Next Article in Journal
Influence of Post-Curing Time and Print Orientation on the Mechanical Behavior of Photosensitive Resins in mSLA 3D Printing
Previous Article in Journal
Electromagnetic Continuously Variable Transmission (EMCVT) System for Precision Torque Control in Human-Centered Robotic Applications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Mechanics
Volume 6
Issue 3
10.3390/applmech6030070
applmech-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparative Analysis of the Mechanical Properties of Eleven 3D Printing Filaments Under Different Printing Parameters

by
Marta Mencarelli
1,*,
Luca Puggelli
1,
Bernardo Innocenti
2,† and
Yary Volpe
1,†
1
Department of Industrial Engineering, University of Florence, Via Di Santa Marta, 3, 50139 Florence, Italy
2
Bio-Electro-And Mechanical Systems (BEAMS) Department, Université Libre de Bruxelles, Av. F. D. Roosevelt 50, 1050 Brussels, Belgium
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Appl. Mech. 2025, 6(3), 70; https://doi.org/10.3390/applmech6030070
Submission received: 30 July 2025 / Revised: 3 September 2025 / Accepted: 9 September 2025 / Published: 11 September 2025
Browse Figures
Versions Notes

Abstract

This study examines the influence of printing parameters and filament composition on the mechanical properties of 3D printed parts, building upon prior research in fused deposition modeling. Two combinations of printing parameters, 75% infill, 0° orientation, four outer shells, with either gyroid and 3D Honeycomb infill patterns—were analyzed across eleven materials, including acrylonitrile butadiene styrene, polylactic acid, polylactic acid-based composites, polyethylene terephthalate glycol, and high-impact polystyrene. Tensile, compression, and bending tests were performed on the printed specimens to determine stiffness and elastic modulus. Each material demonstrated different levels of variability and sensitivity to printing parameters under the various loading conditions, emphasizing that no single configuration is optimal across all scenarios. For example, the gyroid pattern led to increases up to ~35% in bending modules for common thermoplastic filaments and ~30% for stone-filled polymers, while in tensile stiffness, variations between infill patterns remained below 5% for other conventional polymers. These findings underline the load-specific nature of optimal parameter combinations and the influence of material-specific characteristics, such as filler content or microstructural homogeneity. This study provides quantitative insights that can support application-driven parameter selection in additive manufacturing, offering a comparative dataset across widely used and emerging filaments.

1. Introduction

Printing parameters and filament composition heavily influence the mechanical performance of 3D-printed parts [1,2,3,4,5,6,7,8,9], especially in fused deposition modeling (FDM) processes. Prior studies [1,2,3,4,5,6,7,8,9] have demonstrated how infill density, pattern, shell count, and print orientation affect tensile strength, stiffness, and overall part integrity, particularly for commonly used materials such as polylactic acid and acrylonitrile butadiene styrene. However, the mechanical behavior of emerging or modified filaments, such as those containing metal, stone, phosphorescent, or wood-based fillers, remains less explored, despite their increasing relevance across sectors like biomedical engineering, robotics, architecture, prototyping, and consumer product design [10]. Additive manufacturing is increasingly employed in applications where mechanical performance must be carefully tuned to match functional constraints. In biomedical contexts, for example, stone-filled and phosphorescent filaments are used to replicate tissue and bone radiodensity in computed tomography phantoms, requiring not only imaging fidelity but also structural reliability [11,12,13,14,15,16,17,18].
While studies exist for basic polymers such as polylactic acid (PLA), acrylonitrile butadiene styrene (ABS), polyethylene terephthalate glycol (PETG), and high-impact polystyrene (HIPS) [3,6,7,19,20], there is a lack of systematic comparative analyses that quantify how printing parameters affect the mechanical response of a broad range of commercial and composite filaments under different loading conditions. This gap limits both researchers and practitioners when it comes to selecting materials and print strategies for specific mechanical goals.
This study addresses the need for quantitative, application-oriented data linking printing parameters to the mechanical performance of diverse filaments. The aim is to improve material and parameter selection for FDM-printed parts by extending the analysis beyond conventional filaments and establishing a comparative dataset covering both standard and emerging materials.
The novelty of this work lies in the systematic application of a previously identified high-performance parameter set—75% infill, 0° raster orientation, and four outer shells—across eleven filament types. The mechanical effects of two infill patterns, gyroid and 3D honeycomb, are directly compared under tensile, compressive, and flexural loading.
The specific objectives addressed in this study are to (1) quantify tensile, compressive, and flexural stiffness and elastic modulus for eleven filaments, including thermoplastics and composites; (2) compare performance across gyroid and 3D honeycomb infill patterns under fixed optimized parameters; (3) assess the load-specific nature of parameter effectiveness; and (4) provide a comparative dataset and quantitative guidance for material selection and parameter optimization in additive manufacturing.
The present study addresses this gap by analyzing the mechanical properties, namely stiffness and elastic modulus, of eleven different filaments under tensile, compression, and bending loads. Building on prior work [1,9] that identified optimal settings for polylactic acid-based materials, this study applies two high-performing parameter combinations across a broader spectrum of materials, including those with mineral, metallic, and natural fillers. The goal is to inform material selection and parameter tuning strategies in additive manufacturing to adapt to specific requirements.

2. Materials and Methods

2.1. Printing Parameters and Filaments

Following the findings of previous studies carried out using a consistent design of experiment [1,9], featuring four printing settings, namely infill percentage (density of the internal structure of the printed object), orientation (the inclination of the part concerning the printing plane), number of outer shells (layers of material deposited around the perimeter of each printed layer), and infill pattern (the internal structure within a 3D printed object that provides support), this study selected the two combinations of printing parameters that demonstrated superior mechanical performance in terms of stiffness and elastic modulus:
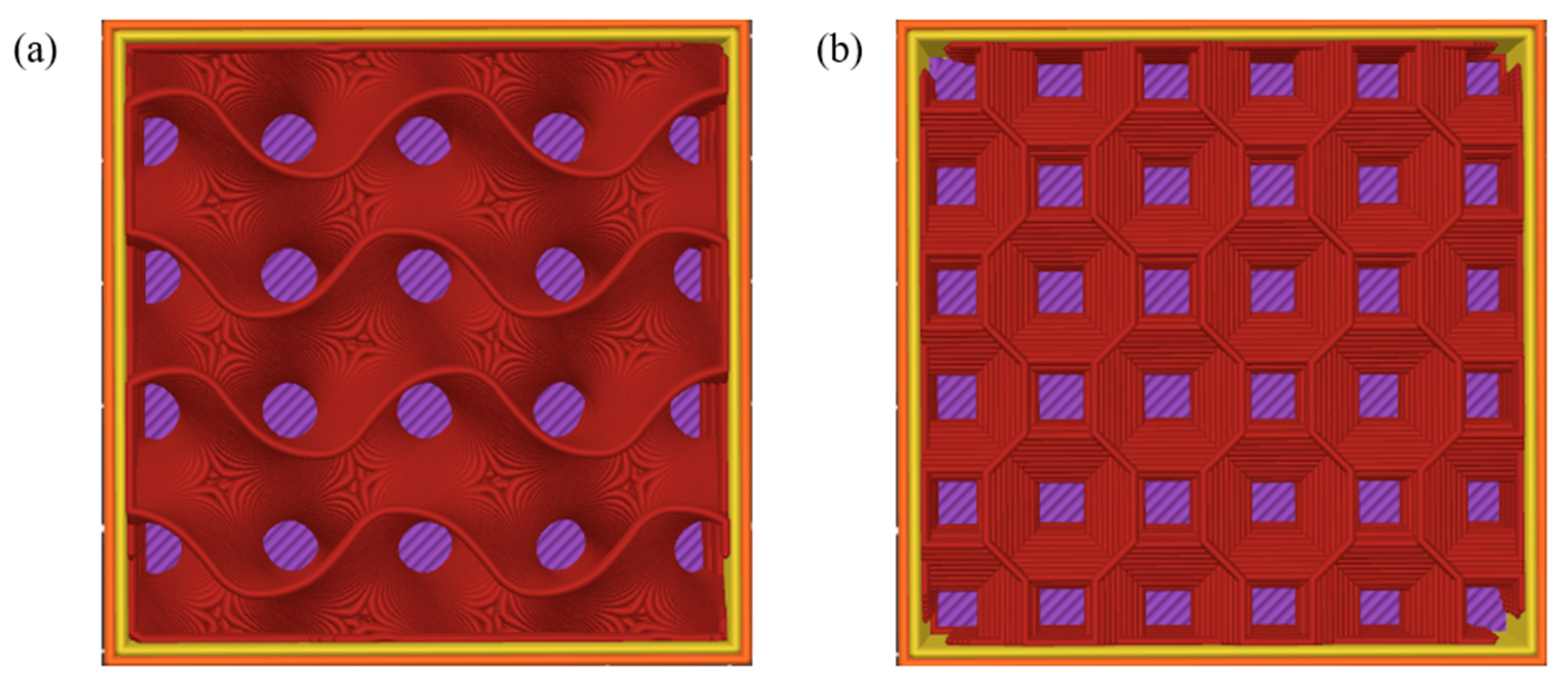
  • Infill: 75%, Orientation: 0°, Shells: 4, Infill Pattern: gyroid
  • Infill: 75%, Orientation: 0°, Shells: 4, Infill Pattern: 3D honeycomb
Based on the results from [1], a 75% infill, 0° print orientation, and four outer shells provide significantly better performance. However, the infill pattern could not be decisively identified as superior. Three patterns, gyroid, 3D honeycomb, and cubic, were initially selected due to their geometrically isotropic structure, which helps counterbalance the directional weaknesses inherent to the 3D printing process. The cubic pattern was excluded due to consistently inferior performance across the tensile, compression, and bending tests performed in Mencarelli et al.’s [1,9] study. In contrast, the gyroid and 3D honeycomb patterns (Figure 1) demonstrated comparable results, making it difficult to identify a dominant configuration.
A comprehensive approach to parameter selection is crucial, as the interplay between infill density, orientation, and shell count has been widely recognized as a critical factor influencing the mechanical integrity of FDM-printed parts [21,22].
The current study further expands the results of previous studies [1,9] on polylactic acid (PLA), StonefilTM Granite (SFG), and Woodfill (WF) by examining 8 additional filaments in terms of stiffness and elastic modulus under tensile, compression, and bending tests. The 11 materials whose mechanical properties in terms of stiffness and elastic modulus when FDM-printed will be analyzed are reported below, alongside the results of a literature analysis:
  • Acrylonitrile Butadiene Styrene (ABS). Characterized by high impact resistance, good toughness, and strength, the ABS used in this study exhibits a tensile strength of 30 MPa [23]. It is recognized for its durability and superior temperature resistance compared to PLA. Previous studies have explored the influence of various printing parameters on its mechanical properties: Samykano et al. [24] investigated the effect of layer height, raster angle, and infill density, while Sood et al. [21] considered layer thickness, orientation, raster angle, raster width, and air gap. Daly et al. [25] also conducted a comprehensive parametric study, and Sumalatha et al. [26] examined the effects of build orientation and infill density. More recently, Haque et al. [27] evaluated its tensile, compressive, and flexural performance across varying key process parameters. Additionally, a recent study by Tzotzis et al. [28] analyzed the influence of structural characteristics on the tensile properties of FDM-fabricated ABS. While ABS’s mechanical properties have been extensively characterized under various printing conditions in the literature, this study distinguishes itself by systematically evaluating its performance under two specific optimized parameter combinations of 11 filaments, thereby including ABS provides a crucial benchmark for direct comparison with less-explored, specialized filaments.
  • Bronzefill (BF). BF, PLA (60–70%) combined with bronze powder (40–30%), is characterized by a higher density than standard PLA (3.9 g/cm3 versus 1.3 g/cm3), which contributes to increased weight and enhanced surface hardness. Its tensile strength, typically around 20–30 MPa [29], is comparatively lower due to the inclusion of metal content. The literature on this filament remains limited, indicating a significant need for further research, except for the study by Kumar et al. [6], who investigated the mechanical properties of bronze infill polylactic acid composites by varying nozzle temperature, printing speed, layer thickness, and infill density, highlighting that tensile strength is primarily influenced by infill density, flexural strength by nozzle temperature, and impact strength predominantly by infill density.
  • Glowfill (GF). Mechanically, GF is comparable to standard PLA, possessing a tensile strength of 50–70 MPa and a flexural strength of 60–80 Mpa [29]. The incorporation of phosphorescent materials (20–30%) into the PLA matrix (70–80%) results in a slight reduction in overall strength. While it has been explored for its bone-like Hounsfield Unit (HU) for CT calibration applications [11,12,13], its mechanical properties under varying printing parameters are yet to be thoroughly characterized.
  • High Impact Polystyrene (HIPS), a flexible material made by polystyrene (85–95%) and rubber (15–5%), exhibits good impact resistance and toughness, with a tensile strength of 20–30 MPa and a flexural strength of 30–50 MPa. Existing studies include Sumalatha et al.’s work on the effect of build orientation and infill density [26], Xu et al.’s study on the effect of crisscross raster orientation, layer thickness, and infill density on the mechanical response of printed HIPS [30], and Pyka et al.’s static tensile and three-point bending tests [31].
  • IronPLA exhibits increased density and hardness compared to regular PLA, though its tensile strength is reduced due to the 30–40% metal powder content, typically ranging from 20–30 MPa. Its magnetic properties, stemming from its iron content, have been a focus in existing literature, particularly for conductive and magnetic applications. However, despite its widespread use in various applications, including magnetic and biomedical devices, there is a distinct lack of studies characterizing its mechanical properties. More research in this area is crucial.
  • Polyethylene Terephthalate Glycol-Modified (PETG) effectively combines strength and flexibility with good chemical resistance. It has a tensile strength of 50–70 MPa and a flexural strength of 60–80 MPa. PETG is less brittle and more durable than PLA [31]. Haque et al., evaluated its tensile, compressive, and flexural performance varying nozzle diameter, infill pattern, infill density, and layer height [27]. Dung et al., demonstrated that the mechanical properties of PETG are significantly influenced by printing speed and layer thickness, with these parameters tending to be inversely proportional to tensile strength [32].
  • Polylactic Acid (PLA) is characterized by high stiffness and good tensile strength, typically 50–70 MPa, and a flexural strength of 60–80 MPa. It is biodegradable but has a lower impact and thermal resistance than ABS. Its mechanical properties have been widely studied and assessed in the literature [1,27,31,33,34].
  • Stonefil Concrete (SFC) offers increased density and surface hardness compared to standard PLA, with the concrete powder (50%) influencing its mechanical properties, typically resulting in a tensile strength of around 40–60 MPa. Studies on this filament are currently sparse, with a primary focus on tissue and bone equivalence in terms of radiodensity [14,15]. There is a notable absence of research addressing the susceptibility of its mechanical properties to varying printing settings.
  • Stonefil Granite (SFG), similar to SFC, provides enhanced surface hardness and density, with a tensile strength around 40–60 MPa, providing a stone-like appearance and feel due to the inclusion of 50% of granite powder into a PLA matrix. Recent studies have highlighted its suitability for biomedical imaging phantoms, particularly in CT-based applications, due to its bone-mimicking radiodensity and favorable interaction with ionizing radiation [16,17,18]. However, despite its promising imaging characteristics, there remains a significant lack of data regarding its mechanical properties in existing literature.
  • Stonefil Terracotta (SFT), like other stone-filled filaments, exhibits an increased surface hardness and density, with a tensile strength of approximately 40–60 MPa. While its radiodensity and tissue-mimicking interaction with ionizing radiation have led to investigations for CT-based biomedical imaging applications [35], its mechanical performance, particularly concerning different printing parameters, is currently undocumented in the available literature.
  • Woodfill (WF), made by a PLA matrix (70%), added with wood fibers (30%) [29], is characterized by a slightly lower tensile strength than standard PLA, typically around 30–50 MPa, while offering enhanced aesthetic properties due to wood fibers. Its fatigue behavior has been extensively studied [36,37,38,39], and the influence of specific parameter combinations on stiffness and elastic modulus was explored in a prior study [9], the results of which are incorporated here. The approach adopted in this study allows for a comparison of the achievable values with these filaments using the two optimized printing parameter combinations.
Main properties for each material are summarized in Table 1.

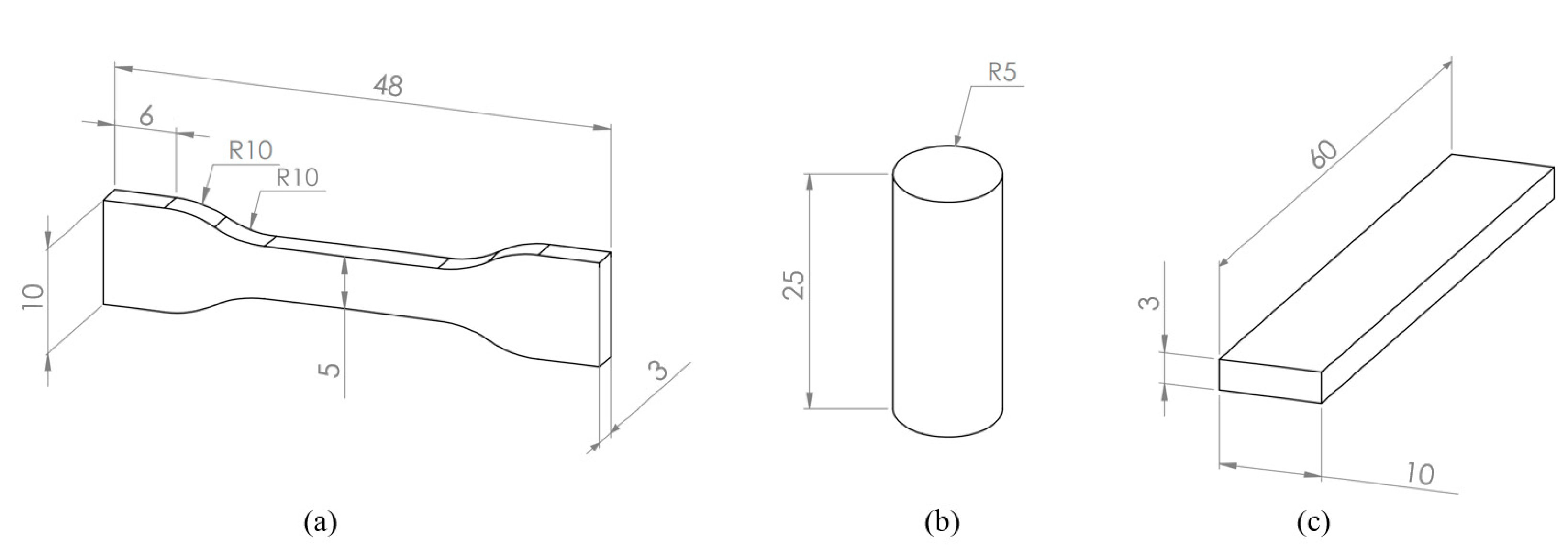
2.2. Specimen Geometry

To align with the previous studies [1,9] the geometries of the specimens were maintained, as well as the testing equipment and procedures. Each specimen was replicated four times to ensure robustness and consistency with the reference studies [1,9]. For tensile tests, dogbone-shaped specimens were used to ensure failure occurred away from the grip areas, maintaining a uniform stress state in the central section. Cylindrical specimens were chosen for compression tests to evenly distribute compressive stresses and reduce the risk of lateral instability. Beam-shaped specimens were used for bending tests to observe stress variation, while rectangular bars were utilized for three-point bending tests due to their easy support and center loading. All specimen designs were created using Solidworks 2023 (Dassault Systemes, Vélizy-Villacoublay, France) CAD software, with detailed geometries and dimensions shown in Figure 2, which reflect commonly adopted configurations in additive manufacturing studies and follow standard testing methodologies.

2.3. Specimen Numerosity

The number of specimens (n = 5) was selected according to ISO 527-1 [40], ISO 527-2 [41], ISO 604 [42], and ISO 178 [43], which recommend a minimum of five replicates per material for tensile, compressive, and flexural testing to ensure statistically meaningful results.

2.4. Specimen Fabrication

For each material, n = 5 specimens per type were printed using a Prusa i3 MK3 (Prusa Research, Prague, Czech Republic) printer using PrusaSlicer-2.7.4 MK3 (Prusa Research, Prague, Czech Republic) as a slicing software. Fabrication was conducted under controlled environmental conditions, maintaining a room temperature of 22 °C and a humidity of 50%. These parameters were kept consistent throughout the entire printing process to minimize any external influences on the results. Layer height and print speed were kept constant, respectively, at 0.15 mm and 60 mm/min. Nozzle and bed temperature were set according to the manufacturer’s instructions. Values are reported in Table 2.

2.5. Mechanical Testing Procedure

Mechanical tests were conducted using the LS1 single-column universal testing machine (Lloyd Materials Testing, Ametek Inc., Berwyn, PA, USA) with a 1 kN load cell. Force-displacement data were recorded, and specimens were aligned using marked guides to ensure repeatability. Dogbone-shaped specimens for tensile tests were clamped to prevent slippage, cylindrical specimens for compression tests were placed between aligned supports, and three-point bending tests used 5 mm radius supports spaced 48 mm apart, with a central loading arm of equal radius (see Figure 3).
Tensile and bending tests resulted in specimen failure, confirming their destructive nature, while compression tests left the cylindrical specimen macroscopically intact. To account for strain rate sensitivity and based on Luo et al. [44], who applied the Cowper-Symonds model to PLA parts, a nominal strain rate of 1.0 mm/min was selected. The testing methodology, based on constant traverse rate conditions for tensile, flexural, and compressive loading, follows the definitions and requirements outlined in ISO 5893 [45] for rubber and plastics. The testing equipment setup is also compliant with relevant aspects of ISO 527-1, ISO 527-2, ISO 604, and ISO 178. According to ISO 527-1 and ISO 527-2, all tests followed the same procedure: preload of 1 N, initial speed of 0.5 mm/min, tensile load set at 900 N, strain rate of 1.0 mm/min, hold time of 5.0 s, and a load limit of 950 N. Temperature and humidity were kept consistent with those used in the manufacturing phase throughout the entire testing process. Recording began once the preload threshold was exceeded. After testing, specimens were disposed of due to the destructive or semi-destructive nature of the methods.

3. Results

3.1. General Overview

After each test, data were collected, and stiffness and elastic modulus were determined from the linear region of the force-displacement and stress–strain curves, respectively. In particular, for bending tests, these values were derived under flexural loading conditions, which introduce additional complexity due to the non-uniform stress distribution across the specimen’s cross-section. In addition to tensile and compression tests, three-point bending tests were performed to provide a more comprehensive mechanical characterization, acknowledging the significant impact of geometrical and inertial properties on stress distribution and material deformation during flexural loading. Unlike in tensile and compression scenarios, where stress distribution is more uniform, bending induces a gradient of tension and compression across the thickness, making theoretical predictions less reliable. For this reason, bending performance cannot be accurately estimated through theoretical calculations alone and requires experimental validation. Incorporating bending tests enhances the understanding of material behavior under various loading conditions, although it requires careful analysis. To ensure reliability, average values were calculated from five test repetitions per specimen. Results are reported in Figure 4. Superimposed load-extension curves of the 11 investigated materials are reported in Supplementary Material (Figures S1–S3).
Consistent with findings from [1], significant variations in mechanical properties were observed among the 11 tested materials based on different printing parameters. Results between stiffness and elastic modules are consistent with each other, except for SFG, for which anomalous behavior is observed for bending E. SFG exhibited anomalous behavior in the bending elastic modulus, which appeared disproportionately high compared to its tensile and compressive counterparts. This discrepancy is likely due to the high variability observed in the raw bending test data, reflected in a large standard deviation. Such variability may originate from the complex nature of the bending test, where multiple factors, such as stress concentration in the outer shells, surface inconsistencies, and non-uniform stress distribution, can amplify small variations in material behavior.
Although the bending E appears significantly higher than the tensile and compressive E, the bending stiffness is much lower due to the strong influence of geometry, particularly the cubic dependence on span length (L3) and the moment of inertia. Additionally, bending tests mainly stress the outer shell regions, leading to an apparent increase in stiffness that may not reflect the bulk material behavior.
The graphs reveal that the combination of parameters and materials that yield the highest values of stiffness and/or elastic modulus varies depending on the type of test conducted. This indicates that different loading conditions and specimen geometries interact uniquely with the chosen parameters, affecting the mechanical properties. For instance, certain materials may perform better under tensile testing with a specific infill pattern—it is the case of IronPLA and SFG that showed increases of approximately 8.4% and 6.9%, respectively, when printed with the gyroid pattern. Others may show superior results in compression tests with another, such as GF, which showed slightly superior performance in compression when printed with the 3D honeycomb pattern, with a 4.5% increase in stiffness. Understanding these variations is crucial for optimizing material selection and printing strategies for specific applications.
Overall, the gyroid pattern tends to enhance mechanical performance in most materials, particularly in bending stiffness and compressive modulus, while exhibiting moderate or negligible effects on tensile-related properties for certain polymers.

3.2. Influence of Infill Pattern on Mechanical Properties

In terms of tensile stiffness, the effect of the infill pattern was marginal for most materials, with percentage differences below ±5% in ABS, PLA, and PETG. Notably, IronPLA and SFG exhibited slightly improved tensile stiffness with the Gyroid structure, with increases of approximately +8.4% and +6.9%, respectively. Conversely, WF showed a minor decrease (−3.2%) with the Gyroid infill with respect to 3D Honeycomb. Compression stiffness showed more sensitivity to the infill geometry. On average, Gyroid improved compressive stiffness by 10–18% in materials like HIPS, SFC, and BF, suggesting enhanced load distribution under axial compression. An exception was observed in GF, where the 3D-Honeycomb slightly outperformed Gyroid (4.5%). The most pronounced improvements due to the Gyroid pattern were seen in bending stiffness. Materials such as PLA, SFT, and ABS displayed increases ranging from +15% to +28% compared to their 3D-Honeycomb counterparts. These gains are attributed to the continuous curvature and isotropic nature of the Gyroid structure, which better resists bending deformation.
For tensile E, variations were moderate. While PETG and BF showed increases up to +12%, others, such as HIPS and WF, registered negligible changes (±2%), indicating that the pattern has limited influence on the elastic response in tension for these materials, reflecting tensile stiffness behavior. Gyroid generally led to improved compressive E across most materials. Increases of over +20% were observed in SFC and PLA, reinforcing the suitability of Gyroid architecture for load-bearing applications. The Gyroid pattern resulted in the most significant gains in bending modulus among all properties. The improvement was particularly notable in ABS (+34.5%) and SFT (+29.1%), highlighting the pattern’s ability to resist bending-induced strain due to its 3D interconnected lattice.

3.3. Statistical Analysis

A Welch’s unpaired two-tailed t-test (α = 0.05) was employed to assess the effects of infill pattern on mechanical properties. This test was selected because the compared groups were independent: a two-tailed approach allows for the detection of any significant differences, whether positive or negative, without assuming a directional trend. Resulting p-values, coherent with the graphs observed in Figure 4, are reported in Table 3.
The analysis reveals that the mechanical response to infill geometry varies notably across different materials, with statistical significance observed in several cases. BF, GF, and the mineral-filled filaments, SFG, SFT, and to a lesser extent, SFC, consistently exhibit p-values well below the threshold across multiple mechanical properties, including tensile stiffness, bending stiffness, and their corresponding elastic moduli. These results suggest a strong sensitivity of these materials to internal structural topology, likely due to the distribution of filler particles and their interaction with stress distribution under different infill geometries.
Specifically, BF shows highly significant differences in tensile stiffness (p = 0.023), bending stiffness (p = 0.008), and their elastic moduli (p = 0.019 and 0.011, respectively), indicating that the chosen infill pattern markedly influences its mechanical integrity. Similarly, GF and SFG show p-values under 0.05 across all properties, underscoring the role of pattern-induced changes in mechanical properties in materials containing luminescent or mineral additives. This sensitivity may be attributed to the discontinuities introduced by fillers, which interact differently with the stress pathways generated by the gyroid or 3D honeycomb architecture.
In contrast, more conventional polymers such as ABS, HIPS, and PETG present high p-values in most categories, suggesting a negligible effect of infill pattern on their global mechanical performance. This behavior may be linked to their more homogeneous microstructure and greater ductility, which makes them less responsive to mesostructural variations. PLA, IronPLA, and WF show an intermediate response, as they demonstrate near-significance in some properties, indicating a moderate dependence on infill geometry. This trend suggests that partially filled or modified PLA-based filaments may exhibit transitional behavior, where the effect of infill is not uniformly distributed across properties.

4. Discussion

The results of this study demonstrate that the optimal combination of parameters and materials for achieving maximum stiffness and elastic modulus varies depending on the type of mechanical test conducted. This load-dependent behavior highlights how different infill geometries engage stress distribution in tensile, compression, and bending modes, revealing the complex interplay between printing settings and material response under different loading conditions (see Figure 4 and Table 2). While the number of outer shells, print orientation, and infill percentage were kept constant based on prior research [9], the variability introduced by different infill patterns yielded notable differences in some materials’ performance across the various mechanical tests conducted.
The mechanical behavior observed in this study can be interpreted through the existing theoretical models for FDM structures. The finding that infill pattern has a minimal effect on the tensile properties of conventional, homogeneous polymers like ABS, HIPS, and PETG aligns with models that prioritize raster orientation and layer adhesion as the dominant factors [21,24,27]. Conversely, the significant influence of infill geometry on composite materials (e.g., BF, GF, SFG) underscores the critical role of microstructural heterogeneity. For these materials, the infill pattern dictates load distribution around the rigid filler particles, a complexity not fully captured by models developed for pure polymers. This explains the pronounced statistical significance seen in the results for composites, a key contribution of this work to the field
Many infill patterns generate rib-like reinforcements or lattices: under bending (or tensile) loads, these reinforcements can align with the principal stress directions and act as stiffeners, effectively increasing bending stiffness or tensile resistance by distributing load along continuous load paths [46,47,48]. However, those same slender struts, when subjected to axial compressive loading, may be prone to local buckling or collapse of individual cells, leading to a drop in compression stiffness [49]. In other words, a geometry that provides favorable load-bearing channels in bending can become a source of instability under compression. This effect is further modulated by anisotropy from layer-by-layer deposition and, for composite filaments, by filler-induced heterogeneities: filler particles may concentrate stresses at strut junctions, exacerbating buckling under compression even as they help carry tensile or bending loads along strut axes [50].
Such trade-offs illustrate why no single infill pattern is universally superior. Designers must therefore choose, or tailor infill geometry based on the dominant service loads (e.g., prioritizing bending stiffness for cantilevered components or selecting more compression-stable architectures for load-bearing columns), or even develop hybrid or graded infill strategies to balance performance across multiple loading modes. Where possible, small-scale prototyping or finite element method (FEM) simulations incorporating actual printed infill geometry can guide pattern selection before full-scale production.
A comparison of the findings of this study with the existing literature reveals both consistencies and unique insights. Studies by Samykano et al. [24] and Daly et al. [25] explored the influence of various printing parameters on ABS mechanical properties, while Haque et al. [27] evaluated a broader range of materials, including PLA and PETG. This work reinforces these findings by demonstrating that the infill pattern has a negligible effect on the global mechanical performance of conventional polymers like ABS, linked to their more homogeneous microstructure.
Conversely, this study extends the findings of Kumar et al. [6], who investigated bronze-filled PLA, by fixing infill density and isolating the effect of the infill pattern, showing significant improvements with the gyroid pattern for this material.
This study also provides specific data for HIPS, complementing the work of Xu et al. [30] by showing that the gyroid pattern can improve compressive stiffness by 10–18%. The present study distinguishes itself through its broad scope, systematically analyzing eleven distinct filaments, including emerging composite materials, under a consistent, optimized parameter set. This approach provides a valuable comparative dataset that is largely absent from the existing literature, which often focuses on a smaller range of materials or a single mechanical property.
This study serves as an initial overview of the mechanical properties associated with eleven 3D printing materials, examining and comparing eleven distinct materials, some of which have been minimally analyzed in existing literature. By focusing on different infill patterns and their influence on stiffness and elastic modulus, the aim was to establish foundational data that elucidates how specific printing settings can affect material performance. It must be noted, however, that the sample size (n = 5 per condition) and the multiple pairwise statistical tests performed (one comparison Gyroid vs. 3D Honeycomb per material and property) may increase the risk of Type I errors; results should be interpreted with caution and, in extended studies, appropriate corrections for multiple comparisons or larger sample sizes are recommended. The insights gained from this research provide critical information for guiding future studies and practical applications in additive manufacturing. By identifying the mechanical characteristics achievable with combinations of print settings and filament types, this work lays the groundwork for optimizing material selection and processing parameters based on the intended load scenarios. Although outer shells, orientation, and infill percentage remained fixed here, varying other parameters (e.g., layer height, print speed, temperature) could further refine performance.
This research offers valuable insights but has limitations. Fixed parameters may restrict exploration of other influential factors. Future work could investigate a wider array of infill patterns in conjunction with varying parameters, which may lead to further optimization of mechanical properties for specific applications, for example, extending Kumar et al. [6] findings by expanding the study to PLA alone. Environmental or printer-related variability (e.g., minor fluctuations in temperature or extrusion consistency) was controlled as far as possible but remains a potential source of scatter. While the results are presented quantitatively, they should be interpreted qualitatively regarding the differences in mechanical performance among the materials because anisotropy from the layer-by-layer process was not explicitly quantified here.
As a preliminary investigation involving numerous unconventional filaments, this research lays the groundwork for future developments. Generating predictive models based on experimental data, whether empirical regressions, machine-learning approaches, or FEM incorporating real printed geometry, is essential to ensure scalability and broader applicability of the results.
Finally, the observed load-specific trade-offs are not a drawback but a crucial insight: they show that infill selection must be context-specific. By recognizing that a pattern beneficial for bending may degrade compression performance, we can guide designers toward application-driven choices or hybrid/graded infill designs that balance multiple requirements.
To support a more informed evaluation, Table 4 reports the finish and the cost of the materials, complementing the data presented in Figure 4.

5. Conclusions

This study provides an analysis of the mechanical properties of FDM-printed parts, focusing on the influence of various printing parameters across eleven distinct materials. The quantitative aims of this study were successfully achieved through systematic testing and analysis. The results can be summarized with the following two take-home messages:
  • The choice of infill pattern significantly affects the stiffness and elastic modulus of printed materials featuring additives, e.g., metal, stone powder, phosphorescent agent, or wood fiber, highlighting the need for careful selection of this parameter based on the specific mechanical requirements and load scenarios. For example, the gyroid pattern led to significant increases in bending modulus, with up to 34.5% in ABS and 29.1% in SFT, and a 10–18% improvement in compressive stiffness in materials like HIPS, SFC, and BF.
  • There is considerable variability in mechanical properties among the 11 materials tested. This variability underscores the importance of material-specific optimization in additive manufacturing to achieve desired performance outcomes.
The optimal combination of printing parameters and materials varies with the type of mechanical test conducted (tensile, compression, or bending). This finding indicates the complex interaction between printing settings and material behavior under different loading conditions. By examining a broad range of materials and focusing on different infill patterns, this study provides a preliminary overview of the achievable mechanical properties, serving as a valuable reference for future research and practical applications. This work offers quantitative guidance for application-driven material and parameter selection, helping designers tune part performance for specific mechanical demands.
The insights gained from this study lay the groundwork for further optimization of 3D printing processes.
Future research could expand on this work by exploring a wider array of infill patterns and varying additional parameters (e.g., densities, print speeds, temperatures), incorporating larger replicates for multiple comparisons, considering directional anisotropy or environmental effects, and developing empirical, machine-learning, or FEM-based predictive models. Ultimately, application-driven selection or hybrid/graded infill strategies informed by these data can lead to 3D-printed parts tailored for their intended loading conditions. While this study focused on commercially available filaments, future work could also consider optimized or functionalized material variants where available, to further explore the influence of material characteristics on performance.
Finally, to address the critical limitation of low fracture resistance often associated with FDM parts, future work will expand this analysis to include fracture mechanics properties, such as toughness and crack propagation resistance, under various loading modes.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/applmech6030070/s1: Figure S1: Superimposed load-extension curves of the 11 investigated materials under tensile testing when printed using Gyroid (a), and 3D Honeycomb pattern (b). Figure S2: Superimposed load-extension curves of the 11 investigated materials under compression testing when printed using Gyroid (a), and 3D Honeycomb pattern (b). Figure S3: Superimposed load-extension curves of the 11 investigated materials under bending testing when printed using Gyroid (a), and 3D Honeycomb pattern (b).

Author Contributions

Conceptualization, M.M., B.I. and Y.V.; methodology, M.M.; validation, M.M. and L.P.; formal analysis, M.M., L.P., B.I. and Y.V.; investigation, M.M.; resources, M.M. and B.I.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, L.P., B.I. and Y.V.; visualization, M.M.; supervision, L.P., B.I. and Y.V.; project administration, B.I. and Y.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to the large volume of data, which requires controlled access for proper interpretation.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Mencarelli, M.M.; Sisella, M.; Puggelli, L.; Innocenti, B.; Volpe, Y. Sensitivity Analysis on 3D-Printing Parameters of Mechanical Properties of FDM-Printed PLA Parts for Biomechanical Modeling. Appl. Mech. 2025, 6, 17. [Google Scholar] [CrossRef]
  2. Yogeshwaran, K.; Das, S. Mechanical properties of fused deposition modelling processed parts: A review. Mater. Today Proc. 2022, 69 Part 2, 412. [Google Scholar] [CrossRef]
  3. Bouzaglou, O.; Golan, O.; Lachman, N. Process Design and Parameters Interaction in Material Extrusion 3D Printing: A Review. Polymers 2023, 15, 2280. [Google Scholar] [CrossRef] [PubMed]
  4. Ćwikła, G.; Grabowik, C.; Kalinowski, K.; Paprocka, I.; Ociepka, P. The influence of printing parameters on selected mechanical properties of FDM/FFF 3D-printed parts. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012033. [Google Scholar] [CrossRef]
  5. Gao, G.; Xu, F.; Xu, J.; Tang, G.; Liu, Z. A Survey of the Influence of Process Parameters on Mechanical Properties of Fused Deposition Modeling Parts. Micromachines 2022, 13, 553. [Google Scholar] [CrossRef]
  6. Kumar, S.; Singh, R.; Singh, T.P.; Batish, A. 3D printed tensile and flexural prototypes of thermoplastic matrix reinforced with multi-materials: A statistical analysis. Mater. Today Proc. 2021, 44, 79–85. [Google Scholar] [CrossRef]
  7. Chadha, A.; Haq, M.I.U.; Raina, A.; Singh, R.R.; Penumarti, N.B.; Bishnoi, M.S. Effect of fused deposition modelling process parameters on mechanical properties of 3D printed parts. World J. Eng. 2019, 16, 550–559. [Google Scholar] [CrossRef]
  8. Mangla, S.K.; Kazancoglu, Y.; Sezer, M.D.; Top, N.; Sahin, I. Optimizing fused deposition modelling parameters based on the design for additive manufacturing to enhance product sustainability. Comput. Ind. 2022, 145, 103833. [Google Scholar] [CrossRef]
  9. Mencarelli, M.; Puggelli, L.; Volpe, Y.; Innocenti, B. Sensitivity on 3D-Printed Parameters of Stiffness and Young’s Modulus of FDM-Printed PLA, Stonefil TM Granite, and Woodfill Filaments: A Comparative Analysis. J. Mech. Med. Biol. 2025, 25, 2454054. [Google Scholar]
  10. Kantaros, A.; Soulis, E.; Petrescu, F.I.T.; Ganetsos, T. Advanced Composite Materials Utilized in FDM/FFF 3D Printing Manufacturing Processes: The Case of Filled Filaments. Materials 2023, 16, 6210. [Google Scholar] [CrossRef]
  11. Ma, X.; Buschmann, M.; Unger, E.; Homolka, P. Classification of X-Ray Attenuation Properties of Additive Manufacturing and 3D Printing Materials Using Computed Tomography from 70 to 140 kVp. Front. Bioeng. Biotechnol. 2021, 9, 763960. [Google Scholar] [CrossRef]
  12. Laidlaw, J.; Earl, N.; Shavdia, N.; Davis, R.; Mayer, S.; Karaman, D.; Richtsmeier, D.; Rodesch, P.-A.; Bazalova-Carter, M. Design and CT imaging of casper, an anthropomorphic breathing thorax phantom. Biomed. Phys. Eng. Express 2023, 9, 025008. [Google Scholar] [CrossRef]
  13. Silberstein, J.; Tran, S.; Wong, Y.H.; Yeong, C.H.; Sun, Z. Development of a 3D-Printed Chest Phantom with Simulation of Lung Nodules for Studying Ultra-Low-Dose Computed Tomography Protocols. Appl. Sci. 2025, 15, 309. [Google Scholar] [CrossRef]
  14. Goodall, S.K.; Rampant, P.; Smith, W.; Waterhouse, D.; Rowshanfarzad, P.; Ebert, M.A. Investigation of the effects of spinal surgical implants on radiotherapy dosimetry: A study of 3D printed phantoms. Med. Phys. 2021, 48, 4586–4597. [Google Scholar] [CrossRef] [PubMed]
  15. Kairn, T.; Zahrani, M.; Cassim, N.; Livingstone, A.G.; Charles, P.H.; Crowe, S.B. Quasi-simultaneous 3D printing of muscle-, lung- and bone-equivalent media: A proof-of-concept study. Phys. Eng. Sci. Med. 2020, 43, 701–710. [Google Scholar] [CrossRef] [PubMed]
  16. Hatamikia, S.; Kronreif, G.; Unger, A.; Oberoi, G.; Jaksa, L.; Unger, E.; Koschitz, S.; Gulyas, I.; Irnstorfer, N.; Buschmann, M.; et al. 3D printed patient-specific thorax phantom with realistic heterogenous bone radiopacity using filament printer technology. Z. Fur Med. Phys. 2022, 32, 438–452. [Google Scholar] [CrossRef]
  17. Bento, M.; Cook, H.; Anaya, V.M.; Bär, E.; Nisbet, A.; Lourenço, A.; Hussein, M.; Veiga, C. Characterisation of 3D-printable thermoplastics to be used as tissue-equivalent materials in photon and proton beam radiotherapy end-to-end quality assurance devices. Biomed. Phys. Eng. Express 2024, 10, 065005. [Google Scholar] [CrossRef]
  18. Mukwada, G.; Hirst, A.; Rowshanfarzad, P.; Ebert, M.A. Development of a 3D printed phantom for commissioning and quality assurance of multiple brain targets stereotactic radiosurgery. Phys. Eng. Sci. Med. 2024, 47, 455–463. [Google Scholar] [CrossRef]
  19. Murali, A.; Vakkattil, M.A.; Parameswaran, R. Investigating the Effect of Processing Parameters on Mechanical Behavior of 3D Fused Deposition Modeling Printed Polylactic Acid. J. Mater. Eng. Perform. 2022, 32, 1089–1102. [Google Scholar] [CrossRef]
  20. Vǎlean, C.; Marşavina, L.; Mǎrghitaşl, M.; Linul, E.; Razavi, N.; Berto, F. Effect of manufacturing parameters on tensile properties of FDM printed specimens. Procedia Struct. Integr. 2020, 26, 313–320. [Google Scholar] [CrossRef]
  21. Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric appraisal of mechanical property of fused deposition modelling processed parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
  22. Syrlybayev, D.; Perveen, A.; Talamona, D. Fused deposition modelling: Effect of extrusion temperature on the accuracy of print. Mater. Today Proc. 2021, 44, 832–837. [Google Scholar] [CrossRef]
  23. 3DJake. Available online: www.3djake.it (accessed on 29 July 2025).
  24. Samykano, M.; Selvamani, S.K.; Kadirgama, K.; Ngui, W.K.; Kanagaraj, G.; Sudhakar, K. Mechanical property of FDM printed ABS: Influence of printing parameters. Int. J. Adv. Manuf. Technol. 2019, 102, 2779–2796. [Google Scholar] [CrossRef]
  25. Daly, M.; Tarfaoui, M.; Chihi, M.; Bouraoui, C. FDM technology and the effect of printing parameters on the tensile strength of ABS parts. Int. J. Adv. Manuf. Technol. 2023, 126, 5307–5323. [Google Scholar] [CrossRef] [PubMed]
  26. Sumalatha, M.; Chennaiah, M.B.; Shoaib, S.K.; Kumar, B.S.; Reddy, T.R.K.; Musthakheem, M.D. Investigation on the Mechanical Properties of 3d Printed CF/ABS Materials by Optimized Process Parameters Using Taguchi and ANOVA Analysis. In Lecture Notes in Mechanical Engineering; Mallaiah, M., Thapliyal, S., Bose, S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2025; pp. 225–239. [Google Scholar]
  27. Haque, M.M.M.; Dhrubo, S.R.; Pranto, A.-F.Z.; Ahmed, A.; Arefin, M.; Arifuzzaman, M.; Islam, S. Impact of process parameters and material selection on the mechanical performance of FDM 3D-Printed components. Hybrid Adv. 2025, 10, 100502. [Google Scholar] [CrossRef]
  28. Tzotzis, A.; Manavis, A.; Efkolidis, N.; García-Hernández, C.; Kyratsis, P. Analysis of the Influence of Structural Characteristics on the Tensile Properties of Fused Filament Fabricated ABS Polymer Using Central Composite Design. Appl. Mech. 2024, 5, 20–35. [Google Scholar] [CrossRef]
  29. ColorFabb. Available online: www.colorfabb.com (accessed on 29 July 2025).
  30. Xu, J.T.; Zhang, G.W.; Chen, M.M. Optimizing mechanical properties of HIPS fabricated with low-cost desktop 3D printers: Investigating the impact of process parameters. Adv. Manuf. 2024, 12, 379–395. [Google Scholar] [CrossRef]
  31. Pyka, D.; Slowinski, J.J.; Kurzawa, A.; Roszak, M.; Stachowicz, M.; Kazmierczak, M.; Stepczak, M.; Grygier, D. Research on Basic Properties of Polymers for Fused Deposition Modelling Technology. Appl. Sci. 2024, 14, 11151. [Google Scholar] [CrossRef]
  32. Dung, H.T.; Van-Long, T.; Quang-Tu, N. Study on Influencing of Processing Parameters on Tensile Strength of 3D Printing Sample. Stroj. Cas. 2025, 75, 27–38. [Google Scholar] [CrossRef]
  33. Murariu, A.C.; SÎRBU, N.-A.; Cocard, M.; Duma, I. Influence of 3D Printing Parameters on Mechanical Properties of the PLA Parts Made by FDM Additive Manufacturing Process. Eng. Innov. 2022, 2, 7–20. [Google Scholar] [CrossRef]
  34. Sagias, V.D.; Papageorgiou, D.G.; Pappas, A.; Stergiou, C.I. Mechanical Properties of AM Polymer Specimens Under Bending Stress. Appl. Mech. 2025, 6, 25. [Google Scholar] [CrossRef]
  35. Okkalidis, N.; Bliznakova, K.; Kolev, N. A filament 3D printing approach for CT-compatible bone tissues replication. Phys. Medica 2022, 102, 96–102. [Google Scholar] [CrossRef]
  36. Travieso-Rodriguez, A.J.; Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J. Fatigue behavior of PLA-wood composite manufactured by fused filament fabrication. J. Mater. Res. Technol. 2020, 9, 8507–8516. [Google Scholar] [CrossRef]
  37. Kianifar, M.; Azadi, M.; Heidari, F. Effect of simulated body fluid on the fatigue resistance of 3D-printed PLA and PLA-wood structures under cyclic bending loading. Int. J. Fatigue 2025, 195, 108876. [Google Scholar] [CrossRef]
  38. Guo, R.; Ren, Z.; Bi, H.; Song, Y.; Xu, M. Effect of toughening agents on the properties of poplar wood flour/poly (lactic acid) composites fabricated with Fusing Deposition Modeling. Eur. Polym. J. 2018, 107, 34–45. [Google Scholar] [CrossRef]
  39. Müller, M.; Šleger, V.; Kolář, V.; Hromasová, M.; Piš, D.; Mishra, R.K. Low-Cycle Fatigue Behavior of 3D-Printed PLA Reinforced with Natural Filler. Polymers 2022, 14, 1301. [Google Scholar] [CrossRef] [PubMed]
  40. ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. International Organization for Standardization: Geneva, Switzerland, 2019.
  41. ISO 527-2:2012; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization: Geneva, Switzerland, 2012.
  42. ISO 604:2002; Plastics—Determination of Compressive Properties. International Organization for Standardization: Geneva, Switzerland, 2002.
  43. ISO 178:2019; Plastics—Determination of Flexural Properties. International Organization for Standardization: Geneva, Switzerland, 2019.
  44. Luo, J.; Luo, Q.; Zhang, G.; Li, Q.; Sun, G. On strain rate and temperature dependent mechanical properties and constitutive models for additively manufactured polylactic acid (PLA) materials. Thin-Walled Struct. 2022, 179, 109624. [Google Scholar] [CrossRef]
  45. ISO 5893:2019; Rubber and Plastics Test Equipment—Tensile, Flexural and Compression Types (Constant Rate of Traverse)—Specification. International Organization for Standardization: Geneva, Switzerland, 2019.
  46. Porter, J.H.; Cain, T.M.; Fox, S.L.; Harvey, P.S. Influence of infill properties on flexural rigidity of 3D-printed structural members. Virtual Phys. Prototyp. 2018, 14, 148–159. [Google Scholar] [CrossRef]
  47. Kwok, T.H.; Li, Y.; Chen, Y. A structural topology design method based on principal stress line, CAD Computer Aided Design. Comput. Des. 2016, 80, 19–31. [Google Scholar] [CrossRef]
  48. Yu, Z.; Savinov, R.; Matura, M.; Zhang, P.; Shi, J. Current research status on advanced lattice structures for impact and energy absorption applications: A systematic review. Thin-Walled Struct. 2025, 215, 113490. [Google Scholar] [CrossRef]
  49. Loughlan, J.; Yidris, N.; Cunningham, P.R. The effects of local buckling and material yielding on the axial stiffness and failure of uniformly compressed I-section and box-section struts. Thin-Walled Struct. 2011, 49, 264–279. [Google Scholar] [CrossRef]
  50. Shinde, V.V.; Wang, Y.; Salek, M.F.; Auad, M.L.; Beckingham, L.E.; Beckingham, B.S. Material Design for Enhancing Properties of 3D Printed Polymer Composites for Target Applications. Technologies 2022, 10, 45. [Google Scholar] [CrossRef]
Applmech 06 00070 g001
Figure 1. Different infill patterns included in this study: (a) Gyroid, and (b) 3D honeycomb.
Figure 1. Different infill patterns included in this study: (a) Gyroid, and (b) 3D honeycomb.
Applmech 06 00070 g001
Applmech 06 00070 g002
Figure 2. Specimen designs: tensile (a), compression (b), and bending (c). Dimensions are expressed in mm.
Figure 2. Specimen designs: tensile (a), compression (b), and bending (c). Dimensions are expressed in mm.
Applmech 06 00070 g002
Applmech 06 00070 g003
Figure 3. Test machine set up for tensile (a), compression (b) and bending test (c).
Figure 3. Test machine set up for tensile (a), compression (b) and bending test (c).
Applmech 06 00070 g003
Applmech 06 00070 g004
Figure 4. Mean tensile, compressive, and bending stiffness and elastic modulus (E) respectively expressed in N/mm and N/mm2 for the two infill patterns (G = Gyroid; 3DH = 3D Honeycomb) used to print the 11 filaments included in the study. Infill: 75%, Orientation: 0°, Shell number: 4.
Figure 4. Mean tensile, compressive, and bending stiffness and elastic modulus (E) respectively expressed in N/mm and N/mm2 for the two infill patterns (G = Gyroid; 3DH = 3D Honeycomb) used to print the 11 filaments included in the study. Infill: 75%, Orientation: 0°, Shell number: 4.
Applmech 06 00070 g004
Table 1. Materials’ key properties.
Table 1. Materials’ key properties.
FilamentCompositionTensile Strength (MPa)Flexural Strength (MPa)Key CharacteristicsRelevant Literature
ABSABS (100%)≈30N/AHigh impact resistance; good thermal resistance[21,23,24,25,26,27,28]
BFPLA (60–70%) + Bronze (30–40%)20–30N/AHigh density and hardness; reduced strength due to metal[6]
GFPLA (70–80%) + Phosphorescent agents (20–30%)50–7060–80Comparable to PLA; slightly reduced strength[11,12,13]
HIPSPolystyrene (85–95%) + Rubber (5–15%)20–3030–50Good toughness and impact resistance[27,30,31]
IronPLAPLA + Iron Powder (30–40%)20–30N/AMagnetic; increased density; lower tensile strengthN/A
PETGPETG (100%)50–7060–80Strong, flexible, chemical resistant[27,31,32]
PLAPLA (100%)50–7060–80High stiffness; biodegradable; brittle[1,27,31,33,34]
SFCPLA + Concrete Powder (~50%)40–60N/AIncreased density and hardness[14,15]
SFGPLA + Granite Powder (~50%)40–60N/ABone-like appearance and radiodensity[16,17,18]
SFTPLA + Terracotta Powder (~50%)40–60N/AStone-like finish; radiodensity use[35]
WFPLA (70%) + Wood Fibers (30%)30–50N/AAesthetic, slightly lower strength[9,36,37,38,39]
Table 2. Nozzle and bed temperature, reported in °C, recommended by the manufacturers of the materials included in the study.
Table 2. Nozzle and bed temperature, reported in °C, recommended by the manufacturers of the materials included in the study.
Nozzle Temperature (°C)Bed Temperature (°C)
ABS245 ± 1590 ± 10
BF205 ± 1555 ± 5
GF205 ± 1555 ± 5
HIPS250 ± 20110 ± 5
IronPLA200 ± 1560
PETG235 ± 575 ± 5
PLA210 ± 560 ± 5
SFC220 ± 560 ± 5
SFG220 ± 560 ± 5
SFT220 ± 560 ± 5
Table 3. p-values. Bold values refer to statistically significant ones (α < 0.05).
Table 3. p-values. Bold values refer to statistically significant ones (α < 0.05).
PropertyABSBFGFHIPSIron PLAPETGPLASFCSFGSFTWF
Tensile Stiffness0.4560.0230.0380.8760.1050.2210.0340.0780.0120.0450.156
Compression Stiffness0.7890.1450.2170.6540.3240.5430.2670.4120.0260.1870.042
Bending Stiffness0.6720.0080.0520.5120.0870.3890.0410.0670.0080.0320.213
Tensile E0.4210.0190.0420.9010.1120.1980.0280.0850.0140.0390.142
Compression E0.8320.1620.1950.7230.2980.6120.3120.38700.0210.2030.038
Bending E0.7150.0110.0610.5890.0760.4320.0370.0590.0070.0280.198
Table 4. Finish and cost of the filaments.
Table 4. Finish and cost of the filaments.
FilamentFinishCost (€/kg)
ABSSmooth, slightly glossy~16
BFMetallic, shiny, bronze-like~82
GFTranslucent, glow-in-the-dark ~55
HIPSSmooth, matte~20
IronPLAMetallic, iron-like, slightly rough~92
PETGSmooth, semi-gloss~17
PLASmooth, glossy~15
SFCMatte, concrete-like~67
SFGSlightly rough, granite-like texture~67
SFTMatte, terracotta-like~67
WFWood-like, textured~70
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mencarelli, M.; Puggelli, L.; Innocenti, B.; Volpe, Y. Comparative Analysis of the Mechanical Properties of Eleven 3D Printing Filaments Under Different Printing Parameters. Appl. Mech. 2025, 6, 70. https://doi.org/10.3390/applmech6030070

AMA Style

Mencarelli M, Puggelli L, Innocenti B, Volpe Y. Comparative Analysis of the Mechanical Properties of Eleven 3D Printing Filaments Under Different Printing Parameters. Applied Mechanics. 2025; 6(3):70. https://doi.org/10.3390/applmech6030070

Chicago/Turabian Style

Mencarelli, Marta, Luca Puggelli, Bernardo Innocenti, and Yary Volpe. 2025. "Comparative Analysis of the Mechanical Properties of Eleven 3D Printing Filaments Under Different Printing Parameters" Applied Mechanics 6, no. 3: 70. https://doi.org/10.3390/applmech6030070

APA Style

Mencarelli, M., Puggelli, L., Innocenti, B., & Volpe, Y. (2025). Comparative Analysis of the Mechanical Properties of Eleven 3D Printing Filaments Under Different Printing Parameters. Applied Mechanics, 6(3), 70. https://doi.org/10.3390/applmech6030070

Article Metrics

Back to TopTop