Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hypothesis on the Method of Adjusting the Stiffness of the Shell Damper
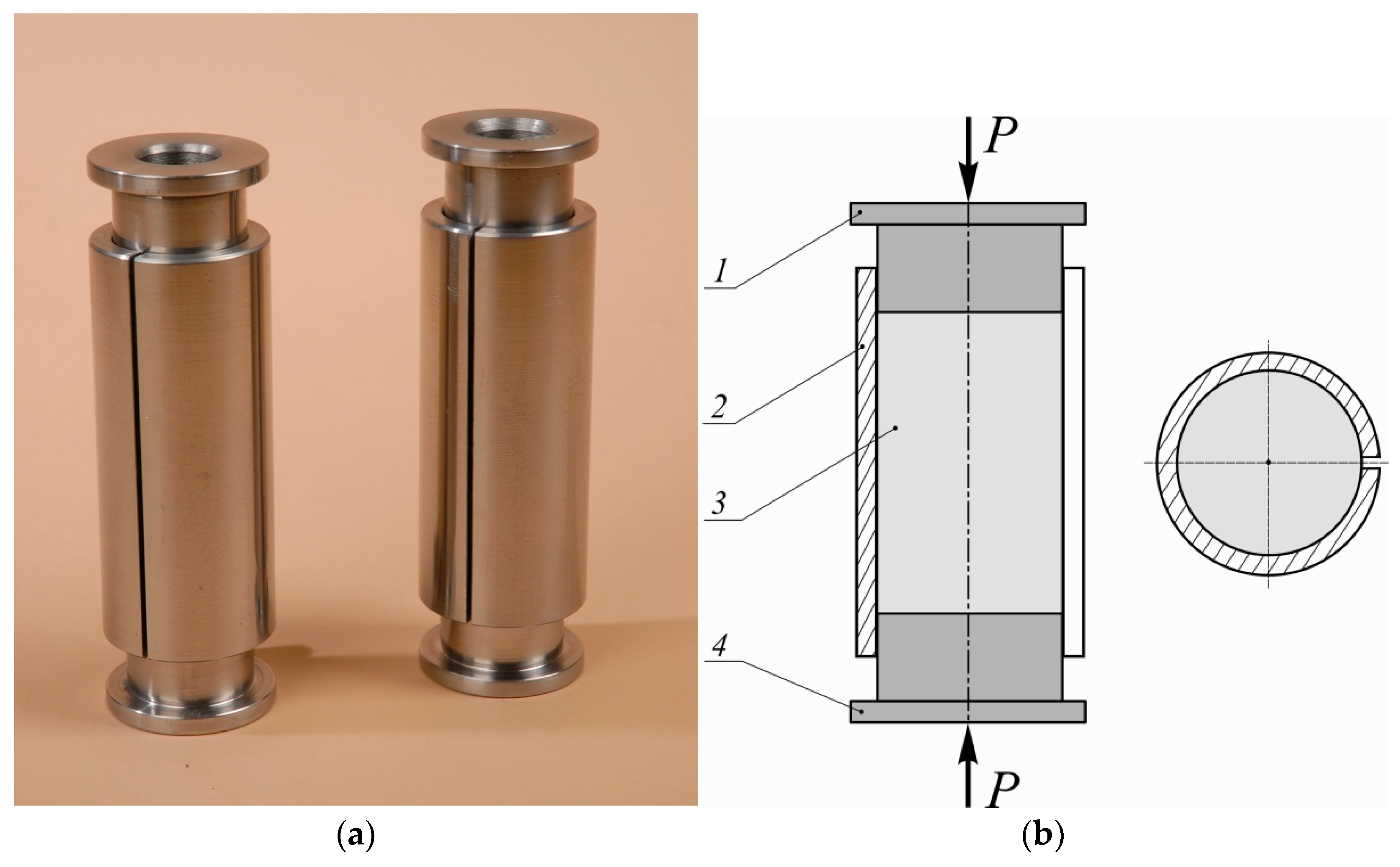
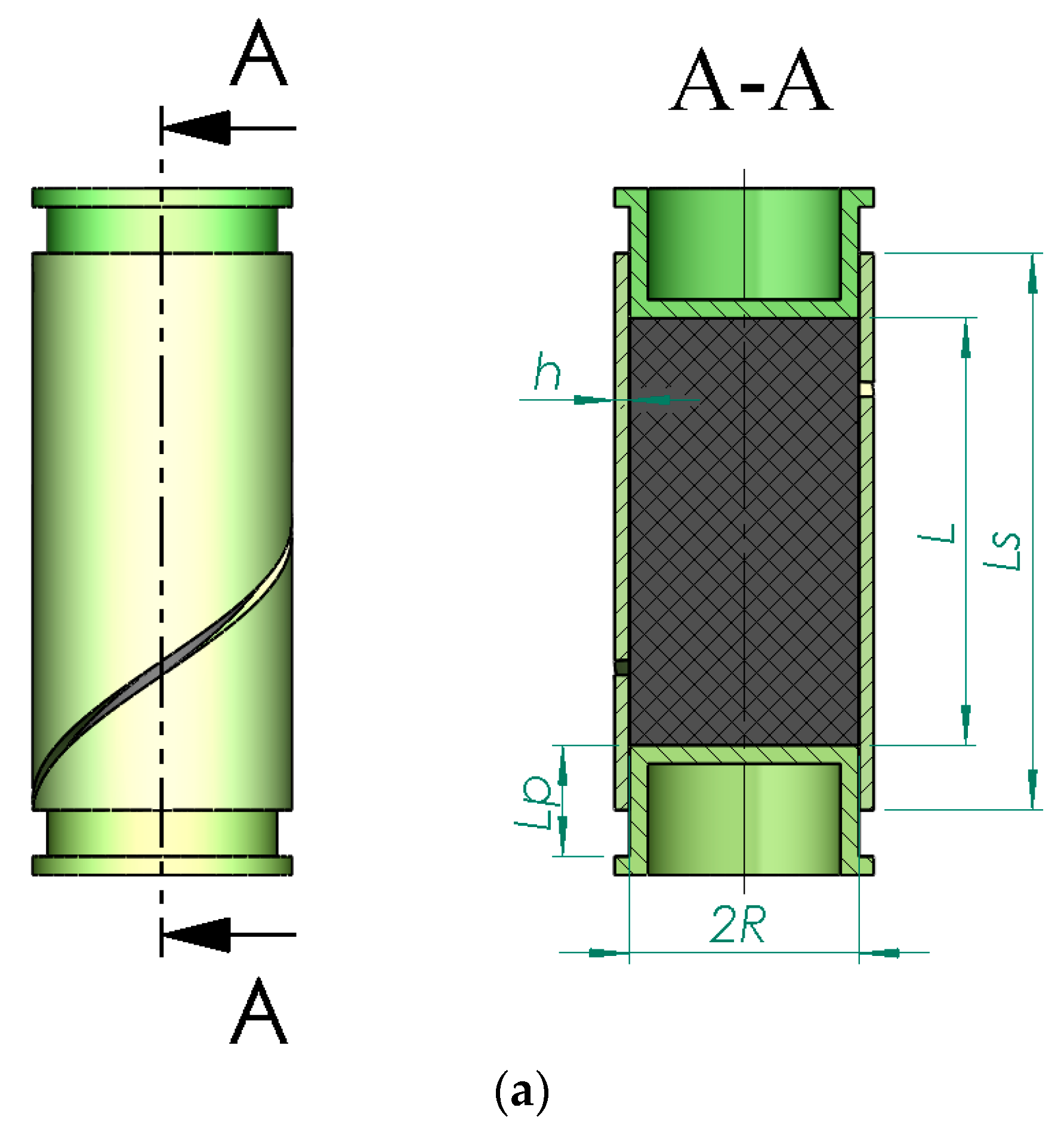
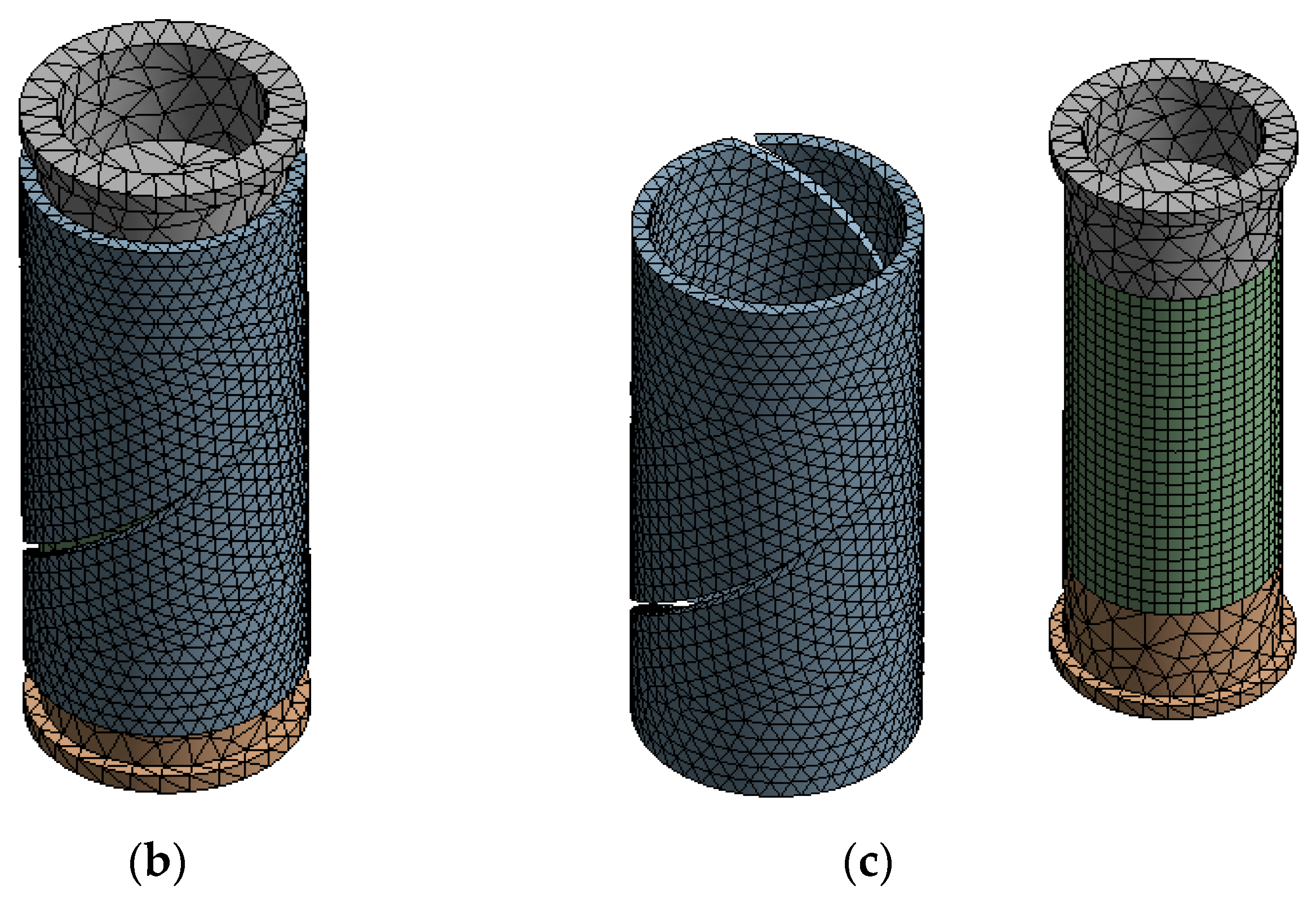
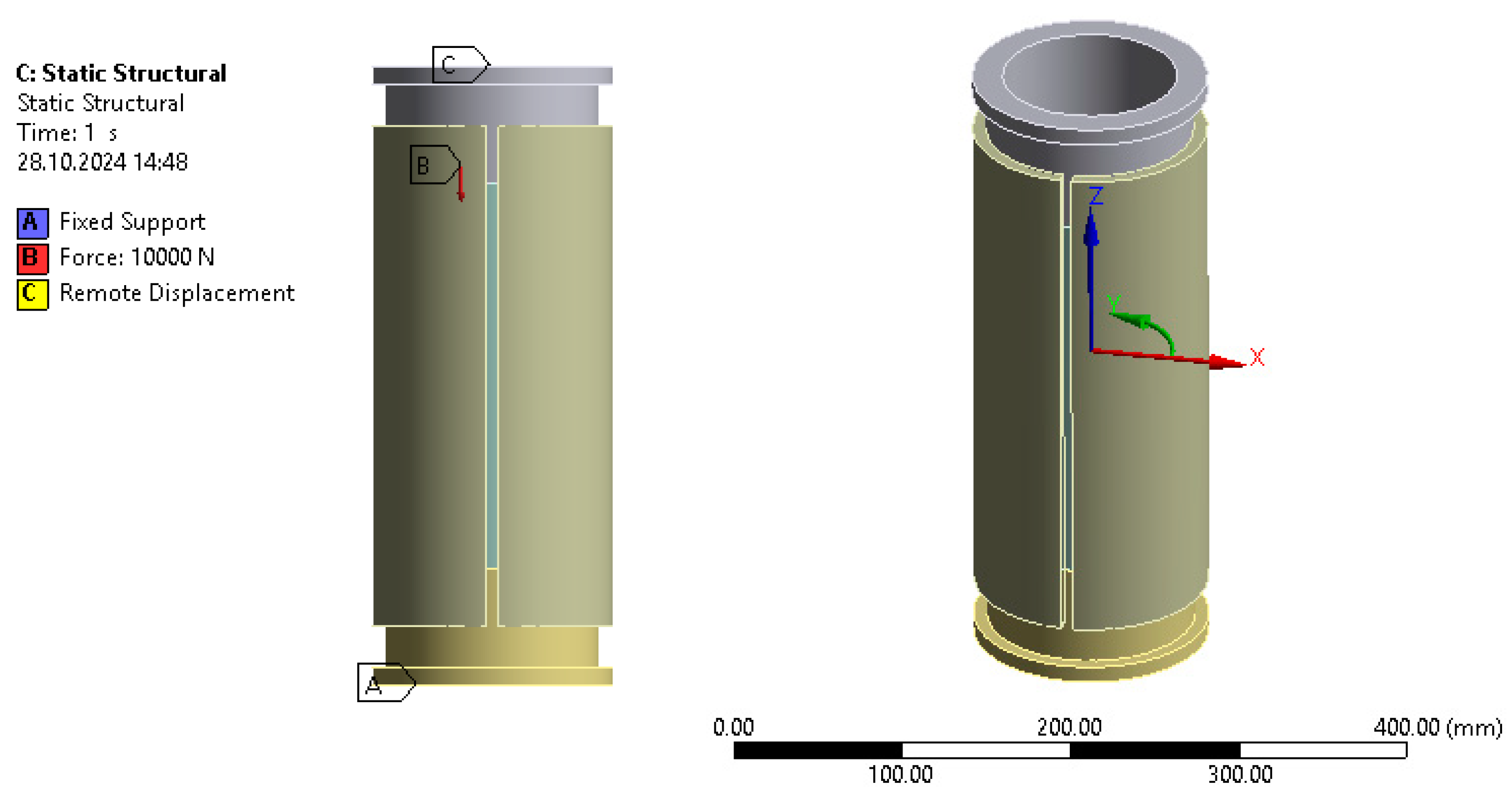
2.2. Numerical Model of a Friction Damper Constructed on the Basis of an Open Shell with a Deformable Filler
3. Results and Analysis
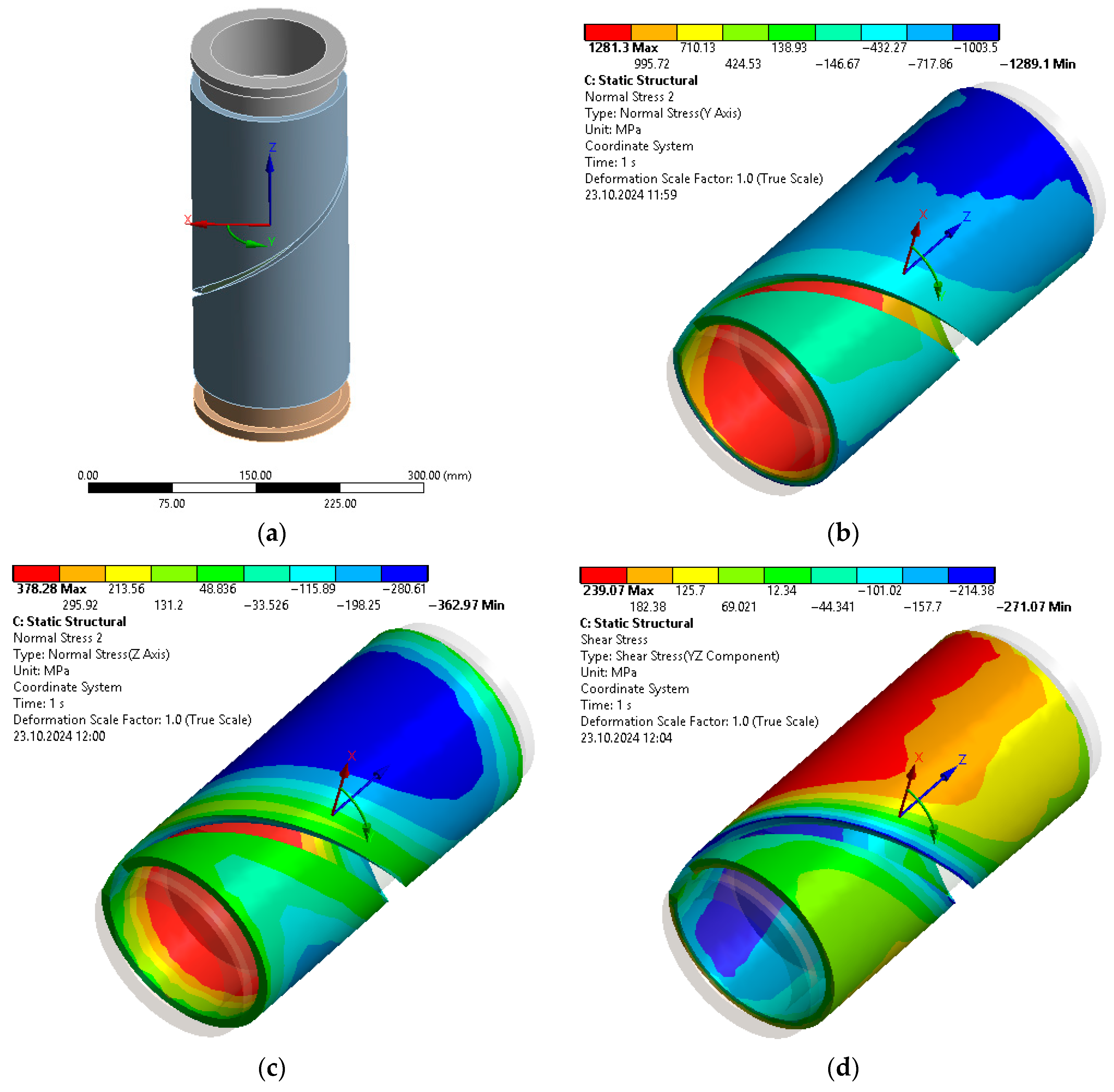
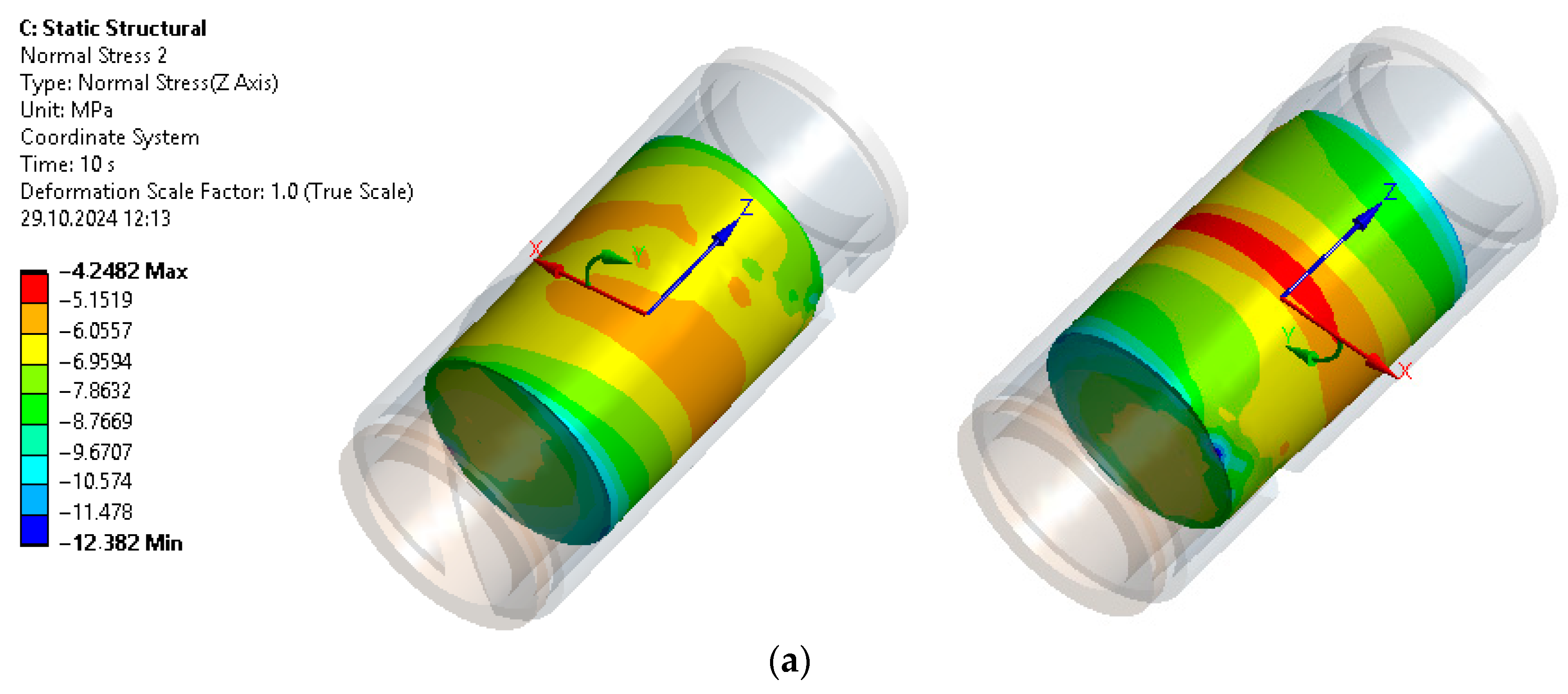
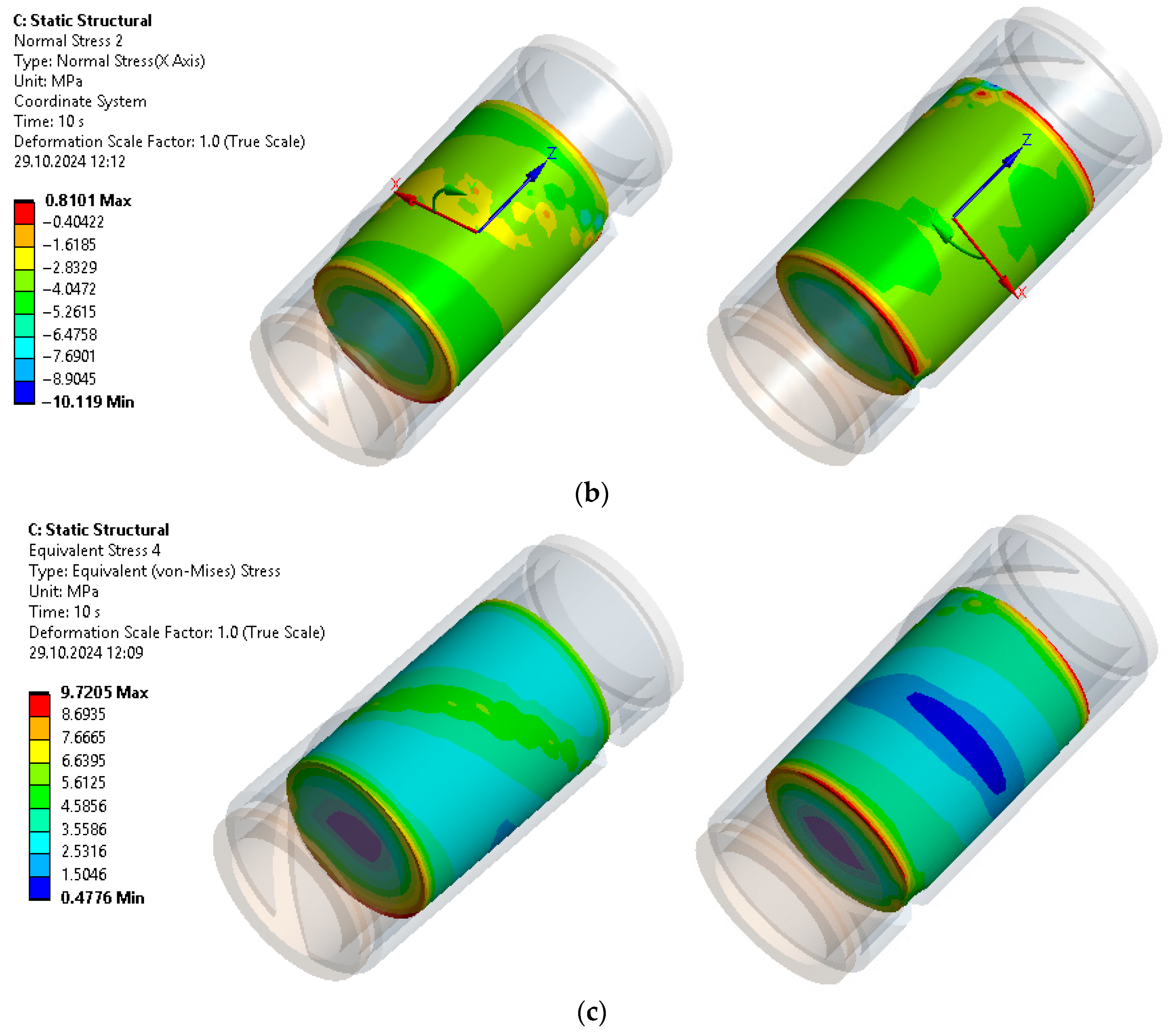
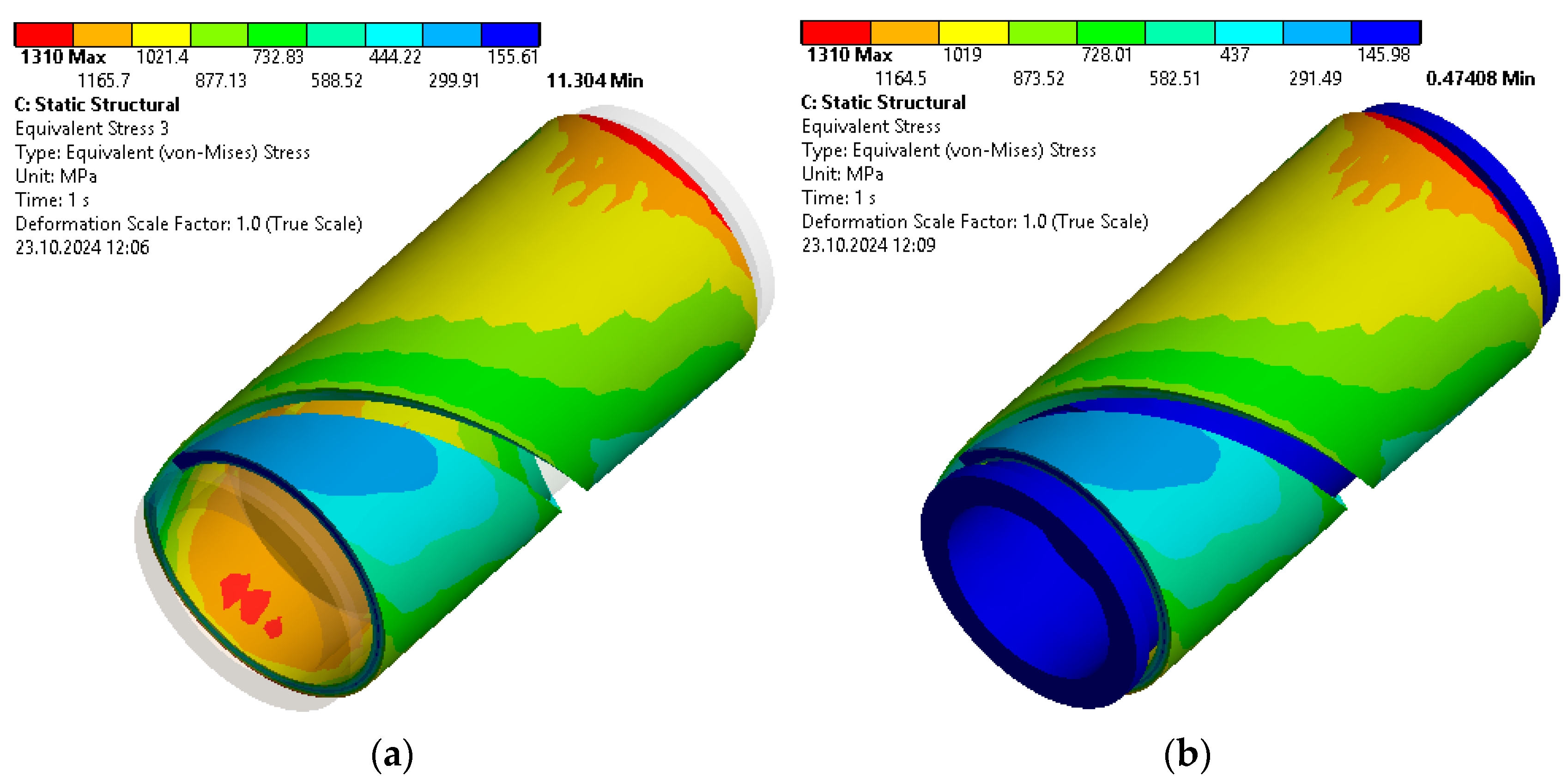
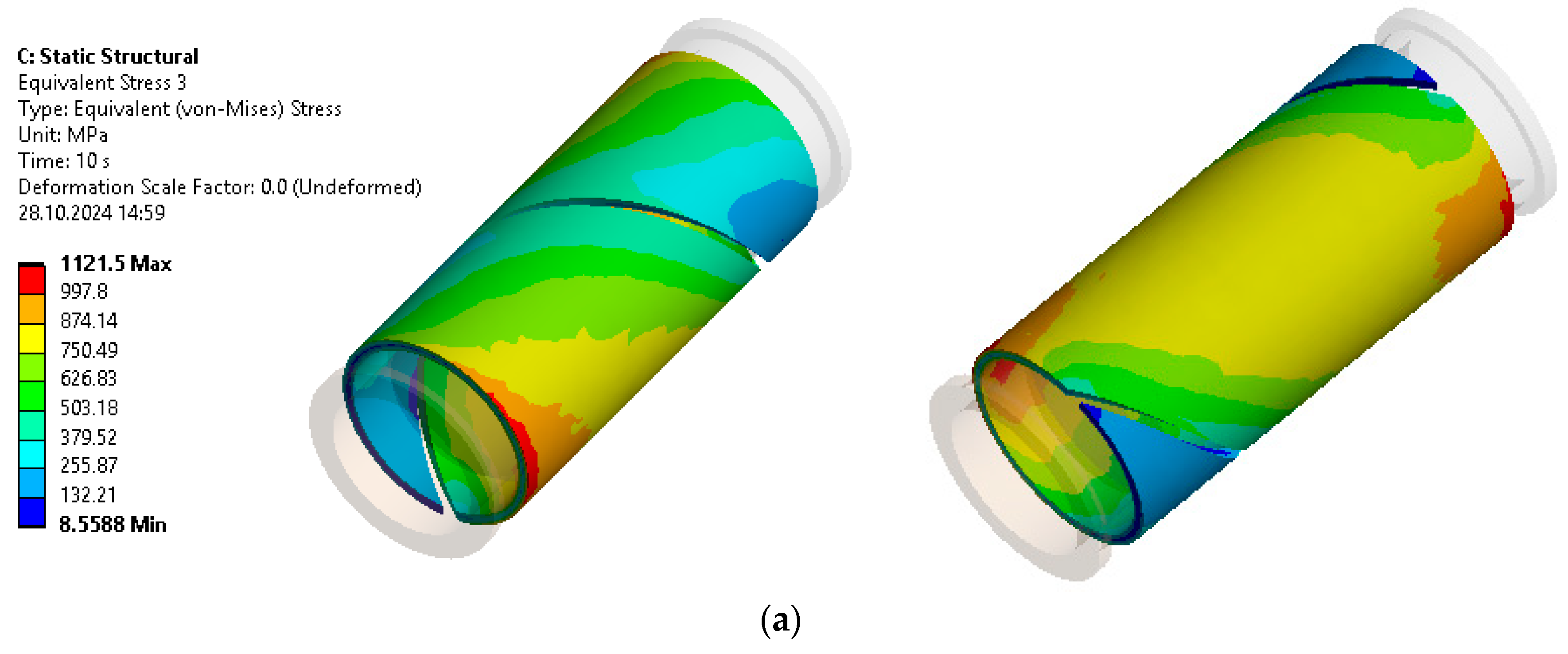
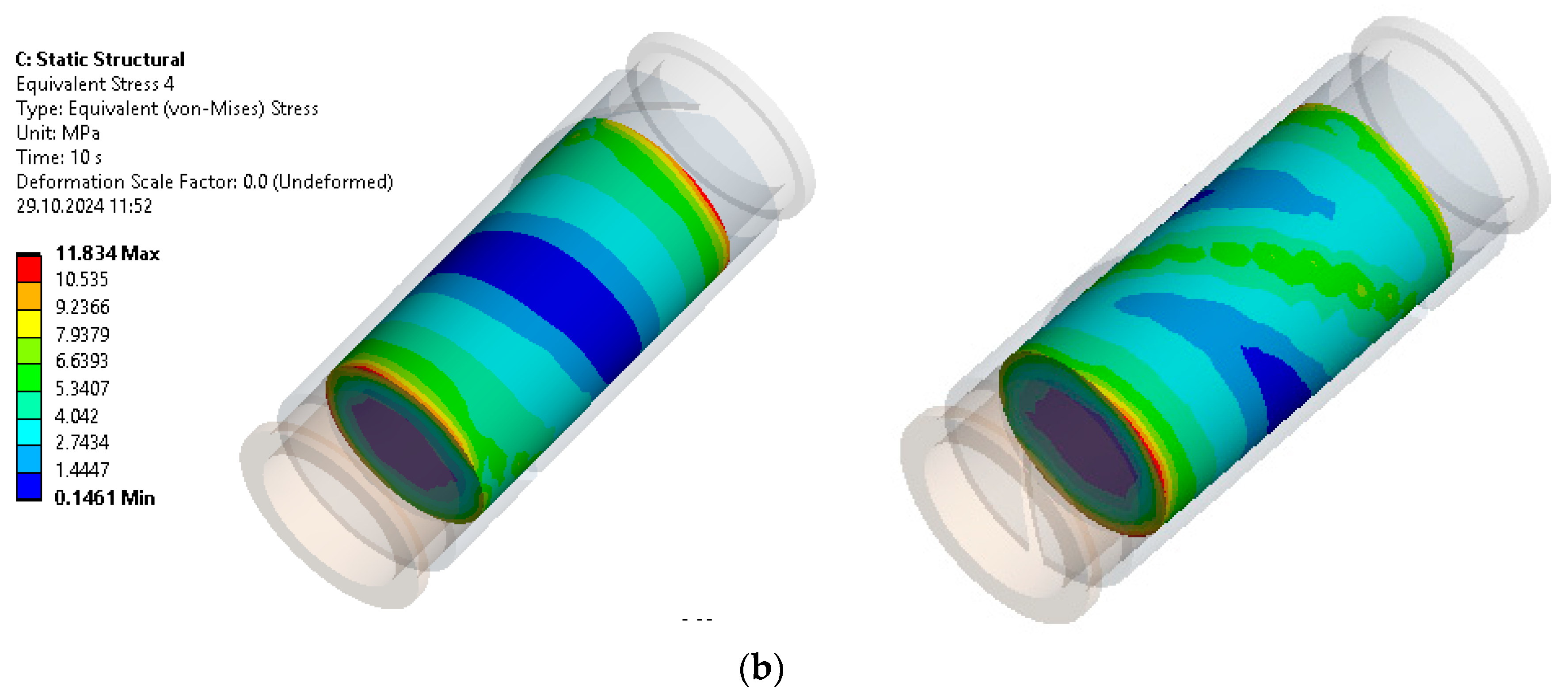
3.1. Stress State Analysis
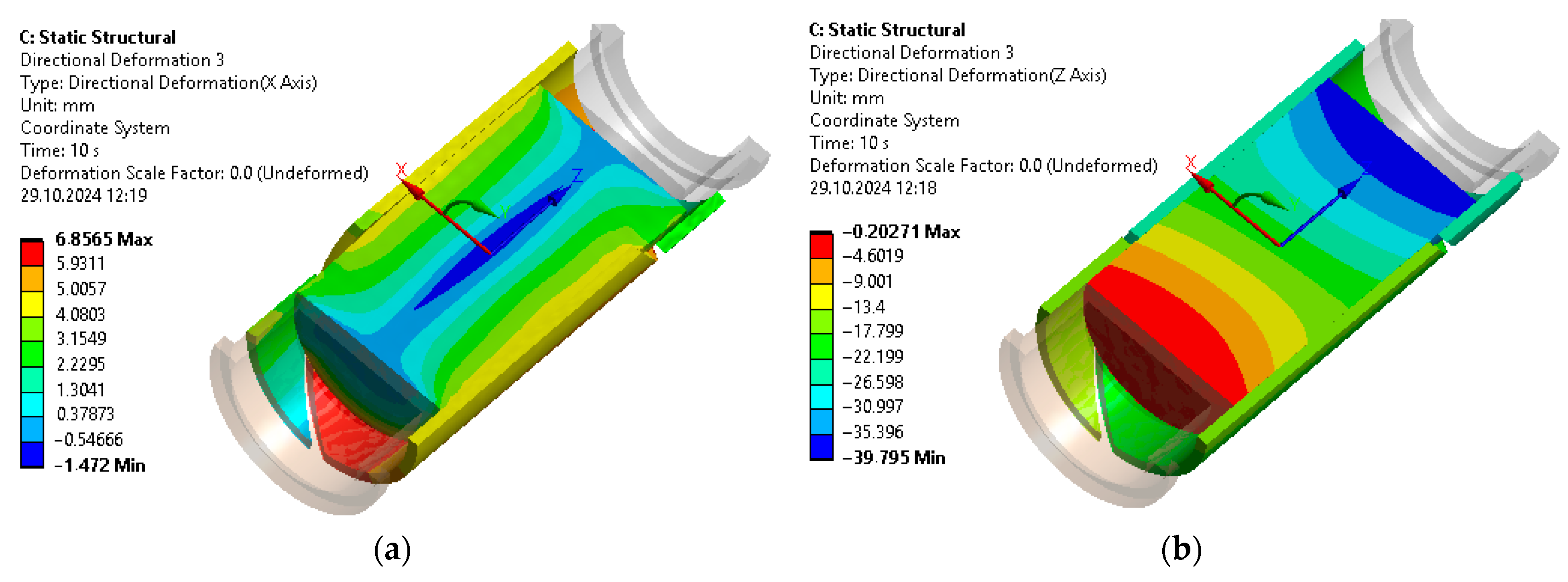
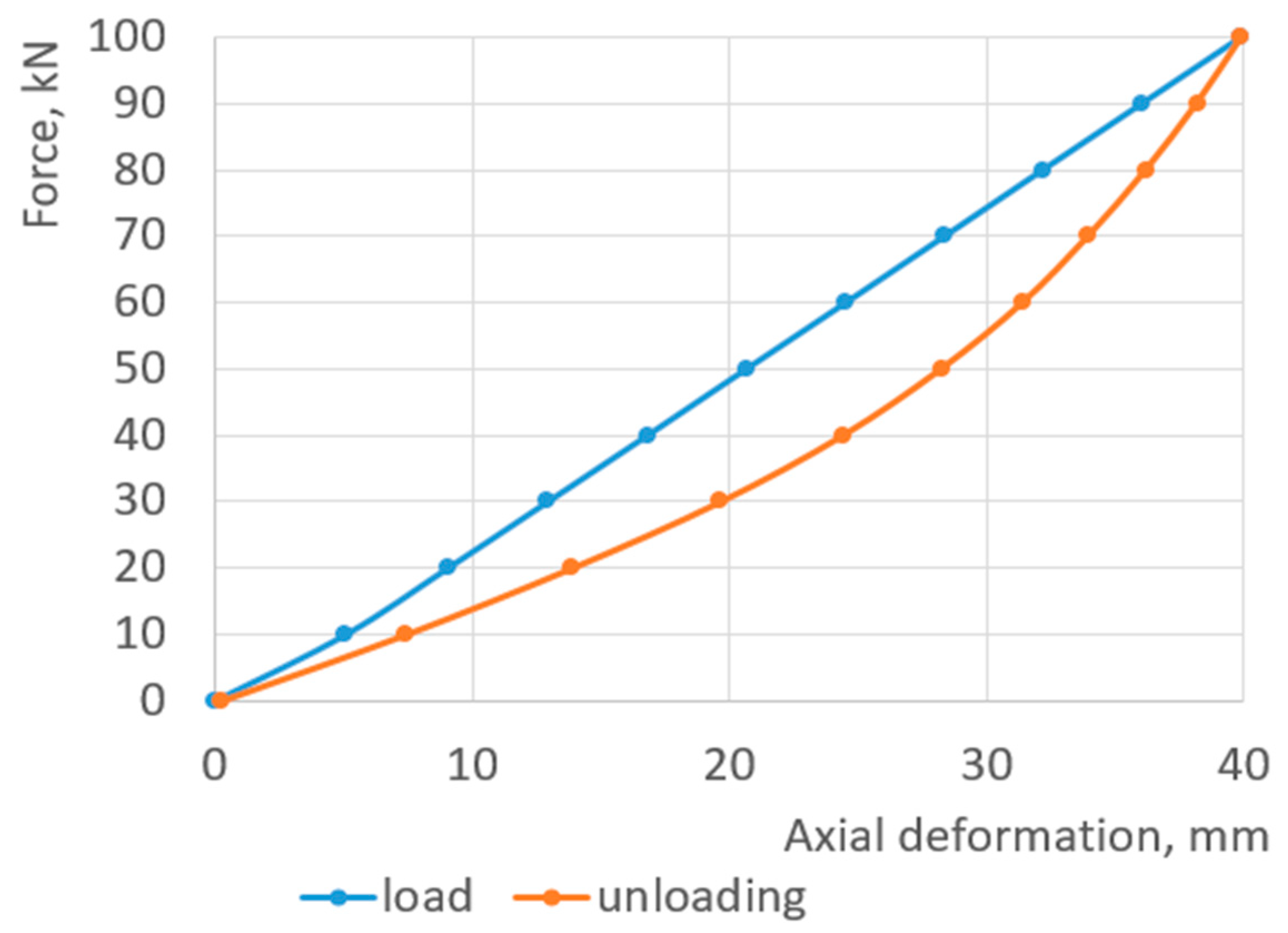
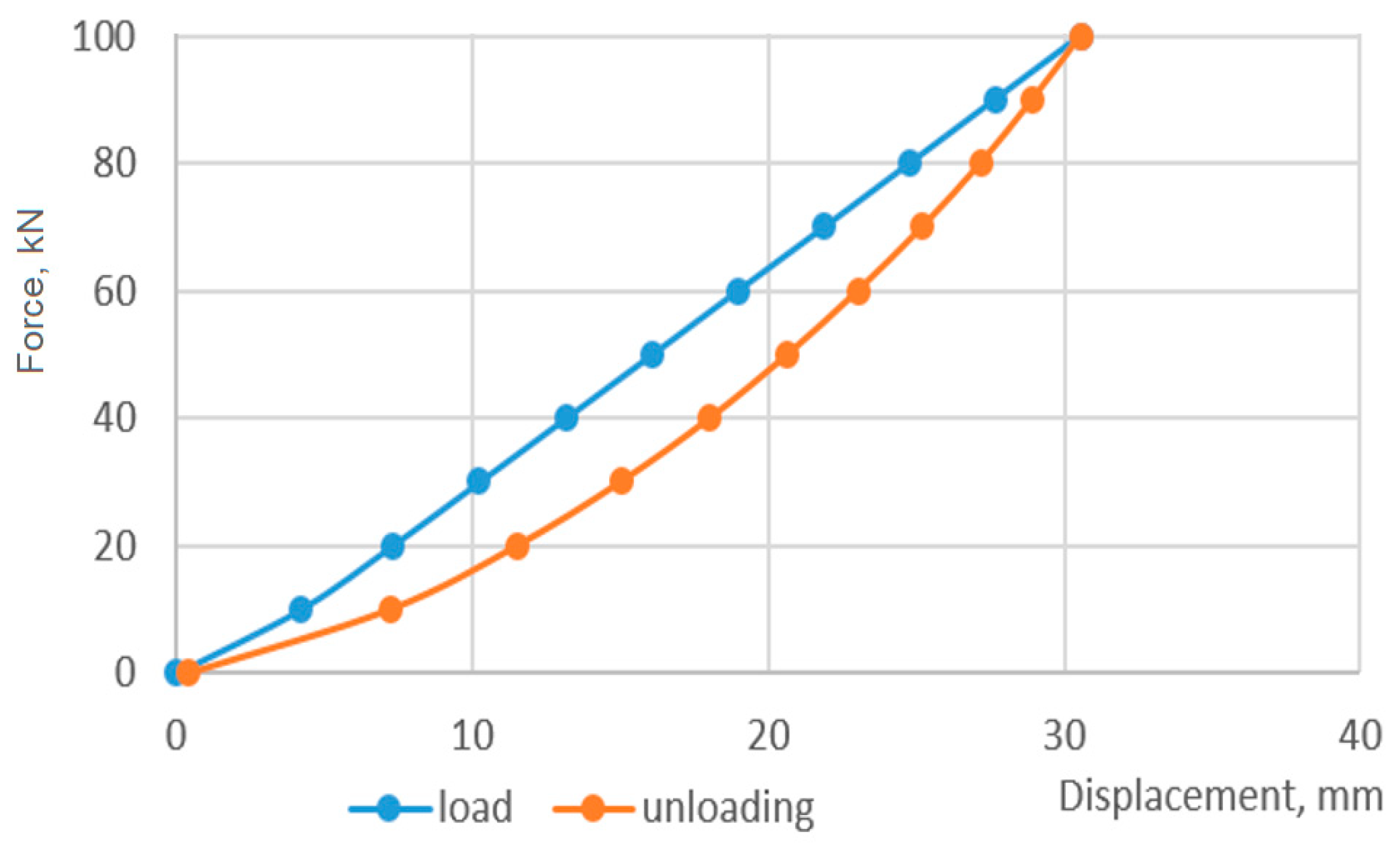
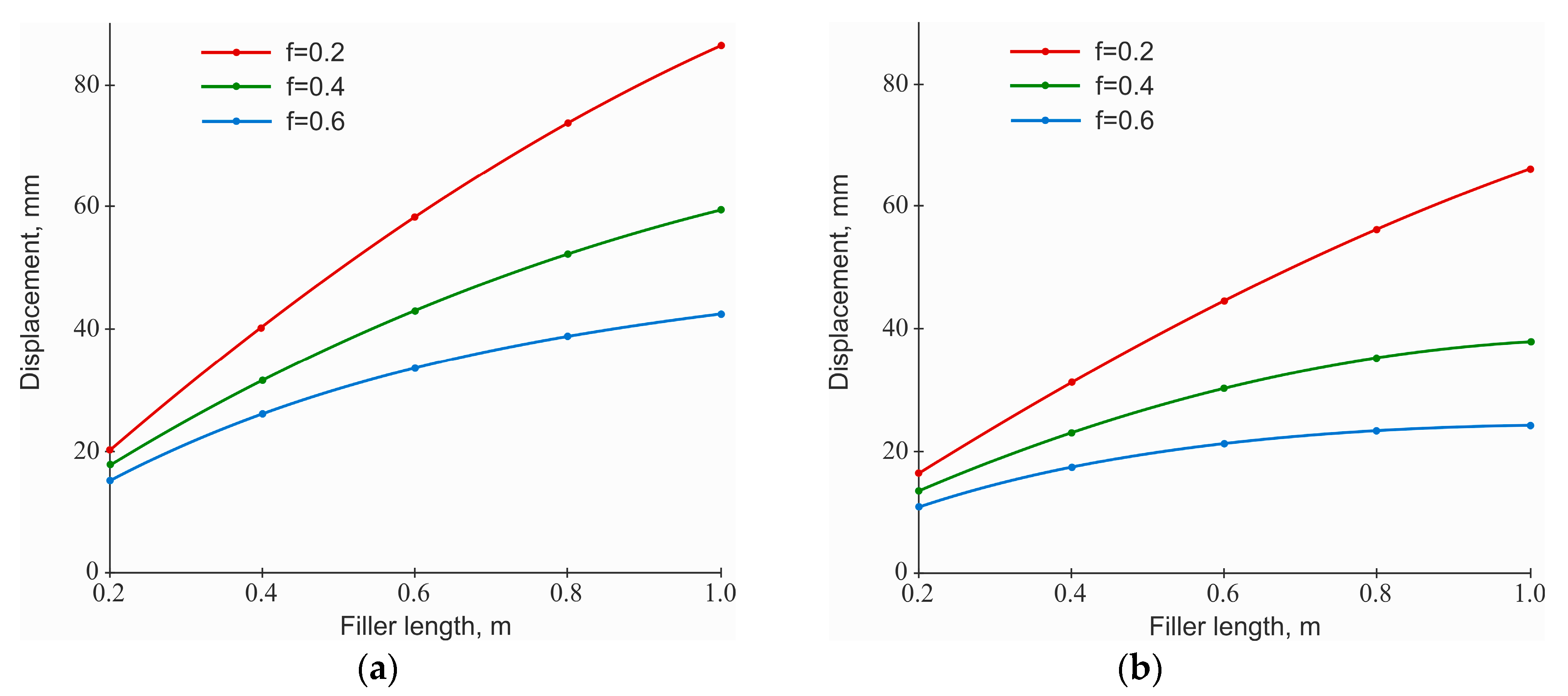
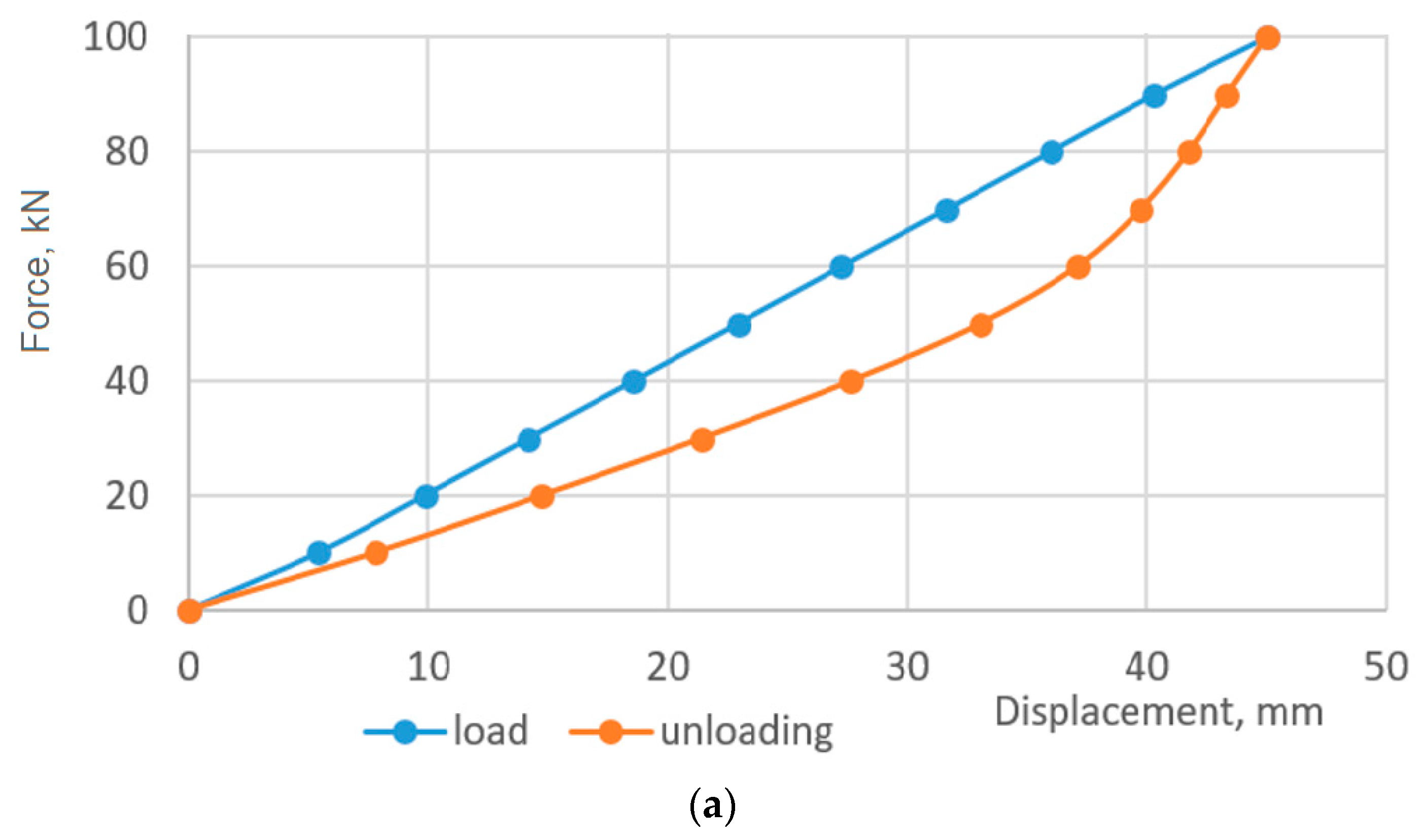
3.2. Displacement Analysis, Settlement-Load Diagram Construction
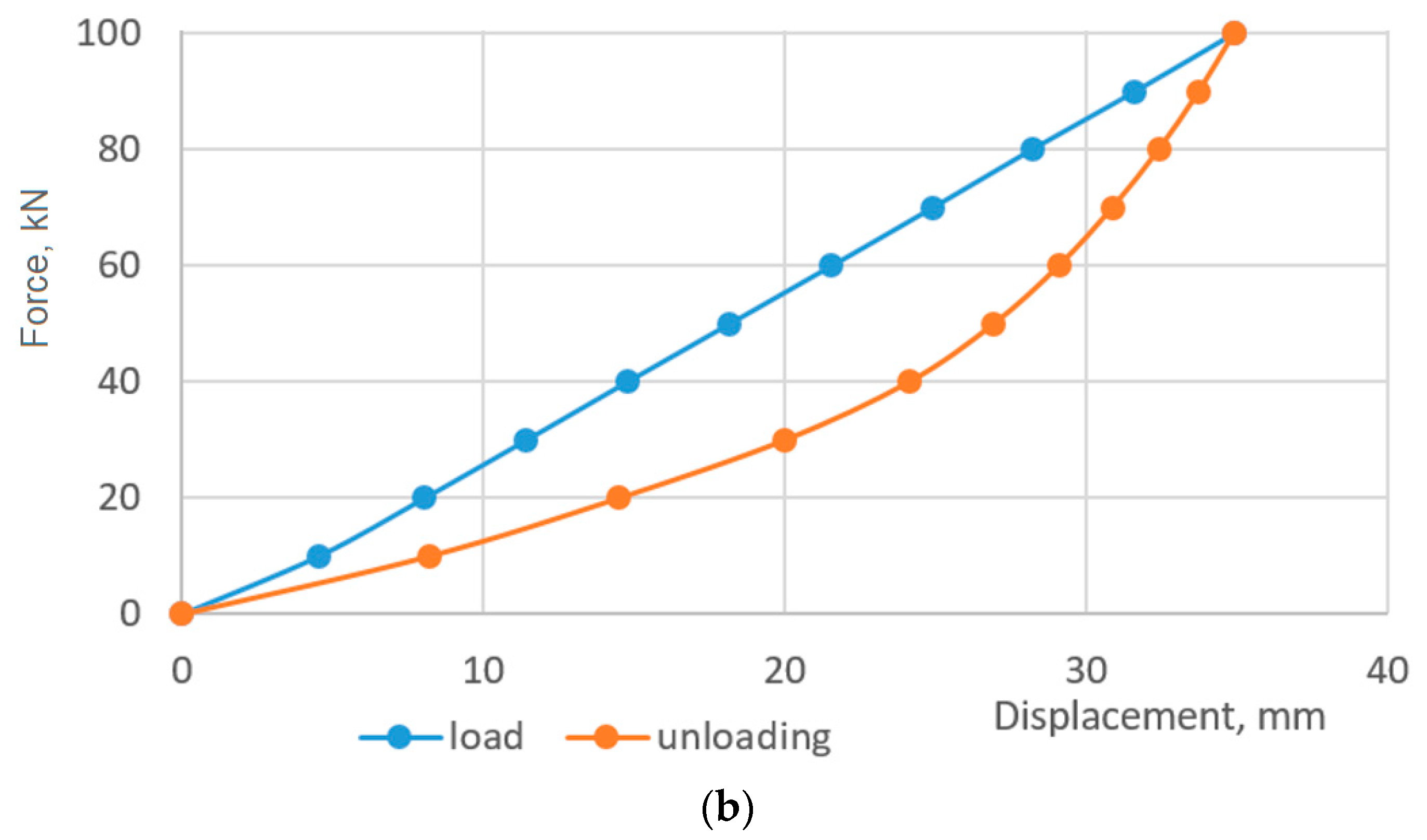
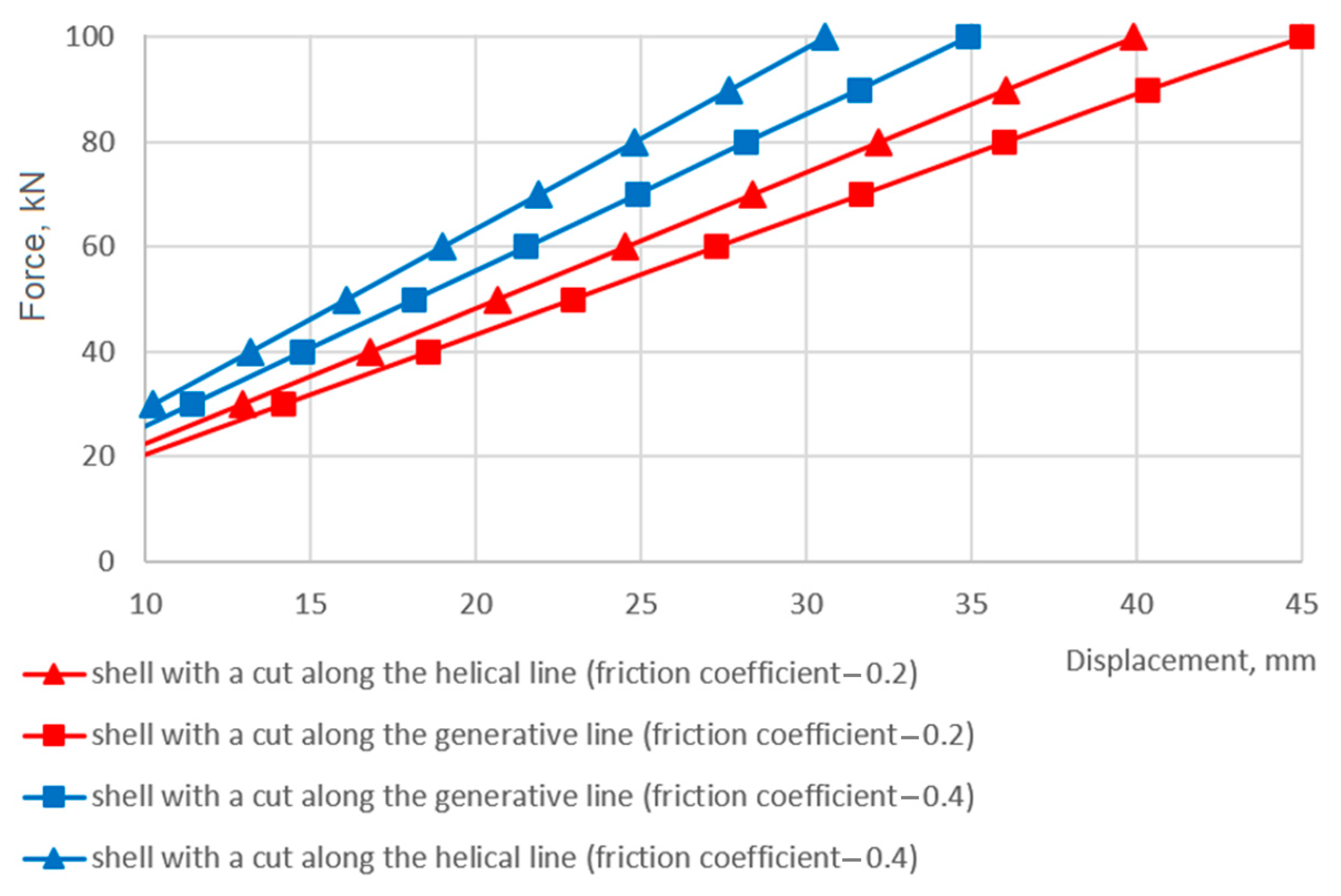
3.3. Comparison of the Stiffness of a Damper Based on a Shell with a Screw Cut with the Stiffness of a Basic Shell Damper Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aydin, E.; Ozturk, B.; Dutkiewicz, M. Analysis of efficiency of passive dampers in multistorey buildings. J. Sound Vib. 2019, 439, 17–28. [Google Scholar] [CrossRef]
- Zhao, Q.; Tan, Y.; Sun, M.; Jiang, Y.; Wang, P.; Meng, F.; Li, Z. Performance of Strengthened Accelerated Oscillator Damper for Vibration Control of Bridges. Appl. Sci. 2024, 14, 6732. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Zheng, X.; Zhao, L.; Qiu, Y. Advancements in Semi-Active Automotive Suspension Systems with Magnetorheological Dampers: A Review. Appl. Sci. 2024, 14, 7866. [Google Scholar] [CrossRef]
- Machado, M.R.; Dutkiewicz, M. Wind turbine vibration management: An integrated analysis of existing solutions, products, and Open-source developments. Energy Rep. 2024, 11, 3756–3791. [Google Scholar] [CrossRef]
- Kang, C.-H.; Park, H.-S.; Seo, S.-W.; Kwag, D.-G. Design and Experiment of a Passive Vibration Isolator for Small Unmanned Aerial Vehicles. Appl. Sci. 2024, 14, 4113. [Google Scholar] [CrossRef]
- Gasparetto, V.E.L.; Reid, J.; ElSayed, M.S.A. Passive-Tuned Mass Dampers for the Pointing Accuracy Mitigation of VLBI Earth-Based Antennae Subject to Aerodynamic Gust. Appl. Mech. 2023, 4, 816–840. [Google Scholar] [CrossRef]
- El Ouni, M.H.; Abdeddaim, M.; Elias, S.; Kahla, N.B. Review of Vibration Control Strategies of High-Rise Buildings. Sensors 2022, 22, 8581. [Google Scholar] [CrossRef]
- Velichkovich, A.S.; Velichkovich, S.V. Vibration-impact damper for controlling the dynamic drillstring conditions. Chem. Pet. Eng. 2001, 37, 213–215. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; John, S. A Comprehensive Review of the Techniques on Regenerative Shock Absorber Systems. Energies 2018, 11, 1167. [Google Scholar] [CrossRef]
- Jacob, K.; Tan, A.S.; Sattel, T.; Kohl, M. Enhancement of Shock Absorption Using Hybrid SMA-MRF Damper by Complementary Operation. Actuators 2022, 11, 280. [Google Scholar] [CrossRef]
- Velichkovich, A.S.; Dalyak, T.M. Assessment of stressed state and performance characteristics of jacketed spring with a cut for drill shock absorber. Chem. Pet. Eng. 2015, 51, 188–193. [Google Scholar] [CrossRef]
- Ehlers, T.; Tatzko, S.; Wallaschek, J.; Lachmayer, R. Design of particle dampers for additive manufacturing. Addit. Manuf. 2021, 38, 101752. [Google Scholar] [CrossRef]
- Pang, F.; Sun, S.; Liu, W.; Zhang, G. Research on reliability test method of MR damper based on damage equivalent. Vibroengin. Procedia 2022, 44, 33–39. [Google Scholar] [CrossRef]
- Pei, Y.; Liu, Z.; Xu, J.; Qi, B.; Cheng, Q. Grouping Preventive Maintenance Strategy of Flexible Manufacturing Systems and Its Optimization Based on Reliability and Cost. Machines 2023, 11, 74. [Google Scholar] [CrossRef]
- Zoccolini, L.; Bruschi, E.; Cattaneo, S.; Quaglini, V. Current Trends in Fluid Viscous Dampers with Semi-Active and Adaptive Behavior. Appl. Sci. 2023, 13, 10358. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.; Wang, S.; Du, D.; Geng, Y. Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects. Machines 2024, 12, 366. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, C.; Zhou, H.; Xu, Z.; Xu, A.; Li, H. Damping Characteristics of a Novel Bellows Viscous Damper. Sensors 2024, 24, 6265. [Google Scholar] [CrossRef] [PubMed]
- Kluczyk, M.; Grządziela, A.; Pająk, M.; Muślewski, Ł.; Szeleziński, A. The Fatigue Wear Process of Rubber-Metal Shock Absorbers. Polymers 2022, 14, 1186. [Google Scholar] [CrossRef] [PubMed]
- Tang, N.; Rongong, J.A.; Sims, N.D. Design of adjustable Tuned Mass Dampers using elastomeric O-rings. J. Sound Vib. 2018, 433, 334–348. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Pan, G.; Huang, Q. Modeling and analysis of a metal rubber vibration isolation system considering the nonlinear stiffness characteristics. Rev. Sci. Instrum. 2023, 94, 015105. [Google Scholar] [CrossRef] [PubMed]
- Landar, S.; Velychkovych, A.; Mykhailiuk, V. Numerical and analytical models of the mechanism of torque and axial load transmission in a shock absorber for drilling oil, gas and geothermal wells. Eng. Solid Mech. 2024, 12, 207–220. [Google Scholar] [CrossRef]
- Jung, H.-Y.; Kim, I.-H.; Jung, H.-J. Feasibility Study of the Electromagnetic Damper for Cable Structures Using Real-Time Hybrid Simulation. Sensors 2017, 17, 2499. [Google Scholar] [CrossRef]
- She, C.; Zhang, M.; Ge, Y.; Tang, L.; Yin, H.; Peng, G. Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems. Aerospace 2022, 9, 113. [Google Scholar] [CrossRef]
- Makowski, M.; Knap, L. Study of a Controlled Piezoelectric Damper. Sensors 2021, 21, 3509. [Google Scholar] [CrossRef]
- Chatziathanasiou, G.M.; Chrysochoidis, N.A.; Rekatsinas, C.S.; Saravanos, D.A. A semi-active shunted piezoelectric tuned-mass-damper for multi-modal vibration control of large flexible structures. J. Sound Vib. 2022, 537, 117222. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, B.L. Robust Static Output Feedback Control of a Semi-Active Vehicle Suspension Based on Magnetorheological Dampers. Appl. Sci. 2024, 14, 10336. [Google Scholar] [CrossRef]
- Sapiński, B.; Jastrzębski, Ł. Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes. Energies 2024, 17, 3436. [Google Scholar] [CrossRef]
- Hao, J.; Wang, Y.; Peng, Y.; Ma, H.; Wei, X. Design and Structure Optimization of Arresting Gear Based on Magnetorheological Damper. Aerospace 2023, 10, 1019. [Google Scholar] [CrossRef]
- Wang, H.; Bi, C.; Liu, W.; Zhou, F. Squeeze Behaviors of Magnetorheological Fluids under Different Compressive Speeds. Materials 2023, 16, 3109. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, L.; Morandini, M.; Ghiringhelli, G.L. A review of friction damping modeling and testing. Arch. Appl. Mech. 2020, 90, 107–126. [Google Scholar] [CrossRef]
- Ma, H.Y.; Li, L.; Wu, Y.G.; Fan, Y.; Gao, Q. Design of dry friction dampers for thin-walled structures by an accelerated dynamic Lagrange method. J. Sound Vib. 2020, 489, 115550. [Google Scholar] [CrossRef]
- Mandziy, T.; Ivasenko, I.; Berehulyak, O.; Vorobel, R.; Bembenek, M.; Kryshtopa, S.; Ropyak, L. Evaluation of the Degree of Degradation of Brake Pad Friction Surfaces Using Image Processing. Lubricants 2024, 12, 172. [Google Scholar] [CrossRef]
- Jaisee, S.; Yue, F.; Ooi, Y.H. A state-of-the-art review on passive friction dampers and their applications. Eng. Struct. 2021, 235, 112022. [Google Scholar] [CrossRef]
- Balaji, P.S.; Karthik SelvaKumar, K. Applications of Nonlinearity in Passive Vibration Control: A Review. J. Vib. Eng. Technol. 2021, 9, 183–213. [Google Scholar] [CrossRef]
- Yuan, J.; Gastaldi, C.; Goy, E.D.; Chouvion, B. Friction damping for turbomachinery: A comprehensive review of modelling, design strategies, and testing capabilities. Prog. Aerosp. Sci. 2024, 147, 101018. [Google Scholar] [CrossRef]
- Baraftabi, E.S.; Elizei, M.H.; Esmaeilabadi, R. Numerical and experimental investigation of a new model of friction damper in diagonal brace under cyclic loading. Structures 2024, 61, 105830. [Google Scholar] [CrossRef]
- Velichkovich, A.S. Shock Absorber for Oil-Well Sucker-Rod Pumping Unit. Chem. Petrol. Eng. 2005, 41, 544–546. [Google Scholar] [CrossRef]
- Rathee, R. Numerical modeling and simulation of friction models for mechanical systems: A brief review. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Barsotti, R.; Bennati, S.; Migliaccio, G. Non-Linear Dynamics of Simple Elastic Systems Undergoing Friction-Ruled Stick–Slip Motions. CivilEng 2024, 5, 420–434. [Google Scholar] [CrossRef]
- Dou, C.; Fan, J.; Li, C.; Cao, J.; Gao, M. On discontinuous dynamics of a class of friction-influenced oscillators with nonlinear damping under bilateral rigid constraints. Mech. Mach. Theory 2020, 147, 103750. [Google Scholar] [CrossRef]
- Ferrotto, M.F.; Cavaleri, L. Variable Friction Dampers (VFD) for a modulated mitigation of the seismic response of framed structures: Characteristics and design criteria. Probabilistic Eng. Mech. 2022, 70, 103375. [Google Scholar] [CrossRef]
- Mrad, C.; Titirla, M.; Larbi, W. Optimal Design of Viscous and Friction Dampers in Symmetric Reinforced Concrete Buildings. In Proceedings of the 7th World Congress on Civil, Structural, and Environmental Engineering, Lisbon, Portugal, 10–12 April 2022. [Google Scholar] [CrossRef]
- Wang, Q.; Shen, H.; Zhang, Z.; Qian, H. Mechanical Behaviors of a Buckling-Plate Self-Centering Friction Damper. Buildings 2023, 13, 440. [Google Scholar] [CrossRef]
- Guglielmino, E.; Edge, K.A. A controlled friction damper for vehicle applications. Control. Eng. Pract. 2004, 12, 431–443. [Google Scholar] [CrossRef]
- Dixon, J.C. The Shock Absorber Handbook, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Sun, Y.; Denimal, E.; Yuan, J.; Salles, L. Geometric design of friction ring dampers in blisks using nonlinear modal analysis and Kriging surrogate model. Struct. Multidiscip. Optim. 2022, 65, 98. [Google Scholar] [CrossRef]
- Velichkovich, A.S. Design features of shell springs for drilling dampers. Chem. Petrol. Eng. 2007, 43, 458–461. [Google Scholar] [CrossRef]
- Velichkovich, A.; Dalyak, T.; Petryk, I. Slotted shell resilient elements for drilling shock absorbers. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2018, 73, 34. [Google Scholar] [CrossRef]
- Bembenek, M.; Grydzhuk, Y.; Gajdzik, B.; Ropyak, L.; Pashechko, M.; Slabyi, O.; Al-Tanakchi, A.; Pryhorovska, T. An Analytical–Numerical Model for Determining “Drill String–Wellbore” Frictional Interaction Forces. Energies 2024, 17, 301. [Google Scholar] [CrossRef]
- Man, J.; Xue, B.; Bian, X.; Yan, W.; Qiao, D.; Zeng, W. Experimental and Numerical Investigations on the Dynamic Response of Blades with Dual Friction Dampers. Aerospace 2023, 10, 977. [Google Scholar] [CrossRef]
- Bruschi, E.; Quaglini, V. Assessment of Non-Linear Analyses of RC Buildings Retrofitted with Hysteretic Dampers According to the Italian Building Code. Appl. Sci. 2024, 14, 2684. [Google Scholar] [CrossRef]
- Lozynskyi, V.; Shihab, T.; Drach, I.; Ropyak, L. The Inertial Disturbances of Fluid Movement in the Chamber of a Liquid Autobalancer. Machines 2024, 12, 39. [Google Scholar] [CrossRef]
- Prysyazhnyuk, P.; Bembenek, M.; Drach, I.; Korzhov, A.; Romanyshyn, L.; Ropyak, L. Restoration of the Impact Crusher Rotor Using FCAW with High-Manganese Steel Reinforced by Complex Carbides. Manag. Syst. Prod. Eng. 2024, 32, 294–302. [Google Scholar] [CrossRef]
- Wahad, H.S.; Tudor, A.; Vlase, M.; Cerbu, N.; Subhi, K.A. The effect of friction in coulombian damper. IOP Conf. Ser. Mater. Sci. Eng. 2017, 174, 012021. [Google Scholar] [CrossRef]
- Shopa, V.M.; Shatskii, I.P.; Popadyuk, I.I. Elementary calculation of structural damping in shell springs. Sov. Eng. Res. 1989, 9, 42–44. [Google Scholar]
- Bedzir, A.A.; Shatskii, I.P.; Shopa, V.M. Nonideal contact in a composite shell structure with a deformable filler. Int. Appl. Mech. 1995, 31, 351–354. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Analytical Study of Nonlinear Vibration in a Rub-Impact Jeffcott Rotor. Energies 2021, 14, 8298. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y. An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration. Aerospace 2021, 8, 302. [Google Scholar] [CrossRef]
- Horvath, H.Z.; Takacs, D. Numerical Analysis on Shimmying Wheels with Dry Friction Damper. Period. Polytech. Mech. Eng. 2023, 67, 118–126. [Google Scholar] [CrossRef]
- Huang, Z.; Tan, J.; Liu, C.; Lu, X. Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers. Symmetry 2021, 13, 281. [Google Scholar] [CrossRef]
- Man, J.; Bian, X.; Zeng, W.; Yan, W.; Qiao, D. Experimental Investigation of the Dynamic Response of a Flat Blade with Dual Dry Friction Dampers. Energies 2023, 16, 7401. [Google Scholar] [CrossRef]
- Wu, Y.G.; Fan, L.; Li, Y.; Ma, H.Y.; Wang, W.J.; Christen, J.-L.; Ichchou, M. Design of semi-active dry friction dampers for steady-state vibration: Sensitivity analysis and experimental studies. J. Sound Vib. 2019, 459, 114850. [Google Scholar] [CrossRef]
- Velichkovich, A.S.; Popadyuk, I.I.; Shopa, V.M. Experimental study of shell flexible component for drilling vibration damping devices. Chem. Pet. Eng. 2011, 46, 518–524. [Google Scholar] [CrossRef]
- Deng, P.; Tan, X.; Bai; Li, H. Influence of Blades’ Shape and Cutters’ Arrangement of PDC Drill Bit on Nonlinear Vibration of Deep Drilling System. J. Sound Vib. 2023, 572, 118165. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Pryhorovska, T.O.; Levchuk, K.H. Analysis of materials and modern technologies for PDC drill bit manufacturing. Prog. Phys. Met. 2020, 21, 274–301. [Google Scholar] [CrossRef]
- Li, L.; Zhang, C.; Wu, A. Study on Mechanism of Stick–Slip Vibration Based on Torque Characteristics of PDC Bit. Appl. Sci. 2024, 14, 6419. [Google Scholar] [CrossRef]
- Shatskii, I.P.; Perepichka, V.V. Shock-wave propagation in an elastic rod with a viscoplastic external resistance. J. Appl. Mech. Tech. Phys. 2013, 54, 1016–1020. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Velychkovych, A.; Andrusyak, A.; Petryk, I.; Kychma, A. Analytical Model of Interaction of an Oil Pipeline with a Support of an Overpass Built in a Mountainous Area. Energies 2023, 16, 4464. [Google Scholar] [CrossRef]
- Shatskyi, I.; Perepichka, V. Problem of dynamics of an elastic rod with decreasing function of elastic-plastic external resistance. In Dynamical Systems in Applications, Proceedings of the DSTA 2017, Lodz, Poland, 11–14 December 2017; Awrejcewicz, J., Ed.; Springer: Cham, Switzerland, 2018; Volume 249, pp. 335–342. [Google Scholar] [CrossRef]
- Yue, F.; Wu, Z. Fracture Mechanical Analysis of Thin-Walled Cylindrical Shells with Cracks. Metals 2021, 11, 592. [Google Scholar] [CrossRef]
- Shats’kyi, I.P. Closure of a longitudinal crack in a shallow cylindrical shell in bending. Mater. Sci. 2005, 41, 186–191. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, J.; Pan, H. Three-Dimension Crack Propagation Behavior of Conical-Cylindrical Shell. Metals 2023, 13, 698. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Analysis of the limiting state of cylindrical shells with cracks with regard for the contact of crack lips. Strength Mater. 2009, 41, 560–565. [Google Scholar] [CrossRef]
- Shatskii, I.P.; Makoviichuk, N.V. Effect of closure of collinear cracks on the stress-strain state and the limiting equilibrium of bent shallow shells. J. Appl. Mech. Tech. Phys. 2011, 52, 464–470. [Google Scholar] [CrossRef]
- Nobili, A.; Radi, E.; Lanzoni, L. A cracked infinite Kirchhoff plate supported by a two-parameter elastic foundation. J. Eur. Ceram. Soc. 2014, 34, 2737–2744. [Google Scholar] [CrossRef]
- Tutko, T.; Dubei, O.; Ropyak, L.; Vytvytskyi, V. Determination of Radial Displacement Coefficient for Designing of Thread Joint of Thin-Walled Shells. In Advances in Design, Simulation and Manufacturing IV, Proceedings of the 4th International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, DSMIE 2021, Lviv, Ukraine, 8–11 June 2021; Ivanov, V., Trojanowska, J., Pavlenko, I., Zajac, J., Peraković, D., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2021; pp. 153–162. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Olejnik, P. Analysis of Dynamic Systems with Various Friction Laws. ASME. Appl. Mech. Rev. 2005, 58, 389–411. [Google Scholar] [CrossRef]
- Velychkovych, A. Numerical model of interation of package of open shells with a weakly compressible filler in a friction shock absorber. Eng. Solid Mech. 2022, 10, 287–298. [Google Scholar] [CrossRef]
- Lu, S.; Liu, J.; Hekkenberg, R. Mesh Properties for RANS Simulations of Airfoil-Shaped Profiles: A Case Study of Rudder Hydrodynamics. J. Mar. Sci. Eng. 2021, 9, 1062. [Google Scholar] [CrossRef]
- Stolarski, T.; Nakasone, Y.; Yoshimoto, S. Application of ANSYS to contact between machine elements. Eng. Anal. ANSYS Softw. 2018, 2018, 375–509. [Google Scholar] [CrossRef]
- Sabri, L.A.; Stojanović, N.; Senatore, A.; Jweeg, M.J.; Abed, A.M.; Abdullah, O.I. Three-Dimensional Finite Element Analysis of Contact Problem in Dry Friction Clutches. Lubricants 2021, 9, 115. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. Frictionless vs. Frictional Contact in Numerical Wear Predictions of Conformal and Non-conformal Sliding Couplings. Tribol. Lett. 2022, 70, 115. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut. Appl. Mech. 2025, 6, 1. https://doi.org/10.3390/applmech6010001
Velychkovych A, Mykhailiuk V, Andrusyak A. Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut. Applied Mechanics. 2025; 6(1):1. https://doi.org/10.3390/applmech6010001
Chicago/Turabian StyleVelychkovych, Andrii, Vasyl Mykhailiuk, and Andriy Andrusyak. 2025. "Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut" Applied Mechanics 6, no. 1: 1. https://doi.org/10.3390/applmech6010001
APA StyleVelychkovych, A., Mykhailiuk, V., & Andrusyak, A. (2025). Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut. Applied Mechanics, 6(1), 1. https://doi.org/10.3390/applmech6010001





