Electromagnetic–Computational Fluid Dynamics Couplings in Tungsten Inert Gas Welding Processes—Development of a New Linearization Procedure for the Joule Production Term
Abstract
1. Introduction
2. Industrial Context
3. CFD Modeling of the Arc and Plasma Flow
- (a)
- The arc is in local thermodynamic equilibrium (LTE), which is a realistic hypothesis when the distance between the tip of the electrode and the surface of the anode is at least 2 mm, as suggested by Griem et al. [30];
- (b)
- A steady-state regime is assumed in the plasma flow;
- (c)
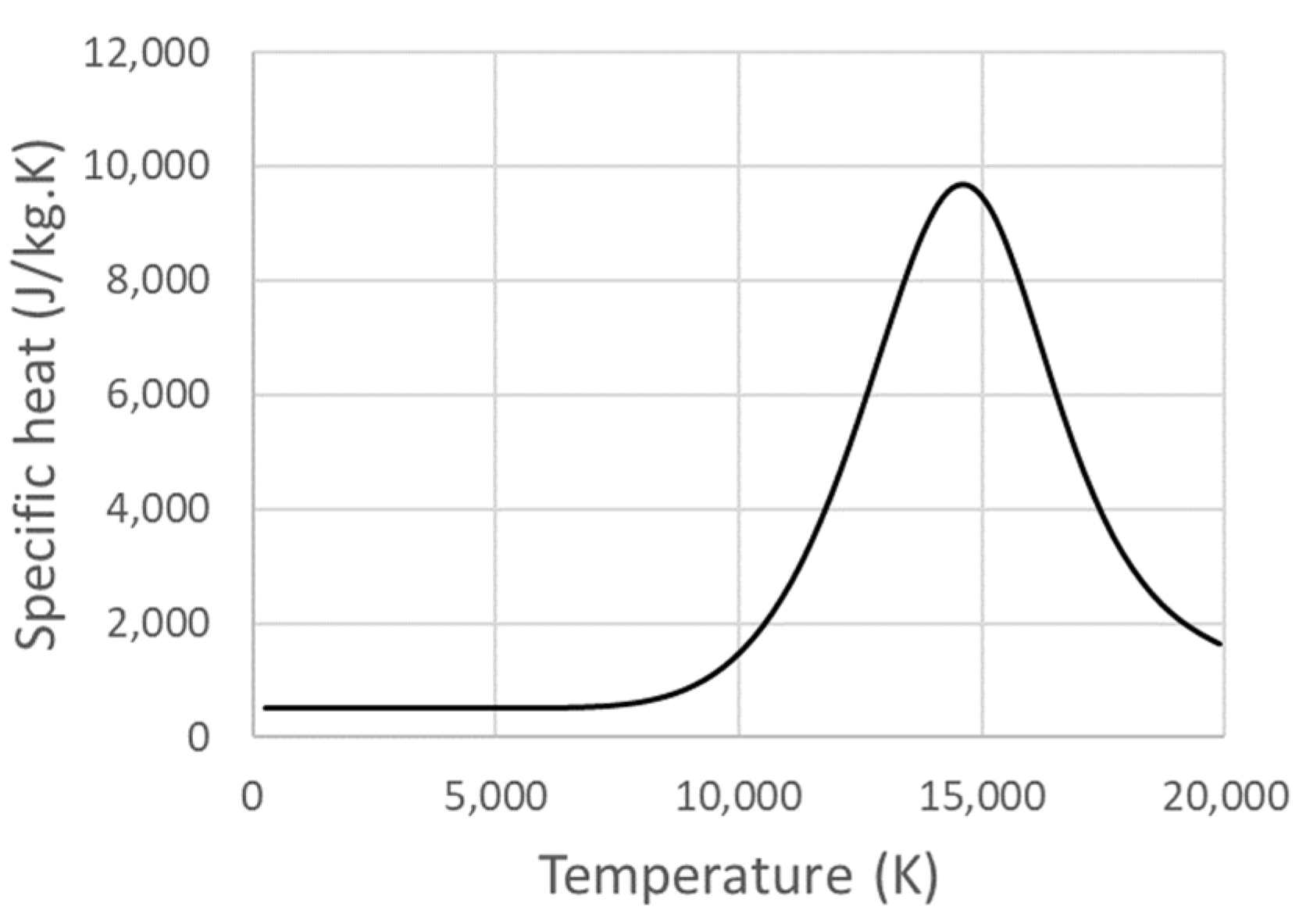
- The effect of metal vapors is neglected because the electric current is lower than 150 A;
- (d)
- The quantity of positive charges almost balances the charge of electrons (quasi-neutral field);
- (e)
- The fluid flow is turbulent.
3.1. Governing Equations
- (1)
- calculating the Lorentz force which plays a key role to describe the behavior of arcing and maintaining of the arc [33];
- (2)
- accounting for the Joule effect to properly solve the energy equation in the plasma flow.
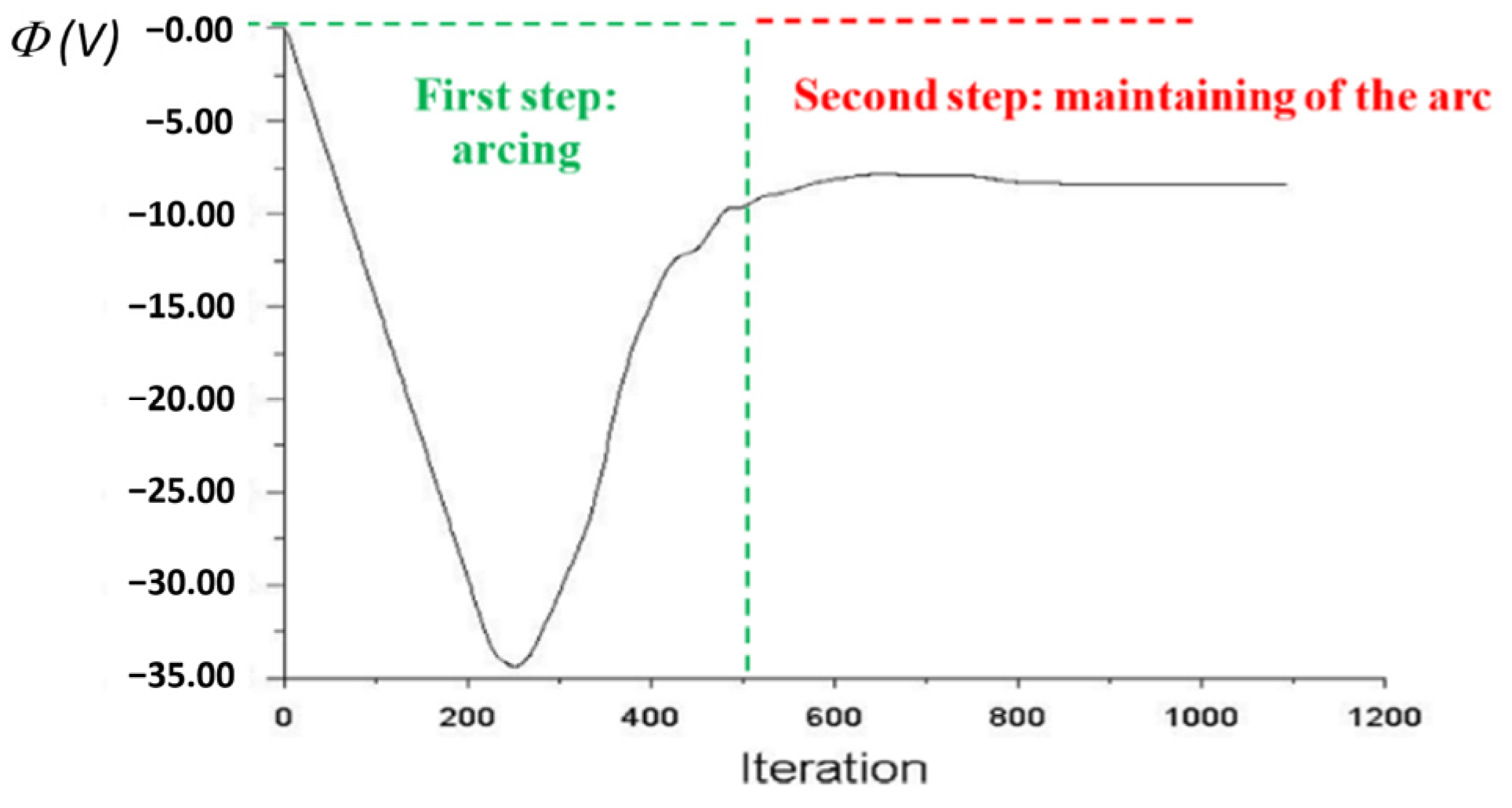
3.2. Arcing and Maintaining of the Welding Arc
- (a)
- The control of the electric current during the welding process (the electric current intensity I is imposed so that the integral of the current density over the cathode tip surface is imposed too);
- (b)
- The variation in the electrical conductibility with temperature.
- (a)
- It avoids under-relaxation in the iterative process applied to solve the energy conservation equation and therefore significantly enhances the convergence of the iterative procedure used to solve Equation (9);
- (b)
- It avoids the use of artificial conductibility in some parts of the domain (i.e., near the surface of electrodes, for example).
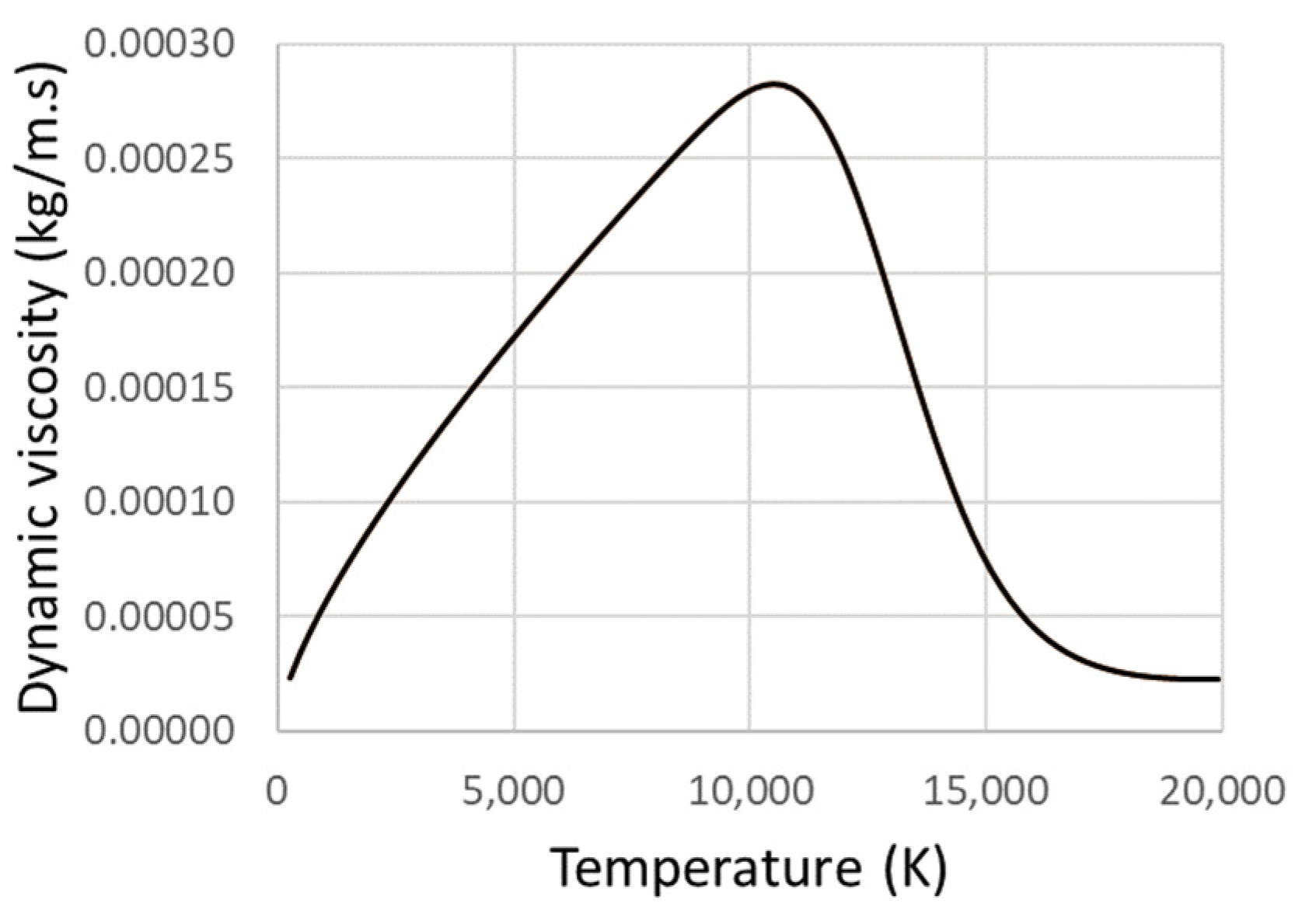
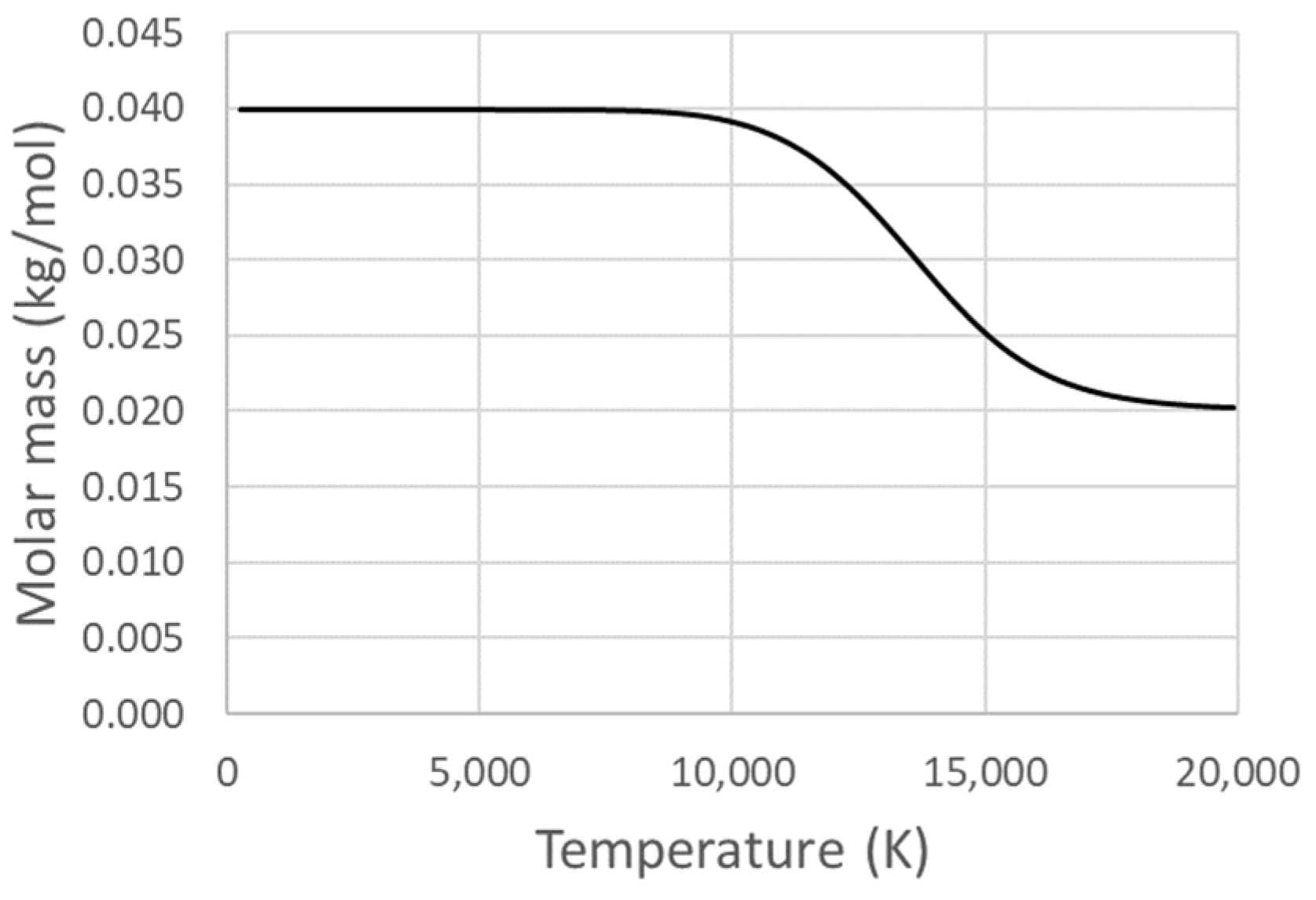
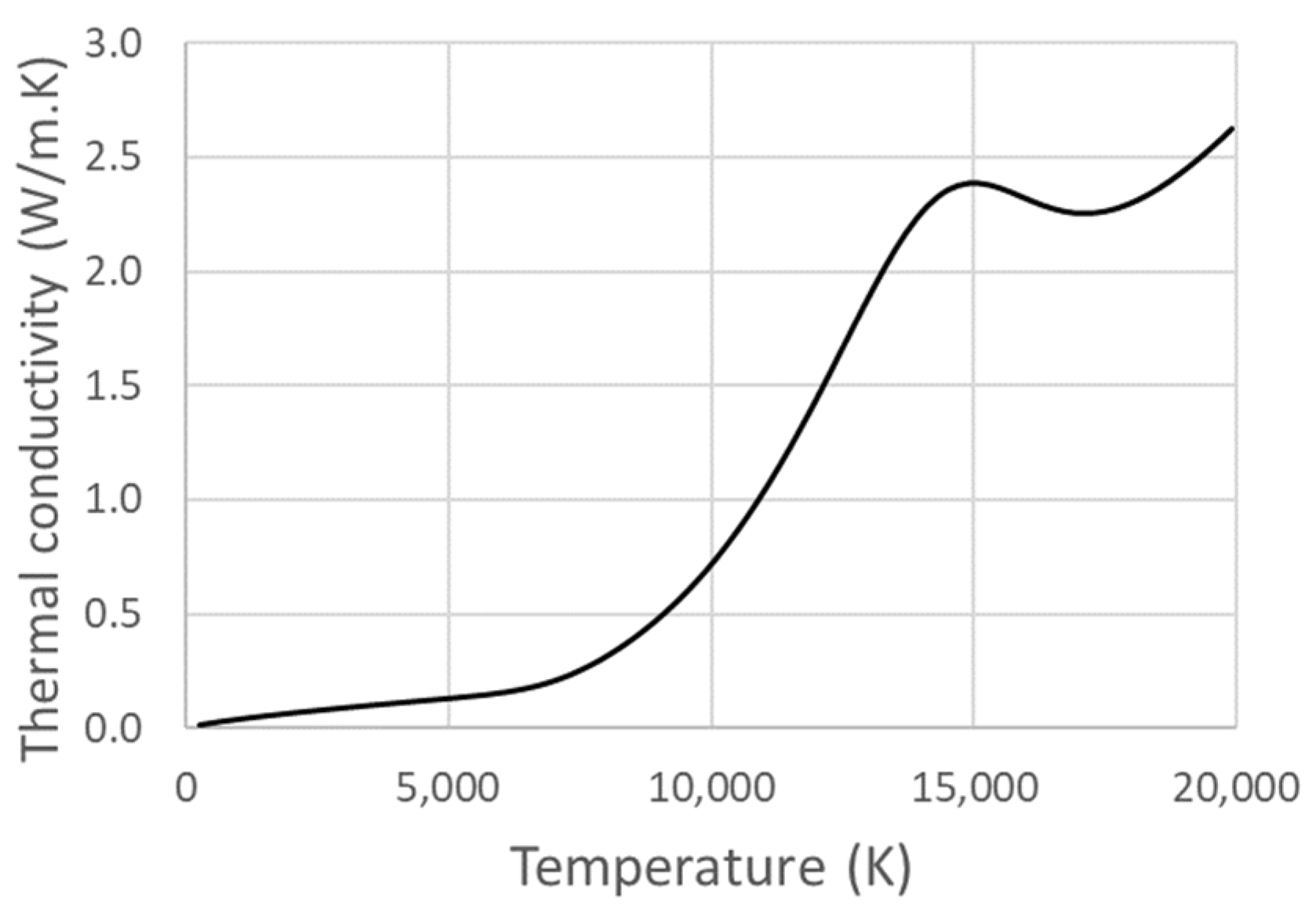
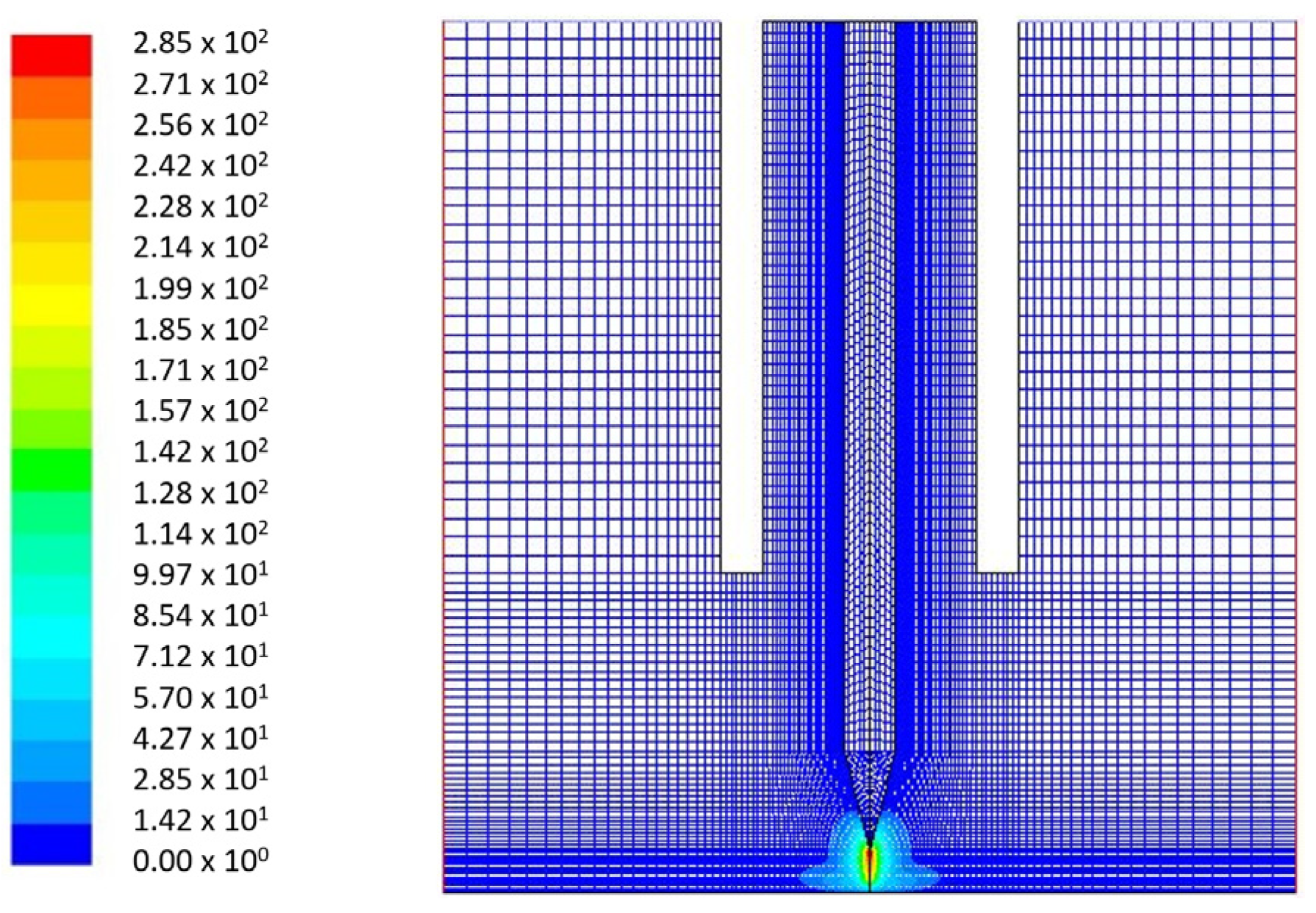
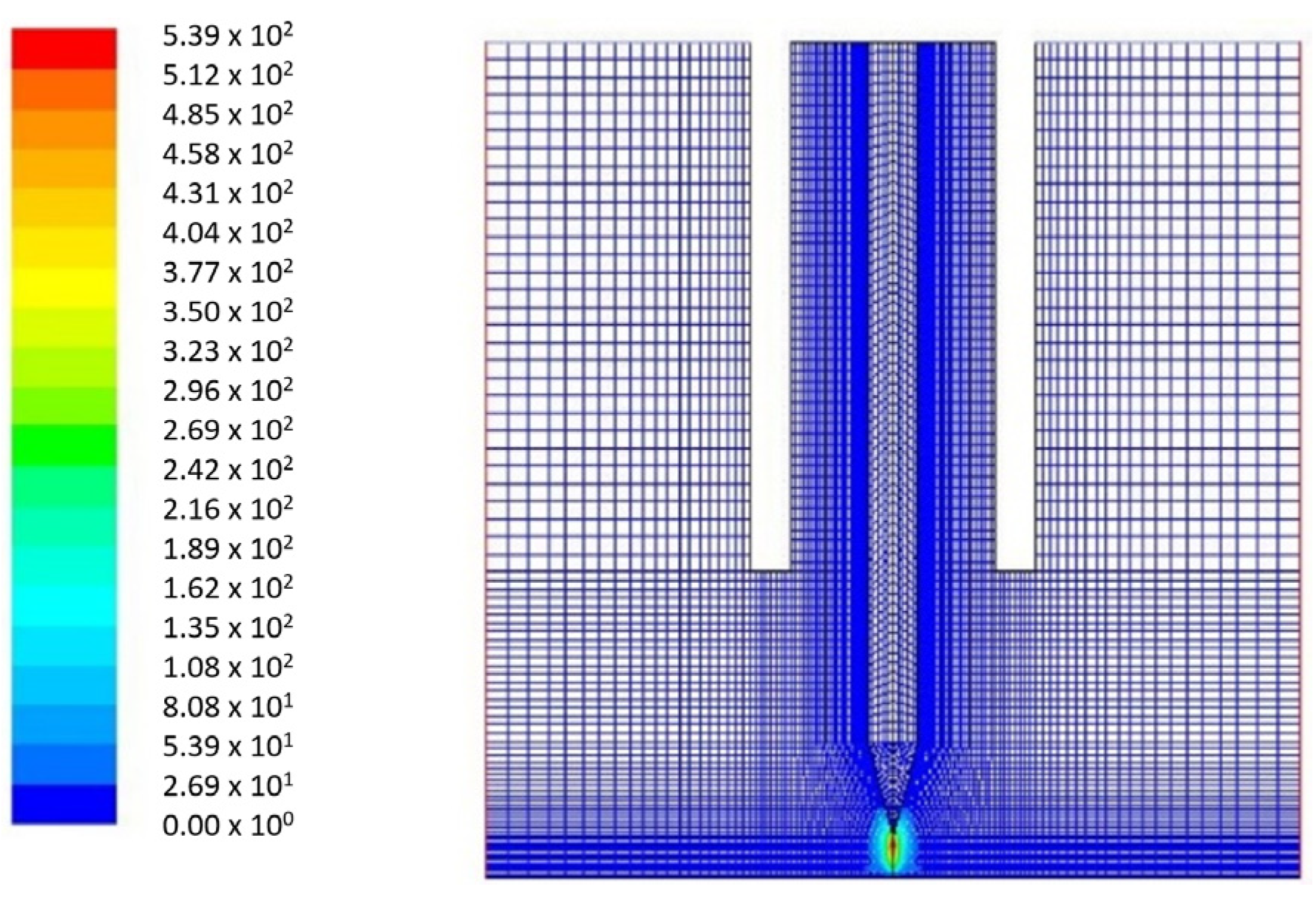
3.3. CFD Model
4. Numerical Results
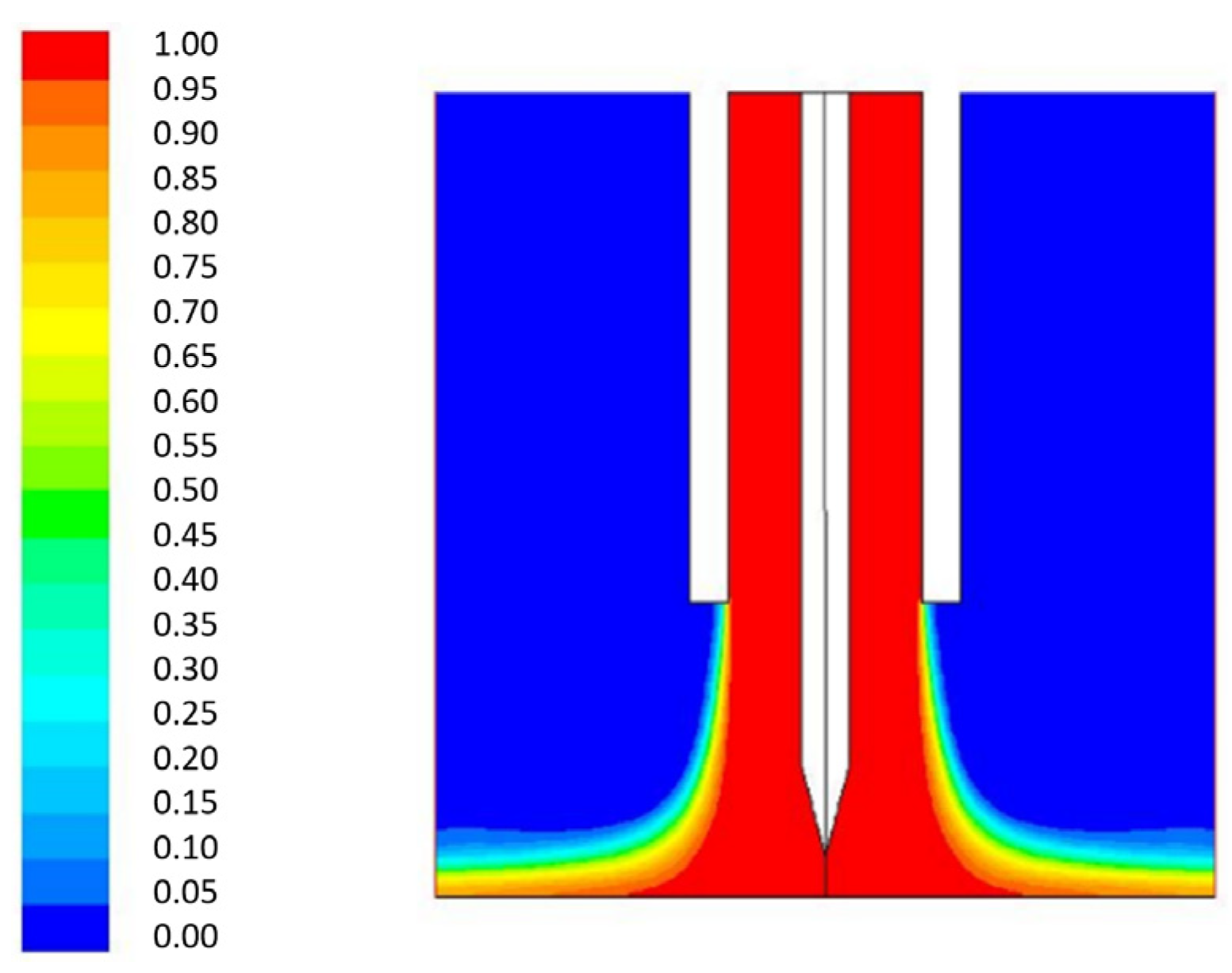
4.1. Argon Mass Fraction
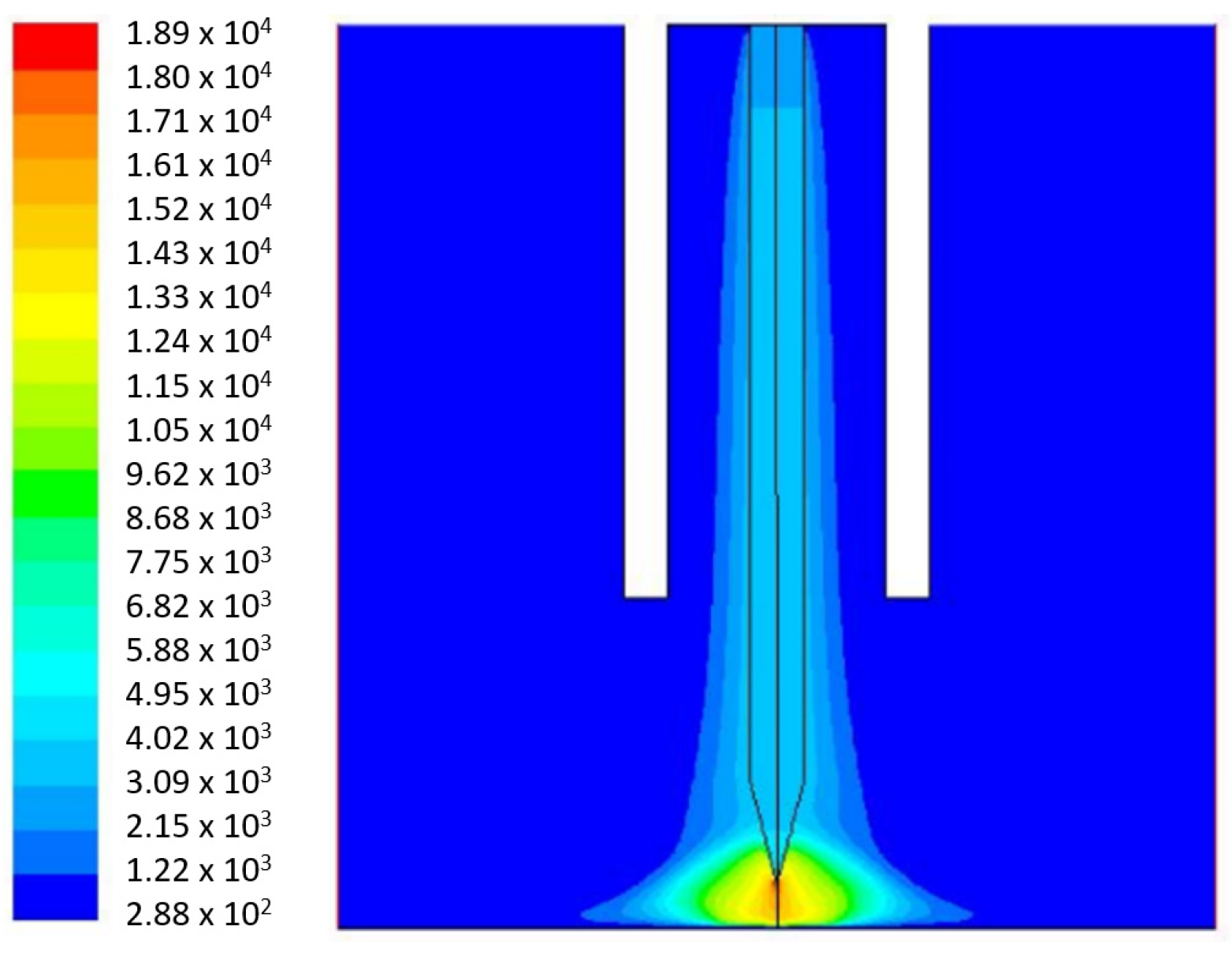
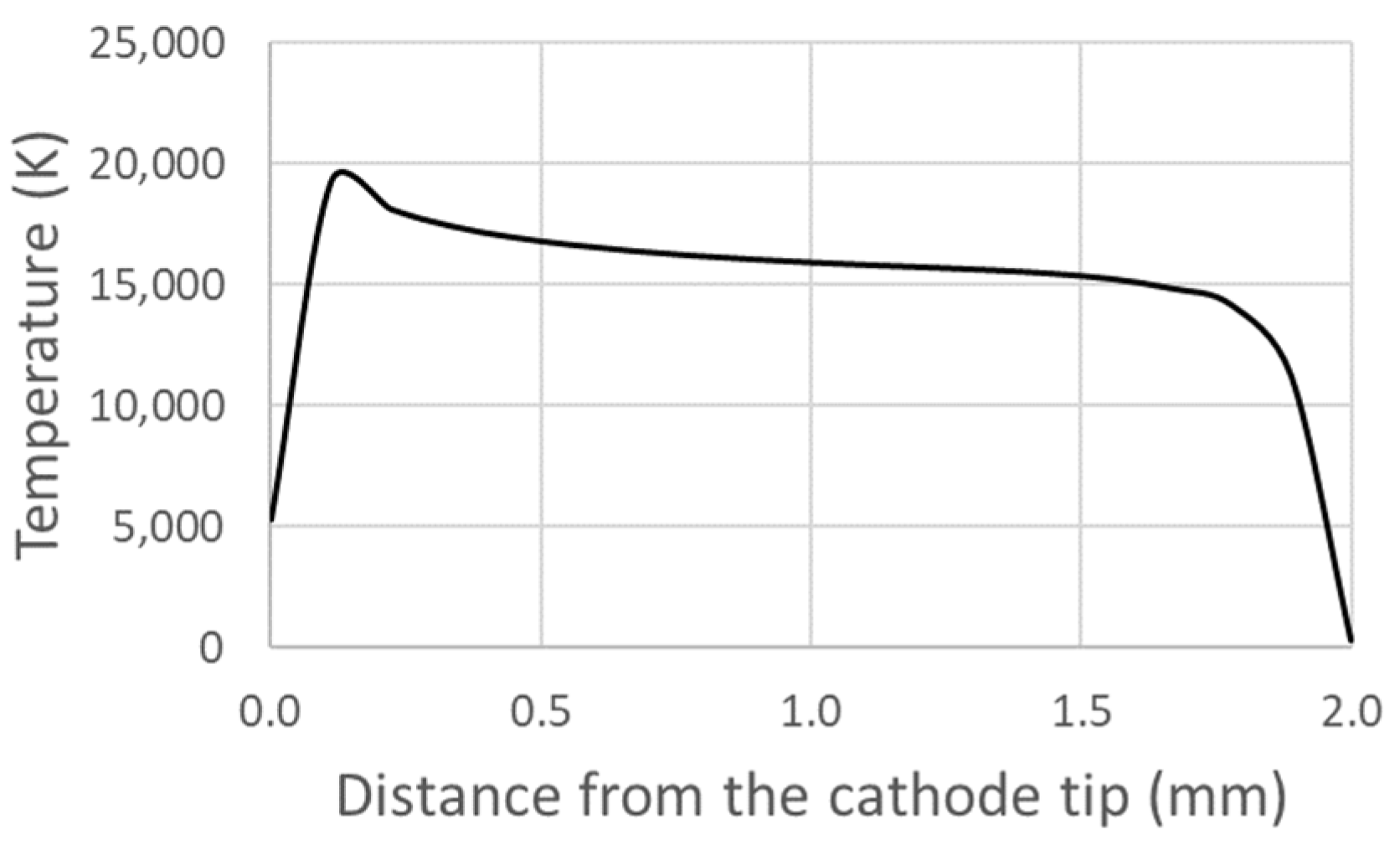
4.2. Temperature Distribution
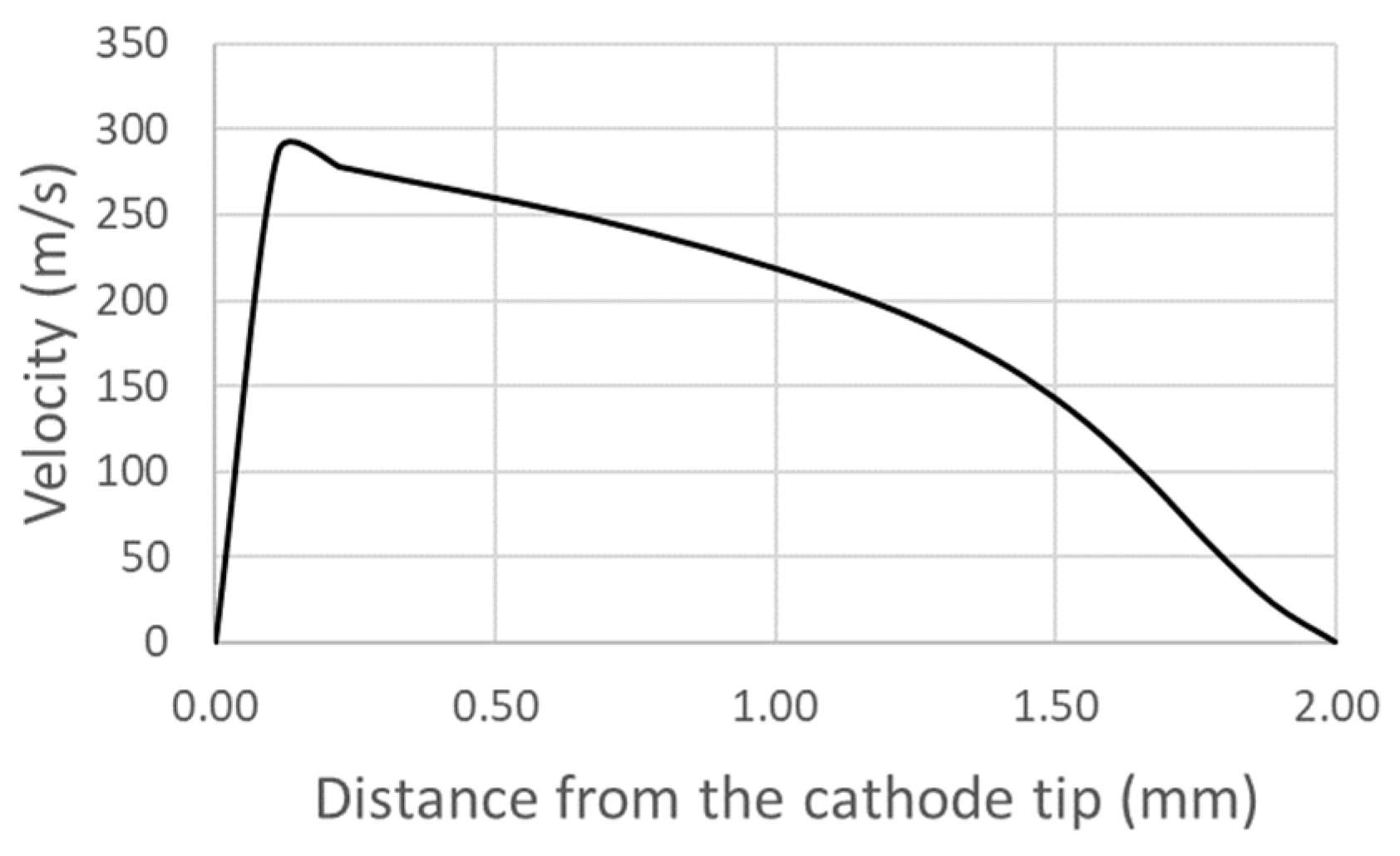
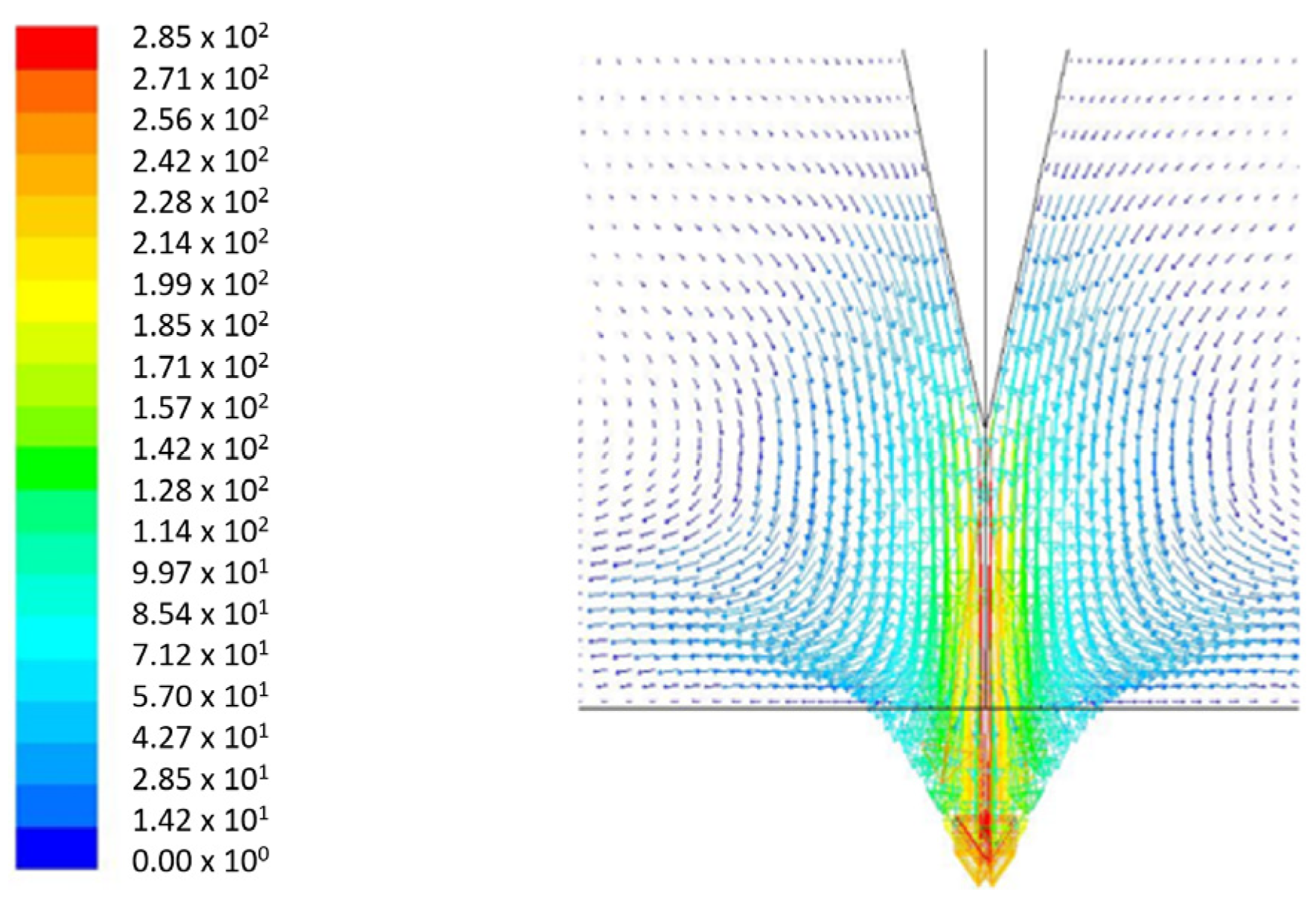
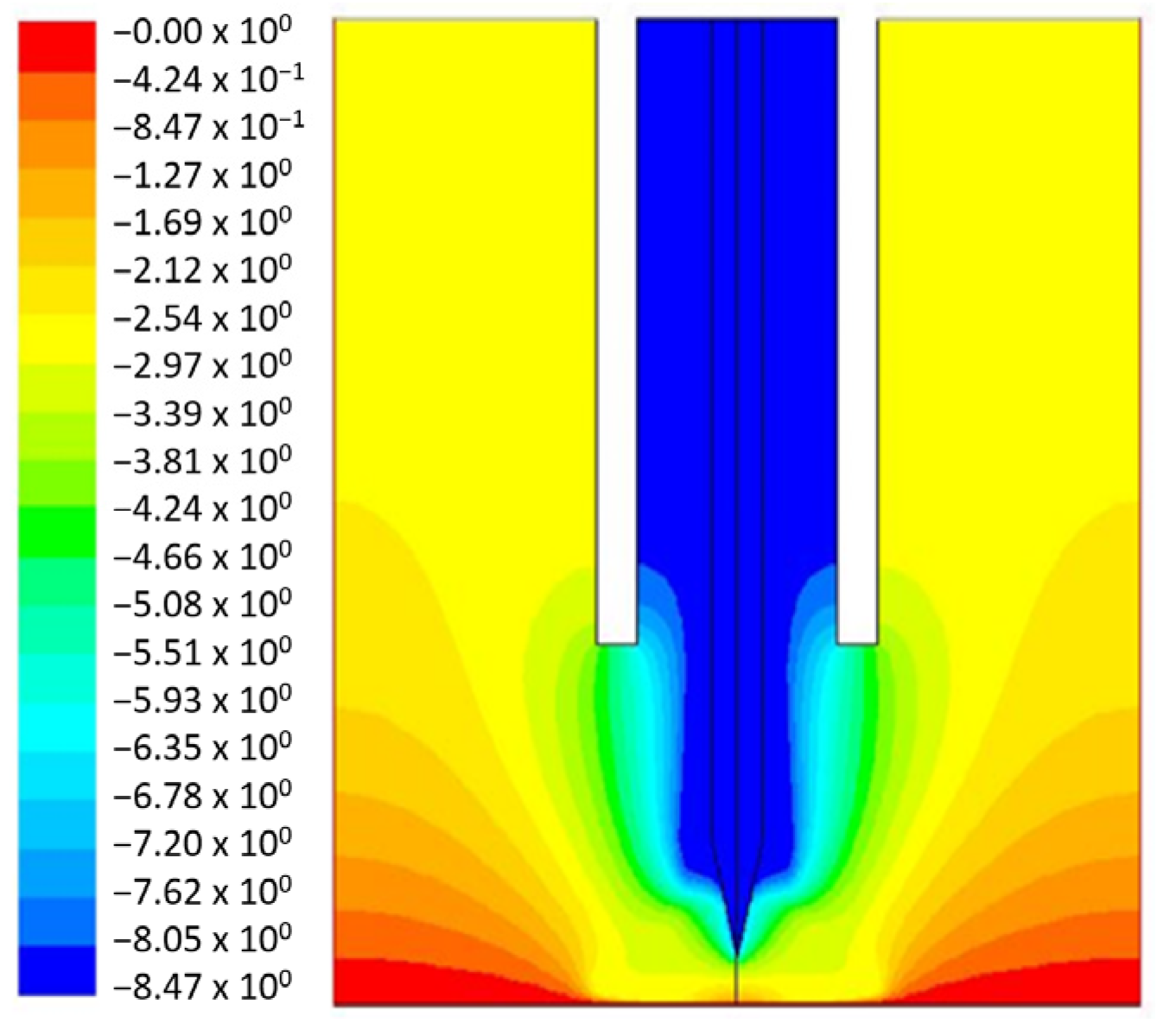
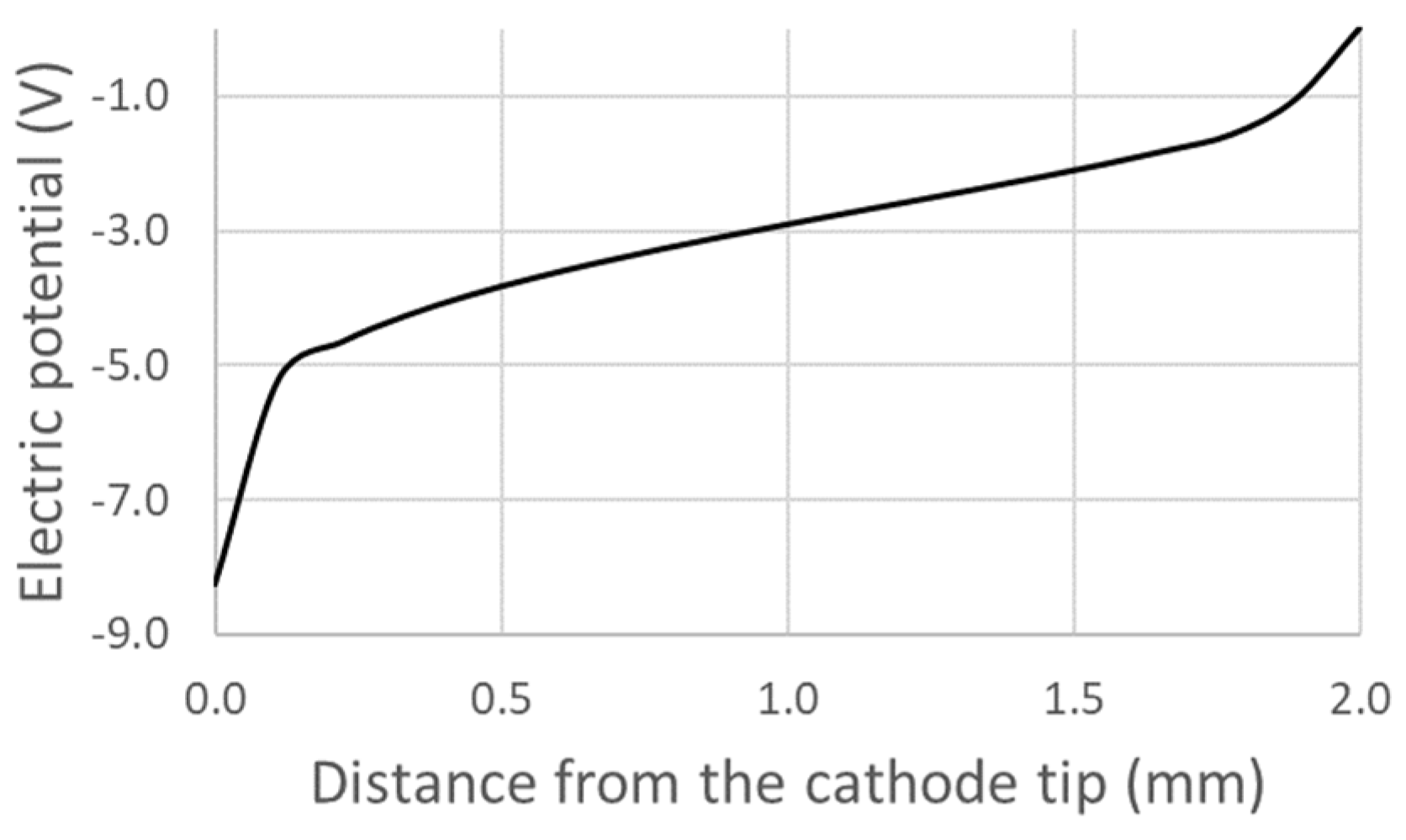
4.3. Velocities, Pressure, and Electric Potential in the Plasma
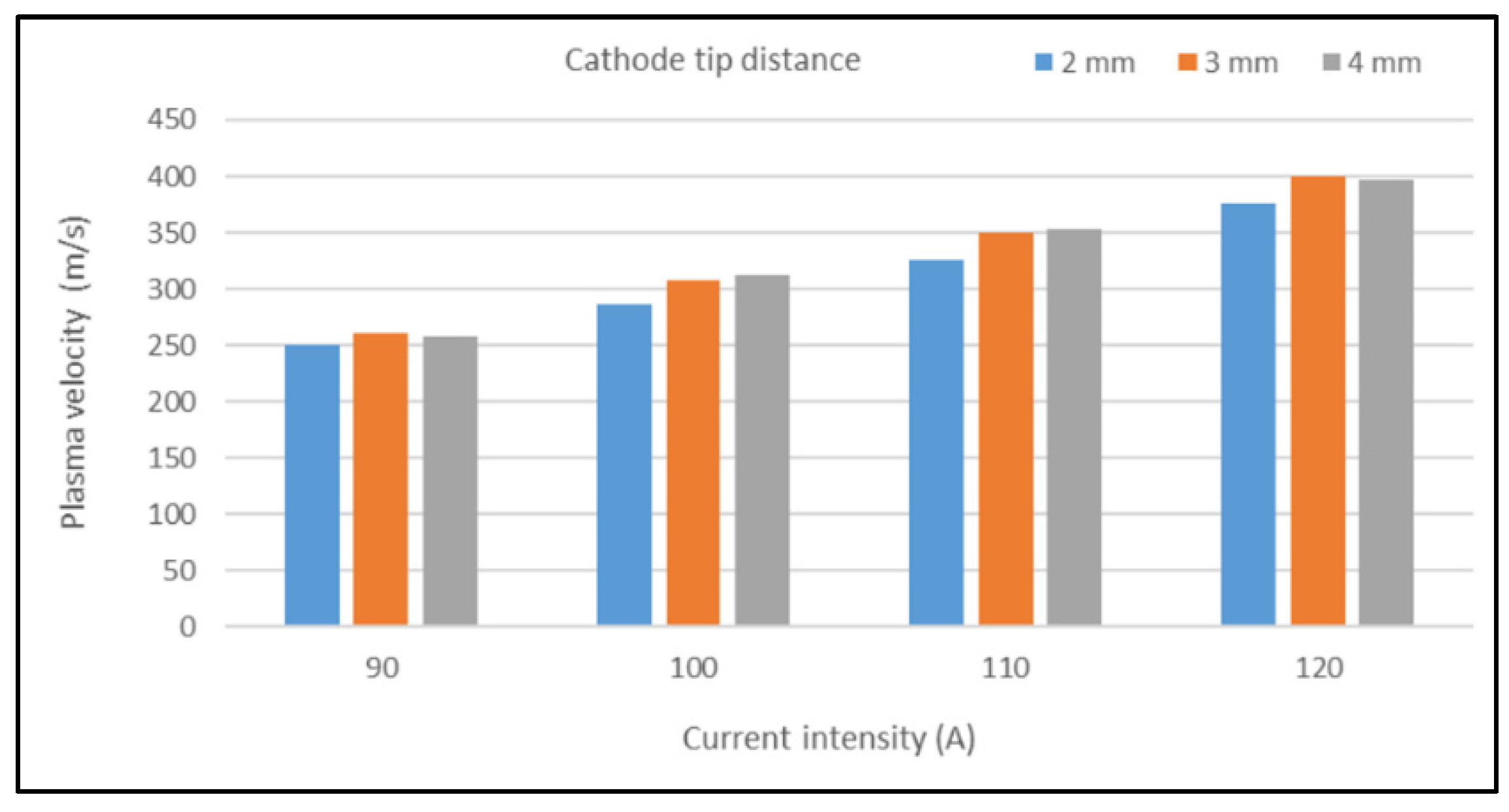
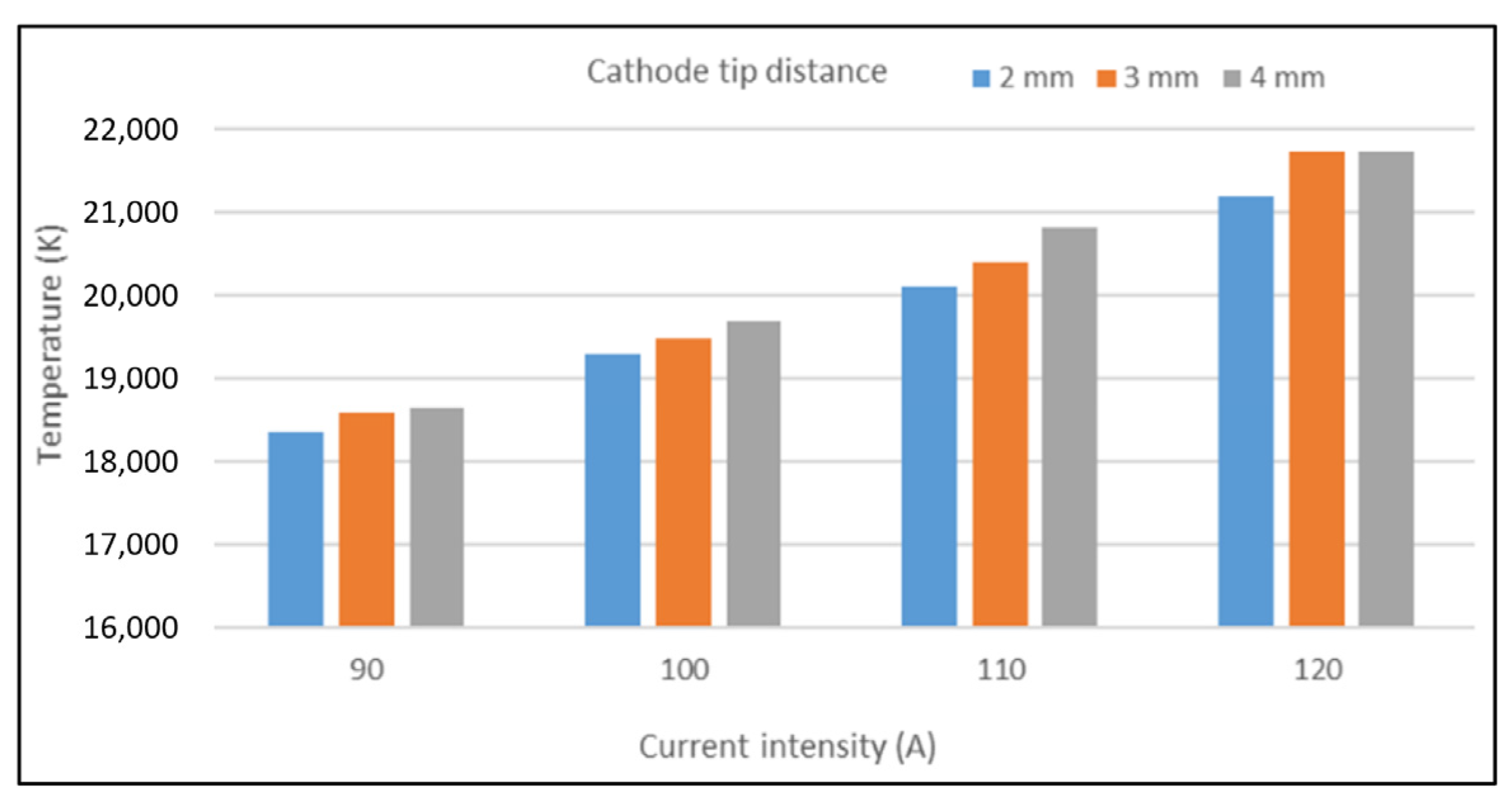
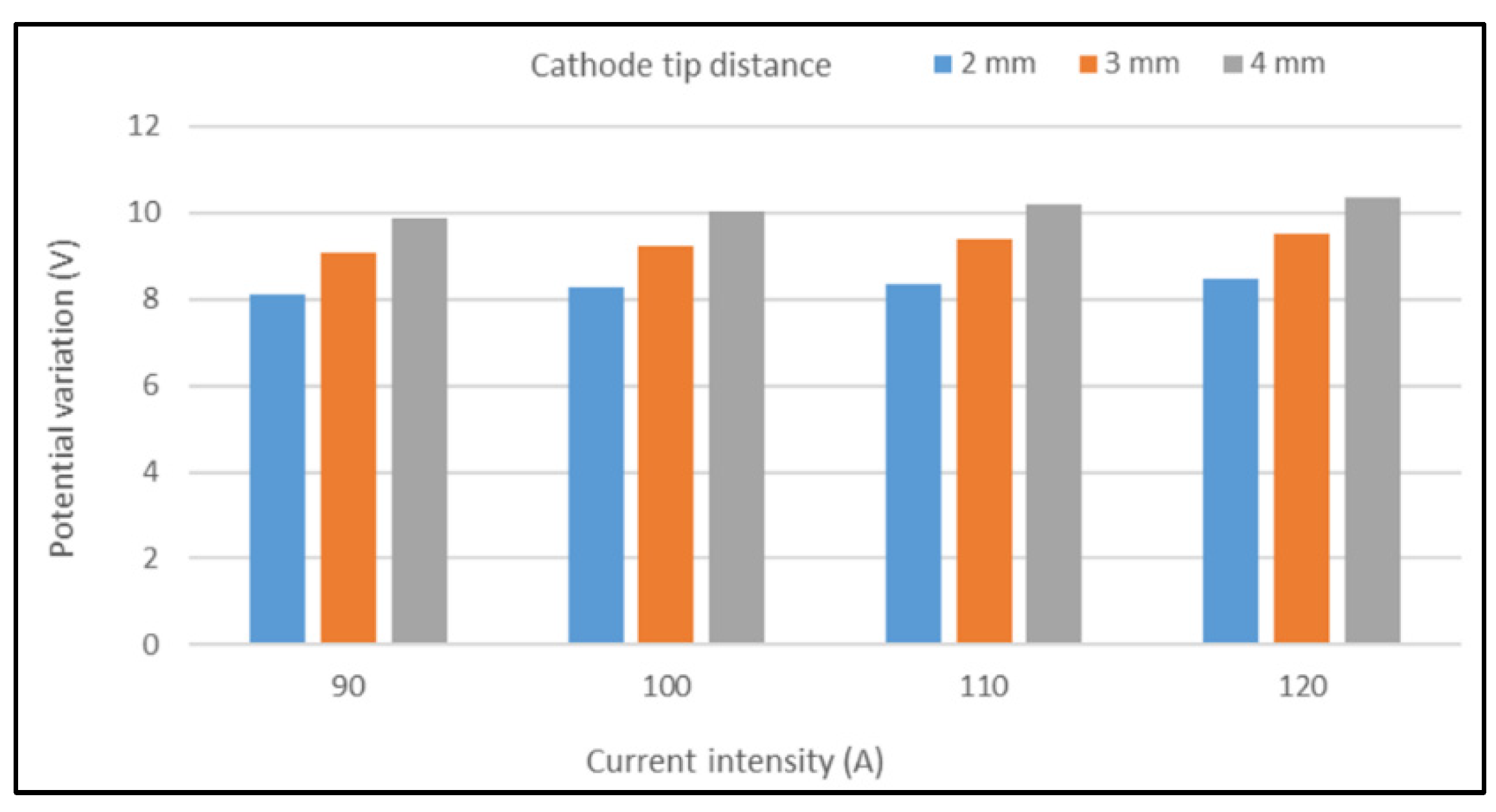
4.4. A Parametric Study of the Welding Operating Parameters
5. Conclusions
- -
- The two additional coupling equations were solved in both fluid and solid regions, including the cathode as a part of the computational domain;
- -
- A new method was implemented for linearization of the Joule heating term in the energy conservation equation;
- -
- This method improves the convergence of the solving procedure (Section 3.2) and makes it possible to attain values closer to the real physical phenomena;
- -
- This method also allows the arc to be maintained without the need for artificial conductibility anywhere in the domain (especially in near wall regions);
- -
- Finally, the adopted numerical procedure improves the convergence and stability during the calculation of electromagnetic couplings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Tashiro, S.; Tanaka, M.; Murphy, A.B. Numerical analysis of non-equilibrium plasma property in anode boundary layer of argon Gas Tungsten Arc. Surf. Coat. Technol. 2010, 205, S115–S119. [Google Scholar] [CrossRef]
- Dal, M.; Fabbro, R. An overview of the state of art in laser welding simulation. Opt. Laser Technol. 2016, 78, 2–14. [Google Scholar] [CrossRef]
- Brickstad, B.; Josefson, B.L. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes. Int. J. Press. Vessel. Pip. 1998, 75, 11–25. [Google Scholar] [CrossRef]
- Capriccioli, A.; Frosi, P. Multipurpose ANSYS FE procedure for welding processes simulation. Fusion Eng. Des. 2009, 84, 546–553. [Google Scholar] [CrossRef]
- Mousavi, A.; Miresmaeili, R. Experimental and numerical analyses of residual stress distributions in TIG welding process for 304L stainless steel. J. Mater. Process. Technol. 2008, 208, 383–394. [Google Scholar] [CrossRef]
- Lundbäck, A.; Alberg, H.; Henrikson, P. Simulation and validation of TIG-Welding and Post Weld Heat Treatment of an Inconel 718 Plate. In Proceedings of the Seventh International Seminar Numerical Analysis of Weldability, Graz, Austria, 29 September–1 October 2003. [Google Scholar]
- Honggang, D.; Hongming, G.; Lin, W. Numerical simulation of fluid flow and temperature field in keyhole double-sided arc welding process on stainless steel. Int. J. Numer. Methods Eng. 2006, 65, 1673–1687. [Google Scholar] [CrossRef]
- Zhan, X.; Zhang, Q.; Wang, Q.; Chen, J.; Liu, H.; Wei, Y. Numerical simulation of flow field in the Invar alloy laser-MIG hybrid welding pool based on different heat source models. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 909–926. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, Y.; Zhan, X.; Chen, J.; Li, H.; Wang, Y. Numerical simulation of keyhole behaviors and droplet transfer in laser-MIG hybrid welding of Invar alloy. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1974–1993. [Google Scholar] [CrossRef]
- Tchoumi, T.; Peyraut, F.; Bolot, R. Influence of the welding speed on the distortion of thin stainless steel plates—Numerical and experimental investigations in the framework of the food industry machines. J. Mater. Process. Technol. 2016, 229, 216–229. [Google Scholar] [CrossRef]
- Dupont, J.N.; Marder, A.R. Thermal Efficiency of Arc Welding Processes. Weld. Res. Suppl. 1995, 74, 406s–416s. [Google Scholar]
- Lu, S.; Fujii, H.; Nogi, K. Arc ignitability, bead protection and weld shape variations for He–Ar–O2 shielded GTA welding on SUS304 stainless steel. J. Mater. Process. Technol. 2009, 209, 1231–1239. [Google Scholar] [CrossRef]
- Arunkumar, V.; Vasudevan, M.; Maduraimuthu, V.; Muthupandi, V. Effect of activated flux on the microstructure and mechanical properties of 9Cr-1Mo steel weld joint. Mater. Manuf. Process. 2012, 27, 1171–1177. [Google Scholar] [CrossRef]
- Lin, H.L.; Wu, T.M. Effects of activating flux on weld bead geometry of Inconel 718 alloy TIG welds. Mater. Manuf. Process. 2012, 27, 1457–1461. [Google Scholar] [CrossRef]
- Venkatesan, G.; George, J.; Sowmyasri, M.; Muthupandi, V. Effect of Ternary Fluxes on Depth of Penetration in A-TIG Welding of AISI 409 Ferritic Stainless Steel. Procedia Mater. Sci. 2014, 5, 2402–2410. [Google Scholar] [CrossRef]
- Dal, M.; Le Masson, P.; Carin, M. A model comparison to predict heat transfer during spot GTA welding. Int. J. Therm. Sci. 2014, 75, 54–64. [Google Scholar] [CrossRef][Green Version]
- Zhu, P.; Lowke, J.J.; Morrow, R. A unified theory of free burning arcs, cathode sheaths and cathodes. J. Phys. D Appl. Phys. 1992, 25, 1221–1230. [Google Scholar] [CrossRef]
- Lowke, J.J.; Morrow, R.; Haidar, J. A simplified unified theory of arcs and their electrodes. J. Phys. D Appl. Phys. 1997, 30, 2033–2042. [Google Scholar] [CrossRef]
- Yamamoto, K.; Tanaka, M.; Tashiro, S.; Nakata, K.; Yamazaki, K.; Yamamoto, E.; Suzuki, K.; Murphy, A.B. Numerical simulation of metal vapor behavior in arc plasma. Surf. Coat. Technol. 2008, 202, 5302–5305. [Google Scholar] [CrossRef]
- Tanaka, M.; Yamamoto, K.; Tashiro, S.; Nakata, K.; Ushio, M.; Yamazaki, K.; Yamamoto, E.; Suzuki, K.; Murphy, A.B.; Lowke, J.J. Metal vapour behavior in gas tungsten arc thermal plasma during welding. Weld. World 2008, 52, 82–88. [Google Scholar] [CrossRef]
- Murphy, A.B.; Tanaka, M.; Yamamoto, K.; Tashiro, S.; Lowke, J.J.; Ostriko, V.K. Modelling of arc welding: The importance of including the arc plasma in the computational domain. Vacuum 2010, 85, 579–584. [Google Scholar] [CrossRef]
- Mougenot, J.; Gonzalez, J.-J.; Freton, P.; Masquere, M. Plasma–weld pool interaction in tungsten inert-gas configuration. J. Phys. D Appl. Phys. 2013, 46, 135206. [Google Scholar] [CrossRef]
- Traidia, A.; Roger, F.; Guyot, E. Optimal parameters for pulsed gas tungsten arc welding in partially and fully penetrated weld pools. Int. J. Therm. Sci. 2010, 49, 1197–1208. [Google Scholar] [CrossRef]
- Traidia, A.; Roger, F. Numerical and experimental study of arc and weld pool behaviour for pulsed current GTA welding. Int. J. Heat Mass Transf. 2011, 54, 2163–2179. [Google Scholar] [CrossRef]
- Hsu, K.C.; Etemadi, K.; Pfender, E. Study of the free-burning high-intensity argon arc. J. Appl. Phys. 1983, 54, 1293–1301. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Kleijn, C.R.; Richardson, I.M. A simulation-based approach to characterise melt-pool oscillations during gas tungsten arc welding. Int. J. Heat Mass Transf. 2021, 164, 120535. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Kleijn, C.R.; Hermans, M.J.M.; Richardson, I.M. The effects of process parameters on melt-pool oscillatory behaviour in gas tungsten arc welding. J. Phys. D Appl. Phys. 2021, 54, 275303. [Google Scholar] [CrossRef]
- Goodarzi, M.; Choo, R.; Toguri, J.M. The effect of the cathode tip angle on the GTAW arc and weld pool: I. Mathematical model of the arc. J. Phys. D Appl. Phys. 1997, 30, 2744–2756. [Google Scholar] [CrossRef]
- Li, L.; Li, B.; Liu, L.; Motoyama, Y. Numerical Modeling of Fluid Flow, Heat Transfer and Arc–Melt Interaction in Tungsten Inert Gas Welding. High Temp. Mater. Proc. 2017, 36, 427–439. [Google Scholar] [CrossRef]
- Griem, H.R. Validity of Local Thermal Equilibrium in Plasma Spectroscopy. Phys. Rev. 1963, 131, 1170–1176. [Google Scholar] [CrossRef]
- Boulos, M.I.; Fauchais, P.; Pfender, E. Thermal Plasmas: Fundamentals and Applications; Plenum Press: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Bolot, R.; Coddet, C.; Allimant, A.; Billieres, D. Modeling of the Plasma Flow and Anode Region Inside a Direct Current Plasma Gun. J. Therm. Spray Technol. 2011, 20, 21–27. [Google Scholar] [CrossRef]
- Nahed, C.; Gounand, S.; Medale, M. A numerical study of the effects of cathode geometry on tungsten inert gas type electric arcs. Int. J. Heat Mass Transf. 2022, 182, 121923. [Google Scholar] [CrossRef]
- Bolot, R.; Li, J.; Coddet, C. Some Key Advices for the Modeling of Plasma Jets using FLUENT, Thermal Spray connects: Explore its surfacing potential. In Proceedings of the International Thermal Spray Conference, Basel, Switzerland, 2–4 May 2005. [Google Scholar]
- Baudry, C. Contribution à la Modélisation Instationnaire et Tridimensionnelle du Comportement Dynamique de L’arc Dans une Torche de Projection Plasma. Ph.D. Thesis, Université de Limoges, Limoges, France, 2003. [Google Scholar]
- Brochard, M. Modèle Couplé Cathode-Plasma-Pièce en Vue de la Simulation du Procédé de Soudage à L’arc TIG. Ph.D. Thesis, IUSTI de L’école Polytechnique Universitaire de Marseille, Marseille, France, 2009. [Google Scholar]
- Lancaster, J.F. The Physics of Welding, 2nd ed.; Oxford Pergamon: Oxford, UK, 1986. [Google Scholar]
- Lago, F.; Gonzalez, J.J.; Freton, P.; Gleizes, A. A numerical modelling of an electric arc and its interaction with the anode: Part I. The two-dimensional model. J. Phys. D Appl. Phys. 2004, 37, 883–897. [Google Scholar] [CrossRef]
- Wilbers, A.T.M.; Beulens, J.J.; Schram, D.C. Radiative energy loss in a two-temperature argon plasma. J. Quant. Spectrosc. Radiat. Transf. 1991, 46, 385–392. [Google Scholar] [CrossRef]
- Sanders, N.A.; Pfender, E. Measurement of anode falls and anode heat transfer in atmospheric pressure high intensity arcs. J. Appl. Phys. 1984, 55, 714–722. [Google Scholar] [CrossRef]
- Dunn, G.J.; Allemand, C.D.; Eagar, T.W. Metal Vapors in Gas Tungsten Arcs: Part I. Spectroscopy and Monochromatic Photography. Metall. Mater. Trans. A 1986, 17, 1851–1863. [Google Scholar] [CrossRef]
- Ushio, M.; Tanaka, M.; Wu, C.S. Analytical Approach to Anode Boundary Layer of Gas Tungsten Arcs. Trans. JWRI 1996, 25, 9–21. [Google Scholar]
- Wu, C.S.; Gao, J.Q. Analysis of the heat flux distribution at the anode of a TIG welding arc. Comput. Mater. Sci. 2002, 24, 323–327. [Google Scholar] [CrossRef]
- Zhu, P.; Lowke, J.J.; Morrow, R.; Haidar, J. Prediction of anode temperatures of free burning arcs. J. Phys. D Appl. Phys. 1995, 28, 1369–1376. [Google Scholar] [CrossRef]
- ISO 14175:2008; Welding Consumables–Gases and Gas Mixtures for Fusion Welding and Allied Processes. ISO: Geneva, Switzerland, 2008.
- Tanaka, M.; Terasaki, H.; Ushio, M.; Lowke, J.J. A Unified Numerical Modeling of Stationary Tungsten-Inert-Gas Welding Process. Metall. Mater. Trans. A 2002, 33, 2043–2052. [Google Scholar] [CrossRef]
- Choo, R.T.C.; Szekely, J.; Westhoff, R.C. On the Calculation of the Free Surface Temperature of Gas-Tungsten-Arc Weld Pools from First Principles: Part I. Modeling the Welding Arc. Metall. Trans. B 1992, 23, 357–369. [Google Scholar] [CrossRef]
- Tetyana, K. Study of Thermal Plasma Jets Generated by DC Arc Plasma Torches Used in Plasma Spraying Applications. Ph.D. Thesis, Charles University in Prague, Faculty of Mathematics and Physics, Prague, Czech Republic, 2006. [Google Scholar]

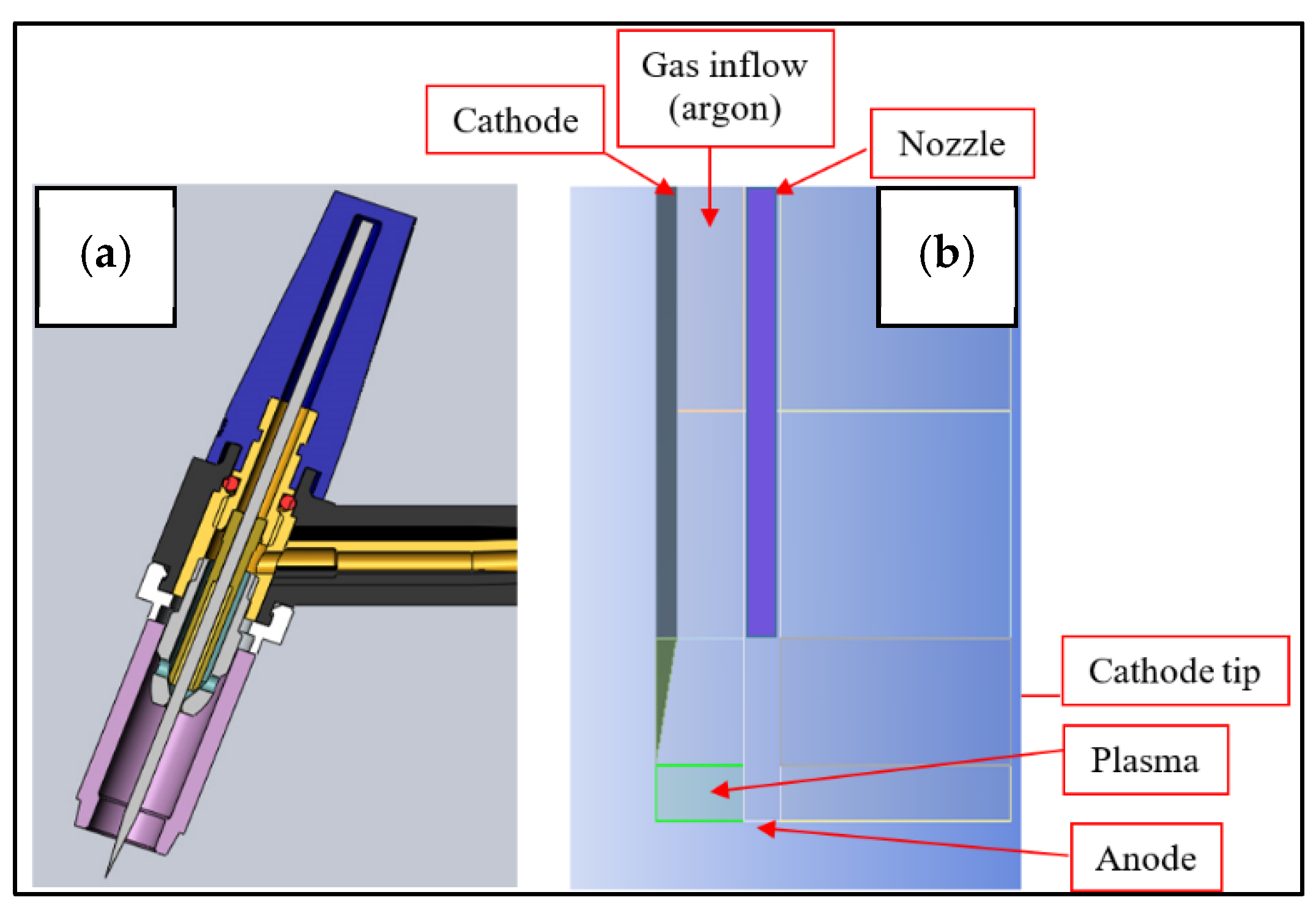

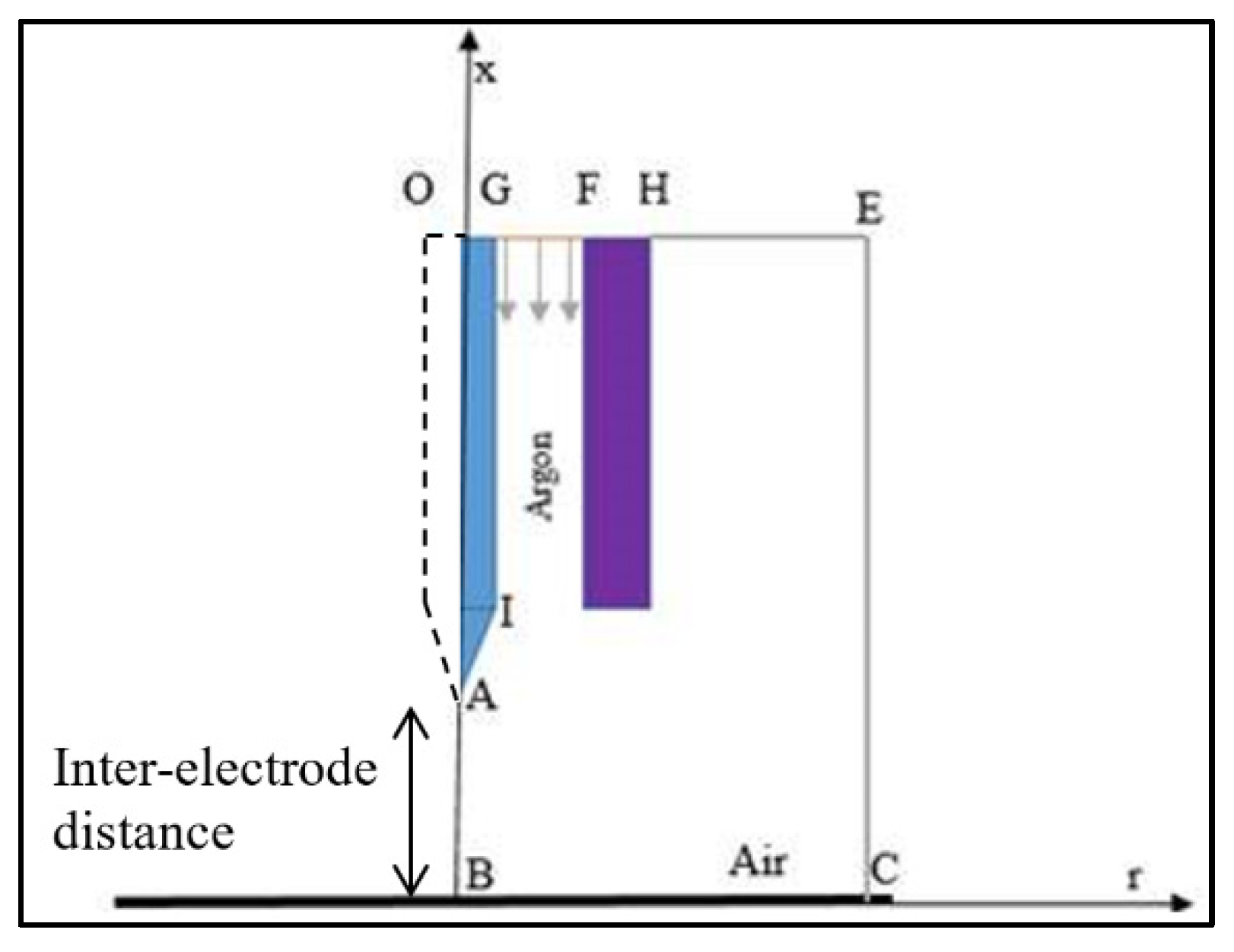


| Plasma: (AB) | Anode: (BC) | Ambient Air: (CE) and (HE) | Gas Inlet: (GF) | Cathode Inlet: (OG) | Cathode Tip: (AI) | |
|---|---|---|---|---|---|---|
| : axial plasma velocity | ||||||
| radial plasma velocity | ||||||
| : temperature | 288 K | 288 K if incoming | 288 K | Solid-fluid coupling | ||
| : electric potential | Solid-fluid coupling | |||||
| : axial component of the magnetic potential vector | Solid-fluid coupling | |||||
| : argon mass fraction | if incoming |
| Inter-Electrode Distance | Current Intensity | ||||
|---|---|---|---|---|---|
| 90 A | 100 A | 110 A | 120 A | ||
| 2 mm | 8 L/min | 8 L/min | 8 L/min | 8 L/min | |
| 10 L/min | 10 L/min | 10 L/min | 10 L/min | ||
| 12 L/min | 12 L/min | 12 L/min | 12 L/min | ||
| 3 mm | 8 L/min | 8 L/min | 8 L/min | 8 L/min | |
| 10 L/min | 10 L/min | 10 L/min | 10 L/min | Argon flow rate | |
| 12 L/min | 12 L/min | 12 L/min | 12 L/min | ||
| 4 mm | 8 L/min | 8 L/min | 8 L/min | 8 L/min | |
| 10 L/min | 10 L/min | 10 L/min | 10 L/min | ||
| 12 L/min | 12 L/min | 12 L/min | 12 L/min | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tchoumi, T.; Peyraut, F.; Bolot, R. Electromagnetic–Computational Fluid Dynamics Couplings in Tungsten Inert Gas Welding Processes—Development of a New Linearization Procedure for the Joule Production Term. Appl. Mech. 2024, 5, 121-140. https://doi.org/10.3390/applmech5010008
Tchoumi T, Peyraut F, Bolot R. Electromagnetic–Computational Fluid Dynamics Couplings in Tungsten Inert Gas Welding Processes—Development of a New Linearization Procedure for the Joule Production Term. Applied Mechanics. 2024; 5(1):121-140. https://doi.org/10.3390/applmech5010008
Chicago/Turabian StyleTchoumi, Thierry, François Peyraut, and Rodolphe Bolot. 2024. "Electromagnetic–Computational Fluid Dynamics Couplings in Tungsten Inert Gas Welding Processes—Development of a New Linearization Procedure for the Joule Production Term" Applied Mechanics 5, no. 1: 121-140. https://doi.org/10.3390/applmech5010008
APA StyleTchoumi, T., Peyraut, F., & Bolot, R. (2024). Electromagnetic–Computational Fluid Dynamics Couplings in Tungsten Inert Gas Welding Processes—Development of a New Linearization Procedure for the Joule Production Term. Applied Mechanics, 5(1), 121-140. https://doi.org/10.3390/applmech5010008





