Comparative Studies between Frequency Domain Analysis and Time Domain Analysis on Free-Field One-Dimensional Shear Wave Propagation
Abstract
1. Introduction
- Stress distribution in rocks around underground silo, published in Ref. [4].
- Silo concrete linings subjected to residual water pressure, published in Ref. [19].
- The 3D silo dynamic analyses subjected to earthquake loads, in preparation.
- Closed-form solutions (SHAKE, SHAKE91, DEEPSOIL, etc.) in the frequency domain are available for one-dimensional shear wave propagation in the linearly viscous elastic system subjected to base accelerations.
- Numerical finite element solutions as the time domain analysis can be directly compared to such closed-form solutions in the free fields including the lateral boundary so that we can assess the accuracy of numerical solutions.
2. Linear Frequency Domain Analysis
2.1. Main Algorithm of the Frequency Domain Analysis
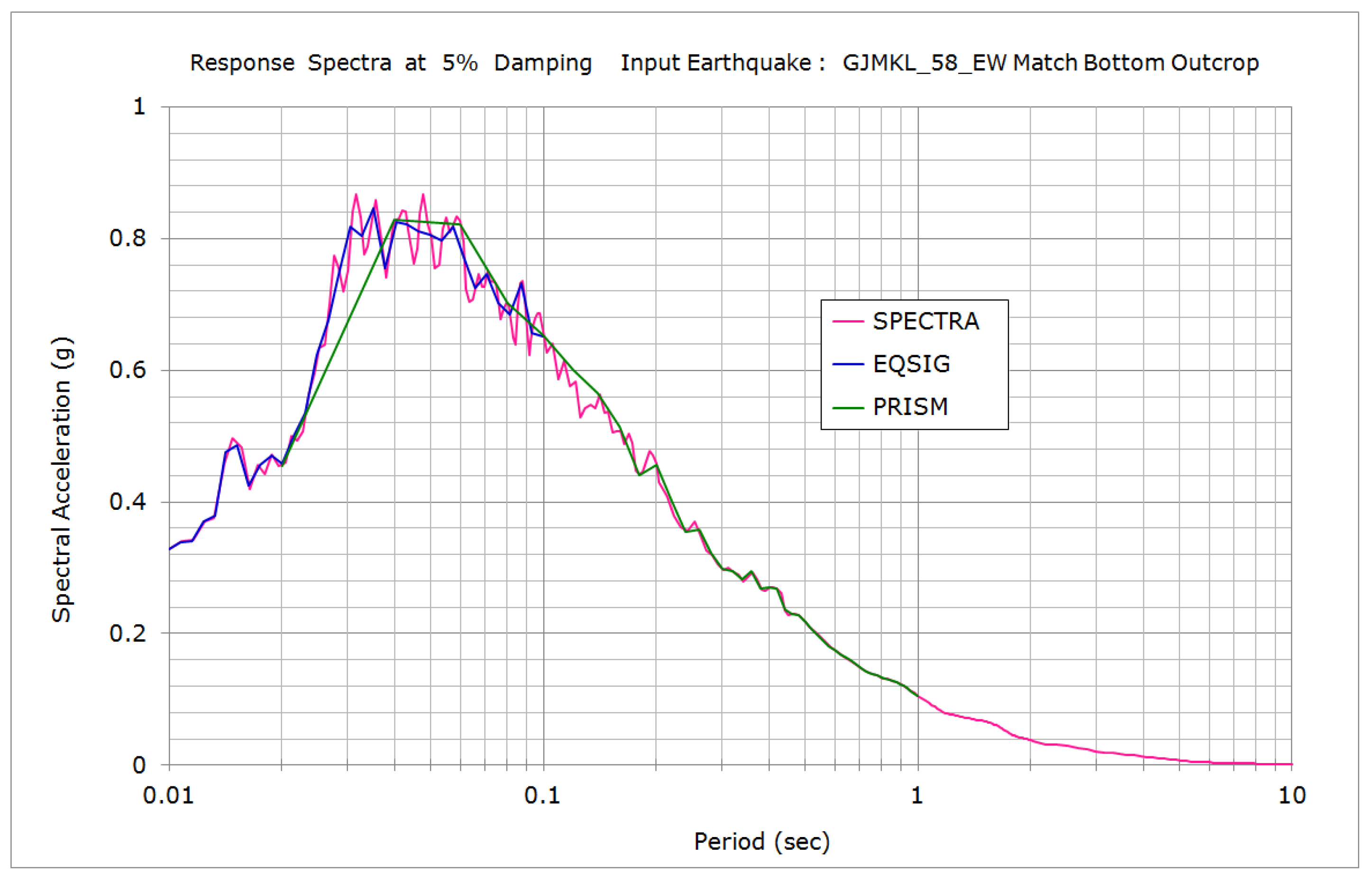
2.2. Site Profile and Response Spectra for Input Earthquake
2.3. Analysis Results
3. Linear Time Domain Analysis
3.1. Finite Element Formulations of Dynamic Equation
3.2. Computer Programs for Free-Field Analysis
- Lumped mass matrix as implicitly used by the frequency domain analysis.
- Transmitting boundary on the bottom of the finite element mesh for the elastic half-space.
- Two methods for applying external earthquake loadings [18].
- The Newmark average acceleration method for the time integration.
3.3. Analysis Results
4. Linear Frequency vs. Linear Time Domain Analysis
4.1. General
4.2. Analysis Results
5. Conclusions
- Closed-form solutions (SHAKE, SHAKE91, DEEPSOIL, etc.) in the frequency domain are available for one-dimensional shear wave propagation in the linearly viscous elastic system subjected to base accelerations.
- Numerical finite element solutions as the time domain analysis can be directly compared to such closed-form solutions in the free fields including lateral boundary so that we can assess the accuracy of numerical solutions.
- (1)
- Two computer programs (SHAKE91 and DEEPSOIL) are selected for the closed-form solutions in the frequency domain. The acceleration time histories on the ground surface which compare SHAKE91 to DEEPSOIL show almost identical responses in the time where strong motions occur. The acceleration time histories at the location of the silo mid-height show also almost identical responses in the time where strong motions occur.
- (2)
- One modal analysis (SRAP-1D) and two finite element computer programs (QUAD-4M, and SMAP-3D) are selected to perform the free-field analysis in the time domain. The acceleration time histories on the ground surface which compare the results of all three computer programs show almost identical responses in the time where strong motions occur. It also shows that Method 1, the conventional procedure, produces almost the same results as Method 2. The acceleration time histories at the location of the silo mid height which compare QUAD-4M to SMAP-3D show almost identical responses in the time where strong motions occur.
- (3)
- SMAP-3D time domain solutions are compared to the exact closed-form frequency domain SHAKE91 solutions for the analysis of free-field responses subjected to vertically propagating shear waves caused by earthquake motions. As a result of comparing SMAP-3D with γ = 0.5 and SHAKE91 to the acceleration time histories on the ground surface, SMAP-3D results show somewhat higher responses in the time where strong motions occur. SMAP-3D results at the location of the silo mid height are closer to SHAKE91 results than we see in those comparisons on the ground surface.
- (4)
- Compared to SHAKE91, SMAP-3D with γ = 1.0 results show significantly damped responses in the time where strong motions occur to the acceleration time histories on the ground surface. Compared to SHAKE91, SMAP-3D results show also moderately damped responses in the time where strong motions occur to the acceleration time histories at the location of the silo mid height.
- (5)
- For the relative displacement time histories on the ground surface, SMAP-3D with γ = 0.5 and γ = 1 results show closer to SHAKE91 results than we see in those comparisons for acceleration histories. It is also noticed that the effect of numerical damping is less significant in the relative displacements. Compared to SHAKE91, SMAP-3D with γ = 0.5 and γ = 1 results in the relative displacement time histories at the location of the silo mid height show the same trends as at the ground surface. Here, also, the numerical damping has a slight influence on the response of relative displacements.
- (6)
- SMAP-3D calculation with numerical damping of γ = 1 to the shear stress time histories at the location of the silo mid height predicts reasonably well SHAKE91 closed-form results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aikas, T.; Anttila, P. Repositories for low- and intermediate-level radioactive wastes in Finland. Rev. Eng. Geol. 2008, 19, 67–71. [Google Scholar] [CrossRef]
- KORAD. Earth & Us; Korea Radioactive Waste Agency: Gyeongju, Republic of Korea, 2018. [Google Scholar]
- Shin, Y.; Lee, J. The status and experiences of LILW disposal facilities construction. J. Korean Soc. Miner Energy Resour. Eng. 2017, 54, 389–396. (In Korean) [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, K.J. Numerical parametric studies on the stress distribution in rocks around underground silo. Appl. Sci. 2022, 12, 1613. [Google Scholar] [CrossRef]
- Park, J.B.; Jung, H.R.; Lee, E.Y.; Kim, C.L.; Kim, G.Y.; Kim, K.S.; Koh, Y.K.; Park, K.W.; Cheong, J.H.; Jeong, C.W.; et al. Wolsong low- and intermediate-level radioactive waste disposal center: Progress and challenges. Nucl. Eng. Techno. 2009, 41, 477–492. [Google Scholar] [CrossRef]
- Bang, J.H.; Park, J.H.; Jung, K.I. Development of two-dimensional near-field integrated performance assessment model for near-surface LILW disposal. J. Nucl. Fuel Cycle Waste Tech. 2014, 12, 315–334. [Google Scholar] [CrossRef]
- Jung, K.I.; Kim, J.H.; Kwon, M.J.; Jeong, M.S.; Hong, S.W.; Park, J.B. Comprehensive development plans for the low- and intermediate-level radioactive waste disposal facility in Korea and preliminary safety assessment. J. Nucl. Fuel Cycle Waste Tech. 2016, 14, 385–410. [Google Scholar] [CrossRef]
- Kim, K.H.; Ree, J.H.; Kim, Y.H.; Kim, S.S.; Kang, S.Y.; Seo, W.S. Assessing whether the 2017 Mw 5.4 Pohang earthquake in South Korea was an induced event. Science 2018, 360, 1007–1009. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.; Lee, J.; Lee, K.; Kyung, J.B.; Kim, Y.S. Earthquake damage and related factors associated with the 2016 ML=5.8 Gyeonju earthquake, southeast Korea. Geosci. J. 2020, 24, 141–157. [Google Scholar] [CrossRef]
- Kim, M.K.; Choi, I.K.; Jeong, J. Development of a seismic risk assessment system for low and intermediate level radioactive waste repository—Current status of year 1 research. In Proceedings of the WM2011 Conference, Phoenix, AZ, USA, 3 March 2011. [Google Scholar]
- Byen, H.; Jeong, G.Y.; Park, J. Structural stability analysis of waste packages containing low- and intermediate-level radioactive waste in a silo-type repository. Nucl. Eng. Techno. 2021, 53, 1524–1533. [Google Scholar] [CrossRef]
- Byeon, H.; Park, J.; Kim, B. Seismic analysis of waste packages stacked in radioactive waste disposal silos. Tunn. Undergr. Sp. Tech. 2023, 140, 105287. [Google Scholar] [CrossRef]
- Mansour, S.; Pieraccini, L.; Foti, D.; Gasparini, G.; Trombetti, T.; Silvestri, S. Comprehensive review on the dynamic and seismic behavior of flat-bottom cylindrical silos filled with granular material. Front. Built Environ. 2022, 7, 2021. [Google Scholar] [CrossRef]
- Foti, D.; Trombetti, T.; Silvestri, S.; Chiacchio, L.; Ivorra, S.; Taylor, C.; Dietz, M. Analysis of the dynamic behavior of squat silos containing grain-like material subjected to shaking table tests-ASESGRAM final report. In Experimental Research in Earthquake Engineering; Taucer, F., Apostolska, R., Eds.; Springer: Cham, Switzerland, 2015; Volume 35. [Google Scholar] [CrossRef]
- Mansour, S.; Silvestri, S.; Sadowski, A.J. The ‘miniature silo’ test; A simple experimental setup to estimate the effective friction coefficient between the granular solid and a horizontally-corrugated cylindrical metal silo wall. Powder Technol. 2022, 399, 117212. [Google Scholar] [CrossRef]
- Dongangun, A.; Karaca, Z.; Durmus, A.; Sezen, H. Cause of damage and failures in silo structures. J. Perform. Constr. Facil. 2009, 23, 65–71. [Google Scholar] [CrossRef]
- Younan, A.H.; Veletsos, A.S. Dynamics of solis-containing tanks. I: Rigid tanks. J. Struct. Eng. 1998, 124, 52–61. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, K.J. Finite element formulations for free field one-dimensional shear wave propagation. Earthquakes Struct. 2024, 26, 163–174. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, K.J. Numerical Study of Structural Behavior of Underground Silo Structures for Low-and-Intermediate-level Radioactive Waste Disposal Facility. J. Comput. Struct. Eng. Inst. Korea 2022, 35, 183–190. (In Korean) [Google Scholar] [CrossRef]
- Idriss, I.M.; Sun, J.I. User’s Manual for SHAKE91: A Computer Program for Conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits; Center for Geotechnical Modeling, Department of Civil & Environmental Engineering, University of California: Davis, CA, USA, 1992. [Google Scholar]
- Hashash, Y.M.A.; Musgrove, M.I.; Harmon, J.A.; Ilhan, O.; Xing, G.; Numanoglu, O.; Groholski, D.R.; Phillips, C.A.; Park, D. DEEPSOIL 7, User Manual; Board of Trustees of University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2020. [Google Scholar]
- Idriss, I.M.; Seed, H.B. Response of Horizontal Soil Layers During Earthquakes; Research Report; Soil Mechanics and Bituminous Materials Laboratory, University of California: Berkeley, CA, USA, 1967. [Google Scholar]
- Hudson, M.; Idriss, I.M.; Beikae, M. User’s Manual for QUAD4M: A Computer Program to Evaluate the Seismic Response of Soil Structures Using Finite Element Procedures and Incorporating a Compliant Base; University of California: Davis, CA, USA, 1994. [Google Scholar]
- Comtec Research. SMAP-3D; Structure Medium Analysis Program, User’s Manual Version 7.03; Comtec Research: Seattle, WA, USA, 2020. [Google Scholar]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE—A Computer Program for Earthquake Response Analysis of Horizontal Layered Sites; Report. No. EERC 71-12; Earthquake Engineering Research Center: Berkeley, CA, USA, 1972. [Google Scholar]
- Ordonez, G.A. SHAKE2000: A Computer Program for the 1-D Analysis of Geotechnical Earthquake Engineering Problems; Geomotion, LLC: Lacey, WA, USA, 2012. [Google Scholar]
- McCallen, D.B. SPECTRA: A Subroutine for Response Spectra Generation; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1991. [Google Scholar]
- Millen, M. EQSIG; A Python Package for Seismic Signal Processing v1.2.10; Pypi. Python Package Repository. 2019. Available online: https://pypi.org/project/eqsig/ (accessed on 19 April 2021).
- Jeong, S.H.; Lee, K.H.; Jang, W.S. PRISM; A Program for seismic response analysis of SDOF system, Version 2.0.0; Department of Architectural Engineering, INHA University: Incheon, Republic of Korea, 2010. [Google Scholar]
- Rayleigh, J.; Lindsay, R. The Theory of Sound; Dover Publications, Inc.: Dover, DE, USA, 1945. [Google Scholar]
- Lai, C.G.; Rix, G.J. Simultaneous Inversion of Rayleigh Phase Velocity and Attenuation for Near-Surface Site Characterization; Report No. GIT-CEE/GEO-98-2; School of Civil and Environmental Engineering, Georgia Institute of Technology: Atlanta, GA, USA, 1988. [Google Scholar]
- Hudson, M. Behavior of Slopes and Earth Dams during Earthquakes. Ph.D. Thesis, University of California, Davis, DE, USA, 1994. [Google Scholar]




























| Name | Analysis Method | Modulus and Damping | Ref. |
|---|---|---|---|
| SHAKE91 | Frequency Domain (1D) | Strain Compatible Values | [20] |
| DEEPSOIL | Frequency Domain (1D) | Strain Compatible Values | [21] |
| SRAP-1D | Time Domain Modal (1D) | Compatible Values Based on Equivalent Uniform Strain | [22] |
| QUAD-4M | Time Domain FEM (2D) | Compatible Values Based on Equivalent Uniform Strain | [23] |
| SMAP-3D | Time Domain FEM (3D) | General Nonlinear Modulus Rayleigh Proportional Damping | [24] |
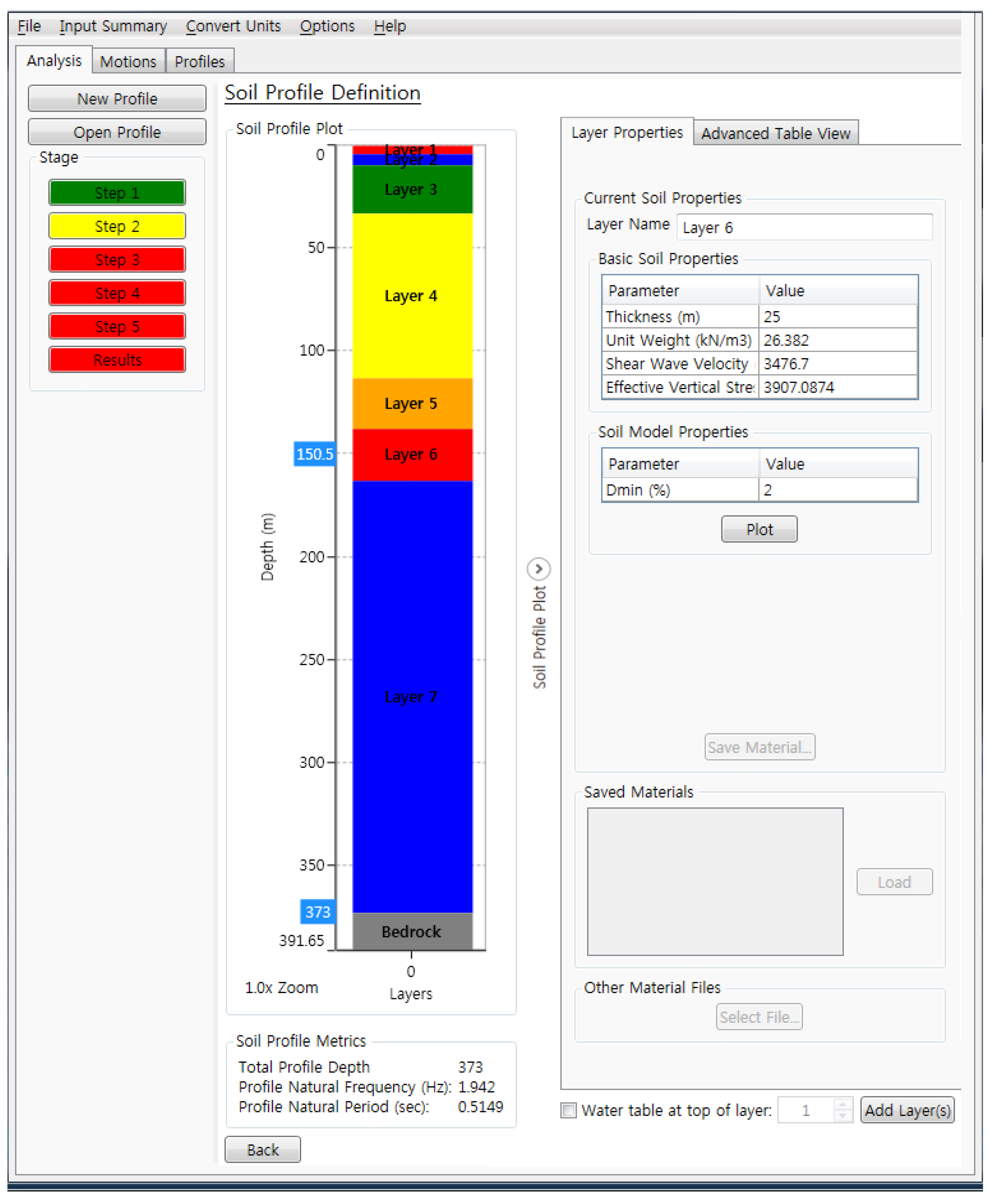
| Ground Layer | Unit Weight (kN/m3) | Shear Wave Velocity (m/s) | Damping Ratio (%) |
|---|---|---|---|
| Soil Layer | 18.63 | 495 | 5 |
| Weathered Rock | 20.59 | 792 | 5 |
| Medium Rock | 26.38 | 1500 | 3 |
| Hard Rock | 26.38 | 3477 | 2 |
| Elastic Half Space | 26.38 | 3607 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-H.; Kim, K.-J. Comparative Studies between Frequency Domain Analysis and Time Domain Analysis on Free-Field One-Dimensional Shear Wave Propagation. Appl. Mech. 2024, 5, 141-161. https://doi.org/10.3390/applmech5010009
Kim S-H, Kim K-J. Comparative Studies between Frequency Domain Analysis and Time Domain Analysis on Free-Field One-Dimensional Shear Wave Propagation. Applied Mechanics. 2024; 5(1):141-161. https://doi.org/10.3390/applmech5010009
Chicago/Turabian StyleKim, Sun-Hoon, and Kwang-Jin Kim. 2024. "Comparative Studies between Frequency Domain Analysis and Time Domain Analysis on Free-Field One-Dimensional Shear Wave Propagation" Applied Mechanics 5, no. 1: 141-161. https://doi.org/10.3390/applmech5010009
APA StyleKim, S.-H., & Kim, K.-J. (2024). Comparative Studies between Frequency Domain Analysis and Time Domain Analysis on Free-Field One-Dimensional Shear Wave Propagation. Applied Mechanics, 5(1), 141-161. https://doi.org/10.3390/applmech5010009





