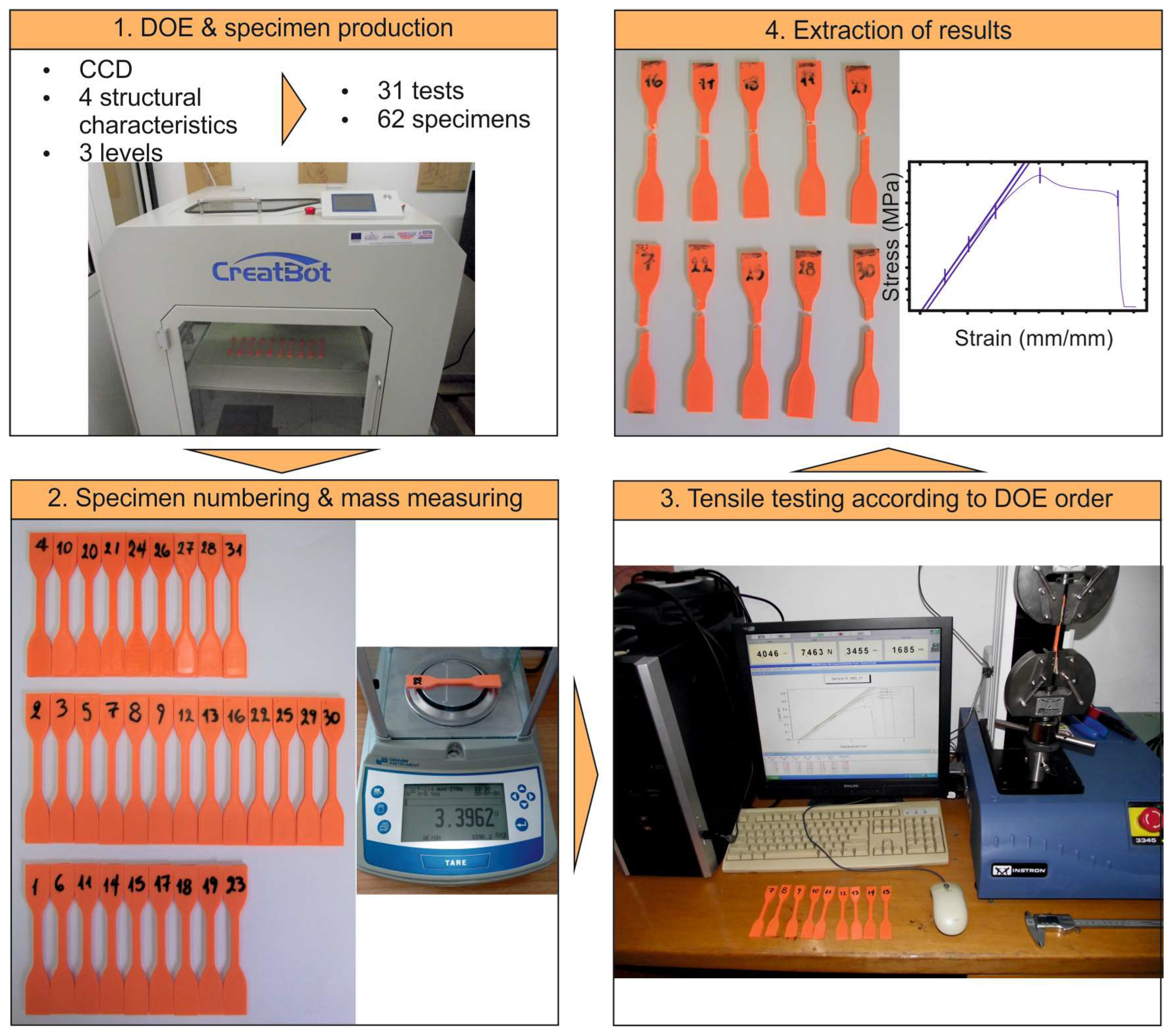
Before processing the output data, a set of magnified images of the specimens at the fracture point were taken.
Figure 4 illustrates the three different fracture lines developed during the tensile testing according to the layer line direction. By observing
Figure 4a, it is evident that the fracture line approximates a curve. However, the individual fractured layer lines indicate that they are perpendicular to the load. Moreover, this observation suggests that shearing is responsible for the weakening and, eventually, the fracturing of the lines, leading to the conclusion that the specific line direction allows for the delamination between layers. Similar findings were reported in [
9], as well.
Figure 4b indicates that due to the 45° layering, the fracture line follows a similar path, possibly causing the abruption of the layers. It is noted that the side layers forming the walls, which follow a perpendicular to the load pattern, fracture in a similar manner to the fracturing discussed in
Figure 4a. Finally,
Figure 4c illustrates the fracture line that developed on a specimen with layer lines deposited at 90°. Weakening marks (white areas) are evident on the side layer lines, which indicate that the load was applied perpendicular to the lines, as opposed to the central layer lines that did not fracture but rather were separated, possibly due to the bonding abruption. In addition, the preliminary results revealed that the best S/M ratio per factor was generated by the 0.3 mm layer thickness (7.12 MPa/g), 20% density (6.91 MPa/g), 0° layer line direction (7.15 MPa/g) and honeycomb pattern (6.74 MPa/g).
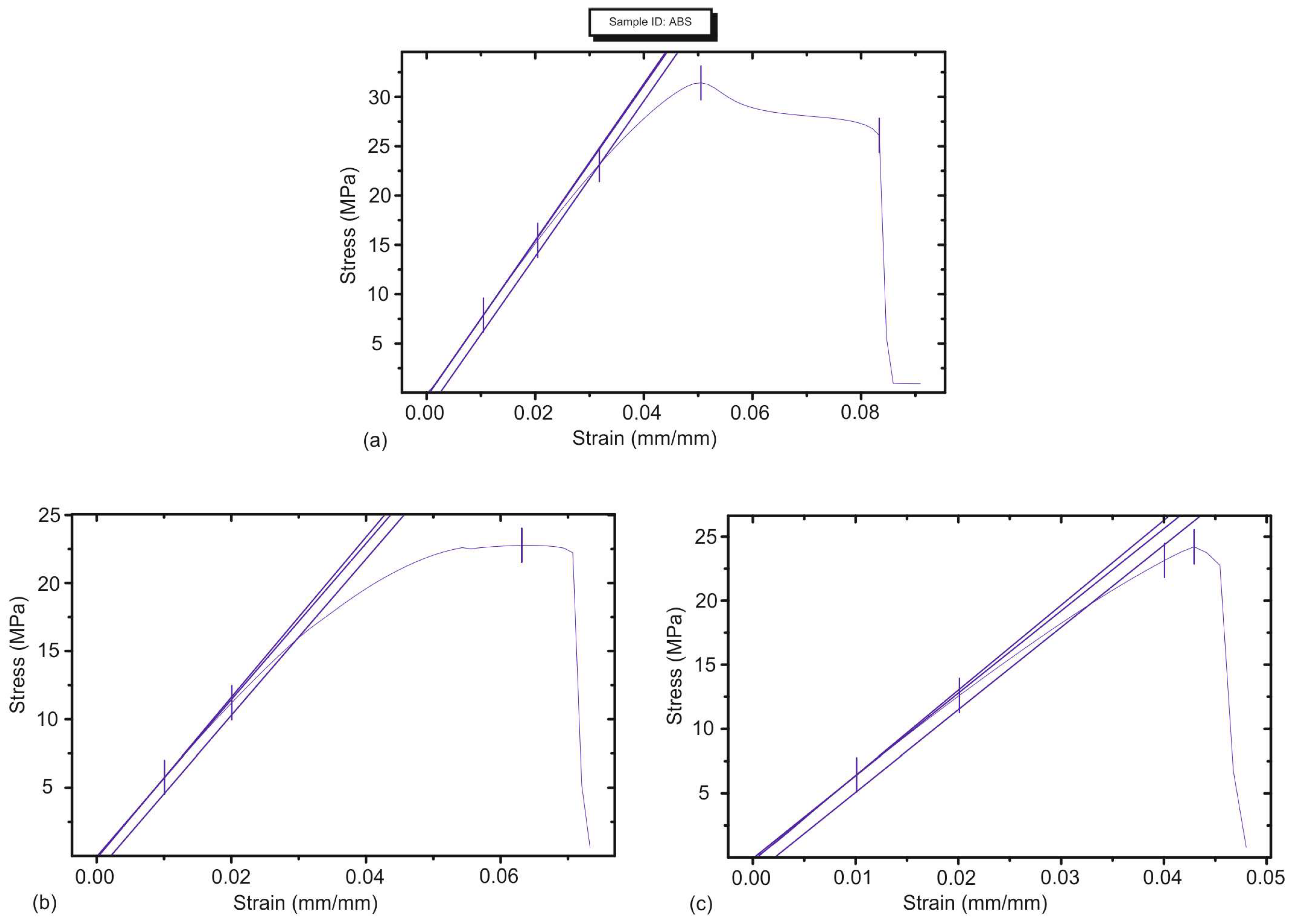
Regarding the direction of the top and bottom layer lines, it was found that it affected the generated stress–strain curve as well. A set of tests that belong to the preliminary study was carried out with specimens of identical parameters (LH = 0.1 mm, FD = 80% and FP = Grid), with the exception of the top/bottom line directions, to assess the generated curves. The 0° direction (
Figure 5a) yielded a curve pattern that included the elastic area where the linear relationship between the stress and strain exists. Additionally, it was observed that the plastic area is larger compared to the ones generated by the 45° (
Figure 5b) and 90° (
Figure 5c) directions. In particular, the 90° layer line angle was responsible for the development of a much smaller plastic area and a rapid fracture point in comparison to the other orientations. Similar findings were mentioned in [
19].
Finally, it should be noted that specimen No 12 was found to be the one with the lowest mass, i.e., 3.361 g. The specimen was built according to the following specifications: LH = 0.2 mm, FD = 20%, LD = 45°, and FP = triangles. The specimen with the highest UTS (32.13 MPa) was No 21, which was fabricated with an LH = 0.3 mm, FD = 80%, LD = 0° and FP = honeycomb. Additionally, specimen No 24 was the one with the highest S/M ratio, calculated as 8.57. It was built with an LH = 0.3 mm, FD = 20%, LD = 0° and FP = honeycomb.
3.2. Analysis and Model Validation
The Analysis of Variance (ANOVA) was carried out to examine the performance [
17] of the developed models in terms of the fit, variance, and prediction capabilities, as well as to check the contribution levels of the terms to the models. Moreover, the interactions between the reactive terms were identified.
Table 4 and
Table 5 contain the ANOVA results for the UTS and the S/M ratio, respectively, by employing a 0.05 confidence level. The calculated coefficient of determination (R-sq) values indicate a strong fit for both models. In addition, the adjusted and predicted values of the coefficient suggest that the model terms included in the models suffice and that the models can predict both the UTS and S/M ratio with increased reliability within the range of conditions of the study.
By examining the
p-values, it is shown that every term with a value lower than 0.05 is statistically significant, and thus, its contribution to the models is considerable. Every term included in
Table 4 and
Table 5 is significant since any high
p-value term was removed during the backward elimination process. In contrast, the remaining errors do not affect the reliability and robustness of the models. Lastly, it is noted that the terms LH × LD and LH × FP were maintained in the S/M ratio model because their
p-value is marginally higher than the significance level. Although they are not considered statistically significant, it was found that their presence in the model positively influenced the generated coefficient of determination.
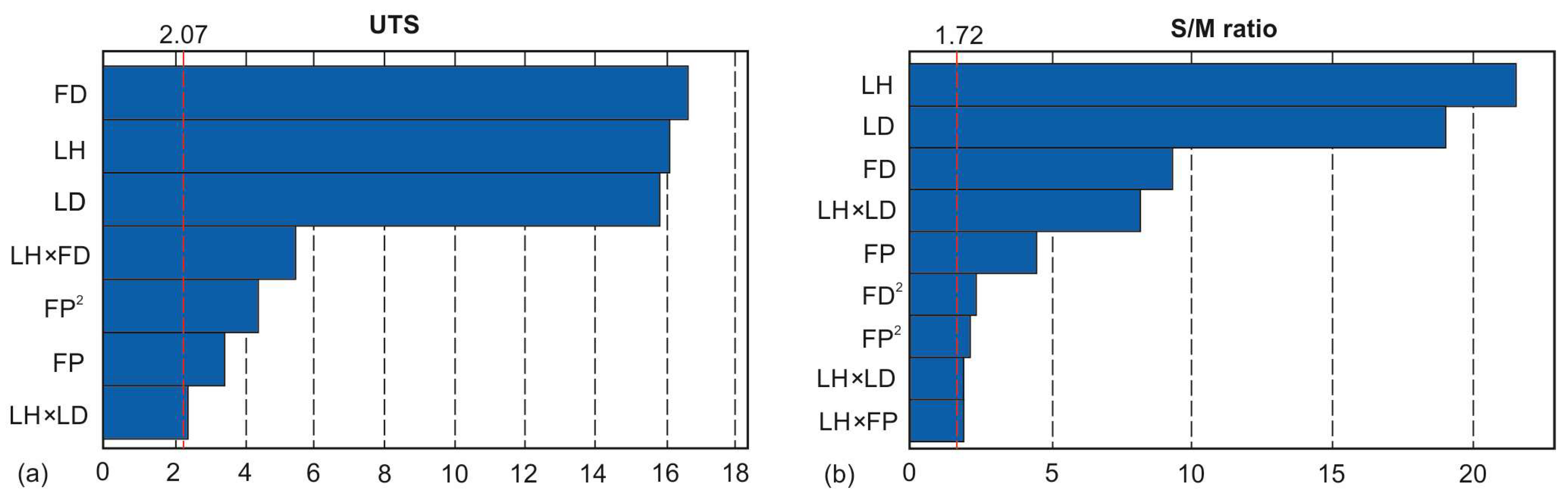
To further analyze the contribution of the factors, as well as to visualize the effects, the Pareto charts were plotted.
Figure 6a displays the effects from the largest effect to the smallest, indicating that the FD, LH and LD contribute the most, with percentages equal to 32.31%, 30.38% and 29.43%, respectively. The magnitudes of the rest of the factors are considerably smaller; however, all terms are significant, as indicated by the reference lines (red dashed lines). Similarly,
Figure 6b highlights the LH and LD as the most important effects, in addition to the FD and LH × LD, which exhibit weaker, but noticeable effects. The percentage levels of the aforementioned terms are 45.61%, 35.44%, 8.55%, and 6.64%, accordingly.
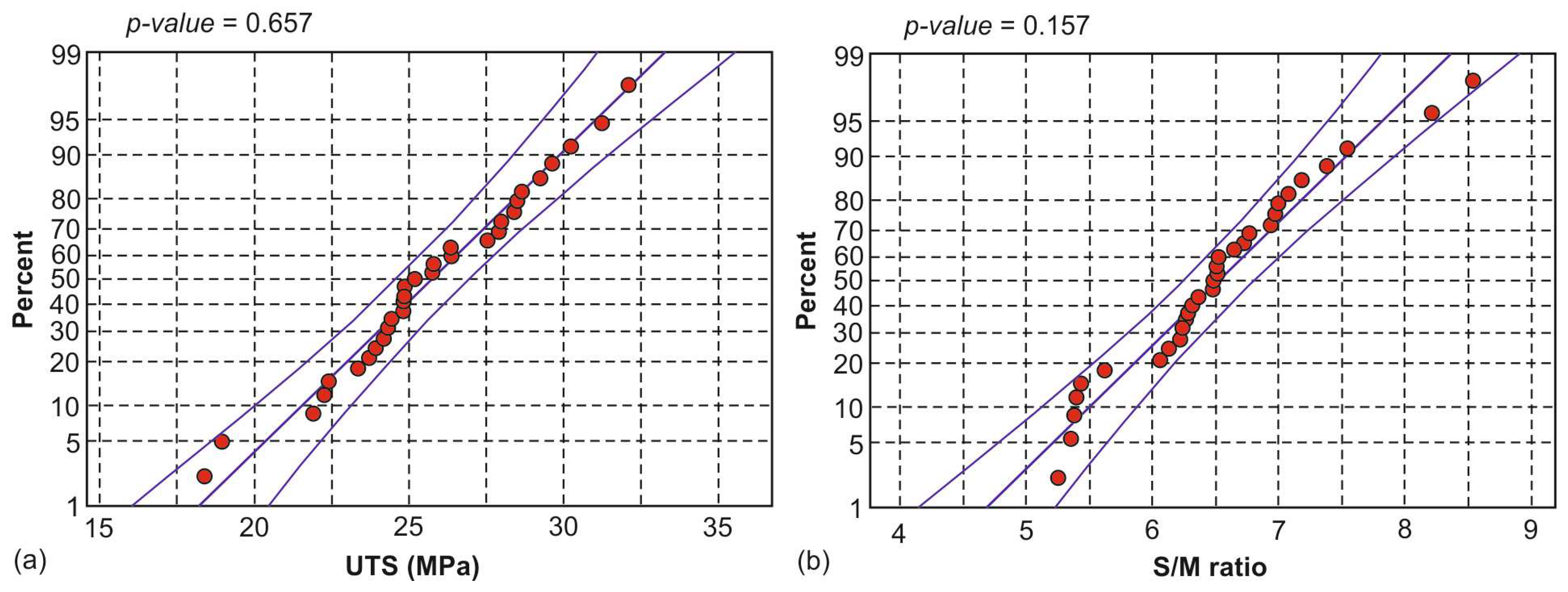
The probability plots (
Figure 7) were used to determine whether the data follow the distribution or not. To assess how well the data points follow the distribution, the vertical distance of each point from the fit line was examined. At first, the
p-value of each one of the plots suggests that the null hypothesis cannot be rejected, and hence, the data follow the distribution. Furthermore, the data points seem to closely follow the fit line, as seen in
Figure 7a,b, which correspond to the UTS and the S/M ratio, accordingly. A number of points pose an exception, one for the UTS and three for the S/M ratio plot, which are more distant compared to the rest of the points. Despite this issue, they are inside the confidence intervals (outer solid lines), a fact that indicates a normal distribution.
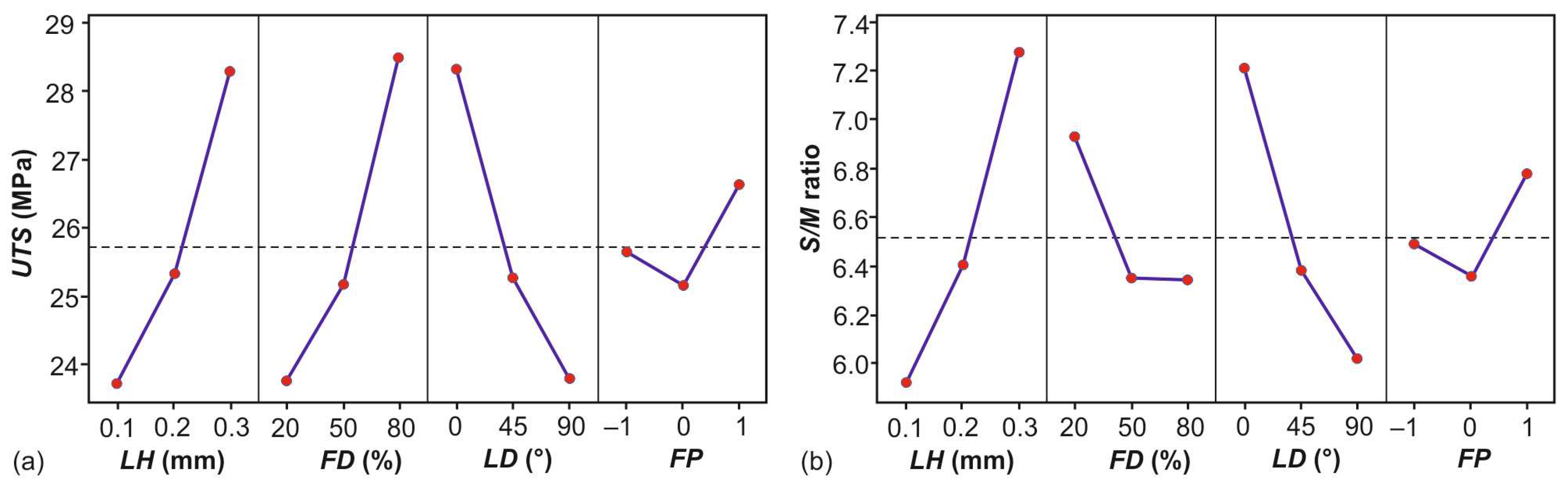
Investigating the main effect plots (
Figure 8) revealed the differences between the level means for the four parameters.
Figure 8a corresponds to the UTS, whereas
Figure 8b represents the mean effect plot for the S/M ratio. By observing
Figure 8a, it is evident that the LH acts increasingly on the generated UTS, and especially the 0.3 mm value. It is also clear that a similar pattern applies for the FD. On the other hand, any increase in the LD negatively affects the UTS. Alafaghani et al. [
33] concluded that increasing the infill percentage and layer thickness have a strong impact on the tensile strength and stiffness of ABS pieces. Lastly, the FP exhibits a different influence scheme. Specifically, the triangle structure seems to contribute the least to the generated UTS, with the grid being slightly better than the triangles. In contrast, the honeycomb pattern is responsible for more rigid structures and, therefore, for higher UTS values. Tanveer et al. reported similar results for the honeycomb structure [
34].
Figure 8b shows that the S/M ratio is affected by both the LH and LD factors, as well as the pattern, in a similar manner to the UTS. Both the 50% and 80% densities produce ratios of approximately equal values. However, the lowest level of density is responsible for increased S/M ratios.
The contour plots of
Figure 9 were used to examine the relationship between an output variable with the predictor variables in pairs. It can be seen that the values for the predictor variables are represented on the x and y axes, whereas the values for the output variable are illustrated as shaded regions, the contours of which are similar to the contours found in the topographical diagrams.
Figure 9a illustrates the relationship between the six different combinations of the input variables and the produced UTS. Similarly,
Figure 9b depicts the same interaction for the S/M ratio. Areas with darker colors indicate higher values of the response, whereas lighter colored regions represent lower values. By observing the FD × LH interaction of
Figure 9a, for instance, it is seen that LH values close to 0.25 mm, coupled with a density of 80%, or FD values close to 65%, combined with a 0.3 mm layer, produce UTS values higher than 28 MPa. Similar patterns, such as triangles and stripes, are observed for the LD × LH interaction, as well as the LD × FD. The rest of the interactive terms tend to form curved regions. According to
Figure 9b, the highest S/M ratios, over 7.5, for the FD × LH interaction are observed in the small triangular area formed by the following combinations: 20% infill and 0.3 mm layer thickness, 20% infill and approximately 0.28 mm LH, and close to 26% FD and 0.3 mm LH.
The performance of the models was further evaluated with the Mean Absolute Percentage Error (MAPE).
Table 6 presents the estimated error values between the experimental and the predicted response values, as well as the MAPE values. The calculated MAPEs were 1.70% and 1.36% for the UTS and the S/M ratio, respectively. Since the error data fluctuate within a reasonable range and extreme values do not exist, it can be safely assumed that each model is able to yield results of acceptable accuracy with respect to the applied range of the input data.
3.3. Structural Parameter Optimization
The combinations that maximize the UTS and S/M ratio individually were identified and discussed at the beginning of
Section 3. It was revealed that the 0.3 mm layer, 0° line direction and honeycomb pattern contribute towards the maximization of both the UTS and S/M ratio. The only difference lies in the infill, with 80% density leading to the maximization of the UTS and 20% density to the S/M ratio.
To identify the combination that maximizes the UTS and S/M ratio simultaneously, the desirability function was utilized in the developed mathematical formulas. This function is widely implemented in studies [
35,
36,
37,
38] based on the Design of Experiments (DOE), such as factorial, Taguchi and RSM. The optimization approach using the desirability function generates operating conditions x that are used for the response calculation based on a graded desirability. The calculated values tend to reach either the maximum or minimum value of a response or a specified target. Therefore, the possible values of a response
Yi(
x) are expressed by a desirability function
di(
Yi) by assigning a number between 0 and 1. The case that
di(
Yi) = 0 denotes that the response generated a completely undesirable value. Contrarily, if
di(
Yi) = 1, the response generated a value of maximized desirability. The overall desirability
D, for
k responses, is estimated by combining the individual disabilities, as shown in Equation (3). Finally, it is pointed out that the desirability rank is affected considerably by how close the response value is to the specified target.
The UTS is one of the most important mechanical properties that indicates the mechanical performance of the fabricated part. In addition, the S/M ratio includes the mass factor, thus, constituting a more complex structural index.
Table 7 contains the constraints and the limits for the optimization process, in addition to
Table 8, which presents the yielded solutions for two cases: one that favors UTS over S/M ratio (Solution 1) and another with the opposite result (Solution 2). Both optimization solutions express the simultaneous maximization of the two responses.
To verify the optimal solutions, four extra specimens, two for each solution, were fabricated and tested under the same conditions.
Table 9 presents the predicted responses for the optimal solutions, as well as the output values extracted from the tests. The calculated relative error values suggest that the models can generate accurate predictions.