A Data-Driven Constitutive Model for 3D Lattice-Structured Material Utilising an Artificial Neural Network
Abstract
1. Introduction
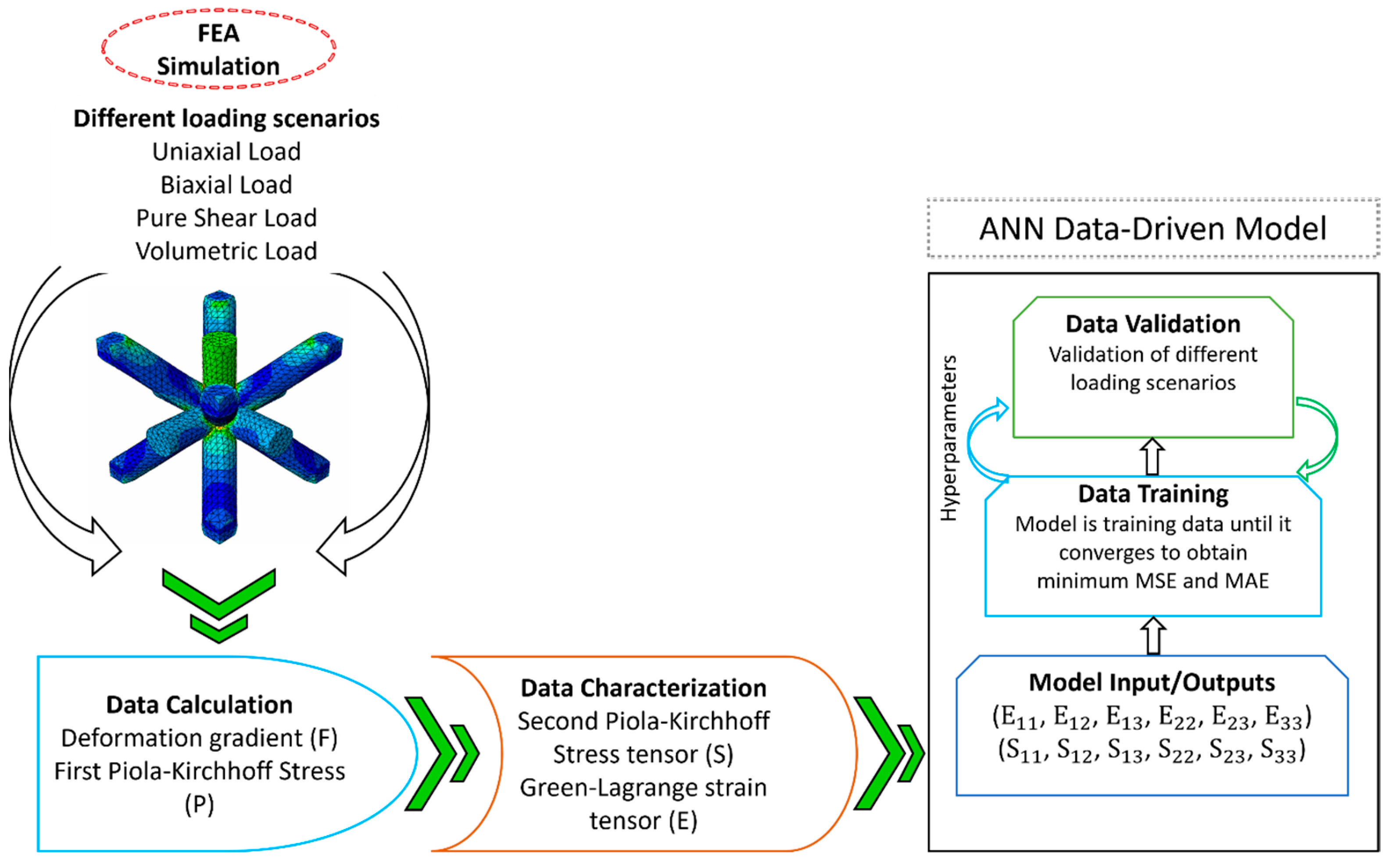
2. Data Collection Method
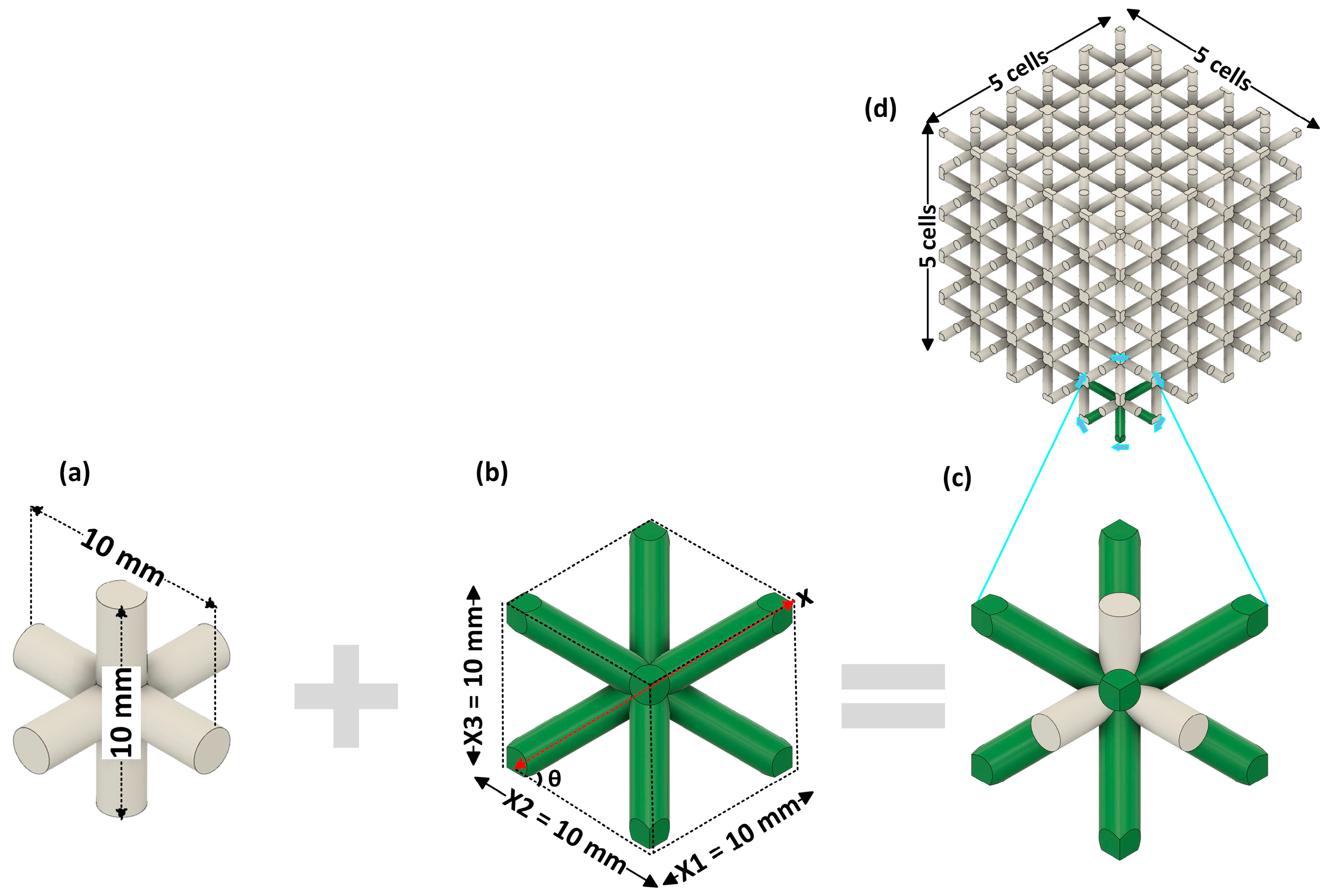
2.1. Unit Cell Design of the Lattice-Structured Material
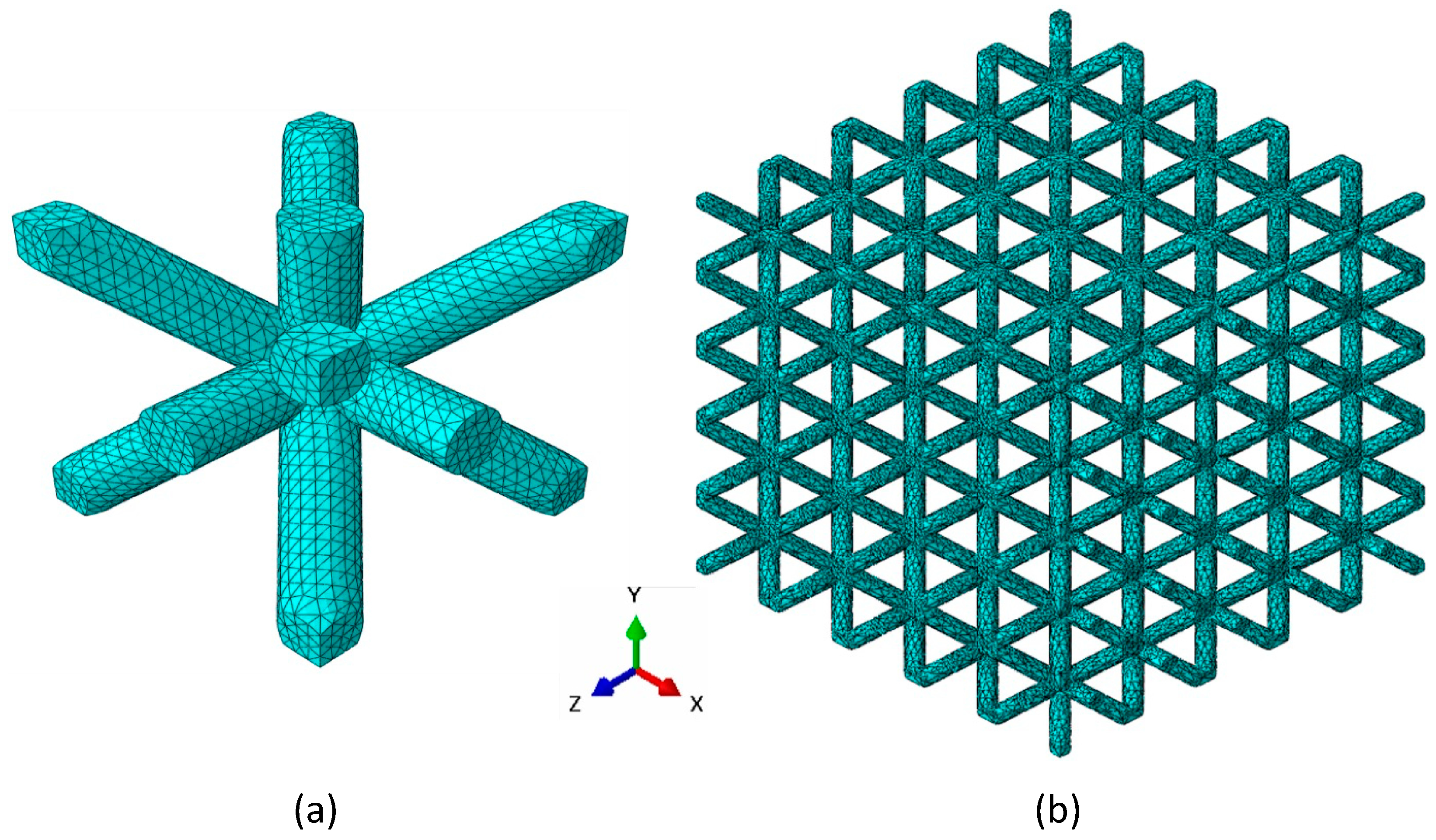
2.2. Data Acquisition through Unit Cell-Level Simulation
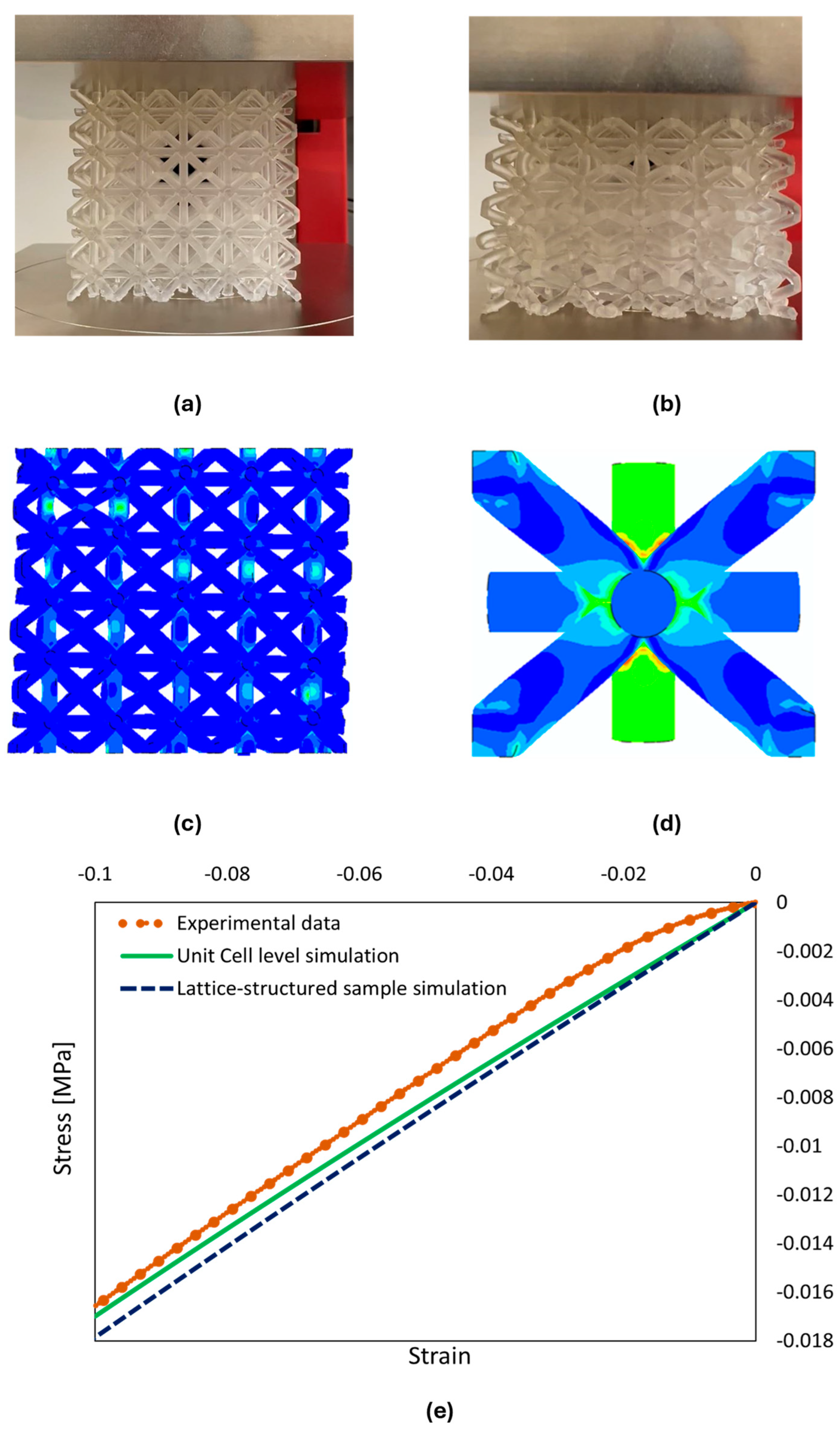
2.3. Additive Manufacturing of Lattice-Structured Specimens
2.4. Experimental Analysis
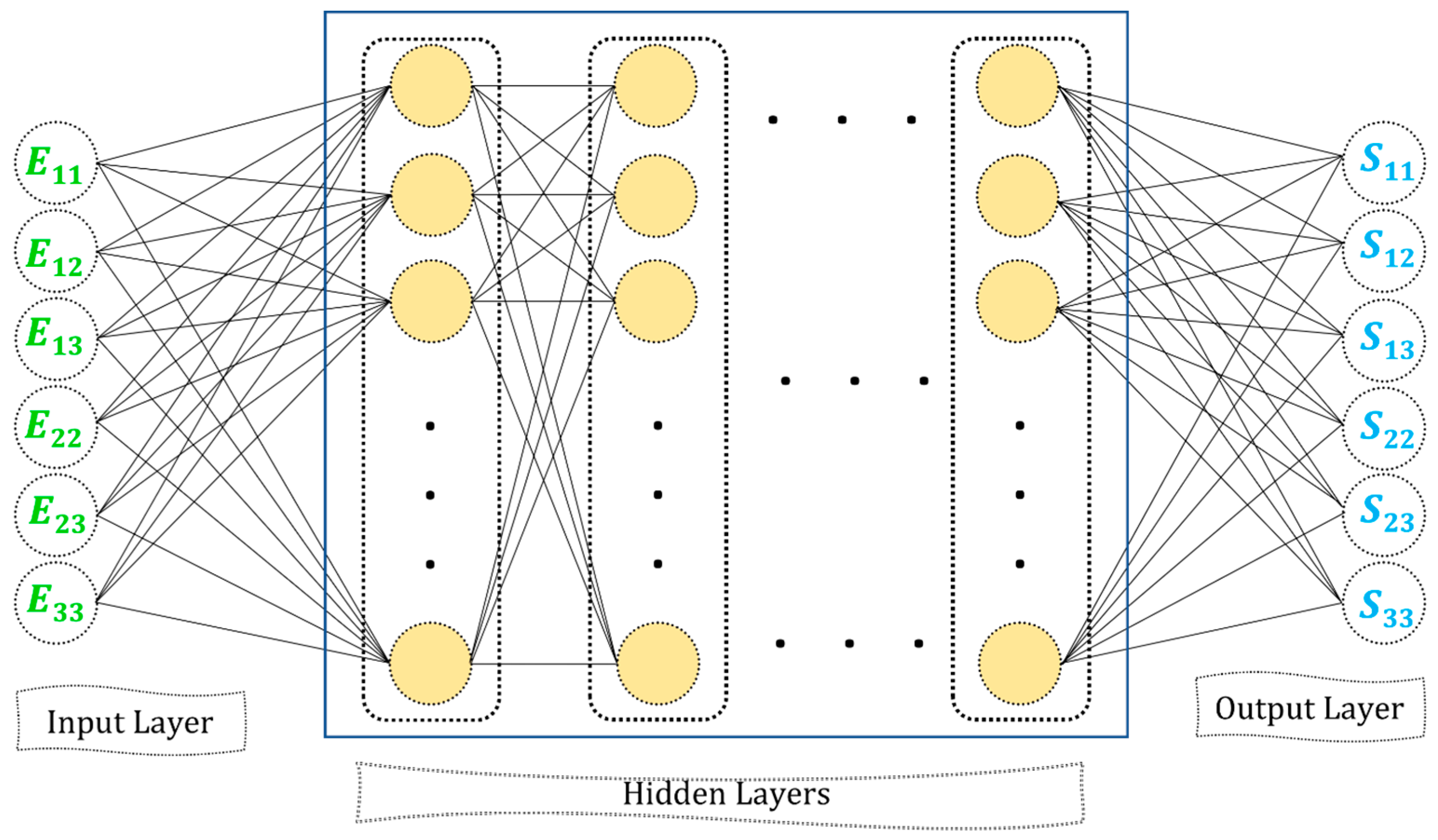
3. An ANN-Based Data-Driven Constitutive Model for Lattice-Structured Materials
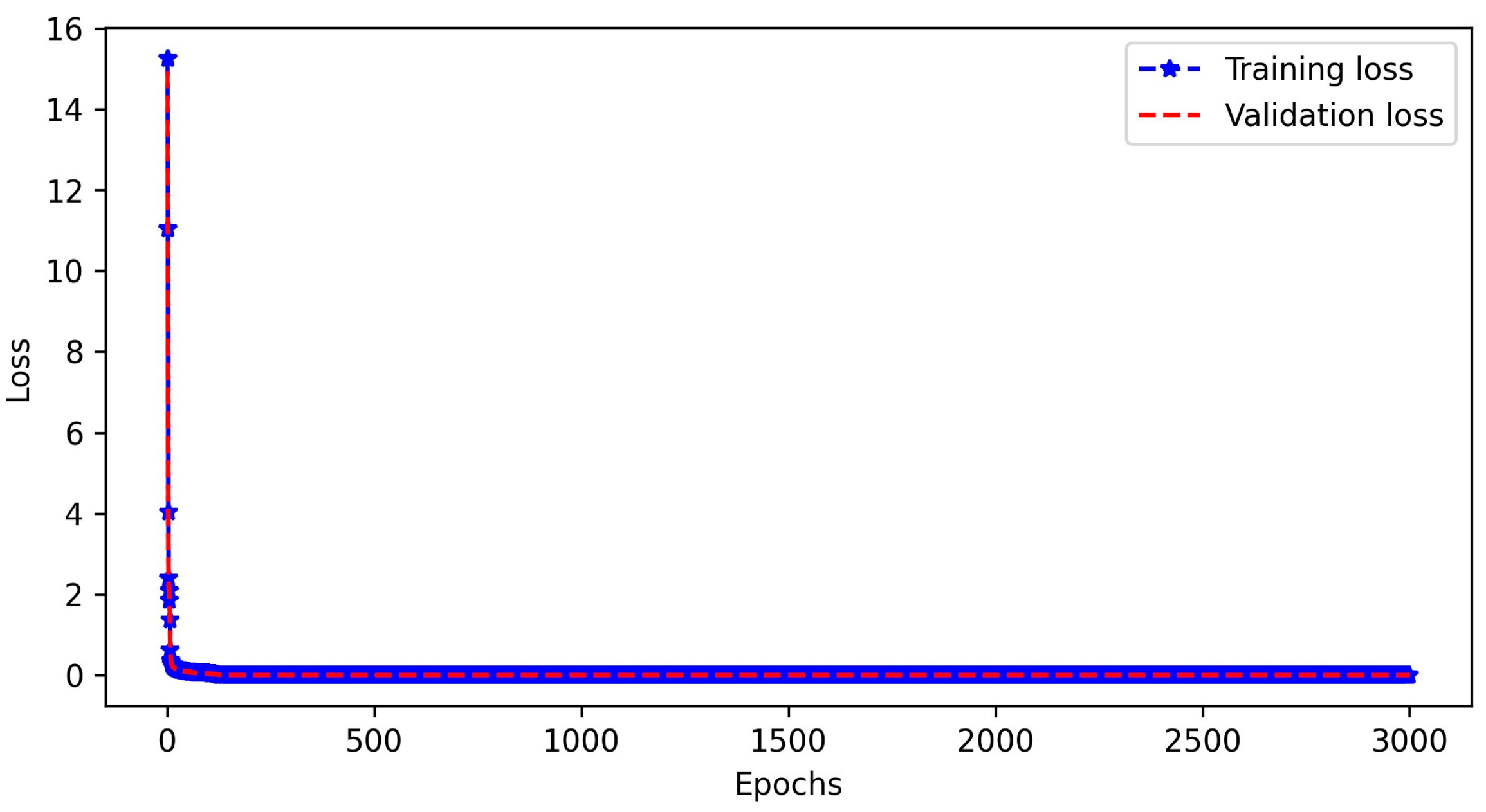
3.1. ANN Model Architecture and Training
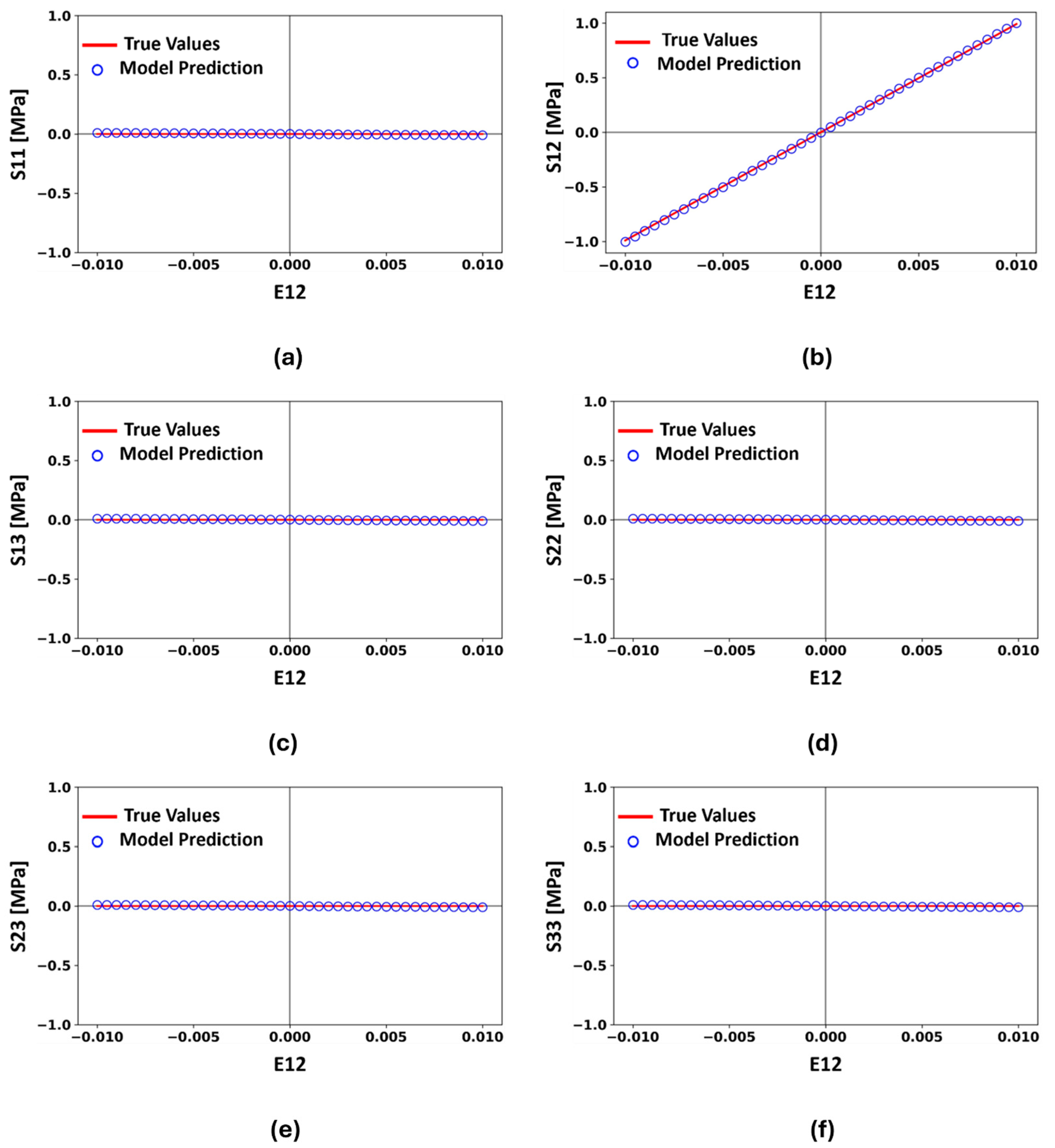
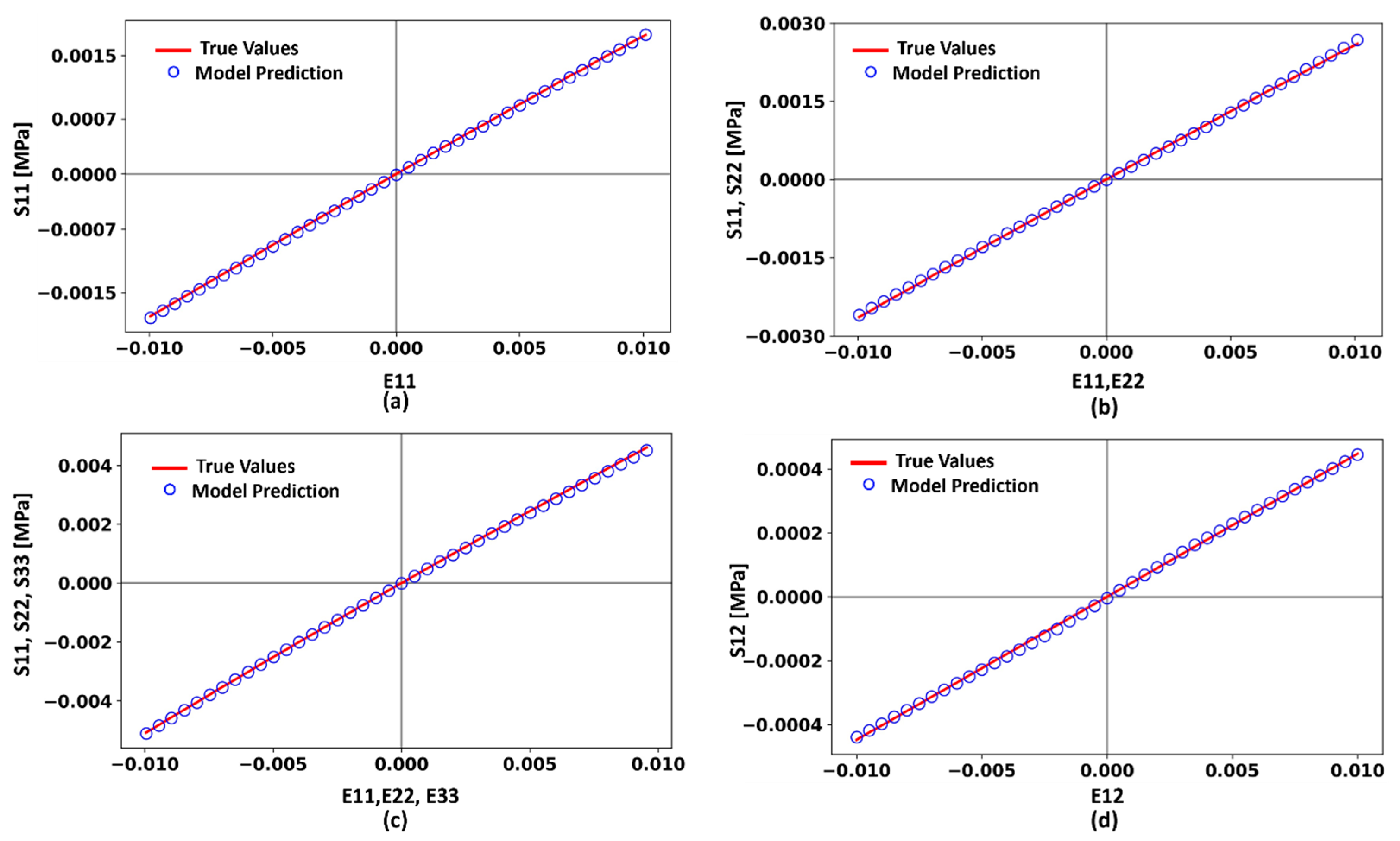
3.2. Performance of Trained ANN Model
4. Results and Discussion
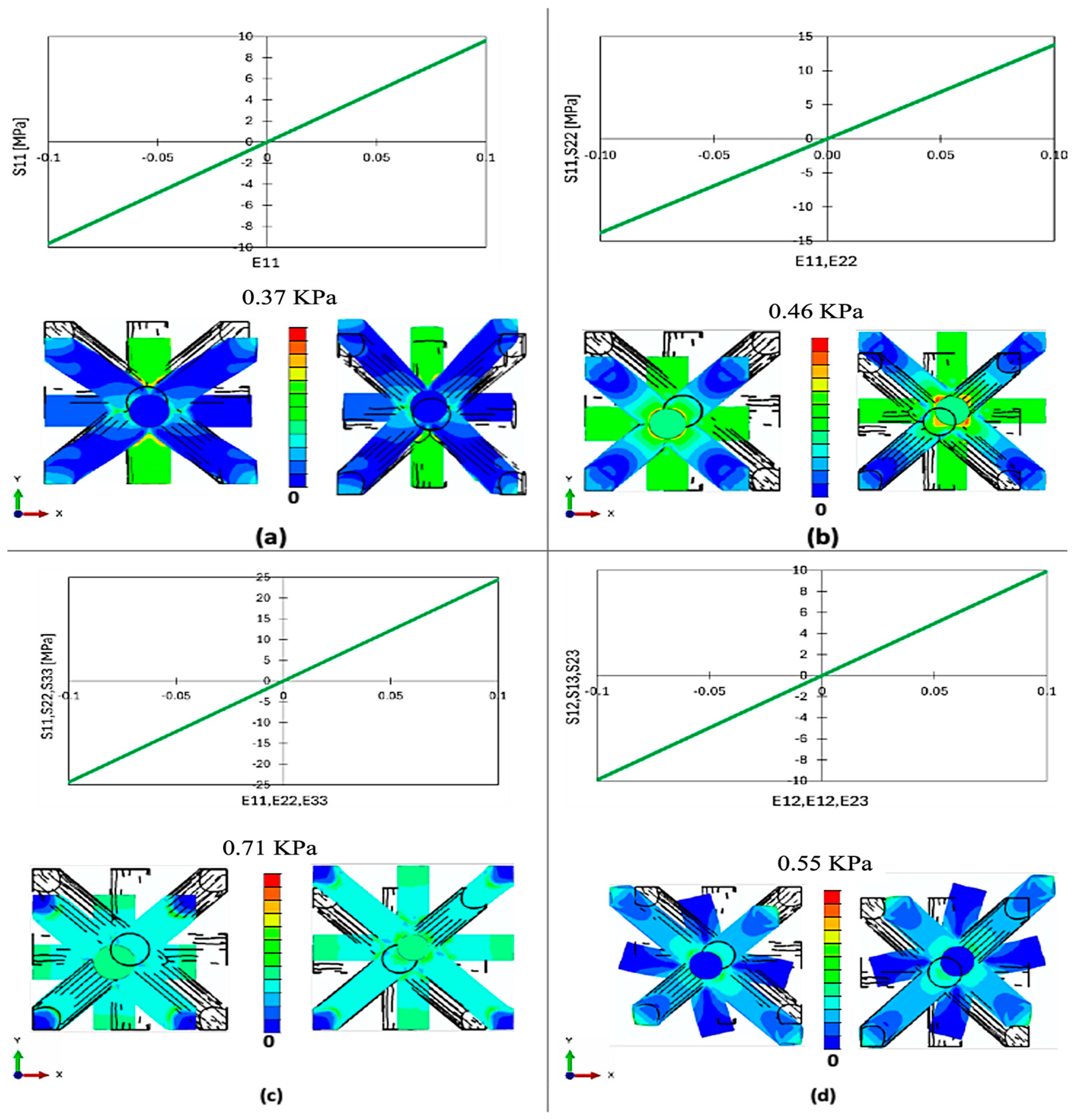
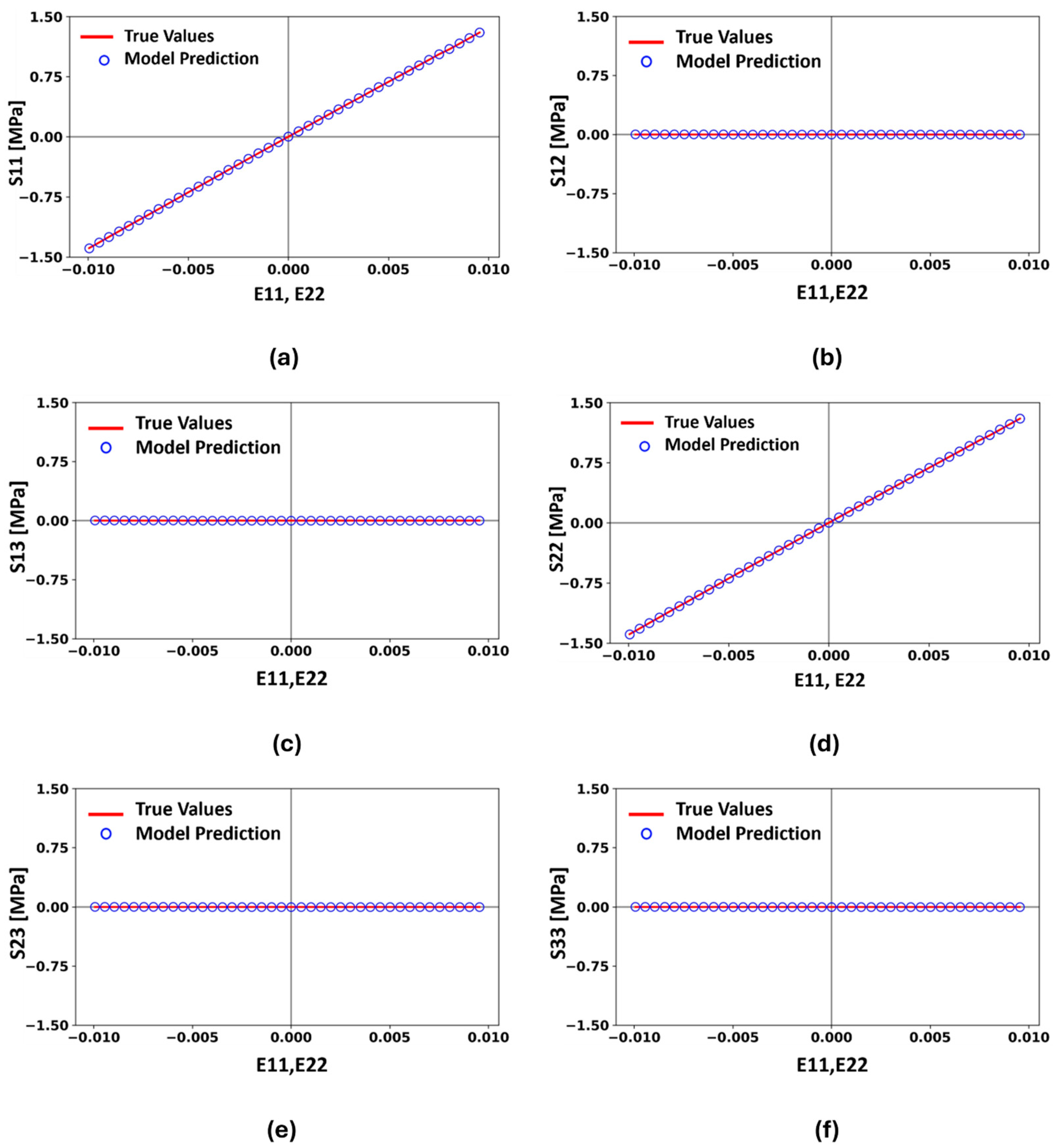
4.1. Validation of the ANN Model under Various Loading Scenarios
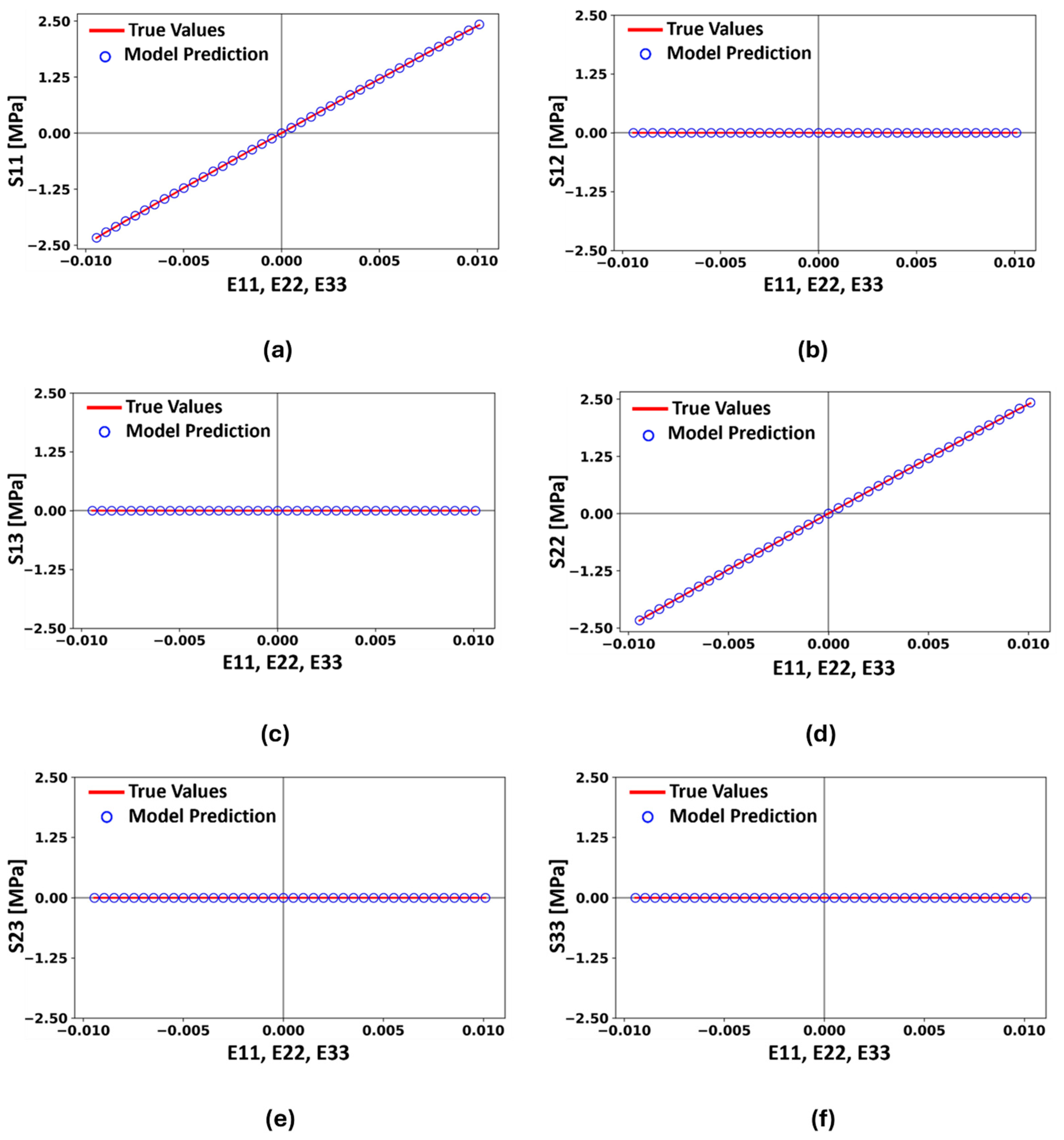
4.2. Generalization of the Model to the Wider Group of Materials
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Yang, F.; Li, P.; Zhang, W.; Lu, G.; Fan, H. Bio-inspired vertex modified lattice with enhanced mechanical properties. Int. J. Mech. Sci. 2023, 244, 108081. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Rahmani, R.; Antonov, M.; Brojan, M. Lightweight 3D printed Ti6Al4V-AlSi10Mg hybrid composite for impact resistance and armor piercing shielding. J. Mater. Res. Technol. 2020, 9, 13842–13854. [Google Scholar] [CrossRef]
- Xiao, R.; Li, X.; Jia, H.; Surjadi, J.U.; Li, J.; Lin, W.; Gao, L.; Chirarattananon, P.; Lu, Y. 3D printing of dual phase-strengthened microlattices for lightweight micro aerial vehicles. Mater. Des. 2021, 206, 109767. [Google Scholar] [CrossRef]
- Syrlybayev, D.; Perveen, A.; Talamona, D. Experimental investigation of mechanical properties and energy absorption capabilities of hybrid lattice structures manufactured using fused filament fabrication. Int. J. Adv. Manuf. Technol. 2023, 125, 2833–2850. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Gan, J.; Li, F.; Li, K.; Li, E.; Li, B. Dynamic failure of 3D printed negative-stiffness meta-sandwich structures under repeated impact loadings. Compos. Sci. Technol. 2023, 234, 109928. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Anti-blast and -impact performances of auxetic structures: A review of structures, materials, methods, and fabrications. Eng. Struct. 2023, 276, 115377. [Google Scholar] [CrossRef]
- Imediegwu, C.; Grimm, U.; Moat, R.; Jowers, I. A computational method for determining the linear elastic properties of 2D aperiodic lattice structures. J. Strain Anal. Eng. Des. 2023, 58, 590–602. [Google Scholar] [CrossRef]
- du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Ramakrishna, D.; Murali, G.B. Bio-inspired 3D-printed lattice structures for energy absorption applications: A review. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 237, 503–542. [Google Scholar] [CrossRef]
- Hulme, J.; Sakhaei, A.H.; Shafiee, M. Mechanical analysis and additive manufacturing of 3D-printed lattice materials for bone scaffolds. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Stainier, L.; Leygue, A.; Ortiz, M. Model-free data-driven methods in mechanics: Material data identification and solvers. Comput. Mech. 2019, 64, 381–393. [Google Scholar] [CrossRef]
- Ibañez, R.; Abisset-Chavanne, E.; Aguado, J.V.; Gonzalez, D.; Cueto, E.; Chinesta, F. A Manifold Learning Approach to Data-Driven Computational Elasticity and Inelasticity. Arch. Comput. Methods Eng. 2018, 25, 47–57. [Google Scholar] [CrossRef]
- Ibáñez, R.; Abisset-Chavanne, E.; González, D.; Duval, J.-L.; Cueto, E.; Chinesta, F. Hybrid constitutive modeling: Data-driven learning of corrections to plasticity models. Int. J. Mater. Form. 2019, 12, 717–725. [Google Scholar] [CrossRef]
- Huang, D.; Fuhg, J.N.; Weißenfels, C.; Wriggers, P. A machine learning based plasticity model using proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2020, 365, 113008. [Google Scholar] [CrossRef]
- Bessa, M.A.; Glowacki, P.; Houlder, M. Bayesian machine learning in metamaterial design: Fragile becomes supercompressible. Adv. Mater. 2019, 31, 1904845. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Kharmanda, G.; Mahdi, E. Constitutive Models for the Prediction of the Hot Deformation Behavior of the 10%Cr Steel Alloy. Materials 2019, 12, 2873. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef]
- Peng, X.-L.; Xu, B.-X. Data-driven inverse design of composite triangular lattice structures. Int. J. Mech. Sci. 2024, 265, 108900. [Google Scholar] [CrossRef]
- Fernández, M.; Jamshidian, M.; Böhlke, T.; Kersting, K.; Weeger, O. Anisotropic hyperelastic constitutive models for finite deformations combining material theory and data-driven approaches with application to cubic lattice metamaterials. Comput. Mech. 2021, 67, 653–677. [Google Scholar] [CrossRef]
- Klein, D.K.; Fernández, M.; Martin, R.J.; Neff, P.; Weeger, O. Polyconvex anisotropic hyperelasticity with neural networks. J. Mech. Phys. Solids 2022, 159, 104703. [Google Scholar] [CrossRef]
- Chung, I.; Im, S.; Cho, M. A neural network constitutive model for hyperelasticity based on molecular dynamics simulations. Int. J. Numer. Methods Eng. 2021, 122, 5–24. [Google Scholar] [CrossRef]
- Bogusz, P.; Popławski, A.; Stankiewicz, M.; Kowalski, B. Experimental Research of Selected Lattice Structures Developed with 3D Printing Technology. Materials 2022, 15, 378. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Meng, J.; Liu, J.; Ao, X.; Lin, S.; Yang, Y. Evaluation of the Equivalent Mechanical Properties of Lattice Structures Based on the Finite Element Method. Materials 2022, 15, 2993. [Google Scholar] [CrossRef] [PubMed]
- Riva, L.; Ginestra, P.S.; Ceretti, E. Mechanical characterization and properties of laser-based powder bed–fused lattice structures: A review. Int. J. Adv. Manuf. Technol. 2021, 113, 649–671. [Google Scholar] [CrossRef]
- Refai, K.; Montemurro, M.; Brugger, C.; Saintier, N. Determination of the effective elastic properties of titanium lattice structures. Mech. Adv. Mater. Struct. 2020, 27, 1966–1982. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. A review on integration of lightweight gradient lattice structures in additive manufacturing parts. Adv. Mech. Eng. 2020, 12, 1687814020916951. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and optimization of lattice structures: A review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- MEGATrends. Abaqus 2022|Dassault Systèmes®. Available online: https://events.3ds.com/abaqus-2022 (accessed on 10 March 2023).
- “Draft Resin for Truly Rapid Prototyping.” N.p., n.d. Web. Available online: https://dental-media.formlabs.com/datasheets/2001477-TDS-ENUS-0.pdf (accessed on 13 March 2024).
- Formlabs. Formlabs 3D Printers Catalog. Available online: https://formlabs.com/uk/3d-printers/catalog/#form-3 (accessed on 7 March 2023).
- Zhang, W.; Zhang, R.; Wu, C.; Goh AT, C.; Lacasse, S.; Liu, Z.; Liu, H. State-of-the-art review of soft computing applications in underground excavations. Geosci. Front. 2020, 11, 1095–1106. [Google Scholar] [CrossRef]
- Argatov, I. Artificial neural networks (ANNs) as a novel modeling technique in tribology. Front. Mech. Eng. 2019, 5, 30. [Google Scholar] [CrossRef]
- Stergiou, K.; Ntakolia, C.; Varytis, P.; Koumoulos, E.; Karlsson, P.; Moustakidis, S. Enhancing property prediction and process optimization in building materials through machine learning: A review. Comput. Mater. Sci. 2023, 220, 112031. [Google Scholar] [CrossRef]
- Hussain, A.; Sakhaei, A.H.; Shafiee, M. Development of an Artificial Neural Network (ANN) Constitutive Model for Mechanical Metamaterials. Am. Soc. Mech. Eng. Digit. Collect. 2023, 3, V003T03A041. [Google Scholar]
- Tomar, A.S.; Sharma, A.; Shrivastava, A.; Rana, A.S.; Yadav, P. A Comparative Analysis of Activation Function, Evaluating their Accuracy and Efficiency when Applied to Miscellaneous Datasets. In Proceedings of the 2023 2nd International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 4–6 May 2023; pp. 1035–1042. [Google Scholar]



| Activation Function | Layers with Neurons | MSE | MAE | Batch Size | Epochs | Params |
|---|---|---|---|---|---|---|
| LeakyReLU, linear | [6,24,16,10,8,6] | 1.43 × 10−5 | 2.93 × 10−2 | 32 | 2500 | 880 |
| LeakyReLU, linear | [6,24,16,10,8,6] | 4.47 × 10−6 | 2.86 × 10−2 | 32 | 3000 | 880 |
| ELU, linear | [6,24,16,10,8,6] | 4.90 × 10−6 | 0.13 × 10−2 | 32 | 2500 | 880 |
| ELU, linear | [6,24,16,10,8,6] | 1.16 × 10−2 | 0.11 × 10−2 | 32 | 3000 | 880 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Sakhaei, A.H.; Shafiee, M. A Data-Driven Constitutive Model for 3D Lattice-Structured Material Utilising an Artificial Neural Network. Appl. Mech. 2024, 5, 212-232. https://doi.org/10.3390/applmech5010014
Hussain A, Sakhaei AH, Shafiee M. A Data-Driven Constitutive Model for 3D Lattice-Structured Material Utilising an Artificial Neural Network. Applied Mechanics. 2024; 5(1):212-232. https://doi.org/10.3390/applmech5010014
Chicago/Turabian StyleHussain, Arif, Amir Hosein Sakhaei, and Mahmood Shafiee. 2024. "A Data-Driven Constitutive Model for 3D Lattice-Structured Material Utilising an Artificial Neural Network" Applied Mechanics 5, no. 1: 212-232. https://doi.org/10.3390/applmech5010014
APA StyleHussain, A., Sakhaei, A. H., & Shafiee, M. (2024). A Data-Driven Constitutive Model for 3D Lattice-Structured Material Utilising an Artificial Neural Network. Applied Mechanics, 5(1), 212-232. https://doi.org/10.3390/applmech5010014







