Abstract
A variety of hollow microneedle (HMN) designs has emerged for minimally invasive therapies and monitoring systems. In this study, a design change limiting the indentation depth of the (3D) printed custom microneedle assembly (circular array of five conical frusta with and without a stopper, aspect ratio = 1.875) fabricated using stereolithography has been experimentally validated and modeled in silico. The micro-indentation profiles generated in confined compression on 1 mm ± 0.073 mm alginate films enabled the generation of a Prony series, where displacement ranged from 100 to 250 µm. These constants were used as intrinsic properties simulating experimental ramp/release profiles. Puncture occurred on two distinct hydrogel formulations at the design depth of 150 µm and indentation rate of 0.1 mm/s characterized by a peak force of 3.5 N (H = 31 kPa) and 8.3 N (H = 36.5 kPa), respectively. Experimental and theoretical alignments for peak force trends were obtained when the printing resolution was simulated. Higher puncture force and uniformity inferred by the stopper was confirmed via microscopy and profilometry. Meanwhile, poroviscoelasticity characterization is required to distinguish mass loss vs. redistribution post-indentation through pycnometry. Results from this paper highlight the feasibility of insertion-depth control within the epidermis thickness for the first time in solid HMN literature.
1. Introduction
Research on microneedle-based cell therapy has shown promising results for tissue regeneration, cancer immunotherapy, skin immune monitoring, targeted cell delivery, drug delivery, and biomarker detection [1]. Microneedle use for transdermal delivery [2,3,4,5,6] involves the transport of active components (such as viable cells [7,8,9], insulin [10,11], nanoparticles [12,13], and exosomes [14]) into the skin. The skin is a multilayered organ that consists of three layers: the epidermis, dermis, and hypodermis. The epidermis is 50 to 200 μm thick and includes sublayers, such as the stratum corneum (10 to 20 μm) and the viable epidermis (~150 μm) [15,16]. Microneedle patches or arrays applied to the skin must be strong enough to pierce the stratum corneum without bending or breaking [15,16] and have the proper length to deliver encapsulated cells into the skin. In cell therapy applications, delivery into the viable epidermis is preferred as drug binding, metabolism and active transport occur here [15,17]. Further, delivery to the viable epidermis avoids contact with nerves and blood vessels in the subcutaneous tissue and decreases pain felt by the patient [15].
Generally, microneedle types can be separated into five categories: solid, coated, dissolving, hydrogel-forming, and hollow [18,19]. Hollow microneedles (HMNs) allow for the administration of drugs or delivery of cells via a “poke-and-flow” mechanism due to their center bore and are fabricated using materials, such as metal, ceramic, glass, silicon, and polymer [1,19]. In order to manufacture hollow microneedle (HMN) arrays, 3D printing technology is often utilized because of its cost efficiency, high throughput, and affinity for customization [19,20]. Conventional 3D printing methods for HMN fabrication include stereolithography (SLA), also known as vat photopolymerization (VPP), the Fused Deposition Method (FDMTM), Selective Laser Sintering (SLS), Continuous Liquid Interface Production (CLIP), and Digital Light Processing (DLP) [21,22,23,24,25]. SLA is a 3D printing process where a UV laser cures liquid monomer molecules in the photoresin, via free radical polymerization, into a cross-linked polymer. SLA has an ink-dependent resolution, making it possible to create complex designs on the micron scale and emerging as a prominent CAD-CAM bio-fabrication method. Specifically, inverted SLA is used because of its ability to produce high-quality designs while having a smaller footprint and lower cost [26,27]. The flexibility of adding new design features printed using recently formulated biocompatible and sterilizable photoresins has increased the biomedical applications of this biofabrication method. Stereolithography is considered an ideal technology for microfluidic device fabrication because of its high printing resolution and flexible design, enabling accelerated process development [27]. Additionally, stereolithography may be used to facilitate the development of personalized drug delivery systems as an alternative to address and treat infectious disease [20], emphasizing the relevance and benefit of 3D printing in biomedical research.
Cell therapy facilitated by microneedle technology is a growing field, with Table 1 summarizing the recent directions [28,29]. Many applications utilize porous or dissolving microneedles for cell therapy, with the full length of the needle being inserted into the tissue to facilitate the delivery of cells. For example, Chang et al. utilized cryogenic microneedles (cryoMNs) in order to deliver ovalbumin-pulsed dendritic cells at a depth of 20 μm to 200 μm to slow melanoma tumor growth [9]. Similarly, Chen et al. describes a maximum penetration depth of 500 μm using their HMN array, leading to potential cell therapy applications to treat vitiligo and alopecia, which requires the delivery of melanocytes into the epidermis at a depth of 200 μm and dermal papilla cells at a depth of 500 μm, respectively [30]. Tang et al. studied the use of cell-microneedle patches for heart regeneration after myocardial infarction, finding that controlling the penetration depth to 500 μm is essential to avoid tissue damage [31]. Zheng et al. describe the use of cryomicroneedles (cryoMNs) for cell delivery, indicating the successful delivery of cells into an agarose gel at a depth ranging from 50 μm to 200 μm using a microneedle structure with an initial height of 700 μm [32]. Ye et al. studied the use of microneedles to regulate insulin secretion from exogenous pancreatic β-cells, indicating that microneedles with a height of 800 μm penetrated approximately 200 μm to the epidermis [33].

Table 1.
Applications of microneedle technology to cell therapy.
Skin phantoms are important tools to assess microneedle integrity and successful puncture, with tensile testing, compression, and indentation used to evaluate the mechanical properties of skin under both static and dynamic conditions to create practical skin phantoms [34]. Materials used to create skin phantoms include polyvinyl alcohol, polyvinyl chloride, gelatin, silicone, agarose, and alginate gels [34]. Alginate remains one of the original biomaterials still used for cell microencapsulation [35,36,37]. It can be crosslinked using a variety of chemical and physical methods, in addition to being integrated in multinetwork hydrogel systems with excellent biocompatibility, specifically the ease of sterilization and mixing [38]. Gradient hydrogels are more complex than homogeneous gels [39], with changing mechanical properties, such as the molecular weight, Young’s Modulus, and degradation rate in stiffness-tunable hydrogels, for example [40,41,42]. Gradient hydrogels can serve as skin phantoms because of their capability to capture the complexities of skin, as the skin is an anisotropic and viscoelastic material with mechanical properties varying depending on the skin thickness, age, anatomical site, etc. [15,16]. While phantoms can be good alternatives for animal and human testing, as they are lower cost and easier to store [34], they must properly mimic the biomechanical properties of human skin to validate microneedle models. When utilizing hydrogels as skin phantoms, factors, such as crosslinking density, rehydration, and creating double networks, improve the mechanical strength and toughness of the hydrogel [43,44,45,46] and thus phantom performance.
In terms of puncture, 6 N is the average force value for human skin puncture [47], meaning a successful skin phantom should withstand this force value in order to model puncture. Other recent studies have quantified puncture force at a lower value [25,48]; however, these studies involve much larger displacements with the goal of delivering drugs beyond the epidermis. Force data collected during puncture are a summation of stiffness, friction, and cutting forces, with the stiffness force producing elastic deformation in the skin surface, cutting force relating to tissue cutting resistance produced when the tip of the needle pierces the skin, and friction force relating to dynamic friction caused by needle movement [47,49]. Puncture force data are quantified via needle insertion tests [25,39,48,50], as well as computation. Trączyński et al. performed needle insertion tests, varying the needle size, insertion speed, and insertion angle to understand the effect of these variables on insertion force, as well as the consistency of force [48]. Then, five low computational cost models were used to model insertion force, finding that a nonlinear regression model [51] best fits the experimental data and allows for an estimation of needle insertion parameters in real time.
Finite element analysis (FEA) software, has been used to simulate and evaluate many applications and characteristics of HMNs, such as drug delivery and diffusion into the skin [52], UV light propagation for sensing and theranostics [53], mechanical and stress analysis [24,54,55,56], insertion [54,55], and failure [24,54,57]. Henriquez et al. performed indentation simulations to find a critical application load to avoid a structural failure during microneedle insertion into human skin for stainless steel and PLGA HMNs [54], with Faraji Rad et al. using simulation to investigate the deflection of HMNs and stress distribution under a lateral bending force [24]. Tamez-Tamez et al. describe the use of simplified versions of microneedles (solid) and skin tissue to simulate insertion, perform stationary and linear buckling analyses, and study the impact of the tip truncation length on puncture [55]. Anbazhagan et al. performed mechanical and stress analysis, with simulation performed by applying axial and bending loading on both conical and pyramidal HMNs [56]. A previous project [57] utilized simulation to investigate the clogged nozzle, deformed nozzle, and suction failure associated with the HMN design and its impact on microencapsulated cell delivery. Overall, the use of simulation is beneficial to understanding the conditions and forces involved in successful microneedle puncture and subsequent drug or cell delivery, with Table 2 summarizing HMN material and dimensions, substrates used for puncture, and the index of biomechanics.

Table 2.
Hollow microneedle characteristics and use in simulations.
At the intersection of HMN bio-fabrication, puncture force/simulation test method development based on custom-designed skin phantoms lies for this proposed biomechanical pre-clinical study. Based on the literature review, there is a need to actively control penetration depth in the epidermis for the painless and precise delivery of cells, which is not currently documented in terms of an existing design feature for microneedles. Currently, the insertion depth is controlled based on the porosity and dissolution rate of microneedle patches [9,30,31,32,33]. Adding a geometric feature, such as a stopper above the microneedle tip at a target distance, prevents the insertion of the HMN beyond the therapeutic region of interest. Furthermore, the height of this feature can be varied accordingly and expand the application of this design control to deeper layers of skin or tissue. Stereolithography is the preferred bio-fabrication method for accommodating this flexible design functionality. Figure 1 is the evolution of the design efforts leading to the unmet need of controlling the insertion depth for cell therapy to the thickness of the epidermis by adding a stopper to the original HMN design. In parallel, puncture feasibility has been improved step-wise by modulating the aspect ratio (AR). Thus, the specific aim of this study is to design a novel HMN to limit the puncture depth to 150 µm, to be validated on a biocompatible alginate phantom formulated to withstand a force of 6 N.
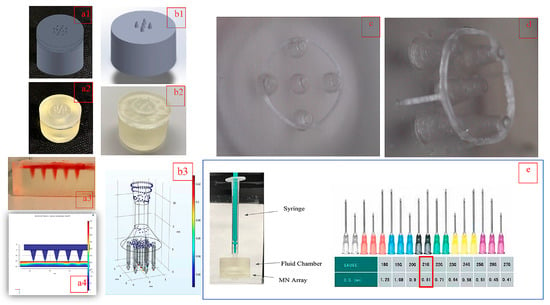
Figure 1.
Timeline of design changes for the custom HMN for microencapsulated cell delivery. (a1,a2) Original low aspect ratio (AR = 0.6) for HMN device design and gel phantom formulation (a3) and simulation (a4) [21]; (b1,b2) HMN device modified for shear modeling [58] and (b3) simulation [57]; (c) introduction of stopper with a low-aspect-ratio design; (d) proposed HMN design with sharper needles (AR = 1.875) and stopper; (e) translational outlook for delivery using design in (d) equivalent to a 21 G hypodermic needle [59].
2. Materials and Methods
2.1. Materials
All the reagents required for hydrogel-based fabrication, including medium-viscosity alginate (Sigma A2033 (μ > 2000 cP, Mv = 900–1000 kDa, M/G ratio 1.6)), and reagent grade salts and solvents were purchased from Sigma Aldrich (St-Louis, MO, USA). The proprietary 3D printing photoresin (RS-F2-GPCL-04, Formlabs Clear Resin Cartridge v4) was procured from Formlabs (Summerville, MA, USA).
2.2. Methods
2.2.1. Device Design Printing and Assembly
Multiple screening runs were conducted prior to the determination of the nominal MN dimensions, co-optimized in terms of the wall thickness, nozzle sharpness, and shrinkage. These runs were conducted to eliminate susceptibility to fracture upon indentation in the hydrogel. Fracture, in turn, can be classified as a slanted tip due to chipping caused by under-curing, as shown in Figure 2, or bending due to an inadequate wall thickness. Buckling has never been observed for neither the HMN nor the HMNS due to uniform mass distribution/symmetry along the z-axis. The choice of the HMN material selection was dictated in turn by the highest theoretical resolution range of 25 μm–50 μm, achievable using a single photoresin formulation. Hence, prototype replication, penetration depth characterization, pycnometry, and simulation will be discussed for the optimal bio-fabrication conditions, summarized in Table 3, applicable to the HMNs without and with the stopper (HMN/HMNS).

Figure 2.
Broken HMN due to incomplete curing. (a) Side view; (b) top view. Dashed white lines indicate chipped nozzles.

Table 3.
Variable settings for the multi-step HMN bio-fabrication.
- Design
The design of the MN device structure comprised two main parts: one containing the array of HMNs, and the other consisting of a fluid chamber (reservoir), as described previously [21], created in SolidWorks 2023 software (Dassault Systèmes, SolidWorks Corporation, Waltham, MA, USA). Two design changes were introduced to the HMN array, one being a reduction of the number of nozzles from 13 to 5 and the other the introduction of a stopper. While the former was introduced to enhance the resolution of characterization by eliminating the overcrowding per surface area, the purpose of the former is to control the prospective insertion depth in the skin phantom based on the nominal epidermis thickness of 150 µm.
The bottom layer (Figure 3a,b) included a 28.5 mm diameter (d2) flat disc of a height of 4.73 mm (h2) with a circular array of 5 microneedles. The dimensions of the cones are as follows: R, the base radius (D = 2R = 1600 μm); r, the tip radius (d = 2r = 800 μm), H the height (H = 3000 μm). The thickness of the stopper (d5 = 300 μm) is given by the difference in the outer diameter (d3) and inner diameter (d4) of the stopper (Figure 3c). The distance between the stopper and the tip of the microneedle (h3) is 150 μm with a needle/stopper fusion length (FL) of 77 μm; as such, the stopper contains two distinction sections, one where the stopper is fused with the microneedle and the other where the stopper is exposed (OL) (Figure 3d). A detailed drawing of the fluid chamber has been previously published [21].
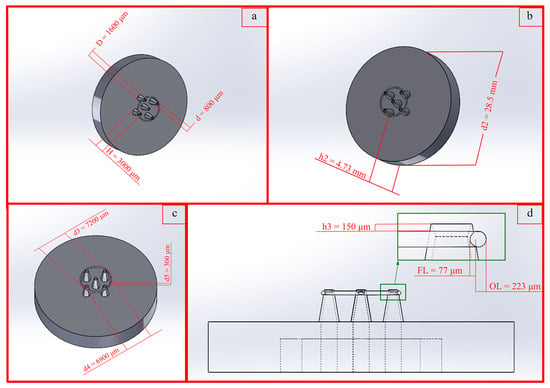
Figure 3.
SolidWorks drawings of the printed device with corresponding dimensioning. (a) Circular array of five hollow microneedles; (b) bottom layer of device; (c) stopper dimensions; (d) side view of bottom layer illustrating stopper–microneedle junction.
- 2.
- 3D Printing
3D printing was executed using a Formlabs Form 2 printer (Formlabs Inc., Sommerville, MA, USA, 2018), operating upon the principle of SLA, with a maximum resolution of 25 μm. To set the orientation of the device and to generate supports, the preprocessing software PreForm (Formlabs Inc., rev.2.16.0) was used. This software confirmed the scale of the part, the orientation, the placement of the build tray, and the resolution for the photoresin to be used. PreForm enabled the mobility of supports, once generated, to ensure that they were not placed at critical feature points of the device. Once these parameters were verified, the device was sent to the printer. Specifically, parts were placed in isopropyl alcohol (IPA, 70% v/v)), bathed for 20 min, and then placed in a HOEFER Scientific Model 1100 UV cross-linking unit, with a pre-set energy function of 120,000 µJ/cm2 for 10 min. The total processing time for 3D printing and washing the parts took over 5 h, with the ability to print three assemblies per batch.
The specific multivariate combination of CAD, 3D printing, and post-processing are summarized in the Table 3.
2.2.2. Inspection of 3D-Printed Parts
A total of 3 devices with and without the stopper design were inspected prior to assembly using transmission microscopy.
Quantitative inspection for the shrinkage at the tip radius (r) was conducted using an Olympus CKX53 transmission microscope/camera (Olympus XM10, Olympus, Waltham, MA, USA) equipped with CellSens Standard imagingsoftware version 1.12. In addition, the open/close state of the nozzles was recorded.
Qualitative inspection of the parts post-indentation tests at the nozzle tip for structural integrity and hydrogel deposition was conducted at a magnification of using a USB Digital Microscope with 300× magnification and a 5 M pixel image sensor (Mustech Electronics, Shenzhen City, China).
2.2.3. Skin Phantom Fabrication
Alginate slabs (3% w/v), made from steam-sterilized polymer, were cross-linked with calcium chloride (CaCl2) fabricated via the polyelectrolyte complexation of alginate after incubation in 1.5% (w/v) divalent salts for 20 min followed by saline washes using a previously established method [60]. Hydrogel films were punched for various tests using an adjustable plastic puncher to a final circular slab with a diameter = 12 mm.
2.2.4. Phantom Dimensional Verification
The average film thickness was measured using a caliper (Mitutoyo model #500–196–30, Kawasaki, Japan) to ensure a minimum thickness of 1 mm. The slabs were left in buffer until testing to avoid shrinkage. Approximately 60 s before testing, hydrogel films were taken out of the aqueous medium prior to mechanical characterization.
2.2.5. Profilometry
Profilometry was used to evaluate the hydrogel phantom flatness prior to and post-indentation. As during the tests the indentations were irreversible, they will be referred to as the puncture. Specifically, the Zeta-20 Optical Profilometer (KLA, Milpitas, CA, USA) was utilized for precise measurements of the puncture depth with and without the stopper design at an uncontrolled indentation rate. The light intensity was calibrated to 27%, and focus control was attained by adjusting the upper and lower limits for scanning by adjusting 200 number of steps. To analyze the punctured alginate slabs, a Gaussian filter with a 16.5 μm low pass and 1317.1 μm high pass was applied. Puncture thickness was then measured using the leveling function. For the unpunctured alginate slabs, no filtering was applied to preserve the surface profile information. For all images, the field of view was held constant at 1679 µm × 1317 µm.
2.2.6. Mechanical Testing
A two-fold mechanical characterization was carried on the hydrogel slabs subjected to microneedle penetration using the MACH-1 mechanical testing systems (Biomomentum Inc., Montreal, QC, Canada) calibrated by provided 10 kg and 25 kg load cells. A custom 3D-printed ring (o.d = 17.mm, i.d. = 15.4 mm, height = 18 mm) was used to confine the punched circular slab. All specimens were deposited on a 1 × 3 mm glass substrate. As the thickness of the slabs is 1 mm, strain and displacement have been used interchangeably in the figures.
- Base Substrate Characterization
According to Hooke’s law (Equation (1)), stress () and strain are proportional () to each where E is Young’s modulus in the elastic region.
Compression testing was conducted using a stainless steel (SS) flat indenter with a diameter of 12.5 mm on crosslinked alginate slabs. The experimentally determined two-dimensional Poisson’s ratio of (Equation (2)) was also calculated using the flat indenter, where εz and εx are strains in the parallel and normal directions to the applied compression. Using Equations (1) and (2), the shear modulus G was calculated using Equation (3).
Compression testing was also conducted using a spherical (SS) indenter (Ri = 3.75 mm) used also for hysteresis measurements. The Oliver Pharr method [61,62] was used to measure the hardness of the base layer based on the stiffness and indentation depth. Contact stiffness (S) is defined as the slope of the tangent line to the unloading hysteresis curve at the maximum indentation depth (hm), extended to the strain axis to obtain the corresponding tangent depth (htan). The contact depth of the spherical indenter (hc), the contact area (Ac), and the resulting hardness can be calculated using the following Equations (4)–(7):
Dynamic mechanical analysis was conducted in axial (compression) mode at a frequency (ω) of 0.05 Hz and displacement of 0.1 mm. The phase (δ), again given by Equations (8) and (9), is a measure of the cross-linking state of the hydrogel slab where E″ and E′ are the storage and loss moduli of the material, respectively. Lower phase angles resulting from a closer superimpostion of the elastic force and viscous strain curves are indicative of a higher degree of cross-linking and viscoelastic solid like behavior. This angle was calculated over multiple cycles and the result was generated by the software.
- 2.
- Viscoelasticity Characterization
Using a 3M™ (6969-2X60, adhesion strength to steel 34 in-lb), the HMN and HMNS configurations were sealed to the flat indenter. Subsequently, stress relaxation experiments were carried out at various amplitudes and compression rates outlined in Table 4 on all films at a constant relaxation rate of 0.01 gf/min. The ratio of the equilibrium force measured at the end of the relaxation period based on the peak force (F∞/Fmax) was plotted to normalize the data. As the experiments were carried out at a constant strain, the magnitude of the ratio was used to classify the relaxation as Maxwell type or Kelvin–Voigt. A ratio of 0.4 was used as the threshold for classification. Only the stress relaxation profiles classified as the Maxwell type were modeled by the Prony series given by Equation (10), where the relaxation modulus (in N/m2) is the sum of , which is the relaxation modulus at equilibrium and the individual moduli () per branch characterized by the respective relaxation constant (τi) [63,64,65].

Table 4.
Layout of experiments.
The curve-fitting app in MATLAB was used to fit the force profile to the Prony series. The projected areas calculated at the maximum indentation depth corresponding to Fmax were used to adjust the units to those of stress. Similarly, in order to generate the hysteresis curves, the ramp release function was used using the combinations outlined in Table 4.
- 3.
- Indentation Parameters
In order to characterize the penetration depth performance and the impact of the stopper, a screening design was used. The metric under observation was the maximum peak force (Fmax). The variables were the insertion depth (Amp), in mm), penetration rate (Rate, in mm/s), and time delay between the forward and reverse portions of the hysteresis loops (Delay, in s). The sequences in Runs A–D were programmed into the biomechanical analyzer and will be referred to as ramp-release experiments. Films named with capital roman letters will be addressed with and without a suffix “S” depending on whether they were subjected to examination via the HMN or HMNS, respectively.
2.2.7. Pycnometry
Density tests for each hydrogel were performed with the Anton-Paar Ultrapyc 5000 (Graz, Austria) in monolith mode where gas is introduced into the sample chamber and then expanded into a second empty chamber with a known volume. The pressure observed after filling the sample cell and the pressure discharged into the expansion chamber are measured, and the volume is calculated using Boyle’s law. Density is calculated by dividing the weight of the sample by the volume. Since the volume of pores is known, the measurement device calculates bulk density. Before measurement, the gels were punched into circles with a radius of 15.6 mm, weighted using a VWR scale model #VWR-224AC (VWR, Radnor, PA, USA) with a resolution 0.1 mg, and then loaded into the calibrated Anton Paar meso sample cell, characterized by a volume of 1.8 cm3 for testing. The pycnometer used nitrogen (N2) gas with a target pressure of 10.00 psi and temperature of 20.00 °C, run under the equilibrium mode. The instrument has a lower limit of detection of 0.1 mg/cm3, and the standard deviation reported for the measurements is a result of three consecutive cycles performed on the same film. The resulting density values were used to confirm the hypothesis of puncture for a subset of films subjected to the conditions of run B, using the following sequence: the baseline densities of each non-punctured hydrogel were determined, puncture testing on each hydrogel was conducted, and the densities of the punctured hydrogels were measured. Residual moisture was removed from the slabs prior to analysis. The hydrogel films were stored in buffer between post-punctures prior to pycnometry analysis.
2.2.8. Simulation
COMSOL (v 6.1) (COMSOL, Stockholm, Sweden) was used to create a time-dependent study of the indentation of a single HMN/HMNS using the Linear Structural Mechanics Module in contact mode. The fundamental equation used was the mechanical energy equation in tensor form (Equations (11) and (12)), where F is the deformation tensor, S is the second Piola Kirchhoff stress, Fv is the deformation force/volume, ∇u is the velocity field, and I is the identity matrix [66]. The geometry option was the 2D-asymmetric where the displacement u in cylindrical coordinates is translated in two-dimensional cartesian coordinates, illustrated by Equation (13).
The two-dimensional-mesh-generation system was used to solve the partial differential equation to be expanded to the 3D visualization of von mises stresses. Compatibility between the initial and boundary conditions of the displacement was established by multiplying the specified prescribed displacement and a piecewise function emulating the behavior of the mechanical analyzer according to the specifications in Table 4. Responses are compared in terms of the maximum force (Fmax) sensed at the tip of the HMN or HMNS by the biomechanical analyzer and simulated peak force using the boundary probe functionality in the software. As recommended by the COMSOL guidelines for contact modeling, the puncture edge of the needle was replaced with a rounded boundary [67]. The fillet radius of 1 × 10−3 µm was chosen across the HMN and HMNS at the location of the boundary probe. At values higher than 1 × 10−3 µm convergence, the system of equations became ill-conditioned. The shape of the stress relaxation plot as the software output converted to force relaxation by dividing the von mises stresses by the maximum projected surface was used as a basis of the comparison between the in silico and empirical findings. At last, the 3D representation of force distribution was consulted to compliment interpretations.
The mechanical properties of cured acrylate have a wide range depending on the formulation [68,69,70,71]. The cured microneedle was modeled as a linear elastic material with bulk properties obtained from the literature E = 3.8 GPa, ν = 0.35, ρ = 1190 kg/m3; the latter intrinsic property was taken from the built-in materials library. The linear viscoelasticity of the hydrogels was modeled using the experimental stress relaxation data, as well as the bulk properties (E, ν, G).
2.2.9. Statistical Analysis
Statistical analysis was conducted using MATLAB version R2021a (MathWorks, Natick, MA, USA). One-sided paired sample t-tests for comparing the bulk densities before and after puncture were conducted at a significance level (α) of 0.05. In addition, two sample t-tests were conducted to compare phantom equivalency priori to puncture for the above-stated density measurements.
3. Results
3.1. Dimensional Inspection of 3D-Printed Parts
Shown in Figure 4 are top views of magnified nozzles with a target CAD diameter of 640 µm (2r). The diameters post-cure are 400 ± 37 µm (N = 15, HMN nozzles) and 480 ± 53 µm (N = 15, HMNS nozzles)) based on the inspection of three parts for each microneedle design. Based on the measurements, the shrinkage at the indentation sites is 37.5% and 25% in the absence and presence of the stopper, respectively.

Figure 4.
Top view of nozzles for HMN (top row (a,b)) and HMNS (bottom row (c,d)) device configurations post-cure, illustrating differential shrinkage rates for the HMN (37.5%) and the HMNS (25%), respectively. The dashed circles represent 3D-printing debris/fibers.
In addition, all nozzles were open; however, the cleaning time needs to be increased to remove the cured fiber-like artefacts of resin on the nozzle, as demonstrated in Figure 4a–c.
3.2. Skin Phantom Fabrication and Dimensional Verifcation
Shown in Figure 5 are the mold-casted slabs characterized by thickness (th) measured using a caliper. Thicker films were fabricated by using 5 mL (th = 2 mm ± 0.28 mm) of alginate instead of 3 mL (th = 1 mm ± 0.073 mm) yielding the thinner slabs. Only the thinner slabs were used for the quantitative characterization of puncture and viscoelasticity.

Figure 5.
Alginate film preparation. (a) Mold-casting on 10 mm × 30 mm microscope slides; (b) cross-linked thin calcium alginate gels; (c) punched specimen for analysis obtained from thin slabs; (d) (top) thicker 2 mm ± 0.28 mm slabs, and (bottom) thin 1 mm ± 0.073 mm slab used for quantitative characterization.
3.3. Profilometry
Shown in Figure 6 are profilometry measurements. For these measurements, the average roughness of the control film is 16.2 µm across (Figure 6a). The puncture depth (dp) for the metallic commercial 0.75 mm blunt-ended syringe is 73.8 µm (~0.74 mm) with a partial but smooth imprint across the perimeter. The purpose of this step was to ensure the proper focus conditions with a relative error of 1.3% for estimating the depth.

Figure 6.
Profilometry measurements on alginate films using uncontrolled displacement rates. (a) Baseline film characterization pre-puncture with an average flatness of 16.2 µm; (b) partial smooth indentation with a standard 0.75 mm blunt-ended needle averaging 73.8 µm in imprint thickness; HMN puncture partial imprint for the middle nozzle (c) and side nozzle (d) averaging 27 µm and 53 µm in thickness, respectively; HMNS, more uniform puncture imprint for middle nozzle (e) and side nozzle (f), averaging 17 µm and 59 µm, respectively. Light orange lines indicate the rough puncture contour characterized by peaks and valleys. The bold orange line and corresponding arrows in the scan illustrate the contribution of the stopper ring in the HMNS. The red scale bar in all images represents the same length of 149 µm.
Shown in Figure 6c–f is the comparison between the HMN and HMNS for the center and right-hand side nozzle. This comparison is essential as the center nozzle is not in contact with the stopper in either of the designs. For both device configurations, the resultant depth denoted by bidirectional red arrows is 50% to 70% less for the center (Figure 6c,e) than the side needles denoted by blue arrows (Figure 6d,f). In fact, the puncture depth of 17 µm for the center nozzle for the HMNS design (Figure 6e) is close to the variation in the film flatness, averaging 16.2 µm. This suggests nozzle-to-nozzle differences in puncture performance and the need for additional post-processing steps, such as surface finish post-cure or a redesign of the center nozzle to be more robust to the curing process. The presence of the stopper in the HMNS design renders the puncture more pronounced and uniform (Figure 6e,f).
Comparing the standard metallic needle imprint (Figure 6b) to the microneedle designs, no concentricity of imprint is observed in the case of the cured parts. There is a threefold explanation behind this discrepancy. The first one is inherent to the slanted design of the microneedle tip. Surface roughness along the imprint contours, highlighted by dashed orange lines in Figure 6, accounts for the second source of imprint non-uniformity. The presence of the stopper is a tertiary contributor to the tip surface roughness, for the nozzle on the edge, resulting in additional peaks and valleys reflected in the profilometer scan (Figure 6f).
3.4. Mechanical Testing
- Substrate Characterization
The range of the properties has been modulated based film drying times of 12 h and 18 h prior to cross-linking. Two batches per drying period have been characterized. The reported averages are translated into ranges and summarized in Table 5.

Table 5.
Mechanical properties of the base substrate.
A subset of hydrogel mechanical characterization was conducted using the spherical indenter (Figure 7a). The shape of the force displacement curve in Figure 7b is indicative of a non-hookean hyperelastic behavior. Based on this hysteresis curve and Equations (3)–(6), the ranges of contact stiffness (S) and hardness (H) were calculated to be 900–1225 N/mm and 31–36.5 (N/mm2) for the phantoms. For these films, the phase angle (δ) ranged between 5 and 11°, determined by the software. A sample dynamic mechanical analysis curve is presented in Figure 7c. There is a negligible lag between the cyclical force and strain curves, indicative of a fully cross-linked alginate film. Initial strain softening can be observed before stabilization at cycle 3. Compression using the spherical indenter did not result in any film puncture.
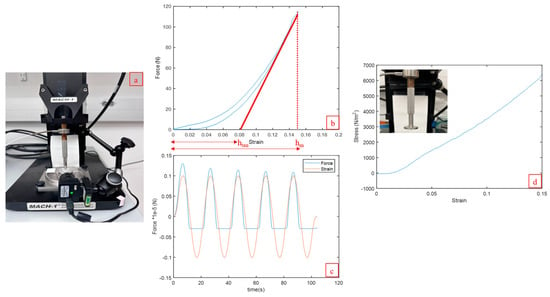
Figure 7.
Mechanical characterization of cross-linked alginate films using the MACH-1biomechanical analyzer. (a) Setup for confined compression enabled by a 3D-printed ring using a metallic spherical indenter; (b) hardness and contact stiffness calculations based on the hysteresis loop using the setup in (a) with the analyzer program to indent 0.15 mm at a rate of 0.1 mm/s with a delay of 1 s prior to unloading (run B); hm and htan are the maximum and tangent indentation depths, respectively; (c) dynamic mechanical analysis programmed for five cycles using the setup in (a) for a frequency of 0.05 Hz and displacement of 0.1 mm scaled to illustrate the negligible lag between the cyclical force and strain curves and initial degree of strain softening as the peak forces decrease before stabilization; (d) nominal stress/strain curve for the determination of Young’s modulus using the flat indenter and the linear portion of the curve.
The shape of the stress–strain is curve was dependent on the projected surface area of the indenter. Specifically for a flat indenter, based on the hookean behavior of the films, the modulus ranged from 41 kPa to 46.5 kPa (Figure 7d). This linear trend differs from the curved loading phase observed in Figure 7a. This discrepancy may be due to the variation in film thickness (1 mm ± 0.073 mm) resulting in uneven contact for the flat indenter.
The batches for which the results were obtained are summarized in Table 5. Film 1 was used for runs in Table 4. Film 2 was used for the confirmation runs.
- 2.
- Viscoelastic Characterization Using Microneedles
Shown in Figure 8a are representative ramp release profiles for the alginate films subjected to indentation experiments comprised of loading, stress relaxation, and unloading cycles programmed to the layout in Table 4. The corresponding experimental set-up is illustrated in Figure 8b. For all runs, the peak force (Fmax) is higher in the presence of the stopper, as reflected in Figure 8c. The maximum difference of 2.31 N is observed for run B for an insertion depth (Amp) of 150 µm, penetration rate (Rate) of 0.1 mm/s, and a 1.5 s time delay (Delay) between the forward and reverse portions of the hysteresis loops.

Figure 8.
Ramp release experiments with the microneedles at varying indentation depths, rates, and time delays between the forward and reverse portions of the hysteresis loops denoted as runs A–D defined in Table 4. (a) Sample stress relaxation profiles for the HMNS; (b) HMN sealed to the analyzer for a viscoelastic characterization connected to the analyzer and inset; (b1) HMNS configuration approaching the confined surface for indentation; (c) peak force difference (ΔFmax) for runs A–D between the HMNS and HMN configurations.
The experimental matrix in Table 4 was duplicated based on the phantoms to focus on the stress relaxation portion of the indentation cycles. The normalized stress relaxation trends subjected to HMN and HMNS are presented in Figure 9a. Based on the criteria of the threshold ratio of 0.4 for the equilibrium force measured at the end of the relaxation period by the peak force (F∞/Fmax), the viscoelastic behavior of the films can be classified as Maxwell behavior. Subsequently, these stress relaxation data were modeled using Equation (10) to find the best fit for the Prony series constants. The constants (Ei), as well as the respective coefficients of determination, R2, are presented in Table 6 and Table 7.
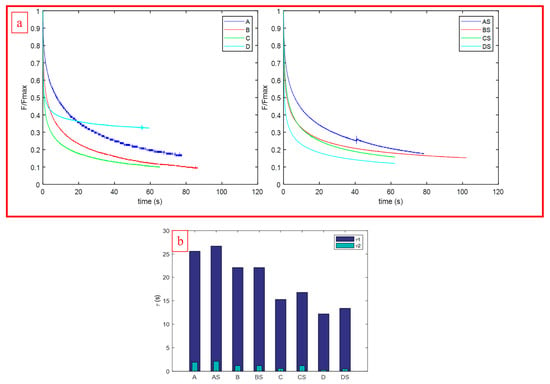
Figure 9.
Stress relaxation experiments with the microneedles at varying indentation depths and rates for viscoelastic behavior classification denoted as runs A–D. The suffix “S” indicates the HMNS configuration. (a) Normalized stress relaxation profiles for the HMN (left) and HMNS (right) configurations displaying biphasic Maxwell behavior. (b) Comparative norms of the biphasic stress relaxation constants (τ1, τ2) modulated based on process parameters.

Table 6.
Summary of stress relaxation results and the goodness of fit for the Prony series.

Table 7.
Prony series constants as a function of differential insertion depth and strain rates.
Shown in Figure 9b is two-fold evidence of phantom uniformity, as the response to stress relaxation plotted in terms of the empirical relaxation constants (τ1, τ2) varies with the indentation rates and parameters, as designed, and the magnitudes of the constants are comparable between microneedle types. In essence, phantom fabrication will not be a noise factor in assessing puncture.
- 3.
- Microneedle Inspection Post-Indentation
Shown in Figure 10 is the comparative examination of HMN and HMNS signature indentation for Run B. This run was chosen as a maximum indentation force difference was registered between the microneedle configurations as previously demonstrated in Figure 8c. Hydrogel and dried saline residues that accumulated as a result of indentation are presented in Figure 10. Hydrogel accumulation is observed mainly on the needles in the absence of the stopper (Figure 10b,c). For the HMNS (Figure 10e,f), the bulk of the hydrogel is distributed between the ring and the nozzles suggesting different indentation/puncture mechanisms in the presence and absence of the stopper. In addition, there was no evidence of fracture or micro needle-bending.
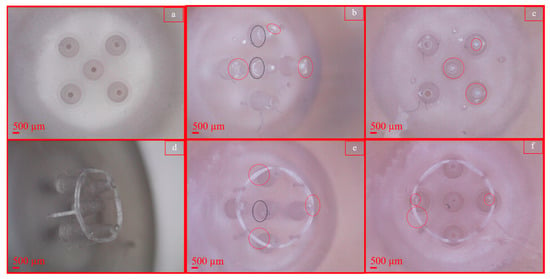
Figure 10.
Microscopic examination of microneedles post-indentation for Run B, Film 1: HMNs (top row), HMNS (bottom row) before (a,d) and after puncture (b,c,e,f). (a,d) Before indentation (control), top view (a), isometric view (d); (b,c) hydrogel residues outlined by red dashed circles present on HMN nozzles; (e,f) hydrogel residues outlined by red dashed circles distributed on the stopper ring and HMNS nozzles. A black dashed circle represents saline residue.
3.5. Pycnometry
In order to distinguish mass re-distribution in soft matter from mass-loss post-indentation, the bulk density was measured for the runs with an indentation depth of 0.15 mm. Results of a paired t-test presented in Table 8 indicate a significant decrease in density pre- (baseline) and post-indentation for both runs examined. At a significance level of α = 0.05, p values of 9.60 × 10−5 and 6.08 × 10−6 were calculated for the HMNS and HMN, respectively, with corresponding recorded mass losses of 28.2 mg and 29.6 mg.

Table 8.
Comparative bulk density measurements between HMN and HMNS.
The effect of phantom-to-phantom variation for baseline calculations may be excluded as there is no significant difference between the bulk densities prior to puncture (p = 0.93).
3.6. Validation of Puncture
The properties of the single alginate hydrogel network were tuned to decrease the phase angle determined based on DMA from 11° (Film 1) to 5° (Film 2) resulting a higher cross-linked phantom.
Using freshly printed HMNS and film-drying conditions extended from 12 h to 18 h prior to crosslinking, the indentation runs A–D were conducted according to the scheme in Table 4 for ramp release experiments. The suffix “S2” associated with these experimental conditions refers to the usage of Film 2 as the phantom. The performance of a 21 G hypodermic stainless steel syringe with a slanted tip (i.d. 0.514 mm, o.d 0.819 mm) subjected to the indentation profile of Run B was also examined. This needle was chosen as the inner diameter is closest to the post-shrinkage average value measurements associated with the HMNS (d = 480 ± 53 µm).
Mechanical analysis of the puncture are represented in Figure 11a,b, as well as complimentary programmed displacement plots (Figure 11c). The large magnitude of the peak force for Run C (33 N) is attributed to the needle touching the surface of the glass substrate on which the hydrogel film is resting (verified visually, not shown). The indentation rate of run D may have been too fast for denting the substrate, as almost no reaction force is detected, as displayed by the flatness of the hysteresis curve (Figure 11b). Puncture occurs for Run B at a peak force of 8.3 N (Figure 11a) for this stiffer substrate (Film 2), as compared to a puncture force of 3.7 N for Film 1 (Figure 8a). Visual proof of puncture for both hydrogel films, for an insertion depth (Amp) of 150 µm, penetration rate (Rate) of 0.1 mm/s, and a 1.5 s time delay (Delay) between the forward and reverse portions of the hysteresis loops, is presented in Figure 12.
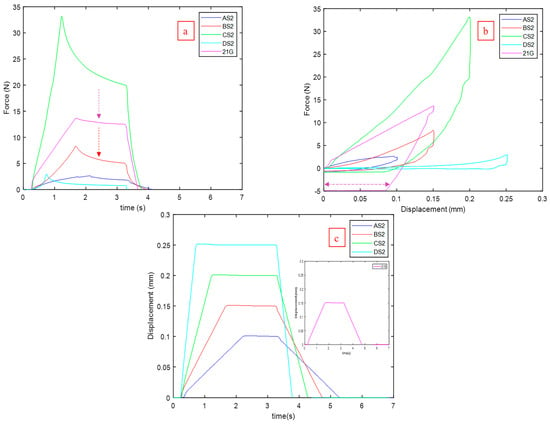
Figure 11.
Mechanical analysis of puncture using a freshly printed HMNS for indentation according to process conditions for runs A–D with the suffix “S2” referring to Film 2, a higher cross-linked phantom. The 21 G needle was indented under the protocol of Run B. Puncture was confirmed for Run B (BS2). (a) Comparative ramp release profiles with dashed arrows comparing the negligible stress relaxation component of the metallic needle to the HMNS relaxation. (b) Comparative hysteresis plots highlighting the plastic strain signature of the 21 G needle denoted by the reversible purple arrow in contrast to viscoelastic recoveries. (c) Programmed displacement profiles corresponding to the ramp release profiles.

Figure 12.
Multi-scale proof of puncture using HMNS on alginate skin phantom. (a,b) Punctured slabs captured with (b) and without (a) a 3D printed compression confinement ring for confirmation of run BS2 on Film 2; (c) puncture imprint for run BS conducted on Film 1; (d) microscopic image obtained from resultant puncture for run BS conducted on Film 1.
The standard 21 G needle puncture was characterized by a peak force of 13.7 N. Visual inspection confirmed that the metallic needle did not touch the glass substrate but punctured the hydrogel. Comparing the hysteresis profiles in Figure 11b, there is a distinct difference between the recovery for the HMNS runs AS2-DS2 and the 21 G needle. For the HMNS, complete viscoelastic recovery was enabled by the mechanical analyzer post-stress relaxation. For the metal, the extent of stress relaxation is minimal and during the unloading period, plastic strain is observed followed by return to the programmed original position. For the same displacement profiles denoted as BS2 and 21 G in Figure 11b, indentation has resulted in irreversible deformation for the SS needle as compared to a plausible local mass redistribution in the presence (Runs BS2 and CS2) and absence of puncture Runs AS2 and DS2).
3.7. Simulation
In the absence of additional metrology and surface finish post-curing, combining the ramp release profiles summarized in Table 4, the bulk and measured viscoelastic phantom properties as inputs, puncture simulations were initiated. Mass loss was not taken into account, as the effect of a single nozzle has been simulated; thus, the density used in the simulation corresponds to the baseline one measured in Run B (ρ = 1.412 g/cm3). The suffix “S” for runs A–D indicates the presence of the stopper.
This simulation process is demonstrated for Run A (Figure 13) for which the model was validated. The reasoning behind this choice is that the indentation depth for this run is 0.1 mm and the HMNS stopper ring theoretically does not touch the surface. Thus, the response for both designs should be very close in terms of the peak force. Validation using identical viscoelastic properties for the films was carried out, with the assumption being that the biphasic relaxation time constants (τ1, τ2) outlined in Table 7 ([τ1HMN = 1.9 s, τ2HMNS = 25.6 s] vs. [τ1HMNS = 2.1 s, τ2HMNS = 26.7 s]) are very close, and the ratio of (F∞/Fmax) levels is at approximately 20% (Figure 9A). The resultant simulated peak forces were 0.7 N and 0.95 N for the HMN and HMNS, with a common shape of the hysteresis loop, as presented in Figure 13b,c. The reason for the discrepancy between the simulated peak forces is that the software takes into account the reactive forces as a result of insertion for the needle/stopper interface, absent in the case of the HMN needle. As the peak force difference is 0.15 N, the model was considered to be validated.
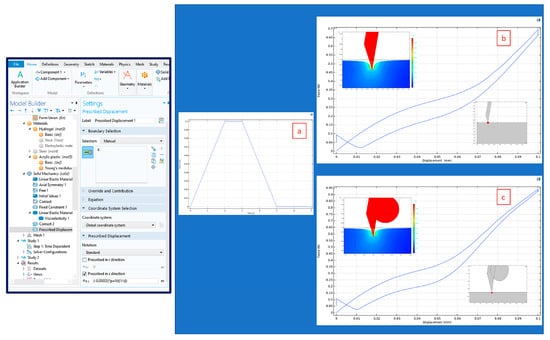
Figure 13.
Model validation using Run A. (a) Generated displacement profile emulating the biomechanical analyzer generated using the COMSOL interface (left); (b) hysteresis plot with inset displacement (top left) measured using the boundary probe (bottom right) for the HMN; (c) hysteresis plot with inset displacement (top left) measured using the boundary probe (bottom right) for the HMNS.
Two sets of CAD dimensions were used for the HMNS. The first set (Original Configuration) includes the dimensions as seen in the SolidWorks file, displayed as Figure 2a–d. The second set includes taking the printing resolution of 25–50 µm into account, combining it with the experimental biomechanical analyzer data, and hypothesizing a likelihood estimate of the geometry (Proposed Configuration).
There is no evidence of nozzle impingement based on the visual inspections shown in Figure 10, and there is evidence of puncture and solid imprint of the stopper on the hydrogel (Figure 12) at the programmed indentation depth of 0.15 mm (Run B). By shortening the fusion length (FL) from 77 µm to 42 µm and reducing the stopper height (h3) from 150 µm to 100 µm, the puncture forces are in the same order of magnitude as the experimental measurements. These modifications are within the printing accuracy range of the V4 Clear resin and reflected in the comparative results presented in Figure 14 and Figure 15.
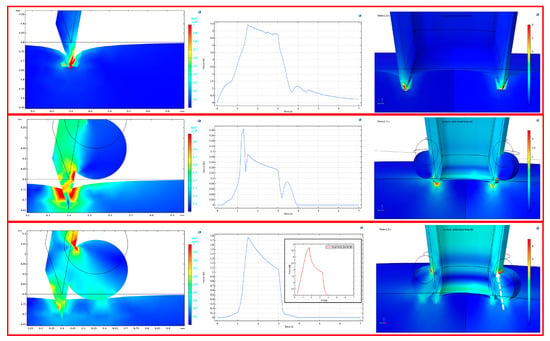
Figure 14.
Simulated indentation for Run B with the displacement profile (left column), stress profile (middle column), and 3D solid view of the puncture at maximum force (right column). (top row) HMN; (middle row) HMNS Original Configuration; (bottom row) HMNS Proposed Configuration, (inset) alignment of the experimental data ramp release profile (red curve) with simulation (blue curve); the white arrow indicates the reaction force at the microneedle fusion interface.
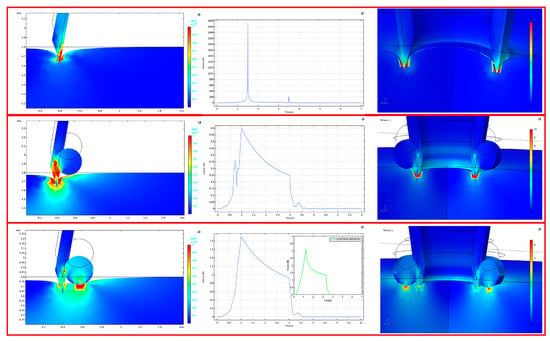
Figure 15.
Simulated indentation for Run C with the displacement profile (left column), stress profile (middle column) and 3D solid view of the puncture at maximum force (right column). (top row) HMN; (middle row) HMNS Original Configuration; (bottom row) HMNS Proposed Configuration, (inset) alignment of the experimental data ramp release profile (green curve) with simulation (blue curve).
The simulated Proposed Configuration confirms the experimental trend and differs from the experimental results by a factor of approximately 2. The shape of simulated force vs. time curves also matches the experimental observations produced by the biomechanical analyzer (Figure 14 and Figure 15, bottom row, inset ramp release profiles). Both the displacement profiles and 3D extrusions highlight the imprint of the stopper on the gel, absent in the Original Configuration.
The comparative experimental and simulation results have been summarized in Table 9. The model is not a good predictor of the HMN performance as the indentation rate and depth increase synergistically (Runs A and C) even after creating a fillet at the nozzle tip to solve the convergence issues. This may be an artefact of not including mass loss in the model. The model also does not converge for runs D and DS (high amplitude, high strain rate), as these rates were experimentally proven to be too fast for effective indentation/puncture in the case of HMNS (Figure 11b, run DS2).

Table 9.
Comparison between measurements and simulation in terms of peak force.
Similarly, without taking into account the hypothesized printing resolution errors and shrinkage in the Original Configuration, the predicted force decreases instead of increasing for runs AS-CS. The convergence of the experimental results for runs BS and CS lends credence to the adoption of the Proposed Configuration.
4. Discussion
4.1. Dimensional Inspection of 3D-Printed Parts
Based on the measurements of the shrinkage at the indentation sites, the presence of the stopper prevents shrinkage by 12.5%. As there is no evidence of nozzle impingement or blockage, future replication and additional metrology measurements should be conducted to validate the trends with the current aspect ratio.
In relation to the collective-material-shrinkage effects (on the h3 deviation from design), the effects of the slant posts are deemed secondary (causing a symmetrical tensile load on the stopper-ring’s peripheral surface), whereas the effects of the stopper-thickness diameter and the nozzle height hold more primary positions, as reflected in the simulation results of the Proposed Configuration.
4.2. Profilometry
Results support the role of the stopper introduction, as the puncture is more uniform for the HMNS. As such, it can be hypothesized that the role of the stopper can be extended to structural support of the peripheral nozzles, as was the case in the shrinkage. Additional surface modifications post-curing, such as surface finish followed by metrology, is recommended to level out the part so that the efficacy of the central needle in the puncture is enhanced.
4.3. Mechanical Testing
The mechanical behavior of alginate is dictated by the shape of the indenter. In case of flat and spherical indenters, hyperelastic and hookean profiles are observed. For spherical indentation, the hardness values for single-network alginate films of 31 kPa and 36.5 kPa enable the classification of the films according to the Density Type durometer scale as extra-soft to soft, with an extrapolated Shore D hardness of 0 [72,73]. According to the literature, cured acrylate-based, from which the microneedles under examination are made, can be classified under Shore D hardness ranging from 47 to 57, classified as hard [69,74]. Young’s modulus of alginate depends on the ratio of the glucuronic to mannuronic constituent acids, morphology of the cross-linked structure (film vs. sphere), cross-linker type and presence of a plasticizer, slab drying method prior to cross-linking, swelling ratio, strain rate, and sterilization scheme [21,46,75,76,77,78,79,80,81]. For calcium alginate, this wide range is 25 kPa–50 MPa. For the films in this study the range is 41 kPa–46,500 kPa, within the same order of magnitude of the hardness range of 31 kPa–36.5 kPa. For Film 1, with a phase angle of 11° determined via DMA, Maxwell relaxation was observed. For Film 2, with a phase angle of 5°, the scope of the modeling will be extended to Voigt relaxation.
Qualitative inspection post-indentation should be extended to quantitative imaging where a reversible imprint should be distinguished from irreversible mass redistribution or mass loss. This in turn will result in a stronger correlation of puncture characterized by mass loss at a given indentation depth. Screening experiments have identified fluorescent microscopy or alternative imaging modalities [59,82] as suitable methods.
4.4. Pycnometry
There is a significant difference in bulk density pre- and post-puncture for the examined films for both the HMNS and HMN designs. This change in density ( may be attributed to two sources. The first contributor is water loss during indentation from the porous slabs. As the films were allowed to rehydrate post-indentation in buffer for at least for 5 min prior to analysis via pycnometry, it could be assumed that there are other contributors to density variation for the puncture. The proposed imaging modalities post-indentation will lend credence to this hypothesis. Furthermore, stress relaxation models have been confined to viscoelasticity. Given the porous nature of the hydrogel, poroviscoelasticity modeling will enable the quantification of solvent diffusion times under stress, and a longer time period than 5 min may be necessary for solvent diffusion into the punctured slab to measure the adequate bulk density [83,84,85].
4.5. Simulation
It is hypothesized that the projected deviation (from design) of the differential height of the nozzle-tip from the stopper (h3) is predominantly governed by the equipment-specified printed-material resolution of 25–50 µm. This is in contrast to other potential contributors to the height differential deviation from design, such as the collective-material shrinkage, including the nozzle, the stopper ring, and the four supporting slant posts connecting the stopper ring to the platform of the printed structure. Although shrinkage was measured, it was assumed that each part shrunk evenly. Additionally, metrology will enable verification of the above assumptions and adequately consider the shrinkage effects.
Using the HMNS design, simulation enabled the illustration of printing resolution limitations using custom viscoelastic properties. At a simulated insertion depth of 0.15 mm (puncture) and 0.2 mm (post-puncture), the simulated peak forces using the proposed configuration are approximately half the empirical values (Table 9). The discrepancy of the peak force magnitudes may be justified as the biomechanical characterization was limited to viscoelasticity and neither poroviscoelasticity nor hyperelasticity were chosen. Another reason for the discrepancy could be the fact that a single needle was modeled instead of the assembly of frusta. Variations were seen in nozzle-to-nozzle performance in the profilometry results, and if the indentation stresses are not normally distributed, the average does not reflect individual deformation. Related to the latter, the Prony series constants were also used as intrinsic properties scaled to the maximum projected area of an ideal CAD dimensioned nozzle.
3D visualization illustrates forces that the biomechanical analyzer does not pick up, namely reaction forces resulting from puncture. From the microneedle perspective, an example of such force could be the microneedle/stopper interface reaction force illustrated in Figure 14 (bottom row, right column) or the hydrogel viscoelastic memory.
4.6. Implications of the Research
In this study, SLA was used for the reproducible feature incorporation of a stopper into solid hollow microneedles in order to actively and precisely control the puncture depth within the alginate skin phantoms. Currently, the epidermis-targeted delivery of cells in peer-reviewed literature is restricted to dissolvable cryoMNs [9] or transport through porous and dissolvable patches [32,33], which are not suitable for microencapsulated cell delivery. The HMNS withstood the mechanical impact of the indentation/puncture, with reproducible puncture observed at the target design height of 150 µm based on two sets of steam-sterilizable alginate slabs with modulated stiffnesses to withstand a range of puncture forces.
Key findings enabling the observations above based on extensive experimentation/simulation and recommendations are summarized below in Table 10.

Table 10.
Key findings and recommendations.
5. Conclusions
The dual objectives of this research study, which were to design a novel HMN feature to limit the puncture depth to 150 µm, using a biocompatible phantom formulated to withstand a force of 6 N, have been met. Visual proof of puncture for a programmed insertion depth (Amp) of 150 µm, penetration rate (Rate) of 0.1 mm/s, and a 1.5 s time delay (Delay) between the forward and reverse portions of the hysteresis loops have been recorded for the HMNS. Puncture was observed for the HMNS and a 21 G SS slanted-tip SS needle under the process conditions stated above at peak forces of 8.3 N and 13.7 N, respectively, by using a 1 mm steam-sterilized alginate cross-linked substrate (S = 1225 N/m, H = 36.5 N/mm2). The alginate layer’s tunable properties may accommodate the injection of extruded mammalian cells into the phantom and will offer a microenvironment to monitor the fate of the cell line. This advantage, in turn, will widen the scope of the pre-clinical study to microencapsulated cell delivery, previously limited by the lack of active control of the HMNS penetration depth. In the absence of costly detailed metrology, simulation using the measured viscoelastic properties of the phantoms in conjunction with the programmed displacement of the mechanical analyzer used as inputs highlighted the possibility of printing resolution errors. With these assumptions, the predicted peak force values were half the empirical ones for the HMNS at depths of 0.15 mm (puncture) and 0.2 mm (post-puncture). Additional metrology is required to decouple shrinkage from the printing resolution, resulting in a more accurate overall process-tolerance estimation for SLA bio-fabrication. Surface finish post-curing may be coupled to metrology to elucidate the effect of surface roughness on the uniformity of the puncture in the presence and absence of the stopper. In parallel, quantitative microscopic test methods and poroviscoelastic modeling need to be explored to improve pycnometry testing protocols in support of the creation of a classification system to distinguish a reversible imprint from irreversible mass redistribution or mass loss as a result of the puncture. At last, there are currently no biomechanical cues indicative of having surpassed the epidermis thickness other than the stopper height, which itself is subject to printing tolerances and unmeasured shrinkage. Future efforts will include the use of biocompatible composite films [39,40,41,42] with a density gradient to be used as soft sensors to compliment the active control feature of the stopper. Based on the successful incorporation of the stopper into the solid microneedles, the insertion height of this feature may be modulated to reach precisely deeper targeted locations in the skin or tissue.
Author Contributions
Conceptualization, M.M.-M. and K.M.D.; methodology, K.M.D., A.Y.S.K., J.R.A., R.A., M.B.M., M.M.D. and L.M.E.; software, M.M.-M., K.M.D., R.A., J.R.A. and A.Y.S.K.; validation, A.Y.S.K. and J.R.A.; formal analysis, J.R.A., A.Y.S.K. and M.M.-M.; investigation, K.M.D., A.Y.S.K., J.R.A. and R.A.; resources, M.M.-M.; data curation, A.Y.S.K.; writing—original draft preparation, K.M.D., J.R.A. and R.A.; writing—review and editing, M.M.-M.; visualization, M.M.-M.; supervision, M.M.-M.; project administration, M.M.-M.; funding acquisition, M.M.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Science Foundation MRI Program (Award ID 2216061) enabling the purchase of the pycnometer. The authors would like to acknowledge the generous support of the Santa Clara University’s School of Engineering Senior Design funds.
Data Availability Statement
The bulk density data generated from pycnometry experiments can be found at the following link: Github.com/SCUMRI/Applied-Mechanics, accessed on 17 March 2024. GitHub—SCUMRI/Applied-Mechanics.
Acknowledgments
The authors would like to acknowledge the generous support of Santa Clara University’s Clare Boothe Luce and Student Research Faculty Development scholarship funds. Access to the profilometry equipment was graciously granted by Emre Araci.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to resolve spelling and grammatical errors in Equation (1). This change does not affect the scientific content of the article.
References
- Chen, B.Z.; Zhao, Z.Q.; Shahbazi, M.A.; Guo, X.D. Microneedle-based technology for cell therapy: Current status and future directions. Nanoscale Horiz. 2022, 7, 715–728. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.; Chen, S.; King, B.; Lin, H.; King, K.; Akhtar, F.; Emaminejad, S.A. 3D-printed microfluidic-enabled hollow microneedle architecture for transdermal drug delivery. Biomicrofluidics 2019, 13, 064125. [Google Scholar] [CrossRef] [PubMed]
- Economidou, S.N.; Uddin, J.; Marques, M.J.; Douroumis, D.; Sow, W.T.; Li, H.; Reid, A.; Windmill, J.F.C.; Podoleanu, A. A novel 3D printed hollow microneedle microelectromechanical system for controlled, personalized transdermal drug delivery. Addit. Manuf. 2021, 38, 101815. [Google Scholar] [CrossRef]
- Hu, Z.; Meduri, C.S.; Ingrole, R.S.J.; Gill, H.S.; Kumar, G. Solid and hollow metallic glass microneedles for transdermal drug-delivery. Appl. Phys. Lett. 2020, 116, 203703. [Google Scholar] [CrossRef]
- Ren, Y.; Li, J.; Chen, Y.; Wang, J.; Chen, Y.; Wang, Z.; Zhang, Z.; Chen, Y.; Shi, X.; Cao, L.; et al. Customized flexible hollow microneedles for psoriasis treatment with reduced-dose drug. Bioeng. Transl. Med. 2023, 8, e10530. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.X.; Nguyen, C.N. Microneedle-Mediated Transdermal Delivery of Biopharmaceuticals. Pharmaceutics 2023, 15, 277. [Google Scholar] [CrossRef] [PubMed]
- Gualeni, B.; Coulman, S.A.; Shah, D.; Eng, P.F.; Ashraf, H.; Vescovo, P.; Blayney, G.J.; Piveteau, L.-D.; Guy, O.J.; Birchall, J.C. Minimally invasive and targeted therapeutic cell delivery to the skin using microneedle devices. Br. J. Derm. 2018, 178, 731–739. [Google Scholar] [CrossRef] [PubMed]
- Iliescu, F.S.; Teo, J.C.M.; Vrtacnik, D.; Taylor, H.; Iliescu, C. Cell therapy using an array of ultrathin hollow microneedles. Microsyst. Technol. 2018, 24, 2905–2912. [Google Scholar] [CrossRef]
- Chang, H.; Chew, S.W.T.; Zheng, M.; Lio, D.C.S.; Wiraja, C.; Mei, Y.; Ning, X.; Cui, M.; Than, A.; Shi, P.; et al. Cryomicroneedles for transdermal cell delivery. Nat. Biomed. Eng. 2021, 5, 1008–1018. [Google Scholar] [CrossRef]
- Xenikakis, I.; Tsongas, K.; Tzimtzimis, E.K.; Katsamenis, O.L.; Demiri, E.; Zacharis, C.K.; Georgiou, D.; Kalogianni, E.P.; Tzetzis, D.; Fatouros, D.G. Transdermal delivery of insulin across human skin in vitro with 3D printed hollow microneedles. J. Drug Deliv. Sci. Technol. 2022, 67, 102891. [Google Scholar] [CrossRef]
- Resnik, D.; Možek, M.; Pečar, B.; Janež, A.; Urbančič, V.; Iliescu, C.; Vrtačnik, D. In Vivo Experimental Study of Noninvasive Insulin Microinjection through Hollow Si Microneedle Array. Micromachines 2018, 9, 40. [Google Scholar] [CrossRef] [PubMed]
- Abd-El-Azim, H.; Tekko, I.A.; Ali, A.; Ramadan, A.; Nafee, N.; Khalafallah, N.; Rahman, T.; Mcdaid, W.; Aly, R.G.; Vora, L.K.; et al. Hollow microneedle assisted intradermal delivery of hypericin lipid nanocapsules with light enabled photodynamic therapy against skin cancer. J. Control. Release 2022, 348, 849–869. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Zheng, G.; Wen, J.; Yang, J.; Yang, Q.; Zheng, X.; Yan, Q. Construction and application of microneedle-mediated photothermal therapy and immunotherapy combined anti-tumor drug delivery system. Drug Deliv. 2023, 30, 2232950. [Google Scholar] [CrossRef] [PubMed]
- Fang, A.; Wang, Y.; Guan, N.; Zuo, Y.; Lin, L.; Guo, B.; Mo, A.; Wu, Y.; Lin, X.; Cai, W.; et al. Porous microneedle patch with sustained delivery of extracellular vesicles mitigates severe spinal cord injury. Nat. Commun. 2023, 14, 4011. [Google Scholar] [CrossRef] [PubMed]
- Makvandi, P.; Kirkby, M.; Hutton, A.R.J.; Shabani, M.; Yiu, C.K.Y.; Baghbantaraghdari, Z.; Jamaledin, R.; Carlotti, M.; Mazzolai, B.; Mattoli, V.; et al. Engineering Microneedle Patches for Improved Penetration: Analysis, Skin Models and Factors Affecting Needle Insertion. Nano-Micro Lett. 2021, 13, 93. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Namjoshi, S.; Benson, H.A.E.; Kumeria, T.; Mohammed, Y. Skin biomechanics: Breaking the dermal barriers with microneedles. Nano TransMed 2022, 1, 9130002. [Google Scholar] [CrossRef]
- Abd, E.; Yousef, S.A.; Pastore, M.N.; Telaprolu, K.; Mohammed, Y.H.; Namjoshi, S.; Grice, J.E.; Roberts, M.S. Skin models for the testing of transdermal drugs. Clin. Pharmacol. Adv. Appl. 2016, 8, 163–176. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Liu, X.; Fu, Y.; Song, Y. Recent advances of microneedles for biomedical applications: Drug delivery and beyond. Acta Pharm. Sin. B 2019, 9, 469–483. [Google Scholar] [CrossRef]
- Kulkarni, D.; Gadade, D.; Chapaitkar, N.; Shelke, S.; Pekamwar, S.; Aher, R.; Ahire, A.; Avhale, M.; Badgule, R.; Bansode, R.; et al. Polymeric Microneedles: An Emerging Paradigm for Advanced Biomedical Applications. Sci. Pharm. 2023, 91, 27. [Google Scholar] [CrossRef]
- Kyser, A.J.; Fotouh, B.; Mahmoud, M.Y.; Frieboes, H.B. Rising role of 3D-printing in delivery of therapeutics for infectious disease. J. Control. Release 2024, 366, 349–365. [Google Scholar] [CrossRef]
- Farias, C.; Lyman, R.; Hemingway, C.; Chau, H.; Mahacek, A.; Bouzos, E.; Mobed-Miremadi, M. Three-Dimensional (3D) Printed Microneedles for Microencapsulated Cell Extrusion. Bioengineering 2018, 5, 59. [Google Scholar] [CrossRef] [PubMed]
- Boehm, R.D.; Jaipan, P.; Yang, K.-H.; Stewart, T.N.; Narayan, R.J. Microstereolithography-fabricated Microneedles for Fluid Sampling of Histamine-contaminated Tuna. Int. J. Bioprinting 2016, 2, 72–80. [Google Scholar] [CrossRef]
- Lim, S.H.; Ng, J.Y.; Kang, L. Three-dimensional Printing of a Microneedle Array on Personalized Curved Surfaces for Dual-pronged Treatment of Trigger Finger. Biofabrication 2017, 9, 015010. [Google Scholar] [CrossRef] [PubMed]
- Faraji Rad, Z.; Nordon, R.; Anthony, C.; Bilston, L.; Prewett, P.; Arns, J.-Y.; Arns, C.; Zhang, L.; Davies, G. High Fidelity Replication of Thermoplastic Microneedles with Open Microfluidic Channels. Microsyst. Nanoeng. 2017, 3, 17034. [Google Scholar] [CrossRef] [PubMed]
- Razzaghi, M.; Akbari, M. The Effect of 3D Printing Tilt Angle on the Penetration of 3D-Printed Microneedle Arrays. Micromachines 2023, 14, 1157. [Google Scholar] [CrossRef] [PubMed]
- Patel, P.; Dhal, K.; Gupta, R.; Tappa, K.; Rybicki, F.J.; Ravi, P. Medical 3D Printing Using Desktop Inverted Vat Photopolymerization: Background, Clinical Applications, and Challenges. Bioengineering 2023, 10, 782. [Google Scholar] [CrossRef] [PubMed]
- Gatto, M.L.; Mengucci, P.; Mattioli-Belmonte, M.; Munteanu, D.; Nasini, R.; Tognoli, E.; Denti, L.; Gatto, A. Features of Vat-Photopolymerized Masters for Microfluidic Device Manufacturing. Bioengineering 2024, 11, 80. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Sheng, T.; Zhang, W.; Feng, H.; Yu, J.; Gu, Z.; Zhang, Y. Microneedle-Mediated Cell Therapy. Adv. Sci. 2024, 11, 2304124. [Google Scholar] [CrossRef]
- Mbituyimana, B.; Adhikari, M.; Qi, F.; Shi, Z.; Fu, L.; Yang, G. Microneedle-based cell delivery and cell sampling for biomedical applications. J. Control. Release 2023, 362, 692–714. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Wang, F.-Y.; Chan, Y.-S.; Huang, C.; Huang, Y.-Y. Biofabricating hollow microneedle array with controllable microstructure for cell transplantation. J. Biomed. Mater. Res. 2022, 110, 1997–2005. [Google Scholar] [CrossRef]
- Tang, J.; Wang, J.; Huang, K.; Ye, Y.; Su, T.; Qiao, L.; Hensley, M.T.; Caranasos, T.G.; Zhang, J.; Gu, Z.; et al. Cardiac cell-integrated microneedle patch for treating myocardial infarction. Sci. Adv. 2018, 4, eaat9365. [Google Scholar] [CrossRef]
- Zheng, M.; Hu, T.; Yang, Y.; Qie, X.; Yang, H.; Zhang, Y.; Zhang, Q.; Yong, K.-T.; Liu, W.; Xu, C. In situ-formed cryomicroneedles for intradermal cell delivery. NPG Asia Mater. 2024, 16, 11. [Google Scholar] [CrossRef]
- Ye, Y.; Yu, J.; Wang, C.; Nguyen, N.Y.; Walker, G.M.; Buse, J.B.; Gu, Z. Microneedles Integrated with Pancreatic Cells and Synthetic Glucose-Signal Amplifiers for Smart Insulin Delivery. Adv. Mater. 2016, 28, 3115–3121. [Google Scholar] [CrossRef]
- Kho, A.S.K.; Béguin, S.; O’Cearbhaill, E.D.; Annaidh, A.N. Mechanical characterization of commercial artificial skin models. J. Mech. Behav. Biomed. Mater. 2023, 147, 106090. [Google Scholar] [CrossRef]
- Chang, T.M.S. Artificial Cells for Cell and Organ Replacements. Artif. Organs 2004, 28, 265–270. [Google Scholar] [CrossRef]
- Kang, S.M.; Lee, J.H.; Huh, Y.S.; Takayama, S. Alginate Microencapsulation for Three-Dimensional In Vitro Cell Culture. ACS Biomater. Sci. Eng. 2021, 7, 2864–2879. [Google Scholar] [CrossRef]
- Desai, T.; Shea, L. Advances in islet encapsulation technologies. Nat. Rev. Drug Discov. 2017, 16, 338–350. [Google Scholar] [CrossRef]
- Tan, J.; Luo, Y.; Guo, Y.; Zhou, Y.; Liao, X.; Li, D.; Lai, X.; Liu, Y. Development of alginate-based hydrogels: Crosslinking strategies and biomedical applications. Int. J. Biol. Macromol. 2023, 239, 124275. [Google Scholar] [CrossRef]
- Zinkovska, N.; Pekar, M.; Smilek, J. Gradient Hydrogels-Overview of Techniques Demonstrating the Existence of a Gradient. Polymers 2022, 14, 866. [Google Scholar] [CrossRef]
- Freeman, F.E.; Kelly, D.J. Tuning Alginate Bioink Stiffness and Composition for Controlled Growth Factor Delivery and to Spatially Direct MSC Fate within Bioprinted Tissues. Sci. Rep. 2017, 7, 17042. [Google Scholar] [CrossRef]
- Luo, T.; Tan, B.; Zhu, L.; Wang, Y.; Liao, J. A Review on the Design of Hydrogels with Different Stiffness and Their Effects on Tissue Repair. Front. Bioeng. Biotechnol. 2022, 10, 817391. [Google Scholar] [CrossRef]
- Garrido, C.A.; Garske, D.S.; Thiele, M.; Amini, S.; Real, S.; Duda, G.N.; Schmidt-Bleek, K.; Cipitria, A. Hydrogels with stiffness-degradation spatial patterns control anisotropic 3D cell response. Biomater. Adv. 2023, 151, 213423. [Google Scholar] [CrossRef]
- Kim, B.; Park, J.; Lee, J.Y. Conductive double-network hydrogel composed of sodium alginate, polyacrylamide, and reduced graphene oxide. Korean J. Chem. Eng. 2023, 40, 352–360. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, R.; Liu, J.; Zhao, L.; Yu, Y. High strength and conductive hydrogel with fully interpenetrated structure from alginate and acrylamide. e-Polymers 2021, 21, 391–397. [Google Scholar] [CrossRef]
- Ji, D.; Park, J.M.; Oh, M.S.; Nguyen, T.L.; Shin, H.; Kim, J.S.; Kim, D.; Park, H.S.; Kim, J. Superstrong, superstiff, and conductive alginate hydrogels. Nat. Commun. 2022, 13, 3019. [Google Scholar] [CrossRef]
- Cui, W.; Zheng, Y.; Zhu, R.; Mu, Q.; Wang, X.; Wang, Z.; Liu, S.; Li, M.; Ran, R. Strong Tough Conductive Hydrogels via the Synergy of Ion-Induced Cross-Linking and Salting-Out. Adv. Funct. Mater. 2022, 32, 2204823. [Google Scholar] [CrossRef]
- Conci, A.; Brazil, A.L.; Popovici, D.; Jiga, G.; Lebon, F. Modeling the behavior of human body tissues on penetration. AIP Conf. Proc. 2018, 1932, 020006. [Google Scholar] [CrossRef]
- Trączyński, M.; Patalas, A.; Rosłan, K.; Suszyński, M.; Talar, R. Assessment of needle–tissue force models based on ex vivo measurements. J. Mech. Behav. Biomed. Mater. 2024, 150, 106247. [Google Scholar] [CrossRef]
- Okamura, A.M.; Simone, C.; O’Leary, M.D. Force modeling for needle insertion into soft tissue. IEEE Trans. Biomed. Eng. 2004, 51, 1707–1716. [Google Scholar] [CrossRef]
- Choo, S.; Jin, S.; Jung, J. Fabricating High-Resolution and High-Dimensional Microneedle Mold through the Resolution Improvement of Stereolithography 3D Printing. Pharmaceutics 2022, 14, 766. [Google Scholar] [CrossRef]
- Gordon, A.; Kim, I.; Barnett, A.C.; Moore, J.Z. Needle Insertion Force Model for Haptic Simulation. In Proceedings of the ASME 2015 International Manufacturing Science and Engineering Conference, Charlotte, NC, USA, 8–12 June 2015; Volume 2: Materials; Biomanufacturing; Properties, Applications and Systems; Sustainable Manufacturing; ASME: New York, NY, USA, 2015; p. V002T03A003. [Google Scholar] [CrossRef]
- Machekposhti, S.A.; Kadian, S.; Vanderwal, L.; Stafslien, S.; Narayan, R.J. Novel hollow biodegradable microneedle for amphotericin B delivery. MedComm 2023, 4, e321. [Google Scholar] [CrossRef]
- Dardano, P.; De Martino, S.; Battisti, M.; Miranda, B.; Rea, I.; De Stefano, L. One-Shot Fabrication of Polymeric Hollow Microneedles by Standard Photolithography. Polymers 2021, 13, 520. [Google Scholar] [CrossRef]
- Henriquez, F.; Morales-Ferreiro, J.O.; Celentano, D. Structural Evaluation by the Finite-Element Method of Hollow Microneedle Geometries for Drug Delivery. Adv. Eng. Mater. 2022, 24, 2200049. [Google Scholar] [CrossRef]
- Tamez-Tamez, J.I.; Vázquez-Lepe, E.; Rodriguez, C.A.; Martínez-López, J.I.; García-López, E. Assessment of geometrical dimensions and puncture feasibility of microneedles manufactured by micromilling. Int. J. Adv. Manuf. Technol. 2023, 126, 4983–4996. [Google Scholar] [CrossRef]
- Anbazhagan, G.; Suseela, S.B.; Sankararajan, R. Effect of hollow microneedle geometry structure on mechanical stability and microfluidic flow for transdermal drug delivery applications. Microfluid. Nanofluid 2023, 27, 25. [Google Scholar] [CrossRef]
- Quisling, S.; Vestal, L.; Enstrom, A. Flow Visualization of Bolus Microcapsule Delivery through 3D Printed Microneedles. Bachelor’s Thesis, Santa Clara University, Santa Clara, CA, USA, June 2021. Available online: https://scholarcommons.scu.edu/bioe_senior/105 (accessed on 13 March 2024).
- Defelippi, K.; Johnson, D. Shear Detection of Microencapsulated Cells for Monoclonal Antibody Production Scaleup. Bachelor’s Thesis, Santa Clara University, Santa Clara, CA, USA, June 2022. Available online: https://scholarcommons.scu.edu/bioe_senior/120 (accessed on 13 March 2024).
- Matheny, M.; Dubus, M.; Eribes, L. Microneedles for Wound Healing. Bachelor’s Thesis, Santa Clara University, Santa Clara, CA, USA, June 2023. Available online: https://scholarcommons.scu.edu/bioe_senior/125/ (accessed on 13 March 2024).
- Johnson, D.; Kim, U.; Mobed-Miremadi, M. Nanocomposite films as electrochemical sensors for detection of catalase activity. Front. Mol. Biosci. 2022, 9, 972008. [Google Scholar] [CrossRef]
- Compression Measurement of Foam with Microindentation. Available online: https://nanovea.com/App-Notes/compressionmeasurement.pdf (accessed on 31 January 2024).
- Xu, D.; Harvey, T.; Begiristain, E.; Domínguez, C.; Sánchez-Abella, L.; Browne, M.; Cook, R.B. Measuring the elastic modulus of soft biomaterials using nanoindentation. J. Mech. Behav. Biomed. Mater. 2022, 133, 105329. [Google Scholar] [CrossRef]
- Webber, R.E.; Shull, K.R. Strain Dependence of the Viscoelastic Properties of Alginate Hydrogels. Macromolecules 2004, 37, 6153–6160. [Google Scholar] [CrossRef]
- Caccavo, D.; Cascone, S.; Lamerti, G.; Barba, A.A. Hydrogels: Experimental characterization and mathematical modelling of their mechanical and diffusive behaviour. Chem. Soc. Rev. 2018, 47, 2357–2373. [Google Scholar] [CrossRef]
- Serra-Aguila, A.; Puigoriol-Forcada, J.M.; Reyes, G.; Menacho, J. Viscoelastic models revisited: Characteristics and interconversion formulas for generalized Kelvin–Voigt and Maxwell models. Acta Mech. Sin. 2019, 35, 1191–1209. [Google Scholar] [CrossRef]
- Analysis of Deformation in Solid Mechanics. Available online: https://www.comsol.com/multiphysics/analysis-of-deformation#strain-tensors (accessed on 31 January 2024).
- Structural Contact Modeling Guidelines. Available online: https://www.comsol.com/support/knowledgebase/1102 (accessed on 31 January 2024).
- Clear Resin. Available online: https://formlabs.com/store/materials/clear-resin/ (accessed on 31 January 2024).
- Teotia, M.; Chauhan, M.; Choudhary, P.; Soni, R.K. Photocured characteristics of fast photocurable acrylic formulations and investigations by differential photo calorimeter. J. Therm. Anal. Calorim. 2019, 137, 133–141. [Google Scholar] [CrossRef]
- Kury, M.; Ehrmann, K.; Gorsche, C.; Dorfinger, P.; Koch, T.; Stampfl, J.; Liska, R. Regulated acrylate networks as tough photocurable materials for additive manufacturing. Polym. Int. 2022, 71, 897–905. [Google Scholar] [CrossRef]
- Plexiglas® G Cell-Cast Acrylic Sheet. Available online: https://associatedplastics.com/forms/acrylic_plastics_data.pdf (accessed on 31 January 2024).
- COI Durometer Conversion Chart. Available online: https://www.coirubber.com/wp-content/uploads/2017/07/COI-Durometer-Conversion-Chart.pdf (accessed on 31 January 2024).
- Rubber Hardness Chart. Available online: https://mykin.com/rubber-hardness-chart (accessed on 31 January 2024).
- ASTM D2240 Durometer Hardness. Available online: https://www.plantech.com/wp-content/uploads/2017/05/ASTM-D2240-Durometer-Hardness.pdf (accessed on 31 January 2024).
- Malektaj, H.; Drozdov, A.D.; deClaville Christiansen, J. Mechanical Properties of Alginate Hydrogels Cross-Linked with Multivalent Cations. Polymers 2023, 15, 3012. [Google Scholar] [CrossRef]
- Brus, J.; Urbanova, M.; Czernek, J.; Pavelkova, M.; Kubova, K.; Vyslouzil, J.; Abbrent, S.; Konefal, R.; Horsky, J.; Vetchy, D.; et al. Structure and Dynamics of Alginate Gels Cross-Linked by Polyvalent Ions Probed via Solid State NMR Spectroscopy. Biomacromolecules 2017, 18, 2478–2488. [Google Scholar] [CrossRef]
- Tong, R.; Ma, Z.; Yao, R.; Gu, R.; Li, T.; Liu, L.; Guo, F.; Zeng, M.; Xu, J. Stretchable and transparent alginate ionic gel film for multifunctional sensors and devices. Int. J. Biol. Macromol. 2023, 246, 125667. [Google Scholar] [CrossRef]
- Gryshkov, O.; Pogozhykh, D.; Hofmann, N.; Pogozhykh, O.; Mueller, T.; Glasmacher, B. Encapsulating Non-Human Primate Multipotent Stromal Cells in Alginate via High Voltage for Cell-Based Therapies and Cryopreservation. PLoS ONE 2014, 9, e0107911. [Google Scholar] [CrossRef]
- Hwang, Y.S.; Cho, J.; Tay, F.; Heng, J.Y.; Ho, R.; Kazarian, S.G.; Williams, D.R.; Boccaccini, A.R.; Polak, J.M.; Mantalaris, A. The use of murine embryonic stem cells, alginate encapsulation, and rotary microgravity bioreactor in bone tissue engineering. Biomaterials 2009, 30, 499–507. [Google Scholar] [CrossRef]
- Chan, E.S.; Lim, T.; Voo, W.; Ravindra, P.; Tey, B.T.; Zhang, Z. Effect of formulation of alginate beads on their mechanical behavior and stiffness. Particuology 2011, 9, 228–234. [Google Scholar] [CrossRef]
- Kaklamani, G.; Cheneler, D.; Grover, L.M.; Adams, M.J.; Bowen, J. Mechanical properties of alginate hydrogels manufactured using external gelation. J. Mech. Behav. Biomed. Mater. 2014, 36, 135–142. [Google Scholar] [CrossRef]
- del Pilar Martin, M.; Weldon, W.C.; Zarnitsyn, V.G.; Koutsonanos, D.G.; Akbari, H.; Skountzou, I.; Jacob, J.; Prausnitz, M.R.; Compans, R.W. Local response to microneedle-based influenza immunization in the skin. mBio 2012, 3, e00012-12. [Google Scholar] [CrossRef]
- Strange, D.G.T.; Fletcher, T.L.; Tonsomboom, K.; Brawn, H.; Zhao, X.; Oyen, M.L. Separating poroviscoelastic deformation mechanisms in hydrogels. Appl. Phys. Lett. 2013, 102, 031913. [Google Scholar] [CrossRef]
- Cai, S.; Hu, Y.; Zhao, X.; Suo, Z. Poroelasticity of a covalently crosslinked alginate hydrogel under compression. J. Appl. Phys. 2010, 180, 113514. [Google Scholar] [CrossRef]
- Ahearne, M.; Siamantouras, E.; Yang, Y.; Lui, K.-K. Mechanical Characterization of biomimetic membranes by micro-shaft. Poking. J. R. Soc. Interface 2009, 6, 471–478. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).