Numerical Analysis of Cracked Double-Beam Systems

Abstract

Based on elasticity theory, this paper discusses the static analysis of a cracked double-beam system in the presence of a Winkler-type medium. It is further assumed that the double-beam system is constrained at both ends by elastically flexible springs with transverse and rotational stiffness. Using a variational formulation, the governing static equations are derived and solved using analytical and numerical approaches. In the first approach, closed-form solutions for the displacement functions are obtained based on the Euler–Bernoulli beam theory. In the second approach, the Cell Discretisation Method (CDM) is performed, whereby the two beams are reduced to a set of rigid bars connected by elastic constraints, in which the flexural stiffness of the bars is concentrated. The resulting stiffness matrix is easily deduced, and the governing equations of the static problem can be immediately solved. A comparative analysis is performed to verify the accuracy and validity of the proposed method. The study focuses on the effect of various parameters, including crack depth and position, boundary conditions, elastic medium and slenderness. The validity of the proposed analysis is confirmed by comparing the current results with those obtained from other approaches. In particular, the results obtained by closed-form solution and CDM are compared with the Finite Element Method (FEM). The accuracy of the results was assessed by making comparisons with results found in the literature and reported in the bibliography. It was shown that the proposed algorithm provides a simple and powerful tool for dealing with the static analysis of a double-beam system. Finally, some concluding remarks are made.

1. Introduction

The literature on the mechanical behaviour of beams is very rich. In most early works, the solutions presented in the literature can be divided into theoretical and numerical. In this context, there are numerous studies on the evaluation of bending, buckling, post-buckling and vibration behaviours of beams using the Euler–Bernoulli and Timoshenko models [1,2,3,4,5,6,7,8,9,10].

It is known that the structural behaviour of beams is sensitive to the presence of cracks. In a beam, their presence introduces a localised increase in bending flexibility, which can lead to excessive deflections and unexpected failures. Given their practical relevance, many studies have been conducted to explore the static response to deflection and vibration of beams with different boundary conditions and resting on various elastic foundations [11,12,13,14,15,16,17]. Some of the works are cited herein. In [11], Biondi and Caddemi studied the problem of integrating the governing static equations for uniform Euler–Bernoulli beams with two kinds of discontinuity and presented closed-form solutions of the governing differential equations. Cicirello and Palmeri [12] dealt with the static analysis of pre-damaged Euler–Bernoulli beams with any number of unilateral cracks and subjected to tensile or compressive forces combined with arbitrary transverse loads. Khaji et al. in [13] developed an analytical approach for the crack identification procedure in uniform Timoshenko beams with an open-edge crack, based on bending vibration measurements. Ghannadiasl and Khodapanah in [14] presented an analytical solution of the dynamic analysis of a cracked Euler–Bernoulli beam on an elastic foundation subjected to a concentrated load. Furthermore, the effects of crack depth and position on the natural frequency and deflection of the cracked beam on an elastic foundation were evaluated. In his doctoral thesis [15], Batihan addressed the transverse vibration of a cracked beam on an elastic foundation and presented the effect of crack and foundation parameters on the natural frequencies of transverse vibration. Yang et al. studied the bending deformation of Timoshenko beams with switching cracks and evaluated the influence of beam slenderness ratio, crack depth and external load on the cracking state and bending performance of the cracked beam [16]. Finally, Alijani et al. studied the static behaviour of cracked Euler–Bernoulli beams resting on an elastic foundation by applying analytical, approximate and numerical approaches [17].

Although single beam models under various types of loads and boundary conditions are the most studied structural solutions, they cannot be used in many engineering applications, such as sandwich or composite beams, nanostructures, bonded joints, floating rails and continuous dynamic vibration absorbers. Based on these assumptions, double-beam systems have attracted much attention from researchers and engineers and play an important role in many fields of structural and foundation engineering.

Double-Beam System (BS) models are structural models consisting of two parallel beam structures interconnected by a uniformly distributed elastic layer, generally regarded as an elastic Winkler medium. It is assumed that the beams are governed by beam theory and that the elastic layers are represented by elastic foundation models. Due to their remarkable structural properties, such as better vibration absorption than a single beam, lower weight and greater strength and stiffness, they have led to an explosion of interest within the scientific community. As a result, recent years have seen progressive research activities on BS, which has been widely used in many fields of engineering. For example, special configurations of multiple-pipe systems and underground auxiliary structures (e.g., passage and drainage systems) can be represented by models of double beam (BS) systems. In the field of civil engineering, this system helps to reduce earthquake energy, and many vibration absorbers have been developed on the basis of this special feature. Although the static and vibration analysis of beams resting on elastic foundations is a widely studied topic, little work can be found in the literature on the static analysis of elastically connected systems. In this sense, by applying theoretical and numerical methods, some significant results have been obtained in the study of beams and nanotubes [18,19,20,21,22,23].

This paper deals with the static analysis of a double-beam system with uniform cracking in the presence of a Winkler medium. It is further assumed that the structure is constrained at both ends by elastically flexible springs with transverse and rotational stiffness. The energy principle is formulated for the static analysis of the double-beam system, and the governing equations are solved analytically and numerically. The Cell Discretisation Method (CDM) is used to discretise and solve the governing equations and boundary conditions. This numerical method has already been used by the authors of [23,24,25,26], Raithel and Franciosi [27] and Franciosi and Franciosi [28] for various structural problems. The analysis is performed by reducing the two beams to a set of rigid bars connected by elastic sections (elastic cells), in which the beam stiffness is appropriately concentrated. In this way, the structure is reduced to a system with a finite number of degrees of freedom, and the global stiffness matrix can be easily calculated.

Numerical examples are then provided to demonstrate the reliability and effectiveness of the current model. Furthermore, in order to highlight the efficiency of the proposed computational model, the authors considered the derivation of a finite beam element and presented the derivation of the stiffness matrix for the cracked double-beam system. The results obtained from the closed-form solution were compared with the CDM and the Finite Element Method (FEM). The accuracy of the results was assessed by making comparisons with results found in the literature. In addition, the effects of different parameters such as crack depth and position, boundary conditions, elastic medium stiffness and slenderness on the static behaviour of the structure were studied. It is shown that the proposed algorithm provides a simple and powerful tool for dealing with the static analysis of a double-beam system. Finally, some concluding remarks are made.

2. Problem Formulation

Consider the system composed of two parallel beams with the same length L and translational and rotational elastic constraints at their ends, as shown in Figure 1. Assuming that the material and geometrical properties of the two beams are the same, let E and I be the Young’s modulus and moment of inertia, respectively. It is assumed that the two beams are joined by a Winkler-type medium with modulus $k_m$. The upper beam is subjected to a uniformly distributed load, q.

Based on the Euler–Bernoulli theory and applying the variational formulation, the total potential energy of the system under consideration takes the following form:

$$\begin{array}{cc}{E}_1+\mathrm{P}=\hfill & \frac{1}{2}\sum _{i=1}^2{\int }_0^{\mathrm{L}}\left[{\mathrm{EI}}_j{\left(\frac{{\partial }^2{\mathrm{v}}_j\left(\mathrm{z}\right)}{\partial {\mathrm{z}}^2}\right)}^2\right]\mathrm{dz}+\frac{1}{2}{k}_{\mathrm{jRL}}{\mathrm{v}}_j^{{}^{\prime }2}(\mathrm{z}=0)+\frac{1}{2}{k}_{\mathrm{jTL}}{\mathrm{v}}_j^2(\mathrm{z}=0)+\hfill \\ & \frac{1}{2}{k}_{\mathrm{jRR}}{\mathrm{v}}_j^{{}^{\prime }2}(\mathrm{z}=\mathrm{L})+\frac{1}{2}{k}_{\mathrm{jTR}}{\mathrm{v}}_j^2(\mathrm{z}=\mathrm{L})-{\int }_0^{\mathrm{L}}\mathrm{q}{\mathrm{v}}_1\left(z\right)\mathrm{dz}+\frac{1}{2}{k}_{\mathrm{jds}}{\left(\Delta v_j^{{}^{\prime }}\left(L_{\mathrm{jc}}\right)\right)}^2\hfill \end{array}$$

(1)

$$E_2=\frac{1}{2}{\int }_0^{\mathrm{L}}\left[k_m{\left({\mathrm{v}}_2\left(\mathrm{z}\right)-{\mathrm{v}}_1\left(\mathrm{z}\right)\right)}^2\right]\mathrm{dz}$$

(2)

where $E_1$ is the strain energy of two beams, P is the potential energy of the applied load and $E_2$ the elastic energy including the contribution of the elastic medium. Let v(z) be the transverse displacement, z be the spatial coordinate, $k_{\mathrm{jRL}}$ and $k_{\mathrm{jTL}}$ be rotational and translational stiffness at z = 0 and $k_{\mathrm{jRR}}$ e $k_{\mathrm{jTR}}$ be rotational and translational stiffnesses at z = L, with j = 1, 2. The index j = 1, 2 refers to the order of the beams: the upper beam is denoted by j = 1 and the lower beam by j = 2. Finally, $k_{\mathrm{jds}}$ is the equivalent rotational stiffness of the two corresponding sections of two beams, and $L_{\mathrm{jc}}$ is their abscissa.

Applying the principle of stationary potential energy, we obtain the following dimensionless form of the static equations of the Euler–Bernoulli beam model:

$$\begin{array}{c}\hfill {\mathrm{v}}_1{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_1\left(\zeta \right)-{\mathrm{v}}_2\left(\zeta \right)\right)=\frac{\mathrm{q}{\mathrm{L}}^4}{\mathrm{EI}}\\ \\ \hfill {\mathrm{v}}_2{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_2\left(\zeta \right)-{\mathrm{v}}_1\left(\zeta \right)\right)=0\end{array}$$

(3)

in which $\zeta =\frac{z}{\mathrm{L}}$. In this way, we shift the domain (0, L) to the domain (0, 1).

As is well known, the presence of a crack or concentrated force introduces a discontinuity, and therefore the displacement function of two beams is not a smooth function of z. Consequently, to calculate the displacement function of the two beams, it is necessary to write a separate system of differential equations for each beam segment between discontinuities. Let n be the number of discontinuities of the upper section and s be those of the lower section, then $n+s+1=m$ systems of differential equations are written. Therefore, the number of systems of equations is the sum of the discontinuities between the upper and lower sections of the two beams.

For the double-beam system under consideration, one obtains:

$$\begin{array}{c}\hfill {\mathrm{v}}_1{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_1\left(\zeta \right)-{\mathrm{v}}_{m+1}\left(\zeta \right)\right)=\frac{\mathrm{q}{\mathrm{L}}^4}{\mathrm{EI}}0<\zeta <{\gamma }_1\\ \\ \hfill {\mathrm{v}}_{m+1}{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_{m+1}\left(\zeta \right)-{\mathrm{v}}_1\left(\zeta \right)\right)=00<\zeta <{\gamma }_1\end{array}$$

(4)

$$\begin{array}{c}\hfill {\mathrm{v}}_i{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_i\left(\zeta \right)-{\mathrm{v}}_{m+i}\left(\zeta \right)\right)=\frac{\mathrm{q}{\mathrm{L}}^4}{\mathrm{EI}}{\gamma }_{i-1}<\zeta <{\gamma }_{i}i=2,\dots ,m-1\\ \\ \hfill {\mathrm{v}}_{m+i}{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_{m+i}\left(\zeta \right)-{\mathrm{v}}_i\left(\zeta \right)\right)=0{\gamma }_{i-1}<\zeta <{\gamma }_{i}i=2,\dots ,m-1\end{array}$$

(5)

$$\begin{array}{c}\hfill {\mathrm{v}}_m{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_m\left(\zeta \right)-{\mathrm{v}}_{2m}\left(\zeta \right)\right)=\frac{\mathrm{q}{\mathrm{L}}^4}{\mathrm{EI}}{\gamma }_{m-1}<\zeta <1\\ \\ \hfill {\mathrm{v}}_{2m}{}^{\prime \prime \prime \prime }\left(\zeta \right)+\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}\left({\mathrm{v}}_{2m}\left(\zeta \right)-{\mathrm{v}}_m\left(\zeta \right)\right)=0{\gamma }_{m-1}<\zeta <1\end{array}$$

(6)

From the first Equations (4)–(6) we obtain, respectively, the displacements ${\mathrm{v}}_{m+i}$($\zeta$) and ${\mathrm{v}}_{2m}\left(\zeta \right)$, which, substituted in the second Equation (4)–(6), lead to:

$${\mathrm{v}}_{m+1}\left(\zeta \right)=\frac{{\mathrm{v}}_1{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_1\left(\zeta \right)-\frac{p}{{\alpha }^4}$$

(7)

$${\mathrm{v}}_{m+i}\left(\zeta \right)=\frac{{\mathrm{v}}_i{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_i\left(\zeta \right)-\frac{p}{{\alpha }^4}i=2,\dots ,m-1$$

(8)

$${\mathrm{v}}_{2m}\left(\zeta \right)=\frac{{\mathrm{v}}_m{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_m\left(\zeta \right)-\frac{p}{{\alpha }^4}$$

(9)

and the following system of equations yields:

$${\mathrm{v}}_1{}^{\prime \prime \prime \prime \prime \prime \prime \prime }\left(\zeta \right)+2{\alpha }^4{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime }}\left(z\right)=p{\alpha }^{4}0<\zeta <{\gamma }_1$$

(10)

$${\mathrm{v}}_i{}^{\prime \prime \prime \prime \prime \prime \prime \prime }\left(\zeta \right)+2{\alpha }^4{\mathrm{v}}_i^{{}^{\prime \prime \prime \prime }}\left(z\right)=p{\alpha }^4{\gamma }_{i-1}<\zeta <{\gamma }_{i}i=2,\dots ,m-1$$

(11)

$${\mathrm{v}}_m{}^{\prime \prime \prime \prime \prime \prime \prime \prime }\left(\zeta \right)+2{\alpha }^4{\mathrm{v}}_m^{{}^{\prime \prime \prime \prime }}\left(z\right)=p{\alpha }^4{\gamma }_{m-1}<\zeta <1$$

(12)

setting

$$\alpha =\sqrt[4]{\frac{k_m{\mathrm{L}}^4}{\mathrm{EI}}};p=\frac{\mathrm{q}{\mathrm{L}}^4}{\mathrm{EI}}$$

(13)

The general solutions are:

$$\begin{array}{cc}{\mathrm{v}}_i\left(\zeta \right)=\hfill & a_{1+(i-1)8}+a_{2+(i-1)8}\zeta +a_{3+(i-1)8}{\zeta }^2+a_{4+(i-1)8}{\zeta }^3+\hfill \\ & a_{5+(i-1)8}\mathrm{Cos}\mathrm{h}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]\mathrm{Sin}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]+a_{6+(i-1)8}\mathrm{Cos}\mathrm{h}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]\mathrm{Cos}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]+\hfill \\ & a_{7+(i-1)8}\mathrm{Sin}\mathrm{h}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]\mathrm{Sin}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]+a_{8+(i-1)8}\mathrm{Sin}\mathrm{h}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]\mathrm{Cos}\left[\frac{\alpha }{\sqrt[4]{2}}\zeta \right]+\hfill \\ & \frac{p{\zeta }^4}{48}i=1,m\hfill \end{array}$$

(14)

where $a_j$ are eight constants that are determined, for each segment, by imposing the boundary conditions. At the n discontinuity point for the upper beam with translational and rotational constraints, the boundary conditions are defined as:

$$\begin{array}{c}{\mathrm{v}}_1^{{}^{″}}(\zeta =0)-K_{1\mathrm{RL}}{\mathrm{v}}_1^{{}^{\prime }}(\zeta =0)=0\hfill \\ \\ {\mathrm{v}}_1^{{}^{‴}}(\zeta =0)+K_{1\mathrm{TL}}{\mathrm{v}}_1(\zeta =0)=0\hfill \end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathrm{v}}_i\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{i+1}\left(\zeta ={\gamma }_i\right)=0i=2,m-1\\ \\ \hfill {\mathrm{v}}_1^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{i+1}^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)+\frac{\mathsf{\Psi }}{\mathrm{L}}{\mathrm{v}}_1^{{}^{″}}\left(\zeta ={\gamma }_i\right)=0\\ \\ \hfill {\mathrm{v}}_i^{{}^{″}}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{i+1}^{{}^{″}}\left(\zeta ={\gamma }_i\right)=0\\ \\ \hfill {\mathrm{v}}_i^{{}^{‴}}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{i+1}^{{}^{‴}}\left(\zeta ={\gamma }_i\right)+F_t=0\end{array}$$

(16)

$$\begin{array}{c}{\mathrm{v}}_m^{{}^{″}}(\zeta =1)+K_{1\mathrm{RR}}{\mathrm{v}}_m^{{}^{\prime }}(\zeta =1)=0\hfill \\ \\ {\mathrm{v}}_m^{{}^{‴}}(\zeta =1)-K_{1\mathrm{TR}}{\mathrm{v}}_m(\zeta =1)=0\hfill \end{array}$$

(17)

For the lower beam, having translational and rotational elastic constraints at the ends and subjected to a concentrated force, the boundary conditions are:

$$\begin{array}{c}{\mathrm{v}}_{m+1}^{{}^{″}}(\zeta =0)-K_{2\mathrm{RL}}{\mathrm{v}}_{m+1}^{{}^{\prime }}(\zeta =0)=0\hfill \\ \\ {\mathrm{v}}_{m+1}^{{}^{‴}}(\zeta =0)+K_{2\mathrm{TL}}{\mathrm{v}}_{m+1}(\zeta =0)=0\hfill \end{array}$$

(18)

$$\begin{array}{c}\hfill {\mathrm{v}}_{m-1+i}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{m+i}\left(\zeta ={\gamma }_i\right)=0i=2,m\\ \\ \hfill {\mathrm{v}}_{m-1+i}^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{m+i}^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)+\frac{\mathsf{\Psi }}{\mathrm{L}}{\mathrm{v}}_{m-1+i}^{{}^{″}}\left(\zeta ={\gamma }_i\right)=0\\ \\ \hfill {\mathrm{v}}_{m-1+i}^{{}^{″}}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{m+i}^{{}^{″}}\left(\zeta ={\gamma }_i\right)=0\\ \\ \hfill {\mathrm{v}}_{m-1+i}^{{}^{‴}}\left(\zeta ={\gamma }_i\right)-{\mathrm{v}}_{m+i}^{{}^{‴}}\left(\zeta ={\gamma }_i\right)+F_t=0\end{array}$$

(19)

$$\begin{array}{c}{\mathrm{v}}_{2m}^{{}^{″}}(\zeta =1)+K_{2\mathrm{RR}}{\mathrm{v}}_{2m}^{{}^{\prime }}(\zeta =1)=0\hfill \\ \\ {\mathrm{v}}_{2m}^{{}^{‴}}(\zeta =1)-K_{2\mathrm{TR}}{\mathrm{v}}_{2m}(\zeta =1)=0\hfill \end{array}$$

(20)

where

$$\begin{array}{c}{F}_t=\frac{F{\mathrm{L}}^3}{\mathrm{EI}}{K}_{j\mathrm{RL}}=\frac{k_{\mathrm{jRL}}\mathrm{L}}{\mathrm{EI}};K_{j\mathrm{RR}}=\frac{k_{\mathrm{jRR}}\mathrm{L}}{\mathrm{EI}};\hfill \\ \\ K_{\mathrm{jTL}}=\frac{k_{\mathrm{jTL}}{\mathrm{L}}^3}{\mathrm{EI}};K_{\mathrm{jTR}}=\frac{k_{\mathrm{jTR}}{\mathrm{L}}^3}{\mathrm{EI}};j=1,2\hfill \end{array}$$

(21)

denoting dimensionless parameters of rotational and translational stiffnesses at two ends, for $\zeta$ = 0 and $\zeta$ = 1, respectively, and taking into account the presence of concentrated non-dimensional force.

By substituting the following equations

$${\mathrm{v}}_{m+1}(\zeta =0)=\frac{{\mathrm{v}}_1{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_1\left(\zeta \right)-\frac{p}{{\alpha }^4}$$

(22)

$${\mathrm{v}}_{m+i}\left(\zeta ={\gamma }_i\right)=\frac{{\mathrm{v}}_i{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_i\left(\zeta \right)-\frac{p}{{\alpha }^4}$$

(23)

$${\mathrm{v}}_{2m}\left(\zeta \right)=\frac{{\mathrm{v}}_n{}^{\prime \prime \prime \prime }\left(\zeta \right)}{{\alpha }^4}+{\mathrm{v}}_m\left(\zeta \right)-\frac{p}{{\alpha }^4}$$

(24)

into Equations (18)–(20), we obtain the following system of equations:

$$\begin{array}{c}\hfill \frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime \prime \prime }}(\zeta =0)}{{\alpha }^4}+{\mathrm{v}}_1^{{}^{″}}(\zeta =0)-K_{2\mathrm{RL}}\left(\frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime \prime }}(\zeta =0)}{{\alpha }^4}+{\mathrm{v}}_1^{{}^{\prime }}(\zeta =0)\right)=0\\ \\ \hfill \frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime \prime \prime \prime }}(\zeta =0)}{{\alpha }^4}+{\mathrm{v}}_1^{{}^{‴}}(\zeta =0)+K_{2\mathrm{TL}}\left(\frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime }}(\zeta =0)}{{\alpha }^4}+{\mathrm{v}}_1(\zeta =0)-\frac{p}{{\alpha }^4}\right)=0\end{array}$$

(25)

$$\begin{array}{cc}\hfill & \frac{{\mathrm{v}}_i^{{}^{\prime \prime \prime \prime }}\left(\left(\zeta ={\gamma }_i\right)\right.}{{\alpha }^4}+{\mathrm{v}}_i\left(\zeta ={\gamma }_i\right)-\frac{{\mathrm{v}}_{i+1}^{{}^{\prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}-{\mathrm{v}}_{i+1}\left(\zeta ={\gamma }_i\right)=0i=2,m-1\hfill \end{array}$$

(26)

$$\begin{array}{c}\\ \hfill & \frac{{\mathrm{v}}_i^{{}^{\prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}+{\mathrm{v}}_i^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)-\frac{{\mathrm{v}}_2^{{}^{\prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}+\hfill \\ & -{\mathrm{v}}_2^{{}^{\prime }}\left(\zeta ={\gamma }_i\right)+\frac{\mathsf{\Psi }}{\mathrm{L}}\left(\frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}+{\mathrm{v}}_1^{{}^{″}}\left(\zeta ={\gamma }_i\right)\right)=0\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & \frac{{\mathrm{v}}_i^{{}^{\prime \prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}+{\mathrm{v}}_i^{{}^{″}}\left(\zeta ={\gamma }_i\right)-\frac{{\mathrm{v}}_2^{{}^{\prime \prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}-{\mathrm{v}}_2^{{}^{″}}\left(\zeta ={\gamma }_i\right)=0\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \frac{{\mathrm{v}}_1^{{}^{\prime \prime \prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}+{\mathrm{v}}_i^{{}^{‴}}\left(\zeta ={\gamma }_i\right)-\frac{{\mathrm{v}}_2^{{}^{\prime \prime \prime \prime \prime \prime \prime }}\left(\zeta ={\gamma }_i\right)}{{\alpha }^4}-{\mathrm{v}}_2^{{}^{‴}}\left(\zeta ={\gamma }_i\right)+F_t=0\hfill \end{array}$$

(29)

$$\begin{array}{c}\frac{{\mathrm{v}}_m^{{}^{\prime \prime \prime \prime \prime \prime }}(\zeta =1)}{{\alpha }^4}+{\mathrm{v}}_m^{{}^{″}}(\zeta =1)+K_{2\mathrm{RR}}\left(\frac{{\mathrm{v}}_m^{{}^{\prime \prime \prime \prime \prime }}(\zeta =1)}{{\alpha }^4}+{\mathrm{v}}_m^{{}^{\prime }}(\zeta =1)\right)=0\hfill \\ \frac{{\mathrm{v}}_m^{{}^{\prime \prime \prime \prime \prime \prime \prime }}(\zeta =1)}{{\alpha }^4}+{\mathrm{v}}_m^{{}^{‴}}(\zeta =1)-K_{2\mathrm{TR}}\left(\frac{{\mathrm{v}}_m^{{}^{\prime \prime \prime \prime }}(\zeta =1)}{{\alpha }^4}+{\mathrm{v}}_m(\zeta =1)-\frac{p}{{\alpha }^4}\right)=0\hfill \end{array}$$

(30)

3. Cracks: Modelling and Method of Solution

3.1. Modelling of Cracks: An Overview of the Discrete Spring Model

The identification of the location and depth of a crack in beam-type structures is an important topic in structural health monitoring and has been the subject of a significant amount of research. The literature on crack modelling is very rich, and various models have been proposed in the technical literature, such as local stiffness reduction, discrete spring models and complex models in two or three dimensions. In this topic, the state of the art can be found in a review works by Alijani et al. [17] and by Palmeri and Cicirello [29]. In both papers, the authors provide a coherent but concise review of as many publications as possible, and the main topics covered are modelling and simulation of the static behaviour of cracked beams.

According to the classification by Friswell and Penny [30], the proposed approach falls into the broad category of “discrete spring models”, being equivalent to an internal hinge coupled with a linear elastic spring. This model is widely adopted when structural analysis focuses on the overall performance of frames and trusses rather than on crack initiation and propagation phenomena. Although very simple, the discrete spring model proves to be very efficient for static problems. The idea of treating cracked beams with linear springs equivalent in crack location is based on the division of each element into undamaged pieces between two consecutive cracks. One of the main advantages of this model is the effective representation of the crack in terms of position and gravity. Several attempts to provide values for the rotational stiffness of the spring using cracking parameters such as depth or geometry can be found in the literature. Among these, Palmeri and Cicirello [29] studied the static analysis of multi-cracked Euler–Bernoulli and Timoshenko beams using this relationship. Subsequently, Okamura et al. [31] showed the buckling behaviour of rectangular-section cracked columns. Furthermore, Ricci and Viola [32] extended the method of Kienzler and Herrmann [33] to evaluate the stress intensity factors of cracked beams and bars and derived two relationships between the stress intensity factor and the rotational stiffness of the spring. In the following analysis, two relationships between the stress intensity factor and the rotational stiffness of the spring were considered, as introduced by Alijani et al. in [17].

Figure 2 shows a beam with a crack in the non-dimensional position ${\gamma }_i$ and depth a. In addition, it is assumed that the shear effect as well as axial and torsional loads are neglected. According to this assumption, the stress intensity factors may be evaluated through the following equations:

$$K_I=\frac{6M}{b{h}^2}\sqrt{\pi a}{F}_m\left(\xi \right)0\le \xi \le 0.6,\xi =\frac{a}{h}$$

(31)

$$K_I=\frac{3.99M}{bh\sqrt{h}\sqrt{{\left(1-{\xi }^2\right)}^3}}0.6\le \xi \le 1.0,\xi =\frac{a}{h}$$

(32)

where $F_m\left(\xi \right)$ is given from the following geometric function

$$F_M\left(\xi \right)=\sqrt{\left(\frac{2}{\pi \xi }\right)tan\frac{\pi \xi }{2}}\frac{0.923+0.199{\left(1-sin\left(\frac{\pi \xi }{2}\right)\right)}^4}{cos\left(\frac{\pi \xi }{2}\right)}$$

(33)

Finally, the following relationship is defined:

$$\frac{1}{k_{\mathrm{ds}}}=\frac{2b\left(1-{\vee }^2\right)}{E}{\int }_0^a{\left(\frac{K_I}{M}\right)}^{2}da$$

(34)

which is used to determine a rotational spring stiffness factor equivalently in terms of the geometrical and material parameters of the crack and where $\mathsf{\Psi }$ in Equation (27) is equal to $\frac{\mathrm{EI}}{k_{\mathrm{ds}}}$ and $k_{\mathrm{ds}}$ is the stiffness of the i-th equivalent spring.

In the present paper, the rotational spring stiffness factor is assumed to be different for each beam. In particular, ${\mathsf{\Psi }}_1$ and ${\mathsf{\Psi }}_2$ denote the rotational spring stiffness factor for the upper and lower beams, respectively.

3.2. Method of Solution: Cell Discretisation Method (CDM)

The Cell Discretisation Method (CDM) is an efficient numerical method for solving linear partial differential equations. It has become an important tool in the field of structural engineering due to its approximation capabilities and ease of implementation. The advent of sophisticated and fully generalised discretisation tools, such as the finite element method and the Boundary Element Method (BEM), has made it possible to simulate the behaviour of structures by taking into account more variables due to the elimination of simplified assumptions, but, on the other hand, such procedures can lead to losing the physical sense of the real behaviour of structures that should always be the basis of engineering studies. In this sense, the CDM can be considered a technique capable of tackling such problems. Since the beginning of the 20th century, this method has found various applications, for example, the dynamics and stability of arches, masonry arches, the static and dynamic analysis of Euler–Bernoulli beams under different load and boundary conditions, the static and dynamic analysis of Timoshenko and Rayleigh beams and the static analysis of plates under different load and boundary conditions [23,24,25,26,27,28]. More recently, some of the present authors have applied the method to the dynamic analysis of single- and double-walled carbon nanotubes, taking into account non-local effects [23,26], and have obtained results showing that the method is able to describe the behaviour of the nanostructure satisfactorily with little computational effort. In several articles, the procedure proves to be very versatile and able to work on a finite number of Lagrangian parameters in each case, bringing the solution within the scope of the usual numerical analysis methods.

In the present paper, the two beams are reduced to a set of t rigid bars with the same length $\mathit{l}$, connected by n = t + 1 elastic cells (see Figure 3). The moment of inertia $I_j$, with j = 1, 2, will be evaluated on the abscissa of the cells, resulting in the concentrated stiffness $k_{1i}=\frac{{\mathrm{EI}}_{1i}}{\mathit{l}}$ and $k_{2i}=\frac{{\mathrm{EI}}_{2i}}{\mathit{l}}$ for the upper and lower beam, respectively. Both quantities can be organised into the so-called unassembled stiffness diagonal matrix ${\mathit{k}}_j$ with dimension (n × n), j = 1, 2 for each of the two beams.

If the cross-section is not uniform, the average inertia across the elastic cell can be considered for each rigid section of length $\mathit{l}$.

In this way, the structure is reduced to a classical holonomic system, with 2n degrees of freedom; in particular, n vertical displacements ${\mathrm{v}}_{1i}$ for the upper beam and n vertical displacements ${\mathrm{v}}_{2i}$ for the lower beam. The abscissa of the cells will be conveniently taken as Lagrangian coordinates and will be organised in the 2n-dimensional vector v. Moreover, for the upper and lower beams, the n − 1 rotations of the rigid bars can be calculated as a function of the Lagrangian coordinates as follows:

$$\begin{array}{c}{\varphi }_{1,i}=\frac{{\mathrm{v}}_{1,i+1}-{\mathrm{v}}_{1,i}}{l}\hfill \\ \\ {\varphi }_{2,i}=\frac{{\mathrm{v}}_{2,i+1}-{\mathrm{v}}_{2,i}}{l}\hfill \end{array}$$

(35)

or, in matrix form, ${\mathit{\varphi }}_{\mathbf{1}}=$ V${\mathbf{v}}_1$ and ${\mathit{\varphi }}_{\mathbf{2}}=$ V${\mathbf{v}}_2$, where $\mathbf{V}$ is a rectangular transfer matrix with n− 1 rows and n columns.

The relative rotations between the two faces of the elastic cells are given by:

$${\psi }_{j,1}={\varphi }_{j,1},{\psi }_{j,i}={\varphi }_{j,i}-{\varphi }_{j,i-1},{\psi }_{j,n}=-{\varphi }_{j,n-1}$$

(36)

or, in matrix form, ${\mathit{\psi }}_{\mathbf{1}}$ = $\mathbf{\Delta }$${\mathit{\varphi }}_{\mathbf{1}}$ for upper rigid bar and ${\mathit{\psi }}_{\mathbf{2}}$ = $\mathbf{\Delta }$${\mathit{\varphi }}_{\mathbf{2}}$ for lower rigid bar, where $\mathbf{\Delta }$ is another rectangular transfer matrix with n rows and n−1 columns.

The strain energies $L_{\mathrm{je}}$, with j = 1, 2, (the first two terms of Equation (1)) are given by:

$$\begin{array}{c}{L}_{1e}=\frac{1}{2}\sum _{i=1}^n{k}_{1,\mathrm{ii}}{\psi }_{1,i}^2\hfill \\ \\ L_{2e}=\frac{1}{2}\sum _{i=1}^n{k}_{2,\mathrm{ii}}{\psi }_{2,i}^2\hfill \end{array}$$

(37)

and they are concentrated at the cells of the upper and lower beams, respectively.

The strain energies should be expressed as functions of the Lagrangian coordinates as follows:

$$\begin{array}{c}\hfill L_{1e}=\frac{1}{2}{\mathit{\psi }}_1^T{\mathit{k}}_1{\mathit{\psi }}_1=\frac{1}{2}{\mathit{\varphi }}_1^T{\mathbf{\Delta }}^T{\mathit{k}}_1\mathbf{\Delta }{\mathit{\varphi }}_1=\frac{1}{2}{{\mathbf{v}}_{\mathbf{1}}}^T\left({\mathit{V}}^T{\mathbf{\Delta }}^T{\mathit{k}}_1\mathbf{\Delta }\mathit{V}\right){\mathbf{v}}_{\mathbf{1}}\\ \\ \hfill L_{2e}=\frac{1}{2}{\mathit{\psi }}_2^T{\mathit{k}}_2{\mathit{\psi }}_2=\frac{1}{2}{\mathit{\varphi }}_2^T{\mathbf{\Delta }}^T{\mathit{k}}_2\mathbf{\Delta }{\mathit{\varphi }}_2=\frac{1}{2}{{\mathbf{v}}_{\mathbf{2}}}^T\left({\mathit{V}}^T{\mathbf{\Delta }}^T{\mathit{k}}_2\mathbf{\Delta }\mathit{V}\right){\mathbf{v}}_{\mathbf{2}}\end{array}$$

(38)

so that the total strain energy can be expressed as:

$$L_e=\frac{1}{2}{\mathbf{v}}^T\left(\begin{array}{cc}{\mathit{K}}_{\mathbf{1}}& \mathbf{0}\\ \mathbf{0}& {\mathit{K}}_{\mathbf{2}}\end{array}\right)\mathbf{v}$$

(39)

where ${\mathit{K}}_{\mathbf{1}}$ = $\left({\mathit{V}}^T{\mathbf{\Delta }}^T{\mathit{k}}_1\mathbf{\Delta }\mathit{V}\right)$ and ${\mathit{K}}_{\mathbf{2}}$ = $\left({\mathit{V}}^T{\mathbf{\Delta }}^T{\mathit{k}}_2\mathbf{\Delta }\mathit{V}\right)$. The global assembled stiffness matrix K, with 2n rows and 2n columns, assumes the following form:

$$\mathit{K}=\left(\begin{array}{cc}{\mathit{K}}_{\mathbf{1}}& \mathbf{0}\\ \mathbf{0}& {\mathit{K}}_{\mathbf{2}}\end{array}\right)$$

(40)

The potential energy, as a function of the Lagrangian coordinates, is given by:

$$P_1=\sum _{i=1}^n{q}_i{\mathrm{v}}_{1,i}$$

(41)

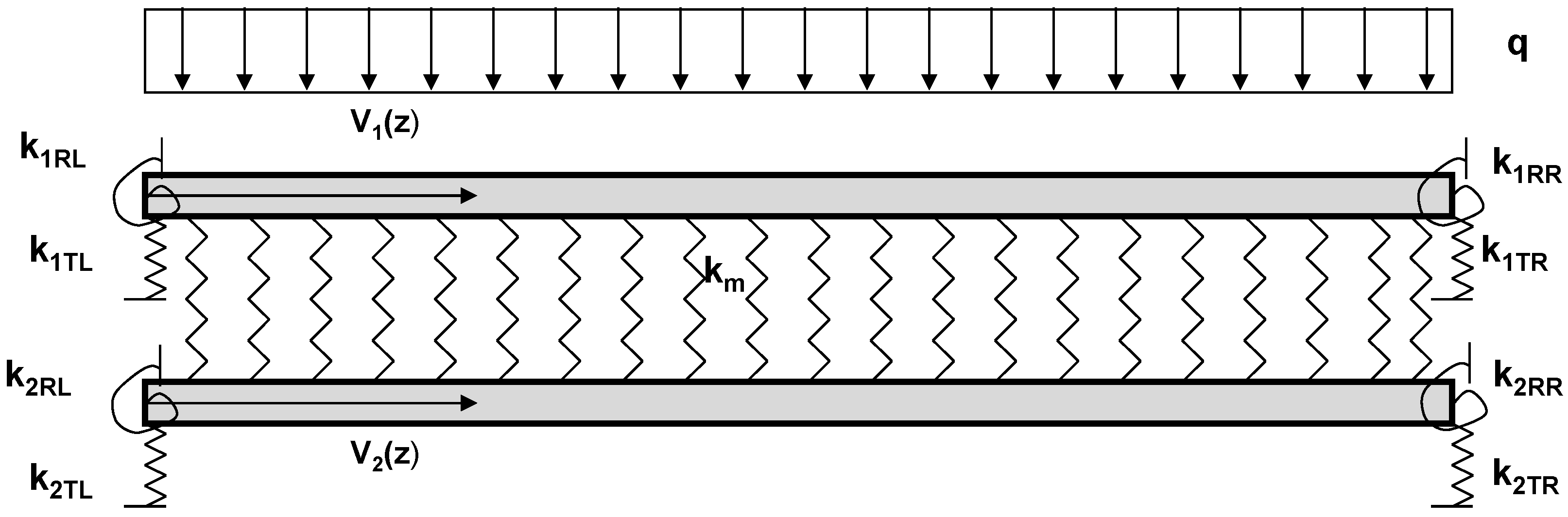
Being the double-beam system subjected to a uniformly distributed load q

$$\mathbf{q}=\left(q_1,\dots ,q_i,\dots ,q_n\right)$$

(42)

with

$$\begin{array}{c}\hfill q_1=ql/2;q_n=ql/2;\\ \hfill q_i=qli=2,\dots ,n-1\end{array}$$

(43)

the global assembled load matrix Q with 2n rows and 2n columns assumes the following form:

$$\mathit{Q}=\left(\begin{array}{cc}\mathit{q}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)$$

(44)

The strain energy due to the elastic medium, Equation (2), can be expressed as:

$$E_2=\frac{1}{2}{\mathbf{v}}^T\mathbf{C}{\mathbf{v}}_1+\frac{1}{2}{\mathbf{v}}_2^T\mathbf{C}{\mathbf{v}}_2-{\mathbf{v}}_1^T\mathbf{C}{\mathbf{v}}_2$$

(45)

The terms of matrix $\mathbf{C}$ are given by:

$$\begin{array}{c}\hfill C_{i,i}=2\frac{l}{3}{k}_m,i=3,n-3\\ \\ \hfill C_{i+1,i}=C_{ii,+1}=\frac{l}{3}{k}_m,i=2,n-2\\ \\ \hfill C_{1,1}=\frac{l}{6}{k}_m,C_{2,2}=\frac{l}{3}{k}_m,C_{1,2}=C_{2,1}=\frac{l}{12}{k}_m\end{array}$$

(46)

Matrix $\mathbf{C}$, with n rows and n columns and half-band widths equal to 2, takes the following form:

$${\mathbf{C}}_t=\left(\begin{array}{cc}\mathbf{C}& -\mathbf{C}\\ -\mathbf{C}& \mathbf{C}\end{array}\right)$$

(47)

Finally, the governing static equation can be written as:

$${\mathit{K}}_t\mathbf{v}=\mathbf{Q}$$

(48)

where ${\mathit{K}}_t$ is the global assembled stiffness matrix:

$${\mathit{K}}_t=\mathbf{K}+{\mathbf{C}}_t$$

(49)

Boundary Conditions in Presence of a Crack

Finally, from the strain energy terms of the flexible constraints at the ends in Equiation (1), the assembled stiffness matrix K must be modified as follows:

$$\begin{array}{c}\hfill K[1,1]=K[1,1]+k_{1\mathrm{TL}};\\ \\ \hfill K[n,n]=K[n,n]+k_{1\mathrm{TR}};\\ \\ \hfill K[n+1,n+1]=K[n+1,n+1]+k_{2\mathrm{TL}};\\ \\ \hfill K[2n,2n]=K[2n,2n]+k_{2\mathrm{TR}}.\end{array}$$

(50)

The rotational stiffnesses of the constraints of each beam can be taken into account by adding the corresponding flexibilities of the rigid bars and obtaining:

$$\begin{array}{c}\hfill k_1[1,1]=\frac{k_1[1,1]k_{1\mathrm{RL}}}{k_{1\mathrm{RL}}+k_1[1,1]}\\ \\ \hfill k_1[n,n]=\frac{k[n,n]k_{1\mathrm{RR}}}{k_{1\mathrm{RR}}+k_1[n,n]}\\ \\ \hfill k_2[1,1]=\frac{k_2[1,1]k_{2\mathrm{RL}}}{k_{2\mathrm{RL}}+k_2[1,1]}\\ \\ \hfill k_2[n,n]=\frac{k_2[n,n]k_{2\mathrm{RR}}}{k_{2\mathrm{RR}}+k_2[n,n]}\end{array}$$

(51)

These terms will be organised in two matrices, ${\mathit{k}}_1$ and ${\mathit{k}}_2$, given in (40). In presence of a crack on the abscissa of cell $j^{\mathrm{ma}}$, the local stiffness of the upper beam is given by:

$$k_1[j+1,j+1]=\frac{k_1[j+1,j+1]k_{1\mathrm{ds}}}{k_{1\mathrm{ds}}+k_1[j+1,j+1]}$$

(52)

whereas at the $s^{\mathrm{ma}}$ cell abscissa relative to the lower beam, the local stiffness is:

$$k_2[s+1,s+1]=\frac{k_2[s+1,s+1]k_{2\mathrm{ds}}}{k_{2\mathrm{ds}}+k_2[s+1,s+1]}$$

(53)

if the height of the crack is different in the two beams. The values $k_{1\mathrm{ds}}$ and $k_{2\mathrm{ds}}$ are derived from Equation (34).

3.3. Method of Solution: Finite Element Method (FEM)

In order to highlight the efficiency of the proposed computational model (CDM), the authors considered the derivation of a finite beam element for the static analysis of a cracked double-beam system. Specifically, a finite element of a cracked double-beam system was developed based on a variational approach, and shape functions for rotational and translational displacements were used to develop the stiffness matrix in the presence and absence of cracks.

For the structure under consideration (see Figure 4), the total potential energy is given by:

$$\begin{array}{cc}{E}_t=\hfill & \frac{1}{2}{\int }_0^{\mathrm{L}}{\mathrm{EI}}_1{\left(\frac{{\partial }^2{\mathrm{v}}_1\left(\mathrm{z}\right)}{\partial {\mathrm{z}}^2}\right)}^2\mathrm{dz}+{\int }_0^{\mathrm{L}}{\mathrm{EI}}_2{\left(\frac{\partial \mathrm{v}\left(\mathrm{z}\right)}{\partial {\mathrm{z}}^2}\right)}^2\mathrm{dz}-{\int }_0^{\mathrm{L}}\mathrm{q}{\mathrm{v}}_1\left(\mathrm{z}\right)\mathrm{dz}+\hfill \\ \hfill & \frac{1}{2}{\int }_0^{\mathrm{L}}{k}_m{\left({\mathrm{v}}_2\left(\mathrm{z}\right)-{\mathrm{v}}_1\left(\mathrm{z}\right)\right)}^2\mathrm{dz}\hfill \end{array}$$

(54)

Using cubic polynomial functions for transverse displacements, the following shape functions are derived:

$${\mathbf{N}}_i=\left(\begin{array}{c}1-\frac{3{\mathrm{z}}^2}{{\mathrm{L}}^2}+\frac{2{\mathrm{z}}^3}{{\mathrm{L}}^3}\\ -\mathrm{z}+\frac{2{\mathrm{z}}^2}{\mathrm{L}}-\frac{{\mathrm{z}}^3}{{\mathrm{L}}^2}\\ \frac{3{\mathrm{z}}^2}{{\mathrm{L}}^2}-\frac{2{\mathrm{z}}^3}{{\mathrm{L}}^3}\\ \frac{{\mathrm{z}}^2}{\mathrm{L}}-\frac{{\mathrm{z}}^3}{{\mathrm{L}}^2}\end{array}\right);$$

(55)

where i = 1, 2 refers to the upper and lower beams, respectively. The transverse displacements are then given as:

$${\mathrm{v}}_i\left(\mathrm{z}\right)={\mathbf{N}}_i^T{\mathbf{d}}_i$$

(56)

where ${\mathbf{d}}_i$ denotes the vector of nodal displacements and is given by:

$${\mathbf{d}}_i={\left({\mathrm{V}}_1^{\left(i\right)},{\mathsf{\Theta }}_1^{\left(i\right)},{\mathrm{V}}_2^{\left(i\right)},{\mathsf{\Theta }}_2^{\left(i\right)}\right)}^T$$

(57)

By deriving the nodal displacements with respect to the spatial coordinate z, the following expressions are obtained:

$$\frac{{\mathrm{dv}}_i\left(\mathrm{z}\right)}{\mathrm{dz}}={\mathbf{N}}_i^{{}^{\prime }T}{\mathbf{d}}_i;\frac{{\mathrm{d}}^2{\mathrm{v}}_i\left(\mathrm{z}\right)}{{\mathrm{dz}}^2}={\mathbf{N}}_i^{″T}{\mathbf{d}}_i$$

(58)

which, substituted for Equation (54), leads to:

$$\begin{array}{cc}{E}_t=\hfill & \frac{1}{2}{\mathbf{d}}_1^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1^{″}\mathrm{EI}{\mathbf{N}}_1^{″T}\mathrm{dz}\right){\mathbf{d}}_1+\frac{1}{2}{\mathbf{d}}_2^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2^{″}\mathrm{EI}{\mathbf{N}}_2^{″T}\mathrm{dz}\right){\mathbf{d}}_2-{\mathbf{d}}_1^T{\int }_0^{\mathrm{L}}\mathrm{q}{\mathbf{N}}_1\mathrm{dz}+\hfill \\ \hfill & \frac{1}{2}{\mathbf{d}}_1^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1+\frac{1}{2}{\mathbf{d}}_2^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2+\hfill \\ \hfill & -{\mathbf{d}}_1^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2-{\mathbf{d}}_2^T\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1\hfill \end{array}$$

(59)

By applying the principle of stationary potential energy, one obtains:

$$\begin{array}{cc}\hfill & \left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1^{″}\mathrm{EI}{\mathbf{N}}_1^{″T}\mathrm{dz}\right){\mathbf{d}}_1+\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1-\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2={\int }_0^{\mathrm{L}}\mathrm{q}{\mathbf{N}}_1\mathrm{dz}\hfill \\ \\ \hfill & \left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2^{″}\mathrm{EI}{\mathbf{N}}_2^{″T}\mathrm{dz}\right){\mathbf{d}}_2+\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2-\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1=\mathbf{0}\hfill \end{array}$$

(60)

Then, rearranging the terms in ${\mathbf{d}}_1$ and ${\mathbf{d}}_2$, one obtains:

$$\begin{array}{cc}\hfill & \left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1^{″}\mathrm{EI}{\mathbf{N}}_1^{″T}\mathrm{dz}+{\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1-\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2={\int }_0^{\mathrm{L}}\mathrm{q}{\mathbf{N}}_1\mathrm{dz}\hfill \\ \\ \hfill & {\int }_0^{\mathrm{L}}{\mathbf{N}}_2^{″}\mathrm{EI}{\mathbf{N}}_2^{″T}\mathrm{dz}+\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_2^T\mathrm{dz}\right){\mathbf{d}}_2-\left({\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_1^T\mathrm{dz}\right){\mathbf{d}}_1=\mathbf{0}\hfill \end{array}$$

(61)

or

$$\left(\begin{array}{cc}{\mathbf{K}}_{11}& -{\mathbf{K}}_{12}\\ -{\mathbf{K}}_{21}& {\mathbf{K}}_{22}\end{array}\right)\left(\begin{array}{c}{\mathbf{d}}_1\\ {\mathbf{d}}_2\end{array}\right)=\left(\begin{array}{c}\mathbf{Q}\\ \mathbf{0}\end{array}\right)$$

(62)

being

$$\begin{array}{c}\hfill {\mathbf{K}}_{11}={\int }_0^{\mathrm{L}}{\mathbf{N}}_1^{″}\mathrm{EI}{\mathbf{N}}_1^{″T}\mathrm{dz}+{\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_1^T\mathrm{dz};\\ \\ \hfill {\mathbf{K}}_{12}={\int }_0^{\mathrm{L}}{\mathbf{N}}_1{k}_m{\mathbf{N}}_2^T\mathrm{dz};\\ \\ \hfill {\mathbf{K}}_{21}={\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_1^T\mathrm{dz};\\ \\ \hfill {\mathbf{K}}_{22}={\int }_0^{\mathrm{L}}{\mathbf{N}}_2^{″}\mathrm{EI}{\mathbf{N}}_2^{″T}\mathrm{dz}+{\int }_0^{\mathrm{L}}{\mathbf{N}}_2{k}_m{\mathbf{N}}_2^T\mathrm{dz};\\ \\ \hfill \mathbf{Q}={\int }_0^{\mathrm{L}}\mathrm{q}{\mathbf{N}}_1\mathrm{dz}.\end{array}$$

(63)

Equation (62) can be rewritten as:

$$\begin{array}{c}{\mathbf{K}}_{11}{\mathbf{d}}_1-{\mathbf{K}}_{12}{\mathbf{d}}_2=\mathbf{Q}\hfill \\ \\ -{\mathbf{K}}_{21}{\mathbf{d}}_1+{\mathbf{K}}_{22}{\mathbf{d}}_2=\mathbf{0}\hfill \end{array}$$

(64)

From the second Equation (64), we obtain ${\mathbf{d}}_1$, which, substituted in the first equation, leads to:

$$\begin{array}{c}{\mathbf{d}}_2={\mathbf{K}}_{22}^{-1}{\mathbf{K}}_{21}{\mathbf{d}}_1;\hfill \\ \\ \left({\mathbf{K}}_{11}-{\mathbf{K}}_{12}{\mathbf{K}}_{22}^{-1}{\mathbf{K}}_{21}\right){\mathbf{d}}_1=\mathbf{Q}\hfill \end{array}$$

(65)

or

$$\begin{array}{c}\hfill {\mathbf{d}}_1={\left({\mathbf{K}}_{11}-{\mathbf{K}}_{22}^{-1}{\mathbf{K}}_{12}{\mathbf{K}}_{21}\right)}^{-1}\mathbf{Q};\\ \\ \hfill {\mathbf{d}}_2={\mathbf{K}}_{22}^{-1}{\mathbf{K}}_{12}{\mathbf{d}}_1\end{array}$$

(66)

In the presence of a crack, the stiffness matrix of finite element with a crack must be modified. In the presence of a crack, the stiffness matrix of the cracked beam element must be modified. Several investigators have derived the stiffness matrix for a cracked beam element and studied the effect of the crack on the stiffness matrix (see, e.g., [34,35]). In the present analysis, the structure under investigation was analysed using finite beam elements that did not take into account the effect of shear forces. Therefore, the stiffness matrix, which represents the relationship between the vector of nodal forces and the vector of nodal displacements, can be expressed as:

$$\begin{array}{c}\hfill {\mathit{K}}_{\mathit{c}}=\frac{\mathrm{EI}}{\delta }\left(\begin{array}{cccc}12a_{11}& -6a_{12}& -12a_{13}& -6a_{14}\\ -6a_{21}& a_{22}& 6a_{23}& a_{24}\\ -12a_{31}& 6a_{32}& 12a_{33}& 6a_{34}\\ -6a_{41}& a_{42}& 6a_{43}& a_{44}\end{array}\right)\end{array}$$

(67)

so as deduced in [35] (see Formula (22)), where $k_r=\frac{\mathrm{EI}}{\mathsf{\Psi }}$, $\delta$ is given by:

$$\delta =L\left(k_r{\mathrm{L}}^3+\mathrm{EI}\left(12{\mathrm{L}}_1^2-12\mathrm{L}{\mathrm{L}}_1+{\mathrm{L}}^{2}4\right)\right)$$

(68)

and where

$$\begin{array}{c}\hfill a_{11}=a_{33}=\left(\mathrm{EI}+k_r\mathrm{L}\right);\\ \\ \hfill a_{22}=\left(12\mathrm{EI}{\mathrm{L}}_1^2+k_r{\mathrm{L}}^{3}4\right);\\ \\ \hfill a_{44}=\left(12\mathrm{EI}{\left(\mathrm{L}-{\mathrm{L}}_1\right)}^2+4k_r{\mathrm{L}}^3\right);\\ \\ \hfill a_{12}=a_{21}=\left(k_r{\mathrm{L}}^2+2\mathrm{EI}{\mathrm{L}}_1\right);\\ \\ \hfill a_{13}=a_{31}=\left(\mathrm{EI}+k_r\mathrm{L}\right);\\ \\ \hfill a_{14}=a_{41}=\left(k_r{\mathrm{L}}^2+2\mathrm{EI}\left(\mathrm{L}-{\mathrm{L}}_1\right)\right);\\ \\ \hfill a_{23}=a_{32}=\left(k_r{\mathrm{L}}^2+2\mathrm{EI}{\mathrm{L}}_1\right);\\ \\ \hfill a_{24}=a_{42}=\left(12\mathrm{EI}\left(\mathrm{L}-{\mathrm{L}}_1\right){\mathrm{L}}_1+2k_r{\mathrm{L}}^3\right);\\ \\ \hfill a_{34}=a_{43}=\left(k_r{\mathrm{L}}^2+2\mathrm{EI}\left(\mathrm{L}-{\mathrm{L}}_1\right)\right).\end{array}$$

(69)

This matrix will be translated into ${\mathbf{K}}_{22}$ at the appropriate abscissa.

4. Numerical Examples: Results and Discussion

To evaluate the effects of the crack, taper ratio, elastic medium parameter, boundary conditions and rotational and translational stiffness on the deflection of the two beams, several numerical examples are presented, using a general code developed in Mathematica [36]. The solutions in terms of the deflection function are derived using analytical and numerical approaches. The results obtained using the Euler–Bernoulli beam model are also presented to demonstrate the validity and reliability of the proposed approach (CDM).

In all numerical examples, the structure under consideration consists of two parallel beams with the same length L equal to 2.5 m and the following material properties: Young’s modulus is 30 GPa and Poisson’s ratio $\nu$ = 0.3. The cross-section of the two beams is rectangular with base and height dimensions of 0.10 m and 0.18 m, respectively. Let $k_m$ = 1 MPa be the average foundation modulus and q = 100 kN/m be a uniformly distributed load applied to the upper beam.

4.1. Case 1: Simply Supported-Simply Supported Double-Beam System in the Presence of a Crack on the Lower Beam and a Uniformly Distributed Load Applied to the Upper Beam

In the first numerical example, the static deflections of a simply supported double girder-system (SS-SS) in the presence of a crack and a uniformly distributed load were studied using a large number of cells, i.e., n = 300. The crack is introduced on the dimensionless abscissa z = 1.25 m from the left end of the lower beam. The non-dimensional height of the crack is assumed to be $\xi$ = 0.5. The upper beam is loaded with a uniformly distributed load q = 100 kN/m.

Figure 5 shows the dimensionless transverse displacements of two beams. Specifically, the dotted line refers to the vertical displacements of the upper beam, while the solid line shows the displacements of the lower beam. As can be seen, the maximum value of the transverse displacement ${\mathrm{v}}_1$ is 0.0291243 m at the dimensionless abscissa z = 1.25 m, while the transverse displacement ${\mathrm{v}}_2$ at the position of the crack (z = 1.25 m) is 0.00890037 m. In order to verify the correctness of the numerical calculations of the CDM, a numerical comparison with the results provided by the closed-form solutions is proposed. Applying the exact procedure, the values of the transverse displacements of the two beams are ${\mathrm{v}}_1$(z = 1.25 m) = 0.0291244 m and ${\mathrm{v}}_2$ (z = 1.25 m) = 0.00890037 m. As can be seen, the deflections of the two beams show very good agreement between the results obtained from the theoretical and numerical procedures. Furthermore, Figure 4 shows the influence of the crack position on the deflection of the two SS-SS beams. This figure emphasises that the deflection will be maximum if the crack position approaches the beam centre line.

To demonstrate the robustness, accuracy and reliability of the proposed numerical method, the structure under investigation was also analysed by implementing the finite elements of the beam.

In the first case, the structure was analysed by implementing finite beam elements that take into account the effect of a crack and a distributed load. The crack was introduced in the middle of the span of the lower beam ($L_1=0.5L$), and a uniformly distributed load is applied only to the upper beam. For different values of the Winkler-type average stiffness $k_m$, the maximum displacements of the beam system were calculated by means of the Finite Element Method (FEM), the closed-form solution and the CD method, and the results obtained are shown in

Table 1. Maximum deflections values of two beams varying $k_m$ in the range $\left[{10}^2,{10}^3,{10}^4,{10}^5\right]$ and with a crack acting on the lower beam, where C-FS = closed-form solution, C = CDM, F = FEM.

${\mathit{k}}_{\mathit{m}}$	v${}_{1max}$ (C-FS)	v${}_{2max}$(C-FS)	v${}_{1max}$ (C)	v${}_{2max}$ (C)	v${}_{1max}$ (F)	v${}_{2max}$ (F)
10${}^2$	0.0348842	1.489 × 10${}^{-6}$	0.0348842	1.489 × 10${}^{-6}$	0.0348842	9.631 × 10${}^{-7}$
10${}^3$	0.0348756	0.0000149	0.0348754	0.0000149	0.0348756	0.0000149
10${}^4$	0.0347895	0.0001479	0.0347894	0.0001479	0.0347895	0.0001479
10${}^5$	0.0339827	0.0013952	0.0339826	0.0013952	0.0340380	0.0013964

. As can be easily seen from the table, using the analytical approach and the proposed numerical methods, the estimated values of the maximum displacements of the double-beam system are in excellent agreement with the numerical calculations based on the FE method. Furthermore, the results obtained show that the displacements decrease as $k_m$ increases.

In the second case, the structure was analysed by implementing finite beam elements that did not take the crack effect into account. In particular, a simply supported double-beam system (SS-SS) subjected to a uniformly distributed load acting only on the upper beam was considered. For different values of $k_m$, the maximum displacements of the beam system were calculated, and the results obtained with the closed-form procedure and the numerical methods based on CDM and FEM were compared and reported in

Table 2. Maximum deflections values of two beams varying $k_m$ in the range $\left[{10}^2,{10}^3,{10}^4,{10}^5\right]$ and in the absence of a crack, where C-FS = closed-form solution, C = CDM, F = FEM.

${\mathit{k}}_{\mathit{m}}$	v${}_{1max}$ (C-FS)	v${}_{2max}$(C-FS)	v${}_{1max}$ (C)	v${}_{2max}$ (C)	v${}_{1max}$ (F)	v${}_{2max}$ (F)
10${}^2$	0.0348842	9.631 × 10${}^{-7}$	0.0348842	9.631 × 10${}^{-7}$	0.0348842	9.631 × 10${}^{-7}$
10${}^3$	0.0348756	9.626 × 10${}^{-6}$	0.0348754	9.626 × 10${}^{-6}$	0.0348756	9.626 × 10${}^{-6}$
10${}^4$	0.0347894	0.0000958	0.0347893	0.0000958	0.0347895	0.0000958
10${}^5$	0.0339723	0.0000913	0.0339721	0.0000913	0.0339271	0.0000913

.

As can be seen from the table, the estimated values of the maximum displacements of the double-beam system are in excellent agreement with the numerical calculations based on the FE method. Furthermore, the results obtained show that the displacements decrease as $k_m$ increases.

4.2. Case 2: Simply Supported-Simply Supported Double-Beam System in the Presence of a Uniformly Distributed Load on the Upper Beam and a Crack on the Upper and Lower Beams

In the second example, a simply supported double-girder system (SS-SS) with two transverse cracks was considered. The transverse cracks are applied to the upper and lower beams at non-dimensional distances of z = 0.5 m and z = 1.75 m, respectively. The top beam is loaded with a uniformly distributed load q = 100 kN/m.

Figure 6 shows the deflections of two beams. In particular, the vertical displacements of the upper beam are shown with a dotted line, while the solid line shows the displacements of the lower beam. As can be seen, for the upper beam, the maximum value of the transverse displacement ${\mathrm{v}}_1$ is 0.0321605 m at the dimensionless abscissa z = 1.18 m, while, for the lower beam, the transverse displacement ${\mathrm{v}}_2$ at the position of the crack (z = 1.2375 m) is 0.00847839 m. The closed-form solution, on the other hand, provides the following results: the maximum value of deflection ${\mathrm{v}}_1$(z = 1.18 m) = 0.0321452 m for the upper beam, and the maximum value of deflection ${\mathrm{v}}_2$(z = 1.2375 m) = 0.0084943 m for lower beam. It can be seen that the predicted results of CDM are in excellent agreement with the closed-form solutions.

4.3. Case 3: Effect of Elastic Constraints and Crack on the Static Behaviour of a Double-Beam System

This example considers a double-beam system with the same geometrical and material properties of the previous numerical examples. The beams are elastically restrained against translation and rotation at either end, with fixed values of $k_{1\mathrm{TL}}$$=k_{2\mathrm{TL}}$$=k_{1\mathrm{TR}}$ = $k_{2\mathrm{TR}}={10}^{10}$ and varying the non-dimensional rotational stiffness in the range [0–$\left.{10}^4\right]$. The transverse crack is located at the mid-span of the lower beam. A uniformly distributed load q = 100 kN/m is applied to the upper beam.

Table 3. Maximum deflections values of two beams varying the non-dimensional rotational stiffness $K_{1\mathrm{RL}}$ = $k_{1\mathrm{RR}}$ = $k_{2\mathrm{RL}}$ = $k_{2\mathrm{RR}}$ = $K_{\mathrm{R}}$ in the range $\left[0,1,10,{10}^2,{10}^3,{10}^4,{10}^{10}\right]$.

${\mathit{K}}_{\mathit{R}}$	v${}_{1max}$	v${}_{2max}$
0	0.0291244	0.00890045
1	0.0220762	0.00509119
10	0.0107519	0.00119981
10${}^2$	0.00713561	0.000536748
10${}^3$	0.00669172	0.000474023
10${}^4$	0.00666452	0.000467836
10${}^{10}$	0.00664013	0.000467150

presents the deflections’ first value for a simply supported double-beam system for different values of the non-dimensional stiffnesses. In Table 3, results involving respective maximum transverse displacements, ${\mathrm{v}}_{1max}$ and ${\mathrm{v}}_{2max}$, at the mid-span for the upper and lower beams are presented. As can be noted, as the stiffness values increase, deflections decrease throughout the two beams, especially near the crack. An analogy between increasing the stiffness and decreasing the deflections is illustrated in Figure 7, which represents the clamped-clamped beam case.

4.4. Case 4: Effect of Taper Ratio Coefficient and Crack on the Static Behaviour of a Double-Beam System

This numerical example considers the influence of taper ratio and crack on the static behaviour of two non-uniform double-beam systems having the following law of moment of inertia:

$$\mathrm{I}\left(z\right)={\mathrm{I}}_0{\left((\beta -1)\frac{z}{\mathrm{L}}+1\right)}^4$$

(70)

where, if $\beta <$ 1, the cross-section decreases with the abscissa; on the contrary, if $\beta >$ 1, the cross-section increases with the abscissa. A uniformly distributed load, q = 100 kN/m, is applied to the upper beam, and a crack is introduced at the mid-span of the lower beam. For varying $\beta$ in the range [0.5–2], the effect of taper ratio is evaluated as obtained by using CDM. In Figure 8 and Figure 9, the displacements diagrams are depicted for $\beta$ = 0.5, 1, respectively. The upper beam is simply supported at the left end and clamped at the right end, while the lower beam is simply supported at either end.

For $\beta$ = 1.5, 2, in Figure 10 and Figure 11, the displacements diagrams are plotted. The upper beam is simply supported at either end, while the lower beam is simply supported at the left end and clamped at the right end.

For varying $\beta$ = 0.5–2, in

Table 4. The maximum deflections value for different values of $\beta$.

$\mathit{\beta }$	v${}_{1max}$	v${}_{2max}$	Figure
0.5	0.051597	0.026785	7
1	0.013401	0.003783	8
1.5	0.005433	0.0010456	9
2	0.002697	0.0004161	10

, the maximum deflections values for two beams are quoted. It is interesting to note that the maximum deflections value decreases when the taper ratio coefficient increases.

4.5. Case 5: Effect of a Concentrated Force and Crack Located at the Mid-Span of the Upper and Lower Beams, Respectively

In this numerical example, the effect of concentrated force is evaluated. Consider a simply supported-simply supported (SS-SS) double-beam system in the presence of a crack. The transverse crack is located at the mid-span of the lower beam, and a concentrated force F is located at the mid-span of the upper beam.

Table 5. The maximum deflections value for different values of dimensional concentrated force F and for height of crack “a” = 0.09 m.

$\mathit{F}\left(\mathbf{N}\right)$	v${}_{1max}$	v${}_{2max}$
10	1.87065 × 10${}^{-6}$	5.59848 × 10${}^{-7}$
10${}^2$	1.87065 × 10${}^{-5}$	5.59848 × 10${}^{-6}$
10${}^3$	1.87065 × 10${}^{-4}$	5.59848 × 10${}^{-5}$
10${}^4$	1.87065 × 10${}^{-3}$	5.59848 × 10${}^{-4}$
10${}^5$	1.87065 × 10${}^{-2}$	5.59848 × 10${}^{-3}$

shows the maximum deflections values for different values of the concentrated force and in the absence of a distributed load. As can be noted, as the value of the concentrated force F increases, the values of displacements at the mid-span of the two beams increase.

For the same numerical example, fixing the force value F = (10${}^4$) N and varying the non-dimensional height of crack $\xi =\frac{a}{h}$ located at the mid-distance of the lower beam, the maximum deflections are calculated and listed in

Table 6. The maximum deflections for different values of crack depth and for a non-dimensional concentrated force $F_t=\left(0.107167\right)$.

$\mathit{\xi }$	v${}_{1max}$	v${}_{2max}$
0.1	0.00184331	0.000397534
0.2	0.00184666	0.000417421
0.3	0.00185267	0.000453055
0.4	0.00186293	0.000513990
0.5	0.00187065	0.000559848

. It is interesting to note that the maximum deflections value increases as the non-dimensional height of the crack increases.

4.6. Case 6: Effect of the Slenderness $\lambda$ on the Deflections for Both Upper and Lower Beams in the Presence of a Crack

This numerical example, to study the effects of the slenderness $\lambda =\frac{L}{h}$ on displacements and rotations, considers a simply supported double-beam system having the same geometrical and material properties of the previous numerical examples. The beam system is submitted to a uniformly distributed load q = 100 kN/m acting on the upper beam only. A crack is introduced in the mid-span of the lower beam.

Setting $\mathsf{\Gamma }=\frac{h}{b}=1.8$ and having $\lambda =\frac{L}{h}$, the expressions of the parameters of Equation (13) become:

$$\alpha =\lambda \sqrt[4]{\frac{12k_m\mathsf{\Gamma }}{\mathrm{E}}};p=\frac{12\mathrm{q}\mathsf{\Gamma }{\lambda }^4}{\mathrm{E}}$$

(71)

Equation (71) denotes the relationship between the deflection and slenderness.

For different values of slenderness $\lambda$ of the two beams, the maximum displacements and the rotations at the left and right ends (for $\zeta$ = 0 and $\zeta$ = 1) are calculated. The results obtained from the closed-form solution and numerical method based on CDM are compared and listed in

Table 7. Numerical comparison among the closed-form solutions (C-FS) and numerical results based on the CDM for different values of length $\lambda$ and ($\zeta$ = 0.5).

$\mathit{\lambda }$	v1(C-FS)	v2(C-FS)	v${}_1\left(\mathbf{CDM}\right)$	v${}_2\left(\mathbf{CDM}\right)$
2	0.00001500	8.5277 × 10${}^{-9}$	0.000014500	8.5276 × 10${}^{-9}$
3	0.00007589	1.6061 × 10${}^{-7}$	0.00007589	1.6061 × 10${}^{-7}$
5	0.00058326	6.7375 × 10${}^{-6}$	0.00058326	6.7374 × 10${}^{-6}$
7	0.00221279	0.00007947	0.00221279	0.00007947
9	0.00588599	0.00048809	0.00588599	0.00048808
13.8889	0.0291243	0.00890046	0.02912429	0.00890037

. As can be easily seen from the table, the displacements values are in excellent agreement. In addition, the results obtained show that the displacements increase as the slenderness $\lambda =\frac{L}{h}$ of the two beams increases.

5. Concluding Remarks

In the present paper, the static behaviour of a double-beam system, in the presence of Winkler medium, carrying a crack at generic position on the lower beam and subjected to a distributed load on the upper beam has been studied. The double-beam system is also supposed to be constrained at the ends by elastically flexible springs with transverse stiffness and rotational stiffness. According to the Euler–Bernoulli beam theory, the static governing equations are derived using a variational formulation and have been solved through implementing analytical and numerical approaches. Among the numerical approaches, the CDM is employed to solve the governing equations, in which the beam is reduced to a set of rigid bars linked together by means of elastic constraints. A comparative analysis has been performed in order to verify the accuracy and validity of the proposed numerical method. The effects of crack, taper ratio, elastic medium parameter, boundary conditions and rotational and translational stiffness on the two beams’ deflections through theoretical and numerical approaches have been presented. Through the obtained results, it can be observed that the maximum deflections value decreases if the transverse stiffness value increases, and if the taper ratio coefficient increases, it decreases. Moreover, the crack plays a key role in the static behaviour of a double-beam system: the maximum deflections value increases when the crack increases.

Finally, the numerical examples demonstrate that the results determined by CDM perfectly match with the solutions from the governing equations of the double-beam model and are in good agreement with the results obtained by FEM. It is shown that the CD method has a good and rapid convergence regardless of the beam theory, crack and elastic foundation parameters.