Closed Form Solution in the Buckling Optimization Problem of Twisted Shafts

Abstract

The counterpart for Euler’s buckling problem is Greenhill’s problem, which studies the forming of a loop in an elastic beam under torsion. In the context of twisted shafts, the optimal shape of the beam along its axis is searched. A priori form of the cross-section remains unknown. For the solution of the actual problem, the stability equations take into account all possible convex and simply connected shapes of the cross-section. The cross-sections are similar geometric figures related by a homothetic transformation with respect to a homothetic center on the axis of the beam and vary along its axis. The distribution of material along the length of a twisted shaft is optimized so that the beam is of the constant volume and will support the maximal moment without spatial buckling. The applications of the variational method for stability problems are illustrated in this manuscript.

1. Introduction

Torsion shafts are tremendously significant mechanical structural elements, which are used in machinery for the transmission of power. Shafts are used broadly in machinery and are often one of the most critical parts of the machine. They are used to transfer mechanical power from the combustion engine or electromotor to a moving component, such as wheels, pulleys, or sprockets. They are used in combination with further mechanical components, such as gears and sprockets, to provide power transmission within a mechanical system. A torsion shaft characteristically consists of a cylindrical rod or bar, but can also be made in other shapes, such as triangle, squares, or hexagonal bars. Shafts are subjected to loads, including bending moments and torsional stresses, which can cause shafts to fail if they are not designed correctly. Generally, shafts are cylindrical bars that can be stepped or have the same diameter from one end to the other. Shafts that measure only one diameter across the whole shaft are much easier and cheaper to produce. Stepped shafts are made to deal with various stress levels that differ along the shaft in a mechanical system. The primary application of the optimal solutions are the moment-transmitting shafts of the engines or of the industrial machinery. Optimally stepped shafts transmit the maximal allowable moment for the predefined mass of the member. The actual manuscript provides the estimation of mass, bucking moment, stored elastic energy and stiffness of the optimally stepped shafts. This information could help the designer to estimate properly the effects of the optimization and allows for the motivated decision making for the specific design of the shafts.

“Rod” means a straight, round stick, shaft, bar, cane, or staff. The term “rod” is frequently used for the members in torsion [1,2,3,4]. In structural optimization, the terms “column” or “beam” are frequently used for the designation of the member in bending state [5,6,7]. A “beam” signifies a structural element that primarily resists loads applied laterally to the beam’s axis. An element designed to carry the primarily axial force would be a “strut” or “column”. The term “column” is applied for the heavy, vertically compressed beams. “Bar” indicates a solid metal object with a uniform (round, square, hexagonal, octagonal, or rectangular) cross-section. However, the term “bar” is hardly ever used in structural mechanics. Greenhill [8] uses the word “shafting” for the designation of the twisted elastic beam. According to [9], there are no principal difference between rods, columns, and shafts in the context of stability problems. In this manuscript, the term “shaft” will be chiefly used for the description of the straight, thin, and elastic “twisted beam”.

In the actual manuscript, a thin elastic shaft with an isotropic cross-section, and twisted by couples applied at its ends only [10], will be considered. The optimization for stability of the simply supported shaft were studied numerically in [1]. The shaft possessed the similarly shaped cross-sections with the varying cross-sectional area. The more advanced problem of a twisted and compressed beam was studied numerically in [6]. The optimization problem consisted in finding the distribution of cross-sectional areas that assigns the largest value to the critical moment. The critical moment causes the loss of stability. The constraint on the volume of material and the constraints on the admissible thickness of the rod were satisfied in the cited article.

The problem of determining the compressed and twisted beam of maximal efficiency was studied in [3]. Following the structural optimization theory for a given load, the shape of the column of minimal weight was determined numerically.

The problem of the optimal design of rods under combined compression and torsion was investigated in [11]. A cross-sectional area varying along the axis of the column, which led to the maximal critical loading, was sought. The varying cross-section was approximated by a function with free parameters. Alternatively, the varying cross-section was determined numerically using Pontryagin’s maximum principle.

Generally speaking, for non-conservative problems, the dynamic approach for stability investigation must be applied [12]. However, Euler’s static approach has proved to be valid for the considered boundary value problem with conditions of fixed axes of rotation, as observed in cases 1 and 2 ([9], §5.4, Table 5.1, Section 1.2, page 127). The twisting couple $\Lambda$ retains its initial direction during buckling and the boundary conditions of fixed axes of rotation are satisfied ([9], cases 1 and 2 in Table 1.1, Section 1.2, page 5). Euler’s static approach is shown to be valid also for an infinite and periodically simply supported shaft. The corresponding boundary-value problems are neither self-adjoint nor conservative in the classical sense. Nevertheless, it is a conservative system of the second kind [13]. Consider a thin elastic shaft with an isotropic cross-section, twisted by couples applied at its ends only (Greenhill’s problem) [2,8]. According to Euler’s theory, the magnitude of the critical moment of the shaft is determined by the smallest positive eigenvalue.

The optimization problem for a column, loaded solely by compression forces is studied in [14]. The vector of the applied forces was parallel to the axis of the column. The critical values of buckling are equal among all competitive designs of the columns. The dimensional analysis eases the mathematical technique for the optimization problem. The moments of inertia of the rod are the powers of the cross-sectional area with the exponent $\alpha$. The dimensional analysis introduces two dimensionless factors, one for the total material volume and one for the total stiffness of the columns. With the method of dimensional analysis, the solution of the nonlinear algebraic equations for the Lagrange multiplier will be superfluous. The closed-form solutions for the Sturm–Liouville and mixed type boundary conditions were derived for an arbitrary positive exponent $\alpha$. The solutions are expressed in terms of the higher transcendental functions. The principal results are the closed-form solution in terms of the hypergeometric and elliptic functions, the analysis of single- and bimodal regimes, and the exact bounds for the masses of the optimal columns. The isoperimetric inequality was formulated as the strict inequality sign, because the optimal solution could not be attained for any finite design parameter. The additional restriction on the minimal area of the cross-section regularized the optimization problem.

The optimal distribution of bending flexure along the axis of the simultaneously compressed and twisted rod was found in [15]. The cross-section that delivers the maximum or the minimum for the critical eigenvalue must be determined among all convex and simply connected domains. The distribution of material along the length of a twisted and compressed rod was optimized so that the rod must support the maximal moment without spatial buckling, presuming its volume remains constant among all admissible rods. The static Euler’s approach is applicable for the simply supported rod (hinged), twisted by the conservative moment and axial compressing force. Notably, the solution of the optimization problem for stability of simultaneously twisted and compressed rods could be determined only for three certain values of the exponent factor $\alpha$. Namely, the solution in the above cited article was determined solely for $\alpha =1$, $\alpha =2,$ and $\alpha =3$. In contrast, the above-cited solution [14] of the optimization of the axially compressed column allows the closed form expressions for an arbitrary positive exponent. There arises a question as to whether the optimal design problem for the shaft allows for the solutions for an arbitrary positive or a real value of the exponent factor $\alpha$.

The principal task of the actual manuscript is the closed-form analytical solutions for the optimal shape of the shaft twisted along its axis. The solutions are sought for real values of the exponent factor $\alpha$.

2. Isoperimetric Inequality for a Twisted Shaft with an Arbitrary Convex and Simply-Connected Cross-Section

In dealing with columns, rods, shafts, etc., it is assumed that they are homogeneous, elastic, and obey Hooke’s law. According to Euler’s theory, the magnitude of critical moment $M$is determined by the smallest positive eigenvalue $\Lambda$. From the beginning, the validity of the static Euler’s approach for the simply supported shaft (hinged), twisted by the conservative moment, is presented. 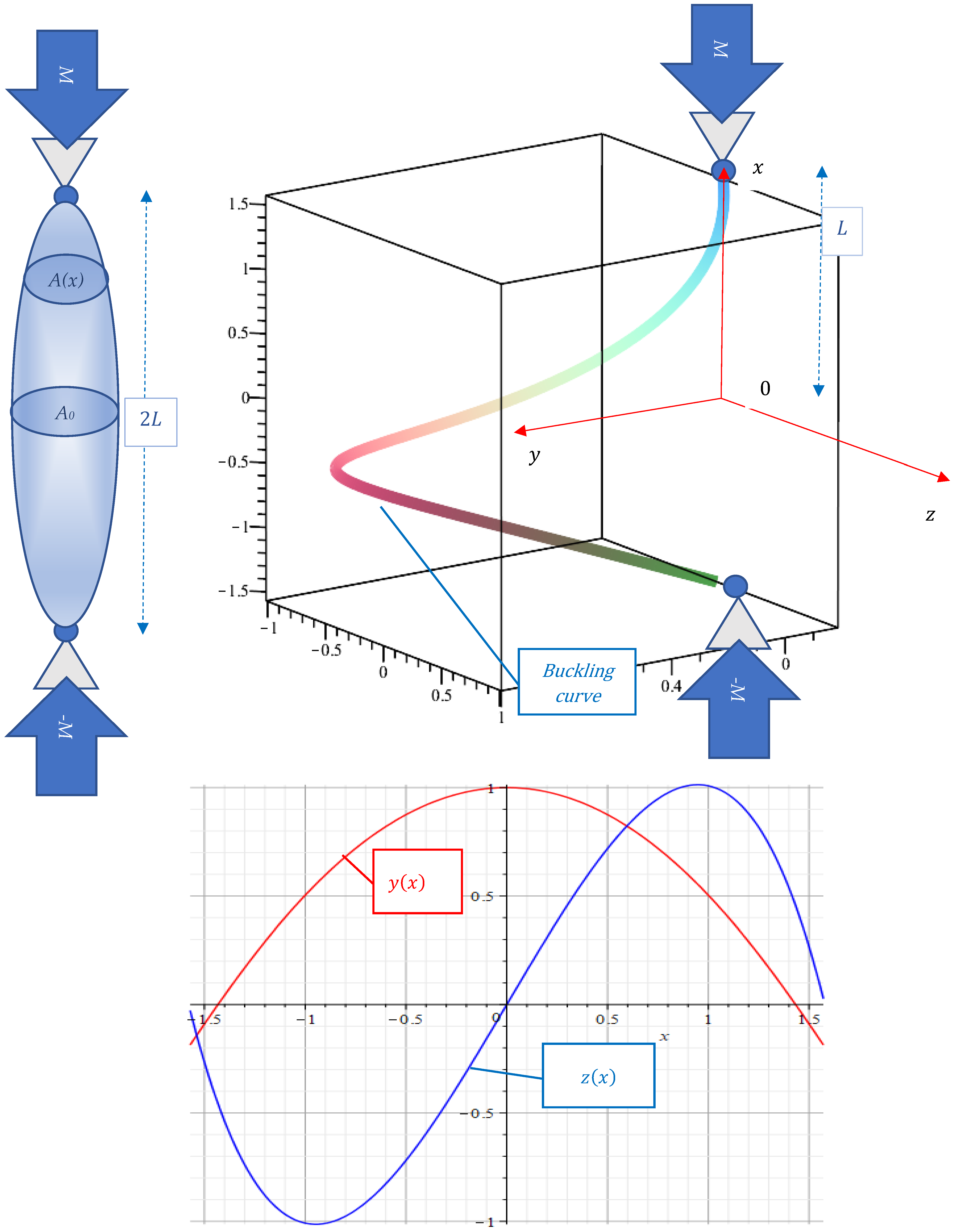The distribution of the material along the length of the shaft is optimized so that the shaft is of the constant volume $V$ and will support the maximal moment without spatial buckling (Figure 1). The cross section that delivers the maximum or the minimum for the critical eigenvalue must be determined among all convex and simply connected domains. A priori form of the cross-section remains unknown. For the solution of the actual problem, the stability equations take into account all possible convex and simply connected shapes of the cross-section. Consequently, the requirement of the equality of the principal moments of inertia for the cross-section could be released.

The cross-sections are similar geometric figures related by a homothetic transformation with respect to a homothetic center on the axis of the shaft and vary along its axis. The area of some reference cross-section $\Omega$ is $A_0$. The area of the cross-section with the coordinate $x$ is $A\left(x\right),-L\le x\le L$. The scaling dimensionless function is positive:

$$\begin{array}{cc}s\left(x\right)=\frac{A\left(x\right)}{A_0}>0, & 0<s<1\end{array}$$

(1)

The function $s\left(x\right)$ is the locally integrable function over the length of the shaft $\left(-L\le x\le L\right)$. The volume of the shaft is equal to $2V$:

$$\frac{1}{2}{{\displaystyle \int }}_{-L}^{L}s\left(x\right)dx=V$$

(2)

For an arbitrary cross-section, the moments of inertia $J_{yy},J_{yz}, J_{zz}$of the transverse cross-sectional area are the power of $s\left(x\right)$. The moments of inertia with respect to lines, passing through a point on the neutral axis of bending and parallel to the axes $y$ and $z$, read:

$$\begin{array}{cccc}{J}_{yy}=I_{yy}{s}^{\alpha }\left(x\right),& J_{yz}=I_{yz}{s}^{\alpha }\left(x\right),& J_{zz}=I_{zz}{s}^{\alpha }\left(x\right),& -L\le x\le L\end{array}$$

(3)

The constants $I_{yy}$, $I_{yz},$ and $I_{zz}$ denote the moments of inertia of the reference cross-section $\Omega$. The moments of inertia$I_{yy}$, $I_{yz},$ and $I_{zz}$ are the components of tensor of the second rank. For an arbitrary angle $\mathsf{\Psi }$ between the principal axis of inertia and y axis, the moments of inertia are

$$\begin{array}{ccc}{I}_{yy}=I_1{\mathit{cos}}^2\mathsf{\Psi }+I_2{\mathit{sin}}^2\mathsf{\Psi },& I_{yz}=\left(I_1-I_2\right)\mathit{sin}\mathsf{\Psi }\mathit{cos}\mathsf{\Psi },& I_{zz}=I_1{\mathit{sin}}^2\mathsf{\Psi }+I_2{\mathit{cos}}^2\mathsf{\Psi }.\end{array}$$

(4)

The angle $\mathsf{\Psi }$ remains constant along the axis of the shaft.

As declared above, the shaft is twisted by conservative couples, such that the torque is constant over the axis of the beam. The bending moments, in terms of curvatures of the shaft are:

$$\begin{array}{cc}{M}_z=E{I}_{yy}{y}^{″}+E{I}_{yz}{z}^{″},& M_y=E{I}_{yz}{y}^{″}+E{I}_{zz}{z}^{″}.\end{array}$$

(5)

The axes $y$ and $z$ are chosen in the direction of principal axes of inertia through the center of gravity ($\mathsf{\Psi }=0$). The curvatures of the axis $k_z, k_y$ in the course of buckling are assumed to be small, such that the geometrically linear equations could be applied for the solutions. The bending moments in terms of curvatures $k_z, k_y$ of the shaft in the principal axes are:

$$\begin{array}{cccc}{M}_z=E{I}_1{k}_z,& M_y=E{I}_2{k}_y,& k_z=y^{″},& k_y=z^{″}\end{array}$$

(6)

At first, it will be assumed that both moments of inertia are proportional to one function$j\left(x\right)$:

$$I_1\left(x\right)={\eta }_1 j\left(x\right), I_2\left(x\right)={\eta }_2 j\left(x\right), j\left(x\right)={\varkappa }_{\alpha }{s}^{\alpha }.$$

The constants are positive values ${\eta }_1>0,{\eta }_2>0.$ The quantity $s^{\alpha }$ is proportional to the flexural rigidity, and the exponent factor $\alpha$ is positive. In the simplest of cases, the exponent factor takes the values of 1, 2, and 3 (Banichuk, 1990). The case $\alpha =2$ corresponds to a congruent change in the form of the cross-section. The optimal convex shape of the simply connected cross-section with the topological genus null was determined [16]. The topological genus of a surface (or Euler characteristic) is in essence the number of its “holes”. The solution grounds on the following isoperimetric equation. Of all convex domains with area $A_{⊿}^{}$, the equilateral triangle yields the maximum of the product$I_1{I}_2$:

$${\sqrt{I_{1}I}}_2\le \frac{\sqrt{3}}{18}{A}_{⊿}^2=I_{⊿}$$

Thus, the shaft with the cross-section in the form of an equilateral triangle delivers the maximum for the critical eigenvalue for all convex and simply-connected domains of the same cross-sectional area$A_{⊿}^{}$. For the cross-section in the form of the equilateral triangle ${\varkappa }_2=\sqrt{3}/18\approx 0.9622.$

For the circular cross-section, the constant is ${\varkappa }_2={\left(4\pi \right)}^{-1}\approx 0.07957.$ The shaft with the circular, simply connected cross-section delivers correspondingly the minimum for the critical eigenvalue:

$${\sqrt{I_{1}I}}_2\ge \frac{1}{4\mathsf{\pi }}{A}_{\odot }^2=I_{\odot }^{}$$

Two other cases describe the situations in which the form of the transverse cross-section undergoes the transformation, such that one of the geometric dimensions of the cross-section changes. For the technically important case of the thin-walled tubes with the variable thickness of wall $t\left(x\right)$ and the mean diameter of tube $D\left(x\right)$, the second moments of:

$$I_1\left(x\right)=I_2\left(x\right)=\frac{\pi }{64}\left[{\left(D+t/2\right)}^4-{\left(D-t/2\right)}^4\right]=\frac{\pi }{16}t{D}^3+\frac{\pi }{64}D{t}^3\approx \frac{\pi }{16}t{D}^3 \mathrm{for} t\ll D$$

The case $\alpha =1$ corresponds to the adjustable wall thickness (as the design variable) and constant mean diameter of the tube. The analogous dependence arises in the case of the bending of sandwich beams [7]. The case $\alpha =3$ corresponds the inconstant mean diameter of the tubular shaft (as the design variable) and constant wall thickness.

Consider the shaft hinged on two supports $x=L$ and $x=-L$:

$$\begin{array}{cccc}y\left(L\right)=0, \hfill & Ej{\eta }_1{y}^{″}\left(L\right)=0\hfill & z\left(L\right)=0,\hfill & Ej{\eta }_2{z}^{″}\left(L\right)=0,\hfill \\ y\left(-L\right)=0,\hfill & Ej{\eta }_1{y}^{″}\left(-L\right)=0,\hfill & z\left(-L\right)=0\hfill & Ej{\eta }_2{z}^{″}\left(-L\right)=0.\hfill \end{array}$$

(7)

The buckling equations of the shaft read:

$${\left(Ej{\eta }_1{y}_{}^{″}\right)}^{″}=-\tilde{\Lambda }{z}^{‴}, {\left(Ej{\eta }_2{z}_{}^{″}\right)}^{″}=\tilde{\Lambda }{y}^{‴}$$

(8)

For the boundary value problem (7) and (8), the actual curvatures and displacements $y^{*},z^{*}$ minimize the quotient:

$$\tilde{\Lambda }\left[j,\tilde{y},\tilde{z}\right]=\frac{{{\displaystyle \int }}_{-L}^{L}Ej\left({\eta }_1{\tilde{y}}^{″}{}^2+{\eta }_2{\tilde{z}}^{″}{}^2\right)dx}{{{\displaystyle \int }}_{-L}^L\left({\tilde{z}}^{″}{\tilde{y}}^{\prime }-{\tilde{z}}^{\prime }{\tilde{y}}^{″}\right)dx}, \tilde{\Lambda }\left[j,y,z\right]\equiv \tilde{\Lambda }\left[{\varkappa }_{\alpha }{s}^{\alpha },y,z\right]=\underset{\tilde{y},\tilde{z}}{\min }\tilde{\Lambda }\left[j,\tilde{y},\tilde{z}\right]$$

(9)

3. Optimization Problem and Isoperimetric Inequality for Stability

Based on the above solution, the distribution of material along the length of a twisted beam will be optimized. The optimal distribution of the cross-sectional area along the span of the beam is denoted by the capital letter$S\left(x\right)$. The optimization problem examines the shaft of the constant volume $2V_0$ that supports the maximal moment without spatial buckling. If the density of the material is $\rho$, the mass 2$\mathfrak{M}$ of the shaft is given by:

$$\begin{array}{ccc}\mathfrak{M}=\rho V,& V\left[s\right]=\frac{1}{2}{{\displaystyle \int }}_{-L}^{L}s\left(x\right)dx& s\left(x\right)>0.\end{array}$$

(10)

The new variables will be introduced:

$$\begin{array}{ccc}Y=\sqrt{{\eta }_1}y, & Z=\sqrt{{\eta }_2}z, & \tilde{\Lambda }=\sqrt{{\eta }_1{\eta }_2}\Lambda \end{array}$$

With the new variables, the formulation of the optimization problem is the following:

$$\Lambda \left[{\varkappa }_{\alpha }{s}^{\alpha },Y,Z\right]=\frac{\tilde{\Lambda }}{\sqrt{{\eta }_1{\eta }_2}}\to \underset{s\left(t\right)}{max}, \frac{1}{2} {{\displaystyle \int }}_{-L}^{L}s\left(x\right)dx=\frac{1}{2} {{\displaystyle \int }}_{-L}^{L}S\left(x\right)dx=V_0,$$

(11)

Particularly, if both principal moments of the second order are equal $I_1\left(x\right)=I_2\left(x\right)$, the factors are: ${\eta }_1={\eta }_2=1$. For example, this setting is valid for the shaft with the cross-section in form of an equilateral triangle or for the shaft with a circular cross-section.

The distribution of material along the length of a shaft is optimized so that the beam is of constant volume and provides the maximal moment without spatial buckling. The variational methods will be applied for the derivation of the necessary optimality conditions. The augmented Lagrangian is related to, but not identical to the method of Lagrange multipliers [10]. Augmented Lagrangian methods are a certain class of algorithms or analytic techniques for solving constrained optimization problems. They have parallels to penalty methods. Both methods replace a constrained optimization problem by a series of unconstrained problems and add a penalty term to the objective. The difference between both methods consists in their penalty terms. The augmented Lagrangian method adds the term with the Lagrange multiplier. The augmented functional for the optimization problem (10) and (11) reads:

$$\mathcal{L}\left[s\right]=V\left[s\right]+\mathsf{\lambda }\Lambda \left[{\varkappa }_{\alpha }{s}^{\alpha },Y,Z\right]$$

(12)

The derivation of the necessary optimality conditions is based on the concept of functionals and the functional derivative. A mathematically precise discussion of the functional derivative can be found in [10] or [17]. The necessary optimality condition follows from the first functional derivative of the augmented Lagrangian (12):

$$\begin{array}{ccc}-c+s^{\alpha -1}{\mathsf{{\rm K}}}^2=0, & {\mathsf{{\rm K}}}^2={\kappa }_y{}^2+{\kappa }_z{}^2 & c={\left(E{k}_{\alpha }\alpha \right)}^{-1}\mathsf{\lambda }.\end{array}$$

(13)

In Equation (13), $c$ an auxiliary constant, that is proportional to Lagrange multiplier $\mathsf{\lambda }$. The spatial curvature is signed in Equation (13) as $\mathsf{{\rm K}}$, where the curvatures of the deformed axis of the shaft in the planes 0xy and 0xz are:

$${\kappa }_y=Z^{″}, {\kappa }_z=Y^{″}$$

The application of Fermat’s principle for the optimization problems leads to the necessary optimality condition:

$$S={\left(\mathsf{{\rm K}}/c\right)}^{2/\left(1-\alpha \right)}$$

(14)

The necessary optimality condition (14) is the requirement that the augmented Lagrangian has a stationary value. The optimal second moment of the cross-section follows from (14) as:

$$J=E{\varkappa }_{\alpha }·{\left(\mathsf{{\rm K}}/c\right)}^{2\alpha /\left(1-\alpha \right)}={\left({Y^{″}}^2+{Z^{″}}^2\right)}^{\alpha /\left(1-\alpha \right)}$$

(15)

The applied method of scaling allows the arbitrary selection of the constant $c$. For the briefness of the governing equations, the constant $c$ is introduced as the positive solution of the equation:

$$E\alpha {\varkappa }_{\alpha }{\left(1/c\right)}^{2\alpha /\left(1-\alpha \right)}=1$$

The bending stiffness reduces with this choice to:

$$E{J}_{}={\left({Y^{″}}^2+{Z^{″}}^2\right)}^{\alpha /\left(1-\alpha \right)}\equiv {\mathrm{K}}^{2\alpha /\left(1-\alpha \right)}$$

(16)

4. Closed-Form Solution of the Governing Equations

The order of both Equations (8) could be reduced by one using the boundary value conditions (7). The buckling equations transform with Equation (16) to:

$${\left({Y^{″}}^2+{Z^{″}}^2\right)}^{\alpha /\left(1-\alpha \right)}{Y}^{″}=-\Lambda Z^{\prime }, {\left({Y^{″}}^2+{Z^{″}}^2\right)}^{\alpha /\left(1-\alpha \right)}{Z}^{″}=\Lambda Y^{\prime }$$

(17)

Two Equations (17) with the corresponding boundary conditions for $Z$ and $Y$ are simultaneous nonlinear ordinary differential equations of the second order. The standard methods for the closed form solutions of such equations were apparently not reported in the literature. The principal task of the actual manuscript is to obtain a closed form solution of Equation (17). As the first step for the solution of two simultaneous Equations (17), the unknowns will be represented over two new functions$\mathsf{{\rm K}}\left(x\right), \theta \left(x\right)$:

$$\begin{array}{cc}{Z}^{″}=\mathsf{{\rm K}}·\mathit{cos}\theta ,& Y^{″}=\mathsf{{\rm K}}·\mathit{sin}\theta .\end{array}$$

(18)

The substitution of Equation (18) in Equation (17) reduces it to two simultaneous equations for the new unknowns $\mathsf{{\rm K}}$ and $\theta$:

$$\begin{gathered} -\left(\alpha -1\right){\mathsf{{\rm K}}}^2{\theta }^{″}+ {\mathsf{{\rm K}}}^{\prime }\left[2\left(\alpha +1\right)\mathsf{{\rm K}} {\theta }^{\prime }+\left(\alpha -1\right){\Lambda \mathsf{{\rm K}}}^{\left(3\alpha -1\right)/\left(\alpha -1\right)}\right]=0, \\ \left(1-{\alpha }^2\right){\mathsf{{\rm K}}}^4 {\mathsf{{\rm K}}}^{″}-{\mathsf{{\rm K}}}^5{\left(1-\alpha \right)}^2{{\theta }^{\prime }}^2+\alpha \left(1+\alpha \right){\mathsf{{\rm K}}}^3{ {\mathsf{{\rm K}}}^{\prime }}^2+{\left(1-\alpha \right)}^2\Lambda {\theta }^{\prime }{\mathsf{{\rm K}}}^{\left(7\alpha -5\right)/\left(\alpha -1\right)}=0. \end{gathered}$$

(19)

The area of the optimal cross-sections $S$ vanishes in the ends of the shaft, where the bending moment and spatial curvature $\mathsf{{\rm K}}$ disappear. This requirement plays the role of the boundary conditions for $\mathsf{{\rm K}}$ and $S$ at $x=\pm L$. The function $\mathsf{{\rm K}}\left(x\right)=\mathsf{{\rm K}}\left(-x\right)$ must be even, and the function is odd $\theta \left(x\right)=-\theta \left(-x\right)$. Thus, from the symmetry considerations are as follows $\theta \left(0\right)=0$.

It is principally possible to solve Equation (19) for$\mathsf{{\rm K}},\theta$, but it is preferable to find the solution for the functions $S,\theta$. With this choice, the solution delivers the optimal cross-section $S$ directly. For this purpose, $\mathsf{{\rm K}}$ in Equation (19) is replaced by $S$ using Equation (14):

$$S^{\alpha +1}{\theta }^{″}+\frac{1}{2}{S}^{\prime }\left[2\left(\alpha +1\right)S^{\alpha }{\theta }^{\prime }{ }^{}+\left(\alpha -1\right)\Lambda S^{\prime }\right]=0$$

(20)

$$2\left(1+\alpha \right)S^{″}-\left(1-{\alpha }^2\right)S^{-1}{S}^{\prime }{}^2-4S^{} {{\theta }^{\prime }}^2+4S^{1-\alpha } \Lambda {\theta }^{\prime }=0$$

(21)

For a given $S\left(x\right)$, the solution to Equation (21) with respect to $\theta \left(x\right)$ reads:

$$\theta \left(x\right)=\frac{\alpha -1}{2}\Lambda \underset{0}{\overset{x}{{\displaystyle \int }}}{S}^{-\alpha }\left(\zeta \right)d\zeta$$

(22)

This choice of the lower integration limit satisfies the symmetry condition:$\theta \left(0\right)=0$. Substitution of $\theta \left(x\right)$ into the Equation (20) leads to an equation in terms of $S$only:

$$\left(1-\alpha \right){S^{\prime }}^2-2S S^{″}+{\Lambda }^2\left(\alpha -1\right)S^{2-2\alpha }=0$$

(23)

The Equation (23) is an ordinary nonlinear differential equation of the second order. For the solution of Equation (23), the dependent and independent variables must be exchanged:

$$\frac{d^{2}x}{d{S}^2}=\frac{1-\alpha }{2A}\left[{\Lambda }^2{S}^{2-2\alpha }{\left(\frac{dx}{dS}\right)}^2-1\right]\frac{dx}{dS}$$

(24)

The Equation (24) is the equation of the second order with missing $x\left(S\right)$. Thus, this equation allows for the order reduction. It follows the differential equation of the first order for the function $\chi =dx/dS$:

$$d\chi /dS=\frac{1-\alpha }{2 S}·\left[{\Lambda }^2{S}^{2-2\alpha }{\chi }^2-1\right]·\chi$$

Its solution with an integration constant $C_1$ reads:

$$\chi \left(S\right)=\pm \frac{1}{\sqrt{C_1 S^{1-\alpha }-{\Lambda }^2{S}^{2-2\alpha }}}$$

The next integration permits the closed form solution of the Equation (24) with two unknown constants $C_1$, $C_2$:

$$\begin{array}{cc}x=-{{\displaystyle \int }}_0^S\frac{t^{\alpha }}{\sqrt{C_1{t}^{\alpha +1}-{\Lambda }^2{t}^2}}dt+C_2 & \mathrm{for} 0<S<1, \mathrm{right} \mathrm{half};\\ x={{\displaystyle \int }}_0^S\frac{t^{\alpha }}{\sqrt{C_1{t}^{\alpha +1}-{\Lambda }^2{t}^2}}dt-C_2& \mathrm{for} 0<S<1, \mathrm{left} \mathrm{half}.\end{array}$$

(25)

According to the symmetry, the optimal solution $S\left(x\right)$ is an even function of x. Thus, $dS/dx$ must vanish in the middle point $x=0$. From this condition follows that $C_2=L$. The integral Equation (25) will be summable, if $C_1={\Lambda }^2$. With this substitution, the quadrature formulas (25) turn into:

$$\begin{array}{cc}x=L-\frac{1}{\Lambda }{{\displaystyle \int }}_0^S\frac{t^{\alpha -1}}{\sqrt{1-t^{\alpha -1}}}dt & \mathrm{for} 0<S<1, \mathrm{right} \mathrm{half};\\ x=\frac{1}{\Lambda }{{\displaystyle \int }}_0^S\frac{t^{\alpha -1}}{\sqrt{1-t^{\alpha -1}}}da-L& \mathrm{for} 0<S<1, \mathrm{left} \mathrm{half}.\end{array}$$

(26)

The function $S\left(x\right),$ as specified by Equation (26), is an even function of the independent variable along the axis of the shaft $-L\le x\le L$. Notably, the singular integral (26) is expressed for the right half in terms of the higher functions [18]:

$$\begin{array}{cc}x=L-\frac{ S^{\alpha }}{\Lambda \alpha }·{}_2{}^{}F{}_2\left(\left[\frac{1}{2},\frac{\alpha }{\alpha -1}\right],\left[\frac{2\alpha -1}{\alpha -1}\right],S^{\alpha -1}\right), & \alpha >1\end{array}$$

(27)

$$\begin{array}{cc}x=L-\frac{1}{\Lambda }\sqrt{\frac{ \pi }{\alpha -1}·}\left[1-erf\left(\sqrt{-ln\left(S\right)}\right)\right]+o\left(\alpha -1\right), & \alpha \to 1,\alpha >1.\end{array}$$

(28)

$$\begin{array}{cc}x=L-\frac{2}{3\Lambda }·\left(2-2\sqrt{1-S}-S\sqrt{1-S}\right)+o\left(\alpha -2\right), & \alpha \to 2\end{array}$$

(29)

$$\begin{array}{cc}x=L-\frac{arcsin\left(S\right)-S\sqrt{1-S^2}}{2\Lambda }+o\left(\alpha -3\right), & \alpha \to 3\end{array}$$

(30)

The functions in Equations (27)–(30) are the real functions of $0<S<1$. The limit in Equation (28) is the right-hand limit $\alpha \to 1+$. The symbol ${}_2{}^{}F{}_2\left(\left[p,q\right],\left[r,s\right],x\right)$ designates the hypergeometric function [18]. The expression $erfx$ in Equation (28) is the Gauss error function.

As required above, the area of the optimal cross-sections vanishes at the ends of the shaft $x=\pm L$, where the bending moment disappears.

Substitution of the condition $S\left(0\right)=1$ into (26) leads to the expression of the half-length of the shaft:

$$L=\frac{1}{\Lambda }{{\displaystyle \int }}_0^1\frac{t^{\alpha -1}}{\sqrt{1-t^{\alpha -1}}}dt$$

(31)

The integral (31) evaluates in terms of the beta-function [19]:

$$L=\frac{1}{\Lambda }\frac{ 1}{\alpha -1}{\rm B}\left(\frac{1}{2},\frac{\alpha }{\alpha -1}\right).$$

(32)

For volume evaluation, the integrand in Equation (31) must be multiplied by area [18]:

$$v=\frac{1}{\Lambda }{{\displaystyle \int }}_0^1\frac{t^{\alpha }}{\sqrt{1-t^{\alpha -1}}}dt=\frac{1}{\Lambda }\frac{ 1}{\alpha -1}{\rm B}\left(\frac{1}{2},\frac{\alpha +1}{\alpha -1}\right)$$

(33)

For estimation of elastic energy $\mathcal{E},$ the integrand in Equation (28) must be multiplied by area $t^{\alpha }$:

$$\epsilon =\frac{1}{\Lambda }{{\displaystyle \int }}_0^1\frac{t^{\alpha +1}}{\sqrt{1-t^{\alpha -1}}}da=\frac{1}{\Lambda }\frac{ 1}{\alpha -1}{\rm B}\left(\frac{1}{2},\frac{2\alpha }{\alpha -1}\right)$$

(34)

The normalized coordinate $X=x/L$ is introduced for the briefness of formulas. The shape $S\left(X\right)$ of the right side is given by the implicit function of the normalized coordinate $-1\le X\le 1$ [18,19]:

$$X=1-\frac{\alpha -1}{\alpha \sqrt{\pi }}·\frac{ \mathsf{\Gamma }\left(\frac{3\alpha -1}{2\alpha -2}\right)}{\mathsf{\Gamma }\left(\frac{\alpha }{\alpha -1}\right)}·{}_2{}^{}F{}_2\left(\left[\frac{1}{2},\frac{\alpha }{\alpha -1}\right],\left[\frac{2\alpha -1}{\alpha -1}\right],S^{\alpha -1}\right)· S^{\alpha }$$

(35)

The expression for the volume of the half of the shaft with the unit length is:

$$V=\frac{v}{L}=\frac{\mathsf{\Gamma }\left(\frac{\alpha -1}{\alpha +1}\right)·\mathsf{\Gamma }\left(\frac{3\alpha -1}{2\alpha -2}\right)}{\mathsf{\Gamma }\left(\frac{3\alpha +1}{2\alpha -3}\right)·\mathsf{\Gamma }\left(\frac{\alpha }{\alpha -1}\right)}$$

(36)

The following formula is valid for an assessment of elastic energy $\mathcal{E}$ in the normalized coordinates:

$$\mathcal{E}=\frac{\epsilon }{L}=\frac{2^{\frac{2\alpha }{\alpha -1}}}{2\sqrt{\pi }}·\frac{{\mathsf{\Gamma }}^2\left(\frac{3\alpha -1}{2\alpha -2}\right)}{\mathsf{\Gamma }\left(\frac{5\alpha -1}{2\alpha -2}\right)}$$

(37)

For practically interesting cases, the shape reduces to the elementary functions, as shown in

Table 1. Normalized cross-sectional area along the span of the shaft, the normalized volume, and normalized elastic energy.

Exponent Factor	Cross-Sectional Area	Normalized Volume	Normalized Elastic Energy	Ratio Elastic Energy to Volume
$\alpha$	$-1\le X\le 1$, $0\le S\le 1$	$V=\frac{v}{L}$	$\mathcal{E}=\frac{\epsilon }{L}$.	$\frac{\mathcal{E}}{V}$
0	$S=1$	$V=1$	$\mathcal{E}=2$	2
$1$	$X=erf\left(\sqrt{-ln\left(S\right)}\right)$	$V=\frac{1}{\sqrt{2}}$	$\mathcal{E}=\frac{1}{\sqrt{2}}$	1
$2$	$X=\sqrt{1-S}+\frac{S\sqrt{1-S}}{2}$	$V=\frac{4}{5}$	$\mathcal{E}=\frac{24}{35}$	$6/7$
$3$	$\frac{\pi }{2}X=arccos\left(S\right)+S\sqrt{1-S^2}$	$V=\frac{8}{3\pi }$	$\mathcal{E}=\frac{32}{15\pi }$	$4/5$

.

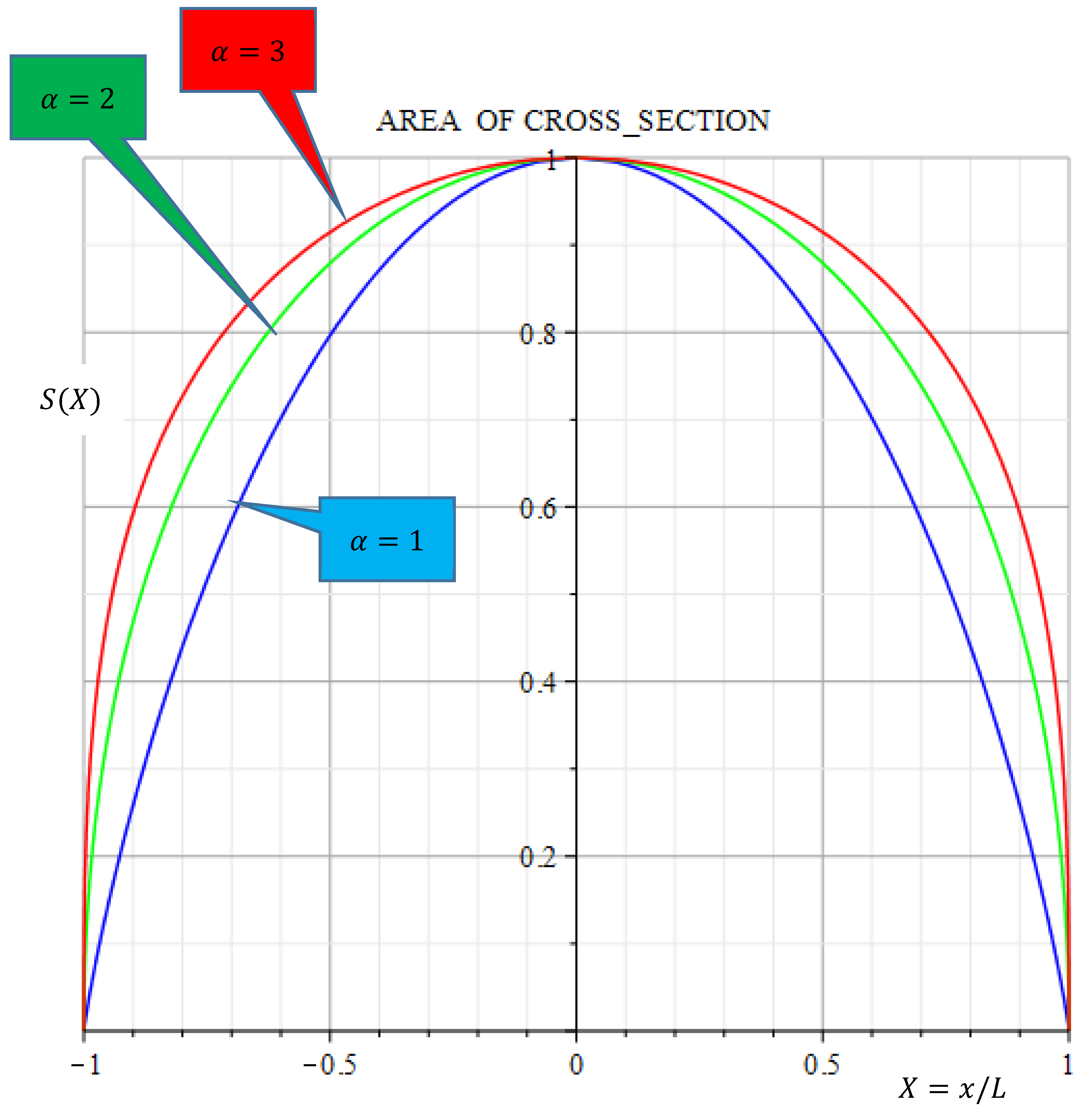
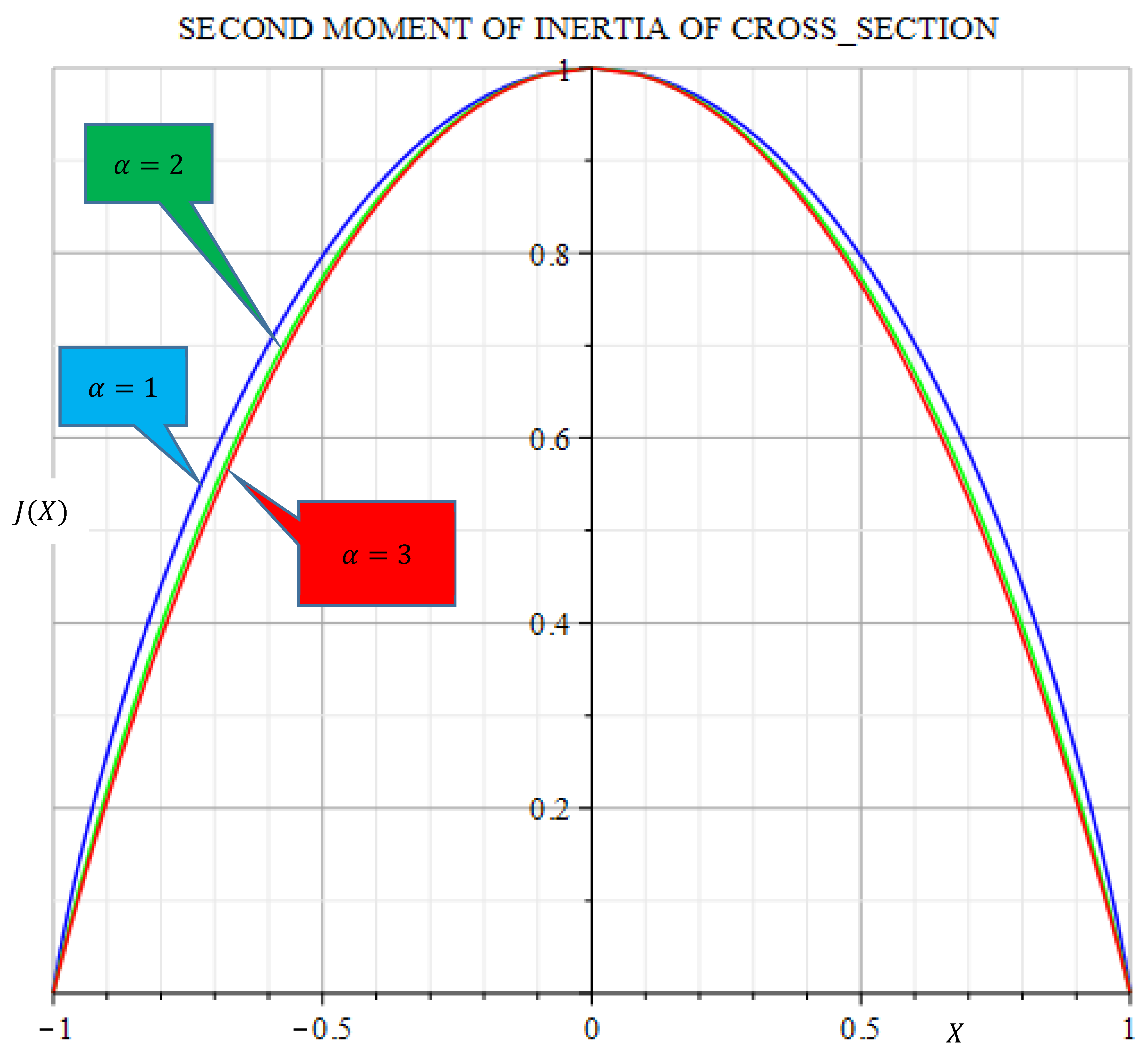
The buckling shape of the twisted column with the simply supported (hinged) ends is demonstrated on Figure 1 for the exponent factor $\alpha =2$. For the other values of parameter $\alpha$, the buckling shapes are similar. Figure 2 displays the areas of cross-sections of the optimal twisted columns for the exponent factors $\alpha =1,2,3$. Second moments of inertia of the cross-sections of the optimal twisted columns are shown for the exponent factors $\alpha =1,2,3$ on Figure 3.

5. Effectiveness

The influence of the exponent $\alpha$ influences the estimations for the optimization effects. Another argument for the introduction of the invariant optimization factors is methodical. In variational calculus, it is common to obtain one factor as the optimization objective and the others as the a priori given constraints. To convert it into an unconstrained problem, the method of Lagrange multipliers is commonly used. The resulting unconstrained problem with Lagrange multipliers increases the number of variables. The new number of unknown variables is the original number of variables plus the original number of constraints. The constraints are usually solved for some of the variables in terms of the others, and the former can be substituted out of the objective function, leaving an unconstrained problem in a smaller number of variables. This method of solution leads to the nonlinear algebraic equations for Lagrange multipliers. These nonlinear equations in most cases do not possess the closed analytical solutions and are solvable only numerically.

The common method for the solution of the optimization problems with stability constraints uses Lagrange multipliers. In the present manuscript, the method of dimensionless factors will be applied for the optimization analysis. This method delivers different lengths and volumes of the optimal shafts. Instead of seeking for the twisted beams of the fixed length and volume, the method of dimensionless factors allows for the comparison of the shafts with the different lengths and cross-sections.

Consider the shafts with the same form of cross-sections. The affine transformation of the shaft is the product of two elementary transformations, namely homothety and scaling. The homothety of ratio $\zeta$ multiplies lengths by $\zeta$. Thus, $\zeta$ is the ratio of magnification, or dilation factor, or scale factor, or similitude ratio. The cross-section function $S\left(\xi \right)$ scales by another factor $\varrho$, such that for the affine transformed shaft, the cross-section function will be $\varrho S\left(\xi \right)$. Apparently, the eigenvalue $\Lambda$ alters in the course of the affine transformation of the shaft.

For each fixed value of $\alpha$, the two dimensionless factors will be studied:

$$F_V=\Lambda \frac{ L^{p_1}}{v^{p_2}}, F_{\mathcal{E}}=2\Lambda \frac{ v^{p_3}}{{\epsilon }^{p_4}}.$$

(38)

The factors $F_V, F_{\mathcal{E}}$(38) will be used for the comparisons of different designs. For arbitrary powers $p_1, p_2,p_3, p_4$, the factors will alter for any affine transformation of the beam. The critical buckling moment $\widetilde{ M}=k_{\alpha }E\Lambda$ inherits the factor $k_{\alpha }$ and is proportional to this value. Evidently, that the ratios of the buckling loads for different designs with the same form of the cross-sections do not depend on the constants $k_{\alpha }$. For different cross-sections, the actual value of $k_{\alpha }$ has to be used.

With the methods of dimensional analysis, the characteristic choice of powers is the following:

$$\begin{array}{cccc}{p}_1=1+\alpha ,& p_2=\alpha ,& p_3=2+\alpha ,& p_4=1+\alpha .\end{array}$$

(39)

Using the expressions (38) and (39), the factors result to:

$$F_V=\frac{L^{1+\alpha }}{v^{\alpha }} F_{\mathcal{E}}=2\frac{v^{2+\alpha }}{{\epsilon }^{1+\alpha }}$$

(40)

With the choice of the powers (38), the factors $F_V, F_{\mathcal{E}}$do not alter for any affine transformation of the shaft. In other words, the factors $F_V, F_{\mathcal{E}}$are the invariants to the affine transformation of the shaft and provide a natural basis for the comparison of different designs.

With the above factor, the estimation of the effect of mass optimization turns out to be trivial. The reference design will be selected with the constant cross-section along the span. The invariant factors for the reference design is ${\tilde{F}}_V$. The factor is the same for all exponents $\alpha$ and for the boundary conditions with both hinged ends. The factor ${\tilde{F}}_V$ reads for the reference design with the constant cross-section as:

$${\tilde{F}}_V=1$$

(41)

The greater the factor, the higher the buckling moment for the given length and volume of the shaft. For example, the buckling force of the reference clamped shaft is four times the buckling force of the reference shaft with the hinged ends.

The dual formulations are typical of the optimization of buckling as well. For the dual formulations, the masses of the shafts for the fixed lengths and fixed buckling moments are compared. The volumes and masses of the optimal and reference shafts relate to each other as the inverse roots of the order $\alpha$ of the factors $F_V$:

$$\frac{\mathrm{V}}{{\tilde{V}}_{ref}}=\sqrt[\alpha ]{\frac{{\tilde{F}}_V}{F_V}}$$

(42)

Specifically, the shaft with the higher value of the factor $F_V$ possesses the lower mass. Consequently, the optimality is expressed for the shaft in the form of the isoperimetric inequalities.

The results of the evaluation of the dimensionless volume factors and volumes for the fixed critical eigenvalue $\Lambda =\pi /2$and the half-length $L=1$ are presented in

Table 2. Dimensionless volume factor and volume for the fixed critical eigenvalue $\Lambda =\pi /2$ and the half-length $L=1$.

$\mathbf{Exponent} \mathbf{Factor} \mathit{\alpha }$	${\mathit{F}}_{\mathit{V}}$	$\mathit{V}\left(\mathit{\Lambda }=\mathit{\pi }/2,\mathit{L}=1\right)$
Constant cross section, reference	1	1
$\alpha =1$	$\sqrt{2}$	$\sqrt{2}/2$
$\alpha =2$	$25/16$	$4/5$
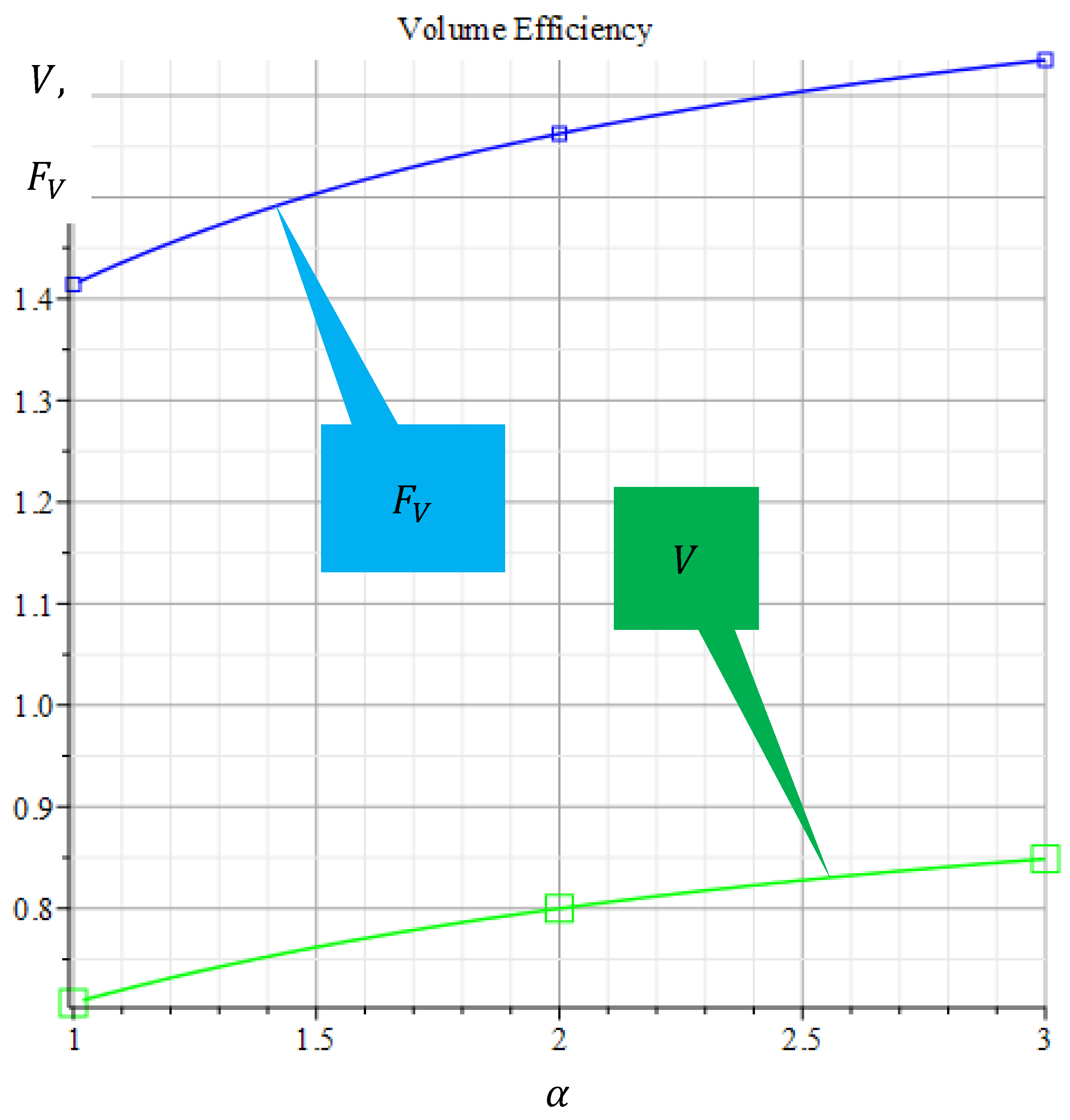
$\alpha =3$	$27{\pi }^3/512$	$8/3\pi$

. The half-volumes of the optimal columns $V$ and the volume optimization factor $F_V$ are shown as the functions $\alpha$ of on Figure 4. Figure 5 demonstrates the half-volumes $V$ and elastic energy $\mathcal{E}$ of the optimal columns. Table 2 displays the dimensionless volume factor and volume for the fixed critical eigenvalue $\Lambda =\pi /2$ and the half-length $L=1$ for different exponent factors $\alpha$. The reference serves the shaft of the constant cross section with the same critical eigenvalue $\Lambda =\pi /2$. The area of its cross-section is one, such that the half volume of the reference shaft is 1.

6. Conclusions

For the shaft, the optimal shape along the axis was searched. The cross section that delivers the maximum or the minimum for the critical eigenvalue was to be determined among all convex and simply connected domains. At the beginning, the validity of the static Euler’s approach for the simply supported beam (hinged), twisted by the conservative moment, was demonstrated. The applied method for integration of the optimization criteria delivers different length and volumes of the optimal twisted beams. Instead of seeking for the twisted shafts of the fixed length and volume, the twisted beams with the different lengths and cross-sections using the invariant factors could be directly compared. The moments of inertia of the rod are the powers of the cross-sectional area with the certain exponent. The exponents are the positive rational numbers, which are equal to or greater than one. For all admissible exponents, the optimal distribution of the cross-sectional area for the shaft was given in the closed form. In the general case, the optimal distribution is stated in terms of the higher transcendental functions. Particularly, for exponents 1, 2, and 3, the solution reduces to certain elementary functions. The final formulas involve the length of the beam, its volume, and critical torque. Remarkably, in the torsion stability problem, the optimal shape of the beam is roughly parabolic along its length. In the torsion stability problem, the optimal shape of the simply connected, convex cross-section is the equilateral triangle. Using the methods of isoperimetric inequalities [20], the exact boundaries for the buckling eigenvalues for the fixed volume and length of the hinged twisted shaft could be stated.

From the presented closed-form solution arises the open questions for the future work. It is well known that different types of boundary conditions on both ends could essentially influence the character of the optimal solution. If the Sturm–Liouville conditions are not satisfied, multimodal buckling regimes are principally possible. The study of the optimization problems for the multimodal buckling could be investigated for the pure twisted and twisted-compressed beams with the presented analytical solution methods. Another task could be the study of the multiplication of supported beams of finite length with the intermediate supports along the span of the beam. Special attention is required for the optimization problem for an infinite, periodically supported shaft.

The applied Euler approach is applicable for the conservative systems and for special classes of non-conservative systems. If the loads are non-conservative, the optimization problems require the application of dynamic stability methods. For example, if the moment direction follows the direction of the deformed axis, the loads will be non-conservative. Seemingly, the closed form solutions of the nonconservative optimization problems are unknown. An interesting question is whether any type of the nonconservative torsion load acknowledges the closed-form solution of the optimization problem.