Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence
Abstract
1. Introduction
2. Fatigue Dataset
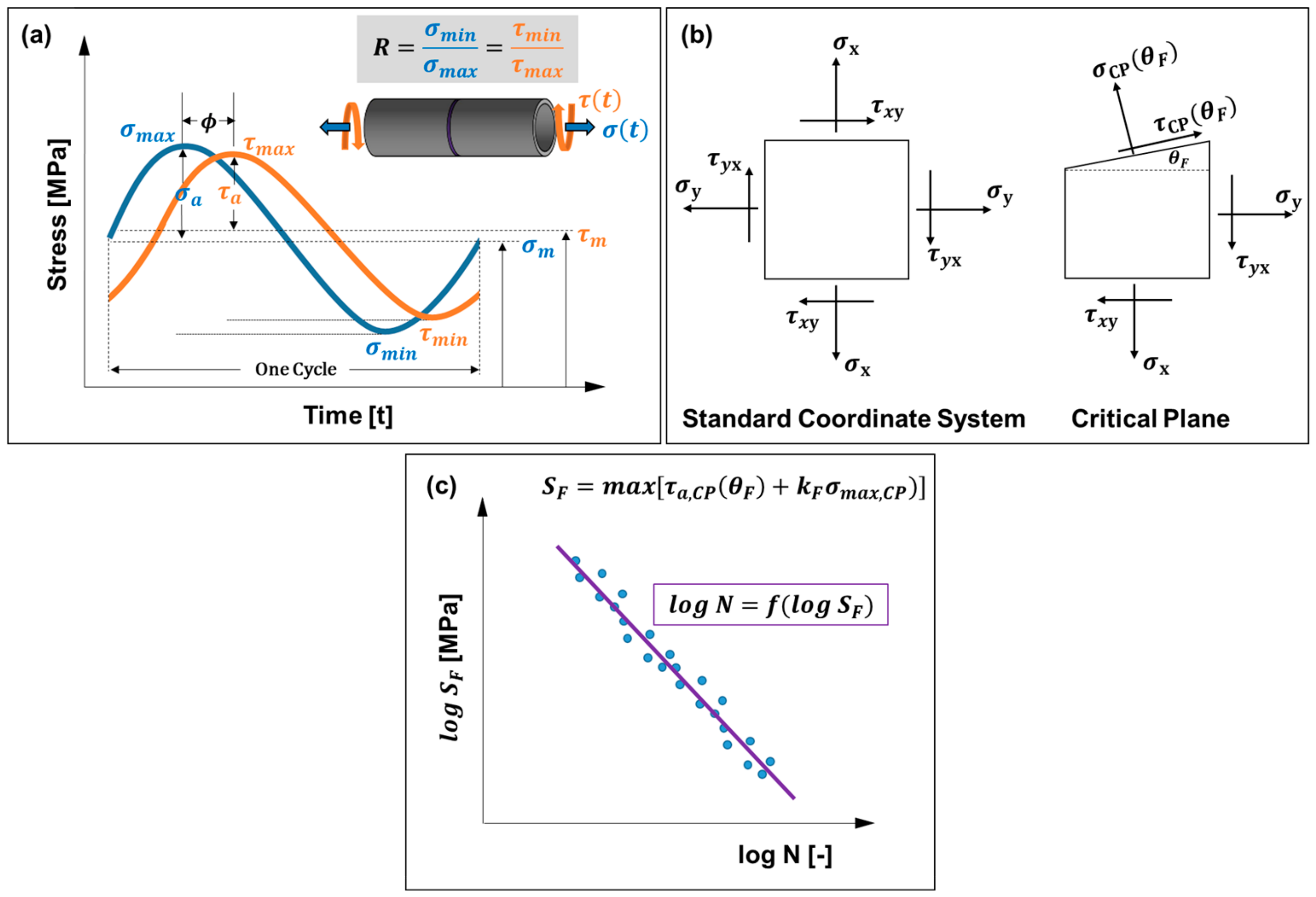
2.1. Fatigue Loading Parameters
2.2. Dataset Description
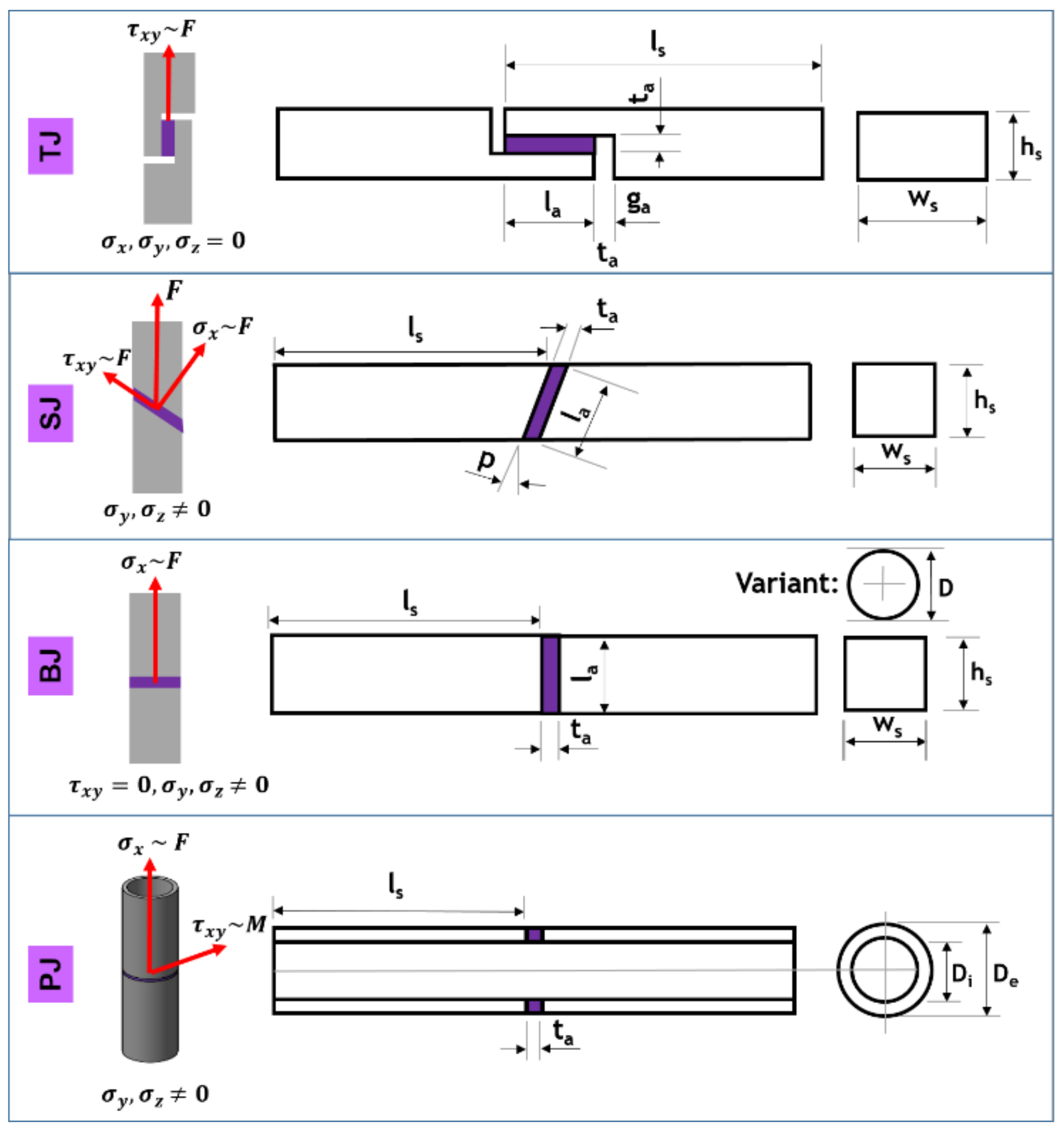
2.3. Adhesives and Joints
- Thick-Adherend-Shear-Test-Joint (TJ) →
- Scarf-Joint (SJ) →
- Butt-Joint (BJ) →
- Pipe-Joint (PJ):
- -
- Pure Axial Load → ;
- -
- Pure Torsional Load →;
- -
- Multiaxial Load →
3. Prediction Models
- Data-driven models (DDMs);
- A physics-based model (PBM);
- Hybrid models (HM):
- -
- Hybrid models based on Findley’s critical plane (HM-F);
- -
- Hybrid models based on invariant stresses (HM-I).
- Split 70tr/30te: 70% of dataset for training and 30% for testing;
- Split 50tr/50te: 50% of dataset for training and 50% for testing;
- Split 30tr/70te: 30% of dataset for training and 70% for testing.
- The fatigue lifetime (number of cycles to failure, N) was modeled using a logarithm scaling based on domain knowledge (e.g., the Basquin’s law [49]);
- By assuming an ideal cohesive failure, and by the fact that the substrates were thick (little deformation), the predictions were carried out ignoring the substrate properties;
- The geometric parameters of the joints were not taken into consideration;
- The frequency () was not taken into consideration.
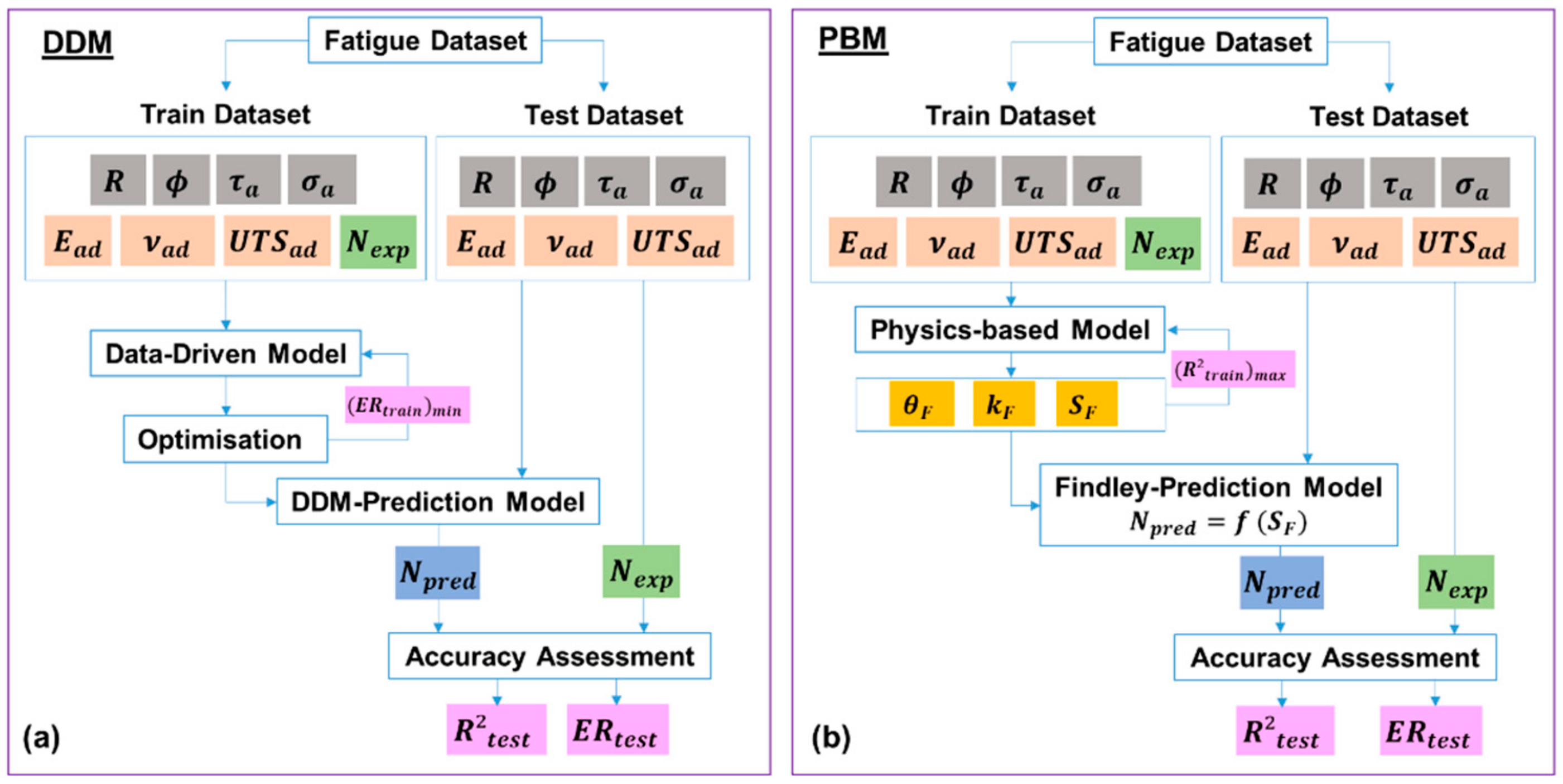
3.1. Data-Driven Model (DDM)
- A particular data split (70Tr/30Te, 50Tr/50Te, or 30Tr/70Te) was selected;
- Parameters of the train dataset (R, , , , , , ) were used to train the model;
- The hyperparameters for the DDM are optimized so as to minimize ER_train (convergence criterion);
- The trained DDM was determined;
- Parameters of the test dataset (R, , , , , ) were used to test the DDM. However, the expected number of cycles to failure () was not used as an input;
- The output of the DDM was the predicted number of cycles to failure ();
- The accuracy indicators of the DDM (R2_test and ER_test) were calculated based on and
- Extra trees regressor (ERT, Python-library: sklearn) [50]: the ERT builds multiple decision trees on random subsets of the data and features. For each split in the tree, a random subset of features is chosen, and the best split is selected based on some criterion, such as reducing the variance or the mean squared error. The final prediction is made by averaging the predictions of all the trees.
- ExtremeXGBoost regressor (XGB, Python-library: xgboost) [51]: the XGB uses gradient boosting to build a sequence of trees, where each tree tries to correct the errors made by the previous tree. The gradient boosting process starts with a weak base learner, such as a decision tree, and trains the next tree to correct the residuals from the previous tree. The final prediction is made by summing up the predictions of all the trees.
- LightGBM regressor (LGBM, Python-library: lightgbm) [52]: the LGBM uses gradient boosting to build a sequence of trees, where each tree tries to correct the errors made by the previous tree. The algorithm uses a novel approach to build trees, called the histogram-based method, which reduces the computational cost compared to traditional gradient boosting algorithms. The histogram-based method splits the data based on histograms of feature values instead of finding the best split by brute force. The final prediction is made by summing up the predictions of all the trees.
- Histogram-based gradient boosting regressor (HGB, Python-library: sklearn) [53]: the HGB is similar to XGB in that it also uses gradient boosting to build a sequence of trees. Moreover, the HGB is inspired (with slight modifications) by the LGBM.
3.2. Physics-Based Model (PBM)
- A particular data split (70Tr/30Te, 50Tr/50Te, or 30Tr/70Te) was selected;
- Since the value of is adhesive-dependent, each adhesive was evaluated separately;
- Parameters of the train set (R, , , , , , ) were used to train the model of each adhesive;
- Train set: the value of was varied between 0 and 2.0;
- Train set: for each data point the value of was varied to maximize ;
- Train set: the value of leading to the maximum correlation of R2_train between and (converge criterion) was determined;
- The optimized PBM determined the relationship: ;
- Based on the parameters of the test dataset (R, , , , , ) the value of was used to test the PBM of each adhesive. However, the expected number of cycles to failure () was not used as an input;
- The output of the PBM was the predicted number of cycles to failure ();
- The and for each adhesive were combined;
- The accuracy indicators of the PBM (R2_test and ER_test) were calculated based on and .
3.3. Hybrid Models (HM)
- A hybrid model using physics-based parameters from the Findley’s critical plane into a data-driven model (HM-F);
- A hybrid model using physics-based stress invariant parameters into a data-driven model (HM-I).
3.3.1. Hybrid Model Using the Findley’s Critical Plane Approach (HM-F)
- A particular data split (70Tr/30Te, 50Tr/50Te, or 30Tr/70Te) was selected;
- Since the value of is adhesive-dependent, each adhesive was evaluated separately;
- Parameters of the train dataset (R, , , , , , ) were used to train a PBM of each adhesive;
- Train set: the value of leading to the maximum correlation R2_train between and was determined;
- The physics-based parameters of the train dataset (, , , , , ) were used to train a DDM regressor;
- The hyperparameters of the DDM regressor were optimized so as to minimize the ER_train (convergence criterion);
- The trained HM-F was determined;
- Parameters of the test dataset (R, , , , , ) were used to test the HM-F. However, the expected number of cycles to failure () was not used as an input;
- The output of the HM-F was the predicted number of cycles to failure ();
- The and for each adhesive were combined;
- The accuracy indicators of the HM-F (R2_test and ER_test) were calculated based on and .
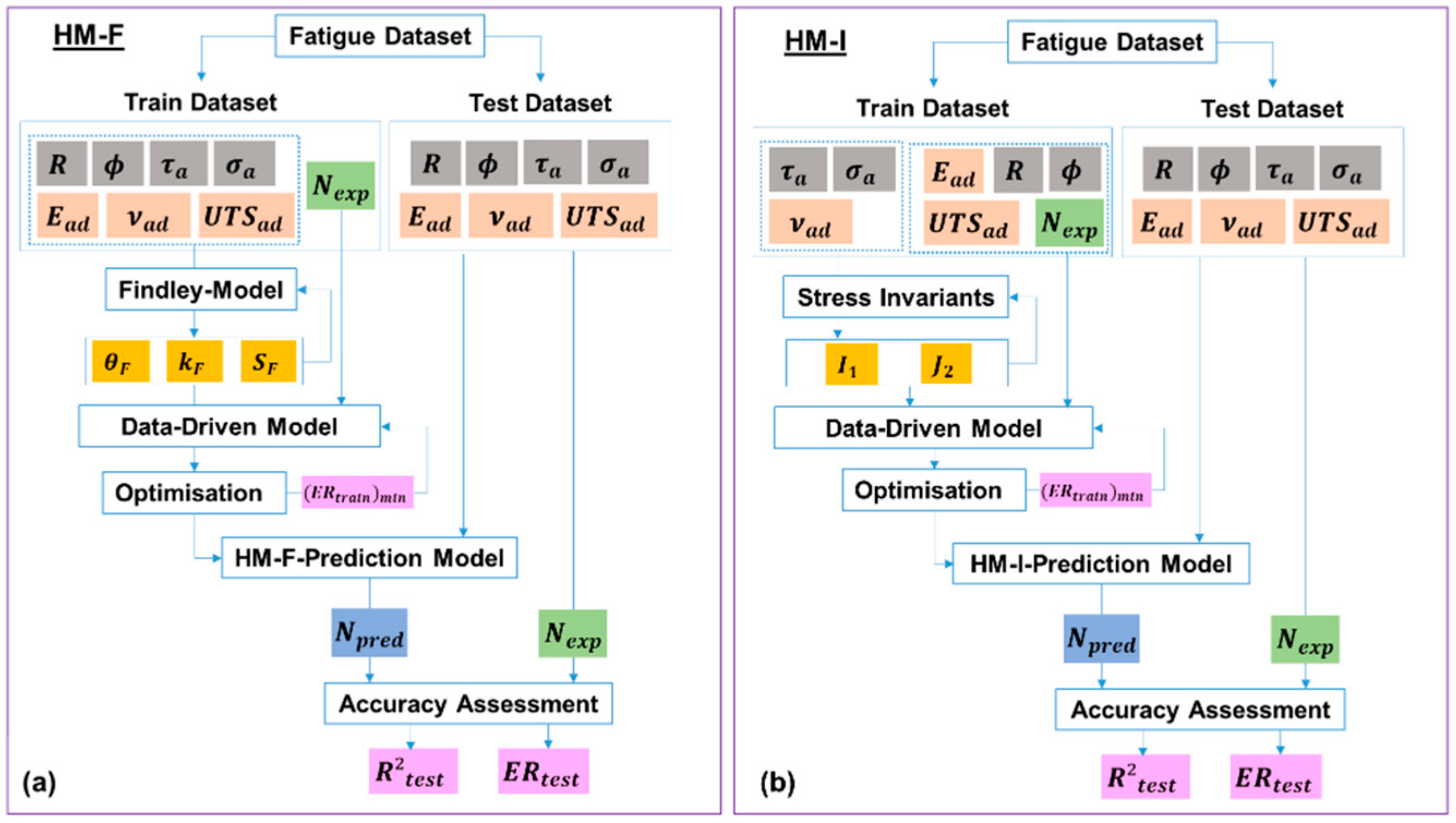
3.3.2. Hybrid Model Using Invariant Stresses (HM-I)
- A particular data split (70Tr/30Te, 50Tr/50Te, or 30Tr/70Te) was selected;
- Train dataset: based on parameters (, ,) the invariant stresses ( and ) were calculated;
- The physics-based parameters of the test dataset (, , , , ,) were used to train a DDM regressor;
- The hyperparameters of the DDM regressor were optimized so as to minimize the ER_train;
- The trained HM-I was determined;
- Parameters of the test dataset (R, , , , , ) were used to test the HM-I. However, the expected number of cycles to failure () was not used as an input;
- The output of the HM-I was the predicted number of cycles to failure ();
- The and for each adhesive were combined;
- The accuracy indicators of the HM-I (R2_test and ER_test) were calculated based on and .
4. Prediction Results
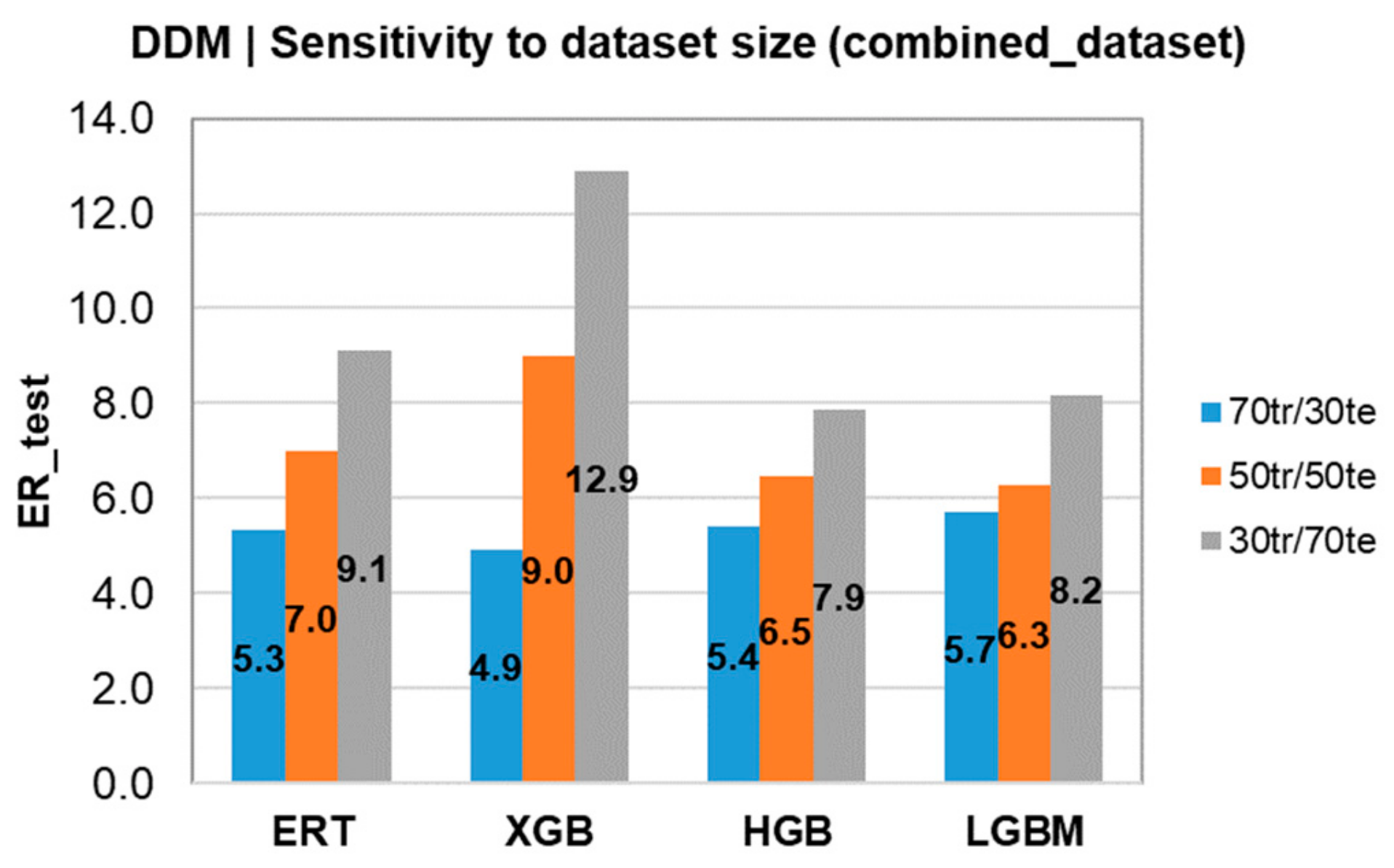
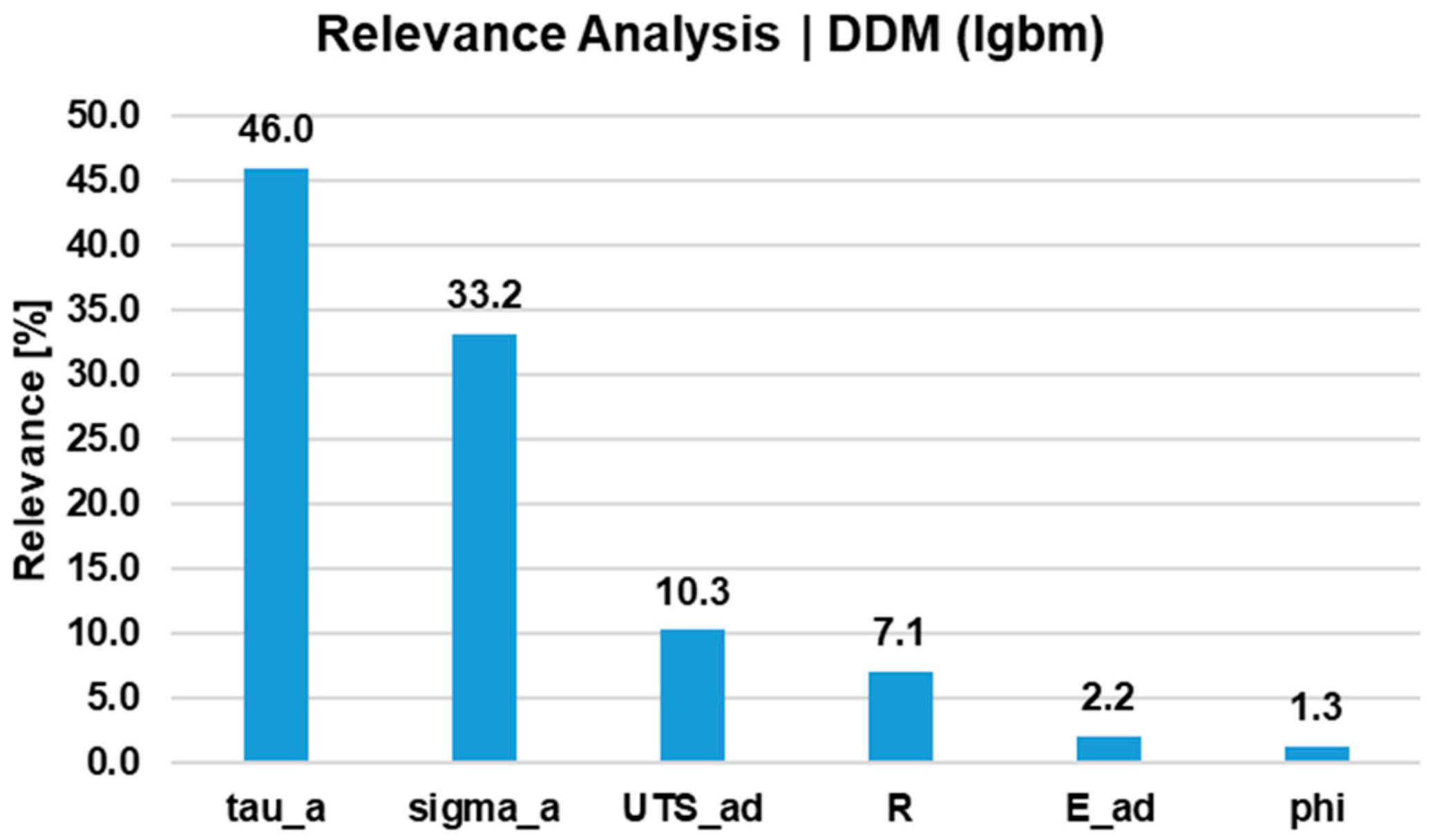
4.1. Predictions by Data-Driven Models
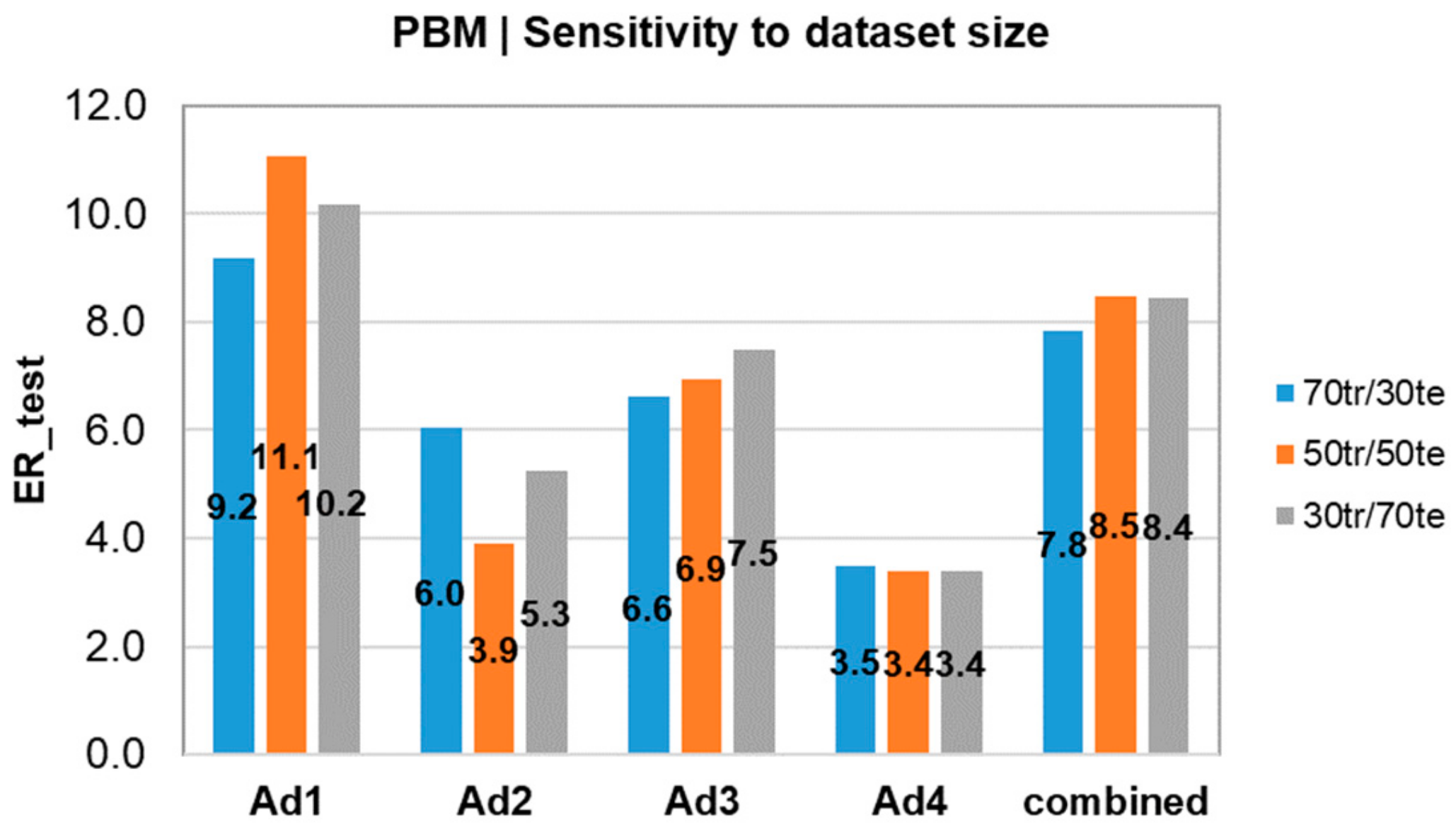
4.2. Predictions Using the Physics-Based Model
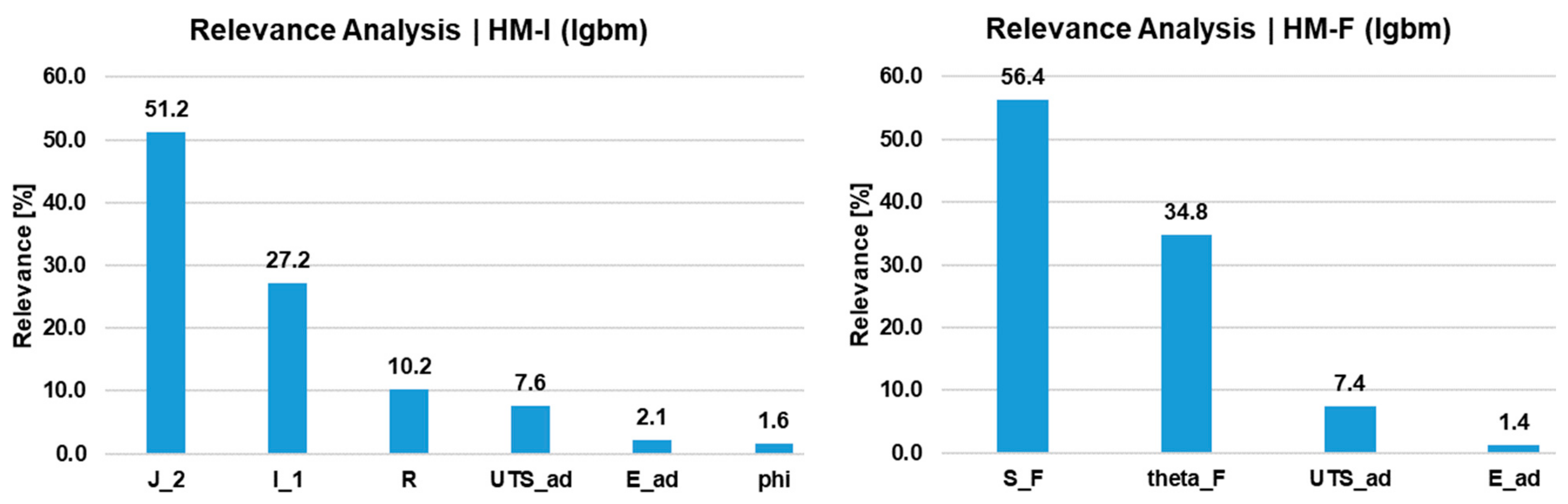
4.3. Predictions Using Hybrid Models
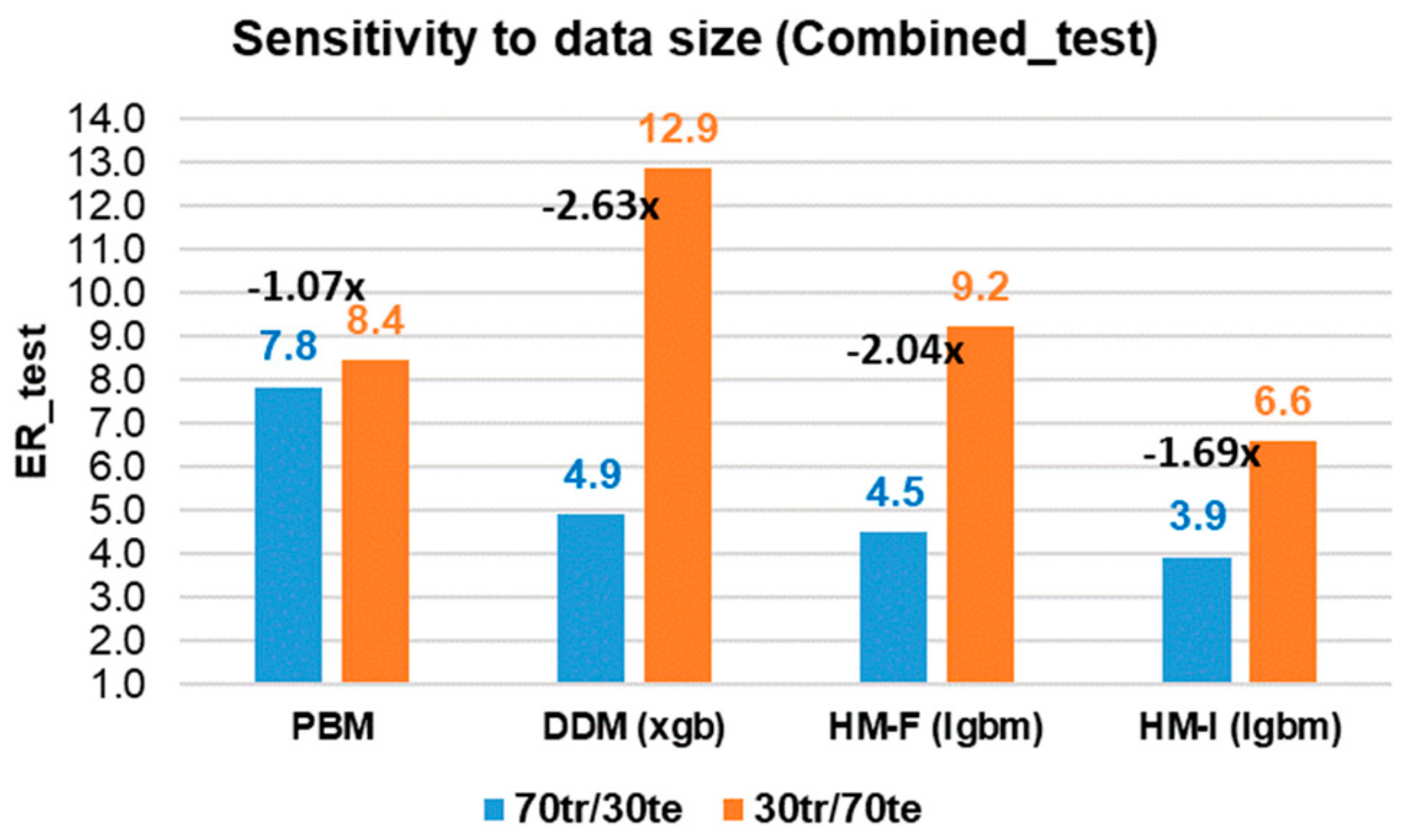
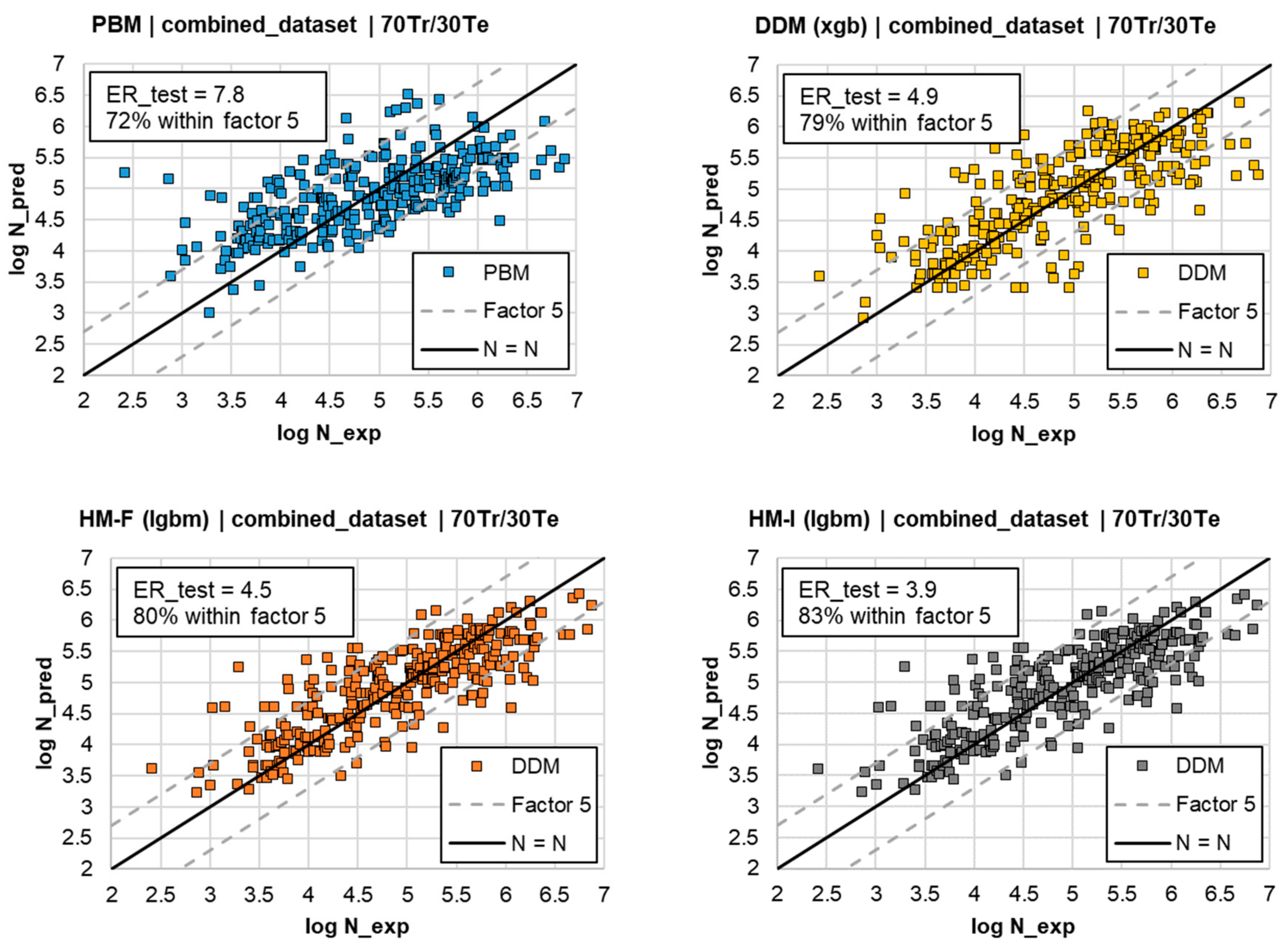
4.4. Performance Comparison between Models and Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation/Symbol | Meaning |
| AI | Artificial intelligence |
| ad | Adhesive |
| BJ | Butt Joint |
| DDM | Data-driven model |
| E | Young’s modulus in [MPa] |
| ER | Error factor |
| ERT | Extremely randomized trees |
| HGBM | Histogram-based gradient boosting model |
| HM-F | Hybrid model based on Findley’s critical plane model |
| HM-I | Hybrid model based on invariant stress |
| LGBM | Light gradient-boosting method |
| LLN | Law of large numbers |
| ML | Machine learning |
| N | Number of cycles to failure |
| n | Number of observations |
| PBM | Physics-based model |
| PJ | Pipe Joint |
| R | Stress ratio |
| RF | Random forest |
| SJ | Scarf Joint |
| sub | Substrate |
| te | Test |
| tr | Train |
| TJ | Thick-Adherend-Shear-Test Joint |
| UTS | Ultimate tensile strength in [MPa] |
| XGB | Gradient boosting method |
| Phase-shift in [°] | |
| Shear stress in [MPa] | |
| Tensile stress in [MPa] | |
| Angle of Findley’s critical plane | |
| Poisson’s ratio | |
| Findley’s critical stress | |
| Findley’s normal stress sensitivity | |
| First invariant of the principal stress tensor in [MPa] | |
| Second invariant of the deviatoric stress tensor in [MPa] |
Appendix A
- Data manipulation
- import os
- import pandas as pd
- import xlwings as wx
- import numpy as np
- import math-Shuffle
- from sklearn.utils import shuffle
- Models applied
- from sklearn.ensemble import ExtraTreesRegressor,HistGradientBoostingRegressor
- import xgboost as xgb
- import lightgbm as ltb
- from sklearn.linear_model import LinearRegression
- Model optimization
- from sklearn.model_selection import GridSearchCV,cross_val_score,KFold,RepeatedKFold,RandomizedSearchCV
- Cross-validation
- cv = KFold(5, shuffle = True, random_state = None)
- gsc = GridSearchCV(
- estimator = ltbreg,
- param_grid = {‘max_depth’: range(5,20,1),
- ‘n_estimators’: (500)
- ‘max_features’: [1,2,3,4],
- ‘min_samples_split’: range(2,5,1)},
- scoring = make_scorer(ER_loss,greater_is_better = False),
- cv = cv,
- verbose = 2, n_jobs = −1)
- Figure manipulation
- import matplotlib.pyplot as plt
References
- Da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology; Springer: Berlin, Germany, 2011; ISBN 978-3-642-01168-9. [Google Scholar]
- Fraunhofer-Institut für Fertigungstechnik und Angewandte Materialforschung IFAM. In Circular Economy and Adhesive Bonding Technology; Fraunhofer Verlag: Stuttgart, Germany, 2020.
- Da Silva, L.F.M.; Öchsner, A. Modeling of Adhesively Bonded Joints; Springer: Berlin, Germany, 2008; ISBN 978-3-540-79055-6. [Google Scholar]
- Abdel Wahab, M.M. Fatigue in Adhesively Bonded Joints: A Review. ISRN Mater. Sci. 2012, 2012, 746308. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Kumatowski, B.; Hanselka, H.; Bruder, T.; Schmidt, H.; Mayer, B.; Schneider, B.; Kehlenbeck, H.; Nagel, C.; Brede, M. Schwingfestigkeitsauslegung von Geklebten Stahlbauteilen des Fahrzeugbaus unter Belastung mit Variablen Amplituden: Forschung für Die Praxis P796, IGF-Nr. 307 ZN; Forschungsvereinigung Stahlanwendung e. V: Düsseldorf, Germany, 2012. [Google Scholar]
- Meschut, G.; Teutenberg, D.; Cavdar, S.; Melz, T.; Rybar, G.; Mayer, B.; Fiedler, A.; Nagel, C.; Matzenmiller, A.; Kroll, U. Analyse der Schwingfestigkeit Geklebter Stahlverbindungen unter Mehrkanaliger Belastung: Forschung für Die Praxis P1028, IGF-Nr. 18107 N; Forschungsvereinigung Stahlanwendung e. V: Düsseldorf, Germany, 2017. [Google Scholar]
- Beber, V.C.; Baumert, M.; Klapp, O.; Nagel, C. Multiaxial elastic, yield and failure behaviour of bonded joints using a hot-curing epoxy film adhesive: Analytical and experimental investigation. J. Adhes. 2020, 98, 526–552. [Google Scholar] [CrossRef]
- Beber, V.C.; Schneider, B. Fatigue of structural adhesives under stress concentrations: Notch effect on fatigue strength, crack initiation and damage evolution. Int. J. Fatigue 2020, 140, 105824. [Google Scholar] [CrossRef]
- Beber, V.C.; Schneider, B.; Brede, M. On the fatigue behavior of notched structural adhesives with considerations of mechanical properties and stress concentration effects. Procedia Eng. 2018, 213, 459–469. [Google Scholar] [CrossRef]
- Beber, V.C.; Fernandes, P.H.E.; Schneider, B.; Brede, M.; Mayer, B. Fatigue lifetime prediction of adhesively bonded joints: An investigation of the influence of material model and multiaxiality. Int. J. Adhes. Adhes. 2017, 78, 240–247. [Google Scholar] [CrossRef]
- Beber, V.C.; Schneider, B.; Brede, M. Influence of Temperature on the Fatigue Behaviour of a Toughened Epoxy Adhesive. J. Adhes. 2015, 92, 778–794. [Google Scholar] [CrossRef]
- Schneider, B.; Beber, V.C.; Brede, M. Estimation of the lifetime of bonded joints under cyclic loads at different temperatures. J. Adhes. 2015, 92, 795–817. [Google Scholar] [CrossRef]
- Schneider, B.; Beber, V.C.; Schweer, J.; Brede, M.; Mayer, B. An experimental investigation of the fatigue damage behaviour of adhesively bonded joints under the combined effect of variable amplitude stress and temperature variation. Int. J. Adhes. Adhes. 2018, 83, 41–49. [Google Scholar] [CrossRef]
- Baumgartner, J.; Schmidt, H.; Rybar, G.; Melz, T.; Ernstberger, L.J.; Teutenberg, D.; Hahn, O.; Meschut, G.; Nagel, C.; Schneider, B. Auslegung von Geklebten Stahlblechstrukturen im Automobilbau für Schwingende Last bei Wechselnden Temperaturen nter Berücksichtigung des Versaensverhaltens; No. 290; FAT: Frankfurt, Germany, 2016. [Google Scholar]
- Fernandes, P.H.E.; Poggenburg-Harrach, L.; Nagel, C.; Beber, V.C. Lifetime calculation of adhesively bonded joints under proportional and non-proportional multiaxial fatigue loading: A combined critical plane and critical distance approach. J. Adhes. 2022, 98, 780–809. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Neural Networks and Information in Materials Science. Stat. Anal. Data Min. 2009, 1, 296–305. [Google Scholar] [CrossRef]
- DOME4.0. Digital Open Marketplace Ecosystem 4.0. Available online: https://dome40.eu/ (accessed on 2 February 2023).
- NFDI-MatWerk. Nationale Forschungsdateninfrastruktur für Materialwissenschat & Werkstofftechnik. Available online: https://nfdi-matwerk.de/ (accessed on 2 February 2023).
- Zhao, S.; Qian, Q. Ontology based heterogeneous materials database integration and semantic query. AIP Adv. 2017, 7, 105325. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. NPJ Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Hao, W.Q.; Tan, L.; Yang, X.G.; Shi, D.Q.; Wang, M.L.; Miao, G.L.; Fan, Y.S. A physics-informed machine learning approach for notch fatigue evaluation of alloys used in aerospace. Int. J. Fatigue 2023, 170, 107536. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Zhang, X.-C.; Gong, J.-G.; Xuan, F.-Z. A physics-informed neural network for creep-fatigue life prediction of components at elevated temperatures. Eng. Fract. Mech. 2021, 258, 108130. [Google Scholar] [CrossRef]
- Tang, A.; Tam, R.; Cadrin-Chênevert, A.; Guest, W.; Chong, J.; Barfett, J.; Chepelev, L.; Cairns, R.; Mitchell, J.R.; Cicero, M.D.; et al. Canadian Association of Radiologists White Paper on Artificial Intelligence in Radiology. Can. Assoc. Radiol. J. 2018, 69, 120–135. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.-Y.; Xu, K.; Deng, H.-X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, T.; Jiao, J.; Chen, Z. The lifetime prediction of epoxy resin adhesive based on small-sample data. Eng. Fail. Anal. 2019, 102, 111–122. [Google Scholar] [CrossRef]
- Mansouri, E.; Manfredi, M.; Hu, J.-W. Environmentally Friendly Concrete Compressive Strength Prediction Using Hybrid Machine Learning. Sustainability 2022, 14, 12990. [Google Scholar] [CrossRef]
- Zhou, K.; Sun, X.; Shi, S.; Song, K.; Chen, X. Machine learning-based genetic feature identification and fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2524–2537. [Google Scholar] [CrossRef]
- Heng, J.; Zheng, K.; Feng, X.; Veljkovic, M.; Zhou, Z. Machine Learning-Assisted probabilistic fatigue evaluation of Rib-to-Deck joints in orthotropic steel decks. Eng. Struct. 2022, 265, 114496. [Google Scholar] [CrossRef]
- Blakseth, S.S.; Rasheed, A.; Kvamsdal, T.; San, O. Combining Physics-Based and Data-Driven Techniques for Reliable Hybrid Analysis and Modeling Using the Corrective Source Term Approach. Appl. Soft Comput. 2022, 128, 1–20. [Google Scholar] [CrossRef]
- Çavdar, S.; Teutenberg, D.; Meschut, G.; Wulf, A.; Hesebeck, O.; Brede, M.; Mayer, B. Stress-based fatigue life prediction of adhesively bonded hybrid hyperelastic joints under multiaxial stress conditions. Int. J. Adhes. Adhes. 2020, 97, 102483. [Google Scholar] [CrossRef]
- Beber, V.C.; Schneider, B.; Brede, M. Efficient critical distance approach to predict the fatigue lifetime of structural adhesive joints. Eng. Fract. Mech. 2019, 214, 365–377. [Google Scholar] [CrossRef]
- Beber, V.C.; Baumert, M.; Klapp, O.; Nagel, C. Fatigue failure criteria for structural film adhesive bonded joints with considerations of multiaxiality, mean stress and temperature. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 636–650. [Google Scholar] [CrossRef]
- Beugre, O.M.R.; Akhavan-Safar, A.; da Silva, L.F.M. Multiaxial Fatigue Life Assessment of Adhesive Joints Based on the Concepts of Critical Planes: Stress-Based Approaches. In Proceedings of the 6th International Conference on Adhesive Bonding 2021, Porto, Portugal, 8–9 July 2021; Da Silva, L.F.M., Adams, R.D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 153–169, ISBN 978-3-030-87667-8. [Google Scholar]
- Chen, J.; Liu, Y. Fatigue modeling using neural networks: A comprehensive review. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 945–979. [Google Scholar] [CrossRef]
- Leininger, D.S.; Reissner, F.-C.; Baumgartner, J. New approaches for a reliable fatigue life prediction of powder metallurgy components using machine learning. Fatigue Fract. Eng. Mater. Struct. 2022, 46, 1190–1210. [Google Scholar] [CrossRef]
- Sekercioglu, T.; Kovan, V. Prediction of static shear force and fatigue life of adhesive joints by artificial neural network. Met. Mater. 2008, 46, 51–57. [Google Scholar]
- Silva, G.C.; Beber, V.C.; Pitz, D.B. Machine learning and finite element analysis: An integrated approach for fatigue lifetime prediction of adhesively bonded joints. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3334–3348. [Google Scholar] [CrossRef]
- Schubert, M.; Kläusler, O. Applying machine learning to predict the tensile shear strength of bonded beech wood as a function of the composition of polyurethane prepolymers and various pretreatments. Wood Sci. Technol. 2020, 54, 19–29. [Google Scholar] [CrossRef]
- Pruksawan, S.; Lambard, G.; Samitsu, S.; Sodeyama, K.; Naito, M. Prediction and optimization of epoxy adhesive strength from a small dataset through active learning. Sci. Technol. Adv. Mater. 2019, 20, 1010–1021. [Google Scholar] [CrossRef] [PubMed]
- Gajewski, J.; Golewski, P.; Sadowski, T. The Use of Neural Networks in the Analysis of Dual Adhesive Single Lap Joints Subjected to Uniaxial Tensile Test. Materials 2021, 14, 419. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Zhao, Y.; Yan, C. MFLP-PINN: A physics-informed neural network for multiaxial fatigue life prediction. Eur. J. Mech. A/Solids 2023, 98, 104889. [Google Scholar] [CrossRef]
- Shutin, D.; Bondarenko, M.; Polyakov, R.; Stebakov, I.; Savin, L. Method for On-Line Remaining Useful Life and Wear Prediction for Adjustable Journal Bearings Utilizing a Combination of Physics-Based and Data-Driven Models: A Numerical Investigation. Lubricants 2023, 11, 33. [Google Scholar] [CrossRef]
- Hennemann, O.-D.; Brede, M.; Nagel, C.; Hahn, O.; Jendrny, J.; Teutenberg, D.; Mihm, K.M.; Schlimmer, M. Methodenentwicklung zur Berechnung und Auslegung Geklebter Stahlbauteile im Fahrzeugbau bei Schwingender Beanspruchung: Forschung für Die Praxis P653, IGF-Nr. 141 ZN; Forschungsvereinigung Stahlanwendung e. V: Düsseldorf, Germany, 2005. [Google Scholar]
- Beber, V.C.; Brede, M. Multiaxial static and fatigue behaviour of elastic and structural adhesives for railway applications. Procedia Struct. Integr. 2020, 28, 1950–1962. [Google Scholar] [CrossRef]
- Da Silva, L.F.; Dillard, D.A.; Blackman, B.; Adams, R.D. (Eds.) Testing Adhesive Joints: Best Practices; Wiley-VCH: Weinheim, Germany, 2012; ISBN 978-3-527-32904-5. [Google Scholar]
- Ajiboye, A.R.; Abdullah-Arshah, R.; Qin, H.; Isah-Kebbe, H. Evaluating the effect of dataset size on predictive model using supervised learning technique. IJSECS 2015, 1, 75–84. [Google Scholar] [CrossRef]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- Basquin, O.H. The exponential law of endurance tests. Proc. Am. Soc. Test. Mater. 1910, 10, 625–630. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Kumar, L.; Sureka, A. Neural network with multiple training methods for web service quality of service parameter prediction. In Proceedings of the 2017 Tenth International Conference on Contemporary Computing (IC3), Noida, India, 10–12 August 2017; pp. 1–7, ISBN 978-1-5386-3077-8. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 1–9. [Google Scholar]
- Macedo, L.; Miguel Matos, L.; Cortez, P.; Domingues, A.; Moreira, G.; Pilastri, A. A Machine Learning Approach for Spare Parts Lifetime Estimation. In Proceedings of the 14th International Conference on Agents and Artificial Intelligence, Online, 3–5 February 2022; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2022; pp. 765–772, ISBN 978-989-758-547-0. [Google Scholar]
- Karolczuk, A.; Macha, E. A Review of Critical Plane Orientations in Multiaxial Fatigue Failure Criteria of Metallic Materials. Int. J. Fract. 2005, 134, 267–304. [Google Scholar] [CrossRef]
- Findley, W.N. Fatigue of Metals Under Combinations of Stresses. Trans. ASME 1957, 79, 1337–1348. [Google Scholar] [CrossRef]
- Beber, V.C.; Fernandes, P.H.E.; Fragato, J.E.; Schneider, B.; Brede, M. Influence of plasticity on the fatigue lifetime prediction of adhesively bonded joints using the stress-life approach. Appl. Adhes. Sci. 2016, 4, 5. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-1-4443-1950-7. [Google Scholar]
- Petrov, A.I.; Betekhtin, V.I.; Zakrevskii, V.A. Influence of hydrostatic pressure on the lifetimes of polymers. Polym. Mech. 1977, 12, 178–183. [Google Scholar] [CrossRef]


| Adhesive | n | Substrate | Sources | |||||
|---|---|---|---|---|---|---|---|---|
| Ad1 | 573 (58.5%) | 34.0 MPa | 1571 MPa | 0.40 | Steel | 210,000 MPa | 0.33 | [5,6,14,44] |
| Ad2 | 174 (17.8%) | 43.6 MPa | 3002 MPa | 0.39 | Steel | 210,000 MPa | 0.33 | [6,15] |
| Ad3 | 180 (18.4%) | 41.3 MPa | 1944 MPa | 0.38 | Aluminum | 70,000 MPa | 0.33 | [45] |
| Ad4 | 52 (5.3%) | 34.5 MPa | 2205 MPa | 0.36 | Steel | 210,00 MPa | 0.33 | [7,33] |
| R [-] | [-] | ||||||
|---|---|---|---|---|---|---|---|
| count | 979 | 979 | 979 | 979 | 979 | 979 | 979 |
| mean | 0.08 | 8.92 | 7.72 | 6.09 | 37.08 | 1927.59 | 356,114.85 |
| std | 0.45 | 31.90 | 7.18 | 5.35 | 4.10 | 532.93 | 708,550.39 |
| min | -1 | 0 | 0 | 0 | 34 | 1571 | 178 |
| 25% | 0.1 | 0 | 0 | 0 | 34 | 1571 | 15,694.5 |
| 50% | 0.1 | 0 | 8.32 | 5.47 | 34 | 1571 | 91,170 |
| 75% | 0.4 | 0 | 12.08 | 9.675 | 41.3 | 1944 | 409,116.5 |
| max | 0.8 | 180 | 37.81 | 28.94 | 43.64 | 3002 | 7,577,945 |
| Joint | /Ad1 | /Ad2 | /Ad3 | /Ad4 | /Combined |
|---|---|---|---|---|---|
| BJ | 40 | 17 | 58 | 20 | 135 (13.8%) |
| PJ | 301 | 124 | 0 | 0 | 425 (43.4%) |
| SJ | 89 | 15 | 54 | 23 | 181 (18.5%) |
| TJ | 143 | 18 | 68 | 9 | 238 (24.3%) |
| Total | 573 | 174 | 180 | 52 | 979 (100%) |
| Dataset | /70tr | /30te | /50tr | /50te | /30tr | /70te |
|---|---|---|---|---|---|---|
| Ad1 | 401 | 172 | 286 | 287 | 171 | 402 |
| Ad2 | 121 | 53 | 87 | 87 | 52 | 122 |
| Ad3 | 125 | 55 | 90 | 90 | 54 | 126 |
| Ad4 | 36 | 16 | 26 | 26 | 15 | 37 |
| Combined | 683 | 296 | 489 | 490 | 292 | 687 |
| Minimum | Maximum | Step | |
|---|---|---|---|
| Maximum depth | 5 | 20 | 1 |
| Maximum features | 1 | 4 | 1 |
| Minimum number of samples to split | 2 | 5 | 1 |
| DDM | 70tr: R2_train/(ER_train) | 30te: R2_test/(ER_test) | 50tr: R2_train/(ER_train) | 50tr: R2_test/(ER_test) | 30tr: R2_train/(ER_train) | 70tr: R2_test/(ER_test) |
|---|---|---|---|---|---|---|
| ERT | 0.96 (1.46) | 0.58/(5.33) | 0.96/(1.36) | 0.58/(7.00) | 0.97/(1.28) | 0.46/(9.12) |
| XGB | 0.95 (1.56) | 0.58/(4.92) | 0.95/(1.43) | 0.54/(9.00) | 0.97/(1.32) | 0.43/(12.88) |
| HGB | 0.79 (3.30) | 0.56/(5.41) | 0.75/(3.01) | 0.49/(6.46) | 0.69/(3.89) | 0.34/(7.86) |
| LGBM | 0.79 (3.26) | 0.56/(5.70) | 0.72/(3.27) | 0.49/(6.27) | 0.66/(4.18) | 0.32/(8.18) |
| PBM | 70tr: R2_train/ (ER_train) | 30te: R2_test/ (ER_test) | 50tr: R2_train/ (ER_train) | 50te: R2_test/ (ER_test) | 30tr: R2_train/ (ER_train) | 70te: R2_test/ (ER_test) | |||
|---|---|---|---|---|---|---|---|---|---|
| Ad1 | 0.8 | 0.24/ (11.48) | 0.38/ (9.19) | 0.9 | 0.25/ 11.06) | 0.3/ (10.10) | 1.0 | 0.29/ (10.92) | 0.27/ (10.17) |
| Ad2 | 0.8 | 0.49/ (4.17) | 0.34/ (6.03) | 0.8 | 0.58/ (3.91) | 0.31/ (5.84) | 1.0 | 0.47/ (4.45) | 0.4/ (5.26) |
| Ad3 | 0.7 | 0.43/ (6.31) | 0.5/ (6.60) | 0.7 | 0.43/ (6.38) | 0.46/ (6.93) | 0.9 | 0.51/ (5.85) | 0.4/ (7.48) |
| Ad4 | 0.7 | 0.62/ (4.60) | 0.5/ (3.48) | 0.7 | 0.61/ (3.38) | 0.59/ (4.72) | 0.6 | 0.49/ (4.40) | 0.65/ (3.38) |
| Combined | - | 0.34/ (8.88) | 0.43/ (7.84) | - | 0.38/ (8.51) | 0.36/ (8.48) | - | 0.38/ (8.50) | 0.34/ (8.44) |
| HM-I | 70tr: R2_train/(ER_train) | 30te: R2_test/(ER_test) | 50tr: R2_train/(ER_train) | 50tr: R2_test/(ER_test) | 30tr: R2_train/(ER_train) | 70tr: R2_test/(ER_test) |
|---|---|---|---|---|---|---|
| ERT | 0.95/(1.46) | 0.61/(5.06) | 0.95/(1.36) | 0.59/(6.78) | 0.97/(1.28) | 0.52/(8.55) |
| XGB | 0.94/(1.54) | 0.59/(6.15) | 0.95/(1.41) | 0.55/(8.96) | 0.97/(1.3) | 0.46/(8.96) |
| HGB | 0.8/(2.67) | 0.64/(4.12) | 0.8/(2.61) | 0.53/(5.83) | 0.75/(3.26) | 0.43/(6.8) |
| LGBM | 0.8/(2.67) | 0.65/(3.92) | 0.78/(2.74) | 0.52/(5.92) | 0.73/(3.35) | 0.43/(6.6) |
| HM-F | 70tr: R2_train/(ER_train) | 30te: R2_test/(ER_test) | 50tr: R2_train/(ER_train) | 50tr: R2_test/(ER_test) | 30tr: R2_train/(ER_train) | 70tr: R2_test/(ER_test) |
|---|---|---|---|---|---|---|
| ERT | 0.95/(1.46) | 0.6/(4.72) | 0.96/(1.36) | 0.51/(8.43) | 0.97/(1.28) | 0.45/(9.95) |
| XGB | 0.94/(1.56) | 0.59/(4.91) | 0.95/(1.41) | 0.52/(8.22) | 0.97/(1.31) | 0.47/(9.48) |
| HGB | 0.78/(2.86) | 0.59/(4.6) | 0.8/(2.62) | 0.51/(6.74) | 0.77/(2.85) | 0.42/(8.24) |
| LGBM | 0.79/(2.81) | 0.59/(4.49) | 0.8/(2.66) | 0.52/(6.9) | 0.76/(3.04) | 0.41/(9.23) |
| Adhesive | n | Homogeneous Dataset: R2_train/(ER_test) | Heterogeneous Dataset: R2_test/(ER_test) |
|---|---|---|---|
| Ad1 | 573 | 0.66/(3.40) | 0.69/(3.24) |
| Ad2 | 174 | 0.37/(8.84) | 0.44/(6.96) |
| Ad3 | 180 | 0.74/(4.18) | 0.78/(3.35) |
| Ad4 | 52 | Not converged | 0.62/(3.12) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, P.H.E.; Silva, G.C.; Pitz, D.B.; Schnelle, M.; Koschek, K.; Nagel, C.; Beber, V.C. Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence. Appl. Mech. 2023, 4, 334-355. https://doi.org/10.3390/applmech4010019
Fernandes PHE, Silva GC, Pitz DB, Schnelle M, Koschek K, Nagel C, Beber VC. Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence. Applied Mechanics. 2023; 4(1):334-355. https://doi.org/10.3390/applmech4010019
Chicago/Turabian StyleFernandes, Pedro Henrique Evangelista, Giovanni Corsetti Silva, Diogo Berta Pitz, Matteo Schnelle, Katharina Koschek, Christof Nagel, and Vinicius Carrillo Beber. 2023. "Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence" Applied Mechanics 4, no. 1: 334-355. https://doi.org/10.3390/applmech4010019
APA StyleFernandes, P. H. E., Silva, G. C., Pitz, D. B., Schnelle, M., Koschek, K., Nagel, C., & Beber, V. C. (2023). Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence. Applied Mechanics, 4(1), 334-355. https://doi.org/10.3390/applmech4010019





