Free-Form Deformation Parameterization on the Aerodynamic Optimization of Morphing Trailing Edge
Abstract
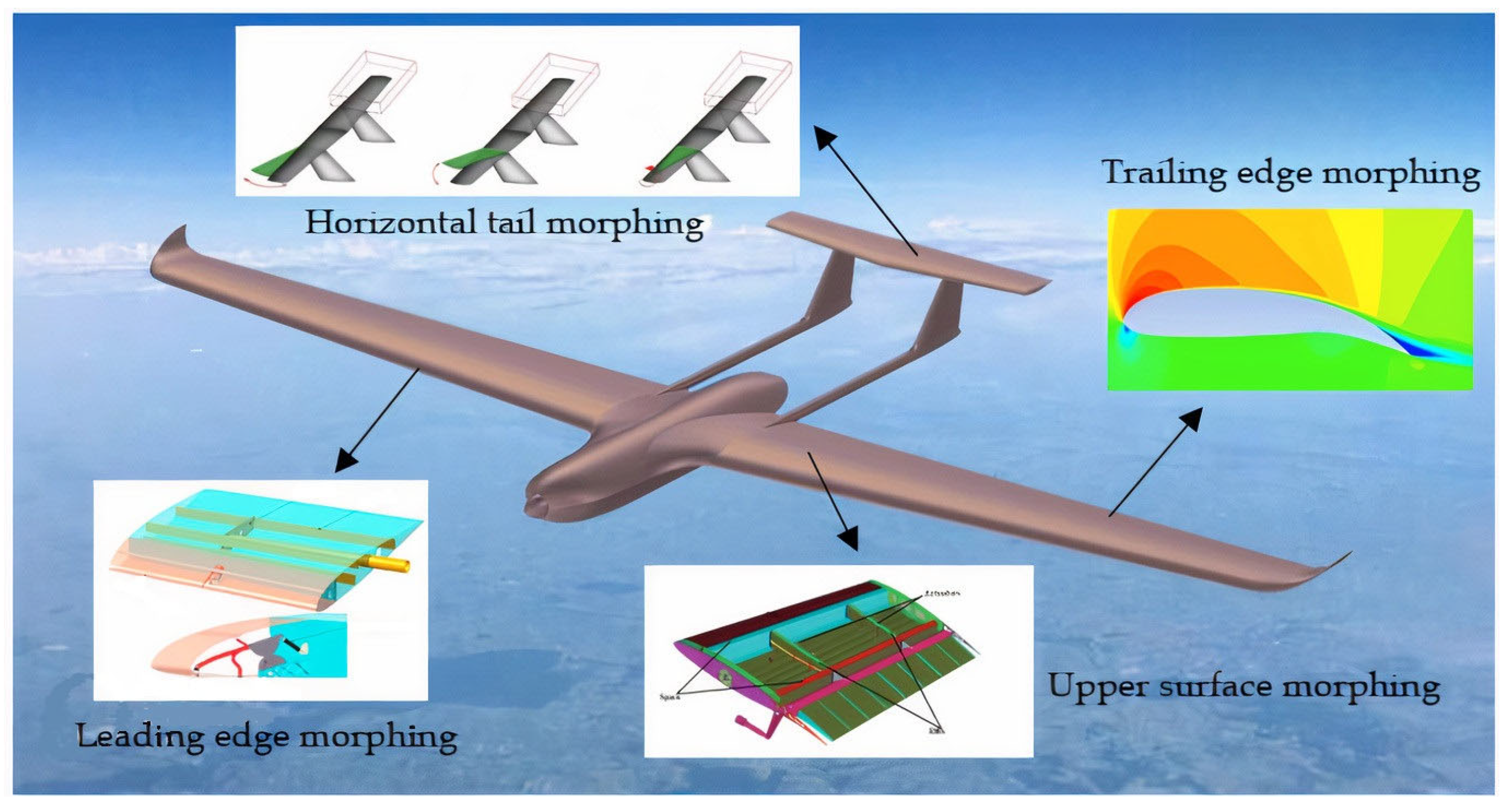
1. Introduction
2. Methodology
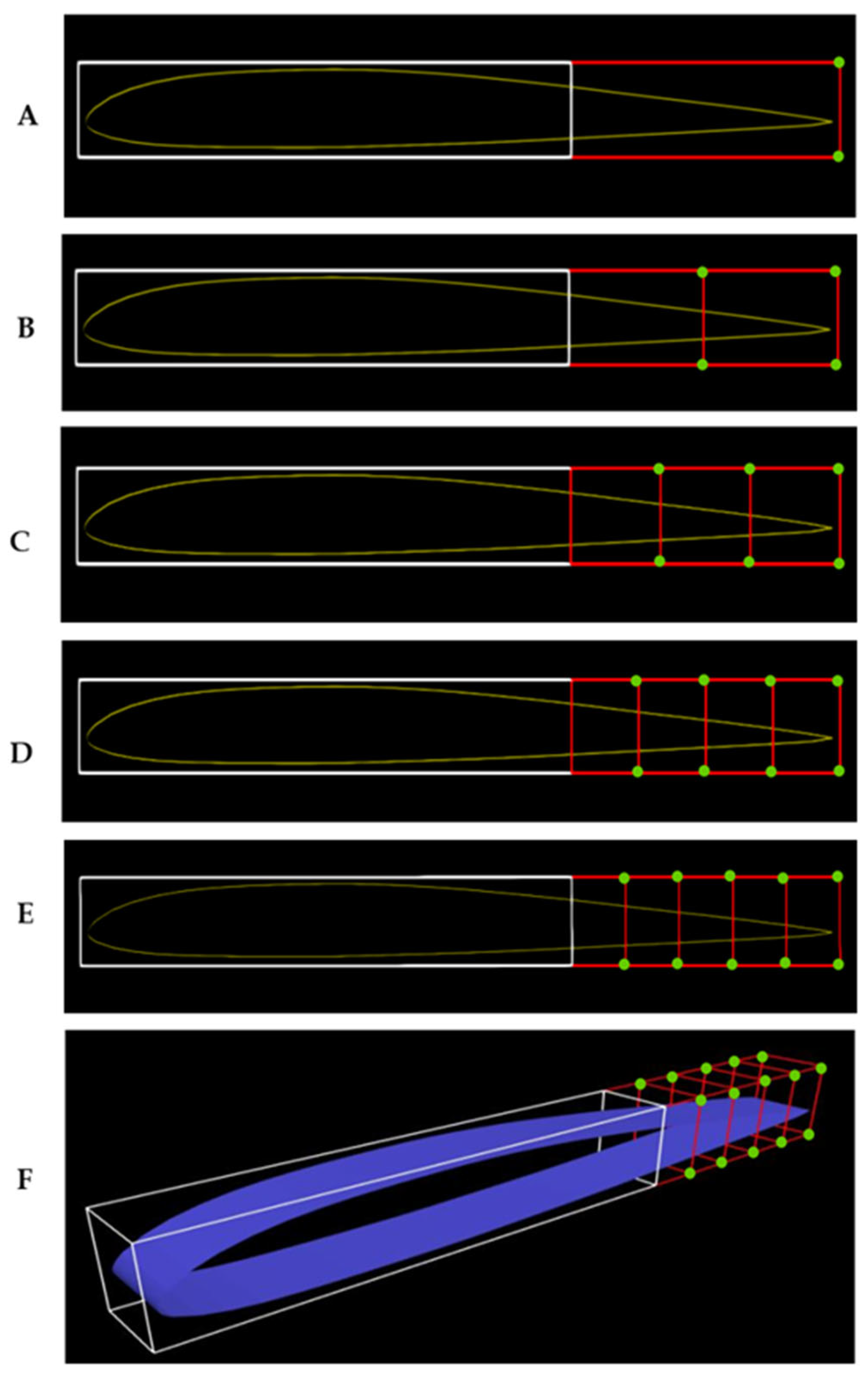
2.1. FFD Parameterization Technique
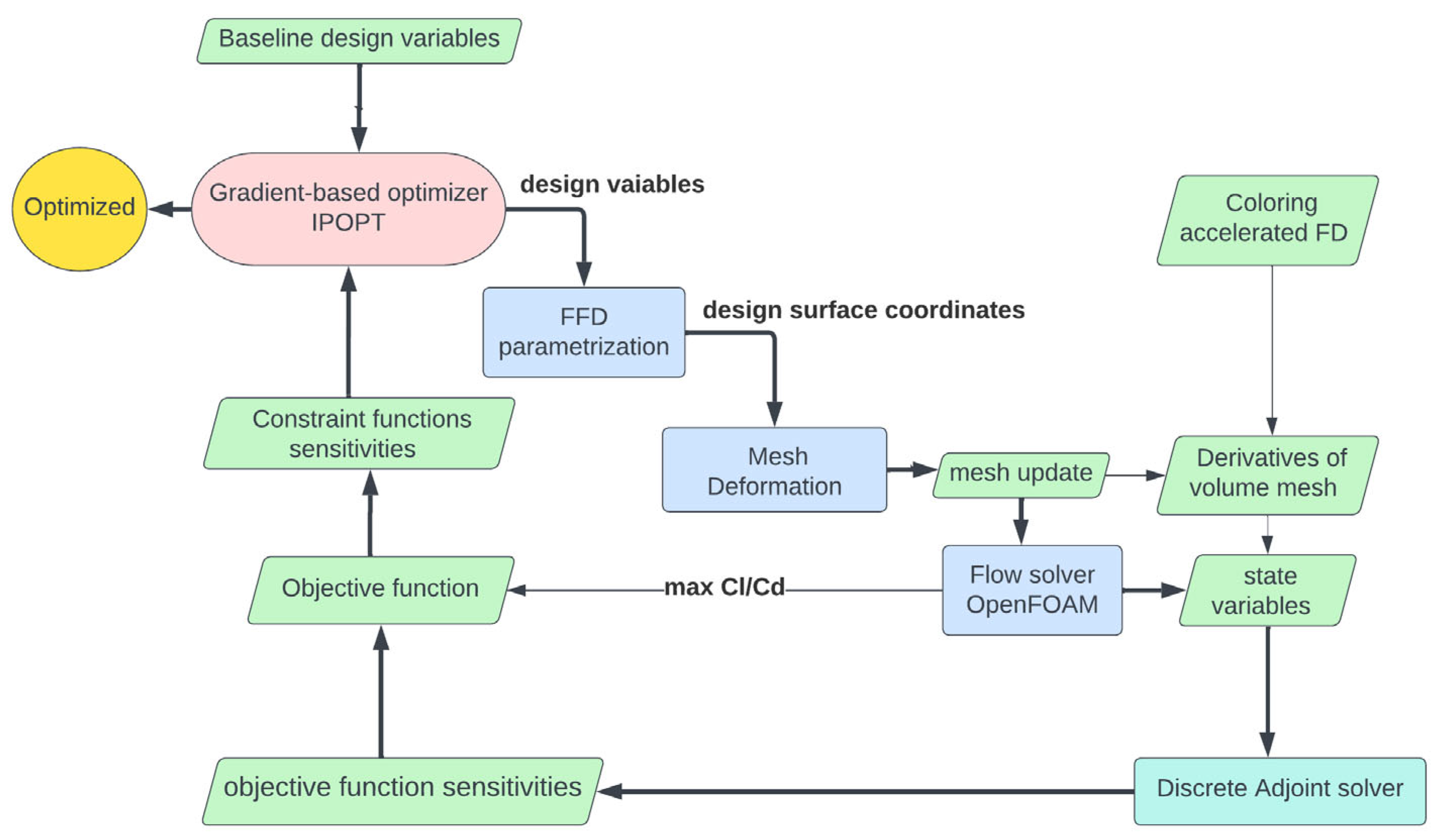
2.2. DAFoam Optimization Framework
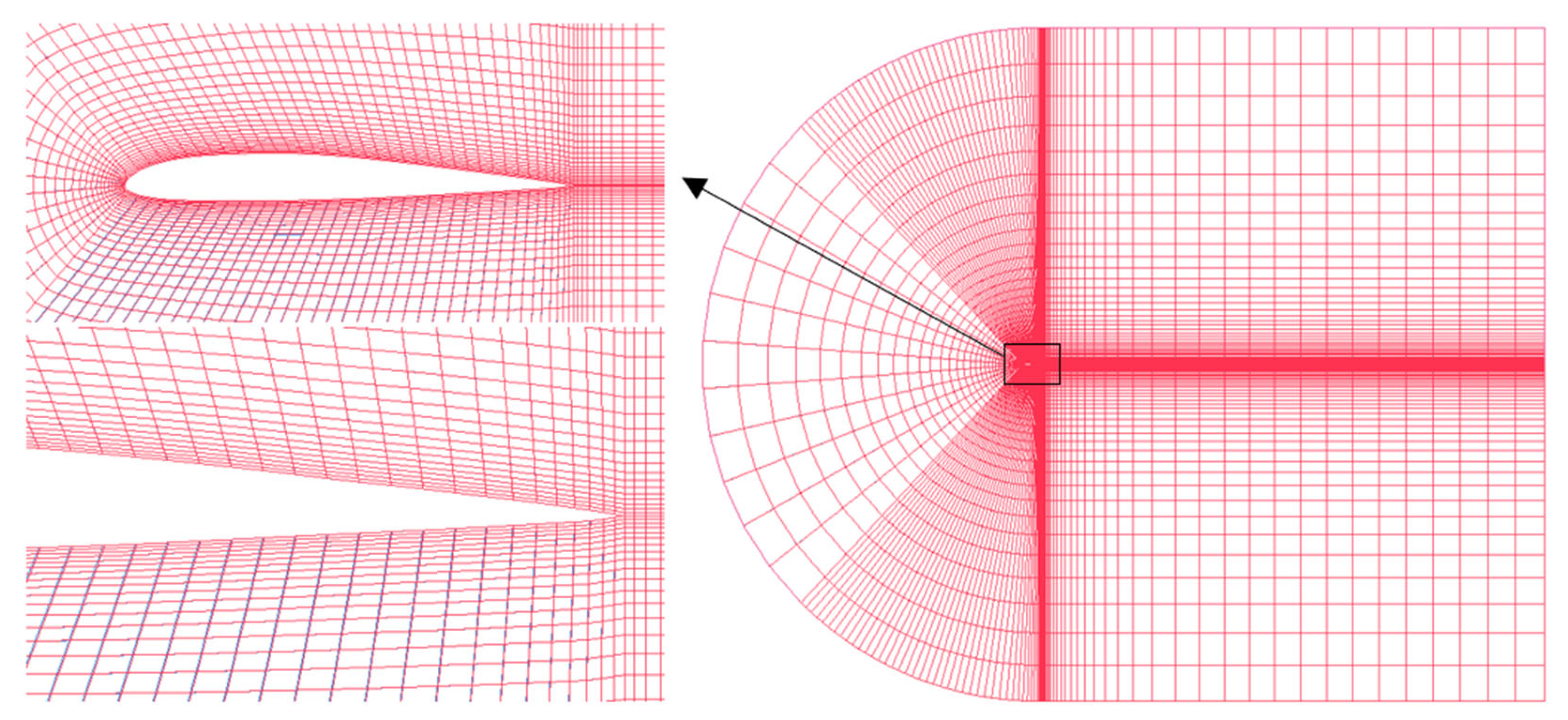
2.3. Optimization Numerical Setup
2.4. Optimization Process for a Morphing Trailing Edge Flap
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khurana, M.S.; Winarto, H.; Sinha, A.K. Airfoil Geometry Parameterization through Shape Optimizer and Computational Fluid Dynamics. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7–10 January 2008; p. 295. [Google Scholar]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef] [PubMed]
- Huynh, N.T.; Nguyen, T.V.; Nguyen, Q.M. Optimum Design for the Magnification Mechanisms Employing Fuzzy Logic-ANFIS. CMC Comput. Mater. Contin. 2022, 73, 5961–5983. [Google Scholar]
- Masters, D.A.; Taylor, N.J.; Rendall, T.; Allen, C.B.; Poole, D.J. Review of Aerofoil Parameterisation Methods for Aerodynamic Shape Optimisation. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Sripawadkul, V.; Padulo, M.; Guenov, M. A Comparison of Airfoil Shape Parameterization Techniques for Early Design Optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; p. 9050. [Google Scholar] [CrossRef]
- Samareh, J.A. Survey of shape parameterization techniques for high-fidelity multidisciplinary shape optimization. AIAA J. 2001, 39, 877–884. [Google Scholar] [CrossRef]
- Sugar Gabor, O.; Simon, A.; Koreanschi, A.; Botez, R.M. Improving the UAS-S4 Éhecal airfoil high angles-of-attack performance characteristics using a morphing wing approach. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 118–131. [Google Scholar] [CrossRef]
- Gabor, O.; Koreanschi, A.; Botez, R. Analysis of UAS-S4 Éhecatl aerodynamic performance improvement using several configurations of a morphing wing technology. Aeronaut. J. 2016, 120, 1337–1364. [Google Scholar] [CrossRef]
- Gabor, O.; Koreanschi, A.; Botez, R.M. A new non-linear vortex lattice method: Applications to wing aerodynamic optimizations. Chin. J. Aeronaut. 2016, 29, 1178–1195. [Google Scholar] [CrossRef]
- Koreanschi, A.; Sugar Gabor, O.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Mamou, M.; Mebarki, Y. Optimization and Design of a Morphing Aircraft Wing Tip Demonstrator at Low Speed for Drag Reduction, Part I–Aerodynamic Optimizations Using 3 Algorithms: Genetic, Bee Colony and Gradient Descent. Chin. J. Aeronaut. 2017, 30, 149–163. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.; Wong, T. Aerodynamic Design Optimization of a Morphing Leading Edge and Trailing Edge Airfoil–Application on the UAS-S45. Appl. Sci. 2021, 11, 1664. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Optimization and Design of a Flexible Droop-Nose Leading-Edge Morphing Wing Based on a Novel Black Widow Optimization Algorithm—Part I. Designs 2022, 6, 10. [Google Scholar] [CrossRef]
- Bashir, M.; Martel, S.L.; Botez, R.M.; Wong, T. Aerodynamic Shape Optimization of Camber Morphing Airfoil based on Black Widow Optimization. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2575. [Google Scholar] [CrossRef]
- Negahban, M.H.; Bashir, M.; Botez, R.M. Aerodynamic Optimization of a Novel Synthetic Trailing Edge and Chord Elongation Morphing: Application to the UAS-S45 Airfoil. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 1582. [Google Scholar]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech Eng. C J. Mech. Eng. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Concilio, A.; Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies—Large Commercial Aircraft and Civil Heli-Copters, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Pecora, R. Morphing wing flaps for large civil aircraft: Evolution of a smart technology across the Clean Sky program. Chin. J. Aeronaut. 2021, 34, 13–28. [Google Scholar] [CrossRef]
- Secanell, M.; Suleman, A.; Gamboa, P. Design of a Morphing Airfoil Using Aerodynamic Shape Optimization. AIAA J. 2006, 44, 1550–1562. [Google Scholar] [CrossRef]
- Botez, R.M. Morphing wing, UAV and aircraft multidisciplinary studies at the Laboratory of Applied Research in Active Controls, Avionics and AeroServoElasticity LARCASE. Aerosp. Lab 2018, 14, 1–11. [Google Scholar]
- Botez, R.M. Overview of Morphing Aircraft and Unmanned Aerial Systems Methodologies and Results–Application on the Cessna Citation X, CRJ-700, UAS-S4 and UAS-S45. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1038. [Google Scholar]
- Lyu, Z.; Martins, J. Aerodynamic Shape Optimization of an Adaptive Morphing Trailing-Edge Wing. J. Aircr. 2015, 52, 1951–1970. [Google Scholar] [CrossRef]
- Lyu, Z.; Kenway, G.K.W.; Martins, J.R.R.A. Aerodynamic Shape Optimization Investigations of the Common Research Model Wing Benchmark. AIAA J. 2015, 53, 968–985. [Google Scholar] [CrossRef]
- Burdette, D.A.; Martins, J.R.R.A. Impact of Morphing Trailing Edges on Mission Performance for the Common Research Model. J. Aircr. 2019, 56, 369–384. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.R.A.; Maki, K. An Object-oriented Framework for Rapid Discrete Adjoint Development using OpenFOAM. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1210. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.; Maki, K.J. An aerodynamic design optimization framework using a discrete adjoint approach with OpenFOAM. Comput. Fluids 2018, 168, 285–303. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.R.A.; Maki, K.J. DAFoam: An Open-Source Adjoint Framework for Multidisciplinary Design Optimization with OpenFOAM. AIAA J. 2020, 58, 1304–1319. [Google Scholar] [CrossRef]
- Abdessemed, C.; Bouferrouk, A.; Yao, Y. Effects of an Unsteady Morphing Wing with Seamless Side-Edge Transition on Aerodynamic Performance. Energies 2022, 15, 1093. [Google Scholar] [CrossRef]
- Negahban, M.H.; Botez, R.M.; Razavi, S.E. New Method for the Flow Modeling around chord-wise Morphing Airfoil. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2574. [Google Scholar] [CrossRef]
- Pecora, R.; Amoroso, F.; Magnifico, M.; Dimino, I. KRISTINA: Kinematic rib-based structural system for innovative adaptive trailing edge. In Industrial and Commercial Applications of Smart Structures Technologies; SPIE: Bellingham, WA, USA, 2016; Volume 9801, pp. 67–77. [Google Scholar]
- Concilio, A.; Dimino, I.; Pecora, R.; Ciminello, M. Structural Design of an Adaptive Wing Trailing Edge for Enhanced Cruise Performance. In Proceedings of the 24th AIAA/AHS Adaptive Structures Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Pecora, R.; Magnifico, M.; Amoroso, F.; Monaco, E. Multi-parametric flutter analysis of a morphing wing trailing edge. Aeronaut. J. 2014, 118, 1063–1078. [Google Scholar] [CrossRef]
- Kuitche, M.A.J.; Botez, R.M. Modeling novel methodologies for unmanned aerial systems—Applications to the UAS-S4 Ehecatl and the UAS-S45 Bálaam. Chin. J. Aeronaut. 2019, 32, 58–77. [Google Scholar] [CrossRef]
- Kuitche, M.A.J.; Botez, R.M.; Guillemin, A.; Communier, D. Aerodynamic modelling of unmanned aerial system through nonlinear vortex lattice method, computational fluid dynamics and experimental validation-application to the UAS-S45 bàlaam: Part 2. INCAS Bull. 2020, 12, 99–115. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Ronzheimer, A. Shape Parameterisation Based on Freeform Deformation in Aerodynamic Design Optimization. In Proceedings of the ERCOFTAC Design Optimization: Methods & Applications, Athens, Greece, 31 March–2 April 2004; p. 400. [Google Scholar]
- Kenway, G.; Kennedy, G.; Martins, J.R. A CAD-free approach to high-fidelity aerostructural optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; p. 9231. [Google Scholar]
- Burdyshaw, C.E.; Anderson, W.K. A General and Extensible Unstructured Mesh Adjoint Method. J. Aerosp. Comput. Inf. Commun. 2005, 2, 401–413. [Google Scholar] [CrossRef]
- Nielsen, E.J.; Kleb, W.L. Efficient Construction of Discrete Adjoint Operators on Unstructured Grids Using Complex Variables. AIAA J. 2006, 44, 827–836. [Google Scholar] [CrossRef]

| Year | Author | Morphing Approach | Optimization Process | Parameterization Method | Objective Functions |
|---|---|---|---|---|---|
| 2015 | Gabor et al. [7] | Upper surface | Artificial Bee Colony (ABC) + BFGS | NURBS | Transition delay |
| 2016 | Gabor et al. [8] | Upper surface | Artificial Bee (ABC) + BFGS | NURBS | Lift-to-drag ratio maximization |
| 2016 | Gabor et al. [9] | Upper surface | Artificial Bee Colony (ABC) | NURBS | Drag minimization |
| 2017 | Koreanschi et al. [10] | Upper surface and aileron | Genetic Algorithm (GA) | Cubic spline | Drag minimization And transition delay |
| 2021 | Bashir et al. [11] | Leading and trailing edge | Particle Swarm Optimization (PSO) | Bezier-PARSEC | Drag minimization and endurance maximization |
| 2022 | Bashir et al. [12] | Leading edge | Black Widow Optimization (BWO) | Class shape transformation (CST) | Drag minimization and endurance maximization |
| 2022 | Bashir et al. [13] | Trailing edge | Black Widow Optimization (BWO) | Makima | Lift-to-drag ratio maximization |
| 2023 | Negahban et al. [14] | Combined chord and trailing edge morphing | Gradient-based optimization with discrete adjoint method | FFD | Drag minimization |
| Function/Variable | Description | Case | ||||
|---|---|---|---|---|---|---|
| Objective function | 1 | 2 | 3 | 4 | 5 | |
| max. / | Lift-to-drag ratio | |||||
| With respect to: | ||||||
| y | TE FFD control points | 8 | 12 | 16 | 20 | 24 |
| α | Angle of attack | 1 | 1 | 1 | 1 | 1 |
| Total design variables | 9 | 13 | 17 | 21 | 25 | |
| Subject to: | ||||||
| Constraint function | ||||||
| Design variable bounds | ||||||
| Linear constraint |
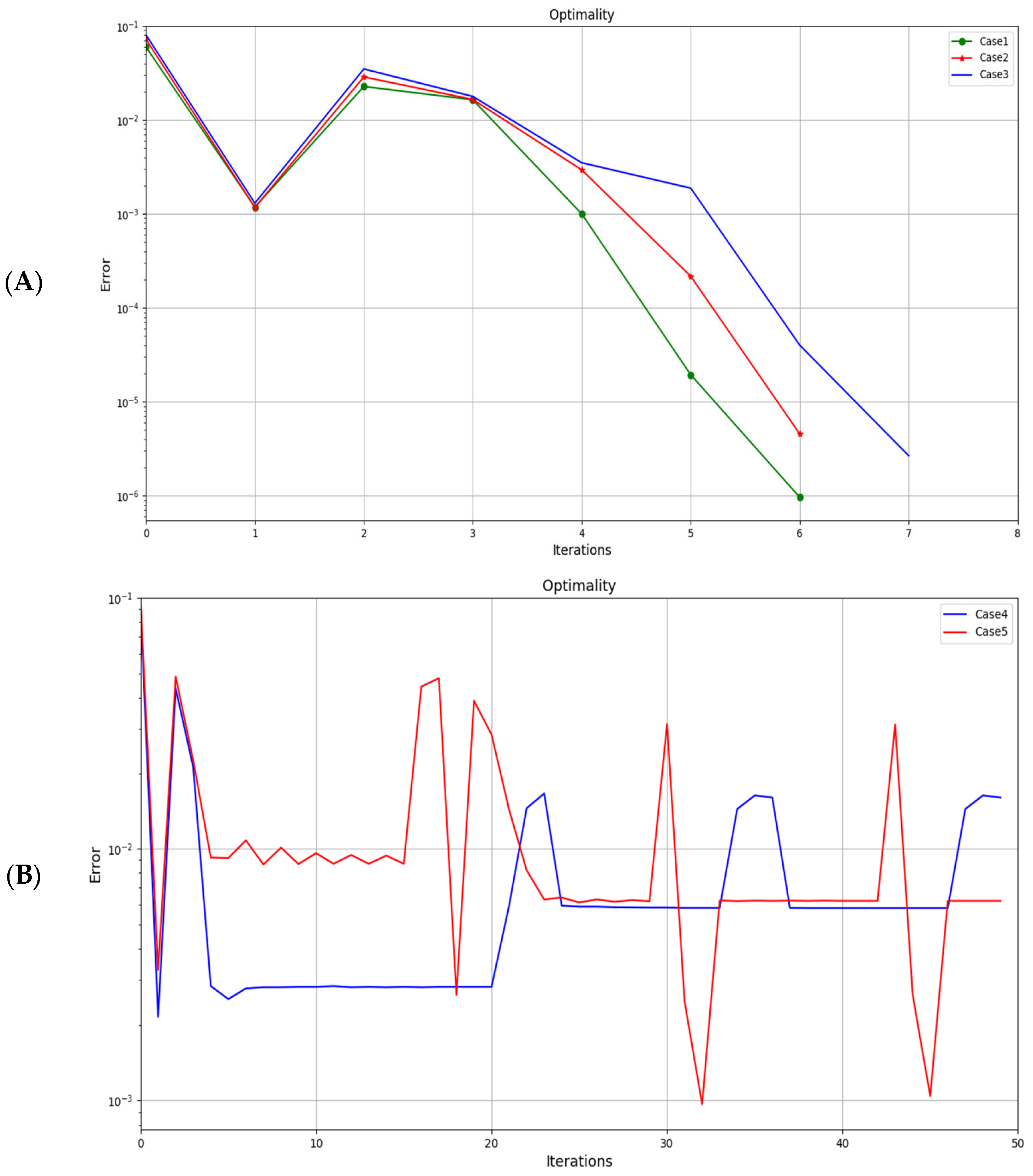
| Case Nr. | Control Points | Run Time (Sec.) | Itr. Nr. | Optimality Error | Initial Cl/Cd | Opt. Cl/Cd | Gain % |
|---|---|---|---|---|---|---|---|
| 1 | 8 | 218.732 | 6 | 9.63 × 10−7 | 34.548 | 38.522 | 10.3 |
| 2 | 12 | 258.512 | 6 | 4.55 × 10−6 | 34.532 | 39.547 | 12.7 |
| 3 | 16 | 504.096 | 7 | 2.67 × 10−6 | 34.524 | 40.058 | 13.8 |
| 4 | 20 | 10,925.43 | 50 | 1.60 × 10−2 | 34.523 | 39.002 | 11.5 |
| 5 | 24 | 12,203.12 | 50 | 6.20 × 10−3 | 34.521 | 38.663 | 10.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negahban, M.H.; Bashir, M.; Botez, R.M. Free-Form Deformation Parameterization on the Aerodynamic Optimization of Morphing Trailing Edge. Appl. Mech. 2023, 4, 304-316. https://doi.org/10.3390/applmech4010017
Negahban MH, Bashir M, Botez RM. Free-Form Deformation Parameterization on the Aerodynamic Optimization of Morphing Trailing Edge. Applied Mechanics. 2023; 4(1):304-316. https://doi.org/10.3390/applmech4010017
Chicago/Turabian StyleNegahban, Mir Hossein, Musavir Bashir, and Ruxandra Mihaela Botez. 2023. "Free-Form Deformation Parameterization on the Aerodynamic Optimization of Morphing Trailing Edge" Applied Mechanics 4, no. 1: 304-316. https://doi.org/10.3390/applmech4010017
APA StyleNegahban, M. H., Bashir, M., & Botez, R. M. (2023). Free-Form Deformation Parameterization on the Aerodynamic Optimization of Morphing Trailing Edge. Applied Mechanics, 4(1), 304-316. https://doi.org/10.3390/applmech4010017






