A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration
Abstract
1. Introduction
1.1. Nonwovens as Acoustic Insulators
- The complex acoustic impedance of the fabric that labels its resistance towards an incoming sound wave.
- The Sound Absorption Coefficient (SAC) that labels the fraction between transmitted and total energy.
- Increasing the thickness improves the SAC. For high frequencies, the SAC increases only up to a thickness of 2 cm.
- Decreasing the fiber diameter improves the SAC at low and medium frequencies.
- There exists an optimal porosity for maximizing the SAC, but the relationship is non-linear.
1.2. Plate Vibration
1.3. Porous Media Mechanics
1.4. Highlights and Content Overview
2. Material Description and Parameters
- 1.
- Opening polypropylene (PP) staple fibers with a staple length of 50 and diameter of 16 by hand.
- 2.
- Carding the fibers using a lab-scale card to form a fiber web.
- 3.
- Folding the fiber web to have a nominal weight per area of 210 .
- 4.
- Mechanical bonding using two-sided needle punching with 1–3 repetitions to increase needlepunch density.
- 5.
- Cut out the samples from the produced nonwovens.
- Sample thickness when subjected to a pressure of 0.5 . For the measurement the sample is placed between two stamps. Weights are placed on the top stamp so that the necessary pressure is achieved. The thickness is the distance between the two stamps.
- Weight per area, which is measured by weighing the sample and dividing by the sample area. Three samples with a circular area of 100 are used.
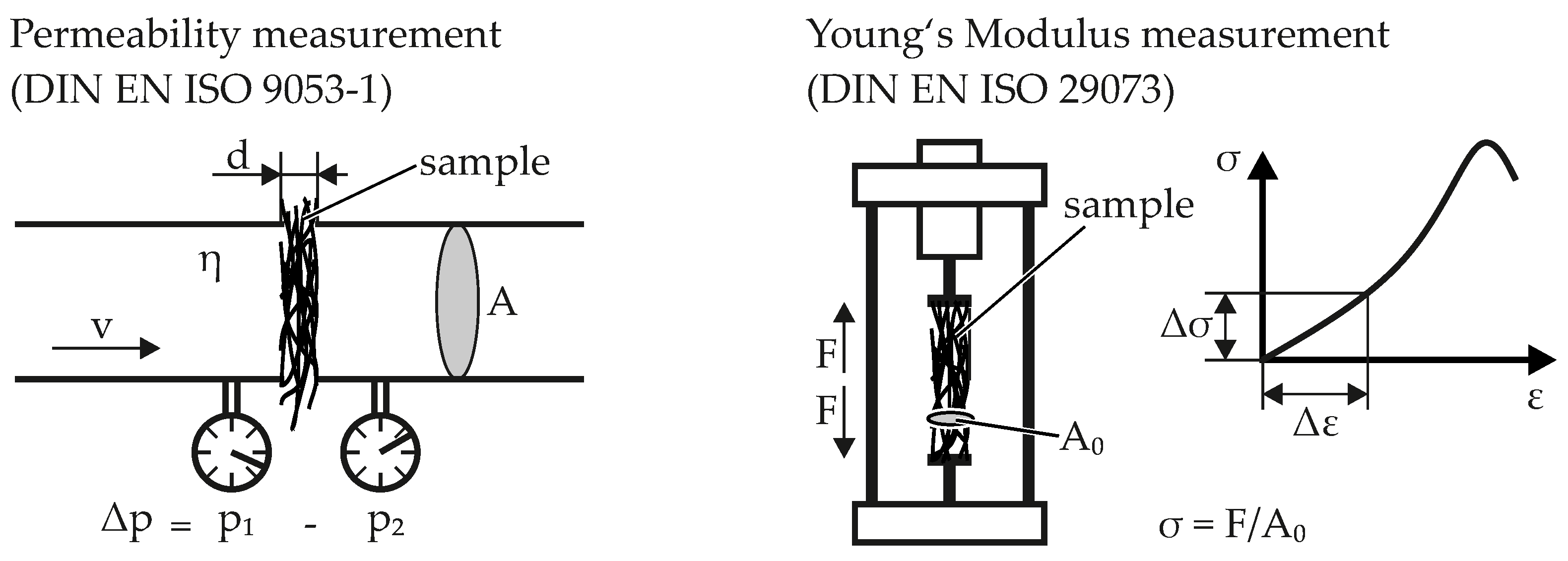
- Air permeability in accordance to DIN EN ISO 9053-1 [7]. The samples are placed in a tube as shown in Figure 1. The air pressure before the sample is kept constant and pressure behind the sample as well as air velocity before are measured. The air permeability is then calculated using Darcy’s law (see Equation (1)).
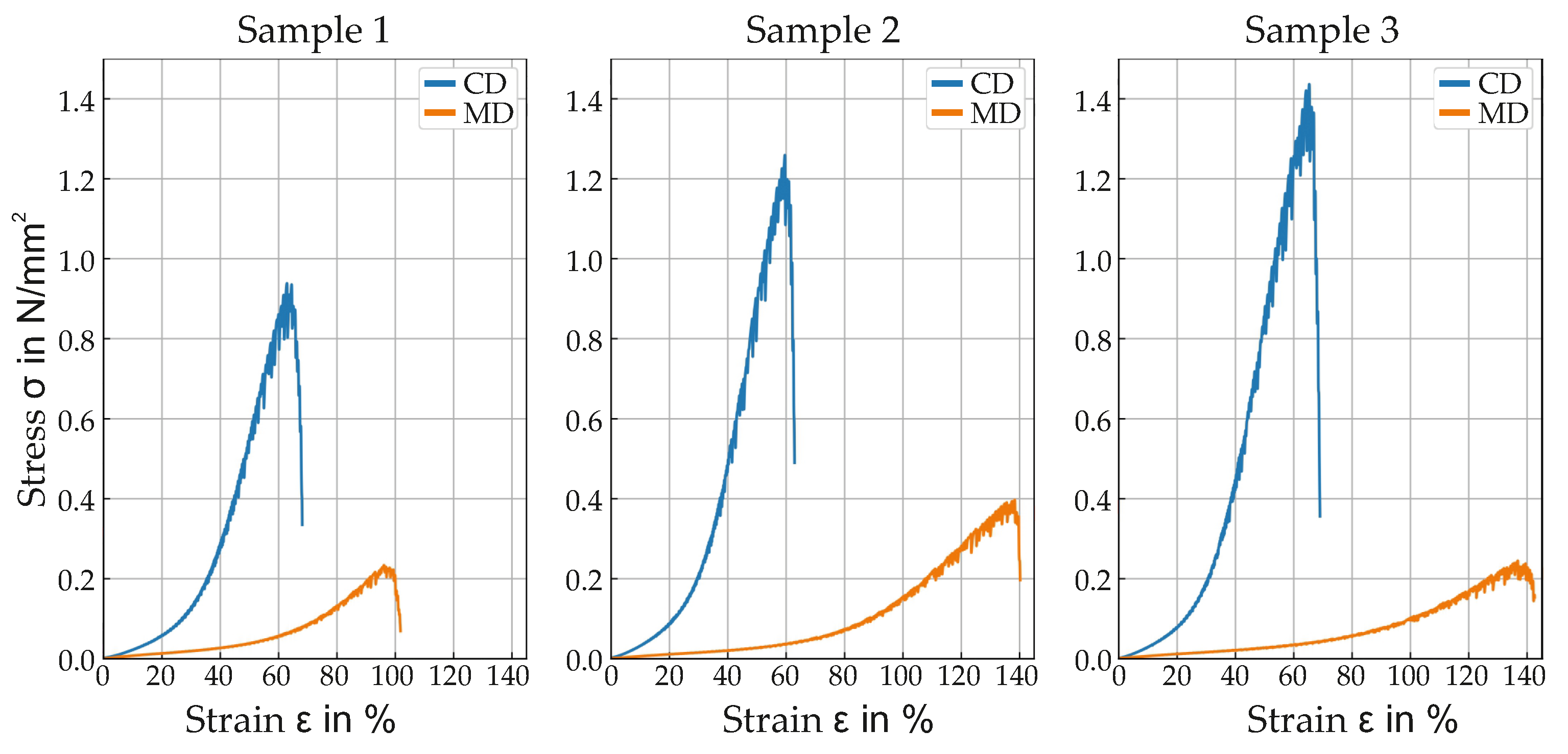
- Young’s Modulus in machine direction (MD) and cross direction (CD) is measured with tensile test in accordance to DIN EN 29073 [8] as shown in Figure 1. For MD measurement the sample strip (width 50 ) is cut out so that the orientation matches the machine direction. For CD measurement the sample strip is cut out so that the orientation is perpendicular to the machine direction. Tensile tests then reveal the stress-strain-curves in both MD and CD. Young’s modulus is the average slope of the linear part of the resulting stress-strain curve. The samples exhibit linear behavior up to an elongation of 10 percent. The stress-strain curves of the samples are shown in Figure 2.
3. Continuum Mechanical Description of Multiphase Anisotropic Fibrous Materials
3.1. Homogenization and Densities
3.2. Kinematics
3.3. Governing Balance Relations
- •
- Overall momentum balance:
- •
- Overall mass balance:
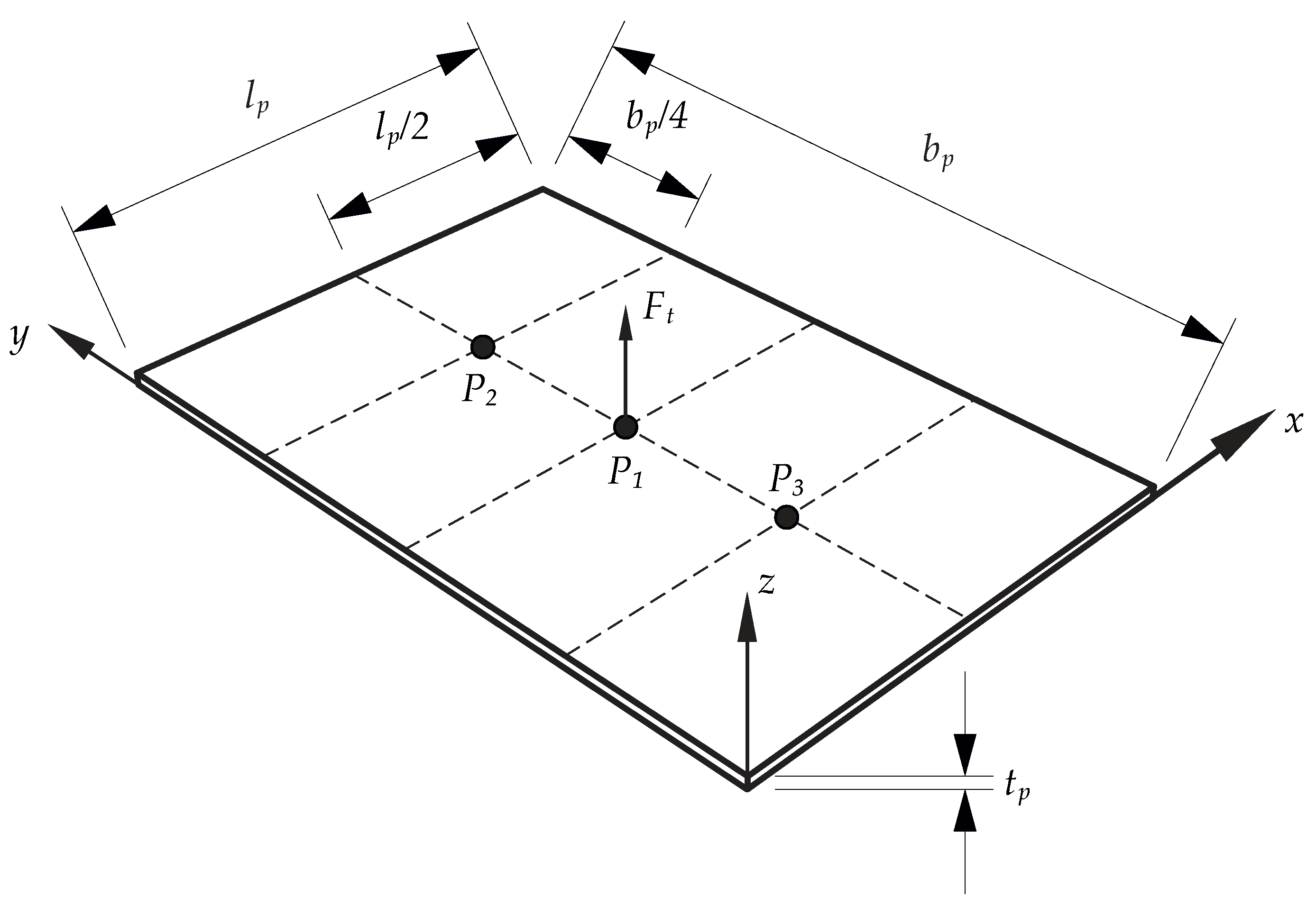
4. Dynamics Analysis of Plate Vibration
4.1. Mathematical Modeling
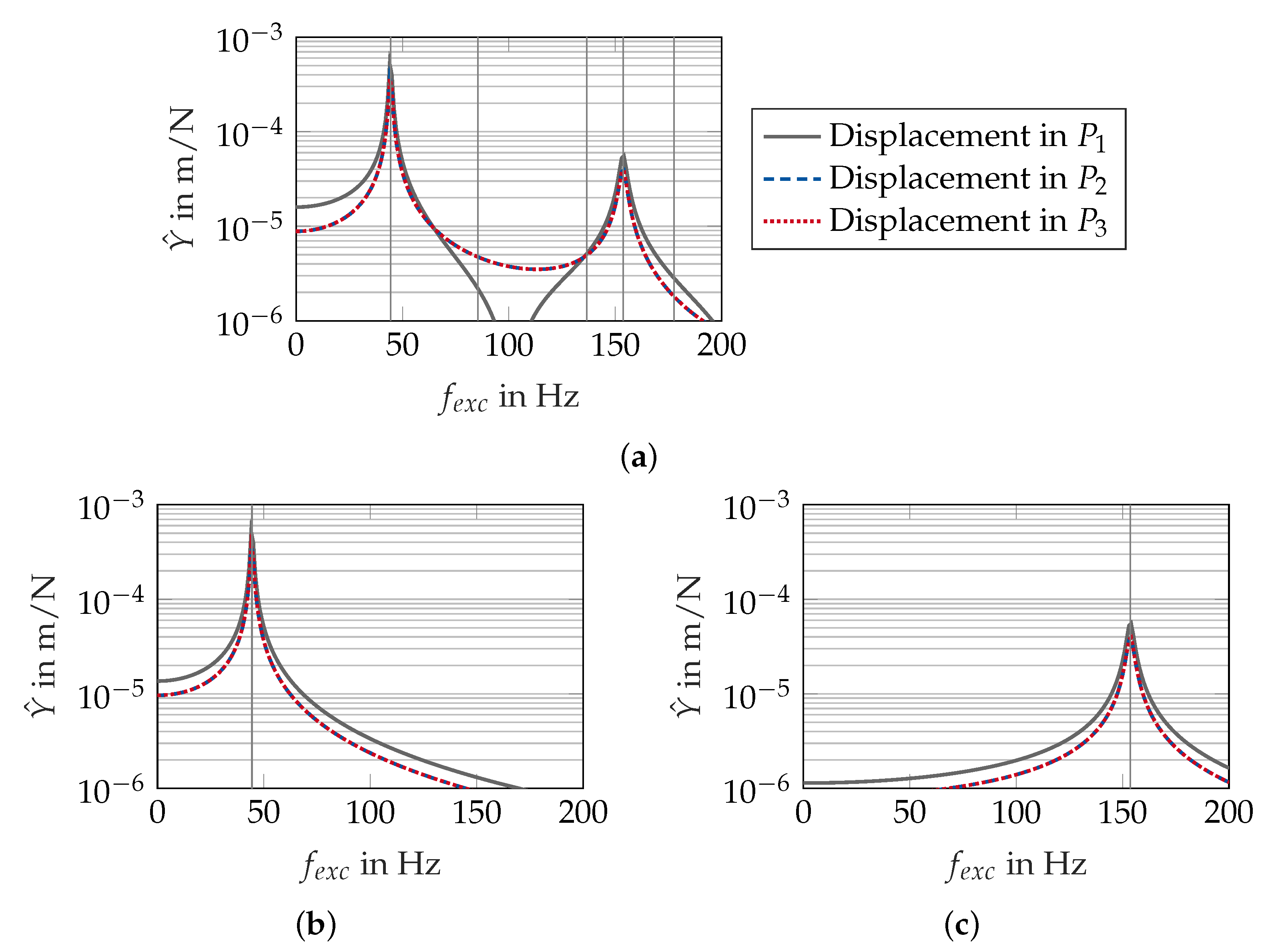
4.2. Numerical Analysis
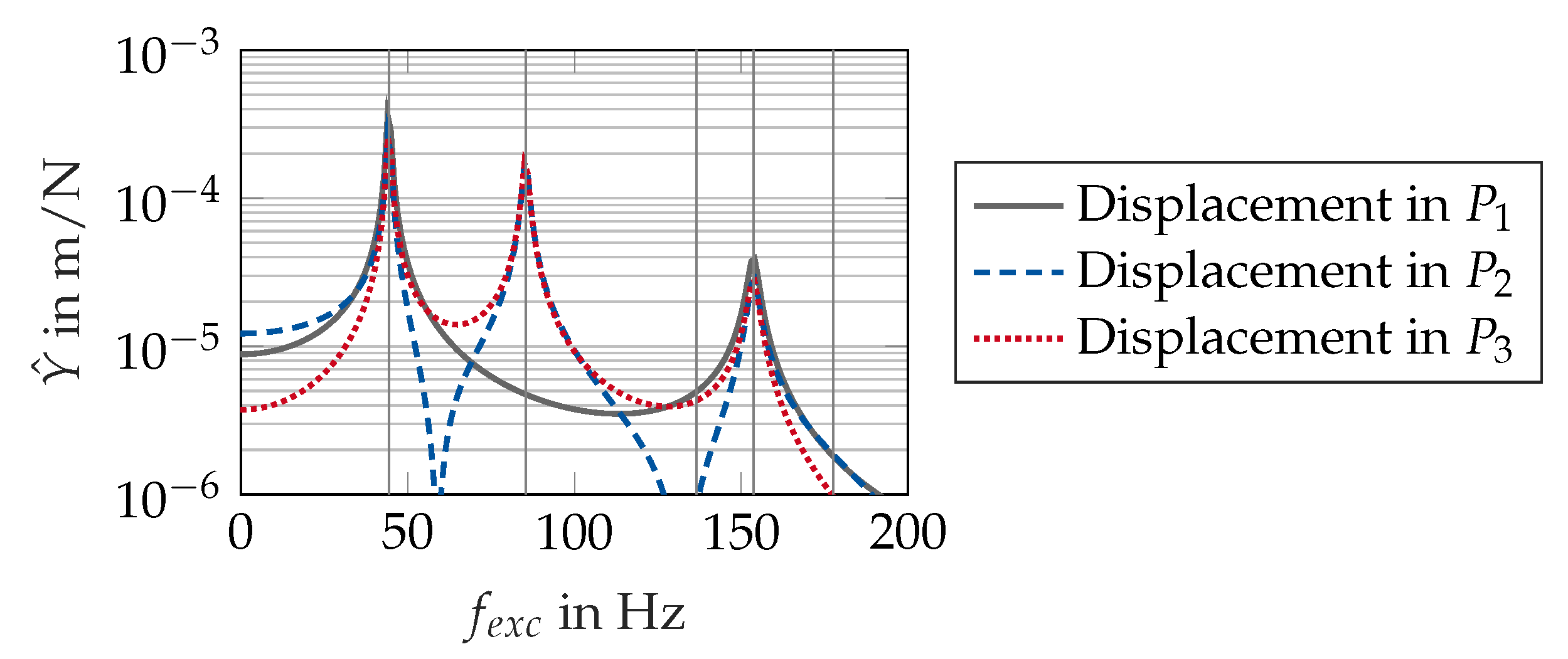
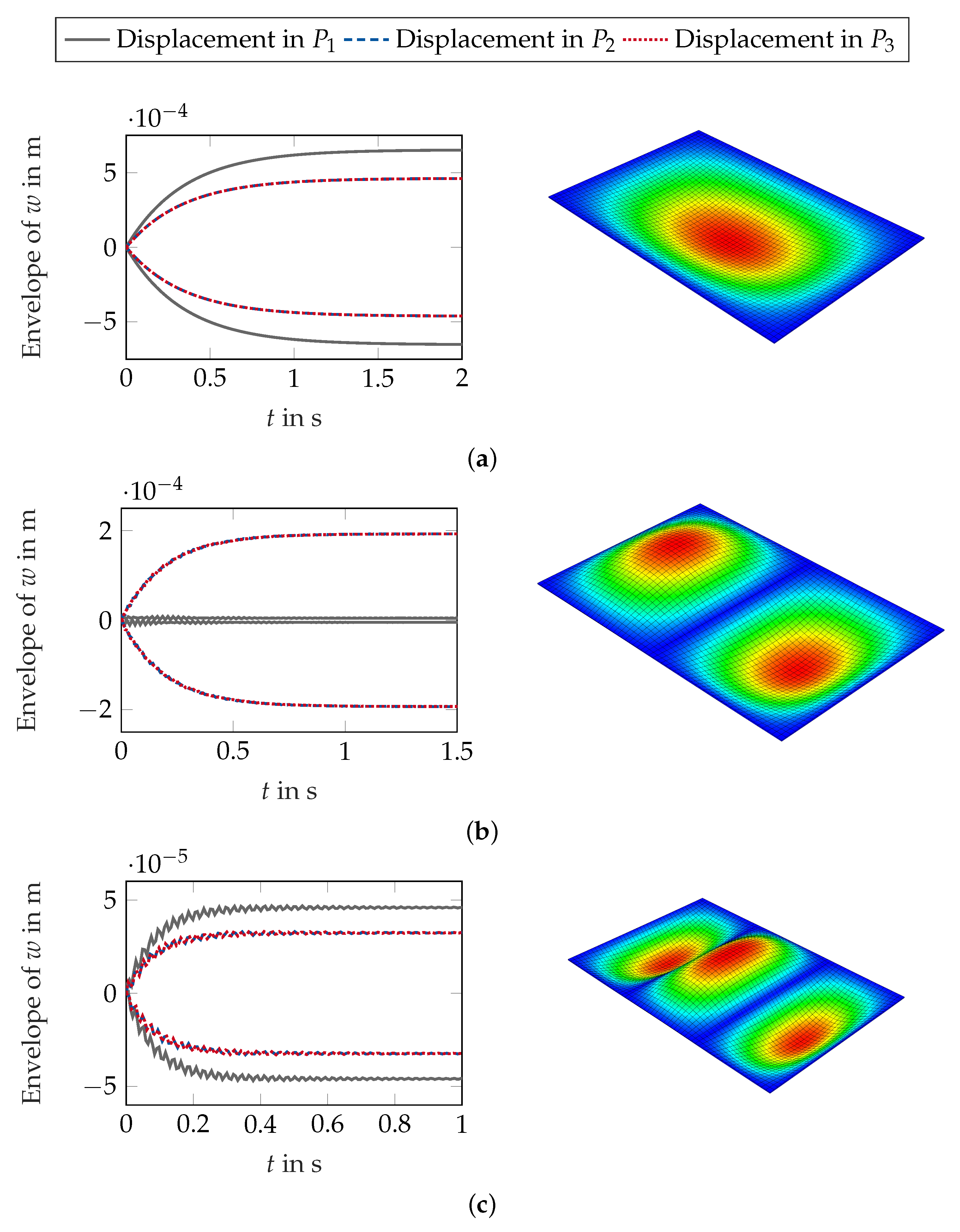
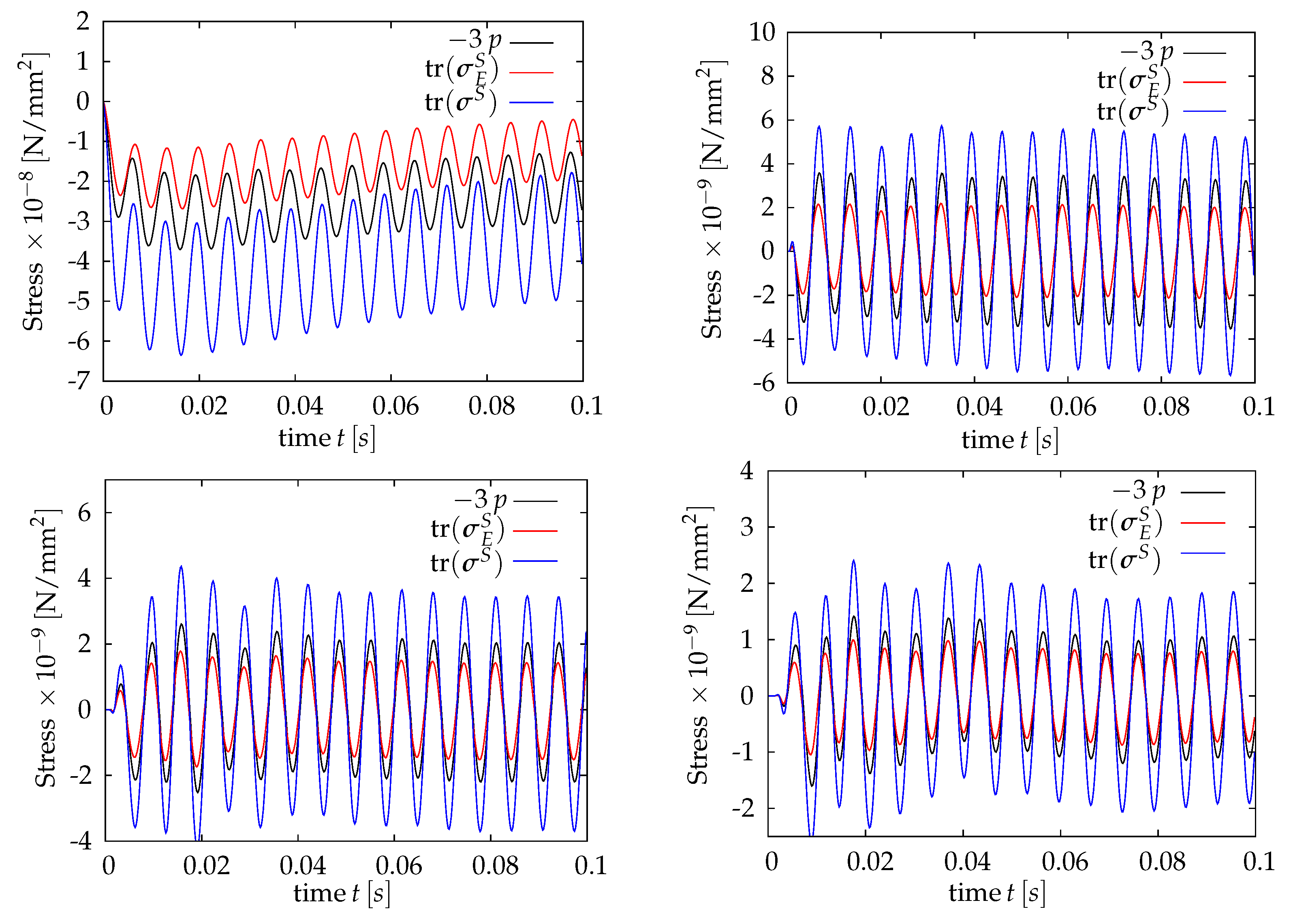
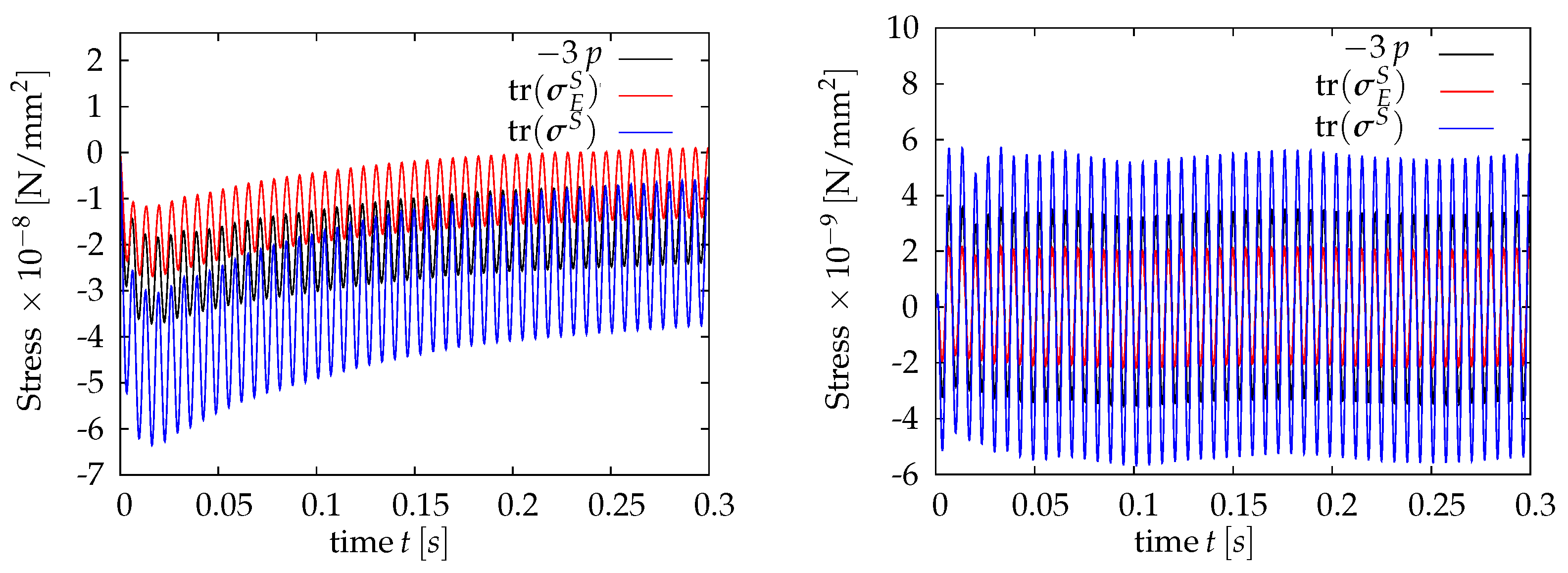
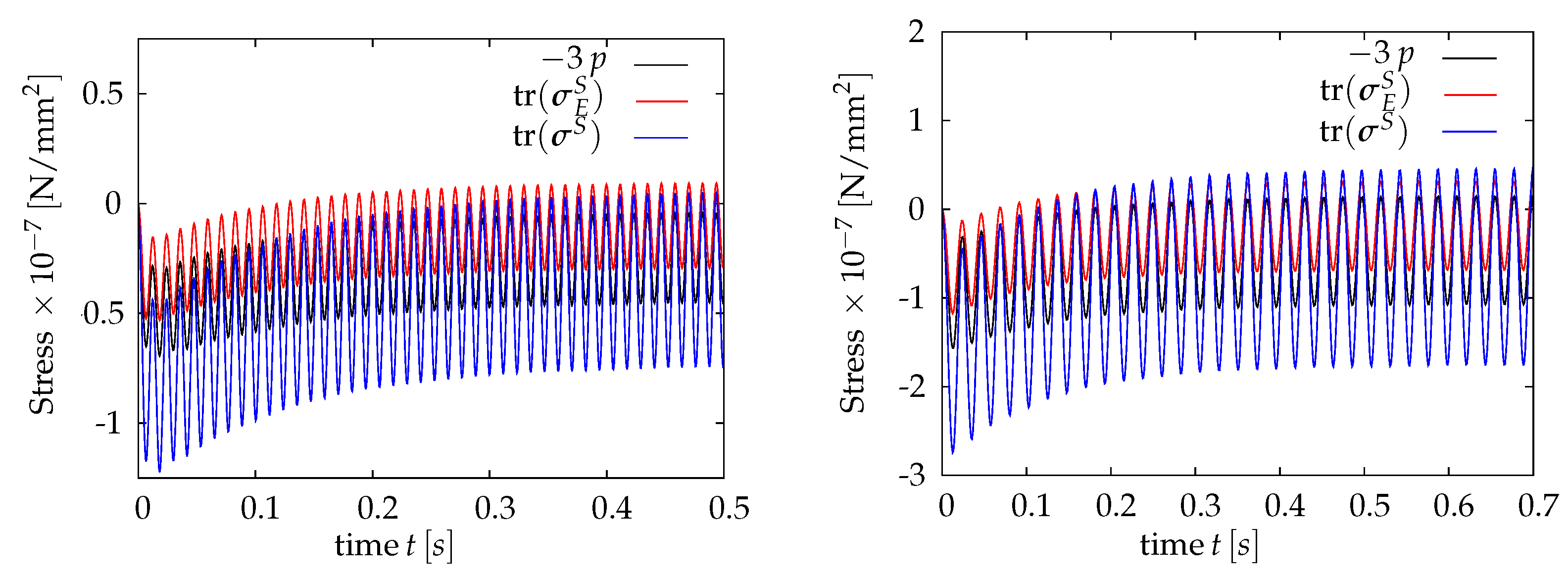
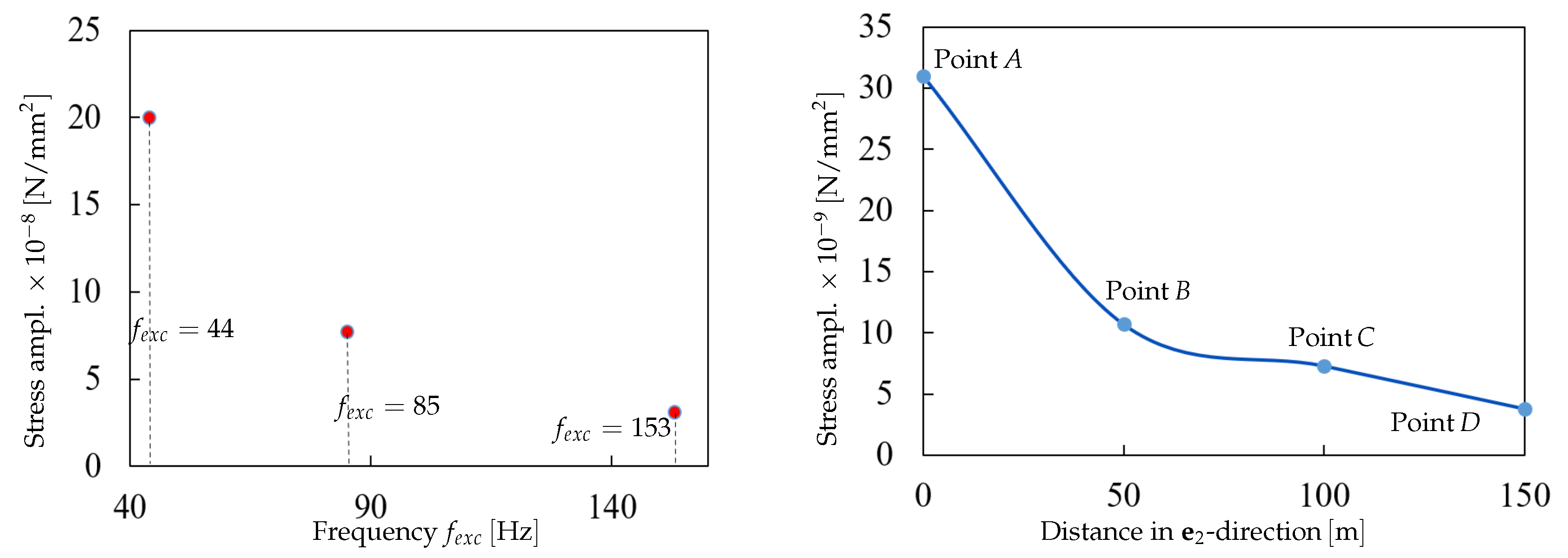
5. Dynamic Response of Nonwovens as Multiphase Porous Media
6. Conclusions and Future Aspects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soltani, P.; Norouzi, M. Prediction of the sound absorption behavior of nonwoven fabrics: Computational study and experimental validation. J. Sound Vib. 2020, 485, 115607. [Google Scholar] [CrossRef]
- Wilson, A. Development of the nonwovens industry. In Handbook of Nonwovens; Russell, S.J., Ed.; Woodhead Publishing Series in textiles; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–16. [Google Scholar]
- Shoshani, Y.; Yakubov, Y. A Model for Calculating the Noise Absorption Capacity of Nonwoven Fiber Webs. Text. Res. J. 1999, 69, 519–526. [Google Scholar] [CrossRef]
- Zarek, J. Sound absorption in flexible porous materials. J. Sound Vib. 1978, 61, 205–234. [Google Scholar] [CrossRef]
- Yang, S.; Yu, W.; Pan, N. Investigation of the sound-absorbing behavior of fiber assemblies. Text. Res. J. 2011, 81, 673–682. [Google Scholar] [CrossRef]
- Beier, H.; Vogel, C.; Haase, J.; Hunger, M.; Schmalz, E.; Sauerkunze, M.; Bergmann, L. Vliesstoffe für technische Anwendungen. In Vliesstoffe; Fuchs, H., Albrecht, W., Eds.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. DIN EN ISO 9053-1: Akustik-Bestimmung des Strömungswiderstands: Teil 1: Verfahren mit statischer Luftströmung; Beuth Verlag GmbH: Berlin, Germany, 2019. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. DIN EN 29 073: Prüfverfahren für Vliesstoffe: Bestimmung der Höchstzugkraft und Höchstzugkraftdehnung; Beuth Verlag GmbH: Berlin, Germany, 1992. [Google Scholar]
- Banerjee, M.M.; Mazumdar, J. A Review of Methods for Linear and Nonlinear Vibration Analysis of Plates and Shells. Procedia Eng. 2016, 144, 493–503. [Google Scholar] [CrossRef][Green Version]
- Ahad, F.E.; Shi, D.Y. Analytical Approaches to Vibration Analysis of Thick Plates Subjected to Different Supports, Loadings and Boundary Conditions—A Literature Survey. Int. J. Eng. Res. Afr. 2015, 17, 43–53. [Google Scholar] [CrossRef]
- Ton-That, H.L.; Nguyen-Van, H.; Chau-Dinh, T. An Improved Four-Node Element for Analysis of Composite Plate/Shell Structures Based on Twice Interpolation Strategy. Int. J. Comput. Methods 2020, 17, 1950020. [Google Scholar] [CrossRef]
- Ton-That, H.L.; Nguyen-Van, H. A Combined Strain Element in Static, Frequency and Buckling Analyses of Laminated Composite Plates and Shells. Period. Polytech. Civ. Eng. 2021, 65, 56–71. [Google Scholar] [CrossRef]
- Phung, M.V.; Nguyen, D.T.; Doan, L.T.; Nguyen, D.V.; Duong, T.V. Numerical Investigation on Static Bending and Free Vibration Responses of Two-Layer Variable Thickness Plates with Shear Connectors. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 1–19. [Google Scholar] [CrossRef]
- Ton-That, H.L.; Nguyen-Van, H.; Chau-Dinh, T. A novel quadrilateral element for analysis of functionally graded porous plates/shells reinforced by graphene platelets. Arch. Appl. Mech. 2021, 91, 2435–2466. [Google Scholar] [CrossRef]
- Zeller, P. Handbuch Fahrzeugakustik: Grundlagen, Auslegung, Berechnung, Versuch, 2nd ed.; ATZ/MTZ-Fachbuch, Vieweg+Teubner Verlag: Wiesbaden, Germany, 2012. [Google Scholar]
- Ramu, I.; Mohanty, S.C. Study on Free Vibration Analysis of Rectangular Plate Structures Using Finite Element Method. Procedia Eng. 2012, 38, 2758–2766. [Google Scholar] [CrossRef]
- Isanaka, B.R.; Akbar, M.A.; Mishra, B.P.; Kushvaha, V. Free vibration analysis of thin plates: Bare versus Stiffened. Eng. Res. Express 2020, 2, 015014. [Google Scholar] [CrossRef]
- Ehlers, W. Foundations of multiphasic and porous materials. In Porous Media: Theory, Experiments and Numerical Applications; Ehlers, W., Bluhm, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 3–86. [Google Scholar]
- Markert, B. A constitutive approach to 3-d nonlinear fluid flow through finite deformable porous continua. Transp. Porous Media 2007, 70, 427. [Google Scholar] [CrossRef]
- Heider, Y.; Avci, O.; Markert, B.; Ehlers, W. The dynamic response of fluid-saturated porous materials with application to seismically induced soil liquefaction. Soil Dyn. Earthq. Eng. 2014, 63, 120–137. [Google Scholar] [CrossRef]
- Ehlers, W.; Wagner, A. Modelling and simulation methods applied to coupled problems in porous-media mechanics. Arch. Appl. Mech. 2019, 89, 609–628. [Google Scholar] [CrossRef]
- Chaaban, M.; Heider, Y.; Markert, B. Upscaling LBM-TPM simulation approach of Darcy and non-Darcy fluid flow in deformable, heterogeneous porous media. Int. J. Heat Fluid Flow 2020, 83, 108566. [Google Scholar] [CrossRef]
- Heider, Y. Multi-Field and Multi-Scale Computational Fracture Mechanics and Machine-Learning Material Modeling; Habilitation, Report No. 13 of Institute of General Mechanics; RWTH Aachen University: Aachen, Germany, 2021. [Google Scholar] [CrossRef]
- Biot, M. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. High-frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Biot, M. Theory of propagation of elastic waves in a fluid-saturated porous solid I. Low-frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Steeb, H. Ultrasound propagation in cancellous bone. Arch. Appl. Mech. 2010, 80, 489–502. [Google Scholar] [CrossRef]
- Schröder, J. Theoretische und algorithmische Konzepte zur phänomenologischen Beschreibung anisotropen Materialverhaltens. Ph.D. Thesis, Inst. f. Baumechanik u. Numerische Mechanik, Universität Hannover, Hanover, Germany, 1996. [Google Scholar]
- Markert, B.; Heider, Y.; Ehlers, W. Comparison of monolithic and splitting solution schemes for dynamic porous media problems. Int. J. Numer. Methods Eng. 2010, 82, 1341–1383. [Google Scholar] [CrossRef]
- Heider, Y. Saturated Porous Media Dynamics with Application to Earthquake Engineering. Ph.D. Thesis, Institute of Applied Mechanics (CE), University of Stuttgart, Stuttgart, Germany, 2012. [Google Scholar]
- Markert, B. A survey of selected coupled multifield problems in computational mechanics. J. Coupled Syst. Multiscale Dyn. 2013, 1, 22–48. [Google Scholar] [CrossRef]
- Padilla, C.A.; Patil, S.P.; Heider, Y.; Markert, B. 3D modelling of brittle fracture using a joint all-atom and phase-field approach. GAMM Mitteilungen 2017, 40, 91–101. [Google Scholar] [CrossRef]
- Ali, B.; Heider, Y.; Markert, B. Residual stresses in gas tungsten arc welding: A novel phase-field thermo-elastoplasticity modeling and parameter treatment framework. Comput. Mech. 2021, 69, 565–587. [Google Scholar] [CrossRef]
- Borja, R.I.; White, J.A. Conservation Laws for Coupled Hydro-Mechanical Processes in Unsaturated Porous Media. In Mechanics of Unsaturated Geomaterials; Wiley-Blackwell: Hoboken, NJ, USA, 2013; Volume Chapter 8, pp. 185–208. [Google Scholar]
- de Boer, R.; Ehlers, W. The development of the concept of effective stresses. Acta Mech. 1990, 83, 77–92. [Google Scholar] [CrossRef]
- Heider, Y.; Wang, K.; Sun, W. SO(3)-invariance of informed-graph-based deep neural network for anisotropic elastoplastic materials. Comput. Methods Appl. Mech. Eng. 2020, 363, 112875. [Google Scholar] [CrossRef]
- Heider, Y.; Bamer, F.; Ebrahem, F.; Markert, B. Self-organized criticality in fracture models at different scales. Examples Counterexamples 2022, 2, 100054. [Google Scholar] [CrossRef]
- Mabuma, J. Multi-Field Modelling and Simulation of the Human Hip Joint. Ph.D. Thesis, Institute of Applied Mechanics (CE), University of Stuttgart, Stuttgart, Germany, 2014. [Google Scholar]
- Tamayol, A.; Bahrami, M. Transverse permeability of fibrous porous media. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 046314. [Google Scholar] [CrossRef]
- Markert, B. A biphasic continuum approach for viscoelastic high-porosity foams: Comprehensive theory, numerics, and application. Arch. Comput. Methods Eng. 2008, 15, 371–446. [Google Scholar] [CrossRef]
- Beckmann, A.; Heider, Y.; Stoffel, M.; Markert, B. Assessment of the viscoelastic mechanical properties of polycarbonate urethane for medical devices. J. Mech. Behav. Biomed. Mater. 2018, 82, 1–8. [Google Scholar] [CrossRef]
- Orban, F. Damping of materials and members in structures. J. Phys. Conf. Ser. 2011, 268, 012022. [Google Scholar] [CrossRef]
- Rahul, B.; Dharani, J.; Balaji, R. Optimal Method for Determination of Rayleigh Damping Coefficients for Different Materials using Modal Analysis. Int. J. Veh. Struct. Syst. 2021, 13. [Google Scholar] [CrossRef]
- Sweidan, A.H.; Heider, Y.; Markert, B. A unified water/ice kinematics approach for phase-field thermo-hydro-mechanical modeling of frost action in porous media. Comput. Methods Appl. Mech. Eng. 2020, 372, 113358. [Google Scholar] [CrossRef]
- Sweidan, A.; Niggemann, K.; Heider, Y.; Ziegler, M.; Markert, B. Experimental study and numerical modeling of the thermo-hydro-mechanical processes in soil freezing with different frost penetration directions. Acta Geotech. 2022, 17, 231–255. [Google Scholar] [CrossRef]
- Heider, Y. A review on phase-field modeling of hydraulic fracturing. Eng. Fract. Mech. 2021, 253, 107881. [Google Scholar] [CrossRef]

| Quantity | Unit | Sample 1 | Sample 2 | Sample 3 |
|---|---|---|---|---|
| Needlepunch iterations | 1 | 2 | 3 | |
| Thickness t | ||||
| Weight per area A | ||||
| Permeability | ||||
| Elasticity modulus MD | ||||
| Elasticity modulus CD | ||||
| Porosity | - |
| Quantity | Unit | Value |
|---|---|---|
| Dimensions: | ||
| Length | 400 | |
| Width | 600 | |
| Thickness | 2 | |
| Material Parameters (Steel): | ||
| Density | 7850 | |
| Elasticity modulus | 210,000 | |
| Poisson’s ratio | - | |
| Viscous damping ratio [41] | - |
| Mode | in | in | Mode Shape |
|---|---|---|---|
| (Analytical) | (FE) | (FE) | |
| Mode 1 (, ) |  | ||
| Mode 2 (, | 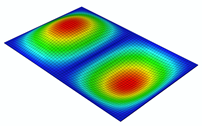 | ||
| Mode 3 (, ) | 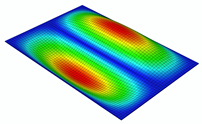 | ||
| Mode 4 (, ) | 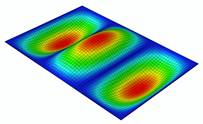 | ||
| Mode 5 (, ) | 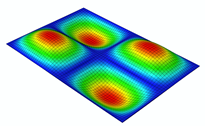 |
| Quantity | Unit | Value |
|---|---|---|
| Dimensions (textile layer): | ||
| Length | 400 | |
| Width | 600 | |
| Thickness | ||
| Material Parameters (textile material): | ||
| Solid material density | 1500 | |
| Elasticity modulus in MD () | ||
| Elasticity modulus in CD () | ||
| Poisson’s ratio | - | |
| 1st Lamé parameter in MD () | ||
| 2nd Lamé parameter in MD () | ||
| 1st Lamé parameter in CD () | ||
| initial porosity | − | |
| Fluid (air) material density | ||
| Effective dynamic fluid viscosity | ||
| Initial intrinsic permeability | ||
| Permeability-related parameter | − | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Archut, J.-L.; Kins, R.; Heider, Y.; Cloppenburg, F.; Markert, B.; Gries, T.; Corves, B. A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration. Appl. Mech. 2022, 3, 496-516. https://doi.org/10.3390/applmech3020029
Archut J-L, Kins R, Heider Y, Cloppenburg F, Markert B, Gries T, Corves B. A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration. Applied Mechanics. 2022; 3(2):496-516. https://doi.org/10.3390/applmech3020029
Chicago/Turabian StyleArchut, Jan-Lukas, Ruben Kins, Yousef Heider, Frederik Cloppenburg, Bernd Markert, Thomas Gries, and Burkhard Corves. 2022. "A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration" Applied Mechanics 3, no. 2: 496-516. https://doi.org/10.3390/applmech3020029
APA StyleArchut, J.-L., Kins, R., Heider, Y., Cloppenburg, F., Markert, B., Gries, T., & Corves, B. (2022). A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration. Applied Mechanics, 3(2), 496-516. https://doi.org/10.3390/applmech3020029






