Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models
Abstract
1. Introduction
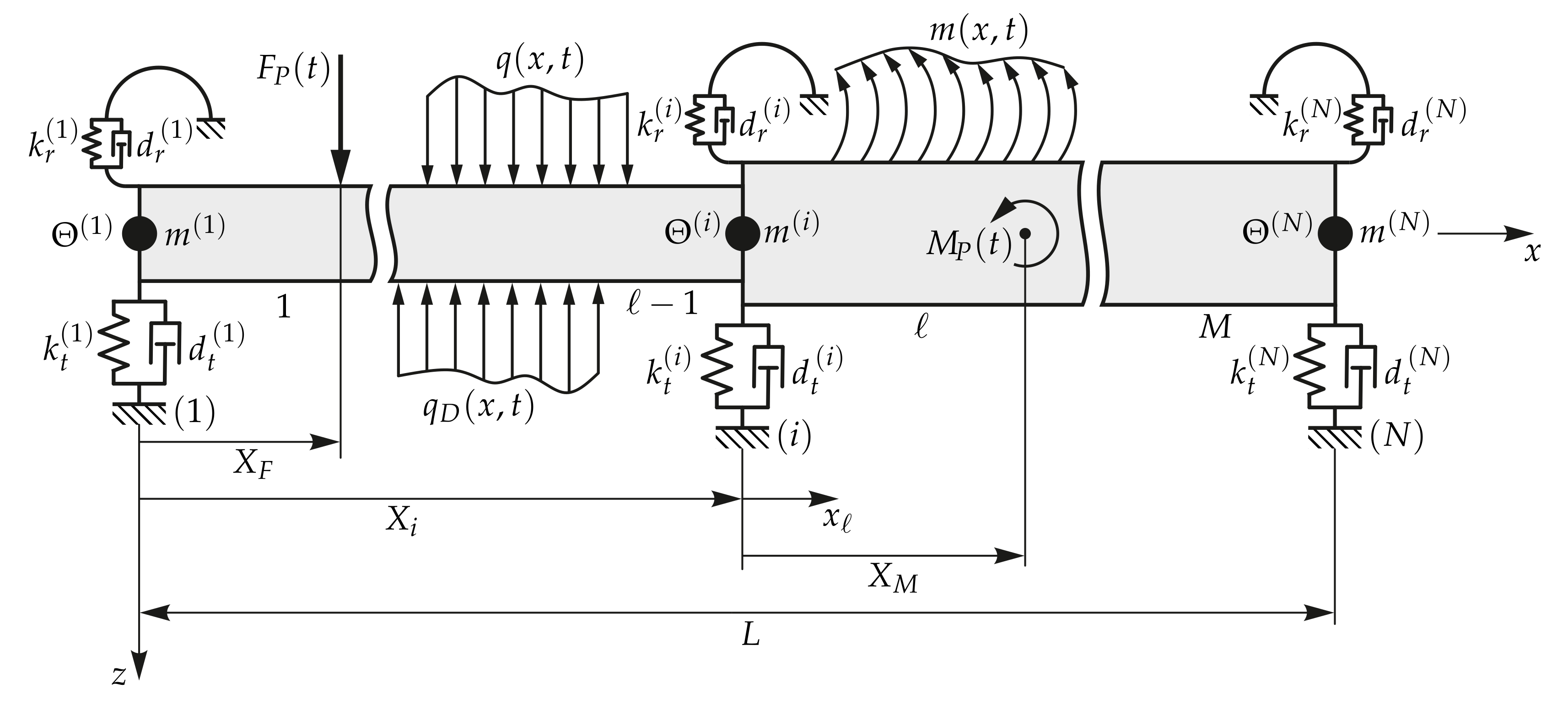
2. Problem Description
2.1. General Viscoelastic Beam Vibration Problem
2.2. Modeling of the Internal Material Damping
2.3. Timoshenko Beam Theory
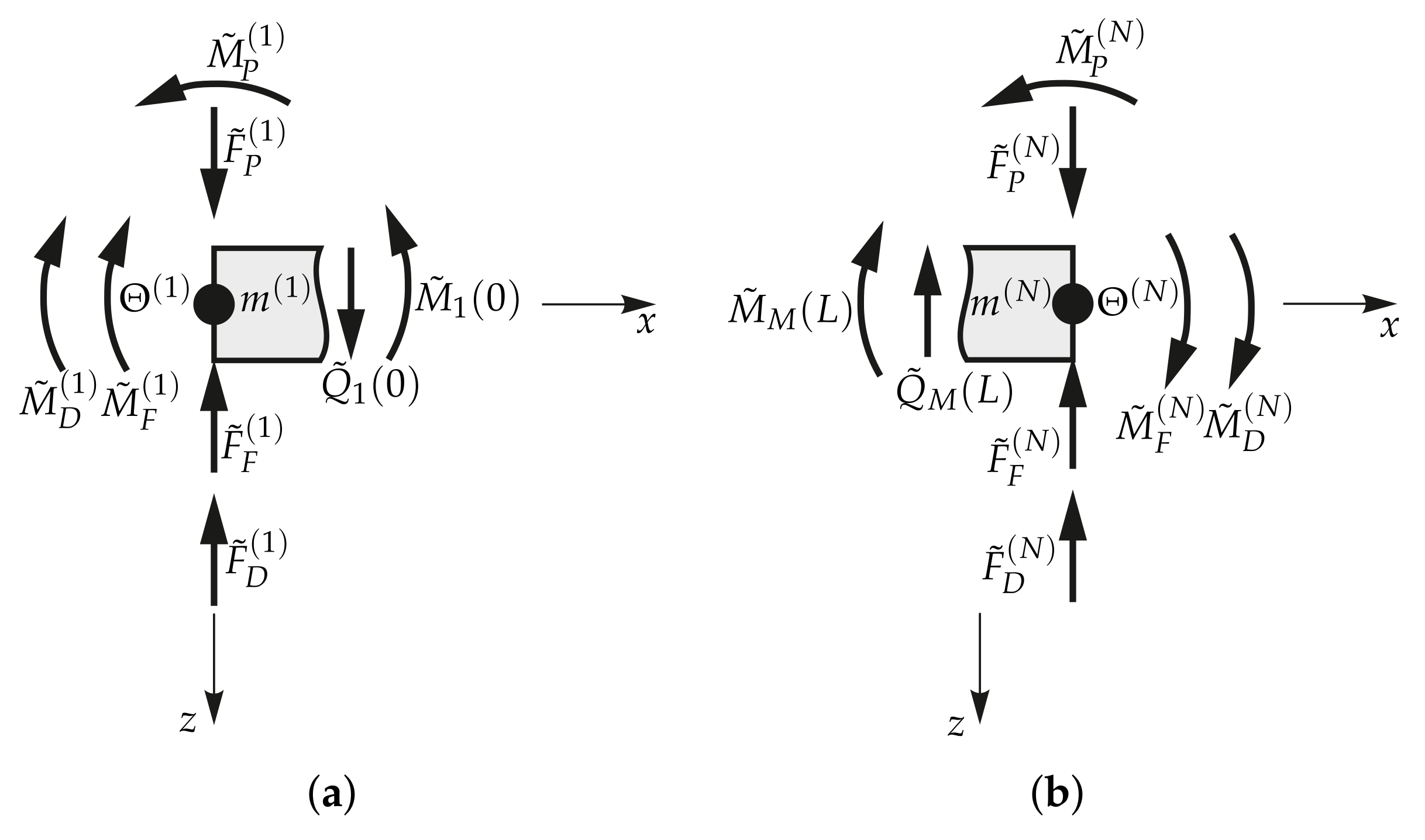
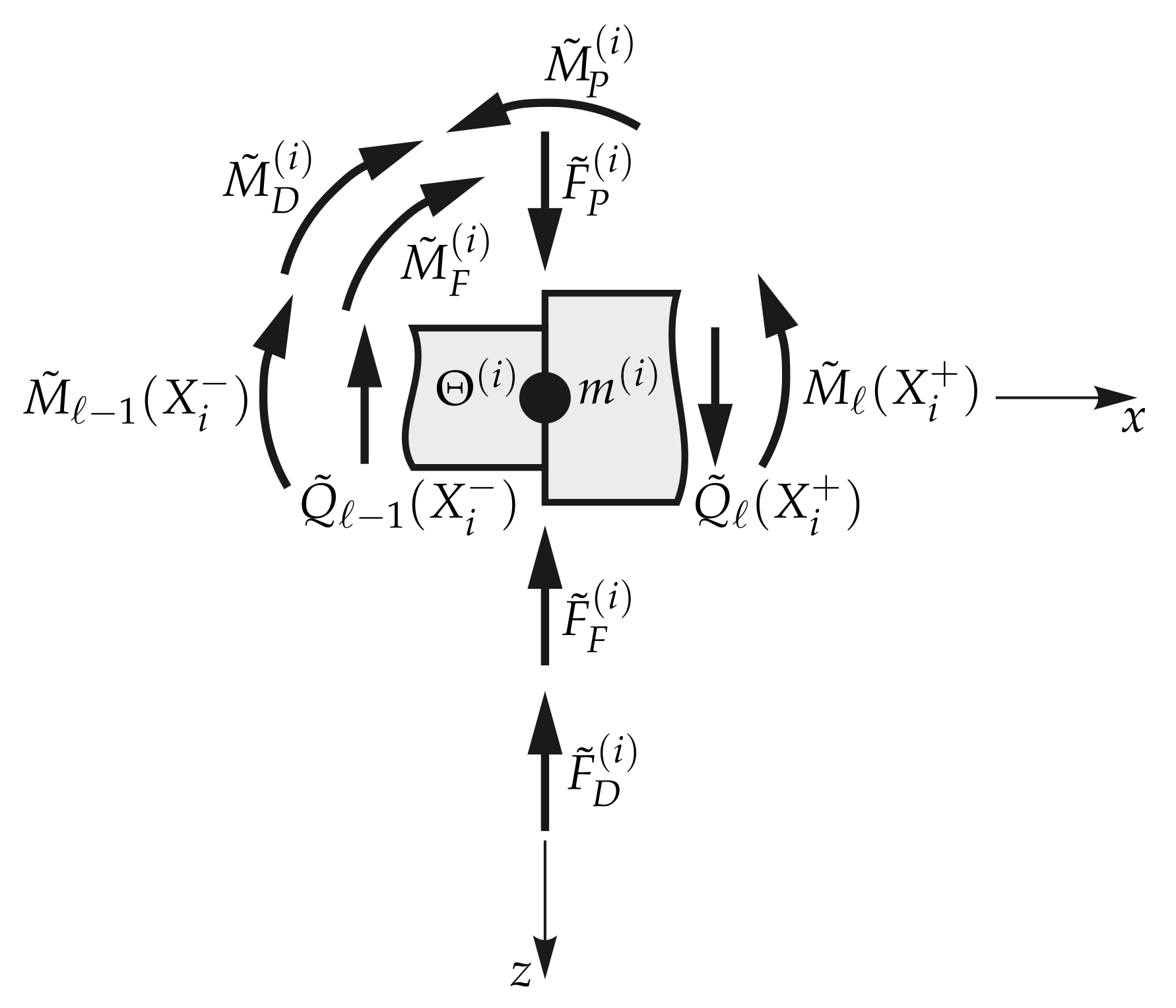
2.4. Boundary and Interface Conditions at the Stations
3. Numerical Assembly Technique
3.1. Homogeneous Solution of the Governing Equations
3.2. Particular Solutions of the Governing Equations
3.2.1. Fourier Transform, Residue Theorem, and Jordan’s Lemma
3.2.2. Concentrated Loads
Point Force
Point Moment
3.2.3. Generally Distributed Loads
Generally Distributed Force
Generally Distributed Moment
3.3. Assembly Procedure and Solution Process
4. Numerical and Experimental Validation Examples
4.1. Numerical Validation Example
4.2. Comparison with Measurement Data
4.2.1. Case 1: Steel Beam (Low Damping)
4.2.2. Case 2: PVC Beam (High Damping)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DSM | Dynamic Stiffness Method |
| FEM | Finite Element Method |
| FRF | Frequency Response Function |
| NAT | Numerical Assembly Technique |
| PVC | Polyvinyl chloride |
| TMM | Transfer Matrix Method |
Appendix A. Integrals
References
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of Transversely Vibrating Beams Using Four Engineering Theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Pirrotta, A.; Cutrona, S.; Di Lorenzo, S. Fractional visco-elastic Timoshenko beam from elastic Euler-Bernoulli beam. Acta Mech. 2015, 226, 179–189. [Google Scholar] [CrossRef]
- Rogers, L. Operators and Fractional Derivatives for Viscoelastic Constitutive Equations. J. Rheol. 1983, 27, 351–372. [Google Scholar] [CrossRef]
- Voigt, W. Ueber innere Reibung fester Körper, insbesondere der Metalle. Ann. Phys. 1892, 283, 671–693. [Google Scholar] [CrossRef]
- Maxwell, J.C. On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Zener, C.M. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 26, 6002–6020. [Google Scholar] [CrossRef]
- Rouleau, L.; Pirk, R.; Pluymers, B.; Desmet, W. Characterization and Modeling of the Viscoelastic Behavior of a Self-Adhesive Rubber Using Dynamic Mechanical Analysis Tests. J. Aerosp. Technol. Manag. 2015, 7, 200–208. [Google Scholar] [CrossRef]
- Pierro, E.; Carbone, G. A new technique for the characterization of viscoelastic materials: Theory, experiments and comparison with DMA. J. Sound Vib. 2021, 515, 116462. [Google Scholar] [CrossRef]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2020, 378, 20200050. [Google Scholar]
- Pritz, T. Analysis of four-parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Tai, Y.; Xu, X.; Shi, G.; Chen, N. Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int. J. Mech. Sci. 2020, 167, 105204. [Google Scholar] [CrossRef]
- Zheng-you, Z.; Gen-guo, L.; Chang-jun, C. Quasi-static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relation. Appl. Math. Mech. 2002, 23, 1–12. [Google Scholar] [CrossRef]
- Pirrotta, A.; Cutrona, S.; Di Lorenzo, S.; Di Matteo, A. Fractional visco-elastic Timoshenko beam deflection via single equation. Int. J. Numer. Methods Eng. 2015, 104, 869–886. [Google Scholar] [CrossRef]
- Usuki, T.; Suzuki, T. Dispersion curves for a viscoelastic Timoshenko beam with fractional derivatives. J. Sound Vib. 2012, 331, 605–621. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of Fractional Calculus for Dynamic Problems of Solid Mechanics: Novel Trends and Recent Results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Loghman, E.; Bakhtiari-Nejad, F.; Kamali, E.A.; Abbaszadeh, M.; Amabili, M. Nonlinear vibration of fractional viscoelastic micro-beams. Int. J. Non-Linear Mech. 2021, 137, 103811. [Google Scholar] [CrossRef]
- Faraji Oskouie, M.; Ansari, R.; Sadeghi, F. Nonlinear vibration analysis of fractional viscoelastic Euler-Bernoulli nanobeams based on the surface stress theory. Acta Mech. Solida Sin. 2017, 30, 416–424. [Google Scholar] [CrossRef]
- Suzuki, J.L.; Kharazmi, E.; Varghaei, P.; Naghibolhosseini, M.; Zayernouri, M. Anomalous Nonlinear Dynamics Behavior of Fractional Viscoelastic Beams. J. Comput. Nonlinear Dyn. 2021, 16, 111005. [Google Scholar] [CrossRef]
- Paunović, S.; Cajić, M.; Karličić, D.; Mijalković, M. A novel approach for vibration analysis of fractional viscoelastic beams with attached masses and base excitation. J. Sound Vib. 2019, 463, 114955. [Google Scholar] [CrossRef]
- Di Paola, M.; Scimemi, F.G. Finite element method on fractional visco-elastic frames. Comput. Struct. 2016, 164, 15–22. [Google Scholar] [CrossRef]
- Wu, J.S.; Chou, H.M. A new approach for determining the natural frequencies and mode shapes of a uniform beam carrying any number of sprung masses. J. Sound Vib. 1999, 220, 451–468. [Google Scholar] [CrossRef]
- Chen, D.W. An exact solution for free torsional vibration of a uniformcircular shaft carrying multiple concentrated elements. J. Sound Vib. 2006, 291, 627–643. [Google Scholar] [CrossRef]
- Yesilce, Y.; Demirdag, O. Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems. Int. J. Mech. Sci. 2008, 50, 995–1003. [Google Scholar] [CrossRef]
- Wu, J.S.; Chen, J.H. An efficient approach for determining forced vibration response amplitudes of a MDOF system with various attachments. Shock Vib. 2012, 19, 57–79. [Google Scholar] [CrossRef]
- Yesilce, Y. Free and forced vibrations of an axially-loaded Timoshenko multi-span beam carrying a number of various concentrated elements. Shock Vib. 2012, 19, 735–752. [Google Scholar] [CrossRef][Green Version]
- Klanner, M.; Ellermann, K. Steady-state linear harmonic vibrations of multiple-stepped Euler-Bernoulli beams under arbitrarily distributed loads carrying any number of concentrated elements. Appl. Comput. Mech. 2020, 14, 31–50. [Google Scholar] [CrossRef]
- Wu, J.S.; Lin, F.T.; Shaw, H.J. Analytical Solution for Whirling Speeds and Mode Shapes of a Distributed-Mass Shaft with Arbitrary Rigid Disks. J. Appl. Mech. 2014, 220, 451–468. [Google Scholar] [CrossRef]
- Klanner, M.; Prem, M.S.; Ellermann, K. Steady-state harmonic vibrations of a linear rotor-bearing system with a discontinuous shaft and arbitrary distributed mass unbalance. Proceedings of ISMA2020 International Conference on Noise and Vibration Engineering and USD2020 International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 7–9 September 2020; pp. 1257–1272. [Google Scholar]
- Klanner, M.; Prem, M.S.; Ellermann, K. Quasi-analytical solutions for the whirling motion of multi-stepped rotors with arbitrarily distributed mass unbalance running in anisotropic linear bearings. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e138999. [Google Scholar]
- Wu, J.S.; Chen, C.T. A continuous-mass TMM for free vibration analysis of a non-uniform beam with various boundary conditions and carrying multiple concentrated elements. J. Sound Vib. 2008, 311, 1420–1430. [Google Scholar] [CrossRef]
- Banerjee, J.R. Review of the dynamic stiffness method for free-vibration analysis of beams. Transp. Saf. Environ. 2019, 1, 106–116. [Google Scholar] [CrossRef]
- Huybrechs, D. On the Fourier Extension of Nonperiodic Functions. SIAM J. Numer. Anal. 2010, 47, 4326–4355. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Structural Analysis—With Applications to Aerospace Structures; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear Models of Dissipation in Anelastic Solids. Riv. Nuovo C. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Gaul, L.; Klein, P.; Kemple, S. Damping description involving fractional operators. Mech. Syst. Signal Process. 1991, 5, 81–88. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A Theoretical Basis for the Application of Fractional Calculus to Viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Hagedorn, P.; DasGupta, A. Vibrations and Waves in Continuous Mechanical Systems; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Mitrinović, D.; Kečkić, J.D. The Cauchy Method of Residues; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Hayek, S.I. Advanced Mathematical Methods in Science and Engineering; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Adcock, B.; Huybrechs, D.; Martín-Vaquero, J. On the Numerical Stability of Fourier Extensions. Found. Comput. Math. 2014, 14, 638–687. [Google Scholar] [CrossRef][Green Version]
- Matthysen, R.; Huybrechs, D. Fast Algorithms for the Computation of Fourier Extensions of Arbitrary Length. SIAM J. Sci. Comput. 2016, 38, A899–A922. [Google Scholar] [CrossRef]
- Lyon, M. A Fast Algorithm for Fourier Continuation. SIAM J. Sci. Comput. 2011, 33, 3241–3260. [Google Scholar] [CrossRef]
- Adcock, B.; Huybrechs, D. On the resolution power of Fourier extensions for oscillatory functions. J. Comput. Appl. Math. 2014, 260, 312–336. [Google Scholar] [CrossRef][Green Version]
- Weiß, M.; Lerch, R.; Rupitsch, S.J. Simulation-Based Material Characterization of Isotropic and Direction-Dependent Polymers for Use in Active Structure Assemblies. Adv. Eng. Mater. 2018, 20, 1800417. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Steinboeck, A.; Kugi, A.; Mang, H.A. Energy-consistent shear coefficients for beams with circular cross sectionsand radially inhomogeneous materials. Int. J. Solids Struct. 2013, 50, 1859–1868. [Google Scholar] [CrossRef]


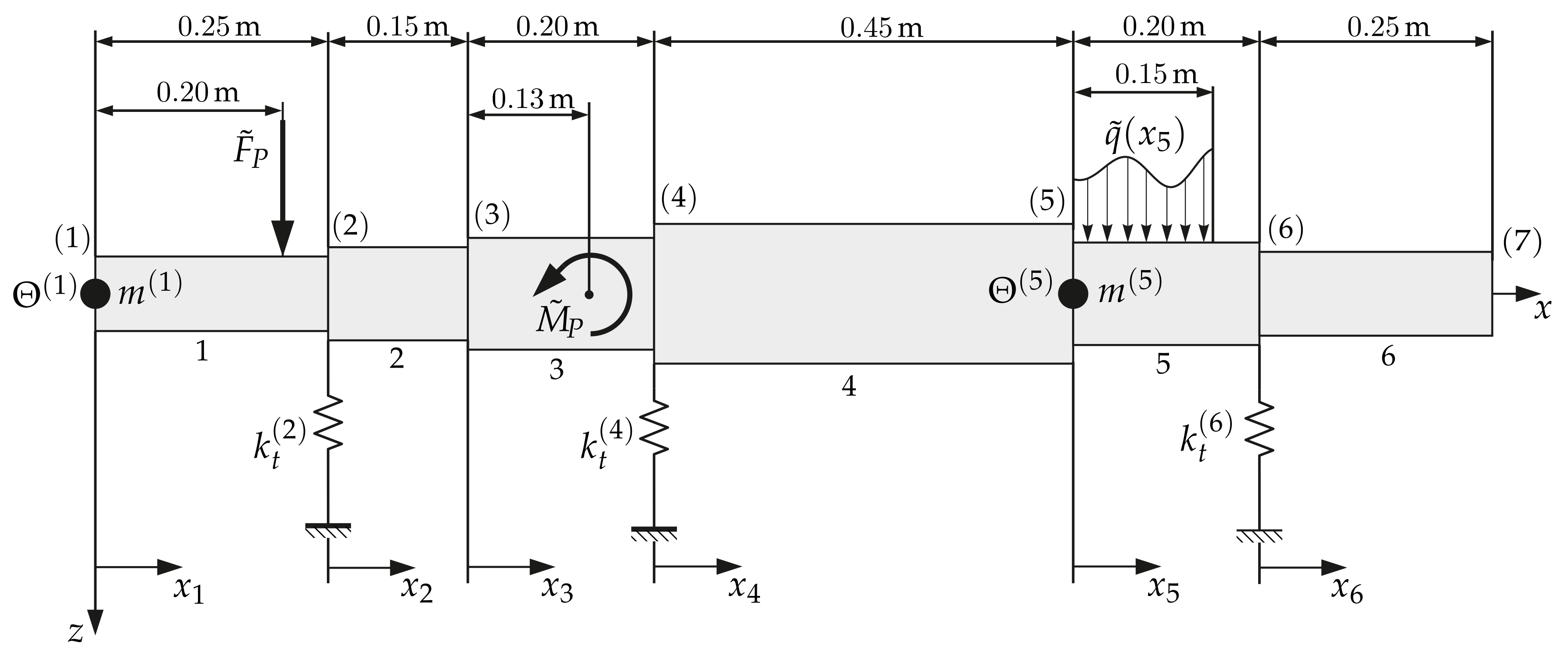
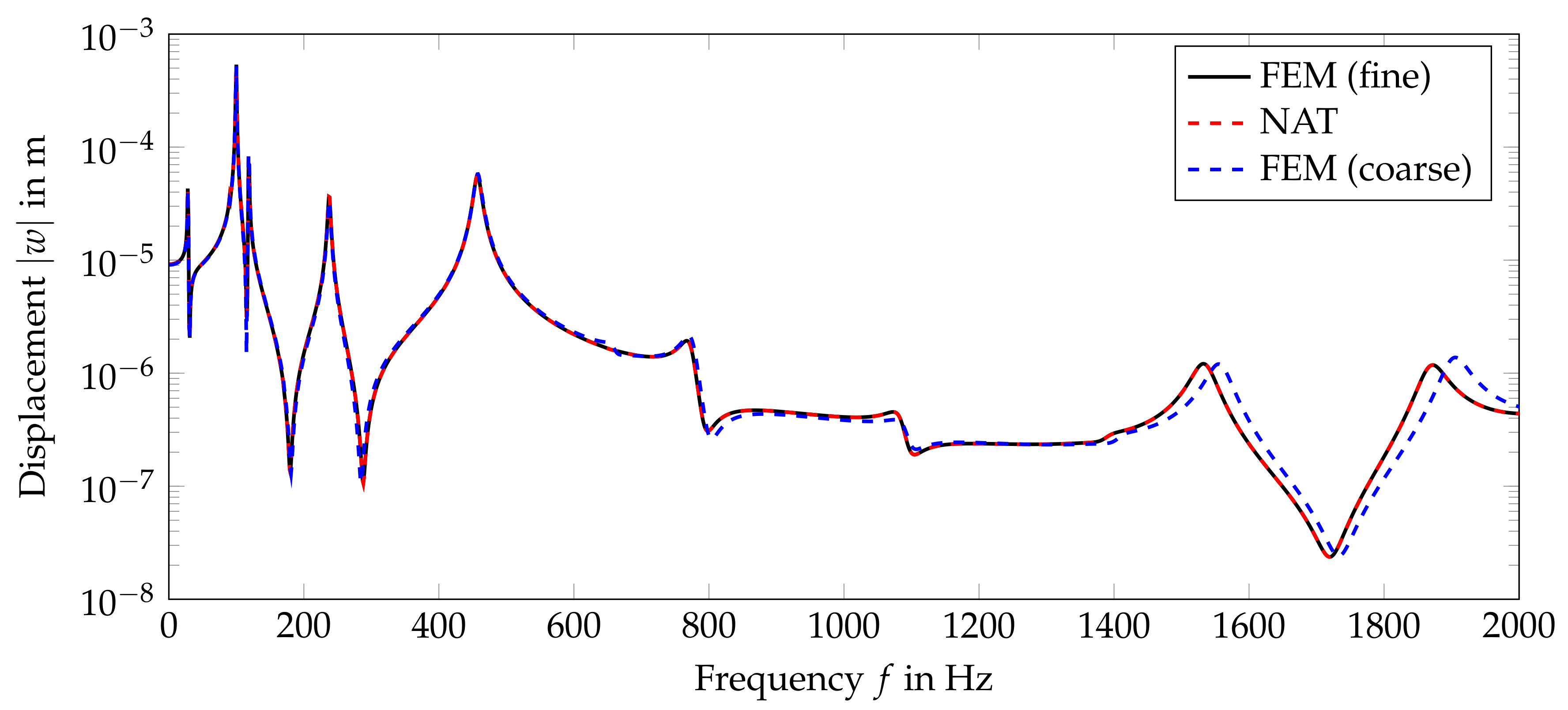
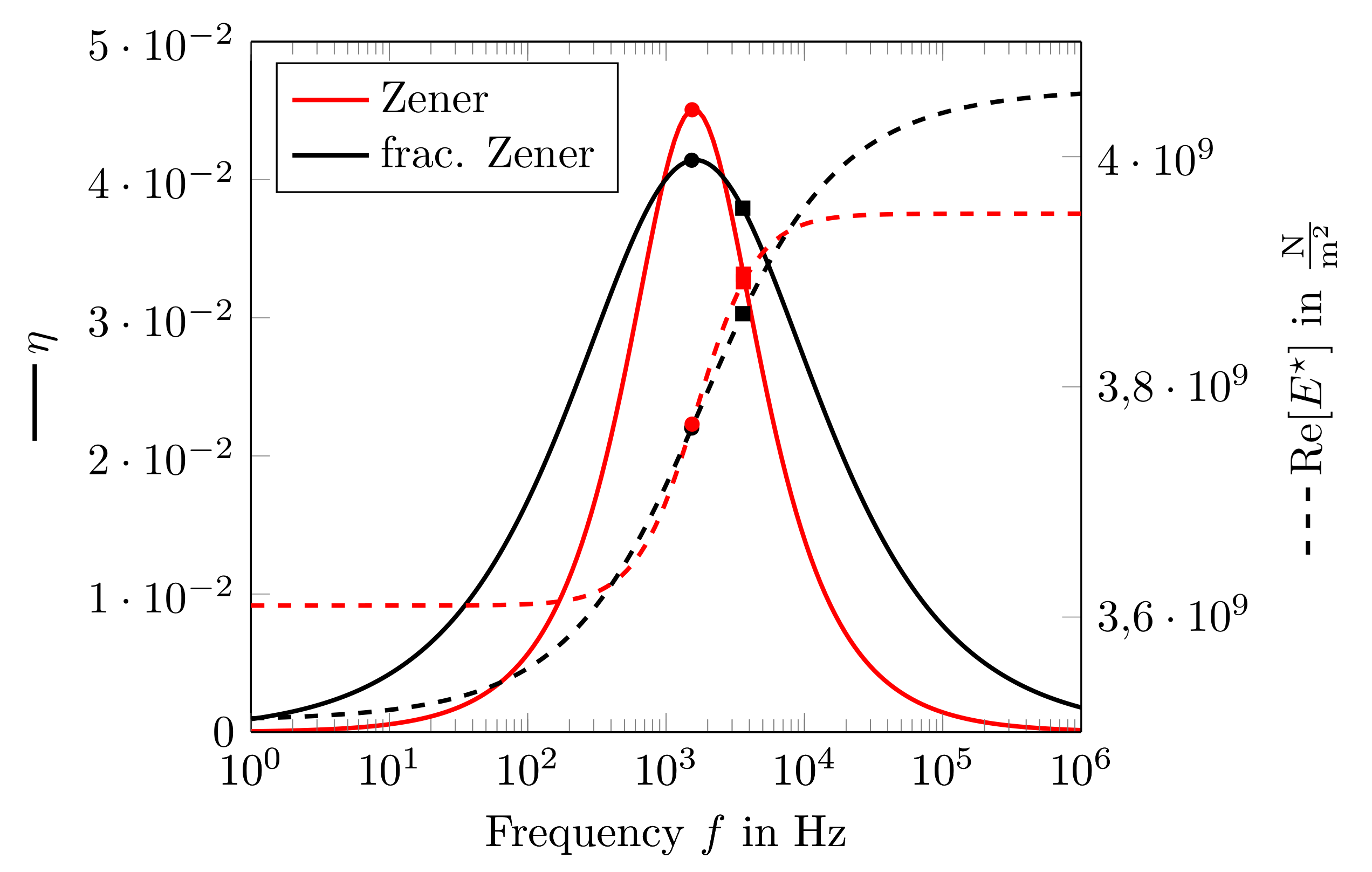
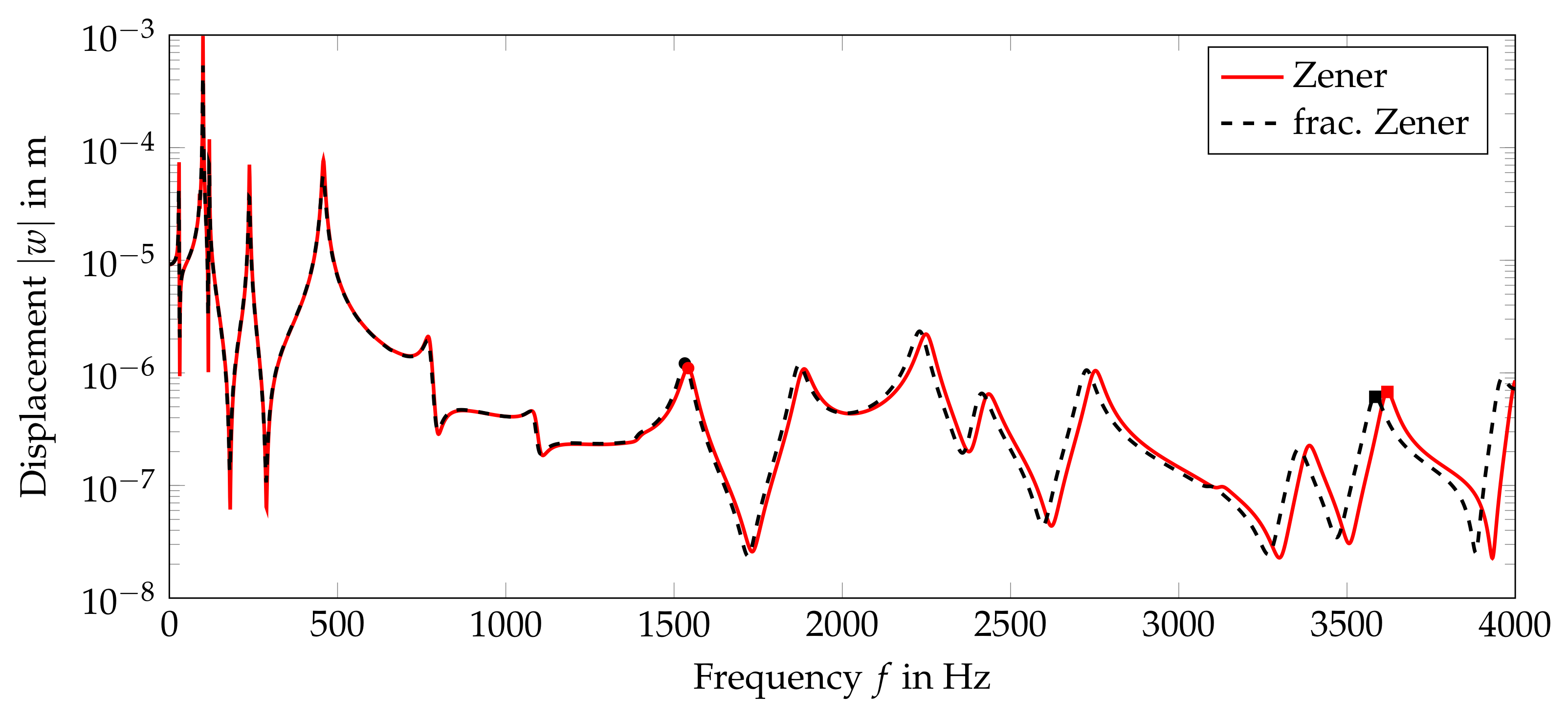

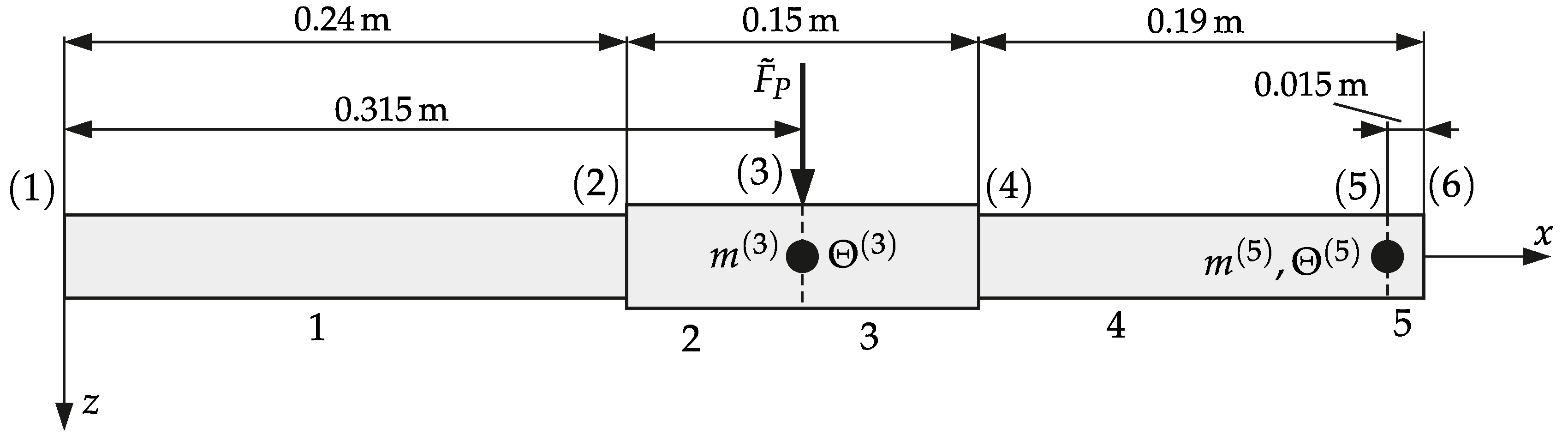


| Station | in | in | in | in |
|---|---|---|---|---|
| 1 | 0.00 | 2.5 | 0.6 | - |
| 2 | 0.25 | - | - | |
| 3 | 0.40 | - | - | - |
| 4 | 0.60 | - | - | |
| 5 | 1.05 | 1.5 | 1.5 | - |
| 6 | 1.25 | - | - | |
| 7 | 1.50 | - | - | - |
| Station | in | in | in |
|---|---|---|---|
| 1 | 0.000 | - | - |
| 2 | 0.240 | - | - |
| 3 | 0.315 | ||
| 4 | 0.390 | - | - |
| 5 | 0.565 | ||
| 6 | 0.580 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klanner, M.; Prem, M.S.; Ellermann, K. Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models. Appl. Mech. 2021, 2, 797-819. https://doi.org/10.3390/applmech2040046
Klanner M, Prem MS, Ellermann K. Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models. Applied Mechanics. 2021; 2(4):797-819. https://doi.org/10.3390/applmech2040046
Chicago/Turabian StyleKlanner, Michael, Marcel S. Prem, and Katrin Ellermann. 2021. "Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models" Applied Mechanics 2, no. 4: 797-819. https://doi.org/10.3390/applmech2040046
APA StyleKlanner, M., Prem, M. S., & Ellermann, K. (2021). Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models. Applied Mechanics, 2(4), 797-819. https://doi.org/10.3390/applmech2040046





