Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics
Abstract
:1. Introduction
2. Onset of Turbulence: Eddies and Vortices in Incompressible Fluids
2.1. Three-Dimensional Incompressible Navier–Stokes Equations
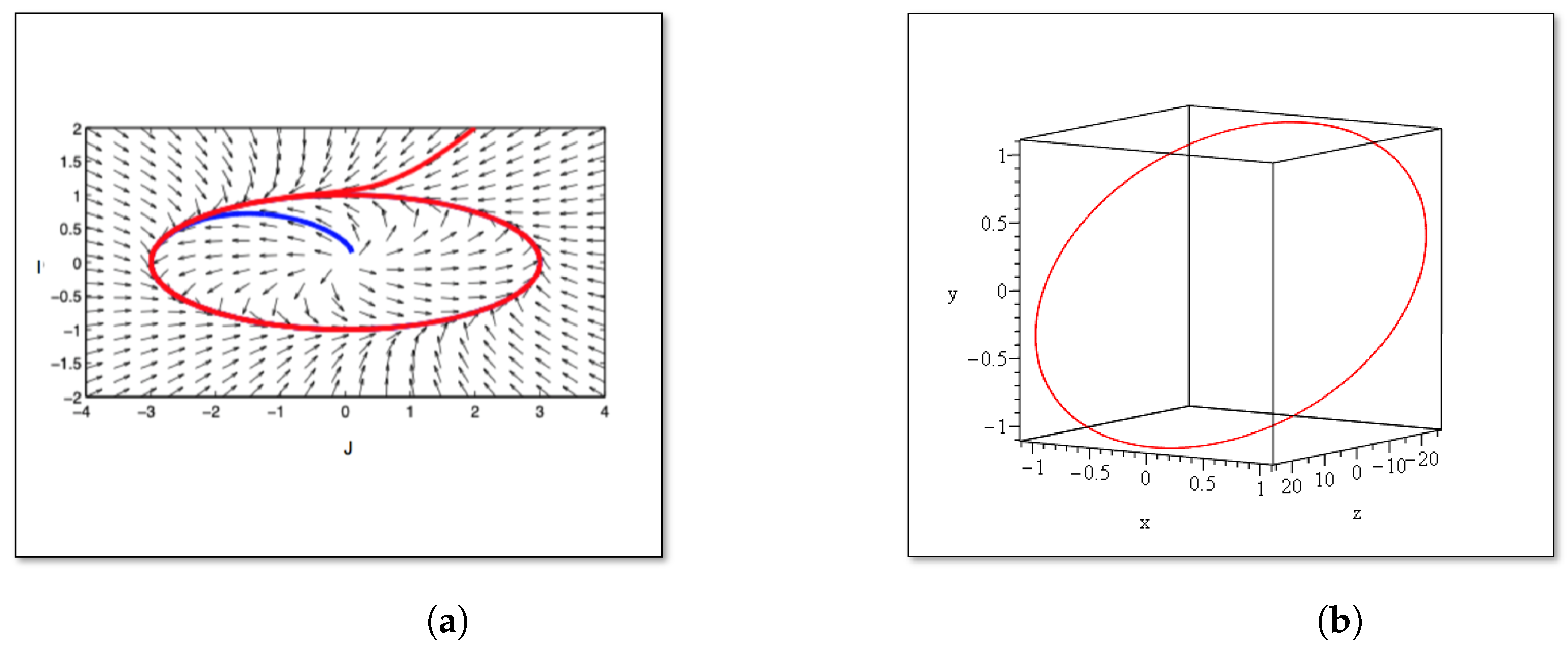
2.2. Decomposition of NSEs, Limit Cycles, and Vortices
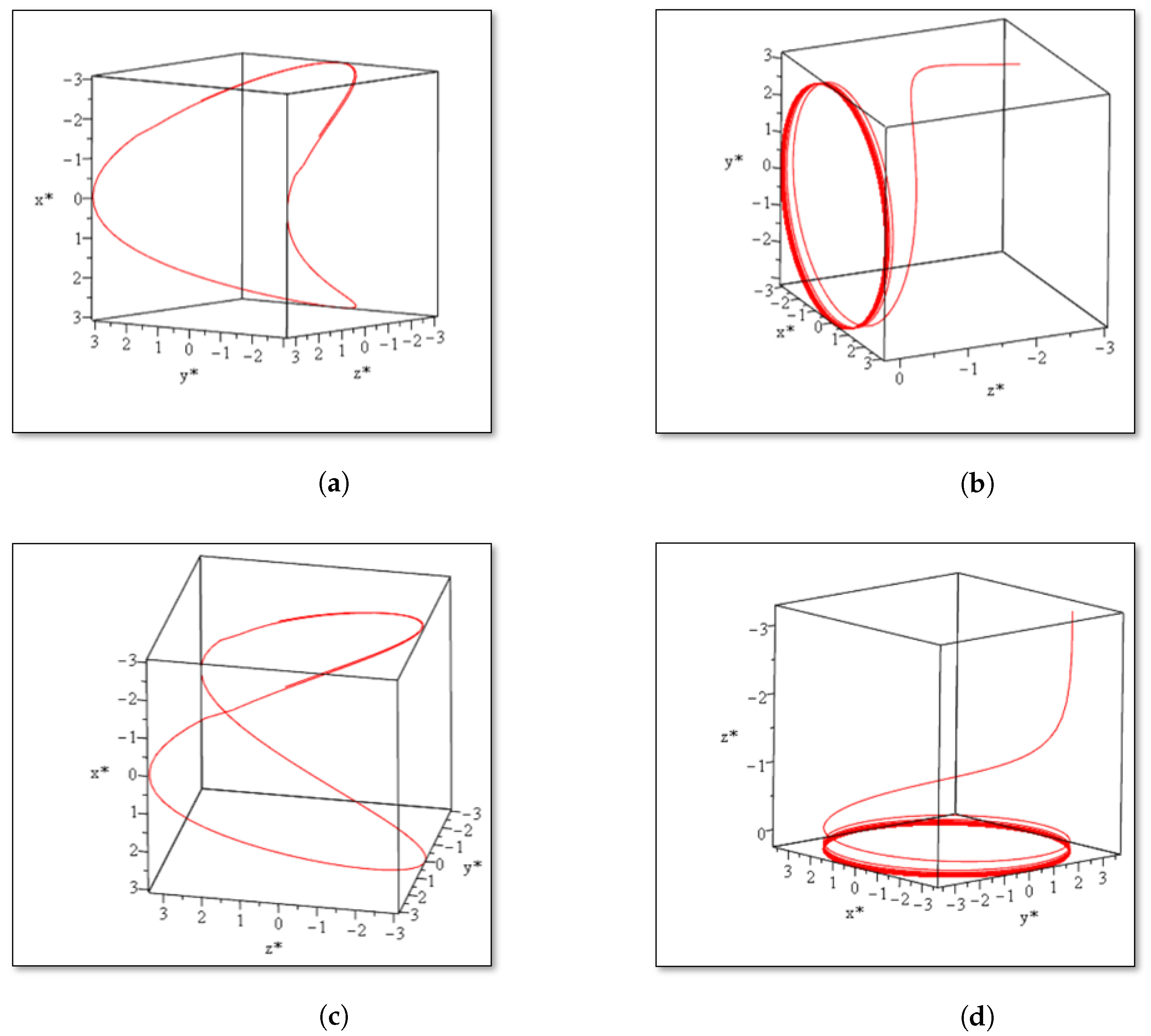
2.3. Convergence and Singularities of Incompressible Eddies and Vortices Along Edge of Cube Lattice
2.4. Norm Analysis of NSE Simplified System
3. Novel Variational Formulation of Cavitation Dynamics
3.1. Membrane Statistical Dynamics as a Variational Technique
3.2. Identifying a Lagrangian Density for the Raleigh–Plesset Equations
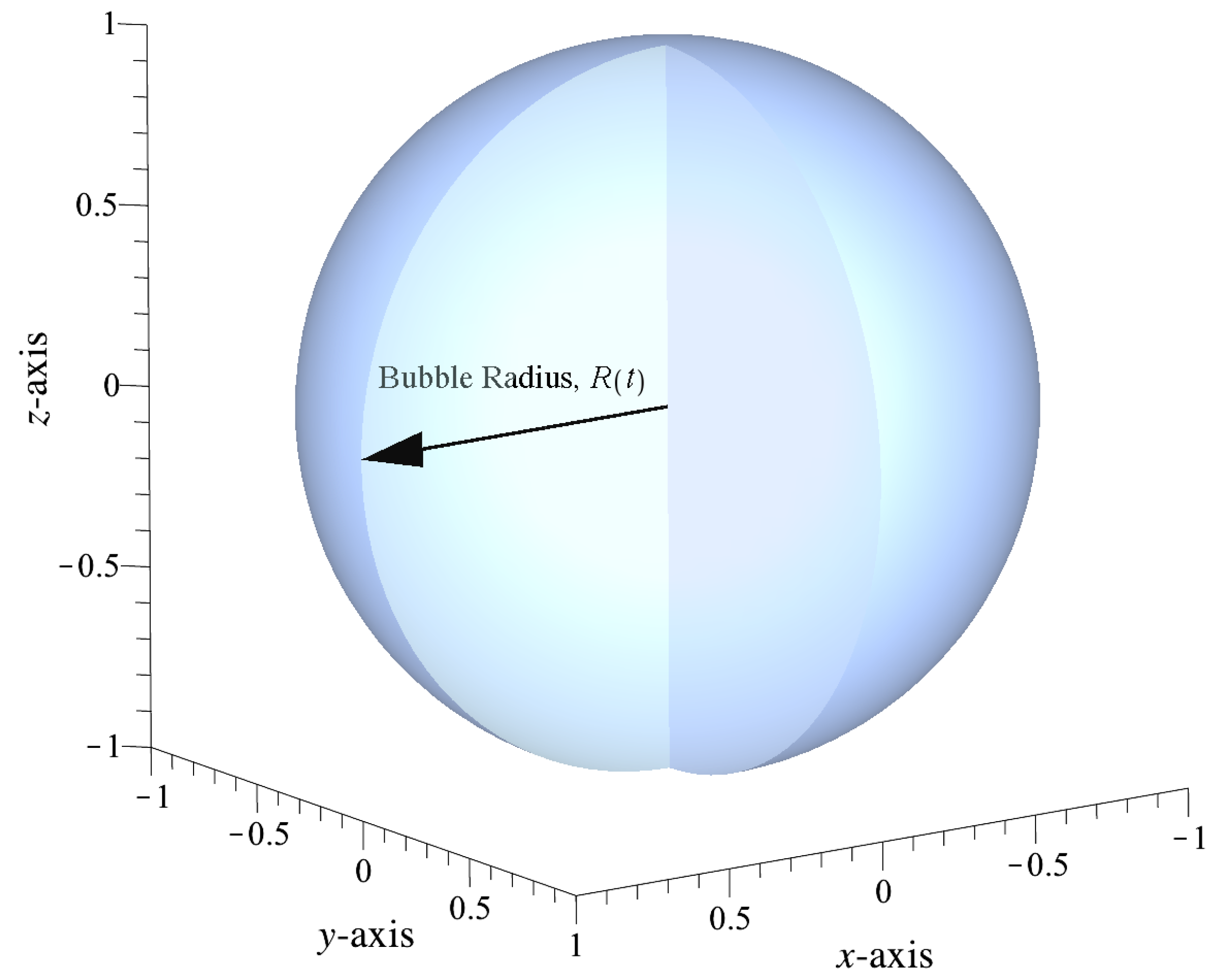
3.3. Spherical Decomposition of Lagrangian Density
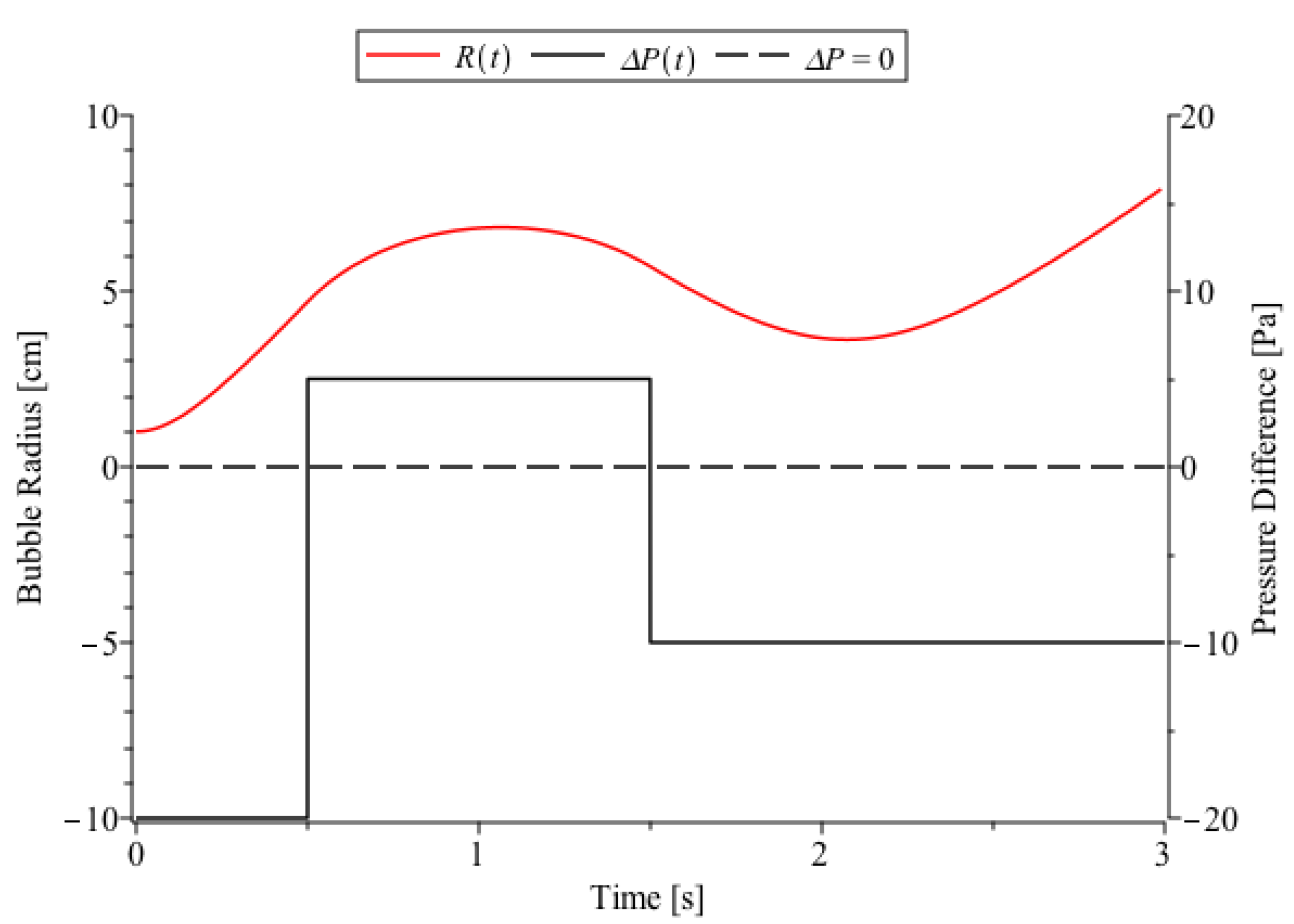
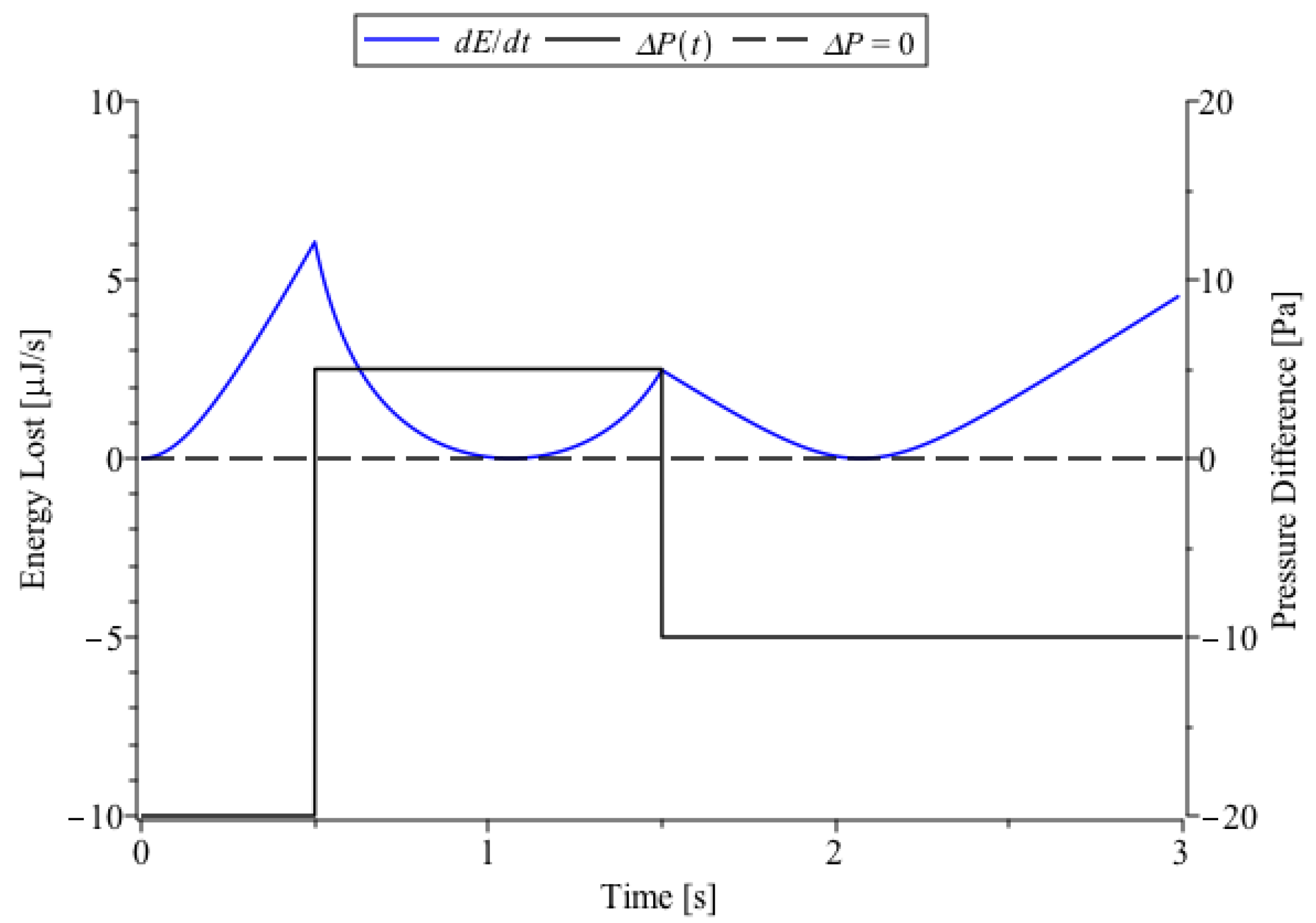
3.4. Accounting for Energy Dissipation in a Raleigh–Plesset Process
4. Conclusions: Incompressible Eddies/Vortices and Cavitation Dynamics
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NSE | Navier–Stokes Equation; |
| PDE | Partial Differential Equation; |
| STC | Spatio-Temporal Chaos; |
| ODE | Ordinary Differential Equation; |
| CMS | Calculus of Moving Surfaces; |
| BVP | Boundary Value Problem. |
Nomenclature
| 3-D Euclidean space | |
| Fluid volumentric density [kg/m] | |
| Cartesian basis vectors | |
| Fluid velocity field | |
| Body force field | |
| Dynamic viscosity | |
| Non-dimensional re-scaling parameter | |
| Pressure field | |
| Gradient and laplacian, respectively |
| Cavitation bubble radius [m] | |
| Surrounding liquid density [kg/m] | |
| Kinematic viscosity of surrounding liquid [m/s] | |
| Cavitation bubble surface tension | |
| Cavitation bubble pressure difference | |
| Lagrangian energy loss proportionality constant [1/s] | |
| Total cavitation bubble energy [J] |
| Embedding of a surface in | |
| Integral over a surface or boundary of a solid , . | |
| Action [J·s], of Lagrangian density [J/m] | |
| Surface tangent vectors, | |
| Metric tensor on surface , | |
| Normal on orientable surface | |
| Curvature tensor/shape operator on surface . | |
| Mean curvature, | |
| C | CMS-invariant normal surface speed [m/s] |
| CMS-invariant time derivative, | |
| Surface variational stress tensor |
Appendix A
References
- Fefferman, C.L. Existence and Smoothness of the Navier Stokes Equation, Millennium Prize Problems. Clay. Math. Inst. Camb. (MA) 2006, 57, 57–676. [Google Scholar]
- Moschandreou, T.E. No Finite Time Blowup for 3D Incompressible Navier Stokes Equations via Scaling Invariance. Math. Stat. 2021, 9, 386–393. [Google Scholar] [CrossRef]
- Moschandreou, T.E.; Afas, K.C. Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions. Mathematics 2019, 7, 1060. [Google Scholar] [CrossRef] [Green Version]
- Cross, M.C.; Hohenberg, P.C. Pattern Formation outside of Equilibrium. Rev. Mod. Phys. 1993, 65, 851–1111. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.C.; Shi, C.; Kosterlitz, J.M.; Zhu, X.; Ao, P.; Potential, G. Topology, and Pattern Selection in a Noisy Stabilized Kuramoto-Sivashinsky Equation. Proc. Natl. Acad. Sci. USA 2020, 117, 23227–23234. [Google Scholar] [CrossRef] [PubMed]
- Brunet, P. The Stabilized Kuramoto-Sivashinsky Equation: A Useful Model for Secondary Instabilities and Related Dynamics of Experimental One-Dimensional Cellular Flows. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 76, 017204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, J. Instability Analysis of Saddle Points by a Local Minimax Method. Math. Comput. (AMS) 2005, 74, 1–21. [Google Scholar] [CrossRef] [Green Version]
- He, K. Embedded Moving Saddle point and its relation to Turbulence in Fluids and Plasmas. Int. J. Mod. Phys. B 2004, 18, 1805–1843. [Google Scholar] [CrossRef]
- Tran, C.V.; Yu, X.; Dritschel, D.G. Velocity-pressure correlation in Navier-Stokes flows and the problem of global regularity. J. Fluid Mech. 2021, 911, A18-1–A18-18. [Google Scholar] [CrossRef]
- Chen, Z.-M.; Price, W.G. Time Dependent Periodic Navier-Stokes Flows on a two-Dimensional Torus. Commun. Math Phys. 1996, 179, 577–597. [Google Scholar] [CrossRef]
- Nelson, D.; Piran, T.; Weinberg, S. Statistical Mechanics of Membranes and Surfaces; World Scientific: Singapore, 2004; ISBN 978-981-4483-22-3. [Google Scholar]
- Finn, R. Capillary Surface Interfaces. Not. AMS 1999, 46, 770–781. [Google Scholar]
- Kudryashov, N.A.; Sinelshchikov, D.I. Analytical solutions of the Rayleigh equation for empty and gas-filled bubble. J. Phys. A Math. Theor. 2014, 47, 405202. [Google Scholar] [CrossRef] [Green Version]
- Pedergnana, T.; Oettinger, D.; Langlois, G.P.; Haller, G. Explicit unsteady Navier-Stokes solutions and their analysis via local vortex criteria. Phys. Fluids 2020, 32, 046603. [Google Scholar] [CrossRef] [Green Version]
- Alzer, H.; Ruscheweyh, S. The Arithmetic Mean—Geometric Mean Inequality for Complex Numbers. Analysis 2002, 22, 277–283. [Google Scholar] [CrossRef]
- Kahan, W. Notes for Math H110. Available online: https://people.eecs.berkeley.edu/~wkahan/MathH110/NORMlite.pdf (accessed on 26 June 2021).
- Duff, G.F.D. Navier Stokes Derivative Estimates in Three Dimensions with Boundary Values and Body Forces. Can. J. Math. 1991, 43, 1161–1212. [Google Scholar] [CrossRef]
- Grinfeld, P. Introduction to Tensor Analysis and the Calculus of Moving Surfaces; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7867-6. [Google Scholar]
- Atland, A.; Simons, B. Condensed Matter Field Theory; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-511-78928-1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschandreou, T.E.; Afas, K.C. Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics. Appl. Mech. 2021, 2, 613-629. https://doi.org/10.3390/applmech2030035
Moschandreou TE, Afas KC. Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics. Applied Mechanics. 2021; 2(3):613-629. https://doi.org/10.3390/applmech2030035
Chicago/Turabian StyleMoschandreou, Terry Eleftherios, and Keith Christian Afas. 2021. "Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics" Applied Mechanics 2, no. 3: 613-629. https://doi.org/10.3390/applmech2030035
APA StyleMoschandreou, T. E., & Afas, K. C. (2021). Existence of Incompressible Vortex-Class Phenomena and Variational Formulation of Raleigh–Plesset Cavitation Dynamics. Applied Mechanics, 2(3), 613-629. https://doi.org/10.3390/applmech2030035




