Modified Polynomial Chaos Expansion for Efficient Uncertainty Quantification in Biological Systems
Abstract
1. Introduction
2. Background and Methodology
2.1. Polynomial Chaos Expansion (PCE) for UQ
2.2. Modified gDRM-Based PCE for UQ
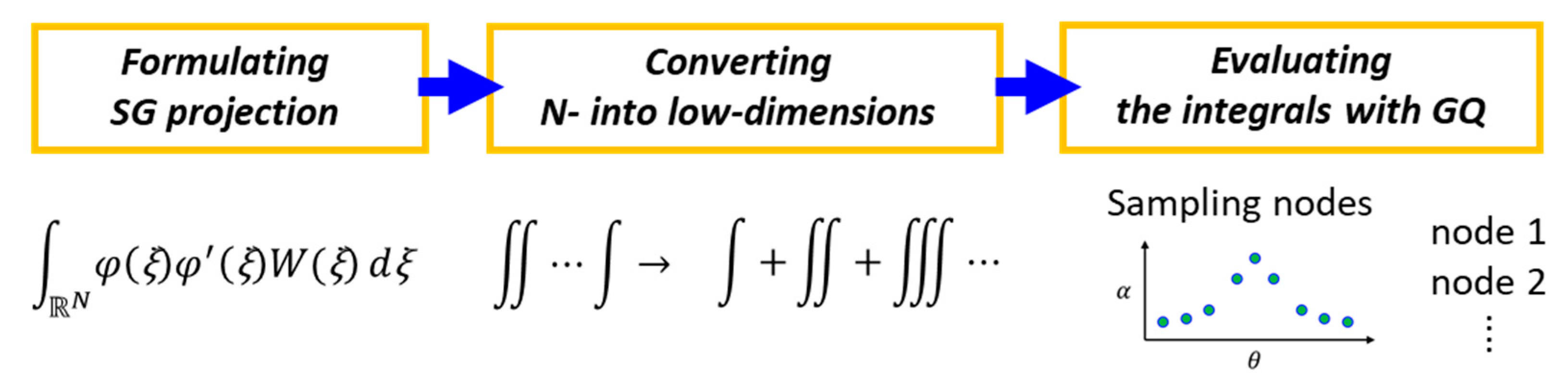
2.2.1. Dimension Reduction Based Stochastic Galerkin Projection
2.2.2. Modified gDRM-Based PCE Sing the Dimension Reduction and Quadrature Rules
2.2.3. Modified gDRM-Based PCE Using the Dimension Reduction and Quadrature Rules
2.3. Sampling-Based Nonintrusive Discrete Projection (NIDP)
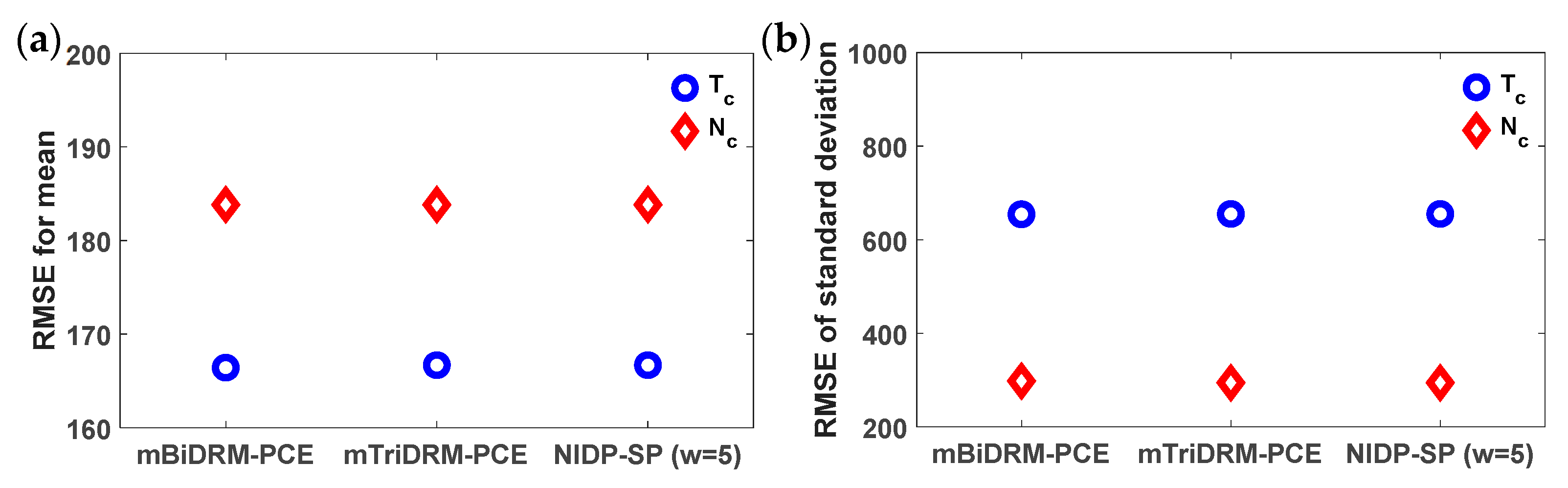
2.4. Root-Mean-Square Error (RMSE) to Evaluate UQ Accuracy
3. Numerical Examples
3.1. Example 1: Nonlinear Algebraic Problems
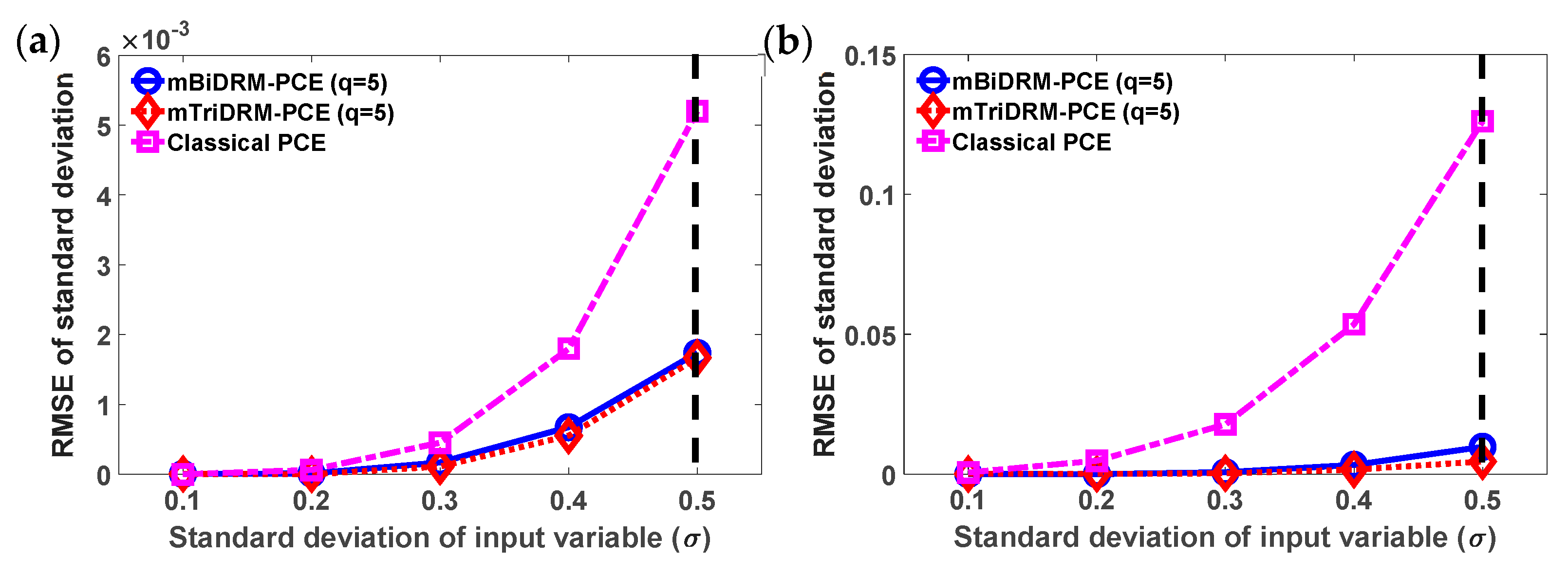
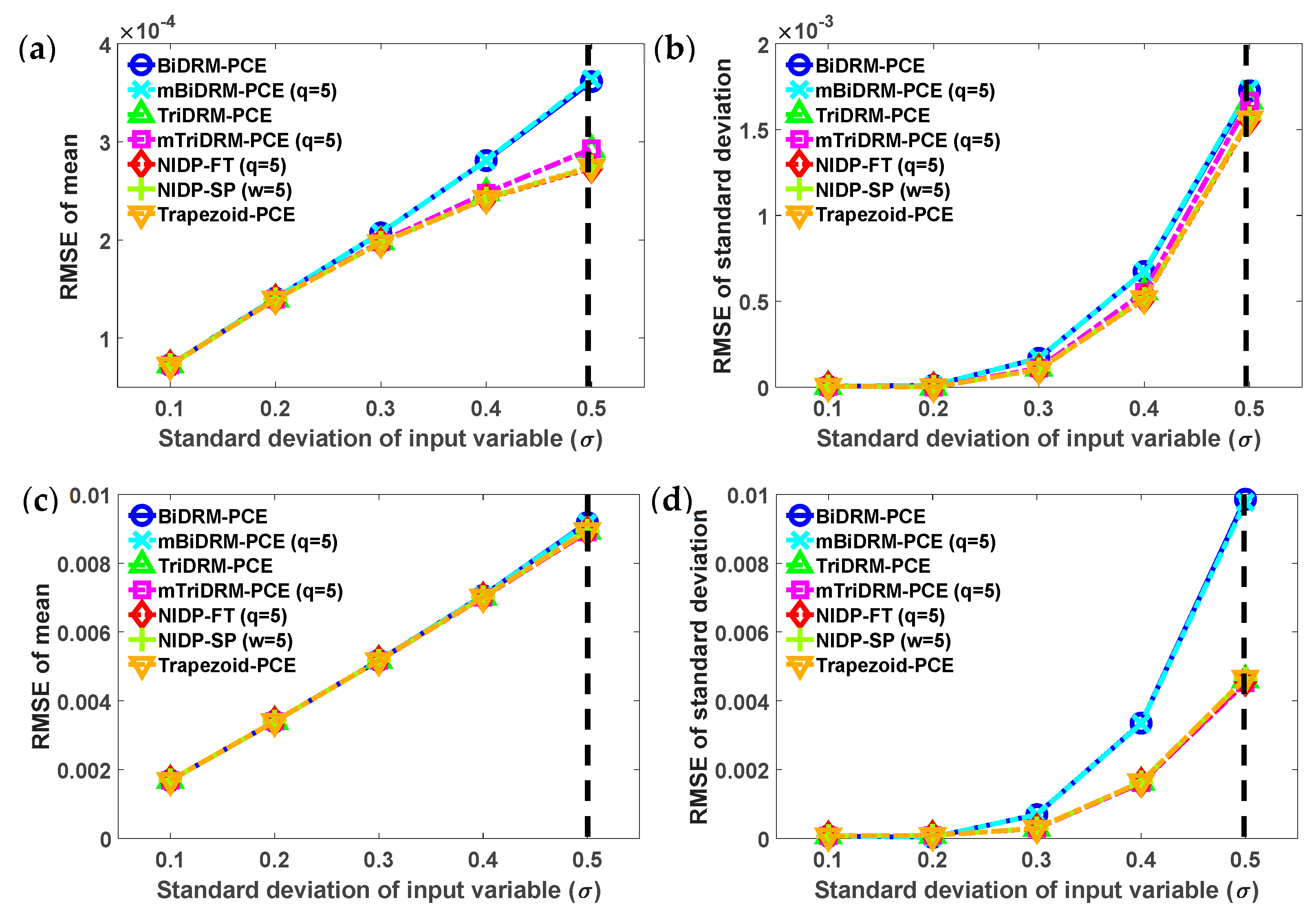
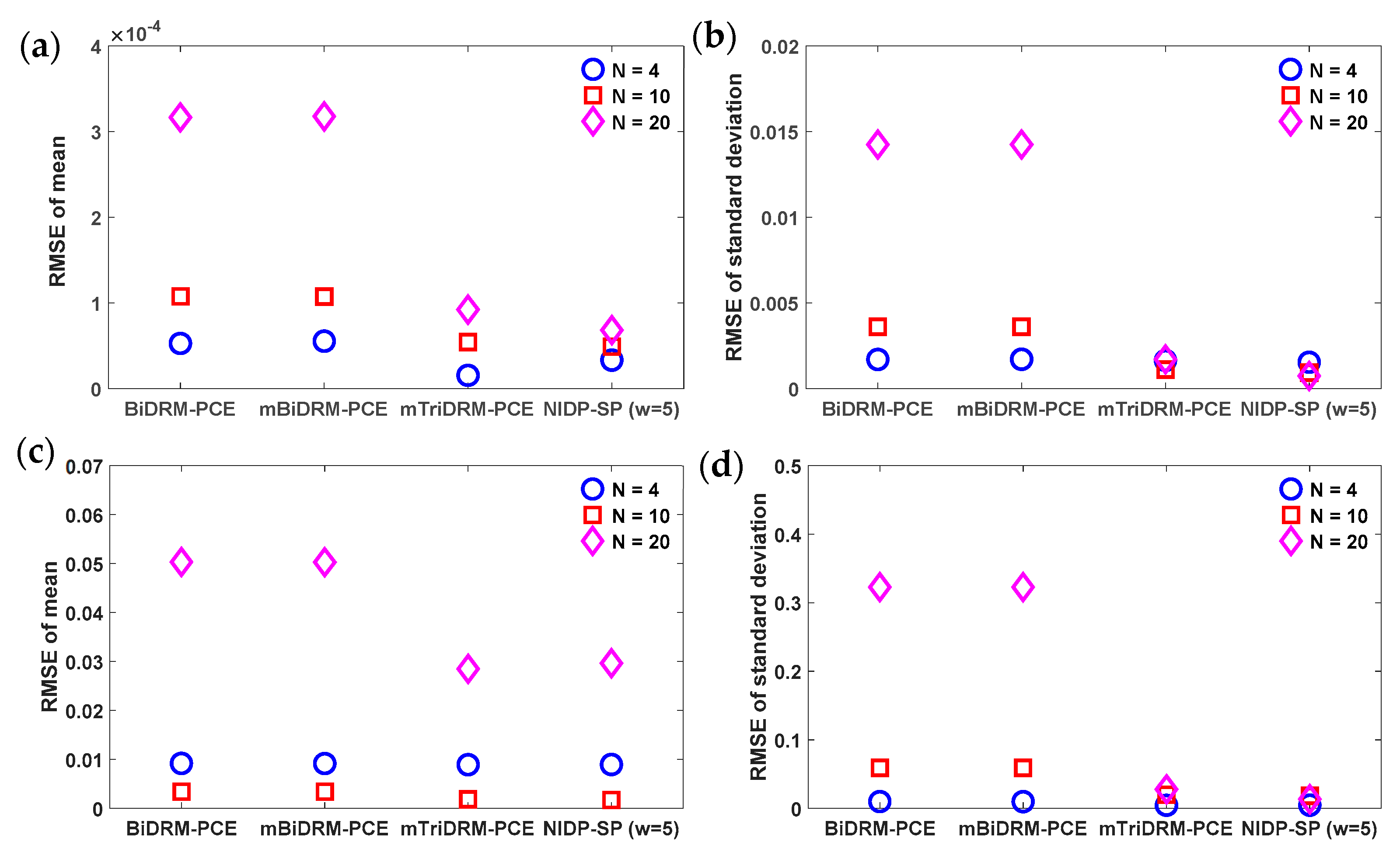
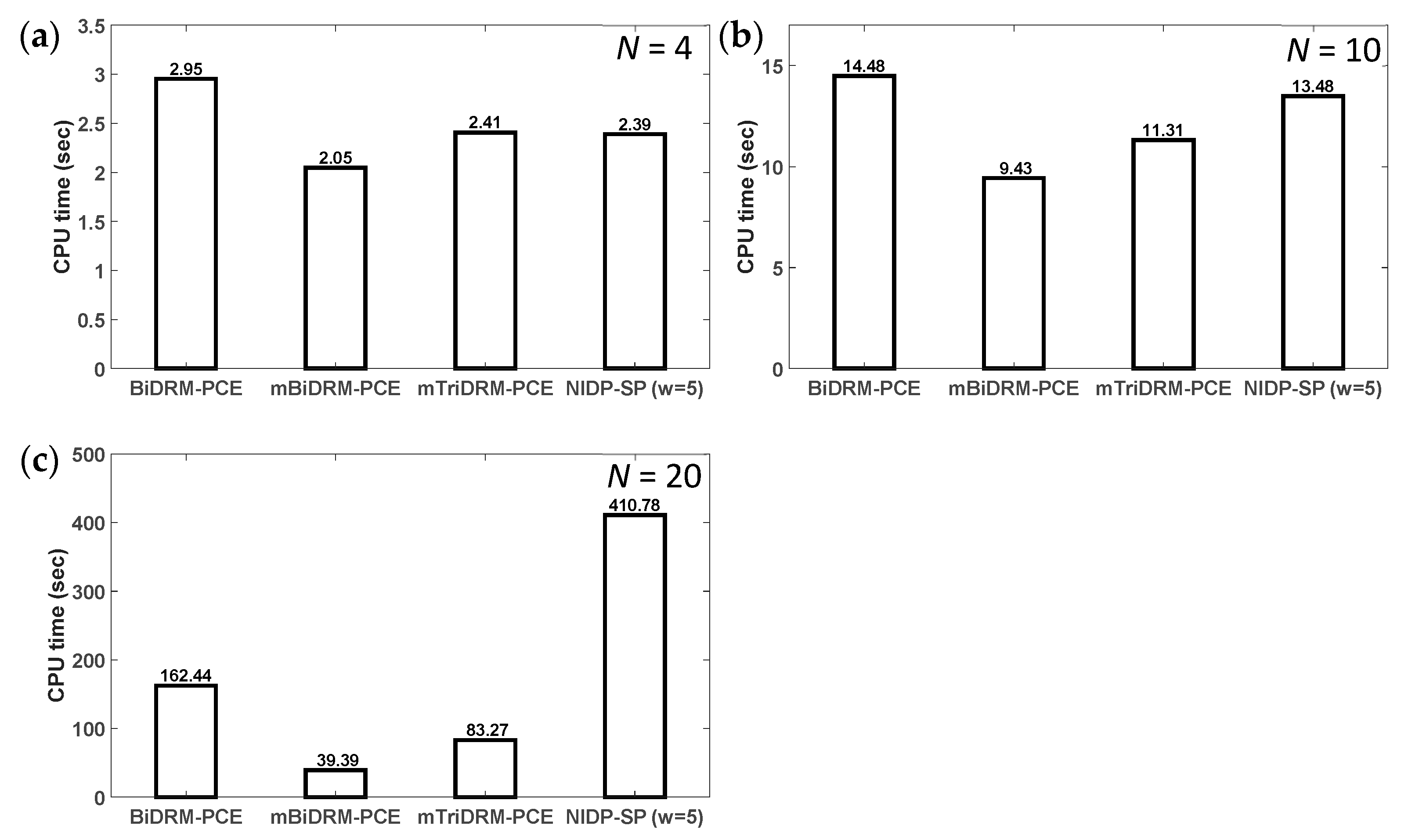
3.2. Example 2: Conjoint Tumor-Normal Cell Models
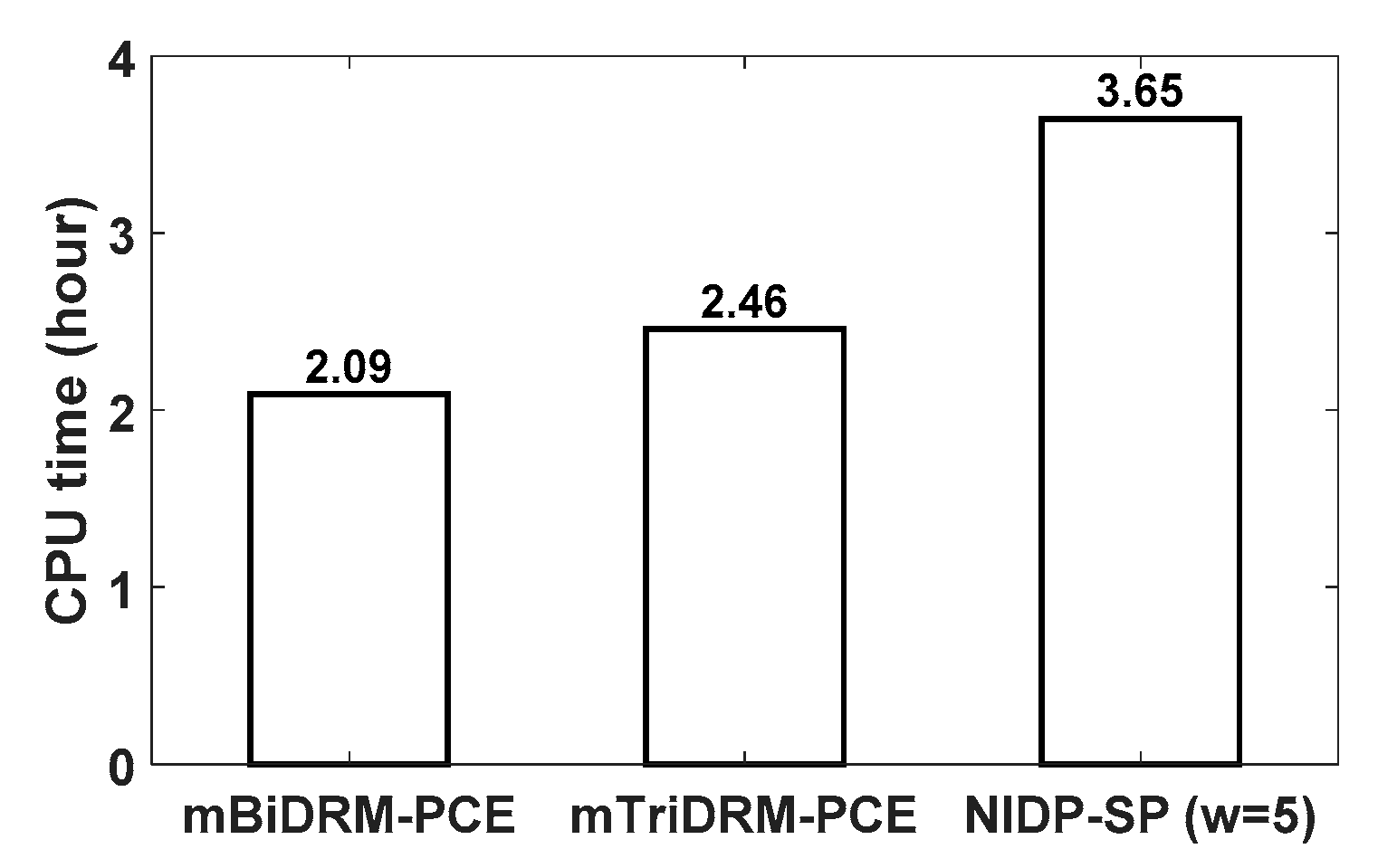
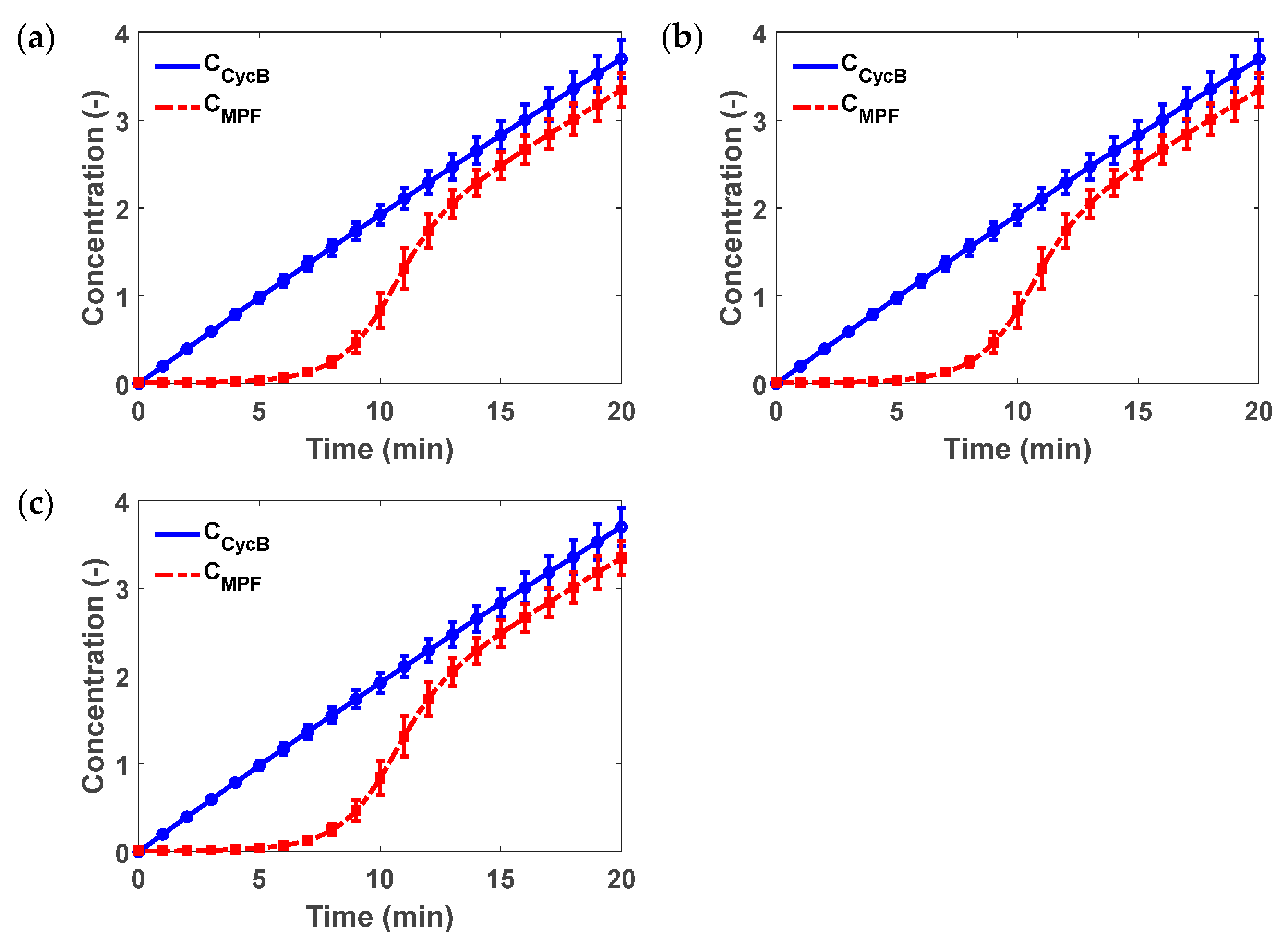
3.3. Example 3: G2 to Mitosis Transition Model for Fission Yeast
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BiDRM | Bivariate dimension reduction method |
| FT | Full tensor grids method used for NIDP-based UQ |
| gDRM | Generalized dimension reduction method |
| GQ | Gaussian quadrature |
| MC | Monte Carlo |
| NIDP | Nonintrusive discrete projection |
| PCE | Polynomial chaos expansion |
| Probability density function | |
| RMSE | Root-mean-square error |
| SC | Stochastic collocation |
| SG | Stochastic Galerkin |
| SP | Sparse grids method used for NIDP-based UQ |
| TriDRM | Trivariate dimension reduction method |
| UQ | Uncertainty quantification |
Appendix A
Appendix B
References
- Champagne, C.; Cazelles, B. Comparison of stochastic and deterministic frameworks in dengue modelling. Math. Biosci. 2019, 310, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Harman, D.B.; Johnston, P.R. Applying the stochastic Galerkin method to epidemic models with uncertainty in the parameters. Math. Biosci. 2016, 277, 25–37. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, T.J. Introduction to Uncertainty Quantification; Springer: Berlin, Germany, 2015. [Google Scholar]
- Marquis, A.D.; Arnold, A.; Dean-Bernhoft, C.; Carlson, B.E.; Olufsen, M.S. Practical identifiability and uncertainty quantification of a pulsatile cardiovascular model. Math. Biosci. 2018, 304, 9–24. [Google Scholar] [CrossRef] [PubMed]
- Vanlier, J.; Tiemann, C.; Hilbers, P.; Van Riel, N.A.W. Parameter uncertainty in biochemical models described by ordinary differential equations. Math. Biosci. 2013, 246, 305–314. [Google Scholar] [CrossRef]
- Gel, A.; Garg, R.; Tong, C.; Shahnam, M.; Guenther, C. Applying uncertainty quantification to multiphase flow computational fluid dynamics. Powder Technol. 2013, 242, 27–39. [Google Scholar] [CrossRef]
- Ma, D.L.; Braatz, R.D. Robust identification and control of batch processes. Comput. Chem. Eng. 2003, 27, 1175–1184. [Google Scholar] [CrossRef]
- Schenkendorf, R.; Xie, X.; Krewer, U. An efficient polynomial chaos expansion strategy for active fault identification of chemical processes. Comput. Chem. Eng. 2019, 122, 228–237. [Google Scholar] [CrossRef]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Wiener, N. The Homogeneous Chaos. Am. J. Math. 1938, 60, 897. [Google Scholar] [CrossRef]
- Streif, S.; Kim, K.-K.K.; Rumschinski, P.; Kishida, M.; Shen, D.E.; Findeisen, R.; Braatz, R.D. Robustness analysis, prediction, and estimation for uncertain biochemical networks: An overview. J. Process. Control. 2016, 42, 14–34. [Google Scholar] [CrossRef]
- Debusschere, B.J.; Najm, H.; Matta, A.; Knio, O.M.; Ghanem, R.; Le Maître, O.P. Protein labeling reactions in electrochemical microchannel flow: Numerical simulation and uncertainty propagation. Phys. Fluids 2003, 15, 2238. [Google Scholar] [CrossRef][Green Version]
- Du, Y.; Budman, H.; Duever, T. Parameter Estimation for an Inverse Nonlinear Stochastic Problem: Reactivity Ratio Studies in Copolymerization. Macromol. Theory Simul. 2017, 26, 1600095. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty Quantification and Polynomial Chaos Techniques in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Knio, O.M.; Le Maître, O. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Debusschere, B.J.; Najm, H.N.; Pébay, P.P.; Knio, O.M.; Ghanem, R.; Le Maître, O.P. Numerical Challenges in the Use of Polynomial Chaos Representations for Stochastic Processes. SIAM J. Sci. Comput. 2004, 26, 698–719. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput. Methods Appl. Mech. Eng. 2002, 191, 4927–4948. [Google Scholar] [CrossRef]
- Babuška, I.; Tempone, R.; Zouraris, G.E. Galerkin Finite Element Approximations of Stochastic Elliptic Partial Differential Equations. SIAM J. Numer. Anal. 2004, 42, 800–825. [Google Scholar] [CrossRef]
- Son, J.; Du, Y. Probabilistic surrogate models for uncertainty analysis: Dimension reduction-based polynomial chaos expansion. Int. J. Numer. Methods Eng. 2019, 121, 1198–1217. [Google Scholar] [CrossRef]
- Son, J.; Du, Y. Comparison of intrusive and nonintrusive polynomial chaos expansion-based approaches for high dimensional parametric uncertainty quantification and propagation. Comput. Chem. Eng. 2020, 134, 106685. [Google Scholar] [CrossRef]
- Xu, H.; Rahman, S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics. Int. J. Numer. Methods Eng. 2004, 61, 1992–2019. [Google Scholar] [CrossRef]
- McClarren, R.G. Gauss Quadrature and Multi-dimensional Integrals. In Computational Nuclear Engineering and Radiological Science Using Python; McClarren, R.G., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 287–299. [Google Scholar]
- Cao, Y.; Chen, Z.; Gunzburger, M. ANOVA expansions and efficient sampling methods for parameter dependent nonlinear PDEs. Int. J. Numer. Anal. Mod. 2009, 6, 256–273. [Google Scholar]
- Eldred, M.; Burkardt, J. Comparison of Non-Intrusive Polynomial Chaos and Stochastic Collocation Methods for Uncertainty Quantification. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Smolyak, S.A. Quadrature and interpolation formulas for tensor products of certain classes of functions. Sov. Math. Dokl. 1963, 4, 240–243. [Google Scholar]
- Judd, K.L.; Maliar, L.; Maliar, S.; Valero, R. Smolyak method for solving dynamic economic models: Lagrange interpolation, anisotropic grid and adaptive domain. J. Econ. Dyn. Control. 2014, 44, 92–123. [Google Scholar] [CrossRef]
- Xiu, D. Efficient collocational approach for parametric uncertainty analysis. Commun. Comput. Phys. 2007, 2, 293–309. [Google Scholar]
- Ganapathysubramanian, B.; Zabaras, N. Sparse grid collocation schemes for stochastic natural convection problems. J. Comput. Phys. 2007, 225, 652–685. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Kim, C.; Lee, Y.; Lee, W.B. Robust Design of Multicomponent Working Fluid for Organic Rankine Cycle. Ind. Eng. Chem. Res. 2019, 58, 4154–4167. [Google Scholar] [CrossRef]
- Feizabadi, M.S. Modeling the Effects of a Simple Immune System and Immunodeficiency on the Dynamics of Conjointly Growing Tumor and Normal Cells. Int. J. Boil. Sci. 2011, 7, 700–707. [Google Scholar] [CrossRef]
- Cheng, T.M.K.; Goehring, L.; Jeffery, L.; Lu, Y.-E.; Hayles, J.; Novak, B.; A Bates, P. A Structural Systems Biology Approach for Quantifying the Systemic Consequences of Missense Mutations in Proteins. PLoS Comput. Boil. 2012, 8, e1002738. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener--Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Reagan, M.T.; Najm, H.N.; Ghanem, R.; Knio, O.M. Uncertainty quantification in reacting-flow simulations through non-intrusive spectral projection. Combust. Flame 2003, 132, 545–555. [Google Scholar] [CrossRef]
- Venkateshan, S.; Swaminathan, P. Computational Methods in Engineering; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Jao, C. Efficient Decision Support Systems: Practice and Challenges from Current to Future; IntechOpen: London, UK, 2011. [Google Scholar]
- Hill, J.M.; Moore, R. Applied Mathematics Entering the 21st Century: Invited Talks from the ICIAM 2003 Congress; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2004. [Google Scholar]
- Griffiths, D.F.; Higham, D.J. Numerical Methods for Ordinary Differential Equations; Springer Science and Business Media: Berlin, Germany, 2010. [Google Scholar]
- Xu, J.; Dang, C. A new bivariate dimension reduction method for efficient structural reliability analysis. Mech. Syst. Signal Process. 2019, 115, 281–300. [Google Scholar] [CrossRef]

| Parameters | Description of Model Parameters | Values | Units |
|---|---|---|---|
| The growth rate for the tumor cells | 0.3 | Time−1 | |
| Carrying capacity of tumor cells | Cells | ||
| The growth rate for the normal cells | 0.4 | Time−1 | |
| Carrying capacity of normal cells | Cells | ||
| Normal-tumor cell interaction rate | 1 | Time−1 | |
| Interaction clearance term | 1 | Cells | |
| Half-saturation for interaction | 1000 | Cells | |
| Tumor-normal cell interaction rate | 0.014 | Time−1 | |
| Critical size of the tumor | Cells |
| Parameters | Description of Model Parameters | Values | Units |
|---|---|---|---|
| Rate constant of CycB synthesis | 0.2 | min−1 | |
| Degradation rates of CycB and MPF | 0.008 | min−1 | |
| Rate constant of Wee1 being activated by a phosphatase | 0.61 | min−1 | |
| Rate constant of Wee1 being inactivated by MPF | 0.71 | min−1 | |
| Rate of Cdc25 being activated by MPF | 0.80 | min−1 | |
| Rate of Cdc25 being inactivated by a phosphatase | 0.35 | min−1 | |
| Turnover coefficient for the activation rate of MPF, | 0.008 | min−1 | |
| Turnover coefficient for the activation rate of MPF, | 0.89 | min−1 | |
| Turnover coefficient for the inactivation rate of MPF, | 0.03 | min−1 | |
| Turnover coefficient for the inactivation rate of MPF, | 0.18 | min−1 | |
| Michaelis constant of MPF for Cdc25 | 0.90 | - | |
| Michaelis constant of MPF for Wee1 | 0.21 | - | |
| Michaelis constant of phosphatase for Cdc25 | 0.19 | - | |
| Michaelis constant of phosphatase for Wee1 | 0.93 | - |
| UQ Methods | RSMEMEAN | RSMESTD | CPU Time (Hour) | ||
|---|---|---|---|---|---|
| mTriDRM-PCE | 0.000155 | 0.000217 | 2.04 × 10−5 | 3.80 × 10−5 | 7.30 |
| NIDP-SP (w = 5) | 0.000278 | 0.000338 | 3.37 × 10−5 | 0.000218 | 11.86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, J.; Du, D.; Du, Y. Modified Polynomial Chaos Expansion for Efficient Uncertainty Quantification in Biological Systems. Appl. Mech. 2020, 1, 153-173. https://doi.org/10.3390/applmech1030011
Son J, Du D, Du Y. Modified Polynomial Chaos Expansion for Efficient Uncertainty Quantification in Biological Systems. Applied Mechanics. 2020; 1(3):153-173. https://doi.org/10.3390/applmech1030011
Chicago/Turabian StyleSon, Jeongeun, Dongping Du, and Yuncheng Du. 2020. "Modified Polynomial Chaos Expansion for Efficient Uncertainty Quantification in Biological Systems" Applied Mechanics 1, no. 3: 153-173. https://doi.org/10.3390/applmech1030011
APA StyleSon, J., Du, D., & Du, Y. (2020). Modified Polynomial Chaos Expansion for Efficient Uncertainty Quantification in Biological Systems. Applied Mechanics, 1(3), 153-173. https://doi.org/10.3390/applmech1030011





