Advances and Optimization Trends in Photovoltaic Systems: A Systematic Review
Abstract
1. Introduction
- A structured taxonomy and critical comparison of traditional optimization techniques, including analytical models, linear programming, dynamic programming, and gradient-based methods emphasizing their applicability, strengths, and limitations across PV system design and control stages.
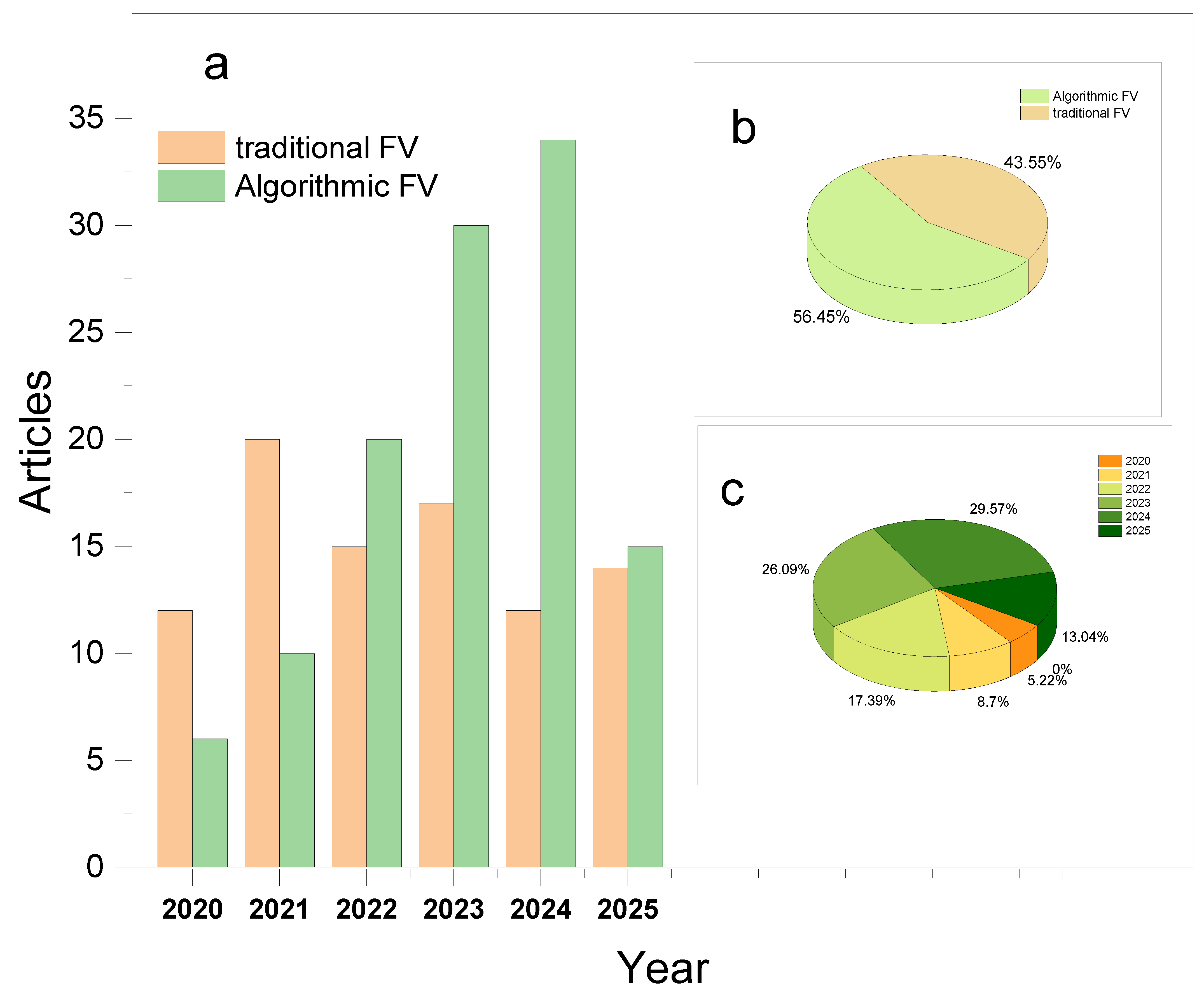
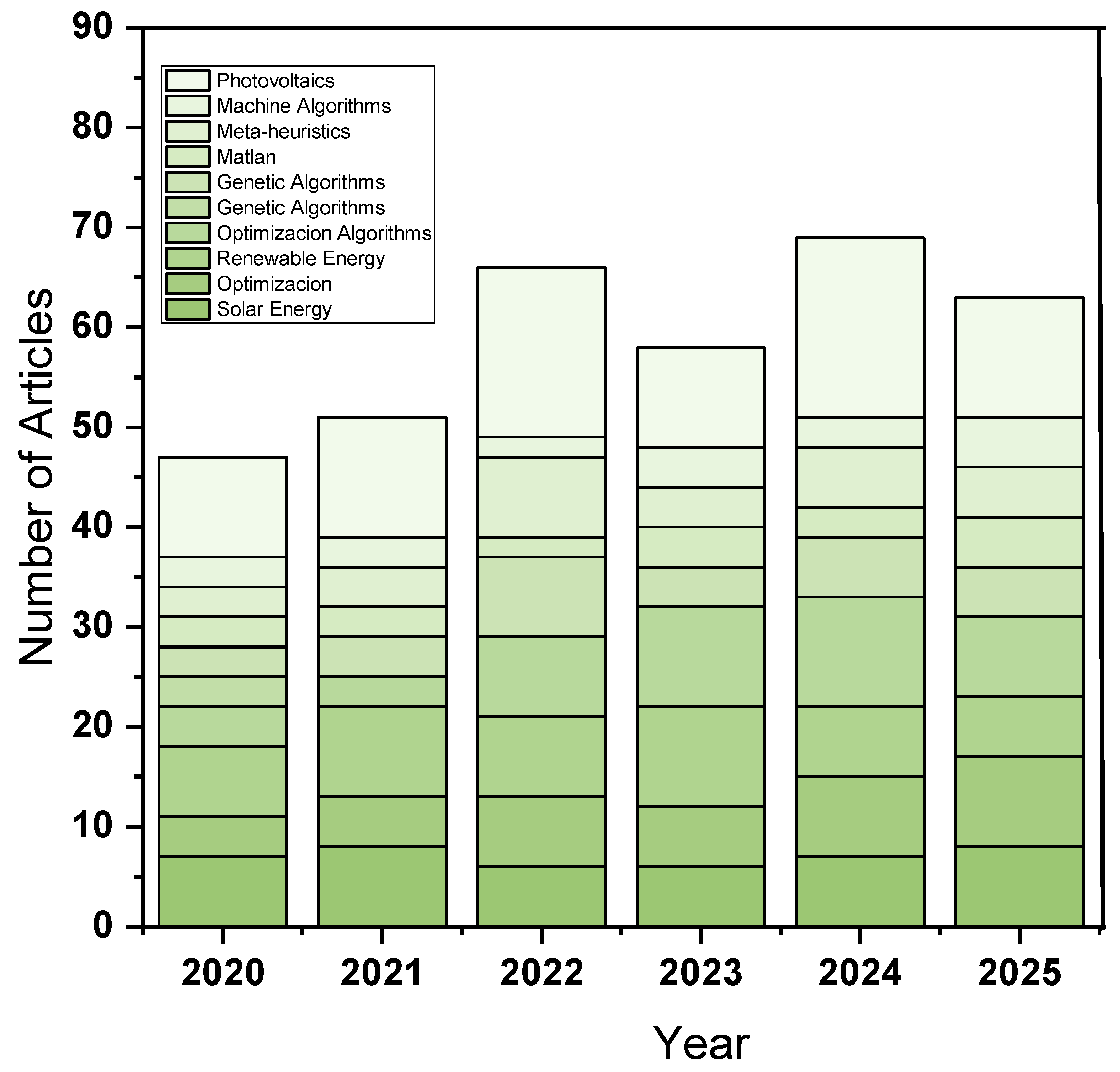
- The application of the Preferred Reporting Items for Systematic Reviews and Meta-Analyses guidelines (PRISMA)-compliant systematic review methodology, enabling the identification, filtration, and synthesis of 314 high-quality studies relevant to PV optimization, with a strong emphasis on structural, operational, and topological improvements.
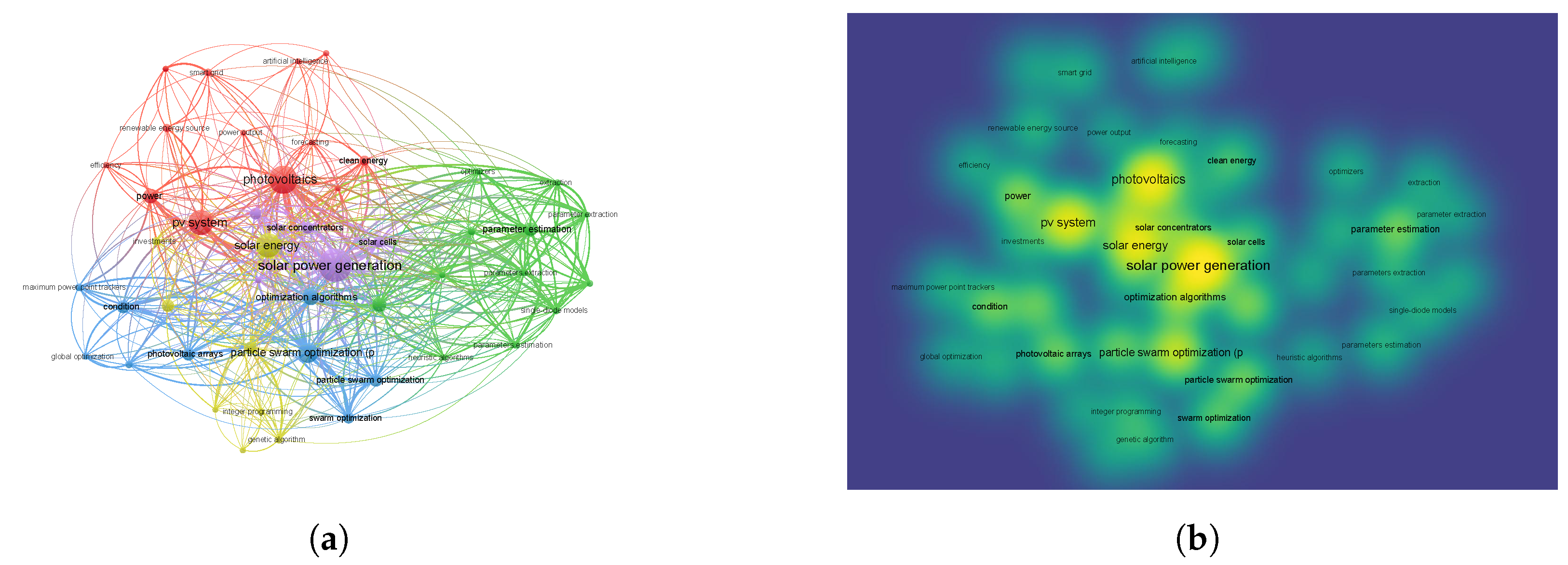
- The integration of bibliometric analysis using VOSviewer 1.6.20 and a multicriteria evaluation framework to highlight key research trends, knowledge clusters, and emerging areas in PV modeling and optimization strategies.
- A detailed examination of metaheuristic and machine learning techniques, including hybrid models applied to MPPT enhancement, PV layout optimization, energy forecasting, fault detection, and real-time energy management, demonstrating their superiority over conventional approaches.
- The formulation of a future research agenda that identifies current limitations such as data quality, model interpretability, and computational cost, proposing the adoption of explainable artificial intelligence (XAI), lightweight algorithms, and edge-computing solutions to enhance practical implementation in intelligent PV systems.
2. Materials and Methods
2.1. Photovoltaic Solar System
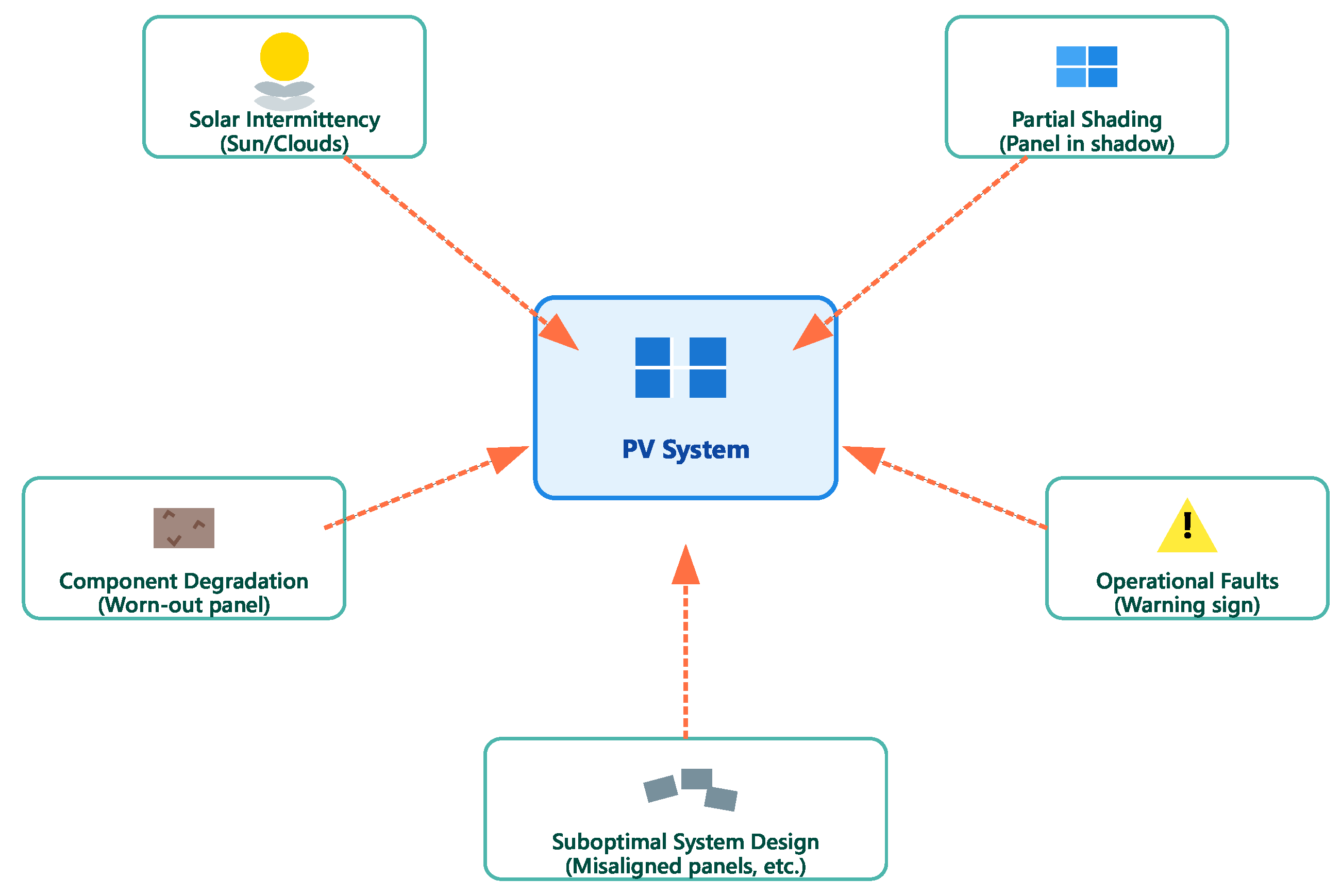
Need for Optimization in PV Systems
- Ensuring that systems capture and convert the maximum possible solar energy by optimizing orientation, tilt angles, and spacing of panels.
- Minimizing energy losses due to resistive wiring, shading, mismatch effects, and thermal inefficiencies.
- Selecting appropriate sizes for PV arrays, inverters, and storage units based on load profiles and solar availability.
- Implementing intelligent algorithms for power flow management, load prioritization, and battery scheduling.
- Increasing overall cost-effectiveness through lifecycle-based financial and technical optimization.
- Module level enhancements: Using high-efficiency solar cells, anti-reflective coatings, and bifacial modules to capture more sunlight.
- System-level improvements: Implementing MPPT algorithms, reducing shading effects through layout optimization, and using tracking systems.
- Energy management: Integrating smart controllers and forecasting tools to align energy production with load demands.
- Hybridization and storage integration: Combining PV with other renewable sources (e.g., wind and biomass) and advanced battery systems to enhance reliability.
2.2. Mathematical Models to Analyze and Optimize Photovoltaic Systems
2.3. Single-Diode Model for PV Modules
- I is the output current of the solar cell (A);
- is the photogenerated current (A);
- is the reverse saturation current of the diode (A);
- q is the elementary charge (C);
- V is the voltage across the cell (V);
- is the series resistance ();
- n is the diode ideality factor;
- k is the Boltzmann constant (J/K);
- T is the temperature (K);
- is the shunt resistance ().
2.4. Two-Diode Model for PV Modules
- I is the output current of the solar cell (A);
- is the photogenerated current (A);
- are the reverse saturation currents of the two diodes (A);
- q is the elementary charge (C);
- V is the voltage across the cell (V);
- is the series resistance ();
- are the ideality factors of the diodes;
- k is the Boltzmann constant (J/K);
- T is the temperature (K);
- is the shunt resistance ().
2.5. Inverter Efficiency Model
- is the inverter efficiency (dimensionless);
- is the maximum inverter efficiency (dimensionless);
- is the DC input power (W);
- is the rated power of the inverter (W);
- is the efficiency adjustment coefficient (dimensionless).
2.6. Battery-Equivalent Circuit Model (Thevenin)
- is the battery voltage (V);
- is the battery open-circuit voltage (V);
- I is the battery charge/discharge current (A);
- is the battery internal resistance ();
- is the voltage across the RC network (V);
- R is the resistance of the RC network ();
- C is the capacitance of the RC network (F);
- t is the time (s).
2.7. MPPT Algorithm: Perturb and Observe (P&O)
- is the power change (W);
- is the power measured at time step k (W);
- is the power measured at time step k-1 (W);
- is the voltage at time step k (V);
- is the voltage change (V).
- If , increase ;
- If , decrease .
Systematic Review Procedure
- 1.
- Define the objective: This step is used to analyze which factors (e.g., tilt angle, orientation, structural arrangement, and material selection) most significantly impact the efficiency and energy production of PSS installations.
- 2.
- Develop a protocol: A protocol is designed, including the main research questions, inclusion and exclusion criteria, relevant databases, and methods, for synthesis and analysis.
- 3.
- Conduct a comprehensive search: Databases such as Scopus, Web of Science and ScienceDirect are queried using advanced search strategies combining terms like “photovoltaic solar system”, “optimization”, “structure”, “efficiency”, and metaheuristic algorithms.
- 4.
- Select studies: Studies are filtered based on scope, publication year, relevance to the engineering and energy fields, and technical alignment with the objectives. A PRISMA flow diagram is used to document the selection process.
- 5.
- Extract data: Key data are collected from each selected article, including optimization objectives, system configurations, methodologies used, and quantitative results on energy output or system performance.
- 6.
- Evaluate the quality of the studies: Methodological quality and risk of bias are assessed through predefined criteria, prioritizing peer-reviewed articles and excluding those with insufficient technical rigor or unrelated focuses.
- 7.
- Analyze the data: The studies are categorized and analyzed based on their optimization approach (traditional vs. AI-based), the energy gains reported, and applicability to structural design improvements in PSS.
- 8.
- Interpret the results: The findings are synthesized to identify trends, common strategies, and gaps in the literature, with a focus on improving the practical implementation of optimization in real-world PSS installations.
2.8. Optimization and Its Application in Photovoltaic Solar Energy
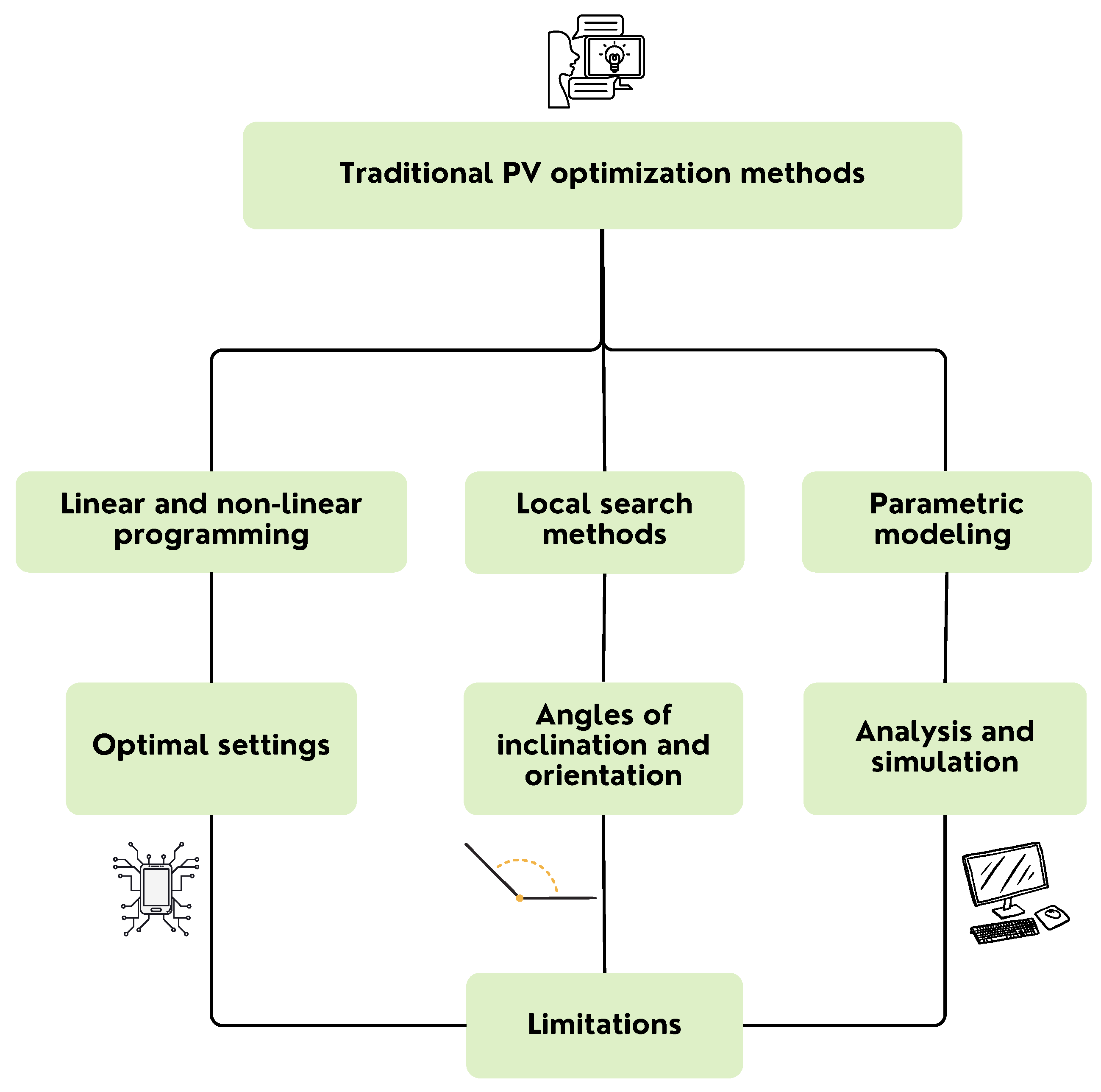
2.8.1. Traditional Optimization Methods
2.8.2. Artificial Intelligence-Based Methods
2.9. Critical Considerations
2.10. Criteria for the Selection and Exclusion of Research
- 1.
- Keyword Focus: Studies must include terms related to solar photovoltaic systems and optimization techniques, such as genetic algorithms, particle swarm optimization, multi-objective or topology optimization.
- 2.
- Publication Date Range: Only documents published between 2020 and 2025 were considered.
- 3.
- Subject Area Filtering: Disciplines unrelated to engineering or computational optimization, such as neuroscience, dentistry, biochemistry, agriculture, materials science, chemistry, sociology, business, arts, economics, medicine, earth sciences, and physics, were excluded.
- 4.
- Document Type: Review articles were excluded to prioritize original research. Patents were excluded as the focus of this review is on peer-reviewed scientific methodologies and results rather than proprietary implementations. However, selected document types, including conference papers, data papers, book chapters, books, discussion papers, editorials, and technical briefs, were allowed.
- 5.
- Thematic Relevance: Articles focusing primarily on unrelated technical topics, such as MPPT, DC-DC converters, electric vehicles, battery systems, emissions, hybrid systems, cost analysis, fuel cells, or hydrogen production, were excluded.
- 6.
- Infrastructure Relevance: Studies that did not explicitly address structural or topological aspects in PV systems, or instead emphasized control systems, inverters, or software development, were also excluded.
- 7.
- Final Search Code: TITLE-ABS-KEY ((“solar photovoltaic system” OR “photovoltaic solar energy” OR “PV system”) AND (“optimization” OR “optimisation” OR “metaheuristic” OR “genetic algorithm” OR “particle swarm” OR “simulated annealing” OR “multi-objective optimization” OR “structural optimization” OR “topology optimization”)) AND PUBYEAR > 2020 AND PUBYEAR < 2025 AND (EXCLUDE (SUBJAREA, “NEUR”) OR EXCLUDE (SUBJAREA, “DENT”) OR EXCLUDE (SUBJAREA, “BIOC”) OR EXCLUDE (SUBJAREA, “AGRI”) OR EXCLUDE (SUBJAREA, “MATE”) OR EXCLUDE (SUBJAREA, “CENG”) OR EXCLUDE (SUBJAREA, “CHEM”) OR EXCLUDE (SUBJAREA, “SOCI”) OR EXCLUDE (SUBJAREA, “BUSI”) OR EXCLUDE (SUBJAREA, “ARTS”) OR EXCLUDE (SUBJAREA, “ECON”) OR EXCLUDE (SUBJAREA, “MEDI”) OR EXCLUDE (SUBJAREA, “EART”) OR EXCLUDE (SUBJAREA, “PHYS”)) AND (EXCLUDE (DOCTYPE, “re”) OR LIMIT-TO (DOCTYPE, “cp”) OR LIMIT-TO (DOCTYPE, “cr”) OR LIMIT-TO (DOCTYPE, “ch”) OR LIMIT-TO (DOCTYPE, “bk”) OR LIMIT-TO (DOCTYPE, “dp”) OR LIMIT-TO (DOCTYPE, “er”) OR LIMIT-TO (DOCTYPE, “tb”) OR LIMIT-TO (DOCTYPE, “ed”)) AND (EXCLUDE (EXACTKEYWORD, “MPPT”) OR EXCLUDE (EXACTKEYWORD, “DC-DC Converter”) OR EXCLUDE (EXACTKEYWORD, “Electric Vehicle”) OR EXCLUDE (EXACTKEYWORD, “Fuzzy Logic”) OR EXCLUDE (EXACTKEYWORD, “Vehicle-to-grid”) OR EXCLUDE (EXACTKEYWORD, “Maximum Power Point Tracking (MPPT)”) OR EXCLUDE (EXACTKEYWORD, “Electric Load Flow”) OR EXCLUDE (EXACTKEYWORD, “Gas Emissions”) OR EXCLUDE (EXACTKEYWORD, “Maximum Power Point”) OR EXCLUDE (EXACTKEYWORD, “Battery Storage”) OR EXCLUDE (EXACTKEYWORD, “Battery Energy Storage Systems”) OR EXCLUDE (EXACTKEYWORD, “Electric Power Distribution”) OR EXCLUDE (EXACTKEYWORD, “Electric Power Generation”) OR EXCLUDE (EXACTKEYWORD, “Secondary Batteries”) OR EXCLUDE (EXACTKEYWORD, “Electric Loads”) OR EXCLUDE (EXACTKEYWORD, “Electric Vehicles”) OR EXCLUDE (EXACTKEYWORD, “Microgrids”) OR EXCLUDE (EXACTKEYWORD, “Greenhouse Gases”) OR EXCLUDE (EXACTKEYWORD, “DC-DC Converters”) OR EXCLUDE (EXACTKEYWORD, “Electric Power System Control”) OR EXCLUDE (EXACTKEYWORD, “Electric Inverters”) OR EXCLUDE (EXACTKEYWORD, “Electric Power Transmission Networks”) OR EXCLUDE (EXACTKEYWORD, “Photovoltaic Cells”) OR EXCLUDE (EXACTKEYWORD, “Maximum Power Point Tracking”) OR EXCLUDE (EXACTKEYWORD, “Fossil Fuels”) OR EXCLUDE (EXACTKEYWORD, “Carbon”) OR EXCLUDE (EXACTKEYWORD, “Electric Batteries”) OR EXCLUDE (EXACTKEYWORD, “Electric Power System Protection”) OR EXCLUDE (EXACTKEYWORD, “Microgrid”) OR EXCLUDE (EXACTKEYWORD, “Fossil Fuel Power Plants”) OR EXCLUDE (EXACTKEYWORD, “Wind Power”) OR EXCLUDE (EXACTKEYWORD, “Extraction”) OR EXCLUDE (EXACTKEYWORD, “Diodes”) OR EXCLUDE (EXACTKEYWORD, “Single-diode Models”) OR EXCLUDE (EXACTKEYWORD, “Single Diode Model”) OR EXCLUDE (EXACTKEYWORD, “Hybrid Systems”) OR EXCLUDE (EXACTKEYWORD, “Renewable Energy Resources”) OR EXCLUDE (EXACTKEYWORD, “Fault Detection”) OR EXCLUDE (EXACTKEYWORD, “Economic Analysis”) OR EXCLUDE (EXACTKEYWORD, “Cost Benefit Analysis”) OR EXCLUDE (EXACTKEYWORD, “Timing Circuits”) OR EXCLUDE (EXACTKEYWORD, “Intelligent Buildings”) OR EXCLUDE (EXACTKEYWORD, “Hydrogen Production”) OR EXCLUDE (EXACTKEYWORD, “Hybrid Energy System”) OR EXCLUDE (EXACTKEYWORD, “Fuel Cells”) OR EXCLUDE (EXACTKEYWORD, “Cost Reduction”) OR EXCLUDE (EXACTKEYWORD, “Cost Of Energies”) OR EXCLUDE (EXACTKEYWORD, “Hybrid System”) OR EXCLUDE (EXACTKEYWORD, “CO 2 Emission”) OR EXCLUDE (EXACTKEYWORD, “Cost Effectiveness”) OR EXCLUDE (EXACTKEYWORD, “OR EXCLUDE (EXACTKEYWORD, “Anomaly Detection”) OR EXCLUDE (EXACTKEYWORD, “Architectural Design”))
2.11. Analysis Guide for Systemic Review
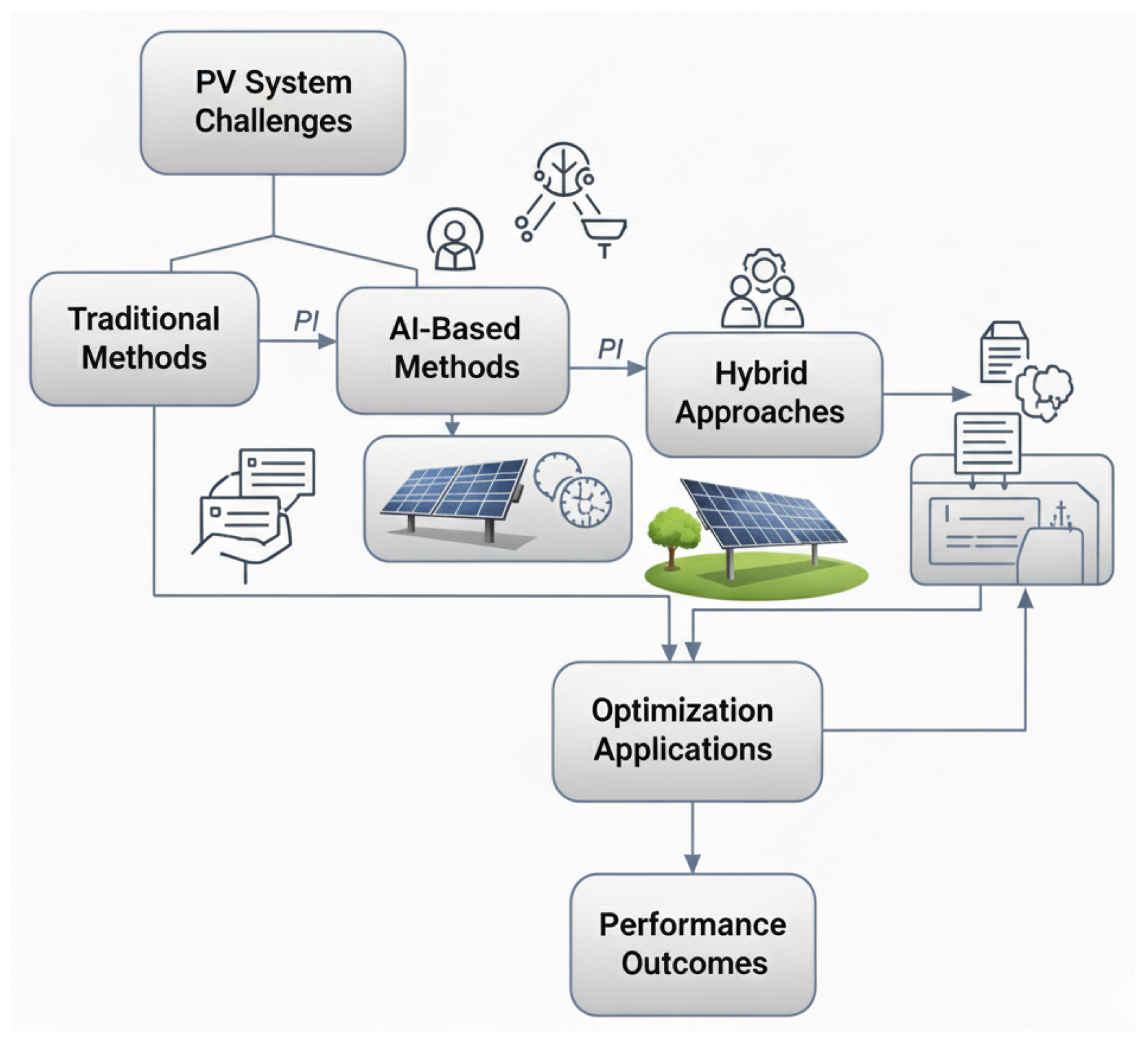
3. Results
3.1. Traditional Optimization Methods in Photovoltaic Solar Energy
Analytical Methods
3.2. Numerical Methods
3.3. Linear Programming
3.4. Dynamic Programming
3.5. Gradient-Based Methods
- A gradient descent MPPT algorithm in solar inverters.
- Calibrating thermal models of PV modules with stochastic gradient descent.
3.6. Critical Comparison of Methods
4. Optimization Methods for Solar Photovoltaic Systems
4.1. Context: The Imperative for Solar PV Optimization
4.2. Metaheuristic Approaches for PV System Optimization
- Evolutionary Algorithms (EAs): Inspired by biological evolution, such as genetic algorithms (GA) [55].
- Swarm Intelligence (SI) Algorithms: Mimicking the collective behavior of social insects or animal groups, such as particle swarm optimization (PSO) [56,57], ant colony optimization (ACO) [58], artificial bee colony (ABC) [59], cuckoo search (CS) [60], gray wolf optimization (GWO) [61], and the firefly algorithm (FA) [62].
- Physics-Based Algorithms: Drawing analogies from physical laws, like simulated annealing (SA) [63].
- Human-Based Algorithms: Modeling human interactions or learning processes, such as teaching–learning-based optimization (TLBO) [64].
4.3. PV Layout and Installation Area Optimization
4.4. Partial Shading Mitigation and MPPT Optimization
- Tracking Speed/Convergence Time: How quickly the algorithm locates the global MPP (GMPP), especially after a change in conditions [73].
- Tracking Accuracy/Efficiency: How close the algorithm operates to the true GMPP [73].
- Steady-State Oscillations: The magnitude of power fluctuations around the MPP once convergence is achieved [76].
- Robustness: The ability to consistently find the GMPP under various dynamic shading patterns and changing environmental conditions [75].
4.5. Tilt and Orientation Optimization for Maximum Yield
4.6. Other Metaheuristic Applications
- Optimizing Power Flow: Managing the flow of energy in transmission and distribution networks incorporating PV [83].
- Reactive Power Dispatch and Volt/Var Control: Optimizing voltage profiles and minimizing losses in distribution systems with PV penetration [83].
- Economic and Emission Dispatch: Scheduling the output of generation units (including PV and storage) to meet demand at minimum cost and/or minimum emissions [83].
- Optimal Placement and Sizing of Distributed Generation (DG): Determining the best locations and capacities for PV systems within a distribution network [83].
- Energy Management Systems (EMS): Developing optimal operating strategies for hybrid systems or microgrids, coordinating PV generation, battery charging/discharging, and load management to achieve specific goals (e.g., cost minimization and self-sufficiency maximization). Advanced optimization algorithms, such as particle swarm optimization (PSO) and genetic algorithms, have been employed to stabilize output power and enhance system reliability in PV systems with battery storage [52].
4.7. Performance Analysis: Effectiveness, Complexity, Advantages, and Limitations
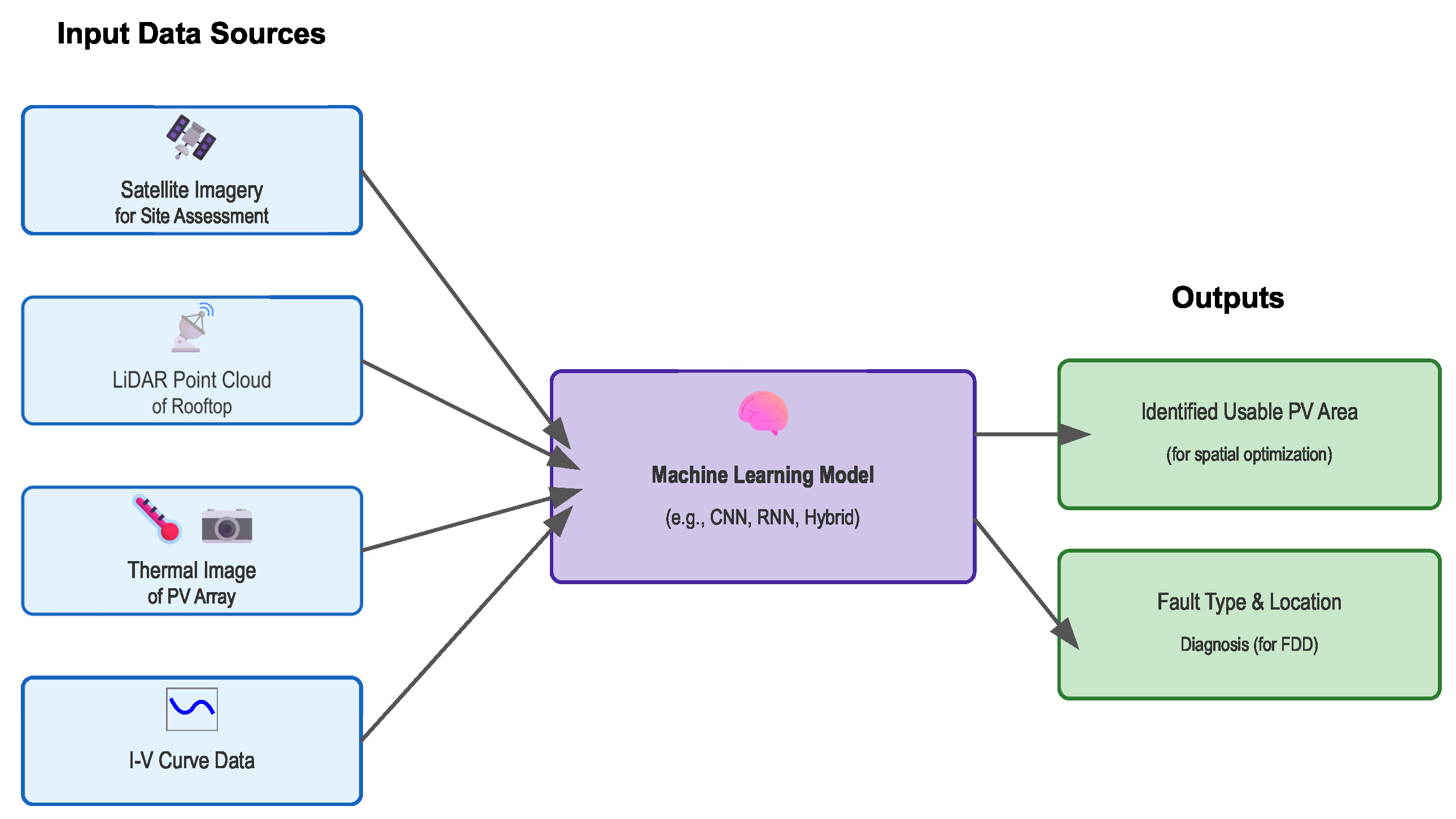
4.8. Machine Learning and Deep Learning Techniques in PV Optimization
4.9. Application in Spatial Optimization and Energy Prediction for Design
4.10. Application in Intelligent MPPT Strategies
4.11. Predictive Optimization and Control
4.12. Application in Fault Detection and Diagnosis for Efficiency Maintenance
4.13. Performance Analysis: Effectiveness, Complexity, Data Needs, Advantages, and Limitations
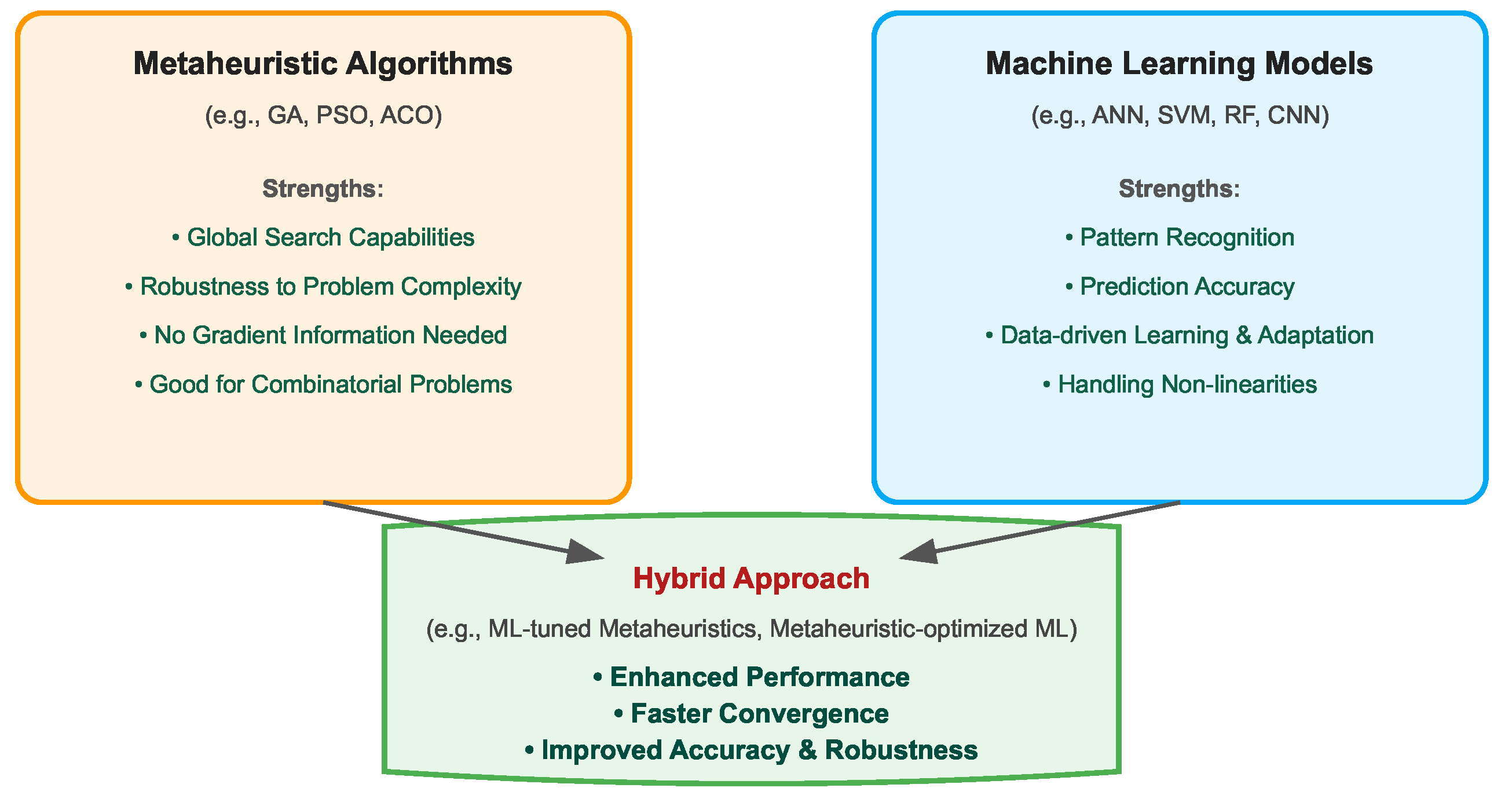
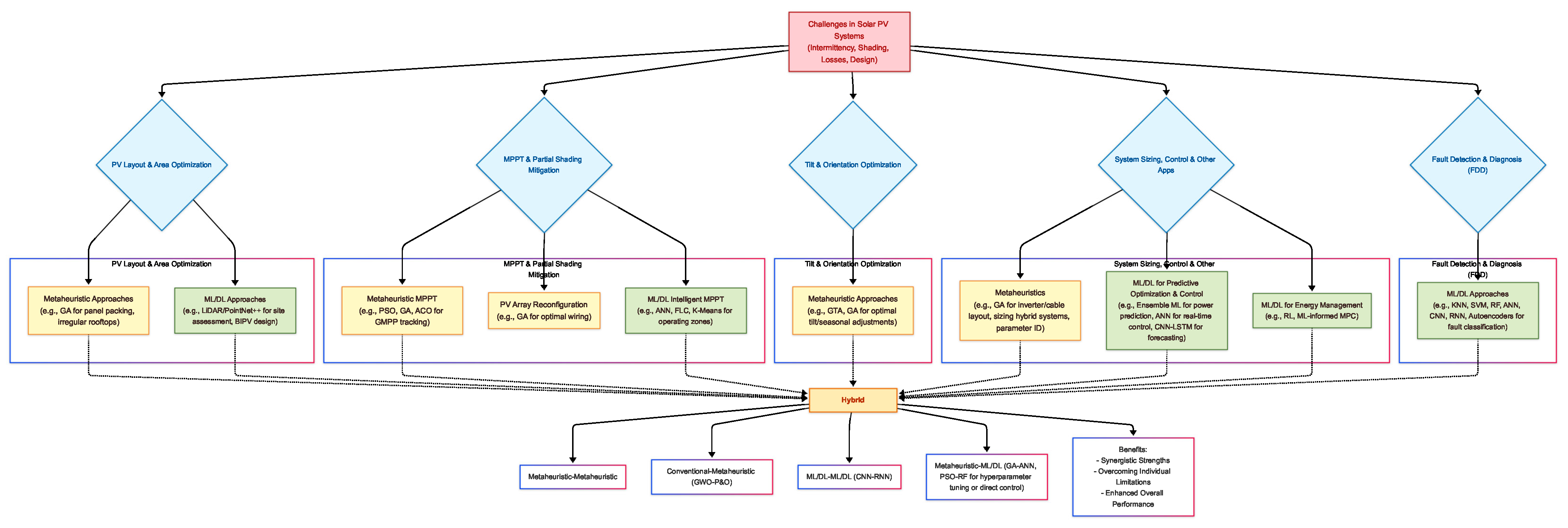
4.14. Comparative Synthesis and Hybrid Methodologies
- MPPT under PSC: Metaheuristics excel due to their inherent global search capabilities, enabling them to locate the GMPP effectively in multi-peaked PV landscapes. ML/DL approaches, including ANNs, FLCs, or clustering methods like K-means, aim to learn the optimal control policy or simplify the search space. A key trade-off exists that metaheuristics might require more online computation during tracking but less offline training data, whereas ML models require potentially extensive offline training but can offer faster inference (decision-making) during operation [75,76].
- Layout Optimization: As noted earlier, direct application of metaheuristics seems less documented recently compared to other tasks. Metaheuristics could theoretically explore the combinatorial space of panel placements, while ML might be better suited for rapidly predicting shading effects or energy yield for numerous candidate layouts generated by another process (e.g., geometric or parametric design tools). The complexity of integrating geometric constraints and detailed shading analysis might favor simulation-based optimization or specialized algorithms.
- System Sizing/Design: Metaheuristics are well-suited for optimizing component sizes (PV, battery, etc.), navigating complex trade-offs between cost, reliability, and performance based on system models. ML primarily contributes by providing accurate forecasts of load demand and renewable generation, which serve as crucial inputs to the sizing optimization process performed by metaheuristics or other optimization solvers [49,55].
- Energy Management: Both paradigms are applicable. Metaheuristics can optimize operational schedules based on predictive models of generation, load, and prices. ML/DL, particularly RL or ML-informed MPC, can learn adaptive control strategies directly from data or use high-accuracy forecasts to optimize decisions in real time or near-real time. ML offers advantages when system dynamics are difficult to model accurately or when adapting to unforeseen changes [52].
- Fault Detection and Diagnosis: This domain is heavily dominated by ML/DL due to their exceptional pattern recognition capabilities applied to electrical signatures, environmental data, or thermal images. Metaheuristics primarily play a supporting role by optimizing the structure or hyperparameters of the ML/DL models used for FDD [92].
4.15. Rise of Hybrid Models: Combining Strengths for Enhanced Performance
4.16. Evaluating Approaches Against Dual Objectives: Area/Energy Maximization vs. Efficiency Preservation
4.17. Critical Analysis of Methods
5. Discussion
New Perspectives on Advances and Trends in Optimization of Photovoltaic Systems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronym | Definition |
| ABC | Artificial Bee Colony |
| ACO | Ant Colony Optimization |
| AI | Artificial Intelligence |
| ANFIS | Adaptive Neuro-Fuzzy Inference Systems |
| ANN | Artificial Neural Networks |
| Bi-GRU | Bidirectional Gated Recurrent Units |
| BIM | Building Information Modeling |
| BIPV | Building-Integrated Photovoltaics |
| CNN | Convolutional Neural Networks |
| CS | Cuckoo Search |
| DC | Direct Current |
| DP | Dynamic Programming |
| DT | Decision Trees |
| EAs | Evolutionary Algorithms |
| EMS | Energy Management Systems |
| FA | Firefly Algorithm |
| FDD | Fault Detection and Diagnosis |
| FHO | Firefly-Host Optimization |
| FLCs | Fuzzy Logic Controllers |
| FPSO | Fuzzy-Particle Swarm Optimization |
| GA | Genetic Algorithms |
| GB | Gradient Boosting |
| GMPP | Global Maximum Power Point |
| GPR | Gaussian Process Regression |
| GRU | Gated Recurrent Units |
| GTA | Gorilla Troop Algorithm |
| GWO | Gray Wolf Optimization |
| HC-ANFIS | Hill Climbing-Adaptive Neuro-Fuzzy Inference System |
| HOMER | Hybrid Optimization of Multiple Energy Resources |
| I–V | Current-Voltage |
| IRT | Infrared Thermography |
| KNN | K-Nearest Neighbors |
| LCOE | Levelized Cost of Energy |
| LiDAR | Light Detection and Ranging |
| LP | Linear Programming |
| LSTM | Long Short-Term Memory |
| MILP | Mixed-Integer Linear Programming |
| MLPs | Multi-Layer Perceptrons |
| MPPT | Maximum Power Point Tracking |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
| OMLP | Optimized Multi-Layer Perceptron |
| OTA | Optimal Tilt Angle |
| P&O | Perturb and Observe |
| PNN | Probabilistic Neural Networks |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSO | Particle Swarm Optimization |
| PSS | Photovoltaic Solar Systems |
| PV | Photovoltaic |
| RF | Random Forest |
| RL | Reinforcement Learning |
| RNNs | Recurrent Neural Networks |
| SA | Simulated Annealing |
| SI | Swarm Intelligence |
| SSAE | Stacked Sparse Auto-Encoders |
| SVM | Support Vector Machines |
| TCT | Total-Cross-Tied |
| TLBO | Teaching-Learning-Based Optimization |
| TOU | Time of Use |
| XAI | Explainable Artificial Intelligence |
| Symbol | Description |
| Power change (W) | |
| Voltage change (V) | |
| Inverter efficiency (dimensionless) | |
| Maximum inverter efficiency (dimensionless) | |
| C | Capacitance of the RC network (F) |
| Battery open-circuit voltage (V) | |
| I | Battery charge/discharge current (A) |
| I | Output current of the solar cell (A) |
| Reverse saturation current of the diode (A) | |
| Reverse saturation current of first diode (A) | |
| Reverse saturation current of second diode (A) | |
| Photogenerated current (A) | |
| k | Boltzmann constant (J/K) |
| Efficiency adjustment coefficient (dimensionless) | |
| n | Diode ideality factor |
| Ideality factor of first diode | |
| Ideality factor of second diode | |
| Power at time step k (W) | |
| Power at time step k − 1 (W) | |
| DC input power (W) | |
| Rated power of the inverter (W) | |
| q | Elementary charge (C) |
| R | Resistance of the RC network () |
| Series resistance () | |
| Battery internal resistance () | |
| Shunt resistance () | |
| T | Temperature (K) |
| t | Time (s) |
| V | Voltage across the cell (V) |
| Voltage at time step k (V) | |
| Battery voltage (V) | |
| Voltage across the RC network (V) |
References
- Kruitwagen, L.; Story, K.; Friedrich, J.; Byers, L.; Skillman, S.; Hepburn, C. A global inventory of photovoltaic solar energy generating units. Nature 2021, 598, 604–610. [Google Scholar] [CrossRef] [PubMed]
- Jean, J.; Brown, P.R.; Jaffe, R.; Buonassisi, T.; Bulović, V. Pathways for solar photovoltaics. Energy Environ. Sci. 2015, 8, 1200–1219. [Google Scholar] [CrossRef]
- Raimi, D.; Campbell, E.; Newell, R.G.; Prest, B.; Villanueva, S.; Wingenroth, J. Global Energy Outlook 2022: Turning Points and Tension in the Energy Transition; Resources for the Future: Washington, DC, USA, 2022; pp. 1723–1742. [Google Scholar]
- Chala, G.; Alshaikh, S.M.A. Solar Photovoltaic Energy as a Promising Enhanced Share of Clean Energy Sources in the Future—A Comprehensive Review. Energies 2023, 16, 7919. [Google Scholar] [CrossRef]
- Gielen, D.; Gorini, R.; Leme, R.; Prakash, G.; Wagner, N.; Janeiro, L.; Collins, S.; Kadir, M.; Asmelash, E.; Ferroukhi, R.; et al. World Energy Transitions Outlook: 1.5 °C Pathway; International Renewable Energy Agency (IRENA): Masdar City, United Arab Emirates, 2021. [Google Scholar]
- Hasan, M.M.U.; Hossain, S.; Mofijur, M.; Kabir, Z.; Badruddin, I.; Khan, T.M.Y.; Jassim, E. Harnessing Solar Power: A Review of Photovoltaic Innovations, Solar Thermal Systems, and the Dawn of Energy Storage Solutions. Energies 2023, 16, 6456. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Ruppert Filho, E. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 1244–1254. [Google Scholar]
- Trejos-Grisales, L.; Bastidas-Rodríguez, J.; Ramos-Paja, C. Mathematical Model for Regular and Irregular PV Arrays with Improved Calculation Speed. Sustainability 2020, 12, 10684. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Accurate MATLAB simulink PV system simulator based on a two-diode model. J. Power Electron. 2011, 11, 179–187. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.; Alsaidan, I.; Abdelaziz, A.; Muyeen, S. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef]
- Salameh, T.; Tawalbeh, M.; Juaidi, A.; Abdallah, R.; Hamid, A. A novel three-dimensional numerical model for PV/T water system in hot climate region. Renew. Energy 2021, 164, 1320–1333. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G. Lead acid battery storage model for hybrid energy systems. Sol. Energy 1993, 50, 399–405. [Google Scholar] [CrossRef]
- Salameh, Z.; Casacca, M.A.; Lynch, W.A. A mathematical model for lead-acid batteries. IEEE Trans. Energy Convers. 1992, 7, 93–98. [Google Scholar] [CrossRef]
- Wang, X.W.; Han, X.Q.; Men, R.J. Modeling and Simulation of Lead-acid Battery in Wind and Solar Power Systems. Shanxi Electr. Power 2009, 2, 23–26. (In Chinese) [Google Scholar]
- Achaibou, N.; Haddadi, M.; Malek, A. Modeling of Lead Acid Batteries in PV Systems. Energy Procedia 2012, 18, 538–544. [Google Scholar] [CrossRef]
- Zhang, J.; Huber, L.; Jovanovic, M.M.; Lee, F.C. Single-stage input-current-shaping technique with voltage-doubler-rectifier front end. IEEE Trans. Power Electron. 2001, 16, 55–63. [Google Scholar] [CrossRef]
- Yu, Y.; Narayan, N.; Vega-Garita, V.; Popovic-Gerber, J.; Qin, Z.; Wagemaker, M.; Bauer, P.; Zeman, M. Constructing Accurate Equivalent Electrical Circuit Models of Lithium Iron Phosphate and Lead–Acid Battery Cells for Solar Home System Applications. Energies 2018, 11, 2305. [Google Scholar] [CrossRef]
- Dürr, M.; Cruden, A.; Gair, S.; McDonald, J. Dynamic model of a lead acid battery for use in a domestic fuel cell system. J. Power Sources 2006, 161, 1400–1411. [Google Scholar] [CrossRef]
- Jlidi, M.; Barambones, O.; Hamidi, F.; Aoun, M. ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC. Energies 2024, 17, 2802. [Google Scholar] [CrossRef]
- Ahessab, H.; Gaga, A.; Elhadadi, B. Enhanced MPPT controller for partially shaded PV systems using a modified PSO algorithm and intelligent artificial neural network, with DSP F28379D implementation. Sci. Prog. 2024, 107, 1–26. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Utama, C.; Meske, C.; Schneider, J.; Ulbrich, C. Reactive power control in photovoltaic systems through (explainable) artificial intelligence. Appl. Energy 2022, 328, 120004. [Google Scholar] [CrossRef]
- Kumar, A.; Dubey, A.; Ramírez, I.S.; del Río, A.M.; Márquez, F.G.G. Artificial Intelligence Techniques for the Photovoltaic System: A Systematic Review and Analysis for Evaluation and Benchmarking. Arch. Comput. Methods Eng. 2024, 31, 4429–4453. [Google Scholar] [CrossRef]
- Susilawati, A.; Al-Obaidi, A.S.M.; Abduh, A.; Irwansyah, F.S.; Nandiyanto, A.B.D. How to do research methodology: From literature Review, bibliometric, step-by-step research stages, to practical examples in science and engineering education. Indones. J. Sci. Technol. 2025, 10, 1–40. [Google Scholar] [CrossRef]
- Khalid, I.L.; Abdullah, M.N.S.; Fadzil, H.M. A systematic review: Digital learning in STEM education. J. Adv. Res. Appl. Sci. Eng. Technol. 2025, 51, 98–115. [Google Scholar] [CrossRef]
- Urrútia, G.; Yepes-Nuñez, J.; Romero-Garcia, M.; Alonso-Fernandez, S. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews Declaración PRISMA 2020: Una Guía Actualizada para la Publicación de Revisiones Sistemáticas. Rev. Esp. De Cardiol. 2021, 74, 790–799. [Google Scholar]
- Peixoto, B.; Pinto, R.; Melo, M.; Cabral, L.; Bessa, M. Immersive virtual reality for foreign language education: A PRISMA systematic review. IEEE Access 2021, 9, 48952–48962. [Google Scholar] [CrossRef]
- Akbari, H.; Browne, M.C.; Ortega, A.; Huang, M.; Hewitt, N.; Norton, B.; McCormack, S. Efficient energy storage technologies for photovoltaic systems. Sol. Energy 2019, 192, 144–168. [Google Scholar] [CrossRef]
- Alsema, E.; Nieuwlaar, E. Energy viability of photovoltaic systems. Energy Policy 2000, 28, 999–1010. [Google Scholar] [CrossRef]
- Eteiba, M.; Barakat, S.; Samy, M.; Wahba, W.I. Optimization of an off-grid PV/Biomass hybrid system with different battery technologies. Sustain. Cities Soc. 2018, 40, 713–727. [Google Scholar] [CrossRef]
- Assareh, E.; Asl, S.S.M.; Ahmadinejad, M.; Parvaz, M.; Ghodrat, M. Optimization of a solar energy system integrating cooling, hot water, and power units in Australian cities: A climate-based analysis and cost-efficiency investigation. Int. J. Hydrogen Energy 2023, 49, 353–375. [Google Scholar] [CrossRef]
- Shin, M.; Kim, J.; Kim, M. Measuring human adaptation to AI in decision making: Application to evaluate changes after AlphaGo. arXiv 2020, arXiv:2012.15035. [Google Scholar]
- Mateo Romero, H.F.; González Rebollo, M.Á.; Cardeñoso-Payo, V.; Alonso Gómez, V.; Redondo Plaza, A.; Moyo, R.T.; Hernández-Callejo, L. Applications of artificial intelligence to photovoltaic systems: A review. Appl. Sci. 2022, 12, 10056. [Google Scholar] [CrossRef]
- Shin, W.G.; Lee, J.S.; Ju, Y.C.; Hwang, H.M.; Ko, S.W. Data preprocessing and machine learning method based on ameliorated mathematical models for inferring the power generation of photovoltaic system. Energy Convers. Manag. 2025, 333, 119793. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A comprehensive MATLAB Simulink PV system simulator with partial shading capability based on two-diode model. Sol. Energy 2011, 85, 2217–2227. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- PVsyst SA. PVsyst|Photovoltaic Software, Design and Simulate Photovoltaic Systems. 2025. Available online: https://www.pvsyst.com/ (accessed on 28 August 2025).
- Aurora Solar Inc. HelioScope|Commercial Solar Design Software. 2025. Available online: https://helioscope.aurorasolar.com/ (accessed on 28 August 2025).
- Wang, Y.; Wu, Z.; Ni, D. Large-Scale Optimization among Photovoltaic and Concentrated Solar Power Systems: A State-of-the-Art Review and Algorithm Analysis. Energies 2024, 17, 4323. [Google Scholar] [CrossRef]
- Ainaoui, K.E.; Zaimi, M.; Assaid, E. Innovative approaches to extract double-diode model physical parameters of a PV module serving outdoors under real-world conditions. Energy Convers. Manag. 2023, 292, 117365. [Google Scholar] [CrossRef]
- Ma, J.; Hong, D.; Wang, K.; Bi, Z.; Zhu, X.; Zhang, J. Analytical modeling and parameter estimation of photovoltaic strings under partial shading conditions. Sol. Energy Mater. Sol. Cells 2022, 235, 111494. [Google Scholar] [CrossRef]
- Zaghba, L.; Borni, A.; Benbitour, M.; Fezzani, A.; Alwabli, A.; Bajaj, M.; Mohammadi, S.A.D.; Ghoneim, S. Enhancing grid-connected photovoltaic system performance with novel hybrid MPPT technique in variable atmospheric conditions. Sci. Rep. 2024, 14, 8205. [Google Scholar] [CrossRef]
- Gündoğdu, A. System Identification Based ARV-MPPT Technique for PV Systems Under Variable Atmospheric Conditions. IEEE Access 2022, 10, 51325–51342. [Google Scholar] [CrossRef]
- Ghaithan, A.; Mohammed, A.; Hanbali, A.A.; Alshibani, A. A Mixed Integer Linear Programming Model for Optimal Sizing of Hydrogen Refueling Station Powered Using a PV-Grid System. Arab. J. Sci. Eng. 2024, 50, 11129–11144. [Google Scholar] [CrossRef]
- Abdellatif, H.; Syed, M.; Hossain, M.; Abido, M.A. Standalone Hybrid Renewable Energy System Optimization Using Linear Programming. Arab. J. Sci. Eng. 2022, 48, 6361–6376. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W. An Algorithmic Model Building Scheme Based on Dynamic Programming Algorithms. J. Phys. Conf. Ser. 2019, 1345, 052080. [Google Scholar] [CrossRef]
- Gammoudi, R.; Brahmi, H.; Dhifaoui, R. Estimation of Climatic Parameters of a PV System Based on Gradient Method. Complex. 2019, 2019, 7385927:1–7385927:10. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Padmanaban, S.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, M.H.; Shafiullah, M.; Malik, M.Z. Investigation of MPPT Techniques Under Uniform and Non-Uniform Solar Irradiation Condition–A Retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Alkabbani, H.; Ahmadian, A.; Zhu, Q.; Elkamel, A. Machine Learning and Metaheuristic Methods for Renewable Power Forecasting: A Recent Review. Front. Chem. Eng. 2021, 3, 665415. [Google Scholar] [CrossRef]
- IEA-PVPS. Trends in PV Applications 2024. Available online: https://iea-pvps.org/trends_reports/trends-in-pv-applications-2024/ (accessed on 30 April 2025).
- Zargarzadeh, S.; Ramnarayan, A.; de Castro, F.; Ohadi, M. ML-Enabled Solar PV Electricity Generation Projection for a Large Academic Campus to Reduce Onsite CO2 Emissions. Energies 2024, 17, 6188. [Google Scholar] [CrossRef]
- Al-Shahri, O.A.; Ismail, F.B.; Hannan, M.A.; Lipu, M.H.; Al-Shetwi, A.Q.; Begum, R.A.; Al-Muhsen, N.F.; Soujeri, E. Solar photovoltaic energy optimization methods, challenges and issues: A comprehensive review. J. Clean. Prod. 2021, 284, 125465. [Google Scholar] [CrossRef]
- Leon-Aldaco, S.E.D.; Calleja, H.; Alquicira, J.A. Metaheuristic Optimization Methods Applied to Power Converters: A Review. IEEE Trans. Power Electron. 2015, 30, 6791–6803. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter Extraction of Solar Photovoltaic Cell and Module Models with Metaheuristic Algorithms: A Review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. An Optimization Sizing Model for Solar Photovoltaic Power Generation System with Pumped Storage. Energy Procedia 2014, 61, 5–8. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Odry, Á. An open-source test environment for effective development of marg-based algorithms. Sensors 2021, 21, 1183. [Google Scholar] [CrossRef]
- Ant colony optimization: Overview and recent advances. In Ant Colony Optimization; Dorigo, M., Stützle, T., Eds.; International Series in Operations Research & Management Science; Springer: Berlin/Heidelberg, Germany, 2019; pp. 311–351. [Google Scholar] [CrossRef]
- Alsamia, S.; Koch, E.; Albedran, H.; Ray, R. Adaptive Exploration Artificial Bee Colony for Mathematical Optimization. AI 2024, 5, 2218–2236. [Google Scholar] [CrossRef]
- Chiroma, H.; Herawan, T.; Fister, I., Jr.; Fister, I. Bio-inspired computation: Recent development on the modifications of the cuckoo search algorithm. Appl. Soft Comput. J. 2017, 61, 149–173. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, X.; Zhang, L. A review of ultra-short-term forecasting of wind power based on data decomposition-forecasting technology combination model. Energy Rep. 2022, 8, 14200–14219. [Google Scholar] [CrossRef]
- Blocho, M. Heuristics, metaheuristics, and hyperheuristics for rich vehicle routing problems. In Smart Delivery Systems: Solving Complex Vehicle Routing Problems; Elsevier: Amsterdam, The Netherlands, 2019; pp. 101–156. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Canturk, D.; Kucukyilmaz, T. A Survey on Pioneering Metaheuristic Algorithms Between 2019 and 2024. 2024. Available online: https://arxiv.org/pdf/2501.14769v1 (accessed on 30 April 2025).
- Barbón, A.; Ghodbane, M.; Bayón, L.; Said, Z. A general algorithm for the optimization of photovoltaic modules layout on irregular rooftop shapes. J. Clean. Prod. 2022, 365, 132774. [Google Scholar] [CrossRef]
- Ren, H.; Sun, Y.; Tse, C.F.N.; Fan, C. Optimal packing and planning for large-scale distributed rooftop photovoltaic systems under complex shading effects and rooftop availabilities. Energy 2023, 274, 127280. [Google Scholar] [CrossRef]
- Aslani, M.; Seipel, S. Rooftop segmentation and optimization of photovoltaic panel layouts in digital surface models. Comput. Environ. Urban Syst. 2023, 105, 102026. [Google Scholar] [CrossRef]
- Pillay, T.L.; Saha, A.K. A Review of Metaheuristic Optimization Techniques for Effective Energy Conservation in Buildings. Energies 2024, 17, 1547. [Google Scholar] [CrossRef]
- Donati, A.V.; Krause, J.; Thiel, C.; White, B.; Hill, N. An Ant Colony Algorithm for Improving Energy Efficiency of Road Vehicles. Energies 2020, 13, 2850. [Google Scholar] [CrossRef]
- Documents: UNGGIM-PSN. Available online: http://unggim-psn.org/documents.html (accessed on 4 May 2025).
- Durango-Flórez, M.; González-Montoya, D.; Trejos-Grisales, L.A.; Ramos-Paja, C.A. PV Array Reconfiguration Based on Genetic Algorithm for Maximum Power Extraction and Energy Impact Analysis. Sustainability 2022, 14, 3764. [Google Scholar] [CrossRef]
- Verma, P.; Alam, A.; Sarwar, A.; Tariq, M.; Vahedi, H.; Gupta, D.; Ahmad, S.; Shah Noor Mohamed, A. Meta-Heuristic Optimization Techniques Used for Maximum Power Point Tracking in Solar PV System. Electronics 2021, 10, 2419. [Google Scholar] [CrossRef]
- Krishnan, G.S.; Kinattingal, S.; Simon, S.P.; Nayak, P.S.R. MPPT in PV systems using ant colony optimisation with dwindling population. IET Renew. Power Gener. 2020, 14, 1105–1112. [Google Scholar] [CrossRef]
- Sutikno, T.; Pamungkas, A.; Pau, G.; Yudhana, A.; Facta, M. A review of recent advances in metaheuristic maximum power point tracking algorithms for solar photovoltaic systems under the partial-shading conditions. Indones. J. Sci. Technol. 2022, 7, 131–158. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A comprehensive review of maximum power point tracking (mppt) techniques used in solar pv systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Abdelaal, A.K.; Alhamahmy, A.I.A.; Attia, H.E.D.; El-Fergany, A.A. Maximizing solar radiations of PV panels using artificial gorilla troops reinforced by experimental investigations. Sci. Rep. 2024, 14, 3562. [Google Scholar] [CrossRef]
- Nascimento, E.O.; Monteiro, P.R.D.; Borges, T.T. Optimization Method for the Internal Distribution Network of a Photovoltaic Plant Using Genetic Algorithm. Curr. J. Appl. Sci. Technol. 2023, 42, 12–27. [Google Scholar] [CrossRef]
- Bouaouda, A.; Sayouti, Y. Hybrid Meta-Heuristic Algorithms for Optimal Sizing of Hybrid Renewable Energy System: A Review of the State-of-the-Art. Arch. Comput. Methods Eng. 2022, 29, 4049–4083. [Google Scholar] [CrossRef]
- Gusain, C.; Tripathi, M.M.; Nangia, U. Study of Meta-heuristic Optimization Methodologies for Design of Hybrid Renewable Energy Systems. Therm. Sci. Eng. Prog. 2023, 39, 101711. [Google Scholar] [CrossRef]
- Navarro, M.A.; Oliva, D.; Ramos-Michel, A.; Haro, E.H. An analysis on the performance of metaheuristic algorithms for the estimation of parameters in solar cell models. Energy Convers. Manag. 2023, 276, 116523. [Google Scholar] [CrossRef]
- Chen, W.; Ren, H.; Zhou, W. Review of multi-objective optimization in long-term energy system models. Glob. Energy Interconnect. 2023, 6, 645–660. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Yu, J.; Li, X.; Yang, L.; Li, L.; Huang, Z.; Shen, K.; Yang, X.; Yang, X.; Xu, Z.; Zhang, D.; et al. Deep Learning Models for PV Power Forecasting: Review. Energies 2024, 17, 3973. [Google Scholar] [CrossRef]
- Lari, A.J.; Sanfilippo, A.P.; Bachour, D.; Perez-Astudillo, D. Using Machine Learning Algorithms to Forecast Solar Energy Power Output. Electronics 2025, 14, 866. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Tran, Q.T.; Ngo, C.T.; Nguyen, D.D.; Tran, V.Q. Solar energy prediction through machine learning models: A comparative analysis of regressor algorithms. PLoS ONE 2025, 20, e0315955. [Google Scholar] [CrossRef]
- Madeti, S.R.; Singh, S.N. Modeling of PV system based on experimental data for fault detection using kNN method. Sol. Energy 2018, 173, 139–151. [Google Scholar] [CrossRef]
- Guessoum, D.; Takruri, M.; Badawi, S.A.; Farhat, M.; ElBadawi, I. Maximum power point tracking using unsupervised learning for photovoltaic power systems. Int. J. Sustain. Eng. 2024, 17, 38–53. [Google Scholar] [CrossRef]
- Bougoffa, M.; Benmoussa, S.; Djeziri, M.; Palais, O. Hybrid Deep Learning for Fault Diagnosis in Photovoltaic Systems. Machines 2025, 13, 378. [Google Scholar] [CrossRef]
- Odry, A.; Kecskes, I.; Pesti, R.; Csik, D.; Stefanoni, M.; Sarosi, J.; Sarcevic, P. NN-augmented EKF for Robust Orientation Estimation Based on MARG Sensors. Int. J. Control. Autom. Syst. 2025, 23, 920–934. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J. Applications and Trends of Machine Learning in Building Energy Optimization: A Bibliometric Analysis. Buildings 2025, 15, 994. [Google Scholar] [CrossRef]
- Amiri, A.F.; Kichou, S.; Oudira, H.; Chouder, A.; Silvestre, S. Fault Detection and Diagnosis of a Photovoltaic System Based on Deep Learning Using the Combination of a Convolutional Neural Network (CNN) and Bidirectional Gated Recurrent Unit (Bi-GRU). Sustainability 2024, 16, 1012. [Google Scholar] [CrossRef]
- Salman, D.; Elmi, Y.K.; Isak, A.M.; Sheikh-Muse, A. Evaluation of MPPT Algorithms for Solar PV Systems with Machine Learning and Metaheuristic Techniques. Math. Model. Eng. Probl. 2025, 12, 115–124. [Google Scholar] [CrossRef]
- Aslani, M.; Seipel, S. A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data. In Proceedings of the International Conference on Geographical Information Systems Theory, Applications and Management, GISTAM-Proceedings, Online, 27–29 April 2022; pp. 56–63. [Google Scholar] [CrossRef]
- Abouelaziz, I.; Jouane, Y. Photogrammetry and deep learning for energy production prediction and building-integrated photovoltaics decarbonization. Build. Simul. 2024, 17, 189–205. [Google Scholar] [CrossRef]
- Nur-E-Alam, M.; Mostofa, K.Z.; Yap, B.K.; Basher, M.K.; Islam, M.A.; Vasiliev, M.; Soudagar, M.E.M.; Das, N.; Kiong, T.S. Machine learning-enhanced all-photovoltaic blended systems for energy-efficient sustainable buildings. Sustain. Energy Technol. Assessments 2024, 62, 103636. [Google Scholar] [CrossRef]
- Odry, Á.; Tadic, V.L.; Odry, P. A stochastic logic-based fuzzy logic controller: First experimental results of a novel architecture. IEEE Access 2021, 9, 29895–29920. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.C.; Lee, S.J. Optimal Photovoltaic Panel Direction and Tilt Angle Prediction Using Stacking Ensemble Learning. Front. Energy Res. 2022, 10, 865413. [Google Scholar] [CrossRef]
- Umasankar, L.; Nithyananthan, K.; Umaeswari, P.; Bindu, K.V. Maximizing Solar PV Performance with Deep Learning Optimization and Advanced Power Regulation. J. Inf. Syst. Eng. Manag. 2025, 10, 331–343. [Google Scholar] [CrossRef]
- Kamal, S.; Ramapraba, P.S.; Kumar, A.; Saha, B.C.; Lakshminarayana, M.; Sanal Kumar, S.; Gopalan, A.; Erko, K.G. Optimization of Solar Panel Deployment Using Machine Learning. Int. J. Photoenergy 2022, 2022, 7249109. [Google Scholar] [CrossRef]
- Hosseini, E.; Saeedpour, B.; Banaei, M.; Ebrahimy, R. Optimized deep neural network architectures for energy consumption and PV production forecasting. Energy Strategy Rev. 2025, 59, 101704. [Google Scholar] [CrossRef]
- Sushmit, M.M.; Mahbubul, I.M. Forecasting solar irradiance with hybrid classical–quantum models: A comprehensive evaluation of deep learning and quantum-enhanced techniques. Energy Convers. Manag. 2023, 294, 117555. [Google Scholar] [CrossRef]
- Benaissa, B.; Kobayashi, M.; Ali, M.A.; Khatir, T.; Elmeliani, M.E.A.E. Metaheuristic optimization algorithms: An overview. HCMCOU J. Sci.—Adv. Comput. Struct. 2024, 14, 33–61. [Google Scholar] [CrossRef]
- Leite, D.; Andrade, E.; Rativa, D.; Maciel, A.M.A. Fault Detection and Diagnosis in Industry 4.0: A Review on Challenges and Opportunities. Sensors 2025, 25, 60. [Google Scholar] [CrossRef] [PubMed]
- Kazem, H.A.; Chaichan, M.T.; Al-Waeli, A.H.; Gholami, A. A systematic review of solar photovoltaic energy systems design modelling, algorithms, and software. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 6709–6736. [Google Scholar] [CrossRef]
- Atawi, I.E.; Al-Shetwi, A.Q.; Magableh, A.M.; Albalawi, O.H. Recent advances in hybrid energy storage system integrated renewable power generation: Configuration, control, applications, and future directions. Batteries 2022, 9, 29. [Google Scholar] [CrossRef]
- Le, P.T.; Tsai, H.L.; Le, P.L. Development and performance evaluation of photovoltaic (PV) evaluation and fault detection system using hardware-in-the-loop simulation for PV applications. Micromachines 2023, 14, 674. [Google Scholar] [CrossRef]
- Zhou, D.; Liu, Y.; Wang, X.; Wang, F.; Jia, Y. Research Progress of Photovoltaic Power Prediction Technology Based on Artificial Intelligence Methods. Energy Eng. 2024, 121, 3573. [Google Scholar] [CrossRef]
- Saxena, A.; Kumar, R.; Sagade, A.A.; Singh, D.B.; Tyagi, V.; Cuce, E.; Goel, V. A state-of-art review on photovoltaic systems: Design, performance, and progress. Process Saf. Environ. Prot. 2024, 190, 1324–1354. [Google Scholar] [CrossRef]
- Datta, S.; Baul, A.; Sarker, G.C.; Sadhu, P.K.; Hodges, D.R. A comprehensive review of the application of machine learning in fabrication and implementation of photovoltaic systems. IEEE Access 2023, 11, 77750–77778. [Google Scholar] [CrossRef]
- Dey, D.; Subudhi, B. Design, simulation and economic evaluation of 90 kW grid connected Photovoltaic system. Energy Rep. 2020, 6, 1778–1787. [Google Scholar] [CrossRef]
- Hassan, Q. Evaluation and optimization of off-grid and on-grid photovoltaic power system for typical household electrification. Renew. Energy 2021, 164, 375–390. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, Y. Collaborative optimization of PV greenhouses and clean energy systems in rural areas. IEEE Trans. Sustain. Energy 2022, 14, 642–656. [Google Scholar] [CrossRef]
- Huang, P.; Sun, Y.; Lovati, M.; Zhang, X. Solar-photovoltaic-power-sharing-based design optimization of distributed energy storage systems for performance improvements. Energy 2021, 222, 119931. [Google Scholar] [CrossRef]
- Faiz, F.U.H.; Shakoor, R.; Raheem, A.; Umer, F.; Rasheed, N.; Farhan, M. Modeling and analysis of 3 MW solar photovoltaic plant using PVSyst at Islamia University of Bahawalpur, Pakistan. Int. J. Photoenergy 2021, 2021, 6673448. [Google Scholar] [CrossRef]
- Bruno Cotelo, R. Optimización de Diseño de Plantas Solares Fotovoltaicas. Master’s Thesis, University of the Republic, Montevideo, Uruguay, 2022. [Google Scholar]
- Zamen, M.; Baghban, A.; Pourkiaei, S.M.; Ahmadi, M.H. Optimization methods using artificial intelligence algorithms to estimate thermal efficiency of PV/T system. Energy Sci. Eng. 2019, 7, 821–834. [Google Scholar] [CrossRef]
- Di Leo, P.; Ciocia, A.; Malgaroli, G.; Spertino, F. Advancements and Challenges in Photovoltaic Power Forecasting: A Comprehensive Review. Energies 2025, 18, 2108. [Google Scholar] [CrossRef]
- Mamodiya, U.; Kishor, I.; Almaiah, M.A.; Hamdi, M.; Shehab, R.; Alkhdour, T. Numerical modeling and neural network optimization for advanced solar panel efficiency. Sci. Rep. 2025, 15, 23492. [Google Scholar] [CrossRef]
- Nyangiwe, N.N.; Kapimkenfack, A.D.; Thantsha, N.; Msimanga, M. Performance monitoring of photovoltaic modules using machine learning based solutions: A survey of current trends. Authorea 2025. [Google Scholar] [CrossRef]
- Abdelsattar, M.; AbdelMoety, A.; Emad-Eldeen, A. Comparative analysis of machine learning techniques for temperature and humidity prediction in photovoltaic environments. Sci. Rep. 2025, 15, 15650. [Google Scholar] [CrossRef]
- Bianchini, G.; Pepe, D.; Vicino, A. Estimation of photovoltaic generation forecasting models using limited information. Automatica 2020, 113, 108688. [Google Scholar] [CrossRef]


| Method | Main Application | Use Case | Advantages | Limitations | Typical Use Stage |
|---|---|---|---|---|---|
| Analytical Methods | Pre-design and estimation | Optimal tilt angle calculation | Low computational cost, easy to interpret | Oversimplified assumptions, limited accuracy | High (conceptual design) |
| Numerical Methods | System modeling and simulation | Hourly PV energy yield estimation | High accuracy, good fit to real conditions | Requires detailed data, not always optimal | High (performance analysis) |
| Linear Programming | Component sizing and energy dispatch | MILP-based microgrid optimization | Scalable, guarantees optimality in linear problems | Only suitable for linear systems | Very high (planning and design) |
| Dynamic Programming | Energy storage scheduling | Battery control under TOU tariffs | Handles multi-stage decisions and uncertainties | High memory and computational demand | High (temporal control and storage) |
| Gradient-Based Methods | Parameter tuning and control | MPPT using P&O or Incremental Conductance | Fast convergence, suitable for embedded systems | Sensitive to local optima, requires gradient information | High (real-time control) |
| Algorithm | Application(s) | Objective(s) | Strengths | Limitations |
|---|---|---|---|---|
| PSO | MPPT, Sizing, ML tuning | GMPP, LCOE, hyperparams | Fast, nonlinear capable, widely used | Premature conv., param. sens., slow end-phase |
| GA | Sizing, MPPT, ML tuning | LCOE, reliability, ML opt. | Robust, flexible, cross-domain use | Slow MPPT, complex ops |
| ACO | MPPT, Mgmt., Packaging | GMPP, CO2/Cost min. | Fast conv., simple logic | Needs complex est. for MPPT |
| GWO | MPPT | GMPP | Stable, no oscill., fast conv. | Cost ↑ with search space size |
| ABC | MPPT, ML tuning | GMPP, ML opt. | Few params, robust, init-indep. | May miss GMPP, slow conv. |
| CS | MPPT | GMPP | Few params, solid conv. | Long calc., perf. loss risk |
| FA | MPPT | GMPP | PSC-capable tracking | Param. tuning (attractiveness) critical |
| SA | General opt. | Cost/Perf. opt. | Simple, well-studied | Sensitive to cooling sched. |
| TLBO | MPPT | GMPP | Easy impl., no control params | Few PV-specific validations |
| Hybrid (e.g., GWO-P&O) | MPPT | GMPP | High perf., speed, synergy | High complexity, comp. load |
| Technique | Application(s) | Objective(s) | Strengths | Limitations |
|---|---|---|---|---|
| ANN/MLP | MPPT, Forecasting, FDD | Yield/load pred., MPP, fault classif. | Nonlinear modeling, broad use | Needs large data, retraining, opaque logic |
| SVM | Forecasting, FDD | Classification, regression | Effective in high dimensions | Kernel choice critical, less scalable |
| RF | Forecasting, FDD | Yield/load/fault prediction | Robust, nonlinear, ensemble power | Slower, less transparent |
| KNN | Forecasting, FDD | Instance-based prediction | Simple, fast inference | Scaling sensitive, low in high dims |
| Boosting (XGB/LGBM) | Forecasting | Accurate yield/load pred. | High accuracy, scalable | Prone to overfit, needs tuning |
| CNN | FDD, Forecasting | Image/I–V curve analysis | Top image feature extractor | Needs large labeled data, GPU cost |
| RNN/LSTM/GRU | Forecasting, FDD | Time-series pred., temporal faults | Good temporal dynamics | Training complexity, vanishing grads |
| Autoencoders | FDD | Feature extraction, anomaly detect. | Unsupervised, reduces dims | Network-dependent performance |
| K-Means | MPPT | Cluster env. states | Simplifies MPPT search | Sensitive to init., assumes shape |
| Hybrid DL | FDD | Fault classification | Merges DL strengths, ↑ accuracy | Complex, high resource use |
| Hybrid ML-Meta. | MPPT | Robust MPPT tracking | Boosts stability/perf. | More algorithmic overhead |
| Task | Metaheuristics | ML/DL | Hybrid | Key Findings |
|---|---|---|---|---|
| MPPT (PSC) | ✓ Global opt.; ✗ slow, unstable | ✓ Fast post-train; ✗ data-hungry | ✓ GWO-P&O, ANN-GA | Hybrids outperform standalone; K-means helps zone detection; improved tracking under PSC. |
| Layout Opt. | ✓ Combinatorial fit; ✗ geometry limits | ✓ Yield prediction; ✗ not direct search | ✓ ML for fitness est. | ML used to evaluate designs; limited hybrid use; more explicit metaheuristic reporting needed. |
| System Sizing | ✓ Multi-obj.; ✗ model sens. | ✓ Load/gen. forecast; ✗ no sizing logic | ✓ ML + GA/NSGA | Common use of ML inputs in HOMER-based sizing; accurate forecasting improves results. |
| Energy Mgmt. | ✓ Schedule opt.; ✗ real-time issues | ✓ RL/MPC; ✗ error propagation | ✓ MPC + DL/RL | RL enables adaptiveness; DL essential for MPC forecasts; growing interest in real-time control. |
| Fault Diagn. | ✗ Not direct use | ✓ Pattern recog.; ✗ rare fault data | ✓ CNN-RNN, AE-MLP | ML/DL dominant (>95% acc.); metaheuristics used for tuning; hybrid DL models perform best. |
| Method | Accuracy | Adaptability | Complexity | Key Insights |
|---|---|---|---|---|
| Traditional (LP, DP) | ✓ Simple cases | ✗ Limited to static env. | Low–Medium | Suitable for sizing/planning; fails in dynamic/nonlinear scenarios; low computational load. |
| Metaheuristics (PSO, GA) | ✓ Versatile | ✗ Param.-sensitive | Medium–High | Effective in complex optimization; widely used in MPPT/design; tuning affects performance. |
| Machine Learning (NN, etc.) | ✓ High precision | ✓ Learns patterns | High | Accurate prediction and control; data-intensive; real-time potential but hard to interpret. |
| Works | Optimization, Control and Efficiency in PV | Mathematical Modeling, Optimization Techniques and IA | Simulation and Embedded Systems | Classical, Data-Driven Physical Models | AI, Machine Learning, and Algorithms | Application of PRISMA Methodology | Period Search |
|---|---|---|---|---|---|---|---|
| [105] | X | X | X | 2017–2021 | |||
| [106] | X | X | 2016–2022 | ||||
| [107] | X | X | X | X | – | ||
| [108] | X | X | X | 2018–2023 | |||
| [109] | X | X | X | – | |||
| [110] | X | X | X | 2017–2022 | |||
| Our Work | X | X | X | X | X | X | 2019–2025 |
| Review (Year) | Main Focus | Compared Algorithms | Systematic Methodology | N. of Articles | Addressed Gaps | Reported Limitations | Period Search |
|---|---|---|---|---|---|---|---|
| [105] | PV system design and modeling | Traditional + GA | No | 127 | Classical modeling only | No embedded system analysis | 2020–2025 |
| [108] | Forecasting and AI methods | ML, DL (CNN, LSTM) | Partial | 82 | Forecasting focus | No comparison with classical optimization | 2020–2024 |
| [93] | MPPT hybrid techniques | GA, PSO, ANN | No | 54 | GMPP tracking only | Does not analyze computational efficiency | 2020–2025 |
| [94] | Fault detection in PV systems | CNN, Bi-GRU | No | 112 | Fault detection techniques | No computational efficiency analysis | 2023–2025 |
| [100] | Optimal tilt and orientation prediction for PV panels | Ensemble Learning | No | 150 | Optimal tilt prediction | No comparison with traditional optimization methods | 2020–2024 |
| [67] | Rooftop PV system optimization under shading | GA | No | 200 | Shading effects on layout | Limited classical optimization techniques | 2020–2023 |
| Our Works | Integrated PV optimization and diagnosis | GA, PSO, ACO, ML/DL | PRISMA + bibliometrics | 314 | Broad integration (optimization, diagnosis, layout) | High data and computation demand | 2019–2025 |
| Location/Case Study | Modules | Power (kWp) | PR (%)/Efficiency | Method/Tool Used | Reference |
|---|---|---|---|---|---|
| India (Technological Institute) | 360 | 90 | 79 | PVsyst | [111] |
| Iraq (Residential) | 15 | 4.3 | 80–85 | Genetic Algorithm | [112] |
| China (PV Greenhouses) | – | – | 80–90 | Collaborative Optimization | [113] |
| Sweden (Distributed Storage) | – | – | 85–90 | Genetic Algorithm | [114] |
| Pakistan (3 MW Plant) | ∼9000 | 3000 | 82–85 | PVsyst + Critical Parameter Validation | [115] |
| Spain (Grid-Connected Plant) | 1200 | 450 | 83–87 | Hybrid Optimization (GA + ML) | [116] |
| Iran (Hybrid PV/T System) | – | – | 80–88 | AI + Metaheuristic Algorithms | [117] |
| Study/Author (Year) | Approach/Compared Methods | Challenges Identified | Key Remarks |
|---|---|---|---|
| Di Leo (2025) [118] | Physical models, statistical approaches, ML, hybrid methods, metaheuristics | Data quality/availability, computational efficiency, adaptability | Systematic review highlighting advantages and limitations of each method; emphasizes robust data and efficient models. |
| Mamodiya et al. (2025) [119] | MPPT (traditional) vs. Deep Learning hybrids (PINNs + RL + CNN-LSTM on Edge AI) | High computational cost, latency, large datasets, limited interpretability | Achieved 10–15% performance improvement, 40–50% faster response; warns about computational demands and lack of transparency. |
| Nyangiwe et al. (2025) [120] | Multiple regression vs. ML (SVM, Random Forest, clustering, Deep Learning) | Data scarcity and quality, computational cost, interpretability | Review showing ML outperforming classical techniques; stresses challenges of data access and model explainability. |
| Abdelsattar et al. (2025) [121] | SVR, regression, decision trees, ensembles (XGBoost, RF, etc.) | Interpretability, adaptability to nonlinear data, environmental variability | Benchmark on ML methods for PV environment forecasting; integration of SHAP for improved interpretability. |
| Bianchini et al. (2019) [122] | PVUSA model with limited data vs. standard forecasting methods | Lack of meteorological data, model complexity, forecasting accuracy | Efficient low-complexity approach requiring only historical generation and temperature forecasts; useful under scarce data conditions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iturralde Carrera, L.A.; Alfonso-Francia, G.; Constantino-Robles, C.D.; Terven, J.; Chávez-Urbiola, E.A.; Rodríguez-Reséndiz, J. Advances and Optimization Trends in Photovoltaic Systems: A Systematic Review. AI 2025, 6, 225. https://doi.org/10.3390/ai6090225
Iturralde Carrera LA, Alfonso-Francia G, Constantino-Robles CD, Terven J, Chávez-Urbiola EA, Rodríguez-Reséndiz J. Advances and Optimization Trends in Photovoltaic Systems: A Systematic Review. AI. 2025; 6(9):225. https://doi.org/10.3390/ai6090225
Chicago/Turabian StyleIturralde Carrera, Luis Angel, Gendry Alfonso-Francia, Carlos D. Constantino-Robles, Juan Terven, Edgar A. Chávez-Urbiola, and Juvenal Rodríguez-Reséndiz. 2025. "Advances and Optimization Trends in Photovoltaic Systems: A Systematic Review" AI 6, no. 9: 225. https://doi.org/10.3390/ai6090225
APA StyleIturralde Carrera, L. A., Alfonso-Francia, G., Constantino-Robles, C. D., Terven, J., Chávez-Urbiola, E. A., & Rodríguez-Reséndiz, J. (2025). Advances and Optimization Trends in Photovoltaic Systems: A Systematic Review. AI, 6(9), 225. https://doi.org/10.3390/ai6090225









