GT-STAFG: Graph Transformer with Spatiotemporal Attention Fusion Gate for Epileptic Seizure Detection in Imbalanced EEG Data
Abstract
1. Introduction
- To the best of our knowledge, we are the first to propose a graph transformer (GT) integrating both spatial and temporal positional encodings for cross-patient seizure detection. The original graph transformer is extended to additionally handle temporal graph sequences with dynamic and evolving functional brain connectivity for EEG seizure detection, omitting the need for a cascaded model design.
- We propose a Spatiotemporal Attention Fusion Gate (STAFG) technique that incorporates self-attention and a fusion gate mechanism to dynamically combine spatial and temporal positional encodings. This technique constructs node embeddings augmented with spatiotemporal information to enhance the learning potential of the original graph transformer.
- We perform cross-patient evaluation in addition to transfer learning experiments to demonstrate the robustness of the proposed model in realistic clinical settings.
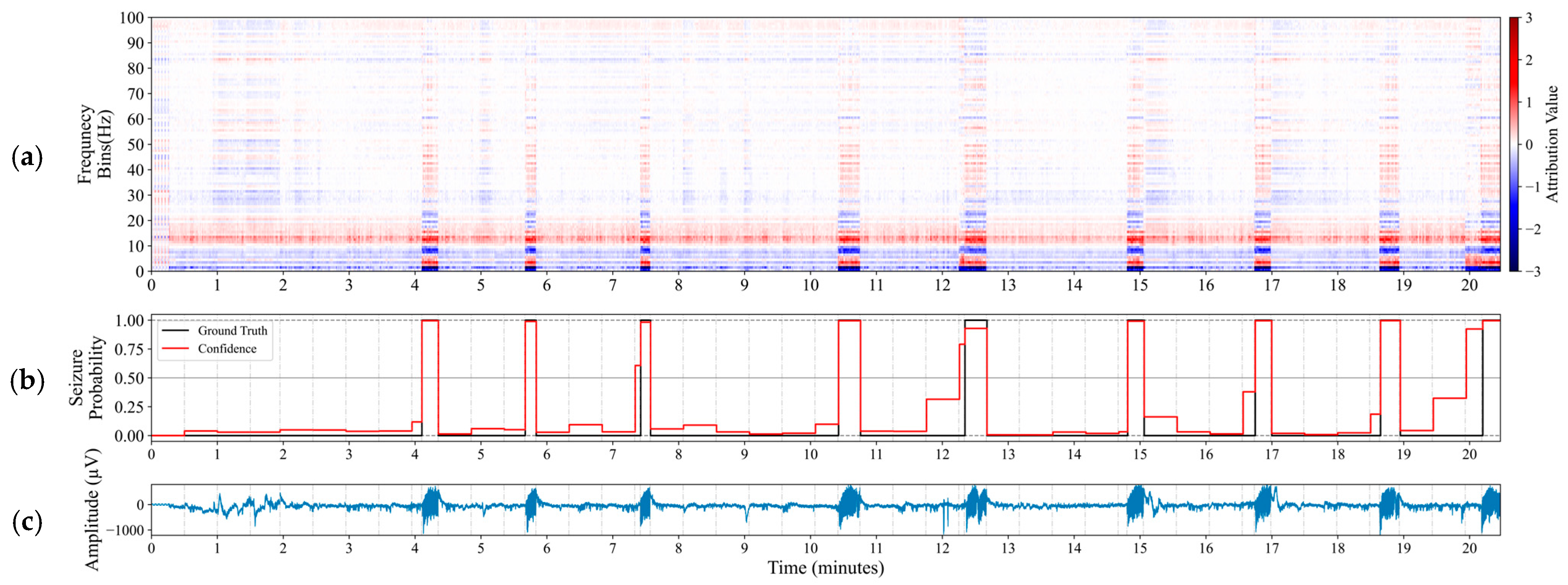
- We utilize Integrated Gradients attribution method to reveal influential frequency bands for identifying seizures and assess the relevance of the proposed model with established clinical biomarkers.
2. Related Works
2.1. Deep Learning for Seizure Detection
2.2. Spatiotemporal Graph Neural Networks
2.3. Transformers and Self-Attention
3. Methods
3.1. Preliminaries
3.2. Proposed Spatiotemporal Attention Fusion Gate
3.3. Feature Attribution Using Integrated Gradients
4. Datasets and Experimental Setup
4.1. Dataset Description and Preparation
4.1.1. TUSZ Dataset
4.1.2. CHB-MIT Dataset
4.1.3. EEG Data Preprocessing
4.1.4. Class Balancing, Data Splitting, and Evaluation Strategy
4.2. Performance and Evaluation Metrics
4.3. Training Setup and Key Parameters
5. Results and Discussion
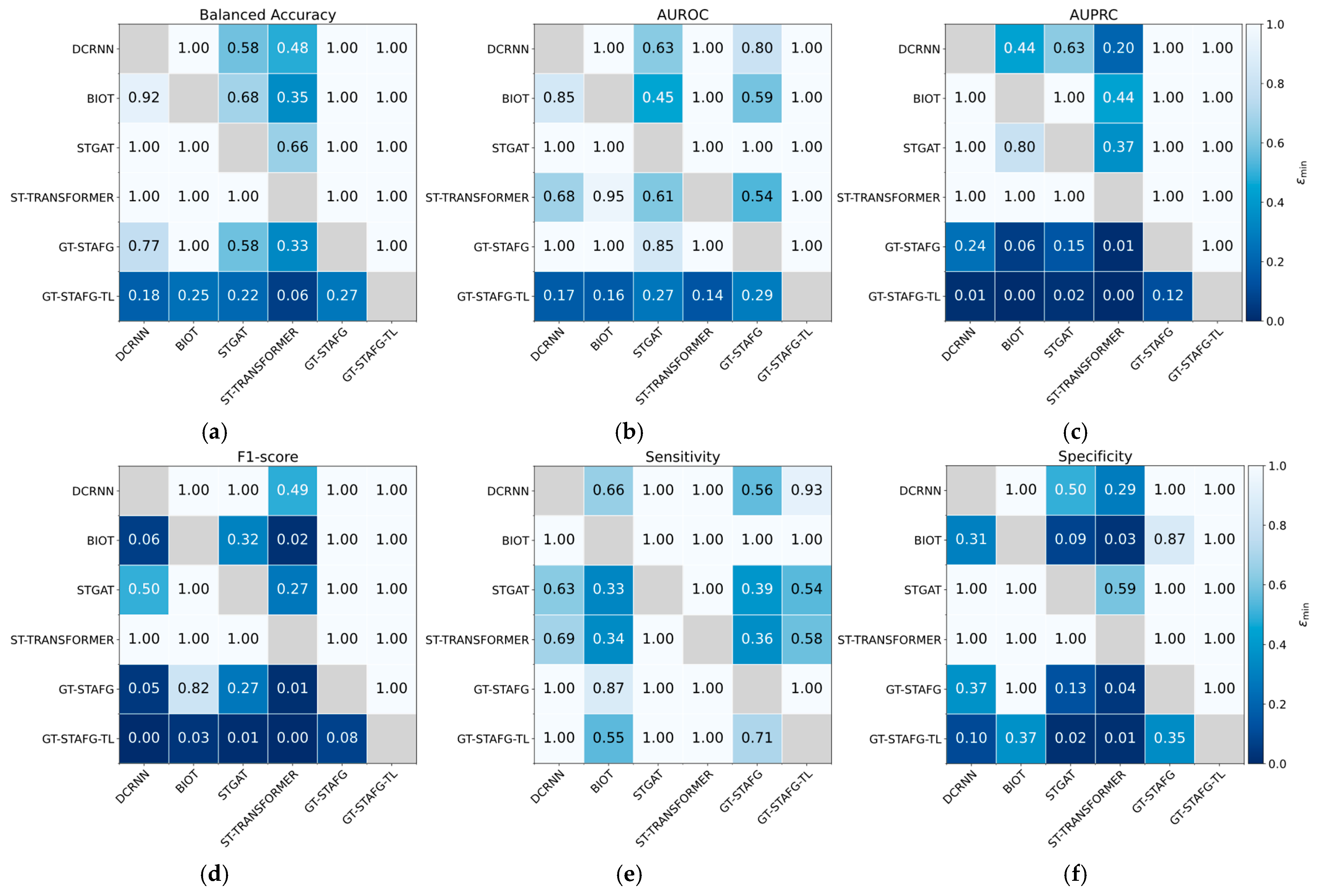
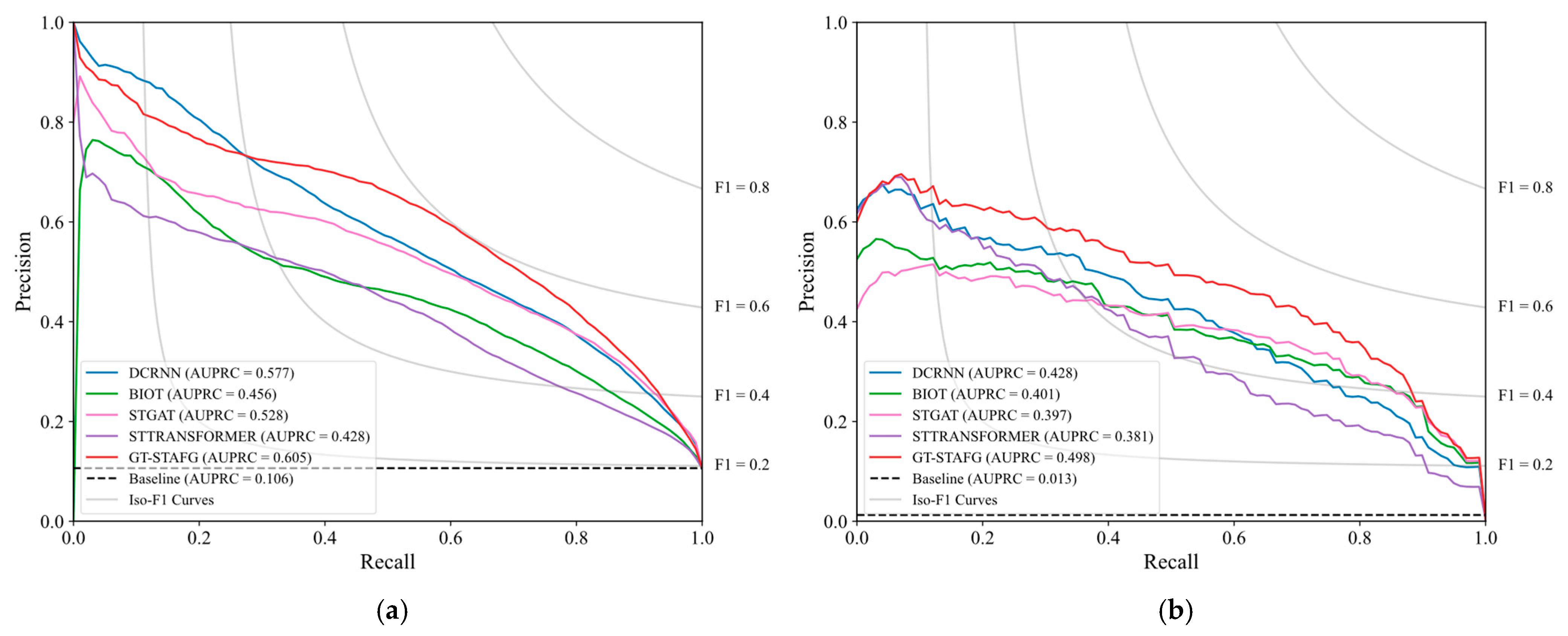
5.1. Performance Compared to Baselines
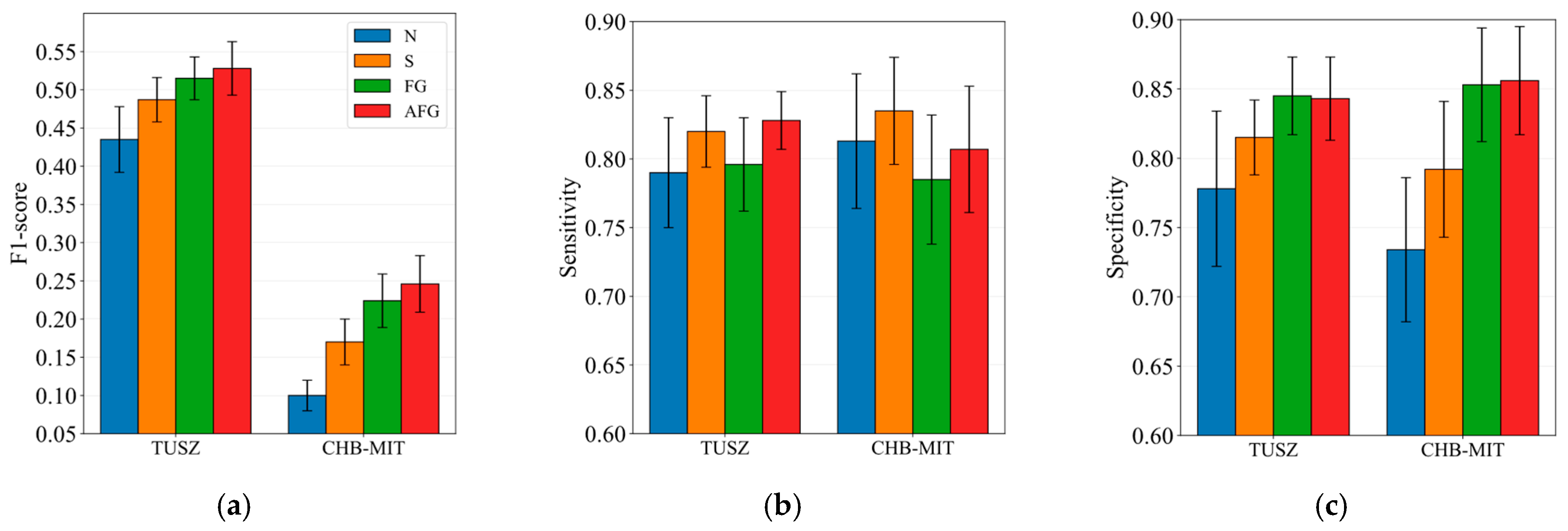
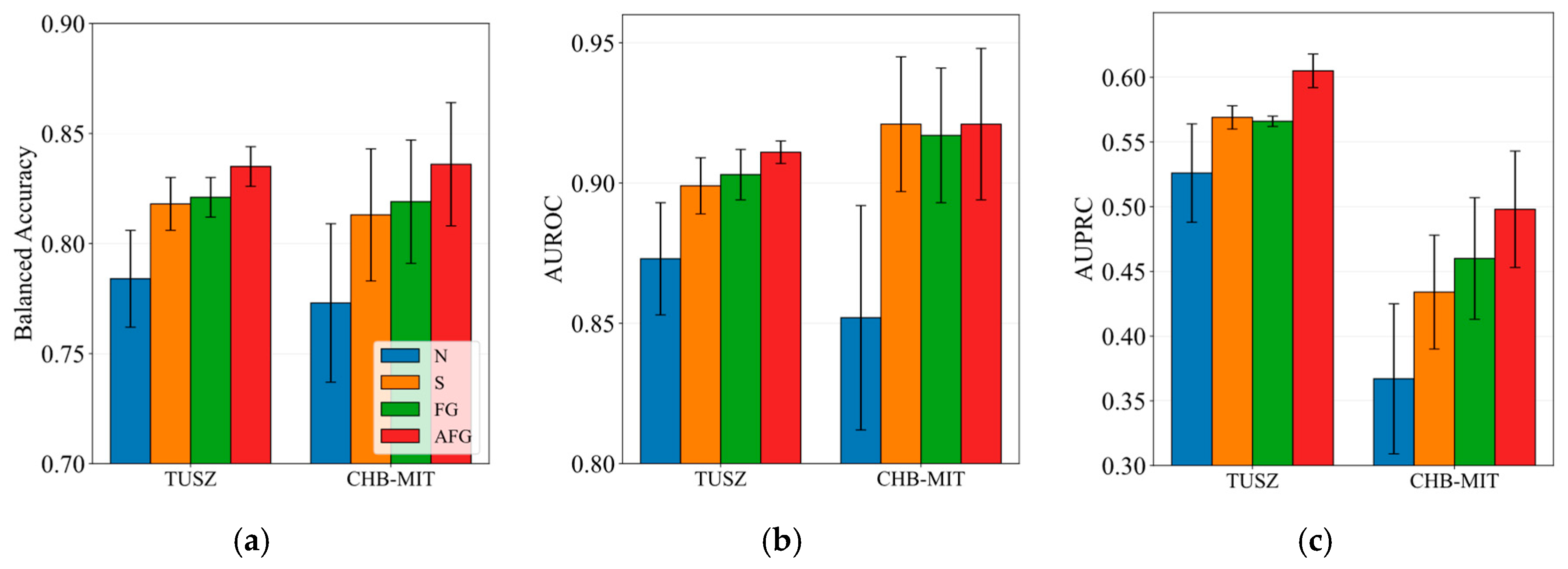
5.2. Impact of Spatiotemporal Attention Fusion Gate
5.3. Feature Attribution and Clinical Practicality
5.4. Transfer Learning
6. Conclusions
- Examine the model’s performance across a range of detection thresholds to find the optimal threshold that aligns with the practical clinical deployment needs.
- Investigate the performance of GT-STAFG on noisy and incomplete EEG data, such as missing and noisy EEG channels.
- Explore Integrated Gradient feature interactions to assess frequency band influence on seizure detection.
- Improve the performance of the transfer learning application.
- Extend the study for seizure type classification and on additional datasets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B
Appendix B.1
| Model | TUSZ | CHB-MIT | ||||
|---|---|---|---|---|---|---|
| F1-Score | Sensitivity | Specificity | F1-Score | Sensitivity | Specificity | |
| DCRNN | 0.490 ± 0.031 | 0.826 ± 0.043 | 0.814 ± 0.043 | 0.139 ± 0.026 | 0.831 ± 0.042 | 0.808 ± 0.045 |
| BIOT | 0.463 ± 0.017 | 0.745 ± 0.037 | 0.824 ± 0.025 | 0.240 ± 0.034 | 0.794 ± 0.040 | 0.860 ± 0.036 |
| STGAT | 0.483 ± 0.062 | 0.835 ± 0.057 | 0.801 ± 0.084 | 0.167 ± 0.034 | 0.847 ± 0.040 | 0.773 ± 0.048 |
| ST-TRANSFORMER | 0.436 ± 0.029 | 0.694 ± 0.078 | 0.820 ± 0.062 | 0.118 ±0.024 | 0.847 ± 0.038 | 0.747 ± 0.051 |
| GT-STAFG (proposed) | 0.528 ± 0.035 | 0.828 ± 0.021 | 0.843 ± 0.030 | 0.246 ± 0.037 | 0.807 ± 0.046 | 0.856 ± 0.039 |

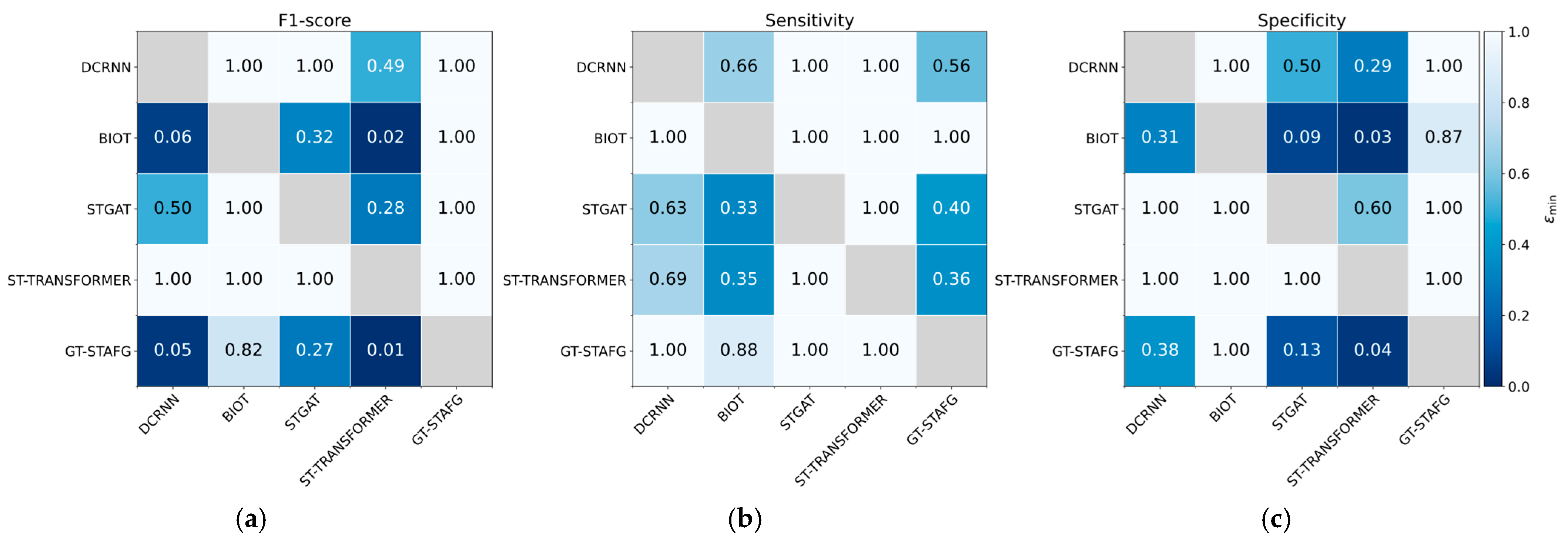
| Model | Pairwise Dominance Points | Rank |
|---|---|---|
| DCRNN | 0 | 3rd * |
| BIOT | 4 | 2nd |
| STGAT | 0 | 4th * |
| ST-TRANSFORMER | 0 | 5th * |
| GT-STAFG (proposed) | 7 | 1st |
Appendix B.2
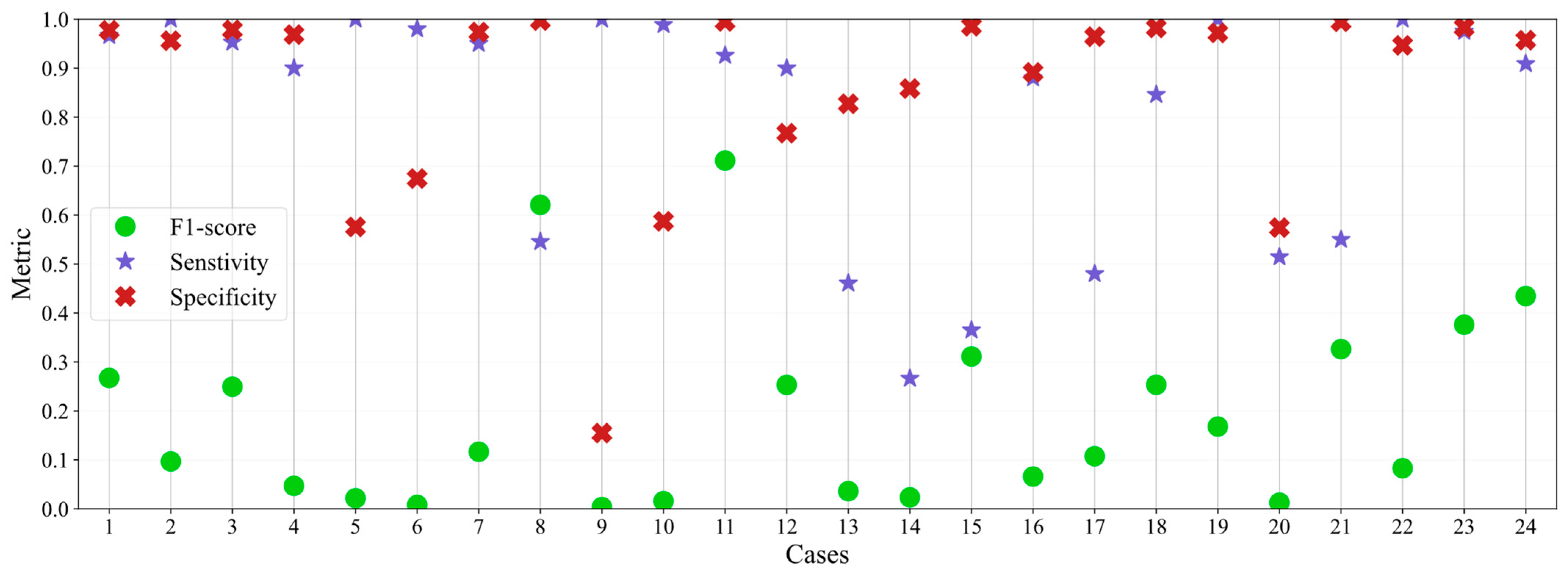
Appendix B.3
Appendix B.4
| F1-Score | Sensitivity | Specificity |
|---|---|---|
| 0.285 ± 0.041 (+0.039) † | 0.820 ± 0.041 (+0.013) † | 0.900 ± 0.032 (+0.044) † |
References
- Nafea, M.S.; Ismail, Z.H. Supervised Machine Learning and Deep Learning Techniques for Epileptic Seizure Recognition Using EEG Signals: A Systematic Literature Review. Bioengineering 2022, 9, 781. [Google Scholar] [CrossRef]
- Saab, K.; Dunnmon, J.; Ré, C.; Rubin, D.; Lee-Messer, C. Weak Supervision as an Efficient Approach for Automated Seizure Detection in Electroencephalography. NPJ Digit. Med. 2020, 3, 59. [Google Scholar] [CrossRef]
- Sinha, S.R.; Sullivan, L.; Sabau, D.; San-Juan, D.; Dombrowski, K.E.; Halford, J.J.; Hani, A.J.; Drislane, F.W.; Stecker, M.M. American Clinical Neurophysiology Society Guideline 1: Minimum Technical Requirements for Performing Clinical Electroencephalography. J. Clin. Neurophysiol. 2016, 33, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Shoeibi, A.; Khodatars, M.; Ghassemi, N.; Jafari, M.; Moridian, P.; Alizadehsani, R.; Panahiazar, M.; Khozeimeh, F.; Zare, A.; Hosseini-Nejad, H.; et al. Epileptic Seizures Detection Using Deep Learning Techniques: A Review. Int. J. Environ. Res. Public Health 2021, 18, 5780. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Yuan, X.; Radfar, M.; Marendy, P.; Ni, W.; O’Brien, T.J.; Casillas-Espinosa, P. Graph Signal Processing, Graph Neural Network and Graph Learning on Biological Data: A Systematic Review. IEEE Rev. Biomed. Eng. 2023, 16, 109–135. [Google Scholar] [CrossRef] [PubMed]
- Cong, S.; Wang, H.; Zhou, Y.; Wang, Z.; Yao, X.; Yang, C. Comprehensive Review of Transformer-based Models in Neuroscience, Neurology, and Psychiatry. Brain-X 2024, 2, e57. [Google Scholar] [CrossRef]
- Craik, A.; He, Y.; Contreras-Vidal, J.L. Deep Learning for Electroencephalogram (EEG) Classification Tasks: A Review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef]
- Klepl, D.; Wu, M.; He, F. Graph Neural Network-Based EEG Classification: A Survey. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 493–503. [Google Scholar] [CrossRef]
- Jang, S.; Moon, S.-E.; Lee, J.S. EEG-Based Video Identification Using Graph Signal Modeling and Graph Convolutional Neural Network. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3066–3070. [Google Scholar]
- Veličković, P.; Casanova, A.; Liò, P.; Cucurull, G.; Romero, A.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–12. [Google Scholar]
- Dwivedi, V.P.; Bresson, X. A Generalization of Transformer Networks to Graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Ye, Z.; Kumar, Y.J.; Sing, G.O.; Song, F.; Wang, J. A Comprehensive Survey of Graph Neural Networks for Knowledge Graphs. IEEE Access 2022, 10, 75729–75741. [Google Scholar] [CrossRef]
- He, J.; Cui, J.; Zhao, Y.; Zhang, G.; Xue, M.; Chu, D. Spatial-Temporal Seizure Detection with Graph Attention Network and Bi-Directional LSTM Architecture. Biomed. Signal Process Control 2022, 78, 103908. [Google Scholar] [CrossRef]
- Shan, X.; Cao, J.; Huo, S.; Chen, L.; Sarrigiannis, P.G.; Zhao, Y. Spatial–Temporal Graph Convolutional Network for Alzheimer Classification Based on Brain Functional Connectivity Imaging of Electroencephalogram. Hum. Brain Mapp. 2022, 43, 5194–5209. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5999–6009. [Google Scholar]
- Li, Q.; Zhang, T.; Song, Y.; Sun, M. Transformer-Based Spatial-Temporal Feature Learning for P300. In Proceedings of the 2022 16th ICME International Conference on Complex Medical Engineering, CME 2022, Zhongshan, China, 4–6 November 2022; pp. 310–313. [Google Scholar]
- Yang, C.; Brandon Westover, M.; Sun, J. BIOT: Biosignal Transformer for Cross-Data Learning in the Wild. Adv. Neural Inf. Process Syst. 2023, 36, 78240–78260. [Google Scholar]
- Tang, S.; Dunnmon, J.A.; Saab, K.; Zhang, X.; Huang, Q.; Dubost, F.; Rubin, D.L.; Lee-Messer, C. Self-Supervised Graph Neural Networks for Improved Electroencephalographic Seizure Analysis. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Tian, X.; Jin, Y.; Zhang, Z.; Liu, P.; Tang, X. Spatial-Temporal Graph Transformer Network for Skeleton-Based Temporal Action Segmentation. Multimed. Tools Appl. 2023, 83, 44273–44297. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Cui, W.G.; Guo, Y.Z.; Huang, H.; Hu, Z.Y. Epileptic Seizure Detection in EEG Signals Using a Unified Temporal-Spectral Squeeze-and-Excitation Network. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 782–794. [Google Scholar] [CrossRef]
- Peng, R.; Zhao, C.; Jiang, J.; Kuang, G.; Cui, Y.; Xu, Y.; Du, H.; Shao, J.; Wu, D. TIE-EEGNet: Temporal Information Enhanced EEGNet for Seizure Subtype Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2567–2576. [Google Scholar] [CrossRef]
- Thuwajit, P.; Rangpong, P.; Sawangjai, P.; Autthasan, P.; Chaisaen, R.; Banluesombatkul, N.; Boonchit, P.; Tatsaringkansakul, N.; Sudhawiyangkul, T.; Wilaiprasitporn, T. EEGWaveNet: Multiscale CNN-Based Spatiotemporal Feature Extraction for EEG Seizure Detection. IEEE Trans. Industr Inform. 2022, 18, 5547–5557. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Cheng, Y.; He, Z.; Wei, X.; Chen, Z.; Zhou, Y. A Spatiotemporal Graph Attention Network Based on Synchronization for Epileptic Seizure Prediction. IEEE J. Biomed. Health Inform. 2023, 27, 900–911. [Google Scholar] [CrossRef]
- Feng, L.; Cheng, C.; Zhao, M.; Deng, H.; Zhang, Y. EEG-Based Emotion Recognition Using Spatial-Temporal Graph Convolutional LSTM with Attention Mechanism. IEEE J. Biomed. Health Inform. 2022, 26, 5406–5417. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Hu, C.; Yin, Z.; Song, Y. Transformers for EEG-Based Emotion Recognition: A Hierarchical Spatial Information Learning Model. IEEE Sens. J. 2022, 22, 4359–4368. [Google Scholar] [CrossRef]
- Wan, Z.; Li, M.; Liu, S.; Huang, J.; Tan, H.; Duan, W. EEGformer: A Transformer–Based Brain Activity Classification Method Using EEG Signal. Front. Neurosci. 2023, 17, 1148855. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, X.; Zhang, B.; Xiao, S.; Weng, S. CTNet: A Convolutional Transformer Network for EEG-Based Motor Imagery Classification. Sci. Rep. 2024, 14, 20237. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A Compact Convolutional Neural Network for EEG-Based Brain–Computer Interfaces. J. Neural Eng. 2018, 15, 56013. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.; Li, Y.; Wu, X.; Dong, Y.; Wen, X.; Niu, Y. Synchronization-Based Graph Spatio-Temporal Attention Network for Seizure Prediction. Sci. Rep. 2025, 15, 4080. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, V.P.; Luu, A.T.; Laurent, T.; Bengio, Y.; Bresson, X. Graph Neural Networks With Learnable Structural and Positional Representations. In Proceedings of the ICLR 2022—10th International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Arevalo, J.; Solorio, T.; Montes-Y-Gómez, M.; González, F.A. Gated Multimodal Units for Information Fusion. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Workshop Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. (Integrated Gradient) Axiomatic Attribution for Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, Australia, 6–11 August 2017; Volume 7, pp. 5109–5118. [Google Scholar]
- Shah, V.; von Weltin, E.; Lopez, S.; McHugh, J.R.; Veloso, L.; Golmohammadi, M.; Obeid, I.; Picone, J. The Temple University Hospital Seizure Detection Corpus. Front. Neuroinform. 2018, 12, 83. [Google Scholar] [CrossRef]
- Shoeb, A.; Guttag, J. CHB-MIT Dataset. In Proceedings of the ICML 2010—Proceedings, 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 975–982. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Del Barrio, E.; Cuesta-Albertos, J.A.; Matrán, C. An Optimal Transportation Approach for Assessing Almost Stochastic Order BT—The Mathematics of the Uncertain: A Tribute to Pedro Gil; Gil, E., Gil, E., Gil, J., Gil, M.Á., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 33–44. ISBN 978-3-319-73848-2. [Google Scholar]
- Dror, R.; Shlomov, S.; Reichart, R. Deep Dominance—How to Properly Compare Deep Neural Models. In Proceedings of the ACL 2019—57th Annual Meeting of the Association for Computational Linguistics, Proceedings of the Conference, Florence, Italy, 28 July–2 August 2019; pp. 2773–2785. [Google Scholar]
- Ulmer, D.; Hardmeier, C.; Frellsen, J. Deep-Significance—Easy and Meaningful Statistical Significance Testing in the Age of Neural Networks. arXiv 2022, arXiv:2204.06815. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process Syst. 2012, 4, 2951–2959. [Google Scholar]
- Rampášek, L.; Galkin, M.; Dwivedi, V.P.; Luu, A.T.; Wolf, G.; Beaini, D. Recipe for a General, Powerful, Scalable Graph Transformer. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35. [Google Scholar]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef]
- Ali, E.; Angelova, M.; Karmakar, C. Epileptic Seizure Detection Using CHB-MIT Dataset: The Overlooked Perspectives. R. Soc. Open Sci. 2024, 11, 230601. [Google Scholar] [CrossRef] [PubMed]
- Weiss, S.; Mueller, H.M. “Too Many Betas Do Not Spoil the Broth”: The Role of Beta Brain Oscillations in Language Processing. Front. Psychol. 2012, 3, 201. [Google Scholar] [CrossRef] [PubMed]
- De Stefano, P.; Carboni, M.; Marquis, R.; Spinelli, L.; Seeck, M.; Vulliemoz, S. Increased Delta Power as a Scalp Marker of Epileptic Activity: A Simultaneous Scalp and Intracranial Electroencephalography Study. Eur. J. Neurol. 2022, 29, 26–35. [Google Scholar] [CrossRef] [PubMed]
- Kakisaka, Y.; Alexopoulos, A.V.; Gupta, A.; Wang, Z.I.; Mosher, J.C.; Iwasaki, M.; Burgess, R.C. Generalized 3-Hz Spike-and-Wave Complexes Emanating from Focal Epileptic Activity in Pediatric Patients. Epilepsy Behav. 2011, 20, 103–106. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Chen, X.; Morehead, A.; Liu, J.; Cheng, J. A Gated Graph Transformer for Protein Complex Structure Quality Assessment and Its Performance in CASP15. Bioinformatics 2023, 39, I308–I317. [Google Scholar] [CrossRef]

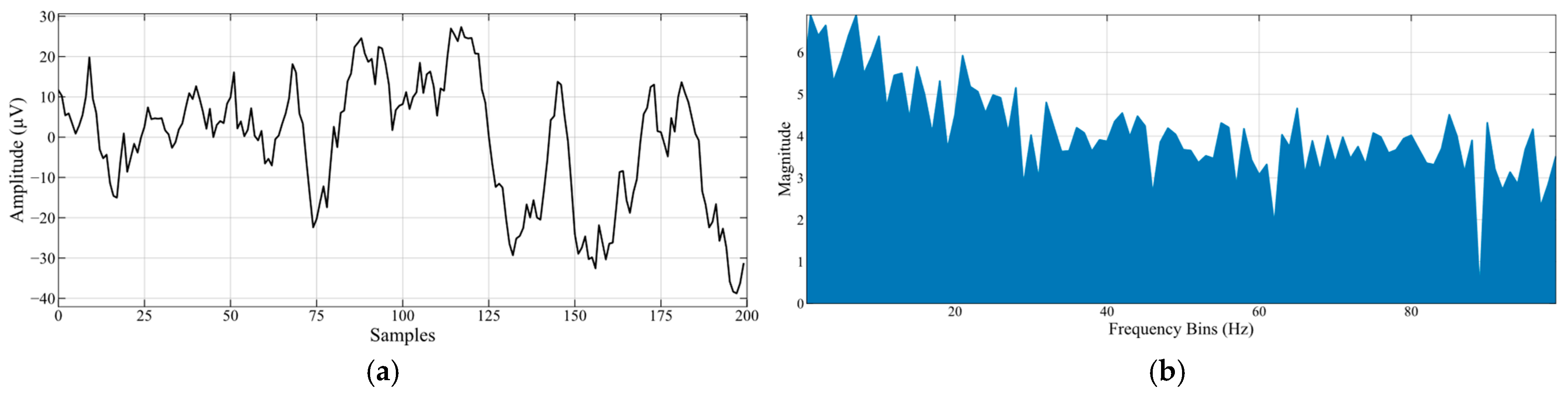


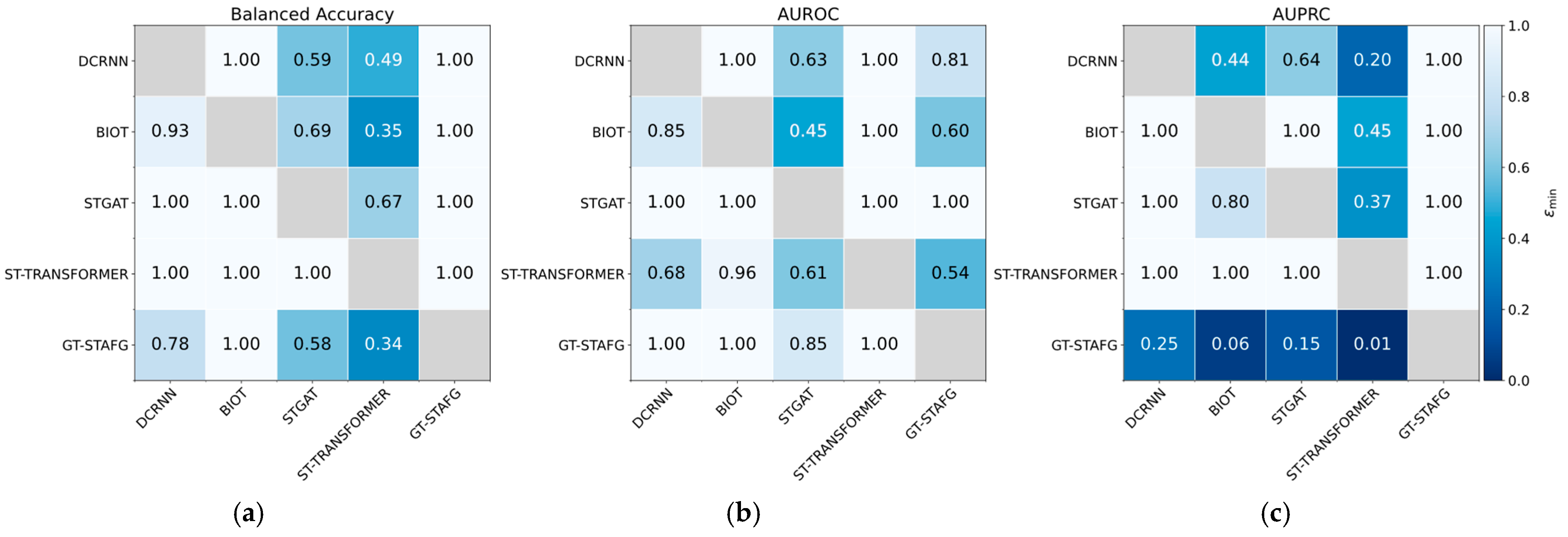


| Dataset | Split | Number of EEG Clips (Non-Seizure) | Number of EEG Clips (Seizure) |
|---|---|---|---|
| TUSZ | Training | 6314 | 5853 |
| Validation | 10,764 | 1058 | |
| Test | 16,671 | 1986 | |
| CHB-MIT | Training * | 1386 | 1311 |
| Validation * | 9687 | 124 | |
| Test * | 4843 | 62 |
| Key Parameter | Value Range | Optimal Value |
|---|---|---|
| ) | {2, 3, 4} | 3 |
| Hidden dimension size (d) | {64, 128, 256} | 128 |
| Spatial positional encoding (SPE) | {LPE, RWPE} | RWPE |
| Number of Random Walk steps | {3, 4, 5, 6} | 4 |
| Number of graph transformer layers | {1, 2, 4, 8} | 4 |
| Attention heads (H)/(P) | {4, 8, 16} | 8/8 |
| Number of FC layers (Classifier Head) | {1, 2, 3, 4} | 2 |
| Dropout probability (GT Layers) | {0.0, 0.1, 0.2} | 0.2 |
| Dropout probability (Classifier Head) | {0.0, 0.1, 0.2} | 0.0 |
| Layer | Input Size | Output Size | Other Parameters | |
|---|---|---|---|---|
| Input Layers | Node embedding | |||
| Edge embedding | ||||
| Node Positional Encoding | TPE embedding | |||
| SPE embedding | ||||
| Spatiotemporal Attention Fusion Gate (STAFG) | TPE attention module | |||
| SPE attention module | ||||
| Fusion Gate | ||||
| Graph Transformer (GT) Block | 4 | |||
| Graph Readout (mean) | ||||
| Classifier Head | FC layer 1 | |||
| FC layer 2 | ||||
| Model | TUSZ | CHB-MIT | ||||
|---|---|---|---|---|---|---|
| BA | AUROC | AUPRC | BA | AUROC | AUPRC | |
| DCRNN | 0.820 ± 0.003 | 0.899 ± 0.003 | 0.577 ± 0.023 | 0.819 ± 0.027 | 0.918 ± 0.023 | 0.428 ± 0.054 |
| BIOT | 0.784 ± 0.008 | 0.864 ± 0.006 | 0.456 ± 0.030 | 0.827 ± 0.025 | 0.924 ± 0.020 | 0.387 ± 0.050 |
| STGAT | 0.818 ± 0.015 | 0.899 ± 0.008 | 0.528 ± 0.028 | 0.810 ± 0.029 | 0.914 ± 0.028 | 0.397 ± 0.059 |
| ST-TRANSFORMER | 0.757 ± 0.008 | 0.847 ± 0.003 | 0.428 ± 0.025 | 0.797 ±0.027 | 0.919 ± 0.017 | 0.351 ± 0.041 |
| GT-STAFG (proposed) | 0.835 ± 0.009 | 0.911 ± 0.004 | 0.605 ± 0.013 | 0.831 ± 0.028 | 0.921 ± 0.027 | 0.498 ± 0.045 |
| Technique | Description |
|---|---|
| N | No positional encodings are used. |
| S | Spatial and temporal positional encodings are directly added to the node embeddings. |
| FG | Spatial and temporal positional encodings are fused via a fusion gate, then added to the node embeddings. |
| AFG (proposed) | Spatial and temporal positional encodings are separately added to the node embeddings, processed by separate attention mechanisms, fused via a fusion gate, and combined with original node embeddings via a residual connection. |
| BA | AUROC | AUPRC |
|---|---|---|
| 0.860 ± 0.022 (+0.029) † | 0.955 ± 0.015 (+0.034) † | 0.581 ± 0.041 (+0.083) † |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafea, M.S.; Ismail, Z.H. GT-STAFG: Graph Transformer with Spatiotemporal Attention Fusion Gate for Epileptic Seizure Detection in Imbalanced EEG Data. AI 2025, 6, 120. https://doi.org/10.3390/ai6060120
Nafea MS, Ismail ZH. GT-STAFG: Graph Transformer with Spatiotemporal Attention Fusion Gate for Epileptic Seizure Detection in Imbalanced EEG Data. AI. 2025; 6(6):120. https://doi.org/10.3390/ai6060120
Chicago/Turabian StyleNafea, Mohamed Sami, and Zool Hilmi Ismail. 2025. "GT-STAFG: Graph Transformer with Spatiotemporal Attention Fusion Gate for Epileptic Seizure Detection in Imbalanced EEG Data" AI 6, no. 6: 120. https://doi.org/10.3390/ai6060120
APA StyleNafea, M. S., & Ismail, Z. H. (2025). GT-STAFG: Graph Transformer with Spatiotemporal Attention Fusion Gate for Epileptic Seizure Detection in Imbalanced EEG Data. AI, 6(6), 120. https://doi.org/10.3390/ai6060120







