Quantum Artificial Intelligence: Some Strategies and Perspectives
Abstract
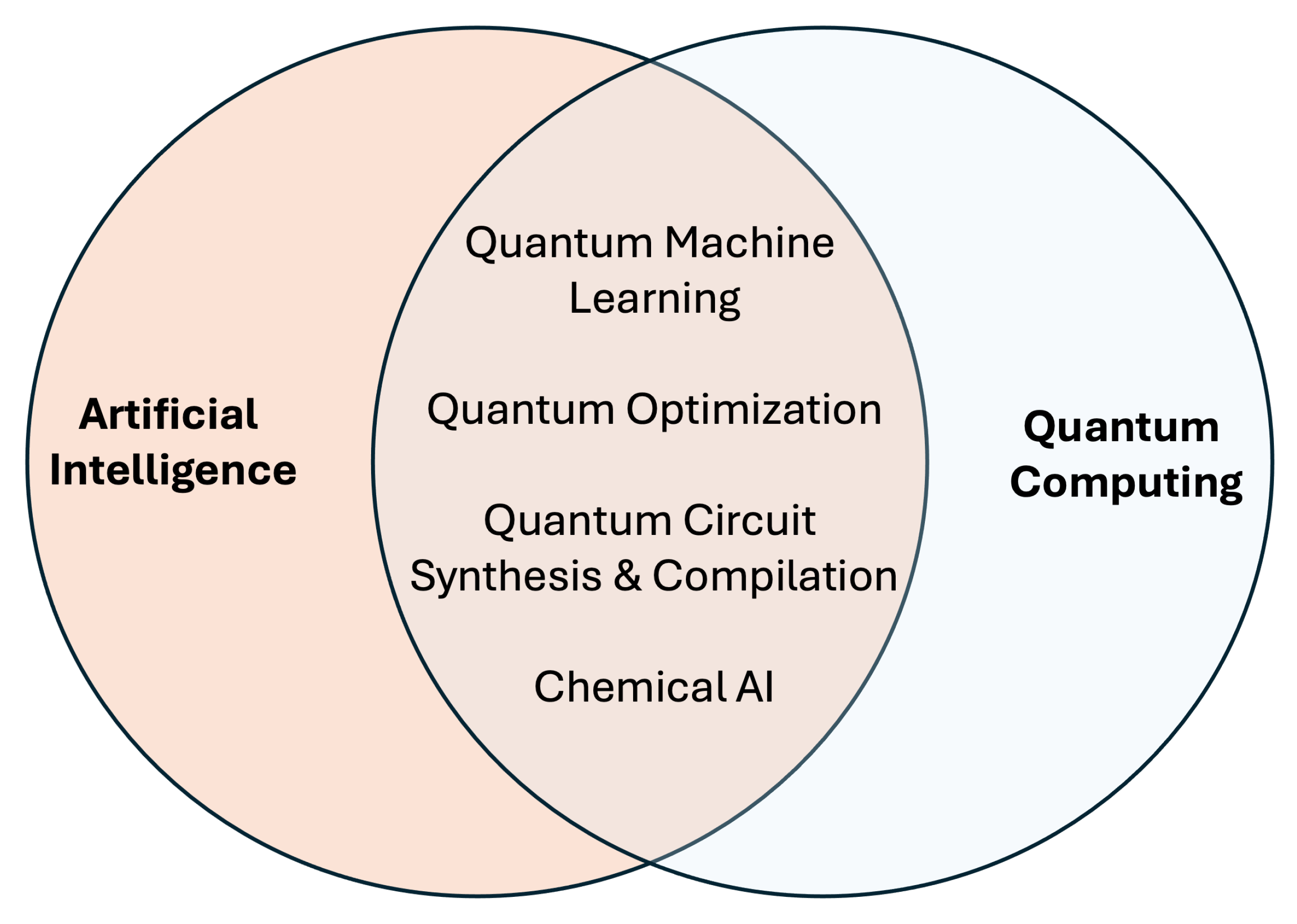
1. Introduction
2. Chemical Contributions to Quantum AI
Perspectives for Chemical AI on QAI
3. Optimisation with Quantum Computing Devices
3.1. Gate Based
3.2. Quantum Annealers
3.3. Perspectives
4. New Paradigms for Quantum Machine Learning
4.1. Incremental Learning
- Unitary nature. Quantum states evolve reversibly, meaning that updates do not erase previously acquired knowledge unless a measurement is performed. Additionally, the intrinsic modularity of quantum circuits may facilitate the selective updating of subspaces within the represented Hilbert space.
- Enhanced representational space. Classical data can be encoded as quantum states corresponding to points in the Hilbert space. This encoding provides access to exponentially larger representation spaces. For example, a classical feature vector with three entries can be mapped to an eight-dimensional quantum space (), enabling richer data representations that may better capture real-world distributions.
- Model adaptability through VQAs. Incremental learning necessitates the use of models that can adapt to new data. Variational quantum circuits are composed of parameterised quantum gates whose parameter values are tuned through a refinement process that embeds the properties of data through the gradual processing of data. Thus, when concept drift occurs, existing quantum models can be adjusted by updating their parameters, ensuring adaptability and extendibility without requiring retraining from scratch. Moreover, quantum circuits often rely on a smaller number of parameters compared to classical neural networks. This can lead to reduced optimisation effort when updating parameters, in contrast to what typically occurs in classical computation.
- Capturing evolving interrelationships. In incremental learning, data often violate the assumptions of independence and identical distributions. Features may be interrelated, and these relationships can evolve over time. Classical deep learning approaches, such as convolutional neural networks, address this property through specialised architectures. In contrast, QC inherently accounts for feature interdependencies using gate-based operations for qubit registers. For instance, controlled gates have the ability to handle relationships of the form event–action. Entanglement circuits, a hallmark of quantum computing, are particularly effective in capturing nonlocal correlations, offering a natural mechanism for modelling complex dependencies without explicitly modelling all pairwise interactions. They have been demonstrated to be accurate in the real-world application of document classification thanks to the accommodation of high-dimensional correlations among words.
- Simultaneous evaluation of hypothesis. To keep the model up-to-date with time, multiple model adaptations or feature-combination strategies are often needed. Superposition enables the evaluation of all these candidate hypotheses in parallel, which can accelerate the search for an optimal update and reduce the overhead of sequential testing.
- Supervised Learning, used to train and update classification models;
- Unsupervised Learning, used to detect significant data changes, triggering model adaptation when necessary.
4.2. Sequence Modelling
4.3. Perspectives
5. The Quantum-Circuit Compilation Problem and Qubit Routing
- a synthesis of recent developments, technologies, and emerging ideas that have shaped the field so far;
- a description and comparison of existing techniques and approaches, highlighting their main characteristics and reported performance;
- a presentation of relevant contributions that provide a foundation for understanding current challenges and potential future directions.
5.1. The Need for Quantum-Circuit Compilation
- Initial Mapping: Initially assigning logical qubits to physical qubits such that the execution is optimised.
- Routing: Ensuring that all two-qubit gates can be executed by inserting additional SWAP gates if necessary.
- Optimisation: Minimising depth, gate count, and error rates to improve execution fidelity.
5.2. Routing Techniques and Compilation Strategies
- 1.
- Heuristic-Based Approaches: Heuristic methods aim to find good, but not necessarily optimal, qubit mappings within a reasonable runtime. Examples include:
- Qiskit’s SABRE (Swap-Based Reordering Algorithm): An iterative heuristic that dynamically selects SWAP gates to optimize circuit depth and reduce overall gate overhead [84]. SABRE is an algorithm designed for NISQ devices regardless of their qubit-connectivity structure. Its high performance is guaranteed by the use of three key strategies that can be individually selected: (i) optimising each individual search step, (ii) refining the initial qubit placement with a unique reverse traversal method, and (iii) incorporating a decay effect to balance circuit depth and gate count. By leveraging these improvements, SABRE has increased its speed considerably compared to the best-known approaches at the time of its presentation.
- t|ket> by Cambridge Quantum Computing: Almost simultaneously with the previous procedure, another routing algorithm was proposed in [85] by the name of t|ket>. t|ket> is a graph-based hardware-agnostic quantum compiler developed by Cambridge Quantum Computing Ltd. that performs qubit allocation and routing efficiently, focusing on minimising the circuit depth. At the time of its introduction, the heuristic method employed in t|ket> achieved circuit mappings that were competitive with or superior to those produced by other systems, minimising both circuit depth and total gate count; it was particularly effective for larger quantum circuits.
- ZX-Calculus Methods: Techniques that use graphical calculus for quantum circuits to optimize and transform circuit layouts [86]. In slightly more detail, ZX-Calculus represents quantum circuits using a diagrammatic notation that makes use of Z-spiders and X-spiders diagrams, with each denoting specific quantum operations. These diagrams enable algebraic manipulations that simplify circuits, making it easier to optimize and transform them for hardware execution. The utilisation of ZX-Calculus for quantum compilation goes typically beyond the acceptance of routing and is particularly useful for the following applications: (i) circuit optimisation, as it allows for algebraic rewrites that reduce gate count and circuit depth; (ii) gate synthesis, as it facilitates the decomposition of high-level quantum operations into hardware-native gates; and (iii) error reduction, as it minimizes the number of error-prone operations like SWAP gates, improving fidelity on NISQ devices.
- These heuristics work well in practical scenarios where exact solutions are computationally prohibitive, offering an effective trade-off between compilation time and circuit efficiency. Additionally, some of these methods integrate error-aware routing strategies, selecting paths that minimize the use of particularly noisy qubits or gates.
- 2.
- Exact Optimisation Methods: Some approaches use combinatorial optimisation techniques to find the best possible routing solutions. These include the following:
- Integer Linear Programming (ILP): Formulating the routing problem as an ILP and solving it using standard solvers to find globally optimal solutions. One remarkable result of this approach is presented in [87], where the goal of adapting a logical quantum circuit to a hardware architecture characterised by constrained two-qubit connectivity is tackled by formulating the problem as an integer linear program (ILP) and employing a network flow-based approach with binary decision variables to simultaneously determine both the initial qubit placement and the routing strategy. The model used here incorporates multiple optimisation objectives, including approximations of circuit fidelity, overall depth, and cross-talk mitigation, all of which can be flexibly integrated. Through numerical experiments on various synthetic datasets and diverse hardware configurations, the authors demonstrate that circuit depth and error rate can be jointly optimised with minimal trade-offs. Additionally, the approach is evaluated on an extensive set of quantum volume circuits, prioritising both fidelity and depth reduction. Obtained results indicate the feasibility of using the method to both decrease the number of CNOT (Controlled-NOT) gates compared to Qiskit’s standard transpilation algorithm, SABRE (see above), and exhibit superior fidelity when executed on real quantum hardware.
- SAT Solvers: Encoding the routing problem as a Boolean satisfiability problem to determine optimal solutions. A representative example of this approach is in reference [88]. In this work, the authors propose a novel approach to circuit mapping that leverages a hybrid incremental and parallel Boolean Satisfiability (SAT) solving strategy. The proposed method introduces an advanced SAT encoding tailored specifically for circuit mapping, significantly enhancing the efficiency of solver-based techniques while offering a flexible balance between compilation speed and output quality. To assess its effectiveness, an extensive benchmarking on 78 test cases was conducted, covering three different quantum algorithms and two distinct quantum hardware architectures. Experimental results show that the proposed approach significantly accelerates compilation compared to existing solver-based methods, reducing processing times from impractical durations to much more feasible ones. Additionally, it outperforms leading heuristic techniques by effectively minimising the number of SWAP gates, thereby enhancing execution fidelity on near-term quantum hardware.
- Constraint Programming (CP) Approaches: Methods that leverage constraint-satisfaction techniques to ensure the best qubit allocation and gate reordering. Beyond the integer linear programming models that solve the qubit-assignment problem and the routing problem optimally by mathematically encoding both constraints and objective functions and leveraging automated solvers to generate hardware-compliant circuits with minimal overhead, alternative approaches that exploit a different optimisation framework, such as constraint programming (CP), can be explored. In [89], the authors use the CP approach and benchmark their results against the ILP for minimising circuit depth. The evaluation was conducted on randomly generated instances across both linear and two-dimensional grid-based hardware architectures and demonstrated that CP-based methods not only achieve superior solution quality but also outperform ILP models in computational efficiency.
- Although exact methods provide optimal solutions, they are often computationally expensive and may not scale well for larger circuits. Moreover, these approaches must also be adapted to account for noise, ensuring that optimality in terms of depth or gate count does not come at the cost of excessive error accumulation.
- 3.
- Machine Learning-Based Methods: Recent advances suggest that reinforcement learning and deep learning techniques can enhance routing strategies by learning optimal SWAP insertion policies from data. Notable contributions include:
- Graph Neural Networks (GNNs) for Compilation: Graph Neural Networks (GNNs) have emerged as powerful tools for tackling the quantum- compilation problem through leveraging of their ability to model the intricate connectivity constraints of quantum hardware, enabling optimised qubit allocation and the implementation of routing decisions that enhance circuit fidelity and execution efficiency. In [90], the authors address the qubit-allocation problem, leveraging reinforcement learning (RL) with techniques from graph neural networks (GNNs). By modelling the quantum hardware’s connectivity as a graph and applying GNN-assisted decision-making, the proposed method identifies optimal initial layouts that reduce error rates. Empirical results demonstrate that this strategy improves output fidelity compared to traditional allocation methods. Another significant example is reference [91], in which a solution is proposed that incorporates Monte Carlo Tree Search (MCTS), allowing an intelligent exploration of routing decisions. Augmented by graph neural networks, this approach evaluates action probabilities and state values, effectively guiding the search toward depth-minimised solutions. Additionally, a novel mutex-lock-inspired technique is introduced to enhance parallelisation, further reducing circuit depth. By respectively integrating GNNs for qubit allocation and MCTS for optimised qubit routing, both previous compilation strategies significantly enhance quantum circuit fidelity and reduce execution overhead. Moreover, the hardware-agnostic nature of these methods ensures broad applicability across various quantum architectures, allowing them to outperform conventional techniques in benchmark evaluations.
- Reinforcement Learning for Circuit Compilation: Using deep Q-networks (DQN) to optimize qubit placement dynamically, this approach reduces the need for manual heuristics. In the literature, there exist some examples in which DQN is being employed for quantum-circuit compilation and routing tasks. One relatively recent example is [92], where the authors present a modified deep Q-learning framework in which actions are represented as sets of parallelisable SWAPs and gates. To efficiently navigate this combinatorial decision space, the agent employs simulated annealing for action selection. To evaluate the effectiveness of the presented method, the authors benchmark their DQN-based routing system against the qubit-based routing strategies implemented in state-of-the-art quantum compilers. The core question driving this research was whether a DQN-based approach could successfully perform qubit routing and, if so, whether it could compete with leading techniques in the field. The results answer both questions in the affirmative. Interestingly, the presented approach not only achieves competitive performance but also outperforms traditional methods in realistic near-term scenarios. Unlike more rigid, pre-defined strategies, reinforcement learning seems to provide a high degree of adaptability, making it particularly advantageous as quantum hardware continues to evolve. The only drawback of this approach seems to be the long runtime, which is much longer than those of other systems such as Qiskit or t|ket>.
- Machine learning-based approaches are promising as they can generalize across different hardware architectures, potentially providing adaptable and efficient compilation strategies. Noise-aware ML models are now being explored, where reinforcement-learning agents consider real-time noise information to make routing decisions that reduce error rates.
- 4.
- Meta-Heuristic Approaches: Like the heuristic methods, meta-heuristics can be used to effectively approximate optimal solutions of complex combinatorial problems such as the quantum-circuit routing problem. The literature includes examples in which such techniques have been used to perform the routing of Quantum Approximate Optimisation Algorithm (QAOA) [61] circuit instances. Solving the routing problem in QAOA instances is particularly challenging, as the typical structure of QAOA circuits entails the presence of commutative gates (i.e., the Phase-shift and Mix gates of the problem Hamiltonian); hence, the routing procedure is called not only to apply the optimal (e.g., minimum) number of SWAP gates to minimise the circuit’s depth, but also to decide the order of the circuit Phase-shift and Mix gates needed to enable the optimal SWAP selection. Below, we list a few significant examples of works in which different meta-heuristics have been tested against the same benchmark, showing how the results have constantly improved over time:
- Rollout-based heuristic: inspired by the approach proposed in [93,94], the authors tackle the quantum-circuit-compilation problem (QCCP) by introducing two different heuristics: the first is a roll-out-based sequential decision-making strategy, which selects the next operation to schedule based on makespan estimates provided by a guiding priority rule; the second approach is a stochastic variant of the roll-out heuristic that alternates between roll-out and a basic priority rule to enhance search space exploration. When compared to the results for the same benchmarks in the recent literature at the time of this work’s publication, the proposed approach demonstrated notable reductions in makespan across various problem instances.
- Ant-Colony Optimisation: In reference [95], the authors propose an Ant-Colony Optimisation (ACO)-based algorithm that introduces an innovative pheromone model and incorporates a heuristic-driven Priority Rule to guide the iterative placement of quantum gates. The performance of the algorithm is compared with the results obtained against the same benchmark and used in the previous works, indicating that the proposed method significantly outperforms state-of-the-art approaches, achieving superior makespan reductions across a large set of test cases, and setting the pace for the resolution of hard combinatorial problems such as the QCCP. Furthermore, the findings highlight the scalability of the proposed approach, reinforcing its potential for tackling increasingly large quantum compilation tasks.
- Genetic Algorithms: in [96], the authors introduce an enhanced genetic algorithm designed to tackle QCCP instances for Quantum Approximate Optimisation Algorithms (QAOA) that is then specifically applied to solving MaxCut and graph coloring problems. The proposed algorithm builds upon the existing Decomposition-Based Genetic Algorithm (DBGA) but incorporates a novel encoding scheme that significantly reduces the number of SWAP gates inserted during the decoding phase, thereby minimising circuit depth. The effectiveness of this newly developed algorithm (DBGA-X) is then demonstrated through comparative experiments against the state-of-the-art methods previously described, confirming the power of genetic algorithms for resolving complex combinatorial problems, and showcasing the importance of a clever coding/decoding scheme to obtain superior performance.
5.3. Perspectives
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimisation |
| CP | Constraint Programming |
| DBGA | Decomposition-Based Genetic Algorithm |
| DQN | Deep Q-Networks |
| GNNs | Graph Neural Networks |
| ILP | Integer Linear Programming |
| LSTM | Long-Short Term Memory (LSTM) neural network |
| MCTS | Monte Carlo Tree Search |
| ML | Machine Learning |
| NISQ | Noisy Intermediate Scale Quantum |
| PQC | Parameterized Quantum Circuit |
| QAI | Quantum artificial intelligence |
| QAOA | Quantum Approximate Optimisation Algorithm |
| QC | Quantum Computing |
| QCCP | Quantum Circuit Compilation Problem |
| QUBO | Quadratic Unconstrained Binary Optimisation |
| RL | Reinforcement Learning |
| SABRE | Swap-Based Reordering Algorithm |
| SAT | Satisfiability |
| VQA | Variational Quantum Algorithm |
| VQE | Variational Quantum Eigensolver |
References
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015, A/RES/70/1. Available online: www.refworld.org/docid/57b6e3e44.html (accessed on 17 April 2025).
- Gentili, P.L. Why is Complexity Science valuable for reaching the goals of the UN 2030 Agenda? Rend. Fis. Acc. Lincei 2021, 32, 117–134. [Google Scholar] [CrossRef] [PubMed]
- Bustamante-Ubilla, M.; Arenas-Torres, F. Epistemological Foundations of Complexity Theory. Sustainability 2022, 14, 13316. [Google Scholar] [CrossRef]
- Goldreich, O. Computational Complexity: A Conceptual Perspective; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–7. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Singapore, 2006. [Google Scholar]
- Rozenberg, G.; Bäck, T.; Kok, J.N. Handbook of Natural Computing; Springer: Berlin, Germany, 2012. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education: Harlow, UK, 2022. [Google Scholar]
- Klusch, M.; Lässig, J.; Müssig, D.; Macaluso, A.; Wilhelm, F.K. Quantum artificial intelligence: A Brief Survey. Künstl. Intell. 2024, 38, 257–276. [Google Scholar] [CrossRef]
- Wichert, A. Principles of Quantum Artificial Intelligence; World Scientific: Singapore, 2020. [Google Scholar]
- Ying, M. Quantum computation, quantum theory and AI. Artif. Intell. 2010, 174, 162–176. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K. Artificial intelligence (AI) for quantum and quantum for AI. Opt. Quant. Electron. 2023, 55, 697. [Google Scholar] [CrossRef]
- Moret-Bonillo, V. Can artificial intelligence benefit from quantum computing? Prog. Artif. Intell. 2015, 3, 89–105. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Mitchell, M. Artificial Intelligence. A Guide for Thinking Humans; Farrar, Strauss and Giroux: New York, NY, USA, 2019. [Google Scholar]
- Bardella, G.; Franchini, S.; Pani, P.; Ferraina, S. Lattice physics approaches for neural networks. iScience 2024, 27, 111390. [Google Scholar] [CrossRef]
- Bardella, G.; Franchini, S.; Pan, L.; Balzan, R.; Ramawat, S.; Brunamonti, E.; Pani, P.; Ferraina, S. Neural Activity in Quarks Language: Lattice Field Theory for a Network of Real Neurons. Entropy 2024, 26, 495. [Google Scholar] [CrossRef] [PubMed]
- Funcke, L.; Hartung, T.; Jansen, K.; Kühn, S. Review on Quantum Computing for Lattice Field Theory. In Proceedings of the 39th International Symposium on Lattice Field Theory, Bonn, Germany, 8–13 August 2022; Volume 430, p. 228. [Google Scholar] [CrossRef]
- Grabowska, D. Quantum simulations of lattice field theories. In Proceedings of the 40th International Symposium on Lattice Field Theory, Atavia, IL, USA, 31 July–4 August 2023; Volume 453, p. 110. [Google Scholar] [CrossRef]
- Zheng, H.; Feng, Y.; Tang, J.; Ma, S. Interfacing brain organoids with precision medicine and machine learning. Cell Rep. Phys. Sci. 2022, 3, 100974. [Google Scholar] [CrossRef]
- Halverson, J. Building quantum field theories out of neurons. arXiv 2021, arXiv:2112.04527. [Google Scholar] [CrossRef]
- Ayoade, O.; Rivas, P.; Orduz, J. artificial intelligence Computing at the Quantum Level. Data 2022, 7, 28. [Google Scholar] [CrossRef]
- Christensen, D.V.; Dittmann, R.; Linares-Barranco, B.; Sebastian, A.; Le Gallo, M.; Redaelli, A.; Slesazeck, S.; Mikolajick, T.; Spiga, S.; Menzel, S.; et al. 2022 roadmap on neuromorphic computing and engineering. Neuromorph. Comput. Eng. 2022, 2, e022501. [Google Scholar] [CrossRef]
- Misra, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing 2010, 74, 239. [Google Scholar] [CrossRef]
- Przyczyna, D.; Zawal, P.; Mazur, T.; Strzelecki, M.; Gentili, P.L.; Szaciłowski, K. In-materio neuromimetic devices: Dynamics, information processing and pattern recognition. Jpn. J. Appl. Phys. 2020, 59, 050504. [Google Scholar] [CrossRef]
- Marković, D.; Grollier, J. Quantum neuromorphic computing. Appl. Phys. Lett. 2020, 117, 150501. [Google Scholar] [CrossRef]
- Ghosh, S.; Nakajima, K.; Krisnanda, T.; Fujii, K.; Liew, T.C.H. Quantum Neuromorphic Computing with Reservoir Computing Networks. Adv. Quantum Technol. 2021, 4, 210005. [Google Scholar] [CrossRef]
- Wasielewski, M.R.; Forbes, M.D.E.; Frank, N.L.; Kowalski, K.; Scholes, G.D.; Yuen-Zhou, J.; Baldo, M.A.; Freedman, D.E.; Goldsmith, R.H.; Goodson, T., 3rd; et al. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. 2020, 4, 490–504. [Google Scholar] [CrossRef]
- Stojanovic, M.N. Some experiments and directions in molecular computing and robotics. Isr. J. Chem. 2011, 51, 99–105. [Google Scholar] [CrossRef]
- Gentili, P.L.; Stano, P. Living cells and biological mechanisms as prototypes for developing chemical artificial intelligence. Biochem. Bioph. Res. Commun. 2024, 720, 150060. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L. Chemical AI in the limelight: The Contribution of Photochromic Materials and Oscillatory Chemical Reactions. Adv. Opt. Mater. 2025, 13, 2500016. [Google Scholar] [CrossRef]
- Stano, P.; Damiano, L. Synthetic cell research: Is technical progress leaving theoretical and epistemological investigations one step behind? Front. Robot. AI 2023, 10, 1143196. [Google Scholar] [CrossRef]
- De Silva, A.P. Molecular Logic-Based Computation; Royal Society of Chemistry: Cambridge, UK, 2013. [Google Scholar]
- Szaciłowski, K. Digital information processing in molecular systems. Chem. Rev. 2008, 108, 3481–3548. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Stano, P. Chemical Neural Networks Inside Synthetic Cells? A Proposal for Their Realisation and Modeling. Front. Bioeng. Biotechnol. 2022, 10, 927110. [Google Scholar] [CrossRef]
- Gentili, P.L.; Zurlo, M.P.; Stano, P. Neuromorphic engineering in wetware: The state of the art and its perspectives. Front. Neurosci. 2024, 18, 1443121. [Google Scholar] [CrossRef] [PubMed]
- Braccini, M.; Collinson, E.; Roli, A.; Fellermann, H.; Stano, P. Recurrent neural networks in synthetic cells: A route to autonomous molecular agents? Front. Bioeng. Biotechnol. 2023, 11, 1210334. [Google Scholar] [CrossRef]
- Gentili, P.L.; Dolnik, M.; Epstein, I.R. “Photochemical Oscillator”: Colored Hydrodynamic Oscillations and Waves in a Photochromic System. J. Phys. Chem. C 2014, 118, 598–608. [Google Scholar] [CrossRef]
- Nakano, T.; Okaie, Y.; Kobayashi, S.; Hara, T.; Hiraoka, Y.; Haraguchi, T. Methods and applications of mobile molecular communication. Proc. IEEE 2019, 107, 1442. [Google Scholar] [CrossRef]
- Gentili, P.L.; Stano, P. Tracing a new path in the field of AI and robotics: Mimicking human intelligence through chemistry. Part II: Systems chemistry. Front. Robot. AI 2023, 10, 1266011. [Google Scholar] [CrossRef]
- Nakano, T. Molecular communication: A 10 Year Retrospective. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2017, 3, 71–78. [Google Scholar] [CrossRef]
- Tomassoli, L.; Silva-Dias, L.; Dolnik, M.; Epstein, I.R.; Germani, R.; Gentili, P.L. Neuromorphic engineering in wetware: Discriminating Acoustic frequencies through their Effects on chemical waves. J. Phys. Chem. B 2024, 128, 1241–1255. [Google Scholar] [CrossRef]
- Lambert, N.; Chen, Y.-N.; Cheng, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10–18. [Google Scholar] [CrossRef]
- Adams, B.; Petruccione, F. Quantum effects in the brain: A review. AVS Quantum Sci. 2020, 2, 022901. [Google Scholar] [CrossRef]
- Erboz, A.; Kesekler, E.; Gentili, P.L.; Uversky, V.N.; Coskuner-Weber, O. Electromagnetic radiation and biophoton emission in neuronal communication and neurodegenerative diseases. Prog. Biophys. Mol. Biol. 2025, 195, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P.J.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, J.; Yao, Y.; Lan, Y. Can Molecular Quantum Computing Bridge Quantum Biology and Cognitive Science? Intell. Comp. 2024, 3, 0072. [Google Scholar] [CrossRef]
- Saleh, I.A.; Srivastava, A. Exploring the Intersection of Fuzzy Logic and Quantum Logic: A New Frontier in Non-Classical Logics. SciWaveBulletin 2023, 1, 27. [Google Scholar] [CrossRef]
- Gentili, P.L. Establishing a New Link between Fuzzy Logic, Neuroscience, and Quantum Mechanics through Bayesian Probability: Perspectives in artificial intelligence and Unconventional Computing. Molecules 2021, 26, 5987. [Google Scholar] [CrossRef]
- Gentili, P.L. The Conformational Contribution to Molecular Complexity and Its Implications for Information Processing in Living Beings and Chemical artificial intelligence. Biomimetics 2024, 9, 121. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Perez-Mercader, J. Quantitative Estimation of Chemical Microheterogeneity through the Determination of Fuzzy Entropy. Front. Chem. 2022, 10, 950769. [Google Scholar] [CrossRef]
- Gentili, P.L. The human sensory system as a collection of specialized fuzzifiers: A conceptual framework to inspire new artificial intelligent systems computing with words. J. Intel. Fuzzy Sys. 2014, 27, 2137–2151. [Google Scholar] [CrossRef]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Extending human perception of electromagnetic radiation to the UV region through biologically inspired photochromic fuzzy logic (BIPFUL) systems. Chem. Comm. 2016, 52, 1474–1477. [Google Scholar] [CrossRef]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Discriminating between the UV-A, UV-B and UVC regions by novel Biologically Inspired Photochromic Fuzzy Logic (BIPFUL) systems: A detailed comparative study. Dyes Pigm. 2016, 135, 169–176. [Google Scholar] [CrossRef]
- Gentili, P.L. Determining Chemical Microheterogeneity from the Analysis of Absorption and Luminescence Transient Signals. J. Phys. Chem. B 2024, 128, 8259–8271. [Google Scholar] [CrossRef]
- Gentili, P.L. The fuzziness of a chromogenic spirooxazine. Dyes Pigm. 2014, 110, 235–248. [Google Scholar] [CrossRef]
- Chicano, F.; Luque, G.; Dahi, Z.A.; Gil-Merino, R. Combinatorial optimisation with quantum computers. Eng. Optim. 2025, 57, 208–233. [Google Scholar] [CrossRef]
- Zahedinejad, E.; Zaribafiyan, A. Combinatorial Optimisation on Gate Model Quantum Computers: A Survey. arXiv 2017, arXiv:1708.05294. [Google Scholar]
- Perez-Ramirez, D.F. Variational Quantum Algorithms for Combinatorial Optimisation. arXiv 2024, arXiv:2407.06421. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimisation Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nature Comm. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Ibrahim, M.; Bronn, N.T.; Byrd, G.T. Crosstalk-Based Parameterized Quantum Circuit Approximation. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Boston, MA, USA, 13–16 June 2022; Volume 01, pp. 39–50. [Google Scholar]
- Wang, S.; Fontana, E.; Cerezo, M.; Sharma, K.; Sone, A.; Cincio, L.; Coles, P.J. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun. 2021, 12, 6961. [Google Scholar] [CrossRef] [PubMed]
- Herrman, R.; Lotshaw, P.C.; Ostrowski, J.; Humble, T.S.; Siopsis, G. Multi-angle quantum approximate optimisation algorithm. Sci. Rep. 2022, 12, 6781. [Google Scholar] [CrossRef]
- Vijendran, V.; Das, A.; Koh, D.E.; Assad, S.M.; Lam, P.K. An expressive ansatz for low-depth quantum approximate optimisation. Quantum Sci. Technol. 2024, 9, 025010. [Google Scholar] [CrossRef]
- Mücke, S.; Piatkowski, N.; Morik, K. Learning Bit by Bit: Extracting the Essence of Machine Learning. In Proceedings of the Conference on “Lernen, Wissen, Daten, Analysen”, Berlin, Germany, 30 September–2 October 2019; Volume 2454, pp. 144–155. [Google Scholar]
- Glover, F.W.; Kochenberger, G.A.; Du, Y. Quantum Bridge Analytics I: A tutorial on formulating and using QUBO models. 4OR 2019, 17, 335–371. [Google Scholar] [CrossRef]
- Verma, A.; Lewis, M.W. Penalty and partitioning techniques to improve performance of QUBO solvers. Discret. Optim. 2022, 44, 100594. [Google Scholar] [CrossRef]
- Vyskocil, T.; Djidjev, H.N. Simple Constraint Embedding for Quantum Annealers. In Proceedings of the International Conference on Rebooting Computing, Tysons, VA, USA, 7–9 November 2018; pp. 1–11. [Google Scholar]
- Kochenberger, G.A.; Hao, J.-K.; Glover, F.W.; Lewis, M.W.; Lü, Z.; Wang, H.; Wang, Y. The unconstrained binary quadratic programming problem: A survey. J. Comb. Optim. 2014, 28, 58–81. [Google Scholar] [CrossRef]
- van de Ven, G.M.; Tuytelaars, T.; Tolias, A.S. Three types of incremental learning. Nat. Mach. Intell. 2022, 4, 1185–1197. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual lifelong learning with neural networks: A review. Neural. Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef]
- Situ, H.; Lu, T.; Pan, M.; Li, L. Quantum continual learning of quantum data realizing knowledge backward transfer. Physica A 2023, 620, 128779. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, S. Quantum continual learning overcoming catastrophic forgetting. Chin. Phys. Lett. 2022, 39, 050303. [Google Scholar] [CrossRef]
- Loglisci, C.; Malerba, D.; Pascazio, S. Quarta: Quantum supervised and unsupervised learning for binary classification in domain-incremental learning. Quantum Mach. Lett. 2024, 6, 68. [Google Scholar] [CrossRef]
- Kashif, M.; Rashid, M.; Al-Kuwari, S.; Shafique, M. Alleviating barren plateaus in parameterized quantum machine learning circuits: Investigating advanced parameter initialisation strategies. In Proceedings of the 2024 Design, Automation & Test in Europe Conference & Exhibition, Valencia, Spain, 25–27 March 2024; pp. 1–6. [Google Scholar]
- Liang, Z.; Liu, G.; Liu, Z.; Cheng, J.; Hao, T.; Liu, K.; Ren, H.; Song, Z.; Liu, J.; Ye, F.; et al. Graph learning for parameter prediction of quantum approximate optimisation algorithm. In Proceedings of the 2023 International Conference on Computer-Aided Design (ICCAD), San Francisco, CA, USA, 28 October–2 November 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Sauvage, F.; Sim, S.; Kunitsa, A.A.; Simon, W.A.; Mauri, M.; Perdomo-Ortiz, A. FLIP: A flexible initializer for arbitrarily-sized parametrized quantum circuits. arXiv 2021, arXiv:2103.08572. [Google Scholar]
- Moussa, C.; Wang, H.; Bäck, T.; Dunjko, V. Unsupervised strategies for identifying optimal parameters in Quantum Approximate Optimisation Algorithm. EPJ Quantum Tech. 2022, 9, 11. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, Y.; Zhang, Y.; Wang, J.; Du, S. Deep learning on multi-view sequential data: A survey. Art. Intell. Rev. 2022, 56, 2819–2857. [Google Scholar] [CrossRef]
- Loglisci, C.; Losavio, V.; De Carolis, B.; Prifti Skenduli, M.; Malerba, D. Parameter prediction for variational quantum algorithms through sequence modeling (Short Paper). In Proceedings of the 23rd International Conference of the Italian Association for artificial intelligence (AIxIA 2024), Bolzano, Italy, 25–28 November 2024; Volume 3913. Available online: https://ceur-ws.org/Vol-3913/short1.pdf (accessed on 1 April 2025).
- Li, G.; Ding, Y.; Xie, Y. Tackling the Qubit Mapping Problem for NISQ-Era Quantum Devices. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ‘19), Providence, RI, USA, 13–17 April 2019; pp. 1001–1014. [Google Scholar] [CrossRef]
- Cowtan, A.; Dilkes, S.; Krajenbrink, A.; Simmons, W.; Sivarajah, S. On the qubit routing problem. arXiv 2019, arXiv:1902.08091. [Google Scholar]
- Kissinger, A.; van de Wetering, J. Picturing Quantum Software: An Introduction to the ZX-Calculus and Quantum Compilation. preprint 2024. [Google Scholar]
- Nannicini, G.; Bishop, L.S.; Günlük, O.; Jurcevic, P. Optimal Qubit Assignment and Routing via Integer Programming. ACM Trans. Quantum Comput. 2023, 4, 7. [Google Scholar] [CrossRef]
- Yang, J.; Kharkov, Y.A.; Shi, Y.; Heule, M.J.H.; Dutertre, B. Quantum Circuit Mapping Based on Incremental and Parallel SAT Solving. Leibniz Int. Proc. Inform. 2024, 305, 29:1–29:18. [Google Scholar] [CrossRef]
- Booth, K.E.C. Constraint Programming Models for Depth-Optimal Qubit Assignment and SWAP-Based Routing (Short Paper). Leibniz Int. Proc. Inform. 2023, 280, 43:1–43:10. [Google Scholar] [CrossRef]
- LeCompte, T.; Qi, F.; Yuan, X.; Tzeng, N.F.; Najafi, M.H.; Peng, L. Graph Neural Network Assisted Quantum Compilation for Qubit Allocation. In Proceedings of the 33rd Great Lakes Symposium on VLSI (GLSVLSI), Knoxville, TN, USA, 5–7 June 2023. [Google Scholar] [CrossRef]
- Sinha, A.; Azad, U.; Singh, H. Qubit Routing Using Graph Neural Network Aided Monte Carlo Tree Search. Proc. Aaai Conf. Artif. Intell. 2022, 36, 9935–9943. [Google Scholar] [CrossRef]
- Pozzi, M.G.; Herbert, S.J.; Sengupta, A.; Mullins, R.D. Using Reinforcement Learning to Perform Qubit Routing in Quantum Compilers. Trans. Quantum Comput. 2022, 3, 10. [Google Scholar] [CrossRef]
- Oddi, A.; Rasconi, R. Greedy randomized search for scalable compilation of quantum circuits. In Integration of Constraint Programming, Artificial Intelligence, and Operations Research; van Hoeve, W.-J., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 446–461. [Google Scholar]
- Chand, S.; Singh, H.K.; Ray, T.; Ryan, M. Rollout based Heuristics for the Quantum Circuit Compilation Problem. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 974–981. [Google Scholar] [CrossRef]
- Baioletti, M.; Rasconi, R.; Oddi, A. A Novel Ant Colony Optimisation Strategy for the Quantum Circuit Compilation Problem. In Evolutionary Computation in Combinatorial Optimisation; Zarges, C., Verel, S., Eds.; EvoCOP 2021. Lecture Notes in Computer Scienc; Springer: Cham, Switzerland, 2021; Volume 12692. [Google Scholar] [CrossRef]
- Arufe, L.; Rasconi, R.; Oddi, A.; Varela, R.; González, M.A. New coding scheme to compile circuits for Quantum Approximate Optimisation Algorithm by genetic evolution. Appl. Soft Comput. 2023, 144, 110456. [Google Scholar] [CrossRef]
- IBM. The future of Computing is Quantum. Tratto da IBM Technology Atlas. 2024. Available online: https://www.ibm.com/roadmaps/quantum/ (accessed on 1 April 2025).
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baioletti, M.; Fagiolo, F.; Loglisci, C.; Losavio, V.N.; Oddi, A.; Rasconi, R.; Gentili, P.L. Quantum Artificial Intelligence: Some Strategies and Perspectives. AI 2025, 6, 175. https://doi.org/10.3390/ai6080175
Baioletti M, Fagiolo F, Loglisci C, Losavio VN, Oddi A, Rasconi R, Gentili PL. Quantum Artificial Intelligence: Some Strategies and Perspectives. AI. 2025; 6(8):175. https://doi.org/10.3390/ai6080175
Chicago/Turabian StyleBaioletti, Marco, Fabrizio Fagiolo, Corrado Loglisci, Vito Nicola Losavio, Angelo Oddi, Riccardo Rasconi, and Pier Luigi Gentili. 2025. "Quantum Artificial Intelligence: Some Strategies and Perspectives" AI 6, no. 8: 175. https://doi.org/10.3390/ai6080175
APA StyleBaioletti, M., Fagiolo, F., Loglisci, C., Losavio, V. N., Oddi, A., Rasconi, R., & Gentili, P. L. (2025). Quantum Artificial Intelligence: Some Strategies and Perspectives. AI, 6(8), 175. https://doi.org/10.3390/ai6080175









