Abstract
In the twenty-first century, humanity is compelled to face global challenges. Such challenges involve complex systems. However, science has some cognitive and predictive limits in dealing with complex systems. Some of these limits are related to computational complexity and the recognition of variable patterns. To overcome these limits, artificial intelligence (AI) and quantum computing (QC) appear to be helpful. Even more promising is quantum AI (QAI), which emerged from the combination of AI and QC. The combination of AI and QC produces reciprocal, synergistic effects. This work describes some of these effects. It shows that QC offers new materials for implementing AI and innovative algorithms for solving optimisation problems and enhancing machine learning algorithms. Additionally, it demonstrates how AI algorithms can help overcome many of the experimental challenges associated with implementing QC. It also outlines several perspectives for the future development of quantum artificial intelligence.
1. Introduction
In this century, humanity is urged to face global challenges. A list of these challenges was reported in the 2030 Agenda compiled by the United Nations ten years ago [1]. Whenever humans cope with global challenges, they have to deal with complex systems [2] such as human beings and their societies, the world economy, urban areas, natural ecosystems, and climate. Unfortunately, whenever we handle complex systems, scientific approaches encounter limitations. in understanding and predicting their behaviour [3]. One such limitation derives from computational complexity: many computational problems involving complex systems are solvable but intractable [4]. It is impossible to determine their exact solutions within a reasonable timeframe, even if the fastest supercomputers in the world are available. Another limitation regards the recognition of variable patterns that are emergent properties of complex systems. We have yet to formulate a universally valid and effective algorithm that can recognize every type of variable pattern [5,6]. To address these limitations, it is necessary to formulate new algorithms, propose new materials and architectures for computation, and develop new methods and models to describe the behaviour of complex systems. In this regard, the interdisciplinary research line of Natural Computing [2,7] is particularly promising. Natural Computing is rooted in the basic idea that any distinguishable physicochemical state of matter or energy can be used to encode information. Therefore, every natural transformation of these states is a computation. Within Natural Computing, two research streams are usually distinguished. In the first case, scientists utilise physicochemical laws to perform computations. For instance, the quantum-mechanical laws can be used to develop quantum computing (QC) [8]. The phenomena of quantum superposition, entanglement, interference, and tunnelling guarantee, at least in principle, computational acceleration compared to computing machines that operate based on the laws of classical physics and electromagnetism, such as conventional electronic computers. In the second research stream of Natural Computing, the intelligent competencies of living beings are mimicked. For example, artificial intelligence (AI) aims to mimic the human capacity to recognize variable patterns easily and make decisions based on deductive reasoning [9]. The urgency of the need to improve our computational capabilities sparked the idea of merging quantum computing (QC) and artificial intelligence (AI) to develop quantum AI (QAI). QAI involves investigating the feasibility and potential of leveraging QC for AI and AI for QC [10,11,12,13,14]. A synergistic effect emerges.
This work presents some of the numerous reciprocal relationships that have been established between the two fields; those described in this work are shown in Figure 1. First, we demonstrate that AI can be supported by materials used in the field of quantum information (paragraph 2). Specifically, it will be shown that thermalised quantum mixed states in liquid solutions allow the imitation of intelligent competencies specific to living beings. Then, it will be explained how the principles of quantum mechanics can support the search for solutions to hard computational problems, such as those of optimisation (paragraph 3) and those involved in the field of machine learning (paragraph 4). The contribution of AI to QC will be demonstrated by the application of AI techniques and algorithms that facilitate quantum-circuit compilation and error mitigation, which are two significant obstacles in the development of quantum technologies (paragraph 5). Finally, some general perspectives are offered in the conclusions of this article.
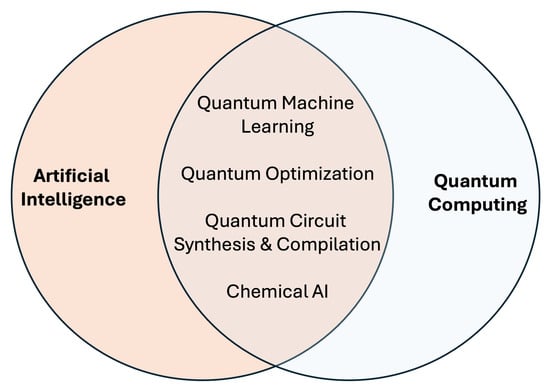
Figure 1.
Main areas of intersection between quantum computing and AI.
2. Chemical Contributions to Quantum AI
There are three principal strategies for developing AI: it can be implemented in (1) software, (2) hardware, and (3) wetware. Generally, AI is implemented in software that runs on classical electronic computers. Among the several strategies used to develop intelligent software, it is worth mentioning the approaches based on the mimicry of (i) rigorous human logic [9], (ii) vague human reasoning (through fuzzy logic) [15], (iii) the structural and functional features of neural networks, and (iv) phenomena specific to living and nonliving matter, such as evolution and minimisation of free energy [16]. Some of these approaches have been enriched by introducing the laws of quantum mechanics. For instance, for modelling the spatiotemporal interactions in neural systems, a framework developed using Lattice Field Theory (i.e., the reference computational paradigm used in Quantum Field Theory) that bridges neuroscience, neural network theory, and quantum mechanics has been introduced [17]. By discretisation of neural activity into binary variables on a spacetime lattice, it has been demonstrated how neural activity can be treated as qubits [18,19,20]. This finding could lead to exciting and promising applications, such as the combined use of Lattice Field Theory and deep learning [21] to program biohybrid circuits, including neuromorphic chips and organoids, thereby paving the way for a new generation of brain-inspired AI. Additionally, this technique could accelerate the development of the groundbreaking idea of using natural neurons to perform physical Lattice Field Theory or quantum simulations [22]. Other examples of how well-established AI algorithms have been enriched through application of the laws of quantum mechanics are described in paragraphs 3 and 4 of this article. The resulting hybrid algorithms can be run on conventional electronic or quantum computers [23].
The second strategy for developing AI relies on the implementation of neural surrogates in hardware to design brain-like computing machines, revolutionising the Von Neumann architecture of current electronic computers in which the processor and memory are physically separated [24,25,26]. Neural networks process classical information when they are composed of silicon-based circuits, inorganic memristors, or organic semiconductors. They process quantum information when the nodes of the networks are made from systems that generate quantum-coherent states. Depending on the quantum computing platform, the various approaches are usually divided into two groups: digital approaches, which use gate-based quantum computers, and analogue approaches, which use analogue quantum computing platforms [27]. Neural networks on gate-based quantum computers are implemented as parameterised quantum circuits through trapped ions or superconducting circuits. Analogue quantum neuromorphic computing relies on the dynamics of a quantum system. It encompasses the adiabatic dynamics of quantum annealers and the more general dynamics of disordered quantum systems, and these are leveraged in the context of reservoir computing. The reservoir can be based on quantum dots, photonic and microwave circuits, nitrogen-vacancy centres in diamond, or nuclear or electron spins in molecules within a magnetic field [28,29].
Recently, authors have proposed a novel strategy for developing AI: chemical AI (CAI) [30,31]. It involves developing chemical systems that mimic biological intelligence competencies in wetware, i.e., liquid solutions, which represent the characteristic phase of life [32,33]. Properly selected molecules and their chemical reactions enable the mimicry of certain biological intelligence functions. For instance, it is possible to process both Boolean and fuzzy logic [32,33,34,35] and implement neural surrogates and the learning capabilities of neural networks [36,37,38,39]. The use of the liquid phase guarantees molecular communication through mechanisms active in living beings, such as thermal diffusion, advection, chemical waves, and supramolecular interactions [40,41,42,43]. Since every chemical process occurs in a microscopic world governed by quantum-mechanical laws, a recently raised hypothesis suggests that some chemical phenomena occurring in living matter and characterizing biological intelligence rely on quantum-coherent phenomena. Avian magnetoreception, olfaction, and, probably, consciousness are biological competencies that involve coherent states, entanglement, and tunnelling [44,45,46,47,48].
Other quantum-like phenomena of living matter are based on quantum mixed states and their fuzzy features [49,50,51]. Quantum mixed states are generated whenever the random Brownian motion of the molecules triggers the collapse of quantum coherent states, which are required for generating qubits (the unit of quantum information in conventional quantum computing). At ordinary temperatures, the collapse occurs relatively quickly, on orders ranging from a few picoseconds s to milliseconds s, depending on the kind of quantum state involved. Quantum mixed states do not have limited lifetimes and can be easily manipulated by physicochemical inputs without the risk of inducing the collapse of superimposed quantum states. A quantum mixed state () is a linear combination of quantum wavefunctions (), as follows:
In Equation (2), represents the weight of the i-th wavefunction and corresponds to its probability. Quantum mixed states allow the implementation of chemical fuzzy sets. When the coefficients are interpreted as the degrees of membership of the different wavefunctions to , the quantum mixed state looks like a chemical fuzzy set. Hence, is also the fuzzy unit of information. The amount of information encoded by a quantum mixed state is the fuzzy entropy, defined as follows: [52]:
Collections of chemical fuzzy sets can granulate the physicochemical variables, guaranteeing computational parallelism. One example in nature is offered by human colour vision. In the centre of the retina (i.e., the fovea), humans have three types of cones: the so-called red, green, and blue cones. Each type of cone has its own characteristic photoreceptor protein. Although the red, green, and blue photoreceptor proteins have the same chromophore, i.e., the 11-cis retinal (see the molecular structure on the top of Figure 2), they differ in the spectral position of their absorption bands (see the bottom part of Figure 2) due to the distinct amino-acid compositions of the pockets containing the retinals.
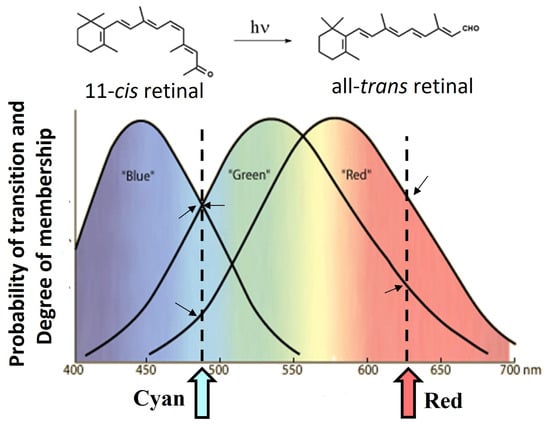
Figure 2.
On top, the molecular structure of 11-cis retinal that photo-isomerizes to all-trans retinal when it absorbs light is shown. At the bottom, the absorption spectra of the three retinals are reported. Lights having distinct hues (for instance, cyan and red) belong to the three bands-chemical fuzzy sets with different degrees, as indicated by the tiny black arrows.
Each absorption band is the result of a characteristic transition moment integral ():
In Equation (3), and refer to the electronic and vibrational wavefunctions of the ground (i) and excited states (f). The three absorption bands correspond to three molecular fuzzy sets that granulate the visible spectral region. Lights of distinct colours, i.e., those having different spectral compositions, are absorbed by the three proteins with different probabilities, these values being related to the extent of the three transition moment integrals (Equation (3)), whose values are wavelength-dependent. In terms of fuzzy sets, lights with distinct hues belong to the three chemical fuzzy sets with different degrees of membership. These diverse degrees of membership or probabilities of absorption constitute the first clue used for distinguishing among hues within the human brain. The granulation of the visible region is a form of quantum parallelism that enables humans to distinguish around 200 hues.
This unconventional form of quantum parallelism, which does not require coherent quantum states, is not restricted to human colour vision, but it is common to all the human sensory systems: the visual, auditory, olfactory, gustatory, somatosensory, vestibular, and thermosensory systems, as has already been demonstrated [53]. The imitation of this feature is pursued by the development of Chemical AI. For instance, in analogy to the system of three photoreceptor proteins, a collection of three or four photochromic compounds, selected by considering their absorption bands as chemical fuzzy sets, has been devised to extend human vision to the UV region of the spectrum [54,55].
A set of thermalised, non-coherent quantum mixed states that operates as a chemical fuzzy set can be easily prepared by using a micro-heterogeneous chemical system, i.e., a compound that exists in many conformations (i.e., structures that have the same molecular skeleton but differ in how the atomic groups are displayed in space) and/or experiences micro-environments with distinct physicochemical features [56,57]. A high degree of computational parallelism is achievable by preparing a mixture of distinct quantum mixed states, i.e., distinct molecular fuzzy sets. The chemical composition of this mixture should be determined based on the goal of achieving the desired granulation of the physicochemical variables. Remarkable examples are found in biology: suffice it to think about human colour vision and the other senses [53]. Their imitation has enabled the implementation of biologically inspired chemical systems that extend human vision into the UV [54,55] and will inspire the development of new quantum sensing systems. The superposition of thermalised quantum mixed states gives rise to an unconventional form of quantum parallelism that does not require the delicate and fragile superposition of coherent quantum states.
Perspectives for Chemical AI on QAI
Chemical AI, referring to the unconventional strategy of mimicking biological intelligence in wetware (i.e., in liquid solutions), will contribute to the development of quantum information science by contributing to new strategies for sensing, computing, and communicating through quantum mixed states. The next grand challenge is to propose quantum-mixed states to solve distinctive, hard computational problems in a reasonable amount of time and prove that their use in QAI is as promising as that of conventional superposed coherent quantum states.
3. Optimisation with Quantum Computing Devices
Quantum computing represents a new approach to solving optimisation problems, exploiting the principles of quantum mechanics to explore solution spaces in ways different from classical methods [58]. Among the various quantum computing architectures, quantum annealers and gate-based quantum computers offer distinct strategies for addressing optimisation problems, with applications ranging from combinatorial optimisation to machine learning and simulations of complex systems.
This section provides an overview of how optimisation problems are formulated and solved using quantum computing devices. We first explore gate-based quantum computing, highlighting its principles, algorithms and applications in optimisation. Next, we examine quantum annealers, focusing on their approach to solving optimisation problems and their suitability for specific tasks.
3.1. Gate Based
Gate-based quantum computing is one of the most promising approaches to tackling combinatorial optimisation problems [59]. Unlike classical methods, which process information sequentially or through parallel computation on conventional hardware, quantum computers operate on the principles of superposition and entanglement. These unique properties allow them to explore vast solution spaces in ways that differ fundamentally from classical approaches.
In optimisation, the challenge is often to find the best configuration among many possible ones. In general, gate-based quantum computers solve these problems with quantum circuits, where qubits represent decision variables and quantum gates guide the computation towards an optimal solution. This approach enables quantum algorithms to explore multiple configurations simultaneously, potentially leading to the development of strategies for more efficient problem-solving.
A widely studied class of methods is the Variational Quantum Algorithms (VQAs), which leverage a hybrid quantum-classical approach [60]. In these algorithms, quantum circuits generate candidate solutions, while classical optimisation methods iteratively refine their parameters to improve the results. VQAs are highly flexible and can be adapted to a wide range of problems, making them particularly promising for near-term quantum devices. A key member of the VQA family is the Quantum Approximate Optimisation Algorithm (QAOA), which was designed to solve combinatorial problems [61]. QAOA encodes the problem into a quantum circuit using a set of parameterised quantum gates that evolve a quantum state toward an optimal or near-optimal solution. A classical optimizer fine-tunes these parameters, improving performance by navigating the solution space efficiently. Another important VQA is the Variational Quantum Eigensolver (VQE), which was developed initially for quantum chemistry but is also applicable to optimization problems [62]. VQE focuses on finding the lowest energy state of a given Hamiltonian, which can be used to represent optimal solutions in various domains, including logistics, finance, and network optimisation. Like QAOA, VQE relies on classical optimisation to iteratively refine quantum circuit parameters, making it well suited for implementation in current quantum hardware.
Variational Quantum Algorithms running on today’s NISQ processors must face two closely related problems. The first problem is the result of hardware noise, such as errors in gate readout, decoherence [63], and crosstalk [64], which accumulate with circuit depth but are problematic because they can affect the estimation of the objective function. Another problem often encountered is the presence of barren plateaus: As the number of qubits grows, the cost function gradients shrink exponentially, leaving classical optimizers with no useful direction. Noise can cause or aggravate these plateaus, and together, they represent a limit to the depth of quantum circuits [65]. Consequently, noise and plateaus limit the size of problems that can be solved on real quantum hardware.
To overcome the above-mentioned limitations of standard QAOA, more expressive but shallower approaches have been proposed to focus on the effectiveness of the algorithm over a small number of levels. This approach reduces exposure to errors and delays the phenomenon of gradient collapse. One of the most promising variants is MA-QAOA (Multi-Angle QAOA), which assigns a pair of independent parameters to each term in the Hamiltonian of the problem (e.g., each constraint or interaction between variables), as well as to mixing operators [66]. A larger parameter space allows better results in terms of solution accuracy, even in the presence of noise, than can be obtained using the standard version of QAOA with the same depth. Another variant that is particularly suitable for noisy scenarios is eXpressive QAOA (XQAOA) [67], where the mixer includes a rotation around the Y axis and each operation on a single qubit is assigned an independent parameter. This approach enhances the circuit’s flexibility, thereby improving its performance in the presence of noise. By packing greater expressivity into low-depth circuits, these variants curb the deleterious impact of noise, delay the onset of barren plateaus and, in turn, extend the practical reach of variational quantum optimisation on current processors.
Despite current hardware limitations, ongoing advances in quantum processors and error-mitigation techniques continue to improve the feasibility of quantum optimisation. As quantum technology advances, gate-based quantum computing is expected to play an increasingly important role in solving large-scale combinatorial problems that remain computationally challenging for classical approaches.
3.2. Quantum Annealers
Quantum annealing is an optimisation approach that leverages quantum mechanical principles to find optimal or near-optimal solutions to complex combinatorial problems. Unlike classical methods, which explore the solution space through deterministic or heuristic techniques, quantum annealing exploits quantum effects such as superposition and tunnelling to traverse energy landscapes more efficiently.
D-Wave has pioneered the development of quantum annealers, specialised hardware designed to solve discrete optimisation problems. These devices operate by encoding an optimisation problem into an energy function, which is then minimised through a quantum-driven process. Quantum annealers are particularly effective in solving large-scale problems where classical approaches struggle due to exponential complexity.
One of the most widely used formulations for programming quantum annealers is the Quadratic Unconstrained Binary Optimisation (QUBO) model. QUBO provides a flexible and expressive framework for encoding various optimisation problems, including SAT (satisfiability) problems, Constraint Satisfaction, Maximum Cut, Graph Coloring, and Maximum Clique, as well as machine learning tasks such as Support Vector Machines, Clustering, and Markov Random Fields [68,69].
A QUBO problem is defined on n binary variables and an upper-triangular matrix Q. The objective is to minimize the function:
which can be rewritten in matrix form as follows:
where represents the transpose of the vector x. The diagonal elements define linear terms, while the off-diagonal elements capture quadratic interactions. The matrix Q can be expressed in a symmetric or upper-triangular form to maintain consistency in representation.
To formulate a constrained optimisation problem as a QUBO, two main steps are required: (i) define a binary encoding of the solution; (ii) add penalty terms to discourage infeasible solutions by penalising constraint violations.
Although QUBO is inherently unconstrained (except for the binary nature of variables), constraints can be incorporated by introducing quadratic penalties into the objective function. This ensures that the augmented objective function aligns with the original problem when penalties approach zero. However, selecting appropriate penalty values is critical: small penalties can result in a function that produces infeasible solutions, while excessively large penalties can increase computational complexity and destabilize optimisation algorithms [70,71]. Research has focused on optimising penalty coefficients and developing effective constraint representations, such as logical constraints modelled by binary multiplication (e.g., for a logical AND).
Quantum annealers solve QUBO problems by embedding the optimisation function into a physical quantum system. The system starts in a low-energy quantum state and evolves according to a time-dependent Hamiltonian. As evolution progresses, the quantum system gradually moves toward the ground state of the final Hamiltonian, which encodes the optimal solution to the QUBO problem. If the annealing process is performed slowly enough, the system remains in the lowest energy state, yielding an optimal or near-optimal solution.
Compared to classical approaches, quantum annealing provides advantages in solving large-scale QUBO problems by leveraging quantum effects to escape local minima and efficiently navigate complex energy landscapes. However, practical limitations such as noise, decoherence, and embedding constraints influence solution quality and require careful consideration in real-world applications.
The continuous development of quantum annealing hardware and hybrid quantum–classical algorithms is expanding the range of solvable optimisation problems. As these technologies evolve, QUBO-based formulations on quantum annealers are expected to play an increasingly significant role in addressing computationally challenging tasks across multiple domains [72].
3.3. Perspectives
As a conclusion, it is possible to say that the two quantum solutions for solving optimisation problems could have different routes and different success in the near future. On the one hand, quantum annealers are a more mature architecture that can be improved by building more powerful machines with a higher number of qubits and increased connectivity. However, the main drawbacks of this approach, namely the too simple mathematical model directly supported and the sparse connectivity, could not be easily overcome in the future without dramatically changing the architecture. On the other hand, QAOA and the other variational algorithms, although designed explicitly for NISQ architectures, could benefit from better architectures, having a higher number of qubits and greater reliability. However, many aspects of this approach require further investigation, particularly its actual advantage over classical solutions.
4. New Paradigms for Quantum Machine Learning
Quantum machine learning has emerged as a transformative approach that promises to tackle machine learning problems that are computationally intractable in classical systems, particularly those involving massive datasets.
In the realm of quantum computing research, the current landscape is dominated by noisy intermediate-scale quantum (NISQ) devices. These devices, although constrained in their computational capacity, can effectively handle small-to medium-scale data problems. Among the most studied approaches, the one used for hybrid frameworks is particularly promising, as it combines classical and quantum methodologies. Due to their capacities to leverage quantum properties and mitigate the limitations of existing quantum hardware, hybrid models represent a practical step forward. Although these technologies are not yet capable of delivering significant speed-ups for large-scale data problems, they lay the groundwork for developing future algorithms tailored to data-intensive challenges.
4.1. Incremental Learning
One prominent category of data-intensive problems in classical computing research is the incremental learning of predictive models. Incremental learning, or more generally lifelong learning, represents a category of machine learning tasks focused on the ability to learn, perpetually maintains model capabilities, and eventually adapts them as needed, depending on whether the learning context changes [73]. In this scenario, the quantum machine has to process data continuously as the data arrive, typically as data blocks, rather than working on the whole dataset. It involves processing data instances sequentially, without the benefit of accessing the entire dataset simultaneously, as in batch learning. This requires models that can make real-time predictions, dynamically adapt to evolving data distributions (concept drifts), and maintain computational efficiency. Even advanced research on deep learning is struggling with these challenges, as evidenced in the literature on catastrophic forgetting [74]. This phenomenon describes the abrupt loss of previously learned knowledge that can occur when a model is exposed to new data. Consequently, the focus on incremental learning shifts from optimising algorithms for massive computation to maintaining high-quality predictions over unbounded data sequences.
Incremental learning aligns well with the current constraints of QC devices. Unlike computationally intensive tasks, incremental learning imposes fewer demands on quantum hardware, making it a promising candidate for implementation on NISQ devices. Although NISQ systems lack the robustness of fully fault-tolerant quantum computers, their computational capacity is sufficient for moderate-scale data problems, positioning them as viable platforms for applications in incremental learning.
Despite its potential, incremental learning remains underexplored in the field of quantum machine learning, in part due to the inherent complexities of the paradigm. However, QC offers unique advantages that can be leveraged to address these challenges, as explained below:
- Unitary nature. Quantum states evolve reversibly, meaning that updates do not erase previously acquired knowledge unless a measurement is performed. Additionally, the intrinsic modularity of quantum circuits may facilitate the selective updating of subspaces within the represented Hilbert space.
- Enhanced representational space. Classical data can be encoded as quantum states corresponding to points in the Hilbert space. This encoding provides access to exponentially larger representation spaces. For example, a classical feature vector with three entries can be mapped to an eight-dimensional quantum space (), enabling richer data representations that may better capture real-world distributions.
- Model adaptability through VQAs. Incremental learning necessitates the use of models that can adapt to new data. Variational quantum circuits are composed of parameterised quantum gates whose parameter values are tuned through a refinement process that embeds the properties of data through the gradual processing of data. Thus, when concept drift occurs, existing quantum models can be adjusted by updating their parameters, ensuring adaptability and extendibility without requiring retraining from scratch. Moreover, quantum circuits often rely on a smaller number of parameters compared to classical neural networks. This can lead to reduced optimisation effort when updating parameters, in contrast to what typically occurs in classical computation.
- Capturing evolving interrelationships. In incremental learning, data often violate the assumptions of independence and identical distributions. Features may be interrelated, and these relationships can evolve over time. Classical deep learning approaches, such as convolutional neural networks, address this property through specialised architectures. In contrast, QC inherently accounts for feature interdependencies using gate-based operations for qubit registers. For instance, controlled gates have the ability to handle relationships of the form event–action. Entanglement circuits, a hallmark of quantum computing, are particularly effective in capturing nonlocal correlations, offering a natural mechanism for modelling complex dependencies without explicitly modelling all pairwise interactions. They have been demonstrated to be accurate in the real-world application of document classification thanks to the accommodation of high-dimensional correlations among words.
- Simultaneous evaluation of hypothesis. To keep the model up-to-date with time, multiple model adaptations or feature-combination strategies are often needed. Superposition enables the evaluation of all these candidate hypotheses in parallel, which can accelerate the search for an optimal update and reduce the overhead of sequential testing.
To our knowledge, there are very few works on this series of challenges, with most focusing on the specific problems of task-incremental learning, where new class labels are introduced over subsequent learning tasks. For instance, reference [75] explores the learning of multiple quantum-state classification tasks using a variational quantum classifier. The authors propose constraining the model updates by projecting the gradient direction onto the region defined by past task gradients. They retain a subset of training data from prior tasks, which is stored in the so-called gradient episodic memory. In [76], it was observed that when quantum classifiers are exposed to new classification tasks, their performance on previously learned tasks tends to degrade. To counteract this effect, the elastic weight-consolidation method has been proposed. This technique operates by identifying and preserving the most important parameters from previously learned tasks, preventing them from undergoing significant modifications during model updates. However, task-incremental learning assumes that the learner is informed when a new task arrives, which turns out to be of little practical use in real-world applications.
Recent research investigated the challenges of quantum-based incremental learning and developed quantum gate-based predictive models that adapt to changing data without knowing when the learning task (to which the data refer) changes [77,78]. Specifically, they design two types of quantum circuits:
- Supervised Learning, used to train and update classification models;
- Unsupervised Learning, used to detect significant data changes, triggering model adaptation when necessary.
A novel aspect of that work is the combined use of different data encodings for the supervised and unsupervised quantum algorithms. This approach strikes a balance between classification accuracy and computational efficiency.
4.2. Sequence Modelling
The continuous computation over data blocks required in incremental learning may necessitate repeated executions of VQAs to keep the model updated. However, this can conflict with real-world applications that require data processing to be completed within strict time constraints. Specifically, adapting the model to each data block requires tuning the PQC (Parameterised Quantum Circuits) parameters through costly optimisation iterations, which may not align with practical time limits. Moreover, the efficiency of parameter optimisation is highly dependent on how the parameters are initialised and refined. In particular, the process is susceptible to vanishing gradients, which can hinder training completion and make it difficult to meet time requirements [78].
Several works in the literature have proposed machine learning algorithms to efficiently search for optimal values and improve the execution of quantum algorithms. Indeed, they are able to systematically estimate parameters thanks to the capabilities of exploring complex high-dimensional spaces and unveiling hidden correlations within the data [79]. Notably, they are characterised by robustness to noise and error. For instance, in [80] the authors propose a meta-learning flexible strategy that trains neural network-based model from families of PQC problems in order to initialize parameters in similar PQC problems. The flexibility lies in the possibility of carrying out predictions on new PQCs differing in the number of qubits, circuit depth, and number of parameters compared to those used during training. This is achieved with an agnostic PQC encoding-decoding scheme that can describe parameters, circuit sizes, and objectives. The PQC families are built either by varying the circuit sizes while keeping the objective fixed, or by varying the cost function while keeping the same ansatz. The method aims at capturing and exploiting patterns in the parameter space that are present in the context of QAOA for max-cut problems. In [81], the authors aim at exploiting the concentration effect, which is the property that arises when optimal parameters identified for a QAOA problem can be reused for another QAOA problem. They consider an unsupervised approach that performs clustering on several inputs, namely, the angle values of training QAOA problems, their features and representation from a graph autoencoder. A fixed number of clusters provide centroids, which are then used as initial indications for the parameters of new QAOA problems. Their findings demonstrated that a machine learning method can effectively estimate QAOA parameters, reducing optimizer calls while maintaining a minimal decrease in the approximation ratio. The results were comparable to those achieved through exhaustive angle optimisation, leading to significant reductions in the required circuit calls.
A common limitation of these methods is that they operate in batch mode, making them unsuitable for incremental learning. Specifically, they struggle to handle changing data, account for time-based properties such as temporal correlations, and update the model over time. Therefore, having tools that can provide reliable estimations sequentially, while avoiding repeated execution of time-consuming optimisation processes, becomes crucial.
A recent research effort explored the contribution of sequential modelling [82] to supporting conventional optimizers in the parameter estimation. They propose a method that combines VQAs and neural networks to forecast the parameter values of the PQC underlying the same VQAs over sequential data [83]. Specifically, the VQA is executed over initial data blocks and identifies refined parameterisation configurations, which become training data to learn a data-driven optimising function. Indeed, these configurations constitute sequences of parameter values (in the form of multi-variate time-series) that feed a sequential neural network. The resulting forecasting model is therefore used in the next data blocks for initialising the parameters (used to start the PQC) and refining the parameters (used to guide the optimisation process).
4.3. Perspectives
QAI envisions leveraging quantum mechanical principles to create new forms of intelligent systems that surpass classical computing. By harnessing phenomena such as superposition, entanglement, and quantum interference, quantum AI could potentially redefine how learning, reasoning, and decision-making tasks are executed, opening up pathways for solving problems that are intractable for classical machines. Within this broad panorama, quantum machine learning (QML) can be considered one of the most active and promising directions. QML is an emerging field but has a promising future, driven by technological advances in quantum hardware and a deeper understanding of machine learning problems through the application of quantum properties and phenomena. A particularly relevant frontier concerns the development of quantum circuits capable of building robust and generalizable models from limited data, exploiting quantum phenomena, such as entanglement and superposition, with the aim of representing and processing information more compactly than classical models can do. Future QML approaches could integrate these quantum resources to achieve greater sampling efficiency, providing opportunities for new applications in contexts where data acquisition is expensive or impractical, at least with current quantum machines. Furthermore, the intersection of QML with recent machine learning paradigms, such as incremental and continual learning, represents a particularly exciting direction. As the stability and scalability of quantum devices improve, the implementation of such learning paradigms may enable the design of quantum circuits that intrinsically avoid, or at least effectively mitigate, catastrophic forgetting by exploiting unitary (reversible) updates or by encoding multi-task knowledge within high-dimensional Hilbert spaces. This could also transform long-term learning scenarios, such as those in adaptive robotics or evolving medical diagnostics. On the other hand, as quantum hardware continues to mature, it will become increasingly important to develop benchmarking frameworks and standardised datasets specific to QML to enable rigorous comparisons with classical methods. This will include schemes to assess learning stability, resilience to noise, and the ability to generalize to unseen data. Additionally, integrating QML with other emerging computational paradigms, such as tensor networks, neuromorphic architectures, and HPC, could lead to synergistic approaches that further push the boundaries of efficiency in model training. Exploring such an interdisciplinary approach could redefine how complex models are trained and deployed, unlocking entire classes of algorithms that go beyond the capabilities of classical AI. Thus, although significant challenges remain, with these including hardware noise, scalability issues, and the question of actual quantum advantage, current research promises to gradually transform QML from a largely theoretical curiosity to a potentially game-changing tool within the machine learning landscape.
5. The Quantum-Circuit Compilation Problem and Qubit Routing
The execution of quantum circuits on NISQ devices poses significant challenges due to hardware constraints. One of the fundamental problems in this domain is quantum-circuit compilation, which includes quantum-circuit routing, a process essential for mapping logical qubits onto physical qubits while satisfying connectivity constraints and minimising gate errors. The compilation process is crucial to ensuring that quantum algorithms can be executed efficiently on real quantum hardware, where noise and connectivity restrictions present significant obstacles.
Basically, quantum-circuit compilation entails transforming an ideal quantum circuit into a form that can be efficiently executed on a specific quantum processor, and thus it is generally a crucial step in the process of preparing quantum algorithms for their execution on real quantum hardware. One of the most significant challenges in quantum-circuit compilation is the problem of qubit routing, which ensures that quantum gates are applied to qubits that are physically connected by the architecture’s topology.
This section provides an overview of the current state of the art in quantum-circuit routing, summarising key methodologies, frameworks, and strategies proposed in the literature. More specifically, our contribution will focus on the following issues:
- a synthesis of recent developments, technologies, and emerging ideas that have shaped the field so far;
- a description and comparison of existing techniques and approaches, highlighting their main characteristics and reported performance;
- a presentation of relevant contributions that provide a foundation for understanding current challenges and potential future directions.
5.1. The Need for Quantum-Circuit Compilation
Quantum circuits are typically designed using an abstract model in which all qubits can interact freely. However, in real quantum hardware, qubit connectivity is limited by the device topology. Most quantum processors, such as those developed by IBM, Rigetti, and Google, impose restrictions on which qubits can perform two-qubit operations directly; consequently, logical circuits must be transformed to conform to these constraints via compilation, which includes the following steps:
- Initial Mapping: Initially assigning logical qubits to physical qubits such that the execution is optimised.
- Routing: Ensuring that all two-qubit gates can be executed by inserting additional SWAP gates if necessary.
- Optimisation: Minimising depth, gate count, and error rates to improve execution fidelity.
As in the classical case, the necessity of compilation in quantum circuits arises from the fundamental mismatch between algorithmic abstractions and hardware implementations. Without an efficient compilation process, logically correct but ideal quantum circuits may be impossible to run (and thus require routing), while even theoretically efficient quantum algorithms may become impractical due to excessive error accumulation and execution delays (and thus require mapping and optimisation).
In addition, noise plays a crucial role in determining the effectiveness of quantum-circuit compilation. The insertion of SWAP gates and additional routing operations increases the number of two-qubit gates, which are typically the noisiest elements in a quantum circuit. Unless the compilation process is not aimed at ideal (i.e., noiseless) quantum hardware backends, a well-designed compilation strategy must not only satisfy connectivity constraints but also minimize noise accumulation to preserve the fidelity of quantum computations. Decoherence times, gate infidelity, and crosstalk errors must be accounted for when designing routing strategies to ensure that compiled circuits can execute within the coherence window of the quantum processor.
5.2. Routing Techniques and Compilation Strategies
Several approaches have been developed to perform quantum-circuit routing efficiently; these techniques can be broadly classified as follows:
- 1.
- Heuristic-Based Approaches: Heuristic methods aim to find good, but not necessarily optimal, qubit mappings within a reasonable runtime. Examples include:
- Qiskit’s SABRE (Swap-Based Reordering Algorithm): An iterative heuristic that dynamically selects SWAP gates to optimize circuit depth and reduce overall gate overhead [84]. SABRE is an algorithm designed for NISQ devices regardless of their qubit-connectivity structure. Its high performance is guaranteed by the use of three key strategies that can be individually selected: (i) optimising each individual search step, (ii) refining the initial qubit placement with a unique reverse traversal method, and (iii) incorporating a decay effect to balance circuit depth and gate count. By leveraging these improvements, SABRE has increased its speed considerably compared to the best-known approaches at the time of its presentation.
- t|ket> by Cambridge Quantum Computing: Almost simultaneously with the previous procedure, another routing algorithm was proposed in [85] by the name of t|ket>. t|ket> is a graph-based hardware-agnostic quantum compiler developed by Cambridge Quantum Computing Ltd. that performs qubit allocation and routing efficiently, focusing on minimising the circuit depth. At the time of its introduction, the heuristic method employed in t|ket> achieved circuit mappings that were competitive with or superior to those produced by other systems, minimising both circuit depth and total gate count; it was particularly effective for larger quantum circuits.
- ZX-Calculus Methods: Techniques that use graphical calculus for quantum circuits to optimize and transform circuit layouts [86]. In slightly more detail, ZX-Calculus represents quantum circuits using a diagrammatic notation that makes use of Z-spiders and X-spiders diagrams, with each denoting specific quantum operations. These diagrams enable algebraic manipulations that simplify circuits, making it easier to optimize and transform them for hardware execution. The utilisation of ZX-Calculus for quantum compilation goes typically beyond the acceptance of routing and is particularly useful for the following applications: (i) circuit optimisation, as it allows for algebraic rewrites that reduce gate count and circuit depth; (ii) gate synthesis, as it facilitates the decomposition of high-level quantum operations into hardware-native gates; and (iii) error reduction, as it minimizes the number of error-prone operations like SWAP gates, improving fidelity on NISQ devices.
- These heuristics work well in practical scenarios where exact solutions are computationally prohibitive, offering an effective trade-off between compilation time and circuit efficiency. Additionally, some of these methods integrate error-aware routing strategies, selecting paths that minimize the use of particularly noisy qubits or gates.
- 2.
- Exact Optimisation Methods: Some approaches use combinatorial optimisation techniques to find the best possible routing solutions. These include the following:
- Integer Linear Programming (ILP): Formulating the routing problem as an ILP and solving it using standard solvers to find globally optimal solutions. One remarkable result of this approach is presented in [87], where the goal of adapting a logical quantum circuit to a hardware architecture characterised by constrained two-qubit connectivity is tackled by formulating the problem as an integer linear program (ILP) and employing a network flow-based approach with binary decision variables to simultaneously determine both the initial qubit placement and the routing strategy. The model used here incorporates multiple optimisation objectives, including approximations of circuit fidelity, overall depth, and cross-talk mitigation, all of which can be flexibly integrated. Through numerical experiments on various synthetic datasets and diverse hardware configurations, the authors demonstrate that circuit depth and error rate can be jointly optimised with minimal trade-offs. Additionally, the approach is evaluated on an extensive set of quantum volume circuits, prioritising both fidelity and depth reduction. Obtained results indicate the feasibility of using the method to both decrease the number of CNOT (Controlled-NOT) gates compared to Qiskit’s standard transpilation algorithm, SABRE (see above), and exhibit superior fidelity when executed on real quantum hardware.
- SAT Solvers: Encoding the routing problem as a Boolean satisfiability problem to determine optimal solutions. A representative example of this approach is in reference [88]. In this work, the authors propose a novel approach to circuit mapping that leverages a hybrid incremental and parallel Boolean Satisfiability (SAT) solving strategy. The proposed method introduces an advanced SAT encoding tailored specifically for circuit mapping, significantly enhancing the efficiency of solver-based techniques while offering a flexible balance between compilation speed and output quality. To assess its effectiveness, an extensive benchmarking on 78 test cases was conducted, covering three different quantum algorithms and two distinct quantum hardware architectures. Experimental results show that the proposed approach significantly accelerates compilation compared to existing solver-based methods, reducing processing times from impractical durations to much more feasible ones. Additionally, it outperforms leading heuristic techniques by effectively minimising the number of SWAP gates, thereby enhancing execution fidelity on near-term quantum hardware.
- Constraint Programming (CP) Approaches: Methods that leverage constraint-satisfaction techniques to ensure the best qubit allocation and gate reordering. Beyond the integer linear programming models that solve the qubit-assignment problem and the routing problem optimally by mathematically encoding both constraints and objective functions and leveraging automated solvers to generate hardware-compliant circuits with minimal overhead, alternative approaches that exploit a different optimisation framework, such as constraint programming (CP), can be explored. In [89], the authors use the CP approach and benchmark their results against the ILP for minimising circuit depth. The evaluation was conducted on randomly generated instances across both linear and two-dimensional grid-based hardware architectures and demonstrated that CP-based methods not only achieve superior solution quality but also outperform ILP models in computational efficiency.
- Although exact methods provide optimal solutions, they are often computationally expensive and may not scale well for larger circuits. Moreover, these approaches must also be adapted to account for noise, ensuring that optimality in terms of depth or gate count does not come at the cost of excessive error accumulation.
- 3.
- Machine Learning-Based Methods: Recent advances suggest that reinforcement learning and deep learning techniques can enhance routing strategies by learning optimal SWAP insertion policies from data. Notable contributions include:
- Graph Neural Networks (GNNs) for Compilation: Graph Neural Networks (GNNs) have emerged as powerful tools for tackling the quantum- compilation problem through leveraging of their ability to model the intricate connectivity constraints of quantum hardware, enabling optimised qubit allocation and the implementation of routing decisions that enhance circuit fidelity and execution efficiency. In [90], the authors address the qubit-allocation problem, leveraging reinforcement learning (RL) with techniques from graph neural networks (GNNs). By modelling the quantum hardware’s connectivity as a graph and applying GNN-assisted decision-making, the proposed method identifies optimal initial layouts that reduce error rates. Empirical results demonstrate that this strategy improves output fidelity compared to traditional allocation methods. Another significant example is reference [91], in which a solution is proposed that incorporates Monte Carlo Tree Search (MCTS), allowing an intelligent exploration of routing decisions. Augmented by graph neural networks, this approach evaluates action probabilities and state values, effectively guiding the search toward depth-minimised solutions. Additionally, a novel mutex-lock-inspired technique is introduced to enhance parallelisation, further reducing circuit depth. By respectively integrating GNNs for qubit allocation and MCTS for optimised qubit routing, both previous compilation strategies significantly enhance quantum circuit fidelity and reduce execution overhead. Moreover, the hardware-agnostic nature of these methods ensures broad applicability across various quantum architectures, allowing them to outperform conventional techniques in benchmark evaluations.
- Reinforcement Learning for Circuit Compilation: Using deep Q-networks (DQN) to optimize qubit placement dynamically, this approach reduces the need for manual heuristics. In the literature, there exist some examples in which DQN is being employed for quantum-circuit compilation and routing tasks. One relatively recent example is [92], where the authors present a modified deep Q-learning framework in which actions are represented as sets of parallelisable SWAPs and gates. To efficiently navigate this combinatorial decision space, the agent employs simulated annealing for action selection. To evaluate the effectiveness of the presented method, the authors benchmark their DQN-based routing system against the qubit-based routing strategies implemented in state-of-the-art quantum compilers. The core question driving this research was whether a DQN-based approach could successfully perform qubit routing and, if so, whether it could compete with leading techniques in the field. The results answer both questions in the affirmative. Interestingly, the presented approach not only achieves competitive performance but also outperforms traditional methods in realistic near-term scenarios. Unlike more rigid, pre-defined strategies, reinforcement learning seems to provide a high degree of adaptability, making it particularly advantageous as quantum hardware continues to evolve. The only drawback of this approach seems to be the long runtime, which is much longer than those of other systems such as Qiskit or t|ket>.
- Machine learning-based approaches are promising as they can generalize across different hardware architectures, potentially providing adaptable and efficient compilation strategies. Noise-aware ML models are now being explored, where reinforcement-learning agents consider real-time noise information to make routing decisions that reduce error rates.
- 4.
- Meta-Heuristic Approaches: Like the heuristic methods, meta-heuristics can be used to effectively approximate optimal solutions of complex combinatorial problems such as the quantum-circuit routing problem. The literature includes examples in which such techniques have been used to perform the routing of Quantum Approximate Optimisation Algorithm (QAOA) [61] circuit instances. Solving the routing problem in QAOA instances is particularly challenging, as the typical structure of QAOA circuits entails the presence of commutative gates (i.e., the Phase-shift and Mix gates of the problem Hamiltonian); hence, the routing procedure is called not only to apply the optimal (e.g., minimum) number of SWAP gates to minimise the circuit’s depth, but also to decide the order of the circuit Phase-shift and Mix gates needed to enable the optimal SWAP selection. Below, we list a few significant examples of works in which different meta-heuristics have been tested against the same benchmark, showing how the results have constantly improved over time:
- Rollout-based heuristic: inspired by the approach proposed in [93,94], the authors tackle the quantum-circuit-compilation problem (QCCP) by introducing two different heuristics: the first is a roll-out-based sequential decision-making strategy, which selects the next operation to schedule based on makespan estimates provided by a guiding priority rule; the second approach is a stochastic variant of the roll-out heuristic that alternates between roll-out and a basic priority rule to enhance search space exploration. When compared to the results for the same benchmarks in the recent literature at the time of this work’s publication, the proposed approach demonstrated notable reductions in makespan across various problem instances.
- Ant-Colony Optimisation: In reference [95], the authors propose an Ant-Colony Optimisation (ACO)-based algorithm that introduces an innovative pheromone model and incorporates a heuristic-driven Priority Rule to guide the iterative placement of quantum gates. The performance of the algorithm is compared with the results obtained against the same benchmark and used in the previous works, indicating that the proposed method significantly outperforms state-of-the-art approaches, achieving superior makespan reductions across a large set of test cases, and setting the pace for the resolution of hard combinatorial problems such as the QCCP. Furthermore, the findings highlight the scalability of the proposed approach, reinforcing its potential for tackling increasingly large quantum compilation tasks.
- Genetic Algorithms: in [96], the authors introduce an enhanced genetic algorithm designed to tackle QCCP instances for Quantum Approximate Optimisation Algorithms (QAOA) that is then specifically applied to solving MaxCut and graph coloring problems. The proposed algorithm builds upon the existing Decomposition-Based Genetic Algorithm (DBGA) but incorporates a novel encoding scheme that significantly reduces the number of SWAP gates inserted during the decoding phase, thereby minimising circuit depth. The effectiveness of this newly developed algorithm (DBGA-X) is then demonstrated through comparative experiments against the state-of-the-art methods previously described, confirming the power of genetic algorithms for resolving complex combinatorial problems, and showcasing the importance of a clever coding/decoding scheme to obtain superior performance.
5.3. Perspectives
Regardless of the particular optimisation techniques used, it is clear how quantum compilation has emerged as one of the central challenges in making the potential of quantum computers truly usable, especially as architectures become increasingly powerful; as the number of available qubits grows and their noise decreases, the way is paved for the execution of increasingly complex circuits. Scientific literature and the most recent reports converge on one key point: the connection between compilation and hardware characteristics is set to become increasingly close and decisive. Since full quantum error correction will not be feasible on NISQ devices [97], algorithms will need to be designed with noise resilience in mind. In this task, techniques like quantum routing will play a crucial role. Indeed, routing algorithms will continue to be essential for executing algorithms on qubits with limited connectivity. As we have seen, strategies based on advanced heuristics, classical optimisation methods, and machine learning are emerging as key tools to tackle these challenges at scale. However, without compilers capable of optimising depth, gate count, routing, and topology based on the actual hardware, this progress risks remaining purely theoretical. The dominant trend is toward hardware-aware compilation, in which compiler decisions are shaped by the real physical and logical constraints of the target machine.
Another major development involves compilers designed for fault-tolerant architectures that can estimate the required resources in advance, including logical qubits, computation time, and error-correction operations. These tools anticipate medium-term to long-term scenarios in which executable circuits will run on systems with hundreds of thousands or even millions of logical qubits.
Hybrid platforms (quantum-classical) and quantum cloud computing already demonstrate how efficient compilers can make the difference between an executable and an impractical circuit. Looking ahead, compilation will no longer be just a technical step, but a true enabler of quantum advantage, i.e., the ability to solve problems better or faster than classical methods. Achieving this goal will require ongoing coordination among hardware design, software development, and algorithmic innovation within an increasingly mature and integrated quantum ecosystem.
6. Conclusions
Understanding and predicting the behaviour of complex systems has long posed a significant challenge to science [2,3]. One of the encountered difficulties is computational complexity: many computational problems regarding complex systems are intractable. Another obstacle regards the recognition of variable patterns, which are emergent properties of complex systems. Therefore, it is an urgent priority to improve the performance of our computational machines and formulate brand-new algorithms. In this regard, AI and QC look undoubtedly promising. QAI is even more attractive, as AI and QC merge to refine themselves in a reciprocal manner. This work shows that QC can boost AI development through three pathways: (1) offering new materials for computing in hardware and wetware; formulating new algorithms for (2) optimisation problems, and (3) machine learning, this last being particularly in vogue in AI. Quantum phenomena such as superposition, entanglement, and tunnelling enhance the capabilities of AI. On the other hand, AI can help overcome many of the experimental difficulties encountered in implementing QC. In this regard, this work describes the ways in which AI algorithms are valuable for quantum-circuit compilation, which is a crucial step in implementing quantum computers based on qubits. A noticeable task in the field of QAI is to develop new algorithms that can exploit the thermalised quantum mixed states described in this work. They could facilitate the solution of particular NP (Non-deterministic Polynomial) problems and the recognition of variable patterns. The manipulation of thermalised quantum mixed states rather than qubits is not affected by decoherent phenomena. Therefore, their use would reduce the waste of the vast amounts of energy currently being spent to preserve conventional qubits from decoherent phenomena. Achieving this goal would be a remarkable feat in the modern world, which consumes vast amounts of energy.
From a technological standpoint, it is possible to outline a potential development trajectory for quantum computing that spans at least the next decade [98]. The primary goal is not to achieve immediate groundbreaking results, but rather to build a reliable foundation by gradually increasing quantum computers’ ability to perform complex operations with ever-greater fidelity; this outcome will largely depend on progress in hardware development. A key early milestone will be surpassing the threshold beyond which classical simulation is no longer feasible; this will mark a critical turning point and a new starting line.
Once this groundwork is laid, the next phase will see theoretical advantages begin to materialize into practical outcomes. The goal will then be to demonstrate, even on a small scale, that quantum computing can solve scientific problems more efficiently or faster than the best classical approaches. This will be a pivotal moment, where theory meets application. In this context, the emergence of error-tolerant quantum modules will be a crucial step toward developing scalable architectures. The next challenge will be to make these benefits more common and accessible across a wider range of application domains.
This will require improvements not only in the coherence and quality of qubits but also in the speed and complexity of executable operations. The ability to link multiple stable modules into a single networked system will ultimately enable the construction of large-scale quantum platforms capable of tackling previously unthinkable tasks. The end goal of this trajectory, although ambitious, is within reach: the creation of a fully error-tolerant quantum system, ready for real-world applications and capable of handling massive computational workloads with unprecedented precision.
Looking even further ahead, it is conceivable that, in the not-too-distant future, these systems will scale to perform billions of quantum operations with thousands of interconnected qubits. At that point, quantum computing’s full potential will be unlocked, making available capabilities that previously had been only imagined, fundamentally transforming how we approach science, industry, and knowledge itself. Although it is not an immediate objective, this vision appears increasingly attainable within the next technological generation, provided that investment continues in basic research, systems engineering, and the development of the skills needed to steer this revolution.
Author Contributions
Conceptualisation, P.L.G. and M.B.; methodology, P.L.G., M.B., C.L., A.O. and R.R.; investigation, P.L.G., F.F., C.L., V.N.L., A.O. and R.R.; writing—original draft preparation, P.L.G., M.B., C.L., A.O. and R.R.; writing—review and editing, P.L.G., M.B., C.L., V.N.L., A.O. and R.R.; visualisation, P.L.G.; supervision, P.L.G., M.B., C.L., A.O. and R.R.; project administration, P.L.G.; funding acquisition, P.L.G. All authors have read and agreed to the published version of the manuscript.
Funding
M. Baioletti acknowledges the financial support from the European Union—NextGenerationEU, Mission 4, Component 2, under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041—VITALITY—CUP J97G22000170005. P.L. Gentili acknowledges the European Union—NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041—VITALITY. He is grateful to Università degli Studi di Perugia and MUR for support within the project Vitality. P.L. Gentili also acknowledged MUR for support through the project PRIN2022-LUNARLIGHT—Prot. 2022NHLX2M. C. Loglisci acknowledges the financial support from the project “PNRR MUR project PE0000023-NQSTI” for this research.
Data Availability Statement
No new data were created for this work.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ACO | Ant Colony Optimisation |
| CP | Constraint Programming |
| DBGA | Decomposition-Based Genetic Algorithm |
| DQN | Deep Q-Networks |
| GNNs | Graph Neural Networks |
| ILP | Integer Linear Programming |
| LSTM | Long-Short Term Memory (LSTM) neural network |
| MCTS | Monte Carlo Tree Search |
| ML | Machine Learning |
| NISQ | Noisy Intermediate Scale Quantum |
| PQC | Parameterized Quantum Circuit |
| QAI | Quantum artificial intelligence |
| QAOA | Quantum Approximate Optimisation Algorithm |
| QC | Quantum Computing |
| QCCP | Quantum Circuit Compilation Problem |
| QUBO | Quadratic Unconstrained Binary Optimisation |
| RL | Reinforcement Learning |
| SABRE | Swap-Based Reordering Algorithm |
| SAT | Satisfiability |
| VQA | Variational Quantum Algorithm |
| VQE | Variational Quantum Eigensolver |
References
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015, A/RES/70/1. Available online: www.refworld.org/docid/57b6e3e44.html (accessed on 17 April 2025).
- Gentili, P.L. Why is Complexity Science valuable for reaching the goals of the UN 2030 Agenda? Rend. Fis. Acc. Lincei 2021, 32, 117–134. [Google Scholar] [CrossRef] [PubMed]
- Bustamante-Ubilla, M.; Arenas-Torres, F. Epistemological Foundations of Complexity Theory. Sustainability 2022, 14, 13316. [Google Scholar] [CrossRef]
- Goldreich, O. Computational Complexity: A Conceptual Perspective; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–7. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Singapore, 2006. [Google Scholar]
- Rozenberg, G.; Bäck, T.; Kok, J.N. Handbook of Natural Computing; Springer: Berlin, Germany, 2012. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education: Harlow, UK, 2022. [Google Scholar]
- Klusch, M.; Lässig, J.; Müssig, D.; Macaluso, A.; Wilhelm, F.K. Quantum artificial intelligence: A Brief Survey. Künstl. Intell. 2024, 38, 257–276. [Google Scholar] [CrossRef]
- Wichert, A. Principles of Quantum Artificial Intelligence; World Scientific: Singapore, 2020. [Google Scholar]
- Ying, M. Quantum computation, quantum theory and AI. Artif. Intell. 2010, 174, 162–176. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K. Artificial intelligence (AI) for quantum and quantum for AI. Opt. Quant. Electron. 2023, 55, 697. [Google Scholar] [CrossRef]
- Moret-Bonillo, V. Can artificial intelligence benefit from quantum computing? Prog. Artif. Intell. 2015, 3, 89–105. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Mitchell, M. Artificial Intelligence. A Guide for Thinking Humans; Farrar, Strauss and Giroux: New York, NY, USA, 2019. [Google Scholar]
- Bardella, G.; Franchini, S.; Pani, P.; Ferraina, S. Lattice physics approaches for neural networks. iScience 2024, 27, 111390. [Google Scholar] [CrossRef]
- Bardella, G.; Franchini, S.; Pan, L.; Balzan, R.; Ramawat, S.; Brunamonti, E.; Pani, P.; Ferraina, S. Neural Activity in Quarks Language: Lattice Field Theory for a Network of Real Neurons. Entropy 2024, 26, 495. [Google Scholar] [CrossRef] [PubMed]
- Funcke, L.; Hartung, T.; Jansen, K.; Kühn, S. Review on Quantum Computing for Lattice Field Theory. In Proceedings of the 39th International Symposium on Lattice Field Theory, Bonn, Germany, 8–13 August 2022; Volume 430, p. 228. [Google Scholar] [CrossRef]
- Grabowska, D. Quantum simulations of lattice field theories. In Proceedings of the 40th International Symposium on Lattice Field Theory, Atavia, IL, USA, 31 July–4 August 2023; Volume 453, p. 110. [Google Scholar] [CrossRef]
- Zheng, H.; Feng, Y.; Tang, J.; Ma, S. Interfacing brain organoids with precision medicine and machine learning. Cell Rep. Phys. Sci. 2022, 3, 100974. [Google Scholar] [CrossRef]
- Halverson, J. Building quantum field theories out of neurons. arXiv 2021, arXiv:2112.04527. [Google Scholar] [CrossRef]
- Ayoade, O.; Rivas, P.; Orduz, J. artificial intelligence Computing at the Quantum Level. Data 2022, 7, 28. [Google Scholar] [CrossRef]
- Christensen, D.V.; Dittmann, R.; Linares-Barranco, B.; Sebastian, A.; Le Gallo, M.; Redaelli, A.; Slesazeck, S.; Mikolajick, T.; Spiga, S.; Menzel, S.; et al. 2022 roadmap on neuromorphic computing and engineering. Neuromorph. Comput. Eng. 2022, 2, e022501. [Google Scholar] [CrossRef]
- Misra, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing 2010, 74, 239. [Google Scholar] [CrossRef]
- Przyczyna, D.; Zawal, P.; Mazur, T.; Strzelecki, M.; Gentili, P.L.; Szaciłowski, K. In-materio neuromimetic devices: Dynamics, information processing and pattern recognition. Jpn. J. Appl. Phys. 2020, 59, 050504. [Google Scholar] [CrossRef]
- Marković, D.; Grollier, J. Quantum neuromorphic computing. Appl. Phys. Lett. 2020, 117, 150501. [Google Scholar] [CrossRef]
- Ghosh, S.; Nakajima, K.; Krisnanda, T.; Fujii, K.; Liew, T.C.H. Quantum Neuromorphic Computing with Reservoir Computing Networks. Adv. Quantum Technol. 2021, 4, 210005. [Google Scholar] [CrossRef]
- Wasielewski, M.R.; Forbes, M.D.E.; Frank, N.L.; Kowalski, K.; Scholes, G.D.; Yuen-Zhou, J.; Baldo, M.A.; Freedman, D.E.; Goldsmith, R.H.; Goodson, T., 3rd; et al. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. 2020, 4, 490–504. [Google Scholar] [CrossRef]
- Stojanovic, M.N. Some experiments and directions in molecular computing and robotics. Isr. J. Chem. 2011, 51, 99–105. [Google Scholar] [CrossRef]
- Gentili, P.L.; Stano, P. Living cells and biological mechanisms as prototypes for developing chemical artificial intelligence. Biochem. Bioph. Res. Commun. 2024, 720, 150060. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L. Chemical AI in the limelight: The Contribution of Photochromic Materials and Oscillatory Chemical Reactions. Adv. Opt. Mater. 2025, 13, 2500016. [Google Scholar] [CrossRef]
- Stano, P.; Damiano, L. Synthetic cell research: Is technical progress leaving theoretical and epistemological investigations one step behind? Front. Robot. AI 2023, 10, 1143196. [Google Scholar] [CrossRef]
- De Silva, A.P. Molecular Logic-Based Computation; Royal Society of Chemistry: Cambridge, UK, 2013. [Google Scholar]
- Szaciłowski, K. Digital information processing in molecular systems. Chem. Rev. 2008, 108, 3481–3548. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Stano, P. Chemical Neural Networks Inside Synthetic Cells? A Proposal for Their Realisation and Modeling. Front. Bioeng. Biotechnol. 2022, 10, 927110. [Google Scholar] [CrossRef]
- Gentili, P.L.; Zurlo, M.P.; Stano, P. Neuromorphic engineering in wetware: The state of the art and its perspectives. Front. Neurosci. 2024, 18, 1443121. [Google Scholar] [CrossRef] [PubMed]
- Braccini, M.; Collinson, E.; Roli, A.; Fellermann, H.; Stano, P. Recurrent neural networks in synthetic cells: A route to autonomous molecular agents? Front. Bioeng. Biotechnol. 2023, 11, 1210334. [Google Scholar] [CrossRef]
- Gentili, P.L.; Dolnik, M.; Epstein, I.R. “Photochemical Oscillator”: Colored Hydrodynamic Oscillations and Waves in a Photochromic System. J. Phys. Chem. C 2014, 118, 598–608. [Google Scholar] [CrossRef]
- Nakano, T.; Okaie, Y.; Kobayashi, S.; Hara, T.; Hiraoka, Y.; Haraguchi, T. Methods and applications of mobile molecular communication. Proc. IEEE 2019, 107, 1442. [Google Scholar] [CrossRef]
- Gentili, P.L.; Stano, P. Tracing a new path in the field of AI and robotics: Mimicking human intelligence through chemistry. Part II: Systems chemistry. Front. Robot. AI 2023, 10, 1266011. [Google Scholar] [CrossRef]
- Nakano, T. Molecular communication: A 10 Year Retrospective. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2017, 3, 71–78. [Google Scholar] [CrossRef]
- Tomassoli, L.; Silva-Dias, L.; Dolnik, M.; Epstein, I.R.; Germani, R.; Gentili, P.L. Neuromorphic engineering in wetware: Discriminating Acoustic frequencies through their Effects on chemical waves. J. Phys. Chem. B 2024, 128, 1241–1255. [Google Scholar] [CrossRef]
- Lambert, N.; Chen, Y.-N.; Cheng, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10–18. [Google Scholar] [CrossRef]
- Adams, B.; Petruccione, F. Quantum effects in the brain: A review. AVS Quantum Sci. 2020, 2, 022901. [Google Scholar] [CrossRef]
- Erboz, A.; Kesekler, E.; Gentili, P.L.; Uversky, V.N.; Coskuner-Weber, O. Electromagnetic radiation and biophoton emission in neuronal communication and neurodegenerative diseases. Prog. Biophys. Mol. Biol. 2025, 195, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P.J.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, J.; Yao, Y.; Lan, Y. Can Molecular Quantum Computing Bridge Quantum Biology and Cognitive Science? Intell. Comp. 2024, 3, 0072. [Google Scholar] [CrossRef]
- Saleh, I.A.; Srivastava, A. Exploring the Intersection of Fuzzy Logic and Quantum Logic: A New Frontier in Non-Classical Logics. SciWaveBulletin 2023, 1, 27. [Google Scholar] [CrossRef]
- Gentili, P.L. Establishing a New Link between Fuzzy Logic, Neuroscience, and Quantum Mechanics through Bayesian Probability: Perspectives in artificial intelligence and Unconventional Computing. Molecules 2021, 26, 5987. [Google Scholar] [CrossRef]
- Gentili, P.L. The Conformational Contribution to Molecular Complexity and Its Implications for Information Processing in Living Beings and Chemical artificial intelligence. Biomimetics 2024, 9, 121. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Perez-Mercader, J. Quantitative Estimation of Chemical Microheterogeneity through the Determination of Fuzzy Entropy. Front. Chem. 2022, 10, 950769. [Google Scholar] [CrossRef]
- Gentili, P.L. The human sensory system as a collection of specialized fuzzifiers: A conceptual framework to inspire new artificial intelligent systems computing with words. J. Intel. Fuzzy Sys. 2014, 27, 2137–2151. [Google Scholar] [CrossRef]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Extending human perception of electromagnetic radiation to the UV region through biologically inspired photochromic fuzzy logic (BIPFUL) systems. Chem. Comm. 2016, 52, 1474–1477. [Google Scholar] [CrossRef]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Discriminating between the UV-A, UV-B and UVC regions by novel Biologically Inspired Photochromic Fuzzy Logic (BIPFUL) systems: A detailed comparative study. Dyes Pigm. 2016, 135, 169–176. [Google Scholar] [CrossRef]
- Gentili, P.L. Determining Chemical Microheterogeneity from the Analysis of Absorption and Luminescence Transient Signals. J. Phys. Chem. B 2024, 128, 8259–8271. [Google Scholar] [CrossRef]
- Gentili, P.L. The fuzziness of a chromogenic spirooxazine. Dyes Pigm. 2014, 110, 235–248. [Google Scholar] [CrossRef]
- Chicano, F.; Luque, G.; Dahi, Z.A.; Gil-Merino, R. Combinatorial optimisation with quantum computers. Eng. Optim. 2025, 57, 208–233. [Google Scholar] [CrossRef]
- Zahedinejad, E.; Zaribafiyan, A. Combinatorial Optimisation on Gate Model Quantum Computers: A Survey. arXiv 2017, arXiv:1708.05294. [Google Scholar]
- Perez-Ramirez, D.F. Variational Quantum Algorithms for Combinatorial Optimisation. arXiv 2024, arXiv:2407.06421. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimisation Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nature Comm. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Ibrahim, M.; Bronn, N.T.; Byrd, G.T. Crosstalk-Based Parameterized Quantum Circuit Approximation. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering, Boston, MA, USA, 13–16 June 2022; Volume 01, pp. 39–50. [Google Scholar]
- Wang, S.; Fontana, E.; Cerezo, M.; Sharma, K.; Sone, A.; Cincio, L.; Coles, P.J. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun. 2021, 12, 6961. [Google Scholar] [CrossRef] [PubMed]
- Herrman, R.; Lotshaw, P.C.; Ostrowski, J.; Humble, T.S.; Siopsis, G. Multi-angle quantum approximate optimisation algorithm. Sci. Rep. 2022, 12, 6781. [Google Scholar] [CrossRef]
- Vijendran, V.; Das, A.; Koh, D.E.; Assad, S.M.; Lam, P.K. An expressive ansatz for low-depth quantum approximate optimisation. Quantum Sci. Technol. 2024, 9, 025010. [Google Scholar] [CrossRef]
- Mücke, S.; Piatkowski, N.; Morik, K. Learning Bit by Bit: Extracting the Essence of Machine Learning. In Proceedings of the Conference on “Lernen, Wissen, Daten, Analysen”, Berlin, Germany, 30 September–2 October 2019; Volume 2454, pp. 144–155. [Google Scholar]
- Glover, F.W.; Kochenberger, G.A.; Du, Y. Quantum Bridge Analytics I: A tutorial on formulating and using QUBO models. 4OR 2019, 17, 335–371. [Google Scholar] [CrossRef]
- Verma, A.; Lewis, M.W. Penalty and partitioning techniques to improve performance of QUBO solvers. Discret. Optim. 2022, 44, 100594. [Google Scholar] [CrossRef]
- Vyskocil, T.; Djidjev, H.N. Simple Constraint Embedding for Quantum Annealers. In Proceedings of the International Conference on Rebooting Computing, Tysons, VA, USA, 7–9 November 2018; pp. 1–11. [Google Scholar]
- Kochenberger, G.A.; Hao, J.-K.; Glover, F.W.; Lewis, M.W.; Lü, Z.; Wang, H.; Wang, Y. The unconstrained binary quadratic programming problem: A survey. J. Comb. Optim. 2014, 28, 58–81. [Google Scholar] [CrossRef]
- van de Ven, G.M.; Tuytelaars, T.; Tolias, A.S. Three types of incremental learning. Nat. Mach. Intell. 2022, 4, 1185–1197. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual lifelong learning with neural networks: A review. Neural. Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef]
- Situ, H.; Lu, T.; Pan, M.; Li, L. Quantum continual learning of quantum data realizing knowledge backward transfer. Physica A 2023, 620, 128779. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, S. Quantum continual learning overcoming catastrophic forgetting. Chin. Phys. Lett. 2022, 39, 050303. [Google Scholar] [CrossRef]
- Loglisci, C.; Malerba, D.; Pascazio, S. Quarta: Quantum supervised and unsupervised learning for binary classification in domain-incremental learning. Quantum Mach. Lett. 2024, 6, 68. [Google Scholar] [CrossRef]
- Kashif, M.; Rashid, M.; Al-Kuwari, S.; Shafique, M. Alleviating barren plateaus in parameterized quantum machine learning circuits: Investigating advanced parameter initialisation strategies. In Proceedings of the 2024 Design, Automation & Test in Europe Conference & Exhibition, Valencia, Spain, 25–27 March 2024; pp. 1–6. [Google Scholar]
- Liang, Z.; Liu, G.; Liu, Z.; Cheng, J.; Hao, T.; Liu, K.; Ren, H.; Song, Z.; Liu, J.; Ye, F.; et al. Graph learning for parameter prediction of quantum approximate optimisation algorithm. In Proceedings of the 2023 International Conference on Computer-Aided Design (ICCAD), San Francisco, CA, USA, 28 October–2 November 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Sauvage, F.; Sim, S.; Kunitsa, A.A.; Simon, W.A.; Mauri, M.; Perdomo-Ortiz, A. FLIP: A flexible initializer for arbitrarily-sized parametrized quantum circuits. arXiv 2021, arXiv:2103.08572. [Google Scholar]
- Moussa, C.; Wang, H.; Bäck, T.; Dunjko, V. Unsupervised strategies for identifying optimal parameters in Quantum Approximate Optimisation Algorithm. EPJ Quantum Tech. 2022, 9, 11. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, Y.; Zhang, Y.; Wang, J.; Du, S. Deep learning on multi-view sequential data: A survey. Art. Intell. Rev. 2022, 56, 2819–2857. [Google Scholar] [CrossRef]
- Loglisci, C.; Losavio, V.; De Carolis, B.; Prifti Skenduli, M.; Malerba, D. Parameter prediction for variational quantum algorithms through sequence modeling (Short Paper). In Proceedings of the 23rd International Conference of the Italian Association for artificial intelligence (AIxIA 2024), Bolzano, Italy, 25–28 November 2024; Volume 3913. Available online: https://ceur-ws.org/Vol-3913/short1.pdf (accessed on 1 April 2025).
- Li, G.; Ding, Y.; Xie, Y. Tackling the Qubit Mapping Problem for NISQ-Era Quantum Devices. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ‘19), Providence, RI, USA, 13–17 April 2019; pp. 1001–1014. [Google Scholar] [CrossRef]
- Cowtan, A.; Dilkes, S.; Krajenbrink, A.; Simmons, W.; Sivarajah, S. On the qubit routing problem. arXiv 2019, arXiv:1902.08091. [Google Scholar]
- Kissinger, A.; van de Wetering, J. Picturing Quantum Software: An Introduction to the ZX-Calculus and Quantum Compilation. preprint 2024. [Google Scholar]
- Nannicini, G.; Bishop, L.S.; Günlük, O.; Jurcevic, P. Optimal Qubit Assignment and Routing via Integer Programming. ACM Trans. Quantum Comput. 2023, 4, 7. [Google Scholar] [CrossRef]
- Yang, J.; Kharkov, Y.A.; Shi, Y.; Heule, M.J.H.; Dutertre, B. Quantum Circuit Mapping Based on Incremental and Parallel SAT Solving. Leibniz Int. Proc. Inform. 2024, 305, 29:1–29:18. [Google Scholar] [CrossRef]
- Booth, K.E.C. Constraint Programming Models for Depth-Optimal Qubit Assignment and SWAP-Based Routing (Short Paper). Leibniz Int. Proc. Inform. 2023, 280, 43:1–43:10. [Google Scholar] [CrossRef]
- LeCompte, T.; Qi, F.; Yuan, X.; Tzeng, N.F.; Najafi, M.H.; Peng, L. Graph Neural Network Assisted Quantum Compilation for Qubit Allocation. In Proceedings of the 33rd Great Lakes Symposium on VLSI (GLSVLSI), Knoxville, TN, USA, 5–7 June 2023. [Google Scholar] [CrossRef]
- Sinha, A.; Azad, U.; Singh, H. Qubit Routing Using Graph Neural Network Aided Monte Carlo Tree Search. Proc. Aaai Conf. Artif. Intell. 2022, 36, 9935–9943. [Google Scholar] [CrossRef]
- Pozzi, M.G.; Herbert, S.J.; Sengupta, A.; Mullins, R.D. Using Reinforcement Learning to Perform Qubit Routing in Quantum Compilers. Trans. Quantum Comput. 2022, 3, 10. [Google Scholar] [CrossRef]
- Oddi, A.; Rasconi, R. Greedy randomized search for scalable compilation of quantum circuits. In Integration of Constraint Programming, Artificial Intelligence, and Operations Research; van Hoeve, W.-J., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 446–461. [Google Scholar]
- Chand, S.; Singh, H.K.; Ray, T.; Ryan, M. Rollout based Heuristics for the Quantum Circuit Compilation Problem. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 974–981. [Google Scholar] [CrossRef]
- Baioletti, M.; Rasconi, R.; Oddi, A. A Novel Ant Colony Optimisation Strategy for the Quantum Circuit Compilation Problem. In Evolutionary Computation in Combinatorial Optimisation; Zarges, C., Verel, S., Eds.; EvoCOP 2021. Lecture Notes in Computer Scienc; Springer: Cham, Switzerland, 2021; Volume 12692. [Google Scholar] [CrossRef]
- Arufe, L.; Rasconi, R.; Oddi, A.; Varela, R.; González, M.A. New coding scheme to compile circuits for Quantum Approximate Optimisation Algorithm by genetic evolution. Appl. Soft Comput. 2023, 144, 110456. [Google Scholar] [CrossRef]
- IBM. The future of Computing is Quantum. Tratto da IBM Technology Atlas. 2024. Available online: https://www.ibm.com/roadmaps/quantum/ (accessed on 1 April 2025).
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).