Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review
Abstract
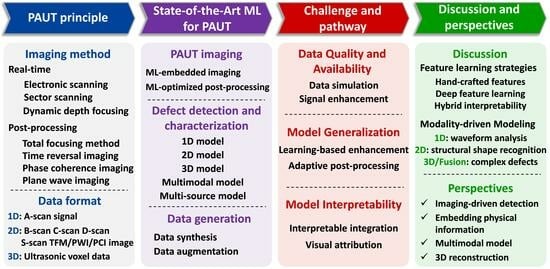
1. Introduction
2. Overview of PAUT Fundamentals
2.1. PAUT Imaging Method
2.1.1. Real-Time Imaging
- Linear scanning
- Sector scanning
- Dynamic depth focusing
2.1.2. Post-Processing Imaging
- Total focusing method
- Time reversal imaging
- Phase coherence imaging
- Plane wave imaging
2.2. PAUT Data Representation
- 1D format
- 2D format
- Three-dimensional volumetric format
3. State-of-the-Art ML for PAUT
3.1. Phased Array Ultrasonic Imaging
3.2. Defect Detection and Characterization
3.2.1. Unimodal Models
- 1.
- One-dimensional model for A-scan
- 2.
- Two-dimensional model for B-scan
- 3.
- Two-dimensional model for C-scan
- 4.
- Two-dimensional model for S-scan
- 5.
- Two-dimensional model for TFM and PWI data
- 6.
- Three-dimensional model for volumetric data
| Application | Reference | ML Model | Input | Dataset Source and Size | Output | Key Metric |
|---|---|---|---|---|---|---|
| Classification | Zhao 2023 [71] | Multi-grained cascade forest (gcForest) | A-scan | Artificial defect specimen 2000 A-scan signals | Size categories of defect (seven classes) | Acc = 97.50% |
| Wang 2022 [44] | GCN | A-scan | N/A | Presence of defect | N/A | |
| Cheng 2023 [46] | 1D-CNN and LSTM | A-scan | Artificial defect specimen 2694 A-scan signals | Presence of defect | Acc = 96.28%, P = 95.22%, R = 96.49% | |
| Siljama 2021 [72] | Improved VGG16 | B-scan | Real defect data and data augmentation 500,000 B-scan images | Presence of defect | Acc = 97.5%, P = 97.26%, R = 96.63% | |
| McKnight 2024 [66] | 3D-CNN | 3D volumetric data | Artificial defect specimen and simulation data 680 3D volumetric data (64 × 1204 × 64) | Presence of defect | Acc = 100.00%, P = 100.00%, R = 100.00% | |
| Dimensional regression | Jia 2024 [61] | Least squares boosting (LSBoost) | S-scan | N/A | Characteristic parameters of interfacial waves | MAPE = 4.38% (Stratified flow) MAPE = 17.26% (Plug flow) |
| Wang 2024 [47] | 1D-CNN | A-scan | Simulation data 21,200 A-scan signals | Surface height | MAE = 0.0237mm (thirty-two elements), MAE = 0.0292mm (eight elements), MAE = 0.0497mm (four elements) | |
| Yang 2016 [48] | RBFNN | A-scan | Real defect data 320 A-scan signals | Defect size and angle | RRMSE = 3.612% (Taper angle), RRMSE = 3.453% (Diameter) | |
| Pyle 2021 [73] | 2D-CNN | Multiple PWI images | Real defect data and simulation data 26,623 PWI images | Defect size and angle | MSE = ±0.29mm (Length), MSE = ±2.9° (Angle) | |
| Bai 2021 [74] | 2D-CNN | Scattering matrix | Simulation data 1156 scattering matrices | Defect size and angle | MAE = 0.08, RMSE = 0.12, R2 = 0.92 (Size) MAE = 4.88, RMSE = 9.54, R2 = 0.92 (Angle) | |
| Object detection | Yuan 2020 [75] | ANN | B-scan | Real defect data and artificial defect specimen 35 B-scan images | Defect location and class (three classes) | Acc = 93.00% |
| Chen 2024 [50] | Improved YOLO v8 | B-scan | Simulation data and public dataset 2286 B-scan images | Defect location and class (two classes) | F1 = 75.68%, IoU = 83.79% | |
| Medak 2022 [53] | 2D-CNN and LSTM | B-scan sequence | Artificial defect specimen Over 4000 B-scan image sequences | Defect location and class (seven classes) | mAP = 91.60% (Conv2d) mAP =91.40% (LSTM) | |
| Tunukovic 2024 [57] | Faster R-CNN | C-scan | Artificial defect specimen and simulation data Over 300 C-scan images | Defect location and class (four classes) | P = 99.80%, R = 96.00%, F1 = 97.80% | |
| Latete 2021 [64] | Faster R-CNN | PWI image | Artificial defect specimen and simulation data 2048 time-trace matrices | Defect location and class (two classes) | R = 70.00% | |
| Segmentation | Liu 2022 [59] | 2D-CNN | C-scan | Artificial defect specimen 1000 C-scan images | Defect mask and class (three classes) | Mean IoU = 75.00% |
| Zhang 2022 [65] | Strongly generalized CNN | Radio frequency data | Public dataset 2900 radio frequency data | Defect mask and class (one class) | IoU = 96.29% F1 = 98.28% | |
| He 2023 [22] | Improved Mask R-CNN | S-scan | Real defect data 3000 S-scan images | Defect mask and class (five classes) | mAP = 98.20% | |
| Zhang 2024 [69] | Improved 3D U-net | 3D volumetric data | Real defect data 196 3D volumetric samples (64 × 128 × 128) | Defect mask and class (one class) | Dice Acc = 90.90% | |
| Anomaly detection | Tunukovic 2024 [56] | DBSCAN and AE | B-scan | Artificial defect specimen 11,750 B-scan images | Presence of defect | AUC = 92.20% (Simple) AUC = 87.90% (Complex) |
| Posilovic 2022 [76] | MobileNet and Patch distribution modeling (PaDiM) | B-scan | Artificial defect specimen 5715 anomalous and 11,709 normal B-scan images | Presence of defect | AUC = 82.00% | |
| Wang 2023 [20] | 2D-CNN and transformer | S-scan and C-scan | Real defect data 90 normal S-scan and C-scan images | Presence of defect | IoU = 15.42% F1 = 25.80% |
3.2.2. Multimodal Models
3.2.3. Multi-Source Models
| Applications | Reference | ML Model | Input 1 | Input 2 | Fusion Method |
|---|---|---|---|---|---|
| Classification | Ortiz de Zuniga 2022 [77] | 2D-CNN and LSTM | S-scan | A-scan | Decision-level fusion of two-branch classification results. |
| Object detection | Li 2021 [78] | YOLO v4 and 1D-CNN | C-scan | A-scan | The C-scan is used to locate defect regions, followed by the extraction of A-scan data from these regions for defect classification. |
| Classification | Cao 2025 [79] | ResNet and GRU | S-scan | A-scan | The two branches perform feature-level fusion for classification. |
| Object detection | Li 2021 [82] | Cascade R-CNN | C-scan | Infrared image | Parallel two-branch feature-level fusion at multiple scales. |
| Segmentation | Caballero 2023 [83] | 2D-CNN | C-scan | XCT slice data | The two data sources are aligned, with the C-scan serving as the model input and XCT slices used as segmentation labels. |
| Segmentation | Sudharsan 2024 [84] | Tri-planar Mask R-CNN | TFM image | Pulsed thermography data | The spatial alignment of the two volumetric data enables pixel-level fusion, followed by feature extraction along the three spatial dimensions. |
3.3. Generation of Phased Array Ultrasonic Data
3.3.1. Data Synthesis
3.3.2. Data Augmentation
| Method | Reference | Approaches | Dataset Type and Size |
|---|---|---|---|
| Data synthesis | Zhang 2022 [88] | PZFlex simulation | 4500 A-scan signals |
| Kumbhar 2023 [89] | COMSOL simulation | A-scan signals N/A | |
| Lee 2023 [90] | CIVA simulation | 498 S-scan images | |
| Gantala 2023 [87] | FE and VASA | 1000 TFM images | |
| Pyle 2021 [73] | FE and ray-based simulation | 25,625 PWI images | |
| Zhang 2023 [97] | CIVA simulation | 2000 PWI images | |
| Liu 2023 [38] | MATLAB Field II simulation | 30,000 sets of paired FMC-TFM data | |
| Pilikos 2020 [37] | MATLAB K-wave simulation | 230 sets of paired FMC–mask data | |
| Latete 2021 [64] | Pogo FEA simulation | 2048 time-trace matrices | |
| Data augmentation | Siljama 2021 [72] | Traditional data augmentation and virtual flaws | 500,000 B-scan images |
| Shi 2020 [98] | Traditional data augmentation | 2050 B-scan images | |
| Virkkunen 2021 [92] | Virtual flaws | 20,000 B-scan images | |
| Sun 2023 [93] | Constrained Cycle GAN | B-scan images N/A | |
| Yang 2024 [55] | PATCH GAN | 1159 sets of paired B-scan–mask data | |
| McKnight 2024 [91] | Cycle GAN | 154 C-scan images | |
| Granados 2023 [94] | Conditional U-net | TFM images N/A | |
| Granados 2024 [99] | Class-conditioned generative adversarial autoencoder | TFM images N/A |
4. Challenges in ML-PAUT Integration
4.1. Data Quality and Availability
4.2. Model Generalization
4.3. Model Interpretability
5. Discussion and Perspectives
5.1. Discussion
5.1.1. Feature Extraction
5.1.2. Modality Selection
5.2. Perspectives
- (1)
- Imaging-driven defect characterization
- (2)
- Fusion of PAUT physical information with ML
- (3)
- Multimodal models for PAUT data
- (4)
- Three-dimensional ultrasonic reconstruction for NDT
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, W.; Zhou, Z.; Li, Y. Inspection of butt welds for complex surface parts using ultrasonic phased array. Ultrasonics 2019, 96, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Satyanarayan, L.; Kumaran, K.B.; Krishnamurthy, C.; Balasubramaniam, K. Inverse method for detection and sizing of cracks in thin sections using a hybrid genetic algorithm based signal parametrisation. Theor. Appl. Fract. Mech. 2008, 49, 185–198. [Google Scholar] [CrossRef]
- Satyanarayan, L.; Rajkumar, K.; Sharma, G.; Jayakumar, T.; Krishnamurthy, C.; Balasubramaniam, K.; Raj, B. Investigations on imaging and sizing of defects using ultrasonic phased array and the synthetic aperture focusing technique. Insight-Non-Destr. Test. Cond. Monit. 2009, 51, 384–390. [Google Scholar] [CrossRef]
- Kleiner, D.; Bird, C.R. Signal processing for quality assurance in friction stir welds. Insight-Non-Destr. Test. Cond. Monit. 2004, 46, 85–87. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Bai, Z.; Chen, S.; Xiao, Q.; Jia, L.; Zhao, Y.; Zeng, Z. Compressive sensing of phased array ultrasonic signal in defect detection: Simulation study and experimental verification. Struct. Health Monit. 2018, 17, 434–449. [Google Scholar] [CrossRef]
- Cruz, F.; Simas Filho, E.; Albuquerque, M.; Silva, I.; Farias, C.; Gouvêa, L. Efficient feature selection for neural network based detection of flaws in steel welded joints using ultrasound testing. Ultrasonics 2017, 73, 1–8. [Google Scholar] [CrossRef]
- Li, J.; Zhan, X.; Jin, S. An automatic flaw classification method for ultrasonic phased array inspection of pipeline girth welds. Insight Non-Destr. Test. Cond. Monit. 2013, 55, 308–315. [Google Scholar] [CrossRef]
- Bai, L.; Velichko, A.; Drinkwater, B.W. Characterization of defects using ultrasonic arrays: A dynamic classifier approach. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 2146–2160. [Google Scholar] [CrossRef]
- He, X.; Jiang, X.; Mo, R.; Guo, J. Quality Classification of Ultrasonically Welded Automotive Wire Harness Terminals by Ultrasonic Phased Array. Russ. J. Nondestruct. Test. 2024, 60, 415–430. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Singh, K. A review on conventional machine learning vs. deep learning. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; pp. 347–352. [Google Scholar]
- Li, F.; Zou, F.; Rao, J. A multi-GPU and CUDA-aware MPI-based spectral element formulation for ultrasonic wave propagation in solid media. Ultrasonics 2023, 134, 107049. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. Adv. Neural Inf. Process. Syst. 2016, 29, 2234–2242. [Google Scholar]
- Latif, S.; Driss, M.; Boulila, W.; Huma, Z.E.; Jamal, S.S.; Idrees, Z.; Ahmad, J. Deep learning for the industrial internet of things (iiot): A comprehensive survey of techniques, implementation frameworks, potential applications, and future directions. Sensors 2021, 21, 7518. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Wang, S.; Yu, P. An efficient perceptual video compression scheme based on deep learning-assisted video saliency and just noticeable distortion. Eng. Appl. Artif. Intell. 2025, 141, 109806. [Google Scholar] [CrossRef]
- Kumar, V.; Lee, P.-Y.; Kim, B.-H.; Fatemi, M.; Alizad, A. Gap-filling method for suppressing grating lobes in ultrasound imaging: Experimental study with deep-learning approach. IEEE Access 2020, 8, 76276–76286. [Google Scholar] [CrossRef]
- Song, H.; Yang, Y. Uncertainty quantification in super-resolution guided wave array imaging using a variational Bayesian deep learning approach. Ndt E Int. 2023, 133, 102753. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Zhang, L.; Yu, J.; Liu, Q. Three-Dimensional Defect Characterization of Ultrasonic Detection Based on GCNet Improved Contrast Learning Optimization. Electronics 2023, 12, 3944. [Google Scholar] [CrossRef]
- Posilović, L.; Medak, D.; Subašić, M.; Petković, T.; Budimir, M.; Lončarić, S. Flaw detection from ultrasonic images using YOLO and SSD. In Proceedings of the 2019 11th International Symposium on Image and Signal Processing and Analysis (ISPA), Dubrovnik, Croatia, 23–25 September 2019; pp. 163–168. [Google Scholar]
- He, D.; Ma, R.; Jin, Z.; Ren, R.; He, S.; Xiang, Z.; Chen, Y.; Xiang, W. Welding quality detection of metro train body based on ABC mask R-CNN. Measurement 2023, 216, 112969. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, S.; Wilcox, P.D.; Croxford, A.J. Deep learning in automated ultrasonic NDE–developments, axioms and opportunities. NDT E Int. 2022, 131, 102703. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Tian, T.; Deng, D.; Hu, M.; Ma, J.; Gao, D.; Zhang, J.; Ma, S.; Yang, L. A review on guided-ultrasonic-wave-based structural health monitoring: From fundamental theory to machine learning techniques. Ultrasonics 2023, 133, 107014. [Google Scholar] [CrossRef] [PubMed]
- Freeman, S.R.; Quick, M.K.; Morin, M.A.; Anderson, R.C.; Desilets, C.S.; Linnenbrink, T.E.; O'Donnell, M. Delta-sigma oversampled ultrasound beamformer with dynamic delays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 320–332. [Google Scholar] [CrossRef] [PubMed]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Fan, C.; Caleap, M.; Pan, M.; Drinkwater, B.W. A comparison between ultrasonic array beamforming and super resolution imaging algorithms for non-destructive evaluation. Ultrasonics 2014, 54, 1842–1850. [Google Scholar] [CrossRef]
- Lev-Ari, H.; Devancy, A. The time-reversal technique re-interpreted: Subspace-based signal processing for multi-static target location. In Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop. SAM 2000 (Cat. No. 00EX410), Cambridge, MA, USA, 16–17 March 2000; pp. 509–513. [Google Scholar]
- Fink, M.; Cassereau, D.; Derode, A.; Prada, C.; Roux, P.; Tanter, M.; Thomas, J.-L.; Wu, F. Time-reversed acoustics. Rep. Prog. Phys. 2000, 63, 1933. [Google Scholar] [CrossRef]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 958–974. [Google Scholar] [CrossRef]
- Miura, K.; Shidara, H.; Ishii, T.; Ito, K.; Aoki, T.; Saijo, Y.; Ohmiya, J. Image quality improvement in single plane-wave imaging using deep learning. Ultrasonics 2025, 145, 107479. [Google Scholar] [CrossRef]
- Holfort, I.K.; Gran, F.; Jensen, J.A. Broadband minimum variance beamforming for ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 314–325. [Google Scholar] [CrossRef]
- Le Jeune, L.; Robert, S.; Villaverde, E.L.; Prada, C. Plane Wave Imaging for ultrasonic non-destructive testing: Generalization to multimodal imaging. Ultrasonics 2016, 64, 128–138. [Google Scholar] [CrossRef]
- Simonetti, F. Multiple scattering: The key to unravel the subwavelength world from the far-field pattern of a scattered wave. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 73, 036619. [Google Scholar] [CrossRef]
- Pimpalkhute, V.A.; Page, R.; Kothari, A.; Bhurchandi, K.M.; Kamble, V.M. Digital image noise estimation using DWT coefficients. IEEE Trans. Image Process. 2021, 30, 1962–1972. [Google Scholar] [CrossRef] [PubMed]
- Luiken, N.; Ravasi, M. A deep learning-based approach to increase efficiency in the acquisition of ultrasonic non-destructive testing datasets. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 3094–3102. [Google Scholar]
- Pilikos, G.; Horchens, L.; Batenburg, K.J.; van Leeuwen, T.; Lucka, F. Fast ultrasonic imaging using end-to-end deep learning. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–4. [Google Scholar]
- Liu, L.; Liu, W.; Teng, D.; Xiang, Y.; Xuan, F.-Z. A multiscale residual U-net architecture for super-resolution ultrasonic phased array imaging from full matrix capture data. J. Acoust. Soc. Am. 2023, 154, 2044–2054. [Google Scholar] [CrossRef] [PubMed]
- Molinier, N.; Painchaud-April, G.; Le Duff, A.; Toews, M.; Bélanger, P. Ultrasonic imaging using conditional generative adversarial networks. Ultrasonics 2023, 133, 107015. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Li, B.; Chen, L.; Wei, X.; Shang, Z.; Liu, C. Ultrasound image super-resolution reconstruction based on semi-supervised CycleGAN. Ultrasonics 2024, 137, 107177. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, X.; Zhu, W.; Zheng, S.; Fan, G.; Li, Z.; Zhang, H.; Zhang, H. Super-resolution reconstruction of ultrasonic Lamb wave TFM image via deep learning. Meas. Sci. Technol. 2023, 34, 055406. [Google Scholar] [CrossRef]
- Shafiei Alavijeh, M.; Scott, R.; Seviaryn, F.; Maev, R.G. Using machine learning to automate ultrasound-based classification of butt-fused joints in medium-density polyethylene gas pipes. J. Acoust. Soc. Am. 2021, 150, 561–572. [Google Scholar] [CrossRef]
- Choung, J.; Lim, S.; Lim, S.H.; Chi, S.C.; Nam, M.H. Automatic Discontinuity Classification of Wind-turbine Blades Using A-scan-based Convolutional Neural Network. J. Mod. Power Syst. Clean Energy 2021, 9, 210–218. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Zhang, L. Semi-Automatic Defect Distinction of PAUT for High Strength Steel Corner Structure. Russ. J. Nondestruct. Test. 2022, 58, 1071–1078. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Lee, J.-R. Automated data evaluation in phased-array ultrasonic testing based on A-scan and feature training. NDT E Int. 2024, 141, 102974. [Google Scholar] [CrossRef]
- Cheng, X.; Ma, G.; Wu, Z.; Zu, H.; Hu, X. Automatic defect depth estimation for ultrasonic testing in carbon fiber reinforced composites using deep learning. NDT E Int. 2023, 135, 102804. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, F.; Zou, F. Deep learning based ultrasonic reconstruction of rough surface morphology. Ultrasonics 2024, 138, 107265. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Xue, B.; Jia, L.; Zhang, H. Quantitative analysis of pit defects in an automobile engine cylinder cavity using the radial basis function neural network-genetic algorithm model. Struct. Health Monit.-Int. J. 2017, 16, 696–710. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, J.; Tian, K.; Wang, A.; Li, J.; Gao, X. Advancing Ultrasonic Defect Detection in High-Speed Wheels via UT-YOLO. Sensors 2024, 24, 1555. [Google Scholar] [CrossRef]
- Chen, H.; Tao, J. Utilizing improved YOLOv8 based on SPD-BRSA-AFPN for ultrasonic phased array non-destructive testing. Ultrasonics 2024, 142, 107382. [Google Scholar] [CrossRef]
- Tan, M.; Pang, R.; Le, Q.V. Efficientdet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, DC, USA, 14–19 June 2020; pp. 10781–10790. [Google Scholar]
- Cheng, X.; Qi, H.; Wu, Z.; Zhao, L.; Cech, M.; Hu, X. Automated Detection of Delamination Defects in Composite Laminates from Ultrasonic Images Based on Object Detection Networks. J. Nondestruct. Eval. 2024, 43, 94. [Google Scholar] [CrossRef]
- Medak, D.; Posilović, L.; Subašić, M.; Budimir, M.; Lončarić, S. Deep learning-based defect detection from sequences of ultrasonic B-scans. IEEE Sens. J. 2021, 22, 2456–2463. [Google Scholar] [CrossRef]
- Medak, D.; Posilovic, L.; Subasic, M.; Budimir, M.; Loncaric, S. Automated Defect Detection From Ultrasonic Images Using Deep Learning. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3126–3134. [Google Scholar] [CrossRef]
- Yang, H.; Shu, J.; Li, S.; Duan, Y. Ultrasonic array tomography-oriented subsurface crack recognition and cross-section image reconstruction of reinforced concrete structure using deep neural networks. J. Build. Eng. 2024, 82, 108219. [Google Scholar] [CrossRef]
- Tunukovic, V.; McKnight, S.; Pyle, R.; Wang, Z.; Mohseni, E.; Pierce, S.G.; Vithanage, R.K.; Dobie, G.; MacLeod, C.N.; Cochran, S. Unsupervised machine learning for flaw detection in automated ultrasonic testing of carbon fibre reinforced plastic composites. Ultrasonics 2024, 140, 107313. [Google Scholar] [CrossRef]
- Tunukovic, V.; McKnight, S.; Mohseni, E.; Pierce, S.G.; Pyle, R.; Duernberger, E.; Loukas, C.; Vithanage, R.K.; Lines, D.; Dobie, G. A study of machine learning object detection performance for phased array ultrasonic testing of carbon fibre reinforced plastics. NDT E Int. 2024, 144, 103094. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, Z.; Zhou, Q.; Zhu, C.; Liu, T.; Wang, B. Damage identification of wind turbine blades based on deep learning and ultrasonic testing. Nondestruct. Test. Eval. 2024, 40, 1–26. [Google Scholar] [CrossRef]
- Liu, K.; Yu, Q.; Lou, W.; Sfarra, S.; Liu, Y.; Yang, J.; Yao, Y. Manifold learning and segmentation for ultrasonic inspection of defects in polymer composites. J. Appl. Phys. 2022, 132, 024901. [Google Scholar] [CrossRef]
- Zhou, L.; Li, W.; Lu, X.; Wang, X.; Liu, H.; Liang, J.; Jiang, F.; Zhou, G. Ultrasonic Image Recognition of Terminal Lead Seal Defects Based on Convolutional Neural Network. In Proceedings of the International Symposium on Insulation and Discharge Computation for Power Equipment; Springer: Berlin/Heidelberg, Germany, 2023; pp. 77–88. [Google Scholar]
- Jia, H.; Wen, J.; Xu, X.; Liu, M.; Fang, L.; Zhao, N. Spatial and temporal characteristic information parameter measurement of interfacial wave using ultrasonic phased array method. Energy 2024, 292, 130472. [Google Scholar] [CrossRef]
- Chen, Y.; He, D.; He, S.; Jin, Z.; Miao, J.; Shan, S.; Chen, Y. Welding defect detection based on phased array images and two-stage segmentation strategy. Adv. Eng. Inform. 2024, 62, 102879. [Google Scholar] [CrossRef]
- Zhang, E.; Wang, S.; Zhou, S.; Cheng, B.; Huang, S.; Duan, W. Intelligent Ultrasonic Image Classification of Artillery Cradle Weld Defects Based on MECF-QPSO-KELM Method. Russ. J. Nondestruct. Test. 2023, 59, 305–319. [Google Scholar] [CrossRef]
- Latete, T.; Gauthier, B.; Belanger, P. Towards using convolutional neural network to locate, identify and size defects in phased array ultrasonic testing. Ultrasonics 2021, 115, 106436. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, L.; Zhang, Y.; Gao, X.; Li, J. A Convolutional Neural Network for Ultrasound Plane Wave Image Segmentation With a Small Amount of Phase Array Channel Data. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2270–2281. [Google Scholar] [CrossRef]
- McKnight, S.; MacKinnon, C.; Pierce, S.G.; Mohseni, E.; Tunukovic, V.; MacLeod, C.N.; Vithanage, R.K.; O’Hare, T. 3-Dimensional residual neural architecture search for ultrasonic defect detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2024, 71, 423–436. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, E.; Zhou, L.; Han, Y.; Liu, W.; Hong, J. 3DWDC-Net: An improved 3DCNN with separable structure and global attention for weld internal defect classification based on phased array ultrasonic tomography images. Mech. Syst. Signal Process. 2025, 229, 112564. [Google Scholar] [CrossRef]
- McKnight, S.; Tunukovic, V.; Pierce, S.G.; Mohseni, E.; Pyle, R.; MacLeod, C.N.; O’Hare, T. Advancing carbon fiber composite inspection: Deep learning-enabled defect localization and sizing via 3-Dimensional U-Net segmentation of ultrasonic data. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2024, 71, 1106–1119. [Google Scholar] [CrossRef]
- Sen, Z.; Zhang, Y. Automated Weld Defect Segmentation from Phased Array Ultrasonic Data Based on U-Net Architecture. NDT E Int. 2024, 146, 103165. [Google Scholar]
- Liu, Y.; Yu, Q.; Liu, K.; Zhu, N.; Yao, Y. Stable 3D Deep Convolutional Autoencoder Method for Ultrasonic Testing of Defects in Polymer Composites. Polymers 2024, 16, 1561. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Yang, K.; Du, X.; Yao, S.; Zhao, Y. Automated quantification of small defects in ultrasonic phased array imaging using AWGA-gcForest algorithm. Nondestruct. Test. Eval. 2023, 39, 1495–1516. [Google Scholar] [CrossRef]
- Siljama, O.; Koskinen, T.; Jessen-Juhler, O.; Virkkunen, I. Automated Flaw Detection in Multi-channel Phased Array Ultrasonic Data Using Machine Learning. J. Nondestruct. Eval. 2021, 40, 67. [Google Scholar] [CrossRef]
- Pyle, R.J.; Bevan, R.L.T.; Hughes, R.R.; Rachev, R.K.; Ali, A.A.S.; Wilcox, P.D. Deep Learning for Ultrasonic Crack Characterization in NDE. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1854–1865. [Google Scholar] [CrossRef]
- Bai, L.; Le Bourdais, F.; Miorelli, R.; Calmon, P.; Velichko, A.; Drinkwater, B.W. Ultrasonic defect characterization using the scattering matrix: A performance comparison study of Bayesian inversion and machine learning schemas. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3143–3155. [Google Scholar] [CrossRef]
- Yuan, M.; Li, J.; Liu, Y.; Gao, X. Automatic recognition and positioning of wheel defects in ultrasonic B-Scan image using artificial neural network and image processing. J. Test. Eval. 2020, 48, 308–322. [Google Scholar] [CrossRef]
- Posilović, L.; Medak, D.; Milković, F.; Subašić, M.; Budimir, M.; Lončarić, S. Deep learning-based anomaly detection from ultrasonic images. Ultrasonics 2022, 124, 106737. [Google Scholar] [CrossRef]
- Ortiz de Zuniga, M.; Prinja, N.; Casanova, C.; Dans Alvarez de Sotomayor, A.; Febvre, M.; Camacho Lopez, A.M.; Rodríguez Prieto, A. Artificial Intelligence for the Output Processing of Phased-Array Ultrasonic Test Applied to Materials Defects Detection in the ITER Vacuum Vessel Welding Operations. In Proceedings of the Pressure Vessels and Piping Conference, Las Vegas, NV, USA, 17–22 July 2022; p. V005T009A006. [Google Scholar]
- Li, C.; He, W.; Nie, X.; Wei, X.; Guo, H.; Wu, X.; Xu, H.; Zhang, T.; Liu, X. Intelligent damage recognition of composite materials based on deep learning and ultrasonic testing. AIP Adv. 2021, 11, 125227. [Google Scholar] [CrossRef]
- Cao, W.; Sun, X.; Liu, Z.; Chai, Z.; Bao, G.; Yu, Y.; Chen, X. The detection of PAUT pseudo defects in ultra-thick stainless-steel welds with a multimodal deep learning model. Measurement 2025, 241, 115662. [Google Scholar] [CrossRef]
- Wang, X.; He, J.; Guo, W.; Guan, X. Three-dimensional damage quantification of low velocity impact damage in thin composite plates using phased-array ultrasound. Ultrasonics 2021, 110, 106264. [Google Scholar] [CrossRef]
- Yang, R.; He, Y.; Zhang, H. Progress and trends in nondestructive testing and evaluation for wind turbine composite blade. Renew. Sustain. Energy Rev. 2016, 60, 1225–1250. [Google Scholar] [CrossRef]
- Li, C.; Nie, X.; Chang, Z.; Wei, X.; He, W.; Wu, X.; Xu, H.; Feng, Z. Infrared and ultrasonic intelligent damage recognition of composite materials based on deep learning. Appl. Opt. 2021, 60, 8624–8633. [Google Scholar] [CrossRef] [PubMed]
- Caballero, J.-I.; Cosarinsky, G.; Camacho, J.; Menasalvas, E.; Gonzalo-Martin, C.; Sket, F. A Methodology to Automatically Segment 3D Ultrasonic Data Using X-ray Computed Tomography and a Convolutional Neural Network. Appl. Sci. 2023, 13, 5933. [Google Scholar] [CrossRef]
- Sudharsan, P.L.; Gantala, T.; Balasubramaniam, K. Multi modal data fusion of PAUT with thermography assisted by Automatic Defect Recognition System (M-ADR) for NDE Applications. NDT E Int. 2024, 143, 103062. [Google Scholar] [CrossRef]
- Mohammadkhani, R.; Zanotti Fragonara, L.; Padiyar, M.J.; Petrunin, I.; Raposo, J.; Tsourdos, A.; Gray, I. Improving depth resolution of ultrasonic phased array imaging to inspect aerospace composite structures. Sensors 2020, 20, 559. [Google Scholar] [CrossRef]
- Uhlig, S.; Alkhasli, I.; Schubert, F.; Tschöpe, C.; Wolff, M. A review of synthetic and augmented training data for machine learning in ultrasonic non-destructive evaluation. Ultrasonics 2023, 134, 107041. [Google Scholar] [CrossRef]
- Gantala, T.; Sudharsan, P.L.; Balasubramaniam, K. Automated defect recognition (ADR) for monitoring industrial components using neural networks with phased array ultrasonic images. Meas. Sci. Technol. 2023, 34, 094007. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, L.; Zhang, H.; Zhang, T.; Zhu, Q. Phased array ultrasonic inspection and automated identification of wrinkles in laminated composites. Compos. Struct. 2022, 300, 116170. [Google Scholar] [CrossRef]
- Kumbhar, S.B.; Sonamani Singh, T. Prediction of Depth of Defect from Phased Array Ultrasonic Testing Data Using Neural Network. In Proceedings of the International Conference on Mechanical Engineering: Researches and Evolutionary Challenges, Warangal, India, 23–25 June 2023; pp. 109–119. [Google Scholar]
- Lee, S.-E.; Park, J.; Yeom, Y.-T.; Kim, H.-J.; Song, S.-J. Sizing-based flaw acceptability in weldments using phased array ultrasonic testing and neural networks. Appl. Sci. 2023, 13, 3204. [Google Scholar] [CrossRef]
- McKnight, S.; Pierce, S.G.; Mohseni, E.; MacKinnon, C.; MacLeod, C.; O'Hare, T.; Loukas, C. A comparison of methods for generating synthetic training data for domain adaption of deep learning models in ultrasonic non-destructive evaluation. NDT E Int. 2024, 141, 102978. [Google Scholar] [CrossRef]
- Virkkunen, I.; Koskinen, T.; Jessen-Juhler, O.; Rinta-aho, J. Augmented Ultrasonic Data for Machine Learning. J. Nondestruct. Eval. 2021, 40, 4. [Google Scholar] [CrossRef]
- Sun, X.; Li, H.; Lee, W.-N. Constrained CycleGAN for effective generation of ultrasound sector images of improved spatial resolution. Phys. Med. Biol. 2023, 68, 125007. [Google Scholar] [CrossRef]
- Granados, G.; Miorelli, R.; Gatti, F.; Robert, S.; Clouteau, D. Towards a multi-fidelity deep learning framework for a fast and realistic generation of ultrasonic multi-modal Total Focusing Method images in complex geometries. NDT E Int. 2023, 139, 102906. [Google Scholar] [CrossRef]
- Gantala, T.; Balasubramaniam, K. Automated Defect Recognition for Welds Using Simulation Assisted TFM Imaging with Artificial Intelligence. J. Nondestruct. Eval. 2021, 40, 28. [Google Scholar] [CrossRef]
- Filipović, B.; Milković, F.; Subašić, M.; Lončarić, S.; Petković, T.; Budimir, M. Automated ultrasonic testing of materials based on C-scan flaw classification. In Proceedings of the 2021 12th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 13–15 September 2021; pp. 230–234. [Google Scholar]
- Zhang, F.; Luo, L.; Li, J.; Peng, J.; Zhang, Y.; Gao, X. Ultrasonic adaptive plane wave high-resolution imaging based on convolutional neural network. NDT E Int. 2023, 138, 102891. [Google Scholar] [CrossRef]
- Shi, J.; Tao, Y.; Guo, W.; Zheng, J. CNN based defect recognition model for phased array ultrasonic testing images of electrofusion joints. In Proceedings of the Pressure Vessels and Piping Conference, Online, 3 August 2020; p. V006T006A026. [Google Scholar]
- Granados, G.; Gatti, F.; Miorelli, R.; Robert, S.; Clouteau, D. Generative domain-adapted adversarial auto-encoder model for enhanced ultrasonic imaging applications. NDT E Int. 2024, 148, 103234. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part V 13. pp. 740–755. [Google Scholar]
- Bevan, R.L.T.J.; Croxford, A.J. Automated detection and characterisation of defects from multiview ultrasonic imaging. NDT E Int. 2022, 128, 102628. [Google Scholar] [CrossRef]
- Schmid, S.; Wei, H.; Grosse, C.U. On the uncertainty in the segmentation of ultrasound images reconstructed with the total focusing method. Sn Appl. Sci. 2023, 5, 108. [Google Scholar] [CrossRef]
- Lei, M.; Zhang, W.; Zhang, T.; Wu, Y.; Gao, D.; Tao, X.; Li, K.; Shao, X.; Yang, Y. Improvement of low-frequency ultrasonic image quality using a enhanced convolutional neural network. Sens. Actuators A Phys. 2024, 365, 114878. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, S.; Croxford, A.J.; Wilcox, P.D. A data-driven approach to suppress artefacts using PCA and autoencoders. NDT E Int. 2023, 139, 102904. [Google Scholar] [CrossRef]
- Jayasudha, J.C.; Lalithakumari, S. Weld defect segmentation and feature extraction from the acquired phased array scan images. Multimed. Tools Appl. 2022, 81, 31061–31074. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, J.; Zhou, S.K.; Rasselkorde, E.M.; Abbasi, W.A. Post-processing of phased-array ultrasonic inspection data with parallel computing for nondestructive evaluation. J. Nondestruct. Eval. 2014, 33, 342–351. [Google Scholar] [CrossRef]
- Herve-Cote, H.; Dupont-Marillia, F.; Belanger, P. Automatic flaw detection in sectoral scans using machine learning. Ultrasonics 2024, 141, 107316. [Google Scholar] [CrossRef]
- Koskinen, T.; Virkkunen, I.; Siljama, O.; Jessen-Juhler, O. The Effect of Different Flaw Data to Machine Learning Powered Ultrasonic Inspection. J. Nondestruct. Eval. 2021, 40, 24. [Google Scholar] [CrossRef]
- Zhang, J.; Bell, M.A.L. Overfit detection method for deep neural networks trained to beamform ultrasound images. Ultrasonics 2025, 148, 107562. [Google Scholar] [CrossRef]
- Pyle, R.J.; Bevan, R.L.T.; Hughes, R.R.; Ali, A.A.S.; Wilcox, P.D. Domain Adapted Deep-Learning for Improved Ultrasonic Crack Characterization Using Limited Experimental Data. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1485–1496. [Google Scholar] [CrossRef]
- Pyle, R.J.; Hughes, R.R.; Wilcox, P.D. Interpretable and explainable machine learning for ultrasonic defect sizing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 277–290. [Google Scholar] [CrossRef]
- Shi, S.; Jin, S.; Zhang, D.; Liao, J.; Fu, D.; Lin, L. Improving Ultrasonic Testing by Using Machine Learning Framework Based on Model Interpretation Strategy. Chin. J. Mech. Eng. 2023, 36, 127. [Google Scholar] [CrossRef]
- Valeske, B.; Tschuncky, R.; Leinenbach, F.; Osman, A.; Wei, Z.; Römer, F.; Koster, D.; Becker, K.; Schwender, T. Cognitive sensor systems for NDE 4.0: Technology, AI embedding, validation and qualification. Tm-Tech. Messen 2022, 89, 253–277. [Google Scholar] [CrossRef]
- Bevan, R.L.; Budyn, N.; Zhang, J.; Croxford, A.J.; Kitazawa, S.; Wilcox, P.D. Data fusion of multiview ultrasonic imaging for characterization of large defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2387–2401. [Google Scholar] [CrossRef] [PubMed]
- Andreades, C.; Fierro, G.P.M.; Meo, M. A nonlinear ultrasonic modulation approach for the detection and localisation of contact defects. Mech. Syst. Signal Process. 2022, 162, 108088. [Google Scholar] [CrossRef]
- Sui, X.; Zhang, R.; Luo, Y.; Fang, Y. Multiple bolt looseness detection using SH-typed guided waves: Integrating physical mechanism with monitoring data. Ultrasonics 2025, 150, 107601. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Peng, L.; Lin, J.; Wang, S.; Zhao, W.; Huang, S. Microcrack defect quantification using a focusing high-order SH guided wave EMAT: The physics-informed deep neural network GuwNet. IEEE Trans. Ind. Inform. 2021, 18, 3235–3247. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, Y.; Xiang, Y.; Li, P.; Liu, X. An Interface Reconstruction Method Based on The Physics-informed Neural Network: Application to Ultrasonic Array Imaging. IEEE Trans. Instrum. Meas. 2024, 74, 2503008. [Google Scholar] [CrossRef]
- Li, N.; Wu, R.; Li, H.; Wang, H.; Gui, Z.; Song, D. M 2 FNet: Multimodal Fusion Network for Airport Runway Subsurface Defect Detection Using GPR Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar]
- Zhao, X.; Zhang, J.; Li, Q.; Zhao, T.; Li, Y.; Wu, Z. Global and local multi-modal feature mutual learning for retinal vessel segmentation. Pattern Recognit. 2024, 151, 110376. [Google Scholar] [CrossRef]
- Ran, Q.-Y.; Miao, J.; Zhou, S.-P.; Hua, S.-h.; He, S.-Y.; Zhou, P.; Wang, H.-X.; Zheng, Y.-P.; Zhou, G.-Q. Automatic 3-D spine curve measurement in freehand ultrasound via structure-aware reinforcement learning spinous process localization. Ultrasonics 2023, 132, 107012. [Google Scholar] [CrossRef]
- Huang, Q.; Zeng, Z. A review on real-time 3D ultrasound imaging technology. BioMed Res. Int. 2017, 2017, 6027029. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, Y.; He, Y.; Deng, B.; Lu, X.; Wang, H.; Wang, L.; Cao, Y. Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review. AI 2025, 6, 124. https://doi.org/10.3390/ai6060124
Na Y, He Y, Deng B, Lu X, Wang H, Wang L, Cao Y. Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review. AI. 2025; 6(6):124. https://doi.org/10.3390/ai6060124
Chicago/Turabian StyleNa, Yiming, Yunze He, Baoyuan Deng, Xiaoxia Lu, Hongjin Wang, Liwen Wang, and Yi Cao. 2025. "Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review" AI 6, no. 6: 124. https://doi.org/10.3390/ai6060124
APA StyleNa, Y., He, Y., Deng, B., Lu, X., Wang, H., Wang, L., & Cao, Y. (2025). Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review. AI, 6(6), 124. https://doi.org/10.3390/ai6060124