Finite Element Analysis and Simulation of 316L Stainless Steel and Titanium Alloy for Orthopedic Hip and Knee Prosthetics

Abstract

Background: Ferrous metals are used extensively in the manufacturing of plates, pins, Kirschner wires (K-wires), and screws, and in the performance of partial and total joint replacement surgeries for the shoulder, elbow, and wrist joints. The primary surgical procedures commonly performed are hip and knee replacement surgeries. Metals possess a combination of high modulus, yield point, and ductility, rendering them well suited for load-bearing applications, as they can withstand significant loads without experiencing substantial deformations or permanent alterations in their dimensions. Application of metals and alloys is of prime importance in orthopedics as they lead the way to overcoming many issues encountered in implant use. In some instances, pure metals are used, but alloys consisting of two or more elements typically exhibit greater material characteristics, including corrosion resistance as well as toughness. The first item to address when selecting a metallic implant material is its biocompatibility. In this regard, three classes of materials are also commonly known as biomedical metals—316L stainless steel, pure titanium, and titanium alloys. Objective: The aim of this work is to create a model describing the material behavior and then simulate the metals under a load of 2300 N, which is equivalent to plastic loading. Methods: Under ten different case studies, a sub-routine was developed to combine the material characteristics of titanium and 316L stainless steel with the software. Results: The outcomes of the research were then investigated. A femur model was created using ANSYS software, and two materials, stainless steel and titanium, were used. The model was then exposed to a force of 2300 N.

1. Introduction

Biomaterials have extensive applications in restoring, substituting, or enhancing damaged or diseased components of the locomotor system (musculoskeletal), including bones, joints, and teeth [1]. The primary criterion for a biomaterial is its compatibility with the surrounding tissue environment, ensuring the absence of adverse or unsuitable interactions. The primary clinical goal is to alleviate discomfort and enhance mobility in the affected area, whereas the engineering goal aims to minimize physiological strain on the remaining bone structures [2]. This ensures the preservation of the operational performance of both the prosthetic and bone materials over an extended period of use. Therefore, materials that are deemed ideal for implantation are those that exhibit high biocompatibility and possess the ability to endure repeated loading within the challenging physiological conditions of the human body [1,2,3].

Based solely on the name “Biomaterial”, one may quickly deduce that it refers to a natural material composed entirely of organic (biological) substances. Indeed, this statement applies to a specific category of biomaterial. However, it is important to note that this is merely the initial stage of a vast and captivating area of research that is seeing consistent and robust expansion. The field has been in existence for roughly fifty years. It combines elements of medicine, biology, chemistry, and material science, making it a multifaceted discipline built around engineering concepts [1,4]. Due to the ongoing research and changing practical requirements of medicine and health care methodology, a variety of medical devices, prostheses, diagnostic products, and disposables are found in the market.

Nevertheless, the variety of applications for these products continues to increase. Aside from conventional medical devices, pharmaceutical preparations, diagnostic products, and healthcare disposables, biomaterial applications are vast and limitless. These applications include, but are not limited to, the following: tissue cultures, bone fracture fixation, cranial repair, joint replacements (such as the knee, hip, shoulder, wrist, and elbow), intelligent drug delivery systems, engineered tissues, breast implants, contact lenses, heart valves, hybrid organs, as well as dental implants for tooth stabilization, etc. So far, tens of millions of individuals have had medical implant procedures. Without question, biomaterials have significantly influenced the field of modern medicine and the treatment of patients, leading to the preservation and enhancement of the lives of both people and animals [2,5].

According to the definition provided by the National Institutes of Health (NIH), “a biomaterial refers to a natural or synthetic substance, or a mix of materials, intended for use in medical applications, whether temporary or long-term. These materials can function on their own or as components of an implanted system to treat, restore, or replace tissues, organs, or bodily functions”. This definition was put forth by Boretos and Eden in 1984, as documented [2,3,4,5]. Various perspectives exist regarding biomaterials, leading to multiple definitions that attempt to capture their essence. It is acknowledged that current definitions of biomaterials are not flawless or exhaustive, yet they serve as valuable references or initial frameworks for discourse.

Irrespective of the specific context, the fundamental procedures in establishing an issue remain consistent. This study aims to establish a predictive model for preventing failure by accurately forecasting fatigue failure resulting from cyclic plastic loading. This objective’s accomplishment necessitates the utilization of approximation constitutive equations to model the physics of failure [6]. The calibration of the constitutive equations is necessary to experimentally define the failure mechanism and accurately estimate the material’s fatigue life when subjected to cyclic loading. In part, geometry is determined through modeling fatigue failure, which is necessary to induce plastic flow in the material under examination. The selection of appropriate equations to characterize the behavior of materials is a pivotal aspect in formulating model calculations. Understanding that utilizing an incorrect model or imprecise material attributes will invariably render the model predictions invalid has significant importance. In the context of this study, a material’s behavior is most accurately characterized through the rate-independent theory of metal plasticity. Rate-independent metal plasticity is employed to compute permanent deformation in metals subjected to loading conditions beyond their yield point [7]. The theory of plasticity for metals with rate-independent behavior was established to accurately predict the mechanical response of these metals under minor strain conditions. Rate-independent plasticity is employed in modeling metals that undergo deformation at low temperatures, namely those materials below 50% of the melting point, and experience moderate strain rates ranging from 0.01 to 10 per second [8].

1.1. 316L Stainless Steel

Stainless steel is a collective term encompassing many types of steel that are predominantly utilized for their ability to withstand corrosion, owing to their elevated chromium (Cr) content. Various types of stainless steel are used in the field of implantation. Nevertheless, the following are extensively and predominantly used for orthopedic implantation due to their affordability and convenient manufacturability: stainless steel 316L, F139, grade 2, and ASTM F138. Austenitic type 316L stainless steel exhibits favorable biocompatibility and other mechanical properties with appropriate density for applications requiring load-bearing capabilities. Consequently, this material is much sought after as a good choice for surgical implants [3,8,9]. The carbon percentage of this steel is <0.030% (wt. %) to mitigate the corrosive implications in biological environments. This steel is marked as “L” in 316L, indicating its low carbon content (CC). The primary purpose of reducing the CC in 316L is to enhance its corrosion resistance. The 316L alloy consists primarily of iron (60–65%) and contains substantial amounts of Cr (17–20%) and nickel (12–14%), along with small quantities of phosphorus (P), manganese (Mn), molybdenum (Mb), nitrogen (N), silicon (Si), and sulfur (S). The primary justification for incorporating alloying additives in 316L pertains to the surface and bulk microstructure of the metal. The primary role of chromium is to facilitate the production of steel resistant to corrosion via the highly adherent surface of a chromium trioxide (Cr₂O₃) layer. Using stainless steel as a significant material in the surgical domain was initially achieved with success [7,10]. The utilization of this biomaterial in orthopedic implants dates back to the 1920s. It has since become the predominant choice for creating bone plates due to its favorable mechanical strength, cost effectiveness, ease of implant production, and malleability during surgical procedures. Various varieties of stainless steels are utilized in orthopedics [11]. However, the AISI 316L stainless steel is commonly employed due to its superior fatigue strength, increased ductility, and improved machinability, resulting in a wide range of biomedical applications.

Nevertheless, the substance in question contains nickel (Ni), which possesses the potential for toxicity, sensitization, and the induction of allergic reactions. Hence, stainless steels without nickel exist for applications inside the orthopedic domain. Overall, titanium alloys exhibit superior corrosion qualities compared with stainless steel, although they contain less than 0.03% (wt, %) carbon to mitigate the risk of in vivo corrosion. Consequently, stainless steel is deemed appropriate for biomedical implants [9,10,11]. The 316L stainless steel has a significantly higher Young’s modulus than bone, roughly ten times greater. This discrepancy in modulus results in stress shielding of the adjacent bone, leading to bone resorption [8,9]. The chromium (Cr) present in stainless steel exhibits a strong inclination towards oxygen, facilitating the development of a chromium oxide film on the steel’s surface at a molecular scale. This layer possesses passive, sticky, tenacious, and self-healing properties. Gorejová et al. [12] have highlighted that stainless steel implants frequently experience degradation because of many corrosion mechanisms, including pitting, crevice, and other corrosion categories, when placed within the human body. The corrosion resistance of these materials can be altered by reducing the Ni content and introducing alloying elements such as manganese (Mn) or nitrogen (N). Austenitic stainless Steel (ASS) has a comparatively low performance in terms of wear resistance [10,13]. Fast loosening is linked to a significant accumulation of wear debris in this case. The limited application of orthopedic joint prostheses is attributed to their inferior corrosion resistance and the potential risk of allergic reactions, which are prevalent among many patients.

Furthermore, it should be noted that the modulus of stainless steel is around 200 GPa—significantly higher than that of human bone (~10–30 GPa) [11,14]. Titanium, with its lower elastic modulus (~110 GPa), better biocompatibility, and superior corrosion resistance, offers a promising complement to stainless steel. The combination of these materials aims to optimize mechanical properties, reduce stress shielding, and improve overall implant performance.

Stainless steels can be categorized into three classifications based on their microstructural characteristics: ferritic, martensitic, and austenitic. Among the several types of stainless steels, the ASS possesses a face-centered cubic structure and exhibits nonmagnetic properties. These steels are composed of chromium (Cr) in the 16–18 wt range (%) and nickel (Ni) in the range of 12–15 wt. (%). The inclusion of Cr enhances the corrosion resistance of the steel, while the presence of nickel ensures the stability of the austenitic phase. The 316L austenitic stainless steel is widely employed as a metallic biomaterial in orthopedic applications, particularly in producing articulated prostheses and structural components for fracture fixation because of its exceptional mechanical strength [12,13,14,15].

1.2. Titanium

The utilization of titanium and the endeavor to employ it as a material for implants may be traced back to the 1930s. Its favorable characteristics are primarily due to its lightweight nature and advantageous mechano-chemical qualities. The study revealed that titanium and stainless steels were both determined to be well tolerated [13,14,15]. The resistance to corrosion property of titanium permits it to act as one of the most effective materials in this regard. Specifically, pure titanium or Ti CP and extra-low interstitial or Ti-6Al-4V (ELI) are the most sought-after biomaterials for biomedical applications. These are categorized as physiologically inert biomaterials. Consequently, these entities undergo small alterations upon transplantation into the human anatomy, as the human body can identify these substances as exogenous and endeavor to sequester them by enveloping them within fibrous tissues. Nevertheless, it is worth noting that these substances do not elicit any negative responses concerning their compatibility with human tissues [5,16].

Several titanium alloys, such as Ti-6Al-4V, Ti-5Al-2.5Fe, and Ti-6Al-7Nb, exhibit adequate strength and corrosion resistance. For example, pure titanium (Ti) and Ti-6Al-4V have elastic moduli that are nearly half that of bone, yet their strength is still about ten times greater. One additional benefit of using titanium-based metals for implants is their advantageous strength-to-density ratio, as supported by previous studies [17]. Nevertheless, it is important to acknowledge the primary drawbacks associated with these materials, which include their substantial expense, subpar wear characteristics, limited shear resistance, and susceptibility to oxygen diffusion during the fabrication and heat treatment processes, and the potential for titanium to become brittle due to the presence of dissolved oxygen. Therefore, specific fabrication and welding techniques are necessary for joining. Titanium is widely recognized for its high passivity, as the passive coating that develops on titanium and its alloys exhibits a notable lack of reactivity. In the context of these alloys, it has been observed that the passive state is not entirely stable, and there are specific conditions under which localized breakdown can occur on a highly microscopic level. As mentioned earlier, the shortcomings observed in applications have necessitated the implementation of surface modification techniques on the material. This approach aims to improve the material’s resistance to corrosion and wear while maintaining its mechanical qualities. Previous studies have documented the occurrence of titanium compounds in the adjacent tissues of these implants [15,16,17,18], as well as the eventual failure of the implants as a result of fatigue, stress corrosion cracking, and inadequate wear resistance [3].

The compatibility of titanium-based biomaterials with blood has not been definitively determined. However, extensive research has demonstrated that it is safe to use on humans, as it does not exhibit any hazardous properties. The safety and tissue compatibility of titanium (Ti) is attributed to its chemical characteristics, particularly its surface qualities. Therefore, understanding these features is of utmost significance [6,19]. The notable characteristics of titanium, such as its lightweight nature and favorable mechano-chemical properties, make it highly suitable for implant applications. According to a study by Zhang et al. [20], titanium has been identified as the sole metal biomaterial capable of osseointegration.

Additionally, Bartolomeu et al. [21] made assumptions regarding the potential bioactive behavior resulting from the gradual synthesis of hydrated titanium oxide on the titanium implant’s surface, facilitating the assimilation of calcium and phosphorus [5]. In the context of orthopedic implants, metallic materials must possess exceptional attributes such as toughness, elasticity, stiffness, strength, and fracture resistance. In the context of complete joint replacement, utilizing metals with high wear resistance properties is imperative. There exist four distinct grades of unalloyed pure titanium that are used for surgical implant applications, with differentiation based on the number of impurities, including oxygen, nitrogen, and iron, present within each grade. The quantity of oxygen that is present influences the ductility and strength of various titanium alloys. Among these alloys, Ti6Al4V is commonly utilized in implant applications. The primary constituents of this material consist of aluminum (Al) and vanadium (V), which serve as the principal alloying elements.

Other titanium alloys commonly utilized include Ti13Nb13Zr, which primarily consists of niobium and zirconium as alloying elements, and Ti3V11Cr3Al, which incorporates Al, Cr, and V as alloying components. The efficacy of titanium as an implant material is attributed to its capacity for osseointegration with the adjacent bone tissue, demonstrating bioactive characteristics that facilitate direct bone development onto its surface. The success of titanium and its alloys as implants can be attributed to several factors [22,23,24,25]. Firstly, it forms an oxide film surface, which serves two important functions during the initial stages of implantation. Thus, it avoids the negative implications of corrosive products in the surrounding tissues, as demonstrated by Wang et al. [22].

Additionally, this oxide film steadily grows in vivo, as observed by Gaval and Solanke [23]. Notably, the composition of this film is stoichiometrically similar to TiO₂, which is known to be biocompatible, as supported by studies conducted by Al-Amin et al. [25]. Furthermore, the surface coating of Ti implants can undergo reformation to a TiOOH matrix. This matrix effectively traps the superoxide created, owing to the inflammatory response, thereby disallowing the release of hydroxyl radicals, as highlighted by Jafari et al. [26].

With regards to the resistance of titanium alloys to corrosion, this is juxtaposed by the elastic moduli, which is approximately half that of stainless steels, resulting in a reduced likelihood of bone stress shielding [9,27]. As such, the Ti-6Al-4V ELI (ASTM F136) alloy comprising titanium, with 6 wt% aluminum and 4wt% vanadium, was selected to enhance the load-bearing capacity in applications like total joint replacements. Additionally, the Ti-6Al-4V alloy has been developed for utilization in aerospace contexts and exhibited exceptional efficacy within the aviation sector, characterized by an elastic modulus of roughly 110 GPa (16 × 106 psi). The utilization of modular femoral heads in total joint replacement (TJR) surgery and the application of long-term medical devices such as pacemakers have been seen. Nevertheless, subsequent investigations have revealed that the existence of vanadium results in cytotoxic effects and unfavorable tissue responses [28].

Consequently, the substitution of vanadium with niobium and iron has been undertaken to create Ti-5Al-2.5Fe and Ti-6Al-7Nb alloys. Additional Ti-15Mo-2.8Nb-3Al and Ti-15Mo-5Zr-3Al alloys have been subjected to experimentation, which has revealed that their discharge of vanadium and aluminum ions can potentially lead to enduring health complications, including peripheral neuropathy, osteomalacia, and Alzheimer’s disease. Therefore, it may be said that Ti-6Al-4V has experienced a decline in its significance as the primary orthopedic alloy [12,28].

The safety and tissue compatibility of titanium (Ti) is attributed to its chemical characteristics, particularly its surface qualities. Therefore, a comprehensive understanding of these features holds significant relevance. Titanium (Ti) exhibits a high degree of thermodynamic activity, making it one of the most easily ionized metallic elements, surpassed only by magnesium (Mg) and beryllium (Be). The inherent reactivity of titanium serves as a fundamental determinant of its chemical attributes, encompassing its challenging workability, corrosion resistance, and safety profile. Despite the strong reactivity of titanium as an element, titanium as a metallic substance exhibits remarkable corrosion resistance. This phenomenon can be attributed to the pronounced reactivity exhibited by titanium [29]. Due to this factor, the level of resistance to corrosion exhibited by the material is significantly higher than that of stainless steel or Co-Cr alloy. The inherent properties of this substance not only provide resistance to corrosion but account for its facile integration into biological systems and its non-toxic nature [14,26]. Titanium is characterized by its low density, resulting in a lightweight material.

The density of the material in question is 4.5 g/cm³, whereas 316 stainless steel has a 7.9 g/cm³ density. Nonetheless, the biomedical application of titanium alloys has been restricted due to their inadequate shear strength and wear resistance [27]. While there has been some progress in enhancing the wear resistance of β-Ti alloys compared with α + β alloys, a comprehensive and basic comprehension of the wear mechanisms involved is necessary to fully assess the suitability of orthopedic titanium alloys as wear components [15,23,28,29]. Stress shielding occurs when there is a disparity in the Young’s moduli of an implant device and the bone, resulting in non-uniform stress transfer between the two entities. This phenomenon is widely recognized in the field. Under such circumstances, bone atrophy ensues, resulting in implant loosening and bone refracturing. Hence, stiffness, also known as Young’s modulus, is preferable, as it is relatively lower than bone. The Young’s moduli of these metallic biomaterials typically exhibit significantly higher values than bone. The Young’s moduli of pure titanium (Ti) and its alloys are generally lower in magnitude than those of stainless steel. As an illustration, titanium (Ti) and its alloy, namely Ti-6Al-4V ELI, are extensively employed in the fabrication of implant devices due to their Young’s modulus measuring approximately 110 GPa.

However, as previously noted, titanium still exhibits a higher modulus than bone, which typically ranges between 10 and 30 GPa.

Titanium alloys are classified into three main categories: α-, (α + β)-, and β-type alloys. The Young’s moduli of α- and (α + β)-type titanium alloys, exemplified by Ti and Ti-6Al-4V ELI, respectively, exhibit higher values compared with β-type titanium alloys. Hence, the utilization of β-type titanium alloys has notable benefits in developing titanium alloys with reduced Young’s modulus, particularly in biomedical applications [29].

Researchers have explored the reduction of Young’s moduli in β-type titanium alloys, intending to utilize them in biomedical contexts due to their composition of elements devoid of toxicity and allergenic properties. Several β-type titanium alloys, which primarily consist of non-toxic and hypoallergenic elements, have been produced or are currently under development [30]. These alloys also exhibit low Young’s moduli. The Young’s moduli of the materials are generally less than 80 GPa under solution-treated conditions. Determining Young’s modulus for a given material may yield varying results based on specific measurement techniques, including tensile, three-point bending, and free resonance methods. The polycrystal β-type titanium alloys, Ti-35Nb-4Sn or Ti-24Nb-4Zr-7.9Sn (TNTZ), when subjected to extreme cold working, exhibit a minimum Young’s modulus value of around 40 GPa, as reported in many sources [17,21,31]. The strength and Young’s modulus of titanium alloys are crucial considerations for their prolonged utilization in biomedical implant applications. Specifically, the significance of dynamic strength, such as fatigue strength, cannot be overstated in this context. The ongoing development of β-type titanium alloys for prosthetics aims to enhance fatigue strength while minimizing Young’s modulus. The present study explores the subject matter in order to establish the appropriate degree of Young’s modulus that effectively prevents stress shielding between a low Young’s modulus β-type titanium alloy implant and the surrounding bone. Previous studies have examined the impact of Young’s modulus on bone atrophy by employing titanium alloy implants with varying Young’s moduli [17,18,32].

Titanium and its alloys have demonstrated superior material quality for orthopedic implants because of their exceptional corrosion resistance, which surpasses that of stainless steel. Additionally, titanium possesses lower moduli than stainless steel, a significant contributing element in stress shielding [33]. It exhibits a favorable strength-to-density ratio, making it compatible with bioinert characteristics. Moreover, it demonstrates good tensile and fatigue strength. However, despite possessing numerous commendable characteristics, it exhibits subpar wear resistance and low shear resistance.

In contrast, stainless steel demonstrates a notable capacity for withstanding wear and shear forces. Extensive efforts have been made, and ongoing research is being conducted, to develop titanium with low moduli, stainless steel with enhanced corrosion resistance, and nickel-free stainless steel. Despite their individual benefits, minimal research has been conducted on integrating the advantageous properties of stainless steel and titanium to develop an optimized biomaterial for orthopedic applications [34,35].

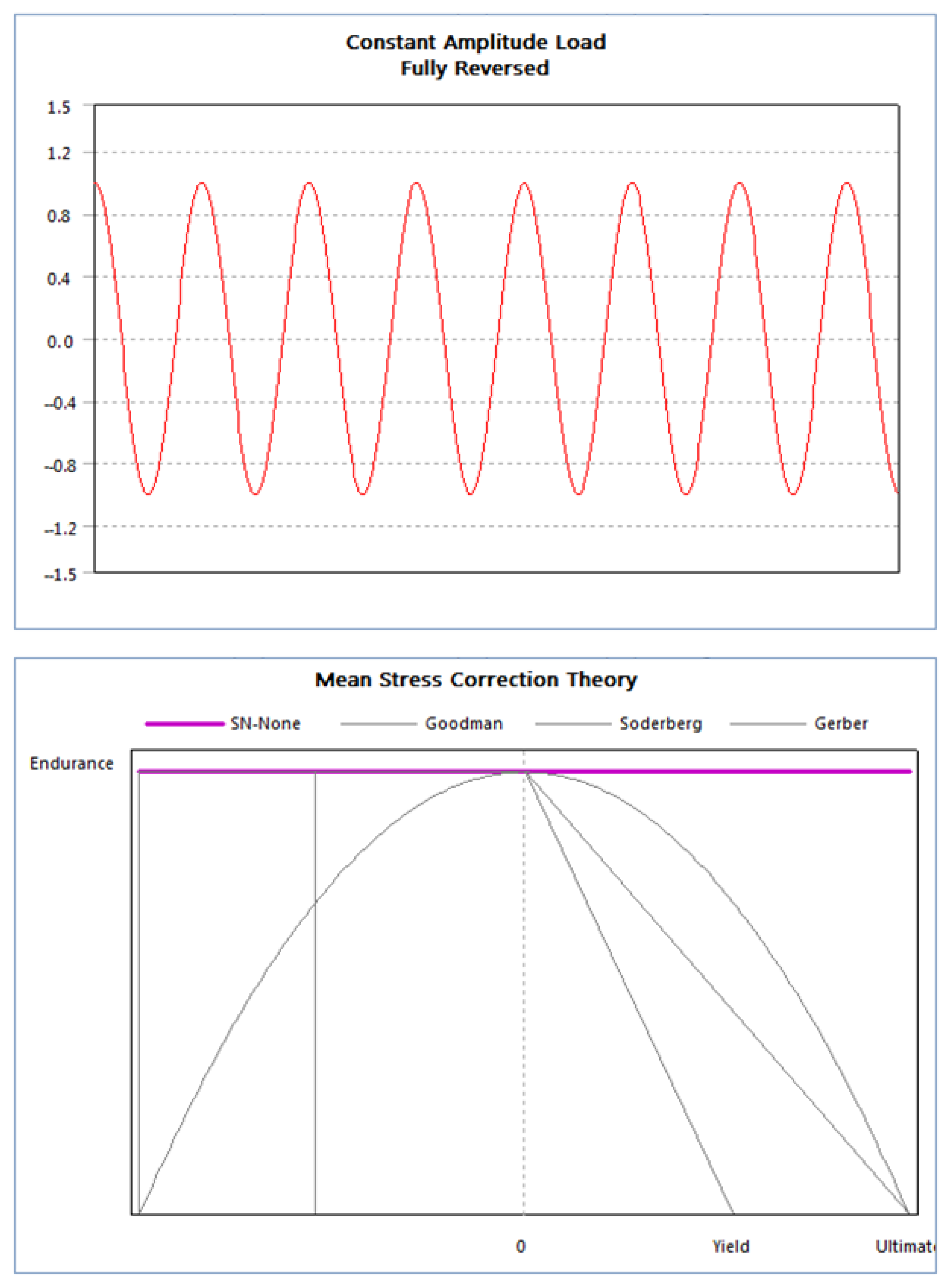
1.3. Applications of Finite Element Method in Prosthesis

The finite element method (FEM) has been instrumental in mechanical and structural engineering since the 1970s, particularly in orthopedic biomechanics, where it was used to assess stress distribution in human bones under functional loads [36]. By the 1980s, finite element analysis (FEA) became increasingly valuable in implant modeling, orthodontics, and the evaluation of deformation under applied forces [37]. This computational approach has since gained widespread acceptance across engineering and biomedical disciplines, particularly in analyzing stress distribution in dental implants, bones, prosthetic structures, and several medical devices [38,39]. Additionally, nano-mechanical testing techniques, such as nano-indentation, have enabled FEM-based assessments of biomechanical properties in nano-coatings, such as hydroxyapatite layers on titanium implants.

According to selected literature on hip implants, FEM has demonstrated its effectiveness in predicting mechanical behavior in a controlled, cost-efficient preclinical setting [37,38,40]. While FEA provides critical insights into the mechanical performance of implant materials, further in vitro, in vivo, and clinical studies are necessary to assess biocompatibility and potential adverse tissue reactions [36,41,42]. The long-term functionality of an implant is influenced by material properties and design factors. While computational FEA serves as a crucial tool in optimizing these aspects during the preclinical phase, allowing researchers to refine designs before clinical validation, the FEM-based simulations offer valuable predictions regarding mechanical performance, and real-world testing remains essential for verifying their safety and efficacy in biomedical applications.

Hip implants must withstand substantial mechanical loads over an extended period, making their design a critical factor in ensuring long-term success. The application of FEM in hip implant analysis enables the evaluation [37,38,40] of key performance indicators, including stress distribution, micromotion at the bone–implant interface, wear resistance, and fatigue life estimation [43]. These computational models simulate various physiological conditions, allowing researchers to refine implant geometries and select appropriate biomaterials before proceeding to physical prototyping. One of the major challenges in hip implant design is achieving optimal load distribution from the implant to the surrounding bone [44]. Insufficient load transfer can lead to stress shielding, where the surrounding bone weakens due to reduced mechanical stimulation. FEM-based simulations help engineers predict and mitigate such issues by adjusting implant material properties and surface textures to promote healthy bone remodeling [45]. By means of FEA, the study by Soliman et al. [46] aggregates and analyzes the performance of the several biomaterials used in total hip implant systems in the pre-clinical stage as well as their performances in in vitro, in vivo, and clinical studies, thus enabling researchers to better understand the prospects and challenges in this field. Pre-clinical computational finite element analysis (FEA) can be applied, according to recent studies, to estimate four mechanical performance parameters of hip implants linked with different biomaterials: von Mises stress and deformation, micromotion, wear estimates, and implant fatigue. The hip implant biocompatibility and the negative local tissue reactions to various biomaterials during the implementation phase are ascertained in vitro, in vivo, and clinically.

Beyond structural optimization, FEM has also played an important role in the evaluation of advanced biomaterials and surface coatings for implants. For instance, nano-mechanical testing techniques such as nano-indentation have been used in conjunction with FEM to assess the biomechanical characteristics of coatings like hydroxyapatite on titanium implants [47,48]. Computational modeling allows researchers to analyze the interaction between these coatings and bone tissue under dynamic loading conditions, aiding in the development of more durable and biocompatible implant surfaces. Overall, FEA serves as a complementary tool to experimental research rather than a standalone solution used for prosthesis study. FEM provides valuable preclinical insights, and its findings must be validated to confirm biocompatibility and long-term functionality. Consequently, computational analyses can predict mechanical performance and potential failure points, but real-world factors such as patient-specific bone density, implant positioning, and biological response must be considered in final design evaluations.

Alaneme et al. [49] presents a comprehensive literature review of finite element analysis applications in the design and selection of titanium-based biometallic alloys for biostructural rehabilitation to understand the practical limitations of computational analysis results for biomaterial design. It has been reported that the biostructural deployment of chosen materials only follows a clinical evaluation approval that is determined by extensive biomechanical assessment. In the review, it was noted that the experimental assessments necessitate significant investments of materials, costs and manpower as well as advanced facilities. Finite element analysis-based computational modelling and simulation techniques represent the preferred route towards a quick and resource-efficient method for evaluating biometallic materials for tissue replacement purposes. This review examines the foundational principles and procedural techniques, along with the results obtained from computational research focusing on Ti-based biometallic systems used for fracture repair and tissue rehabilitation. Vadiraj et al. [50] give detailed review information about biomaterials and FEA applications in implant dentistry while pointing out research areas for future exploration. It was revealed that, in modern dental practice, implantology procedures that use biomaterials alongside simulation techniques have been widely accepted for human apparatus reconstruction. It was noted that a biomaterial that demonstrates compatibility and creates a positive biological interaction with its environment should be chosen to ensure treatment success. Clinical practice makes the prediction of biomechanical parameters within implantology operations in vivo a difficult and challenging task. It was concluded that research and engineering innovations have demonstrated that finite element analysis (FEA) serves as a promising simulation tool to analyze clinical variables and reduce mechanical failures.

The work of Samadhiya et al. [51] was undertaken to generate 3D CAD models of prosthetic knee joints from extant literature and investigate the arrangement of von Mises stresses, contact pressure, total deformation, and, in an identical manner, establishing multiple combinations of biomaterials for femoral and tibial components. Knee implant 3D modeling and the finite element analysis tool in the PRO ENGINEER 5.0 software are used. Von Mises stresses and contact pressure are numerically estimated using ANSYS 12.0. The goal is to determine the FEM results for several flexion angles of knee joint for various biomaterials and also to analyze the results and identify the ideal biomaterial for knee implant design for complete knee replacement.

2. Models, Constitutive Relationships, and Parameter Selection

Irrespective of the specific use case, the fundamental procedure for building up an issue remains consistent: The objective is to establish a model that can aid in preventing failure by accurately anticipating fatigue failure caused by cyclic plastic loading. Only by employing approximation constitutive equations can the physics of failure be accurately modeled. The constitutive equations are mathematical relationships that require experimental calibration to accurately describe the failure mechanism and forecast the fatigue life of the material when subjected to cyclic loading [32,33,34]. The geometry is determined by either modeling fatigue failure or computing the critical loads necessary to induce plastic deformation in the observed material. The most crucial aspect of establishing the model calculation is selecting the appropriate equations to represent the behavior of materials. It is critical to understand that utilizing incorrect, imprecise material attributes or models will consistently render the model predictions invalid [35]. The material behavior is most accurately described as rate-independent metal plasticity for this research. Rate-independent metal plasticity is employed to quantify the permanent deformation in metals when subjected to loads that exceed their yield point. The theory of rate-independent plasticity in metals was created to predict materials/metal behavior under minor strain conditions. Rate-independent plasticity is a modeling technique employed to simulate the behaviors of metals deformed at low temperatures, namely those below half of the melting point or at moderate strain rates ranging from 0.01 to 10 per second [52,53,54,55].

Evaluate the framework of distinct plasticity.

For simplicity, the focus will be limited to tiny deformations. As a result, we will utilize the infinitesimal strain tensor as our chosen method for measuring deformation [37].

$${\epsilon }_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)$$

(1)

Decomposition of Strain into Elastic and Plastic Components

When subjected to uniaxial loading, strain at a given stress can be divided into two components.

$$\epsilon ={\epsilon }^e+{\epsilon }^p$$

(2)

We may improve this process in multiaxial loading by breaking down a general strain increment $d{\epsilon }_j$ into separate elastic and plastic components.

$$d{{\epsilon }_i}_j=d{\epsilon }_{ij}^e+d{\epsilon }_{ij}^p$$

(3)

Yield Criteria

The yield requirement determines the minimum stress required to cause permanent material deformation. In a solid material, the stress ${\sigma }_{ij}$ acting on it can be represented by the primary values of stress, denoted as ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$. Y indicates the yield stress of the material in uniaxial tension.

Von Mises yield criterion:

$$f\left({\sigma }_{ij},\hspace{1em}{\overline{\epsilon }}^p\right)={\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{1}{2}}{\left[{\sigma }_1-{\sigma }_2\right]}^2+{\left[{\sigma }_1-{\sigma }_3\right]}^2+{\left[{\sigma }_2-{\sigma }_3\right]}^2}-Y\left({\overline{\epsilon }}^p\right)=0$$

(4)

Criteria are established in such a manner as it undergoes deformation.

Elastically for $f({\sigma }_{ij})<0$

Plastically for $f({\sigma }_{ij})=0$

Formulating von Mises explicitly in the context is undertaken as follows:

$$f({\sigma }_{ij},\hspace{1em}{\overline{\epsilon }}^p)={\sigma }_e-Y\left({\overline{\epsilon }}^p\right)$$

(5)

where

$${\sigma }_e=\sqrt{{\displaystyle \frac{3}{2}}{S}_{ij}\hspace{1em}{S}_{ij}}\hspace{1em}{S}_{ij}={\sigma }_{ij}-{\displaystyle \frac{1}{3}}{\sigma }_{kk}{\delta }_{ij}$$

(6)

The von Mises effective stress (${\sigma }_e$) represents the deviatoric stress tensor $S_{ij}$.

Strain Hardening

Kinematic hardening is employed as an alternative to the isotropic hardening law in scenarios where components experience cyclic stress, as the latter is typically ineffective [54,55]. The current model fails to consider the Bauschinger effect, leading to the prediction that the solid will undergo a hardening process and eventually exhibit purely elastic behavior after a limited number of cycles. To accommodate the displacement of the center of the yield locus to a specific position ${\alpha }_{1j}$ inside the stress space, a modification is made to the von Mises yield criterion [22]. Figure 1 illustrates the relationship between maximum shear strain values on different types of metals. Figure 2 demonstrates the inclination of shear strain on the different metals employed. In comparison, maximum shear strain for different metals is depicted in Figure 3.

$$f({\sigma }_{ij},\hspace{1em}{\alpha }_{ij})=\sqrt{{\displaystyle \frac{3}{2}}(S_{ij}-{\alpha }_{ij})(S_{ij}-{\alpha }_{ij})}-Y=0$$

(7)

Y is now a constant.

$$d{\alpha }_{ij}={\displaystyle \frac{2}{3}}cd{\epsilon }_{ij}^p$$

(8)

According to the hardening rule, it is postulated that the relationship between stress and plastic strain can be represented by a linear curve, where the slope of this curve is denoted as C. The phenomenon described is called linear kinematic hardening [23,53].

Plastic Flow

To fully characterize the plastic stress–strain behavior, it is vital to establish a methodology for forecasting the plastic strains that arise from subjecting the material to stresses surpassing the yield threshold.

$$d{\epsilon }_{ij}^p=d{\overline{\epsilon }}^p{\displaystyle \frac{\partial f}{\partial {\sigma }_{ij}}}=d{\overline{\epsilon }}^p{\displaystyle \frac{3}{2}}{\displaystyle \frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}}$$

(9)

The yield criterion can be expressed as follows:

$$f({\sigma }_{ij},\hspace{1em}{\alpha }_{ij})=\sqrt{{\displaystyle \frac{3}{2}}(S_{ij}-{\alpha }_{ij})(S_{ij}-{\alpha }_{ij})}-Y$$

(10)

$$S_{ij}={\sigma }_{ij}-{\displaystyle \frac{1}{3}}{\sigma }_{kk}{\delta }_{ij}$$

(11)

The value $d{\overline{\epsilon }}^p$ is chosen based on the requirement that the yield criterion is consistently met during plastic deformation.

This implies the following:

$$f({\sigma }_{ij}+d{\sigma }_{ij},\hspace{1em}{\alpha }_{ij}+d{\alpha }_{ij})=f({\alpha }_{ij}+d{\alpha }_{ij})+{\displaystyle \frac{\partial f}{\partial {\sigma }_{ij}}}d{\sigma }_{ij}+{\displaystyle \frac{\partial f}{\partial {\alpha }_{ij}}}d{\alpha }_{ij}=0$$

(12)

$$d{\alpha }_{ij}={\displaystyle \frac{2}{3}}cd{\epsilon }_{ij}^p=cd{\overline{\epsilon }}^p{\displaystyle \frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}}$$

(13)

By replacing the variables with the Taylor expansion of the yield criterion and subsequently rearranging the expression, the following can be demonstrated:

$$d{\overline{\epsilon }}^p={\displaystyle \frac{1}{c}}{\displaystyle \frac{3}{2}}{\displaystyle \frac{\left(S_{ij}-{\alpha }_{ij}\right)}{Y}}d{\sigma }_{ij}$$

(14)

2.1. Criteria for the Selection of Biomaterials

A biomaterial must possess specific traits and properties that align with its intended purpose within the body to be suitable for implantation. The subsequent section will discuss the design and selection of biomaterials, as outlined [7]. Mechanical attributes and analysis of the host’s immune reaction and the compatibility of a substance with living organisms are the criteria for selecting biomaterials.

2.2. Biocompatibility and Host Response

The host response may be regarded as the physiological reaction of the host organism towards the material implant, which determines the biocompatibility factor. The terms biomaterial’ and ‘biocompatibility’ have been introduced by researchers to denote the biological activities of substances [8,19]. Biomaterials exhibit biocompatibility, a descriptive term denoting the material’s capacity to function in a particular application while eliciting an appropriate host response. Simply put, it denotes the biomaterial’s compatibility or harmony with biological organisms. Biocompatibility refers to the capacity to coexist with human body tissues without inflicting intolerable damage upon the body. It encompasses toxicity and every other detrimental consequence of a substance within a biological system. It is imperative that the interaction between the systemic host environment and the local, including intracellular and extracellular fluids, soft tissues, and plasma ionic composition, is not negatively impacted. It denotes a collection of characteristics a substance must possess to interact with a biological entity safely. It should be non-inflammatory, blood-compatible, non-toxic, carcinogenic, pyrogenic, and allergenic. “Since the patient is alive, it must be biocompatible”, states the operational definition. Roughly speaking, biomedical materials fall into three primary categories determined by the tissue or host response [23,53]. Bioinert substances elicit minimal or no tissue response, retain their structure within the body following implantation, and do not provoke an immune response from the host. Bioactive or active substances promote adhesion to adjacent tissue, as evidenced by the stimulation of new bone growth; these are substances that establish connections with living tissue. The terms “biodegradable” and “resorbable” pertain to substances that undergo hydrolytic degradation within the body, undergoing replacement in the regeneration of natural tissue. Thus, the chemical by-products of these disintegrating substances are assimilated and expelled from the body through metabolic processes. The spectrum of potential uses for biomaterials is extensive. Additionally, the variety of biomaterials is substantial. Biomaterial applications are elaborated upon in the following section: Orthopedic applications employ biomaterials that are metallic, ceramic, or polymeric [2,18].

2.3. Bone’s Biomechanical Characteristics

The biomechanical concept of fragility in bones encompasses three primary variables: strength, brittleness, and work to failure. These factors can be assessed by yield strength, ultimate tensile/compression strength, and toughness [19]. Orthopedic implants are designed to strengthen damaged bones from multiple perspectives. The yield point is the specific point at which a material’s behavior shifts from being elastic to becoming plastic [20]. Yield strength (YS) is the stress level necessary to induce a small plastic deformation. Stress below the YS results in elastic deformation, which is recoverable once the load is removed. If the applied load exceeds the YS, it will result in plastic deformation, leading to permanent deformation of the implant. Thus, the bone (or implant) will fracture when it reaches its maximum strength. The modulus of elasticity (E) represents the relationship between stress and strain in the inelastic state. Materials with a high E exhibit excellent resistance to stress and maintain their shape more effectively. Stiffness, which refers to the ability of a structure to resist bending, is directly related to the modulus of elasticity. The excessive rigidity of the implant leads to issues with stress shielding of the bone throughout the healing process [21]. Characteristics of specific biomaterials’ biomechanical qualities include the way in which certain biomaterials may fracture without undergoing noticeable deformation. Materials with low toughness, such as glass and ceramics, cannot absorb energy before breaking. Depending on its age, bone can exhibit either brittle or ductile properties. However, when compared with other biomaterials, bone generally demonstrates brittle behavior.

3. Finite Element Analysis

When it comes to orthopedic load-bearing implants, like those utilized in hip and knee joints, the implant’s design must endure the anticipated loads without failing or undergoing fatigue. To ensure this, stress analysis is necessary to confirm that all parts of the device perform optimally and are within the fatigue limit. For basic computations, straightforward analytical calculations are typically adequate. Regrettably, analytical solutions are restricted to linear problems and uncomplicated geometries governed by straightforward boundary conditions. In the case of implants used for hip joints, this includes a combination of non-linear materials or geometries, complex geometries, and mixed boundary conditions. Utilizing analytical approaches to address such an issue necessitates making numerous assumptions and simplifications. Another option is to use approximate or numerical techniques. The finite element method (FEM), also known as finite element analysis (FEA), is a popular numerical method for solving problems in continuum mechanics. This is a highly effective analytical tool employed in the design of implants [1,5]. FEA involves the arrangement of points known as nodes, which form a grid (mesh). The intricate configuration is partitioned into numerous smaller components, or elements, with interconnected nodes, each possessing a less complex geometry than the entire system. This mesh is engineered to integrate the material and structural characteristics influencing how the structure reacts to specific loading conditions. Nodes are strategically placed at designated intervals within the material, determined by the anticipated stress levels in particular areas. Those predicted to undergo significant stress typically exhibit a higher concentration of stressors than those with less or no stress [29]. The behavior of the unidentified variable within the element and the form of the component are depicted by uncomplicated functions connected by parameters common to the elements at the nodes. A set of boundary conditions is applied to the problem, forming a complex system of equations. These equations are then solved simultaneously utilizing interactive methods [34].

4. Analysis and Discussion

The provided numbers represent shear strain, a dimensionless quantity measured in mm/mm. The material with the lowest value at 5% error bar is titanium stainless at 0.0000862 ± 4.31 × 10⁻⁶, followed by stainless steel at 0.000135 ± 6.75 × 10⁻⁶, and then titanium with the highest value at 0.000240 ± 1.2 × 10⁻⁵. Therefore, titanium stainless has the lowest shear strain after loading, while stainless and titanium have the maximum shear strain. Existing literature confirms that titanium metal exhibits a relatively low shear resistance [49], whereas stainless steel demonstrates a higher shear resistance. This is evident in the values mentioned before and the graph depicting the properties of titanium and stainless steel. Based on the result, it can be deduced that the poor shear resistance of titanium has been effectively counterbalanced by the strong shear resistance of stainless steel, as indicated by the range of values between the maximum and minimum strain [25]. Figure 3 shows that titanium stainless has the highest resistance to shear strain, as evidenced by its minimal strain recorded.

In comparison, 316 stainless steel has a lower resistance to shear strain, while titanium has the least resistance. Therefore, combining these two metals would result in a superior material choice [49,53]. The analysis of maximum principal stress on different metals employed is displayed in Figure 4, while its rear view is depicted in Figure 5.

The following values represent the most significant primary stress produced, measured in megapascals (MPa). As such, the three metals exhibit a commendable ability to withstand the created stress, as shown in Figure 6 (maximum stress values), with no notable variation observed [2,19]. The material known as stainless, at 5% error bar, has a tensile strength of 8.1281 ± 0.40641 MPa, followed by titanium stainless with a tensile strength of 8.130 ± 0.4065 MPa and then titanium with a tensile strength of 8.1466 ± 0.40733 MPa. Both stainless steel and titanium have demonstrated remarkable yield strength, as evidenced in the literature. From Figure 6, it is evident that stainless steel exhibits the lowest level of stress generated after loading. This may be attributed to its greater modulus of elasticity, which is 190 GPa, compared with titanium’s modulus of 116 GPa. Consequently, materials with higher moduli are more effective in resisting stress. This is considered a negative feature. Therefore, it can be deduced that titanium stainless has contributed to bridging this gap by demonstrating superior stress resistance when compared with titanium, with a lower modulus of 76 GPa [17,19]. The equivalent elastic strain analysis on different metals is illustrated in Figure 7, where the inclination of equivalent strain is shown in Figure 8.

The provided values represent the strain, a dimensionless quantity measured in millimeters per millimeter. The discussion is as follows. The strain values for the materials at 5% error bar, and as shown in Figure 9, are as follows: titanium stainless: 0.000062 ± 3.1 × 10⁻⁶; stainless steel: 0.0000986 ± 4.93 × 10⁻⁶; and titanium: 0.000169 ± 8.45 × 10⁻⁶. This indicates that titanium stainless exhibited the lowest strain value after loading, whereas stainless and titanium had the highest values. Research in the literature has demonstrated that titanium metal exhibits a relatively low shear resistance, whereas stainless steel shows a larger shear resistance, as evidenced by their respective values. The graph provided above serves to support this finding. It can be inferred that the low resistance of titanium to shear has been balanced out by the high resistance of stainless steel to shear. Thus, titanium stainless will exhibit superior load resistance compared with the other two metals [10]. Based on this third investigation, it has been demonstrated that titanium stainless is the optimal material to select. The analysis of equivalent stresses for different metals employed is depicted in Figure 10.

The following values represent the stress created and measured in MPa. As such, and similar to the case of maximum primary stress, the three metals exhibit a high level of resistance to the equivalent stresses created, as shown in Figure 11, which are closely aligned. The material with the lowest value at 5% error bar is titanium stainless, which has a value of 18.874 ± 0.9437 MPa. Stainless has a slightly higher value of 18.905 ± 0.94525 MPa, while titanium has the highest value of 19.069 ± 0.95345 MPa. When considering this study, one immediately thinks of the impressive yield strength of stainless steel and titanium, as documented in the literature [2,3,4,5,19,20]. Upon reviewing the graph once more, it is evident that titanium stainless is the most favorable material to be considered, with stainless and titanium being the least favorable. The analysis of the everyday stresses on the different metals studied is illustrated in Figure 12.

Figure 13 shows the magnitude of the normal stress generated, measured in megapascals (MPa). The ensuing dialogue is presented below: Titanium-stainless is typically disregarded in terms of regular stress [19]. It has the highest stress level produced, which is more of a drawback than a benefit. It was noted that the highest normal stress was observed in titanium stainless steel with the value of 7.7115 ± 0.38557 MPa at 5% error bar, followed by stainless steel with the value of 7.7045 ± 0.38522 MPa and the least of the normal stress was observed in titanium, with the value of 7.6757 ± 0.38379 MPa. Titanium, a substance with lower yield strength, was selected as the preferred material for this study (see Figure 14).

It is widely acknowledged that titanium exhibits a notably low resistance to shear and wear (See Figure 14). On the other hand, stainless steel offers greater resistance and relatively low wear. Our goal is to strike a balance between these two properties. Based on the graph, stainless steel exhibits the highest shear stress value, followed by titanium stainless steel, with titanium having the lowest. This implies that titanium stainless may serve as a connecting element for these characteristics. Figure 15 shows the analysis results of the normal strains on the different metals used.

Units of dimensionlessness (mm/mm) are utilized to represent the normal strain values. After a load was applied, titanium stainless exhibited the least elasticity of strain, as depicted in Figure 16, suggesting that it can withstand greater loads than titanium and stainless steel. Analysis results of shear strain on different metals employed are shown in Figure 17.

Figure 18 provides numbers representing shear strain, a dimensionless quantity measured in mm/mm. These data prove that titanium stainless had the lowest response to shear strain following loading [18]. This indicates that the titanium’s low resistance to shear has been effectively counterbalanced by the stainless steel, as evidenced by the range of strain values observed between the maximum and minimum. Based on the graph above, it can be concluded that titanium stainless exhibits the most substantial resistance to shear strain [19], as evidenced by its minimal strain. In comparison, 316 stainless steel demonstrates a lower resistance to shear strain, while titanium displays the least resistance.

Titanium stainless exhibits the least deformation of the three materials examined (See Figure 19 and Figure 20). This suggests that, for an equivalent load, both stainless steel and titanium would undergo significant deformation, which would not be advantageous in load-bearing applications [23,55]. Consequently, titanium stainless demonstrates superior resistance to deformation [56] and is therefore considered the exceptional material. In addition, the combination of titanium’s and stainless steel’s superior fatigue resistance renders titanium stainless a more suitable material for this investigation. Figure 20 illustrates that titanium stainless steel is more deformation resistant when subjected to load.

The Goodman relationship is a formula used in materials science and fatigue analysis to quantitatively assess how mean and alternating stresses affect a material’s fatigue life. A Goodman chart, also referred to as a Haigh diagram or Haigh–Soderberg diagram, visually represents the correlation between mean stress and alternating stress, indicating the failure point of a material after a specific number of cycles. Experimental data often displayed on a scatter plot can typically be approximated by a parabolic curve known as the Gerber line (See Figure 21). This curve can further be simplified into a straight line called the Goodman line, which serves as a conservative estimate. The Goodman relation suggests that fatigue life generally decreases as mean stress increases, assuming that the applied stress remains constant. This relationship can be graphed to determine the allowable cyclic loading for a component. If the point representing the average and applied stress lies below the curve defined by this relationship, the component is expected to survive.

Conversely, if the point is above the curve, the component will fail and not satisfy the stress criteria. The curve derived from titanium stainless steel indicates that it will withstand stress without failure, as both the yield and ultimate stresses fall within the parabolic range, like the behavior observed in titanium and stainless steel individually [35,54,55,56].

Table 1. Summary of the results of the simulation.

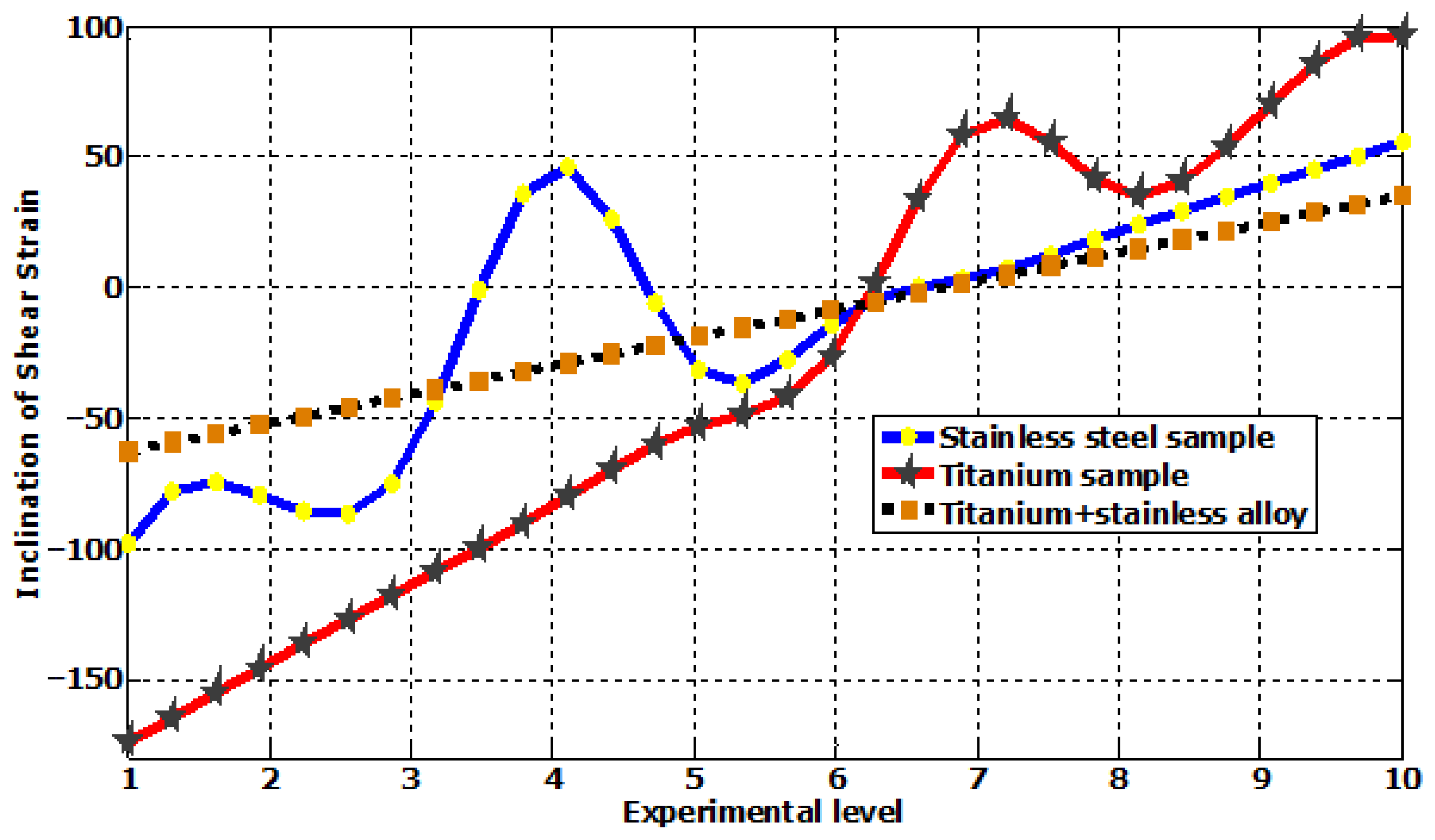
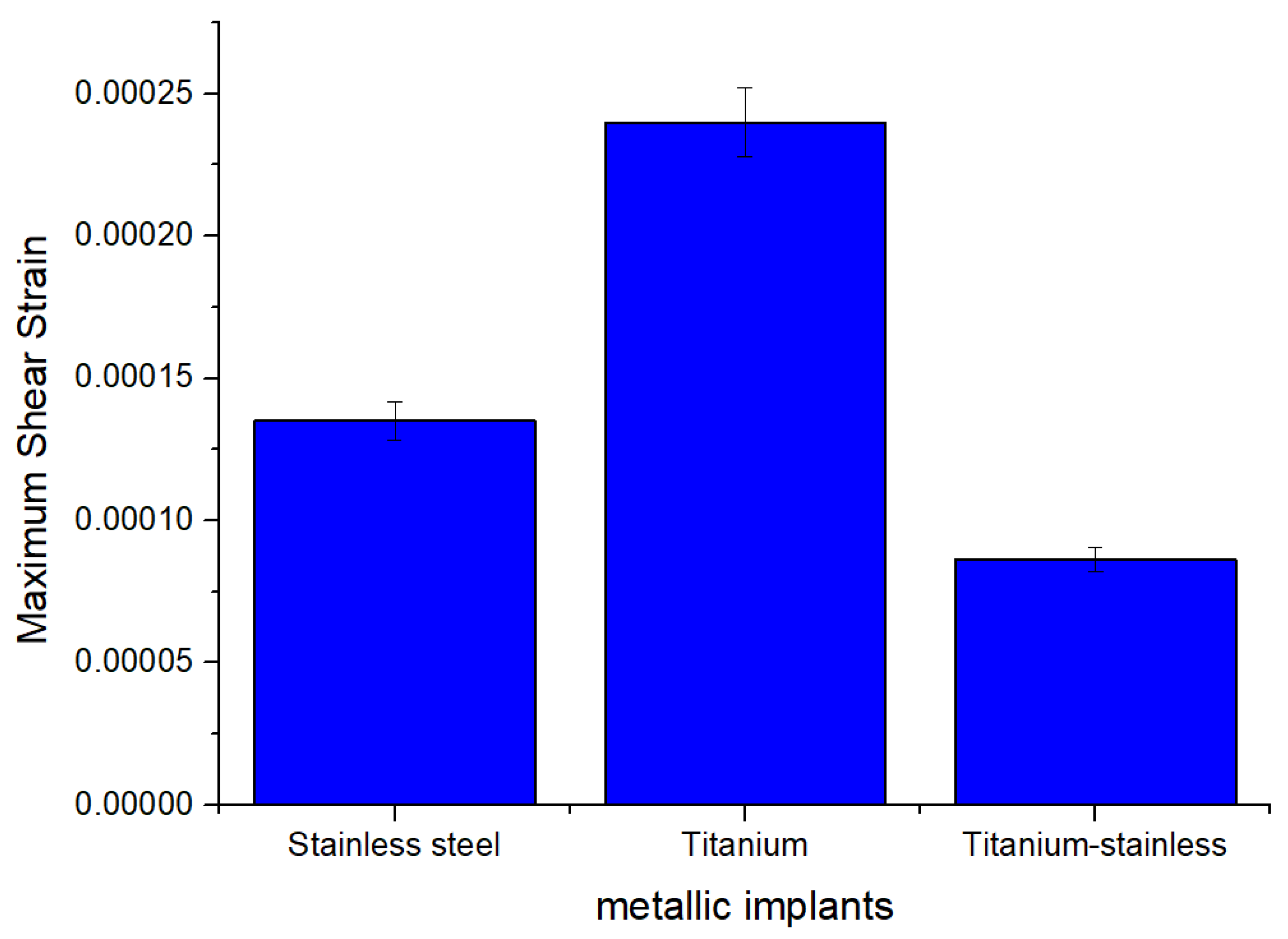
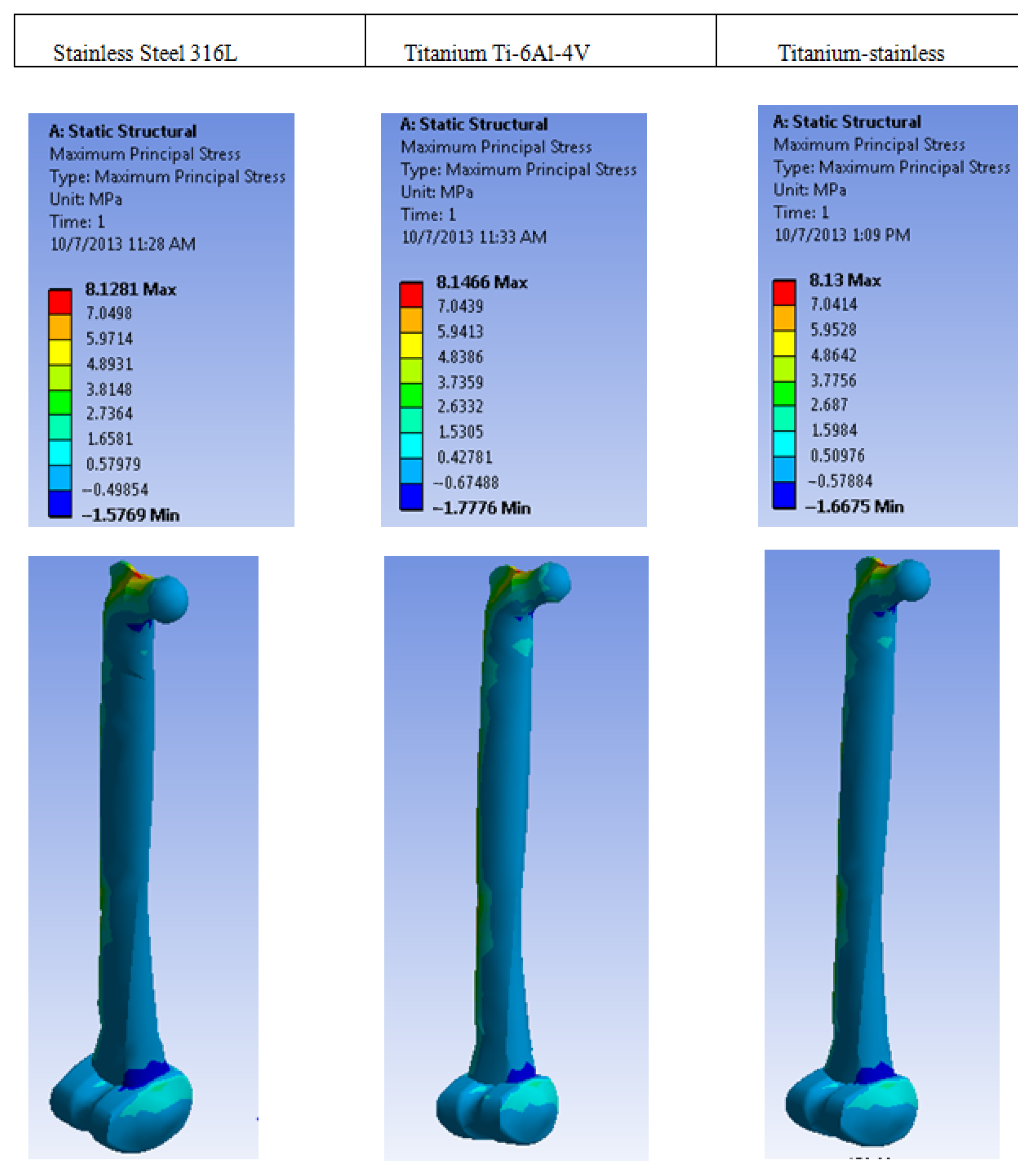
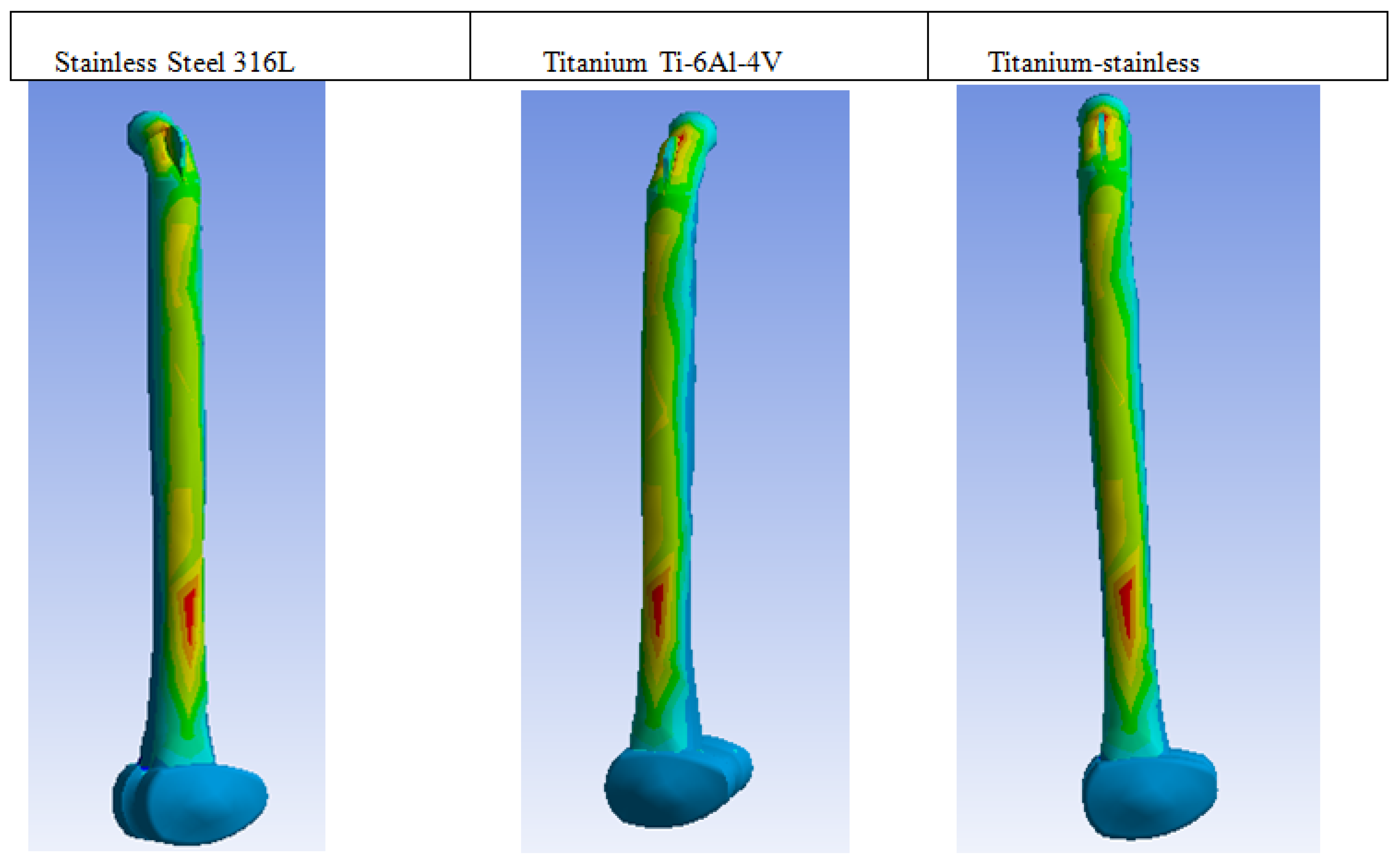
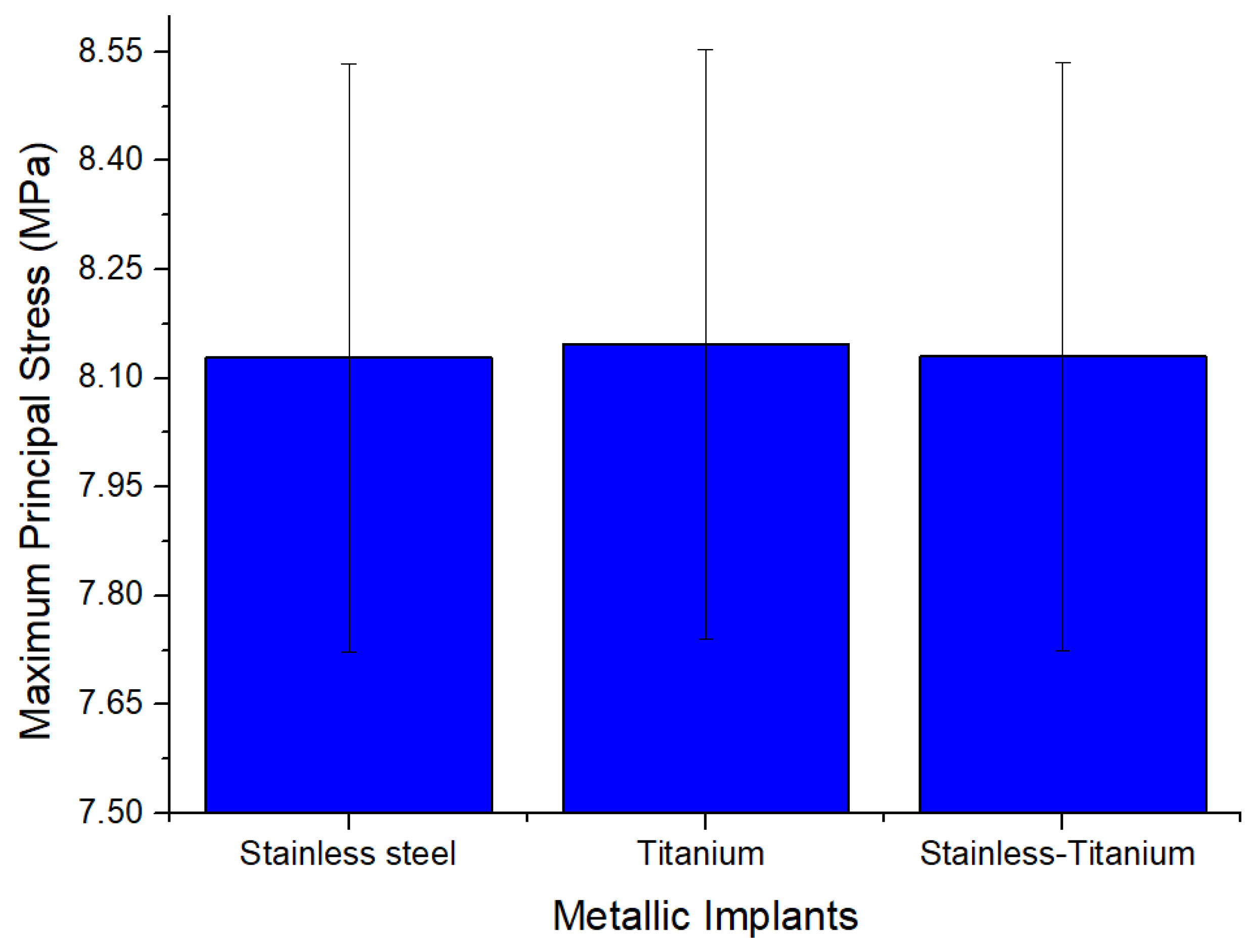
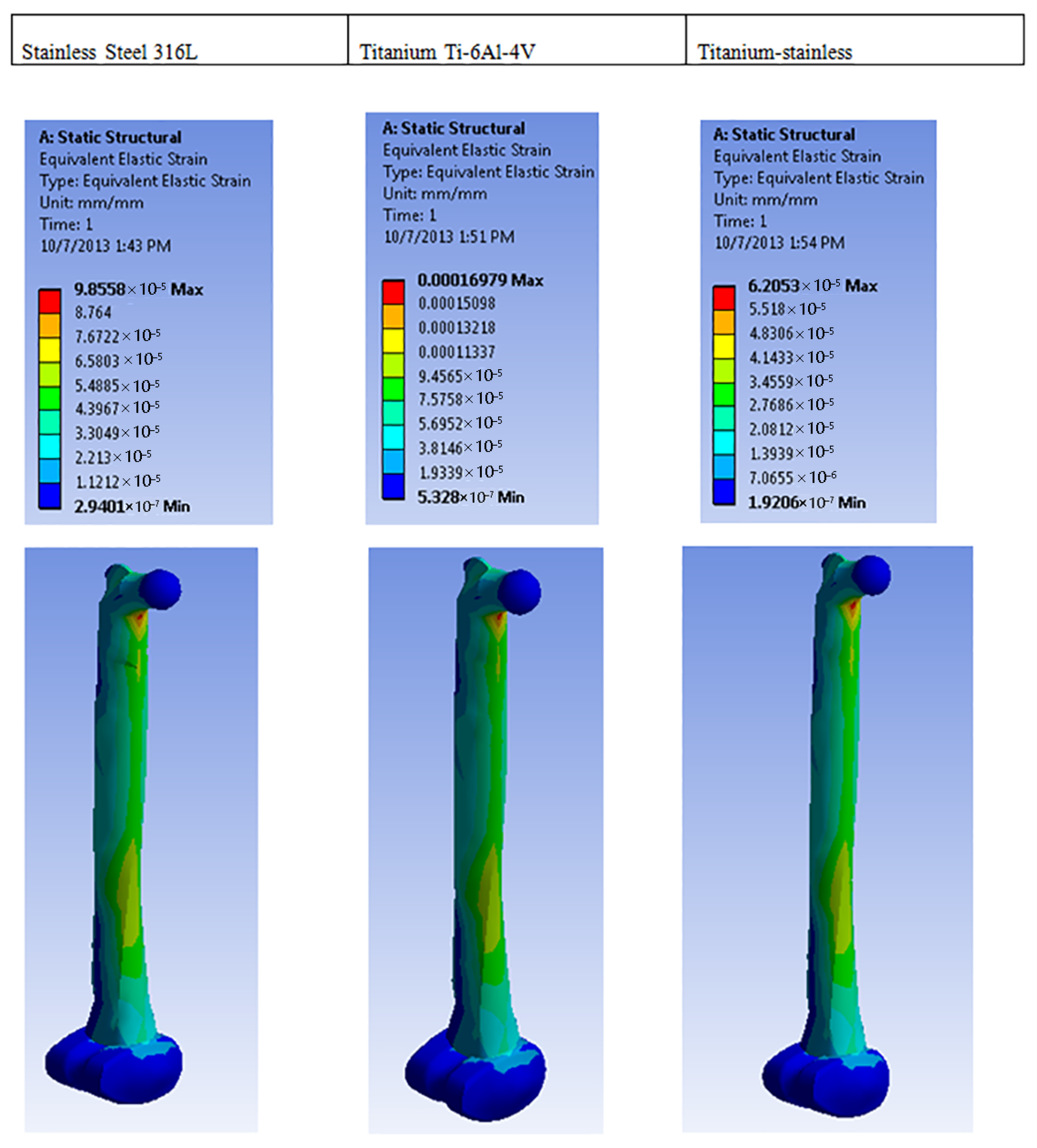
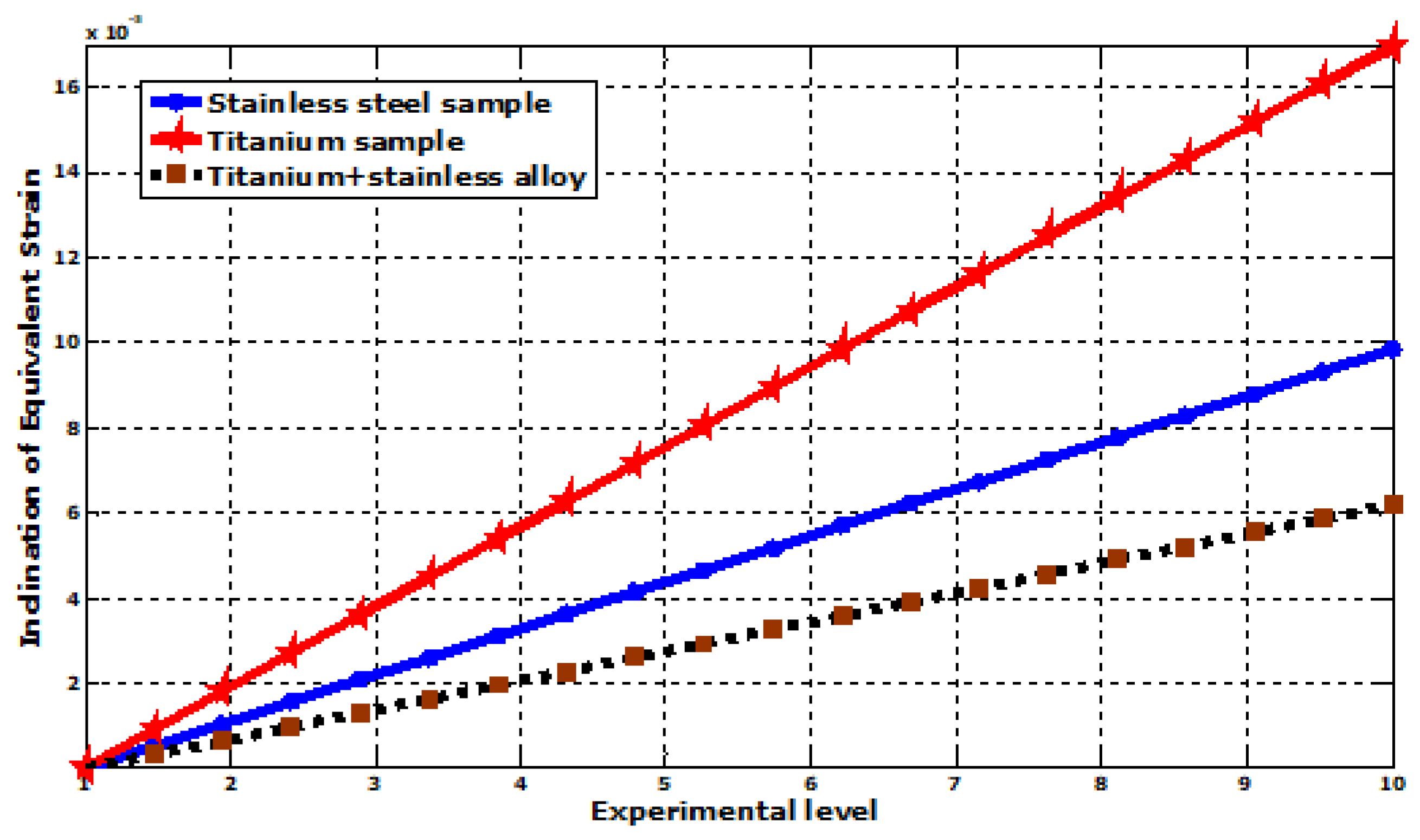
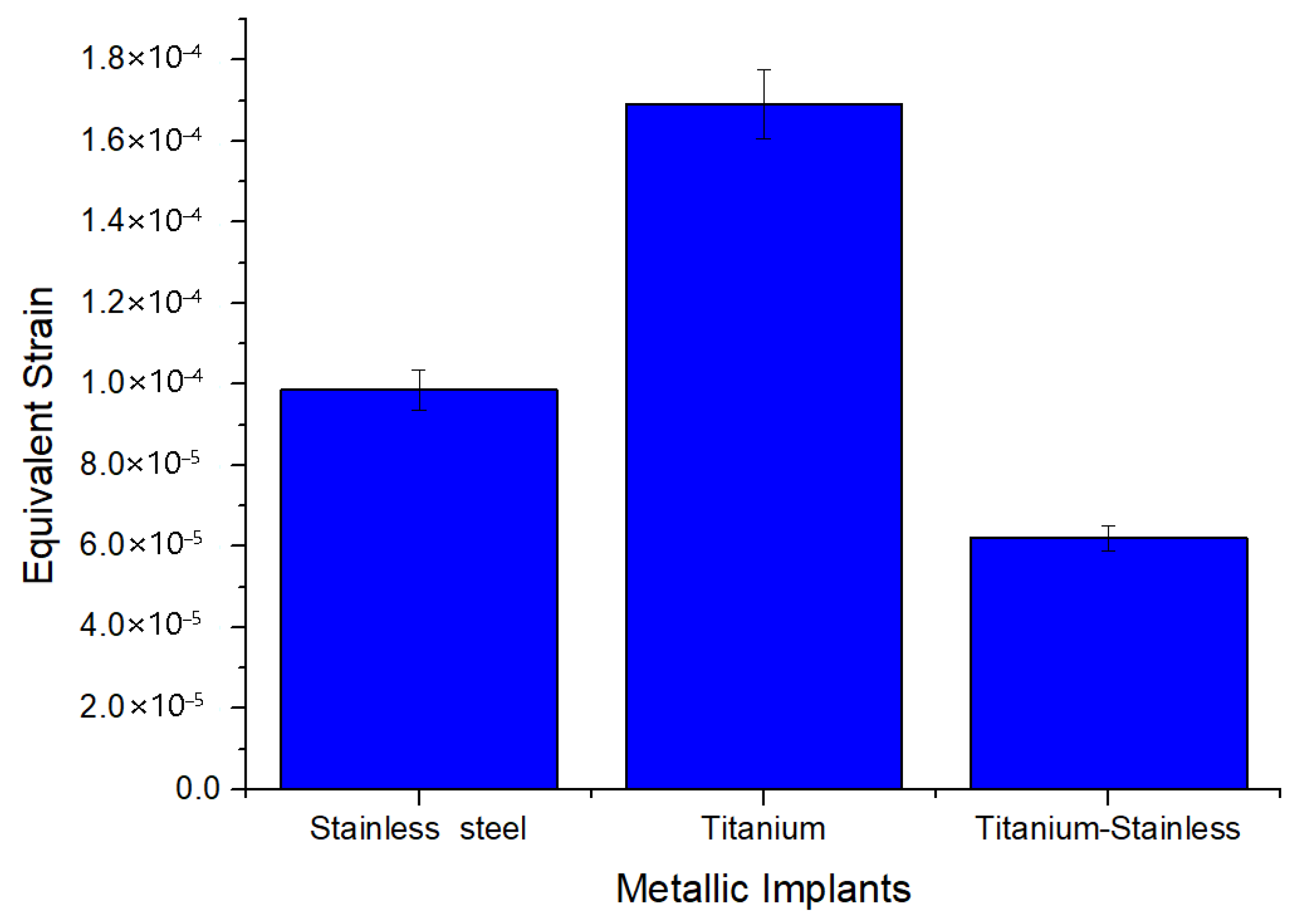
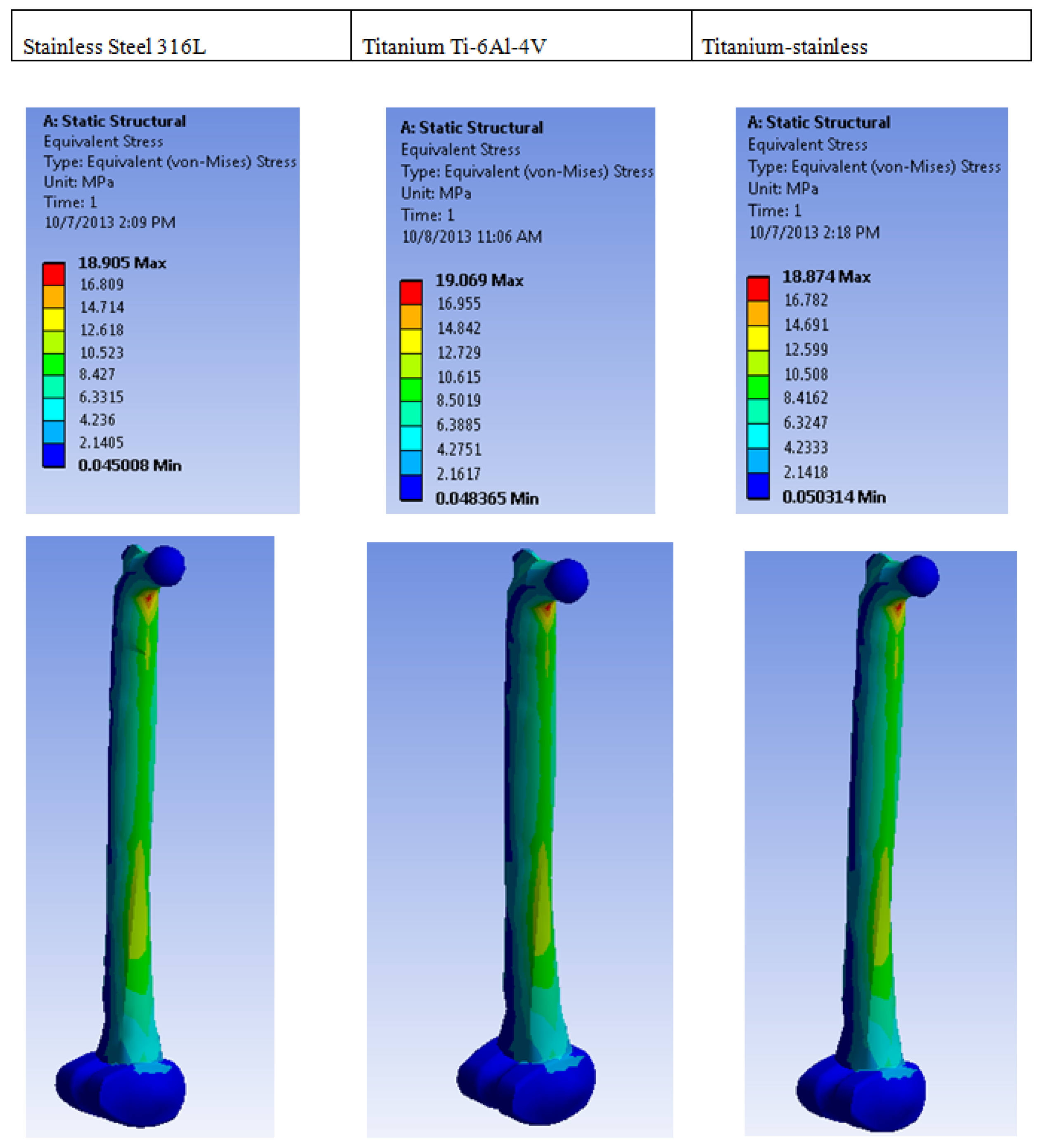
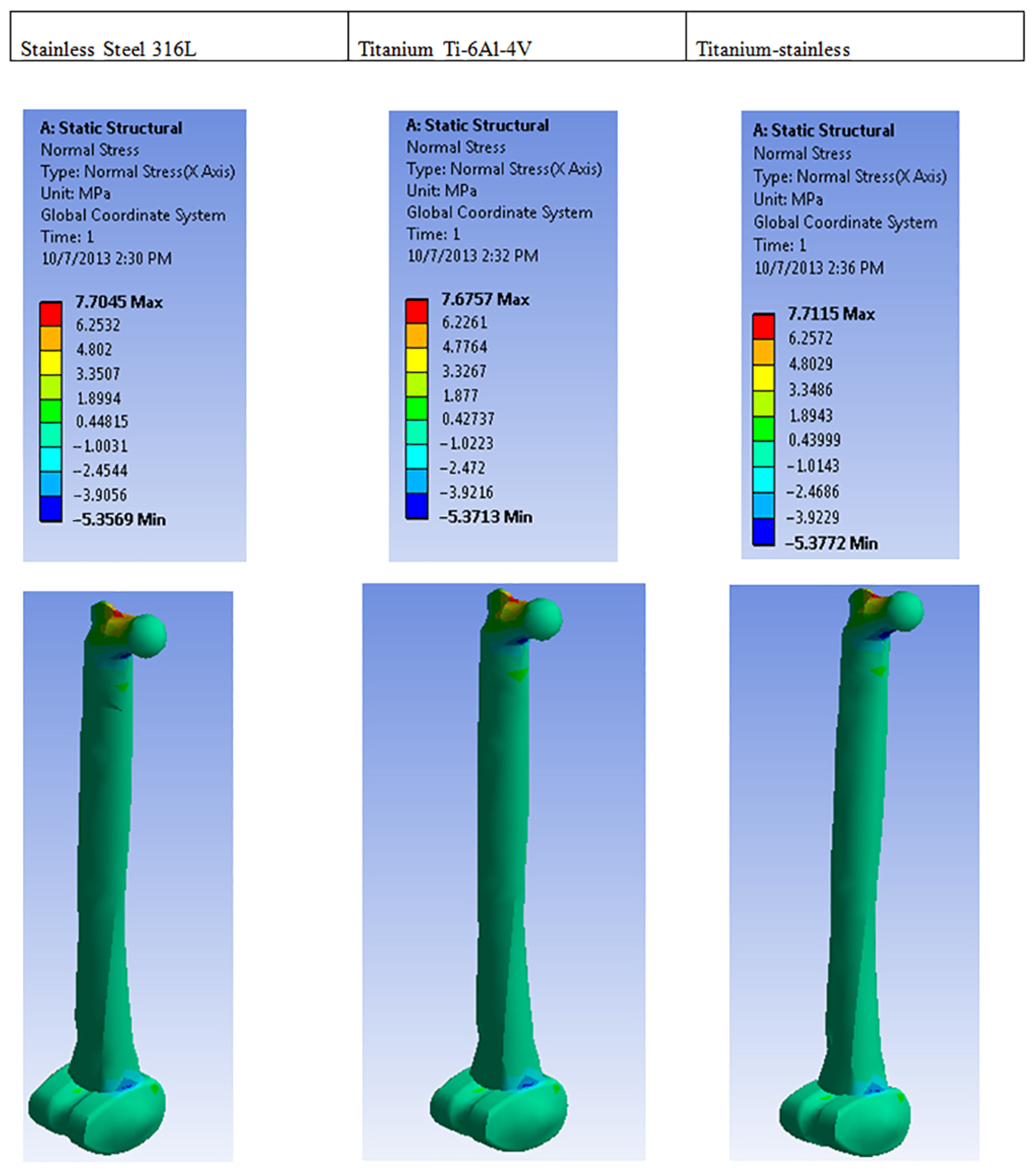
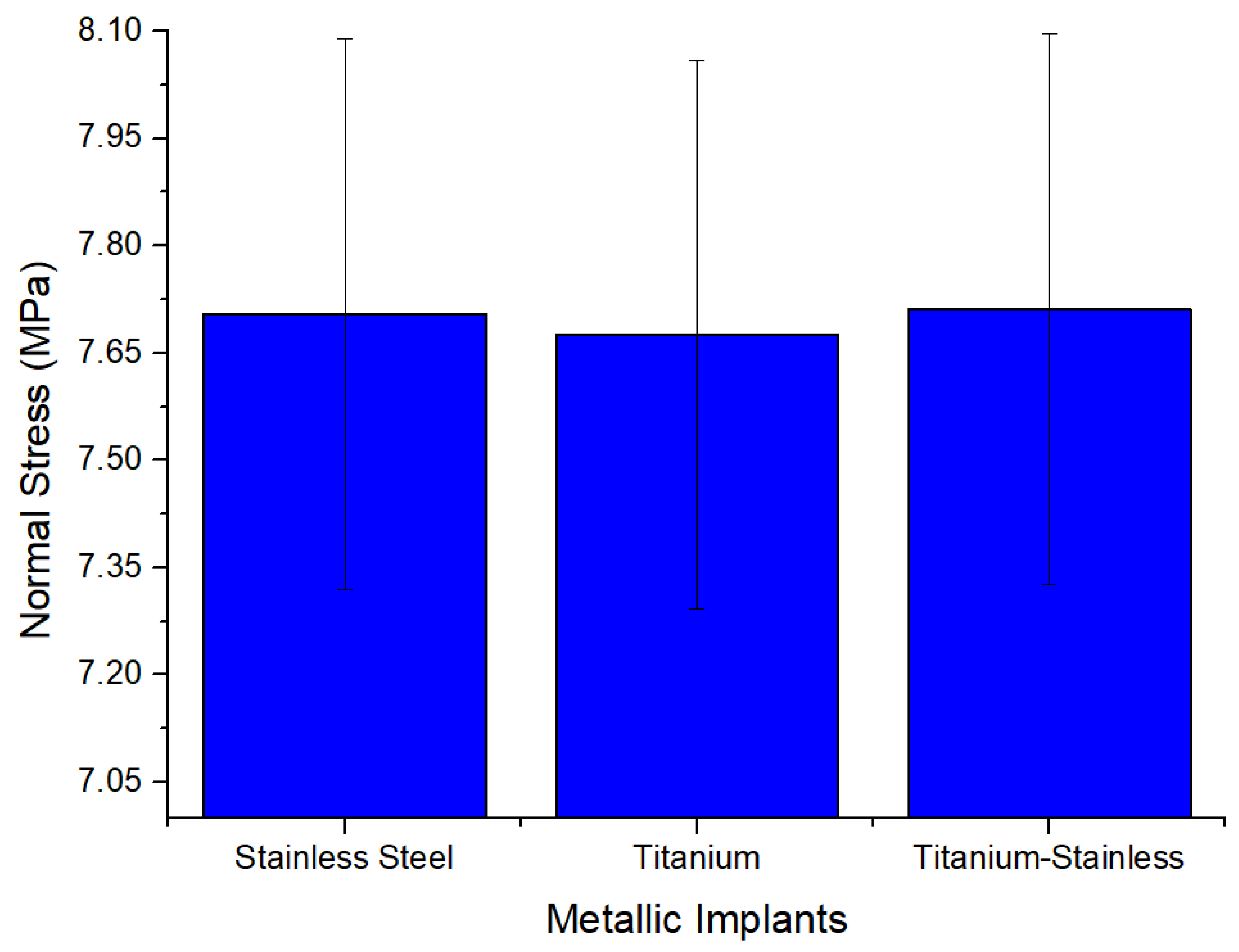
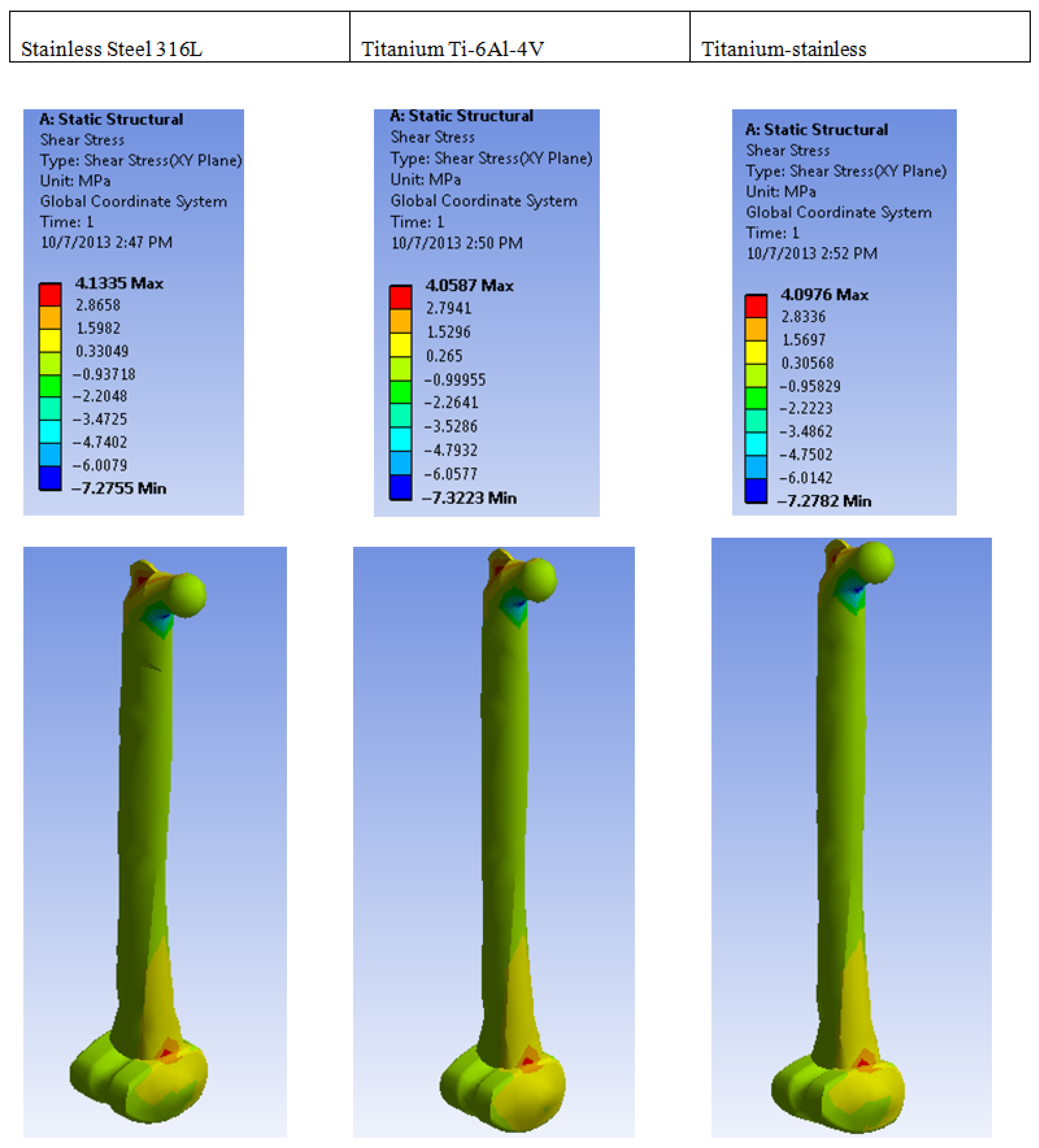
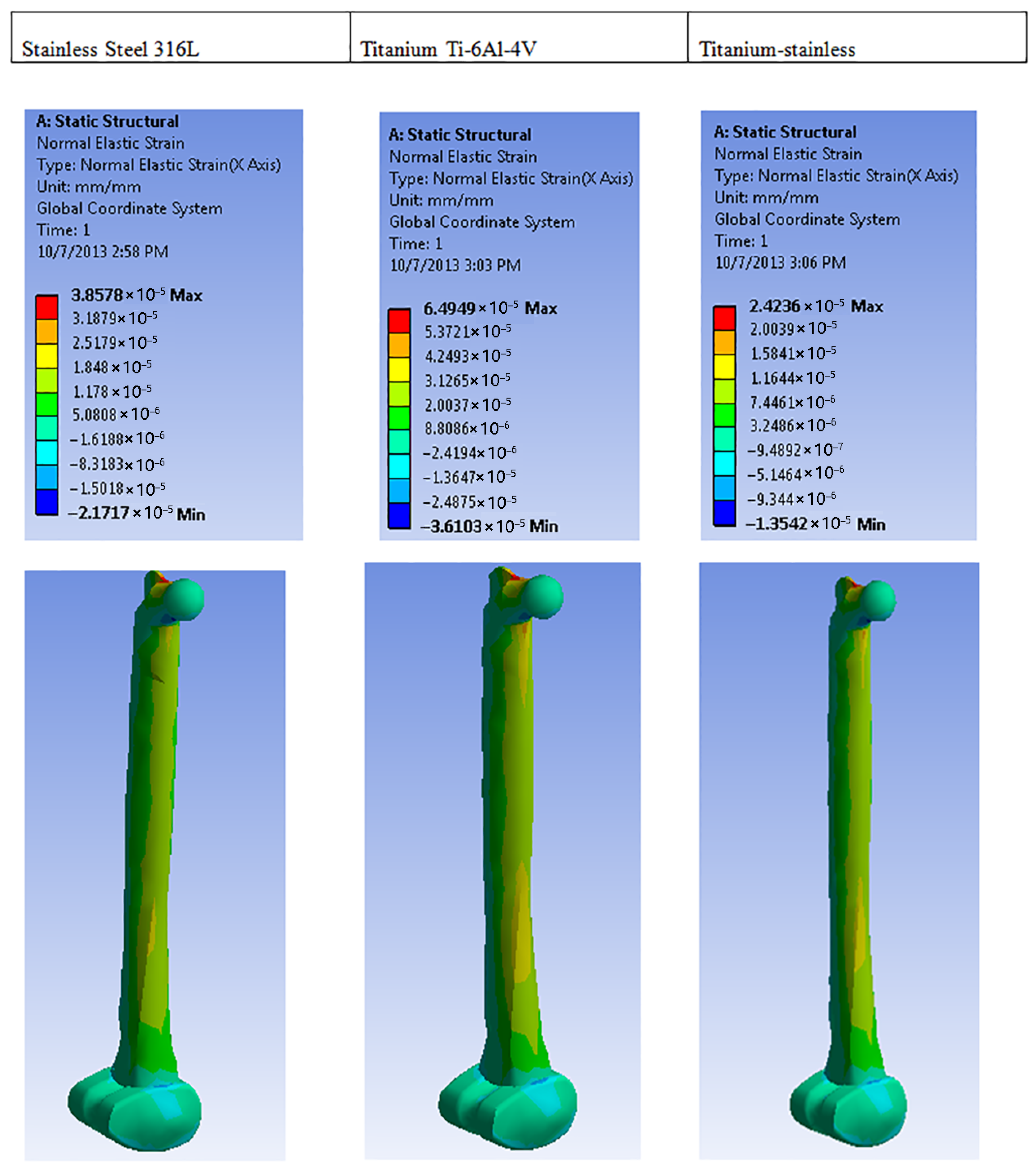
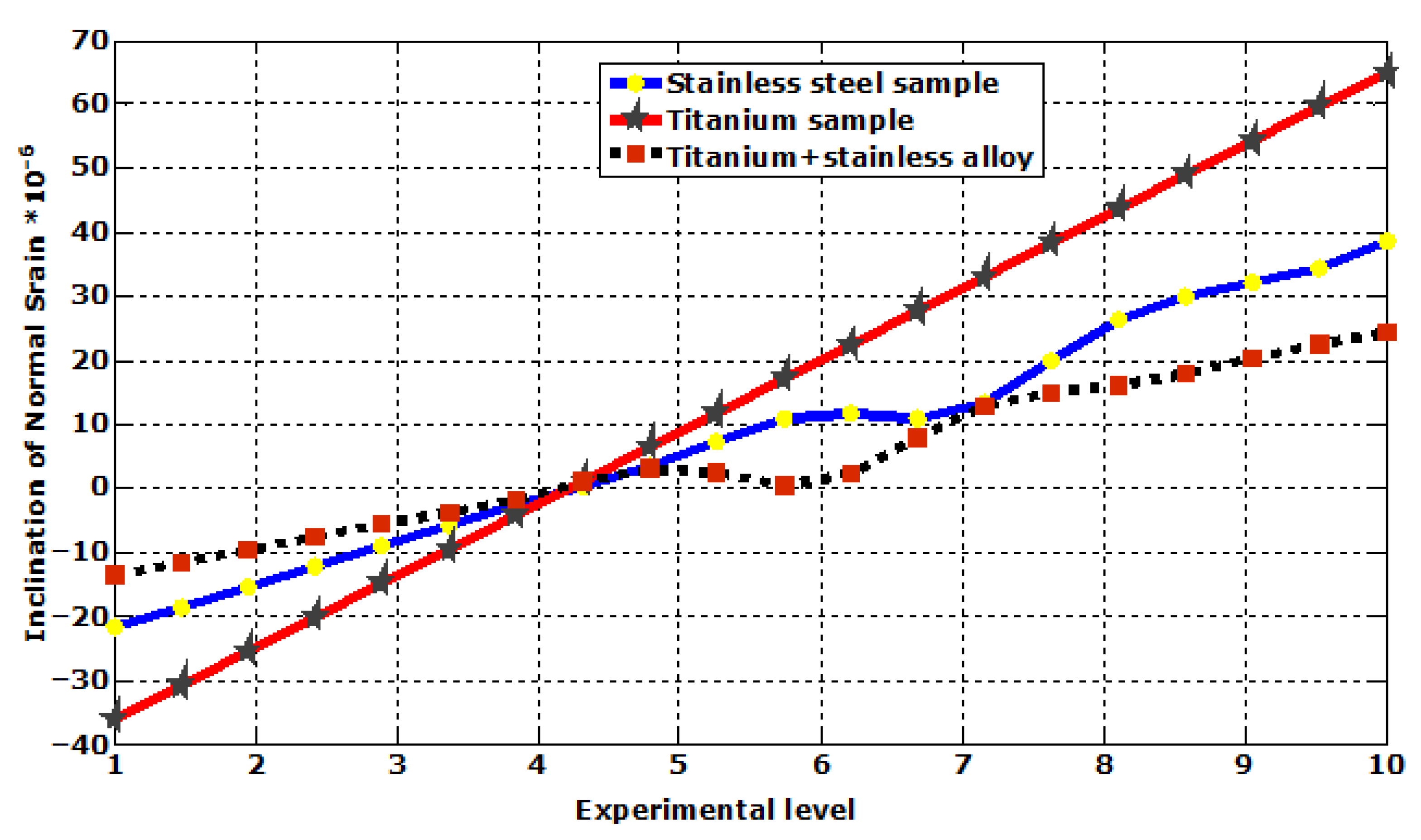
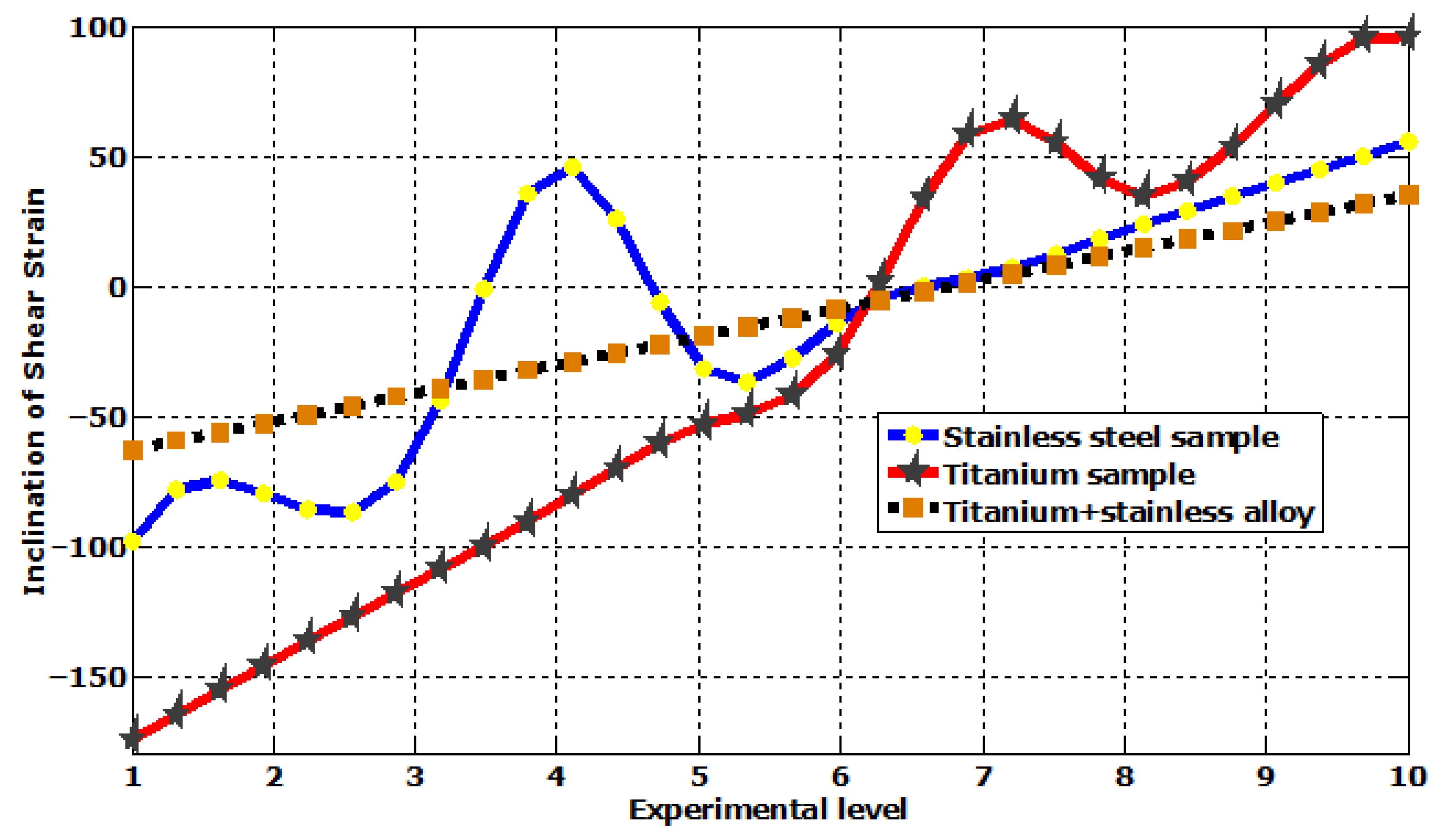
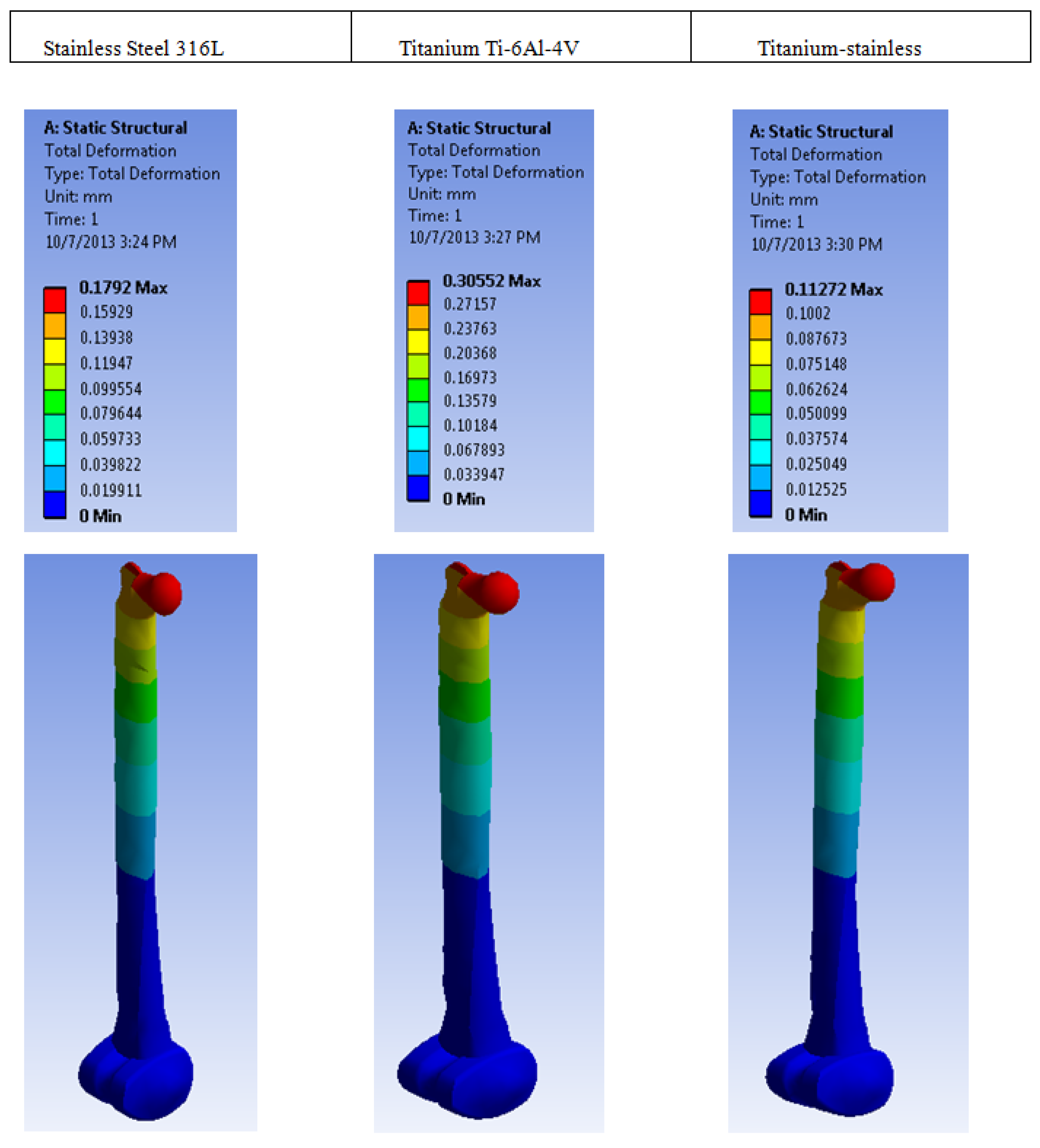
Plastic Study		Stainless	Titanium	Stainless Titanium
Max shear elastic strain (mm)	Max	0.0002401	0.00024011	8.6154 × 10−5
	Min	3.5005 × 10−7	6.6302 × 10−7	2.506 × 10−7
Max Principal Stress (MPa)	Max	8.1281	8.1466	8.13
	Min	−1.5769	−1.7776	−1.6675
Equivalent elastic strain (mm)	Max	9.8558 × 10−5	0.00016979	6.2053 × 10−5
	Min	2.9401 × 10−7	5.328 × 10−7	1.9206 × 10−7
Equivalent stress (MPa)	Max	18.905	19.069	18.874
	Min	0.045008	0.048365	0.050314
Normal stress (MPa)	Max	7.7045	7.6757	7.7115
	Min	−5.3569	−5.3713	−5.3772
Shear stress	Max	4.1335	4.0587	4.0976
	Min	−7.2755	−7.3223	−7.2782
Normal elastic strain	Max	3.8578 × 10−5	6.494 × 10−5	2.4236 × 10−5
	Min	−2.1717 × 10−5	3.6103 × 10−5	1.3542 × 10−5
Shear elastic strain	Max	5.5685 × 10−5	9.6402 × 10−5	3.5352 × 10−5
	Min	9.8012 × 10−5	−0.00017392	−6.2792 × 10−5
Total deformation	Max	0.1792	0.30552	0.11272

presents a summary of the simulation results.

5. Conclusions

Given the challenge of achieving a single material with all of the desirable features of metals without sacrificing any of them, an effort will be made to enhance the current research in biocomposite materials. In essence, this is accomplished by amalgamating several materials or phases in order to use each component’s inherent characteristics. Obtaining a material that is 100% flawless is not possible under ideal conditions. However, it is crucial to understand that there is no perfect material, as each material possesses distinct qualities designed for specific functions within the human body. This research is based on the load-bearing component of the body, namely in orthopedics, which supports the use of metallic materials. This has been extensively debated in the literature. Ten studies were conducted to demonstrate the diverse ways in which the materials exhibited a response. Eight case studies indicate that a combination of titanium and stainless makes for a superior material.

Furthermore, extensive studies have been conducted in the field of cutlery, which has demonstrated its exceptional durability and superior resistance to corrosion compared with standard stainless steel. There is still more work to be done in the realm of biomaterials in terms of the combination of titanium and steel. This study has unequivocally demonstrated that combining these two metals is a superior choice for orthopedic biomaterials. Numerical modeling of prosthesis attachment was not included in this work, though it is suggested for future study. bone modeling which include incorporating more sophisticated bone structures, such as cortical and trabecular differentiation, anisotropic properties, and patient-specific strength parameters, these aspects are missing in this study and are suggested for future study.