Effects of a Semi-Active Two-Keel Variable-Stiffness Prosthetic Foot (VSF-2K) on Prosthesis Characteristics and Gait Metrics: A Model-Based Design and Simulation Study

Abstract

Background/Objectives: Semi-active prosthetic feet present a promising solution that enhances adaptability while maintaining modest size, weight, and cost. We propose a semi-active Two-Keel Variable-Stiffness Foot (VSF-2K), the first prosthetic foot where both the hindfoot and forefoot stiffness can be independently and actively modulated. We present a model-based analysis of the effects of different VSF-2K settings on prosthesis characteristics and gait metrics. Methods: The study introduces a simulation model for the VSF-2K: (1) one sub-model to optimize the design of the keels of VSF-2K to maximize compliance, (2) another sub-model to simulate the stance phase of walking with different stiffness setting pairs and ankle alignment angles (dorsiflexion/plantarflexion), and (3) a third sub-model to simulate the keel stiffness of the hindfoot and forefoot keels comparably to typical mechanical testing. We quantitatively analyze how the VSF-2K’s hindfoot and forefoot stiffness settings and ankle alignments affect gait metrics: Roll-over Shape ($ROS$), Effective Foot Length Ratio ($EFLR$), and Dynamic Mean Ankle Moment Arm ($DMAMA$). We also introduce an Equally Spaced Resampling Algorithm (ESRA) to address the unequal-weight issue in the least-squares circle fit of the Roll-over Shape. Results: We show that the optimal-designed VSF-2K successfully achieves controlled stiffness that approximates the stiffness range observed in prior studies of commercial prostheses. Our findings suggest that stiffness modulation significantly affects gait metrics, and it can mimic or counteract ankle angle adjustments, enabling adaptation to sloped terrain. We show that $DMAMA$ is the most promising metric for use as a control parameter in semi-active or variable-stiffness prosthetic feet. We identify the limitations in $ROS$ and $EFLR$, including their nonmonotonic relationship with hindfoot/forefoot stiffness, insensitivity to hindfoot stiffness, and inconsistent trends across ankle alignments. We also validate that the angular stiffness of a two-independent-keel prosthetic foot can be predicted using either keel stiffness from our model or from a standardized test. Conclusions: These findings show that semi-active variation of hindfoot and forefoot stiffness based on single-stride metrics such as $DMAMA$ is a promising control approach to enabling prostheses to adapt to a variety of terrain and alignment challenges.

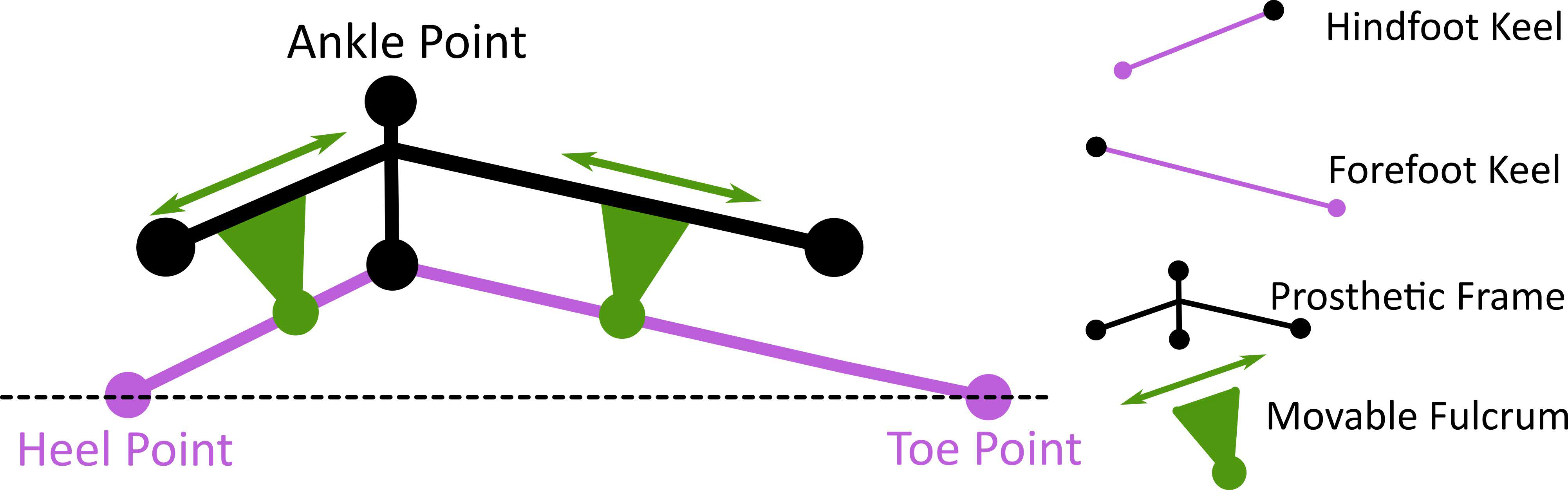
1. Introduction

The adaptability of current commercial ankle-foot prostheses (prosthetic feet) is still not satisfactory, lacking in comfort and overall adaptability. This is mainly constrained by the fact that most commercial prosthetic feet are passive, having constant shape and mechanical characteristics. For example, the fixed stiffness of the prosthetic feet violates the dynamic functionality of a healthy ankle, limiting the users’ ability to adapt to different terrains, different walking speeds, and the transition between walking and standing [1]. Recent developments have led to various powered prosthetic feet to mimic the function of a biological ankle, mostly done by actively providing mechanical power throughout the gait cycle [2,3,4,5,6,7]. However, the high cost, high weight, and high complexity design of these fully active prostheses limit them from gaining a share of the market. The Ottobock Empower [8] is the only fully active powered prosthetic foot on the market now. Some previous research show that using a powered prosthetic foot can reduce the overall metabolic cost, improve the symmetry of walking, and reduce the musculoskeletal pain [9,10,11]. However, a recent study investigating the users’ experience with passive and powered prosthetic feet shows that a substantial proportion of users who had been prescribed a powered prosthetic foot did not experience improvements and had switched back to passive feet [12].

A compromising but viable alternative is the semi-active prosthetic foot. It provides users with better adaptability than a passive prosthetic foot and is less expensive and lighter than the fully active powered prosthetic foot. Specifically, semi-active prosthetic feet use low-power actuators to modulate the mechanical properties of the prosthesis during non-weight-bearing activities (i.e., swing phase during walking), instead of directly providing external mechanical power to assist the user’s movement [13]. For example, the Össur Proprio foot [14], along with the semi-active prosthetic ankles discussed in [15,16], can actively change the sagittal ankle angle during swing phases, in a manner similar to changing the prosthetic foot’s alignment manually in typical passive prostheses. The ankle-foot prosthesis developed in [17] utilizes electromyographic control to adjust both the sagittal and frontal ankle angles through linear actuators, while a more recent innovation [18] employs a non-backdrivable wedge cam mechanism to achieve active control of these angles in a semi-active two-axis prosthetic ankle. Another key idea in some semi-active prosthetic foot designs is to emulate the nonlinear angle-torque relationship in healthy human ankles by using specifically shaped rotated ankle cams [15,19,20] and a lockable spring mechanism [21]. Some other semi-active prosthetic feet, like the Ottobock Meridium [22] and the Blatchford Elan [23], use damping elements to vary resistance at different stages of the gait cycle to improve users’ experience. These semi-active ideas described can provide more adaptability than passive prostheses for different terrains (e.g., steps and slopes). However, with the exception of prosthesis in [20], they cannot vary or control energy storage and return. And with the exception of the Össur Proprio foot, all these commercial prostheses use a hydraulic damper and therefore dissipate energy [24,25].

The Energy Storage and Return (ESR) foot is the most common passive prosthetic foot on the market, where the main idea is to deflect an elastic component, such as a leaf spring keel, to store and release energy back to the user. By using a Controlled Energy Storage and Return prosthetic foot (CESR), previous research [26,27] has shown that the controlled energy recycling (storage and return) can restore ankle push-off and reduce net metabolic cost. Therefore, another promising semi-active idea is to modulate the stiffness of the elastic components to vary the energy storage and return performance of the prosthesis. Several semi-active prosthetic feet [20,28,29] have been successfully developed to implement active stiffness control based on variations of a supported cantilever beam. Another recently developed semi-active prosthetic foot can actively modulate its stiffness using a set of parallel cantilever beams, which can slide or be fixed relative to each other, controlled by solenoid-driven linear actuators [30]. In our previous work [29], we designed the semi-active Variable-Stiffness Foot (VSF; here called VSF-1K, Figure 1a), in which the stiffness of the forefoot keel itself can be modulated through a motor-actuated moving fulcrum during the swing phase of walking. Building on VSF-1K, we now propose and have prototyped the semi-active Two-Keel Variable-Stiffness Foot (VSF-2K), the first prosthetic foot where both the hindfoot and forefoot stiffness can be independently and actively modulated through two movable fulcrums, one on each, shown in Figure 1b. The idea of two-keel-independent modulation is similar to a recently developed passive prosthetic foot prescription tool that can also adjust both hindfoot and forefoot stiffness but requires manual adjustment [31].

Besides the advantage in modulating energy storage and return, a semi-active prosthetic foot with active stiffness control can also provide similar improvement in adaptability as a foot with active ankle-alignment-angle control, like the feet in [11,12] indicated above. Clinically, a common prosthetist’s workaround is to add anterior/posterior bumpers or wedge in the foot to compensate for imperfect foot alignment. However, these add-ons actually change the stiffness of the prosthetic foot; this workaround therefore indicates that modulating prosthetic foot stiffness and changing ankle alignment have similar effects on gait performance. In one previous study, the authors state that by proper ankle alignment, two prosthetic feet with different stiffness in toes and heels can obtain similar walking performance [32]. In another previous study [33], researchers found that addressing knee thrust-forward and hyperextension by varying the stiffness of the hindfoot and forefoot components has a similar effect to changing the alignments in practice. However, all this evidence is empirical and experimental. Therefore, a theoretical understanding of stiffness and ankle alignment interaction in prosthetic feet is needed. And detecting how the stiffness and the ankle alignment affect the walking performance is also important for the practical application of the semi-active prosthetic foot.

In this paper, we demonstrate a simulation model based on Euler-Bernoulli beam theory for the VSF-2K with three sub-models: (1) one sub-model to optimize the design of the keels to reduce the overall minimum achievable stiffness, as a less-stiff prosthesis provides more energy return and a greater range of motion [33], (2) another sub-model to simulate the stance phase of walking on level ground with the optimal VSF-2K, at different stiffness setting pairs (i.e., paired hindfoot-forefoot stiffness combinations) and ankle alignment angles, and (3) a third sub-model to simulate the keel stiffness of the hindfoot and forefoot keels in a way comparable to the mechanical testing of physical prostheses. Through the stance-phase and keel stiffness simulation results, we quantitatively analyze how the VSF-2K’s stiffness setting pair and ankle alignment angle (dorsiflexion/plantarflexion) affect walking mechanics through three gait metrics: Roll-over Shape ($ROS$), Effective Foot Length Ratio ($EFLR$), and Dynamic Mean Ankle Moment Arm ($DMAMA$). $ROS$ is a well-established and proven metric for evaluating gait performance, describing the centers of pressure during the stance phase in the ankle frame [34]. $EFLR$ measures the ratio of the effective foot length to the total foot length, where the effective foot length is the distance from the heel to the end of the $ROS$ [35]. $DMAMA$ is the ratio of sagittal ankle moment impulse to ground reaction force impulse during the entire stance phase [36,37], developed to be a potential control metric in semi-active prostheses [38]. Beyond analyzing gait metrics, we also utilize our model to simulate the angular stiffness of the VSF-2K across various stiffness setting pairs. We explore the interaction between angular stiffness and keel stiffness and validate an angular stiffness prediction model from [39].

There is not much previous work on the modeling and simulation of a semi-active prosthetic foot. Two previous studies aim to provide a simulation method to optimize a prosthetic foot’s design parameters on a user-specific basis, by modeling the VSF-1K [40] and the human gait with VSF-1K [41]. Our intent with this study is to provide more insight into the design, evaluation of performance, and control of a semi-active variable-stiffness prosthetic foot and flexible-keel prostheses in general.

2. Materials and Methods

In this section, we present the details of the three sub-models, their interactions, and their outputs. The simplified version of VSF-2K used in all sub-models is shown in Figure 2. Figure 3 shows a graphical flow and overview of the entire VSF-2K Model. A GitHub repository (link provided in Section A of the Supplementary Materials) contains all the code files and detailed instructions for running this VSF-2K simulation model.

2.1. Model A: Keel Design Optimization Model

Most prosthetic foot users prefer a more compliant foot [42]. To ensure VSF-2K can modulate to a sufficiently low stiffness, we optimize both the hindfoot and forefoot keel designs for maximum possible compliance.

The keel in the VSF-2K is modeled as an Euler-Bernoulli Overhung Beam, shown in Figure 4a. As shown in Figure 4b, the conceptual design includes constant-thickness and linearly tapered sections, and varying width; this design space is chosen so the keel can be machined from rectangular material stock. There are five design inputs for each keel:

(1)

the length of the full keel ($L$),

(2)

the length of the untapered section ($L_{untaper}$),

(3)

the maximum thickness at one end ($h_{max}$),

(4)

the minimum thickness at the other end ($h_{min}$), and

(5)

the maximum displacement of the fulcrum ($a_{max}$).

For the practical implementation of the physical prosthesis, the keel needs to flex past the fulcrum frame on both sides without contacting it. Therefore, we design the keel with a gap in the middle (20 mm wide for hindfoot keel and 25 mm wide for forefoot keel) and with a small portion merged at the toe/heel end. The designed width profile for the keel is then symmetrically divided into two equal parts, as shown in Figure 4c.

The designed keel has a varied thickness profile $h\left(x\right)$, with an untapered section (i.e., constant thickness) and a linearly tapered section, shown in Equation (1). Note that $x$ is defined from the toe/heel end.

$$h\left(x\right)=\left\{\begin{array}{c}{h}_{max}; \left(L-L_{untaper}\right)<x\le L\\ h_{min}+{\displaystyle \frac{h_{max}-h_{min}}{L-L_{untaper}}}x; 0\le x<(L-L_{untaper})\end{array}\right.$$

(1)

The designed keel also has a varied width profile $b\left(x\right)$. Through the five design parameters, we design the width profile through a “Break-Safe” calculation using the Flexure Formula (Equation (2)), where $M\left(x\right)$ is the internal moment, and $I\left(x\right)$ is the area moment of inertia (Equation (3)).

$${\sigma }_{max}(x)={\displaystyle \frac{M\left(x\right)\left(\frac{h\left(x\right)}{2}\right)}{I\left(x\right)}}$$

(2)

$$I(x)={\displaystyle \frac{b\left(x\right){h\left(x\right)}^3}{12}}$$

(3)

We relate the maximum internal tensile stress ${\sigma }_{max}\left(x\right)$ of the keel at each position with its width, under the “Most-Likely-Break” bending scenario (shown in Figure 5a), where the fulcrum is at the maximum displacement (i.e., ${a=a}_{max}$) and a large load ($P_{max}=1200$ N for forefoot keel and $800$ N for hindfoot keel, estimated for a 100 kg person) is applied at the toe/heel end. We set ${\sigma }_{max}$ equal to 90% of the Flexural Strength (${\sigma }_s$) of the selected material to ensure the keel will theoretically not break. Finally, through Equations (2) and (3), the design of the width profile is shown in Equation (4). Based on the force-moment analysis of this scenario (Equation (5)), the break-safe width profile is shown in Equation (6).

$$b(x)={\displaystyle \frac{6M\left(x\right)}{{\sigma }_{max}{h\left(x\right)}^2}}$$

(4)

$$M\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{a}{L-a}}(L-x)P; a<x\le L\\ xP; 0<x\le a\end{array}\right.$$

(5)

$$b(x)=\left\{\begin{array}{c}{\displaystyle \frac{6\frac{a_{max}}{L-a_{max}}(L-x)P_{max}}{0.9{\sigma }_{s}h{\left(x\right)}^2}}; a_{max}<x\le L\\ {\displaystyle \frac{6x{P}_{max}}{0.9{\sigma }_{s}h{\left(x\right)}^2}}; 0<x\le a_{max}\end{array}\right.$$

(6)

We then want to optimize the five keel parameters to lower the keel stiffness. The bending scenario used in this optimization problem is shown in Figure 5b. We use a selected load ($P=800$ N) applied at the toe/heel end, and the fulcrum is set at the midpoint position (i.e., $a=0.5a_{max}$). The deflection of the whole keel ($v\left(x\right)$) caused by the selected load at a contact point (in this scenario, at the toe/heel end) is computed through the Euler-Bernoulli beam theory (Equation (7)), where $E$ is the Elastic Modulus of the selected material, and $M$ is obtained from the force-moment analysis of this scenario (Equation (5)). The details of the derivation of the deflection equations for the entire keel when the load is at the toe/heel end can be found in Section B of the Supplementary Materials.

$${\displaystyle \frac{d^{2}v\left(x\right)}{d{x}^2}}={\displaystyle \frac{M\left(x\right)}{EI\left(x\right)}}$$

(7)

The objective of this optimization problem is to choose the five design parameters in a physically reasonable range that minimize the stiffness $k=P/v\left(0\right)$ (i.e., maximize the deflection), subject to the linear design of the thickness, “Break-Safe” design of the width, moment profile from the force-moment analysis, and the Euler-Bernoulli beam theory. The design optimization framework is shown below:

Keel Design Optimization

$\begin{array}{c} minimize\\ L{,h}_{max},h_{min}, L_{untaper},a_{max}\end{array} k={\displaystyle \frac{P}{ v\left(0\right)}}$ $such that {\displaystyle \frac{d^{2}v(x)}{d{x}^2}}={\displaystyle \frac{M\left(x\right)}{E\frac{b\left(x\right){h\left(x\right)}^3}{12}}}$ $M\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{a}{L-a}}(L-x)P; a<x\le L\\ xP; 0<x\le a\end{array}\right.$ $b(x)=\left\{\begin{array}{c}{\displaystyle \frac{6\frac{a_{max}}{L-a_{max}}(L-x)P_{max}}{0.9{\sigma }_{s}h{\left(x\right)}^2}}; a_{max}<x\le L\\ {\displaystyle \frac{6x{P}_{max}}{0.9{\sigma }_{s}h{\left(x\right)}^2}}; 0<x\le a_{max}\end{array}\right.$ $h(x)=\left\{\begin{array}{c}{h}_{max}; \left(L-L_{untaper}\right)<x\le L\\ h_{min}+{\displaystyle \frac{h_{max}-h_{min}}{L-L_{untaper}}}x; 0\le x<(L-L_{untaper})\end{array}\right.$ $L\in \mathrm{a} \mathrm{r}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}$ $h_{max}\in \mathrm{a} \mathrm{r}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}$ $0.01h_{max}\le h_{min}\le 0.99h_{max}$ $0.01L\le L_{untaper}\le 0.99L$ $0.01L\le a_{max}\le 0.99L$ $60 \mathrm{m}\mathrm{m}\le b\left(x\right)\le 100\mathrm{m}\mathrm{m}$

After obtaining the optimal keel design, we design the two mounting angles of the keels (${\phi }_{hind}$ and ${\phi }_{fore}$) and the height of the ankle ($L_{ankle}$) to ensure the foot sits level in the unloaded state. As shown in Figure 6, when the ankle bar is perpendicular to a horizontal ground and the distal ends of the two keels (i.e., heel and toe) are in contact with the ground without load, we first design ${\phi }_{hind}$, and then calculate ${\phi }_{fore}$ as in Equation (8). According to [43], we set $L_{ankle}$ as 28% of the prosthetic foot length without any cover, i.e., the length from heel to toe of the raw keels ($L_{foo{t}_{raw}}$).

$${\displaystyle \frac{L_{hind}}{sin\left({\phi }_{fore}\right)}}={\displaystyle \frac{L_{fore}}{sin\left({\phi }_{hind}\right)}}$$

(8)

The optimal design of the two keels, the mounting angles of the two keels, and the height of the ankle are later used as the design inputs to the other two models: the Stance Phase Simulation Model and the Keel Stiffness Simulation Model.

2.2. Model B: Stance Phase Simulation Model

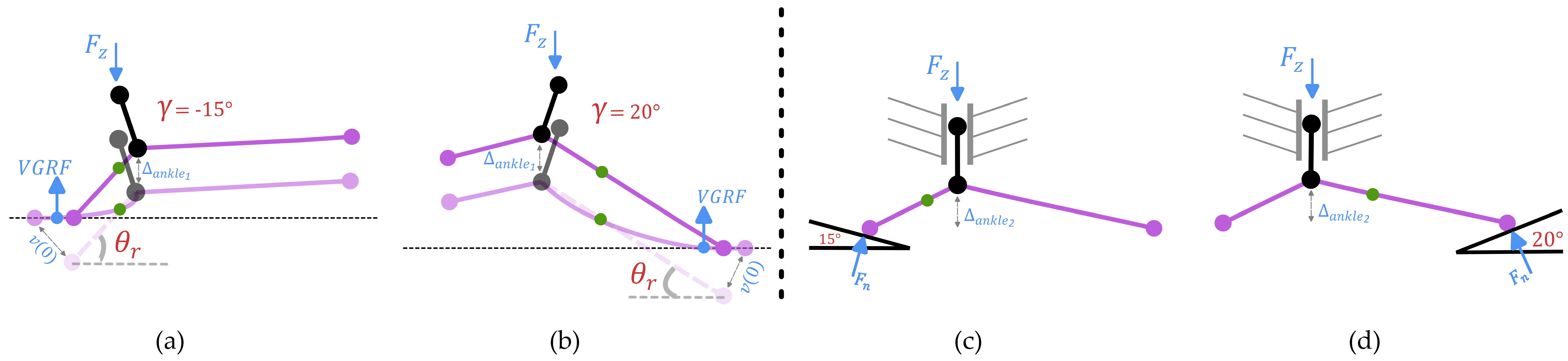
In this section, with the design from the previous section, we use Euler-Bernoulli beam theory again to simulate the stance phase of walking on level ground using the optimal VSF-2K across a variety of stiffness setting pairs (i.e., paired hindfoot-forefoot stiffness combinations) and ankle alignment angles ($\alpha$, varied from plantarflexed $10°$ to dorsiflexed $10°$, where plantarflexion is defined as negative and dorsiflexion as positive). Figure 7 shows the example configurations of VSF-2K at the softest case with dorsiflexed $10°$ ankle alignment, at the medium case with neutral ankle alignment, and at the stiffest case with plantarflexed $10°$ ankle alignment, respectively.

We use the load-time profile (Figure 8a) and angle-time profile (Figure 8b) provided by ISO 22675:2016 [44] as the inputs for sagittal-plane vertical ground reaction force ($VGRF$) and shank angle ($\gamma$) during the stance phase (heel-strike to toe-off). Figure 8c shows the load-angle relationship based on Figure 8a,b. Technically, the load profile in ISO 22675:2016 is determined by the resultant vector of the vertical and horizontal (anterior-posterior) ground reaction forces [44]. In this study, we assume that there is no horizontal ground reaction force, considering its relatively low magnitude. Therefore, we treat the provided load profile as representing pure vertical ground reaction force.

We define four stages in one footstep: (1) Hindfoot-Only Contact, (2) Foot-Flat, and (3) Forefoot-Only Contact. We then divide Stage 2 (Foot-Flat) into two parts: (2.1) the initial half, ending when the portion of the shared $VGRF$ on the hindfoot and forefoot equalize, and (2.2) the latter half, ending when the heel lifts off the ground. Since the load in the hindfoot is higher during Stages 1 and 2.1, we assume the heel is stationary (heel-fixed frame $HFF$) at Stages 1 and 2.1, and the toe is slipping (toe slipping frame $TSF$) at Stage 2.1. Similarly, since the load in the forefoot is higher during Stages 2.2 and 3, we assume the toe is stationary (toe-fixed frame $TFF$) at Stages 2.2 and 3, and the heel is slipping (heel slipping frame $HSF$) at Stage 2.2. We define the world frame ($WF$) at the heel-fixed frame, with the origin (0,0) set at the initial contact point (i.e., heel point at the heel-strike). The overview of the “roll-over” process is shown in Figure 9.

We obtain the whole “roll-over” in a quasi-static way by following these steps:

1.

Equally sample the time from 0 to 600 $\mathrm{m}\mathrm{s}$.

2.

Extract the corresponding shank angle array and $VGRF$ array from the standard profile (Figure 8).

3.

Determine the boundary shank angle and $VGRF$ at all transitions between successive stages.

4.

Correctly split the shank angle and $VGRF$ arrays into the appropriate stages.

5.

Determine how the hindfoot and forefoot share the $VGRF$ at each shank angle during Stage 2.

6.

Determine the contact points of the load for hindfoot and forefoot, the center of pressure, and the ankle position in the world frame ($WF$) at each shank angle.

In the rest of this section, we demonstrate our method for steps (3)–(6). We first show the method for finding the contact point of the load on the undeflected hindfoot/forefoot keel (${x_C}_{ud}$) at a given shank angle, as it serves as the basis for solving all these steps. Figure 10 interprets the idea of finding ${x_C}_{ud}$. In Figure 10, it is important to differentiate between ${x_C}_{ud}$ and ${x_C}_d$. ${x_C}_d$ is the contact point of the load on the deflected hindfoot/forefoot keel (i.e., the actual contact point of the load for hindfoot/forefoot). Since we use the Euler-Bernoulli beam theory, the simulated keel shape will be elongated when it deflects, so ${x_C}_{ud}\ne {x_C}_d$.

2.2.1. Contact Point Identification on the Undeflected Keel

According to Euler-Bernoulli beam theory, there is no internal load in the section of the beam from the distal end (i.e., toe/heel) to the contact point. Theoretically, this section will deflect without deformation, meaning the entire section will retain its linear shape and will remain in contact with the ground, but with no load. Therefore, the contact point of the load should be the point where the keel is no longer tangent to the ground. From Figure 10, we observe that this statement can be interpreted as: the deflection angle (${\theta }_{deflect}$) at the contact point on the undeflected keel of the hindfoot/forefoot keel should satisfy:

$${\left.{\theta }_{deflect}\left(x\right)\right|}_{x={x_C}_{ud}}={\theta }_r,$$

(9)

or equivalently, the deflection slope at the contact point should satisfy:

$${\left.{\displaystyle \frac{dv\left(x\right)}{dx}}\right|}_{x={x_C}_{ud}}=tan({\theta }_r),$$

(10)

where the rolling angle (${\theta }_r$) is defined at a specific shank angle ($\gamma$) with a specific ankle alignment ($\alpha$) as follows:

$${\theta }_{r,hind}={\phi }_{hind}+\alpha -\gamma ;$$

(11)

$${\theta }_{r,fore}={\phi }_{fore}-\alpha +\gamma .$$

(12)

In the force-moment analysis of this scenario (Figure 10, where the load may not be at the distal end), we neglect the effect of the compression load, $VGRF sin\left({\theta }_r\right)$, so the bending load ($F_b$) at the contact point used in Euler-Bernoulli beam theory (Equation (7)) is only the component orthogonal to the beam axis, $VGRF cos\left({\theta }_r\right)$. Based on the force-moment analysis of this scenario and Euler-Bernoulli beam theory (Equation (7)), we can obtain the analytical expressions of $v\left(x\right)$ of the keel at a given bending load and contact point. Therefore, given a shank angle and the $VGRF$ shared by a keel at this shank angle ($VGR{F}_{hind}$ or $VGR{F}_{fore}$), the ${x_C}_{ud}$ of the keel can be solved through Equation (10). The details of the derivation of the deflection equations $v\left(x\right)$ for the entire keel, when the load is not at the distal end (toe/heel), can be found in Section C of the Supplementary Materials.

During Stage 1 and Stage 3, which are single keel contact stages, the $VGRF$ is entirely applied on the hindfoot or forefoot keel at each shank angle (Equations (13) and (14), respectively). Since the $VGRF$ at each shank angle is provided by the standard profile (Figure 8c), the ${x_C}_{ud}$ of the hindfoot or forefoot keel can be solved solely based on the shank angle through Equation (10). During Stage 2, since the given load is shared by hindfoot and forefoot keels (Equation (15)), we need both the shank angle and the $VGRF$ supported by each keel to compute the ${x_C}_{ud}$ of each through Equation (10). The method of determining how the hindfoot and forefoot keels share the $VGRF$ will be discussed later.

$$VGR{F}_{hind@stage1}=VGR{F}_{@stage1}$$

(13)

$$VGR{F}_{fore@stage3}=VGR{F}_{@stage3}$$

(14)

$$VGR{F}_{hind@stage2}+VGR{F}_{fore@stage2}=VGR{F}_{@stage2}$$

(15)

The above analysis aligns with real-world observations. At the beginning of Stage 1 for hindfoot keel, the load is not sufficient to yield a nonzero ${x_C}_{ud}$ whose ${\theta }_{deflect}={\theta }_r$, so the ${x_C}_{ud}=0$ (i.e., the contact point is still at heel). Naturally, as the foot rolls forward, the contact point for hindfoot will gradually shift further from the distal end (${x_C}_{ud}\ne 0$). This phenomenon can be captured by Equation (11): as the foot rolls forward (i.e., with the increase of the shank angle $\gamma$), the rolling angle ${\theta }_r$ decreases. And with forward progression, the load increases, requiring the contact point to shift farther from the distal end (heel) to maintain the smaller ${\theta }_r$.

2.2.2. Boundary Shank Angle Identification Between Successive Stages

Figure 11a,c show the geometry of computing the boundary shank angles between Stages 1 and 2.1 (${\gamma }_{@startFF}$), and Stages 2.2 and 3 (${\gamma }_{@endFF}$), respectively. At these two boundaries, according to Equations (13) and (14), the $VGRF$ is entirely applied on the hindfoot or forefoot keel, respectively, as the opposite keel is just entering or leaving ground contact, respectively. By incorporating with Equations (11) and (12), we can solve ${\gamma }_{@startFF}$ by equaling the height of the keel mounting point ($Q$ in Figure 11) from both sides as follows:

$$L_{fore}sin\left({\theta }_{r,fore@startFF}\right)=n_{@startFF}\mathit{sin}\left({\theta }_{r,hind@startFF}\right),$$

(16)

where $n$ is an intermediate variable and can be derived from Figure 11a as follows:

$$n=L_{hind}-x_{C_{ud},hind}-{\displaystyle \frac{v_{hind}\left(x=x_{C_{ud},hind}\right)}{\mathit{tan}\left({\theta }_{r,hind}\right)}}.$$

(17)

The $x_{C_{ud},hind}$ and $v_{hind}\left(x\right)$ can be solved through Equation (10) and Equation (7), respectively. Similarly, ${\gamma }_{@endFF}$ is solved as follows:

$$L_{hind}sin\left({\theta }_{r,hind@endFF}\right)=m_{@endFF}\mathit{sin}\left({\theta }_{r,fore@endFF}\right),$$

(18)

where another intermediate variable $m$ can be derived as follows:

$$m=L_{fore}-x_{C_{ud},fore}-{\displaystyle \frac{v_{fore}\left(x=x_{C_{ud},fore}\right)}{tan\left({\theta }_{r,fore}\right)}}.$$

(19)

Figure 11b shows the geometry of computing the boundary shank angle (${\gamma }_{@midFF}$) at which Stage 2.1 (hindfoot supporting more $VGRF$) transitions to 2.2 (forefoot supporting more $VGRF$). This boundary is a special case in Stage 2, where the $VGRF$ is equally shared by the two keels (Equation (20)), and the heel and toe are both momentarily stationary. Therefore, similar to Stages 1 and 3, the $x_{C_{ud}}$ of the hindfoot or forefoot keel can be solved solely based on the shank angle through Equation (10), as the $VGRF$ at each shank angle is provided by the standard profile (Figure 8c).

$$VGR{F}_{hind@midFF}=VGR{F}_{fore@midFF}={\displaystyle \frac{VGR{F}_{@midFF}}{2}}$$

(20)

By incorporating with Equations (17) and (19), we compute the keel mounting point (point $Q$ shown in Figure 11) from two frames: heel-fixed frame ($HFF$, i.e., the world frame we defined) and toe-fixed frame ($TFF$), as shown in Equation (21) and Equation (22), respectively.

$$\left\{\begin{array}{c}{z}_Q^{HFF}=sin\left({\theta }_{r,hind@midFF}\right)n_{@midFF}\\ x_Q^{HFF}=\mathit{cos}\left({\theta }_{r,hind@midFF}\right)n_{@midFF}+{\displaystyle \frac{L_{hind}-n_{@midFF}}{cos\left({\theta }_{r,hind@midFF}\right)}} \end{array}\right.$$

(21)

$$\left\{\begin{array}{c}{z}_Q^{TFF}=sin\left({\theta }_{r,fore@midFF}\right)m_{@midFF}\\ x_Q^{TFF}=\mathit{cos}\left({\theta }_{r,fore@midFF}\right)m_{@midFF}+{\displaystyle \frac{L_{fore}-m_{@midFF}}{cos\left({\theta }_{r,fore@midFF}\right)}} \end{array}\right.$$

(22)

We then transform the position calculated from Equation (22) to heel-fixed frame and set it equal to the position calculated from Equation (21). Incorporating with Equations (11) and (12), the shank angle at this instant, ${\gamma }_{@midFF}$, is then solved from Equation (23), where ${shift}_{TFF}^{HFF}$ is the distance from the world frame origin (heel-fixed frame $HFF$) to the toe location at this instant. This toe location is fixed for the remainder of the step, termed the toe-fixed frame $TFF$.

$$\left[\begin{array}{c}{x}_Q^{HFF}\\ z_Q^{HFF}\end{array}\right]=\left[\begin{array}{c}{shift}_{TFF}^{HFF}-x_Q^{TFF}\\ z_Q^{TFF}\end{array}\right]$$

(23)

By obtaining all the boundary shank angles, we can now correctly split the shank angle and $VGRF$ arrays into the appropriate stages.

2.2.3. VGRF Distribution Between Hindfoot and Forefoot in Stage 2

We now show the method to determine how the hindfoot and forefoot share the $VGRF$ in Stage 2. We use the similar equation in finding ${\gamma }_{@midFF}$ (Equations (23) and (15)) to find the shared $VGRF$s of hindfoot and forefoot keels during Stage 2. Similar to Equations (21) and (22) (same equations but with variables at each shank angle of Stage 2), we compute the keel mounting point ($Q$) of the two keels from the two frames again, but with slight difference: heel-fixed frame ($HFF$) and toe-slipping frame ($TSF$) in Stage 2.1, and heel-slipping frame ($HSF$) and toe-fixed frame ($TFF$) in Stage 2.2.

We then merge the keel mounting point calculated from the two frames. At Stage 2.1, we transform the position calculated from the toe-slipping frame to the heel-fixed frame. Conversely, at Stage 2.2, we transform the position calculated from the heel-slipping frame to toe-fixed frame. At each shank angle in Stage 2.1, incorporating with Equations (21) and (22), the $VGRF$s shared by the two keels are then computed from Equation (24), where ${shift}_{TSF}^{HFF}$ is the distance from heel-fixed frame to toe location at each shank angle. Similarly, the $VGRF$s shared by the two keels at each shank angle in Stage 2.2 are computed from Equation (25), where ${shift}_{HSF}^{TFF}$ is the distance from toe-fixed frame to heel location at each shank angle.

$$\left[\begin{array}{c}{x}_Q^{HFF}\\ z_Q^{HFF}\\ VGRF\end{array}\right]=\left[\begin{array}{c}{shift}_{TSF}^{HFF}-x_Q^{TSF}\\ z_Q^{TSF}\\ VGR{F}_{hind}+VGR{F}_{fore}\end{array}\right]$$

(24)

$$\left[\begin{array}{c}{x}_Q^{TFF}\\ z_Q^{TFF}\\ VGRF\end{array}\right]=\left[\begin{array}{c}{shift}_{HSF}^{TFF}-x_Q^{HSF}\\ z_Q^{HSF}\\ VGR{F}_{hind}+VGR{F}_{fore}\end{array}\right]$$

(25)

2.2.4. Center of Pressure and Ankle Position Identification

By identifying the $VGR{F}_{hind}$ and $VGR{F}_{fore}$ at each shank angle of all stages, we can now determine all the contact points of the load on the undeflected keel ($x_{C_{ud}}$) for each keel through Equation (10).The next step is to transform the contact point of the load on the undeflected keel ($x_{C_{ud}}$) to the deflected keel ($x_{C_d}$) in the corresponding deflected frames (see Figure 9): in Stage 1, we have $x_{C_d}^{HFF}$ for hindfoot; in Stage 2.1, we have $x_{C_d}^{HFF}$ for hindfoot and $x_{C_d}^{TSF}$ for forefoot; in Stage 2.2, we have $x_{C_d}^{HSF}$ for hindfoot and $x_{C_d}^{TFF}$ for forefoot; in Stage 3, we have $x_{C_d}^{TFF}$ for forefoot. As indicated before, we assume that the contact point of the load on the deflected keel is the actual contact point of the load for the hindfoot/forefoot. The final step is to transform the contact points on the deflected keels from all the other frames ($x_{C_d}^{HSF}$, $x_{C_d}^{TSF}$, and $x_{C_d}^{TFF}$) to the world frame (i.e., the heel-fixed frame, see Figure 9), resulting in $x_{C_d,hind}^{WF}$ and $x_{C_d,fore}^{WF}$ at each shank angle.

The center of pressure in the world frame ($CO{P}^{WF}$) at each shank angle is then computed as the weighted-arithmetic mean of the two keels’ contact points, weighted by the corresponding $VGRF$:

$$CO{P}^{WF}={\displaystyle \frac{x_{C_d,hind}^{WF}\left(VGR{F}_{hind}\right)+x_{C_d,fore}^{WF}\left(VGR{F}_{fore}\right)}{VGRF}}.$$

(26)

We also calculate the ankle point position $\left(x_{ankle}^{WF},z_{ankle}^{WF}\right)$ at each shank angle in the world frame by using the height of the ankle ($L_{ankle}$), shown in Figure 6. Details of the transformations among various frames—including the heel-undeflected-keel, toe-undeflected-keel (see Figure 10), heel-fixed (world frame), heel-slipping, toe-fixed, and toe-slipping frames—are provided in Section D of the Supplementary Materials. The calculation and transformation of the ankle position in the different frames are also detailed in Section D of the Supplementary Materials.

The center of pressure and the ankle position in the world frame are later used in evaluating the simulated gait metrics and the angular stiffness. They are also used in generating the animation of how the VSF-2K rolls over the ground at a specific stiffness setting pair (i.e., a paired hindfoot-forefoot stiffness combination) and an ankle alignment angle. The animation videos can be found in Section E of the Supplementary Materials.

2.3. Evaluation of Simulated Gait Metrics

We use the center of pressure ($CO{P}^{WF}$) and ankle position $\left(x_{ankle}^{WF},z_{ankle}^{WF}\right)$ obtained from the Stance Phase Simulation Model to evaluate multiple gait metrics of interest in prosthetics research.

2.3.1. Roll-Over Shape ($ROS$)

The Roll-over Shape plot (specifically, the ankle-foot Roll-over Shape indicated in [45]) represents the progression of $COP$ points in the ankle-fixed coordinate frame. We obtain the $ROS$ plot by transforming the $COP$ from the world frame ($WF$) into the ankle frame ($AF$) and then plotting them in the ankle-fixed coordinate frame, at each time step (corresponding to each shank angle). The transformation of coordinates from the world frame to the ankle frame $AF$ (Figure 9) is shown in Equation (27).

$$CO{P}^{AF}={T_{AF}^{WF}}^{-1}CO{P}^{WF},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} T_{AF}^{WF}=\left[\begin{array}{cccc}cos\left(\gamma \right)& 0& sin\left(\gamma \right)& x_{ankle}^{WF}\\ 0& 1& 0& 0\\ -sin\left(\gamma \right)& 0& cos\left(\gamma \right)& z_{ankle}^{WF}\\ 0& 0& 0& 1\end{array}\right]$$

(27)

The Roll-over Shape is commonly conceptualized as containing a circular arc, referred to as the effective rocker shape. We define the effective rocker shape as the section from the first peak of the Roll-over Shape plot to the point corresponding to the opposite-heel-strike, which is commonly standardized at 500$\mathrm{m}\mathrm{s}$ of the stance phase. The portions prior to the first peak and after opposite-heel-strike are ignored because they roughly capture the linear deflections of the hindfoot and forefoot during early contact and late rebound, rather than the forward roll-over modeled as a circle. The effective rocker shape is then fitted as a circle to obtain the two main descriptors of the Roll-over Shape: center position ($x_{ROS},z_{ROS}$) and radius ($r_{ROS}$).

To avoid overfitting the center of pressure points in Stages 1 and 3 (i.e., using least-squares fitting directly will place more weight on these stages due to their greater number of time steps), we develop an “Equally Spaced Resampling Algorithm (ESRA)” (Algorithm 1) to determine the center and the radius of the circle fit to the effective rocker shape of the $ROS$. Figure 12a shows an example $ROS$ plot with the ESRA algorithm.

Algorithm 1: Equally Spaced Resampling Algorithm (ESRA)
	input: Center of Pressure points of the effective rocker shape in ankle frame ($CO{P}^{AF}$)
	output: Center ($x_{ROS},z_{ROS}$) and the radius ($r_{ROS}$) of the circle fit of the input
	initialization: set the change in fit parameters $\left({∆}_x,{∆}_z\right)=\left(\mathrm{10,10}\right)$ mm, the current center position $(x_{old},z_{old})=\left(\mathrm{0,0}\right)$ mm, and number of angular circle segments $n=100$
	while (${∆}_x>1$ mm or ${∆}_z>1$ mm) do:
		- Compute vectors connecting $(x_{old},z_{old})$ with the points at the two ends of the effective rocker shape
		- Equally divide the rocker shape into $n$ equal angular slots between the two vectors for each slot do:     if (the slot has $CO{P}^{AF}$ points in it) do:
		Compute the $CO{P}_{fit}^{AF}$ point by averaging all the $CO{P}^{AF}$ points in this slot    else (i.e., the slot has no $CO{P}^{AF}$ points in it) do:     Connect the two nearest $CO{P}^{AF}$ points that bound the slot to get $lin{e}_{interpolate}$ Compute the $CO{P}_{fit}^{AF}$ point by averaging the two intercepts between this slot’s two boundary lines and $lin{e}_{interpolate}$    end if end for
		- Do least-squares circle fit [46] on the $CO{P}_{fit}^{AF}$ points of all slots to determine the new estimate of the $ROS$ center position $(x_{ROS},z_{ROS})$ and the radius ($r_{ROS}$)
		- Update the change in fit parameters ${∆}_x=\left|x_{ROS}-x_{old}\right|$ and ${∆}_z=\left|z_{ROS}-z_{old}\right|$
		- Update the center position $x_{old}=x_{ROS}$ and $z_{old}=z_{ROS}$
	end

2.3.2. Effective Foot Length Ratio ($EFLR$)

$EFLR$ is calculated as the ratio of the effective foot length versus the total foot length, shown in Equation (28). The effective foot length ($L_{foo{t}_{eff}}$ in Figure 12a) is defined as the horizontal distance from the heel (start point of the $ROS$ plot) to the opposite-heel-strike point of the $ROS$ plot (end of the effective rocker shape) [35]. In this study, we assume the total foot length to be the prosthetic foot length without any cover ($L_{foo{t}_{raw}}$ in Figure 6).

$$EFLR={\displaystyle \frac{L_{foo{t}_{eff}}}{L_{foo{t}_{raw}}}}$$

(28)

2.3.3. Dynamic Mean Ankle Moment Arm ($DMAMA$)

$DMAMA$ is calculated as the ratio of sagittal ankle moment impulse ($M$) to ground reaction force impulse ($GRF$) during the entire stance phase for a single foot:

$$DMAMA={\displaystyle \frac{\int \overrightarrow{M} dt}{\int \overrightarrow{GRF }dt}}={\displaystyle \frac{\overline{M}}{\overline{GRF}}},$$

(29)

where $\overrightarrow{GRF}$ includes the anteroposterior and vertical force components, and $\overrightarrow{M}$ is computed as the sagittal moment of $\overrightarrow{GRF}$ (ignoring inertial effects) about the ankle [36]. In this study, since we assume no anteroposterior ground reaction force, the $DMAMA$ here is equivalent to its simplified version—WACOP, the weighted-average center of pressure, where it ignores anteroposterior forces [36]. Therefore, in this study, $DMAMA$ is calculated in Equation (30). We also compute the normalized version, denoted as $DMAMAn$, by dividing $DMAMA$ by the foot length. For this calculation, we still assume the foot length to be the prosthetic foot length without any cover ($L_{foo{t}_{raw}}$).

$$DMAMA={\displaystyle \frac{\int \left(CO{P}^{WF}-x_{ankle}^{WF}\right)\left(VRGF\right) dt}{\int \left(VGRF\right) dt}}$$

(30)

2.4. Angular Stiffness Evaluation

We use the center of pressure ($CO{P}^{WF}$) and the ankle position ($x_{ankle}^{WF}$) obtained from the Stance Phase Simulation Model to compute the angular stiffness ($k_{angular}$) of VSF-2K at different stiffness setting pairs. At a specific stiffness setting pair, similar to Equation (30), we compute the sagittal ankle moments from the $VGRF$, $CO{P}^{WF}$, and ankle position at $0°$ shank angle during stance phase, for all ankle alignment angles ranging from $10°$ plantarflexion to $10°$ dorsiflexion. Using the instant of $0°$ shank angle ensures that the load is the same across all these cases, and only the ankle alignment angle has changed. These samples yield a plot of moment versus ankle alignment angle which defines the angular stiffness. A typical plot is shown in Figure 13. Angular stiffness is most relevant when both keels contact the ground, so we estimate the angular stiffness of a specific stiffness setting pair by linearly fitting only those samples that occurred in Stage 2 Foot-Flat (i.e., double-keel contact, the middle part shown in Figure 13). The other points occurred in Stage 1 or 3 (i.e., single-keel contact) due to their large magnitude of ankle alignment angles, and so they were excluded from the angular stiffness calculation.

2.5. Model C: Keel Stiffness Simulation Model

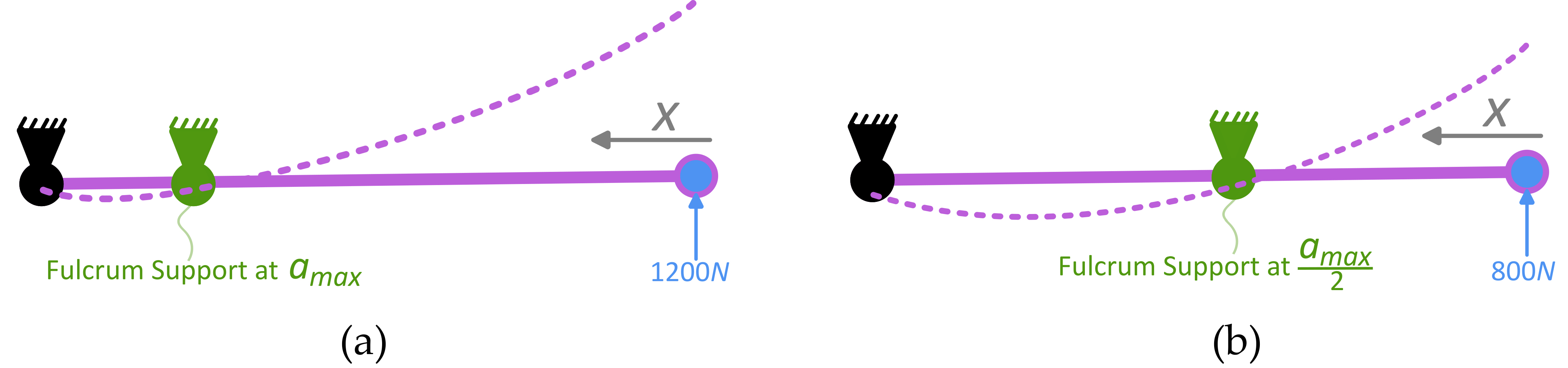
In this section, we generate a model for predicting the keel stiffness at different stiffness settings (i.e., different fulcrum positions) of the hindfoot/forefoot keel, as it would be measured in a standard mechanical test.

The simulation testing setup is shown in Figure 14a,b. Approximating the standard mechanical testing setup (Figure 14c,d) in the Prosthetic Foot Project by AOPA (The American Orthotic and Prosthetic Association) [47], we use a neutral ankle alignment of the prosthesis model and set the shank angle to $-15°$ for the hindfoot and $+20°$ for the forefoot. We simulate a vertical force ($F_z$) compressing the VSF-2K vertically to the ground (i.e., the ankle only moves vertically), by applying $VGRF$ to the keel from 0 to 1230 N [47]. The displacement of the ankle (${∆}_{ankl{e}_1}$) at each $VGRF$ is calculated as:

$${{∆}_{ankle}}_1=\mathit{cos}\left({\theta }_r\right)·v\left(x=0\right).$$

(31)

${\theta }_r$ can be obtained through Equation (11) or (12) with zero ankle alignment angle. Similar to the Stance Phase Simulation Model, at each $VGRF$ (the bending load is only the $cos\left({\theta }_r\right)$ component of the $VGRF$), we first solve the contact point on the undeflected keel (${x_C}_{ud}$) through Equation (10) for the given bending load and shank angle, and then we obtain $v\left(x\right)$ through Equation (7) for the given bending load and contact point. We plot $VGRF$ versus ${∆}_{{ankle}_1}$ for each keel at each stiffness setting; a typical curve of this loading simulation is shown in Figure 15. We obtain two sets of keel stiffness from the plot: (1) the slope of the line connecting the origin and the maximum displacement point from our Keel Stiffness Simulation Model, termed the keel maximum-load stiffness ($k_{max,hind}^{KSSM}$ or $k_{max,fore}^{KSSM}$, shown in red in Figure 15), and (2) the linear fit (with zero intercept) to the entire curve, termed the keel linear stiffness ($k_{linear,hind}^{KSSM}$ or $k_{linear,hind}^{KSSM}$, shown in cyan in Figure 15).

The keel maximum-load stiffness ($k_{max}^{KSSM}$) represents how the keel deflects when the load is at the maximum 1230 N of a specific stiffness setting. This stiffness measurement is comparable to the keel stiffness measured in the testing setup of the Prosthetic Foot Project by AOPA, which uses the displacement at 1230 N to classify the heel and toe compliance. We can relate this stiffness simulated from our Keel Stiffness Simulation Model ($k_{max}^{KSSM}$) and measured from the testing setup by AOPA ($k_{max}^{AOPA}$). From Figure 14, they are calculated as follows:

$$k_{max}^{KSSM}={\displaystyle \frac{1230 \mathrm{N}}{{{∆}_{ankle}}_1}}, \mathrm{a}\mathrm{n}\mathrm{d} k_{max}^{AOPA}={\displaystyle \frac{1230 \mathrm{N}}{{{∆}_{ankle}}_2}}.$$

(32)

From Figure 14c,d, $k_{max}^{KSSM}$ can also be calculated as in Equation (33), where $\beta$ is the testing angle: $-15°$ or $20°$.

$$k_{max}^{KSSM}={\displaystyle \frac{F_n}{cos\left(\beta \right){{∆}_{ankle}}_2}}={\displaystyle \frac{1230 \mathrm{N}/cos\left(\beta \right)}{cos\left(\beta \right){{∆}_{ankle}}_2}}$$

(33)

Therefore, we concluded the relationship between the keel maximum-load stiffness from our model and AOPA’s test as follows:

$$k_{max}^{KSSM}={\displaystyle \frac{k_{max}^{AOPA}}{{\mathit{cos}}^2\left(\beta \right)}}.$$

(34)

This computation makes sense because when $\beta =0$, $k_{max}^{KSSM}=k_{max}^{AOPA}$, indicating the same testing setup. A similar conversion was employed in [48], where the same mathematical relationship (Equation (34)) was used to compute the keel stiffness from a standard testing setup, similar to the one in the AOPA project. By using this relationship, we can approximate the keel stiffness of a standardized testing setup through our simulation model. We can also use this relationship to predict the classification of the VSF-2K’s keel compliance at each stiffness setting, according to guidance in the AOPA Prosthetic Foot Project.

The keel linear stiffness ($k_{linear,hind}^{KSSM}$ or $k_{linear,fore}^{KSSM}$) represents the slope of the fitted line (with zero intercept) of the entire curve in Figure 15. We set this fitted stiffness as the VSF-2K nominal stiffness. We then use this nominal hindfoot/forefoot stiffness ($k_{linear,hind}^{KSSM}$ or $k_{linear,fore}^{KSSM}$) and its corresponding fulcrum position to analyze the interaction between stiffness and the gait metrics at a specific ankle alignment angle. The term “hindfoot/forefoot keel linear stiffness” is shortened to “hindfoot/forefoot stiffness” in some of the following content.

Additionally, as an extension of the AOPA procedure, we can also compute the keel linear stiffness (fitted with zero intercept) measured from the AOPA-like testing setup ($k_{linear,hind}^{AOPA}$ or $k_{linear,fore}^{AOPA}$) using $k_{linear}^{KSSM}$. Equation (34) shows that the deflections from the two setups are related by a factor of ${\mathit{cos}}^2\left(\beta \right)$ at each load point. Therefore, the zero-intercept linear fits for the two loading curves ($k_{linear}^{KSSM}$ and $k_{linear}^{AOPA}$) should also be related by a factor of ${\mathit{cos}}^2\left(\beta \right)$, as in Equation (34).

Both the model-simulated keel linear stiffness ($k_{linear,hind}^{KSSM}$ or $k_{linear,fore}^{KSSM}$, the nominal hindfoot/forefoot stiffness) and the AOPA-like version’s keel maximum-load stiffness ($k_{max,hind}^{AOPA}$ or $k_{max,fore}^{AOPA}$) of the hindfoot/forefoot are used to analyze the interaction of hindfoot/forefoot keel stiffness with the angular stiffness of the VSF-2K.

2.6. Angular Stiffness Prediction

In addition to the simulated angular stiffness ($k_{angular}$) from the Stance Phase Simulation Model, we also aim to estimate and predict the VSF-2K’s angular stiffness from hindfoot/forefoot keel stiffness through an analytical angular stiffness prediction model provided by a previous study [39]. In [39], the author predicted the angular stiffness from the linear stiffness of the hindfoot and forefoot of a two-keel experimental prosthetic foot (Equation (35)) and validated it through linear compression tests at different ground angles.

$${\widehat{k}}_{angular}={\displaystyle \frac{l^2{k}_{fore}{k}_{hind}}{k_{fore}+k_{hind}}}$$

(35)

$k_{hind}$ and $k_{fore}$ represent the linear stiffness of the hindfoot and forefoot keel from vertical compression tests, respectively. We use the two keel stiffness sets (simulated nominal stiffness $k_{linear}^{KSSM}$ and AOPA-like version’s maximum-load stiffness $k_{max}^{AOPA}$) driven from the Keel Stiffness Simulation Model as the input parameters. $l$ is the distance between the contact points of the hindfoot keel and forefoot keel during a vertical compression test on the horizontal ground; it can be approximated as the prosthetic foot length [39]. To test the analytical model’s predictive ability, we fit parameter $l$ to relate the simulated angular stiffness ($k_{angular}$) versus the predicted angular stiffness (${\widehat{k}}_{angular}$). We then compare the best-fit $l$ against the modeled prosthetic foot length ($L_{foo{t}_{raw}}$).

3. Results

All result data and the 3D figures (in .fig format) are provided in the GitHub repository (link provided in Section A of the Supplementary Materials).

3.1. Optimal VSF-2K Design

The keel material we used in the prototype and the model is Gordon Composites-67-UBW [49], which has a high flexural strength ($~1$ GPa) and relatively low flexural modulus ($~33$ GPa). We believe it is likely the most suitable choice on the market for use in prosthetic keel, as it provides both compliance and durability. In this study, the length and the maximum thickness of each keel are preset before the design optimization to respect foot size and raw materials, respectively. Both keels have a maximum thickness of 0.165 inches (4.191 mm), with a hindfoot length of 90 mm and a forefoot length of 165 mm. We also set the hindfoot keel alignment angle (${\theta }_{n,hind}$ as shown in Figure 6) to be $20°$, while the forefoot keel alignment angle is then calculated as 10.752° through Equation (8). According to Figure 6, the prosthetic foot length without any covers ($L_{foo{t}_{raw}}$) is 246.7 mm, and the ankle length ($L_{ankle}$) is 69 mm. The optimal design of each keel is shown in

Table 1. The optimal design parameters for the hindfoot and forefoot keels.

	$\mathit{L}$ (mm)	${\mathit{L}}_{\mathit{u}\mathit{n}\mathit{t}\mathit{a}\mathit{p}\mathit{e}\mathit{r}}$ (mm)	${\mathit{h}}_{\mathit{m}\mathit{a}\mathit{x}}$ (mm)	${\mathit{h}}_{\mathit{m}\mathit{i}\mathit{n}}$ (mm)	${\mathit{a}}_{\mathit{m}\mathit{a}\mathit{x}}$ (mm)
Hindfoot Keel	90	1	4.191	1	90
Forefoot Keel	165	26.57	4.191	1.5	160

, and the resulting keel width design profiles are shown in Figure 16.

Based on the keel length and the maximum fulcrum displacement, we set four fulcrum positions for each keel. With the optimal keel designs, the two sets of keel stiffness ($k_{linear}^{KSSM}$ and $k_{max}^{AOPA}$) of the hindfoot and forefoot at each fulcrum position are shown in Figure 17. A higher stiffness corresponds to a lower fulcrum position value, as we measure the fulcrum position from the distal end (toe/heel). The plots of load versus ankle displacement at each fulcrum position of the hindfoot and forefoot keels (similar to Figure 15) are provided in Section F of the Supplementary Materials.

3.2. Gait Metric Versus Keel Linear Stiffness and Ankle Alignment Angle

3.2.1. Roll-Over Shape (Figure 18)

Overall, the x-coordinate of the $ROS$ center ($x_{ROS}$) increases (i.e., $x_{ROS}$ shifts forward) when the ankle alignment is more plantarflexed. $x_{ROS}$ is less sensitive to the hindfoot stiffness at plantarflexed ankle alignments (remaining almost unchanged) than at dorsiflexed ankle alignments. The x-coordinate of the $ROS$ center decreases (i.e., $x_{ROS}$ shifts rearward) when the hindfoot stiffness increases (i.e., fulcrum moves toward the heel) in most cases, except at the softest forefoot stiffness setting in $10°$ plantarflexed ankle alignment. This can be interpreted from Figure S10 in Section G of the Supplementary Materials, which shows the 2D plots of $x_{ROS}$ versus hindfoot stiffness at each forefoot stiffness level across all ankle alignment angles.

The x-coordinate of the $ROS$ center also generally increases (i.e., $x_{ROS}$ shifts forward) as the forefoot stiffness increases (i.e., fulcrum moves toward the toe), except in dorsiflexed ankle alignments between $3°$ and $10°$. In these specific ankle alignments, at certain high hindfoot stiffness settings, the $x_{ROS}$ initially shifts forward but then shifts rearward as forefoot stiffness continues to increase. Additionally, as dorsiflexion increases within this $3°$ to $10°$ range, this nonmonotonic trend is found in more hindfoot stiffness settings. Specifically, at dorsiflexed $3°$ ankle alignment, this nonmonotonic trend is found only at the stiffest hindfoot setting; at dorsiflexed $10°$ ankle alignment, this trend appears at all four hindfoot stiffness settings. These scenarios can be interpreted from Figure S11 in Section G of the Supplementary Materials, which shows the 2D plots of $x_{ROS}$ versus forefoot stiffness at each hindfoot stiffness level across all ankle alignment angles.

Figure 18. The interaction between keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness), ankle alignment angle, and the x-coordinate of the $ROS$ center ($x_{ROS}$). $x_{ROS}$ increases (i.e., shifts forward) when the ankle alignment is more plantarflexed. $x_{ROS}$ decreases (i.e., shifts rearward) when the hindfoot stiffness increases (i.e., fulcrum moves toward the heel). $x_{ROS}$ generally increases as the forefoot stiffness increases, except in dorsiflexed ankle alignments between $3°$ and $10°$. Detailed 2D plots of $x_{ROS}$ versus hindfoot/forefoot stiffness across different ankle alignment angles are shown in Section G of the Supplementary Materials.

Figure 18. The interaction between keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness), ankle alignment angle, and the x-coordinate of the $ROS$ center ($x_{ROS}$). $x_{ROS}$ increases (i.e., shifts forward) when the ankle alignment is more plantarflexed. $x_{ROS}$ decreases (i.e., shifts rearward) when the hindfoot stiffness increases (i.e., fulcrum moves toward the heel). $x_{ROS}$ generally increases as the forefoot stiffness increases, except in dorsiflexed ankle alignments between $3°$ and $10°$. Detailed 2D plots of $x_{ROS}$ versus hindfoot/forefoot stiffness across different ankle alignment angles are shown in Section G of the Supplementary Materials.

3.2.2. Effective Foot Length Ratio (Figure 19)

Overall, the $EFLR$ is not sensitive to hindfoot stiffness. This can be interpreted from Figure S12 in Section H of the Supplementary Materials, which shows the 2D plots of $EFLR$ versus hindfoot stiffness at each forefoot stiffness level across all ankle alignment angles. For the ankle alignment angle from dorsiflexed $10°$ to plantarflexed $5°$, the $EFLR$ increases when the ankle alignment is more plantarflexed. The $EFLR$ increases when the forefoot stiffness increases for all dorsiflexed and neutral ankle alignments. For the ankle alignment angle from plantarflexed $1°$ to plantarflexed $5°$, the $EFLR$ initially increases but then decreases as forefoot stiffness continues to increase. For the ankle alignment angle from plantarflexed $6°$ to plantarflexed $10°$, the $EFLR$ decreases when the forefoot stiffness increases, conversely. These scenarios can be interpreted from Figure S13 in Section H of the Supplementary Materials, which shows the 2D plots of $EFLR$ versus forefoot stiffness at each hindfoot stiffness level across all ankle alignment angles.

Figure 19. The interaction between keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness), ankle alignment angle, and the Effective Foot Length Ratio. $EFLR$ is not sensitive to hindfoot stiffness. The $EFLR$ increases when forefoot stiffness increases at neutral and all dorsiflexed ankle alignments. The $EFLR$ initially increases but then decreases as forefoot stiffness increases at plantarflexed $1°$ to plantarflexed $5°$ ankle alignment. The $EFLR$ decreases when the forefoot stiffness increases at plantarflexed $6°$ to plantarflexed $10°$ ankle alignments. Detailed 2D plots of $EFLR$ versus hindfoot/forefoot stiffness across different ankle alignment angles are shown in Section H of the Supplementary Materials.

Figure 19. The interaction between keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness), ankle alignment angle, and the Effective Foot Length Ratio. $EFLR$ is not sensitive to hindfoot stiffness. The $EFLR$ increases when forefoot stiffness increases at neutral and all dorsiflexed ankle alignments. The $EFLR$ initially increases but then decreases as forefoot stiffness increases at plantarflexed $1°$ to plantarflexed $5°$ ankle alignment. The $EFLR$ decreases when the forefoot stiffness increases at plantarflexed $6°$ to plantarflexed $10°$ ankle alignments. Detailed 2D plots of $EFLR$ versus hindfoot/forefoot stiffness across different ankle alignment angles are shown in Section H of the Supplementary Materials.

3.2.3. Dynamic Mean Ankle Moment Arm (Figure 20)

Figure 20b shows the interaction between VSF-2K’s keel linear stiffness (the nominal stiffness), ankle alignment angle, and the normalized Dynamic Mean Ankle Moment Arm ($DMAMAn$). Overall, the $DMAMAn$ increases (i.e., shifts forward) nearly uniformly whenever the ankle alignment becomes more plantarflexed. At each ankle alignment, the $DMAMAn$ decreases (i.e., shifts rearward) when the hindfoot stiffness increases, and the $DMAMAn$ increases (i.e., shifts forward) when the forefoot stiffness increases. Figure 20b,c show the trend between $DMAMAn$ and hindfoot/forefoot stiffness at neutral ankle alignment. Each plane is fitted with a left-shifted bi-quadratic hyperbolic surface, with the corresponding fit equation provided in Section K of the Supplementary Materials.

Figure 20a shows the interaction directly between VSF-2K’s fulcrum positions, ankle alignment angle, and the $DMAMAn$. At each ankle alignment, the $DMAMAn$ decreases (i.e., shifts rearward) linearly when the hindfoot fulcrum position decreases (i.e., moves towards the heel, increasing hindfoot stiffness), and the $DMAMAn$ increases linearly (i.e., shifts forward) when the forefoot fulcrum position decreases (i.e., moves towards the toe, increasing forefoot stiffness). Each plane is fitted with a linear surface, with the corresponding fit equation provided in Section K of the Supplementary Materials.

Figure 20. Normalized Dynamic Mean Ankle Moment Arm versus (a) fulcrum position and (b) keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness) across ankle alignment angles. $DMAMAn$ increases steadily with more plantarflexed ankle alignment, with nearly uniform spacing between each plane. $DMAMAn$ increases with higher forefoot stiffness and decreases with higher hindfoot stiffness. $DMAMAn$ has a nearly uniform linear relationship with hindfoot and forefoot fulcrum position at each ankle alignment angle. The fit equations of the neutral ankle alignment planes for (a,b) are shown here. (c) shows $DMAMAn$ versus hindfoot/forefoot stiffness at the neutral ankle alignment. Detailed 2D plots of $DMAMAn$ versus hindfoot/forefoot stiffness and hindfoot/forefoot fulcrum position across different ankle alignment angles are shown in Sections I and J of the Supplementary Materials, respectively.

Figure 20. Normalized Dynamic Mean Ankle Moment Arm versus (a) fulcrum position and (b) keel linear stiffness ($k_{linear}^{KSSM}$, the nominal stiffness) across ankle alignment angles. $DMAMAn$ increases steadily with more plantarflexed ankle alignment, with nearly uniform spacing between each plane. $DMAMAn$ increases with higher forefoot stiffness and decreases with higher hindfoot stiffness. $DMAMAn$ has a nearly uniform linear relationship with hindfoot and forefoot fulcrum position at each ankle alignment angle. The fit equations of the neutral ankle alignment planes for (a,b) are shown here. (c) shows $DMAMAn$ versus hindfoot/forefoot stiffness at the neutral ankle alignment. Detailed 2D plots of $DMAMAn$ versus hindfoot/forefoot stiffness and hindfoot/forefoot fulcrum position across different ankle alignment angles are shown in Sections I and J of the Supplementary Materials, respectively.

3.3. Angular Stiffness Versus Hindfoot and Forefoot Keel Stiffness

Figure 21 shows the interaction between VSF-2K’s hindfoot/forefoot keel stiffness and the angular stiffness. The plot of ankle moment versus ankle alignment angle (similar to Figure 13), used to derive angular stiffness for a specific stiffness setting pair (i.e., a paired hindfoot-forefoot stiffness combination), is provided in Section L of the Supplementary Materials. Figure 21a shows the angular stiffness versus VSF-2K’s keel linear stiffness ($k_{linear}^{KSSM}$), and Figure 21b shows the angular stiffness versus VSF-2K’s keel maximum-load stiffness ($k_{max}^{AOPA}$). In both cases, the angular stiffness increases as the hindfoot and forefoot keel stiffness increases. The fitting results using the model from [39] are also shown for each plot. The best-fit $l$ for $k_{linear}^{KSSM}$ is 244 mm ($R^2=$ 0.968), and for $k_{max}^{AOPA}$, the best-fit $l$ is 223 $\mathrm{m}\mathrm{m}$ ($R^2=$ 0.95).

4. Discussion

4.1. Keel Design Optimization

In this study, we optimized our keel design to achieve a broader range of stiffness modulation, especially in the lower stiffness range. The optimal-designed keels, with the variable-stiffness mechanism, successfully achieve controlled stiffness that approximates the range observed in prior studies of commercial prostheses: hindfoot (44–90 N/mm [50]; 25.5–70.6 N/mm [51]; 31.7–68 N/mm [52]) and forefoot (28–76 N/mm [53]; 16.4–46.5 N/mm [51]; 17.9–47.9 N/mm [52]). The ideal target range for stiffness variation is not fully clear, as different studies have reported stiffness ranges using various testing procedures, including differences in testing angles, testing machines, testing surface [54], the presence or absence of foot shells and shoes, and different stiffness fitting methods. Nevertheless, the stiffness variation achieved by VSF-2K encompasses many of these reported ranges.

Beyond the benefits of increased energy return and a greater range of motion offered by a softer prosthetic foot [33], additional motivation for this design optimization model includes the inherent design challenges associated with achieving a softer keel that maintains structural integrity compared to a stiffer keel. Our design optimization framework aims to provide valuable insight into keel design for bending-beam prosthetic feet.

A recent approach to passive prosthetic foot shape and size design optimization introduced a novel gait metric called Lower Leg Trajectory Error (LLTE) [55,56,57]. This study utilized a finite element model to analyze how a parameterized prosthetic foot rolls over the ground and to quantify the resulting lower leg trajectory. The LLTE is calculated as the error between this trajectory and a scaled standard able-bodied human’s lower-leg trajectory, then it is optimized to identify the optimal prosthetic foot design parameters. This research offers another perspective on prosthetic foot design optimization. Future work could involve extending our stance phase simulation model to encompass the entire lower leg, including the shank segment, enabling us to potentially incorporate optimization of the keel design itself to minimize LLTE, instead of targeting more compliant keels as in the current work.

4.2. Roll-Over Shape

We initially expected that the relationship between the x-coordinate of the $ROS$ center ($x_{ROS}$) and hindfoot/forefoot stiffness would follow the same trend as the relationship between $DMAMA$ and hindfoot/forefoot stiffness. For slightly dorsiflexed to highly plantarflexed ankle alignments, results confirmed this expectation. We believe the nonmonotonic trend at high dorsiflexed ankle alignment is because $ROS$ not only depends on the center position, but also on the radius ($r_{ROS}$). Figure 22 shows the $ROS$ of the VSF-2K at four forefoot stiffness settings, with the highest hindfoot stiffness setting and dorsiflexed 10° ankle alignment. As the forefoot stiffness increases, the $ROS$ rotates downward, so it is intuitive to expect that the $ROS$ center will shift forward if we assume the radii of these four circles are constant. However, the $ROS$ radius generally increases with the increase in forefoot stiffness, since the $ROS$ becomes flatter with the increase in forefoot stiffness (the plot of $ROS$ radius versus hindfoot/forefoot stiffness at different ankle alignment angles is included in Section M of the Supplementary Materials). In settings with a high dorsiflexed ankle alignment, the large $r_{ROS}$ at a high forefoot stiffness setting could push the $x_{ROS}$ rearward, leading to this nonmonotonic trend.

We focus solely on the $ROS$ center position (referring to the x-coordinate of the $ROS$ center $x_{ROS}$, as the z-coordinate is interchangeable with the radius), rather than the $ROS$ radius $r_{ROS}$, because we believe the horizontal shift of the $ROS$ center is more relevant as a controllable gait metric. A major reason is that previous research has shown that foot length actually has a greater impact on gait mechanics than foot radius [58,59], and the $ROS$ center position is strongly impacted by the foot length. Another study also stated that changes in the $ROS$ radius are not clinically significant compared to changes in the $ROS$ center position [60].

Our study further validates the idea that the x-coordinate of $ROS$ center $x_{ROS}$ is a more reasonable gait metric for control purposes. In Figure 18, each plane corresponds to the VSF-2K rolling over level ground at a specific ankle alignment angle. It can also be interpreted as representing the VSF-2K rolling over different inclined ramps with a neutral ankle alignment. For example, the plane at the top corresponds to VSF-2K rolling over “level ground with plantarflexed 10$°$ ankle alignment” but also approximates “10$°$ inclined ramp with neutral ankle alignment”. A previous study found that in healthy individuals, the $ROS$ center position tends to shift rearward (i.e., $x_{ROS}$ decreases) when walking up a ramp, while it remains unchanged when walking down a ramp [61]. The results of this study show that changes in VSF-2K hindfoot and forefoot stiffness could be used to mimic these behaviors. For example, if a user begins to ascend a 10° ramp from level ground (effectively moving from the red plane to the top yellow plane in Figure 18), the user should adjust the stiffness setting pair to achieve a more rearward $ROS$ center position (i.e., a decreased $x_{ROS}$). By referring to Figure 18, at a constant hindfoot stiffness, this can be achieved by lowering the forefoot stiffness. This adjustment makes intuitive sense, as lowering forefoot stiffness when walking uphill could prevent knee hyperextension and increase the energy returned by the prosthesis. These findings are consistent with literature, but the nonmonotonic trend observed at high dorsiflexion and high stiffness suggests that the x-coordinate of the $ROS$ center may not be a reliable control metric.

Additionally, using numerical least-squares circle fitting methods to obtain the $ROS$ center and radius introduces another layer of instability to the metric. Most previous research on fitting the $ROS$ typically applies a direct least-squares circle fit to the center of pressure data in the ankle frame ($CO{P}^{AF}$). This direct method can lead to biased fits that overemphasize the early and late stance phases (i.e., single keel contact, corresponding to Stages 1 and 3 in this study). Specifically, the middle stance phase (i.e., double keel contact, Stage 2 Foot-Flat in this study) generally has fewer time frames, resulting in less center of pressure data during Stage 2 compared to Stages 1 and 3. Consequently, the data from Stage 2 carries less weight in the least-squares circle fit. For example, in Figure 22, the number of data points in Stage 2 is much lower than in Stages 1 and 3, so the raw least-squares fit deviates greatly from the Stage 2 points. To address this issue, we propose the Equally Spaced Resampling Algorithm (ESRA) for fitting the effective rocker shape of the $ROS$. This method ensures that all regions of the effective rocker shape have the same weight in the least-squares circle fit. Figure 23 graphically illustrates the difference between using ESRA and not using it. We believe that Stage 2 Foot-Flat is a crucial phase during stance, as it contains information on how both the hindfoot and forefoot interact with the ground. Therefore, we recommend using the Equally Spaced Resampling Algorithm (Algorithm 1) when performing the circle fit for the effective rocker shape of the Roll-over Shape.

4.3. Effective Foot Length Ratio

The $EFLR$ increases when forefoot stiffness increases at dorsiflexed 10$°$ to plantarflexed 5$°$ ankle alignment. This finding is consistent with previous research [62]. Typically, the $EFLR$ should be less than 1; however, at higher plantarflexed ankle alignment angles, some $EFLR$ values exceed 1. This can be explained by the fact that with a fixed stiffness setting pair, greater plantarflexion causes more deflection of the forefoot. An assumption of the Euler-Bernoulli Beam Theory is that the axial coordinate of each point on the keel does not change under load, which causes the modeled keel shape to elongate under load, in turn causing the forefoot to slip forward more than it should, and leading to an Effective Foot Length larger than the actual foot length ($L_{foo{t}_{raw}}$). At high plantarflexed ankle alignments, increasing forefoot stiffness results in less forefoot deflection, thereby reducing the $EFLR$ value. This likely explains why the $EFLR$ decreases as forefoot stiffness increases at ankle alignment angles from plantarflexed 6° to 10°. This phenomenon is therefore an artifact of the Euler-Bernoulli beam model, which could be improved with an alternative keel model [63]. Nevertheless, the insensitivity of the $EFLR$ to hindfoot stiffness would still limit its effectiveness as a control metric for a two-independent-keel prosthetic foot.

4.4. Dynamic Mean Ankle Moment Arm

$DMAMA$ increases with the increase in forefoot stiffness at each ankle alignment and with more plantarflexed ankle alignments. As discussed in the Roll-over Shape section above, this can also be interpreted as $DMAMA$ increasing with the ramp incline angle. All these results of $DMAMA$ with VSF-2K are consistent with findings from a previous study that used $DMAMA$ as a control metric in the real-world application of the forefoot-only VSF-1K [38]. This study is the first to show that $DMAMA$ (and also the x-coordinate of the $ROS$ center) has a negative monotonic relationship with hindfoot stiffness. Combined with recent research on changes in $DMAMA$ in unimpaired walking across different terrains and walking speeds [37], this provides a basis for the future application of $DMAMA$ as a control metric in real-world walking with advanced prosthetic feet, such as VSF-2K.

At each ankle alignment angle, we fitted the normalized $DMAMA$ versus hindfoot and forefoot stiffness using a left-shifted bi-quadratic hyperbolic surface (Figure 20b) to capture $DMAMA$ behavior at stiffness extremes. Since $DMAMA$ is bound by the foot length, ranging from a negative value (heel-to-ankle) to a positive value (ankle-to-toe), its behavior under extreme stiffness conditions follows specific trends. When the forefoot or hindfoot stiffness approaches infinity, $DMAMA$ converges to a fixed value dependent on the opposing stiffness. Likewise, when either stiffness approaches zero, $DMAMA$ approaches to a value governed by the remaining stiffness. These trends can also be seen in Figure 20b,c. Additionally, the linear relationship between the hindfoot and forefoot fulcrum positions and $DMAMA$ can be attributed to the similarity in the nonlinear trends of “$DMAMA$ versus keel linear stiffness” and “keel linear stiffness versus fulcrum position” (Figure 17), resulting in an offsetting effect of the nonlinearities. The nonlinear relationship between keel linear stiffness and fulcrum position (Figure 17) can be approximated by an inverse-quadratic (i.e., ${\displaystyle \frac{1}{k^2}}$) relationship, as the deflection at the end of an overhung beam relative to the fulcrum position follows a quadratic relationship, which can be derived from standard mechanics of materials principles [64]. This is why we chose to fit $DMAMA$ versus hindfoot/forefoot stiffness using a quadratic hyperbolic (i.e., ${\displaystyle \frac{1}{k^2}}$) surface.

Compared to $ROS$ and $EFLR$, $DMAMA$ exhibits a much more uniform and monotonic relationship with the hindfoot and forefoot stiffness across different ankle alignments (Figure 20). Unlike $ROS$, which cuts off some $COP$ points and weights the remaining ones identically regardless of the applied load, and unlike alternative control metrics that vary throughout the stance phase, such as ankle impedance [65] and ankle quasi-stiffness [66], $DMAMA$ is a single-valued summary metric that captures the dynamics of ankle control throughout the entire stance phase. Additionally, $ROS$ and $EFLR$ can only be measured using a motion capture system, whereas $DMAMA$ can be measured using an embedded pylon load cell or force insole. Therefore, $DMAMA$ could be a suitable control metric for semi-active devices that can adjust only once per stride for out-of-lab testing.

The linear and consistent relationship between the hindfoot and forefoot fulcrum positions and $DMAMA$ across different ankle alignments (Figure 20a) further supports the argument that $DMAMA$ is an excellent metric for variable-stiffness prosthetic feet that use a stiffness modulation mechanism similar to that of the VSF-2K (i.e., based on movable fulcrums), as linear relationships are preferred in control systems. This linear relationship between $DMAMA$ and forefoot fulcrum position is also consistent with the findings in [38]. Even for the nonlinear relationship between $DMAMA$ and keel linear stiffness (Figure 20b), its consistent trend across different ankle alignment angles also makes it a valuable metric for use in other variable-stiffness prosthetic feet that utilize stiffness modulation mechanisms different from that of the VSF-2K. Additionally, a recent study showed that $DMAMA$ is also unaffected by age, further supporting its potential as a promising control metric [67].

If we choose $DMAMA$ as the gait metric for control of the VSF-2K, Figure 20 shows that to achieve an ideal $DMAMA$ value, we can either adjust the ankle alignment angle or modulate the hindfoot or forefoot stiffness. This model-derived evidence supports the idea that changing prosthetic foot stiffness can have the same effect as altering the ankle alignment angle. Therefore, by actively adjusting hindfoot and forefoot stiffness, the VSF-2K can enhance adaptability across different terrains, like other semi-active prosthetic ankle units that can actively change the ankle angle [14,15,16,17,18].

4.5. Angular Stiffness

Another key finding of this study is that we further validate the angular stiffness prediction model from [39] through simulation. The surface fit between angular stiffness and keel linear stiffness ($k_{linear}^{KSSM}$) yields a best-fit value for $l$ that closely matches the actual prosthetic foot length ($L_{foo{t}_{raw}}$ = 246.7$\mathrm{m}\mathrm{m}$). The keel linear stiffness leads to a reasonable estimation, as expected. The hindfoot and forefoot linear stiffness used in the original model used to derive Equation (35) are the linear stiffness values from an experimental two-keel prosthetic foot [39]. This prosthetic foot had small pads attached to the heel and toe, which prevented rolling contact of the keels. Therefore, unlike the load-displacement profile shown in Figure 15—where the initial linear portion is when the contact point is at the toe/heel, followed by a nonlinear portion as the contact point moves proximally due to increased load—the load-displacement profiles of the hindfoot and forefoot keels of the experimental prosthetic foot in [39] were nearly linear because the pads kept the contact points fixed at the heel and toe. To best approximate this model, we derived our keel linear stiffness by linearly fitting the entire curve with a zero intercept ($k_{linear}^{KSSM}$ in Figure 15). This keel linear stiffness can be roughly interpreted as how the keel deflects when the contact point is fixed at the toe/heel (i.e., like adding a pad in [39]), with some added stiffness from the nonlinear portion. The results show that for a two-independent-keel prosthetic foot without any cover, we can accurately estimate its angular stiffness from foot length and the linear stiffness ($k_{linear}^{KSSM}$) of the hindfoot and forefoot keels, as measured from the simulation setup in our Keel Stiffness Simulation Model, using Equation (35).

The reason why we also performed a best-fit surface analysis using the AOPA-like version’s keel maximum-loaded stiffness ($k_{max}^{AOPA}$) is to provide guidance on estimating angular stiffness using a standardized stiffness measurement. As shown in Figure 21b, we suggest that for a two-independent-keel prosthetic foot without any cover, angular stiffness can be estimated using Equation (35), where the stiffness inputs ($k_{hind}$ and $k_{fore}$) are the keel maximum-loaded stiffness measured from the AOPA Prosthetic Foot Project testing setup [47], and $l$ is approximately 90% of the length of the actual prosthetic foot structure (i.e., keels only, without a foot shell).

4.6. Limitations and Future Work

There are a few limitations in our study. First, we neglected the horizontal ground reaction force component (anterior-posterior force) in the load profile provided by ISO 22675:2016, assuming the load profile consists entirely of vertical ground reaction force. We made this assumption because we could not find separate standard load profiles for vertical and horizontal $GRF$, and it is challenging to determine how the hindfoot and forefoot share the horizontal $GRF$. Despite this, we believe our results remain valid, as the horizontal $GRF$ constitutes only a small percentage of the total $GRF$, and the deflection it causes can be reasonably compensated by treating the total $GRF$ as vertical $GRF$.

Another potential limitation is that we employed a quasi-static method using Euler-Bernoulli Beam Theory to simulate the stance phase of the VSF-2K. A comprehensive analysis of a prosthetic foot, which might include horizontal force, inertial effects, and material hysteresis, requires a dynamic model of not just the prosthesis itself but also the human body (at least the lower limb) and nervous system. We believe our model can be extended to a more comprehensive dynamic model, but much more work is needed. Here, we make a quasi-static assumption so that we can use a standard force versus angle gait profile and reduce the complexity of the model. This assumption is justified because the inertial effect of a prosthetic foot during the stance phase is negligible since the acceleration is small. We believe the results derived from this method are reasonable, as many previous studies have used quasi-static methods to evaluate the Roll-over Shape of prosthetic feet [32,68]. In [32], it was found that the Roll-over Shape properties obtained through quasi-static and dynamic methods are similar, and the Roll-over Shape of prosthetic feet is largely governed by their quasi-static mechanical properties.

Another limitation is that all the results are based on the VSF-2K without any cover. We acknowledge that the results might differ when the VSF-2K is enclosed in a foot shell or has a foam pad added to the sole. However, we believe the analysis made in this study is reasonable and valid for understanding the fundamental relationships among keel design, ankle alignment, prosthetic foot stiffness, and gait metrics such as $ROS$, $EFLR$, and $DMAMA$, and for developing controllers for applications of semi-active or variable-stiffness prosthetic feet. Future work could consider how the shape and stiffness of a foot shell or contoured sole attachment alter the geometry and mechanics of ground contact and roll-over, to further inform both design and control.

Another potential limitation of this study is the use of only one keel material. While a different material may yield a different optimal design, we believe our primary findings—the general relationships among gait metrics, prosthetic foot stiffness, and ankle angle alignment—remain robust to variations in material properties and typical manufacturing tolerances. Minor changes in keel stiffness resulting from material variation or manufacturing deviations can be compensated by adjusting the fulcrum position of the VSF-2K. This further highlights the value of active stiffness modulation in prosthetic feet like the VSF-2K.

Finally, the findings are limited by the artifacts inherent in the Euler-Bernoulli beam model. The most notable limitation is the apparent lengthening of the beam under load. Other models that prevent this artifact, such as a spline model [63], an articulated-segment model [40], or a finite-element model of ground contact [56], could improve some details, if chosen carefully for the purpose and with awareness of their alternatives’ limitations.

The major future work is to build an optimized version of the VSF-2K as designed here and test it. Design decisions reflecting durability, actuation, sensing, and control will be made to ensure functional adaptability and usability for prosthetic foot users. We plan to do mechanical testing to validate the property of the device and human subjects testing to determine whether the effects of stiffness on gait metrics occur as predicted. Experimental conditions will include level-ground, ramps, stairs, and different speeds.

5. Conclusions

In this study, we introduced a comprehensive and novel model focused on optimizing the design and simulating the stance phase and keel stiffness of the VSF-2K, a semi-active two-keel variable-stiffness prosthetic foot. The model offers a systematic approach to optimizing the design of leaf spring keels for prosthetic feet to increase low-stiffness range, and it provides a theoretical framework describing how a bending-beam prosthetic foot interacts with level ground. We showed that the optimally designed VSF-2K successfully achieved controlled stiffness that approximates the stiffness range observed in prior studies of commercial prostheses [50,51,52,53]. Our study provides valuable insights into how prosthetic foot stiffness and ankle alignment affect gait metrics, including Roll-over Shape ($ROS$), Effective Foot Length Ratio ($EFLR$), and Dynamic Mean Ankle Moment Arm ($DMAMA$). We analyzed the shortcomings of $ROS$ and $EFLR$ compared to $DMAMA$, primarily showing their nonmonotonic relationship with hindfoot/forefoot stiffness, insensitivity relative to the hindfoot, and inconsistent trends with hindfoot/forefoot stiffness across different ankle alignments. We also highlighted the unequal-weight problem in the least-squares circle fit of the effective rocker shape of the Roll-over Shape and proposed an Equally Spaced Resampling Algorithm (ESRA) to address this issue. Our findings suggest that $DMAMA$ is the most promising metric for use as a control parameter in semi-active or variable-stiffness prosthetic feet. Additionally, we demonstrated that changing stiffness can mimic or counteract the effects of changing ankle angle, enabling adaptation to sloped terrain. Finally, our results confirm that the angular stiffness of a two-independent-keel prosthetic foot can be estimated using either the keel linear stiffness from our simulation model or the keel maximum-load stiffness from a standardized test setup via an angular stiffness prediction model [39]. These findings show that semi-active variation of hindfoot and forefoot stiffness based on single-stride metrics such as $DMAMA$ is a promising control approach to enabling prostheses to adapt to a variety of terrain and alignment challenges.