Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis
Abstract
1. Introduction
2. Materials and Methods
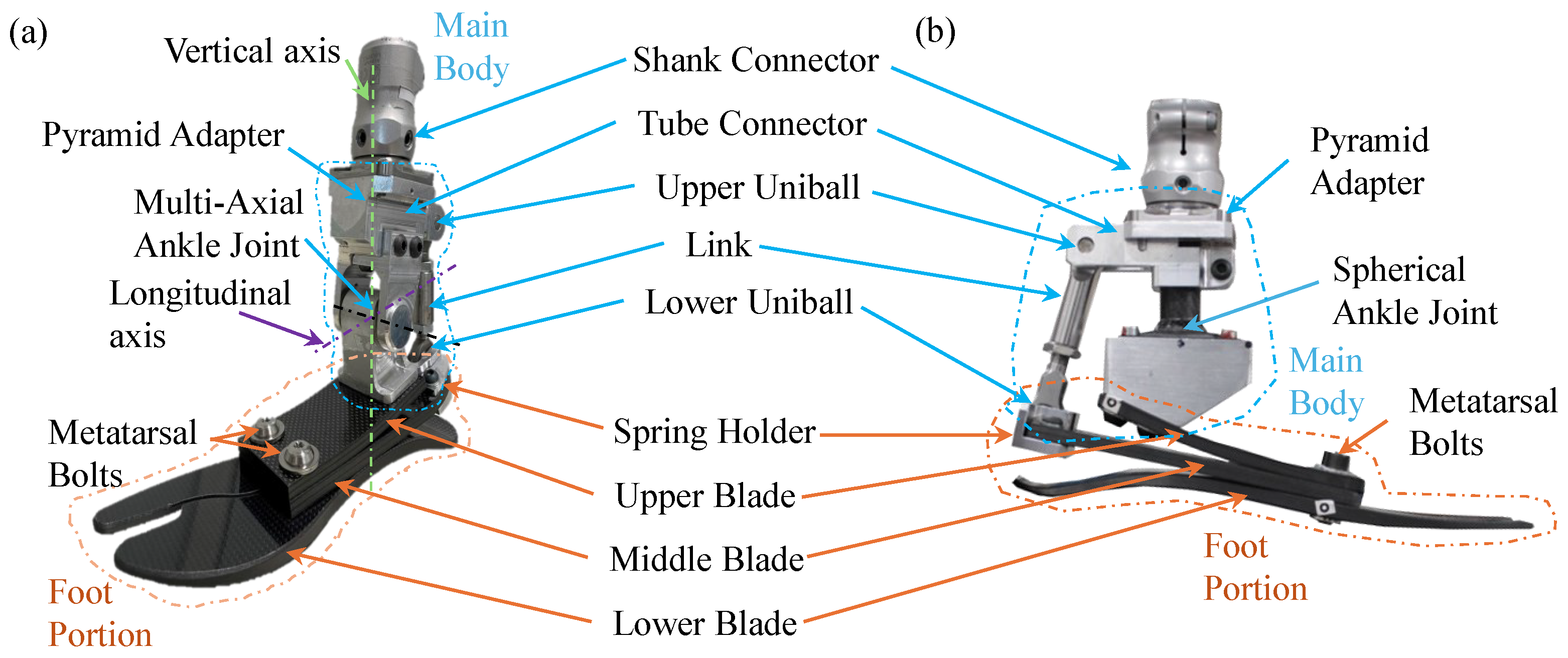
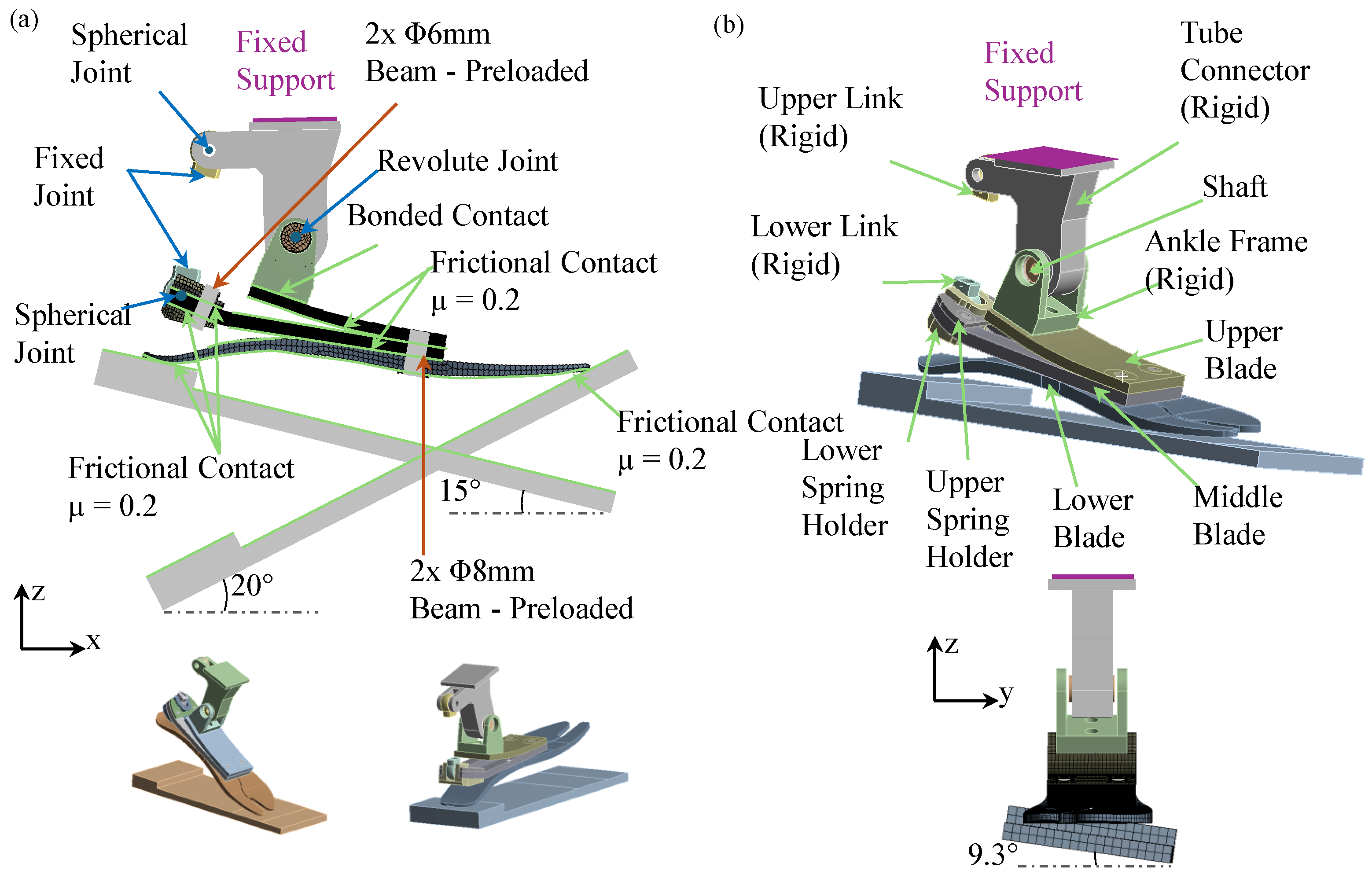
2.1. Concept Design
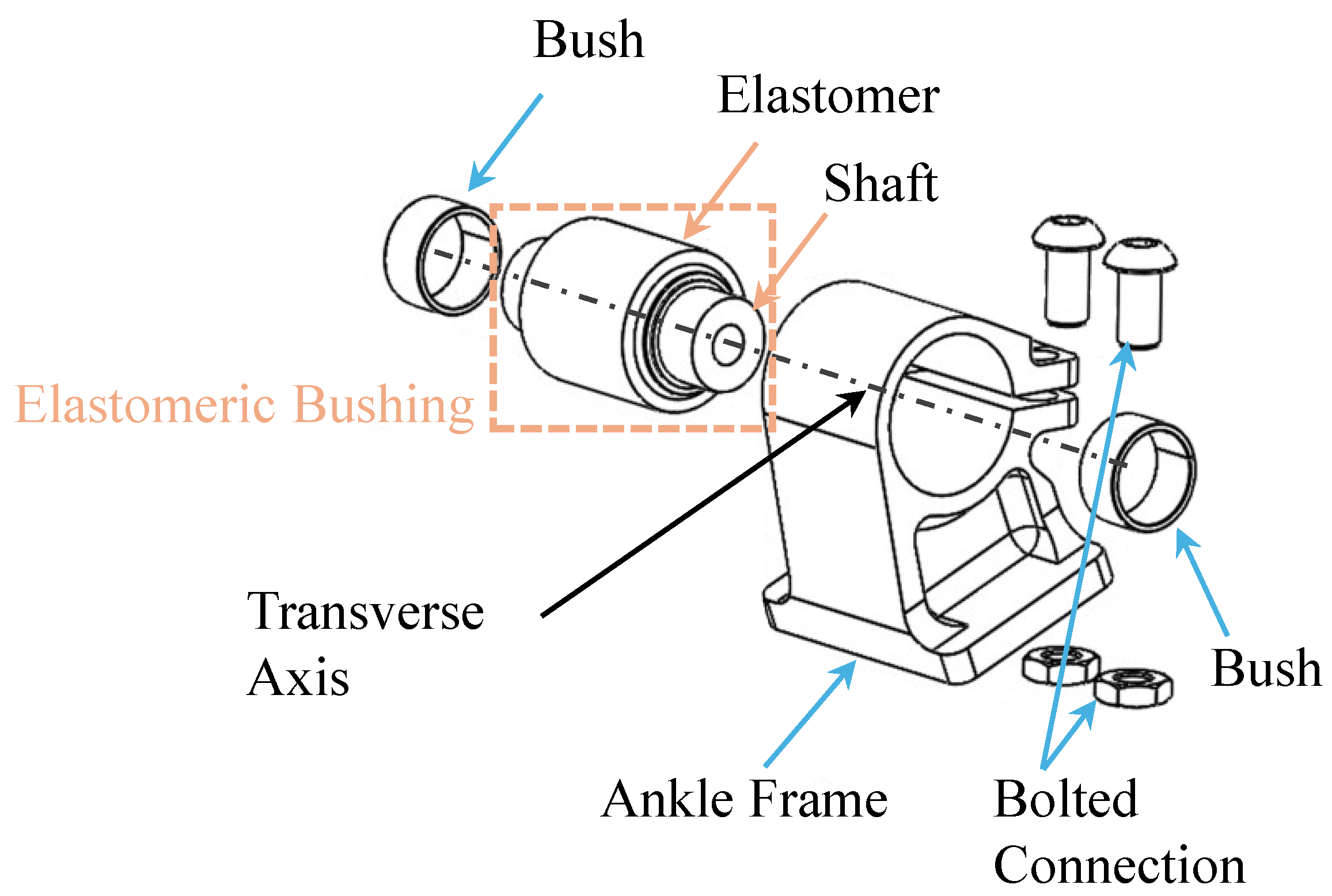
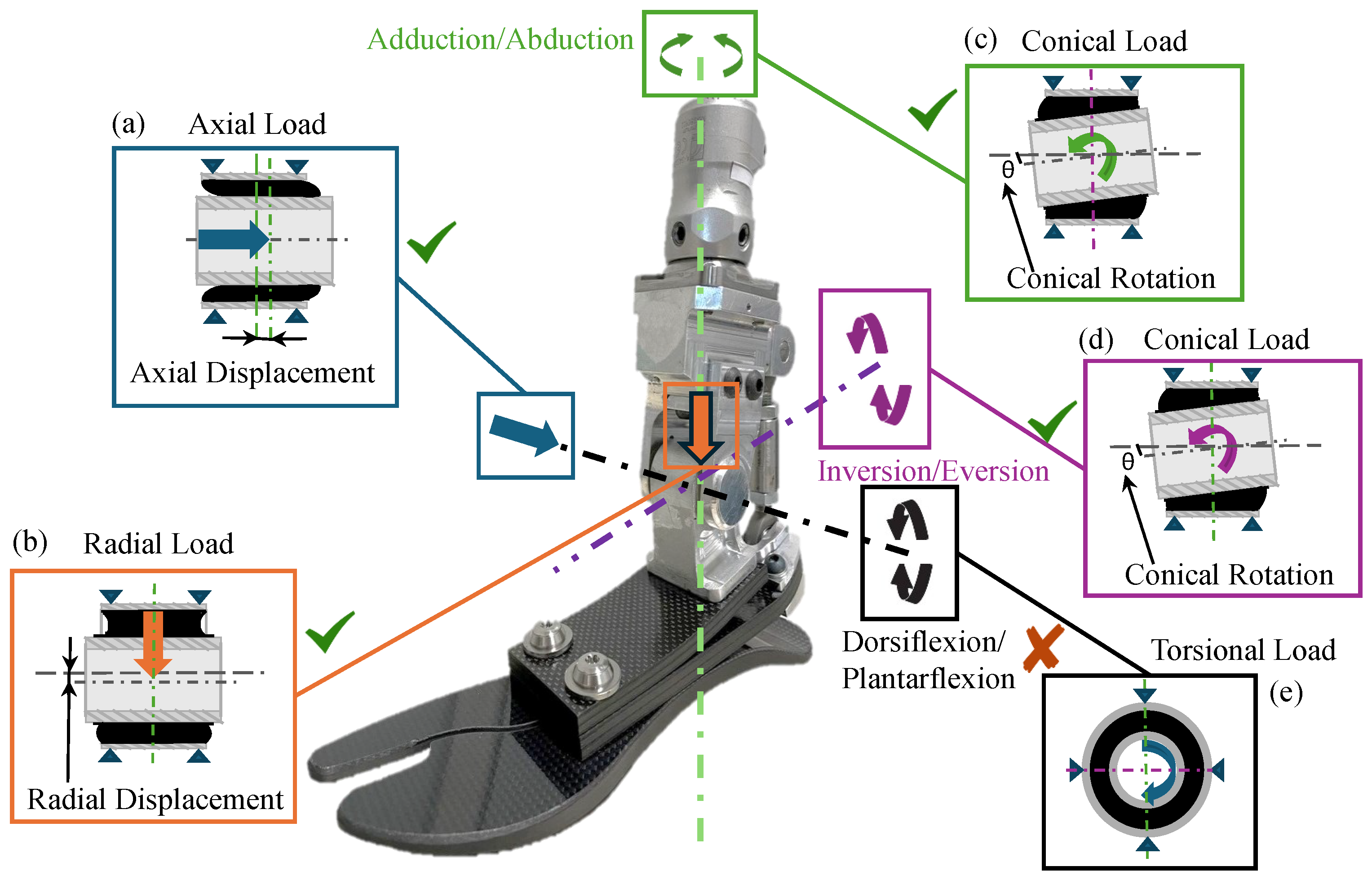
2.2. Design of Experiments of the Multi-Axial Ankle
2.3. ISO 10328 and Cross-Slope Adaptation Test Simulations
2.4. Functionality Verification
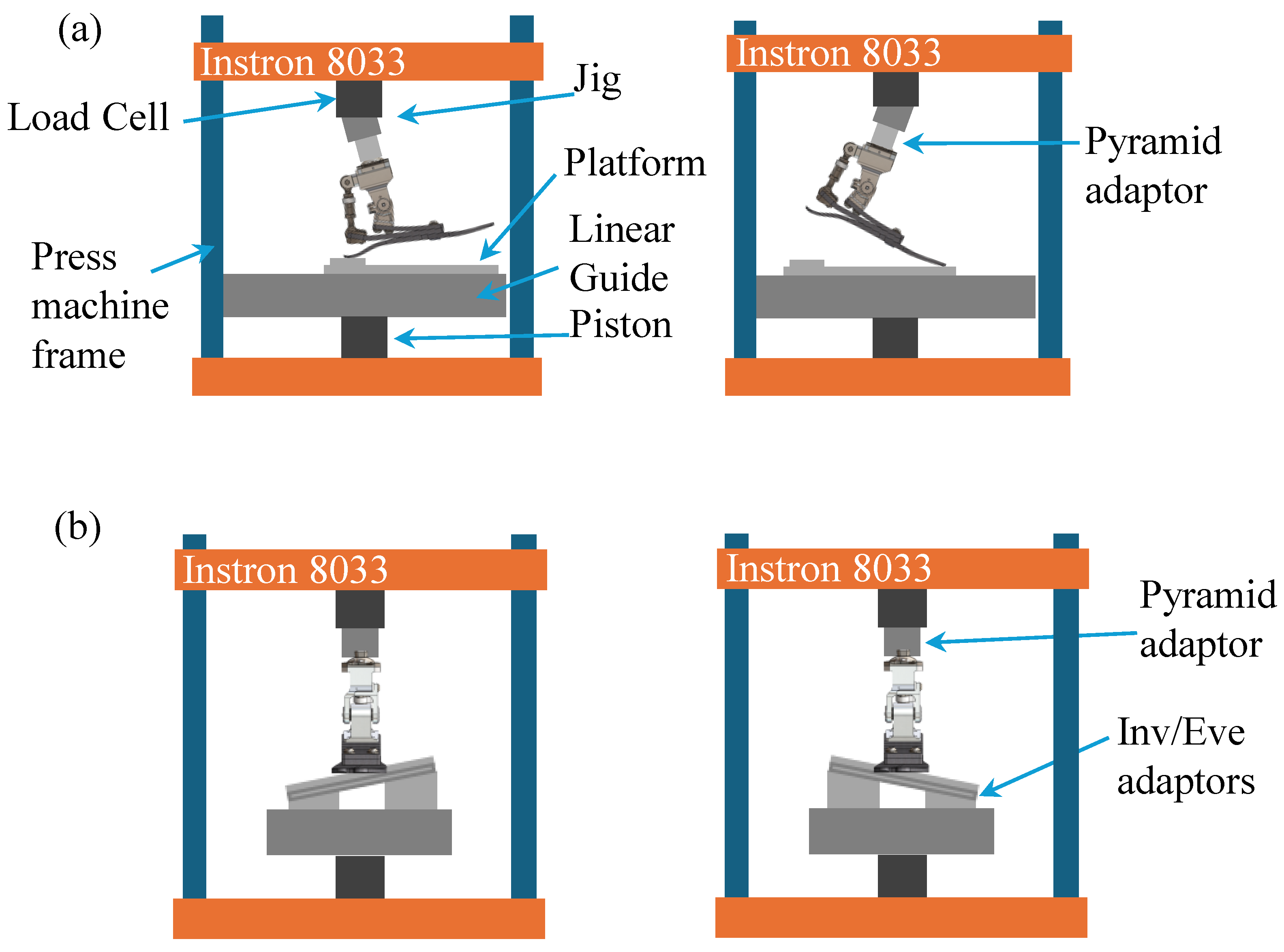
2.5. Testing Method
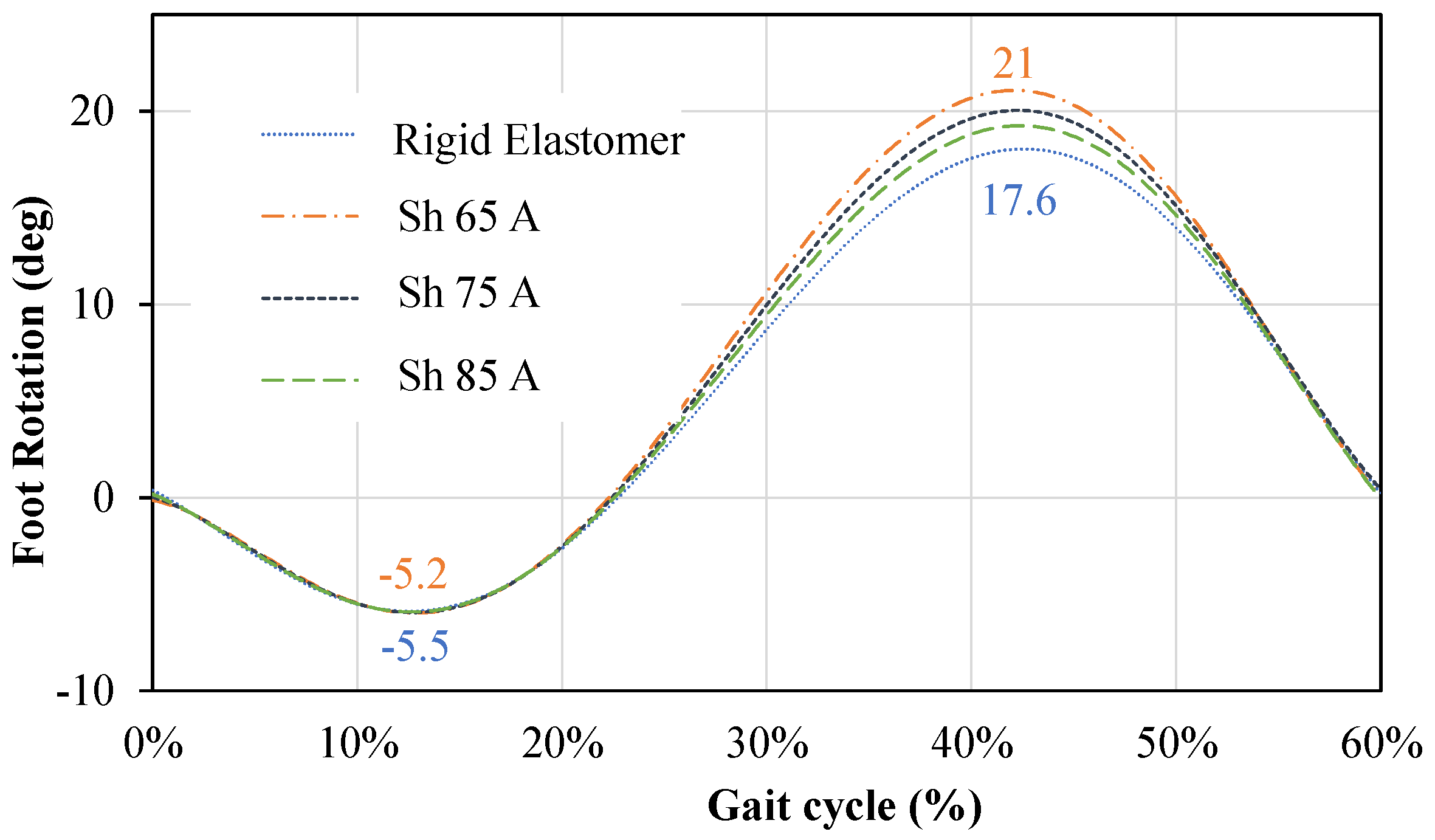
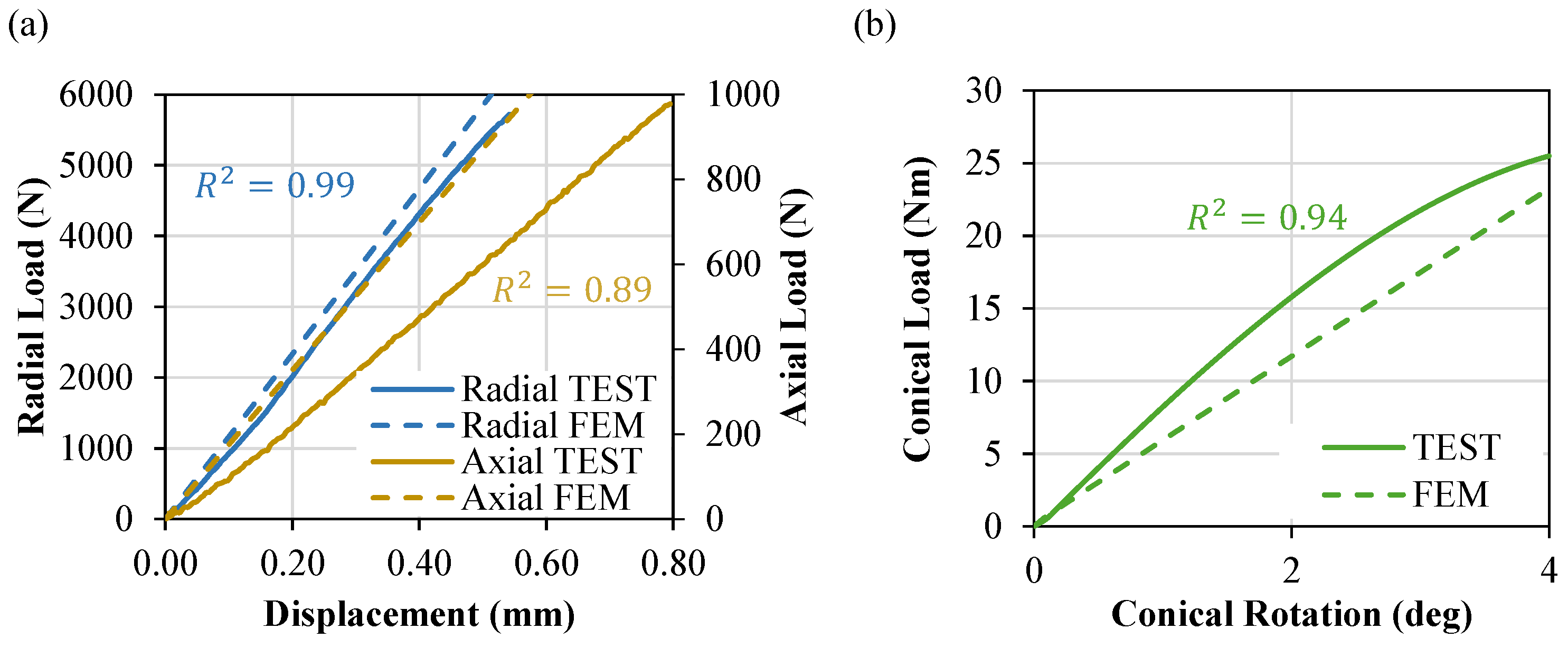
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klute, G.K.; Kallfelz, C.F.; Czerniecki, J.M. Mechanical properties of prosthetic limbs: Adapting to the patient. J. Rehabil. Res. Dev. 2001, 38, 299–307. [Google Scholar]
- Heitzmann, D.W.W.; Salami, F.; De Asha, A.R.; Block, J.; Putz, C.; Wolf, S.I.; Alimusaj, M. Benefits of an increased prosthetic ankle range of motion for individuals with a trans-tibial amputation walking with a new prosthetic foot. Gait Posture 2018, 64, 174–180. [Google Scholar] [CrossRef]
- Su, P.; Gard, S.A.; Lipschutz, R.D.; Kuiken, T.A. The effects of increased prosthetic ankle motion on the gait of persons with bilateral transtibial amputations. NIH Am. J. Phys. Med. Rehabil. 2010, 89, 34–47. [Google Scholar] [CrossRef]
- Hendershot, B.D.; Wolf, E.J. Three-dimensional joint reaction forces and moments at the low back during over-ground walking in persons with unilateral lower-extremity amputation. Clin. Biomech. 2014, 29, 235–242. [Google Scholar] [CrossRef]
- Iosa, M.; Paradisi, F.; Brunelli, S.; Delussu, A.S.; Pellegrini, R.; Zenardi, D.; Paolucci, S.; Traballesi, M. Assessment of gait stability, harmony, and symmetry in subjects with lower-limb amputation evaluated by trunk accelerations. J. Rehabil. Res. Dev. 2014, 51, 623–634. [Google Scholar] [CrossRef]
- Lee, W.C.; Zhang, M.; Mak, A.F. Regional differences in pain threshold and tolerance of the transtibial residual limb: Including the effects of age and interface material. Arch. Phys. Med. Rehabil. 2005, 86, 641–649. [Google Scholar] [CrossRef]
- Highsmith, M.J.; Kahle, J.T.; Klenow, T.D.; Andrews, C.R.; Lewis, K.L.; Bradley, R.C.; Ward, J.M.; Orriola, J.J.; Highsmith, J.T. Interventions to manage residual limb ulceration due to prosthetic use in individuals with lower extremity amputation: A systematic review of the literature. Technol. Innov. 2017, 18, 115–123. [Google Scholar] [CrossRef]
- Glaister, B.C.; Bernatz, G.C.; Klute, G.K.; Orendurff, M.S. Video task analysis of turning during activities of daily living. Gait Posture 2007, 25, 289–294. [Google Scholar] [CrossRef]
- Ficanha, E.M.; Rastgaar, M. Preliminary design and evaluation of a multi-axis ankle-foot prosthesis. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics IEEE, Sao Paulo, Brazil, 12–15 August 2014; pp. 1033–1038. [Google Scholar]
- Dixon, P.C.; Pearsall, D.J. Gait Dynamics on a Cross-Slope Walking Surface. J. Appl. Biomech. 2010, 26, 17–25. [Google Scholar] [CrossRef]
- Damavandi, M.; Dixon, P.C.; Pearsall, D.J. Kinematic adaptations of the hindfoot, forefoot, and hallux during cross-slope walking. Gait Posture 2010, 32, 411–415. [Google Scholar] [CrossRef]
- Madusanka, D.G.K.; Wijayasingha, L.N.S.; Sanjeevan, K.; Ahamed, M.A.R.; Edirisooriya, J.C.W.; Gopura, R.A.R.C. A 3DOF transtibial robotic prosthetic limb. In Proceedings of the 7th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 22–24 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef]
- Moriguchi, C.; Sato, T.; Gil Coury, H. Ankle movements during normal gait evaluated by flexible electrogoniometer. Rev. Bras. Fisioter. 2007, 11, 205–211. [Google Scholar] [CrossRef]
- Ernst, M.; Altenburg, B.; Schmalz, T. Characterizing adaptations of prosthetic feet in the frontal plane. Prosthetics Orthot. Int. 2020, 44, 225–233. [Google Scholar] [CrossRef]
- Agboola-Dobson, A.; Wei, G.; Ren, L. Biologically Inspired Design and Development of a Variable Stiffness Powered Ankle-Foot Prosthesis. J. Mech. Robot. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Bellman, R.D.; Holgate, M.A.; Sugar, T.G. SPARKy 3: Design of an active robotic ankle prosthesis with two actuated degrees of freedom using regenerative kinetics. In Proceedings of the 2nd Biennial IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob.), Scottsdale, AZ, USA, 19–22 October 2008; pp. 511–516. [Google Scholar]
- Masum, H.; Bhaumik, S.; Ray, R. Conceptual Design of a Powered Ankle-foot Prosthesis for Walking with Inversion and Eversion. Procedia Technol. 2014, 14, 228–235. [Google Scholar] [CrossRef]
- Rad, N.F.; Yousefi-Koma, A.; Tajdari, F.; Ayati, M. Design of a novel three degrees of freedom ankle prosthesis inspired by human anatomy. In Proceedings of the 4th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 26–28 October 2016; pp. 428–432. [Google Scholar]
- Tsung-Han Hsieh, B.A. Design and Control of a Two-Degree-of-Freedom Powered Ankle-Foot Prosthesis. Master’s Thesis, Massachussetts Institutes of Technology, Cambridge, MA, USA, September 2019. [Google Scholar]
- Maitland, M.E.; Allyn, K.J.; Ficanha, E.; Colvin, J.M.; Wernke, M.M. Finite Element Simulation of Prosthetic Foot Adaptation to Mediolateral-Angled Cross-Slopes. JPO J. Prosthetics Orthot. 2020, 32, 236–244. [Google Scholar] [CrossRef]
- Maitland, M.E.; Allyn, K.J.; Ficanha, E.M.; Colvin, J.M.; Wernke, M.M. Finite Element Simulation of Frontal Plane Adaptation Using Full-Foot, Split-Toe, and Cam-Linkage Designs in Prosthetic Feet. J. Prosthetics Orthot. 2022, 34, 14–21. [Google Scholar] [CrossRef]
- Wernke, M.M.; Ficanha, E.M.; Thomas, Z.; Maitland, M.E.; Allyn, K.J.; Albury, A.; Colvin, J. Mechanical testing of frontal plane adaptability of commercially available prosthetic feet. J. Rehabil. Assist. Technol. Eng. 2022, 9, 20556683221123330. [Google Scholar] [CrossRef]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. A public dataset of overground and treadmill walking kinematics and kinetics in healthy individuals. PeerJ 2018, 6, e4640. [Google Scholar] [CrossRef]
- James Mahoney, M.E.; Stapleton, D.B.; Renner, K.; Puccinelli, A.; Vardaxis, V. Evaluation of the subtalar joint during gait using 3-D motion analysis: Does the STJ achieve neutral position? Foot Ankle Online J. 2019, 12, 157–163. [Google Scholar]
- Fogelberg, D.J.; Allyn, K.J.; Smersh, M.; Maitland, M.E. What People Want in a Prosthetic Foot: A Focus Group Study. JPO J. Prosthetics Orthot. 2016, 28, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Ma, X.; Chon, T.E.; Fernandez, J.; Gusztav, F.; Kovács, A.; Baker, J.S.; Gu, Y. New Insights Optimize Landing Strategies to Reduce Lower Limb Injury Risk. Cyborg Bionic Syst. 2024, 5, 0126. [Google Scholar] [CrossRef] [PubMed]
- Tabucol, J.; Kooiman, V.G.M.; Leopaldi, M.; Brugo, T.M.; Leijendekkers, R.A.; Tagliabue, G.; Raveendranathan, V.; Sotgiu, E.; Benincasa, P.; Oddsson, M.; et al. The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Appl. Sci. 2022, 12, 4575. [Google Scholar] [CrossRef]
- ISO. Available online: https://www.iso.org/standard/38708.html (accessed on 15 June 2021).
- Oliveira, L.F.; Simpson, D.M.; Nadal, J. Calculation of area of stabilometric signals using principal component analysis. Physiol. Meas. 1996, 17, 305–312. [Google Scholar] [CrossRef] [PubMed]
- Pillet, H.; Bonnet, X.; Lavaste, F.; Skalli, W. Evaluation of force plate-less estimation of the trajectory of the centre of pressure during gait. Comparison of two anthropometric models. Gait Posture 2010, 31, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M.R.; Pappas, I.P.I.; Nakazawa, K.; Keller, T.; Morari, M.; Dietz, V. Stability criterion for controlling standing in able-bodied subjects. J. Biomech. 2000, 33, 1359–1368. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Tabucol, J.; Brugo, T.M.; Povolo, M.; Leopaldi, M.; Oddsson, M.; Carloni, R.; Zucchelli, A. Structural fea-based design and functionality verification methodology of energy-storing-and-releasing prosthetic feet. Appl. Sci. 2022, 12, 97. [Google Scholar] [CrossRef]
- ISO. Available online: https://www.iso.org/standard/69821.html (accessed on 30 May 2021).
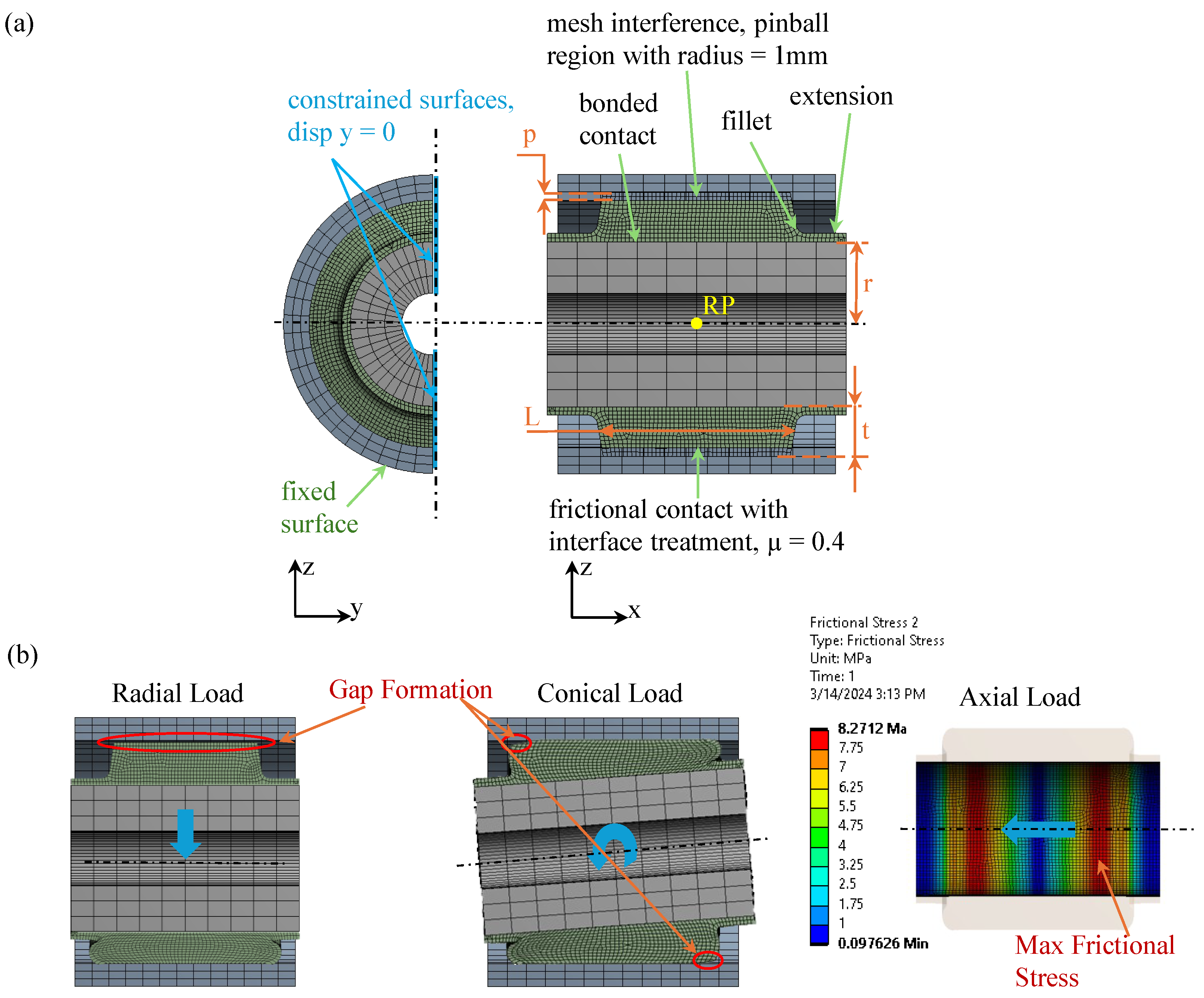
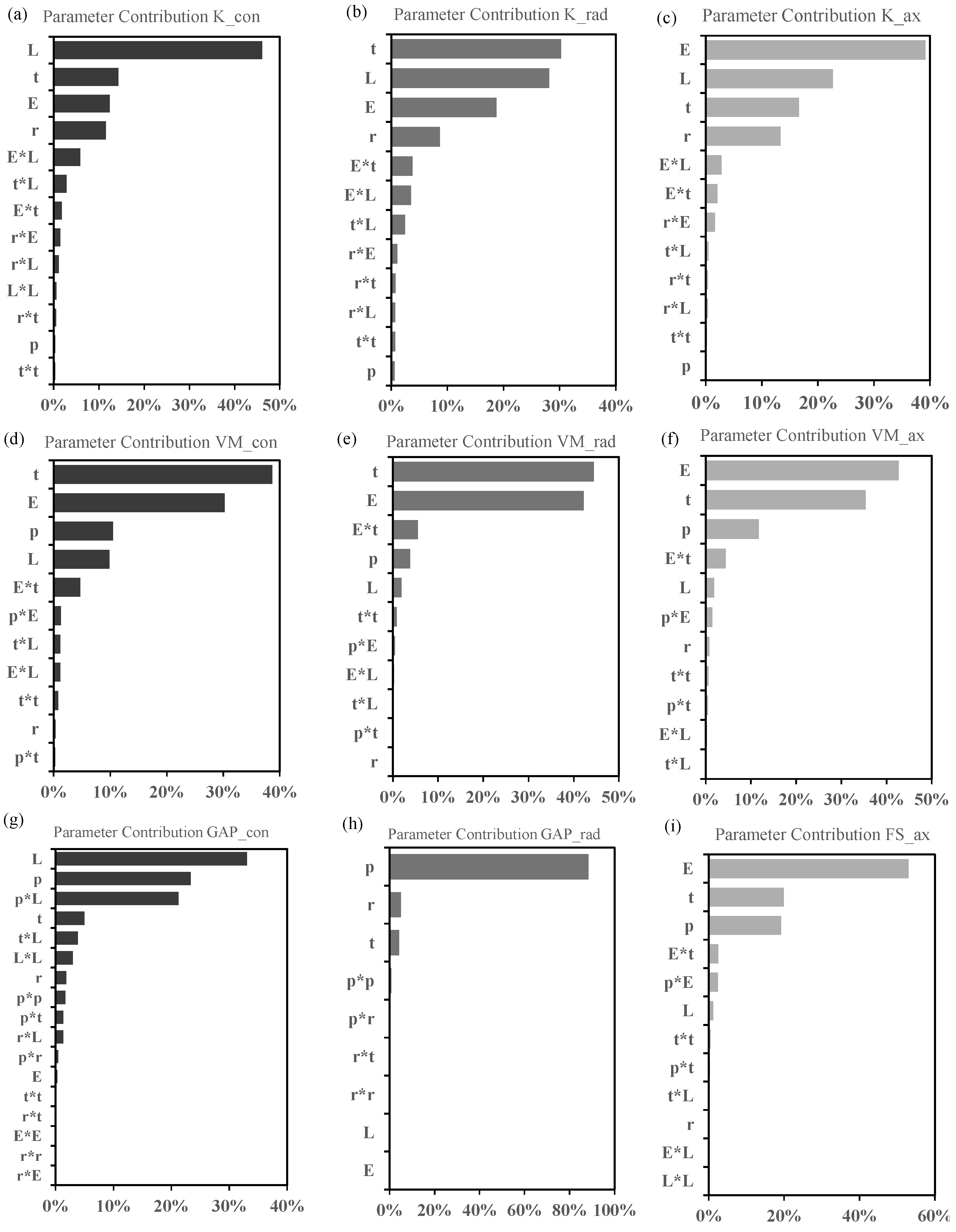




| Parameter | Units | Values |
|---|---|---|
| Pre-compression (p) | mm | 0.5, 0.6, 0.7, 0.8, 0.9 |
| Radius (r) | mm | 6, 7, 9, 11, 12 |
| Young’s Modulus (E) | MPa | 8, 12, 16, 20, 24 |
| Thickness (t) | mm | 3, 3.5, 4.5, 5.5, 6 |
| Length (L) | mm | 12, 14, 18, 22, 24 |
| Prosthesis | Sagittal Plane | Cross-Slope Adaptation |
|---|---|---|
| MyFlex-η | D 19 / P 9 | I 7.2 / E 6.8 |
| MyFlex-δ | D 20 / P 7 | I 4.1 / E 3.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leopaldi, M.; Brugo, T.M.; Tabucol, J.; Zucchelli, A. Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis. Prosthesis 2024, 6, 726-743. https://doi.org/10.3390/prosthesis6040051
Leopaldi M, Brugo TM, Tabucol J, Zucchelli A. Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis. Prosthesis. 2024; 6(4):726-743. https://doi.org/10.3390/prosthesis6040051
Chicago/Turabian StyleLeopaldi, Marco, Tommaso Maria Brugo, Johnnidel Tabucol, and Andrea Zucchelli. 2024. "Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis" Prosthesis 6, no. 4: 726-743. https://doi.org/10.3390/prosthesis6040051
APA StyleLeopaldi, M., Brugo, T. M., Tabucol, J., & Zucchelli, A. (2024). Parametric Design of an Advanced Multi-Axial Energy-Storing-and-Releasing Ankle–Foot Prosthesis. Prosthesis, 6(4), 726-743. https://doi.org/10.3390/prosthesis6040051








