Abstract
Registries have significant roles in assessing the comparative performance of devices. Ideally, early identification of outliers should use a time-to-event outcome while reducing the confounding effects of other components in the device and patient characteristics. Machine learning (ML), which contains self-learning algorithms, is one approach to consider many variables simultaneously to reduce the impact of confounding. The principal objective of this study was to investigate the effectiveness of using either random survival forest (RSF) or regularised/unregularised Cox regression to account for patient and associated device confounding factors in comparison with current standard techniques. This study evaluated RSF and regularised/unregularised Cox regression using data from the Australian Orthopaedic Association National Joint Replacement Registry (AOANJRR) to detect outlier devices among 213 individual primary total hip components performed in 163,356 primary procedures from 1 January 2015 to the end of 2019. Device components and patient characteristics were the inputs, and time to first revision surgery was the primary outcome treated as a censored case for death. The effectiveness of the ML approaches was assessed based on the ability to detect the outliers identified by the AOANJRR standard approach. In the study cohort, the standardised AOANJRR approach identified three acetabular components and seven femoral stems as outliers. The ML approaches identified some but not all the outliers detected by the AOANJRR. Both the methods identified three of the same femoral stems, and the RSF identified the other five components, including two of the same acetabular cups and three of the same femoral stems. In addition, both the RSF and Cox techniques detected a number of additional device components that were not previously identified by the standard approach. The results showed that ML may be able to offer a supplementary approach to enhance the early identification of outlier devices. Random survival forest was a more comparable technique to the AOANJRR standard than the Cox regression, but further studies are required to better understand the potential of ML to improve the early identification of outliers.
1. Introduction
Given their widespread use and the presence of underperforming prostheses, total hip arthroplasty devices are among the most relevant medical devices with a lack of pre- and post-market safety assurances [1,2]. It is known that there is variation in the safety and effectiveness of hip device components [3,4]. While most prostheses perform acceptably, some of them may have higher than anticipated rates of revision. This variability underlines the need for attentive post-market surveillance of hip prostheses for the early detection of poor-performing components within the community [5,6,7]. National arthroplasty registries have played a critically important role in the identification of these devices that are performing poorly [8,9,10,11,12,13]. Data collected and reported by registries exposed the problem and led to the identification of prostheses with higher than anticipated revision rates, called outliers.
There is growing agreement by the community that large-scale multinational evaluations of devices using data from all joint registries are essential for determining if a device is at an increased risk of revision [14,15]. The Australian Orthopaedic Association National Joint Replacement Registry (AOANJRR) has established an effective multistep approach to inform surgeons about the relative performance of prostheses [8]. Arthroplasty devices are composed of multiple components combined in a prosthesis construct to ensure the success of the procedure. Femoral stems and acetabular components are two major components, and revision surgery may mostly occur due to the failure in one or both of these total hip components. Identifying specific components that show an increased risk of revision surgery is challenging, as there are numerous individual components that are used in different combinations.
An initial screening can effectively flag the hip components but may not account for revision rate variations over time [7]. This causes difficulties in detecting a difference if the higher risk of revision happens later in the follow-up time [16]. The method also does not address the possibility of other confounding factors due to device and patient variables. Ideally, a method should be able to identify individual components with an increased risk of revision surgery using a time-to-event endpoint while also limiting the confounding effects of device and patient characteristics in other components. Machine learning (ML) methods are appealing for this type of problem because they are able to handle high-dimensional data, which conventional methods generally cannot. In addition, ML methods address the added complexity introduced by confounding effects. This paper aims to evaluate the use of ML methods for surveillance of primary total hip arthroplasty components. Moreover, it aims to explore the additional primary components that could be potentially detected by ML methods when compared to conventional techniques. The effectiveness of ML methods was determined based on their ability to detect the same outlier prostheses identified by the AOANJRR gold standard.
2. Materials and Methods
The dataset for this research consists of 163,356 primary total conventional hip procedures with a primary diagnosis of osteoarthritis (OA). It is noted that the other primary diagnoses were excluded from this study. The study period was 1 January 2015—when the registry commenced collection of body mass index (BMI) data—to 31 December 2019. The restriction to procedures only for OA accounted for 88.2% of all surgeries over this period. There were 87 acetabular components and 126 femoral stems made by various manufacturers [8]. Patient factors and device components were the predictors, and the elapsed time from primary procedure to first revision was the outcome.
Each device component was distinctly introduced with an indicator variable that showed its model name. Patient covariates comprised of age, gender, BMI, and American Society of Anesthesiologists (ASA) score were treated as potential confounders. Gender and ASA score (less than 3 vs. greater than or equal to 3) were patient covariates with two levels; age (<65, 65–74, and ≥75 years) and BMI (<25, 25–29.9, and ≥30) were classified into three levels. Head size (≤32 mm vs. >32 mm) and bearing surface (modern vs. non-modern) were also categorised as potential confounding variables, with each of the variables divided into two ordinal groups (Table 1).

Table 1.
Descriptive information on patient- and device-related covariates.
Modern bearings are defined as metal or ceramic heads on cross-linked polyethylene and mixed ceramic-on-ceramic. The covariates were selected to control the impacts of relatively few patient characteristics and implant types (i.e., bearing surface, femoral head size) [17]. Missing data were mostly present for the patient covariates (6.35% BMI and 0.41% ASA score) and were handled by multiple imputations using chained equations [18]. Death was treated as a censored case with survival time up to the quit date of the study sample. Patients who did not experience a revision or death had survival times based on their initial implantations and the end of follow-up.
The effectiveness of the ML techniques was assessed to account for patient and associated device confounding factors to the AOANJRR gold standard (first and second stages). The first stage (initial screening test) was done by comparing the revision rate of individual prostheses to twice the average revision rate of all other prostheses that belong to the same broad device class. In addition, the impact of confounding factors was examined by calculating age- and gender-adjusted hazard ratios (HRs) to check if there was a significant difference compared to the combined hazard rate of the comparator group.
The research was conducted according to the ethical principles of the Helsinki Declaration II. The Southern Adelaide Clinical Human Research Ethics Committee provided ethical approval for this study (No. 485.13).
3. ML Statistical Analyses
As the concept of variable selection differs from prediction, ML models need to be trained with a careful selection of hyperparameters. Two feature selection techniques were conducted to explore the significance of inputs and find their contributions effectively in the presence of confounding effects.
For the first approach, we used random survival forest (RSF) as an extension of the random forest algorithm to analyse right-censored survival data [19,20]. Large forests with a group of 2000 trees were used to reduce bias in the highly correlated structure. Each tree of the forest was grown by repetitively performing binary splits of the AOANJRR data using the log-rank test until terminal nodes had no fewer than two revisions [21]. A random set of variables including all device components and covariates were chosen as candidates to split each parent node into two daughter nodes. It is more appropriate to develop the model such that the chance of having substantial variations between variables increases. Each tree needed to be grown deep to have as many levels as possible without limiting the node depth. Variable selection was randomised with the use of the parameter “1 <= mtry <= P”, which was fixed at “P/4” [3]. The number of variables considered at each split was larger than convention (√P) because the bias in variable selection with correlated inputs can be limited by increasing the number of variables considered at each split [22]. A backward selection procedure was then implemented to obtain a reduced set of informative variables by computing a new RSF with the remaining variables. A similar algorithm was suggested by Ishwaran et al. [23] and Dietrich et al. [24]. Rankings of variables are based on minimal depth [25]. In a tree, minimal depth is the distance from the tree’s root node to the node where a variable is first split. The distance for each variable is recorded based on an average taken over all trees, and shorter distances denote variables with stronger effects. A threshold of 0.05 was used for permutation p-values to determine whether the minimal depth of a component exceeded chance [3,26]. Given the small number of permutations performed due to the high computational cost, p-values based on a false discovery rate (FDR) adjustment were not calculated.
The second approach was applied using a combination of ML and a well-recognised conventional regression method. A regularised model with a mixture of L1 (lasso) and L2 (ridge) penalties was used to select a subset of components that are most predictive of survival [27,28]. The extent of the penalties was determined based on choosing a priori value for a parameter (α = 0.5; α ranges from 0 to 1). This is midway between lasso and ridge regression called elastic net. The parameter that specified model complexity–lambda—was chosen using 10-fold cross-validation [27]. No penalty was applied to patient covariates in the model according to a tendency to fully control the effects of relatively few patient characteristics (including age, gender, BMI, and ASA). The regularised Cox model does not report p-values because it does not test variables against null hypotheses. The variables selected by the elastic net were then entered to an unregularised Cox proportional hazards model. The reported p-values are based on a Wald test; the p-values that maintain the FDR at 0.05 were also calculated using the variables selected by the elastic net [29]. The FDR at 0.05 is a much less conservative approach and adjusts for more actual p-value distribution when 5% of all declared positive variables are genuinely negative. R statistical software was used for all analyses, glmnet [30] version 4.1-1 for Cox elastic net, the survival package [31] version 3.2-11 for unregularised Cox regression, randomForestSRC [18] version 2.11.0 for RSF, and MICE package version 3.14.0 for multiple imputations [32].
4. Results
Prostheses survival for 163,356 procedures recorded by the AOANJRR and the yearly number at risk were provided over the study period (Figure 1 and Table 2). The majority of patients had an ASA score of less than 3 (63.47%), were female (53.25%), had an age from 65 to 74 years (36.42%), and had a BMI greater than or equal to 30 kg/m2 (38.86%). In the study cohort, the AOANJRR standardised approach identified three acetabular components and seven femoral stems. It should be noted that the registry did not report a number of these devices at the time of preparing this article due to other confounding effects. However, their continual real-time performance was monitored within the community.
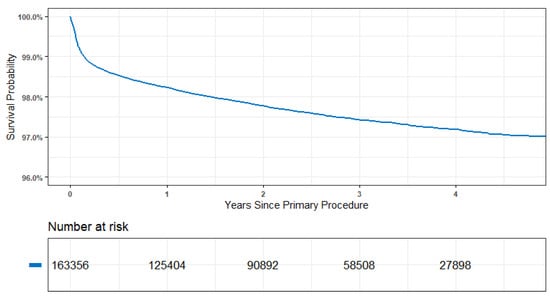
Figure 1.
Time to first revision for 163,356 procedures of AOANJRR data.

Table 2.
Individual outliers identified by the first and second stages of the AOANJRR standard.
The devices IV, V, and VIII were identified using both approaches, and the only undetected components were II and VI (Table 3). The random survival was able to identify eight out of ten outliers identified by the standard. These components included the acetabular I and III and the femoral stems IV, V, VII, VIII, IX, and X. In the case of RSF, a smaller average minimal depth meant more contribution to the prosthesis surveillance. However, given that the exact p-values are unknown, these ranks may not be directly associated with the comparative performance of the components used.

Table 3.
Results for the outliers by the ML methods.
Both the RSF and Cox techniques detected additional device components that were not previously identified by the standardised approach. A number of these devices with at least 10 observations exceeded 1.5 times the revision rate for other contemporary total hip prostheses with a significant difference in HRs (Table 4). The femoral stem XIV was detected by both of the techniques, and the other three components were identified only by one of the approaches.

Table 4.
Results for the additional device components detected by ML.
Given a primary desire to control potential confounding factors, the extent of patient and associated device confounding was evaluated. The coefficients in a Cox regression are related to the HRs of device components given by the exponent of their coefficient. This study compared the HRs for specific components in two models: (a) regularised Cox model with a variable indicating the use of that component adjusted for age and gender (2nd stage of the standard) and (b) unregularised Cox model, which included all the variables selected by the elastic net. This represents the effect of each component after conditioning on the selected variables, including age, gender, BMI, ASA, head size, and bearing surface. Therefore, the difference in the HRs between these two models presents the extent of potential confounding (Figure 2). There was at least reasonable evidence of confounding for most components; relative differences in model coefficients ranged from 38% for Device V to 204% for Device II.
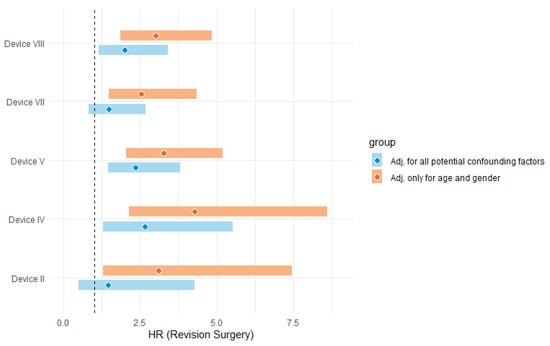
Figure 2.
HR comparison to illustrate the effect of potential confounding (dash line presents HR = 1). Note. %Diff = [ln (HRAdj. for age and gender) − ln (HRAdj. for all potential confounding factors)]/[ln (HRAdj. for all potential confounding factors)].
5. Discussion
Our study showed that the RSF feature selection technique was more comparable to the AOANJRR standard in terms of detecting more outlier prostheses. Of the ten outliers identified by the AOANJRR gold standard, ML was able to identify eight of the same device components, including two acetabular cups and six femoral stems. The group of prostheses detected by both selection techniques included IV, V, and VIII. By contrast, two out of the ten listed components were not identified by either RSF or Cox. The outcome highlights the significance of studying potential confounding effects on the comparative performance of primary total hip prostheses.
The ML methods explored can be effective at detecting outliers. However, a single model may not necessarily be the best choice because the inclusion or exclusion of inputs may affect the strength and even sign of a given predictor. For tree growing, RSF uses random subsets of variables per node that may cause an independent split of correlated variables. This may lead to breaking the structure of highly correlated predictors and providing an interesting approach for explorative variable-selection studies [33]. However, false-positive discoveries due to overfitting are considered to be a major problem [34]. On the other hand, the Cox regression has a significant advantage in terms of computational cost, interpreting variable strength, and documenting confounding effects.
Feature selection may be able to offer a supplementary approach to the initial screening of arthroplasty devices with the potential to identify most of the devices detected by the AOANJRR standardised approach. This similarity in the results becomes more apparent when we look at the outliers reported by the registry after meeting all three stages of the standardised approach due to further investigation of confounding factors. The AOANJRR did not report on the non-detected devices (II and VI). However, the three components identified by both techniques were detected considering larger sample sizes and over longer times [8]. These identified femoral stems included Emperion, Furlong Evolution, and MiniMax total conventional hip prostheses. The current approach used by the registry is effective at identifying the relative performance of prostheses with a higher risk of revision through in-depth knowledge of potential confounding factors.
The current study has several limitations. One important consideration is that the success of the screening process relies on identifying relevant component characteristics. The process will be compromised if some attributes that contribute to prosthesis survival are not accounted for. This study included well-known clinically relevant attributes; head size showed the most significant contribution to the initial screening of total hip devices. However, other factors correlated to surgeons and catalogue ranges could also be investigated. The contrary may be a concern as well; considering too many attributes may cause delayed detection. One possibility to address this issue is to expand the dataset by involving several registries worldwide that have information on the same prostheses. As a research opportunity, the proposed methods can be applied to knee and shoulder arthroplasty devices. Utilising prediction to understand the variables linked with the outcome may improve shared decision making, leading to fewer patients at risk of receiving poor devices.
6. Conclusions
Machine learning may be able to offer a supplementary approach to enhance the early identification of outlier devices within the community. Our study showed that the RSF technique was more comparable to the AOANJRR standardised approach for the initial screening of total hip devices. Further studies are required to better understand the potential of feature selection techniques to improve the early assessment of total hip outlier prostheses.
Author Contributions
K.G.: Writing—original draft, Methodology, Investigation, Formal analysis. S.G.: Writing—review & editing, Supervision, Methodology. R.d.S.: Writing—review & editing, Supervision, Methodology. N.P.: Writing—review & editing, Supervision, Methodology. L.B.S.: Writing—review & editing, Supervision. M.T.: Writing—review & editing, Supervision. R.H.: Writing—review & editing, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting the conclusions of this article will be made available by the authors upon request.
Acknowledgments
We acknowledge the AOANJRR for assisting in the study design and statistical analyses, in addition to the patients, surgeons, and hospitals whose data made this research possible.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pivec, R.; Johnson, A.J.; Mears, S.C.; Mont, M.A. Hip arthroplasty. Lancet 2012, 380, 1768–1777. [Google Scholar] [CrossRef] [PubMed]
- Learmonth, I.D.; Young, C.; Rorabeck, C. The operation of the century: Total hip replacement. Lancet 2007, 370, 1508–1519. [Google Scholar] [CrossRef] [PubMed]
- Cafri, G.; Graves, S.E.; Sedrakyan, A.; Fan, J.; Calhoun, P.; de Steiger, R.N.; Cuthbert, A.; Lorimer, M.; Paxton, E.W. Postmarket surveillance of arthroplasty device components using machine learning methods. Pharmacoepidemiol. Drug Saf. 2019, 28, 1440–1447. [Google Scholar] [CrossRef] [PubMed]
- Anand, R.; Graves, S.E.; de Steiger, R.N.; Davidson, D.C.; Ryan, P.; Miller, L.N.; Cashman, K. What is the benefit of introducing new hip and knee prostheses? J Bone Jt. Surg Am. 2011, 93 (Suppl. 3), 51–54. [Google Scholar] [CrossRef]
- Shah, J.S.; Maisel, W.H. Recalls and safety alerts affecting automated external defibrillators. JAMA 2006, 296, 655–660. [Google Scholar] [CrossRef]
- Resnic, F.S. Postmarketing surveillance of medical devices—Filling in the gaps. N. Engl. J. Med. 2012, 366, 875. [Google Scholar] [CrossRef]
- Steiger, R.N.d.; Miller, L.N.; Davidson, D.C.; Ryan, P.; Graves, S.E. Joint registry approach for identification of outlier prostheses. Acta Orthop. 2013, 84, 348–352. [Google Scholar] [CrossRef]
- Australian Orthopaedic Association National Joint Replacement Registry (AOANJRR). Hip, Knee & Shoulder Arthroplasty: 2020 Annual Report; AOA: Adelaide, Australia, 2020. [Google Scholar]
- Mäkelä, K.; Hailer, N.P. Different, yet strong together: The Nordic Arthroplasty Register Association (NARA). Acta Orthop. 2021, 92, 635–637. [Google Scholar] [CrossRef]
- American Joint Replacement Registry. American Joint Registry 2020 Annual Report; American Joint Replacement Registry: Adelaide, Australia, 2020. [Google Scholar]
- Swedish Hip Arthroplasty Register. Swedish Hip Arthroplasty Register Annual Report; Swedish Hip Arthroplasty Register: Gothenburg, Sweden, 2019. [Google Scholar]
- Guccione, A.A.; Felson, D.T.; Anderson, J.J.; Anthony, J.M.; Zhang, Y.; Wilson, P.; Kelly-Hayes, M.; Wolf, P.A.; Kreger, B.E.; Kannel, W.B. The effects of specific medical conditions on the functional limitations of elders in the Framingham Study. Am. J. Public Health 1994, 84, 351–358. [Google Scholar] [CrossRef]
- The Norwegian Arthroplasty Registry. Annual Report; The Norwegian Arthroplasty Registry: Bergen, Norway, 2020. [Google Scholar]
- Krucoff, M.W.; Sedrakyan, A.; Normand, S.-L.T. Bridging Unmet Medical Device Ecosystem Needs with Strategically Coordinated Registries Networks. Jama 2015, 314, 1691–1692. [Google Scholar] [CrossRef]
- Sedrakyan, A.; Campbell, B.; Graves, S.; Cronenwett, J.L. Surgical registries for advancing quality and device surveillance. Lancet 2016, 388, 1358–1360. [Google Scholar] [CrossRef] [PubMed]
- Hardoon, S.; Lewsey, J.; Gregg, P.; Reeves, B.; van der Meulen, J. Continuous monitoring of the performance of hip prostheses. J. Bone Jt. Surg. Br. Vol. 2006, 88, 716–720. [Google Scholar] [CrossRef]
- Paxton, E.W.; Cafri, G.; Nemes, S.; Lorimer, M.; Kärrholm, J.; Malchau, H.; Graves, S.E.; Namba, R.S.; Rolfson, O. An international comparison of THA patients, implants, techniques, and survivorship in Sweden, Australia, and the United States. Acta Orthop. 2019, 90, 148–152. [Google Scholar] [CrossRef] [PubMed]
- Ishwaran, H.; Kogalur, U.B.; Kogalur, M.U.B. Package ‘randomForestSRC’. Breast 2021, 6, 1–132. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Schmid, M.; Wright, M.N.; Ziegler, A. On the use of Harrell’s C for clinical risk prediction via random survival forests. Expert Syst. Appl. 2016, 63, 450–459. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Ishwaran, H.; Kogalur, U.B.; Chen, X.; Minn, A.J. Random survival forests for high-dimensional data. Stat. Anal. Data Min. ASA Data Sci. J. 2011, 4, 115–132. [Google Scholar] [CrossRef]
- Dietrich, S.; Floegel, A.; Troll, M.; Kühn, T.; Rathmann, W.; Peters, A.; Sookthai, D.; Von Bergen, M.; Kaaks, R.; Adamski, J. Random Survival Forest in practice: A method for modelling complex metabolomics data in time to event analysis. Int. J. Epidemiol. 2016, 45, 1406–1420. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Gorodeski, E.Z.; Minn, A.J.; Lauer, M.S. High-dimensional variable selection for survival data. J. Am. Stat. Assoc. 2010, 105, 205–217. [Google Scholar] [CrossRef]
- Cafri, G.; Calhoun, P.; Fan, J. High dimensional variable selection with clustered data: An application of random multivariate survival forests for detection of outlier medical device components. J. Stat. Comput. Simul. 2019, 89, 1410–1422. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [PubMed]
- Therneau, T.M.; Grambsch, P.M.; Therneau, T.M.; Grambsch, P.M. The Cox Model; Springer: New York, NY, USA, 2000. [Google Scholar]
- Van Buuren, S.; Groothuis-Oudshoorn, K.J. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Siroky, D.S. Navigating random forests and related advances in algorithmic modeling. Stat. Surv. 2009, 3, 147–163. [Google Scholar] [CrossRef]
- Broadhurst, D.I.; Kell, D.B. Statistical strategies for avoiding false discoveries in metabolomics and related experiments. Metabolomics 2006, 2, 171–196. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).