Finite Element Analysis of Zirconia Dental Implant
Abstract
:1. Introduction
2. Materials and Methods
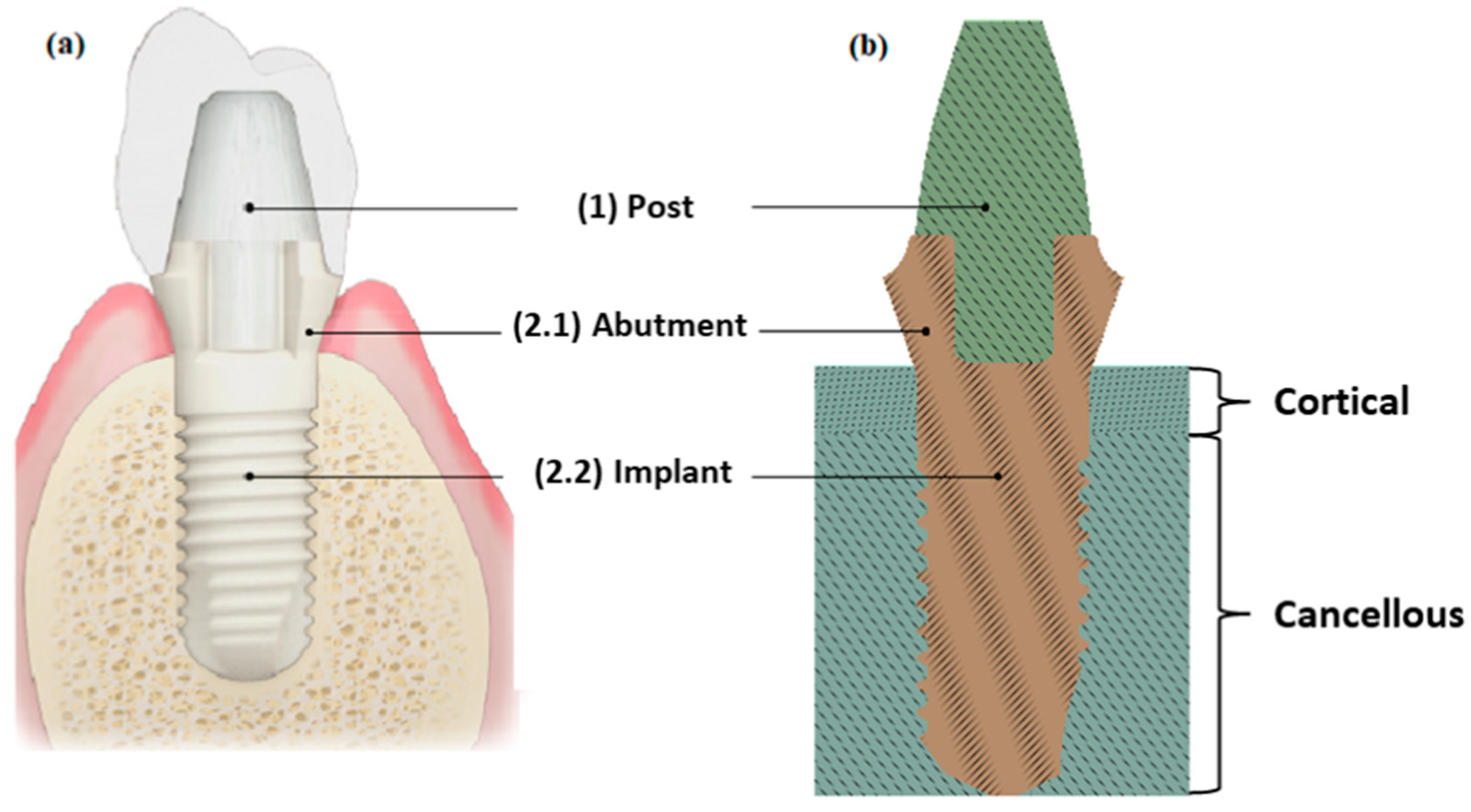
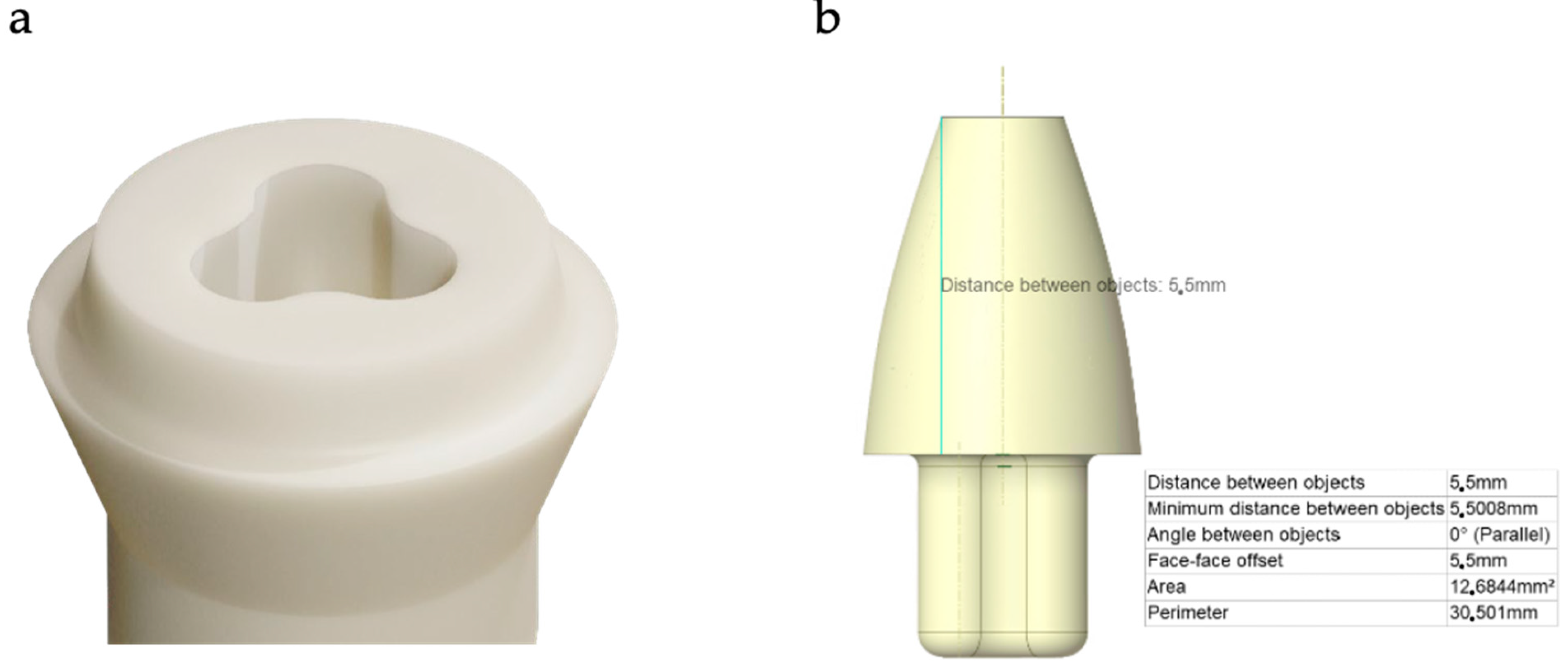
2.1. Materials
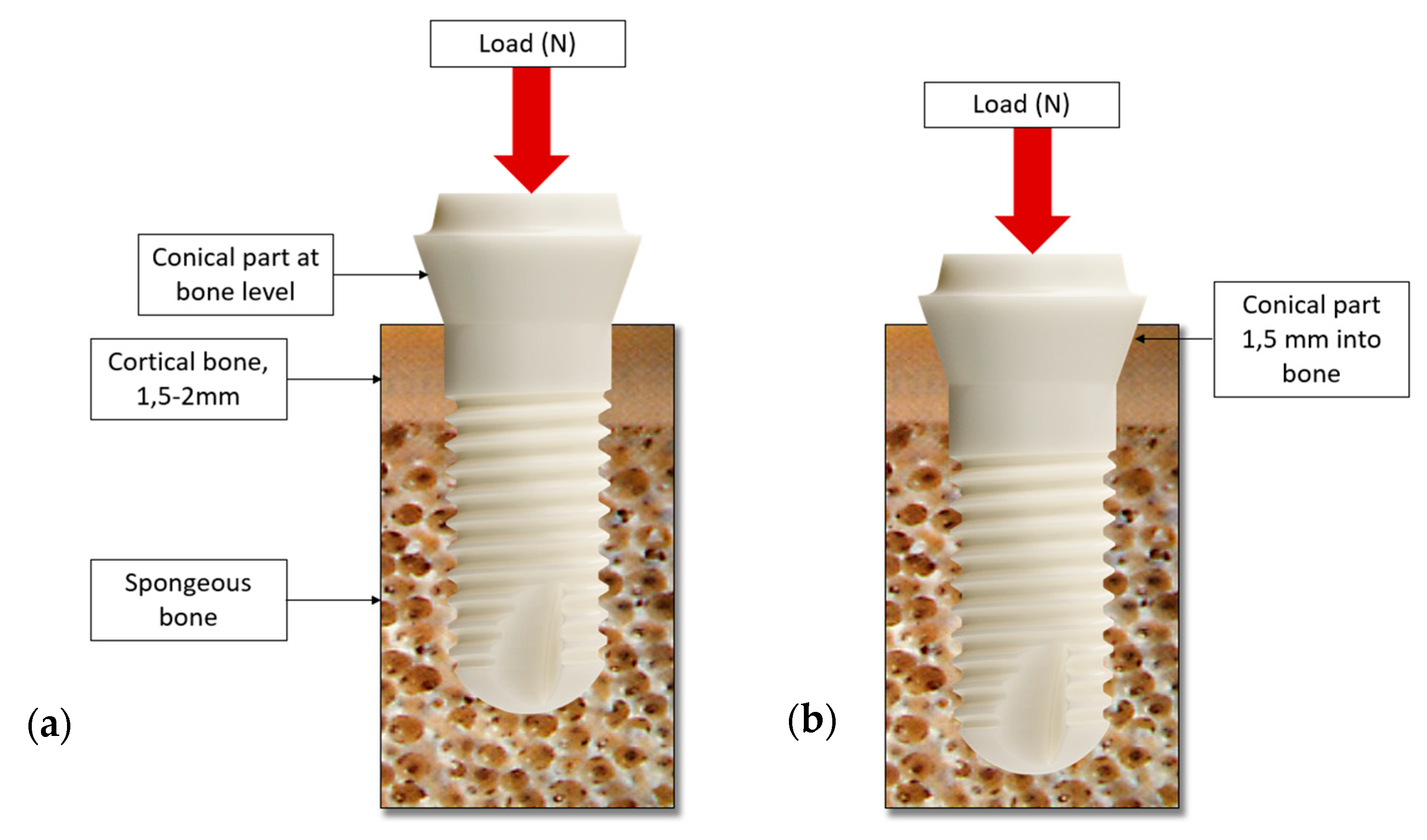
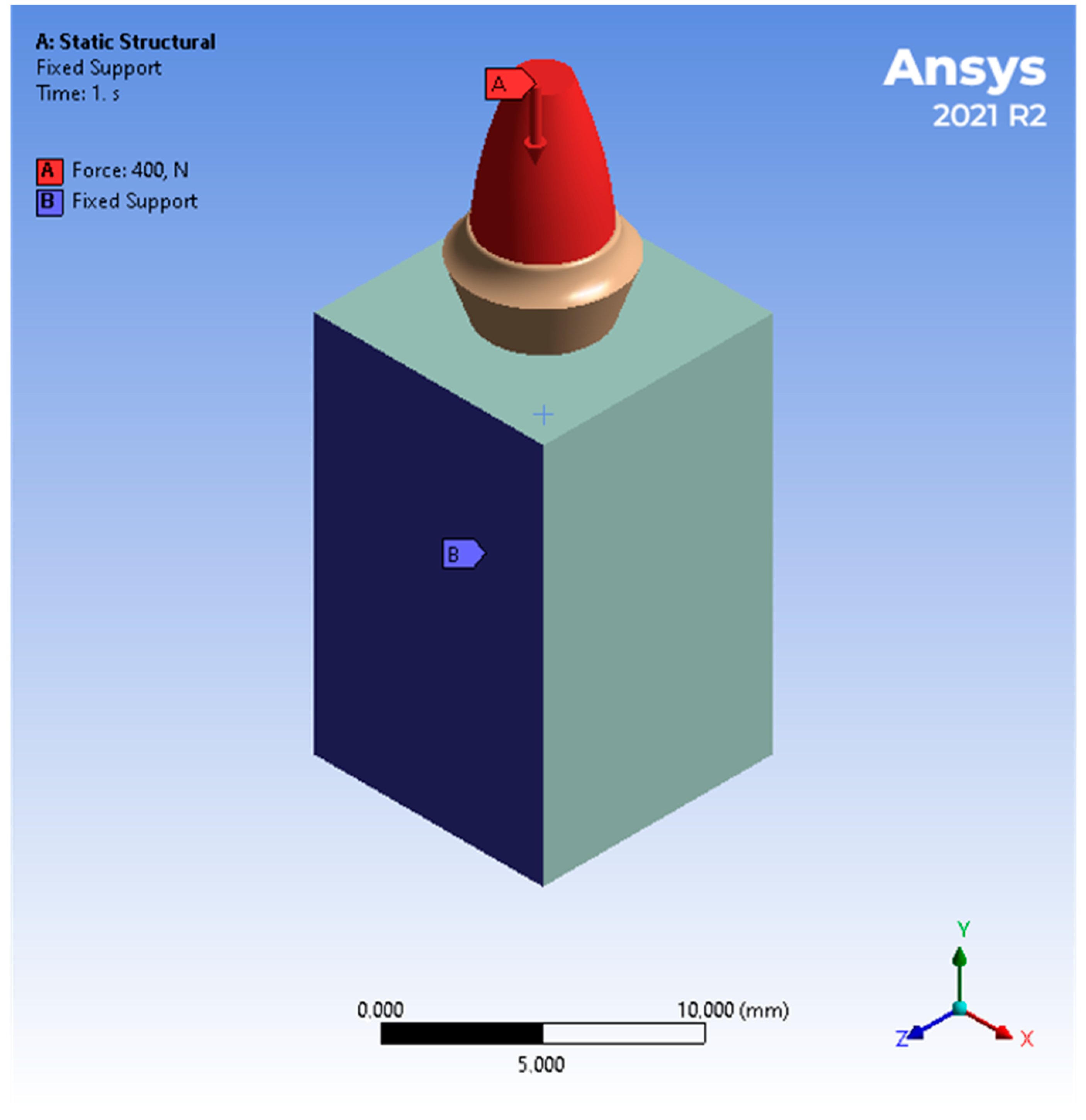
2.2. Boundary Conditions
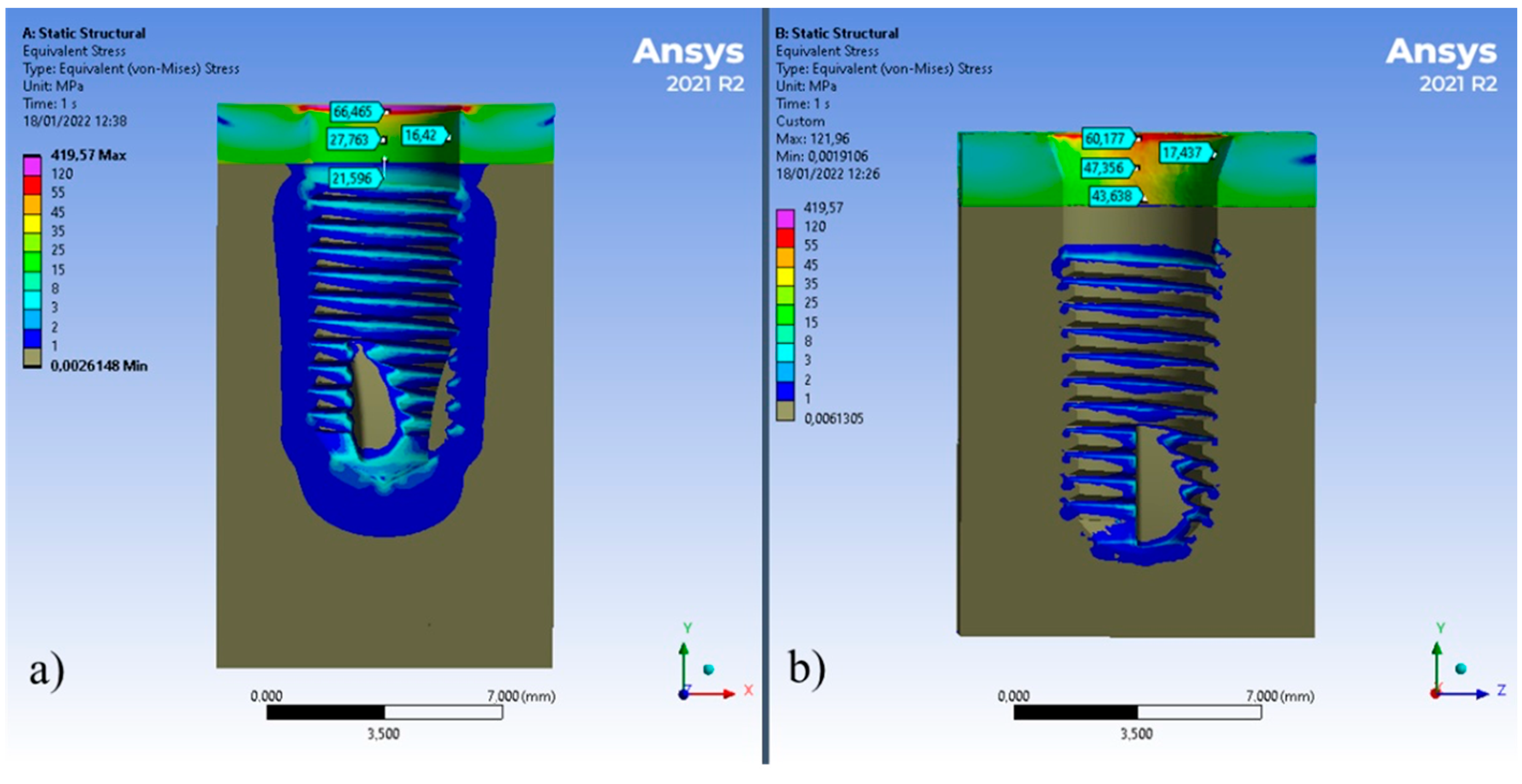
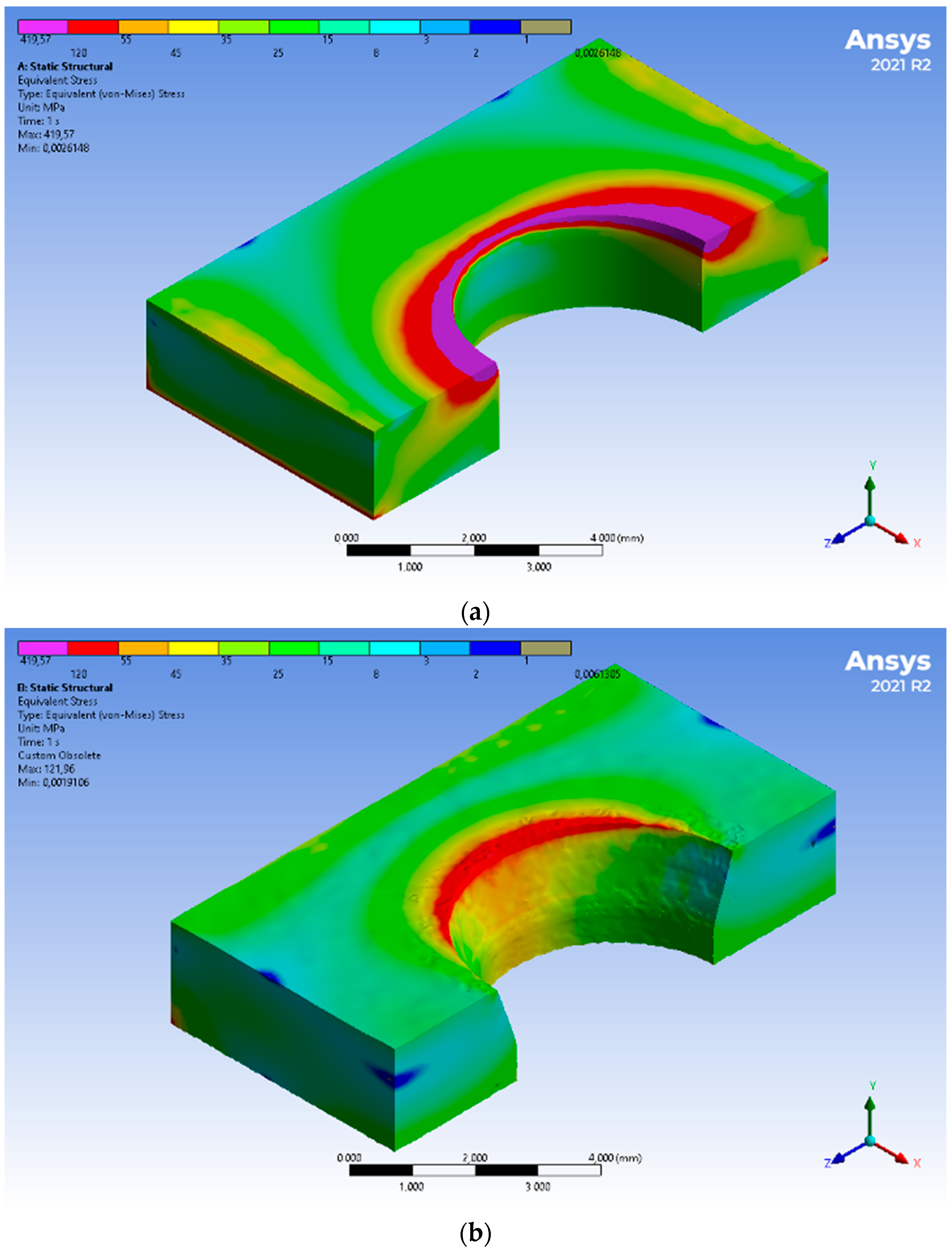
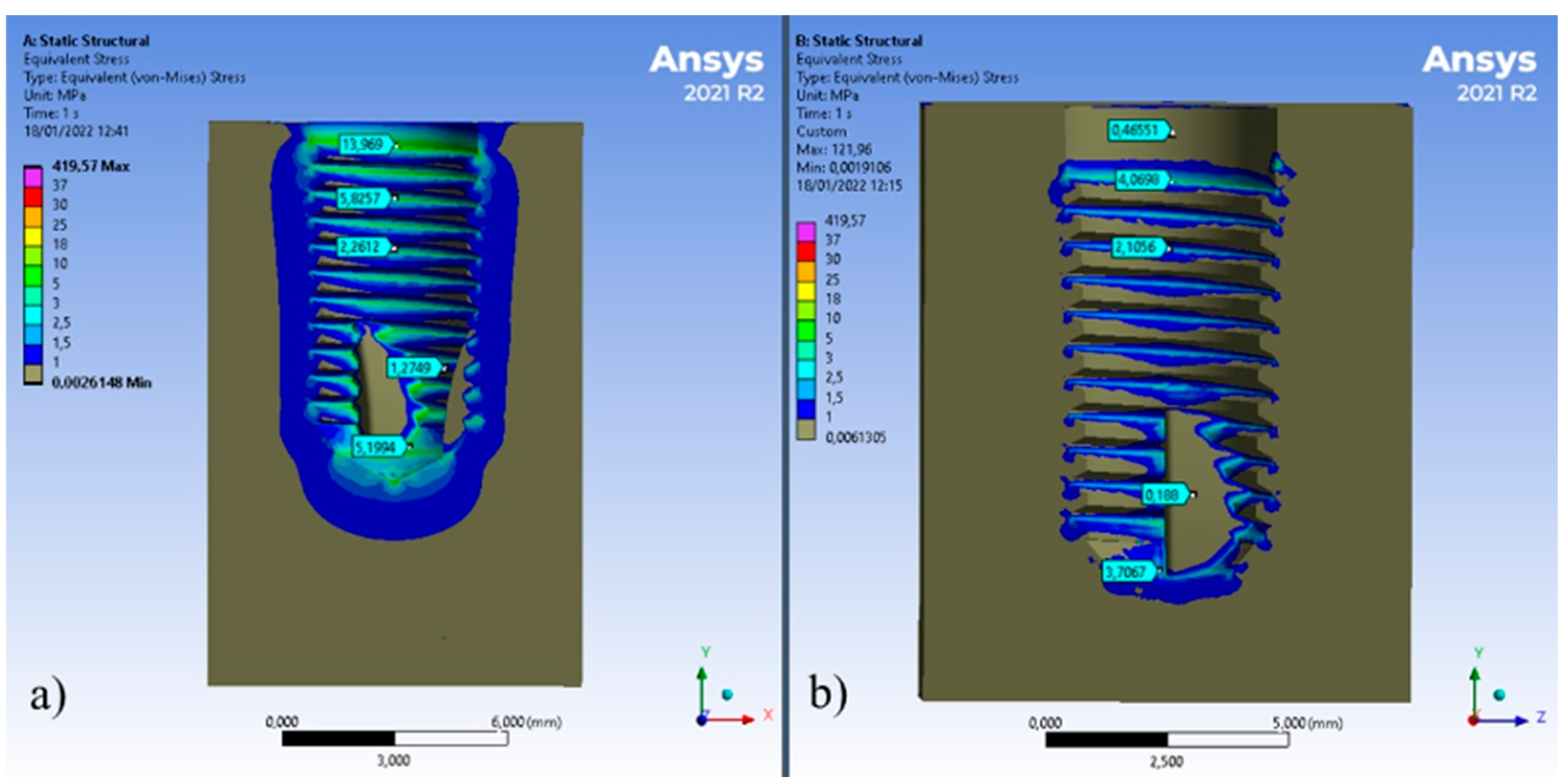
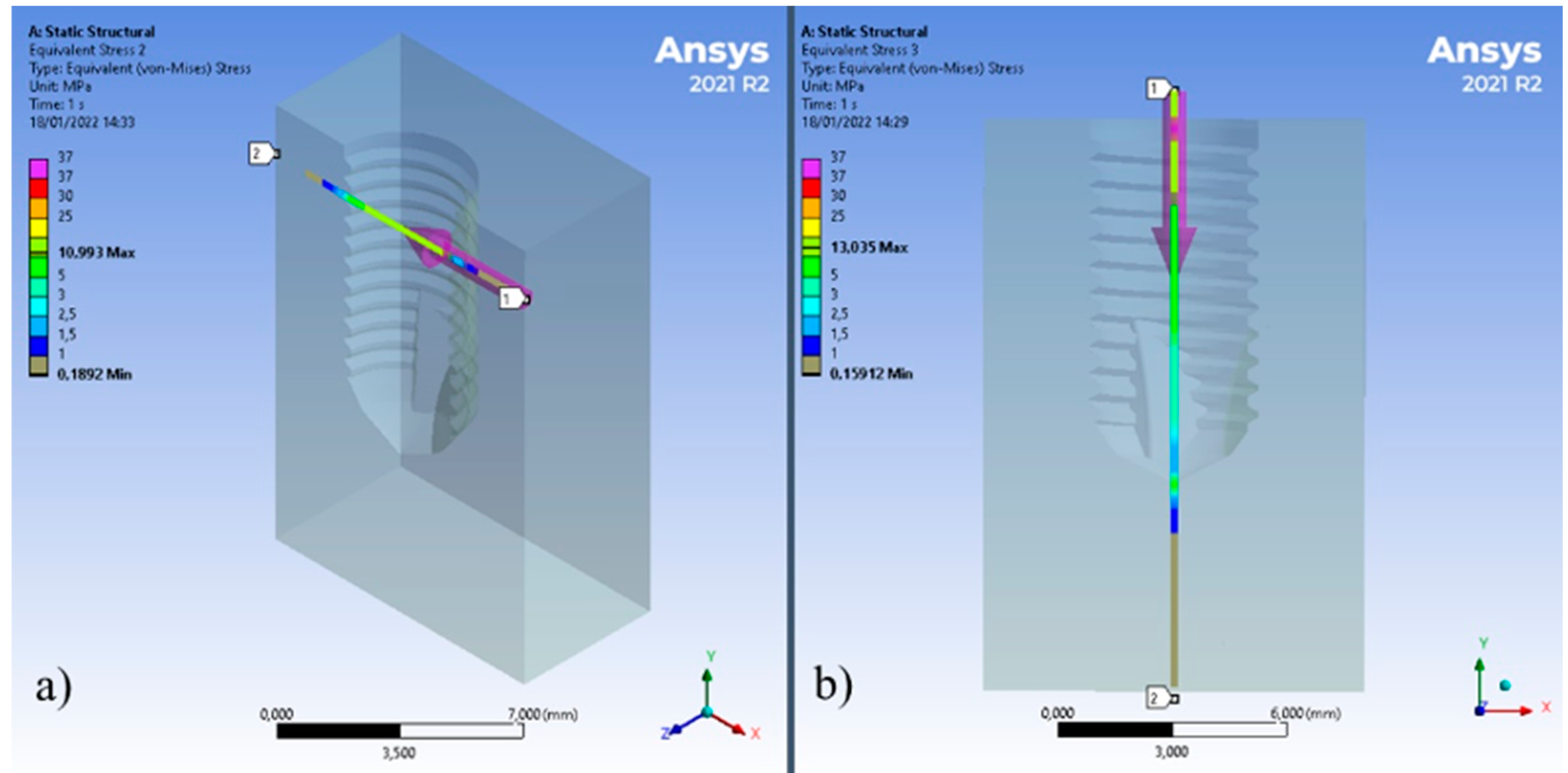
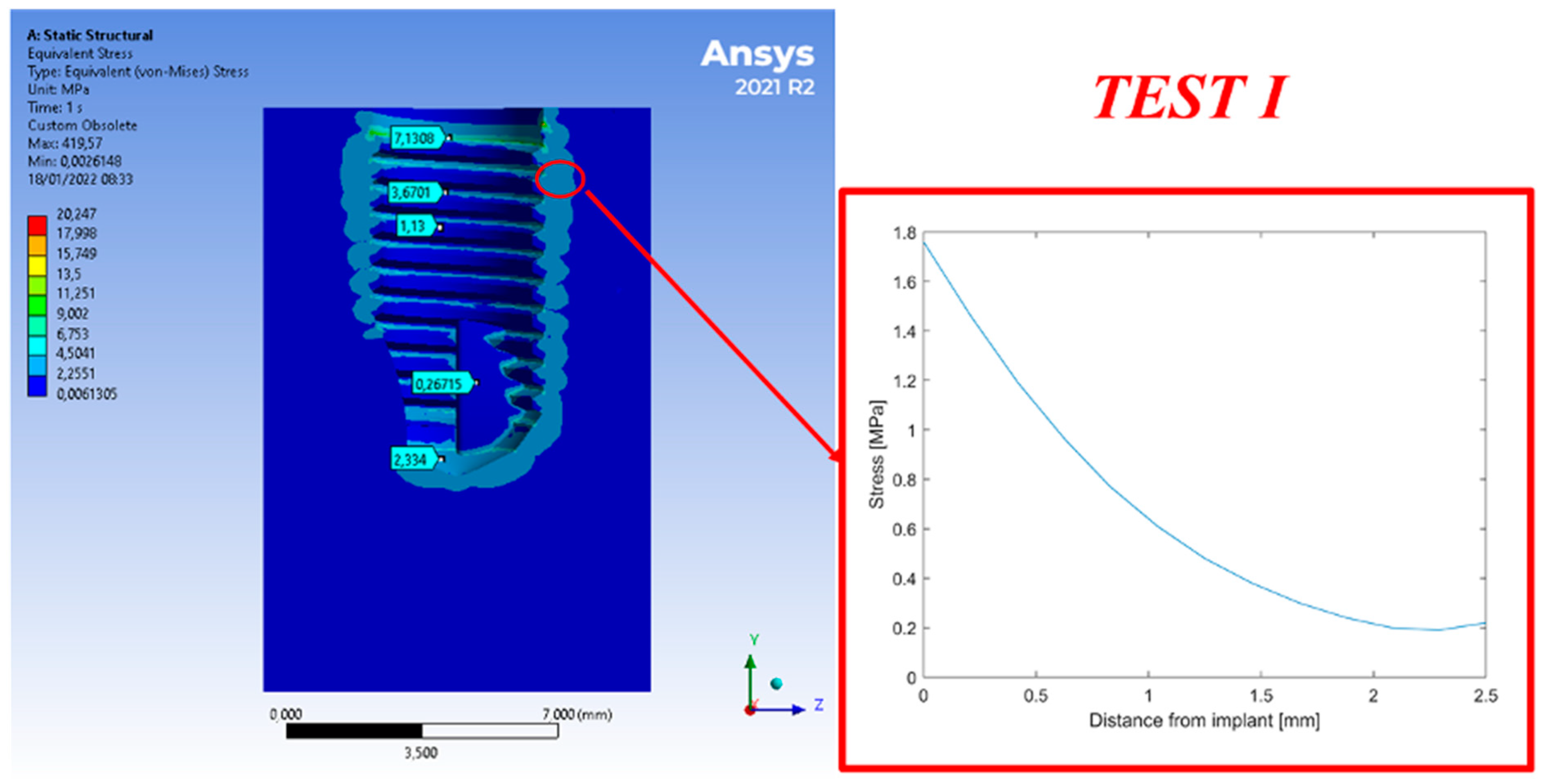
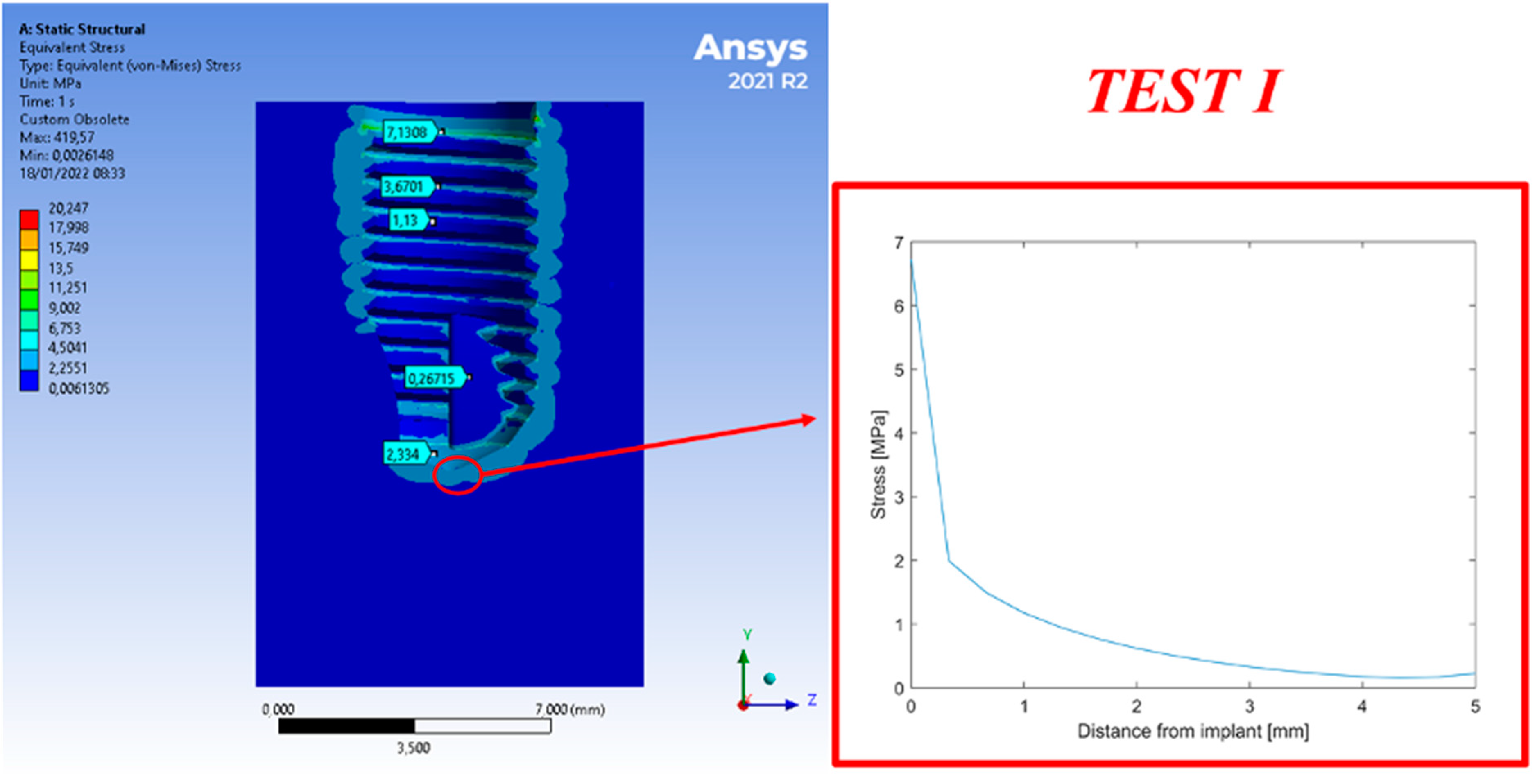
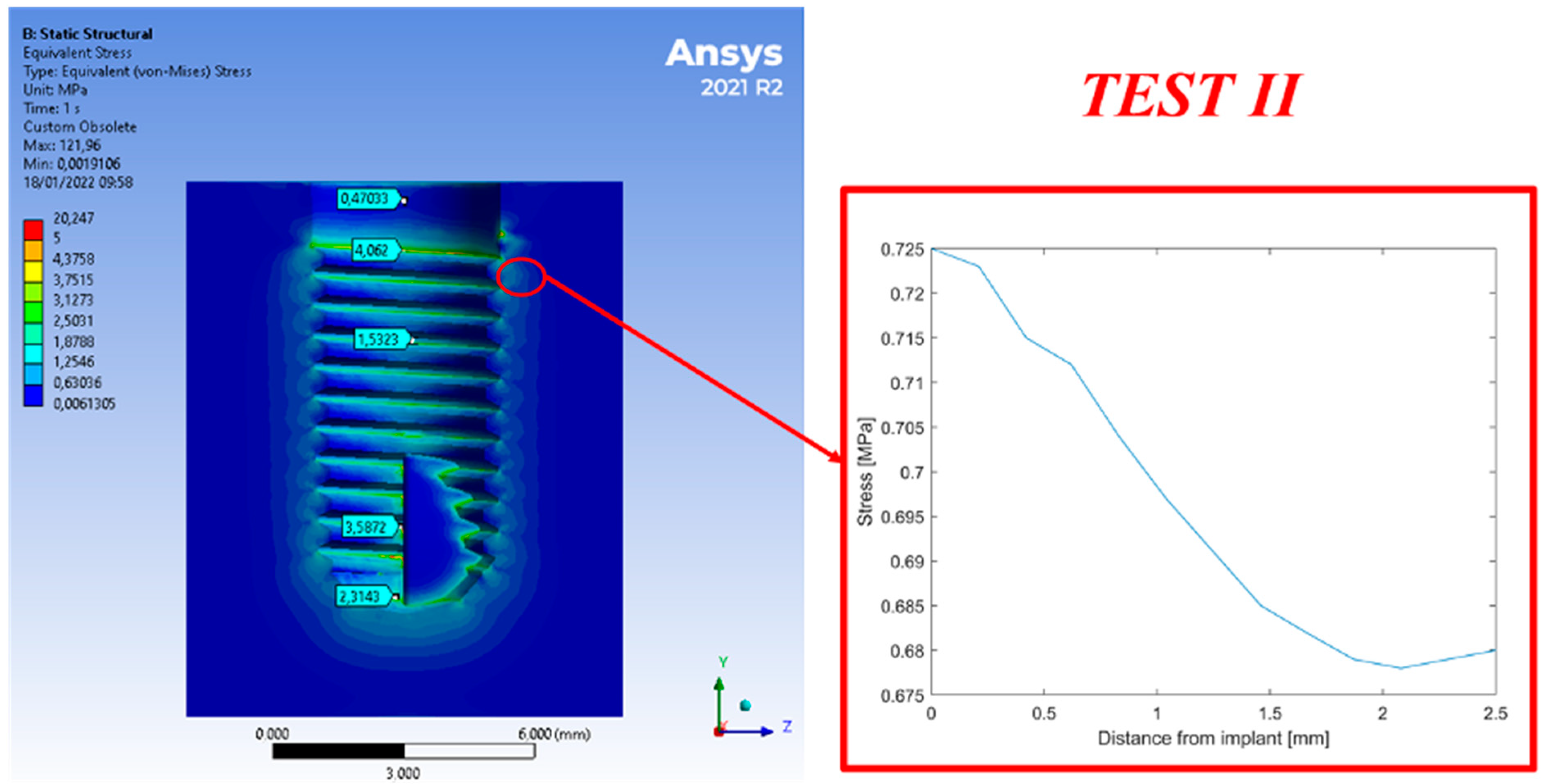
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gordon, L.M.; Cohen, M.J.; MacRenaris, K.W.; Pasteris, J.D.; Seda, T.; Joester, D. Dental materials. Amorphous intergranular phases control the properties of rodent tooth enamel. Science 2015, 347, 746–750. [Google Scholar] [CrossRef] [PubMed]
- Lavorgna, L.; Cervino, G.; Fiorillo, L.; Di Leo, G.; Troiano, G.; Ortensi, M.; Galantucci, L.; Cicciù, M. Reliability of a virtual prosthodontic project realized through a 2d and 3d photographic acquisition: An experimental study on the accuracy of different digital systems. Int. J. Environ. Res. Public Health 2019, 16, 5139. [Google Scholar] [CrossRef]
- Baun, W.L. Phase Transformation at High Temperatures in Hafnia and Zirconia. Science 1963, 140, 1330–1331. [Google Scholar] [CrossRef] [PubMed]
- Roehling, S.; Schlegel, K.A.; Woelfler, H.; Gahlert, M. Zirconia compared to titanium dental implants in preclinical studies-A systematic review and meta-analysis. Clin. Oral Implant. Res. 2019, 30, 365–395. [Google Scholar] [CrossRef] [PubMed]
- Kolata, G.B. The finite element method: A mathematical revival. Science 1974, 184, 887–889. [Google Scholar] [CrossRef] [PubMed]
- Crimi, S.; Defila, L.; Nanni, M.; Cicciù, M.; Fiorillo, L.; Cervino, G.; Marchetti, C.; Bianchi, A. Three-Dimensional Evaluation on Cortical Bone During Orthodontic Surgical Treatment. J. Craniofacial Surg. 2020, 31, 1637–1646. [Google Scholar] [CrossRef]
- D’Andrea, D.; Pistone, A.; Risitano, G.; Santonocito, D.; Scappaticci, L.; Alberti, F. Tribological characterization of a hip prosthesis in Si3N4-TiN ceramic composite made with Electrical Discharge Machining (EDM). Procedia Struct. Integr. 2021, 33, 469–481. [Google Scholar] [CrossRef]
- Fiorillo, L.; Cicciù, M.; D’Amico, C.; Mauceri, R.; Oteri, G.; Cervino, G. Finite Element Method and Von Mises Investigation on Bone Response to Dynamic Stress with a Novel Conical Dental Implant Connection. BioMed Res. Int. 2020, 2020, 2976067. [Google Scholar] [CrossRef]
- Cicciù, M.; Cervino, G.; Terranova, A.; Risitano, G.; Raffaele, M.; Cucinotta, F.; Santonocito, D.; Fiorillo, L. Prosthetic and Mechanical Parameters of the Facial Bone under the Load of Different Dental Implant Shapes: A Parametric Study. Prosthesis 2019, 1, 41–53. [Google Scholar] [CrossRef]
- Zhang, Y.; Lawn, B.R. Evaluating dental zirconia. Dent. Mater. 2019, 35, 15–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Lawn, B.R. Novel Zirconia Materials in Dentistry. J. Dent. Res. 2018, 97, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Hanawa, T. Zirconia versus titanium in dentistry: A review. Dent. Mater. J. 2020, 39, 24–36. [Google Scholar] [CrossRef] [PubMed]
- Filardi, V. Stress shielding FE analysis on the temporomandibular joint. J. Orthop. 2020, 18, 63–68. [Google Scholar] [CrossRef]
- Marcián, P.; Borák, L.; Valášek, J.; Kaiser, J.; Florian, Z.; Wolff, J. Finite element analysis of dental implant loading on atrophic and non-atrophic cancellous and cortical mandibular bone—A feasibility study. J. Biomech. 2014, 47, 3830–3836. [Google Scholar] [CrossRef]
- Crespi, R.; Capparé, P.; Romanos, G.E.; Mariani, E.; Benasciutti, E.; Gherlone, E. Corticocancellous porcine bone in the healing of human extraction sockets: Combining histomorphometry with osteoblast gene expression profiles in vivo. Int. J. Oral Maxillofac. Implant. 2011, 26, 866–872. [Google Scholar]
- Macedo, J.P.; Pereira, J.; Faria, J.; Pereira, C.A.; Alves, J.L.; Henriques, B.; Souza, J.C.M.; López-López, J. Finite element analysis of stress extent at peri-implant bone surrounding external hexagon or Morse taper implants. J. Mech. Behav. Biomed. Mater. 2017, 71, 441–447. [Google Scholar] [CrossRef]
- Clift, S.E.; Fisher, J.; Watson, C.J. Finite element stress and strain analysis of the bone surrounding a dental implant: Effect of variations in bone modulus. Proc. Inst. Mech. Eng. Part H 1992, 206, 233–241. [Google Scholar] [CrossRef]
- Soto-Penaloza, D.; Caneva, M.; Vina-Almunia, J.; Martin-de-Llano, J.J.; Penarrocha-Oltra, D.; Penarrocha-Diago, M. Bone-Healing Pattern on the Surface of Titanium Implants at Cortical and Marrow Compartments in Two Topographic Sites: An Experimental Study in Rabbits. Materials 2018, 12, 85. [Google Scholar] [CrossRef]
- Lakes, R.S.; Katz, J.L.; Sternstein, S.S. Viscoelastic properties of wet cortical bone—I. Torsional and biaxial studies. J. Biomech. 1979, 12, 657–678. [Google Scholar] [CrossRef]
- Brown, C.U.; Norman, T.L.; Kish, V.L., 3rd; Gruen, T.A.; Blaha, J.D. Time-dependent circumferential deformation of cortical bone upon internal radial loading. J. Biomech. Eng. 2002, 124, 456–461. [Google Scholar] [CrossRef]
- Nicholson, W.J. Titanium Alloys for Dental Implants: A Review. Prosthesis 2020, 2, 100–116. [Google Scholar] [CrossRef]
- Fiorillo, L.; Cicciù, M.; Tozum, T.F.; Saccucci, M.; Orlando, C.; Romano, G.L.; D’Amico, C.; Cervino, G. Endosseous Dental Implant Materials and Clinical Outcomes of Different Alloys: A Systematic Review. Materials 2022, 15, 1979. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, L.; D’Amico, C.; Campagna, P.; Terranova, A.; Militi, A. Dental Materials Implant Alloys: An X-Ray Fluorescence Analysis On Fds76®. Minerva Stomatol. 2021, 70, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.Z.; Tsai, P.I.; Kuo, M.Y.; Sun, J.S.; Chen, S.Y.; Shen, H.H. Augmentation of DMLS Biomimetic Dental Implants with Weight-Bearing Strut to Balance of Biologic and Mechanical Demands: From Bench to Animal. Materials 2019, 12, 164. [Google Scholar] [CrossRef]
- Tallarico, M.; Meloni, S.M.; Park, C.-J.; Zadrożny, Ł.; Scrascia, R.; Cicciù, M. Implant Fracture: A Narrative Literature Review. Prosthesis 2021, 3, 267–279. [Google Scholar] [CrossRef]
- Koller, M.; Steyer, E.; Theisen, K.; Stagnell, S.; Jakse, N.; Payer, M. Two-piece zirconia versus titanium implants after 80 months: Clinical outcomes from a prospective randomized pilot trial. Clin. Oral Implant. Res. 2020, 31, 388–396. [Google Scholar] [CrossRef]
- Barazanchi, A.; Li, K.C.; Al-Amleh, B.; Lyons, K.; Waddell, J.N. Mechanical Properties of Laser-Sintered 3D-Printed Cobalt Chromium and Soft-Milled Cobalt Chromium. Prosthesis 2020, 2, 313–320. [Google Scholar] [CrossRef]
- Petrović, Ž.; Šarić, A.; Despotović, I.; Katić, J.; Peter, R.; Petravić, M.; Petković, M. A New Insight into Coating’s Formation Mechanism Between TiO2 and Alendronate on Titanium Dental Implant. Materials 2020, 13, 3220. [Google Scholar] [CrossRef]
- Dong, H.; Liu, H.; Zhou, N.; Li, Q.; Yang, G.; Chen, L.; Mou, Y. Surface Modified Techniques and Emerging Functional Coating of Dental Implants. Coatings 2020, 10, 1012. [Google Scholar] [CrossRef]
- Kohorst, P.; Borchers, L.; Strempel, J.; Stiesch, M.; Hassel, T.; Bach, F.-W.; Hübsch, C. Low-temperature degradation of different zirconia ceramics for dental applications. Acta Biomater. 2012, 8, 1213–1220. [Google Scholar] [CrossRef]
- Pirjamalineisiani, A.; Sarafbidabad, M.; Jamshidi, N.; Esfahani, F.A. Finite element analysis of post dental implant fixation in drilled mandible sites. Comput. Biol. Med. 2017, 81, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Uccioli, U.; Fonzar, A.; Lanzuolo, S.; Meloni, S.M.; Lumbau, A.I.; Cicciù, M.; Tallarico, M. Tissue Recession around a Dental Implant in Anterior Maxilla: How to Manage Soft Tissue When Things Go Wrong? Prosthesis 2021, 3, 209–220. [Google Scholar] [CrossRef]
- Shemtov-Yona, K.; Rittel, D. Fatigue of Dental Implants: Facts and Fallacies. Dent. J. 2016, 4, 16. [Google Scholar] [CrossRef] [PubMed]
- Meijer, H.J.; Kuiper, J.H.; Starmans, F.J.; Bosman, F. Stress distribution around dental implants: Influence of superstructure, length of implants, and height of mandible. J. Prosthet. Dent. 1992, 68, 96–102. [Google Scholar] [CrossRef]

| Properties | Cortical Bone | Cancellous Bone | Zirconia (ZrO2) | Fibreglass Reinforced Resin |
|---|---|---|---|---|
| ρ (g/cm3) | 1.8 | 1.2 | ||
| Exx (GPa) | 9.6 | 0.144 | ||
| Eyy (GPa) | 9.6 | 0.099 | 205 | 20 |
| Ezz (GPa) | 17.8 | 0.344 | ||
| vxx | 0.55 | 0.23 | ||
| vyy | 0.30 | 0.11 | 0.3 | 0.22 |
| vzz | 0.30 | 0.13 | ||
| Gxx (GPa) | 3.10 | 0.053 | ||
| Gyy (GPa) | 3.51 | 0.063 | 78.846 | 8.1967 |
| Gzz (GPa) | 3.51 | 0.045 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorillo, L.; Milone, D.; D’Andrea, D.; Santonocito, D.; Risitano, G.; Cervino, G.; Cicciù, M. Finite Element Analysis of Zirconia Dental Implant. Prosthesis 2022, 4, 490-499. https://doi.org/10.3390/prosthesis4030040
Fiorillo L, Milone D, D’Andrea D, Santonocito D, Risitano G, Cervino G, Cicciù M. Finite Element Analysis of Zirconia Dental Implant. Prosthesis. 2022; 4(3):490-499. https://doi.org/10.3390/prosthesis4030040
Chicago/Turabian StyleFiorillo, Luca, Dario Milone, Danilo D’Andrea, Dario Santonocito, Giacomo Risitano, Gabriele Cervino, and Marco Cicciù. 2022. "Finite Element Analysis of Zirconia Dental Implant" Prosthesis 4, no. 3: 490-499. https://doi.org/10.3390/prosthesis4030040
APA StyleFiorillo, L., Milone, D., D’Andrea, D., Santonocito, D., Risitano, G., Cervino, G., & Cicciù, M. (2022). Finite Element Analysis of Zirconia Dental Implant. Prosthesis, 4(3), 490-499. https://doi.org/10.3390/prosthesis4030040











