Digital Forensics of Quantum Computing: The Role of Quantum Entanglement in Digital Forensics—Current Status and Future Directions

Abstract

As quantum computing advances, traditional digital forensic techniques face significant risks due to the vulnerability of classical cryptographic algorithms to quantum attacks. This review explores the emerging field of quantum digital forensics, with a particular focus on the role of quantum entanglement in enhancing the integrity, authenticity, and confidentiality of digital evidence. It compares classical and quantum forensic mechanisms, examines entanglement-based quantum key distribution (QKD), quantum hash functions, and quantum digital signatures (QDS), and discusses the challenges in practical implementation, such as scalability, hardware limitations, and legal admissibility. The paper also reviews various entanglement detection methods critical to the validation of quantum states used in forensic processes.

1. Introduction

Digital forensics is the science of identifying, preserving, analyzing, and presenting digital evidence in a way that maintains its forensic integrity. With the rise of quantum computing, traditional forensic techniques face potential vulnerabilities, creating a need to shift toward quantum digital forensics. Both approaches focus on ensuring the integrity, authenticity, and confidentiality of digital evidence, but their methods and resilience vary considerably.

Digital forensics is a branch of forensic science that focuses on identifying, acquiring, processing, analyzing, and reporting electronic data. Support from digital forensics is crucial for law enforcement investigations, as electronic evidence is involved in nearly all criminal activities. The main goal of digital forensics is to extract data from electronic evidence, turn it into actionable intelligence, and present the findings for prosecution. To ensure that the results are admissible in court, all procedures must follow solid forensic methodologies [1].

Given the rapid advancement of quantum computing, traditional cryptographic techniques used in digital forensics are increasingly threatened by quantum-based attacks. Current security mechanisms, such as RSA, AES, and SHA-256, depend on computational complexity assumptions that quantum algorithms can easily compromise [2]. The field of quantum cryptography, especially QKD and QDS, presents a promising way to secure forensic investigations in a post-quantum era [3].

Digital forensic science is vital in law enforcement and cybersecurity, ensuring that digital evidence stays authentic, tamper-proof, and legally acceptable [4]. However, as quantum computers become more powerful, forensic methods that depend on traditional cryptographic security may become outdated. Quantum entanglement, a key principle in quantum mechanics, offers a new way to improve evidence authentication and integrity checks in forensic investigations [5].

Research institutions and government agencies have highlighted the importance of Quantum Digital Forensics (QDF). For example, the National Institute of Standards and Technology (NIST) has stressed the need for post-quantum cryptography to protect digital evidence against future cyber threats [6]. Similarly, the European Telecommunications Standards Institute (ETSI) has called for developing quantum-safe cryptographic protocols to safeguard forensic records [7].

The investigation of quantum events has led to the development of a specialized field within physics called “Quantum Mechanics.” It focuses on how particles behave at the subatomic level. All entities in the universe exhibit both particle and wave properties. The core idea of Quantum Mechanics is that the universe is fundamentally probabilistic. Quantum computers use the principles of quantum physics to significantly increase computational speed. They can solve problems that are usually too complex for classical computers [8]. By applying the laws of quantum physics, quantum computing, a relatively new field with the potential to revolutionize various industries, can perform calculations impossible for classical computers. However, quantum computers use quantum bits, called qubits, while classical computers use bits to represent information as either 0 or 1. Qubits can be 0, 1, or both simultaneously because they can exist in a superposition of states.

The increasing complexity of digital technology, while changing modern life, also introduces new challenges to information security. As technology advances, the digital world develops alongside the field of digital forensics.

Many digital forensics researchers and academics predict that quantum computing will become widespread within the next two decades. With the current advancements in quantum computing, cybercrime is likely to increase. Identifying and catching a cybercriminal is always challenging. Even if the criminal is caught, securing a conviction will be difficult due to the lack of standardized digital investigative methods. Observing or measuring quantum data automatically changes its state, creating confusion over whether the observed changes are caused by malicious activity or are just artifacts of the measurement process. The ability of quantum computers to break common encryption schemes raises concerns about the security and integrity of digital evidence stored or transmitted using these techniques. Several new digital forensics investigation models have been developed recently to keep pace with the rapid growth of quantum computing.

This review investigates the role of quantum entanglement in securing digital evidence and examines how emerging quantum technologies can support or replace classical forensic mechanisms. It also discusses the limitations of current approaches and underscores the necessity for QDF that can withstand future cyber threats.

Table 1. Comparison between traditional and quantum digital forensic mechanisms across the core aspects of integrity, authenticity and confidentiality.

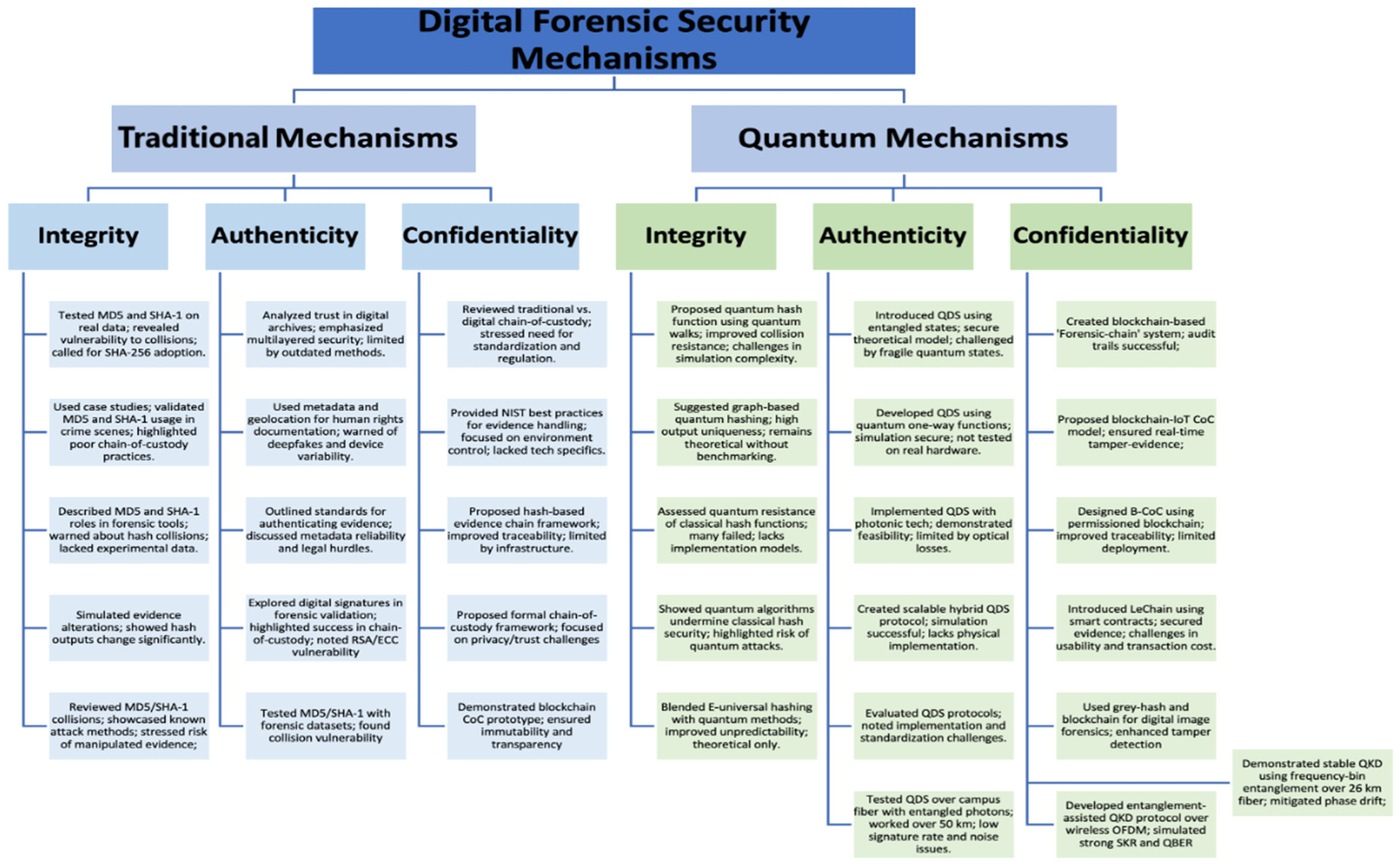
Aspect	Traditional Digital Forensics	Quantum Digital Forensics
Integrity	Uses cryptographic hash functions (MD5, SHA-1, SHA-256); vulnerable to hash collisions and tampering; needs transition to secure algorithms.	Employs quantum hash functions leveraging entanglement and superposition; high resistance to tampering; current methods are theoretical or simulated.
Authenticity	Relies on digital signatures (RSA, ECC); vulnerable to quantum attacks (e.g., Shors algorithm); needs quantum-resistant methods.	Uses Quantum Digital Signatures (QDS) with entangled particles; ensures unforgeability and non-repudiation; limited by hardware and implementation complexity.
Confidentiality	Achieved through AES encryption and secure containers; susceptible to future quantum decryption; lacks blockchain integration.	Uses Quantum Key Distribution (QKD), quantum watermarking, and quantum audit trails; ensures secure key exchange and tamper-evident tracking; challenges in implementation, synchronization, and infrastructure.

highlights the differences between traditional digital forensics and quantum digital forensics in terms of integrity, authenticity and confidentiality.

Figure 1 illustrates a conceptual workflow of a quantum digital forensic process, showing evidence acquisition, integrity verification via quantum hashing, authenticity through QDS, confidentiality with QKD, and final verification for legal admissibility.

The rest of this review is organized as follows: Section 2 covers traditional digital forensic methods, focusing on integrity, authenticity, and confidentiality. Section 3 introduces quantum digital forensic methods and compares them to classical approaches, emphasizing hash functions, digital signatures, and secure communication. Section 4 discusses entanglement detection, its theoretical basis, and the practical challenges of identifying entangled quantum states. Section 5 presents the realization in current experiments. Section 6 presents the findings, while Section 7 explores the implications and possible solutions. Section 8 outlines the challenges of adopting quantum-based forensic technologies, including scalability, standardization, and integration into current legal systems. Finally, Section 9 summarizes the study’s main points and stresses the need for developing quantum-resilient forensic infrastructures.

Figure 2 shows a simple Classification of Digital Forensic Security Mechanisms, contrasting Traditional Methods (hash functions, digital signatures, AES) with quantum approaches (quantum hashing, QDS, QKD). It highlights the shift from classical techniques vulnerable to quantum attacks toward entanglement-assisted mechanisms for forensic integrity, authenticity, and confidentiality.

2. Traditional Digital Forensic Mechanisms

2.1. Integrity

Traditional digital forensics maintains evidence integrity by using cryptographic hash functions such as SHA-256 and MD5 to confirm that evidence remains unaltered [9]. However, these methods can be susceptible to hash collisions and advanced tampering techniques.

The reliability of hash values in forensic investigations has been increasingly questioned due to environmental and technical factors. Simulations indicate that even minor changes to digital evidence can significantly modify hash outputs, emphasizing the importance of understanding hash behavior in forensic training [10]. Studies of MD5 and SHA-1 consistently show their diminishing effectiveness, especially as they are vulnerable to collision attacks [11]. Despite their widespread use in digital forensics, these algorithms lack robustness against modern computational methods, making them unsuitable for maintaining long-term evidence integrity. Researchers have therefore highlighted the urgent need to adopt more secure algorithms like SHA-256, although many existing studies overlook the growing threat posed by quantum computing [11].

Additional literature emphasizes how repeated successful attacks on MD5 and SHA-1 weaken their forensic credibility [12]. Researchers have documented known collision-generation techniques and the risks they pose for accepting tampered evidence as valid. A major challenge highlighted in these studies is the slow industry shift toward adopting stronger cryptographic standards. While informative, some reviews lack experimental validation, indicating a need to update forensic standards [12]. Case studies, like those by K. Kumar and S. Singh, demonstrate the practical use of hashing for verifying evidence authenticity, but also reveal procedural vulnerabilities—especially when the chain of custody is weak or collisions occur in real-world workflows [13]. These limitations underscore the importance of broader integration of secure hashing mechanisms.

In a practical context, Salvation DATA provided an overview of how MD5 and SHA-1 are still used in digital forensic software to acquire, store, and transfer evidence [14]. While the article pointed out their usefulness, it also recognized their weaknesses, especially the increasing risk of hash collisions that can undermine forensic reliability. The content acted more as a user-oriented guide than rigorous academic research and lacked experimental or peer-reviewed backing. Nevertheless, it highlights a significant gap between forensic practice and cryptographic progress, indicating that the community needs to align forensic tools with evolving security standards to maintain the trustworthiness of evidence.

2.2. Authenticity

Authenticity in traditional systems is maintained through digital signatures like RSA or ECC, which depend on public key infrastructure [15]. However, these methods are at risk from Shor’s algorithm, which allows quantum computers to efficiently factor large integers, potentially weakening RSA encryption [16].

Legal standards for authenticating digital evidence in court emphasize how electronic records can fulfill evidentiary requirements. A key part of this process is validating metadata, especially through cryptographic hash verification, to demonstrate authenticity [17]. However, maintaining the long-term integrity of metadata poses ongoing challenges. The changing nature of file formats and systems can create discrepancies that make verification difficult. In legal settings, additional complexities come from hearsay rules and the admissibility of digital records, which demand clear, consistent custody chains backed by verifiable technical evidence.

In an early foundational study, C. Lynch emphasized that technological measures alone—such as cryptography—are insufficient without a supporting institutional trust framework [18]. His work in the archival and library sciences advocated for a multi-layered model of authenticity that combines organizational policies with technical safeguards. Although published in 2000, and thus not addressing modern advances like blockchain or quantum-resistant encryption, Lynch’s argument remains relevant: digital authenticity must be rooted in both reliable systems and trustworthy institutions. A central challenge he identified is the risk of digital obsolescence, where formats and verification tools may no longer be supported in the future.

The significance of metadata and digital validation techniques is further illustrated in human rights investigations, where digital videos and mobile data are submitted to international criminal courts. Ulbricht et al. demonstrated how metadata such as geolocation, timestamps, and file signatures can improve the credibility of evidence [19]. Their case studies also revealed risks like deepfakes, metadata manipulation, and device dependency, especially in regions with inconsistent technological standards. Importantly, they emphasized the ethical obligation to protect the identities and safety of victims and witnesses during digital verification.

The discussion of authenticity tools also covers digital signatures and cryptographic hash functions. Digital signatures, when used with public key infrastructure (PKI), are effective for verifying data origin and preserving the chain of custody in forensic investigations [20]. However, these signatures depend on the strength of their underlying algorithms—such as RSA or ECC—which are facing new threats from quantum computing. As noted in Section 2.1, vulnerabilities of MD5 and SHA-1 undermine forensic reliability; Jordaan and Schmitt further emphasized this point, calling for the adoption of stronger standards such as SHA-256 and quantum-resistant hash functions

2.3. Confidentiality

Confidentiality in classical digital forensics is typically achieved using AES encryption and secure containers [15]. However, these encryption methods are vulnerable to future quantum attacks.

Creating a framework for managing the digital evidence chain of custody in modern forensic settings is vital because of changing challenges related to privacy, trust, and compliance. Such a framework would enhance evidence management among multiple stakeholders through formal modeling and automation for real-time tracking [21]. However, implementing this in diverse systems adds complexity, especially when integrating dynamic data contexts with legal requirements. The flexibility of policies is essential to maintain the validity of digital evidence, but deploying this solution broadly remains challenging due to technological diversity and limited resources.

Maintaining the integrity of digital evidence is essential for guaranteeing authenticity throughout the chain of custody. D. Banwani and Y. Kalra proposed a framework that uses cryptographic hash functions and secure logging mechanisms to improve traceability and detect tampering [22]. Their findings showed reliability in controlled settings, but challenges arose for low-budget agencies lacking technical skills. Their solution, although effective, was limited by scalability issues and reliance on trusted infrastructures. The authors recommended developing more user-friendly tools to encourage widespread use and preserve evidence credibility.

Practical guidance for handling digital evidence was provided by B. Guttman, D. R. White, and T. Walraven through a NIST publication that highlighted best practices such as environment control, forensic integrity, and secure storage protocols [23]. They used real-world scenarios to demonstrate proper procedures, aiming to reduce contamination and maintain chain of custody. A major challenge they identified was the risk of human error due to the absence of standardized training. Although the guidance was thorough, its general description limited its technical relevance. The authors suggested implementing certification programs to improve the professionalism of digital evidence management.

Emerging technologies like blockchain provide innovative solutions for chain-of-custody issues in digital forensics. A 2023 study showed how blockchain systems using smart contracts can guarantee immutability, transparency, and secure evidence transfers [24]. Despite encouraging results, challenges included integrating with existing forensic tools and performance problems in large-scale deployments. Cost and technical complexity also hindered wider adoption. Supporting this, D’Anna et al. conducted a comparative analysis of traditional and digital chain-of-custody practices, highlighting risks such as data volatility and metadata manipulation in digital contexts [25]. They emphasized the need for standardized protocols and legal harmonization across different jurisdictions, although their suggestions were mostly theoretical, underscoring the need for more practical research and implementation strategies.

3. Quantum Digital Forensic Mechanisms

3.1. Integrity

Quantum digital forensics uses quantum hash functions that rely on properties like superposition and entanglement. These quantum features make it nearly impossible to alter evidence without detection, because any measurement collapses the quantum state and reveals interference [26].

Quantum hash functions have become promising tools for improving data integrity in the post-quantum era. P. Hou et al. introduced a quantum hash function using Controlled Alternate Lively Quantum Walks to boost collision resistance [27]. Their method utilized quantum mechanical unpredictability to generate secure hash values, surpassing classical hash functions in simulated quantum attack scenarios. A key challenge was the complexity of modeling quantum walks and maintaining algorithmic stability. Although the results were encouraging, the study was limited by the lack of real-device testing and reliance on simulations. Similarly, Ziatdinov’s 2016 work proposed quantum hash constructions based on graph structures and quantum walks, highlighting the uniqueness of quantum graph-based outputs [28]. However, converting theoretical models into efficient quantum algorithms proved difficult, and the study remained mostly conceptual with minimal empirical evaluation.

Further research by B. Hamlin and F. Song focused on evaluating the quantum resilience of classical hash functions by introducing property-preservation under iterated hashing [29]. Their findings showed that many commonly used classical hash schemes lose collision resistance when facing quantum adversaries. The challenge was in formalizing realistic quantum threat models applicable to practical hashing systems. Although their models were abstract and lacked implementation examples, their work established foundational principles for assessing and redesigning cryptographic functions for quantum environments. Complementing this, a 2018 study presented quantum algorithms capable of finding collisions in homomorphic hash functions using quantum parallelism [30]. This research demonstrated how quantum capabilities greatly speed up collision discovery, revealing vulnerabilities in current cryptographic designs. However, the study’s limitation was its focus on simulation rather than practical, real-world demonstration.

In the quest for practical quantum-resistant hashing, F. Ablayev and M. Ablayev proposed hybrid quantum hashing methods based on classical ε-universal hashing schemes [31]. Their approach combined classical hashing universality with quantum encoding to enhance resistance against both classical and quantum attacks. Results indicated increased unpredictability and security, though the authors faced challenges in defining robust quantum measurement rules and managing decoherence. Like many theoretical studies, the lack of hardware-based testing limited its immediate usefulness. Nonetheless, this work represented a crucial step toward integrating quantum-safe hashing into digital forensic systems, encouraging further development of hybrid and scalable solutions for post-quantum environments.

Beyond hash functions, understanding the computational foundations of quantum advantage is vital for forensic and cryptographic applications. R. Jozsa and N. Linden explored the role of quantum entanglement in enabling exponential speed-up in quantum algorithms [32]. They showed that entanglement is a necessary condition for pure-state quantum algorithms to outperform classical computation, demonstrating that non-entangled systems can be simulated easily with classical methods. A key finding was identifying a threshold level of entanglement needed to achieve quantum advantage. However, rigorously quantifying entanglement in complex quantum states remains a significant challenge. Additionally, their study was limited by focusing on pure states and specific algorithm categories. Despite these limitations, the research offered valuable insights into the computational power of entanglement and laid the foundation for future research into quantum resources in secure systems.

3.2. Authenticity

Quantum digital forensics introduces QDS, which uses entangled particles and the no-cloning theorem, ensuring that any attempt to copy or forge the signature is fundamentally forbidden by the laws of quantum physics [33].

QDS has become an essential part of developing post-quantum secure communication systems. The foundational work by D. Gottesman and I. Chuang introduced a QDS scheme using non-repudiable and unforgeable quantum states distributed over quantum channels [34]. Their model showed that quantum-based signatures can offer greater security than classical digital signatures. However, the fragile nature of quantum states and the restrictions of the no-cloning theorem make practical implementation very challenging. The need for perfect quantum channels and the lack of experimental validation at that time were significant limitations, but their pioneering framework set the stage for future QDS advancements. Building on this, X. Lu and D.-G. Feng developed a protocol based on quantum one-way functions to improve authentication and non-repudiation [35]. Their simulation results indicated advantages over traditional cryptographic methods, though implementing it with current hardware remains a major obstacle. While not yet tested in physical systems, their work provided important conceptual progress toward making practical QDS systems possible.

Experimental breakthroughs in QDS occurred with the 2013 study by P. J. Clarke et al., who developed a QDS system using phase-encoded coherent light states [34]. Their experiments showed that photonic technologies can withstand common attacks such as beam-splitting and intercept-resend strategies, confirming the feasibility of QDS in real-world networks. However, challenges like optical loss and limited transmission range restrict the scalability of these systems. Despite this, their results mark an important step toward the practical deployment of quantum cryptographic tools. In a more recent effort, M. I. García Cid et al. proposed a hybrid signature scheme combining quantum primitives with classical cryptographic components [36]. Their design allows signing messages of any length while remaining flexible across various security assumptions. Key challenges include synchronizing quantum and classical components, especially regarding latency. Although still theoretical, their approach paves the way for near-term deployment of quantum-enhanced digital signatures.

A broader overview of QDS systems was provided by H. Duan, who categorized existing QDS protocols and evaluated their relevance to future secure communications [37]. The study highlighted QDS’s benefits in post-quantum scenarios, such as increased resistance to forgery and repudiation. However, several challenges were identified, especially in establishing secure key distribution and reducing the impact of quantum decoherence. Duan also pointed out the gap between rapid theoretical progress and the slower development of supporting hardware. He called for standardizing QDS protocols and integrating them with classical infrastructure as key steps for widespread adoption. Supporting this, J. C. Chapman et al. successfully tested an entanglement-based QDS system over a deployed fiber-optic campus network [38]. Using polarization-entangled photon pairs, they kept quantum bit error rates (QBERs) below 5% over a 50 km distance. While the experiment demonstrated real-world applicability, issues such as polarization misalignment, detector noise, and low signature rates limited overall efficiency. Still, the study showed that existing infrastructure could support QDS deployment.

Exploring scalability and advanced communication models, a high-dimensional QDS scheme was proposed that uses entanglement swapping and super-dense coding to enable secure multi-party communication [39]. Unlike traditional two-dimensional QDS systems, this method operates in N-dimensional quantum space, greatly increasing noise resilience and data capacity. The system eliminates the need for quantum memory, which is often a limiting factor in QDS implementations. However, maintaining entanglement authenticity during swapping and handling the experimental complexity of high-dimensional states pose significant challenges. As the proposal remains theoretical and untested, practical implementation is still pending. Despite this, the approach indicates promising directions for creating scalable, secure, and memory-free quantum signature systems for next-generation networks.

3.3. Confidentiality

In quantum systems, QKD provides a way to securely share encryption keys. Any eavesdropping attempt creates detectable anomalies, ensuring security [14]. Additionally, quantum watermarking or quantum audit trails enable tracking of who accessed or tampered with the evidence, maintaining custody’s chain [15].

Blockchain-based systems have increasingly been explored to secure the digital evidence chain of custody in forensic investigations. In 2019, A. H. Lone and R. N. Mir introduced “Forensic-chain,” a Hyperledger Composer proof-of-concept blockchain model designed to deliver tamper-proof audit trails [40]. The system succeeded in simulated environments, reinforcing trust in digital forensic processes. However, reconciling blockchain immutability with legal admissibility presented challenges. Limitations included dependence on private networks and the need for specialized user training. The authors emphasized the importance of integrating technical innovations with legal standards and recommended extending the system to support multi-jurisdictional use cases. Similarly, A. A. Khan et al. proposed a secure chain-of-custody model using blockchain and IoT for multimedia forensics, leveraging Hyperledger Sawtooth to ensure tamper-evident sensor data tracking [41]. Despite validating real-time monitoring, they encountered challenges in synchronizing heterogeneous media inputs and managing scalability. Their proposal to incorporate edge computing aimed to enhance system performance and scalability.

S. Bonomi et al. introduced B-CoC, a blockchain-based chain-of-custody system that combines secure evidence storage methods with a permissioned blockchain framework [42]. Their design significantly enhances evidence traceability, access control, and auditability. However, the system faces challenges with metadata growth and aligning with strict legal standards for admissibility. Additionally, the absence of live deployment limits its immediate practicality. The authors recommend future research to incorporate B-CoC into existing forensic platforms to manage the entire digital evidence lifecycle more reliably. In a related effort, M. Li et al. developed LeChain, a blockchain-based management platform using smart contracts to automate access auditing and evidence verification [43]. While the system shows strong security and operational efficiency, it encounters usability issues for non-technical users and challenges related to blockchain transaction costs and privacy. They suggest adopting a hybrid on-chain/off-chain architecture and aligning policies with legal regulations to improve deployment feasibility.

Focusing on multimedia forensics, M. Ali et al. introduced a new approach using grey hashing and blockchain technology to trace digital image evidence and verify its authenticity [44]. Their method proved effective in detecting image tampering and offered visually verifiable forensic trails. A major challenge was adapting cryptographic hash functions to handle the variability in multimedia content. Limitations included high computational costs and reliance on specific image formats. The authors recommended more extensive testing across various image types to confirm scalability. Their framework supports tamper-evident storage and verification of visual evidence and meets emerging needs in image-based digital forensics.

In the field of QKD, various models have been developed to enhance communication security against quantum attacks. Ahammed and Kadir proposed a hybrid entanglement-assisted and teleportation-based QKD system using OFDM modulation, which was simulated against BB84 under different attack scenarios [45]. The system achieved high secure key rates (SKRs) and low quantum bit error rates (QBERs), demonstrating robustness against quantum noise and classical interference. However, the absence of quantum memory, phase noise, and decoherence presented challenges for real-world implementation. Borghi et al. experimentally demonstrated a frequency-bin entanglement-based QKD protocol with active phase-drift compensation over 26 km fiber lengths [46]. Their use of wavelength multiplexing and a custom Mach-Zehnder interferometer maintained fidelity above 0.975 but faced limitations due to environmental fluctuations, system complexity, and dependence on high-performance photon sources.

Other quantum-secure models aim to improve QKD resilience and verification through theoretical innovations. Li et al. introduced a Modified Entanglement-based QKD (MEQKD) protocol resistant to intercept-resend attacks by modeling Bell-state entanglement disturbances [47]. Although theoretical, their protocol achieved a low attacker success probability of 5/8 and showed resistance to eavesdropping. However, real-world implementation depends on quantum hardware reliability and environmental noise reduction. Earlier, Curty, Lewenstein, and Lütkenhaus argued that entanglement is crucial for unconditionally secure QKD and developed witness operators based on measurable quantum correlations [48]. Their work, applied to 4-state and 6-state protocols, demonstrated security certification at higher error thresholds. Despite the lack of experimental validation and limited noise modeling, their theoretical framework effectively linked entanglement conditions to protocol security, reinforcing the fundamental role of quantum correlations in secure communication.

Table 2. Overview of current research on traditional and quantum digital forensic mechanisms, summarizing contributions in integrity, authenticity, and confidentiality.

Traditional Digital Forensic Mechanisms			Quantum Digital Forensic Mechanisms
Key Aspect	Author	Contribution Summary	Key Aspect	Author	Contribution Summary
Integrity	V. Schmitt and J. Jordaan [11]	Tested MD5 and SHA-1 on real data; revealed vulnerability to collisions; called for SHA-256 adoption.	Integrity	P. Hou et al. [27]	Proposed quantum hash function using quantum walks; improved collision resistance; challenges in simulation complexity.
	K. Kumar and S. Singh [13]	Used case studies; validated MD5 and SHA-1 usage in crime scenes; highlighted poor chain-of-custody practices.		Ziatdinov, M. [28]	Suggested graph-based quantum hashing; high output uniqueness; remains theoretical without benchmarking.
	SalvationDATA [14]	Described MD5 and SHA-1 roles in forensic tools; warned about hash collisions; lacked experimental data.		B. Hamlin & F. Song [29]	Assessed quantum resistance of classical hash functions; many failed; lacks implementation models.
	A. Thakar et al. [10]	Simulated evidence alterations; showed hash outputs change significantly; emphasized usefulness for investigator training; lacked discussion of stronger hash alternatives.		J. C. Garcia-Escartin et al. [30]	Showed quantum algorithms undermine classical hash security; highlighted risk of quantum attacks.
				F. Ablayev & M. Ablayev [31]	Blended E-universal hashing with quantum methods; improved unpredictability; theoretical only.
	Rasjid Z.E. et al. [12]	Reviewed MD5/SHA-1 collisions; showcased known attack methods; stressed risk of manipulated evidence; lacked experimental validation; urged updates in forensic standards.		R. Jozsa and N. Linden [32]	Explored entanglement’s role in computational speed-up; found entanglement essential in pure-state algorithms; limited to theoretical models and pure states.
			Authenticity	D. Gottesman & I. Chuang [34]	Introduced QDS using entangled states; secure theoretical model; challenged by fragile quantum states.
Authenticity	C. Lynch [18]	Analyzed trust in digital archives; emphasized multilayered security; limited by outdated methods.		X. Lu & D.-G. Feng [35]	Developed QDS using quantum one-way functions; simulation secure; not tested on real hardware.
	Ulbricht et al. [19]	Used metadata and geolocation for human rights documentation; warned of deep fakes and device variability.		P. J. Clarke et al. [33]	Implemented QDS with photonic tech; demonstrated feasibility; limited by toptical losses.
	P. Grimm and G. P. Joseph [17]	Outlined standards for authenticating evidence; discussed metadata reliability and legal hurdles.		M. I. Garcia Cid et al. [36]	Created scalable hybrid QDS protocol; simulation successful; lacks physical implementation.
	Dogra, K. [20]	Explored digital signatures in forensic validation; highlighted success in chain-of-custody; noted RSA/ECC vulnerability; promoted quantum-resistant protocols; limited by cryptographic dependency.		H. Duan [37]	Evaluated QDS protocols; noted implementation and standardization challenges.
				J. C. Chapman et al. [38]	Tested QDS over campus fiber with entangled photons; worked over 50 km; low signature rate and noise issues.
				A.Aktaş & I. Yılmaz [39]	Proposed high-dimensional QDS using entanglement swapping and super-dense coding; improved security; remains theoretical without implementation.
	V. Schmitt and J. Jordaan [11]	Tested MD5/SHA-1 with forensic datasets; found collision vulnerability; warned about outdated tool use; called for updates; did not include SHA-256.	Confidentiality	A. H. Lone & R. N. Mir [40]	Created blockchain-based ‘Forensic-chain’ system; audit trails successful; challenged by training and legal fit.
				A. A. Khan et al. [41]	Proposed blockchain-IoT CoC model; ensured real-time tamper-evidence; issues with multimedia and privacy.
Confidentiality	T. D’Anna et al. [25]	Reviewed traditional vs. digital chain-of-custody; stressed need for standardization and regulation.		S. Bonomi et al. [42]	Designed B-CoC using permissioned blockchain; improved traceability; limited deployment.
	B. Guttman et al. [23]	Provided NIST best practices for evidence handling; focused on environment control; lacked tech specifics.		M. Li et al. [43]	Introduced LeChain using smart contracts; secured evidence; challenges in usability and transaction cost.
	D. Banwani and Y. Kalra [22]	Proposed hash-based evidence chain framework; improved traceability; limited by infrastructure.		M. Ali et al. [44]	Used grey-hash and blockchain for digital image forensics; enhanced tamper detection; computationally intensive.
	S. Nath et al. [21]	Proposed formal chain-of-custody framework; focused on privacy/trust challenges; emphasized policy adaptability; limited by complexity in heterogeneous systems.		Ahammed and Kadir [45]	Developed entanglement-assisted QKD protocol over wireless OFDM; simulated strong SKR and QBER; limited by decoherence, memory, and hardware feasibility.
				Borghi et al. [46]	Demonstrated stable QKD using frequency-bin entanglement over 26 km fiber; mitigated phase drift; constrained by complexity and photon source limitations.
	J. Machhi et al. [24]	Demonstrated blockchain CoC prototype; ensured immutability and transparency; noted tool integration issues and latency; limited by cost and adoption barriers.		Shang, T. et al. [47]	Suggested intercept-resistant MEQKD; modeled errors from eavesdropping; showed robustness in theory; limited by reliance on ideal quantum hardware.
				Curty, M. et al. [48]	Proved entanglement is necessary for secure QKD; used entanglement witnesses in 4- and 6-state protocols; theoretical only, lacking noise validation.

represents an overview of the current research on traditional and quantum digital forensic mechanisms, summarizing contributions in integrity, authenticity, and confidentiality. The table contrasts classical approaches (e.g., MD5, RSA, AES, blockchain) with quantum solutions (quantum hashing, QDS, QKD), highlighting key results, limitations, and feasibility for forensic applications.

4. Entanglement Detection

Entanglement detection is a vital area in quantum computing, as entanglement is a crucial resource for many quantum algorithms and protocols, including quantum error correction, quantum cryptography, and quantum communication. Detecting and quantifying entanglement helps ensure that quantum systems function as intended and can be effectively utilized in quantum computations. It is widely believed that entanglement detection has gained popularity over time, and several methods are available; however, some have application and system scale limitations. The primary physical process in quantum computers is quantum entanglement. Entanglement is a key resource for a wide variety of tasks in quantum computing, such as quantum computing, quantum teleportation, quantum cryptography, and forensics [49,50]. Quantum entanglement has the potential to be applied in digital forensics by enabling faster and more efficient data analysis via quantum computing. This technology is still in the early stages of development and faces significant challenges related to hardware limitations and error correction, which could help investigators identify hidden patterns and correlations within large datasets, especially in complex cybercrime investigations, by leveraging the unique properties of entangled quantum states [51].

Determining whether a specific unknown state is entangled can be very complex. The first challenge is theoretical; even if an unknown state is fully identified through full state tomography (FST), verifying whether a known state is entangled can still be difficult. The second challenge arises from practical laboratory conditions, which introduce imperfections and noise, making it harder to perform FST or directly assess whether an unknown state is entangled or separable. In practice, it may not be necessary to carry out FST if the goal is simply to test for entanglement. Additionally, the sample complexity involved in FST does not provide a straightforward measurement or sample complexity for entanglement detection. Over the past two decades, many theoretical and practical methods have been proposed for detecting and quantifying entanglement. These include entanglement witnesses, Bell’s inequalities, the realignment criterion, the range criterion, and the majorization criterion [52]. Many of these methods generally assume that some prior knowledge of the target state is available.

Quantum state tomography and density matrix reconstruction are direct methods for acquiring this information. However, the number of measurement parameters needed grows exponentially with the size of the system, making tomography impractical [53,54]. Entanglement can be identified using Bell’s inequalities, as a system that violates a Bell inequality shows correlations between measurements that cannot be explained by classical physics, indicating entanglement between particles. Essentially, if the measured correlations surpass the limit set by the Bell inequality, entanglement exists. Bell’s inequalities are frequently used to detect quantum entanglement because they provide a way to determine if a system has correlations that defy classical explanations. Violating a Bell inequality signifies that the system is entangled.

• Bell’s Theorem: States that no local hidden variable theory can reproduce all the predictions of quantum mechanics, and observing a violation of the Bell inequality proves that the system is entangled.
• CHSH Inequality: A common form of Bell’s inequality that involves measuring pairs of entangled particles. If the measured correlations go beyond the classical limit, it shows entanglement.

Entanglement Detection Limitations [55,56]:

• Scalability: Detecting entanglement becomes more challenging as the number of qubits increases because the Hilbert space grows exponentially.
• Noise and Imperfections: In real-world quantum systems, noise and imperfections can hide entanglement, making it more difficult to detect.
• Mixed States: Many quantum systems exist in mixed states rather than pure states, and detecting entanglement in such mixed states is more complex.

While a wide range of entanglement detection methods exists, not all are equally feasible in applied forensic contexts. Full state tomography provides complete information about a quantum state, but its exponential scaling makes it impractical for more than a few qubits [53]. Similarly, criteria such as the range or majorization tests [52] remain primarily theoretical due to their heavy reliance on prior knowledge of the state and significant computational overhead. By contrast, Bell inequality violations and entanglement witnesses are among the most practical tools for forensic integration. Bell tests have been successfully demonstrated in photonic platforms and superconducting qubits to verify non-classical correlations [54], making them suitable for small-scale forensic prototypes. Entanglement witnesses, which require fewer measurements, offer a scalable alternative and have been shown effective in detecting multipartite entanglement with limited experimental data [52]. However, their reliability diminishes under noisy or mixed-state conditions, a common feature of real-world systems. Recent progress in machine-learning-assisted entanglement detection also suggests promising near-term applications [56], though such methods require further validation in forensic workflows. Overall, while tomography and advanced criteria remain largely theoretical, Bell tests and entanglement witnesses stand out as the most realistic detection strategies for forensic use in current experimental environments.

Recent developments in practical entanglement distribution and quantum network testbeds further support the feasibility of applying entanglement-based methods in digital forensics. For instance, E. Arbel et al. demonstrated an optical emulation of quantum state tomography and Bell tests as an undergraduate experiment, highlighting that entanglement verification techniques can now be realized with relatively low-cost photonic setups [57]. Similarly, I. César-Cuello et al. reported progress toward lithium niobate photonic integrated circuits for quantum sensing, showing that scalable and compact quantum photonic platforms are rapidly emerging [58]. These advances indicate that entanglement detection and distribution are no longer limited to specialized laboratories, but are transitioning toward practical and educational settings, thereby bridging the gap between theoretical forensic models and real-world quantum infrastructure.

5. Realization in Current Experiments

Although the proposed scheme is largely theoretical, recent experimental progress shows that it can be realized with current quantum technologies. Entanglement-based QDS have already been implemented over deployed optical fiber networks, demonstrating stable operation across 50 km with polarization-entangled photons, albeit with low signature rates and sensitivity to polarization misalignment [38]. Similarly, experimental demonstrations of QDS using coherent light states confirmed resistance to beam-splitting and intercept–resend attacks, validating the feasibility of photonic platforms [33]. For con-fidentiality, frequency-bin entanglement-based QKD has been experimentally shown over 26 km with active phase stabilization, maintaining fidelity above 0.975 [46]. Satellite and free-space QKD have also been experimentally verified, confirming feasibility for global deployment [59]. In addition, entanglement verification techniques such as Bell inequality tests and state tomography have been demonstrated with superconducting qubits [54]. Taken together, these results indicate that small-scale experimental prototypes using entangled photons, optical fibers, and superconducting qubits can already realize essential components of the proposed forensic framework. This suggests that integration of entanglement-based integrity, authenticity, and confidentiality mechanisms into forensic practice is feasible in the near term, provided that scalability and noise-resilience challenges are addressed.

6. Findings

This review highlights several key findings regarding the role of quantum entanglement in improving digital forensic practices. First, traditional forensic methods—such as hash functions, digital signatures, and encryption—remain effective but are increasingly vulnerable to quantum-based attacks. Studies on MD5 and SHA-1 consistently demonstrate their weaknesses against collision attacks, while RSA and ECC signatures could become obsolete with the use of Shor’s algorithm. These limitations emphasize the need to adopt post-quantum solutions for lasting forensic reliability.

Second, quantum forensic mechanisms offer promising theoretical solutions. Quantum hash functions, based on superposition and entanglement, provide significantly higher resistance to tampering. QDS verify authenticity through the no-cloning theorem, creating signatures that cannot be forged or denied. Likewise, QKD guarantees strong confidentiality, as eavesdropping attempts leave detectable traces. However, these solutions remain mostly experimental, facing challenges in scalability, synchronization, hardware stability, and real-world implementation.

Third, entanglement detection becomes an essential tool for quantum forensics. Techniques such as entanglement witnesses, Bell inequalities, and tomography verify the integrity of quantum states used in forensic procedures. Despite progress, detection faces challenges due to scalability issues, noise, and difficulties in managing mixed quantum states. These technical barriers limit the immediate use of entanglement-based systems in forensic investigations.

Finally, the review shows that beyond technical readiness, legal and procedural issues remain key. Challenges such as the admissibility of quantum-secured evidence, lack of standardization, and limited professional training create obstacles for incorporating quantum technologies into existing forensic workflows. Although blockchain-based audit trails and hybrid classical-quantum frameworks have potential to bridge this gap, they also need to align with legal systems across different jurisdictions.

In summary, quantum entanglement could greatly enhance the integrity, authenticity, and confidentiality of digital forensic evidence. However, its benefits depend on overcoming hardware constraints, creating scalable detection methods, and establishing supportive legal and procedural frameworks. The findings indicate that quantum digital forensics is not yet fully practical, but it is a quickly advancing field with significant future implications for secure evidence management.

7. Discussion

The main issue this review emphasizes is the vulnerability of traditional digital forensic methods in the era of quantum computing. As highlighted in Section 2, traditional cryptographic primitives such as MD5 and SHA-1 are already known to be collision-prone, further underscoring the urgency of adopting quantum-resistant mechanisms. Moreover, security measures like AES encryption and conventional chain-of-custody procedures are at risk of being decrypted or manipulated by quantum attackers. Without reliable protections, forensic evidence could lose its credibility in courtrooms and criminal cases, directly impacting justice and cybersecurity.

To address these challenges, this research focuses on utilizing quantum entanglement as a key method for preserving the integrity, authenticity, and confidentiality of digital forensic evidence.

1-

Integrity: Using entanglement-based quantum hash functions ensures that any unauthorized change to digital evidence will collapse the quantum state, making tampering immediately detectable. This method aims to address the collision vulnerabilities of classical hashes while offering a future-proof solution resistant to quantum attacks.

2-

Authenticity: QDS, based on entangled particles and governed by the no-cloning theorem, are explored as a way to verify that forensic evidence comes from a trusted source. Unlike RSA or ECC, QDS cannot be forged or denied, strengthening its admissibility in legal cases.

3-

Confidentiality: Entanglement-assisted QKD and quantum audit trails will be used to protect the transmission and storage of forensic evidence. These methods create tamper-evident custody chains, where any interception causes detectable anomalies, ensuring evidence stays private and traceable throughout its lifecycle.

The proposed approach does not aim to replace traditional forensic tools entirely, but to create a hybrid quantum-classical framework where entanglement boosts essential forensic guarantees. This integration will allow current forensic systems to gradually shift toward quantum-secure infrastructures. By confirming entanglement through detection methods such as Bell inequalities and entanglement witnesses, the research will ensure that forensic protocols remain trustworthy even in noisy, real-world environments.

Ultimately, the goal is to show that quantum entanglement can create tamper-proof, unforgeable, and secure forensic systems, thus addressing the weaknesses of classical cryptography in the quantum era. This work will contribute both technically—through prototype models in Qiskit—and procedurally, by proposing frameworks that align quantum forensic methods with legal and investigative standards.

8. Challenges

Quantum-based technologies show promise for securing digital forensic evidence, but their implementation still faces many technological, procedural, and legal hurdles. To verify authenticity, QDS are designed to confirm that messages or evidence come from a verifiable sender and have not been altered. However, practical QDS systems encounter several limitations. A key challenge in quantum communication is the fragility and difficulty of transmitting quantum states—particularly over long distances where photon loss and environmental noise degrade the information and although early QDS protocols attempted to address this by requiring quantum memory for state storage until verification, practical quantum memories remain limited by short coherence times and high error rates [59,60]. More recent protocols aim to eliminate the need for memory by using immediate measurement and classical forwarding, which increases operational complexity and demands stricter timing and coordination [61]. Scalability remains a major obstacle, particularly when involving multiple recipients and signers, as each extra user adds complexity to the distribution and verification of signatures. Furthermore, since QDS protocols are relatively new, there is no universal standard for their use, making it hard to integrate into traditional forensic workflows and raising legal validation issues.

Regarding integrity, QKD is a method that uses entangled quantum particles to create and exchange encryption keys that cannot be intercepted or copied without detection. While QKD offers information-theoretic security that is resistant to attacks by quantum computers, deploying it in the real world faces several challenges. First, range limitations affect most QKD systems: in fiber-optic channels, photon loss becomes too significant over distances greater than about 100 km without quantum repeaters, which are not yet commercially available [62]. Free-space QKD and satellite-based QKD provide alternatives, but they require substantial investment and are impacted by atmospheric conditions and limited accessibility [63]. Additionally, even if the QKD protocol itself is mathematically secure, hardware vulnerabilities such as detector blinding, timing attacks, and power fluctuations can weaken the overall security of key exchanges [64]. Another obstacle is compatibility with traditional systems: forensic environments rely on a variety of digital tools and evidence storage systems, and QKD devices must interface seamlessly with them without compromising the quantum security guarantees. Furthermore, key management and authentication protocols need to be adapted to support long-term use and preserve archival integrity—particularly important in legal and forensic contexts where evidence may be examined years after collection.

For chain-of-custody improvements, quantum technologies provide tamper-evident and non-repudiable evidence tracking, but they also introduce their own complex challenges. Quantum systems are governed by the no-cloning theorem, which prevents creating copies of unknown quantum states. While this helps prevent forgery, it also means that traditional digital auditing methods—such as duplicating logs or making multiple backups—cannot be directly applied to quantum-tagged evidence [65]. Quantum timestamping and entanglement-based tracking require precise synchronization among all involved parties. If the timing or entanglement correlation is disrupted by environmental noise, network delays, or technical failures, the quantum evidence record may be invalidated. In practice, forensic evidence often changes hands across multiple jurisdictions and institutions, so a continuous and universally trusted quantum-secured infrastructure would need to be in place. Currently, such global or even national-scale systems are not yet deployed. Additionally, many forensic professionals and legal experts are unfamiliar with quantum principles, raising concerns about user education, trust, and legal standardization [66]. Without clear regulatory guidelines, quantum-protected chains of custody might face skepticism or rejection in court despite their theoretical strength [67].

Influence of External Environments

The current study focuses on closed quantum systems; however, in real-world implementations, the interaction of qubits with their surrounding environments significantly affects performance. Environmental decoherence can be broadly categorized as Markovian or non-Markovian. Markovian processes, where noise is memoryless, tend to cause exponential decay of entanglement, leading to reduced fidelity of quantum hash functions, QDS, and QKD systems [68]. By contrast, non-Markovian effects involve back-flow of information from the environment to the system, which can temporarily restore coherence and entanglement, thus influencing the security and reliability of forensic protocols [69,70]. For instance, the presence of structured reservoirs or strong system–environment coupling can induce non-Markovian behavior that alters entanglement lifetimes, thereby changing error rates and detection probabilities. These findings suggest that practical deployment of entanglement-based forensic mechanisms must incorporate error mitigation strategies and adaptive entanglement witnesses designed for open quantum systems.

9. Conclusions

In conclusion, this study highlights the growing importance of quantum digital forensics as a response to the limitations of traditional forensic methods faced with emerging quantum threats. The research demonstrates that quantum entanglement can significantly enhance the integrity, authenticity, and confidentiality of digital evidence through innovations like quantum hash functions, quantum digital signatures, and quantum key distribution. Additionally, the review of entanglement detection techniques underscores their vital role in verifying quantum states, although they still face challenges related to scalability and noise. Results suggest that while quantum solutions offer theoretical strength and future-proofing, practical implementation encounters obstacles such as hardware limitations, legal standardization, and infrastructure development. Nonetheless, integrating quantum technologies into digital forensics presents promising opportunities to transform the field and ensure secure, tamper-evident forensic practices in the post-quantum era.