Abstract
We investigate a three-level system in the context of the fractional Schrödinger equation by considering fractional differential operators in time and space, which promote anomalous relaxations and spreading of the wave packet. We first consider the three-level system omitting the kinetic term, i.e., taking into account only the transition among the levels, to analyze the effect of the fractional time derivative. Afterward, we incorporate a kinetic term and the fractional derivative in space to analyze simultaneous wave packet transition and spreading among the levels. For these cases, we obtain analytical and numerical solutions. Our results show a wide variety of behaviors connected to the fractional operators, such as the non-conservation of probability and the anomalous spread of the wave packet.
1. Introduction
Many phenomena in nature, such as in complex viscoelastic media [1,2], electrical spectroscopy impedance [3,4,5], wave propagation in porous media [6,7], microflows of viscoelastic fluids [8], and gas transport in heterogeneous media [9,10,11] are associated with different types of scenarios, such as non-Markovian processes, which can be connected to memory effects, long-range correlations, and long-range interactions, among others. In this context, fractional calculus brings new possibilities in which the standard approach is unsuitable for describing these effects in connection with the experimental data. With a simple extension of the differential operator to the non-integer index, significant changes are incorporated into the standard approach, such as memory effects, long-range correlations, and other effects in complex systems [12,13]. Fractional extensions have been shown to be more suitable for capturing the experimental behavior when compared with integer-order models [14,15]. For instance, extending the dengue epidemic model using the Caputo derivative is more accurate than the standard model [16]. In the photothermal phenomena, the fractional operators are considered an extension of Fourier’s law to study the heat propagation in non-homogeneous solids, which present different regimes of diffusivity [17]. These different regimes of diffusivity, such as subdiffusion and superdiffusion, can be modeled with different values of fractional order. Another application of fractional calculus is in the study of cardiac rhythm [18]. The normal rhythms of the heart are associated with a fractional order close to one; however, signals generated by hypertensive patients are modeled by a different fractional order. The hypertension model with fractional extension also was studied in Ref. [19]. Other applications of fractional calculus are found in Refs. [20,21,22,23,24,25,26] and the references therein. These fractional operators, and the processes connected to them, have been widely analyzed in several fields, particularly in quantum mechanics, as a fundamental physics theory that describes the physical properties of nature in lighting on a subatomic and atomic level. The pioneer works of N. Laskin [27,28,29] (based on extensions of the path integral formulation [30]), lead us to a fractional Schrödinger equation and have been followed by other extensions incorporating fractional differential operators in time and space [31], non-local terms [32,33], constraints among the different spatial coordinates (comb-model) [34,35,36,37,38], and others [39,40]. Space and time fractional derivatives in the Schrödinger equation were considered to obtain soliton-type solutions in the optical field [41], while numerical solutions for the fractional Schrödinger equations were obtained in Ref [42]. Other applications can be found in Refs. [43,44,45,46,47]. It is important to stress that, in these scenarios, anomalous relaxation processes [48] are present due to the extension of the differential operators of integer order to fractional ones. It is also worth mentioning that, from the analytical and numerical point of view, it is a challenge to obtain solutions when fractional derivatives in time and space are considered.
The main goal is to investigate the implications of considering time-dependent potentials in the fractional Schrödinger equation [49] given by
where the fractional differential operator is the Caputo fractional time derivative, written as
where , , and [31]. The fractional time derivative is defined as a convolution integral between a kernel (power law) and the wave function. We apply analytical and numerical methods to analyze Equation (1). As mentioned in Ref. [49], we can also extend the Schrödinger equation as follows:
Equations (1) and (3) are possible extensions and have been considered in many situations, such as optical solitons [50], resonant mode conversions [51], and two-level systems [52] as an extension of Rabi’s model. However, note that when a Wick rotation is performed, the imaginary unit is increased to the same power as the time coordinates considered for Equation (1). Another point between the two equations involves the temporal behavior of the solution, which for the first case, is more suitable than for the second one, which decreases or grows with time instead of demonstrating a sinusoidal behavior. For these reasons, we consider Equation (1) in our developments.
Hence, we consider a three-level system in Equation (1) perturbed by an external electromagnetic field. Firstly, we analyze the system described by the time-dependent Hamiltonian in the form
where the terms stand for the external perturbation, here understood as an external oscillatory field, with a frequency equal to . The terms are associated with the coupling between i and j, and means the energy eigenvalues of with (). After analyzing the dynamics of the Schrödinger equations under the Hamiltonian given by Equation (4), we incorporate the kinetic terms with fractional powers yielding
Note that the kinetic terms in Equation (5) can be related to a spatial fractional derivative, i.e., , where , and , refer to the Fourier transforms, respectively. This definition corresponds to the Riesz derivative [53,54].
We consider a three-level system because the atom shows a wide variety of effects in its interaction with the electromagnetic field, such as laser cooling, lasing without inversion, loss-free pulse propagation, and population transfer, compared to the two-level atom. Jing and Yu [55] presented an accurate quantum trajectory approach for a dissipative three-level model and developed a convolutionless stochastic Schrödinger equation called the time-local quantum state diffusion (QSD) equation without Markov approximation. They showed that this exact time-local QSD equation is suitable for exploring quantum dynamics for a higher dimensional quantum system with a non-Markovian environment. Castanos et al. [56] showed that the atoms with and configurations present double points. This means that there are two independent quantum states with the same energy, which depends on the values of the dipole strengths of the interaction between the atoms and the radiation field. Robustness against the noise source is a big challenge for realizing quantum devices. In this way, based on generic three-level systems, Petiziol et al. [57] proposed a protocol according to the widespread stimulated Raman adiabatic passage technique. Their protocol realizes adiabatic acceleration by applying additional control fields to the optical excitation. They illustrated that the proposed method is efficient over various control parameters and brings the timescales close to the quantum speed limit when an environmental disturbance exists. Other applications of three-level systems can be found in Refs. [58,59,60] and the references therein.
Due to the additional degree of freedom, three-level systems are richer dynamically when compared with two-level ones. However, little attention has been devoted to them, mainly in the context of fractional quantum mechanics. In this context, we dedicate this research to studying a three-level system under the influence of an external perturbation. Our contribution to the fractional quantum mechanics field is to propose analytical and numerical solutions for this system. Aiming to understand the effects of fractional operators, we first analyze the Hamiltonian in the context of standard quantum mechanics, i.e., with integer-order operators. After, we extend the differential operators to a non-integer order by incorporating the fractional differential operators in that time and space. Our results suggest that the probability density follows an anomalous relaxation process due to the fractional operators. These developments are performed in Section 2 and Section 3 by considering the analytical and numerical calculations for these Hamiltonians and analyzing the spreading behavior of the wave packet in different conditions. Finally, we present our discussions and conclusions in Section 4.
2. Schrödinger Equation without Kinetic Terms
The standard Schrödinger equation is defined by
where i is the imaginary unit, is the wave function, ℏ is the Planck’s constant, and is the Hamiltonian [61]. The following Hamiltonian can give a three-level system
Considering Equation (6) with the Hamiltonian given by Equation (7) and, for simplicity, , we obtain the following equations
The system described by Equation (10) corresponds to a coupled three-level system, respectively. A particular case was considered in Ref. [52] for a two-level system. This system of linear differential equations can be analyzed from analytical and numerical points of view. From the analytical point of view, we can use the Laplace transform to obtain the solutions for a given initial condition. We apply this approach combined with the Fourier transform to obtain the solution when the kinetic term is present in the Hamiltonian, i.e., when the Hamiltonian is given by Equation (26). Applying the Laplace transform and , we achieve the system of algebraic equations written as
Solving Equations (12) and (13) for the , we find that
with and , while the solutions for and read as
and
A particular case from the previous one arises when with the corresponding solutions :
It is worth mentioning that the inverse Laplace transform can be found using the method of partial fractions, which implies finding the roots of a third-degree polynomial. For example, the case , , with results in the following equations
By applying the inverse of the Laplace transform to the functions , we obtain the corresponding given by
and
We can use the numerical approach presented in Ref. [62] to find the solution to the previous set of equations. Numerical solutions for the probability densities (red line), (green line), and (blue line) related to Equations (8)–(10) are presented in Figure 1. We consider , , , , , , in panel (a), and in panel (b). The choice of parameters is arbitrary. We chose these values due to the fact that some behaviors are highlighted with them. The probability of finding the system in one of the states obeys an oscillatory behavior. When no frequency is considered (panel (a)), the system stays more intense in the state . However, when the oscillatory dynamics of the field are considered (), the system transit between the first () and third states () using the second state () as an edge of transition. This transition shows that the is the coupling between and . When no frequency is considered (panel (a)), the system stays more intense in the state . However, when the oscillatory dynamics of the field are considered (), the system transitions between the first () and third state () using the second state () as an edge of transition. This transition shows that the is the coupling between and . These solutions show that if particles populated the first state initially, the transition for the third state depends on the second one. Moreover, the transmission of the particles depends on the parameters of the coupling and external field properties, such as the frequency.
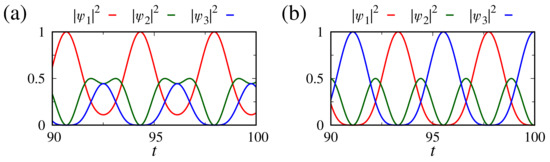
Figure 1.
Times series of probability density (red line), (green line), and (blue line). We consider , , , , , , in panel (a), and in panel (b).
Now, we extend the previous scenario by incorporating fractional time derivatives. For this case, we have that
Interestingly, the Caputo fractional time derivative produces an anomalous relaxation for the solutions, which are usually asymptotically characterized by power laws. Similar to the previous case, we use a numerical calculation to obtain the behavior of the solutions of this set of coupled equations for an initial condition. In particular, for determining the numerical solutions for Equations (23)–(25), we use the Predictor–Evaluate–Corrector–Predictor method (PECE) [63] (see Appendix A for more details).
Considering , , , , , , and , the solutions for , , and are displayed in Figure 2 by the red, green, and blue lines, respectively. Panel (a) exhibits the case with , i.e., a constant potential. This situation shows how drastically the dynamics change front fractional operators. Now occurs a competition between the first and second states in terms of their probability amplitudes, while the third state is less populated. On the other hand, if the potential oscillates, i.e., , the second state works just as an edge between the first and third states, which are populated with the same amplitude, as seen in Figure 2b. In both cases, the probability amplitude goes proportionally with . This result is expected when considering , as found in Ref. [64] for a particular case. The resulting probability increases can be interpreted as the creation of particles.
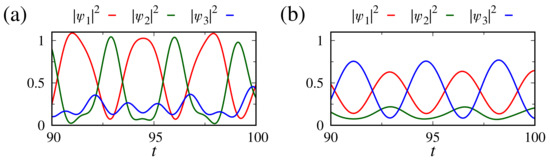
Figure 2.
Times series of probability density (red line), (green) line, and (blue line). We consider , , , , , , , , in panel (a), and in panel (b).
3. Schrödinger Equation with Kinetic Dependences
The kinetic terms can be considered in Equation (4) by the following transformation , , and which yields
For simplicity, we consider and and the one-dimensional case. Taking into account the kinetic terms, the dynamics of the three-level system are described by
The analytical solution for this set of equations can be obtained using the Laplace and Fourier ( and ) transforms. Applying the integral transforms to the previous set of equations assuming the initial conditions , , and , we obtain the corresponding set of algebraic equations, written in the form:
From Equation (32), we relate the solutions and by means of
The former result combined with Equation (31) fixes the function in terms of according to
which, applied to Equation (30), leads to
By applying the inverse of the Laplace transform to Equation (35), we obtain the wave function in the form
where
Similarly, the functions and read as
with and determined from
and
The inverse of the Fourier transform of the previous equations is given by
for 1, 2, and 3 with
The discretization of Equations (27)–(29) can be obtained by the finite difference scheme [65]. For this, we consider a grid defined by with boundary conditions equal to . The time is discretized according to , where with a time step equal to ; each space coordinate is given by where with a space step equal to (see Appendix B for more details). To avoid numerical boundary problems, the origin of our space coordinate is located in . With these considerations, Equations (27)–(29) are given by
The numerical solutions for Equations (43)–(45) are displayed in Figure 3 in panels (a)–(f). Panels (a)–(c) show the probability amplitude (color scale) distribution in time and space for , , and . As time advances, the Gaussian package that is centered in spreads along the second () and third states (). The packet scattering is more evident when we look for the density plot in Figure 3d–f, for , , and . These results show that the probability of finding particles in a given state decreases in amplitude as time advances and becomes wider in the space domain. Furthermore, the particles transition from the first state to the second one, and, just after populating the second one, they go into the third state. This oscillatory transition reflects the effects of the potential and external perturbation. For these results, we consider , , , , and the initial condition with , .
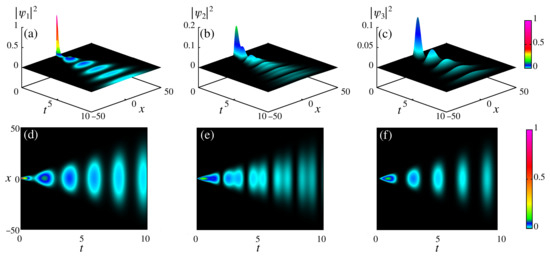
Figure 3.
Probability amplitude (color scale) spread in panels (a–c) for , , and . Density plot of the probability distributions in panels (d–f) for , , and . We consider , , , , , and the initial condition with , .
The profiles of , , and are exhibited in Figure 4, respectively, by panels (a)–(c). The red line is for , the green line is for in panel (a) and in panels (b) and (c), and the blue line is for in panel (a) and in panels (b) and (c). From these profiles, we note the distribution of the Gaussian package among the three states. The Gaussian shape spreads along space as time evolves.
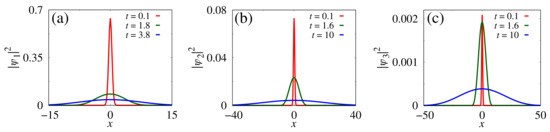
Figure 4.
Profiles for the Gaussian package distribution for the probabilities , , and in panels (a–c), respectively. The red line is for , the green line is for in (a) and in (b,c), and the blue line is for in (a) and in (b,c). We consider , , , , , and the initial condition with , .
One way to measure a probability package’s spread is by computing the mean square displacement (), which is displayed in Figure 5. The red line is associated with , while the black and blue lines are associated with and , respectively. In dealing with the standard formulation, the displacements evolve proportionally linearly with , which characterizes the standard spreading of the wave packet. Due to the numerical imprecision and the potential effects, our respective slopes for , , and are 1.95, 2.01, and 1.83. The oscillations in the displacements reflect the oscillatory character of the potential, which causes a non-linear transmission among the states. It is worth mentioning that the position in relation to the -axis is translated to consider all the curves in the same figure without superposition. This shift does not alter the slope, which is an important parameter for our study.
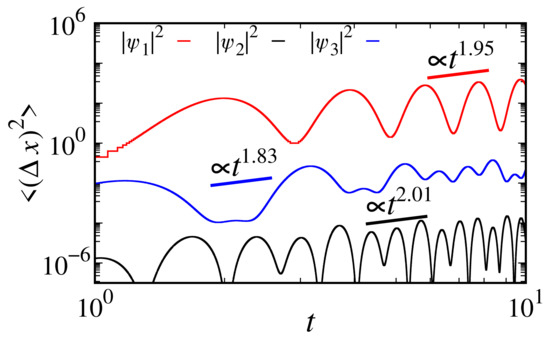
Figure 5.
Mean square displacement for (red line), (black line), and (blue line). The respective slopes are 1.95, 2.01, and 1.83. We consider , , , and the initial condition with , .
Let us extend the previous result by incorporating a fractional differential in space. For this case, the previous set of equations can be written as follows:
The solution for the previous set of equations is given by
for 1, 2, and 3 with
which resembles the form of the Lévy distribution found in anomalous diffusion processes. In Equation (50), we have the H Fox function [66], usually represented [31] by
In Equation (51), the function reads
which involves Mellin–Barnes integrals [31] (for more details see also Ref. [66]). The asymptotic behavior of Equation (50) in the limit of is given by , which is different from the usual one characterized by the Gaussian behavior. Note that this result for the asymptotic limit can be obtained by using the approach employed in Ref. [67]. It is essentially an integration over the Mellin-Branes integral poles, which represents Equation (50). This feature is directly connected to the presence of spatial fractional differential operators in Equations (46)–(48).
For numerical investigation, we consider the same method as in the standard case, i.e., the finite differences. Considering this scheme, the discretization of Equations (46)–(48), yields
where .
The inclusion of fractional space derivatives (e.g., ) in the Schrödinger three-level systems implies a delay in the probability spread, as shown by Figure 6a–c for , , and , respectively. Furthermore, the scattering gains more evidence of the potential, which is seen through a sinuous scattering, as displayed by panels (d)–(f), in Figure 6, for , , and , respectively.
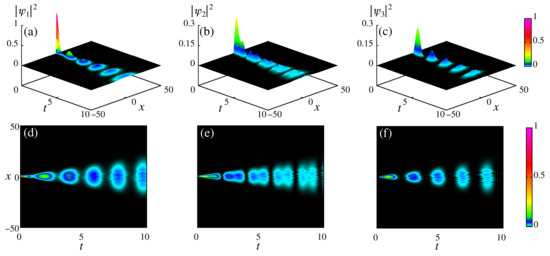
Figure 6.
Effects of fractional space derivative with in the probability amplitude (color scale) spread (panels (a–c), for , , and ) and in the density plot of the probability distributions in panels (d–f) for , , and . We consider , , , , and the initial condition with , .
Profiles for , , and are displayed in Figure 7, respectively, in panels (a–c). We note from the profiles that the spread has a higher amplitude than the standard case and occurs in sinusoidal form due to the potential effects. The higher amplitude shows the package spread with a low velocity when was considered.
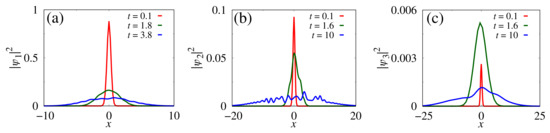
Figure 7.
Profiles for the Gaussian package distribution for the probabilities , , and in panels (a–c), respectively. We consider . The red line is for , the green line is for in (a) and in (b,c), and the blue line is for in (a) and in (b,c). We consider , , , , and the initial condition with , .
The mean square displacement for (red line), (black line), and (blue line) with is exhibited in Figure 8. The mean square displacement increases by , for ; , for ; and , for . The sinusoidal form reflects the potential effects and transitions among the states.
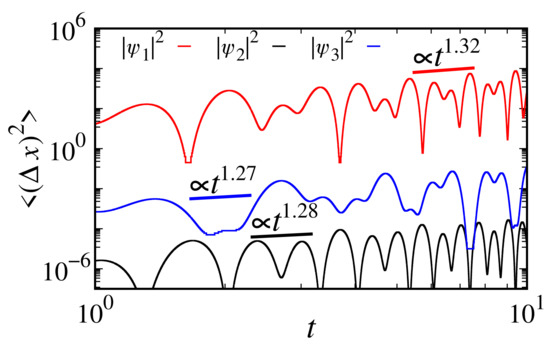
Figure 8.
Mean square displacement for (red line), (black line), and (blue line), considering . The respective slopes are 1.32, 1.28, and 1.27. We consider , , , and the initial condition with , .
4. Discussions and Conclusions
We have investigated a three-level system described by a fractional Schrödinger equation, with a time-dependent potential and an external electromagnetic field. We considered fractional extensions of the Schrödinger equation in terms of differential operators of non-integer order in space and time. We first analyzed the three-level system by considering the transition among the levels to investigate how the probability evolves, in time, according to the conditions considered. Considering that one state is initially populated, our results suggest that the other two states become populated over time. This transition occurs in an oscillatory way, depending on the parameters related to the external field, e.g., oscillation frequency. We verified that extending the time operator to a fractional one introduces an anomalous relaxation and oscillation among the levels. Afterward, we incorporated a kinetic term into the previous scenarios. This feature allows the spreading of the wave packet at each level while the transition between the levels occurs. For this case, we also extended the differential operators to fractional differential operators in space. Extending the space operators to fractional ones, we verify an anomalous relaxation process related to the probability transition among the states. The transition process can be amplified according to the parameter’s range. For example, if we address different weight coupling, the higher weight state will be populated earlier, and this state can bind the particles. Another way to change the probability transition is by changing the frequency. The frequency of the external field is directly connected with the probability transition frequency.
In summary, we have considered the fractional operator defined by a power-law kernel, which is well known as the Caputo derivative for the fractional time derivative. One of the most relevant aspects obtained with this extension of the time derivative is the possibility of describing different effects not present in the standard approach, such as memory effects and long-range correlations. These aspects have implications for the relaxation processes of these systems, which are different from the usual ones. These relaxation processes emerge from the fact that we may connect the solutions with the Mittag–Lefler functions, which are asymptotically governed by power laws. In future works, we will consider other fractional time derivatives with different kernels, which imply different relaxation processes. For the spatial operator, we considered the Riesz fractional operator, which also produces an anomalous relaxation with distributions asymptotically governed by power laws. Finally, we hope the results presented here can be useful in discussing anomalous processes and fractional Schrödinger equations.
Author Contributions
Conceptualization, E.K.L., E.C.G., E.S., A.S.M.d.C., J.T. and A.M.B.; methodology, E.K.L., E.C.G., E.S., A.S.M.d.C., J.T. and A.M.B.; formal analysis, E.K.L., E.C.G., E.S., A.S.M.d.C., J.T. and A.M.B.; investigation, E.K.L., E.C.G., E.S., A.S.M.d.C., J.T. and A.M.B.; writing—original draft preparation, E.K.L., E.C.G., E.S., A.S.M.d.C., J.T. and A.M.B.; writing—review and editing, E.K.L., E.C.G.,E.S., A.S.M.d.C., J.T. and A.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
E.K.L. acknowledges the support of CNPq (Grant No. 301715/2022-0). E.C.G. acknowledges the support of CAPES (Grant No. 88887.650484/2021-00). A.M.B acknowledges the support of CNPq, CAPES and Fundação Araucária.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Fractional Ordinary Differential Equations
One numerical method to solve fractional ordinary differential equations based on Caputo’s definition is a generalization of the Adams–Bashforth–Moulton method, which is known as the Predictor–Evaluate–Corrector–Predictor method (PECE) [63].
Given an initial problem, defined by
with as the initial condition. The problem is solved, according to Ref. [63] by the following discretization
where
The coefficients are defined by
and
where , and n is associated with the discrete time window, T, which is discrete in with where .
Appendix B. Fractional Partial Differential Equations
In this work, Equations (46)–(48) are discretized according to the finite difference method [65]. The extensions for the fractional partial differential equations (FPDE) of this method are found in Refs. [68,69]. The first step in building this method is to consider a grid defined by . The space and time are discretized by: , where and . In this way, the space and time steps are, respectively: and . To avoid numerical problems, we translate the origin of our space to , without loss of generality. To solve the FPDE, it is necessary to be informed of the boundary conditions and initial conditions for all states. For simplicity, we consider boundary conditions equal to and the initial conditions and . Then, the discrete forms of Equations (46)–(48) are given by
where .
These equations are solved numerically by the Algorithm A1, described below.
| Algorithm A1 Algorithm to solve space FPDE |
|
We performed our numerical simulation using the language C, and the graphs were plotted using Gnuplot 5.2.
Appendix C. List of Symbols
A list of symbols used in this work is shown in Table A1.

Table A1.
List of symbols.
Table A1.
List of symbols.
| Symbol | Meaning |
|---|---|
| i | Imaginary unity. |
| ℏ | Reduced Planck constant. |
| Time fractional order. | |
| Wave function. | |
| Hamiltonian operator. | |
| Time Caputo derivative. | |
| Time Caputo derivative. | |
| Eigenvalue of energy. | |
| Strenght coupling between i and j. | |
| Frequency of external perturbation. | |
| Momentum operator. | |
| Space fractional order. | |
| Fractional momentum operator. | |
| m | Mass. |
| Fourier transformation. | |
| Laplace transformation. | |
| Probability density. | |
| Time step. | |
| Space step. | |
| Standard deviation. | |
| Mean square displacement. | |
| Green function. | |
| H Fox function. | |
| Gamma function. |
References
- Pandey, V.; Holm, S. A fractional calculus approach to the propagation of waves in an unconsolidated granular medium. J. Acoust. Soc. Am. 2015, 138, 1766. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Rosseto, M.; Evangelista, L.; Lenzi, E.; Zola, R.; Ribeiro de Almeida, R. Frequency-Dependent Dielectric Permittivity in Poisson-Nernst-Planck Model. J. Phys. Chem. B 2022, 126, 6446–6453. [Google Scholar] [CrossRef] [PubMed]
- Scarfone, A.M.; Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem 2022, 2, 163–178. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Guilherme, L.; da Silva, B.; Koltun, A.; Evangelista, L.R.; Zola, R. Anomalous diffusion and electrical impedance response: Fractional operators with singular and non-singular kernels. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105907. [Google Scholar] [CrossRef]
- Chen, W.; Hu, S.; Cai, W. A causal fractional derivative model for acoustic wave propagation in lossy media. Arch. Appl. Mech. 2016, 86, 529–539. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Fang, J.; Holm, S. A survey on fractional derivative modeling of power-law frequency-dependent viscous dissipative and scattering attenuation in acoustic wave propagation. Appl. Mech. Rev. 2018, 70, 030802. [Google Scholar] [CrossRef]
- Jiang, Y.; Qi, H.; Xu, H.; Jiang, X. Transient electroosmotic slip flow of fractional Oldroyd-B fluids. Microfluid. Nanofluidics 2017, 21, 7. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.; Zhang, Y.; Zheng, C.; Min, F. Spatial fractional Darcy’s law to quantify fluid flow in natural reservoirs. Phys. A Stat. Mech. Its Appl. 2019, 519, 119–126. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.; Zheng, C.; Lu, B.; Lu, C.; Ma, R.; Zhang, Y. A time fractional convection–diffusion equation to model gas transport through heterogeneous soil and gas reservoirs. Phys. A Stat. Mech. Its Appl. 2018, 502, 356–369. [Google Scholar] [CrossRef]
- Pandey, V.; Holm, S. Connecting the grain-shearing mechanism of wave propagation in marine sediments to fractional order wave equations. J. Acoust. Soc. Am. 2016, 140, 4225–4236. [Google Scholar] [CrossRef]
- Ali, M.; Narayanan, G.; Shekher, V.; Alsaedi, A.; Ahmad, B. Global Mittag-Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105088. [Google Scholar]
- Sultana, M.; Arshad, U.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry 2022, 14, 1653. [Google Scholar] [CrossRef]
- Almeida, R. What is the best fractional derivative to fit data? Appl. Anal. Discret. Math. 2017, 11, 358–368. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Somer, A.; Novatski, A.; Serbena, F.C.; Lenzi, E.K. Interplay between super and subdiffusive behaviors in photothermal phenomena. Int. J. Therm. Sci. 2021, 159, 106539. [Google Scholar] [CrossRef]
- Templos-Hernández, D.; Quezada-Téllez, L.; Gonzáles-Hernández, B.; Rojas-Vite, G.; Pineda-Sánchez, J.; Fernández-Anaya, G.; Rodriguez-Torres, E. A fractional-order approach to cardiac rhythm analysis. Chaos Solitons Fractals 2021, 147, 110942. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Aboelkassem, Y.; Laleg-Kirati, T.M. Human Hypertension Blood Flow Model Using Fractional Calculus. Front. Physiol. 2022, 13, 838593. [Google Scholar] [CrossRef]
- Cius, D.; Menon, L., Jr.; dos Santos, M.A.F.; de Castro, A.S.M.; Andrade, F.M. Unitary evolution for a two-level quantum system in fractional-time scenario. Phys. Rev. E 2022, 106, 054126. [Google Scholar] [CrossRef]
- Ullah, I.; Ahmad, S.; Arfan, M.; De la Sen, M. Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator. Fractal Fract. 2023, 7, 300. [Google Scholar] [CrossRef]
- dos Santos, M.A.F. Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting. Physics 2019, 1, 40–58. [Google Scholar] [CrossRef]
- Tarasov, V.E. On History of Mathematical Economics: Application of Fractional Calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- de Barros, L.C.; Lopes, M.M.; Pedro, F.S.; ao Esmi, E.; dos Santos, J.P.C.; Sánchez, D.E. The memory effect on fractional calculus: An application in the spread of COVID-19. Comput. Appl. Math. 2021, 40, 72. [Google Scholar] [CrossRef]
- Magin, R.; Ortigueira, M.D.; Podlubny, I.; Trujillo, J. On the fractional signals and systems. Signal Process. 2011, 91, 350–371. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Martynyuk, V.; Kosenkov, V.; Batista, A.G. A New Look at the Capacitor Theory. Fractal Fract. 2023, 7, 86. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechanics; World Scientific Publishing Company: Singapore, 2018. [Google Scholar]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Laskin, N. Fractals and quantum mechanics. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 780–790. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Time-dependent Schrödinger-like equation with nonlocal term. J. Math. Phys. 2014, 55, 092105. [Google Scholar] [CrossRef]
- Lenzi, E.K.; de Oliveira, B.F.; da Silva, L.R.; Evangelista, L.R. Solutions for a Schrödinger equation with a nonlocal term. J. Math. Phys. 2008, 49, 032108. [Google Scholar] [CrossRef]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Generalized time-dependent Schrödinger equation in two dimensions under constraints. J. Math. Phys. 2018, 59, 012104. [Google Scholar] [CrossRef]
- Petreska, I.; de Castro, A.S.M.; Sandev, T.; Lenzi, E.K. The time-dependent Schrödinger equation in three dimensions under geometric constraints. J. Math. Phys. 2019, 60, 032101. [Google Scholar] [CrossRef]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Constrained quantum motion in δ-potential and application of a generalized integral operator. Comput. Math. Appl. 2019, 78, 1695–1704, Advances in Fractional Differential Equations (V): Time-space fractional PDEs. [Google Scholar] [CrossRef]
- Iomin, A. Fractional-time Schrödinger equation: Fractional dynamics on a comb. Chaos Solitons Fractals 2011, 44, 348–352. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Ribeiro, H.V.; Magin, R.L. Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models. Quantum Rep. 2022, 4, 296–308. [Google Scholar] [CrossRef]
- Meften, G.A.; Ali, A.H. Continuous dependence for double diffusive convection in a Brinkman model with variable viscosity. Acta Univ. Sapientiae Math. 2022, 14, 125–146. [Google Scholar] [CrossRef]
- Meften, G.A.; Ali, A.H.; Yaseen, M.T. Continuous dependence for thermal convection in a Forchheimer-Brinkman model with variable viscosity. AIP Conf. Proc. 2023, 2457, 020005. [Google Scholar]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Analytic and numerical solutions for systems of fractional Schrödinger equation. J. Inequalities Appl. 2015, 12, 23. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgül, A. A novel approach for solving linear and nonlinear time-fractional Schrödinger equations. Chaos Solitons Fractals 2022, 162, 112487. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Heydari, M.; Atangana, A. A cardinal approach for nonlinear variable-order time fractional Schrödinger equation defined by Atangana-Baleanu-Caputo derivative. Chaos Solitons Fractals 2009, 128, 339–348. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A.; Anukool, W. A family of nonlinear Schrödinger equations and their solitons solutions. Chaos Solitons Fractals 2023, 166, 112907. [Google Scholar] [CrossRef]
- Ain, Q.T.; He, J.H.; Anjum, N.; Ali, M. The fractional complex transform: A novel approach to the time-fractional Schrödinger equation. Fractals 2020, 28, 2050141. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Zola, R.S.; Petreska, I.; Sandev, T. Fractional Schrödinger equation and anomalous relaxation: Nonlocal terms and delta potentials. Mod. Phys. Lett. A 2021, 36, 2140004. [Google Scholar] [CrossRef]
- Naber, M. Time fractional Schrödinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar] [CrossRef]
- Okposo, N.I.; Veeresha, A.; Okposo, E.N. Solutions for time-fractional coupled nonlinear Schrödinger equations arising in optical solitons. Chin. J. Phys. 2022, 77, 965–984. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, R.; Zhong, H.; Zhang, J.; Belić, M.R.; Zhang, Y. Resonant mode conversions and Rabi oscillations in a fractional Schröridinger equation. Opt. Express 2017, 25, 32401–32410. [Google Scholar] [CrossRef]
- Gabrick, E.C.; Sayari, E.; de Castro, A.S.M.; Trobia, J.; Batista, A.M.; Lenzi, E.K. Fractional Schrödinger Equation and Time Dependent Potentials. Commun. Nonlinear Sci. Numer. Simul. 2023, 123, 107275. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer Nature: Berlin, Germany, 2023. [Google Scholar]
- Bayin, S.S. Definition of the Riesz derivative and its application to space fractional quantum mechanics. J. Math. Phys. 2016, 57, 123501. [Google Scholar] [CrossRef]
- Jing, J.; Yu, T. Non-Markovian Relaxation of a Three-Level System: Quantum Trajectory Approach. Phys. Rev. Lett. 2010, 105, 240403. [Google Scholar] [CrossRef]
- Castanos, O.; Cordero, S.; Lopez-Pena, R.; Nahmad-Achar, E. Single and collective regimes in three-level systems interacting with a one-mode electromagnetic field. J. Phys. Conf. Ser. 2014, 512, 012006. [Google Scholar] [CrossRef]
- Petiziol, F.; Arimondo, E.; Giannelli, L.; Mintert, F.; Wimberger, S. Optimized three-level quantum transfers based on frequency-modulated optical excitations. Sci. Rep. 2020, 10, 2185. [Google Scholar] [CrossRef] [PubMed]
- Borzì, A.; Stadler, G.; Hohenester, U. Optimal quantum control in nanostructures: Theory and application to a generic three-level system. Phys. Rev. A 2002, 66, 053811. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, A.; Cao, N.; Xu, H.; Zheng, K.; Poon, Y.T.; Sze, N.S.; Xu, P.; Zeng, B.; Zhang, L. Observing Geometry of Quantum States in a Three-Level System. Phys. Rev. Lett. 2020, 125, 150401. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, L.P.; Li, Y.; Sun, C.P. Quantum Routing of Single Photons with a Cyclic Three-Level System. Phys. Rev. Lett. 2013, 111, 103604. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Diethelm, K.; Ford, N.; Freed, A.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Lu, L.; Yu, X. Time fractional evolution of the two-level system interacting with light field. Laser Phys. Lett. 2017, 14, 115202. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function; Springer: New York, NY, USA, 2010. [Google Scholar]
- Saxena, R.; Mathai, A.; Haubold, H. Fractional reaction-diffusion equations. Astrophys. Space Sci. 2006, 305, 289–296. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F. Error analysis of an explicit finite difference approximation for the space fractional diffusion equation with insulated ends. Anziam J. 2005, 46, C871–C887. [Google Scholar] [CrossRef]
- Liu, F.; Shen, S.; Turner, I.W. Analysis of a Discrete non-Markovian Random Walk Approximation for the Time Fractional Diffusion Equation. Anziam J. 2005, 46, C488–C504. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).