Abstract
Over the past few decades, confined quantum systems have emerged to be a subject of considerable importance in physical, chemical and biological sciences. Under such stressed conditions, they display many fascinating and notable physical and chemical properties. Here we address this situation by using two plasma models, namely a weakly coupled plasma environment mimicked by a Debye-Hückel potential (DHP) and an exponential cosine screened Coulomb potential (ECSCP). On the other hand, the endohedral confinement is achieved via a Woods-Saxon (WS) potential. The critical screening constant, dipole oscillator strength (OS) and polarizability are investigated for an arbitrary state. A Shannon entropy-based strategy has been invoked to study the phase transition here. An increase in Z leads to larger critical screening. Moreover, a detailed investigation reveals that there exists at least one bound state in such plasmas. Pilot calculations are conducted for some low-lying states () using a generalized pseudo spectral scheme, providing optimal, non-uniform radial discretization.
1. Introduction
Since its inception, confined quantum systems have emerged as a subject of topical interest. Under such stressed conditions the rearrangement in atomic orbitals leads to significant changes in their energy spectra, causing fascinating behavior in hyper-fine splitting, ionization potential, static and dynamic polarizability, magnetic screening constants etc. [1,2,3,4,5]. Interestingly, in this environment the inert chemical systems like N, He, and Ar become reactive; also, the sintering effect in organo-metallic catalysts gets reduced. It is needless to mention that the discovery of such artificial systems has opened up several interesting possibilities in almost all fields of science, and in technology. For example, in the realm of quantum computers, researchers have proposed an alternative way where the qubits are formed using the concept of confinement. This is possible because of the isolating property of endohedral fullerenes which almost perfectly isolate the atomic properties, particularly the spin of an atom/ion trapped inside, as it plays a vital role in carrying the information [6,7,8,9]. More applications can be found in photo-voltaic materials [10], semiconducting nano-crystals [11], fusions experiments [12], hydrogen storage [13] and medicinal science [14].
Ever since the early stage of their discovery, endohedral systems like fullerene [15] and supra-molecular structures like crown ether, graphene tubes were utilized to trap quantum systems. The variety in size and shape of cavity (which is directly dependent on number of carbon atoms) has helped researchers to trap systems as small as H atom to larger ones like HO, alkali atoms, Xe [16,17,18] etc. Several spectroscopic quantities like oscillator strength (OS) [19,20], polarizability [21], photo ionization cross-section [22] and stopping cross-sections [23] were reported in such scenarios. Apart from that, Shannon entropy and Fisher information [24] were also studied. Interestingly, these systems can also explain the shell-confinement model. In recent works, Gaussian well and Woods-Saxon (WS) model potentials are used to mimic endohedral confinement, besides the square well potential [24,25,26,27,28]. It appears that, generally speaking, the WS model is a better fit when compared with experimental observations in such confinement studies. The presence of a smoothing parameter in the potential gives an advantage in changing the nature of the curve from soft to sharp and vice-versa.
In a plasma environment, Coulomb and thermal energy play a pivoting role in determining the strength of coupling. Moreover, factors like electron density (n) and temperature (T) are critical because they equilibrate the bound states of a given system. The coupling constant is expressed as the ratio of average Coulomb energy and average thermal energy,
where Q signifies the charge of particle, a refers to the inner-particle separation, is the usual Boltzmann constant. This presents two different scenarios: (i) , when n is low and T is high, making thermal energy larger than Coulomb energy; this is generally known as weak coupled plasma, (ii) , when n is high but T is low, causing thermal energy smaller than Coulomb energy; this is usually referred to as strongly coupled plasma.
A prototypical example of weakly coupled plasma is Debye-Hückel potential (DHP), provided by introducing an exponential term in the Coulomb potential [29]. It has been investigated extensively; the literature is quite vast. Energy spectra, [30,31,32,33], transition probabilities with electron-impact excitation [34,35], OS, polarizability [36,37,38,39,40,41], inelastic electron-ion scattering [42,43], two-photon transition [44,45], Shannon entropy and Fisher information [46], mean-excitations energy [47] were studied with great interest. Research was also conducted to estimate the critical screening parameter [48], , beyond which no bound state exists.
When the Debye radius becomes comparable to the de broglie wavelength, a quantum effect starts to appear. Thus, we use exponential cosine screened Coulomb potential (ECSCP), where a cosine function is multiplied with the usual DHP; this invokes the composite screening and wake effect around a slow-moving charge in a low-density quantum plasma. This is due to the fact that statistical pressure is preponderated by the quantum force of plasma electrons. This potential is examined intensely using the perturbation and variational method, the shooting method, the super-symmetric perturbation method, the Padé scheme, basis-expansion with Slater-type orbitals, the generalized pseudo-spectral (GPS) method, the Laguerre polynomial and so on. Besides eigenvalues and eigenfunctions, several important spectroscopic properties like OS, polarizability and the photo-ionization cross-section were under examination [48,49,50,51,52,53,54,55,56,57,58].
In a recent work, astrophysicists have discovered the existence of fullerene entrapped plasmas in interstellar space. This also includes radioactive atoms and fusion products [59,60,61]. This has triggered the investigation of such systems in both free and confined conditions. As a consequence, properties like , OS (dipole), photo-ionization cross-section, static dipole polarizability, mean excitation energy and electronic stopping cross-section were investigated for different well depths, including the avoided crossing region in endohedral H atom embedded in a Debye plasma [62]. To the best of our knowledge, the literature is rather scarce for the current system under study. In this context, we want to explore the trapping of an H-like plasma (modeled through DHP and ECSCP) under endohedral environment. In order to proceed, at first we engage the accurate and efficient GPS method for calculating eigenvalues and eigenfunctions of the corresponding Schrödinger equation (SE). Then quantities like , OS and polarizability are studied. Later we also explore the behavior of such a system under external high pressure. For this, we have used two different models, namely, (i) DHP under WS (DHPWS) and (ii) ECSCP under WS (ECSCPWS). Following [63], where the s were estimated through a Shannon entropy criterion for free DHP and ECSCP, here we employ the same procedure to report these under a confinement environment. This is performed for ℓ values ranging from 0–4, while Z remains 1 or 2. The OS and polarizability are calculated varying for some selective values of confinement radius, , and for some large (≈∞) with for 1s, 2s and 2p states. The article is organized as follows: Section 2 gives a brief introduction to the theoretical formalism, Section 3 discusses the obtained results, and finally some concluding remarks are made in Section 4.
2. Theoretical Formalism
The time-independent radial SE for the spherically confined plasma system is expressed as (in a.u.):
Here, the total wave function is of which is the radial wave function and is the spherical harmonics. The first term of this equation denotes the usual kinetic energy of electrons. To represent the excited states, we need to add the angular contribution and thus the second term. The last two terms signify the potential models characterizing the plasma through , and the fullerene cavity through . To calculate energy and spectroscopic properties, we have employed a non-uniform, optimal radial discretization scheme via GPS method. Its accuracy and efficiency in calculating various bound-state properties have been reported in our previous papers in the case of several central potentials in both free and confined condition. For more detailed information, readers are referred ([64,65,66,67,68,69] and therein).
In this article, we employ three different plasma model potentials to simulate the experimental environment. First, a DHP model, where the collective screening by plasma electron is mapped and expressed as,
Here, the probability of finding plasma electrons inside the Debye sphere is negligible. Moreover, the inequalities ensure that the charge cloud remains confined. The second model used is called ECSCP, which accounts for the fact that with an increase in plasma density the Debye radius becomes commensurable to de Broglie wavelength, which emerges in the form of quantum effects [70]. This is accomplished by taking a potential of the following form,
The cosine function helps to achieve a stronger screening effect than the DHP. Then, we also make use of the (WS) potential to model fullerene as an external confinement. Within this framework, to get the desired effect of endohedral fullerene confinement, parameters like the radius of the fullerene cavity , thickness of fullerene shell , as well as two fitting parameters, namely (defining well depth) and (a suitable smoothing parameter) are necessary. It is mathematically expressed as,
In this work, parameters are fixed as follows: , , and , which are used to describe endohedral confinement in numerous references [71,72,73,74,75,76].
2.1. Oscillator Strength and Polarizability
The static multi-pole polarizability can be expressed in following form,
There are mainly two approaches to calculating static polarizability. The first one is direct computation using a perturbation theory framework. The second one is a sum-over-state method. The latter is more convenient to express and has a compact form in nature. That is why we have used this approach. Accordingly, the -pole static polarizability is expressed as,
On the right, the two terms signify the polarizability contributions from bound states and continuum states, respectively. Moreover, denotes multi-pole OS where k is a positive integer, while is the energy difference between the transition states.
The -pole OS can be expressed as:
Designating the initial and final states as and , one derives the mean OS as,
This is a necessary part because the mean OS does not depend on the magnetic quantum number. Thereafter we apply Wigner-Eckart theorem and sum rule for 3j symbol [77] leading us to,
The transition matrix element may be expressed by the following,
In this article, we aim to compute dipole polarizability and OS for states. The relevant selection rule for dipole OS () for these states are ( or 2),
It is important to mention that there exists an OS sum rule [78,79] in literature. To show that all the transition states are rendered properly it is customary to verify what it holds. It is denoted by and the respective sum rule is given by,
2.2. Shannon Entropy
Shannon entropy (S) is a statistical quantity and a function of density. It is the arithmetic mean of uncertainty associated with a given state. Therefore, it can be aptly used to measure the change in density at the point of transition from bound to continuum state. It has been observed before that, at that point, jumps suddenly. It is recently used to investigate confined systems [80,81,82,83]. Mathematically, these are written as,
Here, is the normalized position-space density, while corresponds to momentum-space density. This work incorporates to characterize in the mixed potential condition.
3. Result and Discussion
The result will be discussed in three subsections. At the onset, it may be noted that all calculations are achieved by keeping the pseudo-spectral parameter fixed at (mapping parameter) and (number of grid points). At first, we present the calculated s for both DHPWS and ECSCPWS through Shannon entropy. This will allow us to investigate the phase transition in plasma systems. Then we look into the dipole OS and polarizability for these pair of H-like plasmas embedded in the fullerene cavity, taking . It is necessary to mention that, for the purpose of calculation, we have kept . Pilot calculations are conducted in ℓ = 0–5 states using the experimental values mentioned in Section 2.
3.1. Critical Screening Constant in DHPWS and ECSCPWS
In a plasma system, the number of bound state decreases with an increase in . The characteristic at which a bound state vanishes is termed as , i.e., beyond which no bound state exists. In the present endeavor, our objective is to find the effect of the fullerene environment on . In practice, is determined by the sign change argument of energy (−ve for bound state and +ve continuum state). Interestingly, in a recent paper [63], the authors have successfully used to determine the same. At , it jumps suddenly to a higher value indicating the conversion from a bound to a continuum state. Thus, at that point , explaining a first-order phase transition. In general, this occurs when . We know that, is a function of T. Therefore, one can identify as a first-order phase transition point. Figure 1 depicts the behavior of calculated against for circular node-less states, having 0–2 in DHPWS (panel I) and ECSCPWS (panel II), having . Similarly, Figure 2 portrays the variation of as functions of for some other states like, , with and 2 in DHPWS (panels I) and ECSCPWS (panels II) systems. A detailed analysis of these figures reveals the following:
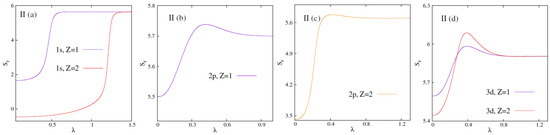
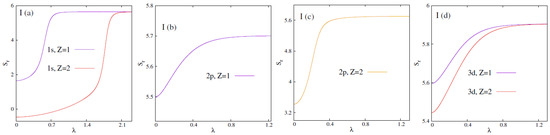
Figure 1.
Plot of as function of for states; bottom (I) and top (II) panels refer to DHPWS and ECSCPWS, having . See text for details.
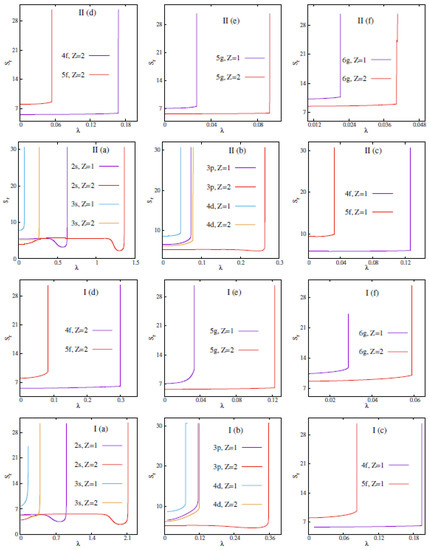
Figure 2.
Plot of as function of for ; bottom (I) and top (II) panels refer to DHPWS and ECSCPWS, having . See text for details.
- At the onset, it should be mentioned that the qualitative behaviour of with in DHPWS and ECSCPWS are quite similar.
- Panels (I), (II) in Figure 1 show that there exists at least three bound states in either of the fullerene trapped plasmas. Because, in both cases, circular or node-less states with 0–2 are never going to be deleted. As a consequence, no abrupt jump in is observed. In these states increases with and finally converges to the respective limiting values.
- Panels (I), (II) of Figure 2 suggest that, for a given state, there exists a characteristic at which the value jumps suddenly, signifying the phase transition. The position of these gets right shifted with a rise in Z. Here, a first order phase transition happens in both the plasmas involving states.
- These observations lead us to the conjecture that, in these two fullerene trapped plasmas, phase transition occurs for all states. However, for 0–2 states, a similar phenomenon occurs only when .
Apart from the above procedure, we have also estimated using the usual sign-change argument of energy for the same set of states explored above. Results are collected in Table 1 at two selected Z (1, 2) for both DHPWS and ECSCPWS. It is worth mentioning that these results corroborate all the inferences drawn from Figure 1 and Figure 2. Moreover, the present result of in DHPWS is in complete consonance with the observation (obtained by energy sign change) given in [62], as evident from the entries provided in the footnote of Table 1. However, the pattern in ECSCPWS could not be found in the literature; here they are reported for the first time. Now, we move to investigate dipole OS and polarizability for these pair of fullerene-trapped plasmas in both the confined condition and at the free regime as a limiting case. Note that some of the entries are left blank indicating no in such occasions.

Table 1.
Calculated for H-like ions for states in DHPWS and ECSCPWS (). See text for details.
3.2. Dipole Oscillator Strength
In this section, we aim to discuss dipole OS for free and confined fullerene-trapped plasmas. It may be noted that, acts as a cornerstone in estimating several spectroscopic properties, like polarizability, mean excitation energy etc. The ve value of indicates absorption, whereas a ve value signifies emission. With progress in , the probability of radiative transition increases in comparison to its non-radiative counterpart. On the contrary, explains non-radiative transitions. Here, calculations are conducted at three selected values, namely and infinity.
In the case of , the selection rule for dipole transition is . Thus, the transition may be possible only to states. However, for p and d states, transitions may occur to and states, respectively. Table 2, at first, reports the calculated for 1s, 2p and 3d states at several selected , keeping fixed at and , addressing all possible modes of transition allowed by the selection rule. Here, columns 2–6 represent DHPWS and columns 7–10 signify ECSCPWS. In both situations, at a given Z and , decreases to reach a minimum, and then rises to a maximum before achieving the limiting value. Further, at a fixed , on moving from to 2, the position of the minimum gets right shifted. On the contrary, for indicates emission. Here, at a fixed Z and , increases to attain a maximum and declines thereafter; the position of the maximum moves toward the right with Z. The transition suggests absorption. In this case, imprints a distinctly different pattern in DHPWS and ECSCPWS. In DHPWS a shallow maximum is seen at , . However, at it decreases with . On the contrary, at and it passes through a maximum. In ECSCPWS for (when ) it reduces with . However, at , it decreases to reach a minimum then climbs a maximum and then again declines to a minimum. As expected, explains emission. In this case, we observe more or less an opposite pattern to . In DHPWS, abates with at and . However, in case of it passes through a maximum. Now, we move to discuss the behavior of in either of the plasmas at involving these five transitions. Table 3 records the same for these two plasmas at some selected value, keeping and 2. It is observed that variation of in free systems is different from their confined counterparts. Moreover, at drops sharply to reach a minimum and then climbs up to a maximum. Similarly, for , it passes through a minimum. For the transition we observe a reverse trend. Now, for transition, in DHPWS (i) we observe a decreasing pattern at (ii) but at , we see a maximum. In ECSCPWS, at , a minimum is noticed. At , there appears a maximum followed by a minimum. Here, imprints similar trends to . Finally, we derive a decreasing curve for transition in both the plasmas.

Table 2.
values for DHPWS and ECSCPWS for fixed and , using and .

Table 3.
values for DHPWS and ECSCPWS for and , using and .
The above observations of Table 2 and Table 3 are rather sketchy. To derive a clearer picture, we have plotted for DHPWS and ECSCPWS in Figure 3 and Figure 4 as function of , respectively, at three selected values, keeping and 2. The transitions shown correspond to (a) (b) (c,d) (e,f) and (g,h) . Panels (c,e,g) correspond to while (d,f,h) produce the same for . It is found that in DHPWS and ECSCPWS are quite similar. A careful examination reveals that, all these plots corroborate the inferences drawn from Table 2 and Table 3.
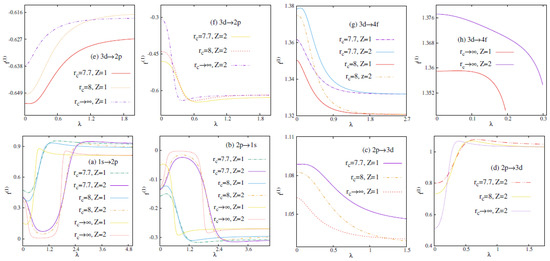
Figure 3.
Plot of as function of in DHPWS potential for selected transitions mentioned in the panels (a–h), for . See text for details.
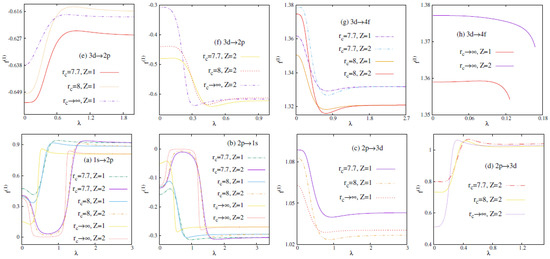
Figure 4.
Plot of as function of in ECSCPWS potential for selected transitions mentioned in the panels, for . See text for details.
3.3. Polarizability
In this subsection now, we proceed to discuss for states. It can have ve as well as ve values. When emission predominates over absorption, we derive ve values. On the contrary, a ve values indicates that, absorption contribution has overcome the respective emission part. For the ground state, it is always ve. However, for excited states, it can have either sign. Here, results are presented for states involving infinity having Z values 1 and 2.
In Table 4, we have shown the results for for these three states at and . Columns three to six represent DHPWS while ECSCPWS results are tabulated in columns seven to ten. At a given Z and , in state it always increases with . At a given , these decrease with Z. Conversely, at a given Z, it increases with . Interestingly, for and , the pattern behavior of is not that straightforward. Depending upon the values it can have either a ve or ve sign. However, the absolute numerical values abate with Z and progress with . Table 5 indicates for both the plasmas in states at at . In state, as usual it grows with a rise in . However, in the other two cases, we observe both ve and ve results.

Table 4.
values for DHPWS and ECSCPWS for and , using and .

Table 5.
values for DHPWS and ECSCPWS for →∞ and , using and .
To probe further, we have now plotted as a function of at and infinity, keeping Z fixed at . Figure 5 and Figure 6 represent DHPWS and ECSCPWS cases, respectively. Panels (a,b) correspond to state. Similarly, panels (c–e) give the plots for state, and finally results are produced in panels (f–i). It complements the conclusion discussed in Table 4 and Table 5. However, for , and curves, one can observe discontinuities. This may appear due to a sign change in .
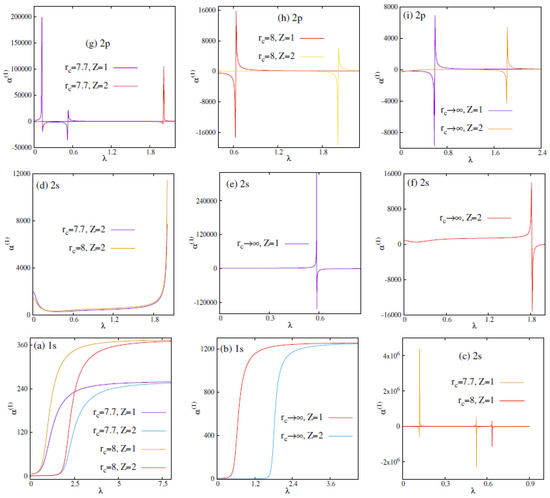
Figure 5.
Plot of as function of in DHPWS potential, for states as mentioned in the panels, for . See text for details.
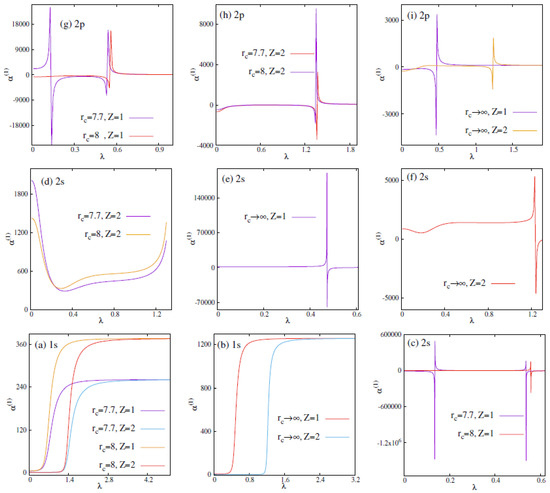
Figure 6.
Plot of as function of in ECSCPWS potential, for states as mentioned in the panels, for . See text for details.
4. Conclusions
Multi-pole oscillator strength and polarizability are estimated for H-like plasmas inside a fullerene cavity under high pressure and with special emphasis on excited states. The desired confinement condition has been imposed primarily by trapping the system under a endohedral cavity. Illustrative calculations have been undertaken for states. Negative values of and are reported here for certain excited states. The qualitative behavior of does not change with or Z. Moreover, has been studied in a free condition using . A thorough analysis reveals that, under a fullerene cavity states will never be deleted. However, for other states, at , jumps suddenly indicating a first-order phase transition. A detailed inspection of and in many-electron systems under confinement would throw some light on their understanding. Investigation of several other properties like the photo-ionization cross-section, the mean excitation energy, and the electronic stopping cross-section may also be undertaken in future.
Author Contributions
Conceptualization, N.M.; Formal analysis, N.M.; Investigation, N.M.; Resources, A.K.R.; Data curation, S.C.; Writing–original draft, N.M.; Writing—review and editing, S.C. and A.K.R.; Supervision, A.K.R.; Funding acquisition, A.K.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by SERB-DST, India (sanction order: CRG/2019/000293) and CSIR, New Delhi (grant number: 01(3027)/21/EMR-II).
Data Availability Statement
Data will be available on request.
Acknowledgments
The authors thank two anonymous referees for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Suryanarayana, D.; Weil, J.A. On the hyperfine splitting of the hydrogen atom in a spherical box. J. Chem. Phys. 1976, 64, 510. [Google Scholar] [CrossRef]
- Ley-Koo, E.; Rubinstein, S. The hydrogen atom inside boxes with paraboloidal surfaces. J. Chem. Phys. 1980, 73, 887. [Google Scholar] [CrossRef]
- Kilcoyne, A.L.D.; Aguilar, A.; Müller, A.; Schippers, S.; Cisneros, C.; Alna’Washi, G.; Aryal, N.B.; Baral, K.K.; Esteves, D.A.; Thomas, C.M.; et al. Confinement resonances in photoionization of Xe@C60+. Phys. Rev. Lett. 2010, 105, 213001. [Google Scholar] [CrossRef]
- Ndengué, S.A.; Motapon, O. Electric response of endohedrally confined hydrogen atoms. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 045001. [Google Scholar] [CrossRef]
- Motapon, O.; Ndengué, S.A.; Sen, K.D. Static and dynamic dipole polarizabilities and electron density at origin: Ground and excited states of hydrogen atom confined in multiwalled fullerenes. Int. J. Quantum Chem. 2011, 111, 4425. [Google Scholar] [CrossRef]
- Benjamin, S.C.; Ardavan, A.; Briggs, G.A.D.; Britz, D.A.; Gunlycke, D.; Jefferson, J.; Jones, M.A.G.; Leigh, D.F.; Lovett, B.W.; Khlobystov, A.N.; et al. Towards a fullerene-based quantum computer. J. Phys. Condens. Matt. 2006, 18, S867. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, B.W.; Meng, H.B.; Xu, M.X.; Wang, T.S.; Wang, B.W.; Wang, C.R.; Jiang, S.D.; Gao, S. Qubit crossover in the Endohedral fullerene Sc3C2@C80. Chem. Sci. 2018, 9, 457. [Google Scholar] [CrossRef]
- Yang, W.L.; Xu, Z.Y.; Wei, H.; Feng, M.; Suter, D. Quantum-information-processing architecture with endohedral fullerenes in a carbon nanotube. Phys. Rev. A 2010, 81, 032303. [Google Scholar] [CrossRef]
- Harneit, W. Fullerene-based electron-spin quantum computer. Phys. Rev. A 2002, 65, 032322. [Google Scholar] [CrossRef]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.O.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; Van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 2009, 8, 208. [Google Scholar] [CrossRef]
- Ornes, S. Core Concept: Quantum dots. Proc. Natl. Acad. Sci. USA 2016, 113, 2796. [Google Scholar] [CrossRef] [PubMed]
- Nishikawa, K.; Wakatani, M. Plasma Physics: Basic Theory with Fusion Applications. In Plasma Physics: Basic Theory with Fusion Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pupysheva, O.V.; Farajian, A.A.; Yakobson, B.I. Fullerene nanocage capacity for hydrogen storage. Nano Lett. 2008, 8, 767. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, H. Endohedral metallofullerenes. Rep. Prog. Phys. 2000, 63, 843. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S.; Becker, U. Strong oscillations in the photoionization of 5s electrons in Xe@C60 endohedral atoms. Phys. Rev. A 2000, 62, 012701. [Google Scholar] [CrossRef]
- Patil, S.H.; Sen, K.D.; Varshni, Y.P. Alkali atoms confined to a sphere and to a fullerene cage. Can. J. Phys. 2005, 83, 919. [Google Scholar] [CrossRef]
- Kurotobi, K.; Murata, Y. A single molecule of water encapsulated in fullerene C60. Science 2011, 333, 613. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Dolmatov, V.K. Confinement and correlation effects in the Xe@C60 generalized oscillator strengths. Phys. Rev. A 2011, 84, 063201. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Manson, S.T. A unique situation for an endohedral metallofullerene. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L395. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. Electron elastic scattering off A@C60: The role of atomic polarization under confinement. Phys. Rev. A 2015, 92, 042709. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Manson, S.T. Photoionization of atoms encapsulated in endohedral ions A@C60±z. Phys. Rev. A 2006, 73, 013201. [Google Scholar] [CrossRef]
- Moretto-Capelle, P.; Bordenave-Montesquieu, D.; Rentenier, A.; Bordenave-Montesquieu, A. Interaction of protons with the C60 molecule: Calculation of deposited energies and electronic stopping cross sections (v ≤ 5 au). J. Phys. B At. Mol. Opt. Phys. 2001, 34, L611. [Google Scholar] [CrossRef]
- Martínez-Flores, C. Shannon entropy and Fisher information for endohedral confined one-and two-electron atoms. Phys. Lett. A 2021, 386, 126988. [Google Scholar] [CrossRef]
- Martínez-Flores, C.; Cabrera-Trujillo, R. Derived properties from the dipole and generalized oscillator strength distributions of an endohedral confined hydrogen atom. J. Phys B At. Mol. Opt. Phys. 2018, 51, 055203. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Baltenkov, A.S.; Connerade, J.P.; Manson, S.T. Structure and photoionization of confined atoms. Radiat. Phys. Chem. 2004, 70, 417. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2010, 44, 015003. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Photoionization of atoms encapsulated by cages using the power-exponential potential. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 145001. [Google Scholar] [CrossRef]
- Bates, D.; Bederson, B. Advances in Atomic and Molecular Physics; Academic Press: Cambridge, MA, USA, 1989; Volume 25. [Google Scholar]
- Soylu, A. Plasma screening effects on the energies of hydrogen atom. Phys. Plasmas 2012, 19, 072701. [Google Scholar] [CrossRef]
- Bahar, M.K.; Soylu, A. The hydrogen atom in plasmas with an external electric field. Phys. Plasmas 2014, 21, 092703. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Hydrogen atoms in Debye plasma environments. Phys. Plasmas 2009, 16, 063302. [Google Scholar] [CrossRef]
- Bahar, M.K.; Soylu, A.; Poszwa, A. The hulthén potential model for hydrogen atoms in debye plasma. IEEE Trans. Plasma Sci. 2016, 44, 2297. [Google Scholar] [CrossRef]
- Jung, Y.D. Semiclassical transition probabilities for the electron-impact excitation of hydrogenic ions in dense plasmas. Phys. Plasmas 1995, 2, 332. [Google Scholar] [CrossRef]
- Jung, Y.D.; Yoon, J.S. Plasma-screening effects on semiclassical ionization probabilities for the electron-impact ionization of hydrogenic ions in dense plasmas. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 3549. [Google Scholar] [CrossRef]
- Saha, B.; Mukherjee, P.K. Effect of Debye plasma on the structural properties of compressed positronium atom. Phys. Lett. A 2002, 302, 105. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Bound-bound transitions in hydrogenlike ions in Debye plasmas. Phys. Rev. A 2008, 78, 062511. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Static dipole polarizability of hydrogenlike ions in Debye plasmas. Phys. Rev. A 2009, 80, 032502. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wu, Y.; Wang, J.G.; Qu, Y.Z. The generalized oscillator strengths of hydrogenlike ions in Debye plasmas. Phys. Plasmas 2009, 16, 023502. [Google Scholar] [CrossRef]
- Das, M. Transition energies and polarizabilities of hydrogen like ions in plasma. Phys. Plasmas 2012, 19, 092707. [Google Scholar] [CrossRef]
- Kang, S.; Yang, Y.C.; He, J.; Xiong, F.Q.; Xu, N. The hydrogen atom confined in both Debye screening potential and impenetrable spherical box. Cent. Eur. J. Phys. 2013, 11, 584. [Google Scholar] [CrossRef]
- Gutierrez, F.A.; Diaz-Valdes, J. Effects of non-spherical screening for inelastic electron-ion scattering. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 593. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jung, Y.D. Spherical versus nonspherical plasma-screening effects on semiclassical electron–ion collisional excitations in weakly coupled plasmas. Phys. Plasmas 1996, 3, 3291. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Three-photon transitions in the hydrogen atom immersed in Debye plasmas. Phys. Rev. A 2009, 79, 032714. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Two-photon transitions in hydrogen atoms embedded in weakly coupled plasmas. Phys. Plasmas 2008, 15, 073301. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-theoretic measures of hydrogen-like ions in weakly coupled Debye plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Bassi, M.; Baluja, K.L. Polarizability of screened Coulomb potential. Indian J. Phys. 2012, 86, 961. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Effects of screened Coulomb (Yukawa) and exponential-cosine-screened Coulomb potentials on photoionization of H and He+. Eur. Phys. J. D 2010, 57, 21. [Google Scholar] [CrossRef]
- Lam, C.S.; Varshni, Y.P. Bound eigenstates of the exponential cosine screened coulomb potential. Phys. Rev. A 1972, 6, 1391. [Google Scholar] [CrossRef]
- Lai, C.S. Energies of the exponential cosine screened Coulomb potential. Phys. Rev. A 1982, 26, 2245. [Google Scholar] [CrossRef]
- Dutt, R.; Mukherji, U.; Varshni, Y.P. Energy levels and oscillator strengths for the exponential-cosine screened Coulomb potential in the shifted large-dimension expansion theory. J. Phy. B At. Mol. Phys. 1986, 19, 3411. [Google Scholar] [CrossRef]
- Bayrak, O.; Boztosun, I. Application of the asymptotic iteration method to the exponential cosine screened Coulomb potential. Int. J. Quantum Chem. 2007, 107, 1040. [Google Scholar] [CrossRef]
- Singh, D.; Varshni, Y.P. Accurate eigenvalues and oscillator strengths for the exponential-cosine screened Coulomb potential. Phys. Rev. A 1983, 28, 2606. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Solution of the generalized exponential cosine screened Coulomb potential. Comput. Phys. Commun. 2011, 182, 130. [Google Scholar] [CrossRef]
- Nasser, I.; Abdelmonem, M.S.; Abdel-Hady, A. J-Matrix approach for the exponential-cosine-screened Coulomb potential. Phys. Script. 2011, 84, 045001. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Bound-bound transitions in hydrogen-like ions in dense quantum plasmas. Phys. Plasmas 2016, 23, 073302. [Google Scholar] [CrossRef]
- Roy, A.K. Studies on some exponential-screened coulomb potentials. Int. J. Quantum Chem. 2013, 113, 1503. [Google Scholar] [CrossRef]
- Lai, H.F.; Lin, Y.C.; Lin, C.Y.; Ho, Y.K. Bound-state energies, oscillator strengths, and multipole polarizabilities for the hydrogen atom with exponential-cosine screened coulomb potentials. Chin. J. Phys. 2013, 51, 73. [Google Scholar]
- Kuganathan, N.; Arya, A.K.; Rushton, M.J.D.; Grimes, R.W. Trapping of volatile fission products by C60. Carbon 2018, 132, 477. [Google Scholar] [CrossRef]
- Brocławik, E.; Eilmes, A. Density functional study of endohedral complexes M@C60 (M = Li, Na, K, Be, Mg, Ca, La, B, Al): Electronic properties, ionization potentials, and electron affinities. J. Chem. Phys. 1998, 108, 3498. [Google Scholar] [CrossRef]
- Kikuchi, K.; Kobayashi, K.; Sueki, K.; Suzuki, S.; Nakahara, H.; Achiba, Y.; Tomura, K.; Katada, M. Encapsulation of radioactive 159Gd and 161Tb atoms in fullerene cages. J. Am. Chem. Soc. 1994, 116, 9775. [Google Scholar] [CrossRef]
- Martínez-Flores, C.; Cabrera-Trujillo, R. Dipole and generalized oscillator strength derived electronic properties of an endohedral hydrogen atom embedded in a Debye-Hückel plasma. Matter Radiat. Extreme 2018, 3, 227. [Google Scholar] [CrossRef]
- Mukherjee, N.; Patra, C.N.; Roy, A.K. Confined hydrogenlike ions in plasma environments. Phys. Rev. A 2021, 104, 012803. [Google Scholar] [CrossRef]
- Roy, A.K. Studies on bound-state spectra of Manning–Rosen potential. Mod. Phys. Lett. A 2014, 29, 1450042. [Google Scholar] [CrossRef]
- Roy, A.K. Confinement in 3D polynomial oscillators through a generalized pseudospectral method. Mod. Phys. Lett. A 2014, 29, 1450104. [Google Scholar] [CrossRef]
- Roy, A.K. Ro-vibrational spectroscopy of molecules represented by a Tietz–Hua oscillator potential. J. Math. Chem. 2014, 52, 1405. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Quantum mechanical virial-like theorem for confined quantum systems. Phys. Rev. A 2019, 99, 022123. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Analysis of Compton profile through information theory in H-like atoms inside impenetrable sphere. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 235002. [Google Scholar] [CrossRef]
- Zhu, L.; He, Y.Y.; Jiao, L.G.; Wang, Y.C.; Ho, Y.K. Revisiting the generalized pseudospectral method: Radial expectation values, fine structure, and hyperfine splitting of confined atom. Int. J. Quantum Chem. 2020, 120, e26245. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Photodetachment of H− in dense quantum plasmas. Phys. Rev. E 2010, 81, 016403. [Google Scholar] [CrossRef]
- Xu, Y.B.; Tan, M.Q.; Becker, U. Oscillations in the photoionization cross section of C60. Phys. Rev. Lett. 1996, 76, 3538. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; King, J.L.; Oglesby, J.C. Diffuse versus square-well confining potentials in modelling A@C60 atoms. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 105102. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Lakshmi, P.A.; Manson, S.T. Electron structure of endohedrally confined atoms: Atomic hydrogen in an attractive shell. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L239. [Google Scholar] [CrossRef]
- Hasoğlu, M.F.; Zhou, H.L.; Manson, S.T. Correlation study of endohedrally confined alkaline-earth-metal atoms A@C60. Phys. Rev. A 2016, 93, 022512. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181. [Google Scholar] [CrossRef] [PubMed]
- Madjet, M.E.; Chakraborty, H.S.; Rost, J.M.; Manson, S.T. Photoionization of C60: A model study. J. Phys B At. Mol. Opt. Phys. 2008, 41, 105101. [Google Scholar] [CrossRef]
- Yan, Z.C.; Babb, J.F.; Dalgarno, A.; Drake, G.W.F. Variational calculations of dispersion coefficients for interactions among H, He, and Li atoms. Phys. Rev. A 1996, 54, 2824. [Google Scholar] [CrossRef]
- Luyckx, R.; Coulon, P.H.; Lekkerkerker, H.N.W. Dispersion interaction between helium atoms. Chem. Phys. Lett. 1977, 48, 187. [Google Scholar] [CrossRef]
- Bartolotti, L.J. Oscillator strength sum rule and the hydrodynamic analogy to quantum mechanics. Chem. Phys. Lett. 1979, 60, 507. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures in free and confined hydrogen atom. Int. J. Quantum Chem. 2018, 118, e25596. [Google Scholar] [CrossRef]
- Estanón, C.R.; Aquino, N.; Puertas-Centeno, D.; Dehesa, J.S. Two-dimensional confined hydrogen: An entropy and complexity approach. Int. J. Quantum Chem. 2020, 120, e26192. [Google Scholar] [CrossRef]
- Jiao, L.G.; Zan, L.R.; Zhang, Y.Z.; Ho, Y.K. Benchmark values of Shannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Salazar, S.J.C.; Laguna, H.G.; Dahiya, B.; Prasad, V.; Sagar, R.P. Shannon information entropy sum of the confined hydrogenic atom under the influence of an electric field. Eur. Phys. J. D 2021, 75, 127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).