Centering the Born Rule

Abstract

The centered Everett interpretation solves a problem that various approaches to quantum theory face. In this paper, I continue developing the theory underlying that solution. In particular, I defend the centered Everett interpretation against a few objections, and I provide additional motivation for some of its key features.

1. Introduction

This paper is about a particular solution, to a particular problem, that arises for many different versions of the Everett interpretation of quantum theories. The problem is that these interpretations have trouble reconciling the deterministic evolution of the universe with the indeterministic outcomes of experiments. In this paper, I discuss my preferred solution at length, developing several subtle aspects of it.

Here is the problem in a little more detail. According to many different versions of the Everett interpretation, the complete physical state of the universe evolves deterministically. That state is aptly represented by a wavefunction whose evolution conforms to the deterministic Schrödinger equation. However, according to the Born rule—different versions of which are endorsed by different versions of the Everett interpretation—experimental outcomes are indeterministic. The probability that certain z-spin up electrons will eventually be seen in the x-spin up state, for example, is $\frac{1}{2}$. So the problem is: the deterministic evolution of the universe seems incompatible with the indeterministic outcomes of experiments. It is unclear what should be made of the apparent conflict between (i) the universe being deterministic, and (ii) experimental outcomes being indeterministic. Call this the ‘probability problem’ for various versions of the Everett interpretation.

To solve this problem, in other work, I formulate and defend the centered Everett interpretation of quantum theories [1]. Roughly put, according to that interpretation, the universe evolves deterministically over one class of propositions, while experimental outcomes are indeterministic over another class of propositions. The indeterminism derives from an unappreciated, and largely overlooked, kind of chance [2,3]: basically, as I argue, objective chances can be assigned to irreducibly subjective propositions such as “I will see the electron in the x-spin up state”. The objectively chancy character of those subjective propositions supports a striking, compelling solution to the probability problem; one which, among other things, avoids the shortcomings of standard solutions based on rational credences [1] (pp. 1033–1038). The principle that assigns objective chances to these subjective propositions is what I call the ‘centered Born rule’. That rule is the key to the probability problem’s solution.

Unfortunately, the centered Everett interpretation is quite complicated. In addition to drawing on theories in the philosophy of science and the philosophy of physics, it also draws on theories in linguistics, philosophy of language, logic, metaphysics, and formal epistemology. All of those moving parts make the details of the centered Everett interpretation hard to absorb.

In addition, the basic posit of the centered Everett interpretation—that apparently subjective propositions such as “I will see the electron in the x-spin up state” have objective chances of obtaining—might seem quite odd. It is unclear how the proposition expressed by that sentence, which uses the indexical ‘I’, could have an objective chance of obtaining. For this reason too, the centered Everett interpretation strikes many as bizarre.

In the present paper, I seek to clarify all this by continuing to develop the theory of the centered Everett interpretation. For starters, I defend the centered Everett interpretation against two objections that are often raised against it. Then I explain why certain posits of the centered Everett interpretation are far more attractive, and far less strange, than they might initially seem to be.

In Section 2, I present the centered Everett interpretation in more detail. In Section 3, I defend the centered Everett interpretation against an objection that, though common, is based on a false assumption about the propositions that indexicals are used to express: the objection mistakenly supposes that sentences such as “I will see the electron in the x-spin up state” sometimes express the same proposition as sentences such as “Susie will see the electron in the x-spin up state”. In Section 4, I defend the centered Everett interpretation against an objection that, though also common, is based on a false assumption about how to count branches in the Everettian universe: the objection mistakenly claims that the centered Born rule holds on a negligibly small percentage of branches. In Section 5, I explain why a certain view of the metaphysics of agents—that the centered Everett interpretation endorses—is better, overall, than alternative views of what agents are: I focus, in particular, on a view which utilizes temporal counterpart theory. Finally, in Section 6, I explain why a particular implication of the centered Everett interpretation is not as strange as one might have thought: the centered Everett interpretation implies that some laws only hold relative to particular branches, but as I argue, there is nothing problematic about that.

2. The Centered Everett Interpretation

In this section, I summarize the centered Everett interpretation. To start, I provide a rough, big-picture summary of the key idea with which the centered Everett interpretation solves the probability problem. Then I present the centered Everett interpretation itself.

By way of preparation, it is worth reviewing the distinction between uncentered propositions and centered propositions. Roughly put, uncentered propositions are expressed by sentences that do not contain any indexicals. The sentence “Susie will see the electron in the x-spin up state”, for instance, expresses an uncentered proposition since this sentence contains the name ‘Susie’. Centered propositions, in contrast, are expressed by sentences that contain indexicals. The sentence “I will see the electron in the x-spin up state”, for instance, expresses a centered proposition since this sentence contains the indexical ‘I’.

A brief but important aside: my approach to indexicals and centered propositions is based on the theory developed by Kaplan [4,5], as well as on the philosophical and logical foundations of indexicals, demonstratives, centered propositions, and de se content discussed in [6,7,8,9,10]. Now, the physics and philosophy of physics literature—surrounding Everett in particular—discuss a kind of agential subjectivity that is, in some pre-theoretic sense or other, connected to the intuitive ideas that these theories in linguistics, logic, and the philosophy of language make rigorous. However, there is a large gap between the discussions of those intuitive ideas that occur in the physics and philosophy of physics literature, and the corresponding discussions that occur in the linguistics, logic, and philosophy of language literature. This paper, along with [1], helps close that gap.

It is extremely important to note that the proposition expressed by “Susie will see the electron in the x-spin up state” is different from the proposition expressed by “I will see the electron in the x-spin up state”. In fact, the propositions are different even when both sentences are uttered by Susie. Of course, when Susie utters the latter sentence, the ‘I’ ultimately refers to her. However, the proposition she expresses, by uttering the latter sentence, is centered—and so that proposition is different from the uncentered proposition that Susie expresses by uttering the former sentence.

This distinction, between uncentered propositions and centered propositions, can be used to solve the probability problem. In rough outline, the solution is as follows: the universe evolves deterministically with respect to uncentered propositions but indeterministically with respect to centered propositions. More precisely, the universe is deterministic in the following sense: for each time t and each time $t^{\prime }$ later than t, (i) the uncentered propositions that describe various physical states of the universe at $t^{\prime }$, are determined by (ii) whatever uncentered proposition completely describes the physical state of the universe at t. The Schrödinger equation captures all of that. However, the universe is indeterministic in the following sense: for each time t and each time $t^{\prime }$ later than t, (i) the centered propositions that describe various physical states of the universe at $t^{\prime }$, are generally not determined by (ii) any of the propositions, centered or uncentered, which describe the physical state of the universe at t. That is what the Born rule captures.

Think of it this way. The Schrödinger equation implies that the universe is deterministic over the algebra of uncentered propositions—the algebra, that is, containing one proposition for each possible quantum state of the universe at each time—that describe physical reality. That is perfectly compatible with the universe being indeterministic, in the manner in which the Born rule implies, over the algebra of centered propositions which describe physical reality. So there is no conflict whatsoever between (i) the universe being deterministic and (ii) experimental outcomes being indeterministic. The determinism of the universe is confined to an algebra of uncentered propositions, and the indeterminism of the universe is confined to an algebra of centered propositions. That solves the probability problem.

The centered Everett interpretation provides an account of how, exactly, the Born rule assigns probabilities to centered propositions. In summary, the centered Everett interpretation has three components: a metaphysical account of branches and agents, a version of the Born rule that assigns objective chances to centered propositions, and an analysis of the metaphysics of those chances. Let us consider each component in turn; for more details, see [1].

First, the metaphysics of branches and agents: both branches and agents are four-dimensional entities. They extend through time as well as through space. So they are often called ‘spacetime worms’, and this view of branches and agents is often called the ‘worm view’.

Given the worm view, there is an elegant way to think about how branching works. Each branch is an approximately isolated region of the wavefunction that evolves, more-or-less, like a classical world. Each agent is part of some branch or other. For periods of time, some branches are exact physical duplicates of one another, and some agents are exact physical duplicates of one another too. However, when certain sorts of events occur—quantum experiments, for instance—some branches cease to be exact physical duplicates of some others, and the agents in those branches cease to be exact physical duplicates of each other as well.

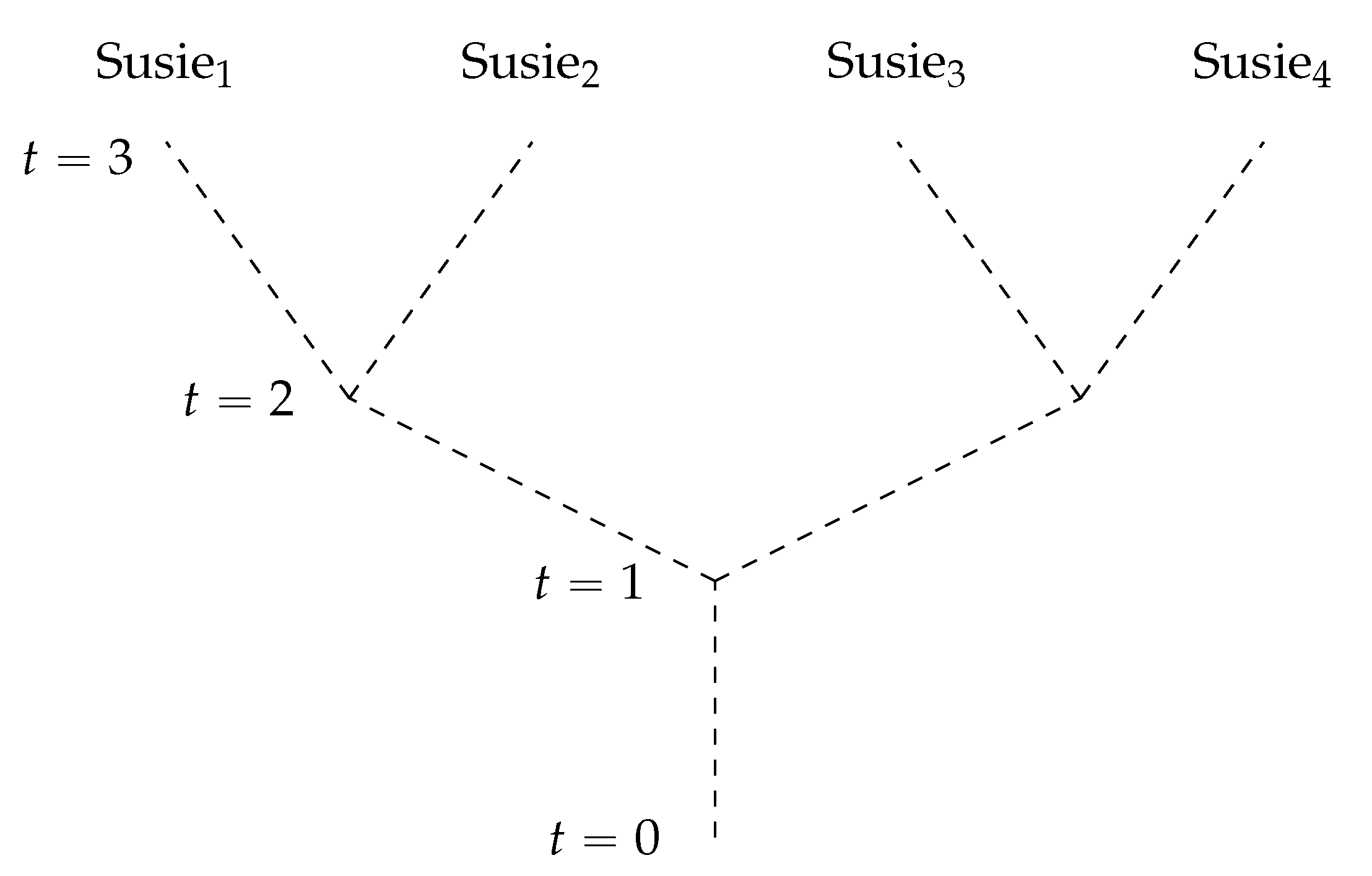
The following picture illustrates all this Figure 1.

In this picture, there are four branches, each represented by a dotted line that begins at $t=0$ and ends at $t=3$. From $t=0$ to $t=1$, all four branches are exact physical duplicates of one another; this is represented, in the picture, by the four lines overlapping. At $t=1$, a measurement occurs, and so the branches divide into two groups of two: the left two branches remain exact physical duplicates of each other, the right two branches remain exact physical duplicates of each other, but the left two branches are no longer exact physical duplicates of the right two branches. Then at $t=2$, measurements occur again: afterwards, none of the four branches are exact physical duplicates of any other branch.

Second, a version of the Born rule: this version assigns $\psi$-squared chances to centered propositions. In particular, for simplicity, let E be an agent who performs a measurement, or a community of agents who measure something, or a branch that contains some agents who perform some measurements. Let $|\psi$⟩ be the wavefunction before measurement occurs. Let $|a$⟩ be a branch, or a collection of branches, into which the wavefunction splits. Let $O_a$ be the centered proposition expressed by the sentence “I am in one of the $|a$⟩ branches”. Let $C{h}_{E,\psi }$ be a probability function that assigns chances to centered propositions such as $O_a$: think of $C{h}_{E,\psi }$ as assigning chances to propositions expressed by sentences of the form “I am in one of the thus-and-so branches”, where the chances in question are relativized to agents and to wavefunctions before measurement. Suppose that E is unsure of which branch is theirs—as all agents, in the actual world, in fact are. Then

$$C{h}_{E,\psi }\left(O_a\right)={\left|〈a|\psi 〉\right|}^2$$

Call this the ‘centered Born rule’.

Basically, the centered Born rule assigns objective chances to centered propositions. Relative to, for instance, an agent E, and relative to a wavefunction $|\psi$⟩ before measurement, the chance of the proposition expressed by “I am in one of the thus-and-so branches” obtaining is just the usual $\psi$-squared probability. These chances, which the centered Born rule associates with centered propositions, are called ‘centered chances’.

Third, the metaphysics of centered chance: the centered chances, which the centered Born rule posits, can be analyzed using the ideas that underlie the best system account of lawhood. By way of preparation for that analysis, it is worth reviewing what the best system account of lawhood is. Basically, according to that account, laws are useful summaries. To be a law, in particular, is to be an implication of the best deductive systems, where a deductive system is best just in case it best balances a variety of theoretical virtues that scientists generally value and that good summaries generally have: simplicity, strength, fit, calculational tractability, and more [11,12,13,14,15].

Uncentered chances—that is, objective chances of uncentered propositions—can be analyzed using the best system account of laws. According to that analysis, an uncentered chance is a proposition that (i) assigns a probability to some uncentered proposition, and (ii) follows from the best deductive system. Basically, an uncentered chance contributes to the best overall summary of the world, by summarizing the frequency with which a corresponding uncentered proposition, such as the proposition that a particular electron will be in the x-spin up state, obtains.

Likewise for centered chances. Basically, according to the analysis that I propose, a centered chance is a proposition that (i) assigns a probability to some centered proposition, and (ii) follows from the best deductive system. So think of it like this: a centered chance contributes to the best overall summary of the world, by summarizing the frequency with which a corresponding centered proposition—such as the proposition that I will see a particular electron in the x-spin up state after measurement—obtains.

A striking consequence of this analysis: it implies that the centered Born rule holds on some branches but not others. On some branches, namely branches where propositions expressed by sentences such as “I will see the electron in the x-spin up state” obtain with the standard $\psi$-squared frequency, the centered Born rule provides a great summary of the frequency facts; so on those branches, the centered Born rule holds. On other branches, however, the summary that the centered Born rule would provide—of the frequency facts on those branches—is terribly inaccurate, so the centered Born rule does not hold. For example, on one such branch, the proposition expressed by the sentence “I will see the electron in the x-spin up state” obtains with a frequency of 1, which of course is not the $\psi$-squared frequency that the centered Born rule would predict. On another such branch, the proposition expressed by the sentence “I will see the electron in the x-spin up state” obtains with a frequency of 0; that too is incompatible with the centered Born rule. So the centered Born rule is a law on many branches but not on all. The lawhood of the centered Born rule is branch-relative.

To summarize: the centered Everett interpretation says, basically, that the universe is deterministic over uncentered propositions and indeterministic over centered propositions. The centered Born rule captures, in precise detail, the universe’s indeterministic evolution. The four-dimensional account of the metaphysics of branches, and of agents, facilitates that. And the best system account of lawhood extends to an analysis of how centered propositions can be objectively chancy in the manner that the centered Born rule implies.

3. Utterances of Indexicals

In this section, I discuss an objection to the chances that the centered Born rule assigns. One might be tempted to make some seemingly natural assumptions about the propositions that utterances of certain sentences—featuring indexicals—express. Those assumptions imply that the chances of the centered propositions at issue must be either 0 or 1. However, as I will explain, those assumptions are false. So contrary to the objection, the relevant centered propositions can have non-null, non-unit chances, as the centered Born rule implies.

Here is the sort of situation that often leads to confusion. In Figure 1, suppose that the splits all correspond to x-spin measurements of a particular electron which, just before time $t=1$, has z-spin up. In addition, suppose that at $t=1$, the following situation obtains.

• On Susie₁’s branch and Susie₂’s branch, the electron is found to have x-spin up.
• On Susie₃’s branch and Susie₄’s branch, the electron is found to have x-spin down.

Suppose that before $t=1$, Susie₁–Susie₄ all utter the sentence “I will see the electron in the x-spin up state”: so Susie₁’s utterance is true, Susie₂’s utterance is true, Susie₃’s utterance is false, and Susie₄’s utterance is false. In addition, suppose that the centered Born rule holds on all four branches in the figure; and suppose, moreover, that each of Susie₁–Susie₄ has conducted thousands of experiments on their branch which confirm exactly that. So in the times before $t=1$, Susie₁–Susie₄ have found that centered propositions expressed by sentences of the form “I am in one of the branches where systems with thus-and-so quantum state are found, after measurement, to have such-and-such quantum state” obtain with the frequencies that the centered Born rule predicts. Therefore, each of Susie₁–Susie₄ knows that the centered Born rule holds on their branch.

Note that before t = 1, there really are four utterances which Susie₁–Susie₄ make; so long, that is, as Susie₁–Susie₄ each have a distinct temporal part at the time of utterance. Susie₁–Susie₄ are physical duplicates of each other, of course. But their temporal parts, at the time when they each utter the sentence “I will see the electron in the x-spin up state”, are distinct. That is why the problem discussed by Tappenden does not arise [16] (p. 311): Susie₁–Susie₄ successfully refer to themselves, when the utterance of that sentence occurs, because they do not literally share temporal parts at that time. And all this vindicates the view, discussed in detail by Saunders and Wallace, that agents in the Everettian universe can experience de se uncertainty before measurement [17] (p. 301).

One might object that the situation here, as I described it, is incoherent. In particular, one might object by claiming that there is a conflict between (i) the fact that Susie₁ and Susie₂ find the electron to have x-spin up while Susie₃ and Susie₄ find the electron to have x-spin down, and (ii) the fact that the centered Born rule holds on the branches containing Susie₁–Susie₄. For the chance assigned to the proposition expressed by the sentence “I will see the electron in the x-spin up state”, one might claim, should be 0 or 1, depending on the agent Susie₁–Susie₄ at issue. After all, on the branches containing Susie₁ and Susie₂, that proposition obtains: therefore, one might claim that relative to Susie₁ and relative to Susie₂—and relative to the wavefunction prior to measurement—that proposition’s chance is 1. Additionally, on the branches containing Susie₃ and Susie₄, that proposition does not obtain: therefore, one might claim that its chance—relative to those agents, and to the wavefunction prior to measurement—is 0. So the proposition expressed by the sentence “I will see the electron in the x-spin up state” cannot be assigned chance $\frac{1}{2}$. But that is the chance that the centered Born rule, if true on the branches of Susie₁–Susie₄, would assign to that proposition. So given (i), it follows that (ii) is false: given what Susie₁–Susie₄ actually observe, the centered Born rule does not hold on their branches.

This objection contains several mistakes. It is true, of course, that the proposition expressed by the sentence “I will see the electron in the x-spin up state” obtains on the branches containing Susie₁ and Susie₂. But it does not follow that the chance of this proposition, relative to Susie₁ and relative to Susie₂—and relative to the wavefunction prior to measurement—must be 1. Similarly, it is true that this proposition does not obtain on the branches containing Susie₃ and Susie₄. But it does not follow that the chance of this proposition, relative to Susie₃ and relative to Susie₄—and relative to the wavefunction prior to measurement—must be 0. Each of Susie₁–Susie₄ utter the sentence “I will see the electron in the x-spin up state”. Susie₁ and Susie₂ speak truly: relative to them, the proposition which that sentence expresses is true. Susie₃ and Susie₄ speak falsely: relative to them, the proposition which that sentence expresses is false. But it simply does not follow, from any of this, that the chance of this proposition must be 1–relative to Susie₁ and Susie₂ (and to the wavefunction prior to measurement)–or 0–relative to Susie₃ and Susie₄ (and to the wavefunction prior to measurement).

I suspect that the confusion underlying this objection derives from a failure to properly distinguish centered propositions from uncentered propositions. By way of illustration, consider Susie₁. The objector might think that Susie₁’s utterance of the sentence “I will see the electron in the x-spin up state” expresses the proposition that Susie₁ will see the electron in the x-spin up state; for after all, Susie₁’s utterance of ‘I’ refers to Susie₁. That proposition obtains deterministically: given the initial wavefunction, that proposition must hold. So the objector concludes that the proposition expressed by Susie₁’s utterance of the sentence “I will see the electron in the x-spin up state” must have chance 1.

The mistake in the paragraph above is as follows: Susie₁’s utterance of the sentence “I will see the electron in the x-spin up state” does not express the proposition that Susie₁ will see the electron in the x-spin up state. That proposition is uncentered: it is expressed without using indexicals. But the sentence “I will see the electron in the x-spin up state” contains an indexical and because of that—and for many other reasons too—expresses a centered proposition [18,19]. So the objector is wrong to claim that the proposition expressed by Susie₁’s utterance of the sentence “I will see the electron in the x-spin up state” must have chance 1. The proposition that Susie₁ will see the electron in the x-spin up state does, of course, have chance 1 of obtaining. But the proposition expressed by Susie₁’s utterance of the sentence “I will see the electron in the x-spin up state” is definitely not that proposition; so the proposition expressed by that utterance need not have chance 1, and so that proposition can have the chance assigned by the centered Born rule.

This point is worth belaboring because it is so easy to forget. Suppose that Susie₁ utters two sentences:

(1)

“I will see the electron in the x-spin up state”

and

(2)

“Susie₁ will see the electron in the x-spin up state.”

Relative to Susie₁, the propositions expressed by those sentences are true. Nevertheless, the propositions expressed by those sentences are, despite the fact that Susie₁ is the speaker—and so Susie₁’s utterance of ‘I’ refers to herself—different: (1) expresses a centered proposition, and (2) expresses an uncentered proposition. So while the truth value of the proposition expressed by (2) is completely fixed by the deterministic evolution of the wavefunction, the truth value of the proposition expressed by (1) is not.

A crucial, related aside: when each of Susie₁–Susie₄ utter sentence (1), they each express the very same proposition, despite the fact that their respective uses of the indexical ‘I’ refer to different agents. This is simply how the standard semantics for centered propositions works [4]. If you and I both utter the sentence “I like apple pie”, for instance, then we both express the same proposition, despite the fact that our respective utterances of ‘I’ have different referents. This is related, of course, to the fact that truth values are only ever assigned—to centered propositions—relative to centers.

To summarize: there is no conflict between (i) the fact that Susie₁ and Susie₂ find the electron to have x-spin up while Susie₃ and Susie₄ find the electron to have x-spin down, and (ii) the fact that the centered Born rule holds on the branches containing Susie₁–Susie₄. Relative to Susie₁ and Susie₂—and relative to the wavefunction prior to measurement—the proposition expressed by the sentence “I will see the electron in the x-spin up state” is indeed true, and relative to Susie₃ and Susie₄—and relative to the wavefunction prior to measurement—the proposition expressed by this sentence is indeed false. But it is not the case that this sentence, when uttered by Susie₁ say, expresses the proposition that Susie₁ will see the electron in the x-spin up state. So the proposition expressed by this sentence need not be assigned chance 1. It can be assigned the chance given by the centered Born rule.

One final point: all this connects to a concern that P. Lewis raises for various versions of the Everett interpretation [20]. Basically, P. Lewis claims that no extant version of the Everett interpretation can account for non-trivial probability assignments to measurement outcomes, for the following reason: each such version of the Everett interpretation implies that prior to measurement, every agent knows with certainty (i) where they are, and (ii) what will happen to them in the future [20] (pp. 12–13). Regardless of whether that is correct for other versions of the Everett interpretation, it is not correct for the centered Everett interpretation under discussion here. Because the centered Everett interpretation is consistent with the claim that before measurement, agents cannot tell which branch they are on, the agents’ epistemic states are compatible with being on many, many different branches that are all physical duplicates of one another.

4. Counting Branches

In this section, I discuss an objection regarding the number of branches on which the centered Born rule holds. One might be tempted to assume that the centered Born rule obtains on very few branches; and on that basis, one might object to the centered Born rule. But that assumption is incorrect. Given the proper way of measuring how many branches there are, the centered Born rule obtains on most of the branches.

Here is the objection to which this confusion, about the number of branches in the universe, gives rise. Every outcome of every quantum experiment obtains on some branch or other. So there are branches in which $\frac{1}{2}$ of z-spin up electrons are found to have x-spin up, as the centered Born rule predicts. But there are also branches in which $\frac{1}{3}$ of z-spin up electrons are found to have x-spin up, and there are branches in which $\frac{2}{3}$ of z-spin up electrons are found to have x-spin up, and so on; and on all of these branches, the centered Born rule is false. Therefore, one might claim, the centered Born rule holds on a negligibly small percentage of branches. And therefore, we have no good reason for thinking that the centered Born rule holds on our branch in particular.

The main mistake, in this objection, is the claim that the centered Born rule holds on a negligibly small percentage of branches. It is certainly true that there are branches in which the centered Born rule fails. There are branches where $\frac{1}{3}$ of z-spin up electrons are found to have x-spin up; there are branches where $\frac{2}{3}$ of z-spin up electrons are found to have x-spin up; and so on. But it does not follow, from this alone, that the centered Born rule holds on very few branches. In order to draw any conclusions about the number of branches on which the centered Born rule holds, some sort of measure—over the set of all branches—must be used. For reasons I will explain, the best measure to use is the $\psi$-squared measure that the centered Born rule invokes. And given that measure, it follows that on the vast majority of branches, the centered Born rule holds. Let us see why.

By way of preparation, note that Figure 1 is a simplified depiction of branches. Strictly speaking, branches do not form discrete, countable units. There are densities of branches. So it is not as if there are exactly four branches, of which Susie₁–Susie₄ are parts. There are continuum-many branches in the Everettian universe [21] (p. 20).

Because $\mathcal{B}$ is uncountable, it can be equipped with many different measures. That is, the set $\mathcal{B}$, taken on its own—absent any considerations about chance, or the dynamics of the wavefunction, or decoherence, or any such thing—does not select out any one measure as the best way of quantifying the sizes of subsets which $\mathcal{B}$ contains; it is not as if $\mathcal{B}$ has the intrinsic structure of the real numbers, for instance. Of course, if $\mathcal{B}$ were finite, then one measure would clearly be best: the counting measure. However, since $\mathcal{B}$ is uncountable, there are many sigma-algebras and many measures that—again, absent any considerations about chance, or the dynamics of the wavefunction, or decoherence, or any such thing—all do more-or-less equally good jobs of assigning sizes to subsets that $\mathcal{B}$ contains.

All this raises a question: what is the right measure to use, for assigning sizes to subsets of $\mathcal{B}$? Which measure, that assigns sizes to those sets, is best? Which one gets the sizes of those sets right?

Note that for the purposes of evaluating the objection above, these questions really matter. To see why, let $\mathcal{C}$ be the set of branches on which the centered Born rule holds. Some measures will imply that $\mathcal{C}$ is quite large. Other measures will imply that $\mathcal{C}$ is negligibly small. So the right measure to use, for assigning sizes to subsets of $\mathcal{B}$, will determine how large $\mathcal{C}$ is. And that, in turn, will determine whether or not the centered Born rule holds on most branches, or a negligibly small percentage of branches, or something in between.

As shown by Everett, there is a natural measure to use for assigning sizes to subsets of $\mathcal{B}$: the $\psi$-squared measure [22,23]. That measure satisfies a series of reasonable conditions for quantifying the sizes of sets which $\mathcal{B}$ contains [24,25]. For instance, that measure is a function of the amplitudes of coefficients of branches in certain superpositions. Furthermore, that measure is conserved, in a certain precise sense, under the linear dynamics of the Schrödinger equation. So given reasonable constraints based on the structures of amplitudes and on wavefunction dynamics, that is the best measure for assigning sizes to sets that $\mathcal{B}$ contains.

It follows that the centered Born rule holds on the vast majority of branches. For the $\psi$-squared measure assigns a size of nearly 1 to $\mathcal{C}$. (A little more precisely: given the $\psi$-squared measure, as the number of quantum experiments increases without bound, the measure of the set of branches where the outcomes of those experiments conform to the centered Born rule converges to 1. Put in terms of the notion of typicality, which I prefer to use when quantifing the distribution of branches in the Everettian universe: in the set of all branches, the centered Born rule typically holds.) So it is false to claim that the centered Born rule holds on a negligibly small percentage of branches. The centered Born rule obtains on nearly all branches in the Everettian universe.

Let me be clear about what I have not argued. Nowhere did I claim that the centered Born rule holds on our branch because the centered Born rule holds on nearly all branches whatsoever. That sort of justification, for the centered Born rule obtaining on our branch, may be circular. For the notion of ‘nearly all’, which that sort of justification invokes, is precisified using the $\psi$-squared measure. And the $\psi$-squared measure is basically just the measure that the centered Born rule invokes. So the claim in question—that the centered Born rule holds on our branch because the centered Born rule holds on nearly all branches—may amount to a circular explanation: it may be using the centered Born rule to justify the centered Born rule. And that, of course, would be problematic.

What I have argued, rather, is this: the best measure to use, for assigning sizes to subsets of $\mathcal{B}$, is the $\psi$-squared measure. For that measure concerns the structure of wavefunction amplitudes, the sorts of dynamics which the Schrödinger equation expresses, and so on. Furthermore, according to that measure, the centered Born rule holds on nearly all branches whatsoever. So the original objection, with which this section began, is based on a false assumption.

One might respond to all this by asking: so why does the centered Born rule hold on our branch? The answer: the centered Born rule holds on our branch because it provides the best summary of the frequencies with which, on our branch, propositions expressed by sentences such as “I am in one of the thus-and-so branches” obtain. In other words, the explanation of the centered Born rule’s truth, on our branch in particular, appeals to the metaphysical view of centered chance that the centered Everett interpretation provides; the explanation of the centered Born rule’s truth, on our branch in particular, does not appeal to any claims about numbers of branches.

5. Metaphysics of Agents

In this section, I provide some motivation for the worm view that the centered Everett interpretation endorses. To do so, I discuss an alternative account of the metaphysics of agents. According to that alternative account, agents are not four-dimensional worms: they only exist at instantaneous moments. In addition, according to that alternative account, the truth conditions for tensed sentences about agents at particular times invoke other agents at other times. If all that were true, of course, then the worm view—and therefore, the centered Everett interpretation—would be false. However, as I argue, that account faces a problem that the worm view avoids, and that is a reason to endorse the worm view.

The basic idea, underlying the alternative account of the metaphysics of agents, is this: at time $t=0$, just one agent exists; let us call her ‘Susie’. So it is not as if four agents exist at $t=0$, namely, Susie₁–Susie₄. Only Susie exists at that time. And so the metaphysics of agents, which I used to formulate the centered Everett interpretation, is false.

There are many different versions of this view. According to one version, each agent is an instantaneous time-slice, and agents that exist at different times are numerically distinct from one another [26,27]. Susie, for instance, is the clump of matter that exists, just for an instant, at time $t=0$. In addition, at each specific time between $t=0$ and $t=1$, exactly one agent exists. But also, between $t=0$ and $t=1$, continuum-many agents exist: one for each particular, specific time in that range. Similarly, at each particular, a specific time between $t=1$ and $t=2$, two agents exist: one exists on the left branch of Figure 1, and the other exists on the right branch of that figure. But also, between $t=1$ and $t=2$, continuum-many agents exist on the left branch and continuum-many agents exist on the right branch: one on the left, and one on the right, for each particular, specific time in that range. And similarly for the range of times between $t=2$ and $t=3$.

A brief aside: a similar view is discussed by Vaidman [28]. Vaidman often describes the underlying issue here in terms of the meaninglessness of certain linguistic expressions [28] (p. 254). In my view, there is a better way to describe the underlying issue. The claim that certain linguistic expressions are meaningless is empirically false: it contradicts the empirical science of linguistics. It is better to claim that those linguistic expressions, while meaningful, feature in sentences that—if true—would have certain problematic implications for the metaphysics of agents. The formulation of the issue, in terms of the metaphysics of agents rather than the meaninglessness of utterances, is my focus in this section.

Temporal counterpart theory, which provides an account of the semantics of tensed sentences, can be used to express tensed facts about all these agents [26]. According to this account, temporal sentences about agents are true at the present time because of similar agents—call them ‘temporal counterparts’—at other times. These temporal counterparts are defined as follows: given an agent $A_t$ who exists at time t, a temporal counterpart of $A_t$ at time $t^{\prime }$ is an agent $A_{t^{\prime }}$ who is at least as similar to $A_t$ as each other agent at $t^{\prime }$ is. The similarity relation varies from context to context: two agents might count as extremely similar in one context but extremely dissimilar in another.

Now for temporal counterpart theory. Let t be a time, let $A_t$ be an agent who exists at t, let c be a context, and let $\varphi$ be a sentence. Then a sentence of the form “$A_t$ will be such that $\varphi$” is true at t in c if and only if at some time $t^{\prime }$ earlier than t, a temporal counterpart of $A_t$ is such that $\varphi$. Likewise, a sentence of the form “$A_t$ will be such that $\varphi$” is true at t in c if and only if at some time $t^{\prime }$ later than t, a temporal counterpart of $A_t$ is such that $\varphi$ [26] (pp. 188–208).

When combined with the Everett interpretation of quantum mechanics, however, temporal counterpart theory—and the corresponding view of the metaphysics of agents—faces a problem. To see why, let $|a_1$⟩ and $|a_2$⟩ be any two distinct possible outcomes of a measurement which occurs immediately after time $t=0$. Let Susie be the sole agent who, according to the theory currently under consideration, exists at that time. Then consider the sentence below.

(3)

Susie will be such that she finds herself on branch $|a_1$⟩, and Susie will be such that she finds herself on branch $|a_2$⟩.

Intuitively and pre-theoretically, this sentence is false. When physicists say things such as “We only ever see one outcome of a given quantum experiment”, they are best understood as claiming that sentences like (3) are falsified, empirically, by experiments in quantum physics. So a good metaphysical theory of agents in the branching Everettian universe, and a good semantic theory for tensed expressions about those agents, would imply the falsity of (3).

The problem, for temporal counterpart theory, is this: it implies that (3) is true. To see why, let c be the present context. Then according to temporal counterpart theory, for each possible outcome $|a$⟩ of a measurement that occurs immediately after $t=0$, the sentence “Susie will be such that she finds herself on branch $|a$⟩” is true at $t=0$ in c: for given any such $|a$⟩, a future time $t^{\prime }$ exists such that a temporal counterpart of Susie exists on branch $|a$⟩ at $t^{\prime }$. Therefore, according to temporal counterpart theory, the sentence “Susie will be such that she finds herself on branch $|a_1$⟩” is true at $t=0$ in c, and the sentence “Susie will be such that she finds herself on branch $|a_2$⟩” is true at $t=0$ in c. Therefore, (3)—which is the conjunction of those two sentences—is true at $t=0$ in c as well. And that seems problematic.

Note that this line of argument relies on an assumption about the logical form of (3). To see how, suppose that the language of temporal counterpart theory is a ‘Priorian object language’, in particular, a first-order language supplemented with the one-place tense operators ‘F’ and ‘P’, where ‘F’ is the analog of the English expression ‘It will be the case that’ and ‘P’ is the analog of the English expression ‘It was the case that’ [29]. Let ‘$A_{1}s$’ be the formal analog of the English sentence “Susie will be such that she finds herself on branch $|a_1$⟩”, and let ‘$A_{2}s$’ be the formal analog of the English sentence “Susie will be such that she finds herself on branch $|a_2$⟩”. Then there are two reasonable candidate translations of (3) into the Priorian object language: in particular, the sentences below.

(3.1)

$F\left(A_{1}s\right)\wedge F\left(A_{2}s\right)$

(3.2)

$F(A_{1}s\wedge A_{2}s)$

For the reasons given in the main text, temporal counterpart theory implies that (3.1) is true. In addition, temporal counterpart theory implies that (3.2) is false: for (3.2) is true if and only if there exists a future temporal counterpart of Susie who finds herself on both branches $|a_1$⟩ and $|a_2$⟩, and given some plausible assumptions about the initial wavefunction, there is no such counterpart. Now, when I claimed that temporal counterpart theory implies the truth of (3), what I meant was this: temporal counterpart theory implies the truth of the sentence which best translates (3) into the Priorian object language, namely, sentence (3.1). So I was implicitly assuming that (3.1)—not (3.2)—is the best translation of (3) into the language of temporal counterpart theory. And one might claim that (3.2) is a better translation of (3) into the language of temporal counterpart theory than (3.1) is, in which case temporal counterpart theory should be understood as implying the falsity of (3) after all.

This claim is, however, rather implausible. The English analog of (3.2) is “Susie will find herself on both branches $|a_1$⟩ and $|a_2$⟩”, which is quite different from (3). So the logical form of (3), in the Priorian object language of temporal counterpart theory, seems to be (3.1) rather than (3.2). Therefore, temporal counterpart theory really should be understood as implying, problematically, the truth of (3).

The worm view of agents, which the centered Everett interpretation invokes, does not have this problematic implication. And this is a serious point in favor of the worm view. When supplemented with a standard semantics, the worm view implies that at time $t=0$ in context c, the sentence “Susie will be such that she finds herself on branch $|a_1$⟩” is true—given the stipulation that ‘Susie’ denotes the worm which exists on branch $|a_1$—and the sentence “Susie will be such that she finds herself on branch $|a_2$⟩” is false. Therefore, when supplemented with a standard semantics, the worm view implies that at time $t=0$ in context c, (3) is false as well. So we should endorse the worm view over the alternative view, of the metaphysics of agents, discussed above.

6. Branch Relativity

In this section, I discuss a common concern about the branch-relativity of the centered Born rule. This branch-relativity might strike some as strange. But it is not strange at all. For as I explain below, the branch-relativity of the centered Born rule is an instance of a more general phenomenon: namely, that scientific laws often only hold in some regions, or regimes, of the universe.

By way of illustration, consider Mendel’s law of independent assortment. According to this law, alleles for separate traits are passed down, from parents to offspring, independently of each other. The chance of a pea inheriting a particular color from its parents, for instance, is independent of the chance of that pea inheriting a particular shape from its parents.

Quite plausibly, Mendel’s law of independent assortment only holds in some regions of the universe. As numerous experiments have confirmed, it holds—to a reasonably high degree of accuracy—for evolutionary processes on Earth. But there may be other planets, out there in the universe, on which Mendel’s law of independent assortment does not hold. The evolutionary processes that these worlds support would be quite different, of course, from the evolutionary processes that Earth supports. But those other worlds, with those other evolutionary processes, are still perfectly possible. And in fact, on certain branches in the Everettian universe, there will almost certainly be planets like these: there will almost certainly be planets on which life evolves, but on which Mendel’s law of independent assortment is false.

So Mendel’s law of independent assortment is region-relative. It holds in some regions of the Everettian universe, but not in others. Its lawhood varies from place to place.

Likewise for the centered Born rule. On some branches in the Everettian universe, the centered Born rule holds. But on other branches, where the frequencies with which certain propositions obtain differ from the $\psi$-squared probabilities, the centered Born rule is false. So the lawhood, of the centered Born rule, varies from place to place. That is all it means to claim that the centered Born rule is a law on some branches but not on others. That is all it means to claim that the lawhood, of the centered Born rule, is branch-relative.

So do not be too bothered by the branch-relativity of the centered Born rule. Plenty of special science laws exhibit an entirely analogous kind of relativity. In fact, arguably, pretty much every scientific law ever discovered exhibits a relativity of roughly this sort. For pretty much all such laws only hold in some domain or other. Laws of evolutionary biology only hold for certain sorts of biospheres. Laws of economics only hold for certain sorts of monetary systems. Even laws of quantum field theories, like the equations of motion generated by the Lagrangian density for quantum electrodynamics, only hold in certain energy regimes; for sufficiently short length scales, the physics is unknown.

Note that I have not proposed an account of what it is, exactly, for a law to hold relative to a region of the universe. There are many such accounts with which the centered Everett interpretation is compatible. Let me list three.

First, perhaps lawhood is a two-place relation rather than a one-place property. This two-place relation obtains between (i) certain regularities, and (ii) certain corresponding regions of reality. So for instance, it is incorrect to say that Mendel’s law of independent assortment is a law, full-stop. It is correct, instead, to say that Mendel’s law of independent assortment stands in the lawhood relation to a particular region, such as Earth. Similarly, it is incorrect to say that the centered Born rule is a law, full-stop. Rather, it is correct to say that the centered Born rule stands in the lawhood relation to our branch. And strictly speaking, it is incorrect to say that the Schrödinger equation is a law, full-stop. Rather, it is correct to say that the Schrödinger equation stands in the lawhood relation to the entire Everettian universe.

Second, perhaps there are many numerically distinct one-place properties of lawhood, one for each region that the universe contains. The regions basically function as indices on different lawhood predicates. So there is the one-place property of being a law_Earth, the one-place property of being a law_{our branch}, and so on.

Third, perhaps laws always come equipped with certain statements that specify those laws’ domains of applicability. So strictly speaking, the sentence “Alleles for separate traits are passed down, from parents to offspring, independently of each other” does not itself express a law. Rather, the relevant law here is expressed by something like this: “On Earth, alleles for separate traits are passed down, from parents to offspring, independently of each other”. Similarly, the earlier statement of the centered Born rule does not, itself, express a law. Rather, the relevant law is expressed by something like this: “On our branch, …,” where the statement of the centered Born rule goes in for the ellipses. And statements of nomic regularities which hold absolutely everywhere, like the Schrödinger equation, would not themselves express laws. Rather, the relevant laws would be expressed by something like this: “Absolutely everywhere, …,” where again, the statement of the law at issue goes in for the ellipses.

The centered Everett interpretation is compatible with each of these accounts of what it is for a law to hold relative to a region of the universe. The reader is welcome to adopt whichever they prefer. Or the reader is welcome to develop their own account of the region-relativity of regularities such as Mendel’s law of independent assortment, the centered Born rule, and so on. That would also be compatible with the centered Everett interpretation.

7. Conclusions

According to the centered Everett interpretation, the universe (i) evolves deterministically with respect to uncentered propositions, but (ii) evolves indeterministically with respect to centered propositions. The Schrödinger equation describes the universe’s deterministic evolution. The centered Born rule, which assigns objective chances to centered propositions, describes the universe’s indeterministic evolution.

There is much to like about the centered Everett interpretation. It avoids a problem connected to the propositions expressed by sentences featuring indexicals. It avoids a problem connected to the number of branches in the Everettian universe. It is based on a view of agents—the worm view—which is better than a standard alternative. And it posits a form of branch relativity that is entirely analogous to the more general phenomenon of some laws only ever holding in some regions of the universe. So the centered Everett interpretation is worth taking seriously.