Tuning Logical Phi-Bit State Vectors in an Externally Driven Nonlinear Array of Acoustic Waveguides via Drivers’ Phase

Abstract

We experimentally navigate the Hilbert space of two logical phi-bits supported by an externally driven nonlinear array of coupled acoustic waveguides by parametrically changing the relative phase of the drivers. We observe sharp phase jumps of approximately 180° in the individual phi-bit states as a result of the phase tuning of the drivers. The occurrence of these sharp phase jumps varies from phi-bit to phi-bit. All phi-bit phases also possess a common background dependency on the drivers’ phase. Within the context of multiple time scale perturbation theory, we develop a simple model of the nonlinear array of externally driven coupled acoustic waveguides to shed light on the possible mechanisms for the experimentally observed behavior of the logical phi-bit phase. Finally, we illustrate the ability to experimentally initialize the state of single- and multiple- phi-bit systems by exploiting the drivers’ phase as a tuning parameter. We also show that the nonlinear correlation between phi-bits enables parallelism in the manipulation of two- and multi-phi-bit superpositions of states.

1. Introduction

A “phi-bit” [1] is a two-state degree of freedom in an acoustic wave (an acoustic spin), which can be in a coherent superposition of states with complex amplitude coefficients. Phi-bits are, therefore, analogs of qubits. So far, phi-bits have been theoretically, computationally, and experimentally studied in the externally driven nonlinear arrays of coupled acoustic waveguides [2]. Acoustic quantum analogs readily extend beyond the qubit paradigm into qutrit and even qudit analogs [3]. Subsequently, we theoretically, computationally, and experimentally (demonstrated) introduced the notion of a logical phi-bit [4]. A logical phi-bit is a two-state degree of freedom in the spectral domain of nonlinear acoustic modes supported by the externally driven arrays of coupled waveguides. We demonstrated the exponentially complex and scalable Hilbert space of the states of multiple logical phi-bits (≤16 with 2¹⁶-dimensional space) and the nonseparability of coherent superpositions [4]. The applicability of logical phi-bits to the development of a classical, acoustic-based quantum-inspired information processing platform necessitates that phi-bits and their supporting array of waveguides satisfy the DiVincenzo five criteria for the physical construction of a quantum computer [5].

Criterion 1: “A scalable physical system with well-characterized qubit”. Logical phi-bits live within the same driven nonlinear array of coupled acoustic waveguides. They occupy the same real estate—the phi-bit physical system does not need to scale physically. Since phi-bits are acoustic modes in the spectral domain with a bandwidth of a few tens of Hz, there is a lot of room in the ultrasonic domain for numbers of phi-bits exceeding 50, which is considered to be the threshold for quantum advantage.

Criterion 2: “The ability to initialize the state of the qubits to a simple fiducial state”. A logical phi-bit can be prepared in states spanning the Bloch sphere [4]. Multiple phi-bits can be prepared in classical entangled states (i.e., nonseparable superpositions of states) [4]. That is, a multipartite system composed of N two-level correlated logical phi-bits can support coherent superpositions of nonlinear acoustic modes spanning exponentially complex Hilbert spaces of dimension 2^N [4]. The complete Hilbert space of multi-phi-bit systems can be tiled through their representation (i.e., the choice of the basis) and by tuning the system’s driving conditions, such as the drivers’ frequency [6].

Criterion 3: “Long relevant decoherence times”. Coherent superpositions of phi-bit states are complex acoustic amplitudes. These states are not subjected to decoherence, in contrast to the probability amplitude of quantum systems, which are composed of superconducting or trapped ion qubits.

Criterion 4: “A ‘universal’ set of quantum gates”. We experimentally demonstrated the phase, Hadamard [7], and C-NOT gates [8] that form the components of a universal set. We further showed a three-phi-bit gate that would challenge qubit-based computing platforms [9].

Criterion 5: “A qubit-specific measurement capability”. Measurements in conventional quantum computing approaches, including photonic platforms [10], entail the collapse of the wavefunction. This is the destruction of the coherent superposition of states that is at the heart of the exponential scaling that leads to quantum advantage. In contrast, measurements in phi-bit systems do not alter the wave function, which persists as long as the drivers are applied.

An understanding of the nonlinear phenomena that underlie the manipulation of and correlations between phi-bits is critical to the use of phi-bits as qubit analogs for the development of quantum-analog computing platforms that can support and navigate scalable, exponentially complex Hilbert spaces. The navigation of phi-bit states in multiple correlated phi-bit Hilbert spaces is necessary to initialize (criterion 2) and operate (criterion 4) on the state of phi-bits in ways that are analogous to quantum initialization, operations, and gates. This is carried out by exploiting the correspondence between the state of correlated logical phi-bits represented in a low-dimensional linearly scaling physical space and their state representation in a high-dimensional, exponentially scaling Hilbert space. The navigation necessitates control of the state of logical phi-bits in response to parametric changes in the physical system that supports them. In Ref. [6], we utilized the frequency of the drivers to parametrically explore the phi-bit states. Here, we experimentally demonstrate the manipulation of logical phi-bits states by tuning the relative phase of the external drivers applied to the nonlinear array of coupled acoustic waveguides. Within simple models of nonlinear arrays of externally driven coupled acoustic waveguides, we also propose the possible mechanisms for the experimentally observed behaviors.

2. Materials and Methods

Logical phi-bits are supported by a nonlinear metamaterial composed of coupled elastic waveguides [4]. The waveguides are aluminum rods arranged in a linear array with epoxy-filled lateral gaps (Figure 1).

Ultrasonic longitudinal contact transducers drive and detect the acoustic field at the rod ends. Separate waveform generators excite the top and bottom driving transducers with sinusoidal signals of the same magnitude at frequency $f_1=f_3$. Another signal generator drives the middle transducer at the frequency $f_2$. With the same magnitude as the outer transducers. The relative phase, $\mathsf{\Delta }\theta$, between the signal generators’ exciting transducers 1 and 3 is controlled and can be tuned over the entire range [0–360°]. Three detecting transducers at the opposite ends collect data on the displacement field, providing temporal and spatial information across the array. Details of the experimental system are given in Ref. [6]. Temporal Fourier transforms of output signals generate spectral information. The displacement field measured at the waveguide’s detection ends is the Fourier sum of modes with the primary frequencies $f_1$ and $f_2$ as well as secondary nonlinear modes, the frequencies of which are a linear combination of the driving frequencies: $p{f}_1+q{f}_2$, where $p$ and $q$ are integers. The measured displacement field of a nonlinear mode can be expressed in the compact form:

$${\widetilde{\stackrel{\rightharpoonup }{U}}}^{\left(p,q\right)}=\left(\begin{array}{c}{C}_1{e}^{i{\phi }_1}\\ C_2{e}^{i{\phi }_2}\\ C_3{e}^{i{\phi }_3}\end{array}\right)e^{i\left(p{\omega }_1+q{\omega }_2\right)t},$$

(1)

where ${\omega }_i=2\pi f_i;i=1,2$ is the angular frequency and $C_j$ is the magnitude of the displacement of the waveguide $j;j=1,2,3$. The phases ${\phi }_1$, ${\phi }_2$, and ${\phi }_3$ arise from the complex nature of the resonant amplitudes of the driven system as well as any nonlinear effect combining these resonant amplitudes and the drivers’ phases. Equation (1) can be reformulated by normalizing the amplitude to that of the first waveguides and expressing the field in terms of phase differences only:

$$\frac{1}{C_1{e}^{i{\phi }_1}}{\widetilde{\stackrel{\rightharpoonup }{U}}}^{\left(p,q\right)}=\left(\begin{array}{c}1\\ {\widehat{C}}_2{e}^{i{\phi }_{12}}\\ {\widehat{C}}_3{e}^{i{\phi }_{13}}\end{array}\right)e^{i\left(p{\omega }_1+q{\omega }_2\right)t}$$

(2)

where ${\widehat{C}}_2$ and ${\widehat{C}}_3$ are normalized to $C_1$ and ${\phi }_{12}={\phi }_2-{\phi }_1$ and ${\phi }_{13}={\phi }_3-{\phi }_1$. We reduce this expression by dropping the direct reference to waveguide 1. We now define the displacement field at the end of the waveguides by the renormalized $2\times 1$ vector:

$${\stackrel{\rightharpoonup }{U}}^{\left(p,q\right)}=\left(\begin{array}{c}{\widehat{c}}_2{e}^{i{\phi }_{12}}\\ {\widehat{c}}_3{e}^{i{\phi }_{13}}\end{array}\right)e^{i\left(p{\omega }_1+q{\omega }_2\right)t}$$

(3)

We redefine the state of the logical phi-bit {p, q} in terms of phase difference of the displacement field only by constructing the nontemporal part of the field as the normalized complex amplitude state vectors:

$$\psi =\frac{1}{\sqrt{2}}\left(\begin{array}{c}{e}^{i{\phi }_{12}}\\ e^{i{\phi }_{13}}\end{array}\right)=\frac{1}{\sqrt{2}}\left(e^{i{\phi }_{12}}\left(\begin{array}{c}1\\ 0\end{array}\right)+e^{i{\phi }_{13}}\left(\begin{array}{c}0\\ 1\end{array}\right)\right)$$

(4)

This state vectors live in single phi-bit 2D Hilbert space, with a basis of $\left\{\left(\begin{array}{c}1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 1\end{array}\right)\right\}$. The quantities $e^{i{\phi }_{12}}$ and $e^{i{\phi }_{13}}$ represent the complex coefficient in a linear combination of the 2D basis vectors.

We can now define a logical phi-bit as a two-level, secondary nonlinear mode of vibration, the state of which is characterized by the set of frequency coefficients $\left\{p,q\right\}$ and the spatial mode associated with two independent relative phases of the displacement between the waveguides.

The mixed frequency, $p{\omega }_1+q{\omega }_2$, serves as a good quantum number for defining a logical phi-bit. The amplitude and phases at the waveguide ends can be measured unambiguously. A single phi-bit state lives in a 2D Hilbert space $h_{\left(j\right)}$. Employing Dirac’s ket notation to represent the basis vectors of that space, Equation (4) reduces to

$$\psi =\frac{1}{\sqrt{2}}\left(e^{i{\phi }_{12}}\left|0\right.\rangle +e^{i{\phi }_{13}}\left|1\right.\rangle \right)$$

(5)

A single phi-bit state represented in this form spans the Bloch sphere and is analogous to a quantum bit (qubit). Equation (5) is effectively a coherent superposition of $\left|0\right.\rangle$ and $\left|1\right.\rangle$ states with complex amplitudes, $\frac{1}{\sqrt{2}}{e}^{i{\phi }_{12}}$ and $\frac{1}{\sqrt{2}}{e}^{i{\phi }_{13}}$.

3. Results

We have conducted an experiment with the system in Figure 1 by driving waveguides 1 and 3 at the same frequency $f_1=f_3=62 \mathrm{kHz}$ and the middle waveguide 2 at a frequency of $f_2=66 \mathrm{kHz}.$The reason for choosing these driving frequencies is that, at these frequencies, the experimental aluminum rod’s (McMaster-Carr 1615T172: diameter = 1/2 inch, length = 0.6096 m, and density = 2660 kg/m³) longitudinal waves have a wavelength of around 10 cm, making propagation along rod-like waveguides almost one-dimensional [2]. 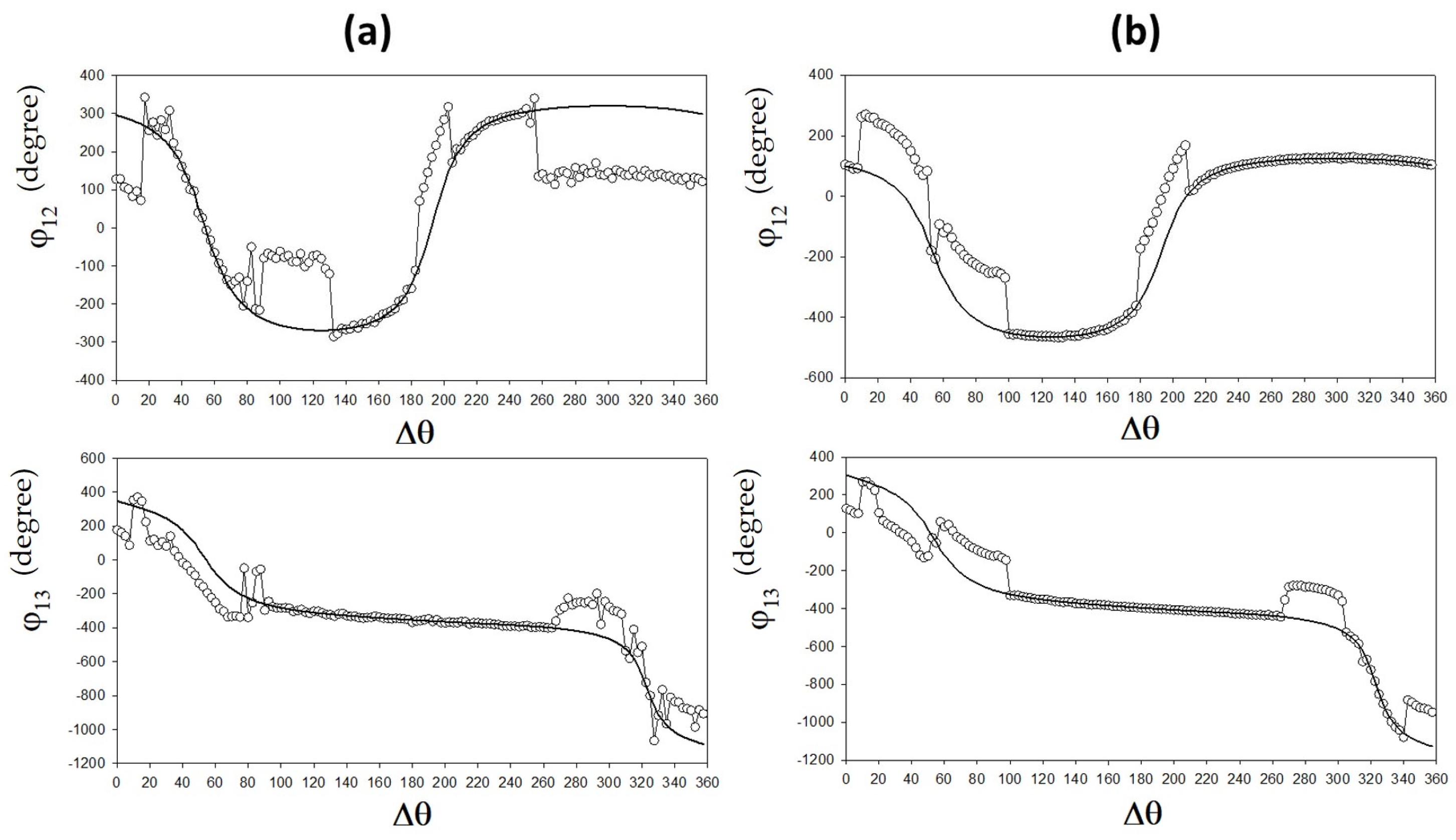Additionally, the transducers provide appropriate driving and detecting amplitudes at these frequencies, and the linear longitudinal modes of finite-length waveguides are well-defined [2]. Initially, drivers 1 and 3 are in phase, and their relative phase, $\mathsf{\Delta }\theta$, is increased by increments of 2.5° up to 360°. The displacement field at the detection ends of the waveguides is Fourier transformed. The Fourier spectrum includes primary peaks at the two frequencies $f_1$ and $f_2$ and secondary peaks at multiple frequencies, $p{f}_1+q{f}_2$, corresponding to nonlinear phi-bit modes. The complex amplitude of each phi-bit mode at the ends of the three waveguides is used to calculate the phase differences ${\phi }_{12}$ and ${\phi }_{13}$. In Figure 2, we illustrate these phase differences for two phi-bit modes, namely a phi-bit (a) with nonlinear frequency $f_a=4f_1-2f_2$ ({p = 4, q = −2}) and a phi-bit (b) with frequency $f_b=4f_1-f_2$ ({p = 4, q = −1}). In addition to the response to $\mathsf{\Delta }\theta$ of the phase differences ${\phi }_{12}$ and ${\phi }_{13}$, from phi-bits (a) and (b), we have also measured the phases ${\phi }_{12 }\left(f_{1,2}\right)$ and ${\phi }_{13 }\left(f_{1,2}\right)$ for the primary modes observed at the frequencies $f_1$ and $f_2$. We have also calculated the quantities ${\phi }_{12}^0\left(a\right)=4{\phi }_{12 }\left(f_1\right)-2{\phi }_{12 }\left(f_2\right)$ and ${\phi }_{13}^0\left(a\right)=5{\phi }_{13 }\left(f_1\right)-2{\phi }_{13 }\left(f_2\right)$, as well as ${\phi }_{12}^0\left(b\right)=4{\phi }_{12 }\left(f_1\right)-{\phi }_{12 }\left(f_2\right)$ and ${\phi }_{13}^0\left(b\right)=5{\phi }_{13 }\left(f_1\right)-{\phi }_{13 }\left(f_2\right)$. These quantities (${\phi }_{12}^0$ and ${\phi }_{13}^0$, with the superscript 0) would represent the phase differences of the phi-bits if these were simple linear combinations of ${\phi }_{12}$ and ${\phi }_{13}$ in the primary linear modes. The response of the two phi-bits is composed of two separate sets of features. ${\phi }_{12}$ and ${\phi }_{13}$ of both phi-bits (a) and (b) follow the trend of ${\phi }_{12}^0\left(a\right)$, ${\phi }_{12}^0\left(b\right)$, ${\phi }_{13}^0\left(a\right)$, and ${\phi }_{13}^0\left(b\right)$ as functions of $\mathsf{\Delta }\theta$. The variations following the linear combinations of primary mode phases will be subsequently called backgrounds. Sharp phase jumps that happen within a few degrees overlap with the backgrounds. These phase jump amount to less than 180°. Similar behaviors are observed for other phi-bit nonlinear modes.

These experimental results broach the challenging questions of the origin of the experimentally observed trends and jumps in the phases ${\phi }_{12}$ and ${\phi }_{13}$; this is in the context of enabling manipulation of phi-bit states (Equation (5)) within the Bloch sphere. The subsequent section develops a perturbative model of a nonlinear array of externally driven acoustic waveguides to offer possible answers to this question.

3.1. Model of Nonlinear Logical Phi-Bit and Effect of Drivers’ Phase on Phi-Bit State Vector

We consider a model of the acoustic metamaterial composed of three one-dimensional elastic waveguides coupled elastically along their length (Figure 3). Each waveguide is driven externally at its end at the position $x=0$. $x$ represents the position along the waveguides.

The nonlinear elastic wave equation in the long wavelength limit is written as

$$\begin{array}{l}\left[\right(\frac{{\partial }^2}{\partial t^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}+2\mu \frac{\partial }{\partial t})\overleftrightarrow{I}+{\alpha }^2\overleftrightarrow{M}]\stackrel{\rightharpoonup }{U}+\epsilon \stackrel{\rightharpoonup }{G}\left(\stackrel{\rightharpoonup }{U}\right)\\ ={\stackrel{\rightharpoonup }{F}}_1{\delta }_{x=0}\cos \left({\omega }_{1}t+{\theta }_1\right)+{\stackrel{\rightharpoonup }{F}}_2{\delta }_{x=0}\cos \left({\omega }_{2}t+{\theta }_2\right)+{\stackrel{\rightharpoonup }{F}}_3{\delta }_{x=0}\cos \left({\omega }_{3}t+{\theta }_3\right)\end{array}$$

(6)

The parameter β is proportional to the speed of sound along the waveguides. The parameter $\mu$ represents damping. $\overleftrightarrow{I}$ is the identity matrix. $\alpha$ measures the elastic coupling strength between waveguides due to epoxy. $\overleftrightarrow{M}$ is the matrix characterizing the elastic coupling between the three waveguides. In the case of our planar array of waveguides, the coupling matrix takes the form

$$\overleftrightarrow{M}=\left(\begin{array}{ccc}1& -1& 0\\ -1& 2& -1\\ 0& -1& 1\end{array}\right)$$

(7)

${\stackrel{\rightharpoonup }{F}}_1$, ${\stackrel{\rightharpoonup }{F}}_2$, and ${\stackrel{\rightharpoonup }{F}}_3$ are 3 × 1 vectors representing the external driving harmonic forces for the three different driving angular frequencies ${\omega }_1=2\pi f_1$, ${\omega }_2=2\pi f_2$, and ${\omega }_3=2\pi f_3$. ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ are the phases of the driving forces.

The displacement in waveguides 1, 2, and 3 is represented by the 3 × 1 vector $\stackrel{\rightharpoonup }{U}=\left(U_1,U_2,U_3\right)$. $\epsilon \stackrel{\rightharpoonup }{G}\left(\stackrel{\rightharpoonup }{U}\right)$ is a nonlinear term with strength $\epsilon$.

We seek analytical approximations to the nonlinear Equation (6) with three frequency excitations. For this, we consider a variation on that equation that enables us to use frequency detuning with multiple time scale perturbation theory [11,12].

$$\begin{array}{l}\left[\right(\frac{{\partial }^2}{\partial t^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}+2\epsilon \mu \frac{\partial }{\partial t})\overleftrightarrow{I}+{\alpha }^2\overleftrightarrow{M}]\stackrel{\rightharpoonup }{U}+\epsilon \delta \stackrel{\rightharpoonup }{G}(\stackrel{\rightharpoonup }{U})\\ ={\stackrel{\rightharpoonup }{F}}_1{\delta }_{x=0}\cos \left({\omega }_{1}t+{\theta }_1\right)+{\stackrel{\rightharpoonup }{F}}_2{\delta }_{x=0}\cos \left({\omega }_{2}t+{\theta }_2\right)\\ +{\stackrel{\rightharpoonup }{F}}_3{\delta }_{x=0}\cos \left({\omega }_{3}t+{\theta }_3\right)\end{array}$$

(8)

Note the additional parameter $\delta$ and the dependency of damping on $\epsilon$. A factor of 2 for multiplying the damping parameter is introduced in Equations (6) and (8) to simplify the derivation that follows. The function, $\stackrel{\rightharpoonup }{G}(\stackrel{\rightharpoonup }{U})$, models the nonlinearities that act on the waveguides along their length. It may, therefore, qualitatively represent the effect of the nonlinear elasticity of epoxy.

We introduce two time scales: ${\tau }_0=t$ and ${\tau }_1=\epsilon t$. We also expand the displacement field as the sum of the zero-order (linear) and first-order (nonlinear) terms, as follows: $\stackrel{\rightharpoonup }{U}={\stackrel{\rightharpoonup }{U}}^{\left(0\right)}\left({\tau }_0,{\tau }_1\right)+ϵ{\stackrel{\rightharpoonup }{U}}^{\left(1\right)}\left({\tau }_0,{\tau }_1\right)$. The first-order and second-order time derivatives take the form

$$\frac{\partial \stackrel{\rightharpoonup }{U}}{\partial t}=\frac{\partial {\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_0}+\epsilon \left(\frac{\partial {\stackrel{\rightharpoonup }{U}}^{\left(1\right)}}{\partial {\tau }_0}+\frac{\partial {\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_1}\right)$$

(9a)

$$\frac{{\partial }^2\stackrel{\rightharpoonup }{U}}{\partial t^2}=\frac{{\partial }^2{\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_0{}^2}+\epsilon \left(\frac{{\partial }^2{\stackrel{\rightharpoonup }{U}}^{\left(1\right)}}{\partial {\tau }_0{}^2}+2\frac{{\partial }^2{\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_1\partial {\tau }_0}\right)$$

(9b)

The wave equation to the 0th order in $\epsilon$ is effectively the linear equation:

$$\left[\left(\frac{{\partial }^2}{\partial {\tau }_0{}^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\overleftrightarrow{I}+{\alpha }^2\overleftrightarrow{M}\right]{\stackrel{\rightharpoonup }{U}}^{\left(0\right)}={\stackrel{\rightharpoonup }{F}}_1{\delta }_{x=0}\cos \left({\omega }_1{\tau }_0+{\theta }_1\right)+{\stackrel{\rightharpoonup }{F}}_2{\delta }_{x=0}\cos \left({\omega }_2{\tau }_0+{\theta }_2\right)+{\stackrel{\rightharpoonup }{F}}_3{\delta }_{x=0}\cos \left({\omega }_3{\tau }_0+{\theta }_3\right)$$

(10)

Note that there is no damping coefficient in Equation (10) as the effect of damping is now included in the first-order equation. We will see later that the phase associated with damping (included now in the first-order equation) will come back as a correction to the complex amplitude of the zero-order solution.

We can solve this equation by defining ${\lambda }_n$ and ${\stackrel{\rightharpoonup }{E}}_n$ with n = 1, 2, 3: the eigenvalues and eigen vectors of the $\overleftrightarrow{M}$ matrix, where ${\stackrel{\rightharpoonup }{E}}_n$ represents the spatial eigenmodes across the waveguides with components $E_{n,j}$, $j=1,2,3$. We write

$$\overleftrightarrow{M}{\stackrel{\rightharpoonup }{E}}_n={\lambda }_n\overleftrightarrow{I} {\stackrel{\rightharpoonup }{E}}_n$$

(11)

The eigenmodes have eigenvalues ${\lambda }_1=0, {\lambda }_2=1$ and ${\lambda }_3=3$, and are given by

$${\stackrel{\rightharpoonup }{E}}_1=\left(\begin{array}{c}{E}_{1,1}\\ E_{1,2}\\ E_{1,3}\end{array}\right)=\frac{1}{\sqrt{3}}\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right),{\stackrel{\rightharpoonup }{E}}_2=\left(\begin{array}{c}{E}_{2,1}\\ E_{2,2}\\ E_{2,3}\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right), {\stackrel{\rightharpoonup }{E}}_3=\left(\begin{array}{c}{E}_{3,1}\\ E_{3,2}\\ E_{3,3}\end{array}\right)=\frac{1}{\sqrt{6}}\left(\begin{array}{c}1\\ -2\\ 1\end{array}\right)$$

We now expand the displacement vector on the complete orthonormal basis, $\{{\stackrel{\rightharpoonup }{E}}_n\}$:

$${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}={\displaystyle \sum }_n{u}_{0,n}{\stackrel{\rightharpoonup }{E}}_n$$

(12)

The $3\times 1$ vectors, ${\stackrel{\rightharpoonup }{F}}_l$, are also expanded on the basis $\{{\stackrel{\rightharpoonup }{E}}_n\}$:

$${\stackrel{\rightharpoonup }{F}}_l={\displaystyle \sum }_n{F}_n^{\left(l\right)}{\stackrel{\rightharpoonup }{E}}_n$$

(13)

Inserting Equations (11)–(13) into Equation (10) yields a set of three equations, giving the form of

$$\left(\frac{{\partial }^2}{\partial {\tau }_0{}^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}+{\alpha }^2{\lambda }_n\right)u_{n,l}^{\left(0\right)}=F_n^{\left(1\right)}{\delta }_{x=0}\cos \left({\omega }_1{\tau }_0+{\theta }_1\right)+F_n^{\left(2\right)}{\delta }_{x=0}\cos \left({\omega }_2{\tau }_0+{\theta }_2\right)+F_n^{\left(3\right)}{\delta }_{x=0}\cos \left({\omega }_3{\tau }_0+{\theta }_3\right)$$

(14)

By employing plane wave expansions, the solutions to the homogeneous equation take the form of

$$u_{0,n}^h={\displaystyle \sum }_{k_{jn}}{\mathrm{A}}_n\left(k_{jn},{\tau }_1\right)e^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}+{\displaystyle \sum }_{k_{jn}}{\mathrm{A}}_n^{*}\left(k_{jn},{\tau }_1\right)e^{-i{k}_{jn}x}{e}^{-i{\omega }_{0,n}{\tau }_0}$$

(15)

with the dispersion relation: ${\omega }_{0,n}^2\left(k_{jn}\right)={\beta }^2{k}_{jn}^2+{\alpha }^2{\lambda }_n$. $k_{jn}$ is the jth wave number for mode n. The star in Equation (15) stands for the complex conjugate, and the superscript $h$ stands for the homogeneous solution. The summations in Equation (15) cover a discrete set of wave numbers since the waveguides have a finite length.

The particular solutions of Equation (14) that follow the temporal dependency of the driving forces are found in the form

$$\begin{array}{ll}{u}_{0,n}^p={\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,1}\left(k_{jn}\right)& e^{i{k}_{jn}x}{e}^{i\left({\omega }_1{\tau }_0+{\theta }_1\right)}+{\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,2}\left(k_{jn}\right)e^{i{k}_{jn}x}{e}^{i\left({\omega }_2{\tau }_0+{\theta }_2\right)}+{\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,3}\left(k_{jn}\right)e^{i{k}_{jn}x}{e}^{i\left({\omega }_3{\tau }_0+{\theta }_3\right)}\\ & +{\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,1}\left(k_{jn}\right)e^{-i{k}_{jn}x}{e}^{-i\left({\omega }_1{\tau }_0+{\theta }_1\right)}+{\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,2}\left(k_{jn}\right)e^{-i{k}_{jn}x}{e}^{-i\left({\omega }_2{\tau }_0+{\theta }_2\right)}\\ & +{\displaystyle \sum }_{k_{jn}}{\Lambda }_{n,3}\left(k_{jn}\right)e^{i{k}_{jn}x}{e}^{-i\left({\omega }_3{\tau }_0+{\theta }_3\right)}\end{array}$$

(16)

The quantities ${\mathsf{\Lambda }}_{n,l}\left(k_{jn}\right)=\frac{1}{2}\frac{F_n^{\left(l\right)}}{{\omega }_{0,n}^2\left(k_{jn}\right)-{\omega }_l^2}$ are real resonant amplitudes. In Equation (16), the superscript $p$ stands for a particular solution. In order to obtain Equation (16), we have expanded the cosine functions into complex exponentials.

The complete solution, therefore, takes the form

$${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}={\displaystyle \sum }_{n=1}^3{\stackrel{\rightharpoonup }{E}}_n\left(u_{0,n}^h+u_{0,n}^p\right)$$

(17)

To obtain a first order in perturbation, the wave equation is given by

$$\left[\left(\frac{{\partial }^2}{\partial {\tau }_o{}^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\overleftrightarrow{I}+{\alpha }^2\overleftrightarrow{M}\right]{\stackrel{\rightharpoonup }{U}}^{\left(1\right)}=-2\frac{{\partial }^2{\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_1\partial {\tau }_0}-2\mu \frac{\partial {\stackrel{\rightharpoonup }{U}}^{\left(0\right)}}{\partial {\tau }_0}-\delta \stackrel{\rightharpoonup }{G}({\stackrel{\rightharpoonup }{U}}^{\left(0\right)})$$

(18)

Note that the external driving force does not appear in Equation (18) as its full contribution was accounted for in the zeroth order equation. Here, the zeroth order solution now serves as a driver for the first-order equation.

We now choose a form for the nonlinear term $\stackrel{\rightharpoonup }{G}({\stackrel{\rightharpoonup }{U}}^{\left(0\right)})$ that enables us to proceed analytically and illustrate the effect of the phases ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ on nonlinear modes:

$$\stackrel{\rightharpoonup }{G}({\stackrel{\rightharpoonup }{U}}^{\left(0\right)})={{\displaystyle \sum }}_{n=1}^3{\stackrel{\rightharpoonup }{E}}_n{\left(u_{0,n}\right)}^3$$

(19)

This form assumes that the spatial modes, ${\stackrel{\rightharpoonup }{E}}_n$, do not interact with each other. However, for each spatial mode, the plane wave modes, $e^{i{k}_{jn}x}$, may interact with each other. We use a third order nonlinearity for the sake of analytical tractability.

Defining ${\stackrel{\rightharpoonup }{U}}^{\left(1\right)}={{\displaystyle \sum }}_{n=1}^3{\stackrel{\rightharpoonup }{E}}_n{u}_{1,n}$ and using Equation (14), we can rewrite Equation (18) as a set of three equation, each one corresponding to a different spatial mode:

$$\left[\frac{{\partial }^2}{\partial {\tau }_o{}^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}+{\alpha }^2{\lambda }_n\right]u_{1,n}=-2\frac{{\partial }^2{u}_{0,n}}{\partial {\tau }_1\partial {\tau }_0}-2\mu \frac{\partial u_{0,n}}{\partial {\tau }_0}-\delta {\left(u_{0,n}\right)}^3$$

(20)

The terms on the right-hand side of Equation (20) can lead to secular behavior.

In order to calculate ${\left(u_{0,n}\right)}^3$, we rewrite equation (17) as

$${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}=u_{0,n}={\displaystyle \sum }_{k_{jn}}{\xi }_n{e}^{i{k}_{jn}x}+{\displaystyle \sum }_{k_{jn}}{\xi }_n^{*}{e}^{-i{k}_{jn}x}$$

(21)

with ${\xi }_n={\mathrm{A}}_n{e}^{i{\omega }_{0,n}{\tau }_0}+{\mathsf{\Lambda }}_{n,1}{e}^{i\left({\omega }_1{\tau }_0+{\theta }_1\right)}+{\mathsf{\Lambda }}_{n,2}{e}^{i\left({\omega }_2{\tau }_0+{\theta }_2\right)}+{\mathsf{\Lambda }}_{n,3}{e}^{i\left({\omega }_3{\tau }_0+{\theta }_3\right)}$. With this, we rewrite the cubic term in Equation (20) as

$${\left(u_{0,n}\right)}^3=\left({\displaystyle \sum }_{k_{jn}}{\xi }_n{e}^{i{k}_{jn}x}+{\displaystyle \sum }_{k_{jn}}{\xi }_n^{*}{e}^{-i{k}_{jn}x}\right)\left({\displaystyle \sum }_{k_{jn}^{\prime }}{\xi }_n^{\prime }{e}^{i{k}_{jn}^{\prime }x}+{\displaystyle \sum }_{k_{jn}^{\prime }}{\xi }_n^{\prime *}{e}^{-i{k}_{jn}^{\prime }x}\right)\left({\displaystyle \sum }_{k_{jn}^{″}}{\xi }_n^{″}{e}^{i{k}_{jn}^{″}x}+{\displaystyle \sum }_{k_{jn}^{″}}{\xi }_n^{″*}{e}^{-i{k}_{jn}^{″}x}\right)$$

(22)

In this expression, since we have the product of three summations over the wave numbers, we introduced three different wave numbers, $k_{jn}$, $k_{jn}^{\prime }$, $k_{jn}^{″}$. However, to simplify the problem, we investigate the self-interaction of one single mode $k_{jn}$. We will more carefully examine two types of terms from Equation (22), those that contain the resonant frequencies of the system, ${\omega }_{0,n}$, and those corresponding to the driving frequencies, ${\omega }_n$. Beginning with those involving resonant frequencies, we seek terms in Equation (22) with a time dependency given by $e^{i{\omega }_{0,n}{\tau }_0}$. These terms will contribute to the secular behavior of Equation (20) and are grouped as

$$T_1=3A_n^2{A}_n^{*}{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}+3A_n{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}2\left({\mathsf{\Lambda }}_{n,1}^2+{\mathsf{\Lambda }}_{n,2}^2+{\mathsf{\Lambda }}_{n,3}^2\right)$$

(23)

Furthermore, we seek terms in $e^{i{k}_{jn}x}$ but without a time dependency of the form $e^{i{\omega }_{0,n}{\tau }_0}$, which correspond to a mixing of the driving frequencies and phases. We focus on terms mixing the frequency and phase of driver 2 with either drivers 1 or 3, which we group as

$$T_2=3({\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}{e}^{i{k}_{jn}x}{e}^{i\left((2{\omega }_2-{\omega }_1){\tau }_0+2{\theta }_2-{\theta }_1\right)}+{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,3}{e}^{i{k}_{jn}x}{e}^{i\left((2{\omega }_2-{\omega }_3){\tau }_0+2{\theta }_2-{\theta }_3\right)})$$

(24)

In order to make contact with the experimental conditions, we now take ${\omega }_1={\omega }_3$ and ${\theta }_1=-\mathsf{\Delta }\theta /2$, ${\theta }_3=+\mathsf{\Delta }\theta /2$, where $\mathsf{\Delta }\theta$ is the phase difference between drivers 1 and 3.

In the experiment, since the outer transducers are driven with the same magnitude, ${\stackrel{\rightharpoonup }{F}}_{l=1}=F\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$ and ${\stackrel{\rightharpoonup }{F}}_{l=3}=F\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$, according to Equation (13), we need to consider two cases. Case I corresponds to the spatial modes $n=1,3$ for which the $F_n^{\left(l\right)}$ are the same, leading to ${\mathsf{\Lambda }}_{n,1}={\mathsf{\Lambda }}_{n,3}$. Case II corresponds to the spatial mode $n=2$, for which ${\mathsf{\Lambda }}_{n,3}=-{\mathsf{\Lambda }}_{n,1}$.

In both cases, $T_1=3A_n^2{A}_n^{*}{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}+3A_n{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}2(2{\mathsf{\Lambda }}_{n,1}^2+{\mathsf{\Lambda }}_{n,2}^2)$.

3.1.1. Case I: $n=1$ or 3

In this case, we rewrite Equation (24) in the simpler form:

$$T_2=3{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}{e}^{i{k}_{jn}x}{e}^{i\left((2{\omega }_2-{\omega }_1){\tau }_0+2{\theta }_2\right)}2\cos \frac{\mathsf{\Delta }\theta }{2}$$

(25)

We now introduce a detuning parameter: $\sigma =\frac{1}{\epsilon }\left(2{\omega }_2-{\omega }_1-{\omega }_{0,n}\right)$ and redefine $T_2$ as

$$T_2=3{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}{e}^{i\left(\sigma {\tau }_1+2{\theta }_2\right)}2\cos \frac{\mathsf{\Delta }\theta }{2}$$

(26)

By regrouping all the terms contributing to secular behavior and setting them to zero, we obtain the relation

$$2\frac{{\partial }^2{u}_{0,n}}{\partial {\tau }_1\partial {\tau }_0}+2\mu \frac{\partial u_{0,n}}{\partial {\tau }_0}+\delta (T_1+T_2)=0$$

(27)

Using $u_{0,n}=u_{0,n}^h+u_{0,n}^p$, Equations (15) and (16) for the wave number $k_n$, and Equations (23) and (26), after some algebraic manipulations, we obtain

$$2i{\omega }_{0,n}\left(A_n^{\prime }+\mu A_n\right)+2\delta {\mathsf{\Gamma }}_1{\omega }_{0,n}{A}_n+3\delta A_n^2{A}_n^{*}+\delta {\mathsf{\Gamma }}_2{e}^{i\left(\sigma {\tau }_1\right)}2\cos \frac{\mathsf{\Delta }\theta }{2}=0$$

(28)

where ${\mathsf{\Gamma }}_1=\frac{3}{{\omega }_{0,n}}\left(2{\mathsf{\Lambda }}_{n,1}^2+{\mathsf{\Lambda }}_{n,2}^2\right)$ and ${\mathsf{\Gamma }}_2=\frac{3}{{\omega }_{0,n}}{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}$. In Equation (28), the primed quantity is a derivative with respect to ${\tau }_1$. We have also chosen ${\theta }_2=0$ without consequence on the rest of the derivation. We now take $A_n\left({\tau }_1\right)=\frac{1}{2}a\left({\tau }_1\right)e^{ib\left({\tau }_1\right)}$. We also define: $\eta =\sigma {\tau }_1-b$ such that $b^{\prime }=\sigma -\eta \prime$. By inserting these into Equation (28) and considering only steady state behavior (that is, $a^{\prime }=0$ and ${\eta }^{\prime }=0$), the regrouping of the real and imaginary terms into two separate equations results in

$$a+\frac{\delta {\mathsf{\Gamma }}_2}{\mu }2\cos \frac{\mathsf{\Delta }\theta }{2}\sin \eta =0$$

(29a)

$$a\left[\sigma -\delta {\mathsf{\Gamma }}_1-\frac{3\delta }{8{\omega }_{0,n}}{a}^2\right]-\delta {\mathsf{\Gamma }}_{2}2\cos \frac{\mathsf{\Delta }\theta }{2}\cos \eta =0$$

(29b)

We can get the amplitude-frequency response of the specific nonlinear mode, $2{\omega }_2-{\omega }_1$ due to self-interaction by eliminating the phase $\eta$ using the trigonometric relation ${\sin }^2\eta +{\cos }^2\eta =1$. That response takes the form of

$$\sigma =\delta {\mathsf{\Gamma }}_1+\frac{3\delta }{8{\omega }_{0,n}}{a}^2\pm {\left(\frac{{\left(\delta {\mathsf{\Gamma }}_{2}2\cos \frac{\mathsf{\Delta }\theta }{2}\right)}^2}{a^2}-{\mu }^2\right)}^{1/2}$$

(30)

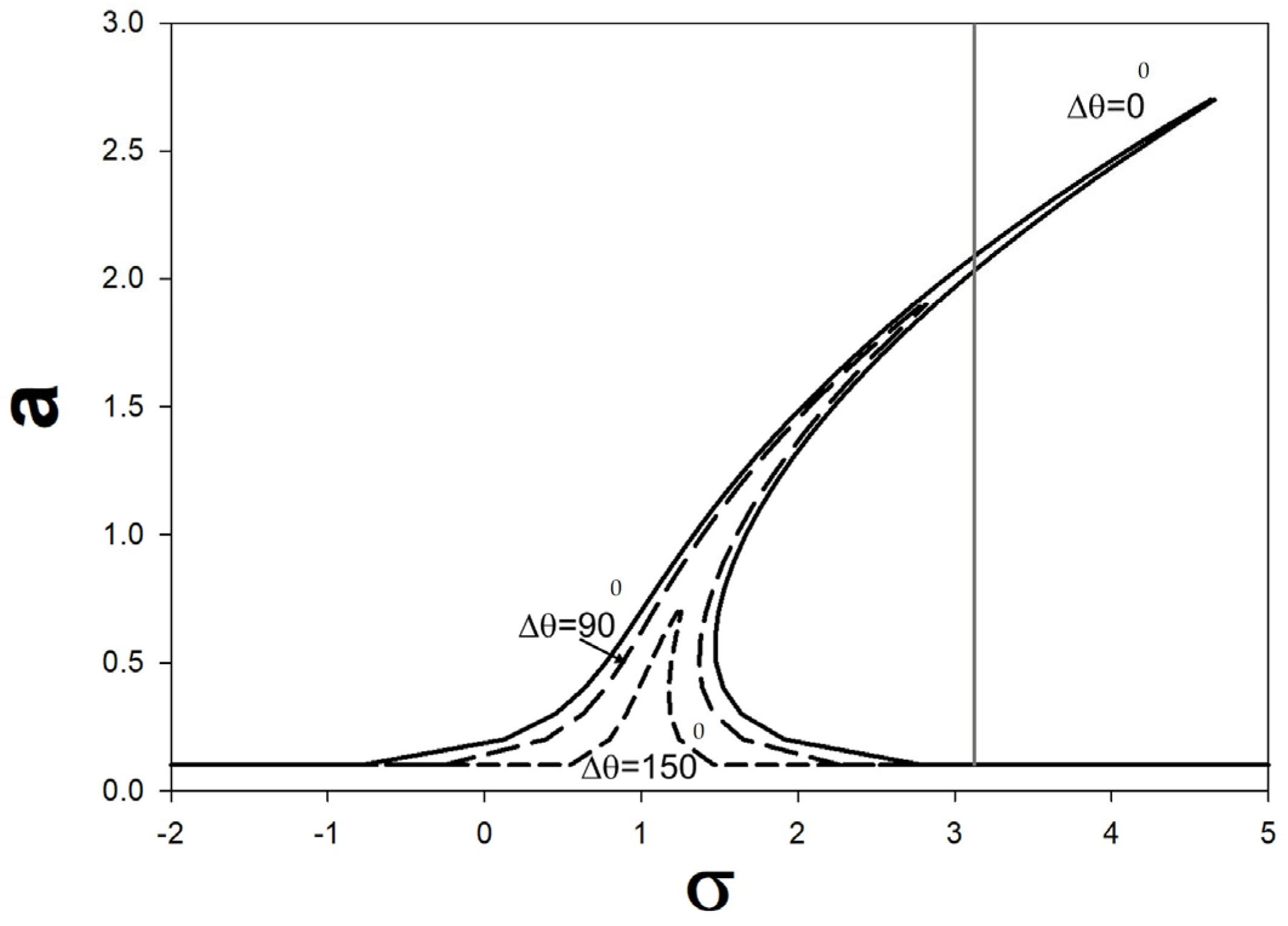
Recall that $a$ is the correction to the amplitude ${\mathrm{A}}_n\left(k_{jn}\right)$ solution of the homogenous zeroth order wave equation as a result of the nonlinear perturbation. In some frequency ranges, $\sigma$, the amplitude frequency response may not be a single-valued function. The amplitude may show overhangs to a high frequency or low frequency depending on the sign of $\delta$. It is centered on the backbone curve given by $\sigma =\delta {\mathsf{\Gamma }}_1+\frac{3\delta }{8{\omega }_{0,n}}{a}^2$, where the amplitude decays to zero when $\sigma =\delta {\mathsf{\Gamma }}_1$. The maximum value of the amplitude is obtained by setting the square root term to zero, $a_m=\frac{\left|\delta {\mathsf{\Gamma }}_{2}2\cos \frac{\mathsf{\Delta }\theta }{2}\right|}{\mu }$. The maximum amplitude is, therefore, dependent on the phase difference between drivers 1 and 3.

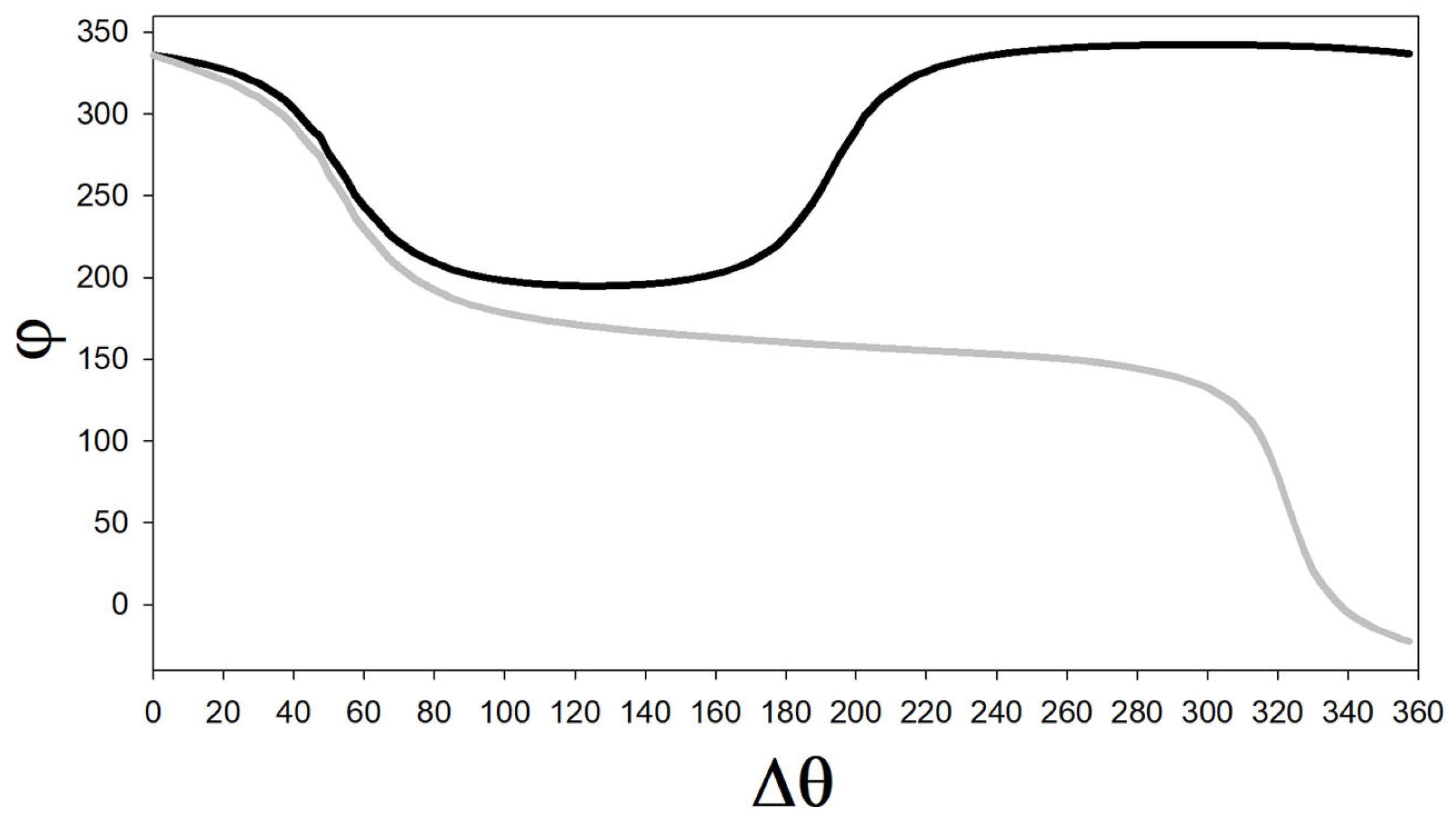
In Figure 4, we note that the amplitude of the nonlinear mode depends on the phase difference between the two drivers, 1 and 3. We note that for $\mathsf{\Delta }\theta$ = 180°, the amplitude a = 0 and the spatial modes ${\stackrel{\rightharpoonup }{E}}_1$ and ${\stackrel{\rightharpoonup }{E}}_3$ do not contribute to the nonlinear correction of the solution of Equation (15). In particular, we note that, at a fixed frequency, $\sigma$~3.1 (vertical line in the figure), changing the drivers’ phase difference $\mathsf{\Delta }\theta$ from 0° to 90° reduces the number of solutions for the amplitude from 3 to 1. This dependency will impact the behavior of the phase, $\eta$. We obtain the phase from Equation (29a) as $\sin \eta =sgn\left(\delta {\mathsf{\Gamma }}_2\right)\frac{a}{a_m}$. 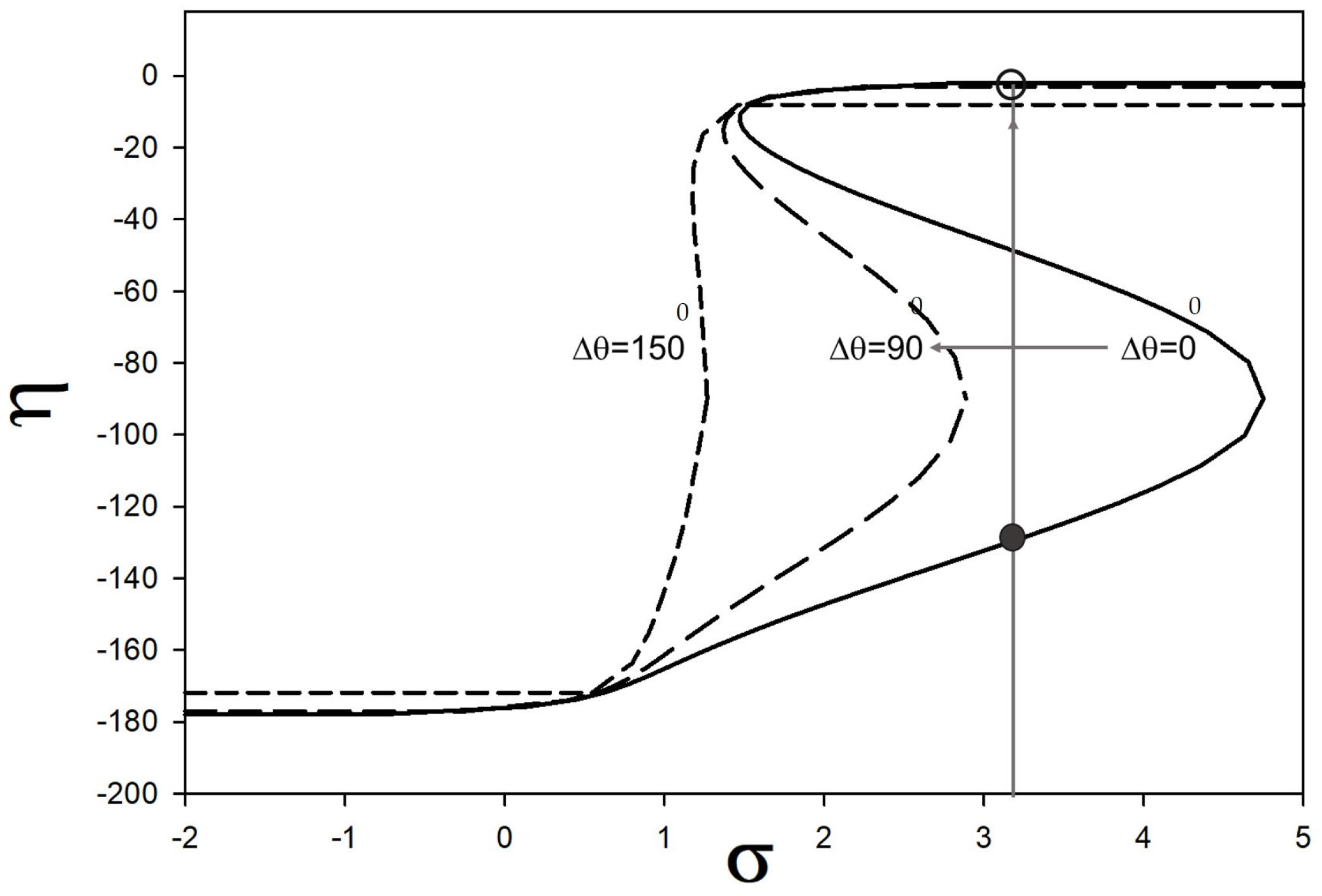In Figure 4, we illustrate the effect of a change in the drivers’ phase on $\eta$ as a function of frequency. Let us suppose that we prepared the nonlinear mode shown by the closed circle in Figure 5. This is carried out by setting $\mathsf{\Delta }\theta =0$ and by slowly increasing the frequency $\sigma$ from −2 to 3.1, i.e., by moving along the upper part of the solid line amplitude-frequency response of Figure 4 up to an amplitude a~2.0. In that state, $\eta ~{130}^{\mathrm{o}}$. Increasing the phase difference between drivers 1 and 3 to $\mathsf{\Delta }\theta =90°$ reduces the maximum amplitude of the nonlinear mode (long dashed curve) in Figure 4, which now occurs at a frequency $\sigma$ < 3.

Under this condition, the amplitude-frequency response is single value and corresponds to the state illustrated as an open circle in Figure 5. This state has a single value $\eta ~0$. The change in the driver phase difference leads to a near 130° change in the phase of the nonlinear mode. This jump in phase carries to ${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}$ through $A_n$ and $u_{0,n}$.

Indeed, we can now rewrite $A_n$ in the form

$$A_{n=1,3}=a_{1,3}\left({\sigma }_{1,3}\right)e^{i\left(\sigma {\tau }_1-{\eta }_{1,3}\right)}$$

(31)

Here, we are using indices 1 and 3 to specify that the amplitude and phase correspond to the spatial modes ${\stackrel{\rightharpoonup }{E}}_1$ and ${\stackrel{\rightharpoonup }{E}}_3$. Inserting the definition of: ${\sigma }_{1,3}=\frac{1}{\epsilon }\left(2{\omega }_2-{\omega }_1-{\omega }_{0,n=1,3}\right)$, ${\tau }_0=t$ and ${\tau }_1=\epsilon t$, we rewrite Equation (31) as

$$A_{n=1,3}=a_{1,3}\left({\sigma }_{1,3}\right)e^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}{e}^{-i{\eta }_{1,3}}{e}^{-i{\omega }_{0,n=1,3}{\tau }_0}$$

(32)

Considering a single $k_{jn}$ and ${\theta }_2=0$ in Equation (21) and focusing our attention on the complex term (keeping aside the complex conjugate in that equation), we obtain

$$u_{0,n=1,3}=\left({\mathrm{A}}_{n=1,3}{e}^{i{\omega }_{0,n=1,3}{\tau }_0}+2{\mathsf{\Lambda }}_{n=1,3,1}{e}^{i{\omega }_1{\tau }_0}2\cos \frac{\mathsf{\Delta }\theta }{2}+{\mathsf{\Lambda }}_{n=1,3,2}{e}^{i{\omega }_2{\tau }_0}\right)e^{i{k}_{jn=1,3}x}$$

(33)

Inserting Equation (32) into Equation (33) yields

$$u_{0,n=1,3}=\left(a_{1,3}\left({\sigma }_{1,3}\right)e^{-i{\eta }_{1,3}}{e}^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}+2{\mathsf{\Lambda }}_{n=1,3,1}{e}^{i{\omega }_1{\tau }_0}2\cos \frac{\mathsf{\Delta }\theta }{2}+{\mathsf{\Lambda }}_{n=1,3,2}{e}^{i{\omega }_2{\tau }_0}\right)e^{i{k}_{jn=1,3}x}$$

(34)

The last two terms correspond to the primary linear modes observed experimentally. The first term corresponds to one of the possible nonlinear phi-bit modes, namely {p = 2, q = −1}.

3.1.2. Case II: $n=2$

In this case, Equation (24) becomes

$$T_2=3{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}{e}^{i{k}_{jn}x}{e}^{i{\omega }_{0,n}{\tau }_0}{e}^{i\left(\sigma {\tau }_1+2{\theta }_2\right)}2i\sin \frac{\mathsf{\Delta }\theta }{2}$$

(35)

The secular Equation (27) yields

$$2i{\omega }_{0,n}\left(A_n^{\prime }+\mu A_n\right)+2\delta {\mathsf{\Gamma }}_1{\omega }_{0,n}{A}_n+3\delta A_n^2{A}_n^{*}+\delta {\mathsf{\Gamma }}_2{e}^{i\left(\sigma {\tau }_1\right)}2i\sin \frac{\mathsf{\Delta }\theta }{2}=0$$

(36)

where again ${\mathsf{\Gamma }}_1=\frac{3}{{\omega }_{0,n}}\left(2{\mathsf{\Lambda }}_{n,1}^2+{\mathsf{\Lambda }}_{n,2}^2\right)$ and ${\mathsf{\Gamma }}_2=\frac{3}{{\omega }_{0,n}}{\mathsf{\Lambda }}_{n,2}^2{\mathsf{\Lambda }}_{n,1}$. Choosing ${\theta }_2=0$, $A_n\left({\tau }_1\right)=\frac{1}{2}a\left({\tau }_1\right)e^{ib\left({\tau }_1\right)}$ and defining $\eta =\sigma {\tau }_1-b$ such that $b^{\prime }=\sigma -\eta \prime$, Equation (36) becomes at steady state (i.e., $a^{\prime }=0$ and ${\eta }^{\prime }=0$)

$$a+\frac{\delta {\mathsf{\Gamma }}_2}{\mu }2\sin \frac{\mathsf{\Delta }\theta }{2}\cos \eta =0$$

(37a)

$$a\left[\sigma -\delta {\mathsf{\Gamma }}_1-\frac{3\delta }{8{\omega }_{0,n}}{a}^2\right]+\delta {\mathsf{\Gamma }}_{2}2\sin \frac{\mathsf{\Delta }\theta }{2}\sin \eta =0$$

(37b)

Equations (37a) and (37b) result from the imaginary and real parts of Equation (36), respectively. Note that in case II, the effect of the phase difference $\mathsf{\Delta }\theta$ occurs through a sine function instead of a cosine function, as was the case in case I. Additionally, note the swapping between $\sin \eta$ and $\cos \eta$ compared to case I.

We can obtain the amplitude-frequency response of the specific nonlinear mode, $2{\omega }_2-{\omega }_1,$ for mode n = 2 due to self-interaction by eliminating phase $\eta$ using the trigonometric relation: ${\sin }^2\eta +{\cos }^2\eta =1$. That response takes the form of

$$\sigma =\delta {\mathsf{\Gamma }}_1+\frac{3\delta }{8{\omega }_{0,n}}{a}^2\mp {\left(\frac{{\left(\delta {\mathsf{\Gamma }}_{2}2\sin \frac{\mathsf{\Delta }\theta }{2}\right)}^2}{a^2}-{\mu }^2\right)}^{1/2}$$

(38)

This equation has the same backbone curve as that of case 1. The only difference resides in the way the amplitude varies with the phase difference $\mathsf{\Delta }\theta$ through $\sin \frac{\mathsf{\Delta }\theta }{2}$ instead of $\cos \frac{\mathsf{\Delta }\theta }{2}$. Now, for $\mathsf{\Delta }\theta =0$, that is $\sin \frac{\mathsf{\Delta }\theta }{2}=0$, Equations (37a) and (37b) give a = 0. Spatial mode 2 does not contribute to the nonlinear displacement field. Case II mirrors case I with a $\pi$ phase lag in $\mathsf{\Delta }\theta$. The second spatial mode contributes to phase jumps in $\eta$ with, again, a $\pi$ phase lag in $\mathsf{\Delta }\theta$. Considering a single $k_{jn}$ in Equation (21) for spatial mode ${\stackrel{\rightharpoonup }{E}}_2$, we obtain

$$u_{0,n=2}=\left(a_2\left({\sigma }_2\right)e^{-i{\eta }_2}{e}^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}+2{\mathsf{\Lambda }}_{n=2,1}{e}^{i{\omega }_1{\tau }_0}2i\sin \frac{\mathsf{\Delta }\theta }{2}+{\mathsf{\Lambda }}_{n=2,2}{e}^{i{\omega }_2{\tau }_0}\right)e^{i{k}_{jn=2}x}$$

(39)

Again, in Equation (39), we apply a subscript of 2 to the amplitude a and phase $\eta$ to highlight the fact that, in case II, one deals with the spatial mode n=2.

Let us now combine cases I and II. The first-order correction (due to the self-interaction of the $k_{jn}$ wave number to the complete displacement field of Equation (12), ${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}={{\displaystyle \sum }}_n{u}_{0,n}{\stackrel{\rightharpoonup }{E}}_n$) is now

$$\begin{array}{ll}{\stackrel{\rightharpoonup }{U}}^{\left(0\right)}=\left[\right(a_1\left({\sigma }_1\right)& e^{-i{\eta }_1}{e}^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}+2{\Lambda }_{n,1}{e}^{i{\omega }_1{\tau }_0}2\cos \frac{\Delta \theta }{2}\\ & +{\Lambda }_{n,2}{e}^{i{\omega }_2{\tau }_0}){\stackrel{\rightharpoonup }{E}}_1{e}^{i{k}_{jn=1}x}\\ & +(a_2\left({\sigma }_2\right)e^{-i{\eta }_2}{e}^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}+2{\Lambda }_{n,1}{e}^{i{\omega }_1{\tau }_0}2i\sin \frac{\Delta \theta }{2}\\ & +{\Lambda }_{n,2}{e}^{i{\omega }_2{\tau }_0}){\stackrel{\rightharpoonup }{E}}_2{e}^{i{k}_{jn=2}x}\\ & +(a_3\left({\sigma }_3\right)e^{-i{\eta }_3}{e}^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}+2{\Lambda }_{n,1}{e}^{i{\omega }_1{\tau }_0}2\cos \frac{\Delta \theta }{2}\\ & +{\Lambda }_{n,2}{e}^{i{\omega }_2{\tau }_0}\left){\stackrel{\rightharpoonup }{E}}_3{e}^{i{k}_{jn=3}x}\right]\end{array}$$

(40)

In the Fourier spectrum of the displacement field, the displacement associated with the nonlinear logical phi-bit mode with a frequency of $2{\omega }_2-{\omega }_1$ measured at x = 0 is given by

$${\stackrel{\rightharpoonup }{U}}^{\left(0\right)}\left(2{\omega }_2-{\omega }_1\right)=\left(\begin{array}{c}{C}_1{e}^{i{\phi }_1}\\ C_2{e}^{i{\phi }_2}\\ C_3{e}^{i{\phi }_3}\end{array}\right)e^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}=\left[a_1\left({\sigma }_1\right)e^{-i{\eta }_1}{\stackrel{\rightharpoonup }{E}}_1+a_2\left({\sigma }_2\right)e^{-i{\eta }_2}{\stackrel{\rightharpoonup }{E}}_2+a_3\left({\sigma }_3\right)e^{-i{\eta }_3}{\stackrel{\rightharpoonup }{E}}_3\right]e^{i\left(2{\omega }_2-{\omega }_1\right){\tau }_0}$$

(41)

The driver phase difference, $\mathsf{\Delta }\theta$, can, therefore, be used through its impact on ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ to tune the complex amplitudes $\frac{1}{\sqrt{2}}{e}^{i{\phi }_{12}}$ and $\frac{1}{\sqrt{2}}{e}^{i{\phi }_{13}}$ of a logical phi-bit. These amplitudes may exhibit large phase jumps, which are associated with the phase jumps in ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$, which is a behavior that is consistent with the experimental observation of the sharp phase jumps reported in Section 3.

We now address the possible origin of the phi-bit phase background as a function of $\mathsf{\Delta }\theta$. Let us consider the particular solution part of Equation (40) evaluated at x = 0:

$${\stackrel{\rightharpoonup }{U}}_p^{\left(0\right)}\left({\omega }_1,{\omega }_2\right)=2{\mathsf{\Lambda }}_{n,1}\left(2\cos \frac{\mathsf{\Delta }\theta }{2}\left({\stackrel{\rightharpoonup }{E}}_1+{\stackrel{\rightharpoonup }{E}}_3\right)+2i\sin \frac{\mathsf{\Delta }\theta }{2}{\stackrel{\rightharpoonup }{E}}_2\right)e^{i{\omega }_1{\tau }_0}+{\mathsf{\Lambda }}_{n,2}\left({\stackrel{\rightharpoonup }{E}}_1+{\stackrel{\rightharpoonup }{E}}_2+{\stackrel{\rightharpoonup }{E}}_3\right)e^{i{\omega }_2{\tau }_0}$$

(42)

In the Fourier spectrum of the total displacement field, the two terms in Equation (42) correspond to the primary modes. We rewrite Equation (42) by introducing

$${\stackrel{\rightharpoonup }{U}}_p^{\left(0\right)}\left({\omega }_1,{\omega }_2\right)=\left(\begin{array}{c}{C}_1\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_1\left({\omega }_1,\mathsf{\Delta }\theta \right)}\\ C_2\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_2\left({\omega }_1,\mathsf{\Delta }\theta \right)}\\ C_3\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_3\left({\omega }_1,\mathsf{\Delta }\theta \right)}\end{array}\right)e^{i{\omega }_{1}t}+\left(\begin{array}{c}{C}_1\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_1\left({\omega }_2,\mathsf{\Delta }\theta \right)}\\ C_2\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_2\left({\omega }_2,\mathsf{\Delta }\theta \right)}\\ C_3\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_3\left({\omega }_2,\mathsf{\Delta }\theta \right)}\end{array}\right)e^{i{\omega }_{2}t}$$

(43)

In Equation (43), we have replaced ${\tau }_0$ with t. As seen in Figure 1, the array of coupled acoustic waveguides is only part of a system that includes transducers and their ultrasonic coupling agent at the ends of the waveguides. These system components may possess nonlinear as well as damping characteristics, which will be able to mix the frequencies associated with the linear displacement of Equation (43). Indeed, let us consider a model of the transducer/coupling agent component of the system in the form of extrinsic nonlinear damped oscillators at the waveguide ends driven by the displacement ${\stackrel{\rightharpoonup }{U}}_p^{\left(0\right)}\left({\omega }_1,{\omega }_2\right)$:

$$\left(\frac{d^2}{d{t}^2}+{\omega }_R^2+{\mu }_R\frac{d}{dt}\right)\overrightarrow{V}+{\epsilon }_R\stackrel{\rightharpoonup }{G}\left(\stackrel{\rightharpoonup }{V}\right)=K{\stackrel{\rightharpoonup }{U}}_p^{\left(0\right)}\left({\omega }_1,{\omega }_2\right)$$

(44)

where ${\omega }_R$ and ${\mu }_R$ are the characteristic frequency and damping coefficient, respectively. $\stackrel{\rightharpoonup }{G}$ is the nonlinear function with a strength ${\epsilon }_R$. $\overrightarrow{V}=\left(V_1,V_2,V_3\right)$ where the $V_i^{\prime };i=1,2,3,$ are displacement degrees of freedom associated with the extrinsic oscillators at the ends of rods, i = 1, 2, 3. $K$ is some proportionality constant converting displacement into force. Note that since the transducers/coupling agent at the ends of the waveguides are independent of each other, the components, $V_i$, in Equation (44) are also independent of each other. So we can rewrite Equation (44) in the form of three independent equations:

$$\left(\frac{d^2}{d{t}^2}+{\omega }_R^2+{\mu }_R\frac{d}{dt}\right)V_i+{\epsilon }_R{V}_i^Q=K{C}_i\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_{i\left({\omega }_1,\mathsf{\Delta }\theta \right)}}{e}^{i{\omega }_{1}t}+K{C}_i\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_{i\left({\omega }_2,\mathsf{\Delta }\theta \right)}}{e}^{i{\omega }_{2}t}$$

(45)

In Equation (45), we have chosen the nonlinear function, $G_i,$ in the form of a power $V_i^Q$. We can solve Equation (45) using perturbation theory. We seek solutions in the form: $V_i=V_i^{\left(0\right)}+{\epsilon }_R{V}_i^{\left(1\right)}$. Regarding the zeroth order in ${\epsilon }_R$, the equation reduces to a linear form:

$$\left(\frac{d^2}{d{t}^2}+{\omega }_R^2+{\mu }_R\frac{d}{dt}\right)V_i^{\left(0\right)}=K{C}_i\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_{i\left({\omega }_1,\mathsf{\Delta }\theta \right)}}{e}^{i{\omega }_{1}t}+K{C}_i\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_{i\left({\omega }_2,\mathsf{\Delta }\theta \right)}}{e}^{i{\omega }_{2}t}c$$

(46)

By seeking zeroth order harmonic solutions with the same frequencies as the driving displacement, we obtain

$$V_i^{\left(0\right)}=\frac{K{C}_i\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_i\left({\omega }_1,\mathsf{\Delta }\theta \right)}}{-{\omega }_1^2+{\omega }_R^2+i{\mu }_R{\omega }_1}{e}^{i{\omega }_{1}t}+\frac{K{C}_i\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_i\left({\omega }_2,\mathsf{\Delta }\theta \right)}}{-{\omega }_2^2+{\omega }_R^2+i{\mu }_R{\omega }_2}{e}^{i{\omega }_{2}t}$$

(47)

Regarding the first order in ${\epsilon }_R$, Equation (45) becomes

$$\left(\frac{d^2}{d{t}^2}+{\omega }_R^2+{\mu }_R\frac{d}{dt}\right)V_i^{\left(1\right)}+{\left(V_i^{\left(0\right)}\right)}^Q=0$$

(48)

Here, the zeroth order solution drives through the nonlinear term to the first-order solution. Inserting Equation (47) into the nonlinear Equation (48) leads to a series of terms with the general form of

$D{\left(\frac{K{C}_i\left({\omega }_1,\mathsf{\Delta }\theta \right)e^{i{\phi }_i\left({\omega }_1,\mathsf{\Delta }\theta \right)}}{-{\omega }_1^2+{\omega }_R^2+i{\mu }_R{\omega }_1}\right)}^p{\left(\frac{K{C}_i\left({\omega }_2,\mathsf{\Delta }\theta \right)e^{i{\phi }_i\left({\omega }_2,\mathsf{\Delta }\theta \right)}}{-{\omega }_2^2+{\omega }_R^2+i{\mu }_R{\omega }_2}\right)}^q{e}^{i\left(p{\omega }_1+q{\omega }_2\right)t}$, where D is a proportionality constant and $p+q=Q$. By focusing on one of these terms, corresponding to one of the logical phi-bits with $\left\{p,q\right\},$ Equation (48) yields

$$\left(\frac{d^2}{d{t}^2}+{\omega }_R^2+{\mu }_R\frac{d}{dt}\right)V_i^{\left(1\right)}+D{\left(\frac{K{C}_i\left({\omega }_1,\mathsf{\Delta }\theta \right)}{-{\omega }_1^2+{\omega }_R^2+i{\mu }_R{\omega }_1}\right)}^p{\left(\frac{K{C}_i\left({\omega }_2,\mathsf{\Delta }\theta \right)}{-{\omega }_2^2+{\omega }_R^2+i{\mu }_R{\omega }_2}\right)}^q{e}^{i\left(p{\phi }_i\left({\omega }_1,\mathsf{\Delta }\theta \right)+q{\phi }_i\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}{e}^{i\left(p{\omega }_1+q{\omega }_2\right)t}=0$$

(49)

A particular solution of Equation (49) may be written as

$$\begin{gathered} V_i^{\left(1\right)}=\frac{1}{-{\left(p{\omega }_1+q{\omega }_2\right)}^2+{\omega }_R^2+i{\mu }_R\left(p{\omega }_1+q{\omega }_2\right)}{\left(\frac{K}{-{\omega }_1^2+{\omega }_R^2+i{\mu }_R{\omega }_1}\right)}^p{\left(\frac{K}{-{\omega }_2^2+{\omega }_R^2+i{\mu }_R{\omega }_2}\right)}^q \\ {\left(C_i\left({\omega }_1,\mathsf{\Delta }\theta \right)\right)}^p{\left(C_i\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}^q{e}^{i\left(p{\phi }_i\left({\omega }_1,\mathsf{\Delta }\theta \right)+q{\phi }_i\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}{e}^{i\left(p{\omega }_1+q{\omega }_2\right)t} \end{gathered}$$

(50)

The fraction prefactors in Equation (50) are the same for each component “$i$” of ${\overrightarrow{V}}^{\left(1\right)}$ and add the same general phase of each component. Therefore, we have

$${\overrightarrow{V}}^{\left(1\right)}\propto \left(\begin{array}{c}{\left(C_1\left({\omega }_1,\mathsf{\Delta }\theta \right)\right)}^p{\left(C_1\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}^q{e}^{i\left(p{\phi }_1\left({\omega }_1,\mathsf{\Delta }\theta \right)+q{\phi }_1\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}\\ {\left(C_2\left({\omega }_1,\mathsf{\Delta }\theta \right)\right)}^p{\left(C_2\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}^q{e}^{i\left(p{\phi }_2\left({\omega }_1,\mathsf{\Delta }\theta \right)+q{\phi }_2\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}\\ {\left(C_3\left({\omega }_1,\mathsf{\Delta }\theta \right)\right)}^p{\left(C_3\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}^q{e}^{i\left(p{\phi }_3\left({\omega }_1,\mathsf{\Delta }\theta \right)+q{\phi }_3\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}\end{array}\right)e^{i\left(p{\omega }_1+q{\omega }_2\right)t}$$

(51)

Note that the coefficients ${\left(C_i\left({\omega }_1,\mathsf{\Delta }\theta \right)\right)}^p{\left(C_i\left({\omega }_2,\mathsf{\Delta }\theta \right)\right)}^q$ are real. The Fourier spectrum of the displacement detected by the transducers will include the contribution of Equation (51) to the phase of the nonlinear phi-bit mode, {p,q}. These phases are linear combinations of the phase of primary linear modes at frequencies ${\omega }_1$ and ${\omega }_2$ with linear coefficients p and q. They will, therefore, contribute the background of the phases of a phi-bit that can be determined from the phases of the primary modes, as was shown it Section 3. Here, the background in the logical phi-bit phase clearly depends on the parameter $\mathsf{\Delta }\theta$ in accordance with the experimental observation. However, to gain full insight into the effect of $\mathsf{\Delta }\theta$ on the phi-bit phase, one needs to go beyond the particular solution of Equation (42). Indeed, this solution does not include the effect of damping as it was lumped into the perturbation of Equation (8) in order to use frequency detuning with multiple time scale perturbation theory and shed light on the nonlinear amplitude-frequency response of a phi-bit. In order to illuminate the dependency of the phase of the primary modes, that is, the background of the phi-bit phase, on $\mathsf{\Delta }\theta$, we now reconsider the linear version of Equation (6), with a single driving frequency, $\omega$, applied to the three waveguides with different phases, namely

$$\left[\left(\frac{{\partial }^2}{\partial t^2}-{\beta }^2\frac{{\partial }^2}{\partial x^2}+2\mu \frac{\partial }{\partial t}\right)\overleftrightarrow{I}+{\alpha }^2\overleftrightarrow{M}\right]\stackrel{\rightharpoonup }{U}={\stackrel{\rightharpoonup }{F}}_1{\delta }_{x=0}\cos \left(\omega t+{\theta }_1\right)+{\stackrel{\rightharpoonup }{F}}_2{\delta }_{x=0}\cos \left(\omega t+{\theta }_2\right)+{\stackrel{\rightharpoonup }{F}}_3{\delta }_{x=0}\cos \left(\omega t+{\theta }_3\right)$$

(52)

We simplify this equation by working with a complex exponential instead of a cosine function for the driving force. That is, we reformulate the driving force on the right-hand side of Equation (52) as

$$\overrightarrow{F}={\delta }_{x=0}\left(\begin{array}{c}A\\ B{e}^{i{\theta }_{12}}\\ C{e}^{i{\theta }_{13}}\end{array}\right)e^{i\omega t}$$

(53)

where we have expressed the phase difference between drivers 2 and 3 relative to driver 1 as ${\theta }_{12}$ and ${\theta }_{13}$. The coefficients $A$, $B$, and $C$ are the magnitudes of the forces. We define $C=rA$. Note that our experiment is conducted with $r=1$. However, because we use different transducers for each waveguide, that condition may not be exactly realized.

Expanding $\overrightarrow{F}$ on the basis of spatial modes ${\stackrel{\rightharpoonup }{E}}_1$, ${\stackrel{\rightharpoonup }{E}}_2$, and ${\stackrel{\rightharpoonup }{E}}_3$ gives the three components:

$$f_1=A+B{e}^{i{\theta }_{12}}+C{e}^{i{\theta }_{13}}$$

(54a)

$$f_2=A-C{e}^{i{\theta }_{13}}$$

(54b)

$$f_3=A-2B{e}^{i{\theta }_{12}}+C{e}^{i{\theta }_{13}}$$

(54c)

We also expand the left-hand side of Equation (52) on the basis of spatial modes; that is, we define $\stackrel{\rightharpoonup }{U}={{\displaystyle \sum }}_n{u}_n{\stackrel{\rightharpoonup }{E}}_n$. Equation (52) takes the form of three equations, each one corresponding to a spatial mode. We seek solutions for $u_n$ in the form of superpositions of plane waves. The complex resonant amplitudes are obtained for each spatial mode as

$H_1=\frac{f_1}{{\omega }_{0,1}^2-{\omega }^2+i2\mu \omega }$, $H_2=\frac{f_2}{{\omega }_{0,2}^2-{\omega }^2+i2\mu \omega }$, and $H_3=\frac{f_3}{{\omega }_{0,3}^2-{\omega }^2+i2\mu \omega }$, where ${\omega }_{0,n}^2\left(k_{jn}\right)={\beta }^2{k}_{jn}^2+{\alpha }^2{\lambda }_n$ for n = 1, 2, 3, wave number, $k_{jn}$, and spatial mode eigenvalue, ${\lambda }_n$, as was defined earlier. Inserting Equations (54a)–(54c) into the resonant amplitudes and determining their corresponding phase, as defined by $H_i=\left|H_i\right|e^{i{\varphi }_{\left(i\right)}}$, yields

$${\varphi }_{\left(1\right)}={\tan }^{-1}\left(\frac{r\sin {\theta }_{13}}{1+r\cos {\theta }_{13}}\right)$$

(55a)

$${\varphi }_{\left(2\right)}={\tan }^{-1}\left(\frac{-r\sin {\theta }_{13}}{1-r\cos {\theta }_{13}}\right)$$

(55b)

$${\varphi }_{\left(3\right)}={\varphi }_{\left(1\right)}$$

(55c)

These phases are independent of ${\theta }_{12}$. We can now redefine ${\theta }_{13}=\mathsf{\Delta }\theta$. We note that as $\mathsf{\Delta }\theta$ passes through 180° for r = 1, the phases ${\varphi }_{\left(1\right)}={\varphi }_{\left(3\right)}$ undergo a π jump. There is no such jump in ${\varphi }_{\left(2\right)}$. In order to see how such a jump would carry to a phase jump in the phase of the primary linear mode and subsequently to the background of a phi-bit, we write the complete solution for $\stackrel{\rightharpoonup }{U}$:

$$\stackrel{\rightharpoonup }{U}=\left[{\displaystyle \sum }_{k_{jn=1}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}{\stackrel{\rightharpoonup }{E}}_1{e}^{i{k}_{jn=1}x}+{\displaystyle \sum }_{k_{jn=2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}{\stackrel{\rightharpoonup }{E}}_2{e}^{i{k}_{jn=2}x}+{\displaystyle \sum }_{k_{jn=3}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}{\stackrel{\rightharpoonup }{E}}_3{e}^{i{k}_{jn=3}x}\right]e^{i\omega t}$$

(56)

Note that the $\left|H_i\right|$ depends on the wave number and eigenvalue of the spatial mode. Since the $\left|H_i\right|$ correspond to a Lorentzian resonance, we can assume that for a given driving frequency, there might be a single plane wave for each spatial mode that dominates the contribution to $\stackrel{\rightharpoonup }{U}$. Choosing also to detect the displacement at x = 0, Equation (56) reduces to

$$\stackrel{\rightharpoonup }{U}~[\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}{\stackrel{\rightharpoonup }{E}}_1+\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}{\stackrel{\rightharpoonup }{E}}_2+\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}{\stackrel{\rightharpoonup }{E}}_3] e^{i\omega t}$$

(57)

The components of the amplitude of $\stackrel{\rightharpoonup }{U}$ are given by

$$U_1=C_1{e}^{i{\phi }_1}=\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}+\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}$$

(58a)

$$U_2=C_2{e}^{i{\phi }_2}=\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}+0-\frac{2}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}$$

(58b)

$$U_3=C_3{e}^{i{\phi }_3}=\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}-\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}$$

(58c)

We can now try to evaluate the behavior of ${\phi }_{12 }$. For instance, we first calculate

$${\phi }_1={\tan }^{-1}\left(\frac{Im\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}+\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}{Real\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}+\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}\right)$$

(59a)

$${\phi }_2={\tan }^{-1}\left(\frac{Im\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}-\frac{2}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}{Real\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}-\frac{2}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}\right)$$

(59b)

$${\phi }_3={\tan }^{-1}\left(\frac{Im\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}-\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}{Real\left(\frac{1}{\sqrt{3}}\left|H_1\right|e^{i{\varphi }_{\left(1\right)}}-\frac{1}{\sqrt{2}}\left|H_2\right|e^{i{\varphi }_{\left(2\right)}}+\frac{1}{\sqrt{6}}\left|H_3\right|e^{i{\varphi }_{\left(3\right)}}\right)}\right)$$

(59c)

We observe that in this simple model, if we change ${\varphi }_{\left(1\right)}={\varphi }_{\left(3\right)}$ to ${\varphi }_{\left(1\right)}+\pi ={\varphi }_{\left(3\right)}+\pi$, ${\phi }_1$ and ${\phi }_3$ will effectively interchange. We, therefore, expect no jump in the difference of ${\phi }_{13}.$ However, in contrast, a localized change is expected in the difference of ${\phi }_{12}$. Furthermore, the phases ${\phi }_1$, ${\phi }_2$, and ${\phi }_3$ will undergo sharp π jumps when the denominator of the argument of the inverse tangent of Equations (59a)–(59c) becomes zero. Such zeros will not occur for the same value of $\mathsf{\Delta }\theta$, leading to several possible phase jumps.

This model indicates that for some specific values of the difference in the phase between drivers 1 and 3, $\mathsf{\Delta }\theta$, one may observe localized changes in the phase of the primary linear modes and subsequently in the background phase of phi-bits (which was shown to be a linear combination of the primary phases). This is consistent with the results of Figure 2.

In the next sections, we show how we exploit the parallelism of nonlinearly correlated phi-bits and the features of the phi-bit phase (nonlinear phase jumps and background phase) arising from variations in the drivers’ parameter $\mathsf{\Delta }\theta$ to initialize the state of individual phi-bits and the superposition of states of multi-phi-bits.

3.2. Example of Initialization Using Nonlinear Phase Jumps

We can subtract the background phases from the measured ${\phi }_{12}$ and ${\phi }_{13}$ of phi-bits (a) and (b). The quantities $\mathsf{\Delta }{\phi }_{12}\left(a,b\right)={\phi }_{12}\left(a,b\right)-{\phi }_{12}^0\left(a,b\right)$ and $\mathsf{\Delta }{\phi }_{13}\left(a,b\right)={\phi }_{13}\left(a,b\right)-{\phi }_{13}^0\left(a,b\right)$ reflect only the sharp phase jumps associated with changes in $\mathsf{\Delta }\theta$. For the sake of illustration, we reduce the complex representation of the phi-bit states to their real part, namely

$${\psi }_r=\frac{1}{\sqrt{2}}\left(\cos \mathsf{\Delta }{\phi }_{12}\left(\begin{array}{c}1\\ 0\end{array}\right)+\cos \mathsf{\Delta }{\phi }_{13}\left(\begin{array}{c}0\\ 1\end{array}\right)\right)$$

(60)

In Figure 6, we report the components of ${\psi }_r\left(a\right)$ and ${\psi }_r\left(b\right)$ as functions of the drivers’ phase tuning parameter $\mathsf{\Delta }\theta$.

Figure 6 illustrates the ability to initialize the system composed of the two phi-bits (a) and (b) into all possible two-phi-bit states, which are the tensor products of selected two single phi-bit states. The single phi-bit states lie in a two-dimensional Hilbert space. The Hilbert space of the two phi-bit states has exponentially scaled dimensions: 2². By driving the physical system with $\mathsf{\Delta }\theta ~{122}^{\mathrm{o}},$ one can realize the two-phi-bit state labeled (1): $\left(\begin{array}{c}-1\\ 1\end{array}\right)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)$. Similarly, at $\mathsf{\Delta }\theta ~{157}^{\mathrm{o}}$, ${187}^{\mathrm{o}}$, and ${207}^{\mathrm{o}}$, one can initialize the system into the states: (2): $\left(\begin{array}{c}1\\ 1\end{array}\right)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)$, (3): $\left(\begin{array}{c}-1\\ 1\end{array}\right)\otimes \left(\begin{array}{c}-1\\ 1\end{array}\right)$ and (4): $\left(\begin{array}{c}1\\ 1\end{array}\right)\otimes \left(\begin{array}{c}-1\\ 1\end{array}\right)$, respectively. The two phi-bit states are constructed as the tensor products of single-phi-bit states and are, therefore, separable (i.e., not classically entangled). However, entanglement is not necessary to correlate the two phi-bits, as would be the case with two qubits, in order to enable parallelism in two-bit operations. Here, the two phi-bits (a) and (b) are correlated via the nonlinearity of the elasticity of the physical system. For phi-bits, classical entanglement would only be needed to initialize two different phi-bit states. This can be achieved with the current data by using a different representation (i.e., basis) of the two phi-bit states. We can see that through a single action on the nonlinear array of coupled acoustic waveguides, that is, tuning the drivers’ phase difference $\mathsf{\Delta }\theta ,$ one can parametrically change the states of phi-bits (a) and (b) and, therefore, simultaneously change the four components of the two phi-bit state vector. This action is actually a controllable operation on two phi-bit states. For instance, changing $\mathsf{\Delta }\theta$ from ${122}^{\mathrm{o}}$ to ${157}^{\mathrm{o}}$ results in the following unitary transformation acting on state (1) and producing state (2) to within a global phase of π:

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& -1\end{array}\right)\left(\begin{array}{c}-1\\ 1\\ -1\\ 1\end{array}\right)=-\left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right)$$

(61)

This unitary transformation is a phase gate that adds π to the second and fourth components of the two-phi-bit state vector. Changing $\mathsf{\Delta }\theta$ from ${157}^{\mathrm{o}}$ to ${187}^{\mathrm{o}}$ adds a phase of π to the second and third components of state vector (2) and produces state vector (3). Changing $\mathsf{\Delta }\mathsf{\theta }$ from ${187}^{\mathrm{o}}$ to ${207}^{\mathrm{o}}$ adds a phase of π to the first and third components of state vector (3) to produce state vector (4). This is only a simple illustration of how one can exploit the sharp phase jumps in logical phi-bit phases associated with the parametric variation of the relative phase between drivers in a nonlinear array of acoustic waveguides. Here, the difference in the phase response of the two phi-bits provides the complexity necessary to realize a complete set of two phi-bit states. This approach is scalable, and it can be applied readily to more than many logical phi-bits (which exist effectively in the spectral domain) without increasing the footprint of the physical system.

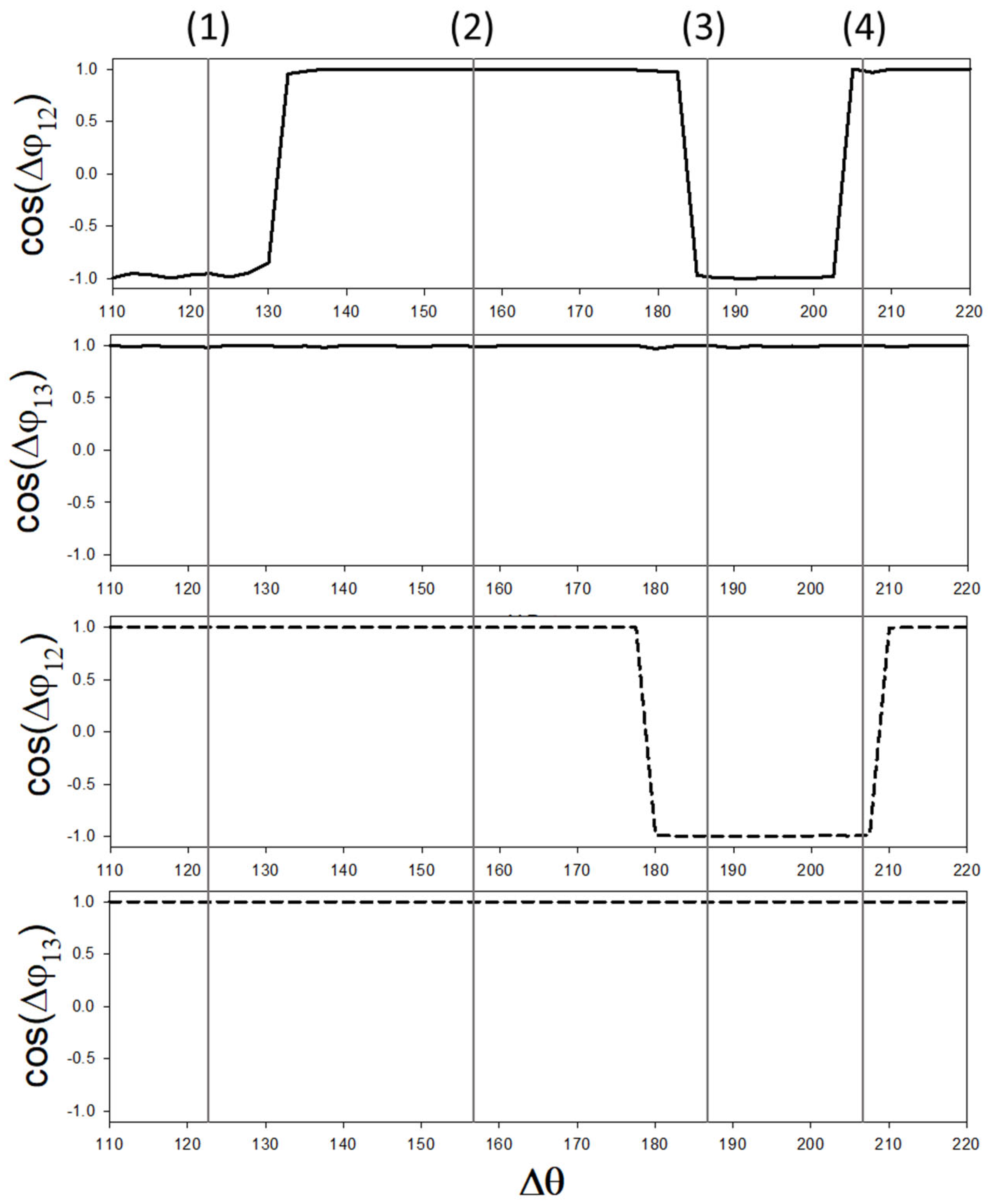
3.3. Example of Initialization Using Phi-Bit Background Phase

As seen in Figure 7 and observed in Section 2, a background in the phi-bit phase response is common to all phi-bits. This background arises from the phases of the primary mode at the frequency $f_1=2\pi /{\omega }_1$: ${\phi }_{12}\left(f_1\right)$ and ${\phi }_{13}\left(f_1\right)$. Since $\mathsf{\Delta }\theta$ only applies to drivers 1 and 3, which are driven at $f_1$, the phases of the primary modes at $f_2=2\pi /{\omega }_2$, ${\phi }_{12}\left(f_2\right)$ and ${\phi }_{13}\left(f_2\right)$ remain constant. Correlations between phi-bits make their background phases react simultaneously to a change in $\mathsf{\Delta }\theta$ in the same way.

When considering (for illustrative purposes) N phi-bits with the same background phases, (we have experimentally verified that in addition to phi-bits (a) and (b) presented in this paper, all other phi-bits investigated possess the same background phases. We recall that the state of each phi-bit “I” is given by Equation (5): ${\psi }^I=\frac{1}{\sqrt{2}}\left(e^{i{\phi }_{12}^I}{\left|0\right.\rangle }_I+e^{i{\phi }_{13}^I}{\left|1\right.\rangle }_I\right)$, I = a, b, …, m, n is the phi-bit index. The state of a multipartite composite system constituting N phi-bits can be constructed as a tensor product of individual phi-bit states, ${\psi }^I$’s, that is, $\mathsf{\Psi }={\psi }^a\otimes {\psi }^b\otimes \dots \otimes {\psi }^m\otimes {\psi }^n$. This multi-phi-bit state is defined in an exponentially scaling Hilbert space, $H$, of dimension $2^N$, and can be written as

$$\mathsf{\Psi }=\frac{1}{2^{N/2}}\left(\begin{array}{c}{e}^{i\left({\phi }_{12}^a+{\phi }_{12}^b\dots +{\phi }_{12}^m+{\phi }_{12}^n\right)}\\ e^{i\left({\phi }_{12}^a+{\phi }_{12}^b\dots +{\phi }_{12}^m+{\phi }_{13}^n\right)}\\ e^{i\left({\phi }_{12}^a+{\phi }_{12}^b\dots +{\phi }_{13}^m+{\phi }_{12}^n\right)}\\ .\\ .\\ e^{i\left({\phi }_{13}^a+{\phi }_{13}^b\dots +{\phi }_{13}^m+{\phi }_{13}^n\right)}\end{array}\right)$$

(62)

The basis for that representation is $\left\{{\left|0\right.\rangle }_a{\left|0\right.\rangle }_b\dots {\left|0\right.\rangle }_m{\left|0\right.\rangle }_n,{\left|0\right.\rangle }_a{\left|0\right.\rangle }_b\dots {\left|1\right.\rangle }_n,\dots , {\left|1\right.\rangle }_a{\left|1\right.\rangle }_b\dots {\left|1\right.\rangle }_m{\left|1\right.\rangle }_n \right\}$.

In order to construct other complex representations of the multi-phi-bit states, we can apply unitary transformations to the Hilbert space, $H$, which are equivalent to changes in the basis, i.e., a change in the co-ordinate system. Since the experimental background in ${\phi }_{12}^I$, and ${\phi }_{13}^I$ is the same for all phi-bits, we can use different representations to gain the ability to initialize multi-phi-bits states into any desired fiducial state. The choice of representation introduces complexity in multi-phi-bit states composed of identical single phi-bit states by differentiating them.

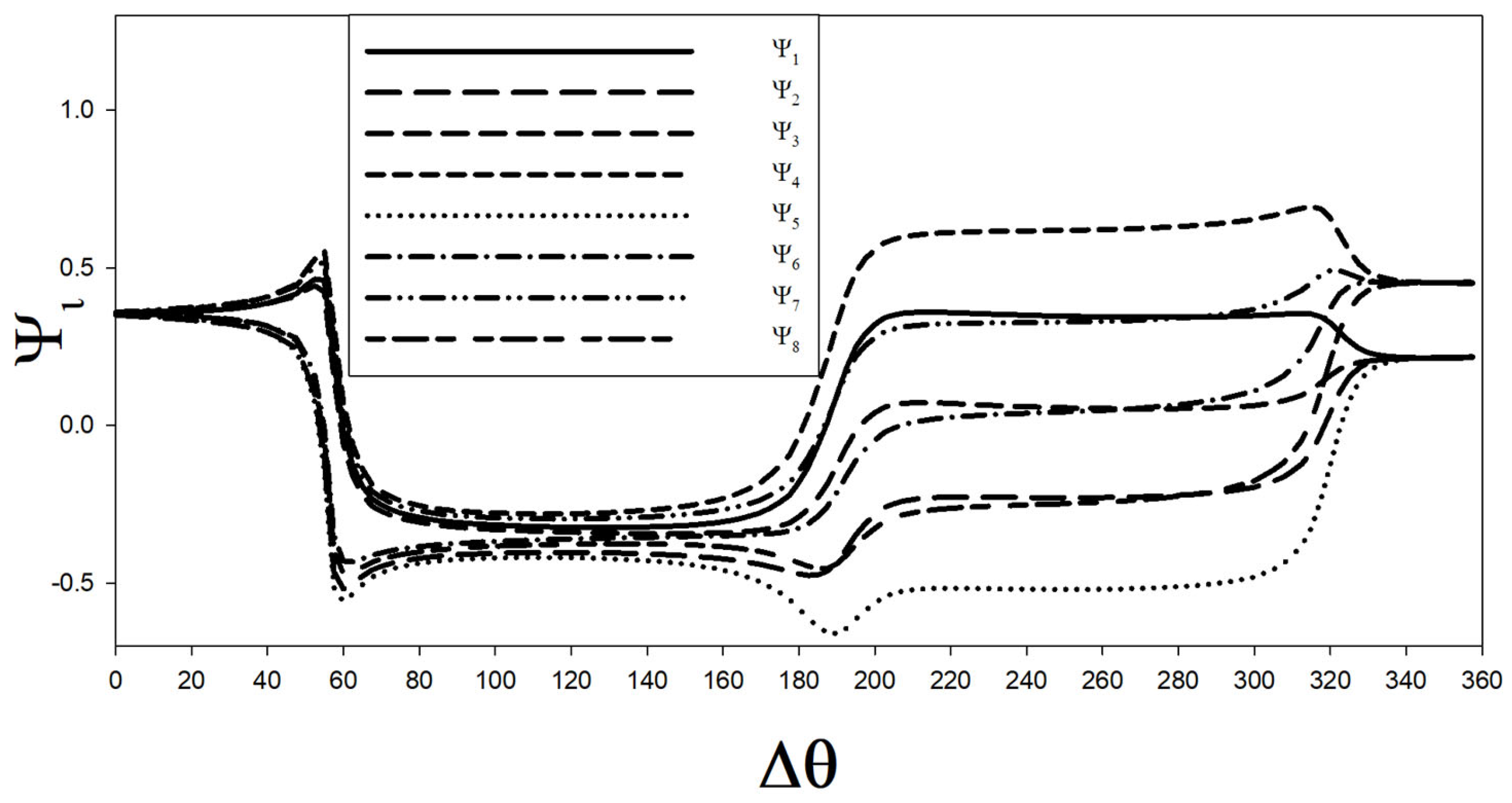
As an example, let us consider the following three-phi-bit representation:

$$\Psi =\left(\begin{array}{c}{\Psi }_1\\ {\Psi }_2\\ {\Psi }_3\\ {\Psi }_4\\ {\Psi }_5\\ {\Psi }_6\\ {\Psi }_7\\ {\Psi }_8\end{array}\right)=\frac{1}{Norm}\left\{\begin{array}{c}a\cos A\left({\phi }_{12}^a-{\delta }_{12}^a\right)+b\cos B\left({\phi }_{12}^b-{\gamma }_{12}^b\right)+c\cos C\left({\phi }_{12}^c-{\rho }_{12}^c\right)\\ a\cos A\left({\phi }_{12}^a-{\delta }_{12}^a\right)+b\cos B\left({\phi }_{12}^b-{\gamma }_{12}^b\right)+c\cos C\left({\phi }_{13}^c-{\rho }_{13}^c\right)\\ a\cos A\left({\phi }_{12}^a-{\delta }_{12}^a\right)+b\cos B\left({\phi }_{13}^b-{\gamma }_{13}^b\right)+c\cos C\left({\phi }_{12}^c-{\rho }_{12}^c\right)\\ a\cos A\left({\phi }_{13}^a-{\delta }_{13}^a\right)+b\cos B\left({\phi }_{12}^b-{\gamma }_{12}^b\right)+c\cos C\left({\phi }_{12}^c-{\rho }_{12}^c\right)\\ a\cos A\left({\phi }_{12}^a-{\delta }_{12}^a\right)+b\cos B\left({\phi }_{13}^b-{\gamma }_{13}^b\right)+c\cos C\left({\phi }_{13}^c-{\rho }_{13}^c\right)\\ a\cos A\left({\phi }_{13}^a-{\delta }_{13}^a\right)+b\cos B\left({\phi }_{12}^b-{\gamma }_{12}^b\right)+c\cos C\left({\phi }_{13}^c-{\rho }_{13}^c\right)\\ a\cos A\left({\phi }_{13}^a-{\delta }_{13}^a\right)+b\cos B\left({\phi }_{13}^b-{\gamma }_{13}^b\right)+c\cos C\left({\phi }_{12}^c-{\rho }_{12}^c\right)\\ a\cos A\left({\phi }_{13}^a-{\delta }_{13}^a\right)+b\cos B\left({\phi }_{13}^b-{\gamma }_{13}^b\right)+c\cos C\left({\phi }_{12}^c-{\rho }_{13}^c\right)\end{array}\right\}$$

(63)

where Norm is a normalization factor. In Figure 8, we report, as an example, these eight components for the set of parameters: $a=1$, $b=0.5$, $c=1$, $A=0.3$, $B=1$, $C=1$, ${\delta }_{12}^a={\delta }_{13}^a=0$, ${\gamma }_{12}^b={\rho }_{13}^c={10}^{\mathrm{o}}$, and ${\gamma }_{13}^b={\rho }_{12}^c=0^{\mathrm{o}}$. This representation enables the initialization of the approximate states (to within 15%), as expressed in the transpose form

$${\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta =0\right)\cong 0.35\left(1,1,1,1,1,1,1,1\right)$$

$${\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={55}^{\mathrm{o}}\right)\cong \left(0.5,0,0.5,0.5,0,0,0.5,0\right)$$

$${ \mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={60}^{\mathrm{o}}\right)\cong \left(0,-0.5,0,0,-0.5,-0.5,0,-0.5\right)$$

$${\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={120}^{\mathrm{o}}\right)\cong -0.35\left(1,1,1,1,1,1,1,1\right)$$

$${\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={270}^{\mathrm{o}}\right)\cong \left(0.33,-0.22,0,0.5,-0.5,0,0.33,-0.22\right)$$

$${\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={360}^{\mathrm{o}}\right)\cong 0.21\left(1,1,1,2,1,2,2,2\right)$$

One may notice the simple relations between some of these states, which may be viewed as resulting from nontrivial unitary transformations. For instance, ${ \mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={60}^{\mathrm{o}}\right)=\overleftrightarrow{T}{\mathsf{\Psi }}^T\left(\mathsf{\Delta }\theta ={55}^{\mathrm{o}}\right)$ with, for instance,

$$\overleftrightarrow{T}=\left(-1\right)\left(\begin{array}{cccccccc}0& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right)$$

This is only an example of the use of representation as a means of initializing multiple phi-bit states. While we are here, we have exploited the background phase of the phi-bit, and we can also use the nonlinear phase jumps in combination with representations to add complexity to the multi-phi-bit states that can be realized. Note that since the phi-bits are nonlinearly correlated, an initializing operation, such as $\overleftrightarrow{T}$, can be achieved experimentally with a single action of tuning the drivers’ phase difference.

4. Conclusions

We demonstrated how one could navigate the Hilbert space of two logical phi-bits by parametrically changing the physical system that supports them. We experimentally showed the manipulation of logical phi-bits state vectors by tuning the relative phase of the external drivers applied to a nonlinear array of coupled acoustic waveguides. We observed sharp phase jumps in the phi-bit states as a result of tuning the relative phase between drivers. These sharp phase jumps amount to approximately 180°. While the occurrence of the sharp phase jumps varies from phi-bit to phi-bit, all phi-bit phases possess a common background that is dependent on the drivers’ phase. We introduced simple models of the nonlinear arrays of externally driven coupled acoustic waveguides to shed light on the possible mechanisms that may underlie the experimentally observed behavior. Finally, by exploiting the sharp phase jumps, we illustrated the ability to initialize a system composed of two logical phi-bits into all possible two phi-bit states, which are tensor products of a selected subset of single phi-bit states. We also showed an approach to initialize exponentially complex states of multiple phi-bits by introducing multi-phi-bit representations and by tuning the phase background common to all phi-bits. The correlation between phi-bits resulting from the nonlinear elasticity of the physical system is critical to the parallelism of unitary operations on multiple phi-bit states.

This work provides only a simple demonstration of how phi-bits, which are acoustic, classical analogs of qubits, can bring us closer to realizing a classical acoustic physical system that meets DiVincenzo’s criteria. Logical phi-bits exist in the spectral domain of the nonlinear array of acoustic waveguides; thus, a phi-bit-based approach is scalable without increasing the footprint of the physical system. Phi-bits are classical nonlinear acoustic modes, and as such, their coherent superpositions of states can be measured without suffering from the fragility of quantum systems.