Abstract
Because of the sustained growth of information and mobile users transmitting a great amount of data packets, modern network performances are being seriously affected by congestion problems. In fact, congestion management is a challenging task that can be roughly summarized as a trade off between transmission latency and cost. In order to contribute to solve the congestion problem on communication networks, a novel framework based on a quantum game model is proposed, where network packets compete selfishly for their fastest route. Simulations show that final network routing and traveling times achieved with the quantum version outperform those obtained with a classical game model with the same options for packet transmission for both. Pareto optimality and Nash equilibrium are studied as well as the influence of simulated and real noise in the quantum protocol. This leads to the opportunity of developing full-stack protocols that may be capable of taking advantage of the quantum properties for optimizing communication systems. Due to its generality, this game approach can be applied both in classical complex networks and in future quantum networks in order to maximize the performance of the quantum internet.
1. Introduction
Congestion is a significant issue in the more diverse environments, from supermarket queuing, urban traffic, transport, local networks to 5G and LTE-A networks.
Congestion problems arise when users compete over a set of limited resources causing an increase in the latency to all contenders. Latency, for its part, depends on the number of agents that use a resource. A common example of congestion is at rush hour when the city’s vehicle flow is saturated due to excess demand for roads by drivers. When the number of vehicles surpass the capacity of the roads, there is a decrease in velocities that cause waste of time and excessive fuel consumption. Likewise, delays, loss of efficiency and increase of transmission time occur when networks are too demanded [1].
At present, the constant increase in the number of packets sent over networks evidences the congestion problems and suggests that more research is needed when designing efficient communication systems. By their nature, the congestion problems become appropriate for being modeled by Game Theory [2,3], because selfish decisions of agents (packets on the network or vehicles in a city) cause the whole system performance to be adversely affected.
In the case of Wireless Sensor Networks (WSN), a type of network that faces a more challenging environment compared to traditional networks, several works on the threat mitigation problem have recently been published. In [4], for instance, the authors present a survey of several game-theoretic defense strategies for Wireless Sensor Networks. Due to their dynamic nature, WSN are exposed to malicious intruders. Such a security situation involving an interaction between the defender(s) and attacker(s) is directly mapped to a game among players where each player strives to promote its own benefit.
Besides, in [5], a game theory model to control congestion in wireless body sensor networks supported on intelligent drop packet mechanisms is proposed. Moreover, a repeated game approach is proposed to sensor nodes protection in a clustered WSN in [6], where the proposed model outperforms non-cooperative defense mechanism to prevent cluster members from dropping the high priority packets.
Furthermore, today we know that if game theory models harness the capabilities of quantum computing [7,8] better outcomes can emerge. Moreover, the authors of [9] present an interesting work that address the Nash equilibria and correlated equilibria of classical and quantum games in the context of their Pareto efficiency. They focus their study in three classical games: the prisoner’s dilemma, battle of the sexes and the game of chicken and show that the Nash equilibria of these games in quantum mixed Pauli strategies are closer to Pareto optimal results than their classical counter-parts. Quantum routing games were first proposed in [10] where the Braess’ paradox was studied along with an analysis of the flow in a network with quantum resources, more exactly, networks that provide quantum entangled particles to the players before they play their strategies. In addition, in [11] a quantum game is applied to diminish spectrum allocation times and power consumption in quantum communication networks [12].
In this work, we start by modeling a network that allows both classical and quantum packets and then propose a routing protocol designed using the Game Theory formalism. After that, different variables with information about the dynamics of the network were measured and we point out that the protocol that makes use of the quantum game theory rules [13] significantly outperforms its classical equivalent. We demonstrate how to avoid congestion in a network and decrease the traveling time per packet in a system with a high number of packets that selfishly decide which decision is the best for everyone of them.
There have already been efforts to try to mitigate congestion in networks using quantum technologies (mainly coming from the automotive industry [14,15,16]) but they focus on a centralized optimization approach using quantum annealing. In this work, we propose a decentralized self-organization approach using gate-based quantum computers. Finally, due to the absence of ideal quantum computers that we suffer today, the influence of noise in our system is studied. This is achieved by both doing simulations using quantum noise models and using current IBM noisy quantum computers available on the web [17].
The work is organized as follows. In Section 2, the problem and the system are presented in detail. In Section 3, we explain the two possible strategies for modeling the network and develop in depth the quantum model. In Section 4, the results of each protocol are compared and their performance is graphically analyzed under different types of environment: ideal case, simulated noise and real devices. Finally, the work is concluded in Section 5 with a debate on its consequences.
2. Modeling the Congestion Problem
Our goal is to minimize the total transmission time, which is formed by the sum of the routing time and the traveling time. The routing time measures how long it takes for a packet to find a path for going from origin to destination. More precisely, in our model, the routing time is a quantity proportional to the number of games a packet must play before finding its final path. The greater the number of possible paths that a packet considers, the longer the routing time. The traveling time, for its part, measures how long it takes for a packet to travel from origin to destination when the path is chosen. This means, the sum of the weights of all the edges that a final path has.
Therefore, , where is the time it takes to play one game, is the number of games played by the player i, is the maximum distance between two nodes in the network, is the number of edges of the final path of player i and is the weight of the edge connecting the nodes e and .
The communication network model has nodes and packets to be sent between nodes. The net is generated using the Erdős–Rényi–Gilbert model [18] with (where is the number of nodes and the probability that two nodes are connected to each others) with the condition that every node has at least one connection to other node. The maximum capacity of every channel is assumed to be one packet, with linearly declining performance from there on. This decline will be reflected in our model by increasing the corresponding weight, , of each channel proportionally to the number of packets going through it. An example of a nodes network is shown in Figure 1 where the packets traveling through are represented with different colors.
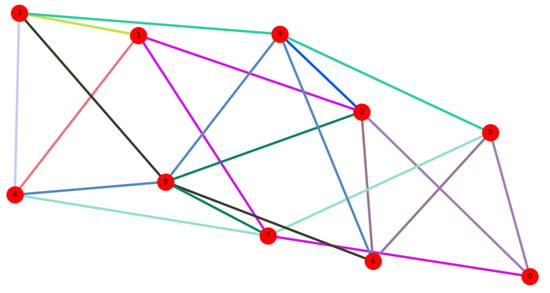
Figure 1.
Example of network model for .
In a congested channel it will take much longer traveling time for a given packet than in an idle one. In other words, as the number of packets traveling through the same channel increases, the traveling time for each packet increases. This situation is analogous to city transport where the time a vehicle takes to travel a route increases as the number of vehicles on that route increases. If this situation is not handled well, this may result in heavy traffic congestion [19].
Every packet is thought as a player in a game that prefers the shortest path channel. The traveling channel choice is made by playing a game. Whenever many players choose the same channel, the traveling time for that channel increases. Channel congestion makes traveling time much longer. Finally, on every congested channel packets play game, each of them has two options: to travel through the preferred channel or to search another path.
If every player decides to choose their shortest path, some network channels will be overloaded with all the packets that are disputing for it, slowing down the network. Therefore, if players behave in a selfish way, always choosing their shortest path, the whole communication network will be harmed. On the other hand, if every player decides to look for idle channels, the routing time increases and the network would be also slowed down. This simple model reflects the massive problem faced in modern communication technologies which poses a severe challenge to the existing routing strategies [20]. This phenomenon is called congestion dilemma, as we will observe in the following sections, the routing time may decrease by increasing traveling time or traveling time may decrease by increasing routing time.
3. Classical and Quantum Strategies
It is well known that a game is defined by three elements: players, strategies, and rewards. In this case, our game has a non-cooperative nature, that is, it is a game with competition between individual players, the players being the packets that travel through the network. The strategies are to take or not a channel when there are enough packets to congest the channel. Lastly, the reward is the total time that is specified by adding the routing and traveling time (with a negative sign since the lower the time, the bigger the reward).
If more than one packet is interested in a channel, because it is part of their currently shortest path, each packet has two possible strategies: choose this preferred channel (risking that other packets will also select it and then congest the channel) or search for its following shortest path (longer but possibly idler). These two strategies will be called option 1 and 0, respectively. For example, in the first game of a player, he has two options: (1) Take the shortest path risking that the congestion increases their traveling time significantly. (0) Try with their second shortest path, where there might be no congestion. In Table 1, an example of a situation where two packets are interested in the same channel, is presented.

Table 1.
Example of two packets interested in the same channel.
The playing games may be of different kind, that is classical or quantum. Let us consider first classical games. The player’s mixed classical strategies are probabilistic, that is, option 0 is chosen with probability p and option 1 with probability . Then, probability p near zero corresponds to greedy players, since players will tend to always take the shortest path even when many players are competing for that channel. A value of p closer to one will create players more patiently looking for another idler route.
To study the quantum game for channel choice we follow the EWL protocol for 2 players [8] and then extended for N players [21]. The first step is to assign a quantum state to each of the possible strategies. The quantum protocol is exactly the same as the classical one, the only difference being that strategies 0 and 1 were previously represented on a bit and now they are represented on a qubit. Strategy 0 (leave the preferred route) is mapped to the quantum state and strategy 1 (take the preferred route) to the quantum state . The second step is to create a quantum circuit where each player will be assigned a qubit that will start in state . The third step is to create a maximally entangled state between all the players. This is done by applying the entangling operator , as seen in Figure 2, where the number of players is .
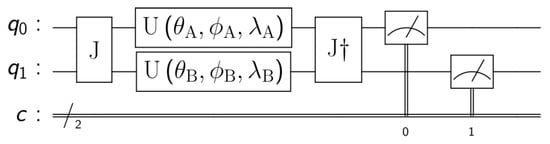
Figure 2.
EWL game model for 2 players. Where and are the initial quantum states of the players and c is a classical register where the qubits measurements are stored.
In the fourth step, every player chooses her most suitable strategy individually and independently. This is done by modifying the state of her own qubit locally. To do this, every player applies one or more one-qubit gates, modifying the state of her qubit. A general one-qubit gate is a unitary matrix that can be represented as [22]:
We can already highlight the fact that while classic players have only one parameter to choose their mixed strategy: p, quantum players have three parameters to choose in order to select their own pure strategy: , and . The fifth step is to apply the operator (J conjugate transpose) after the players’ strategies. Furthermore, finally, the sixth step consists of measuring the state of the qubits to know the output of the circuit and, therefore, the final action of each player.
4. Results
In this section, we compare the results of classic and quantum protocols. The simulations were done averaging the performance of 50 simulations for different auto-generated random network configurations. The prospect of Pareto optimality and Nash equilibrium in each case is considered. The quantum protocol is also analyzed under non-ideal conditions, by modeling a noisy channel and also using the quantum devices available from IBM.
4.1. Pareto Optimality and Nash Equilibrium
Numerical simulations are performed since we do not have an analytical representation of the model due to its complexity. In the classic case with mixed strategies we will accomplish this by sweeping in p, while in the quantum case with pure strategies, as explained below, sweeping in , and .
4.1.1. Mixed Classical Strategies
Simulations of the classical game, where all players have the probability p, are shown in Figure 3. Figure 3a displays the average traveling time per packet increase with the increasing number of packets for different probabilities p. The variation of the average routing time with the number of packets is shown alongside in Figure 3b.
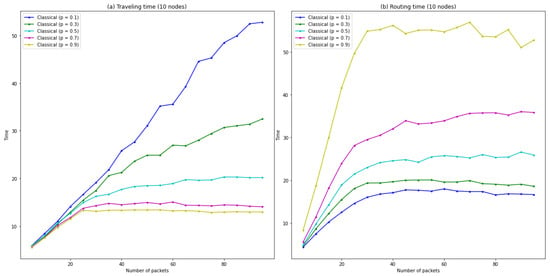
Figure 3.
Graphs for different probabilities p of: (a) Traveling time as a function of the number of packets. (b) Routing time as a function of the number of packets.
The simulations were done on networks of nodes and a value of packets from to packets and averaging the performance of 50 different cases. The qualitative behavior of the network, that is, the dynamics reflected in the graphs, is independent of the number of nodes. The only difference is the number of packets needed for the network to stabilizes, the larger the network, the greater the number of packets required to saturate it. Analyzing the graphs for an increasing number of nodes it is possible to conclude that there is a kind of trade-off between traveling and routing time. Given a fixed number of packets and a low p, the traveling time per packet increases but the routing time decreases. On the other hand, as p increases, the traveling time per packet decreases but the routing time increases.
This effect can be seen in Figure 4 where traveling and routing time for different probabilities p are shown. These results are obtained when the system reaches steady state with a high number of packets ().
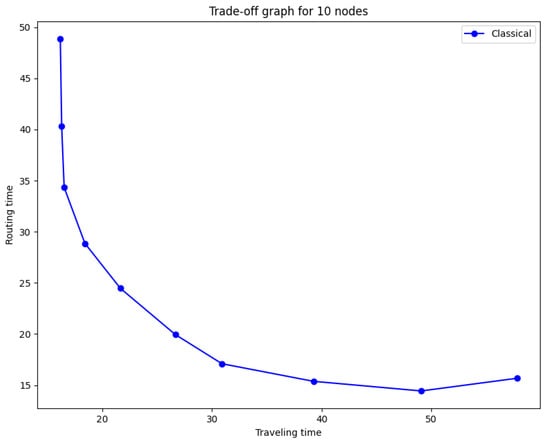
Figure 4.
Trade-off between traveling and routing time for different p values between 0 and . Values of p closer to 0 give a high traveling time and low routing time. Values of p closer to 1 give a low traveling time and high routing time.
4.1.2. Pure Quantum Strategies
As mentioned earlier, the quantum player’s strategy consists of a sequence of 1 qubit quantum gates. To demonstrate the potential that quantum strategies have, we are going to start by studying a particular case: the system with rotations in the X, Y and Z axes. The one-qubit quantum gate matrices for rotations are:
Therefore, every player must choose 3 angles that we will call , and . In our design, we propose the strategy , and for every player as shown in Figure 5.
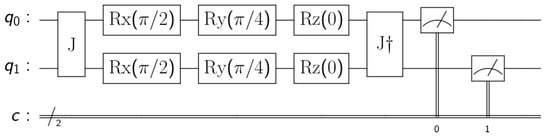
Figure 5.
Game model for 2 players.
In Figure 6a,b the quantum protocol performance when all players are using is shown against the classical performance. The quantum game shows the lowest traveling time and a medium routing time compared to the classical one. With this in mind we can recalculate Figure 4 and add the quantum case. By doing this we obtain Figure 7 where we can observe how the classical traveling-routing time trade-off barrier is crossed by this quantum protocol. Thus, we will obtain a performance that enhances any classical performance by simultaneously reaching less routing time and less traveling time.
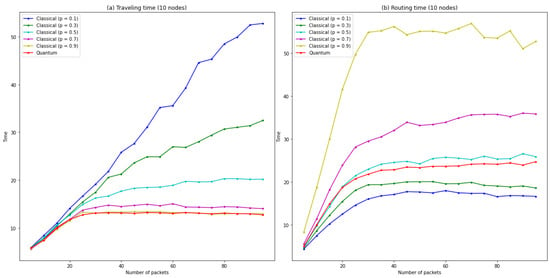
Figure 6.
Graphs for different probabilities p and the quantum case: (a) Traveling time as a function of the number of packets. (b) Routing time as a function of the number of packets.
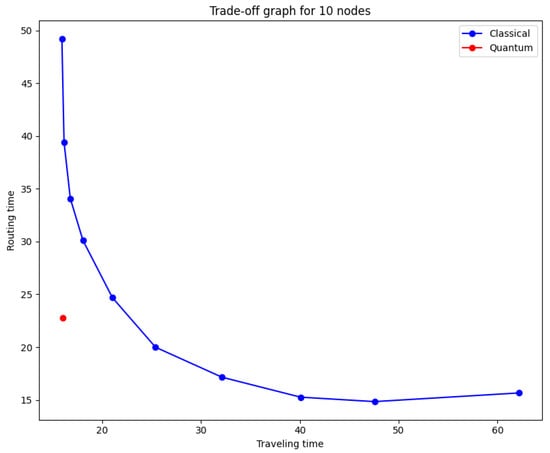
Figure 7.
Trade-off barrier broken by quantum protocol. In red the quantum strategy, in blue different mixed classical strategies with p values between 0 and .
Another way of visualizing the advantage of the quantum protocol is by measuring the total_time = routing_time + traveling_time. In Figure 8, it is clear that when the total time is measured, the performance of the quantum protocol surpass the performance of the classical protocol as the number of packets increases and the network becomes increasingly congested.
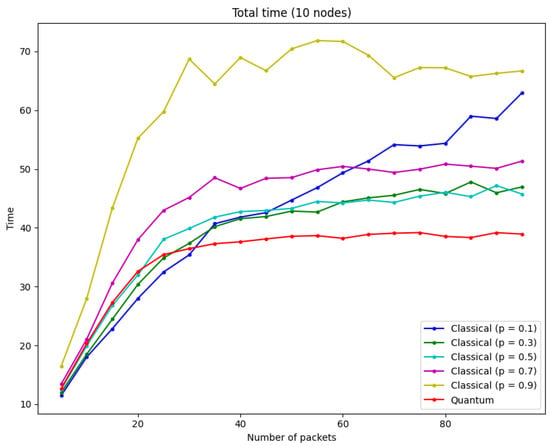
Figure 8.
Total time = routing time + traveling time, it is evident that the minimum total time correspond to the quantum case when the number of packets increases.
This advantage may be understood considering the quantum state of the circuit for two players (Figure 5) just before measuring, is: .
That is, state will be measured with a 50% probability and state with a 50% probability. This strategy turns out to be Pareto optimal since no player can improve their performance without worsening someone else’s. This means that one of the two players will always take the channel and the other will not. By avoiding state we are avoiding the case where the two players take the channel, therefore, avoiding network congestion.
By taking advantage of the entanglement generated at the beginning of the circuit in the quantum game, an unattainable behavior in the classical case is obtained: having a medium routing time with minimal traveling time.
However, is just one of the possible pure strategies. In Figure 9, the performance of different quantum strategies is shown. The quantum protocol may enhance (points under the classical trade-off curve) or worsen (points over the classical trade-off curve) the network performance depending on the different quantum strategies selected by the players if they change the values of , and .
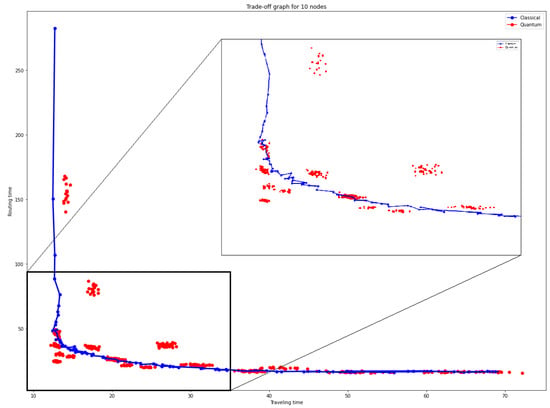
Figure 9.
Trade-off barrier broken by quantum protocol. In red different pure quantum strategies, in blue different mixed classical strategies with p values between 0 and .
4.1.3. Mixed Quantum Strategies
It is interesting to know if is also a Nash equilibrium. For an strategy to be a Nash equilibrium, no player will have any incentive to individually modify their strategy. It turns out that there exists a strategy that is beneficial to an individual player assuming that the rest apply , therefore is not a Nash equilibrium. It also turns out that is Pareto optimal and is not a Nash equilibrium, since there exists a that is beneficial for an individual player assuming that the rest apply . Again, is Pareto optimal and not a Nash equilibrium, since there exists another that is beneficial for an individual player assuming that the rest apply . Furthermore, finally, is Pareto optimal and not a Nash equilibrium since an individual player can apply to benefit himself!
In short, , , and are all pure strategies. All of them are Pareto optimal in our problem, since no player can improve their performance without worsening someone else’s and if all the players apply the same strategy maximum performance can be obtained and the network congestion be avoided. However, none of them is a Nash equilibrium since there is always a dominant strategy that would increase the benefit of an individual player thus encouraging players to individually modify their strategy.
Finally, we can build a mixed strategy that applies the four strategies , , and with equal probability . turns out to be Pareto optimal since no one can improve their own performance without worsening someone else’s and it also appears to be Nash equilibrium since we could not find any strategy that a player can apply individually to increase their own performance assuming that the other players are applying .
The rigorous proof that is a Nash equilibrium will be left for future work and its difficulty relies on the fact that the strategy space is infinite. Another interesting work that remains for the future is the study of the equilibrium strategies of the system formulated as a generic infinitely repeated quantum game [23]. , and are already continuous variables, and for proving that is a Nash equilibrium it is necessary to demonstrate that there is no mixed strategy in the entire space (three probability density function, over , and ) that has the incentive to deviate.
Observing the outcome of the system when all players apply the mixed strategy , we see in Equation (6) how we avoid congestion. States and are absent, therefore, the congestion is avoided.
4.2. Noise Influence
To date, we have been studying the system without considering noise and decoherence of quantum states. In this section, quantum noise on the system is considered.
4.2.1. Decoherence Simulation
In order to add quantum noise to the model we use the quantum depolarization channel [22]. This channel depends on a parameter C that maps from the state (from Equation (6)) to the maximally mixed state () following the equation: , with I the identity matrix and d the dimension of the quantum state.
Figure 10 is obtained by plotting the performance of the system for a Pareto optimal case and different values of C (from to , respecting the condition of complete positivity). The performance becomes more and more similar to the classical case as the original quantum state tends to the maximally mixed state. Finally, as expected, the maximally mixed state () and the classical mixed strategy with have the same performance.
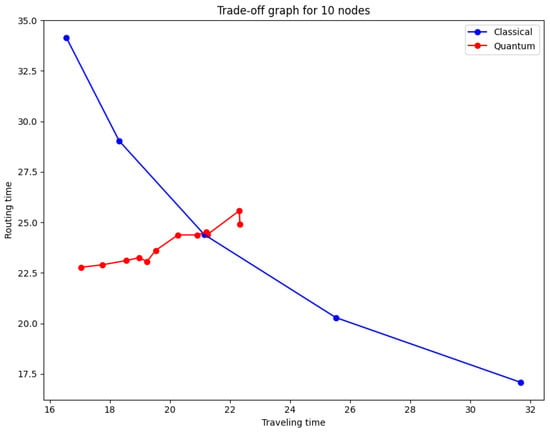
Figure 10.
Effect of decoherence in the trade-off barrier by quantum protocol. As the value of C moves away from (ideal case), the quantum case looks more and more like the classical case. p values between and .
4.2.2. Real Device Noise
In order to test our proposal, the IBM quantum computers [17] were used to simulate the quantum games. IBM quantum computer are denominated NISQ (Noisy Intermediate-Scale Quantum) devices [24], this means that the quantum processors are very sensitive to the environment and may lose their quantum state due to quantum decoherence. In the NISQ era, the quantum processors are not sophisticated enough to continuously implement quantum error correction, that is why it is important to test our algorithm in these type of quantum devices. The results can be observed in Figure 11.
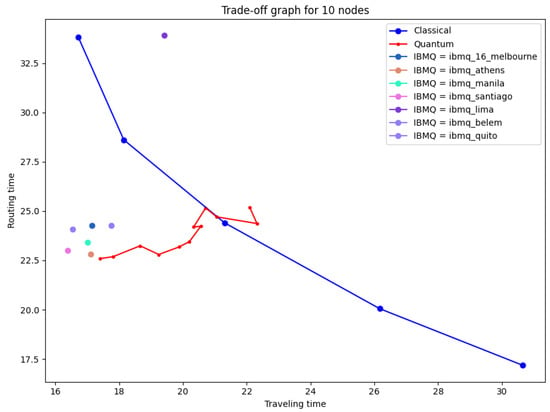
Figure 11.
Effect of real devices in the trade-off barrier by quantum protocol. Congestion can be mitigated by making use of IBM NISQ quantum computers. p values between and .
Importantly, the protocol performance is actually very high. This is because the games were implemented playing in 2-player batches, that is, 2-qubit quantum circuits, while available quantum computers are still very noisy for large quantum systems, they perform well when dealing with few qubits and shallow quantum gates circuits.
4.3. Outline
To sum up, mixed classical strategies are constrained by a trade-off between the routing and traveling time. By allowing quantum strategies, it is possible to break this trade-off and many Pareto optimal points that outperform the protocol with classical games are obtained. However, they do not correspond to a Nash equilibrium. In order to achieve this goal it is necessary to switch to mixed quantum strategies where we propose a strategy that is Pareto optimal and appears to be a Nash equilibrium.
5. Conclusions
Communication networks are facing increasing congestion problems associated with the tremendous growth of the number of packets sent over the networks. In order to get an improvement on the communication network performance classical and quantum network protocols based on game theory are proposed in this work. Classical game protocols lead to a routing and traveling time constraint that deteriorates the network performance for an increasing number of packets.
The quantum model is obtained with quantum strategies as proposed by the EWL protocol of quantum games. Quantum strategies are represented by a three-parameter one-qubit quantum gate model. Then, the players strategies are extended when passing from classical to quantum.
The trade-off barrier between routing and traveling time present in the classic probabilistic protocol is surpassed by many quantum game strategies leading to an enhancement of the network performance for increasing packet number. The stability of the quantum strategies is associated with Nash equilibrium. As pure quantum strategies are not Nash equilibrium, mixed strategies have been studied. In this way, a mixed strategy that is Pareto optimal and seems to be Nash equilibrium was shown. Additionally, it was also shown that under the influence of simulated noise and real quantum devices the quantum protocol benefits still remain.
We have shown that a quantum game formalism applied to the communication network enhances its efficiency when dealing with congestion problems. Consequently, a new world of opportunities could emerge in these types of complex systems when taking advantage of the possibilities offered by quantum computing. Moreover, they might bring with them solutions that create remarkably more efficient systems.
Author Contributions
Conceptualization, A.S.; Formal analysis, A.S.; Investigation, A.S., O.G.Z. and C.M.A.; Project administration, C.M.A.; Software, A.S.; Supervision, O.G.Z. and C.M.A.; Validation, O.G.Z.; Writing—original draft, A.S. and O.G.Z.; Writing—review & editing, C.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and scripts that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Niyato, D.; Hossain, E. Modeling user churning behavior in wireless networks using evolutionary game theory. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March–3 April 2008; pp. 2793–2797. [Google Scholar]
- Morgenstern, O.; Von Neumann, J. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Nash, J.F., Jr. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdalzaher, M.S.; Seddik, K.; Elsabrouty, M.; Muta, O.; Furukawa, H.; Abdel-Rahman, A. Game theory meets wireless sensor networks security requirements and threats mitigation: A survey. Sensors 2016, 16, 1003. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.Y.; Li, S.P.; Mansour, H. An intelligent packet drop mechanism in wireless body sensor network for multiple class services based on congestion control. Procedia Comput. Sci. 2019, 154, 453–459. [Google Scholar] [CrossRef]
- Abdalzaher, M.S.; Seddik, K.; Muta, O. Using repeated game for maximizing high priority data trustworthiness in wireless sensor networks. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 552–557. [Google Scholar]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052. [Google Scholar] [CrossRef] [Green Version]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef] [Green Version]
- Szopa, M. Efficiency of classical and quantum games equilibria. Entropy 2021, 23, 506. [Google Scholar] [CrossRef]
- Solmeyer, N.; Dixon, R.; Balu, R. Quantum routing games. J. Phys. Math. Theor. 2018, 51, 455304. [Google Scholar] [CrossRef] [Green Version]
- Zabaleta, O.G.; Barrangú, J.P.; Arizmendi, C.M. Quantum game application to spectrum scarcity problems. Phys. Stat. Mech. Its Appl. 2017, 466, 455–461. [Google Scholar] [CrossRef] [Green Version]
- Bassoli, R.; Boche, H.; Deppe, C.; Ferrara, R.; Fitzek, F.H.; Janssen, G.; Saeedinaeeni, S. Quantum Communication Networks; Springer: Berlin/Heidelberg, Germany, 2021; Volume 23. [Google Scholar]
- Khan, F.S.; Solmeyer, N.; Balu, R.; Humble, T.S. Quantum games: A review of the history, current state, and interpretation. Quantum Inf. Process. 2018, 17, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Neukart, F.; Compostella, G.; Seidel, C.; Von Dollen, D.; Yarkoni, S.; Parney, B. Traffic flow optimization using a quantum annealer. Front. ICT 2017, 4, 29. [Google Scholar] [CrossRef]
- Yarkoni, S.; Leib, M.; Skolik, A.; Streif, M.; Neukart, F.; von Dollen, D. Volkswagen and quantum computing: An industrial perspective. Digitale Welt 2019, 3, 34–37. [Google Scholar] [CrossRef]
- Yarkoni, S.; Neukart, F.; Tagle, E.M.G.; Magiera, N.; Mehta, B.; Hire, K.; Narkhede, S.; Hofmann, M. Quantum shuttle: Traffic navigation with quantum computing. In Proceedings of the 1st ACM SIGSOFT International Workshop on Architectures and Paradigms for Engineering Quantum Software, Virtual, 13 November 2020; pp. 22–30. [Google Scholar]
- IBM Quantum Experience. Available online: http://www.research.ibm.com/quantum (accessed on 10 June 2021).
- Gilbert, E.N. Random graphs. Ann. Math. Stat. 1959, 30, 1141–1144. [Google Scholar] [CrossRef]
- Jabbarpour, M.R.; Zarrabi, H.; Khokhar, R.H.; Shamshirband, S.; Choo, K.K.R. Applications of computational intelligence in vehicle traffic congestion problem: A survey. Soft Comput. 2018, 22, 2299–2320. [Google Scholar] [CrossRef]
- Ding, R.; Yang, Y.; Liu, J.; Li, H.; Gao, F. Packet routing against network congestion: A deep multi-agent reinforcement learning approach. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 932–937. [Google Scholar]
- Benjamin, S.C.; Hayden, P.M. Multiplayer quantum games. Phys. Rev. A 2001, 64, 030301. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ikeda, K.; Aoki, S. Infinitely repeated quantum games and strategic efficiency. Quantum Inf. Process. 2021, 20, 1–24. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).