Simple Analytical Expression of the Voigt Profile
Abstract
1. Introduction
2. Evaluation of the Voigt Profile
2.1. Expression of in Terms of the Humbert Function
2.2. A Simple Approximation of the Voigt Profile
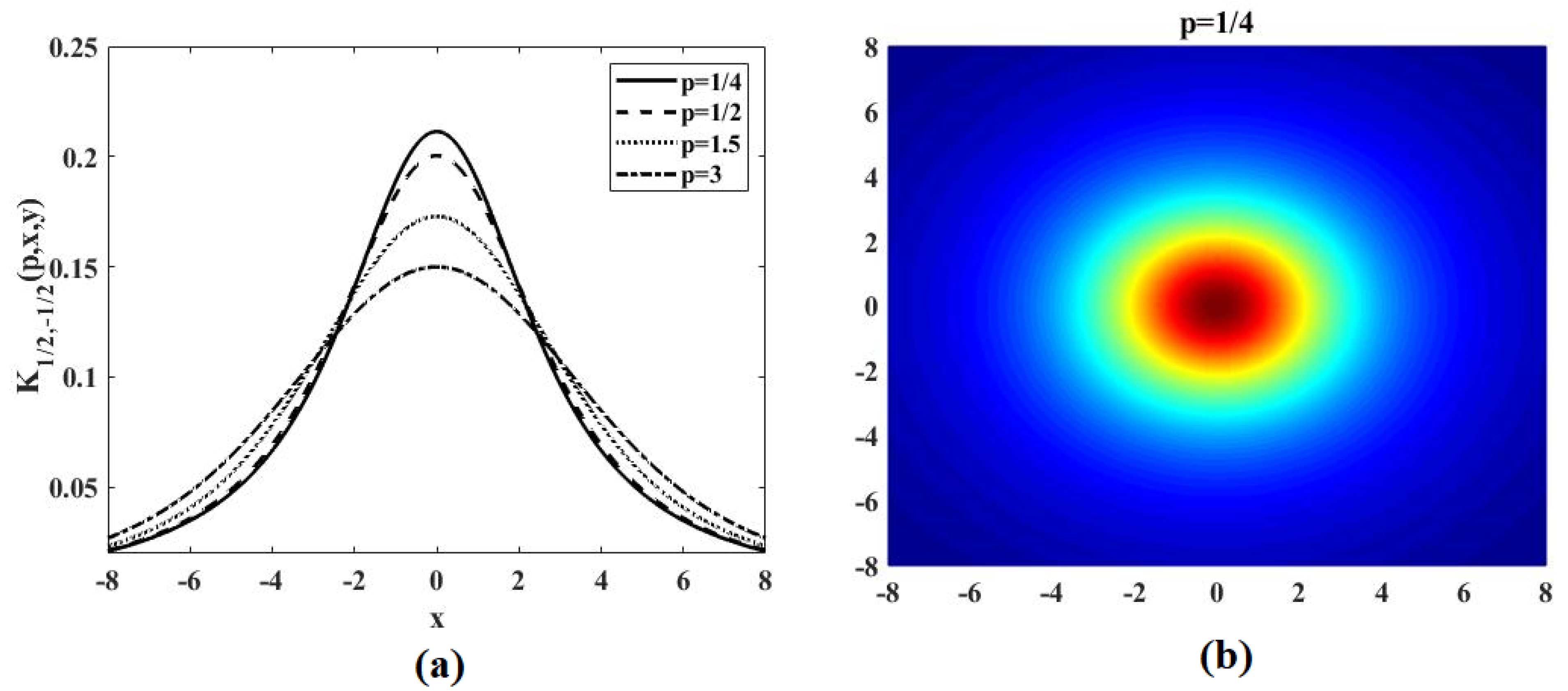
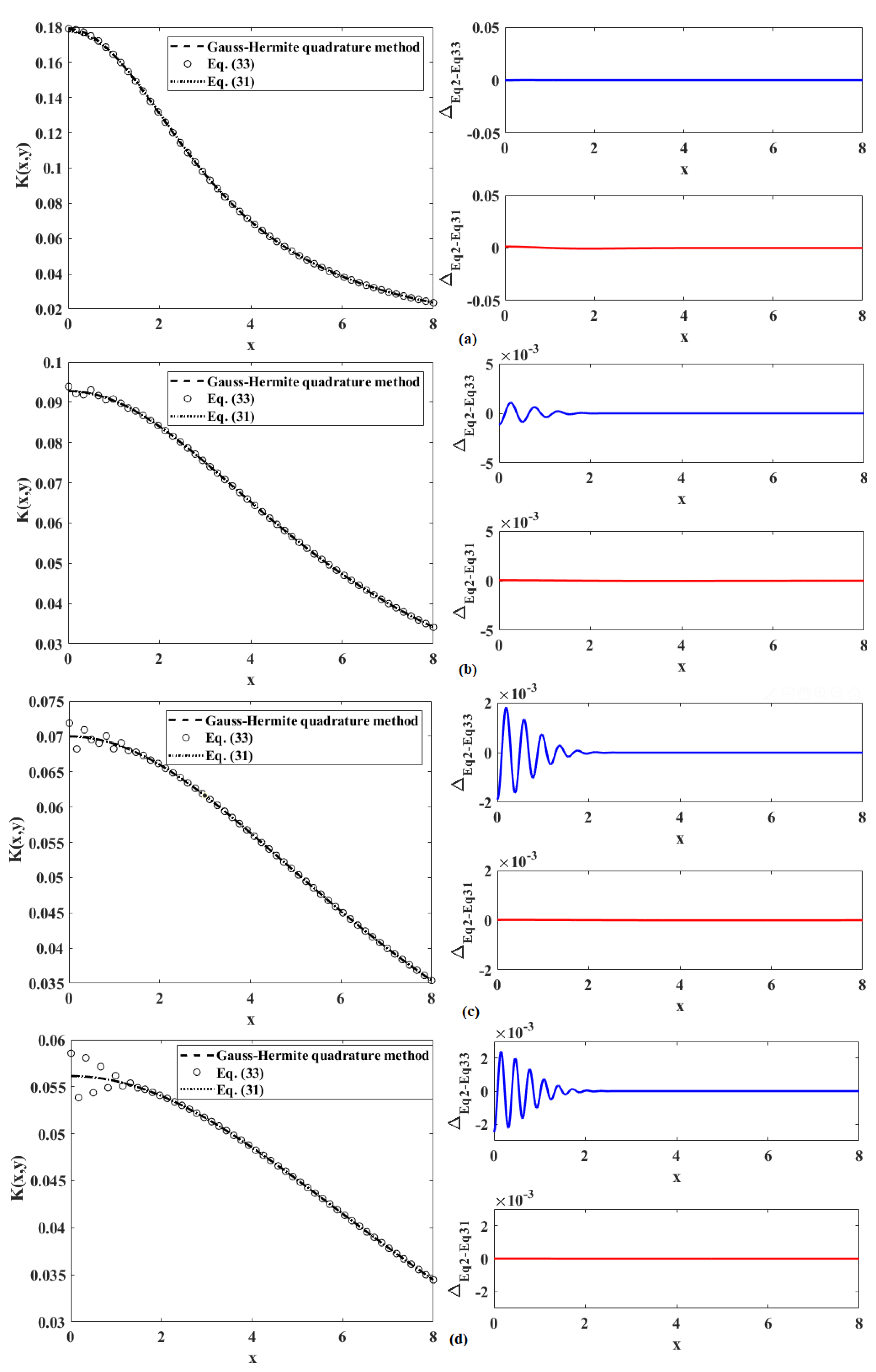
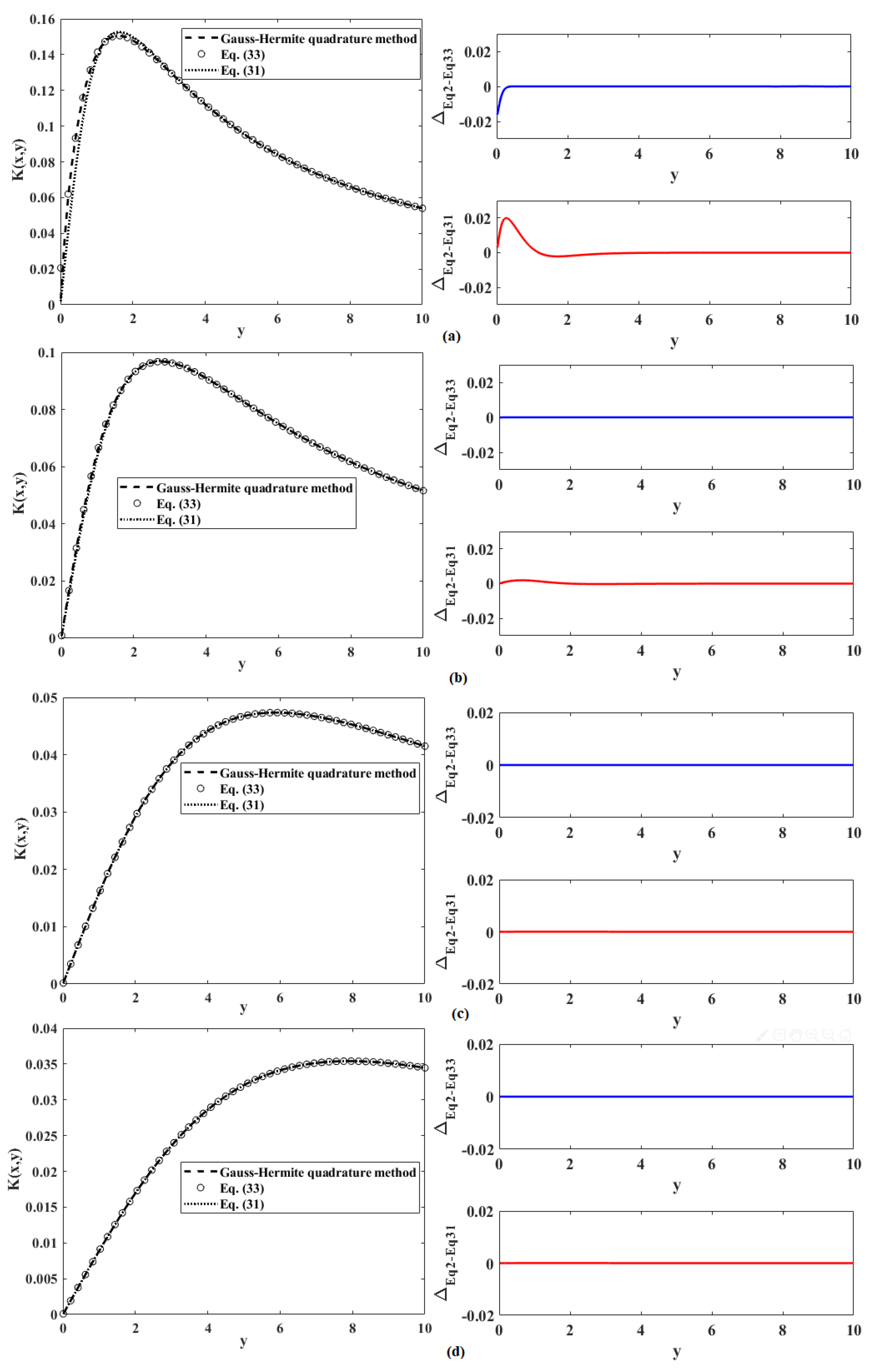
3. Analysis and Numerical Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reiche, F. Uber die emission, absorption and intensitats vertcitung von spektrallicien. Ber. Deutsch. Phys. Ges. 1913, 15, 3–21. [Google Scholar]
- Benedict, W.S.; Herman, R.; Moore, G.E.; Silverman, S. The Strengths, Widths, and Shapes of Infrared Lines: I. General Considerations. Can. J. Phys. 1956, 34, 830–849. [Google Scholar] [CrossRef]
- Hummer, D.G. Non-Coherent Scattering: I. The Redistribution Function with Doppler Broadening. Mon. Not. R. Astron. Soc. 1962, 125, 21–37. [Google Scholar] [CrossRef]
- Armstrong, B. Spectrum line profiles: The Voigt function. J. Quant. Spectrosc. Radiat. Transf. 1967, 7, 61–88. [Google Scholar] [CrossRef]
- Young, C. Calculation of the absorption coefficient for lines with combined Doppler and Lorentz broadening. J. Quant. Spectrosc. Radiat. Transf. 1965, 5, 549–552. [Google Scholar] [CrossRef][Green Version]
- Yamada, H. Total radiances and equivalent widths of isolated lines with combined Doppler and collision broadened profiles. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 1463–1473. [Google Scholar] [CrossRef][Green Version]
- Haubold, H.J.; John, R.W. Spectral line profiles and neutron cross sections: New results concerning the analysis of Voigt functions. Astrophys. Space Sci. 1979, 65, 477–491. [Google Scholar] [CrossRef]
- Whiting, E. An empirical approximation to the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 1379–1384. [Google Scholar] [CrossRef]
- Rodgers, C.; Williams, A. Integrated absorption of a spectral line with the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 1974, 14, 319–323. [Google Scholar] [CrossRef]
- Drayson, S. Rapid computation of the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 1976, 16, 611–614. [Google Scholar] [CrossRef]
- Minguzzi, P.; Di Lieto, A. Simple Padé approximations for the width of a Voigt profile. J. Mol. Spectrosc. 1985, 109, 388–394. [Google Scholar] [CrossRef]
- Flores-Llamas, H.; Cabral-Prieto, A.; Jiménez-Domínguez, H.; Torres-Valderrama, M. An expression for an approximation of the Voigt profile I. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1991, 300, 159–163. [Google Scholar] [CrossRef]
- Teodorescu, C.; Esteva, J.; Karnatak, R.; El Afif, A. An approximation of the Voigt I profile for the fitting of experimental X-ray absorption data. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 345, 141–147. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, J.; Huang, G.; Guo, Y.; Duan, C. Simple empirical analytical approximation to the Voigt profile. J. Opt. Soc. Am. B 2001, 18, 666–672. [Google Scholar] [CrossRef]
- Asfaw, A. A fast method of modeling spectral lines. J. Quant. Spectrosc. Radiat. Transf. 2001, 70, 129–137. [Google Scholar] [CrossRef]
- Letchworth, K.L.; Benner, D.C. Rapid and accurate calculation of the Voigt function. J. Quant. Spectrosc. Radiat. Transf. 2007, 107, 173–192. [Google Scholar] [CrossRef]
- Di Rocco, H.; Cruzado, A. The Voigt Profile as a Sum of a Gaussian and a Lorentzian Functions, when the Weight Coefficient Depends Only on the Widths Ratio. Acta Phys. Pol. A 2012, 122, 666–669. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Miller, E.A. A unified presentation of the Voigt functions. Astrophys. Space Sci. 1987, 135, 111–118. [Google Scholar] [CrossRef]
- Errera, Q.; Vanderauwera, J.; Belafhal, A.; Fayt, A. Absolute Intensities in 16O12C32S: The 2500–3100 cm−1. J. Mol. Spectrosc. 1995, 173, 347–369. [Google Scholar] [CrossRef]
- Belafhal, A. The shape of spectral lines: Widths and equivalent widths of the Voigt profile. Opt. Commun. 2000, 177, 111–118. [Google Scholar] [CrossRef]
- AlOmar, A.S. Accurate Chebyshev Approximations for the Width of the Voigt Profile, Differential Peaks, and Deconvolution of the Lorentzian Width. Optik 2021, 225, 165533. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A. Table of Integrals, Series, and Products, 7th ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2007. [Google Scholar]
- Srivastava, H.M.; Karlsson, P.W. Multiple Gaussian Hypergeometric Series; Ellis Horwood: Chichester, UK, 1985. [Google Scholar]
- Singh, D. On Some Representations of Voigt Functions. Ph.D. Thesis, Aligarh Muslim University, Aligarh, India, 2004. [Google Scholar]
- Huang, Q.; Coëtmellec, S.; Duval, F.; Louis, A.; Leblond, H.; Brunel, M. Analytical expressions for diffraction-free beams through an opaque disk. J. Eur. Opt. Soc. Rapid Publ. 2011, 6, 11031–11037. [Google Scholar] [CrossRef]
- Belafhal, A.; Chib, S.; Khannous, F.; Usman, T. Evaluation of integral transforms using special functions with applications to biological tissues. Comput. Appl. Math. 2021, 40, 1–23. [Google Scholar] [CrossRef]



| 1 | 0.2453407083009 | (−1) 4.622436696006 |
| 2 | 0.7374737285454 | (−1) 2.866755053628 |
| 3 | 1.2340762153953 | (−1) 1.090172060200 |
| 4 | 1.7385377121166 | (−2) 2.481052088746 |
| 5 | 2.2549740020893 | (−3) 3.243773342238 |
| 6 | 2.7888060584281 | (−4) 2.283386360163 |
| 7 | 3.3478545673832 | (−6) 7.802556478532 |
| 8 | 3.9447640401156 | (−7) 1.086069370769 |
| 9 | 4.6036824495507 | (−10) 4.399340992273 |
| 10 | 5.3874808900112 | (−13) 2.229393645534 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chib, S.; Belafhal, A. Simple Analytical Expression of the Voigt Profile. Quantum Rep. 2022, 4, 36-46. https://doi.org/10.3390/quantum4010004
Chib S, Belafhal A. Simple Analytical Expression of the Voigt Profile. Quantum Reports. 2022; 4(1):36-46. https://doi.org/10.3390/quantum4010004
Chicago/Turabian StyleChib, Salma, and Abdelmajid Belafhal. 2022. "Simple Analytical Expression of the Voigt Profile" Quantum Reports 4, no. 1: 36-46. https://doi.org/10.3390/quantum4010004
APA StyleChib, S., & Belafhal, A. (2022). Simple Analytical Expression of the Voigt Profile. Quantum Reports, 4(1), 36-46. https://doi.org/10.3390/quantum4010004







