Polarization in Quasirelativistic Graphene Model with Topologically Non-Trivial Charge Carriers
Abstract
:1. Introduction
2. Methods
2.1. High-Energy Hamiltonian
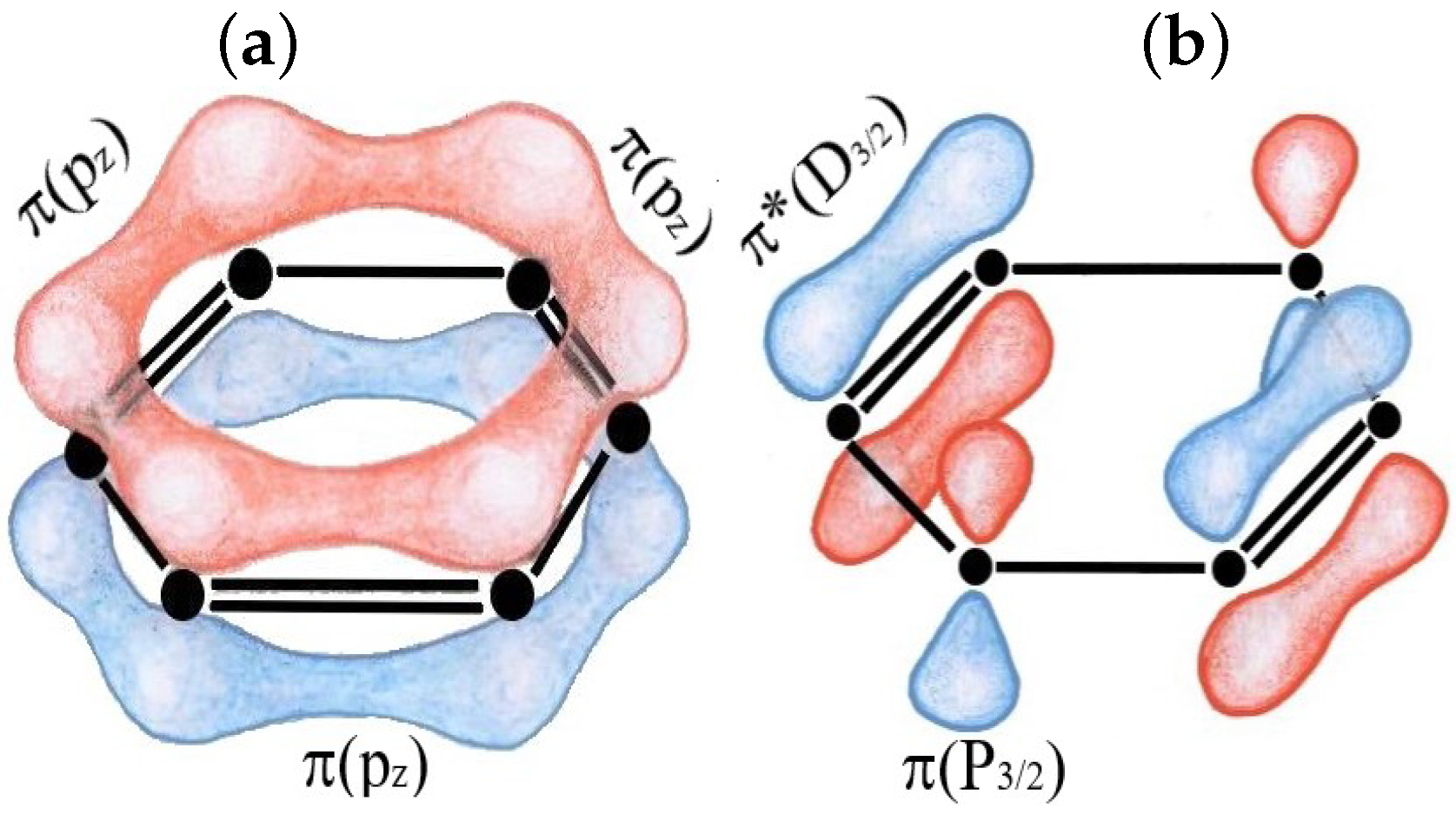
2.2. Non-Abelian-Zak-Phase Analysis of Emerging Polarization
2.3. Non-Abelian Currents in Quasi-Relativistic Graphene Model
3. Results and Discussion
3.1. Band Structure Simulations
3.2. Low-Frequency Dielectric Permittivity of Graphene
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elias, D.C.; Gorbachev, R.V.; Mayorov, A.S.; Morozov, S.V.; Zhukov, A.A.; Blake, P.; Ponomarenko, L.A.; Grigorieva, I.V.; Novoselov, K.S.; Guinea, F.; et al. Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 2012, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Wyrick, J.; Natterer, F.D.; Nieva, J.R.; Lewandowski, C.; Watanabe, K.; Taniguchi, T.; Levitov, L.; Zhitenev, N.B.; Stroscio, J.A. Creating and Probing Electron Whispering Gallery Modes in Graphene. Science 2015, 348, 672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef]
- Yu, T.; Kennes, D.M.; Rubio, A.; Sentef, M.A. Nematicity Arising from a Chiral Superconducting Ground State in Magic-Angle Twisted Bilayer Graphene under In-Plane Magnetic Fields. Phys. Rev. Lett. 2021, 127, 127001. [Google Scholar] [CrossRef]
- Cao, Y.; Rodan-Legrain, D.; Park, J.M.; Yuan, F.N.; Watanabe, K.; Taniguchi, T.; Fernandes, M.; Fu, L.; Jarillo-Herrero, P. Nematicity and Competing Orders in Superconducting Magic-Angle Graphene. Science 2021, 372, 264–271. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, H.; Lewandowski, C.; Peng, Y.; Thomson, A.; Polski, R.; Zhang, Y.; Watanabe, K.; Taniguchi, T.; Alicea, J.; et al. Interaction-driven Band Flattening and Correlated Phases in Twisted Bilayer Graphene. Nat. Phys. 2021, 17, 1375–1381. [Google Scholar] [CrossRef]
- Guinea, F.; Walet, N.R. Electrostatic effects, band distortions and superconductivity in twisted graphene bilayers. Proc. Nat. Acad. Sci. USA 2018, 115, 13174–13179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cea, T.; Walet, N.R.; Guinea, F. Electronic band structure and pinning of Fermi energy to van Hove singularities in twisted bilayer graphene: A self-consistent approach. Phys. Rev. B 2019, 100, 205113. [Google Scholar] [CrossRef] [Green Version]
- Xie, M.; MacDonald, A.H. Weak-field Hall Resistivity and Spin/Valley Flavor Symmetry Breaking in MAtBG. Phys. Rev. Lett. 2021, 127, 196401. [Google Scholar] [CrossRef]
- Lewandowski, C.; Nadj-Perge, S.; Chowdhury, D. Does filling-dependent band renormalization aid pairing in twisted bilayer graphene? NPJ Quantum Mater. 2021, 6, 82. [Google Scholar] [CrossRef]
- Wang, J.-R.; Liu, G.-Z. Eliashberg theory of excitonic insulating transition in graphene. J. Phys. Condens. Matter 2011, 23, 155602. [Google Scholar] [CrossRef]
- Li, L.L.; Zarenia, M.; Xu, W.; Dong, H.M.; Peeters, F.M. Exciton states in a circular graphene quantum dot: Magnetic field induced intravalley to intervalley transition. Phys. Rev. B 2017, 95, 045409. [Google Scholar] [CrossRef] [Green Version]
- Grushevskaya, H.V.; Krylov, G.G.; Kruchinin, S.P.; Vlahovic, B.; Bellucci, S. Electronic properties and quasi-zero-energy states of graphene quantum dots. Phys. Rev. B. 2021, 103, 235102. [Google Scholar] [CrossRef]
- Claassen, M.; Kennes, D.M.; Zingl, M.; Sentef, M.A.; Rubio, A. Universal Optical Control of Chiral Superconductors and Majorana Modes. Nat. Phys. 2019, 15, 766–770. [Google Scholar] [CrossRef]
- Yu, T.; Claassen, M.; Kennes, D.M.; Sentef, M.A. Optical Manipulation of Domains in Chiral Topological Superconductors. Phys. Rev. Res. 2021, 3, 013253. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed-matter simulation of a three-dimensional anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [Green Version]
- Bistritzer, R.; MacDonald, A.H. Moiré bands in twisted double-layer graphene. Proc. Nat. Acad. Sci. USA 2011, 108, 12233. [Google Scholar] [CrossRef] [Green Version]
- Grushevskaya, G.V.; Komarov, L.I.; Gurskii, L.I. Exchange and correlation interactions and band structure of non-close-packed solids. Phys. Solid State 1998, 40, 1802–1805. [Google Scholar] [CrossRef]
- Gorbachev, R.V.; Song, J.C.W.; Yu, G.L.; Kretinin, A.V.; Withers, F.; Cao, Y.; Mishchenko, A.; Grigorieva, I.V.; Novoselov, K.S.; Levitov, L.S.; et al. Detecting topological currents in graphene superlattices. Science 2014, 346, 448–451. [Google Scholar] [CrossRef] [Green Version]
- San-Jose, P.; JLado, L.; Aguado, R.; Guinea, F.; Fernández-Rossier, J. Majorana Zero Modes in Graphene. Phys. Rev. X 2015, 5, 041042. [Google Scholar] [CrossRef]
- Eschrig, H.; Richter, M.; Opahle, I. Relativistic Solid State Calculations. Theor. Comput. Chem. 2004, 13, 723–776. [Google Scholar]
- Grushevskaya, H.; Krylov, G. Vortex Dynamics of Charge Carriers in the Quasi-Relativistic Graphene Model: High-Energy Approximation. Symmetry 2020, 12, 261. [Google Scholar] [CrossRef] [Green Version]
- Grushevskaya, H.V.; Krylov, G.G. Massless Majorana-Like Charged Carriers in Two-Dimensional Semimetals. Symmetry 2016, 8, 60. [Google Scholar] [CrossRef] [Green Version]
- Grushevskaya, H.V.; Krylov, G. Semimetals with Fermi Velocity Affected by Exchange Interactions: Two Dimensional Majorana Charge Carriers. J. Nonlin. Phenom. Complex Syst. 2015, 18, 266–283. [Google Scholar]
- Grushevskaya, H.V.; Krylov, G.; Gaisyonok, V.A.; Serow, D.V. Symmetry of Model N = 3 for Graphene with Charged Pseudo-Excitons. J. Nonlin. Phenom. Complex Syst. 2015, 18, 81–98. [Google Scholar]
- Grushevskaya, H.V.; Krylov, G.G. Chapter 9. Electronic Structure and Transport in Graphene: QuasiRelativistic Dirac-Hartree-Fock Self-Consistent Field Approximation. In Graphene Science Handbook: Electrical and Optical Properties; Aliofkhazraei, M., Ali, N., Milne, W.I., Ozkan, C.S., Mitura, S., Gervasoni, J.L., Eds.; Taylor and Francis Group: Oxford, UK; CRC Press: Boca Raton, FL, USA, 2016; Volume 3, pp. 117–132. [Google Scholar]
- Kutzelnigg, W.; Liu, W. Quasirelativistic theory I. Theory in terms of a quasi-relativistic operator. Int. J. Interface Chem. Phys. 2006, 104, 2225–2240. [Google Scholar] [CrossRef]
- Fock, V.A. Foundations of Quantum Mechanics; Science Publishing Company: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef]
- Muechler, L.; Alexandradinata, A.; Neupert, T.; Car, R. Topological Nonsymmorphic Metals from Band Inversion. Phys. Rev. X 2016, 6, 041069. [Google Scholar] [CrossRef] [Green Version]
- Davydov, A.S. Quantum Mechanics; Science Publishing Company: Moscow, Russia, 1973. (In Russian) [Google Scholar]
- Falkovsky, L.A.; Varlamov, A.A. Space-time dispersion of graphene conductivity. Eur. Phys. J. 2007, 56, 281. [Google Scholar] [CrossRef] [Green Version]
- Halina, V. Grushevskaya, George Krylov, and Victor A. Gaisyonok Non-Abelian Currents in Quasi-Relativistic Graphene Model: General Theory. J. Nonlin. Phenom. Complex Syst. 2018, 21, 278–308. [Google Scholar]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Sodano, P. Stretched quantum states emerging from a Majorana medium. J. Phys. B 2007, 40, 1479–1488. [Google Scholar] [CrossRef]
- Grushevskaya, H.V.; Krylov, G.G. Non-Abelian Majorana-Like Quasi-Excitation in Dirac Materials. J. Nonlin. Phenom. Complex Syst. 2017, 20, 153–169. [Google Scholar]
- Kraeft, V.D.; Kremp, D.; Ebeling, W.; Röpke, G. Quantum Statistics of Charged Particle Systems; Akademie: Berlin, Germany, 1986. [Google Scholar]



| , K | ||||||
|---|---|---|---|---|---|---|
| N = 2 | N = 3 | N = 2 | N = 3 | |||
| Massless | Mass Case | Massless | Mass Case | |||
| 13.3 | −0.025 | 3 | 3.312 | 3.308 | 3.32 | |
| − | 0.191 | 0.191 | 0.194 | |||
| 0 | − | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grushevskaya, H.; Krylov, G. Polarization in Quasirelativistic Graphene Model with Topologically Non-Trivial Charge Carriers. Quantum Rep. 2022, 4, 1-15. https://doi.org/10.3390/quantum4010001
Grushevskaya H, Krylov G. Polarization in Quasirelativistic Graphene Model with Topologically Non-Trivial Charge Carriers. Quantum Reports. 2022; 4(1):1-15. https://doi.org/10.3390/quantum4010001
Chicago/Turabian StyleGrushevskaya, Halina, and George Krylov. 2022. "Polarization in Quasirelativistic Graphene Model with Topologically Non-Trivial Charge Carriers" Quantum Reports 4, no. 1: 1-15. https://doi.org/10.3390/quantum4010001
APA StyleGrushevskaya, H., & Krylov, G. (2022). Polarization in Quasirelativistic Graphene Model with Topologically Non-Trivial Charge Carriers. Quantum Reports, 4(1), 1-15. https://doi.org/10.3390/quantum4010001






