Topological Photonics for Optical Communications and Quantum Computing
Abstract
1. Introduction
- Superposition concerns the property of quantum objects to stay in a linear combination of multiple states until they are observed;
- Entanglement is defined as the possibility that two or more quantum objects stay intrinsically linked in an intertwined composite state, regardless of how far apart the objects are from one another. Recently, hyperentanglement has been discovered, defined as the entanglement in multiple degrees of freedom (DOFs) of a quantum system, such as the polarization, spatial mode, orbital angular momentum, time-bin and frequency DOFs of photons;
- Measurement regards the collapse and disruption of a quantum state from a coherent, probabilistic superposition state into a discrete one.
- A scalable physical system with well characterized qubits;
- The ability to initialize the state of the qubits to a simple fiducial state;
- Long, relevant decoherence times;
- A universal set of quantum gates;
- A qubit-specific measurement capability.
- A brief description of a vision aiming at the integration of optical communications and quantum optical computing;
- A description of some key concepts and definitions on topological photonics, with a focus on the adoption of orbital angular momentum (OAM) for optical communications, networking and quantum optical computing;
- An overview of the state-of-the-art future challenges and applications.
2. Quantum Communications and Quantum Optical Computing
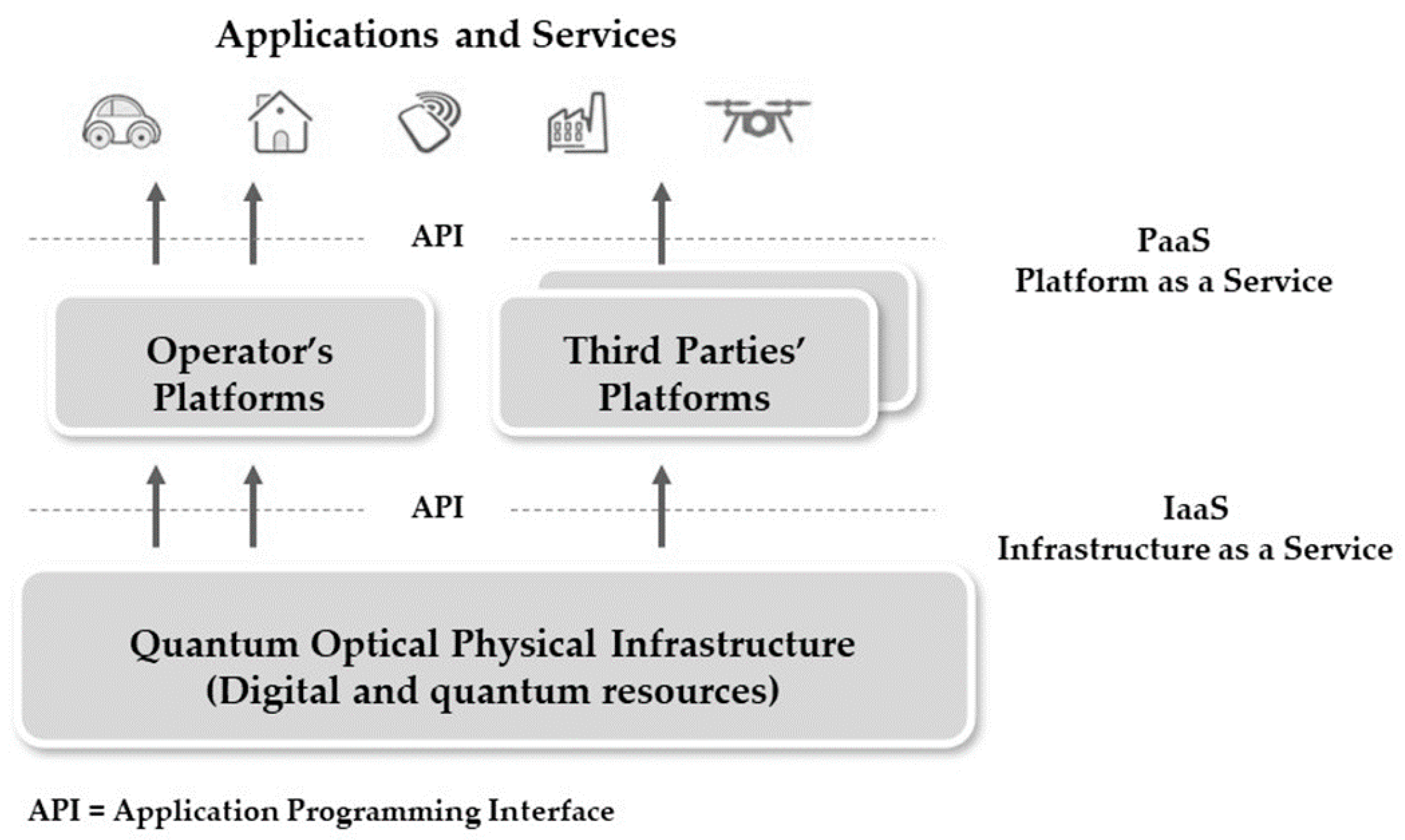
- Infrastructure architectural integration;
- ○
- Management, control and orchestration (abstractions and interfaces) of digital and quantum resources and services;
- Optics integration;
- ○
- Integrated photonic components and sub-system systems;
- Channels integration;
- ○
- Quantum optical vs. classical optical links.
3. Topological Photonics and OAM
3.1. Basic Concetps on Topology
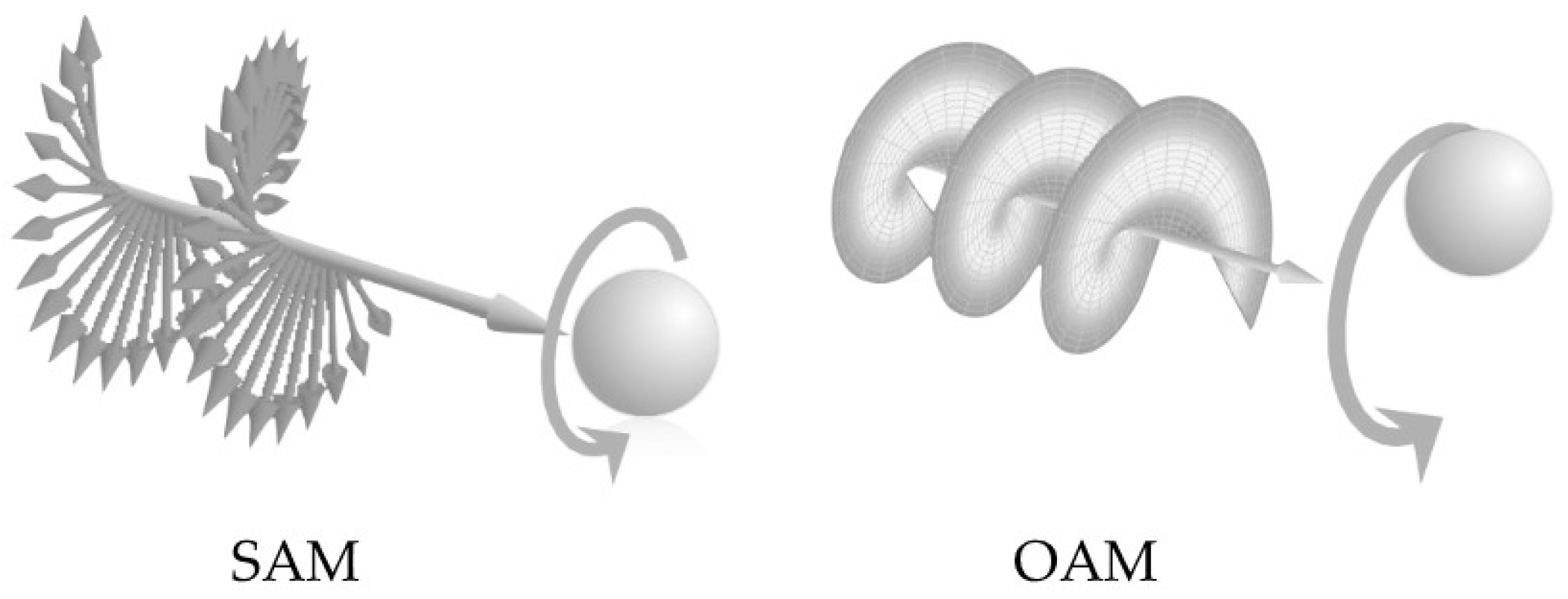
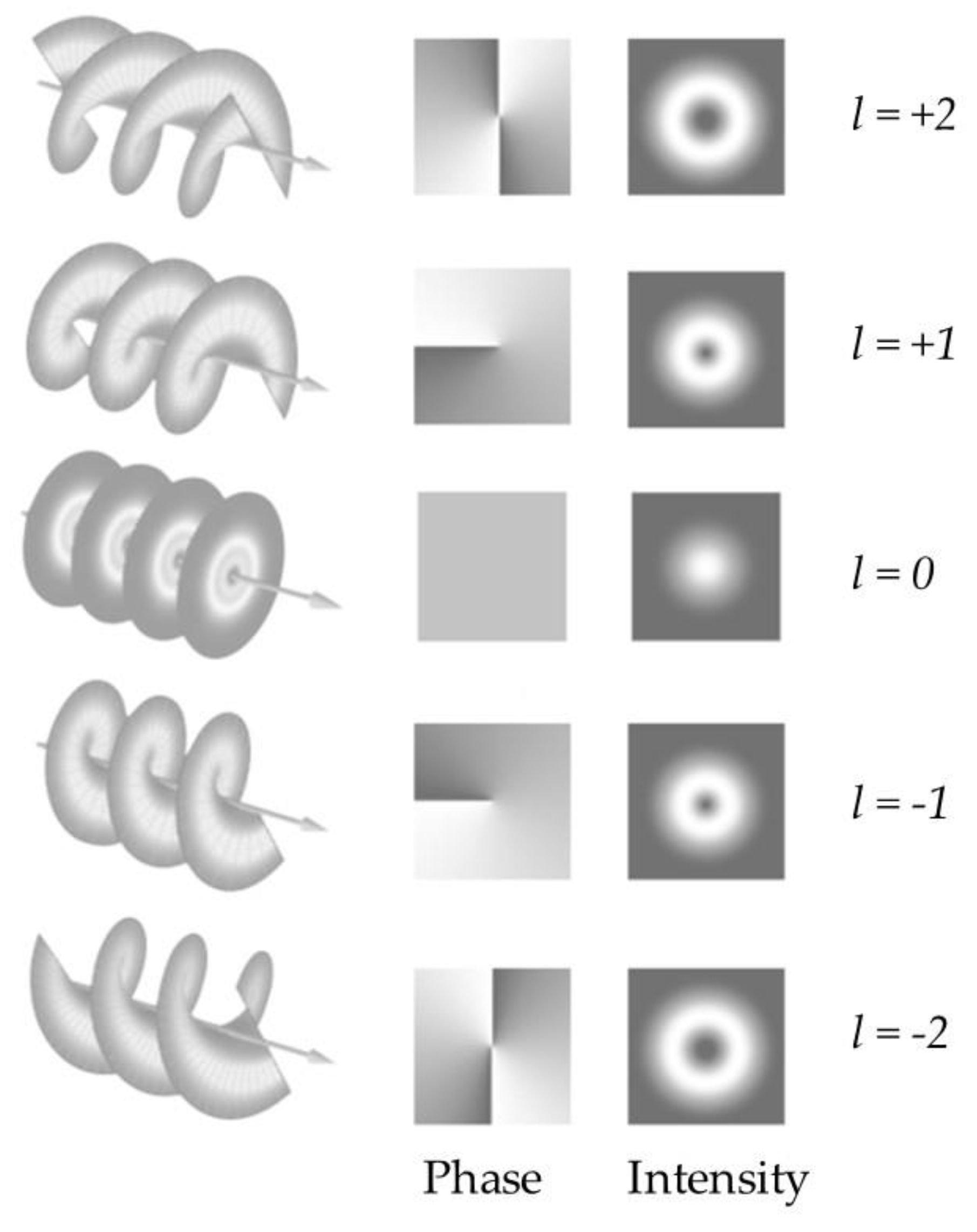
3.2. Topological Photonic: Vortex and Qubits
4. Quantum Materials
5. Conclusions and Outlook
Funding
Conflicts of Interest
References
- Kozlowski, W.; Wehner, S.; Meter, R.V.; Rijsman, B.; Cacciapuoti, A.S.; Caleffi, M. Architectural Principles for a Quantum Internet. In Internet-Draft Draft-Irtf-Qirg-Principles-03; Internet Engineering Task Force: Fremont, CA, USA, 2020. [Google Scholar]
- Cacciapuoti, A.S.; Caleffi, M.; Van Meter, R.; Hanzo, L. When entanglement meets classical communications: Quantum teleportation for the quantum Internet. IEEE Trans. Commun. 2020, 6, 3808–3833. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1973, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Cacciapuoti, A.S.; Caleffi, M.; Tafuri, F.; Cataliotti, F.S.; Gherardini, S.; Bianchi, G. Quantum internet: Networking challenges in distributed quantum computing. IEEE Netw. 2019, 34, 137–143. [Google Scholar] [CrossRef]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.; Ömer, B.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481–486. [Google Scholar] [CrossRef]
- Żukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. Event-ready-detectors Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef]
- Pan, J.-W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Pan, J.-W.; Simon, C.; Brukner, Č.; Zeilinger, A. Entanglement purification for quantum communication. Nature 2001, 410, 1067–1070. [Google Scholar] [CrossRef]
- Pan, J.-W.; Gasparoni, S.; Ursin, R.; Weihs, G.; Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 2003, 423, 417–422. [Google Scholar] [CrossRef]
- Chou, C.W.; Laurat, J.; Deng, H.; Choi, K.S.; De Riedmatten, H.; Felinto, D.; Kimble, H.J. Functional quantum nodes for entanglement distribution over scalable quantum networks. Science 2007, 316, 1316–1320. [Google Scholar] [CrossRef]
- Moehring, D.L.; Maunz, P.; Olmschenk, S.; Younge, K.C.; Matsukevich, D.N.; Duan, L.M.; Monroe, C. Entanglement of single-atom quantum bits at a distance. Nature 2007, 449, 68–71. [Google Scholar] [CrossRef]
- Yuan, Z.S.; Chen, Y.A.; Zhao, B.; Chen, S.; Schmiedmayer, J.; Pan, J.W. Experimental demonstration of a BDCZ quantum repeater node. Nature 2008, 454, 1098–1101. [Google Scholar] [CrossRef]
- Zwerger, M.; Dür, W.; Briegel, H.J. Measurement-based quantum repeaters. Phys. Rev. A 2012, 85, 062326. [Google Scholar] [CrossRef]
- Munro, W.; Stephens, A.; Devitt, S.; Harrison, K.; Nemoto, K. Quantum communication without the necessity of quantum memories. Nat. Photonics 2012, 6, 777–781. [Google Scholar] [CrossRef]
- Muralidharan, S.; Kim, J.; Lütkenhaus, N.; Lukin, M.D.; Jiang, L. Ultrafast and fault-tolerant quantum communication across long distances. Phys. Rev. Lett. 2014, 112, 250501. [Google Scholar] [CrossRef]
- Chen, L.K.; Yong, H.L.; Xu, P.; Yao, X.C.; Xiang, T.; Li, Z.D.; Liu, C.; Lu, H.; Liu, N.L.; Yang, T.; et al. Experimental nested purification for a linear optical quantum repeater. Nat. Photonics 2017, 11, 695–699. [Google Scholar] [CrossRef]
- Xu, P.; Yong, H.L.; Chen, L.K.; Liu, C.; Xiang, T.; Yao, X.C.; Lu, H.; Li, Z.D.; Liu, N.L.; Li, L.; et al. Two-hierarchy entanglement swapping for a linear optical quantum repeater. Phys. Rev. Lett. 2017, 119, 170502. [Google Scholar] [CrossRef]
- Kalb, N.; Reiserer, A.A.; Humphreys, P.C.; Bakermans, J.J.; Kamerling, S.J.; Nickerson, N.H.; Benjamin, S.C.; Twitchen, D.J.; Markham, M.; Hanson, R. Entanglement distillation between solid-state quantum network nodes. Science 2017, 356, 928–932. [Google Scholar] [CrossRef]
- Zhong, H.S.; Li, Y.; Li, W.; Peng, L.C.; Su, Z.E.; Hu, Y.; Ding, X.; Zhang, W.; Li, H.; Zhang, L.; et al. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys. Rev. Lett. 2018, 121, 250505. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Paesani, S.; Ding, Y.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mančinska, L.; Bonneau, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef]
- Asorey, M. Space, matter and topology. Nat. Phys. 2016, 12, 616–618. [Google Scholar] [CrossRef][Green Version]
- Castelvecchi, D. The strange topology that is reshaping physics. Nat. News 2017, 547, 272. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 1982, 48, 1559. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 1983, 50, 1395. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Stern, A.; Lindner, N.H. Topological quantum computation—From basic concepts to first experiments. Science 2013, 339, 1179–1184. [Google Scholar] [CrossRef]
- Kouwenhoven, L. Majorana Qubits. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018. [Google Scholar]
- Franz, M.; Pikulin, D.I. Quantized, finally. Nat. Phys. 2018, 14, 334–336. [Google Scholar] [CrossRef]
- Meade, R.D.; Winn, J.N.; Joannopoulos, J.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 1–29. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Pang, K.; Song, H.; Zhao, Z.; Zhang, R.; Song, H.; Xie, G.; Li, L.; Liu, C.; Du, J.; Molisch, A.F.; et al. 400-Gbit/s QPSK free-space optical communication link based on four-fold multiplexing of Hermite-Gaussian or Laguerre-Gaussian modes by varying both modal indices. Opt. Lett. 2018, 43, 3889–3892. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.J.; Erkmen, B.I.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Lett. 2014, 39, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E. Communication with a twist. IEEE Spectr. 2016, 53, 34–39. [Google Scholar] [CrossRef]
- Bouchard, F.; Heshami, K.; England, D.; Fickler, R.; Boyd, R.W.; Englert, B.-G.; Sanchez-Soto, L.L.; Karimi, E. Experimental investigation of high-dimensional quantum key distribution protocols with twisted photons. Quantum 2018, 2, 111. [Google Scholar] [CrossRef]
- Qu, Z.; Djordjevic, I.B. High-speed free-space optical continuous variable quantum key distribution enabled by three-dimensional multiplexing. Opt. Express 2017, 25, 7919–7928. [Google Scholar] [CrossRef]
- Larocque, H.; Gagnon-Bischoff, J.; Mortimer, D.; Zhang, Y.; Bouchard, F.; Upham, J.; Grillo, V.; Boyd, R.W.; Karimi, E. Generalized optical angular momentum sorter and its application to high-dimensional quantum cryptography. Opt. Express 2017, 25, 19832–19843. [Google Scholar] [CrossRef]
- Jaeger, G.; Simon, D.S.; Sergienko, A.V. Topological qubits as carriers of quantum information in optics. Appl. Sci. 2019, 9, 575. [Google Scholar] [CrossRef]
- Liu, C.; Liu, J.; Niu, L.; Wei, X.; Wang, K.; Yang, Z. Terahertz circular Airy vortex beams. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- García-Escartín, J.C.; Chamorro-Posada, P. Universal quantum computation with the orbital angular momentum of a single photon. J. Opt. 2011, 13, 064022. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, T. Why I am optimistic about the silicon-photonic route to quantum computing. APL Photonics 2017, 2, 030901. [Google Scholar] [CrossRef]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef]
- Yuen-Zhou, J.; Saikin, S.K.; Yao, N.Y.; Aspuru-Guzik, A. Topologically protected excitons in porphyrin thin films. Nat. Mater. 2014, 13, 1026–1032. [Google Scholar] [CrossRef] [PubMed]
- Karzig, T.; Bardyn, C.E.; Lindner, N.; Refael, G. Topological polaritons from quantum wells in photonic waveguides or microcavities. arXiv 2014, arXiv:1406.4156. [Google Scholar]
- Prodan, E.; Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 2009, 103, 248101. [Google Scholar] [CrossRef]
- Shindou, R.; Matsumoto, R.; Murakami, S.; Ohe, J.I. Topological chiral magnonic edge mode in a magnonic crystal. Phys. Rev. B 2013, 87, 174427. [Google Scholar] [CrossRef]
- Giustino, F.; Bibes, M.; Lee, J.H.; Trier, F.; Valentí, R.; Winter, S.M.; Son, Y.W.; Taillefer, L.; Heil, C.; Figueroa, A.I. The 2020 Quantum Materials Roadmap. J. Phys. Mater. 2020. [Google Scholar] [CrossRef]
- Capasso, F. The future and promise of flat optics: A personal perspective. Nanophotonics 2018, 7, 953–957. [Google Scholar] [CrossRef]
- Staude, I.; Schilling, J. Metamaterial-inspired silicon nanophotonics. Nat. Photonics 2017, 11, 274–284. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzalini, A. Topological Photonics for Optical Communications and Quantum Computing. Quantum Rep. 2020, 2, 579-590. https://doi.org/10.3390/quantum2040040
Manzalini A. Topological Photonics for Optical Communications and Quantum Computing. Quantum Reports. 2020; 2(4):579-590. https://doi.org/10.3390/quantum2040040
Chicago/Turabian StyleManzalini, Antonio. 2020. "Topological Photonics for Optical Communications and Quantum Computing" Quantum Reports 2, no. 4: 579-590. https://doi.org/10.3390/quantum2040040
APA StyleManzalini, A. (2020). Topological Photonics for Optical Communications and Quantum Computing. Quantum Reports, 2(4), 579-590. https://doi.org/10.3390/quantum2040040




