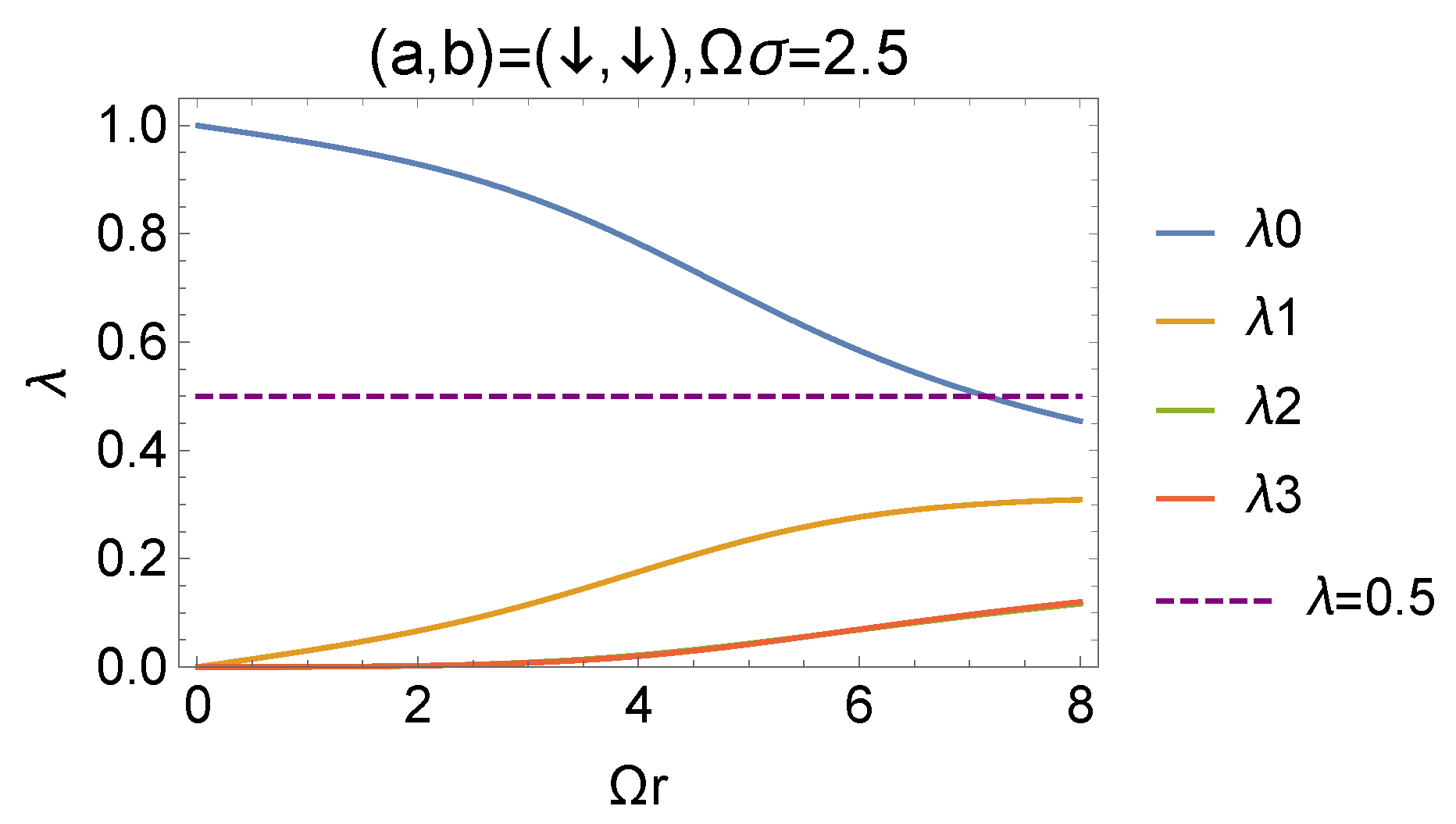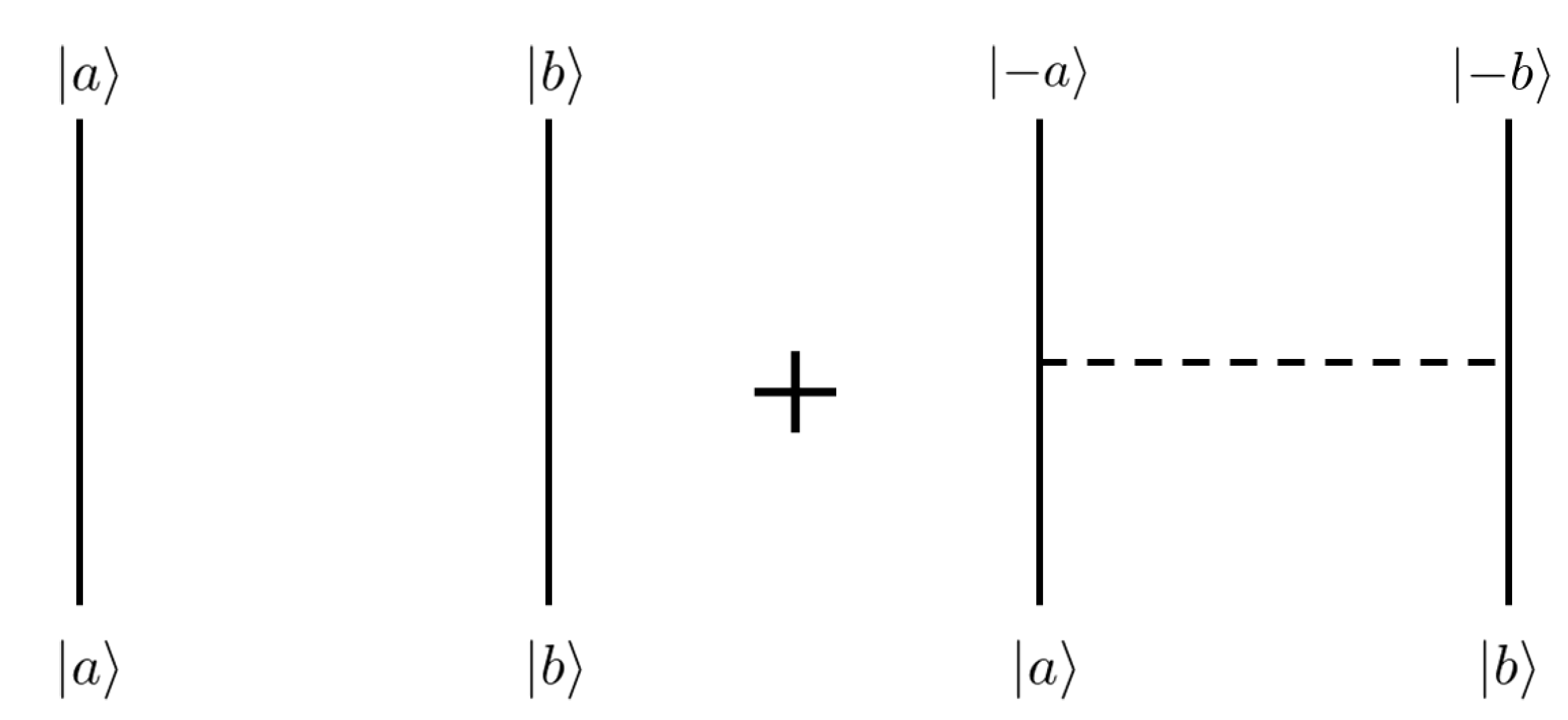Abstract
We investigate quantum correlations appearing for two-qubit detectors which are initially uncorrelated and locally coupled to a massless scalar field in a vacuum state. Under the perturbation up to the second order in the coupling, the state of the detectors can be entangled through the interaction with the scalar field but satisfies the Bell-CHSH inequality. The violation of the Bell-CHSH inequality for such an entangled state is revealed by local filtering operations. In this paper, we construct the optimal filtering operations for the qubit detectors and derive the success probability of the filtering. The success probability characterizes the reliability of revealing the violation of the Bell-CHSH inequality by the filtering operations. Through these analyses, we demonstrate a trade-off relation between the success probability and the size of parameter region showing the violation of the Bell-CHSH inequality.
1. Introduction
In quantum information theory, quantum entanglement is known as a crucial property which describes a nonlocal correlation [1]. As well as quantum entanglement, the Bell-CHSH inequality also characterizes a nonlocal correlation in quantum mechanics [2]. The Bell-CHSH inequality [3] is satisfied for local hidden variable theories, and a quantum state violating this inequality cannot be described in that framework. The two aspects of quantum correlations, quantum entanglement and the violation of the Bell-CHSH inequality, are not equivalent, and it was shown that a given quantum state violating the Bell-CHSH inequality has quantum entanglement [4,5].
In quantum field theory, it is known that quantum correlations appear in various states of a quantum field. Reeh and Schlieder showed that arbitrary states of a quantum field can be approximated by acting some local operators on the Minkowski vacuum state [6], and such a property implies that the vacuum state is spatially entangled. Furthermore, it was shown that the vacuum state violates the Bell-CHSH inequality by examining the correlation of bounded observables between two spatial separated regions [7]. The vacuum of a quantum field displays quantum entanglement and the violation of the Bell-CHSH inequality, and these correlations characterize nonlocal features of the quantum field.
In connection with the quantum correlations of the vacuum of a quantum field, the detection of such correlations by local observers has been investigated. The so-called detector model is adopted to characterize how quantum resources in the vacuum is available, and provides a suitable experimental setting to detect the quantum correlation of the vacuum. The detector model is often described by spatially localized harmonic oscillators [8,9,10] or qubit systems [11,12,13,14,15,16,17,18]. Reznik et al. [11] considered the detection of quantum correlation by two-qubit detectors. These detectors are locally coupled to a massless scalar field and do not interact directly with each other. It was shown that quantum entanglement can be extracted and the violation of the Bell-CHSH inequality was found by applying a local filtering [19]. The local filtering operation is a kind of measurement processes acting on each qubit by local observers Alice and Bob. The operation is constructed by post-selected (probabilistic) local operations and classical communication (LOCC). The proper choice of the operation reveals the violation of the Bell-CHSH inequality of the state of the detectors. This method is also applied to the cosmological situation to reveal the quantum nonlocality in the early universe [20]. In quantum information theory, the optimal construction of local filters which give the maximal violation of the Bell-CHSH inequality was provided in the previous works [21,22].
In this paper, we investigate the quantum correlations in a vacuum through the model of two-qubit detectors. The initial state of the detectors is usually assumed to be an uncorrelated ground state, however, we also consider the excited state of detectors. By such a generalization of the initial state of the detectors, we clarify what is playing a crucial role to reveal the quantum entanglement and the violation of Bell-CHSH inequality in the vacuum. As an entanglement measure, we compute the negativity of the qubit detectors, which completely characterizes the entanglement for two-qubit system [23]. We also construct the optimal filtering operation for the two detectors by the method given in Ref. [22] to reveal the violation of the Bell-CHSH inequality. We show that the constructed local filtering corresponds to that given previously in Ref. [11] and derive the explicit formula of the success probability of the filtering operation. From the formulas of quantum correlations and the success probability, it is shown that the quantum correlations between the detectors decreases and the success probability of the optimal filtering increases as the transition probability of the spontaneous emission grows. This behavior means that there is a trade-off relation between the size of the parameter region indicating the quantum correlation and the success probability.
This paper is organized as follows. In Section 2, we introduce the system composed of two-qubit detectors and a massless scalar field. Up to the second order in the coupling, we solve the dynamics assuming that the initial state of the total system is a product state of the detectors and the field in the Minkowski vacuum. We obtain the reduced density matrix of the detectors represented by an X state. In Section 3, we calculate the negativity and the expectation value of the Bell operator for an X state. In Section 4, we explicitly construct the optimal filtering for an X state and derive the success probability of the filtering. In Section 5, we discuss the quantum entanglement and the violation of the Bell-CHSH inequality of detectors’ system and show the quantum correlation is determined by the coherence and the spontaneous emission of scalar particles. In Section 6, we discuss the effect of local emissions on the violation of the Bell-CHSH inequality and find the trade-off relation between the parameter region revealing the violation of the Bell-CHSH inequality and the success probability of the optimal filter. Section 6 is devoted to the summary and conclusion.
2. Perturbative Dynamics of Two Detectors Coupled to Scalar Field
The vacuum state of a quantum field has nonlocal quantum correlations [6,7]. To investigate the extraction of the quantum correlations by local observers, we consider a free theory of a massless scalar field and introduce qubit detectors locally coupled to the scalar field. The free Hamiltonian of the total system is with
where is the Pauli matrix, is the energy gap of the qubits, is the free Hamiltonian of the massless scalar field and is the conjugate momentum of the scalar field. The interaction Hamiltonian is
where and denote each spatial position of the two detectors, that is, the two detectors are at rest at each position and locally interact with the scalar field. We assume that the switching function has the Gaussian form
where is a coupling constant and is a time interval while the interaction turns on. Roughly speaking, the detectors interact with the scalar field for . We assume that the initial state of the total system is a product state
where denote eigenvalues of and is the vacuum state of the scalar field. We also use the notation to represent the state of qubits. In the interaction picture, the out-state up to the second order in the coupling is given by
where is the interaction Hamiltonian in the interaction picture, denotes the time ordering, and the operators and acting on the state of the scalar field are defined by
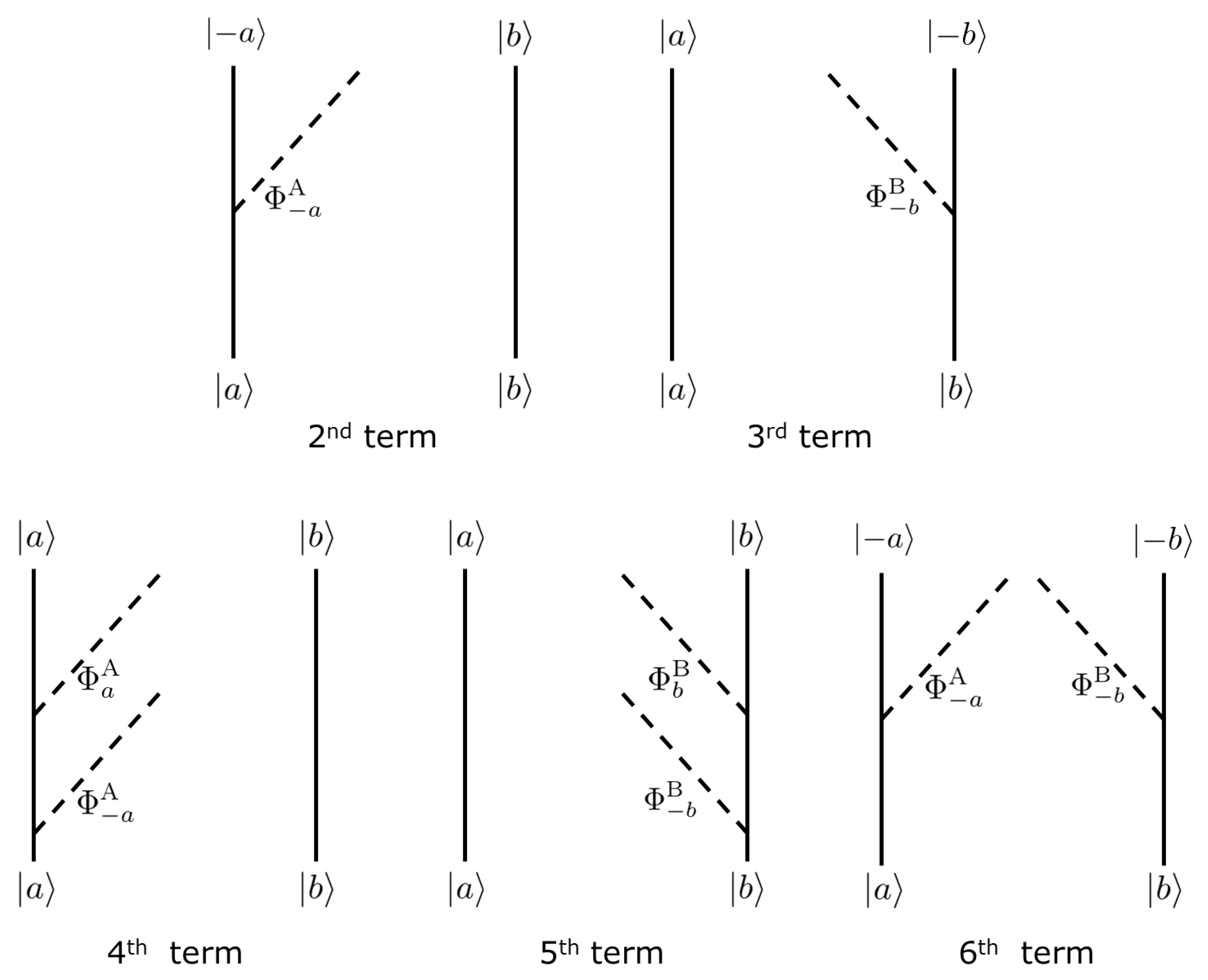
Each term in Equation (5) can be interpreted using the diagrammatic representation shown in Figure 1. For example, the second term in Equation (5) denotes that detector A interacts once with the scalar field, and the qubit A is flipped.
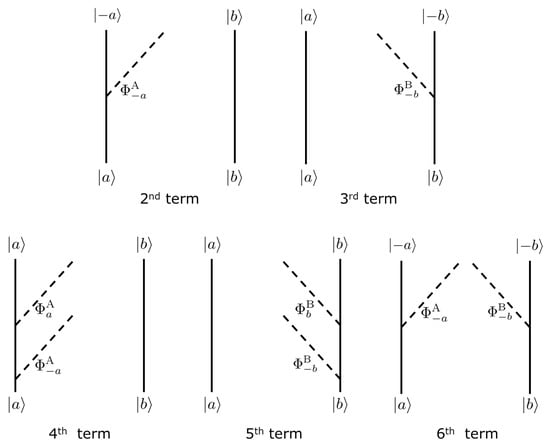
Figure 1.
The diagrammatic representation of each term appeared in Equation (5).
The reduced density matrix of the two detectors after the interaction is
where we assumed the basis . The density matrix with only non-diagonal components and is called an X state, which has only the quantum coherences of the superpositions or and this property makes the analysis of the quantum correlations easier. Concretely, the non-diagonal components of the density matrix (7) are
where is the one-particle state for the scalar field. The diagonal components are given as
where and the formula of is derived by the Wick theorem. Note that the non-diagonal components and depends on the Wightman function for the massless scalar field
where is the UV cutoff parameter. Hence the detectors with an initial product state can be entangled by the local interaction with the scalar field in Equation (2) through the two-point function. We can explicitly compute and as
where is the complementary error function defined by
The detailed derivation (17) and (18) is presented in Appendix A. From the explicit formulas for the density matrix, the quantum correlation of the scalar field detected via the two detectors can be computed.
3. Negativity and Bell-CHSH Inequality for X State
As the state of the detectors depends on the two-point function for the scalar field, we expect that the initial product state of the detectors becomes correlated first inequalityafter the interaction. To evaluate the quantum correlation between the two detectors, we consider the negativity and the Bell-CHSH inequality. The negativity is defined by the eigenvalues, , of a partial transposed density matrix as
If the negativity does not vanish, then the state is entangled. Especially, the converse the statement is true when the Hilbert space is or [24]. Thus, the negativity completely characterizes whether the state of the detectors is entangled or not. For an X state
the negativity is explicitly obtained as
The conditions or are rewritten in the simple form as
For the detectors’ density matrix (7), the first inequality in (25) is not satisfied because we find
to the leading order in the coupling , where , and . Hence we can obtain the condition of nonzero negativity for the detectors’ density matrix as
For a detailed understanding of the quantum correlation, it is important to evaluate the Bell-CHSH inequality [3] given by the correlation function for the qubit A and B. To compute the Bell-CHSH inequality, we introduce the Bell operator
where and are unit vectors, and are the Pauli matrices. We consider the maximum expectation value of the Bell-CHSH operator
For separable states, satisfies the following Bell-CHSH inequality
The inequality (30) holds for the local hidden variable theory, which includes any separable states. For any physical states, has the upper bound called the Tsirelson bound [25]
For an X state, the maximum value can be calculated explicitly as
where we used the Horodecki theorem [26] which provides the method to obtain the explicit form of from the singular value of the matrix . Note that the Bell-CHSH inequality is satisfied for the state of the two detectors system given by (15)–(18) within our perturbative treatment. Since the order of the coupling for the non-diagonal components and X is , and for a small are evaluated as
where and are . The maximum expectation value of the Bell operator is smaller than unity and the Bell-CHSH inequality is always satisfied. On the other hand, it is possible for the detectors to have a nonzero negativity because the condition for the entangled state (27) does not depend on the strength of coupling (both sides of the inequality (27) have the same order for the coupling). Figure 2 shows the contour plot of the negativity in space for the detectors’ initial state . The dashed line denotes the “null” curve and we find that the negativity has a nonzero value for a region .
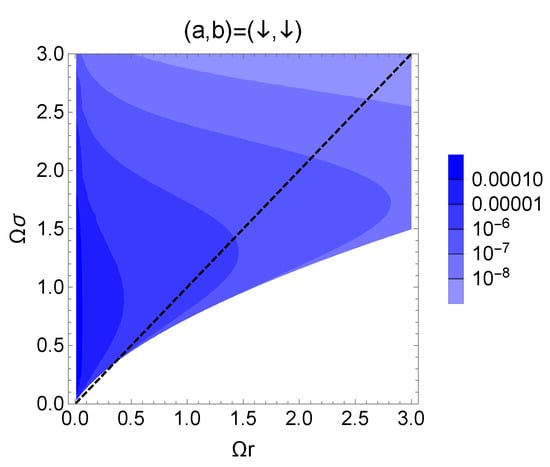
Figure 2.
The contour plot of the negativity in the parameter space with the initial detectors’ state . The dashed line represents the null curve .
As we have seen above, the state of the detectors is entangled and satisfies the Bell-CHSH inequality. Interestingly, it is known that the violation of the Bell-CHSH inequality for such a state can be revealed by a local filtering operation [19].
4. Local Filtering Operation for X States
We introduce a local filtering operation for a two-qubit system. The local filtering operation is performed as follows: qubit locally interacts with a measurement apparatus and then an observer picks up one outcome from the measurement apparatus. When two local observers, Alice and Bob, perform the local filtering operation for each qubit, the filtered state is given by
where is an initial density operator of a two-qubit system, and are local operators ( matrices) for each subsystem. The success probability, p, to attain the filtered state is
Those operators and have inverse and satisfy the conditions and , where and are the identity operators on each Hilbert space of the qubit systems. It is known that the local filtering is adopted to reveal the violation of Bell-CHSH inequality for the bipartite qubit system [19,21,22].
4.1. Key Theorems
There are two important theorems to reveal the violation of Bell-CHSH inequality by the local filtering operation [21,22]:
Theorem 1
([21]). By a local filtering operation, a two-qubit state can be uniquely transformed into a Bell diagonal state.
Theorem 2
([22]). If the optimized over all local operations and is larger than unity, then the filtered state is a Bell diagonal state. The statement is represented by
where and .
According to the above theorems, we need the local operation which transforms a given state into a Bell diagonal form to reveal the violation of Bell-CHSH inequality. In general, it is complicated to construct such a local operation, however, we easily get it for an X state. We note that a Bell diagonal state has the form of an X state with its components given by
This state corresponds to the X state with
All we have to do is to transform a given X state into the X state satisfying these conditions (40) by an appropriate filtering operation. We apply the local z rotation to a given X state. The diagonal components are invariant and the non-diagonal components are transformed as
We can choose the parameters so that are positive and satisfy . Without loss of generality, we assume that the diagonal components satisfy . From Theorem 1, we can uniquely transform the two-qubit system to a Bell diagonal form by a local filtering operation. Hence it is sufficient to find one of the filtering operations converting a given X state to a Bell diagonal state. For this purpose, we consider the local operation defined by
where and . This operation corresponds to the amplitude damping channel with a post selection and was used in Ref. [11] to detect the Bell-CHSH nonlocality. Under the local operations (42), the X state is transformed to
where . If the parameters and satisfy , that is,
then the X state becomes the Bell diagonal state with the spectrum given by
Equation (44) provides the optimal filters for the detection of the violation of Bell-CHSH inequality with the success probability p
This probability characterizes the reliability of detecting the violation of Bell-CHSH inequality by the local filtering operation.
4.2. Quantum Correlation of the Bell Diagonal State and Coherence of X State
To get a clear understanding of the quantum correlation for the X state, we investigate the detailed properties of the Bell diagonal state and its relationship to the X state. The entanglement of the Bell diagonal state is completely characterized by the negativity. The conditions of non-zero negativity (25) for the Bell diagonal state are equivalent to
where we used Equation (39). Hence, whenever the largest eigenvalue of exceeds (the spectrum is biased towards any one of the four Bell states), then the Bell diagonal state is entangled.
Let us focus on the violation of Bell-CHSH inequality for the Bell diagonal state. When the maximum value is larger than 1 (that is, or in Equation (32)), the eigenvalues satisfy
where and are imposed by Equation (45). If we assume then and because . We obtain the inequalities
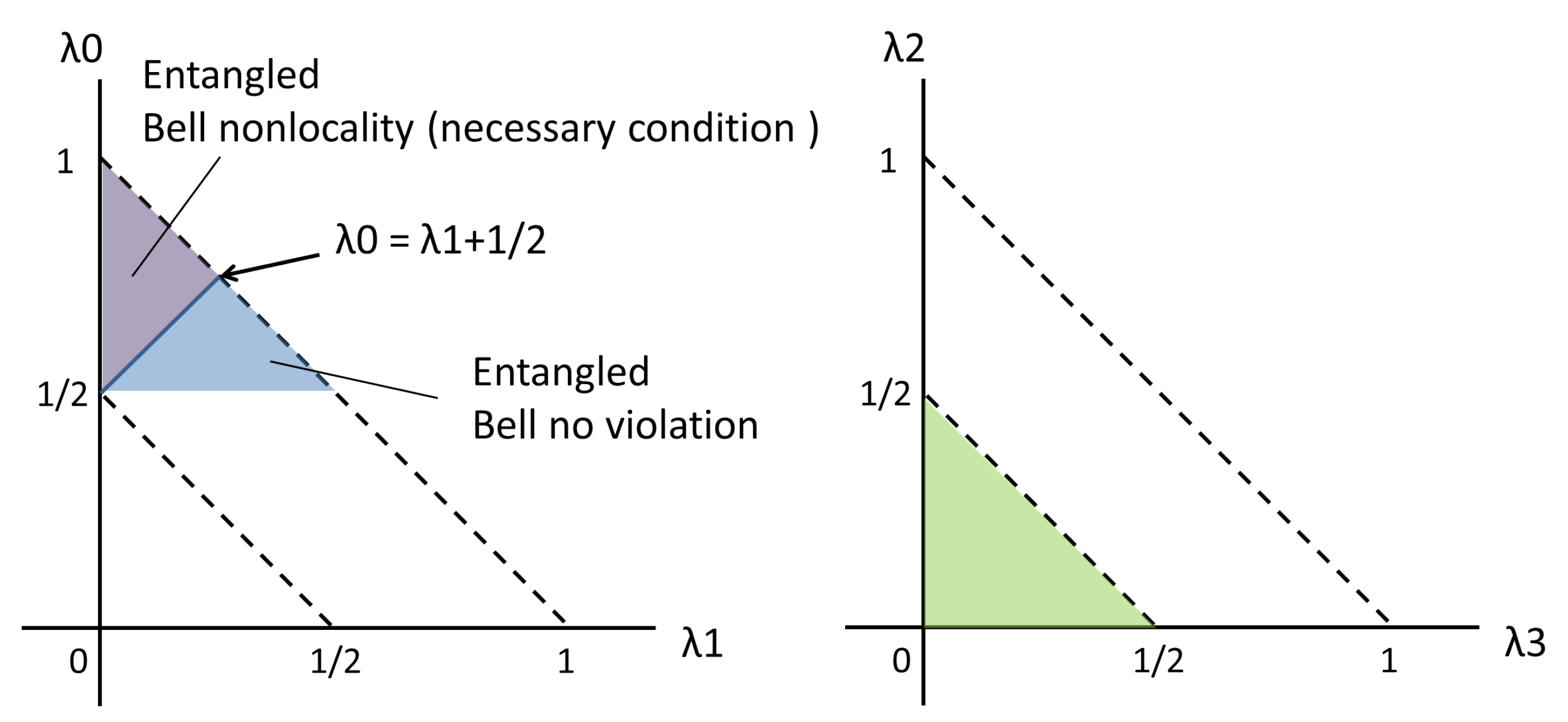
as the necessary condition of the violation of the Bell-CHSH inequality. To summarize, the typical region of the spectra satisfying the entanglement condition (47) and the violation of Bell-CHSH inequality (necessary) conditions (49) are presented in Figure 3. The Bell diagonal state has the Bell-CHSH nonlocal correlation when one of the spectra approaches unity.
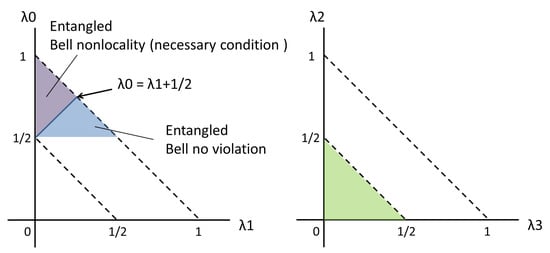
Figure 3.
The typical region of revealing the quantum entanglement and the violation of Bell-CHSH inequality.
In Equation (45), the spectra depend on the components of the X state and their dominant terms are and . To show the violation of the Bell-CHSH inequality, one of these terms, and the associated coherence that it represents, need to dominate the other.
5. Violation of Bell-CHSH Inequality by Using Optimal Local Filtering
In this section, we examine the quantum entanglement and the violation of Bell-CHSH inequality for the model of two-qubit detectors with the initial conditions and . For the detection of the violation of Bell-CHSH inequality, we apply the local filter to the qubit detectors’ state given in Section 4.
5.1. The Initial Condition
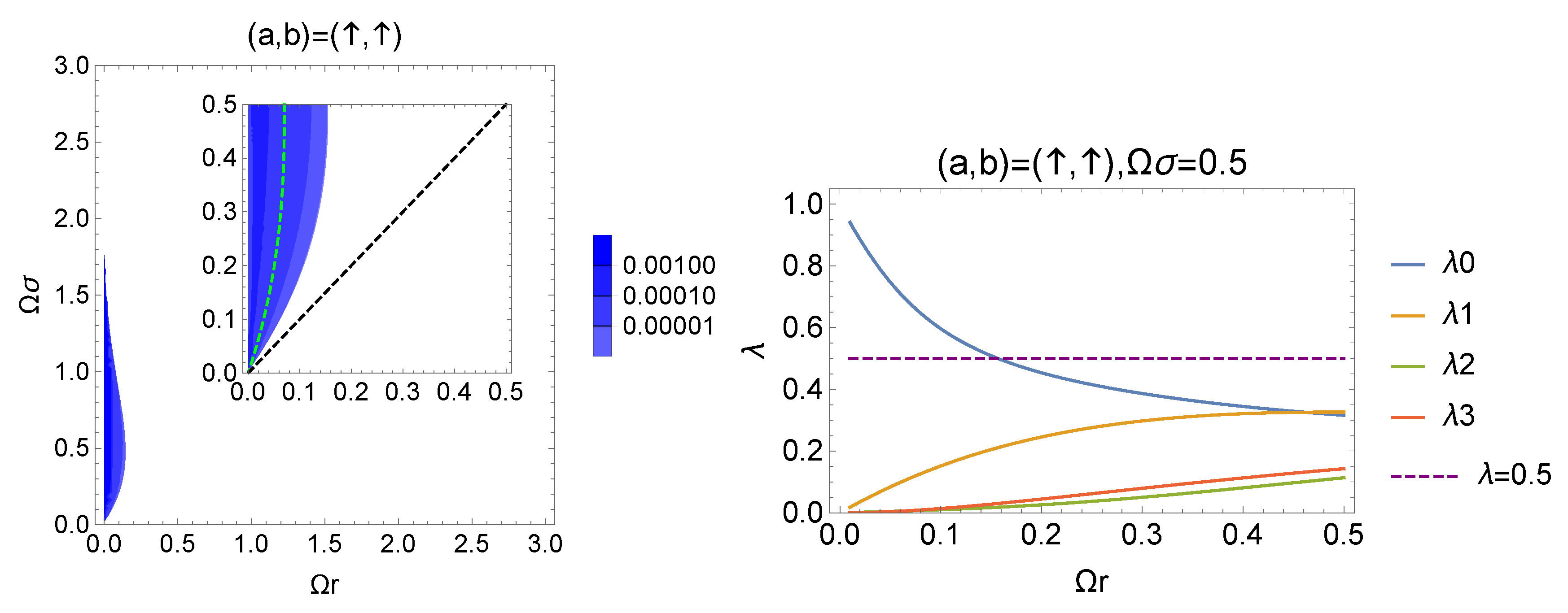
We consider the initial condition of the detectors corresponding to the state . From Equations (15)–(18), we derive
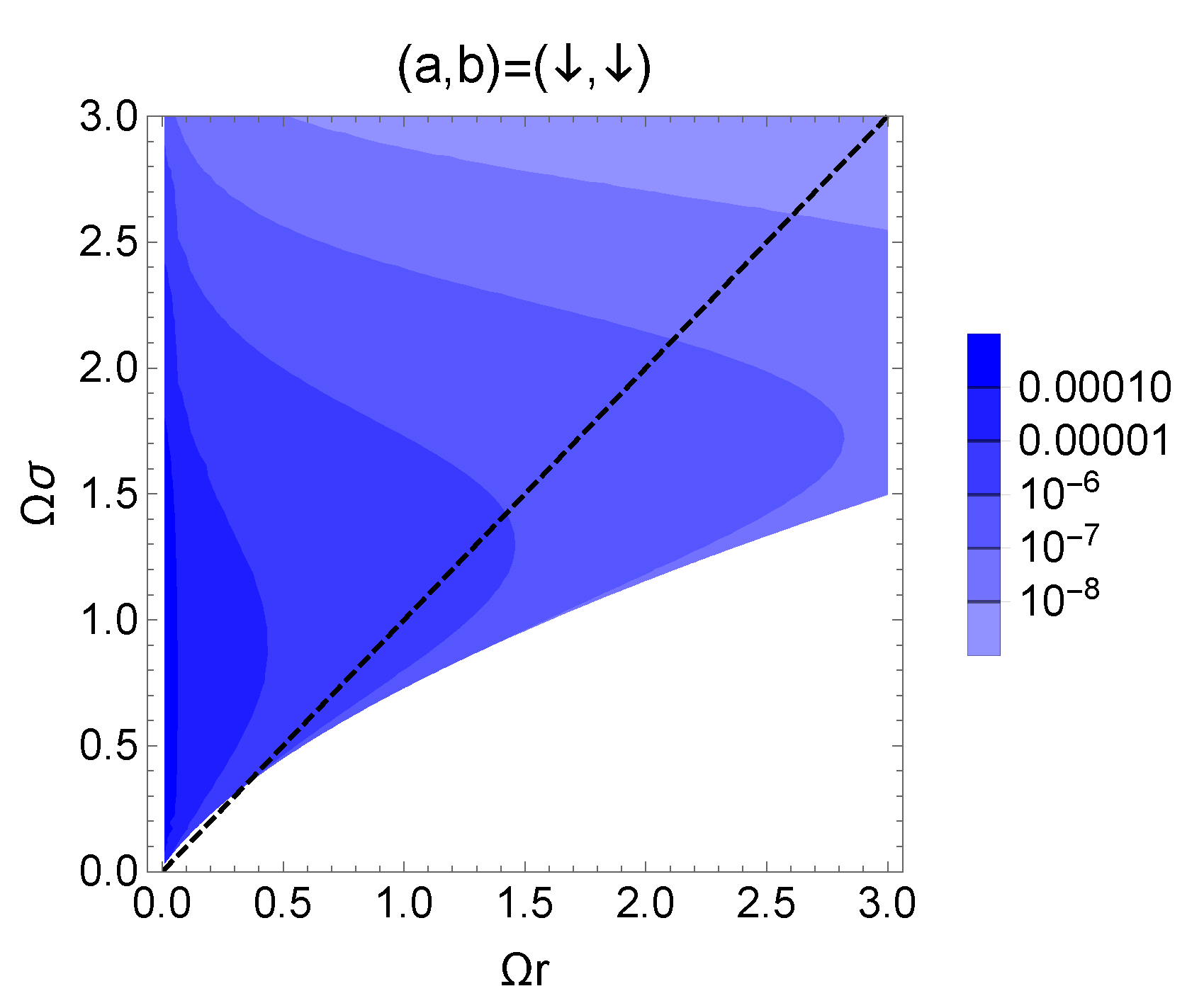
and . Figure 4 shows the contour plot of the negativity for the filtered X state with the initial condition . The coupling is fixed to .
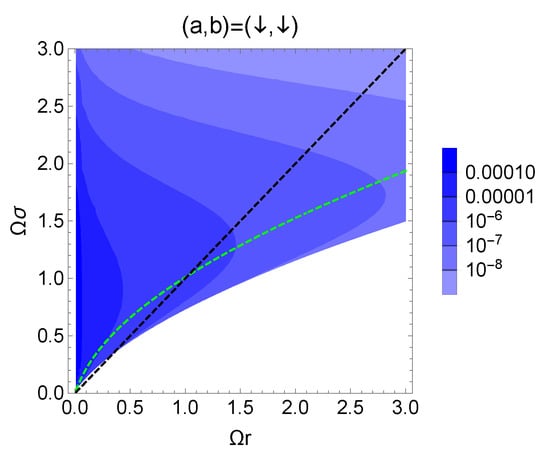
Figure 4.
The contour plot of the negativity with the initial condition . The green dashed line denotes , and the above this line .
The green dashed line denotes , and the region above this line represents where the Bell-CHSH inequality is violated. In addition, we observe the existence of the region where the violation of Bell-CHSH inequality is not found even if the optimal filtering is acted on each detector.
We analyze how the quantum correlation of the scalar field is detected through the detectors. In Section IV, we give the simple form (45) of the spectrum obtained from the components of the X state. Figure 5 shows the behavior of those spectra with and we observe that is dominant compared to the others.
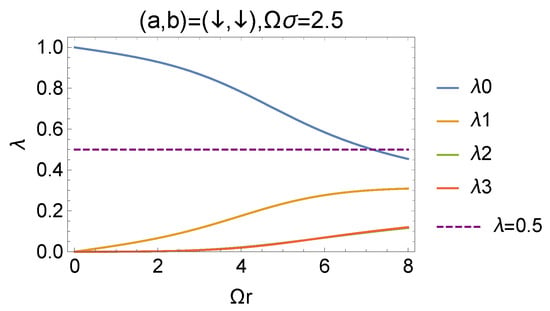
Figure 5.
The behavior of the spectrum of the Bell diagonal state with fixed and . The initial condition of the detectors’ state is . is larger than the other eigenvalues, that is, the coherence is dominant.
From Equation (45) we note that the eigenvalue for a small coupling is evaluated as
Hence the condition is equivalent to , and Figure 5 means that the coherence of the superposition in the basis is larger than . To understand why the coherence dominates, we remind that the state of the detectors depends on the two-point function of the scalar field. The quantum superposition in the basis is realized by the exchange of the real or virtual scalar field. Figure 6 corresponds to the diagrammatic picture to generate the coherence in the second order dynamics.
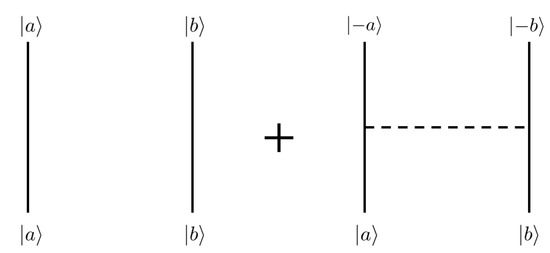
Figure 6.
The diagrammatic picture of the coherence generation by the exchange of the scalar field.
5.2. The Initial Condition
We consider the detection of the quantum correlation for the initial state . The components and X of the reduced density matrix are
and . We find that , that is, those coherences with the two different initial conditions are equivalent. Due to the facts that the vacuum is invariant under time translation and time reversal and that the switching function has the symmetric property , we can derive that the transition probability of is the same as of . The detail calculation is presented in the Appendix B.
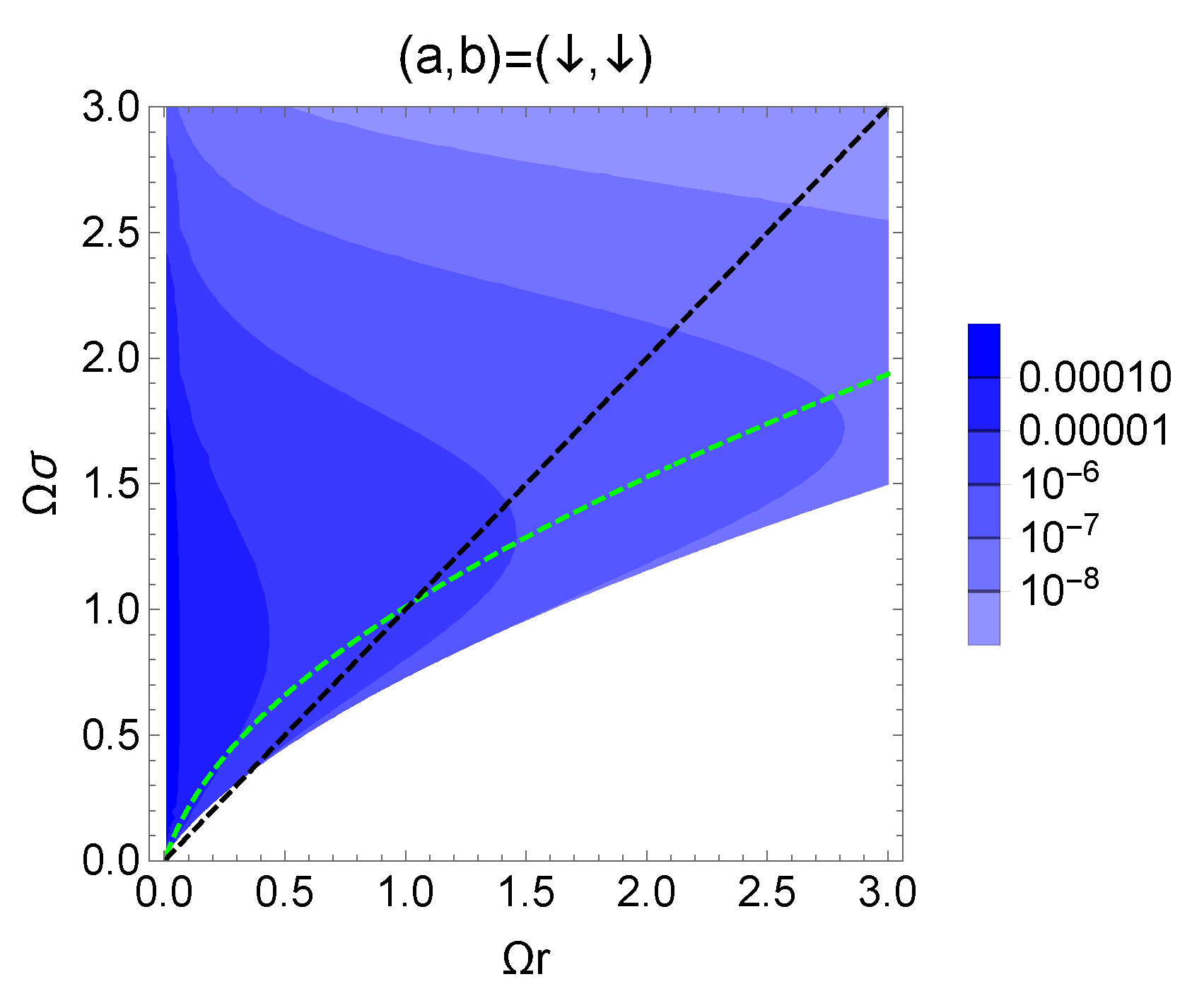
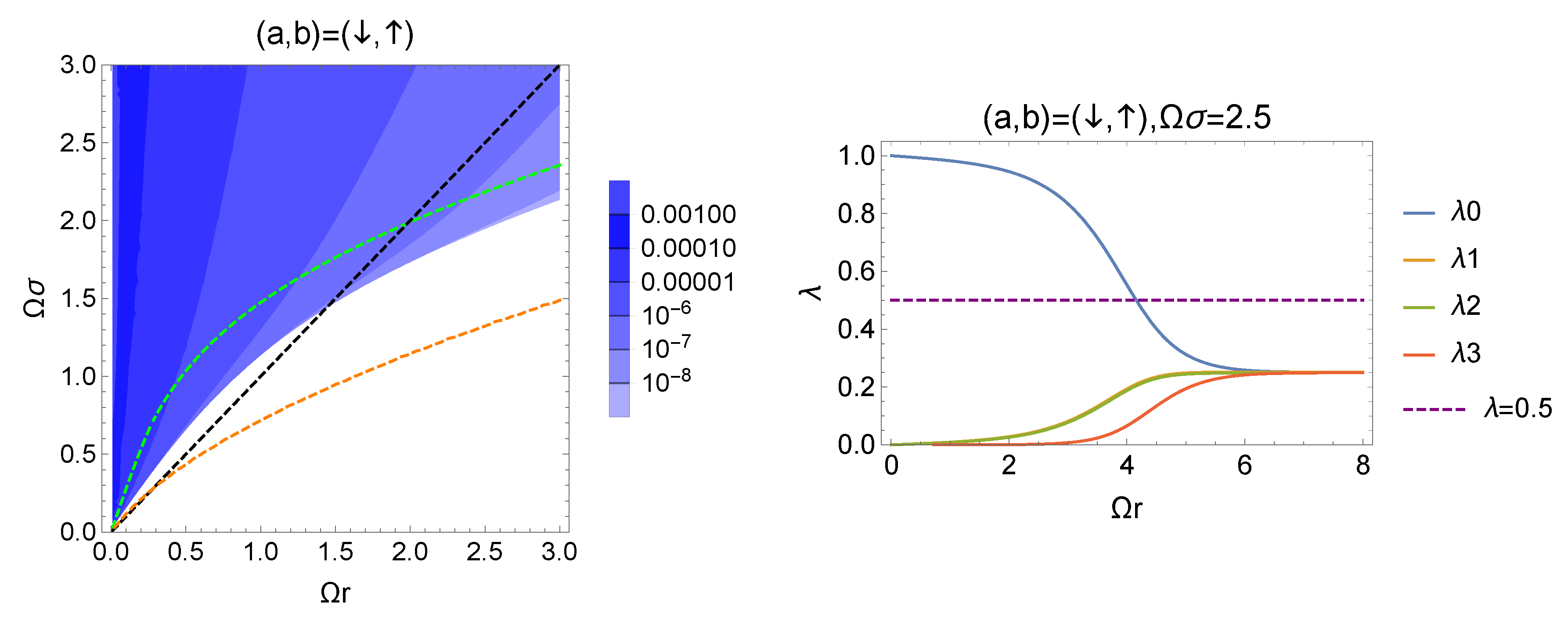
The left panel of Figure 7 presents the contour plot of the negativity with the initial state . The region with the nonzero negativity is much smaller compared to the result obtained with the initial state (similar to the case for , in the right panel of Figure 7, we can confirm that the quantum correlation of the X state is generated by the exchange of the scalar particle because dominates). To understand the different feature of quantum correlations from that for the case , we focus on the diagonal components and , which are the transition probabilities of and , respectively. Evaluating the difference , we obtain
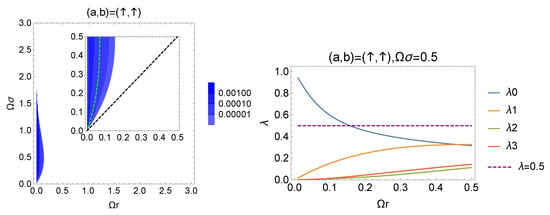
Figure 7.
(left): The contour plot of the negativity with the initial condition . The inset is the enlarged version of the contour plot. The green dotted line represents . region does not extend to the region . (right): The behavior of the spectrum of the Bell diagonal state with fixed and . The eigenvalue is dominant due to the exchange of the scalar particle.
The inequality also holds. and correspond to the probabilities of spontaneous emissions, which are determined by the local dynamics and prevent the detection of nonlocal correlations (indeed, the equality and the inequalities and imply that the spectrum given by (53) is reduced). Therefore, it is difficult to reveal the entanglement and the violation of Bell-CHSH violation with the initial excited state .
5.3. The Initial Condition
We consider the detectors’ initial condition . The components and X of the reduced density matrix are given as
The left panel of Figure 8 shows the contour plot of the negativity with the green dotted line . Further, we add the orange line which denotes for the initial state .
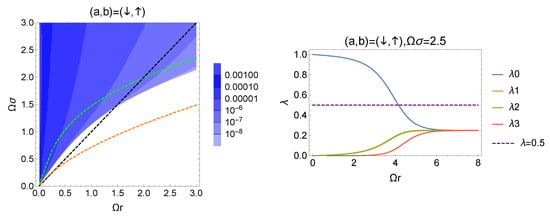
Figure 8.
(left): The contour plot of the negativity with the initial condition . The orange dashed line denotes the boundary of the nonzero negativity with the initial state . In this case, the size of the parameter region which shows the quantum correlations is smaller compared to the case . (right): The behavior of the spectrum as a function of with fixed and .
We observe that the region with the nonzero negativity is smaller compared to that for the initial state but larger than that for the initial state . This is because the probability of spontaneous emission is large () and the generation of quantum correlations are suppressed compared to the case with the initial condition
6. Effect of Local Emissions for the Detection Region of Bell Nolocality and Its Success Probability
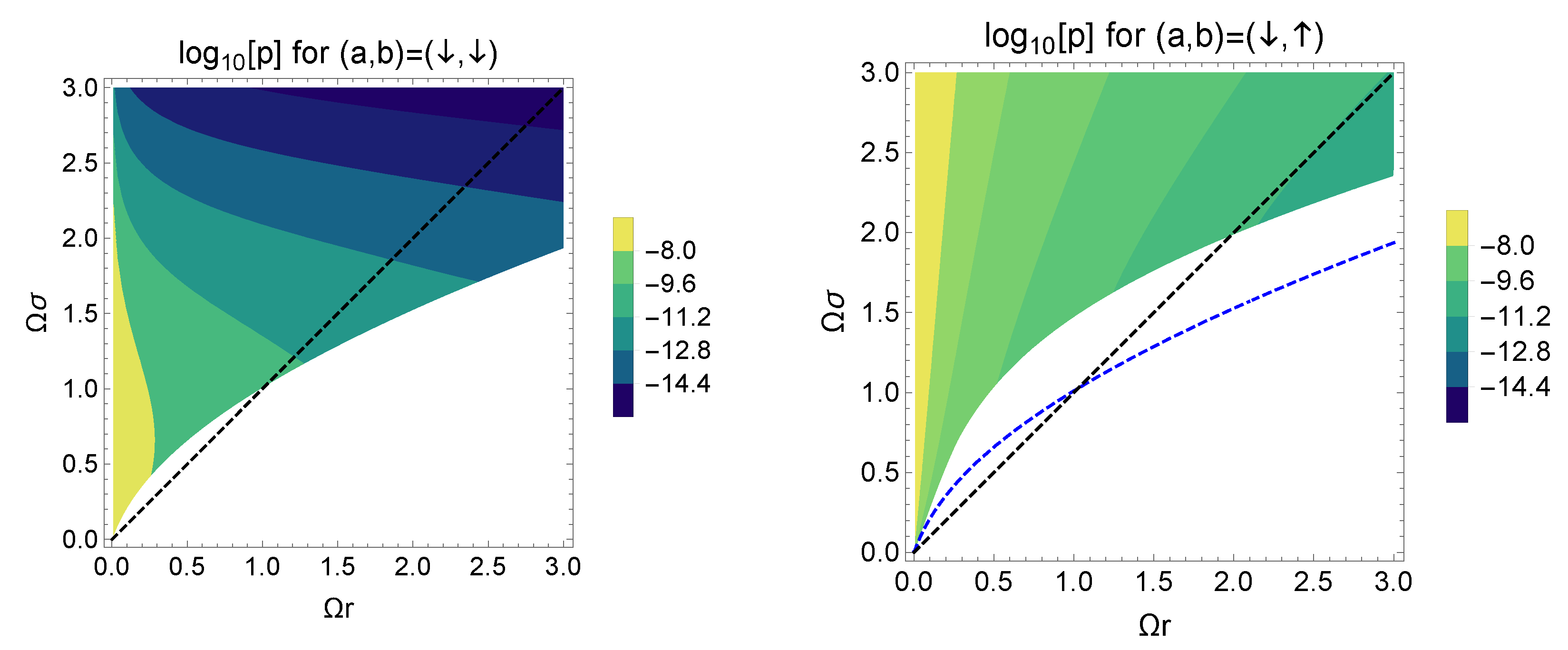
In this section, we focus on the success probability of the optimal filtering for the initial conditions and . In the left panel of Figure 9, we present the contour plot of the success probability with the violation of the Bell-CHSH inequality (that is, ) in common logarithms scale for the initial condition and observe that the probability decreases as the distance between the two detectors or the interaction time increase.
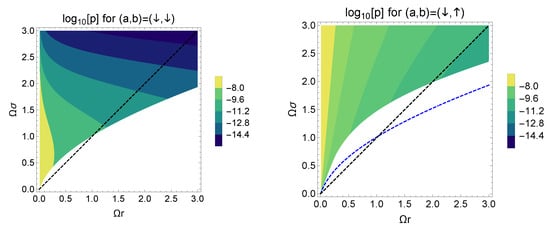
Figure 9.
(left): The contour plot of the success probability p in common logarithms scale for the initial condition . The colored region denotes that is larger than unity in the parameter space . As the distance or the interaction time increase, the probability becomes small. (right): The contour plot of the success probability p in common logarithms scale with for the initial condition . The blue dotted curve represents the curve for the initial condition equals to unity. The detection region of the violation of the Bell-CHSH inequality is reduced, but its probability increases from the case for the initial condition .
The right panel of Figure 9 is the contour plot of p in common logarithms scale for the initial condition . Comparing to the case , the behavior of the probability for the interaction time is different. To understand the behavior of p for , we should note that the success probability in the leading order of the coupling is
where we substituted Equations (10)–(13) into the formula of the probability (46). Here let us denote and as the success probability for each initial condition and . For the switching function is effectively regarded as the constant . Hence the total system is invariant under a time translation and the total energy is conserved. By the energy conservation for , each component and X is
where and correspond to the amplitudes of each transition process. According to the behaviors of and X, we find that the probabilities and approach zero and for a large , respectively. In Figure 9, this different feature appears as the shape of the contour of p for each initial condition.
In the right panel of Figure 9, we also observe that the success probability is improved compared to the initial condition while the detection region of the violation of the Bell-CHSH inequality in the parameter space is reduced. This trade-off relation is explained by the formulas of the eigenvalue (53) and the success probability p (62). The eigenvalue is given by the difference , and the success probability depends on the sum . As the transition probability or of the spontaneous emission grows, the eigenvalue decreases and the success probability p increases. This means that the process of the local emission has two effects: one is the reduction of the detection region of the violation of the Bell-CHSH inequality, and the other is the increase of the efficiency for the detection of that violation. The local dynamics of each detector plays an important role in the reliable detection of the Bell-CHSH inequality.
7. Summary and Conclusions
We investigated the detection of quantum correlations of a massless scalar field for the model of two-qubit detectors. We considered the two-qubit detectors coupled to the scalar field in a Minkowski vacuum. Under the second-order perturbation of the total dynamics, we examined the negativity and the violation of the Bell-CHSH inequality for the detectors’ state. It is demonstrated that the state of the detectors can be entangled but satisfies the Bell-CHSH inequality within our perturbative treatment. To reveal the violation of the Bell-CHSH inequality, we used the optimal filtering operations acting on each detector. In general, it is complicated to construct these operations. It is simpler to obtain the optimal filtering for the out-state of the detectors described by an X state. Such a filtering is given by the two steps; passing through an amplitude damping channel and choosing a specific outcome after the channel. The success probability to perform the filtering characterizes the efficiency of the detection of the violation of Bell-CHSH inequality.
By examining the negativity and the violation of the Bell-CHSH inequality under the optimal filter, we found that the detection of the quantum correlations strongly depends on the initial state of the detectors. When the detectors are initially in the ground state, the detection region in the parameter space showing the quantum correlation is larger than that obtained for the case of initially excited states. This is because the excited detectors spontaneously emit the scalar particles and such local dynamics prevent the detection of quantum correlations by the detectors.
Further we focused on the success probability of the optimal filtering for the violation of Bell-CHSH inequality for the initial condition and . Then we demonstrated the trade-off relation between the parameter region of the violation of Bell-CHSH inequality and the success probability. Due to this trade-off relation, the reliable detection of the violation of Bell-CHSH inequality becomes non-trivial, and we found that the setting with the initial state of the detectors leads to the violation of the Bell-CHSH inequality with a high efficiency and large parameter regions. This result gives a suitable model for the detection of the violation of Bell-CHSH inequality through the two-qubit detectors.
Author Contributions
A.M. and Y.N. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the JSPS KAKENHI Grant Number 15K05073.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Components of Reduced Density Matrix
The diagonal components and are obtained from . According to Equation (8), the non-diagonal component are represented by
where note that the inner product of and n-particle state for or is zero. We introduce the regularized mode function of the Minkowski vacuum
where . The inner product are calculated as
The component is computed as
We get Equation (17) by taking the limit . Next we derive the formula of X. Using the Wightman function given by Equation (14), the non-diagonal component is
where the integral variables and are changed as
and we carried out the x integration. By using the identity
the above Equation (A5) can be rewritten as
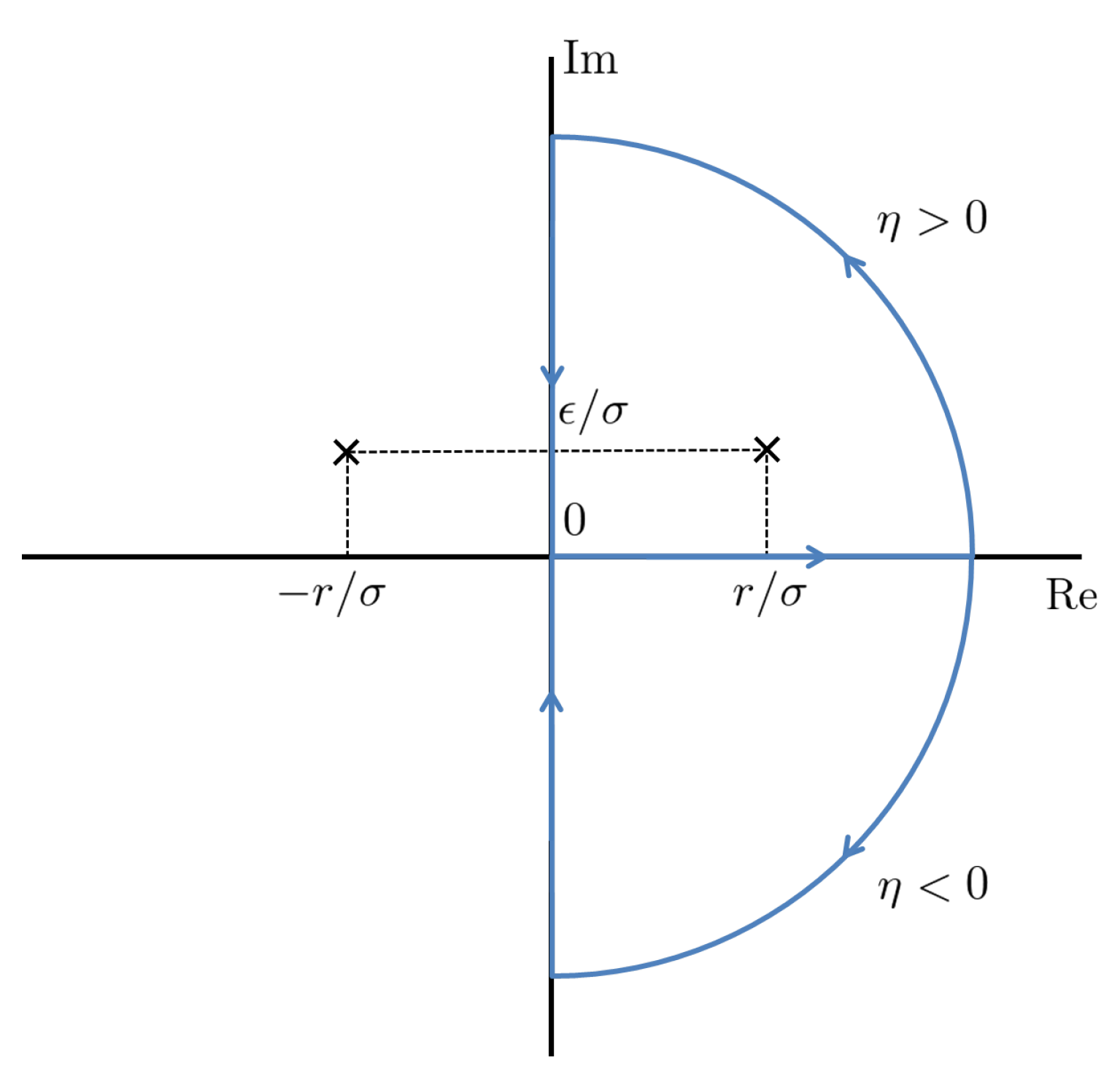
The y integration is equivalent to the complex integration given in Figure A1. Hence,
where the second and third terms are the integration along the imaginary axis. For the sum of those terms is an odd function, and then it does not contribute to the integration (note that the function of in front of Equation (A9) is an even function).
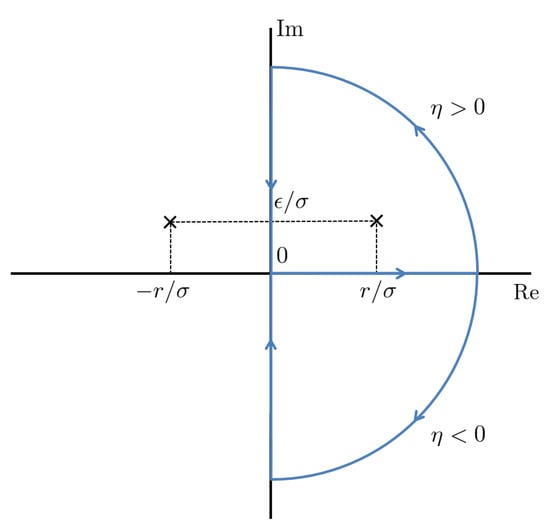
Figure A1.
The contour of the complex integration to compute the non-diagonal component .
Figure A1.
The contour of the complex integration to compute the non-diagonal component .
Thus we get the following formula
Appendix B. Equality of |X(−1,−1)| and |X(+1,+1)|
Let us show the equality of and . Under the second order of the coupling, the non-diagonal components and is
where we used the translation invariant of the vacuum state for Equation (A11). Due to the time reversal invariance of the Minkowski vacuum, is rewritten as
The switching function is a Gaussian function, and holds. Thus,
and we get the equality .
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bell, J. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Clauser, J.; Horne, M.; Shimony, A.; Holt, R. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Werner, R. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Reeh, H.; Schlieder, S. Bemerkungen zur unitäräquivalenz von lorentzinvarianten feldern. Nuovo Cimento 1961, 22, 1051. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R. The vacuum violates Bell’s inequalities. Phys. Lett. A 1985, 110, 257. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Hu, B.L. Accelerated detector-quantum field correlations: From vacuum fluctuations to radiation flux. Phys. Rev. D 2006, 73, 124018. [Google Scholar] [CrossRef]
- Brown, E.G.; Martin-Martinez, E.; Menicucci, N.C.; Mann, R.B. Detectors for probing relativistic quantum physics beyond perturbation theory. Phys. Rev. D 2013, 87, 084062. [Google Scholar] [CrossRef]
- Brown, E.G. Thermal amplification of field-correlation harvesting. Phys. Rev. A 2013, 88, 062336. [Google Scholar] [CrossRef]
- Reznik, B.; Retzker, A.; Silman, J. Violating Bell’s inequalities in vacuum. Phys. Rev. A 2005, 71, 042104. [Google Scholar] [CrossRef]
- Retzker, A.; Cirac, J.I.; Reznik, B. Detecting Vacuum Entanglement in a Linear Ion Trap. Phys. Rev. Lett. 2005, 94, 050504. [Google Scholar] [CrossRef] [PubMed]
- Silman, J.; Reznik, B. Long-range entanglement in the Dirac vacuum. Phys. Rev. A 2007, 75, 052307. [Google Scholar] [CrossRef]
- Leon, J.; Sabin, C. Entanglement swapping between spacelike-separated atoms. Phys. Rev. A 2008, 78, 052314. [Google Scholar] [CrossRef]
- Pozas-Kerstjens, A.; Martin-Martinez, E. Harvesting correlations from the quantum vacuum. Phys. Rev. D 2015, 92, 064042. [Google Scholar] [CrossRef]
- Salton, G.; Mann, R.B.; Menicucci, N.C. Acceleration-assisted entanglement harvesting and rangefinding. New J. Phys. 2015, 17, 035001. [Google Scholar] [CrossRef]
- Sachs, A.; Mann, R.B.; Martin-Martinez, E. Entanglement harvesting and divergences in quadratic Unruh-DeWitt detector pairs. Phys. Rev. D 2017, 96, 085012. [Google Scholar] [CrossRef]
- Pozas-Kerstjens, A.; Louko, J.; Martin-Martinez, E. Degenerate detectors are unable to harvest spacelike entanglement. Phys. Rev. D 2017, 95, 105009. [Google Scholar] [CrossRef]
- Gisin, N. Hidden quantum nonlocality revealed by local filters. Phys. Lett. A 1996, 210, 151. [Google Scholar] [CrossRef]
- Nambu, Y.; Ohsumi, Y. Classical and quantum correlations of scalar field in the inflationary universe. Phys. Rev. D 2011, 84, 044028. [Google Scholar] [CrossRef]
- Verstraete, F.; Dehaene, J.; DeMoor, B. Local filtering operations on two qubits. Phys. Rev. A 2001, 64, 010101. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M. Entanglement versus Bell Violations and Their Behavior under Local Filtering Operations. Phys. Rev. Lett. 2002, 89, 170401. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, R.; Horodecki, P. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]
- Tsirelson, B. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M. Violating Bell inequality by mixed spin-1/2 states: Necessary and sufficient condition. Phys. Lett. A 1995, 200, 340. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).