Abstract
Several methods for exploiting quantum effects in radar have been proposed, and some have been shown theoretically to outperform any classical radar scheme. Here, a model is presented of quantum-enhanced noise radar enabling a similar analysis. This quantum radar scheme has a potential advantage in terms of ease of implementation insofar as it requires no quantum memory. A significant feature of the model introduced is the inclusion of quantum noise consistent with the Heisenberg uncertainty principle applied to simultaneous determination of field quadratures. The model enables direct comparison to other quantum and classical radar schemes. A bound on the probability of an error in target detection is shown to match that of the optimal classical-state scheme. The detection error is found to be typically higher than for ideal quantum illumination, but orders of magnitude lower than for the most similar classical noise radar scheme.
1. Introduction
Microwave quantum optics may enable new radar technologies that outperform existing approaches founded on the classical model of electromagnetic waves [1,2,3,4,5,6,7,8]. Radar and other remote sensing technologies generally rely on illuminating a region of interest with waves whose properties are well known so that waves received from that region can be classified as reflected by a target or not, thereby revealing the presence or absence of the target. Properties of the received waves can further indicate the range and velocity of the target, the identity of the target, and other characteristics of interest. Uncertainty in the properties of the illuminating waves or in detection of the received waves impairs the ability to gather such information about the target. Classical physics allows for infinitely precise wave properties. However, the classical description fails at the extreme of weak intensity where a quantum description is most accurate and where the fundamental limits to radar sensitivity lie.
Aspects of the quantum description of the electromagnetic field have been recognized to offer an opportunity for a quantum advantage over technology based on classical physics. To understand these phenomena, recognize that the closest quantum approximation to a classical wave is the coherent state, a wave whose intensity and phase are defined only to within the resolution allowed by a Heisenberg uncertainty relation. This uncertainty is often thought of in terms of quantum noise that accompanies an otherwise largely classical wave [9]. However, other quantum states exist in which this inherent quantum noise can be squeezed into components of the field that are not relevant to a particular measurement. Additionally, two quantum systems can be entangled so that their quantum noise is correlated. Thus, quantum physics offers opportunities to improve radar performance that cannot be derived from any classical model.
Several approaches to quantum radar have been investigated in theoretical and experimental studies [1,2,3,4,5,6,7,8]. Quantum solutions to basic radar tasks, such as target detection and ranging, as well as more advanced functions, such as low probability of interception, have been explored. The most widely studied method, known as quantum illumination, was originally proposed for optical target detection or imaging [3,8,10]. The subject of this article is another approach known as quantum-enhanced noise radar or quantum two-mode squeezing radar [5,6,11,12]. This approach aims to detect the presence of a target while maintaining a low probability of intercept. Quantum-enhanced noise radar has been demonstrated in a laboratory environment and described theoretically in terms of a covariance matrix and radar performance metrics [6,11,12,13]. However, a quantum optics model that can easily be compared with other methods like quantum illumination has not been elaborated in detail.
Here, such a model is presented. The model utilizes the same treatment of loss and noise most widely used in the quantum illumination literature [10,14]. An important, unique aspect of the current model is the treatment of the simultaneous determination of field quadratures as a minimum uncertainty, non-projective measurement [15]. The description of field measurements is shown to have a direct bearing on predicted radar performance. Within this model, a bound on target detection error is derived in terms similar to those used in the quantum illumination literature. In the regime of low signal power, weak reflection and strong background noise, the error bound indicates a probability of detection error that equals that of the optimal classical-state radar scheme. An adaptation of the model used to provide error bounds for two-mode noise radar, the most similar classical noise radar scheme, shows the dramatic advantage of quantum-enhanced noise radar. Thus, the results presented clarify the place of quantum-enhanced noise radar among other proposed quantum radar methods and existing classical technologies.
2. Quantum-Enhanced Noise Radar
In general, a noise radar of any type uses a complicated, random or pseudo-random waveform to probe a vicinity of interest [16]. Assuming the receiver has a record of the irregular shape of the waveform, the signal is easier to recognize after reflection and severe attenuation than would be a simple sine wave or other periodic signal. The performance of the receiver is, therefore, limited by, among other things, the fidelity of the receiver’s record of the transmitted waveform. The presence of quantum noise fundamentally limits the precision of the receiver’s description of the transmitted waveform. Quantum-enhanced noise radar utilizes a non-classical state of the electromagnetic field to push this limit.
Signal generation in quantum-enhanced noise radar is performed by a superconducting microwave circuit that produces two spatially separated output fields, referred to conventionally as the signal and idler modes, in a quantum state called a two-mode squeezed vacuum [5,6]. As the name indicates, the quantum noise in this state is squeezed insofar as its effects on the two modes are strongly correlated. In the radar scheme, the idler mode is immediately detected, while the signal mode is transmitted to the region of interest. The receiver collects radiation from the region of interest and looks for a correlation with the idler measurements. If the correlation is strong enough, the received radiation is likely to be the reflected signal mode and the target is deemed present. Other information about the target can also be gathered. For example, the time of flight of the reflected signal reveals the range to the target. However, other functions besides target detection are outside the scope of this article.
The signal and idler modes are generated through the nonlinear process of spontaneous parametric down conversion in which single microwave photons arising from vacuum fluctuations interact with the nonlinear circuit components to produce pairs of photons, with one photon in each of the two output modes [5,6]. Individually, the signal and idler modes resemble thermal fields commonly associated with spontaneous emission. The thermal fluctuations may act as a sort of camouflage reducing the probability of interception by an adversary. However, since the signal and idler photons are always generated pairwise, the fields have strongly correlated fluctuations. Detection of both the idler mode and the received radiation involves simultaneous measurements of the quadratures of the respective fields. The receiver can then compute the correlation between these measurements and compare the result to a detection threshold to decide whether a target is likely to be present.
Since field quadratures are the physical observables of interest, it is convenient to describe the quantum state of the two-mode squeezed vacuum in terms of the real quadrature representation [17,18] in which
where and are the real quadratures of the signal and idler modes, respectively, and R is a parameter related to the mean photon number of both modes by the equation . The correlated nature of the two modes ensures that they have the same mean photon number. This quantum state is characterized by mean values and variance , and the same values for the corresponding imaginary quadratures.
Immediately before the signal mode is transmitted, and , the real and imaginary field quadratures of the idler field, respectively, are measured simultaneously. It is important to recognize that the quadratures of any single mode electromagnetic field are non-commuting observables. As such, they can only be determined simultaneously to within the precision allowed by the Heisenberg uncertainty relation . As a result, the most common approach to describing measurements in quantum mechanics (i.e., that of projective measurements) is not appropriate. Instead, these observations must be treated as generalized measurements with finite precision. Here, we apply the formalism of generalized measurements where the measurement devices are assumed to be in minimum-uncertainty quantum states [15,19]. These states are not intended to represent physically realistic models of experimentally implementable devices. Rather, the goal is to define the detector states purely in terms of the optimum performance allowed by quantum physics. In effect, this is a limiting case in which no classical noise is added by the measurements and quantum noise is as weak as possible.
The effect of simultaneous minimum-uncertainty measurements of the idler quadratures is represented by the measurement operator , where is a coherent state with mean quadratures and [15,19]. The probability density for obtaining the values and from a simultaneous measurement is
Note that the probability distribution for either quadrature corresponding to this density has a variance that is the sum of the variance for a projective measurement of a single quadrature (i.e., ) and the variance of the minimum uncertainty measurement device, (i.e., 1/2). The contribution of the finite precision measurement will later be seen to have a direct impact on target detection error.
Since this measurement is not projective, it does not leave the signal and idler modes in quadrature eigenstates [15,19]. Instead, the density operator after a measurement that results in values and is
Once the measurements and are recorded, no further use is made of the idler mode. Thus, a partial trace over the idler mode is performed and the density operator of the signal to be transmitted becomes
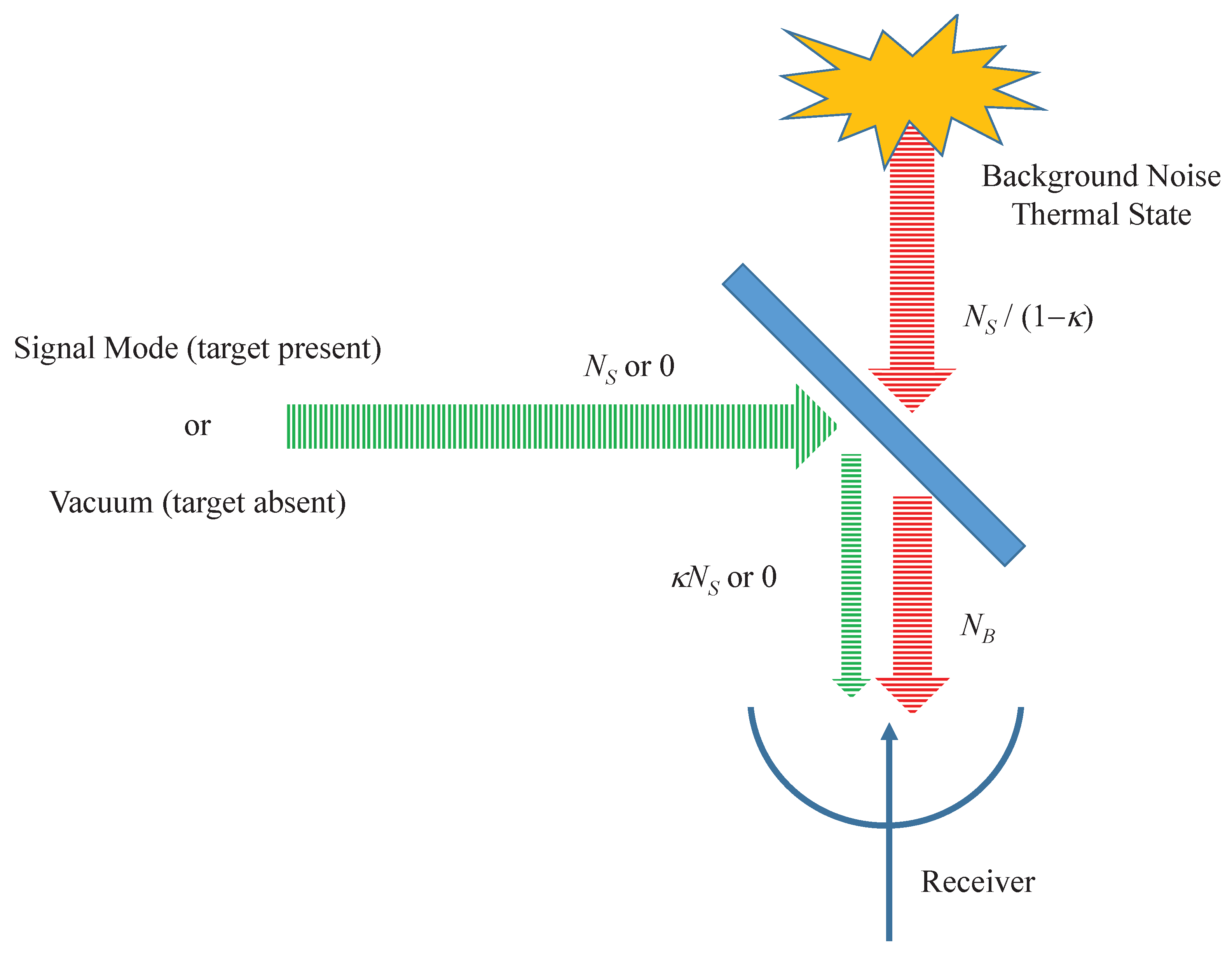
Having determined the quantum state of the transmitted field, the model of loss and noise is now introduced. This model, widely used in the literature on quantum illumination [10,14], is depicted schematically in Figure 1. In this model, the signal mode is subjected to loss and contaminated by background noise before reception. The background noise is accounted for by the introduction of a single mode thermal field which is combined with the signal mode in a beam splitter. The signal mode is reflected by the splitter with a reflectance representing all loss mechanisms. Losses in remote sensing are typically substantial. First, and foremost, this is true because only a small fraction of the transmitted energy actually falls on the target and is reflected into the receiver. Some other sources of loss include absorption by the target or the atmosphere, detector inefficiency, multi-path fading, and Doppler shifts. Consequently, the reflectance . The background mode is transmitted with a transmittance . The mean photon number of the background thermal field at the input to the beam splitter is set to so that the mean photon number of the noise field emerging from the beam splitter is simply . To model the received radiation when no target is present, the signal field of Equation (4) is replaced by a vacuum state.
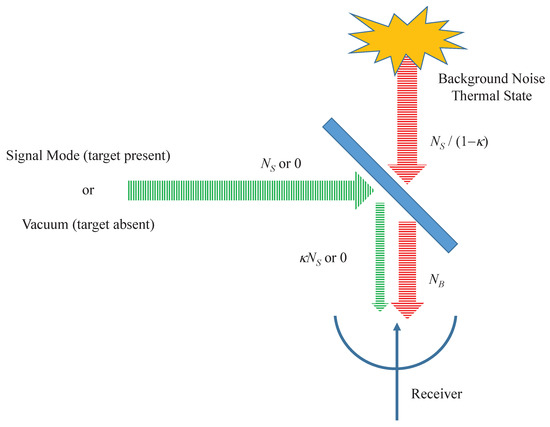
Figure 1.
A schematic representation of the loss and noise mechanisms in the model of quantum-enhanced noise radar.
A single mode thermal field can be written as a Gaussian-distributed mixture of coherent states [9]. Thus, we represent the thermal field input to the beam splitter by the density operator
where is a coherent state with complex amplitude and mean real and imaginary quadratures and , respectively.
The combined quantum state of the inputs to the beam splitter is . The effect of the beam splitter is represented by a unitary transformation on this density operator resulting in a new density operator whose two modes represent the two output modes of the splitter, which we will label 1 and 2 [18]. The physically significant output 1 is that which results from reflection of the signal mode and transmission of the thermal mode. Thus, a partial trace is necessary over the unused output mode 2. Finally, we have the density operator for the field emerging from the beam splitter
The receiver makes simultaneous measurements of the quadratures of this field. Using the same formalism as for the idler measurements, the probability density for obtaining the values and for the real and imaginary quadratures, respectively, conditioned on having found the corresponding values for the idler to be and is
In the case where the target is absent, the lack of a reflected beam is modeled by replacing the signal beam with a vacuum state, i.e., setting , giving
Multiplying these conditional densities by the idler measurement density in Equation (2) gives the unconditional probability density
when the target is present, and
when the target is absent.
At this point, it is helpful to consider the covariance matrices corresponding to these densities. These quantities, which have been studied extensively in the literature on quantum enhanced noise radar, reveal the structure of correlations between the various measurements providing insight into entanglement of the fields and its exploitation in possible receiver designs [5,6,11,12,13]. The covariance matrix C, in terms of the vector , is defined by components of the form , where the braces indicate the quantum expectation value. From Equation (10), it follows that, when the target is present,
and, from Equation (11), when the target is absent
In these matrices, the elements on the diagonal quantify the spread in the various measured quantities due to quantum noise. Note that the treatment of the simultaneous quadrature measurements as non-projective contributes 1/2 to these terms beyond what their values would be for individual measurements. The off-diagonal elements quantify correlations between the measurements. When the target is present, the real quadratures, and , are correlated while the imaginary quadratures and are anti-correlated. Physically, these correlations are remnants of the entanglement of the two-mode squeezed vacuum state that survive the effects of measurements, loss, and contamination by noise. The only non-zero difference between the diagonal elements when the target is present and absent is proportional to , which is typically very small. In contrast, the off-diagonal elements differ in proportion to . Thus, receiver designs proposed in the literature utilize the latter [5,6,11,12].
The receiver takes the measured quadrature values of the idler and received fields and forms a scalar that can be compared to one or more thresholds in order for the receiver to infer the presence or absence of the target. Several possible scalars have been considered in the literature [5,6,11,12]. In what follows, the discussion is limited to the quantity , but it would be straightforward to adapt the results to other scalars. The densities in Equations (10) and (11) can be used to derive the probability density for c. The first step is to find the cumulative probability distributions for the products and and differentiate to get the corresponding densities. Then, the density for the difference of these two products is a convolution of the product densities giving
when the target is present and
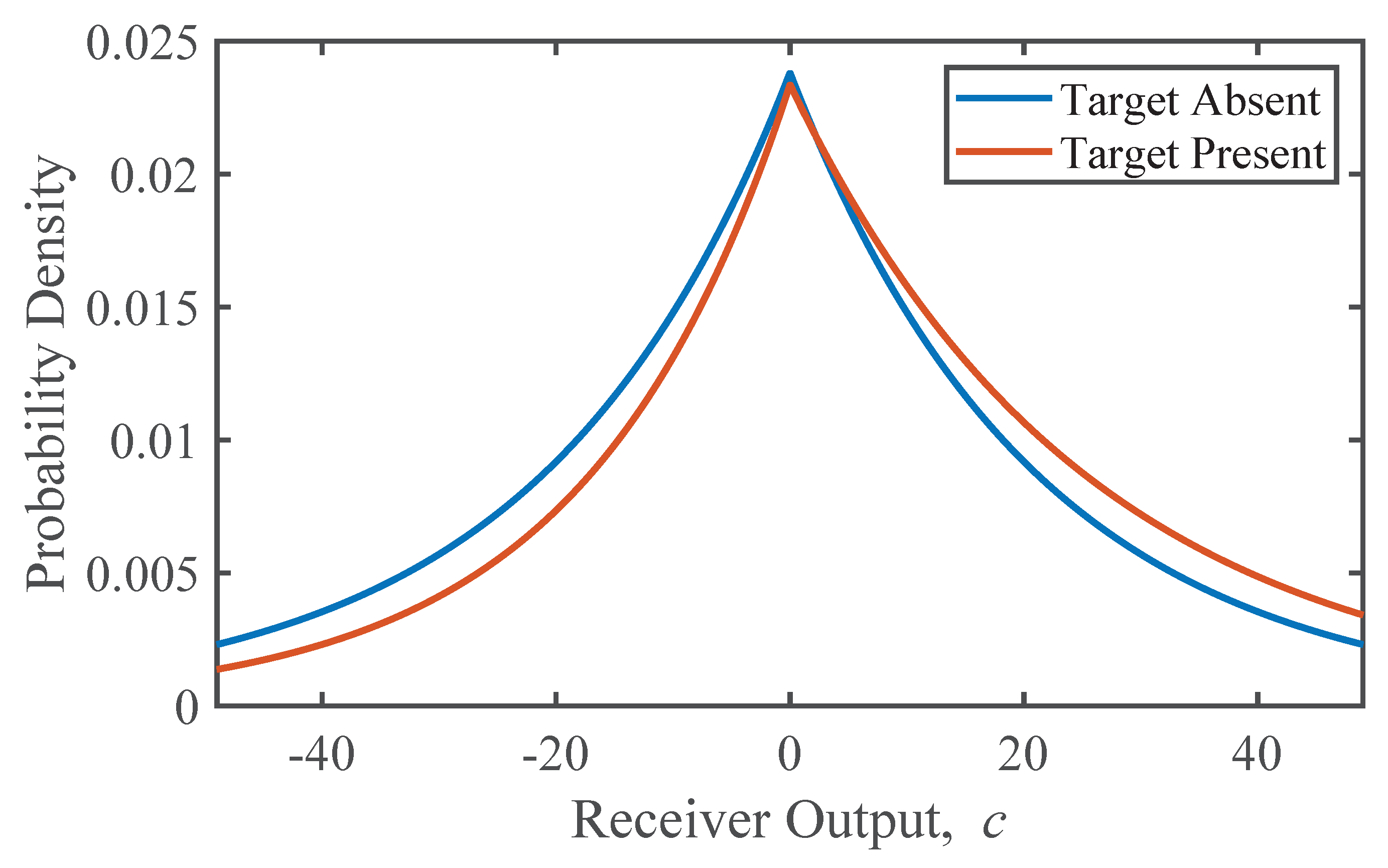
when the target is absent (see Appendix A for details of the derivation). Figure 2 shows examples of these densities in the case where and . These relatively large values of and were chosen to exaggerate the differences between the densities to make them more perceptible. It is seen that the presence of he target is indicated by a subtle bias of the receiver output towards non-zero values.
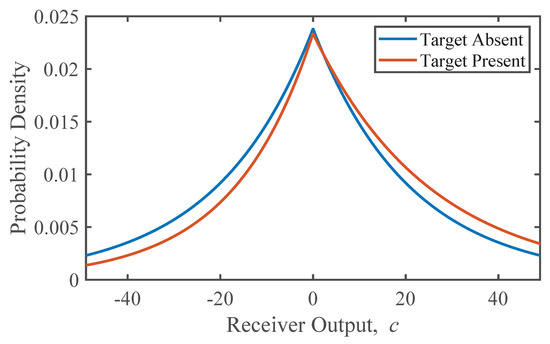
Figure 2.
Probability densities for the receiver output when the target is absent (blue) and present (red), with , and . These parameters are chosen to exaggerate the difference between the two functions.
However, before any further analysis of the receiver output, the next section presents analogous densities and covariance matrices for the classical noise radar scheme that most closely resembles quantum-enhanced noise radar.
3. Two-Mode Noise Radar
The same article that first introduced quantum-enhanced noise radar also described the closest approximation allowed by a classical model of the field [5]. This classical radar was later named two-mode noise radar [6,11,12]. Two-mode noise radar provides an important benchmark for quantum-enhanced noise radar because, unlike many other classical radars, it aims to fulfill both design goals of target detection and low probability of intercept. Understanding the performance differences between these two radar schemes is central to understanding the nature and extent of the advantage to be gained by incorporating quantum physics into radar.
The two mode noise radar mimics quantum-enhanced noise radar by generating two microwave fields that are out of phase by radians and whose amplitudes are identically modulated by band-limited Gaussian noise. Thus, at any arbitrary moment in time, the fields can be viewed as coherent states with a relative phase shift and a random amplitude as represented by the density operator
where is a coherent state with complex amplitude and mean real and imaginary quadratures and , respectively, and is the variance of the classical Gaussian noise. This model of the field remains valid at other times, as well, as long as they are separated by intervals at least as long as the inverse bandwidth of the Gaussian noise so that the noise values at these times are effectively independent. The resemblance of this state to a thermal state such as that of Equation (5) gives it the property of low probability of intercept that is often viewed as an advantage of noise radar over more conventional radar signals. Since the modes of the two-mode squeezed vacuum observed individually resemble thermal states with mean photon number , it is reasonable to set , as is done in all that follows.
Apart from the mechanism for generating the signal and idler beams, two mode radar is identical to quantum enhanced noise radar. Thus, Equations (6) and (7) may be applied directly, and analogous reasoning leads to the probability densities of measured quadratures of the idler and received field in the form
when the target is present, and Equation (11) when the target is absent. The covariance matrix when the target is present then takes the form
By comparison with Equation (12), it can be seen that the correlations between the received field and the idler are weaker for two-mode noise radar, most significantly when or smaller. In particular, as the correlations for two mode radar decrease in proportion to while those of quantum enhanced noise radar decrease at the slower rate of . Thus, for example, when , the correlation in the quantum radar scheme is an order of magnitude larger. On the other hand, when , there is very little difference between the two covariance matrices. Thus, it can be seen already that the regime of significant quantum advantage is that of low signal strength.
Assuming the same receiver operation as in the previous section, the probability density for the receiver output following from Equation (17) is
4. Bounds on Detection Error
In practice, target detection is conducted in situations where, given only a single sample, the probability of a detection error is very high. Thus, detection decisions are usually made on the basis of many samples. This raises the question of how to quantify receiver performance as the number of samples increases. One approach used widely in the quantum illumination literature is to derive bounds on the probability of a detection error as a function of the number of samples [3,8,10,14,20]. In what follows, this approach is applied to quantum-enhanced noise radar.
To be clear, two types of error are possible: the target may be deemed present when it is absent, and the target may be deemed absent when it is present. That these errors typically have distinct probabilities motivates a variety of detection strategies in radar technology. For example, one may design a receiver to limit the probability of one type of error while trying to minimize the probability of the other. In this article, consideration is limited to the specific objective of minimizing the total probability of error, which is the sum of the probabilities of the two types of error, assuming the target is equally likely to be present or absent. Thus, a bound on the total error probability as a function of the number of samples is sought for quantum-enhanced noise radar.
Of course, it would be ideal to calculate the total probability of error directly as a function of the number of samples. However, for most probability densities, this approach becomes unwieldy as the number increases beyond a few samples. Fortunately, bounds can be placed on this probability that are tractable as follows [21,22]. These bounds are based on the Bhattacharya distance B between the two densities, defined as
Then, , the total probability of a detection error given M samples, is bounded above and below by the relation
Exact or approximate Bhattacharya bounds have been given for several target detection schemes in the quantum illumination literature [3,20]. Two important examples are cited here for later comparisons.
First, for target detection using a single coherent state with optimal quantum reception [14], the Bhattacharya distance is
This result was derived under the assumption that the receiver has perfect knowledge of the field quadratures of the coherent state. Thus, this ‘’perfect measurement bound” can be seen to limit any real implementation of coherent state illumination. Moreover, it has been argued that no other classical scheme, viewed as a mixture of coherent states, can provide a Bhattacharya distance larger than this idealized coherent state illumination. Hence, Equation (22) can be construed as bounding all classical radar performance in target detection.
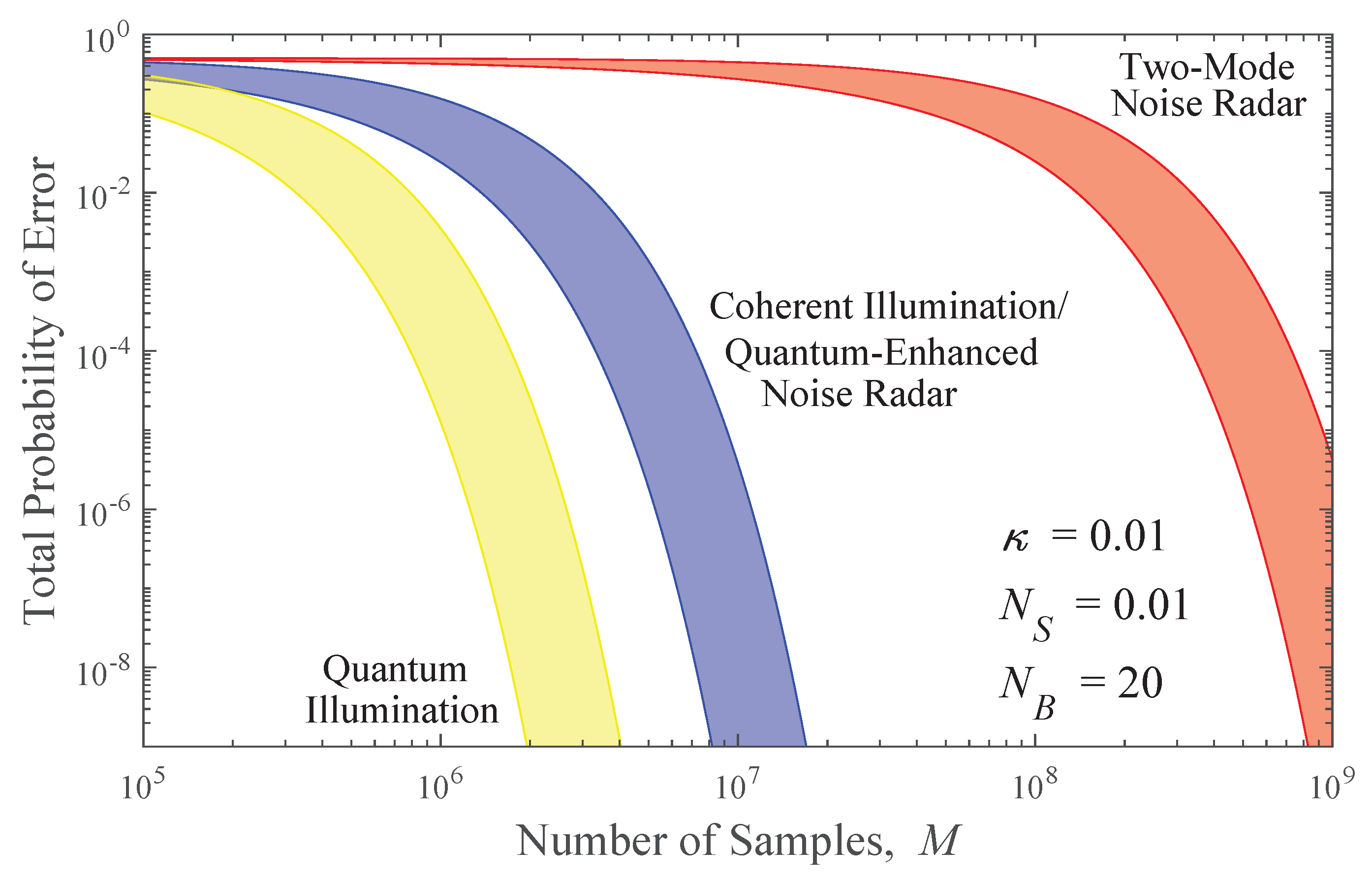
The range of probabilities bounded by Equation (22) and in Equation (21) as a function of the number of samples, M, is depicted by the blue region in Figure 3 for the specific parameters , , and . This choice of values is located in parameter space well within the regime where quantum illumination is most advantageous, i.e., the region of low signal power, weak reflection, and strong background [10,14]. In the figure, blue solid lines (with matching shading in between) indicate the upper and lower bounds for total detection error for coherent state illumination (which later will be shown to coincide with the bounds for quantum-enhanced noise radar to within the resolution of the figure).
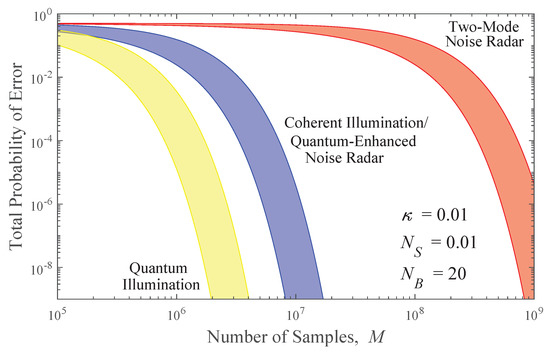
Figure 3.
Bounds on total probability of error in target detection using coherent state illumination or quantum enhanced noise radar (blue), quantum illumination (yellow), and two-mode noise radar (red). The upper and lower bounds are indicated by solid lines with matching shading in between.
A second important example is the Bhattacharya distance for quantum illumination [14]. That approach to target detection is similar to quantum-enhanced noise radar insofar as it uses a two-mode squeezed vacuum state. However, it differs in that the idler field is held in a quantum memory until a joint measurement can be made of the idler and received fields. Although the general expression is lengthy, in the regime where , , and , and assuming optimal quantum reception, the Bhattacharya distance is approximately
In the same regime, the distance for coherent state illumination given by Equation (22) is approximately one quarter of this value. Because of this advantage in the Bhattacharya distance, quantum illumination, given enough measurements, can have an error probability orders of magnitude lower than any classical target detection scheme. This advantage is apparent in Figure 3 where the probability of error for quantum illumination lies in the yellow region bounded by Equation (22) and Equation (21). Of course, some practical difficulties are not captured in this model that hinder full realization of this advantage. For example, the experimental implementation of the optimal joint measurement of the saved idler and the received field is non-trivial [23,24]. Nonetheless, this result may be interpreted as a bound on the advantage that may be obtained, in principle, by optimally exploiting the two-mode squeezed vacuum.
The definition of the Bhattacharya distance in Equation (20) can be applied directly to the densities of Equations (14), (15), and (19). For quantum-enhanced noise radar, the surprisingly concise result is
when , , and , i.e., the regime where quantum illumination offers a significant advantage over classical approaches, the value becomes approximately
which closely matches the distance in Equation (22) for idealized coherent state illumination in this regime [14]. In Figure 3, the probability of error for quantum-enhanced noise radar lies in the blue region and coincides with that of coherent illumination to within the resolution of the figure.
For the two-mode noise radar, the classical scheme most similar to quantum-enhanced noise radar, the Bhattacharya distance is
This expression is too unwieldy to glean much insight from direct inspection. However, in Figure 3, where the probability of error for two-mode noise radar lies in the red region, the orders-of-magnitude advantage of quantum-enhanced noise radar is manifest.
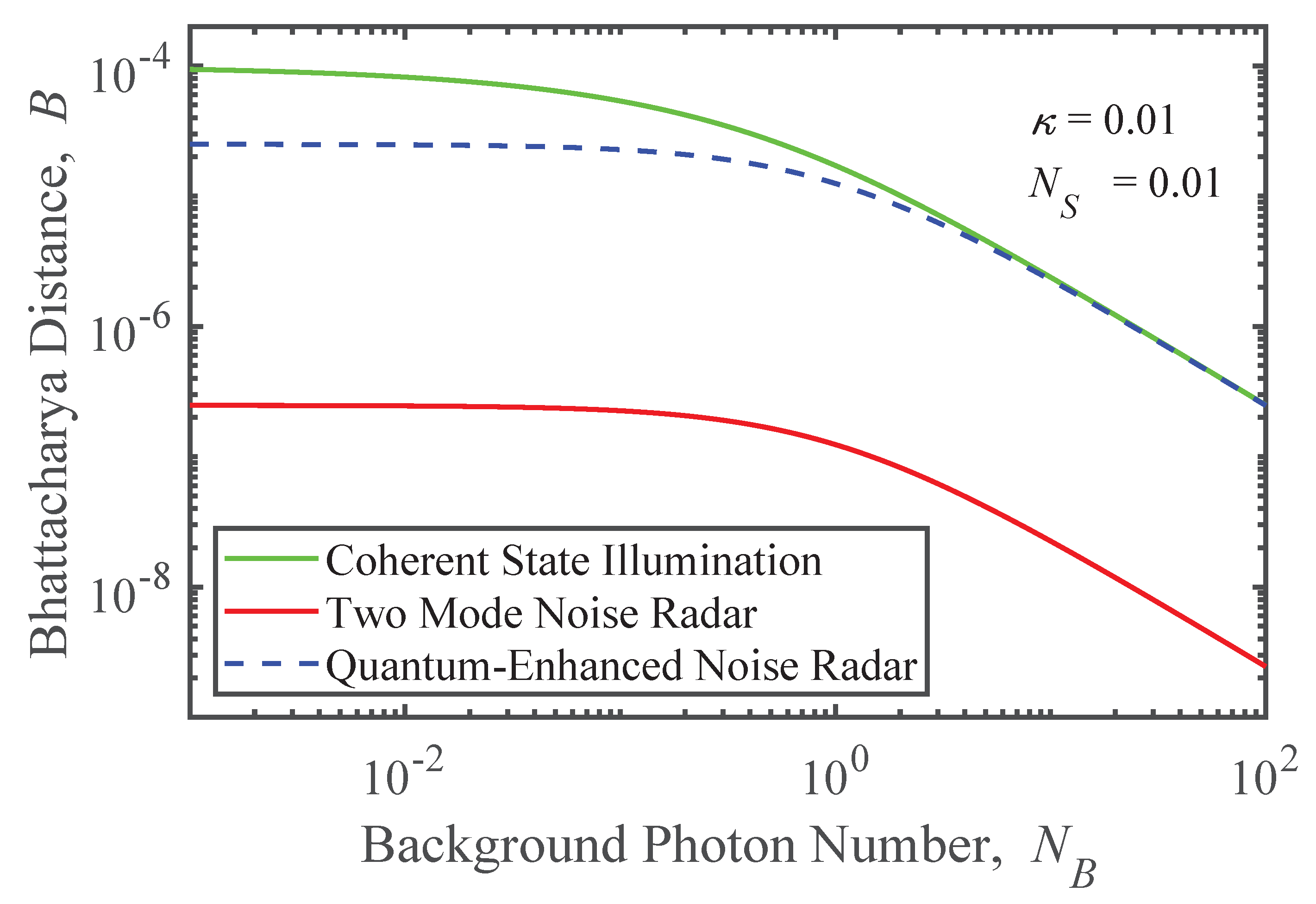
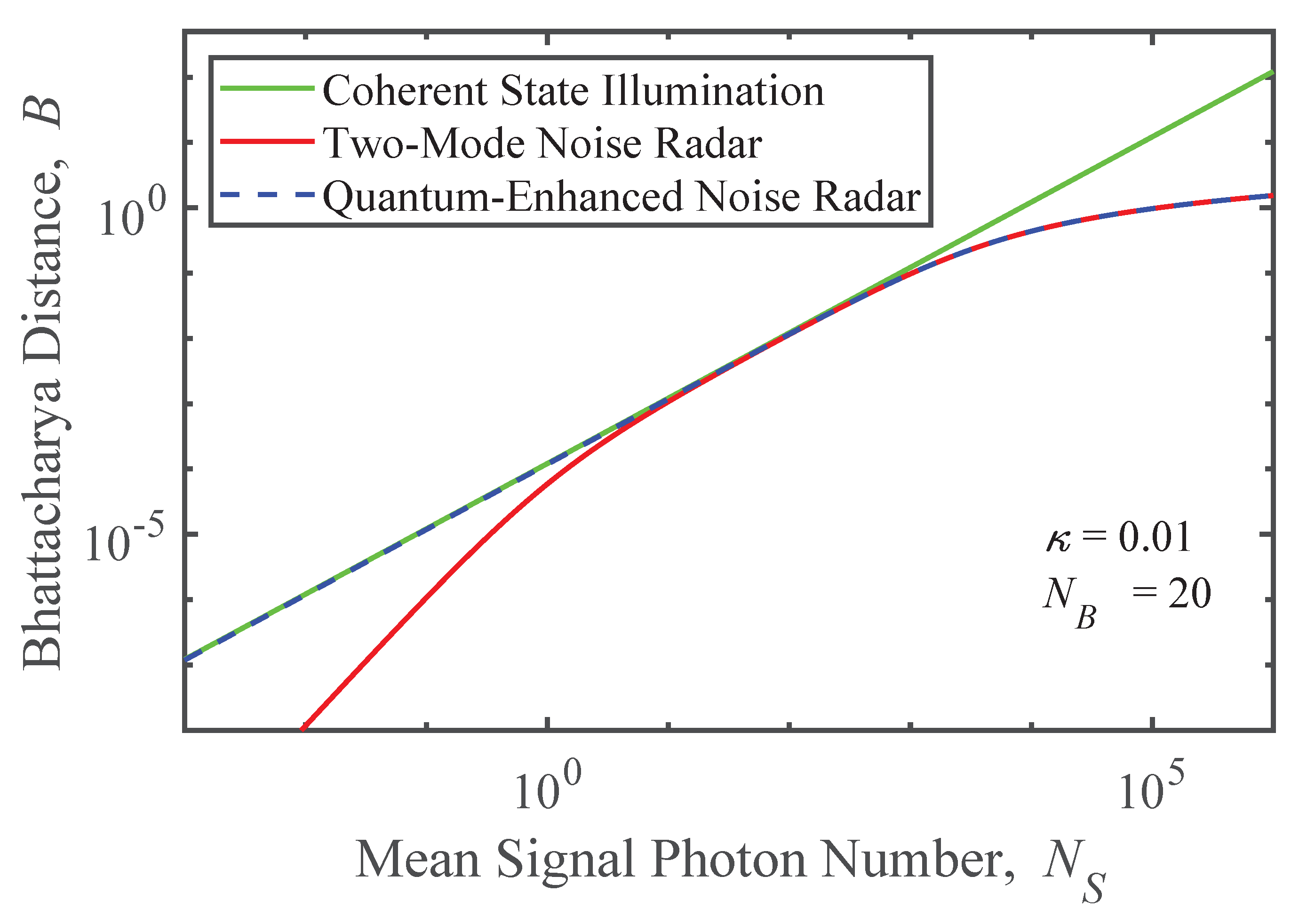
Further insight can be gained from varying the parameters in Equations (22), (24) and (26) beyond the regime of validity of Equation (23). Figure 4 shows the Bhattacharya distances for coherent state illumination (green), two-mode noise radar (red), and quantum-enhanced noise radar (blue dashed) as functions of the mean background noise photon number, , when and . When , all distances decline monotonically as the background noise increasingly dominates the signal field. The distance for quantum-enhanced noise radar closely approaches that of coherent state illumination, while the advantage over two-mode radar is a fixed multiplicative factor. At the other extreme, when , all three curves flatten as the background becomes effectively a vacuum state.
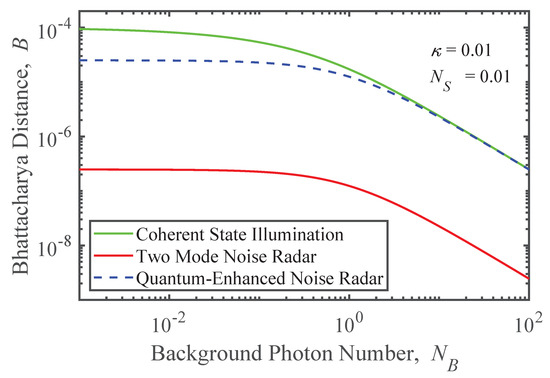
Figure 4.
Bhattacharya distance as a function of background noise mean photon number for quantum enhanced noise radar (blue), two mode noise radar (red), and coherent state illumination with perfect measurement (green). The blue line is dashed so that it remains visible as it overlaps the other curves.
The ordering of the curves in this limit correlates inversely with the amount of noise inherent to each scheme. The coherent state, being a minimum uncertainty state, has the least noise (quantum or classical). Moreover, its state is assumed to be perfectly measurable. Thus, it is plausible that it would have the largest Bhattacharya distance. The quantum-enhanced noise radar and the two-mode noise radar both have the measurement noise of a minimum uncertainty state plus thermal-like noise proportional to . However, the thermal noise between modes is correlated in the former case and uncorrelated in the latter. This is consistent with the larger Bhattacharya distance for quantum-enhanced noise radar.
Figure 5 similarly shows the Bhattacharya distances for coherent state illumination (green), two-mode noise radar (red), quantum-enhanced noise radar (blue dashed) as functions of the mean signal photon number, , when and . When , the quantum noise of the coherent state is relatively insignificant and the field increasingly resembles a true classical field. In contrast, the two forms of noise radar contain thermal noise that grows with resulting in a smaller Bhattacharya distance and an increased probability of detection errors. At the other extreme, where , the coherent state is dominated by its quantum noise, which is the same magnitude as the measurement noise in the noise radar schemes. Notably, the difference in the strength of correlations in the remaining thermal noise that was noted in Section 3 becomes increasingly important.
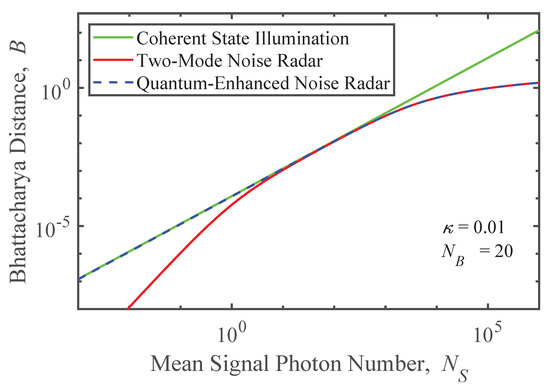
Figure 5.
Bhattacharya distance as a function of mean signal photon number for quantum enhanced noise radar (blue), two mode noise radar (red), and coherent state illumination with perfect measurement (green). The blue line is dashed so that it remains visible as it overlaps the other curves.
5. Discussion
Bounds on the probability of detection error were derived for quantum-enhanced noise radar enabling comparison with alternative quantum and classical schemes. The derivation incorporated the model of loss and noise most widely used in the quantum illumination literature. Additionally, the effect of simultaneous measurements of non-commuting field quadratures was incorporated. Since these measurements introduce additional quantum noise they have direct impact on the fundamental limits of detection sensitivity of quantum-enhanced noise radar. In the regime of a weak signal, weak reflection and a strong background, where quantum illumination provides the most advantage, it was found that quantum-enhanced noise radar is subject to the same bound as an idealized coherent state illumination, which in turn bounds the performance of any classical-state radar scheme.
Quantum-enhanced noise radar was also compared to two-mode noise radar, the most similar classical approach. As has been pointed out previously, this comparison is perhaps of greater practical significance than that with coherent state illumination. A primary motivation for interest in noise radar is its low probability of intercept. Coherent state illumination has no such property. Therefore, it is often not an appropriate candidate for applications of noise radar. The dramatic advantage of quantum-enhanced noise radar over two-mode noise radar demonstrated here may then be the result of most practical importance.
Funding
This research received no external funding.
Acknowledgments
The author gratefully acknowledges discussions with Ned J. Corron and Shawn D. Pethel that were helpful in clarifying aspects of the model presented in this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The probability density in Equation (14) for the output of the quantum-enhanced noise radar receiver when the target is present can be derived from that of Equation (10) for the quadrature measurements as follows. From Equation (10), it can be seen that the joint density for and is
The cumulative probability distribution for the product is then
Invoking the fundamental theorem of calculus, the derivative of Equation (A2) with respect to z is the probability density
where is the zeroth-order, modified Bessel function of the second kind. Similarly, it follows that, for the product ,
where the sign difference in the exponential term reflects the fact that the imaginary quadratures are anti-correlated. The density of Equation (14) corresponding to the difference is simply the convolution of these last two densities, where it is helpful to invoke
which holds for constants , , and c. (This last relation can be verified by taking the Fourier transform of both sides).
References
- Lanzagorta, M. Quantum Radar; Morgan & Claypool: New York, NY, USA, 2012. [Google Scholar]
- Jiang, K.; Lee, H.; Gerry, C.C.; Dowling, J.P. Super-resolving quantum radar: Coherent-state sources with homodyne detection suffice to beat the diffraction limit. J. Appl. Phys. 2013, 114, 193102. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave quantum illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar] [CrossRef]
- Brandsema, M.J.; Narayanan, R.M.; Lanzagorta, M. Theoretical and computational analysis of the quantum radar cross section for simple geometrical targets. Quant. Inform. Process. 2017, 16, 32. [Google Scholar] [CrossRef]
- Chang, C.S.; Vadiraj, A.M.; Bourassa, J.; Balaji, B.; Wilson, C.M. Quantum-enhanced noise radar. Appl. Phys. Lett. 2019, 114, 112601. [Google Scholar] [CrossRef]
- Luong, D.; Chang, C.S.; Vadiraj, A.M.; Damini, A.; Wilson, C.M.; Balaji, B. Receiver operating characteristics for a prototype quantum two-mode squeezing radar. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2041–2060. [Google Scholar] [CrossRef]
- Maccone, L.; Ren, C. Quantum radar. Phys. Rev. Lett. 2020, 124, 200503. [Google Scholar] [CrossRef] [PubMed]
- Barzanjeh, S.; Pirandola, S.; Vitali, D.; Fink, J.M. Microwave quantum illumination using a digital receiver. Sci. Adv. 2020, 6, eabb0451. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.; Zoller, P.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 2008, 321, 1463–1465. [Google Scholar] [CrossRef] [PubMed]
- Luong, D.; Rajan, S.; Balaji, B. Quantum two-mode squeezing radar and noise radar: Correlation coefficients for target detection. IEEE Sens. J. 2020, 20, 5221–5228. [Google Scholar] [CrossRef]
- Luong, D.; Balaji, B. Quantum two-mode squeezing radar and noise radar: Covariance matrices for signal processing. IET Radar Sonar Navig. 2020, 14, 97–104. [Google Scholar] [CrossRef]
- Bowell, R.A.; Brandsema, M.J.; Ahmed, B.M.; Narayanan, R.M.; Howell, S.W.; Dilger, J.M. Electric field correlations in quantum radar and the quantum advantage. In Radar Sensor Technology XXIV (Vol. 11408); International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 114080S. [Google Scholar]
- Tan, S.H.; Erkmen, B.I.; Giovannetti, V.; Guha, S.; Lloyd, S.; Maccone, L.; Pirandola, S.; Shapiro, J.H. Quantum illumination with Gaussian states. Phys. Rev. Lett. 2008, 101, 253601. [Google Scholar] [CrossRef] [PubMed]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Pace, P.E. Detecting and Classifying Low Probability of Intercept Radar; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Lvovsky, A.I. Squeezed light. In Photonics: Scientific Foundations, Technology and Applications; Andrews, D.L., Ed.; Wiley: New York, NY, USA, 2015; pp. 121–163. [Google Scholar]
- Leonhardt, U. Measuring the Quantum State of Light; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Scott, A.J.; Milburn, G.J. Quantum nonlinear dynamics of continuously measured systems. Phys. Rev. A 2001, 63, 042101. [Google Scholar] [CrossRef]
- Guha, S.; Erkmen, B.I. Gaussian-state quantum-illumination receivers for target detection. Phys. Rev. A 2009, 80, 052310. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition, 2nd ed.; Academic Press: Boston, MA, USA, 1990. [Google Scholar]
- Lopaeva, E.D.; Berchera, I.R.; Degiovanni, I.P.; Olivares, S.; Brida, G.; Genovese, M. Experimental realization of quantum illumination. Phys. Rev. Lett. 2013, 110, 153603. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Tengner, M.; Zhong, T.; Wong, F.N.; Shapiro, J.H. Entanglement’s benefit survives an entanglement-breaking channel. Phys. Rev. Lett. 2013, 111, 010501. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).