Generation of Entanglement between Two Two-Level Atoms Coupled to a Microtoroidal Cavity Via Thermal Field
Abstract
1. Introduction
2. Theoretical Model
3. Entanglement Dynamics between the Two Atoms
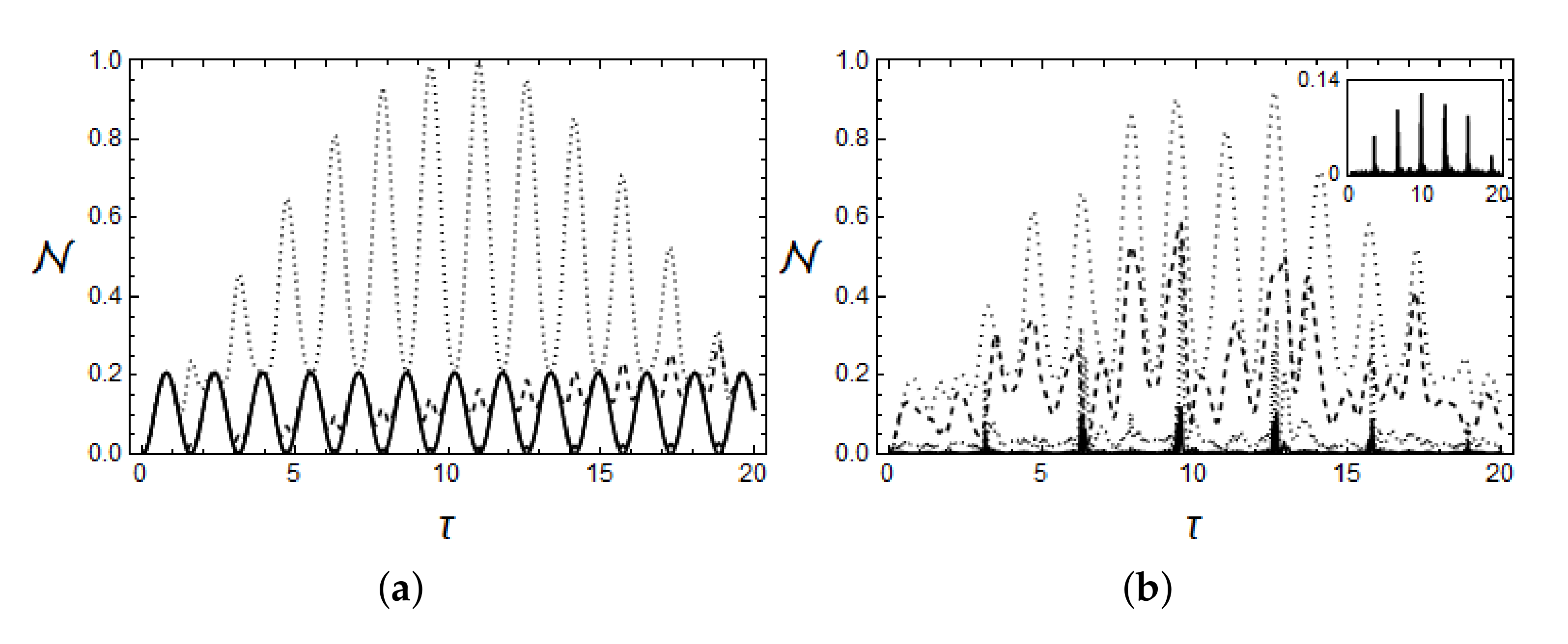
3.1. Two Atoms Coupled to an Ideal Resonator (J = 0)
3.2. Two Atoms Coupled to a Non-Ideal Resonator (J ≠ 0)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Walther, H.; Varcoe, B.T.H.; Englert, B.G.; Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 2006, 69, 1325–1382. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281–324. [Google Scholar] [CrossRef]
- Thompson, J.K.; Simon, J.; Loh, H.; Vuletić, V. A high-brightness source of narrowband, identical-photon pairs. Science 2006, 313, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Plenio, M.B.; Knight, P.L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 1998, 70, 101–144. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F.; Beige, A.; Knight, P.L. Cavity-loss-induced generation of entangled atoms. Phys. Rev. A 1999, 59, 2468–2475. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Xiao, M. Entangling Two Macroscopic Mechanical Resonators at High Temperature. Phys. Rev. Appl. 2020, 13, 034030. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, J.; Ahn, D.; Knight, P.L. Entanglement induced by a single-mode heat environment. Phys. Rev. A 2002, 65, 040101. [Google Scholar] [CrossRef]
- Galve, F.; Pachón, L.A.; Zueco, D. Bringing Entanglement to the High Temperature Limit. Phys. Rev. Lett. 2010, 105, 180501. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Fuentes-Guridi, I.; Knight, P.L.; Vedral, V. Subsystem Purity as an Enforcer of Entanglement. Phys. Rev. Lett. 2001, 87, 050401. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, L.S.; Munhoz, P.P.; Vidiella-Barranco, A.; Roversi, J.A. The entanglement of two dipole–dipole coupled atoms in a cavity interacting with a thermal field. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S769–S771. [Google Scholar] [CrossRef]
- Spillane, S.M.; Kippenberg, T.J.; Painter, O.J.; Vahala, K.J. Ideality in a Fiber-Taper-Coupled Microresonator System for Application to Cavity Quantum Electrodynamics. Phys. Rev. Lett. 2003, 91, 043902. [Google Scholar] [CrossRef]
- Spillane, S.; Kippenberg, T.; Vahala, K. Ultralow-threshold Raman laser using a spherical dielectric microcavity. Nature 2002, 415, 621–623. [Google Scholar] [CrossRef]
- Li, P.B.; Gao, S.Y.; Li, F.L. Quantum-information transfer with nitrogen-vacancy centers coupled to a whispering-gallery microresonator. Phys. Rev. A 2011, 83, 054306. [Google Scholar] [CrossRef]
- Song, W.; Yang, W.; Chen, Q.; Hou, Q.; Feng, M. Entanglement dynamics for three nitrogen-vacancy centers coupled to a whispering-gallery-mode microcavity. Opt. Express 2015, 23, 13734–13751. [Google Scholar] [CrossRef]
- Shen, L.T.; Yang, Z.B.; Wu, H.Z.; Chen, X.Y.; Zheng, S.B. Control of two-atom entanglement with two thermal fields in coupled cavities. J. Opt. Soc. Am. B 2012, 29, 2379–2385. [Google Scholar] [CrossRef]
- Sousa, E.H.; Roversi, J. The role of dipole-dipole interaction and the scattering strength in entanglement dynamics between atoms surrounding a microtoroidal cavity. Eur. Phys. J. Plus 2019, 134, 607. [Google Scholar] [CrossRef]
- Rahachou, A.I.; Zozoulenko, I.V. Effects of boundary roughness on a Q factor of whispering-gallery-mode lasing microdisk cavities. J. Appl. Phys. 2003, 94, 7929–7931. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Modal coupling in traveling-wave resonators. Opt. Lett. 2002, 27, 1669–1671. [Google Scholar] [CrossRef] [PubMed]
- Dayan, B.; Parkins, A.; Aoki, T.; Ostby, E.; Vahala, K.; Kimble, H. A photon turnstile dynamically regulated by one atom. Science 2008, 319, 1062–1065. [Google Scholar] [CrossRef]
- Aoki, T.; Parkins, A.S.; Alton, D.J.; Regal, C.A.; Dayan, B.; Ostby, E.; Vahala, K.J.; Kimble, H.J. Efficient Routing of Single Photons by One Atom and a Microtoroidal Cavity. Phys. Rev. Lett. 2009, 102, 083601. [Google Scholar] [CrossRef]
- Sousa, E.H.S.; Roversi, J.A. Selective Engineering for Preparing Entangled Steady States in Cavity QED Setup. Quantum Rep. 2019, 1, 63–70. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Jozsa, R. Fidelity for Mixed Quantum States. J. Mod. Opt. 1994, 41, 2315–2323. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, E.H.S.; Roversi, J.A. Generation of Entanglement between Two Two-Level Atoms Coupled to a Microtoroidal Cavity Via Thermal Field. Quantum Rep. 2020, 2, 343-351. https://doi.org/10.3390/quantum2030024
Sousa EHS, Roversi JA. Generation of Entanglement between Two Two-Level Atoms Coupled to a Microtoroidal Cavity Via Thermal Field. Quantum Reports. 2020; 2(3):343-351. https://doi.org/10.3390/quantum2030024
Chicago/Turabian StyleSousa, Emilio H. S., and J. A. Roversi. 2020. "Generation of Entanglement between Two Two-Level Atoms Coupled to a Microtoroidal Cavity Via Thermal Field" Quantum Reports 2, no. 3: 343-351. https://doi.org/10.3390/quantum2030024
APA StyleSousa, E. H. S., & Roversi, J. A. (2020). Generation of Entanglement between Two Two-Level Atoms Coupled to a Microtoroidal Cavity Via Thermal Field. Quantum Reports, 2(3), 343-351. https://doi.org/10.3390/quantum2030024




