Abstract
The ideas of classical communication and holographic encoding arise in different parts of physics. Here, we show that they are equivalent. This allows for us to reformulate the holographic principle independently of spacetime, as the principle that holographic screens encode interaction eigenvalues.
1. Introduction
The idea that classical information can be encoded on a holographic screen originated in black-hole (BH) physics [1,2] and it remains of interest primarily in the context of quantum gravity [3,4]. The idea that quantum systems can be restricted to interacting via a classical information channel arises in the theories of measurement [5,6] and decoherence [6,7]. An information channel and, hence, any communication employing such a channel, is classical if and only if the exchanged information is fully fungible, i.e., encodable in a finite bit string [8]. Classical channels are relevant whenever classical communication is included within a broader operational protocol, e.g., in a local operations, classical communication (LOCC) protocol [9]. Studies of parallel quantum and classical communication, however, involve multipartite decompositions, e.g., into agents Alice and Bob, a shared quantum system, a shared classical channel, shared, non-fungible reference frames, and a shared environment that provides free energy and absorbs waste heat. Hence, they require explicit consideration of a large number of distinct physical interactions [10,11]. Therefore, in what follows, we restrict our attention to simple, bipartite decompositions in which two quantum systems A and B interact exclusively with each other via a single, shared, classical information channel.
Here, we study, in this simple bipartite setting, the relationship between the seemingly-disparate ideas of holographic screens and classical information channels, and show that they are, in fact, equivalent: holographic screens are classical information channels and vice-versa. Any physical situation involving classical communication can, in particular, be reformulated as a situation in which the communicating entities are separated by, and encode information on, a holographic screen. If the classical information channel is considered ancillary to the physics of the communicating systems, as in practice it generally is, then the equivalent holographic screen is also ancillary, i.e., the interaction does not depend on its spatial coordinates. Hence, our result effectively generalizes the holographic principle (HP) from a principle stated in spacetime [1,2,3,4] to a principle stated independently of spacetime (see [12] for further details). However, situations in which systems occupying distinct regions of spacetime that are separated by a holographic screen, e.g., the interior and exterior of a BH, can be similarly reformulated as situations in which their physical interaction is confined to a classical information channel.
Let U be an isolated, finite quantum system (i.e. the Hilbert space has finite dimension d) and be a bipartite decomposition that satisfies the separability condition at least up to some recoherence time that is long with respect to other times of interest. Classical communication between A and B clearly requires such separability; if is an entangled state, A and B by definition cannot exchange classical, i.e., fungible information. Moreover, the separability of is, in this situation, also sufficient to restrict A and B to classical communication. The overall Hamiltonian can be written as , where the last term fully specifies the interaction. This interaction is, because d is finite, fully specified by a finite set of real, finite-resolution eigenvalues and, hence, by a finite bit string. Therefore, we can regard A and B as exchanging finite bit strings via an ancillary channel, i.e., a channel with degrees of freedom on which does not depend. It is natural, in this case, to regard A as “observing” B and vice-versa. Zurek has termed the encoding of such bit strings by an “observing” environment “einselection” [7,13]. The locus of einselection is the locus of interaction, i.e., the nominal boundary at which is defined. We show below that the exchanged bits can in this case be regarded as written on, and read from, an intervening, ancillary holographic screen located at this boundary.
We begin by reviewing the implementation of classical communication by , and show that any classical channel can be implemented by an ancillary qubit array. We assume the HP in its covariant form [3] as a fundamental principle of physics, and use it to relate the width in bits of either timelike and lightlike classical channels to areas on which the transmitted information is encoded; these areas are ancillary if the channels are ancillary. We then state and prove our main result relating bipartite separability, classical communication, and holographic encoding. This allows for us to reformulate the holographic principle without reference to an embedding in spacetime, as the principle that holographic screens encode interaction eigenvalues. We briefly discuss three implications of this equivalence: (i) channel serialization induces decoherence; (ii) net mass-energy flows between A and B can either increase or decrease channel width; and, (iii) the channel width decreases as for systems embedded in a surrounding environment in which they have a non-ancillary spacelike separation r.
2. Implementation of Classical Communication by
The associativity of the Hilbert-space tensor product ⊗ (equivalently, the additivity of the Hamiltonian) renders bipartite decompositions completely general: given any bipartite decomposition , the interaction is independent of further decompositions of A or B. Any physical situation involving many interacting components can, therefore, without a loss of generality be described as a set of bipartite interactions between single systems and their complements . In order to characterize any such interaction as classical communication, we require separability, as discussed above: . With this assumption and finite d, we can assume has n eigenvalues, each of which can be represented with m bits, such that , d the dimension of , as above. The interaction can then be fully specified with N bits. Following [10,11,12], we choose a basis in which:
where or B, the are Hermitian operators with eigenvalues in , the are such that , is Boltzmann’s constant, is k’s temperature, and ln 2 is an inverse measure of k’s thermodynamic efficiency that depends on the internal dynamics . The are traditionally regarded as (binary) “measurement” operators that can be considered “questions to nature” with one-bit answers [14]; this interpretation depends critically on the separability of , without which the concepts of “question” and “answer” and, hence, of “measurement” are meaningless [15]. In this separable setting in which interaction can be considered classical communication, it is natural to think of as measuring the computational resources required for k to process one-bit [11].
Communication between A and B being classical implies that exchanged bits are irreversibly sent and received; hence, each bit incurs a thermodynamic cost of [16]. If transferring N bits requires time , the action is:
where . Here, and the channel is both symmetric and parallel in units of . The thermodynamic entropy of A as measured by B is, therefore, N bits, as is the thermodynamic entropy of B as measured by A. However, note that A cannot measure the entanglement entropy of B, as A has no observational access to . As is separable, the entanglement entropy of the decomposition is, by definition, zero.
The communication channel defined by (1) and (2) is ideal by definition: no energy is lost, and no third system exists to contribute noise [11]. The channel has no degrees of freedom on which depends, and, in particular, no spatial degrees of freedom on which depends; hence, it is entirely ancillary. As a concrete implementation of an ideal, ancillary classical information channel with fixed bandwidth, consider an array of N mutually-non-interacting qubits, as shown in Figure 1. Here, the operators each implement z-spin operators either as preparation or measurement; we assume equal efficiencies and equivalent z-spin reference frames for A and B a priori [10]. We can view each qubit in the array as sequentially prepared by A and then measured by B during a time step of duration , and then prepared by B and measured by A during the next time step of duration . This alternating interaction is effectively bipartite; letting C be the channel, A effectively prepares , and then B effectively measures . This entanglement swap induces decoherence [17], as discussed in Section 5.1 below, confirming that any such channel is classical.
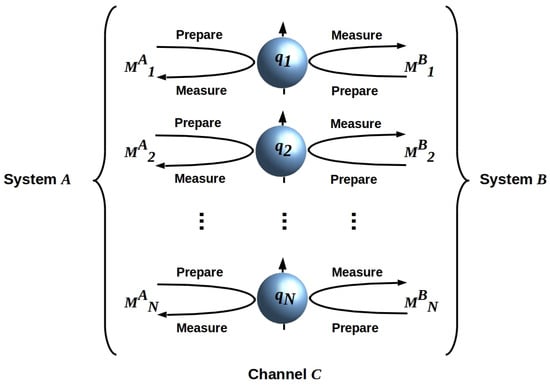
Figure 1.
An N-qubit array serving as a classical channel C between A and B. The two systems alternate preparing and measuring the state of the array.
It is natural to interpret the qubit array in Figure 1 as an input/output register via which two quantum computers, A and B, communicate. Because A and B interact by preparing and then measuring, using equivalent reference frames, the states of the qubits in the register, their interaction is classical.
3. Timelike and Lightlike Communication Channels
The Hamiltonian (1) describes an interaction between spin-like degrees of freedom, with no dependence on the spatial degrees of freedom. However, any realistic classical channel must be physically implemented [18], e.g., by photons. The HP specifies a minimal area, i.e., a minimal set of spatial degrees of freedom, for any such physically-implemented channel; an N-qubit array such, as shown in Figure 1, requires a minimal area of , the Planck length [3,4]. These spatial degrees of freedom remain strictly ancillary to (1); they are, however, effectively incorporated into the sending system by the receiving system as above. Hence, they induce decoherence.
Let us first consider an ideal, unidirectional, purely-timelike channel, corresponding to an ideal classical memory that B writes N-bit strings on at t and A reads N-bit strings from at some , . As A and B, in this case, only have timelike separation, it is natural to interpret them as alternating "snapshots" of a single system writing on and reading from its ideal, internal, classical memory. Special relativity restricts the information written on the memory at t to the past light cone of the memory. The HP in its covariant form [3],
with the classical, thermodynamic entropy of any light-sheet of the (spacelike) boundary of the channel C and the area of the boundary in Planck units, relates the quantity of this writable classical information to the area of the memory written on. Consistent with the discussion above, the classical information holographically encoded on tells an external observer nothing about the entanglement entropy of the system contained within ; the relationship between these two entropies remains an open question [19,20]. Indeed, in this covariant formulation of the HP, it is not even necessary that be closed [3]. As shown in Figure 2a, when only considering the upward arrows, the same holographic considerations apply to the process of reading from the memory: the obtained information can only flow into the forward light cone of the memory. A and B both experience causality when interacting with this channel; for both systems, information flows from the past and into the future.
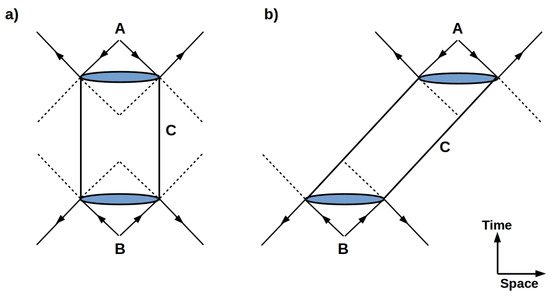
Figure 2.
The holographic principle relates the quantity of information writable on or readable from a channel to its spacelike area. (a) a purely-timelike channel, e.g., an ideal memory. Upward arrows indicate unidirectional B to A information flow; downward arrows indicate A to B information flow. With both sets of arrows, the channel is reversible. Both of the systems experience past-to-future causality in both unidirectional and bidirectional scenarios. (b) a ideal lightlike channel, equivalent to an ideal memory with its input and output surfaces displaced in space.
The downward arrows presented in Figure 2a show A writing on the memory and B reading from it. When considering both sets of arrows, the interaction and, hence, the channel is bidirectional. Provided that reading and writing alternate, as in Figure 1, both systems still experience causality; information flows unidirectionally from past to future when B writes and A reads, and also flows unidirectionally, with the sign of t reversed to capture the alternating action, from past to future when A writes and B reads. Thus, alternating reads from and writes to the memory renders reversibility of the dynamics consistent with irreversible encoding of the received bits.
Figure 2b shows a lightlike communication channel. This channel is equivalent to that in Figure 2a, except the two ends, and, hence, the sending and receiving systems, are separated in space. Here, the natural interpretation is the usual one of spatially-separated observers communicating via an ancillary classical channel. Any such communication channel can, thus, also be considered to be a classical memory; the only difference between timelike and lightlike channels lies in where, in an ancillary space, relative to the writing location, the memory is read. The data encoded by the memory are insufficient for determining this spatial relationship, which, as before, is ancillary to ; therefore, neither a writer on or a reader of the memory can distinguish a timelike from a lightlike channel. We consider in Section 5.3 below the situation in which A and B are embedded in a non-ancillary space, and show that in this case, the channel width decreases with their non-ancillary spacelike separation r.
The width of the channel in time can be decreased to a minimum of . In this case, the channel can be considered to have the structure of Figure 1, with each qubit confined to a minimal voxel with volume .
4. Holographic Screens Encode Interaction Eigenvalues
The considerations above can be summarized by the following:
Theorem 1.
Let be a bipartite decomposition of a finite quantum system U into components A and B. The following statements are equivalent:
- A:
- The state is separable: .
- B:
- The systems A and B communicate via an ideal, ancillary classical information channel with finite capacity.
- C:
- The eigenvalues of the interaction are written on a finite, ancillary holographic screen at the boundary.
Proof.
- A → B:
- ([11] Theorem 1) If A and B are separable, the interaction can be written in the form (1), with the N Hermitian operators , or B, having binary eigenvalues. The interaction at any time t is, in this case, completely specified by an N-bit string. Hence, nothing is lost by replacing the interaction with an exchange of N-bit strings, i.e., with finite-bandwidth classical communication. There are no intervening systems to introduce noise and energy is perfectly conserved; hence the channel is ideal and can be considered to be ancillary.
- B → C:
- A classical information channel can be timelike or lightlike. The information encoded into the channel by A (B) must be within the past lightcone of A’s (B’s) end of the channel, while the information that is received from the channel by A (B) can only flow into the future lightcone of A’s (B’s) end of the channel. These past and future light cones are light-sheets of the two ends of the channel, and define equal areas of the boundaries and of the two channel ends by (3). These boundaries are by definition holographic screens for A and B, respectively. As the only information exchanged through the channel consists of encodings of eigenvalues of , this is the only information on the relevant light-sheets and the only information encoded on the boundaries. The boundaries have no degrees of freedom on which depends; hence, they are ancillary.
- C → B:
- The eigenvalues of have a finite binary encoding, hence the intervening screen has finite area. As it encodes classical information that is accessible to both A and B, it is a classical channel between A and B.
- B → A:
- In order for A and B to exchange finite classical information specifying their states, their states must be well-defined. As , must be separable as .
☐
This equivalence allows us to generalize the HP to the claim that if A and B are components of a finite separable system , they can be regarded as separated by an ancillary holographic screen that classically encodes the eigenvalues of their interaction at a density no greater than one-bit per . This formulation assumes no embedding of A or B into spacetime, so can be regarded as a purely quantum principle that effectively defines the spatial area of the screen in terms of the information it encodes (cf. [12]).
The independence of Theorem 1 from spacetime and, therefore, from geometric considerations is of particular relevance in BH physics. It is standardly assumed that unitarity requires entanglement between a BH and its Hawking radiation and, in consequence, entanglement between early and late Hawking radiation [21,22,23]. If this is the case, the BH and its Hawking radiation constitute, at all times, a single system B in an entangled state . For this state to be observable from the BH exterior A, it must be separable from the state of the exterior, i.e., the joint state must be separable as and, hence, have identically zero entanglement entropy. In this case, Theorem 1 applies, the horizon separating B from A becomes a holographic screen that classically encodes the eigenvalues of , and the HP stipulates that this holographic screen must have area , N the total number of bits required to classically encode the eigenvalues of . However, this holographic screen is not simply connected when observed from A, as a component of the holographic screen surrounds each "particle" (e.g. photon) of Hawking radiation and encodes the eigenvalues of its local interaction with A. This is precisely the situation envisaged in Susskind’s “octopus” model of Hawking radiation, each component of which is connected by an Einstein-Rosen bridge to the parent BH [24].
5. Discussion
Here, we briefly consider three additional straightforward consequences of Theorem 1.
5.1. Serialization Induces Decoherence
In any purely quantum-theoretic setting, classical communication requires decoherence. Theorem 1 shows that holographic screens are resources for decoherence. The decoherence time is the temporal width of the screen, with a minimum of for each observer, as above.
Consider a physically-implemented screen C as in Figure 1, above. Let us drop the assumption that C is ancillary, but require that (the qubits in Figure 1 have no mutual interactions) and that (A and B alternate their interactions with C). In this case, A interacts exclusively with , while B interacts exclusively with . This is an entanglement swap, with C playing the role of the “environment” [17]. The decoherence time is the swap time, with a minimum of , the minimum time required for one complete measurement cycle. As the only role of C here is as a decoherence resource, it is effectively ancillary; the encoded eigenvalues are just the eigenvalues of .
The more interesting case is the one in which A’s operators are deployed in two sequential sets, which can be labeled (dropping the superscript A) and for “environment” and “system” observables, respectively. This is the situation, for example, when A must identify S by distinguishing it from E [25]; clearly, such a distinction requires separability [11]. We can then think of A interacting with B through two sequential, mutually-exclusive channels and . As , the physical situation is again an interaction when the channel is accessed alternating with an interaction when the channel is accessed. The entanglement swap induces decoherence, as above. Angelo et al. [26] provide a detailed analysis of this scenario with A, E, and S all represented by single particles.
5.2. Net Mass-Energy Transfer Alters Channel Width
Classical communication is, by definition, discrete, with a minimal unit of one bit. If the average free energy per received bit that is available to a system k drops below , where, as above, is an inverse thermodynamic efficiency, receiving and irreversibly recording the received bits becomes no longer possible. Therefore, at fixed T, the width of any system’s classical communication channel depends on its inverse efficiency , with the width going to zero, i.e., the channel “evaporating” as . Any system thermodynamically incapable of information processing is thus isolated, undetectable by and irrelevant to the physics of surrounding systems.
Away from thermodynamic equilibrium, net mass-energy flows between A and B. A net transfer of mass-energy X from B to A, e.g., infall of X into a BH A, can be represented as a change in decomposition , where and . As , such a decompositional change alters nothing physically, in particular, it can have no effect on separability or on . Moreover, the idea of a “net” transfer is classical; hence, it also requires separability . Therefore, the interaction can be written in the form (1) and Theorem 1 applies.
The two extreme cases for transfers of X from B to A, and are considered in Figure 3. If and transfers bits (Figure 3a), the post-transfer interaction has a channel width of bits, i.e., the channel width increases by bits with the transfer. This case captures, for example, the situation in which an observer falls from an initially-distant position into a BH [22,23]. However, if and transfer bits (Figure 3b), the post-transfer interaction has a channel width of only N bits, i.e., the channel width decreases by bits with the transfer. This case corresponds to a BH B “evaporating” a particle X with which it has no interaction and is ipso facto not entangled. Non-extremal interactions are intermediate between these cases.
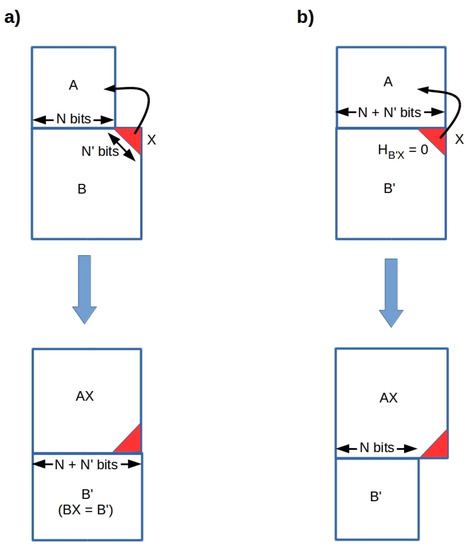
Figure 3.
Net mass-energy transfers from B to A. (a) transferring a system X (red triangle) with which B interacts but A does not increases the horizon width. (b) transferring a system X with which A interacts, but B does not decrease the horizon width.
5.3. Spacelike Separation Decreases Communication Bandwidth
Thus far, we have relaxed the assumption of an ancillary channel or screen only for non-spatial degrees of freedom. We now consider a case in which A and B are embedded in a spacetime with which they interact only by radiating information. We consider, in particular, the case in which A and B are separated by a lightlike channel, as in Figure 2b, but interpret their separation in terms of a physical distance r.
If B send a lightlike message to A, but also radiates information uniformly into a physical embedding space, the horizon area of B’s future-directed light-sheet increases as , as shown in Figure 4. This area contains all possible foci of A’s future-directed light-sheet, the light-sheet that encodes information that A can receive. Hence the width of the B-to-A channel decreases by for , being the purely-timelike case. This is, obviously, simply a consequence of the Divergence Theorem for a uniform flux density. The focal point of A’s future-directed light-sheet plays the role in this construction played by the test mass m in Verlinde’s construction of Newtonian gravity from a holographic screen [27]; here, we do not consider effective masses (proportional to for system k), so only recover the behavior.
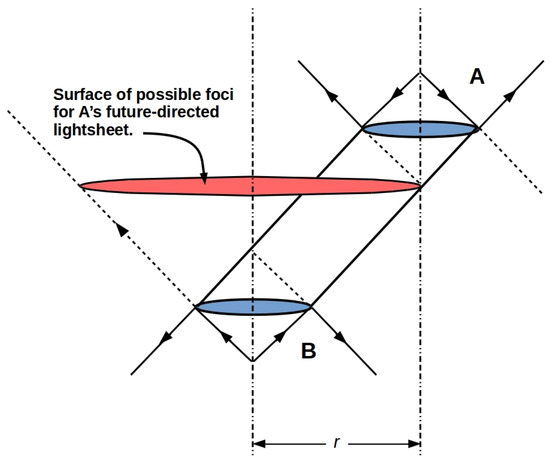
Figure 4.
The area that can be both encoded by future directed light-sheets of B and sampled by future-directed light-sheets of A decreases by , where r is the spacelike separation of A and B.
6. Conclusions
Here we have shown that, given a bipartite decomposition of a finite-dimensional quantum system U that satisfies the separability condition , the interaction can be described as noise-free classical communication via an ancillary information channel, which itself can be represented as a holographic screen with area , N the number of bits required to encode the eigenvalues of . This result generalizes the HP to a purely quantum principle that is independent of spacetime embedding and, hence, of geometry.
We have shown elsewhere that the HP in this generalized form implies gauge invariance [12]; hence, we expect that a generalization of the usual AdS/CFT duality [28] will be possible. Currently, we are investigating the question of how the entanglement entropy within a BH relates to the thermodynamic entropy of the horizon [29]. We defer to future work a full analysis of the BH information paradox [22,23], which requires at least a tripartite decomposition (Alice, the BH, and everything else) for its formulation.
Author Contributions
Conceptualization, C.F. and A.M.; writing—original draft preparation, C.F.; writing—review and editing, C.F. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federico and Elvia Faggin Foundation (CF), the Shanghai Municipality, Grant No. KBH1512299 (AM), and by Fudan University, Grant No. JJH1512105 (AM).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviation is used in this manuscript:
| AdS/CFT | Anti de Sitter/Conformal Field Theory |
| BH | Black hole |
| HP | Holographic Principle |
| LOCC | Local operations, classical communication |
References
- ’t Hooft, G. Dimensional reduction in quantum gravity. In Salamfestschrift; Ali, A., Ellis, J., Randjbar-Daemi, S., Eds.; World Scientific: Singapore, 1993; pp. 284–296. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and information theory. Contemp. Phys. 2004, 45, 31–43. [Google Scholar] [CrossRef]
- Landsman, N.P. Between classical and quantum. In Handbook of the Philosophy of Science: Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 417–553. [Google Scholar]
- Schlosshauer, M. Decoherence and the Quantum to Classical Transition; Springer: Berlin, Germany, 2007. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar] [CrossRef]
- Chitambar, E.; Leung, D.; Mančinska, L.; Ozols, M.; Winter, A. Everything you always wanted to know about LOCC (but were afraid to ask). Comms. Math. Phys. 2014, 328, 303–326. [Google Scholar] [CrossRef]
- Fields, C.; Marcianò, A. Sharing nonfungible information requires shared nonfungible information. Quantum Rep. 2019, 1, 252–259. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F. Representing measurement as a thermodynamic symmetry breaking. Symmetry 2020, 12, 810. [Google Scholar] [CrossRef]
- Addazi, A.; Chen, P.; Fabrocini, F.; Fields, C.; Greco, E.; Lutti, M.; Marcianò, A.; Pasechnik, R. Generalized holographic principle, gauge invariance and the emergence of gravity à la Wilczek. arXiv 2020, arXiv:2004.13751v1. [Google Scholar]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 2005, 72, 042113. [Google Scholar] [CrossRef]
- Wheeler, J.A. Law without law. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton University Press: Princeton, NJ, USA, 1983; pp. 182–213. [Google Scholar]
- Bohr, N. The quantum postulate and the recent development of atomic theory. Nature 1928, 121, 580–590. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Devel. 1961, 5, 183–195. [Google Scholar] [CrossRef]
- Fields, C. Decoherence as a sequence of entanglement swaps. Results Phys. 2019, 12, 1888–1892. [Google Scholar] [CrossRef]
- Landauer, R. Information is a physical entity. Phys. A 1999, 263, 63–67. [Google Scholar] [CrossRef]
- Rovelli, C. Black holes have more states than those giving the Bekenstein-Hawking entropy: A simple argument. arXiv 2017, arXiv:1710:00218. [Google Scholar]
- Rovelli, C. The subtle unphysical hypothesis of the firewall theorem. Entropy 2019, 21, 839. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Susskind, L.; Thorlacius, L. Gedanken experiments involving black holes. Phys. Rev. D 1994, 49, 966–974. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or firewalls? J. High Energy Phys. 2013, 2013, 62. [Google Scholar] [CrossRef]
- Susskind, L. Entanglement is not enough. arXiv 2014, arXiv:1411.0690. [Google Scholar] [CrossRef]
- Fields, C. Some consequences of the thermodynamic cost of system identification. Entropy 2018, 20, 797. [Google Scholar] [CrossRef]
- Angelo, R.M.; Brunner, N.; Popescu, S.; Short, A.J.; Skrzypczyk, P. Physics within a quantum reference frame. J. Phys. A 2011, 2011 44, 145304. [Google Scholar] [CrossRef]
- Verlinde, E. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Maldacena, J. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Chen, P.; Chiang, H.-W.; Fields, C.; Marcianò, A. (Center for Field Theory and Particle Physics & Department of Physics, Fudan University, Shanghai 200433, China). Work in progress.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).