Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive
Abstract
1. Quantum Clouds as Collections of Intertwined Contexts and Their Classical Doubles
- (i)
- a quantum mechanical realization in terms of intertwining orthonormal bases, as mentioned earlier;
- (ii)
- a pseudo-classical realization in terms of partition logic, which in turn have automaton logic or generalized urn models;
- (iii)
- a classical realization if there is only a single context involved;
- (iv)
- none of the above (such as a tightly interlinked “triangle” configuration of three contexts with two vertices per context).
2. Enforcing Classical Two-Valued States
- (I)
- The “measures” or value assignments employed in so-called “contextuality inequalities” merely assume that every proposition is either true or false, regardless of the other propositions in that context, which are simultaneously measurable [32]. This allows all possible possibilities of value assignments in a d-dimensional context with d vertices, thereby vastly expanding the multitude of possible value assignments. With this expansion, all Kochen–Specker sets trivially allow value assignments.
- (II)
- The prevalent assumption of two-valued states or value assignments, also used by Kochen and Specker [19], as well as Pitowsky [33], is that only a single one of the d vertices within a d-dimensional context is true, and all the others are false; therefore, any isolated d-dimensional context can have only d such standard two-valued value assignments.
- (III)
- An even more restricted rule of value assignment abandons uniform definiteness and supposes [11,12,34] that, if all but one vertex in a d-dimensional context are false, the remaining one is true, and if one vertex within a d-dimensional context is true, all remaining vertices are false. These latter value assignments allow for partial functions, which can be undefined.
- (u)
- unital, if for every , there is a two-valued state such that ;
- (s)
- separating, if for every distinct pair of vertices with , there is an such that ;
- (f)
- full, if for every nonadjacent pair of vertices , there is an such that .
3. Chromatic Separability
4. Formation of Gadgets as Useful Subgraphs for the Construction of Clouds
- Zeroth order gadget: a single context (also known as clique/block/Boolean (sub)algebra/ maximal observable/orthonormal basis). This can be perceived as the most elementary form of a true-implies-false (TIFS/10) [14]/01-(maybe better 10)-gadget [50,52] configuration, because a truth/value one assignment of one of the vertices implies falsity/value zero assignments of all the others;
- First order “firefly” gadget: two contexts connected in a single intertwining vertex;
- Second order gadget: two first order firefly gadgets connected in a single intertwining vertex;
- Third order house/pentagon/pentagram gadget: one firefly and one second order gadget connected in two intertwining vertices to form a cyclic orthogonality hypergraph;
5. Quantum Clouds Enforcing Particular Features When Interpreted Classically
- (a)
- (b)
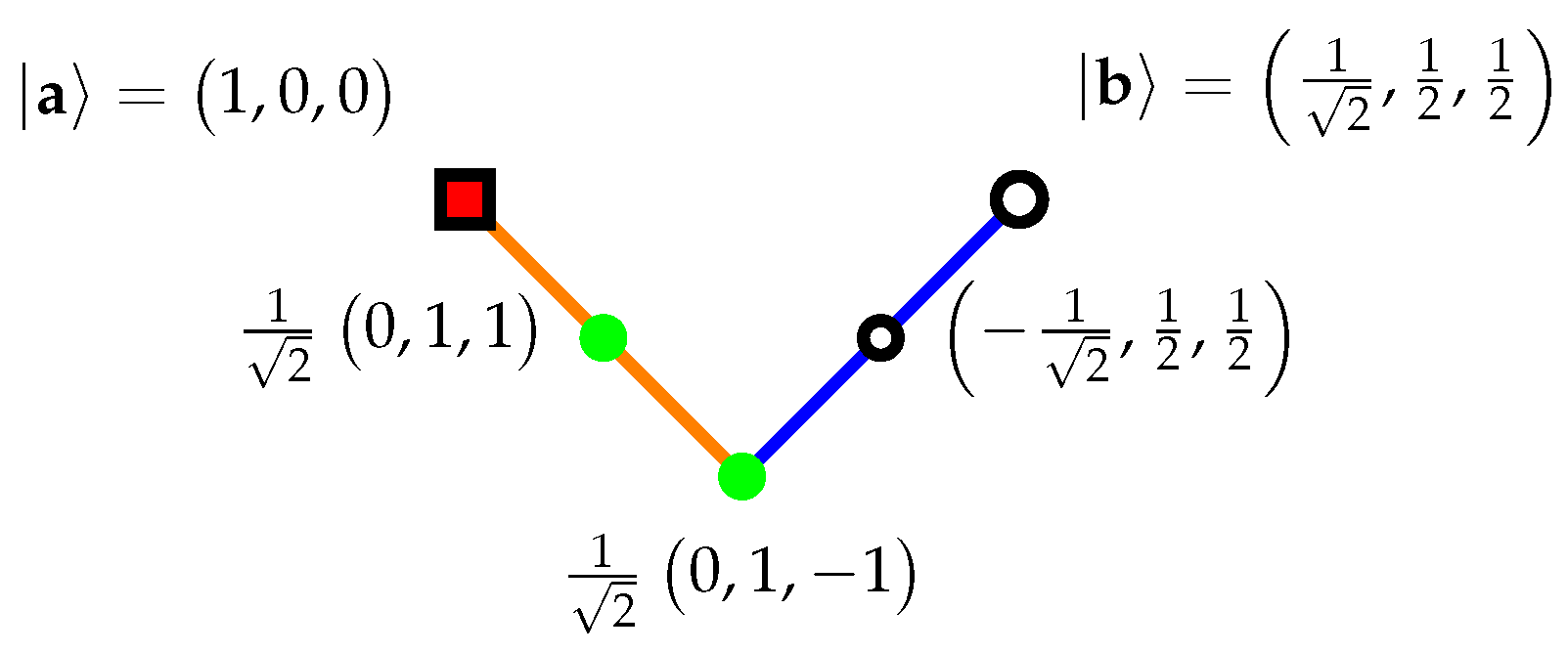
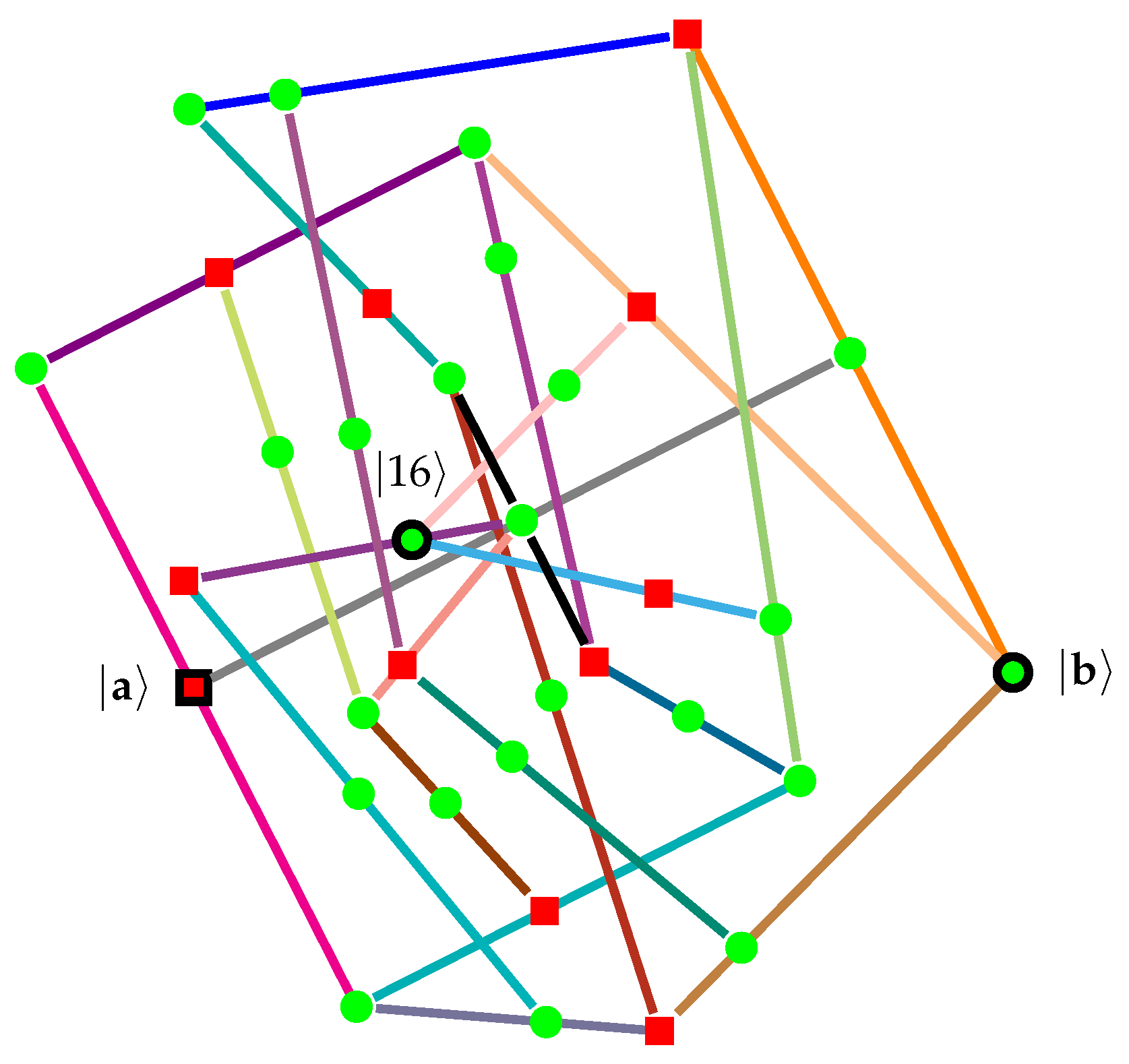
- Already, Kochen and Specker utilized quantum clouds enforcing classical true-implies- false predictions and their compositions in the construction of a configuration that does not allow a uniform truth assignment (of Type (II)). Stairs ([54], pp. 588–589) has pointed out that the Specker bug ([9], Figure 1, p. 182) is a quantum cloud configuration that classically enforces true-implies- false: if a quantum system is prepared in such a way that is true—that is, if it is in the state –and measured along , and and are not orthogonal or collinear, then any observation of given amounts to a probabilistic proof of nonclassicality: because although quantum probabilities do not vanish, classical value assignments predict that never occurs. Minimal quantum cloud configurations for classical true-implies- false, as well as true-implies- true value assignments (of Type (II)) can be found in [14].As Cabello has pointed out [69,70], the original Specker bug configuration cannot go beyond the quantum prediction probability threshold because the angle between and cannot be smaller than radians (). A configuration ([71], Figure 5a) allowing Type (III) TIFS truth assignments with “maximally unbiased” quantum prediction probability is a sublogic of a quantum logic whose realization was enumerated in [12], Table. 1, p. 102201-7. This is depicted in Figure 3. A proof of Theorem 2 in [50] contains an explicit parametrization of a single TIFS/10 cloud allowing the full range of angles .
- (c)
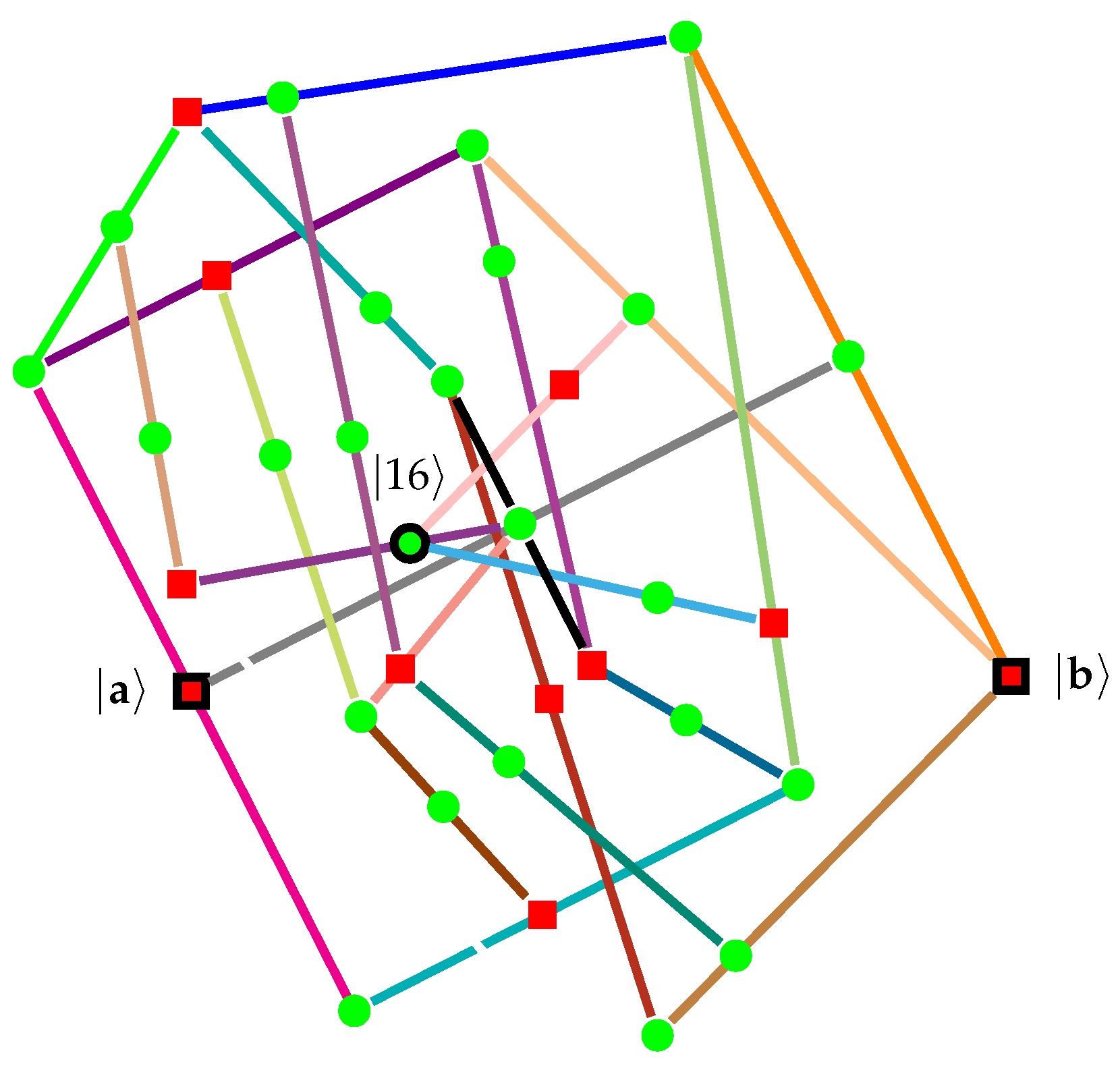
- Clifton (note added in the proof to Stairs ([54], pp. 588–589)) presented a true-implies- true (TITS) cloud ([56,72,73], Sects. II, III, Figure 1) inspired by Bell ([57], Figure C.l. p. 67) (cf. also Pitowsky ([58], p. 394)), as well as by the Specker bug logic ([56], Sects. IV, Figure 2). Hardy [59,60,61], as well as Cabello, among others [50,63,64,65,66,67,69,70], utilized similar scenarios for the demonstration of nonclassicality ([74], Chapter 14). Figure 4 depicts an 11-gadget ([71], Figure 5b) with identical endpoints as the 10-gadget discussed earlier and depicted in Figure 3.
- (d)
- Various parallel and serial compositions of 10- and 11-gadgets serve as a “gadget toolbox” to obtain clouds, which, if they are interpreted classically, exhibit other interesting relational properties. For instance, the parallel composition (pasting) of two quantum clouds of the 10-gadget type: one 10-gadget classically demanding true-implies- false and the other 10-gadget classically demanding true-implies- false, results in a quantum cloud that has two observables and , which are classically always “opposite”: if one is true, the other one is false, and vice versa.
- (e)
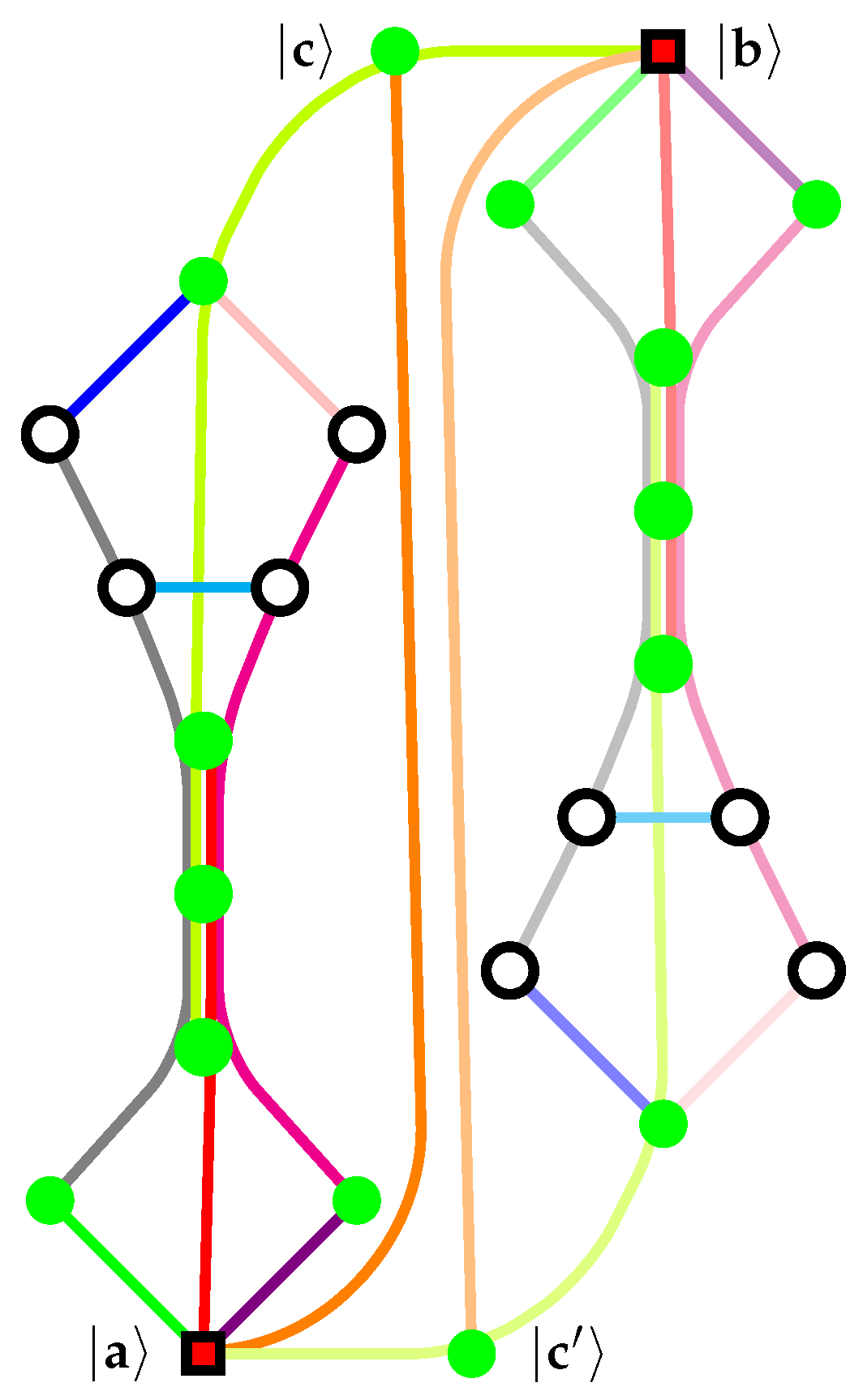
- The parallel composition (pasting) of two quantum clouds of the TITS type, with one TITS, classically demanding true-implies- true and the other TITS classically demanding true-implies- true, results in a quantum cloud that has two observables and , which are classically nonseparable, which is a sufficient criterion for nonclassicality ([19], Theorem 0, p. 67). As pointed out by Portillo [75], this is equivalent to is true if and only if is true (TIFFTS). Figure 5 depicts a historic example of such a construction. The serial composition of suitable TITS of the form true-implies- true-implies- true eventually yields two or more vectors and that are mutually orthogonal; a technique employed by Kochen and Specker for the construction of a quantum cloud admitting no Type (II) truth assignment ([19], , p. 69).
- (f)
- The parallel composition (pasting) of the two quantum clouds that respectively represent a 10-gadget and an 11-gadget and identical endpoints and yields a true-implies- value indefinite cloud discussed in [12].
6. Some Technical Issues of Gadget Construction
7. Discussion
- if the quantum cloud allows both values, then the claim is that there is no determination of the outcome; the event “popped up” from nowhere, ex nihilo, or, theologically speaking, has come about by creatio continua (cf. Kelly James Clark’s God-as-Curler metaphor [76]);
- in the case of a 10-gadget, the system is truly quantum and cannot be classical;
- in the case of an 11-gadget, the system could be classical;
- in the case of a cloud inducing value indefiniteness, the claim can be justified that the system cannot be classical, as no such event (not even its absence) should be recorded. Indeed, relative to the assumptions made, the (non)occurrence of any event at all is in contradiction to the classical predictions.
- as mentioned earlier, if the quantum cloud allows both values, then there exists creatio continua (currently, this appears to be the orthodox majority position);
- in the case of a 10-gadget, the system could be classical;
- in the case of an 11-gadget, the system is truly quantum and cannot be classical;
- just as mentioned earlier, in the case of a cloud inducing value indefiniteness, the claim can be justified that the system cannot be classical, as no such event (not even its absence) should be recorded.
Funding
Acknowledgments
Conflicts of Interest
References
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Everett III, H. ’Relative State’ Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Wigner, E.P. Remarks on the mind-body question. In The Scientist Speculates; Good, I.J., Ed.; Heinemann and Basic Books: London, UK, 1961; New York, NY, USA, 1962; Springer: Berlin, Germany, 1995; pp. 284–302. [Google Scholar] [CrossRef]
- Everett, H., III. The Theory of the Universal Wave Function. In The Everett Interpretation of Quantum Mechanics: Collected Works 1955–1980 with Commentary; Barrett, J.A., Byrne, P., Eds.; Princeton University Press: Princeton, NJ, USA, 2012; pp. 72–172. [Google Scholar]
- Berkeley, G. A Treatise Concerning the Principles of Human Knowledge; Aaron Rhames for Jeremy Pepyat, Bookseller: Skinner–Row, Dublin, 1710. [Google Scholar]
- Stace, W.T. The Refutation of Realism. Mind 1934, 43, 145–155. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. Logical Structures arising in quantum theory. In The Theory of Models: Proceedings of the 1963 International Symposium at Berkeley; North Holland: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1965; pp. 177–189. [Google Scholar]
- Kochen, S.; Specker, E.P. The calculus of partial propositional functions. In Proceedings of the 1964 International Congress for Logic, Methodology and Philosophy of Science, Jerusalem; North Holland: Amsterdam, The Netherlands, 1965; pp. 45–57. [Google Scholar]
- Abbott, A.A.; Calude, C.S.; Conder, J.; Svozil, K. Strong Kochen-Specker theorem and incomputability of quantum randomness. Phys. Rev. A 2012, 86, 062109. [Google Scholar] [CrossRef]
- Abbott, A.A.; Calude, C.S.; Svozil, K. A variant of the Kochen-Specker theorem localising value indefiniteness. J. Math. Phys. 2015, 56, 102201. [Google Scholar] [CrossRef]
- Kleene, S.C. General recursive functions of natural numbers. Math. Ann. 1936, 112, 727–742. [Google Scholar] [CrossRef]
- Cabello, A.; Portillo, J.R.; Solís, A.; Svozil, K. Minimal true-implies-false and true-implies-true sets of propositions in noncontextual hidden-variable theories. Phys. Rev. A 2018, 98, 012106. [Google Scholar] [CrossRef]
- Quisquater, J.J.; Quisquater, M.; Quisquater, M.; Quisquater, M.; Guillou, L.; Guillou, M.A.; Guillou, G.; Guillou, A.; Guillou, G.; Guillou, S. How to Explain Zero-Knowledge Protocols to Your Children. In Advances in Cryptology—CRYPTO’ 89 Proceedings; Brassard, G., Ed.; Springer: New York, NY, USA, 1990; pp. 628–631. [Google Scholar] [CrossRef]
- Specker, E. Die Logik nicht gleichzeitig entscheidbarer Aussagen. Dialectica 1960, 14, 239–246. [Google Scholar] [CrossRef]
- Goldschmidt, T.; Pearce, K.L. Idealism: New Essays in Metaphysics; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Bridgman, P.W. A Physicist’s Second Reaction to Mengenlehre. Scr. Math. 1934, 2, 101–117, 224–234. [Google Scholar]
- Kochen, S.; Specker, E.P. The Problem of Hidden Variables in Quantum Mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Svozil, K. Logical equivalence between generalized urn models and finite automata. Int. J. Theor. Phys. 2005, 44, 745–754. [Google Scholar] [CrossRef]
- Moore, E.F. Gedanken-Experiments on Sequential Machines. In Automata Studies (AM-34); Shannon, C.E., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–153. [Google Scholar]
- Wright, R. The state of the pentagon. A nonclassical example. In Mathematical Foundations of Quantum Theory; Marlow, A.R., Ed.; Academic Press: New York, NY, USA, 1978; pp. 255–274. [Google Scholar]
- Wright, R. Generalized urn models. Found. Phys. 1990, 20, 881–903. [Google Scholar] [CrossRef]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Godsil, C.D.; Newman, M.W. Coloring an Orthogonality Graph. SIAM J. Discret. Math. 2008, 22, 683–692. [Google Scholar] [CrossRef]
- Halmos, P.R. Finite-Dimensional Vector Spaces; Undergraduate Texts in Mathematics; Springer: New York, NY, USA, 1958. [Google Scholar]
- Lovász, L.; Saks, M.; Schrijver, A. Orthogonal representations and connectivity of graphs. Linear Algebra Its Appl. 1989, 114, 439–454. [Google Scholar] [CrossRef]
- Solís-Encina, A.; Portillo, J.R. Orthogonal Representation of Graphs. arXiv 2015, arXiv:1504.03662. [Google Scholar]
- Greechie, R.J. Orthomodular lattices admitting no states. J. Comb. Theory Ser. A 1971, 10, 119–132. [Google Scholar] [CrossRef]
- Navara, M.; Rogalewicz, V. The pasting constructions for orthomodular posets. Math. Nachr. 1991, 154, 157–168. [Google Scholar] [CrossRef]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61. [Google Scholar] [CrossRef]
- Cabello, A. Experimentally Testable State-Independent Quantum Contextuality. Phys. Rev. Lett. 2008, 101, 210401. [Google Scholar] [CrossRef]
- Pitowsky, I. Infinite and finite Gleason’s theorems and the logic of indeterminacy. J. Math. Phys. 1998, 39, 218–228. [Google Scholar] [CrossRef]
- Abbott, A.A.; Calude, C.S.; Svozil, K. Value-indefinite observables are almost everywhere. Phys. Rev. A 2014, 89, 032109. [Google Scholar] [CrossRef]
- Svozil, K.; Tkadlec, J. Greechie diagrams, nonexistence of measures in quantum logics and Kochen–Specker type constructions. J. Math. Phys. 1996, 37, 5380–5401. [Google Scholar] [CrossRef]
- Tkadlec, J. Greechie diagrams of small quantum logics with small state spaces. Int. J. Theor. Phys. 1998, 37, 203–209. [Google Scholar] [CrossRef]
- Boole, G. On the Theory of Probabilities. Philos. Trans. R. Soc. Lond. 1862, 152, 225–252. [Google Scholar] [CrossRef]
- Froissart, M. Constructive generalization of Bell’s inequalities. Il Nuovo Cim. B (1971–1996) 1981, 64, 241–251. [Google Scholar] [CrossRef]
- Tsirelson, B.S. Some results and problems on quantum Bell-type inequalities. Hadron. J. Suppl. 1993, 8, 329–345. [Google Scholar]
- Pitowsky, I. The range of quantum probabilities. J. Math. Phys. 1986, 27, 1556–1565. [Google Scholar] [CrossRef]
- Pitowsky, I. Quantum Probability—Quantum Logic. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1989; Volume 321. [Google Scholar]
- Pitowsky, I. From George Boole to John Bell: The origin of Bell’s inequality. In Bell’s Theorem, Quantum Theory and the Conceptions of the Universe; Kafatos, M., Ed.; Fundamental Theories of Physics; Kluwer Academic Publishers, Springer: Dordrecht, The Netherlands, 1989; Volume 37, pp. 37–49. [Google Scholar] [CrossRef]
- Pitowsky, I. Correlation polytopes their geometry and complexity. Math. Program. 1991, 50, 395–414. [Google Scholar] [CrossRef]
- Pitowsky, I. George Boole’s ‘Conditions of Possible Experience’ and the Quantum Puzzle. Br. J. Philos. Sci. 1994, 45, 95–125. [Google Scholar] [CrossRef]
- Pitowsky, I.; Svozil, K. New optimal tests of quantum nonlocality. Phys. Rev. A 2001, 64, 014102. [Google Scholar] [CrossRef]
- Svozil, K. How much contextuality? Nat. Comput. 2012, 11, 261–265. [Google Scholar] [CrossRef][Green Version]
- Zierler, N.; Schlessinger, M. Boolean Embeddings of Orthomodular Sets and Quantum Logic. In The Logico-Algebraic Approach to Quantum Mechanics: Volume I: Historical Evolution; Hooker, C.A., Ed.; Springer: Dordrecht, The Netherlands, 1975; pp. 247–262. [Google Scholar] [CrossRef]
- Tutte, W.T. A Short Proof of the Factor Theorem for Finite Graphs. Can. J. Math. 1954, 6, 347–352. [Google Scholar] [CrossRef]
- Szabó, J. Good characterizations for some degree constrained subgraphs. J. Comb. Theory Ser. B 2009, 99, 436–446. [Google Scholar] [CrossRef]
- Ramanathan, R.; Rosicka, M.; Horodecki, K.; Pironio, S.; Horodecki, M.; Horodecki, P. Gadget structures in proofs of the Kochen-Specker theorem. arXiv 2018, arXiv:1807.00113. [Google Scholar]
- Svozil, K. Physical [A]Causality. Determinism, Randomness and Uncaused Events; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany; New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Svozil, K. Quantum Scholasticism: On Quantum Contexts, Counterfactuals, and the Absurdities of Quantum Omniscience. Inf. Sci. 2009, 179, 535–541. [Google Scholar] [CrossRef]
- Cohen, D.W. An Introduction to Hilbert Space and Quantum Logic; Problem Books in Mathematics; Springer: New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Stairs, A. Quantum logic, realism, and value definiteness. Philos. Sci. 1983, 50, 578–602. [Google Scholar] [CrossRef]
- Yu, S.; Oh, C.H. State-Independent Proof of Kochen-Specker Theorem with 13 Rays. Phys. Rev. Lett. 2012, 108, 030402. [Google Scholar] [CrossRef]
- Clifton, R.K. Getting contextual and nonlocal elements-of-reality the easy way. Am. J. Phys. 1993, 61, 443–447. [Google Scholar] [CrossRef]
- Belinfante, F.J. A Survey of Hidden-Variables Theories. In International Series of Monographs in Natural Philosophy; Pergamon Press: Oxford, UK; Elsevier: New York, NY, USA, 1973; Volume 55. [Google Scholar] [CrossRef]
- Pitowsky, I. Substitution and Truth in Quantum Logic. Philos. Sci. 1982, 49, 380–401. [Google Scholar] [CrossRef]
- Hardy, L. Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories. Phys. Rev. Lett. 1992, 68, 2981–2984. [Google Scholar] [CrossRef] [PubMed]
- Hardy, L. Nonlocality for two particles without inequalities for almost all entangled states. Phys. Rev. Lett. 1993, 71, 1665–1668. [Google Scholar] [CrossRef] [PubMed]
- Boschi, D.; Branca, S.; De Martini, F.; Hardy, L. Ladder Proof of Nonlocality without Inequalities: Theoretical and Experimental Results. Phys. Rev. Lett. 1997, 79, 2755–2758. [Google Scholar] [CrossRef]
- Cabello, A.; García-Alcaine, G. A hidden-variables versus quantum mechanics experiment. J. Phys. A Math. Gen. Phys. 1995, 28, 3719–3724. [Google Scholar] [CrossRef]
- Cabello, A.; Estebaranz, J.M.; García-Alcaine, G. Bell-Kochen-Specker theorem: A proof with 18 vectors. Phys. Lett. A 1996, 212, 183–187. [Google Scholar] [CrossRef]
- Cabello, A. No-hidden-variables proof for two spin- particles preselected and postselected in unentangled states. Phys. Rev. A 1997, 55, 4109–4111. [Google Scholar] [CrossRef]
- Badzia̧g, P.; Bengtsson, I.; Cabello, A.; Granström, H.; Larsson, J.A. Pentagrams and Paradoxes. Found. Phys. 2011, 41, 414–423. [Google Scholar] [CrossRef]
- Chen, J.L.; Cabello, A.; Xu, Z.P.; Su, H.Y.; Wu, C.; Kwek, L.C. Hardy’s paradox for high-dimensional systems. Phys. Rev. A 2013, 88, 062116. [Google Scholar] [CrossRef]
- Cabello, A.; Badziag, P.; Terra Cunha, M.; Bourennane, M. Simple Hardy-Like Proof of Quantum Contextuality. Phys. Rev. Lett. 2013, 111, 180404. [Google Scholar] [CrossRef]
- Dvurečenskij, A.; Pulmannová, S.; Svozil, K. Partition Logics, Orthoalgebras and Automata. Helv. Phys. Acta 1995, 68, 407–428. [Google Scholar]
- Cabello, A. A simple proof of the Kochen-Specker theorem. Eur. J. Phys. 1994, 15, 179–183. [Google Scholar] [CrossRef]
- Cabello, A. Pruebas Algebraicas de Imposibilidad de Variables Ocultas en Mecánica Cuántica. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 1996. [Google Scholar]
- Svozil, K. New Forms of Quantum Value Indefiniteness Suggest That Incompatible Views on Contexts Are Epistemic. Entropy 2018, 20, 406. [Google Scholar] [CrossRef]
- Johansen, H.B. Comment on “Getting contextual and nonlocal elements-of-reality the easy way”. Am. J. Phys. 1994, 62, 471. [Google Scholar] [CrossRef]
- Vermaas, P.E. Comment on “Getting contextual and nonlocal elements-of-reality the easy way”. Am. J. Phys. 1994, 62, 658. [Google Scholar] [CrossRef]
- Svozil, K. Physical (A)Causality. In Fundamental Theories of Physics; Springer International Publishing: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2018; Volume 192. [Google Scholar] [CrossRef]
- Portillo, J.R. Logical equivalence of nonseparability and “true if and only if” (TIFFTS). Universidad de Sevilla: Sevilla, Spain, 2018; Private Conversation. [Google Scholar]
- Clark, K.J. Is God a Bowler or a Curler? Presented at the Randomness and Providence Workshop, Kalamazoo, MI, USA, 9 May 2017. [Google Scholar]
- Clavadetscher-Seeberger, E. Eine Partielle Prädikatenlogik. Ph.D. Thesis, ETH-Zürich, Zürich, Switzerland, 1983. [Google Scholar]
- Peres, A. Unperformed experiments have no results. Am. J. Phys. 1978, 46, 745–747. [Google Scholar] [CrossRef]

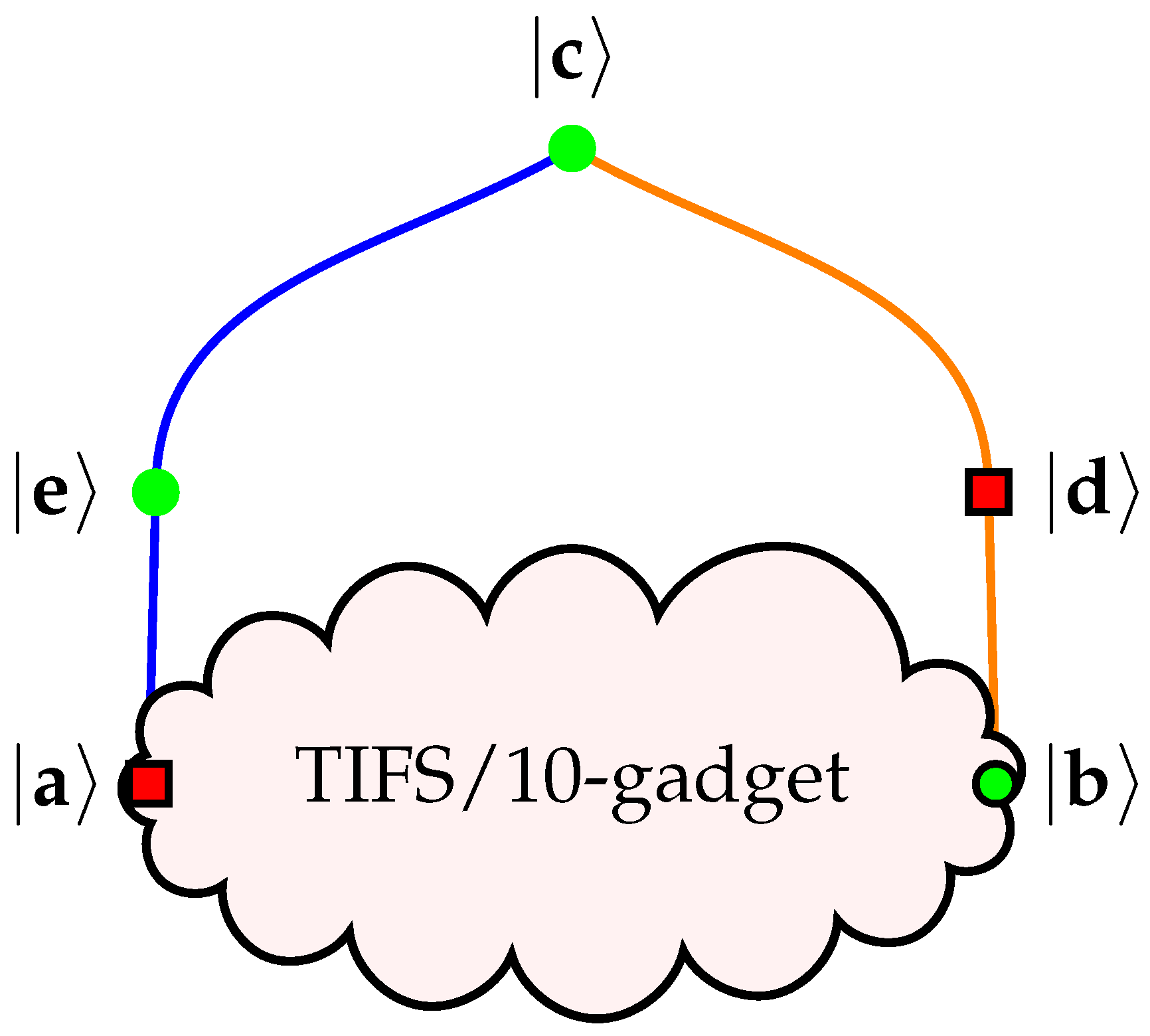
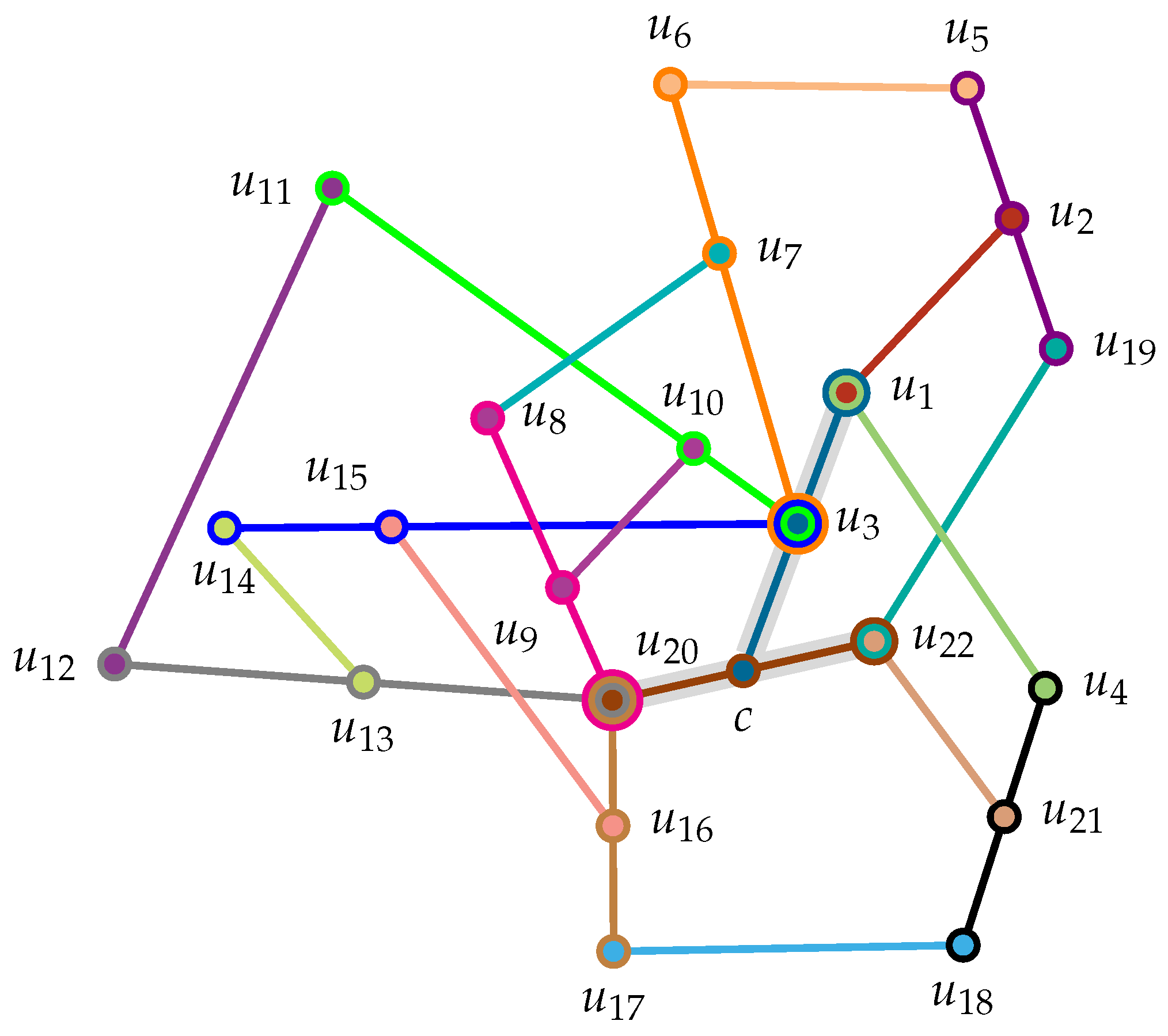
| If A is True Classical Value Assignments | Anecdotal, Historic Quantum Realization | Reference to Utility or Relational Properties |
|---|---|---|
| imply is independent (arbitrary) | firefly logic ([53], pp. 21, 22) | |
| imply false (TIFS/10) | Specker bug logic ([9], Figure 1, p. 182) | ([54], pp. 588–589), [14,55] |
| imply true (TITS) | extended Specker bug logic | ([19], , p. 68), |
| ([56], Sects. II, III, Figure 1), | ||
| ([57], Figure C.l. p. 67), | ||
| ([58], p. 394), [59,60,61], | ||
| [14,62,63,64,65,66,67] | ||
| iff true (nonseparability) | combo of intertwined Specker bugs | ([19], , p. 70) |
| imply value indefiniteness of | depending on Type (II), (III) assignments | [12,33] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svozil, K. Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive. Quantum Rep. 2020, 2, 278-292. https://doi.org/10.3390/quantum2020018
Svozil K. Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive. Quantum Reports. 2020; 2(2):278-292. https://doi.org/10.3390/quantum2020018
Chicago/Turabian StyleSvozil, Karl. 2020. "Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive" Quantum Reports 2, no. 2: 278-292. https://doi.org/10.3390/quantum2020018
APA StyleSvozil, K. (2020). Classical Predictions for Intertwined Quantum Observables Are Contingent and Thus Inconclusive. Quantum Reports, 2(2), 278-292. https://doi.org/10.3390/quantum2020018





