Scattering–Like Control of the Cheshire Cat Effect in Open Quantum Systems

Abstract

We study the Quantum Cheshire Cat effect in an open system coupled to a finite environment. We consider a very special type of coupling—pure dephasing—and show that there is a scattering-like mechanism which can be utilized to construct an open-loop control strategy for the weak values of the Cat and its grin.

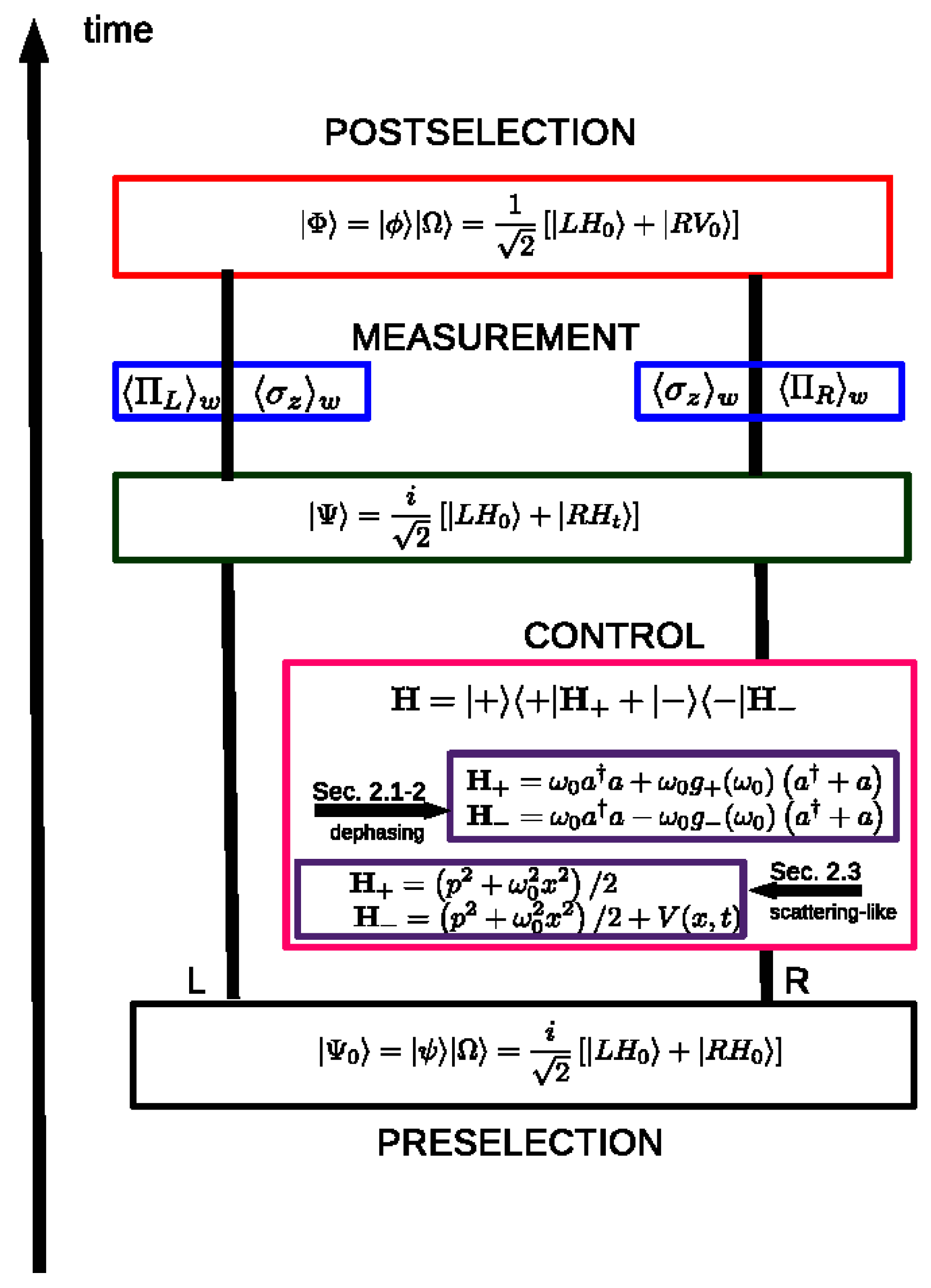
1. Introduction

Quantum weak values [1] attract the increasing attention of physicists who apply them to analyze otherwise difficult problems. Let us mention two examples: The continuous and sometimes controversial discussion what the history of quantum particle really is [2,3] or one of the most spectacular counter-intuitive effects—the Quantum Cheshire Cat [4]. There are many effective methods [5] to design quantum dynamics leading to desired expectation values of certain observables. However, quantum control of weak values needs further attention.

Weak values seem to be of particular usefulness in all the circumstances which require the simultaneous measurement of otherwise non comeasurable observables one applies there the weak measurement scheme [4,6,7]. Both the interpretations and the broad possible applications of the quantum weak values are presented in Refs. [6,7]. Here we simply recall the weak value related to an observable X as

$$\begin{array}{c}\hfill {\langle X\rangle }_w=\frac{\langle \Phi \left|X\right|\Psi \rangle }{\langle \Phi |\Psi \rangle }\end{array}$$

(1)

and utilize its basic interpretation as a change of the detection probability $|\langle \Phi |\Psi \rangle |$ in a presence of a (weak) interaction generated by X. Although the weak value is generically complex, it is a measurable quantity [8]. None of the quantum systems, maybe except the whole Universe, is closed. Consider that a quantum system separated from its environment is always an approximation which is better or worse depending on the detailed circumstances. It is common wisdom that decoherence is to blame for many limitations of, e.g., ‘practical’ quantum computing due to an unavoidable leakage of information from a quantum system into its environment. In this paper, however, we discuss how an environment can help to design a control strategy leading to the desired properties of weak values. We focus on the Cheshire Cat coupled to (or controlled by) an environment attached to an internal degree of freedom, i.e., to ‘a smile’ of the Cat. We consider two exactly solvable cases: The first is a pure decoherence in a presence of an finite bosonic bath, the second, having the same symmetry leading to its exact solvability, is a scattering-like mechanism of interaction between the finite environment and the Cat.

This paper is organized as follows: In the Introduction we review the Cheshire Cat effect in terms of weak values as introduced in Ref. [4] and its modification in the presence of a dephasing environment studied recently in Ref. [9]. In the Results section we study the Cheshire Cat effect controlled by a finite environment consisting of a harmonic oscillator. We study both symmetric and asymmetric dephasing and we introduce scattering-like approximation suitable for non-linear or time-driven systems. Our results compete and extend the discussion provided in Ref. [9] which was solely devoted to infinite baths studied in pure dephasing and almost pure dephasing approximation. Finally we conclude our work.

For the sake of making our discussion self-consistent we review a very basic idea of the Cheshire Cat effect introduced in Ref. [4] and our recent studies [9] of an effect of decoherence. The Quantum Cheshire Cat effect [4] is a separation of internal and ‘external’ degrees of freedom of a quantum particle. For simplicity we assume that both types of degree of freedom are qubits, i.e., that the state space of the system is $\mathcal{H}={\mathbb{C}}^2\otimes {\mathbb{C}}^2=\mathrm{span}\left\{\right|L\rangle ,|R\rangle \}\otimes \mathrm{span}\left\{\right|\leftrightarrow \rangle ,|\updownarrow \rangle \}$ where $L,R$ and $\leftrightarrow ,\updownarrow$ label the ‘external’ and internal degrees of freedom respectively. The archetypal Cheshire Cat [4] effect takes place in a Mach–Zehnder setting with a path ‘chosen’ by the photon—either left L or right R—and photonic polarization—horizontal ↔ or vertical ↕ as presented in Figure 1 of Ref. [4]. Although photonic terminology is invoked, all the considerations of this paper can be applied, at least in principle, to any quantum system with a state space $\mathcal{H}$. Detection of the Cat’s position corresponds to a measurement related to the projectors:

$$\begin{array}{c}\hfill {\mathsf{\Pi }}_L=|L\rangle \langle L|,{\mathsf{\Pi }}_R=|R\rangle \langle R|,\end{array}$$

(2)

whereas a measurement of its grin (an internal degree of freedom) in a given (either left or right) position requires the projectors

$$\begin{array}{c}\hfill {\sigma }_L={\mathsf{\Pi }}_L{\sigma }_z,{\sigma }_R={\mathsf{\Pi }}_R{\sigma }_z,\end{array}$$

(3)

where ${\sigma }_z=|+\rangle \langle +|-|-\rangle \langle -|$ for $|\pm \rangle =\left[\right|\leftrightarrow \rangle \pm i|\updownarrow \rangle ]/\sqrt{2}$. According to the proposal in [4], the system is preselected in

$$\begin{array}{c}\hfill |\psi \rangle =\frac{1}{\sqrt{2}}\left(i|L\leftrightarrow \rangle +|R\leftrightarrow \rangle \right)\end{array}$$

(4)

and postselected in

$$\begin{array}{c}\hfill |\varphi \rangle =\frac{1}{\sqrt{2}}\left(|L\leftrightarrow \rangle +|R\updownarrow \rangle \right).\end{array}$$

(5)

In the meantime, one measures the weak values of Equation (1) and of the quantities Equations (2) and (3), i.e., the weak values of internal and external degrees of freedom. Counterintuitively, one obtains [4]

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w=1,{\langle {\mathsf{\Pi }}_R\rangle }_w=0\end{array}$$

(6)

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w=0,{\langle {\sigma }_R\rangle }_w=1\end{array}$$

(7)

which, according to [4], indicates the separation of internal and external degrees freedom of the considered system and justifies the terminology originating from L. Carroll’s novel Alice’s Adventures in Wonderland adopted in many further studies. The quantities in Equation (2) denote the Cheshire Cat’s position and in Equation (3) the Cheshire Cat’s grin respectively.

One of the first and most natural extensions and modifications of the Cheshire Cat setting introduced recently in Ref. [9] is to attach an environment coupled locally to an internal degree of freedom of the Cheshire Cat (its grin) as presented in Figure 1. The state space enlarges then to a triple $\mathcal{H}={\mathbb{C}}^2\otimes {\mathbb{C}}^2\otimes {\mathcal{H}}_E$. The last term of the tensor product corresponds to an environment E. Let us notice that the state space ${\mathcal{H}}_E$ of an environment, in Ref. [9] assumed to be an infinite bosonic bath, here has no specified dimension yet. Let us emphasize that in the following we assume that the environment E couples to internal degree of freedom (the Cat’s grin) only locally in one of the two sectors L or R. For simplicity, we also assume that prior to any interaction the environment is prepared in a pure state $|\Omega \rangle \in {\mathcal{H}}_E$. The time evolution of the Cat-and-environment system includes the interaction between an environment and the Cat’s grin only. The Cat’s position (external degree of freedom) remains uncoupled to an environment. The time evolution in the ${\mathbb{C}}^2\otimes {\mathcal{H}}_E$ subspace accommodating the Cat’s grin and an environment is given by a unitary (as the total system is assumed closed) operator $U\left(t\right)$ such that

$$\begin{array}{c}\hfill |H_t\rangle =U\left(t\right)|\leftrightarrow \rangle |\Omega \rangle \in {\mathbb{C}}^2\otimes {\mathcal{H}}_E\end{array}$$

(8)

and $U\left(0\right)=\mathcal{I}$ (the identity at $t=0$). Following Ref. [9], we consider one of two noisy preselections: the first, where the internal degree of freedom, the Cat’s grin, is affected by E in a R–sector (right path using photonic terminology),

$$\begin{array}{c}\hfill |{\Psi }_R\rangle =\frac{1}{\sqrt{2}}\left(i|L{H}_0\rangle +|R{H}_t\rangle \right)\in {\mathbb{C}}^2\otimes {\mathbb{C}}^2\otimes {\mathcal{H}}_E\end{array}$$

(9)

and the second, for E affecting the Cat’s grin in the L–sector (left path),

$$\begin{array}{c}\hfill |{\Psi }_L\rangle =\frac{1}{\sqrt{2}}\left(i|L{H}_t\rangle +|R{H}_0\rangle \right)\in {\mathbb{C}}^2\otimes {\mathbb{C}}^2\otimes {\mathcal{H}}_E.\end{array}$$

(10)

Moreover, we assume that the post–selection is not affected by the presence of the environment, i.e., it remains given by

$$\begin{array}{c}\hfill |\Phi \rangle =|\varphi \rangle |\Omega \rangle \in {\mathbb{C}}^2\otimes {\mathbb{C}}^2\otimes {\mathcal{H}}_E\end{array}$$

(11)

with $|\varphi \rangle$ given in Equation (5) as in the original, noiseless proposal formulated in Ref. [4]. The weak values Equation (6)—figure of merit for the Cheshire Cat effect—then become modified by decoherence [9]. With preselection of Equation (9) and

$$\begin{array}{c}\hfill |V_0\rangle =|\updownarrow \rangle |\Omega \rangle \in {\mathbb{C}}^2\otimes {\mathcal{H}}_E,\end{array}$$

(12)

one obtains

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^R=\frac{i}{2N_R},{\langle {\mathsf{\Pi }}_R\rangle }_w^R=\frac{\langle V_0|H_t\rangle }{2N_R}=\frac{\langle V_0|H_t\rangle }{i+\langle V_0|H_t\rangle }\end{array}$$

(13)

for the Cat’s position and

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^R=0,{\langle {\sigma }_R\rangle }_w^R=\frac{\langle V_0\left|{\sigma }_z\right|H_t\rangle }{2N_R}\end{array}$$

(14)

for the Cat’s grin, where

$$\begin{array}{c}\hfill N_R=\langle \Phi |{\Psi }_R\rangle =\frac{1}{2}\left(i+\langle V_0|H_t\rangle \right),N_L=\langle \Phi |{\Psi }_L\rangle =\frac{i}{2}\langle H_0|H_t\rangle .\end{array}$$

(15)

Weak values in Equations (13) and (14) can be interpreted as follows: For the preselected Equation (9), decoherence affects the Cat’s position, originally residing [4] in the (noiseless) L–sector with the grin being solely confined to the R–sector of the system. This is in contrast to that what occurs for the preselection Equation (10). In that case [9] (indicated by the superscript L below), corresponds to a noisy L-sector, originally occupied by the Cat [4], and the Cat’s position remains confined to the L-sector of the system

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^L=\frac{i\langle H_0|H_t\rangle }{2N_L}\equiv 1,{\langle {\mathsf{\Pi }}_R\rangle }_w^L=0,\end{array}$$

(16)

but the Cat’s grin becomes wiped off by decoherence,

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^L=\frac{i\langle H_0\left|{\sigma }_z\right|H_t\rangle }{2N_L},{\langle {\sigma }_R\rangle }_w^L=\frac{i}{2N_R},\end{array}$$

(17)

and appears in both the R– and L–sectors of the system.

Following Ref. [9] we exemplify our discussion using probably the simplest model of decoherence—the pure dephasing model [10,11]. This model is suitable if one operates on the time scales much shorter than (negligible in that case) the energy exchange between the system and its environment [12] and all the formulas below are formally valid with no matter if the environment E is such that one can neglect an energy exchange between the system and its environment [12], and formulas reviewed below are formally valid regardless of a dimension of an environment E being finite or not. For the pure decoherence of the system-environment, Hamiltonian is assumed to have the particular form

$$\begin{array}{c}\hfill \mathbf{H}=|+\rangle \langle +|\otimes {\mathbf{H}}_{+}+|-\rangle \langle -|\otimes {\mathbf{H}}_{-},\end{array}$$

(18)

indicating its highly symmetric block-diagonal structure which simplifies time evolution of the decoherence-affected preselected state. We assume that the initially internal degrees of freedom $\leftrightarrow \rangle ,\updownarrow \rangle$ and an initial state of the environment $|\Omega \rangle$ are separated and read

$$\begin{array}{c}\hfill |V_0\rangle =\frac{i}{\sqrt{2}}\left(|-\rangle -|+\rangle \right)|\Omega \rangle ,\end{array}$$

(19)

$$\begin{array}{c}\hfill |H_0\rangle =\frac{1}{\sqrt{2}}\left(|-\rangle +|+\rangle \right)|\Omega \rangle .\end{array}$$

(20)

For both the preselected Equation (9) and Equation (10), the internal degree of freedom ↔ becomes modified by the decoherence. For any pure decoherence generated by Equation (18) one obtains

$$\begin{array}{c}\hfill |H_t\rangle =\frac{1}{\sqrt{2}}\left(|+\rangle |{\Omega }_t^{+}\rangle +|-\rangle |{\Omega }_t^{-}\rangle \right),\end{array}$$

(21)

where $|{\Omega }_t^{\pm }\rangle =exp(-i{\mathbf{H}}_{\pm }t)|\Omega \rangle$. Hence, an effect of (pure) decoherence on the Cheshire Cat is fully governed by a quantity

$$\begin{array}{c}\hfill Q_{\pm }=\langle \Omega |{\Omega }_t^{+}\rangle \pm \langle \Omega |{\Omega }_t^{-}\rangle ,\end{array}$$

(22)

which is a sum/difference of overlaps between the initial and time-evolving states of the environment and which controllability results in controllability of the weak values for the Cat’s grin and position.

For the ‘noise-affected’ preselected Equation (9), one gets the following weak values for the Cat’s position:

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^R=\frac{1}{1+Q_{-}/2},{\langle {\mathsf{\Pi }}_R\rangle }_w^R=\frac{Q_{-}}{2(1+Q_{-}/2)},\end{array}$$

(23)

and for the Cat’s grin,

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^R=0,{\langle {\sigma }_R\rangle }_w^R=\frac{Q_{+}}{2(1+Q_{-}/2)}.\end{array}$$

(24)

The preselected Equation (9) describes the case when an environment couples to the R–sector of an external degree of freedom, i.e., the one occupied by the grin Equation (6). It is in contrast to the case of the preselection Equation (10) when the environment couples to the L–sector. Such a configuration does not modify the Cat’s position:

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^L=1,{\langle {\mathsf{\Pi }}_R\rangle }_w^L=0,\end{array}$$

(25)

but rather the Cat’s grin now appears in the L–sector:

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^L=Q_{-}/Q_{+},{\langle {\sigma }_R\rangle }_w^L=2/(2+Q_{-}).\end{array}$$

(26)

This is in accordance with our previous conclusion formulated in Ref. [9] that the decoherence attracts the cat for the preselected Equation (9) and the grin for Equation (10) respectively.

2. Results

In this section we apply general considerations reviewed in the Introduction and study the best-known simple models of pure decoherence caused by a bath of bosonic oscillators that affect the grin of the Cheshire Cat, i.e., a bath coupled to an internal degree of freedom of our system. Instead of a full quantum statistical model [11] of a bath consisting of an infinity of oscillators, we consider its finite version, and in all explicit calculations we assume that an internal degree of freedom of the system (the Cat’s grin) couples to a single oscillator as presented in Figure 1.

2.1. Symmetric Dephasing

Typically, pure decoherence or dephasing models [11,13] are described by a linear coupling of a system to a bosonic bath:

$$\begin{array}{c}\hfill {\mathbf{H}}_{\pm }={\int }_0^{\infty }d\omega h\left(\omega \right)a^{†}\left(\omega \right)a\left(\omega \right)\pm {\int }_0^{\infty }d\omega h\left(\omega \right)g_{\pm }\left(\omega \right)\left(a^{†}\left(\omega \right)+a\left(\omega \right)\right),\end{array}$$

(27)

where $h\left(\omega \right)$ describes spectral properties of the bath [14]. However, in this paper we consider a finite version of a pure dephasing model—a limiting case of a bath consisting of just a single oscillator $h\left(\omega \right)={\omega }_0\delta (\omega -{\omega }_0)$ coupled to an internal degree of freedom (the grin) of the Cheshire Cat. Then, ${\mathbf{H}}_{\pm }$ terms in the Hamiltonian Equation (18) read as follows

$$\begin{array}{c}\hfill {\mathbf{H}}_{\pm }^{fin}={\omega }_0{a}^{†}\left({\omega }_0\right)a\left({\omega }_0\right)\pm {\omega }_0{g}_{\pm }\left({\omega }_0\right)\left(a^{†}\left({\omega }_0\right)+a\left({\omega }_0\right)\right),\end{array}$$

(28)

where $a\left({\omega }_0\right),a^{†}\left({\omega }_0\right)$ generate the Heisenberg–Weyl algebra [15,16]. The model Equation (28) is simple enough to obtain its exact solution for a time-evolving system Equation (21) with

$$\begin{array}{c}\hfill |{\Omega }_t^{\pm }\rangle =e^{i{K}_{\pm }\left(t\right)}D\left(\pm \frac{g_{\pm }\left({\omega }_0\right)}{{\omega }_0}(1-e^{i{\omega }_{0}t}\right)|\Omega \rangle ,\mathrm{with}{K}_{\pm }\left(t\right)={\left(\frac{g_{\pm }\left({\omega }_0\right)}{{\omega }_0}\right)}^2\left({\omega }_{0}t-sin\left({\omega }_{0}t\right)\right),\end{array}$$

(29)

and the displacement operator [16] $D\left(x\right):=exp(x{a}^{†}\left({\omega }_0\right)-h.c)$. As a result, one obtains the explicit form for $Q_{\pm }$ in Equation (22). In particular, for the most natural symmetric dephasing corresponding to the van Hove model [17] $g_{+}\left({\omega }_0\right)=g_{-}\left({\omega }_0\right)$, one obtains $Q_{-}=0$ and $Q_{+}=Q$ with $Q=\langle \Omega |{\Omega }_t^{+}\rangle$ and

$$\begin{array}{c}\hfill Q=e^{i{K}_{+}\left(t\right)}{\Phi }_{+}\left(t\right)+e^{i{K}_{-}\left(t\right)}{\Phi }_{-}\left(t\right)\end{array}$$

(30)

$$\begin{array}{c}\hfill {\Phi }_{\pm }\left(t\right)=exp\left[-\frac{g_{\pm }{\left({\omega }_0\right)}^2}{{\omega }_0^2}\left(1-cos\left({\omega }_{0}t\right)\right)\right].\end{array}$$

(31)

Equation (30) follows solely from the symmetry of the model Equations (27) and (28) and depends on none of the particular values of parameters involved in the Hamiltonian. For the preselections $|{\Psi }_{L,R}\rangle$, Equations (9) and (10), weak values of the Cat’s position and its grin in the L–sector of an external degree of freedom are not affected by decoherence,

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^{L,R}=1,{\langle {\mathsf{\Pi }}_R\rangle }_w^{L,R}=0,{\langle {\sigma }_L\rangle }_w^{L,R}=0,\end{array}$$

(32)

whereas the grin in the R–sector,

$$\begin{array}{c}\hfill {\langle {\sigma }_R\rangle }_w^L=2/Q,{\langle {\sigma }_R\rangle }^R=Q/2,\end{array}$$

(33)

and, similarly to the symmetric case of an infinite bath considered in Ref. [9], differ only quantitatively from the noise–less archetype [4].

2.2. Asymmetric Dephasing

Complementary to the van Hove symmetric case discussed above let us consider the asymmetric Friedrichs-like model [18] with $g_{+}\left({\omega }_0\right)\ne 0$ and $g_{-}\left({\omega }_0\right)=0$. Such a model can serve as a simple approximation of an anisotropic coupling between polarization [19] or spin [20] and an external bosonic degree of freedom controlling the system. For Equations (28) and (29) in the asymmetric model of coupling we obtain $Q_{-}=Q_{+}=Q/2$. For the ’noise-affected’ preselection Equation (9) one gets the Cat’s position

$$\begin{array}{c}\hfill {\langle {\mathsf{\Pi }}_L\rangle }_w^R=\frac{4}{4+Q},{\langle {\mathsf{\Pi }}_R\rangle }_w^R=\frac{Q}{4+Q},\end{array}$$

(34)

and the Cat’s grin

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^R=0,{\langle {\sigma }_R\rangle }_w^R=\frac{Q}{4+Q},\end{array}$$

(35)

whereas for the preselection Equation (10) one obtains

$$\begin{array}{c}\hfill {\langle {\sigma }_L\rangle }_w^L=1,{\langle {\sigma }_R\rangle }_w^L=4/(4+Q).\end{array}$$

(36)

Let us notice that seemingly artificial asymmetric model allows for qualitatively new results in quantum communication [21] and becomes very useful in spintronics [20].

2.3. Scattering–Like Control

In this section we consider the modified asymmetric model and assume time-dependent and possibly non-linear coupling between the Cat’s grin and a finite environment-controlling time evolution. We consider a class of dephasing models Equation (18) with

$$\begin{array}{c}\hfill {\mathbf{H}}_{+}^{fin}={\overline{H}}_0,{\mathbf{H}}_{-}^{fin}={\overline{H}}_0+V(x,t),\end{array}$$

(37)

where ${\overline{H}}_0={\omega }_0{a}^{†}\left({\omega }_0\right)a\left({\omega }_0\right)=\left(p^2+{\omega }_0^2{x}^2\right)/2$ is a Hamiltonian of the harmonic oscillator and $V(x,t)$ is a (possibly time-dependent and non-linear) control (time-dependent departure form harmonicity) with $x,p=-i\partial /\partial x$ indicating position and momentum of the oscillator respectively. Such a coupling, both non–linear and time–dependent, despite its simplicity, allows for an effective control of the Cheshire Cat effect via V–dependent modification of the weak values of desired quantities.

Let us notice that the coupling Equation (37) $|\langle \Omega |{\Omega }_t^{+}\rangle |=1$ and the quantities $Q_{\pm }$ in Equation (22) responsible for the weak values of the Cat’s grin and the Cat’s position are governed mainly by $A_t=\langle \Omega |{\Omega }_t^{-}\rangle$. In the following we simplify the model Equation (37) one step further and assume that an effective interaction between the Cat’s grin and the finite bath under consideration has a short duration in comparison with a total time-evolution considered in the Cheshire Cat effect. Such an approximation, know as a singular coupling limit, is also useful in the modelling of quantum open systems [11,14] and continuous measurement [22]. In other words, we assume that a finite environment was prepared in a distant past ($t_0\to -\infty$), and a postselection is performed in a far future ($t\to \infty$). As a result one arrives to an approximation

$$\begin{array}{c}\hfill A:=A_{\infty }=\langle \Omega |{\Omega }_{\infty }^{-}\rangle =\langle \Omega |S_{-}\Omega \rangle ,\mathrm{where}{S}_{-}=\underset{t\to \infty }{lim}\underset{t_0\to -\infty }{lim}exp\left(-i({\overline{H}}_0+V(x,t))(t-t_0)\right),\end{array}$$

(38)

which is of a particular usefulness since it allows us to reduce (at least formally) a control of the Cheshire Cat effect to the single particle scattering process of the Cat’s grin in the presence of an external control potential $V(x,t)$.

Below we exemplify the scattering-type approximation in Equation (38), using two most elementary and highly symmetric models. The first is a time-dependent but linear shift in the coupling in Equation (37):

$$\begin{array}{c}\hfill V(x,t)=-f\left(t\right)x.\end{array}$$

(39)

Here the function $f\left(t\right)$ is an open-loop control [5] affecting the oscillator and, indirectly, the Cat’s grin in a presence of finite environment. For technical reasons the control $f\left(t\right)$ is assumed to vanish in the past and in the future, i.e., ${lim}_{t\to \pm \infty }f\left(t\right)=0$. A control strategy given in Equation (39) allows for a particularly simple analytic treatment, since a time evolution of a finite environment governed by Equation (37) with $V(x,t)$ given in Equation (39)—in the interaction picture with respect to ${\overline{H}}_0$—reads as $d|{\tilde{\Omega }}_t\rangle =[if\left(t\right)/\sqrt{2{\omega }_0}]\left[e^{i\omega t}{a}^{†}\left({\omega }_0\right)-h.c\right]|{\tilde{\Omega }}_t\rangle dt$. Hence, it is given in terms of coherent states related to the Heisenberg–Weyl symmetry of the system [16]:

$$\begin{array}{ccc}\hfill |{\tilde{\Omega }}_t\rangle & \sim & D\left(\kappa \right)|\Omega \rangle ,\hfill \end{array}$$

(40)

where [16,23]

$$\begin{array}{c}\hfill \kappa =\frac{i}{\sqrt{2{\omega }_0}}{\int }_{-\infty }^{\infty }f\left(t\right)exp\left(i{\omega }_{0}t\right)dt\end{array}$$

(41)

is a Fourier transform of the force $f\left(t\right)$ at the oscillator frequency ${\omega }_0$ and $D\left(x\right)=exp(x{a}^{†}-h.c)$ is a displacement operator. The scattering amplitude (38) for the $|n\rangle \to |n\rangle$ transition, including the celebrated vacuum-to-vacuum transition [24] for $n=0$, is given by matrix elements of the displacement operator $D\left(\kappa \right)$ and reads [23]

$$\begin{array}{c}\hfill A={exp(-|\kappa |}^2/2)L_n^0{\left(\right|\kappa |}^2),\end{array}$$

(42)

where $L_n^0$ are the Laguerre polynomials and

$$\begin{array}{c}\hfill \kappa =\frac{i}{\sqrt{2{\omega }_0}}{\int }_{-\infty }^{\infty }f\left(t\right)exp\left(i{\omega }_{0}t\right)dt\end{array}$$

(43)

is a Fourier transform of the force $f\left(t\right)$ at the oscillator frequency ${\omega }_0$. For a Gaussian profile which is easy to calculate,

$$\begin{array}{c}\hfill f\left(t\right)=bexp(-\pi {\gamma }^2{t}^2/4),\left|\kappa \right|=\frac{2b}{\gamma \sqrt{2{\omega }_0}}exp\left(-\frac{{\omega }_0^2}{\pi {\gamma }^2}\right).\end{array}$$

(44)

We note that for $\kappa$ to exist it is enough to design an absolutely integrable control $f\left(t\right)$. The scattering amplitude A depends on $\left|\kappa \right|\in [0,\infty )$. As there are many processes (i.e., various control strategies $f\left(t\right)$) leading to the same value of $\left|\kappa \right|$ one can identify a class of scattering processes leading to the same effect. By changing $\left|\kappa \right|$ from zero to infinity, we can take into account all admissible scattering processes for a desired A–dependent $Q_{\pm }$.

As a second exactly solvable example of scattering–like approximation in Equation (38), we study the quadratic time-dependent correction in Equation (37):

$$\begin{array}{c}\hfill V\left(t\right)=\frac{1}{2}f\left(t\right)x^2,\end{array}$$

(45)

such that, effectively, $H_{-}$ becomes an oscillator with a time-varying frequency ${\omega }^2\left(t\right)={\omega }_0^2+f\left(t\right)$ leading to the parametric excitation of a quantum oscillator. Let us observe that Equation (37) with $V(x,t)$ given by Equation (45) can be expanded in terms of generators of the $SU(1,1)$ group

$$\begin{array}{c}\hfill {\mathbf{H}}_{-}^{fin}=r_0{K}_0-r_1{K}_1-r_2{K}_2=ib{K}_{+}-\overline{b}{K}_{\_}ig{K}_0,\end{array}$$

(46)

where $r_{0/1}={\omega }_0[{(\omega \left(t\right)/{\omega }_0)}^2\pm 1],r_2=0$ and

$$\begin{array}{c}\hfill [K_1,K_2]=-i{K}_0,[K_2,K_0]=i{K}_1,[K_0,K_1]=i{K}_2,\mathrm{and}{K}_{\pm }=K_1\pm i{K}_2.\end{array}$$

(47)

Solutions of the corresponding Schrödinger equation

$$\begin{array}{c}\hfill |{\Omega }_t^{-}\rangle \sim T\left(\begin{array}{c}ab\\ \overline{b}\overline{a}\end{array}\right){|\Omega \rangle ,|a|}^2+{\left|b\right|}^2=1\end{array}$$

(48)

can be expressed in terms of matrix elements of a generalized displacement operator $T(·)$ (squeezing operator [16]) and coherent states corresponding to one of the discrete series of the $SU(1,1)$ representations [16] directly related to the celebrated squeezed states [25]. The scattering amplitude A calculated for an $|n\rangle \to |n\rangle$ transitions, reads as follows [26]

$$\begin{array}{c}\hfill A={(1-\sigma )}^{\frac{1}{4}}{P}_n^0\left({(1-\sigma )}^{\frac{1}{2}}\right),\end{array}$$

(49)

where $P_n^0$ are the Legendre polynomials and $\sigma ={\left|b\right|}^2/{\left|a\right|}^2$. Equation (49) holds true when $\omega \left(t\right)$ attains its limits ${\omega }_{\pm }$ sufficiently fast [26] for $t\to \pm \infty$, respectively. Again, the scattering amplitude A depends on $\sigma \in [0,1]$. By changing $\sigma$ from zero to one, we can take into account all admissible scattering processes leading to different values of $Q_{\pm }$.

3. Discussion

An effective control of quantum systems [5] allows one to confine their properties to a desired range. We presented a simple but exactly solvable model of how an environment affecting the ‘grin’ of the Cheshire Cat serves to control weak values that indicate the Cheshire Cat paradox. Our central result—the scattering-like control strategy—allows one to utilize the well developed methods of scattering theory. Although there is an intensive experimental effort concerning the Cheshire Cat effect [27,28], the role of weak values as a theoretical tool for its proper description is argued [29,30] similarly to the continuing debate concerning a past of a quantum particle [2,3,31,32] which is far from being concluded.

Our studies are a modest contribution to a general problem of the effect of noise on weak quantum values [33]. In particular, if one continues our program and abandons a simplifying assumption of the finite environment, one can utilize tools originating from a mature branch of quantum field theory. If in addition one decides to scarify exact solvability to the perturbative approximations [34] and makes a step beyond pure dephasing [35], one can utilize a plenitude of methods developed in quantum field theory [24]. Experimental investigations [27,28] of the Quantum Cheshire Cat effect and other subtle quantum effects demanding weak measurements require conditions which are most convenient for verification of theoretical predictions. Effective control strategies can help experimentalists to approve or to reject the controversial and counter-intuitive theoretical approaches.

4. Materials and Methods

Pure dephasing models, both symmetric and asymmetric, studied in this work allow for exact results obtained using standard methodology suitable for the open quantum systems [10,11].