Entanglement Dynamics of Three and Four Level Atomic System under Stark Effect and Kerr-Like Medium
Abstract
:1. Introduction
2. Introduction to Quantum Fisher Information (QFI) and Van Neumann Entropy
2.1. Quantum Fisher Information (QFI)
2.2. Von Neumann Entropy
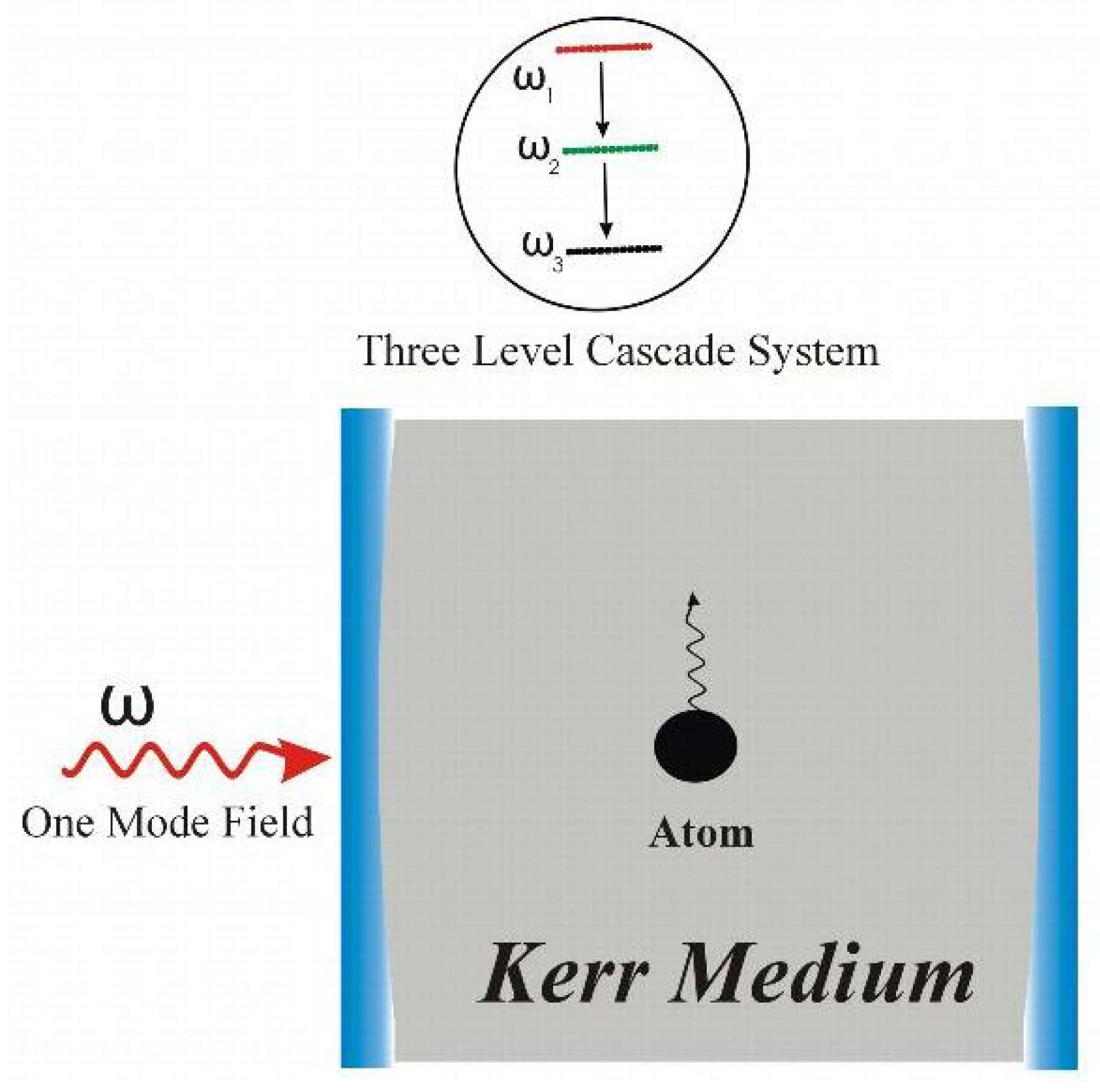
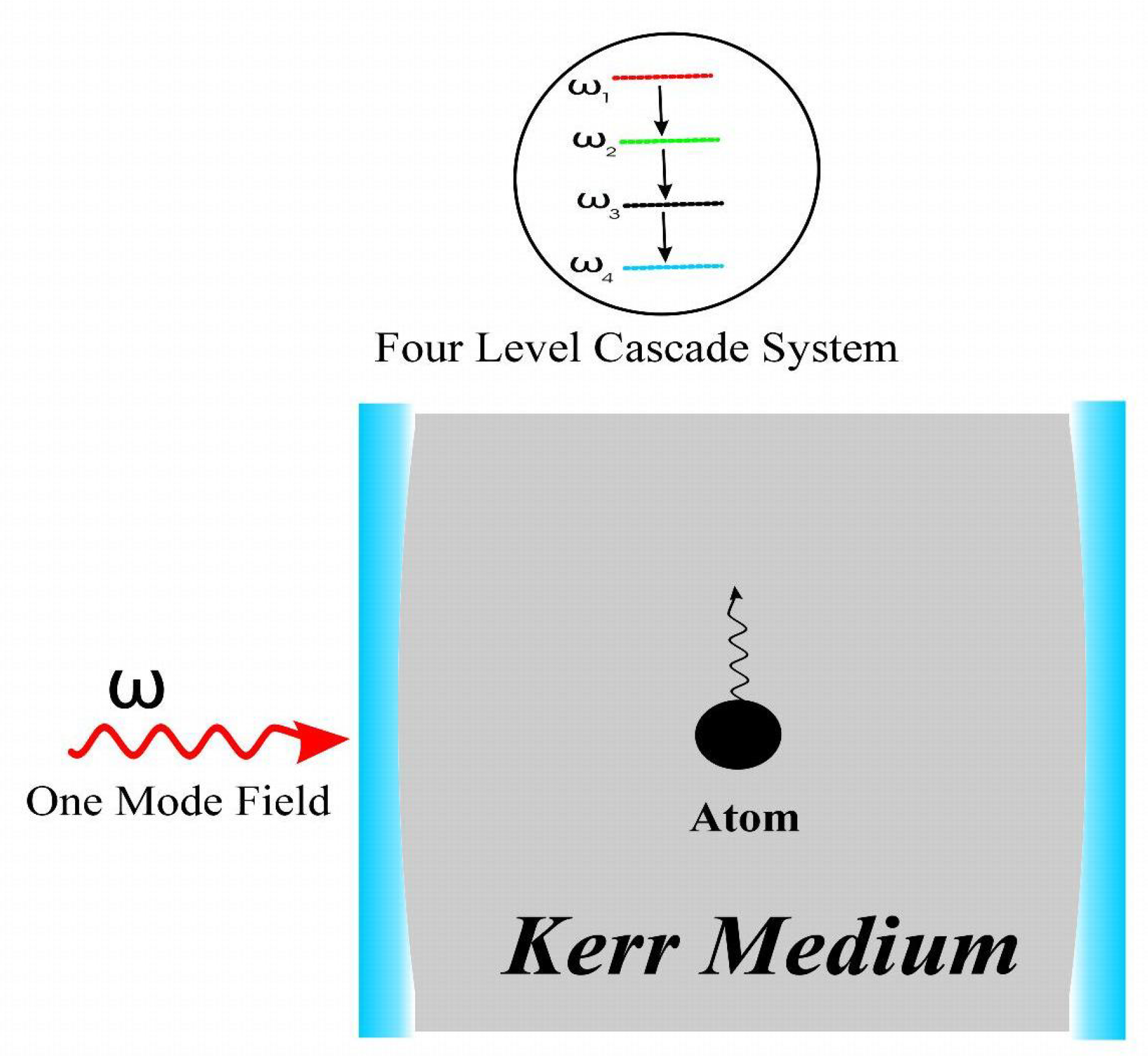
3. Model and Hamiltonian
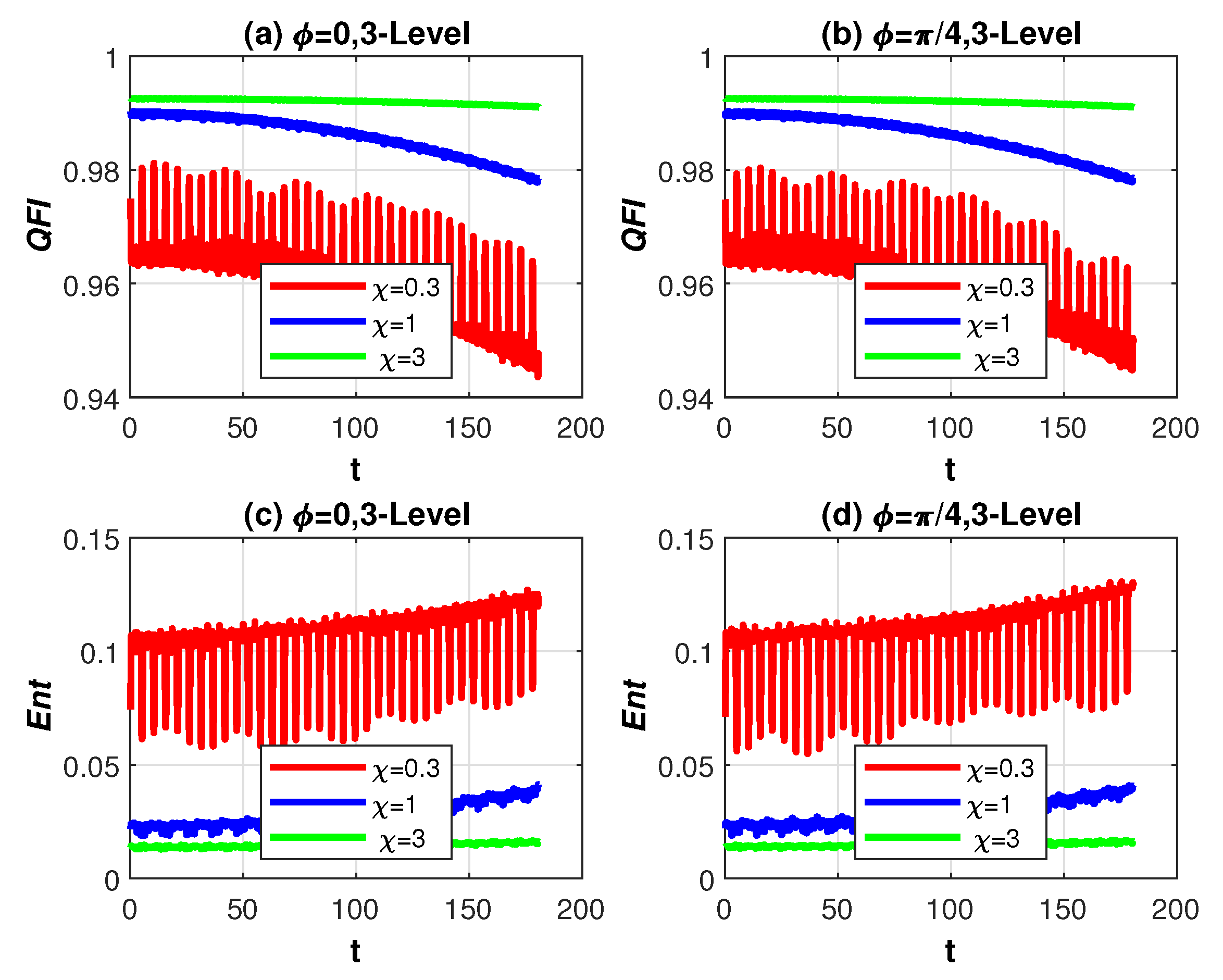
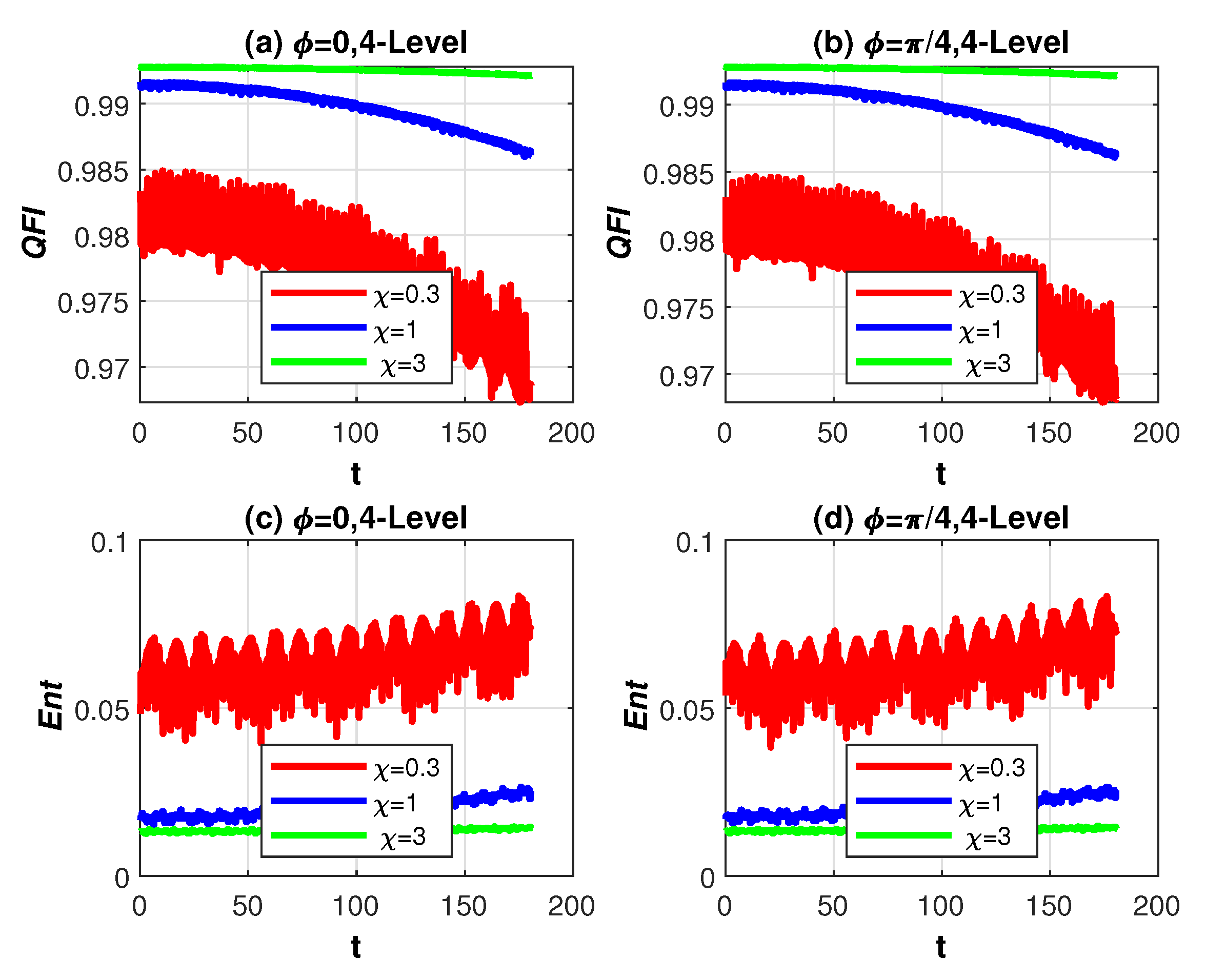
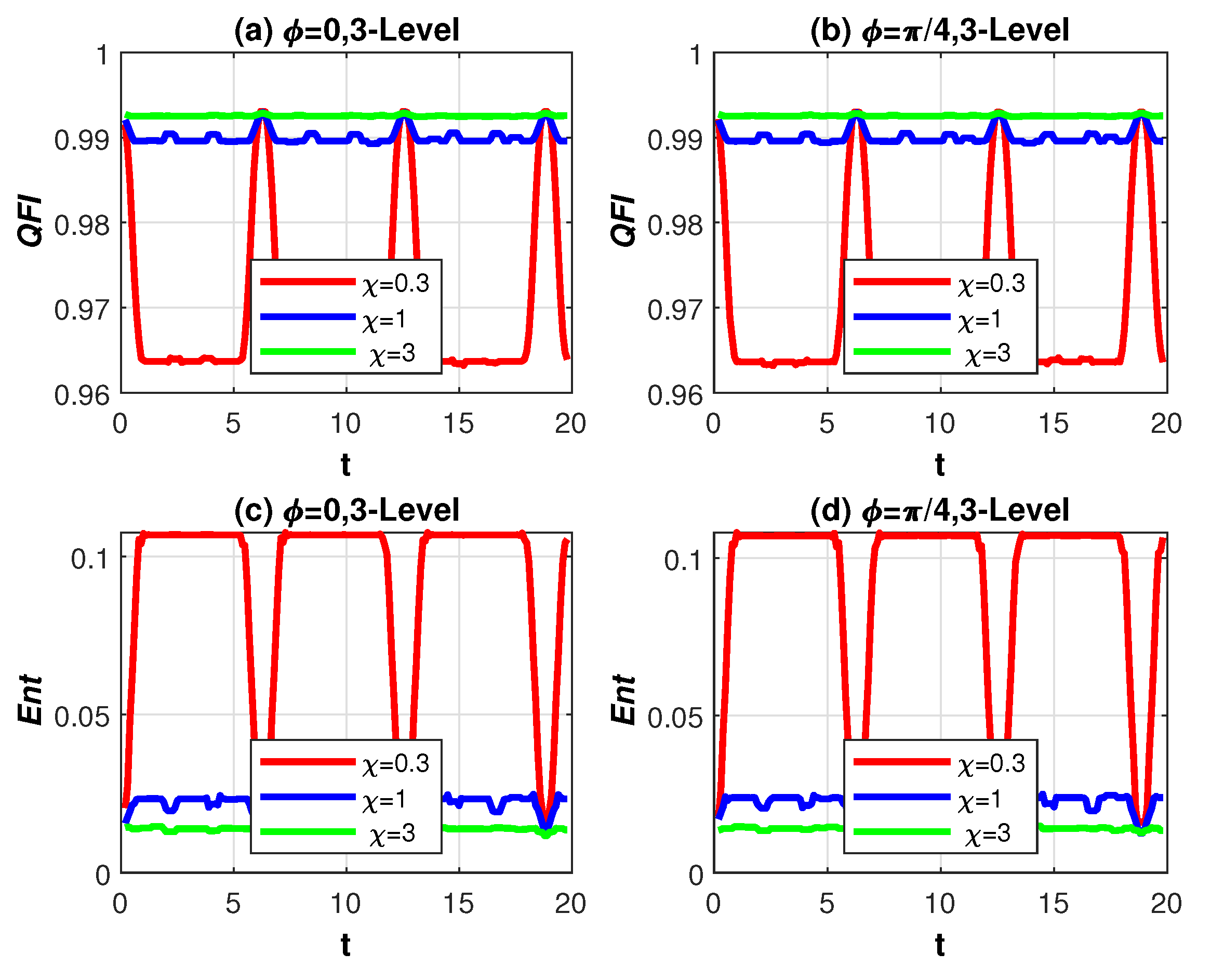
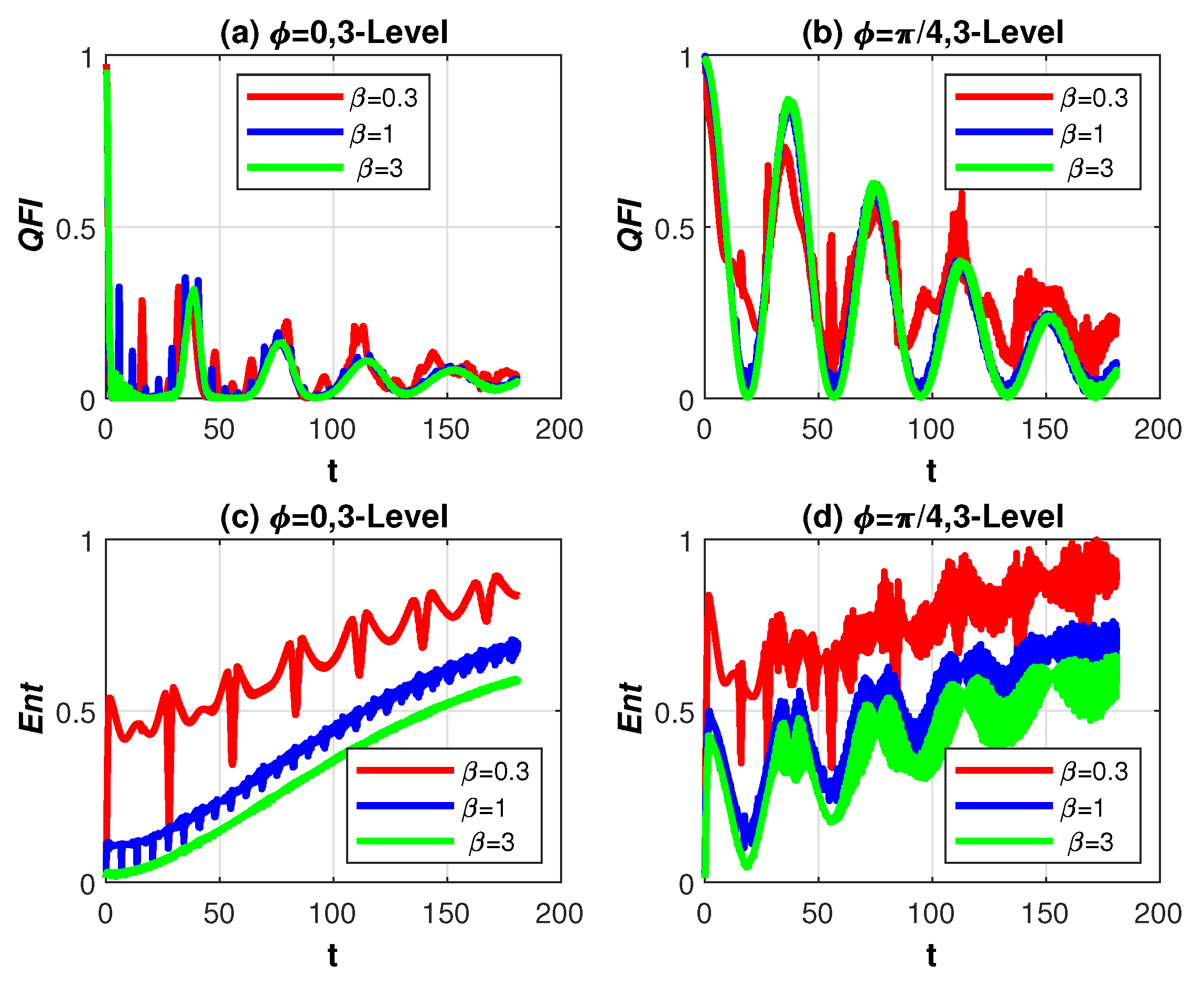
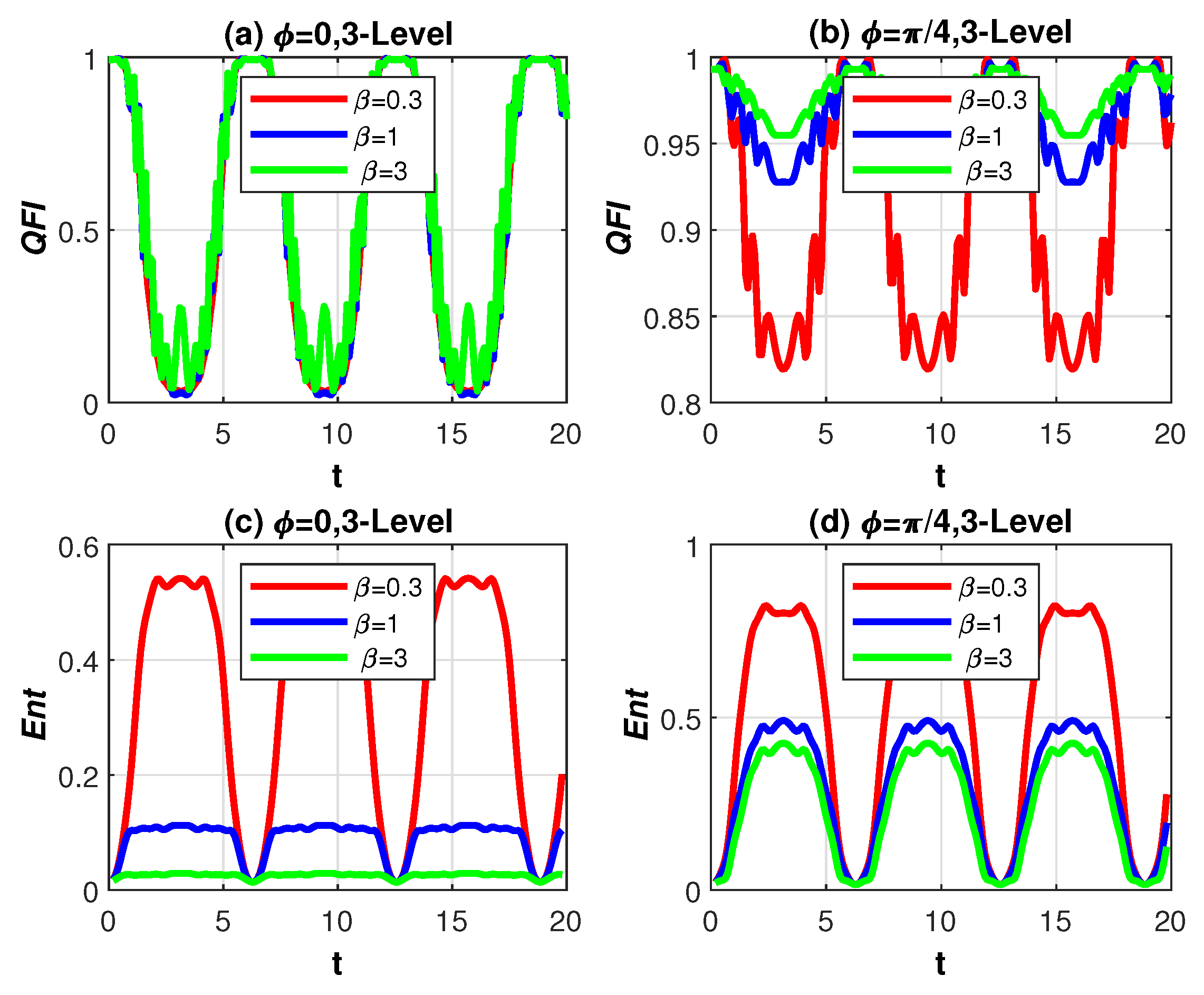
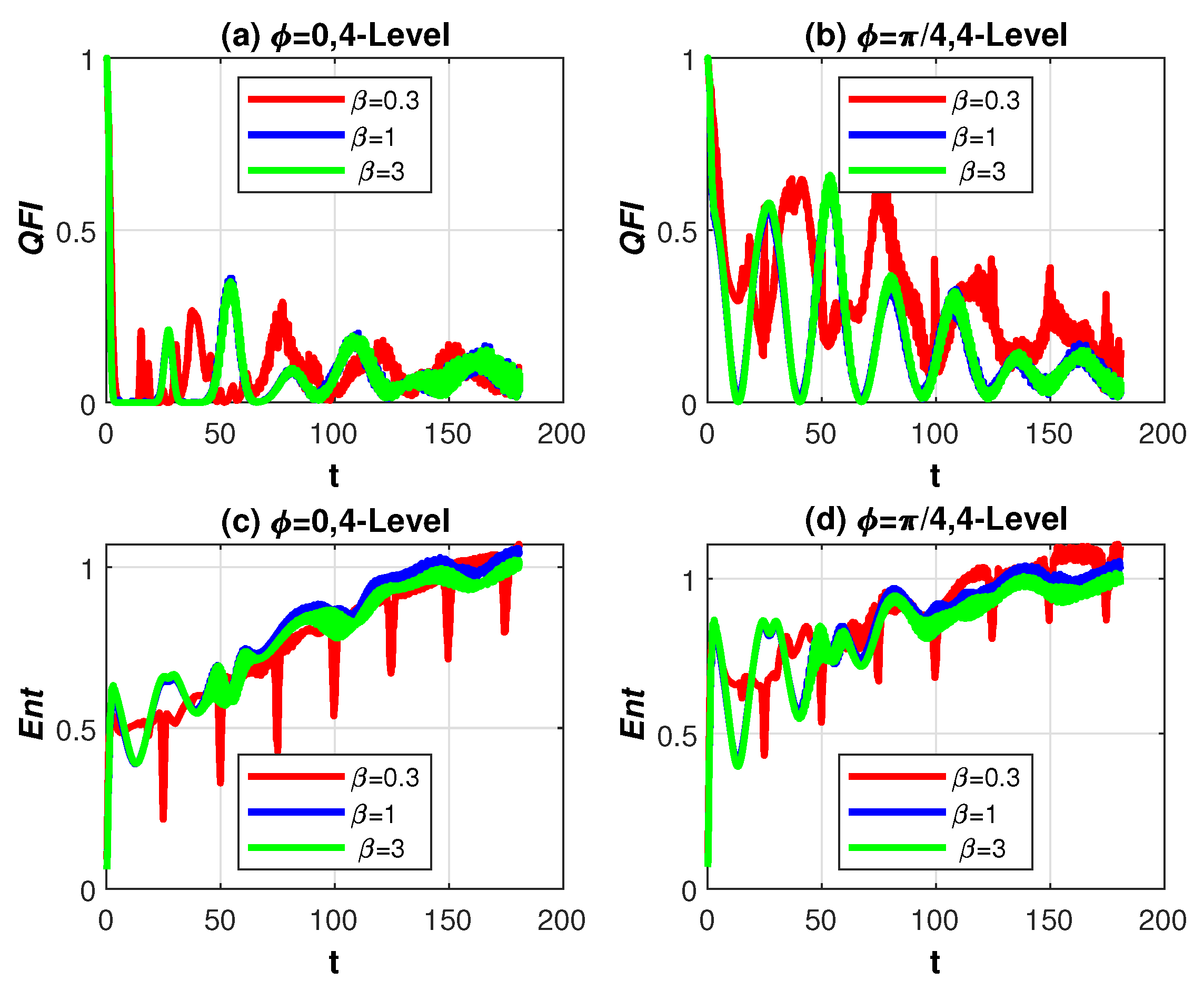
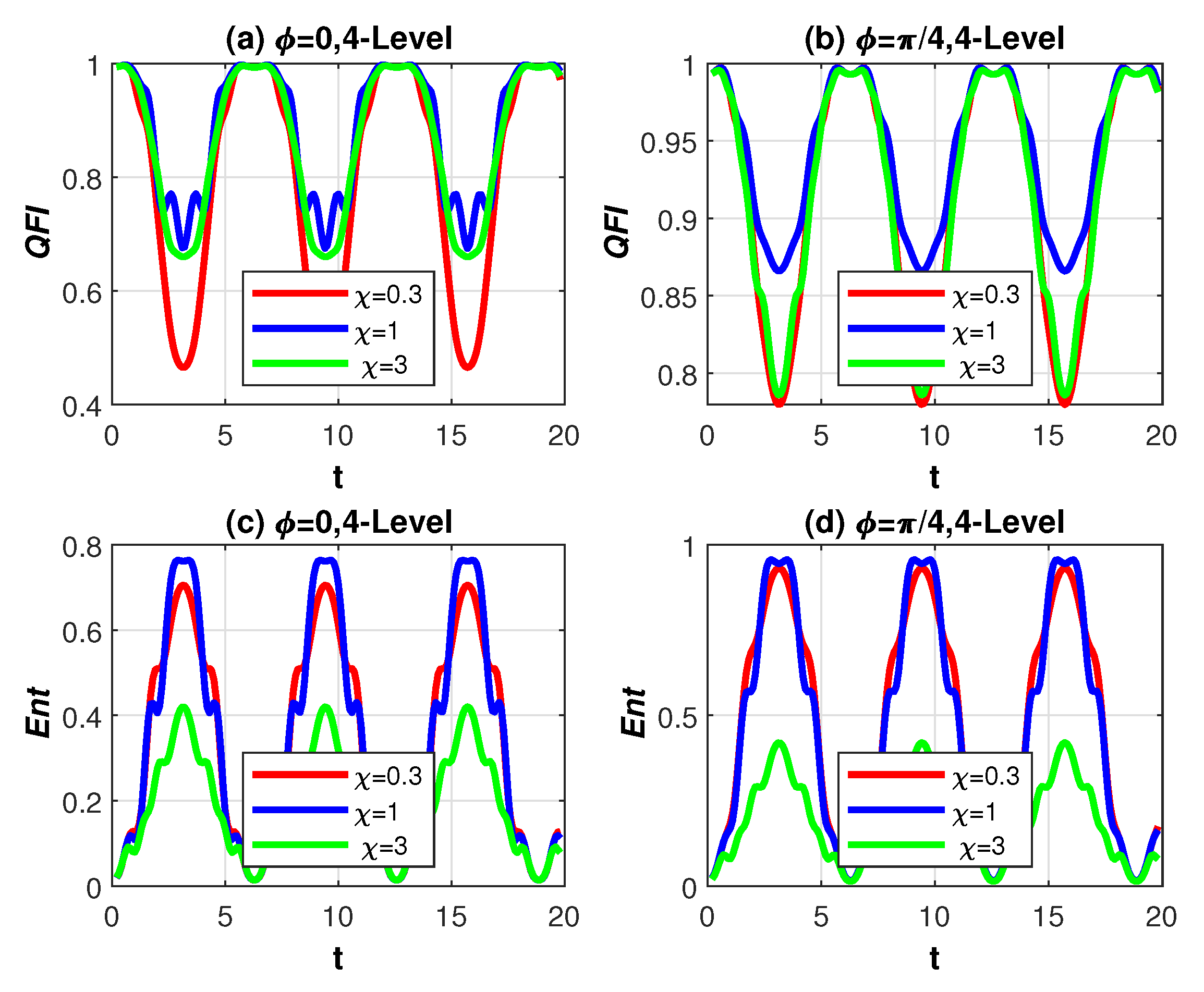
4. Discussion of Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Dowling, J. Quantum optical metrology – the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Holevo, A.S. Statistical Structure of Quantum Theory; North-Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; Caves, C.M.; Milburn, G.J. Generalized uncertainty relations: Theory, examples, and Lorentz invariance. Ann. Phys. 1996, 247, 135. [Google Scholar] [CrossRef]
- Hübner, M. Explicit computation of the Bures distance for density matrices. Phys. Lett. A 1992, 163, 239. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. Proc. Camb. Phil. Soc. 1935, 31, 555. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bell, J. On the einstein podolsky rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Clauser, J.; Horne, M.; Shimony, A.; Holt, R. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Huver, S.D.; Wildfeuer, C.F.; Dowling, J.P. Entangled Fock states for robust quantum optical metrology, imaging, and sensing. Phys. Rev. A 2008, 78, 063828. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K. Quantum metrology with SU (1, 1) coherent states in the presence of nonlinear phase shifts. Phys. Rev. A 2013, 88, 013817. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M.; Pombo, C.; Furtado, C.; Khrennikov, A.Y.; Pedrosa, I.A.; Spicka, V. Quantum Foundations and Open Quantum Systems; World Scientific: Singapore, 2014. [Google Scholar]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Meschede, D. Radiating atoms in confined space: From spontaneous emission to micromasers. Phys. Rep. 1992, 211, 201–250. [Google Scholar] [CrossRef]
- Hansch, T.W.; Walther, H. Quantum theory. Rev. Mod. Phys. 1999, 71, 5242. [Google Scholar]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353. [Google Scholar] [CrossRef] [PubMed]
- Buck, B.; Sukumar, C.V. Exactly soluble model of atom-phonon coupling showing periodic decay and revival. Phys. Lett. A 1981, 81, 132–135. [Google Scholar] [CrossRef]
- Sukumar, C.V.; Buck, B. Multi-phonon generalisation of the Jaynes-Cummings model. Phys. Lett. A 1981, 83, 211–213. [Google Scholar] [CrossRef]
- Fan, A.-F.; Wang, Z.-W. Phase, coherence properties, and the numerical analysis of the field in the nonresonant Jaynes-Cummings model. Phys. Rev. A 1994, 49, 1509. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13. [Google Scholar] [CrossRef] [PubMed]
- Gora, P.; Jedrzejek, C. Nonlinear jaynes-cummings model. Phys. Rev. A 1992, 45, 6816. [Google Scholar] [CrossRef] [PubMed]
- Buzek, V.; Jex, I. Dynamics of a two-level atom in a Kerr-like medium. Opt. Commun. 1990, 78, 425–435. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Eied, A.A.; Al-Kader Abd, G.M. Treatment of the emission and absorption spectra of a general formalism Λ-type three-level atom driven by a two-mode field with nonlinearities. Laser Phys. 2008, 18, 1164–1175. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Krepelka, J.; Perina, J. Effect of Kerr-like medium on a two-level atom in interaction with bimodal oscillators. J. Phys. B Atom. Mol. Opt. Phys. 2006, 39, 1563–1577. [Google Scholar] [CrossRef]
- Lai, Y.Z.; Li, W.D.; Liang, J.Q. Adiabatic transfer of atomic level-occupation probability induced by Kerr-like medium. Opt. Commun. 1999, 160, 240–244. [Google Scholar] [CrossRef]
- Berlin, G.; Aliaga, J. Quantum dynamical properties of a two-photon non linear Jaynes-Cummings model. Mod. Opt. 2001, 48, 1819–1829. [Google Scholar] [CrossRef]
- Schlicher, R.R. Jaynes-Cummings model with atomic motion. Opt. Commun. 1989, 70, 97. [Google Scholar] [CrossRef]
- Liu, J.-R.; Wang, Y.-Z. Motion-quantized Jaynes-Cummings models with an arbitrary intensity-dependent medium. Phys. Rev. A 1996, 54, 2326. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H.; Amin, M.E.; Mourad, M.F. Influence of the Stark shift and the detuning parameters on the entanglement degree in a two-mode coupling systemJ. Phys. Soc. Jpn. 2002, 71, 2129. [Google Scholar] [CrossRef]
- Zait, R.A.; Abdel-Wahab, N.H. Nonresonant interaction between a three-level atom with a momentum eigenstate and a one-mode cavity field in a Kerr-like medium. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 353701. [Google Scholar] [CrossRef]
- Zait, R.A.; Abdel-Wahab, N.H. Influence of Detuning and Kerr-like Medium on the Interaction of a three-level Atom with Squeezed two-mode Cavity Field. J. Phys. Scr. 2002, 66, 452. [Google Scholar] [CrossRef]
- Abdel-aty, M. Influence of a Kerr-like medium on the evolution of field entropy and entanglement in a three-level atom. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 2665. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H. N-level Atom in a Momentum Eigenstate Interacting with an (N- 1) Mode Cavity Field 2005. Phys. Scr. 2005, 71, 132. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H.; Amin, M.E.; Taha, M. One-mode interaction with a four-level atom in a momentum eigenstate. FIZIKA (Zagreb) 2006, 2, 113. [Google Scholar]
- Abdel-Wahab, N.H. A moving four-level N-type atom interacting with cavity fields. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 105502. [Google Scholar] [CrossRef]
- Haken, H.; Wolf, H.C. Atom- und Quantenphysik, 8th ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Alsing, P.; Guo, D.-S.; Carmichael, H.J. Dynamic Stark effect for the Jaynes-Cummings system. Phys. Rev. A 1992, 45, 5135. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.-S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162. [Google Scholar] [CrossRef]
- Alsing, P.; Zubairy, M.S. Collapse and revivals in a two-photon absorption process. J. Opt. Soc. Am. B 1987, 4, 177. [Google Scholar] [CrossRef]
- Swain, S. Systematic method for deriving effective Hamiltonians. Phys. Rev. A 1994, 49, 2816. [Google Scholar] [CrossRef]
- Brune, M.; Raimond, J.M.; Haroche, S. Theory of the Rydberg-atom two-photon micromaser. Phys. Rev. A 1987, 35, 154. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Puri, R.R. Exact quantum-electrodynamics results for scattering, emission, and absorption from a Rydberg atom in a cavity with arbitrary Q. Phys. Rev. A 1986, 33, 1757. [Google Scholar] [CrossRef]
- Obada, A.S.F.; Ahmed, M.M.A.; Khalil, E.M.; Ali, S.I. Entangled two two-level atoms interacting with a cavity field in the presence of the stark shift terms. Opt. Commun. 2013, 287, 215–223. [Google Scholar] [CrossRef]
- Jamal Anwar, S.; Ramzan, M.; Khan, K. Dynamics of entanglement and quantum Fisher information for N-level atomic system under intrinsic decoherence. Quantum Inf. Process 2017, 16, 142. [Google Scholar] [CrossRef]
- Abdel-Khalek, S. Quantum Fisher information for moving three-level atom. Quantum Inf. Process 2013, 12, 3761–3769. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Obada, A.S.F. Quantum Fisher information for a qubit system placed inside a dissipative cavity. Phys. Lett. A 2012, 376, 1412–1416. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Raymond Ooi, C.H. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86, 033823. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27. [Google Scholar]
- Lu, X.; Wang, X.; Sun, C.P. Quantum Fisher information flow and non-Markovian processes of open systems. Phys. Rev. A 2010, 82, 042103. [Google Scholar] [CrossRef]
- Enaki, N.A.; Ciobanu, N. Horopter measured as a function of wavelength. J. Mod. Opt. 2008, 55, 589–598. [Google Scholar]
- Barndorff-Nielsen, O.E.; Gill, R.D.; Jupp, P.E. On quantum statistical inference. J. R. Stat. Soc. B 2003, 65, 775–816. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University: Princeton, NJ, USA, 1955. [Google Scholar]
- Abdel-Khalek, S. Dynamics of a moving five-level atom interacting with cavity fields. J. Russ. Laser Res. 2011, 32, 86. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, S.J.; Ramzan, M.; Usman, M.; Khan, M.K. Entanglement Dynamics of Three and Four Level Atomic System under Stark Effect and Kerr-Like Medium. Quantum Rep. 2019, 1, 23-36. https://doi.org/10.3390/quantum1010004
Anwar SJ, Ramzan M, Usman M, Khan MK. Entanglement Dynamics of Three and Four Level Atomic System under Stark Effect and Kerr-Like Medium. Quantum Reports. 2019; 1(1):23-36. https://doi.org/10.3390/quantum1010004
Chicago/Turabian StyleAnwar, S. Jamal, M. Ramzan, M. Usman, and M. Khalid Khan. 2019. "Entanglement Dynamics of Three and Four Level Atomic System under Stark Effect and Kerr-Like Medium" Quantum Reports 1, no. 1: 23-36. https://doi.org/10.3390/quantum1010004




