Quantum Computing, Seifert Surfaces, and Singular Fibers
Abstract
:1. Introduction
1.1. Motivation of the Work
1.2. Contents of the Work
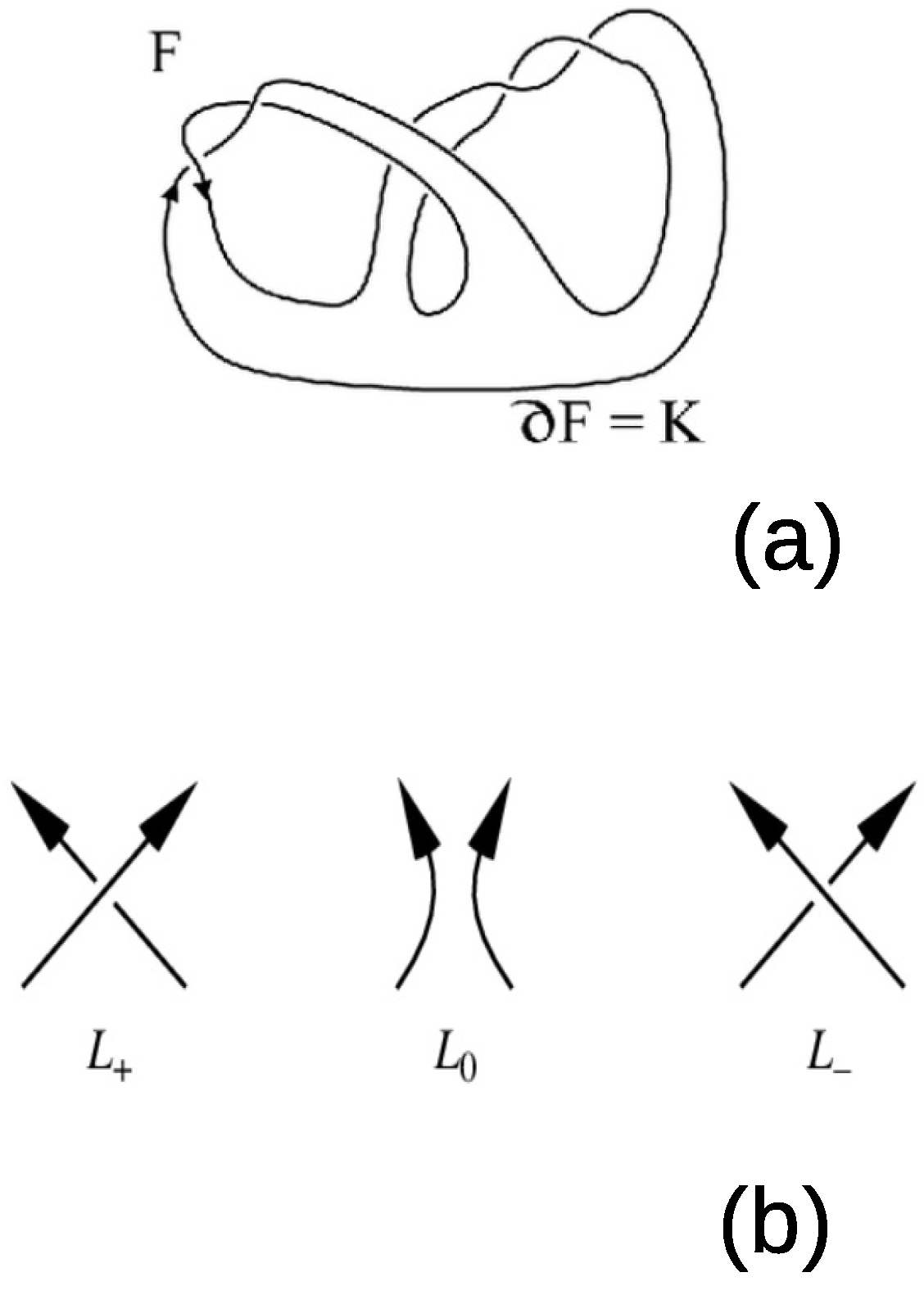
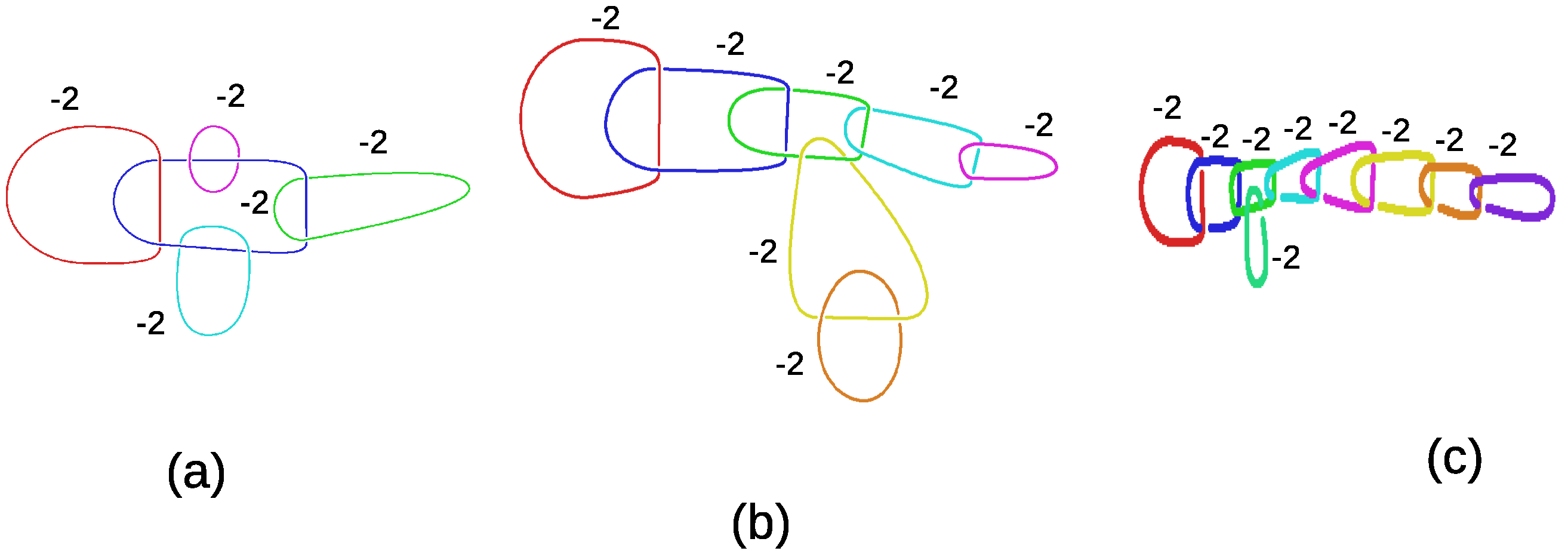
2. Seifert Surfaces and Braids from d-Fold Coverings of the Trefoil Knot Manifold (or of Hyperbolic Three-Manifolds)
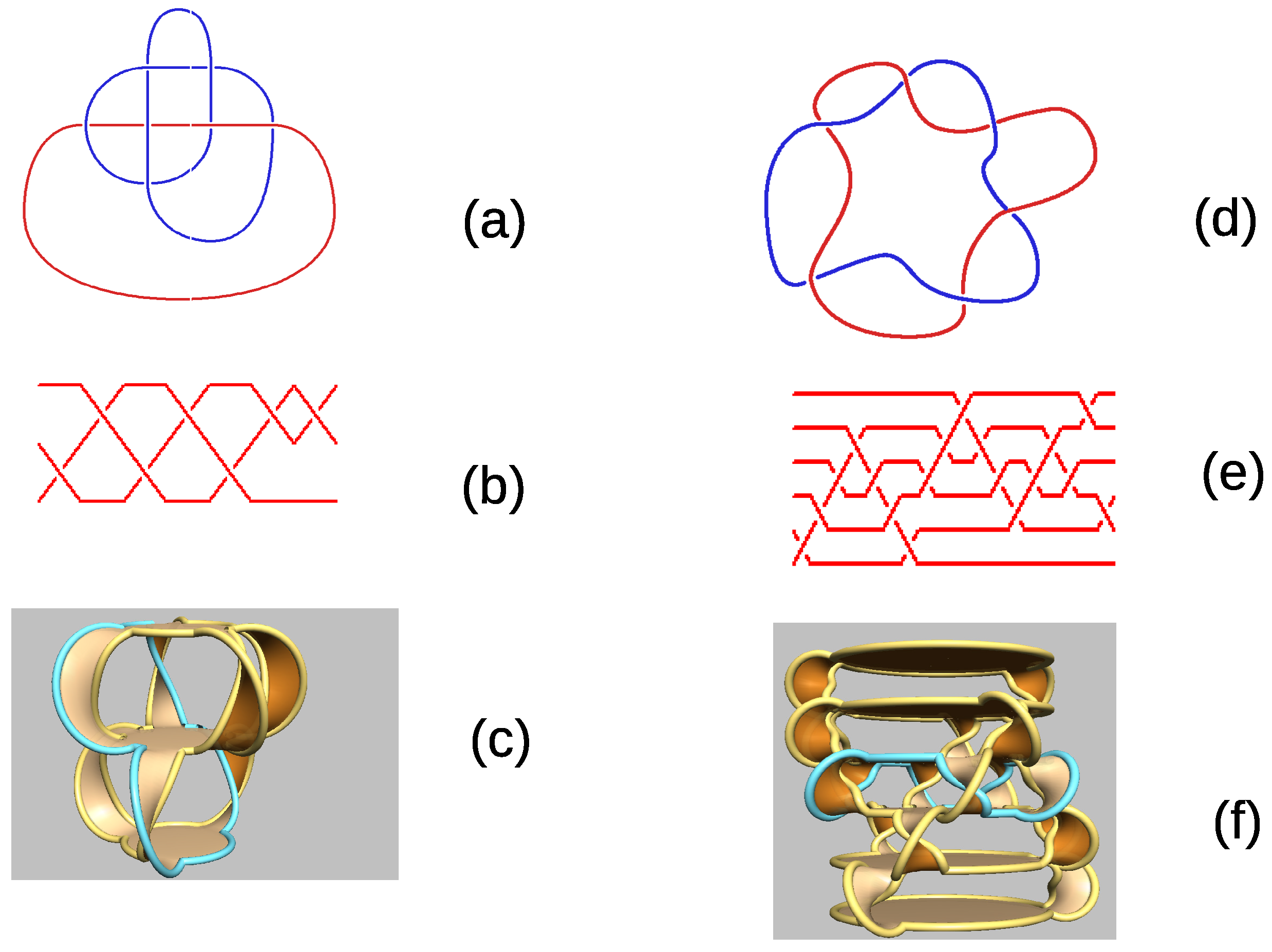
2.1. The Braids Built from the Trefoil Knot that Are Associated with the Qutrit Link and the Two-Qubit Link
2.2. The Braid Built from the Trefoil Knot that Is Associated with the 6-dit Link and Related Braids with the Same Fundamental Group
The Six-Cover of the Trefoil Knot Manifold Corresponding to the Congruence Subgroup of
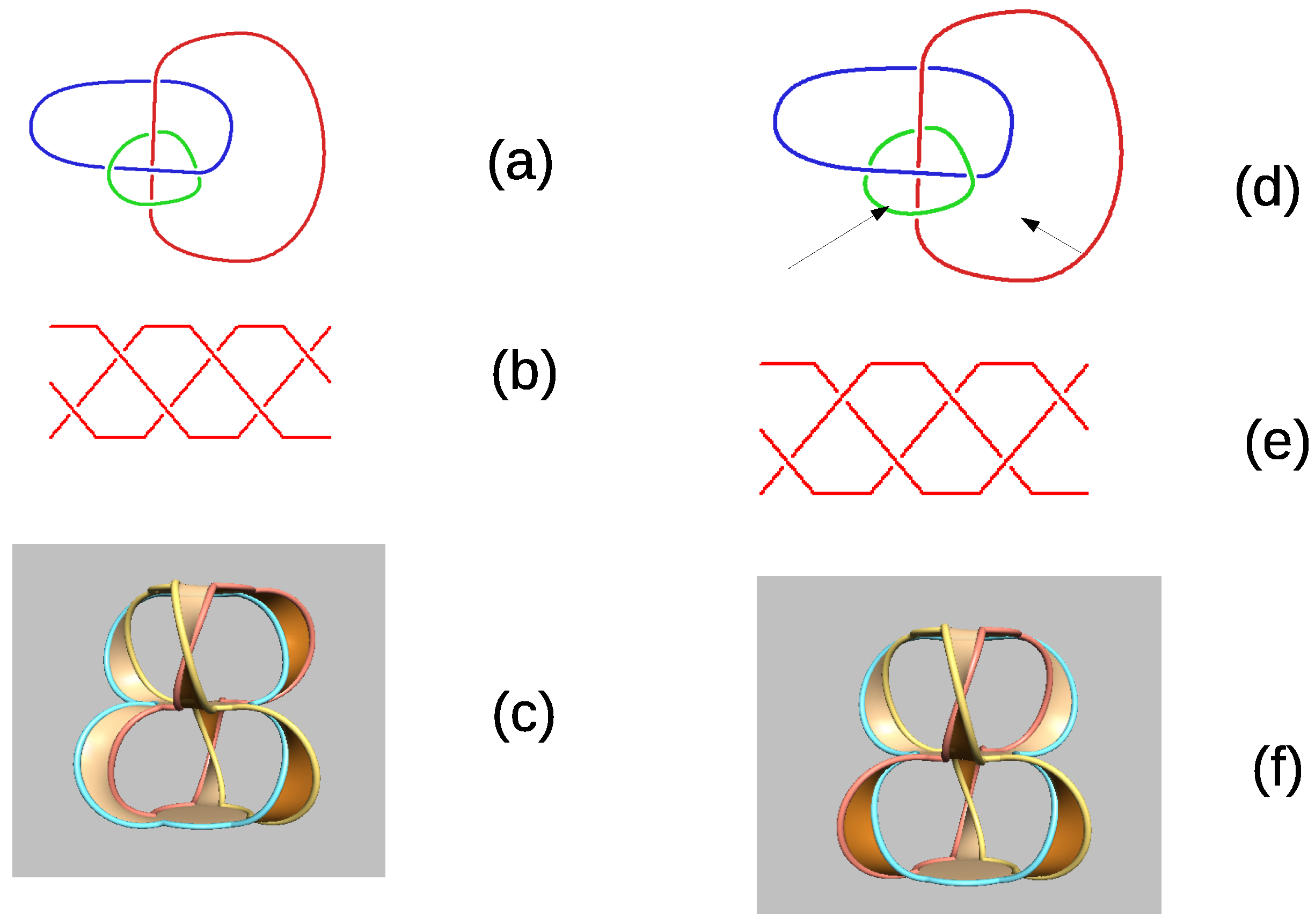
2.3. The Braid Built from the Trefoil Knot that Is Associated with the Two-Qubit/Qutrit MIC with Icosahedral Symmetry of the Permutation Representation
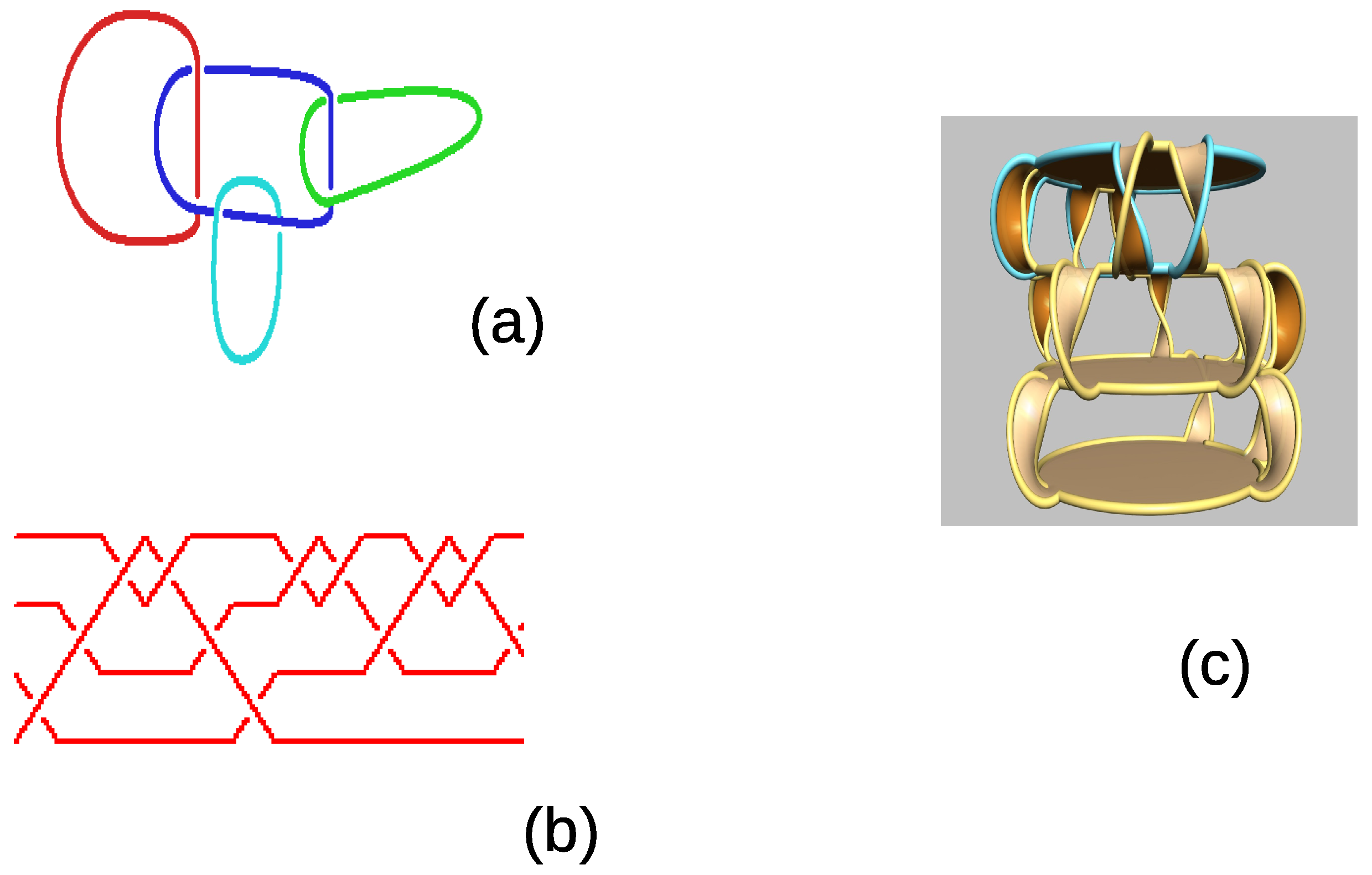
2.4. Braids from d-Fold Coverings of Hyperbolic Three-Manifolds
2.4.1. The Hyperbolic Link and Its Zero-Surgery
2.4.2. Further Results
3. Quantum Computing from Affine Dynkin Diagrams
Reidemeister Torsion of the Manifold
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. 2005, A71, 022316. [Google Scholar] [CrossRef]
- Veitch, V.; Mousavian, S.A.; Gottesman, D.; Emerson, J. The resource theory of stabilizer quantum computation. New J. Phys. 2014, 16, 013009. [Google Scholar] [CrossRef]
- Seddon, J.R.; Campbell, E. Quantifying magic for multi-qubit operations. arXiv 2019, arXiv:1901.03322. [Google Scholar]
- Planat, M.; Haq, R.U. The magic of universal quantum computing with permutations. Adv. Math. Phys. 2017, 217, 5287862. [Google Scholar] [CrossRef]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef]
- Planat, M. The Poincaré half-plane for informationally complete POVMs. Entropy 2018, 20, 16. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Universal quantum computing and three-manifolds, Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef]
- Freedman, M.; Kitaev, A.; Larsen, M.; Wang, Z. Topological quantum computation. Bull. Am. Math. Soc. 2003, 40, 31. [Google Scholar] [CrossRef]
- Kauffman, L.H.; Lomonacco, S.J. Braiding, Majorana fermions, Fibonacci particles and topological quantum computing. Quant. Inf. Proc. 2018, 17, 201. [Google Scholar] [CrossRef]
- Nayak, C. Non-Abelian Anyons and Topological Quantum Computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Adams, C.C. The Knot Book, An Elementary Introduction to the Mathematical Theory of Knots; W. H. Freeman and Co.: New York, NY, USA, 1994. [Google Scholar]
- Weeks, J.R. The Shape of Space, 2nd ed.; Chapman & Hall: Boca Raton, FL, USA, 2001; 408p. [Google Scholar]
- Chelnokov, G.; Deryagina, M.; Meldnykh, A. On the coverings of Euclidean manifolds 1 and 2. Commun. Algebra 2017, 45, 1558. [Google Scholar] [CrossRef]
- Gompf, R.E.; Stipsicz, A.I. four-Manifolds and Kirby Calculus; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1999; p. 129. [Google Scholar]
- Akbulut, S. four-Manifolds; Oxford Graduate Texts in Mathematics 25; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Scorpian, A. The Wild World of four-Manifolds; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Kauffman, L.H. State models and the Jones polynomial. Topology 1987, 26, 395–407. [Google Scholar] [CrossRef]
- Milnor, J. A duality theorem for Reidemeister torsion. Ann. Math. Sec. Ser. 1962, 76, 137–147. [Google Scholar] [CrossRef]
- Nicolaescu, L.I. Notes on the Reidemeister Torsion. Available online: http://www.nd.edu/~lnicolae/ (accessed on 1 February 2019).
- Van Wijk, J.J.; Cohen, A.M. Visualization of Seifert surfaces. IEEE Trans. Vis. Comput. Graph. 2006, 12, 485–496. [Google Scholar] [CrossRef]
- Collins, J. Seifert Matrix Computations. Available online: www.maths.ed.ac.uk/~v1ranick/julia/index.htm (accessed on 1 November 2018).
- van Wijk, J.J.; Cohen, A.M. SeifertView a Program to Visualize Seifert Surfaces in 3D. Available online: www.win.tue.nl/~vanwijk/seifertview (accessed on 1 November 2018).
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of three-Manifolds. Available online: http://snappy.computop.org (accessed on 1 November 2018).
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions; University of Sydney: Sydney, Australia, 2017; 5914p. [Google Scholar]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing with Bianchi groups. arXiv 2018, arXiv:1808.06831. [Google Scholar]
- Mednykh, A.D. A new method for counting coverings over manifold with finitely generated fundamental group. Dokl. Math. 2006, 74, 498–502. [Google Scholar] [CrossRef]
- Liskovets, V.A.; Mednykh, A.D. On the number of connected and disconnected coverings over a manifold. Ars. Math. Contemp. 2009, 2, 181. [Google Scholar] [CrossRef]
- Kirby, R.C.; Scharlemann, M.G. Eight faces of the Poincaré homology three-sphere. In Geometric Topology; Academic Press: New York, NY, USA, 1979; pp. 113–146. [Google Scholar]
- Kirby, R.C.; Melvin, P. The E8-manifold, singular fibers and handlebody decompositions. Geom. Topol. Publ. 1998, 2, 233–258. [Google Scholar]
- Akbulut, S.; Larson, K. Brieskorn spheres bounding rational balls. Proc. Am. Math. Soc. 2018, 146, 1817–1824. [Google Scholar] [CrossRef]
- Hilden, H.; Lozano, M.T.; Montesinos-Amilibia, J.M. On a remarkable polyhedron geometrizing the figure eight cone manifolds. J. Math. Sci. Univ. Tokyo 1995, 2, 501–561. [Google Scholar]
- Aschheim, R.; Irwin, K. Constructing numbers in quantum gravity: Infinions. In Proceedings of the Group32 Conference, Prague, Czech Republic, 9–13 July 2018. [Google Scholar]
- Wu, Y.-Q. Seifert fibered surgery on Montesinos knots. arXiv 2012, arXiv:1207.0154. [Google Scholar]
- Atiyah, M.; Marcolli, M. Anyons in geometric models of matter. J. High Energ. Phys. 2017, 76. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Król, J. How to obtain a cosmological constant from small exotic 4. Phys. Dark Univ. 2018, 19, 66–77. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity, 1st ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Amaral, M.; Aschheim, R.; Irwin, K. Quantum gravity at the fifth root of unity. arXiv 2019, arXiv:1903.10851. [Google Scholar]
| Source | Target | MIC | Braid Word | Alexander Polynomial |
|---|---|---|---|---|
| trefoil | L7n1 | QTHesse | ||
| . | L6a3 | 2QBdoily | ||
| . | 6-ditMIC | |||
| . | Dynkin | 2QB-QT MIC | ||
| fig. eight | L10n46 | 2QB doily | ||
| . | L14n55217 | 7-dit MIC | ||
| Whitehead | L12n1741 | QT Hesse | AbcDEFeDCBDacBdcdEdfCbdCddddeD | |
| . | L13n11257 | 5-dit MIC | AbCCbDaCBcDcDcbCD | |
| L12n2181 | QT Hesse | ABcdEFceGbdFaedCBcdEdfcEgbdfedc | ||
| . | L14n63905 | 2QB doily | AbCddEdFedcBdaEdfCbceDccDcBC | |
| L6a5 | L14n63788 | QT Hesse | ABCdEEEFEDcebdacEbEED | |
| ceDefedCeBdCEDe |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum Computing, Seifert Surfaces, and Singular Fibers. Quantum Rep. 2019, 1, 12-22. https://doi.org/10.3390/quantum1010003
Planat M, Aschheim R, Amaral MM, Irwin K. Quantum Computing, Seifert Surfaces, and Singular Fibers. Quantum Reports. 2019; 1(1):12-22. https://doi.org/10.3390/quantum1010003
Chicago/Turabian StylePlanat, Michel, Raymond Aschheim, Marcelo M. Amaral, and Klee Irwin. 2019. "Quantum Computing, Seifert Surfaces, and Singular Fibers" Quantum Reports 1, no. 1: 12-22. https://doi.org/10.3390/quantum1010003
APA StylePlanat, M., Aschheim, R., Amaral, M. M., & Irwin, K. (2019). Quantum Computing, Seifert Surfaces, and Singular Fibers. Quantum Reports, 1(1), 12-22. https://doi.org/10.3390/quantum1010003






