Integrated Sensing and Communication for UAV Beamforming: Antenna Design for Tracking Applications

Abstract

Unmanned Aerial Vehicles (UAVs) are promising nodes for Integrated Sensing and Communication (ISAC), but accurate Direction-of-Arrival (DoA) estimation on a small airframe is challenged by platform loading, motion, attitude, and multipath. Traditionally, DoA algorithms have been developed and evaluated for stationary, ground-based (or otherwise mechanically stable) antenna arrays. Extending them to UAVs violates these assumptions. This work designs a six-element Uniform Circular Array (UCA) at 2.4 GHz (radius $\approx 0.5\lambda$) for a quadrotor and introduces a Pose-Aware MUSIC (MUltiple SIgnal Classification) estimator for DoA. The novelty is a MUSIC formulation that (i) applies pose correction using the drone’s instantaneous roll–pitch–yaw (pose correction) and (ii) applies a Doppler correction that accounts for platform velocity. Performance is assessed using data synthesized from embedded-element patterns obtained by electromagnetic characterization of the installed array, with additional channel/hardware effects modeled in post-processing (Rician LOS/NLOS mixing, mutual coupling, per-element gain/phase errors, and element–position jitter). Results with the six-element UCA show that pose and Doppler compensation preserve high-resolution DoA estimates and reduce bias under realistic flight and platform conditions while also revealing how coupling and jitter set practical error floors. The contribution is a practical PA-MUSIC approach for UAV ISAC, combining UCA design with motion-aware signal processing, and an evaluation that quantifies accuracy and offers clear guidance for calibration and field deployment in GNSS-denied scenarios. The results show that, across 0–25 dB SNR, the proposed hybrid DoA estimator achieves <$0.5^{°}$ RMSE in azimuth and elevation for ideal conditions and ≈5°–$6^{°}$ RMSE when full platform coupling is considered, demonstrating robust performance for UAV ISAC tracking.

1. Introduction

Unmanned Aerial Vehicles (UAVs) are increasingly used in surveillance, reconnaissance, search and rescue, and spectrum monitoring missions. Their ability to operate in remote, inaccessible, or dangerous areas makes them ideal platforms for radio frequency (RF) sensing tasks, including Direction-of-Arrival (DoA) estimation. Accurate DoA estimation enables UAVs to locate ground-based emitters, support jamming avoidance, enhance navigation in GPS-denied environments, and assist in electronic warfare and disaster response scenarios [1]. DoA estimation is a key component of RF-based localization because it provides the angular bearings necessary to track drones. It relies on measuring the phase or amplitude differences of a signal received by multiple spatially separated antennas. Classic subspace-based algorithms such as multiple signal classification (MUSIC) operate on the covariance matrix of the array output and exploit the orthogonality between signal and noise subspaces. For uniform linear arrays (ULAs), MUSIC can localize multiple emitters in azimuth, but it suffers from front–back ambiguity and end-fire errors. It also cannot distinguish elevation [2]. Uniform Circular Arrays (UCAs) mitigate these issues by offering 360° azimuth coverage and the ability to estimate elevation, albeit at the cost of more complex calibration and processing.

1.1. Motivation

Phased array antennas offer the capability to steer beams electronically without moving parts, which is particularly advantageous for UAV applications where size, weight, and power (SWaP) are constrained. By applying controlled phase shifts to the individual elements, these arrays can enhance gain in a desired direction and suppress interference, allowing for real-time tracking of RF sources. Previous works have demonstrated phased array systems for DoA estimation in terrestrial and maritime environments [3,4], and some recent studies have explored their integration on aircraft and satellites [5,6]. At the same time, broader research within the UAV and wireless communication community has addressed interference mitigation, adaptive swarm mission planning, UAV positioning using 5G New Radio, and digital-twin-empowered optimization for UAV networks [7,8,9,10,11,12], all of which highlight the increasing demand for resilient and intelligent UAV sensing architectures.

Accurate DoA estimation also depends on array geometry, inter-element spacing and platform effects. When antennas are mounted on UAVs, electromagnetic interactions with the airframe can distort the radiation pattern, potentially degrading estimation accuracy. Current research explores several hardware architectures to address these challenges [13]. For example, a low-cost switched-beam system uses six circularly arranged directional antennas connected to a single receiver through RF switches to estimate the angle of arrival of drone video signals [14]. It achieved a mean error below $5^{°}$ while eliminating multi-receiver synchronization. Distributed phased-array concepts for UAV swarms are also being explored. A recent prototype uses magnetic, hands-free RF connectors to dock multiple UAVs mid-flight, maintaining precise inter-element spacing and phase coherence while steering beams toward multiple directions [15,16]. These developments complement earlier work in communication system analysis and optimization for future aviation and wireless networks [17,18,19,20].

Recent work has strengthened ISAC foundations specifically for UAVplatforms. On the network side, Bithas et al. analyze aerial ISAC networks and quantify the sensing–communication trade-off (coverage probability vs. detection probability) under shadowing and interference, including a UAV selection policy that improves performance [21]. At the channel level, Li et al. propose a UAV ISAC channel model with joint/shared clusters and birth–death (B–D) evolution to capture altitude-dependent angular/delay statistics, offering a physics-grounded basis for UAV ISAC link design [22]. For algorithmic coupling between radar and comms, Ding et al. present a fully distributed joint radar–communication optimization for distributed airborne radar that explicitly enforces communication constraints while maximizing AOA-based localization performance [23]. At the waveform level, Li et al. design complementary-sequence JRC waveforms (and a Doppler-resilient variant) that reduce range sidelobes without degrading BER, directly relevant to ISAC tracking on moving aerial platforms [24]. From a hardware and phased-array integration perspective, Sen et al. review RF front-ends, antenna/beamformer options, and self-interference cancellation for JCRS, highlighting practical constraints for compact arrays and co-designed transceivers [25]. These studies complement our focus on UAV-mounted UCA manifolds, platform coupling, and pose/Doppler-aware MUSIC, and they motivate our hybrid WAA–CTF estimator and platform-aware validation.

1.2. Research Gap and Contributions

A major challenge in implementing phased arrays on UAVs lies in accounting for electromagnetic interactions between the antenna array and the drone body. The proximity of motors, arms, and batteries can distort the radiation pattern, reduce gain, and introduce multipath effects. These platform-specific influences are often overlooked in simplified array models, and limited work has been carried out on simulating compact phased arrays mounted on UAVs, especially under non-planar surfaces and platform-induced distortions. This paper presents a simulation-based study of a drone-mounted phased array using Altair FEKO. A compact circular array is designed and evaluated for its Direction-of-Arrival (DoA) estimation capability across a range of steering angles and incidence scenarios. Unlike prior work that assumes ideal free-space conditions, this study incorporates the full 3D electromagnetic model of a quadcopter to capture realistic loading, shadowing, and scattering effects. The results provide new insights into angular resolution, main lobe accuracy, and side lobe performance for airborne RF sensing.

Furthermore, a  Pose-Aware, Doppler-Aware MUSIC algorithmis developed to address UAV dynamics. Standard MUSIC assumes a fixed array; however, UAVs experience pose variations (yaw, pitch, roll) and Doppler shifts due to motion. The proposed algorithm compensates for both effects by modifying the array manifold and covariance modeling. To enhance efficiency, a  hybrid Coarse-to-Fine (CTF) and Weighted Average Algorithm (WAA) framework is introduced, where the CTF stage identifies coarse candidate regions and the WAA stage refines estimates via intelligent spectrum search. This reduces computational complexity by orders of magnitude compared with exhaustive searches while retaining high resolution.

The contributions of this paper are

• Development of a phased array antenna model for UAV integration and simulation of platform effects.
• Introduction of a novel Pose-Aware, Doppler-Aware MUSIC algorithm with hybrid CTF–WAA optimization for robust, real-time DoA estimation.
• Quantitative analysis of UAV-based DoA performance for low-altitude, passive RF localization tasks.

This study supports the demand for lightweight and accurate RF sensing on UAVs and provides a foundation for experimental validation and system-level deployment.

2. Phased Array Antenna Design

In UAV-based RF sensing systems, the design of a compact and lightweight phased array antenna is crucial for ensuring omnidirectional angular coverage, robust beam steering, and integration within the platform’s size, weight, and power (SWaP) constraints. This section presents the design methodology of a Uniform Circular Array (UCA), including element selection, frequency choice, array geometry, and beam steering principles tailored to UAV integration.

A half-wavelength dipole was selected as the fundamental antenna element owing to its omnidirectional radiation in the azimuth plane, simple structure, and ease of simulation. The operating frequency is set to 2.4 GHz, corresponding to the industrial, scientific, and medical (ISM) band commonly used for UAV command and control, telemetry, and real-time video transmission. This frequency ensures moderate propagation range, low atmospheric loss, and manageable element size, making it suitable for both simulation and physical implementation.

To achieve ${360}^{°}$ azimuthal coverage and reduce direction-dependent performance variations, a Uniform Circular Array (UCA) configuration was chosen over a Uniform Linear Array (ULA). Unlike ULAs, which suffer from reduced performance at endfire angles, UCAs offer rotational symmetry, making them inherently robust to changes in UAV yaw or heading. This makes them well-suited for airborne platforms operating in dynamic environments [26]. The detailed rationale behind each array parameter is summarized in

Table 1. UCA Design Parameters and Rationale for UAV-Based DoA Estimation.

Parameter	Value/Description	Rationale
Frequency	2.4 GHz	Common ISM band used for UAV telemetry, control, and video transmission. Provides moderate propagation range, low atmospheric loss, and compact element size ($\lambda =125$ mm). This wavelength yields ∼7.5 cm array diameter suitable for small multirotor top plates.
Element Type	Half-wavelength dipole	Omnidirectional azimuthal radiation and simple geometry enabling rapid modeling and simulation without substrate modeling.
Array Configuration	UCA	Ensures ${360}^{°}$ steering and yaw-independent response. Mitigates front–back ambiguity of ULAs and supports azimuth/elevation estimation.
No. of Elements	6	Provides 60° uniform element spacing ($s\approx \lambda /2$), giving fine angular resolution without excessive coupling or feed complexity; increasing N beyond 6 offers marginal resolution gain while adding ports, weight, and computation.
Array Radius (R)	$0.3\lambda$ (≈37.5 mm)	Maintains inter-element spacing ≈$\lambda /2$ to suppress grating lobes. Larger radii (>$0.5\lambda$) could introduce mechanical overhang on compact UAVs.
Polarisation	Linear (horizontal)	Matches typical ground-based transmitters and simplifies feeding geometry.
Substrate	N/A	Omitted to avoid unnecessary dielectric modeling in free-space characterization; simplifies early-stage array optimization.
Beam Steering Range	0°–360° (azimuth)	Full circular tracking capability using electronic phase control without mechanical rotation.
Target UAV	Small quadcopter	Maintains low mass and compact footprint for platform-mounted evaluation.

. In addition, similar UCA settings are used in recent Direction Finding (DF) systems (e.g., a  six-element UCA operating at 2.4 GHz with approximately half-wavelength inter-element spacing), contributing to the progress of similar existing work [1].

Table 1 provides a concise justification of the chosen configuration. The six-element, 2.4 GHz UCA with radius $0.3\lambda$ offers an optimal balance between spatial resolution, coupling control, and ease of airframe integration. A half-wavelength dipole was selected as the array element due to its omnidirectional azimuthal radiation pattern, compact size, and ease of simulation in free space. Dipoles provide uniform angular sensitivity, which is ideal for 360° Direction-of-Arrival (DoA) estimation in Uniform Circular Arrays (UCAs). Unlike microstrip patches, dipoles do not require substrate modeling, simplifying design and reducing computational complexity. Their symmetric radiation and structural simplicity make them well-suited for circular arrangements on small UAV platforms, enabling effective beam steering analysis with minimal fabrication constraints.

From a simulation standpoint, dipoles can be efficiently modeled using thin-wire segments in Altair FEKO, allowing for rapid iteration and reduced meshing complexity. This facilitates focused evaluation of array behavior without the added overhead of substrate modeling, dielectric losses, or feed structure optimization typically associated with microstrip antennas. Moreover, dipoles are lightweight, structurally simple, and commonly used in UAV telemetry systems, making them viable for eventual physical integration.

2.1. Single Dipole Element Design

A half-wavelength dipole antenna was designed and simulated at 2.4 GHz using Altair FEKO to serve as the element for the Uniform Circular Array. The parameters used to design the dipole element is summarized in

Table 2. Design Parameters for Half-Wavelength Dipole Element at 2.4 GHz.

Parameter	Value	Description
Operating Frequency ($f_0$)	2.4 GHz	Center frequency in the ISM band
Wavelength ($\lambda$)	125 mm	Free-space wavelength at 2.4 GHz
Total Dipole Length (L)	62.5 mm	Half-wavelength dipole (0.5 $\lambda$)
Arm Length (L/2)	31.25 mm	Each dipole arm measured from the feedpoint
Feed Gap	2 mm	Small gap at the center for voltage source excitation
Wire Radius	0.5 mm	Thin wire approximation for ideal dipole
Material	PEC (Perfect Electric Conductor)	Idealized conductor for simulation
Simulation Tool	Altair FEKO (MoM)	Method of Moments solver in CADFEKO
Matching Bandwidth ($S_{11}$ < −10 dB)	2.13–2.53 GHz	−10 dB return loss bandwidth from simulation
Maximum Simulated Gain	∼1.7 dBi	Gain in the azimuthal plane (xy-plane)
Polarization	Linear	Electric field aligned with the z-axis

below.

The dipole consists of two wire segments, each 31.25 mm in length, and fed by a discrete voltage source at the center. Full-wave simulations were carried out to evaluate return loss and radiation characteristics in free space.

The simulated $S_{11}$ curve (Figure 1) shows a −10 dB impedance bandwidth spanning from 2.13 GHz to 2.53 GHz, with a minimum reflection coefficient of −14.7 dB near 2.33 GHz. This indicates good impedance matching across the desired ISM band. The corresponding 3D radiation pattern (Figure 2) exhibits the expected doughnut-shaped profile, characteristic of a dipole in free space, with peak gain oriented in the azimuthal plane and deep nulls along the vertical (z-axis). The maximum gain is approximately 1.7 dBi, providing an omnidirectional response suitable for circular array deployment.

2.2. UCA Construction and Steering Setup

2.2.1. UCA Geometry Construction

A six-element Uniform Circular Array (UCA) was designed in Altair FEKO (CADFEKO) using half-wave dipole antennas tuned to resonate at 2.4 GHz. Each dipole was modeled with a wire of an overall length of approximately $0.47\lambda$ and a radius of 0.5 mm, fed by a delta-gap voltage source at the center split.

The dipole elements were positioned uniformly on a circular ring of radius R. For the present configuration, a normalized radius of $0.5\lambda$ was selected to ensure arc spacing close to $\lambda /2$, thereby minimizing mutual coupling while avoiding grating lobes during azimuthal beam steering. The element azimuths are given by

$${\varphi }_n={\varphi }_{start}+{\displaystyle \frac{2\pi (n-1)}{N}},n=1,2,...N$$

(1)

where N is the number of elements (here, N = 6), and ${\varphi }_{start}$ denotes the angular reference of the first element relative to the array axis. The constructed UCA and the corresponding radiation pattern without any individual excitation are shown in Figure 3. The array geometry is defined in the UAV body–frame coordinates and later rigidly attached to the quadcopter model (Section 3), so the same analytically specified element positions and geometry are used in both free-space and platform-integrated simulations.

2.2.2. Beam Steering Setup in FEKO

Each dipole element was excited with a voltage source of equal magnitude (1 V), and progressive phase shifts were applied to the sources according to the steering law. CADFEKO’s scripting interface (Lua API) was used to automate the calculation and assignment of excitation phases.

1.

Phase steering law

The required excitation phase for element n to form a beam in the desired direction $({\theta }_0,{\varphi }_0)$ is derived from the UCA array factor:

$${\psi }_n=-kR\sin {\theta }_0\cos ({\varphi }_n-{\varphi }_0)$$

(2)

where

• $k={\displaystyle \frac{2\pi }{\lambda }}$ is the wave number;
• R is the array radius;
• ${\theta }_0$ and ${\varphi }_0$ are steering elevation and azimuth angles;
• ${\varphi }_n$ is the angular position of the element n.

Converting to degrees (as required in FEKO)

$$\psi {[}^{°}]=-{\displaystyle \frac{{360}^{°}R}{\lambda }}\sin {\theta }_0\cos {\varphi }_n-{\varphi }_0$$

(3)

for azimuthal steering (${\theta }_0={90}^{°}$), this reduces to

$$\psi {[}^{°}]=-{\displaystyle \frac{{360}^{°}R}{\lambda }}\cos {\varphi }_n-{\varphi }_0$$

(4)

2.

Excitation assignment

In CADFEKO, a single solution configuration (StandardConfiguration1) was defined. The Lua script iterates over all sources (VoltageSource1...VoltageSourceN) and assigns the computed ${\psi }_n$ values to the Phase property of each source. Magnitudes remain unity unless amplitude tapering is introduced (e.g., Taylor distribution for sidelobe suppression).

3.

Pseudocode for UCA steering

The .luascript was structured to minimize user effort, with interactive forms for input and automatic generation of phase-steered models. The high-level pseudocode is shown in Algorithm 1.

The Lua script was implemented to automatically assign progressive phase excitations to the six dipole ports in the Uniform Circular Array (UCA). By varying the steering azimuth ${\varphi }_0$, new excitation sets were created without manual intervention. This enabled rapid generation of multiple steering cases, significantly reducing modeling time and potential errors.

The steering angles evaluated were

$${\varphi }_0\in \{0^{°},{60}^{°},{120}^{°},{180}^{°},{240}^{°},{300}^{°}\},{\theta }_0={90}^{°}$$

corresponding to six uniformly distributed beam directions in the azimuth plane.

The excitation phases obtained from the Lua script for six steering angles are summarized in

Table 3. Excitation phases (in degrees) for each port of the six-element UCA.

Steering Angle $({\mathit{\theta }}_0,{\mathit{\varphi }}_0)$	VS1	VS2	VS3	VS4	VS5	VS6
${90}^{°},0^{°}$	179.88	$-90.06$	$90.06$	$-179.88$	$90.06$	$-90.06$
${90}^{°},{60}^{°}$	$-90.06$	179.88	$-90.06$	90.06	$-179.88$	90.06
${90}^{°},{120}^{°}$	90.06	$-90.06$	179.88	$-90.06$	90.06	$-179.88$
${90}^{°},{180}^{°}$	$-179.88$	90.06	$-90.06$	179.88	$-90.06$	90.06
${90}^{°},{240}^{°}$	90.06	$-179.88$	90.06	$-90.06$	179.88	$-90.06$
${90}^{°},{300}^{°}$	$-90.06$	90.06	$-179.88$	90.06	$-90.06$	179.88

. Each voltage source corresponds to one dipole element of the UCA, with equal magnitude excitations of 1 V and phase shifts as listed. The table highlights the symmetry of the UCA: opposite elements are excited with approximately conjugate phases, and the patterns repeat with ${180}^{°}$ periodicity. Small deviations from exact multiples of ${90}^{°}$ or ${180}^{°}$ (e.g., $179.{88}^{°}$ instead of ${180}^{°}$) arise from numerical precision in the steering law computation. These phase assignments ensure that the main beam is directed towards the desired azimuth angle ${\varphi }_0$ while maintaining the array’s circular symmetry.

Algorithm 1 Lua Script for UCA Steering Setup

1: Get FEKO application instance 2: Define: 3: Frequency f (GHz) 4: Number of elements N 5: Array radius R (mm) 6: Steering angles $({\theta }_0,{\varphi }_0)$ (degrees) 7: Start angle ${\varphi }_{\mathrm{start}}$ of element #1 8: Compute wavelength $\lambda =c/f$ 9: Compute wavenumber $k=2\pi /\lambda$ 10: for $n=1$ to N do 11:     Compute element angle: $${\varphi }_n={\varphi }_{\mathrm{start}}+{\displaystyle \frac{2\pi (n-1)}{N}}$$ 12:     Compute excitation phase (degrees): $${\psi }_n=-{\displaystyle \frac{360R}{\lambda }}\sin {\theta }_0\cos ({\varphi }_n-{\varphi }_0)$$ 13:     Wrap ${\psi }_n$ to range $[-{180}^{°},{180}^{°}]$ 14:     Identify source name “VoltageSource$\left[n\right]$” 15:     Retrieve source properties 16:     Set Phase = ${\psi }_n$, Magnitude = 1 V 17:     Update properties in configuration 18: end for 19: Save updated model as $theta\_{\theta }_0\_phi\_{\varphi }_0.cfx$

2.3. Evaluation of Reflection Coefficient

The $S_{11}$ plots at each $\varphi$ are shown in Figure 4. In all cases, the $-10$ dB passband consistently spans

$$f_L\approx 2.265\mathrm{GHz}\mathrm{to}{f}_H\approx 2.670\mathrm{GHz},$$

with variations of only a few megahertz across ${\varphi }_0$. The corresponding fractional bandwidth is

$$\mathrm{FBW}\approx {\displaystyle \frac{f_H-f_L}{(f_H+f_L)/2}}\approx {\displaystyle \frac{0.405}{2.4675}}\approx 16.4\%.$$

The minimum of $|S_{11}^{\mathrm{active}}|$ occurs close to the design frequency of 2.4 GHz for every steering case, with a depth of approximately $-12.3\pm 0.2$ dB. Importantly, at 2.4 GHz, the active reflection coefficient remains below $-10$ dB for all ${\varphi }_0$, confirming adequate matching across the ISM band. The near-invariance of $f_L$, $f_H$, and the notch depth with steering demonstrates that the UCA maintains stable impedance characteristics under azimuthal scan, which is beneficial for downstream DoA processing.

2.4. Far Field Patterns for the UCA

Figure 5 shows the normalized 2D azimuth patterns ($\theta ={90}^{°}$) for six steering angles ${\varphi }_0\in \{0^{°},{60}^{°},{120}^{°},{180}^{°},{240}^{°},{300}^{°}\}$. In each case, the main beam aligns with the commanded azimuth, confirming correct phase excitation. A complementary back lobe appears at ${\varphi }_0+{180}^{°}$, as expected for a single-ring UCA.

The measured half-power beamwidths (HPBWs) from the FEKO plots are listed in

Table 4. Measured HPBW and first SLL for each steering angle at $f=2.4$ GHz, $\theta ={90}^{°}$.

Steering Angle ${\mathit{\varphi }}_0$	HPBW (deg)	SLL
$0^{°}$	58.66	$-6.49$
${60}^{°}$	42.71	$0.01$
${120}^{°}$	42.71	$0.01$
${180}^{°}$	58.66	$-6.49$
${240}^{°}$	42.71	$0.01$
${300}^{°}$	42.71	$0.01$

. The broader beams at ${\varphi }_0=0^{°}$ and ${180}^{°}$ compared to the ∼$42.7^{°}$ HPBW at the other scan angles are attributed to the interaction between the element pattern and the active array factor under scan.

In the cuts shown in Figure 5, the sidelobe level (SLL) is reported in linear units and defined as the ratio between the maximum beam strength and the second-largest beam. The apparent variation between $\mathrm{HPBW}\approx {59}^{°}$ and ≈${43}^{°}$, and between the corresponding SLL values in Table 4, is primarily a consequence of how the fixed $\theta ={90}^{°}$ cut is taken for each steered beam in the global reference frame. Depending on the steering angle, this cut may intersect the main lobe together with its complementary back lobe, or only small local ripples, so the extracted HPBW/SLL values are cut-dependent rather than reflecting a true physical asymmetry between, for example, $0^{°}$ and ${180}^{°}$. The underlying 3D UCA beams are rotationally symmetric, and hence the intrinsic angular resolution of the array is essentially uniform with azimuth. In the MUSIC results that follow, the full 3D manifold is used, so any mild scan-angle dependence of the local pseudospectrum shape is captured without implying a change in the fundamental array resolution.

2.5. Three-Dimensional Far-Field Radiation Patterns

Figure 6 presents the three-dimensional realized gain patterns of the six-element UCA at $f=2.4$ GHz for steering angles ${\varphi }_0\in \{0^{°},{60}^{°},{120}^{°},{180}^{°},{240}^{°},{300}^{°}\}$ with ${\theta }_0={90}^{°}$. In each case, the main lobe is directed towards the commanded azimuth, validating the excitation control.

The 3D plots confirm the observations made from the 2D azimuth cuts:

• For ${\varphi }_0=0^{°}$ and ${180}^{°}$, the main beams are broad ($\mathrm{HPBW}\approx {59}^{°}$) with sidelobe levels around $-6.5$ dB.
• For ${\varphi }_0={60}^{°}$, ${120}^{°}$, ${240}^{°}$, and ${300}^{°}$, the beams are narrower ($\mathrm{HPBW}\approx {43}^{°}$) but exhibit higher sidelobe levels (≈0 dB relative to the main lobe).
• A complementary back lobe appears at ${\varphi }_0+{180}^{°}$, as expected for a single-ring UCA.

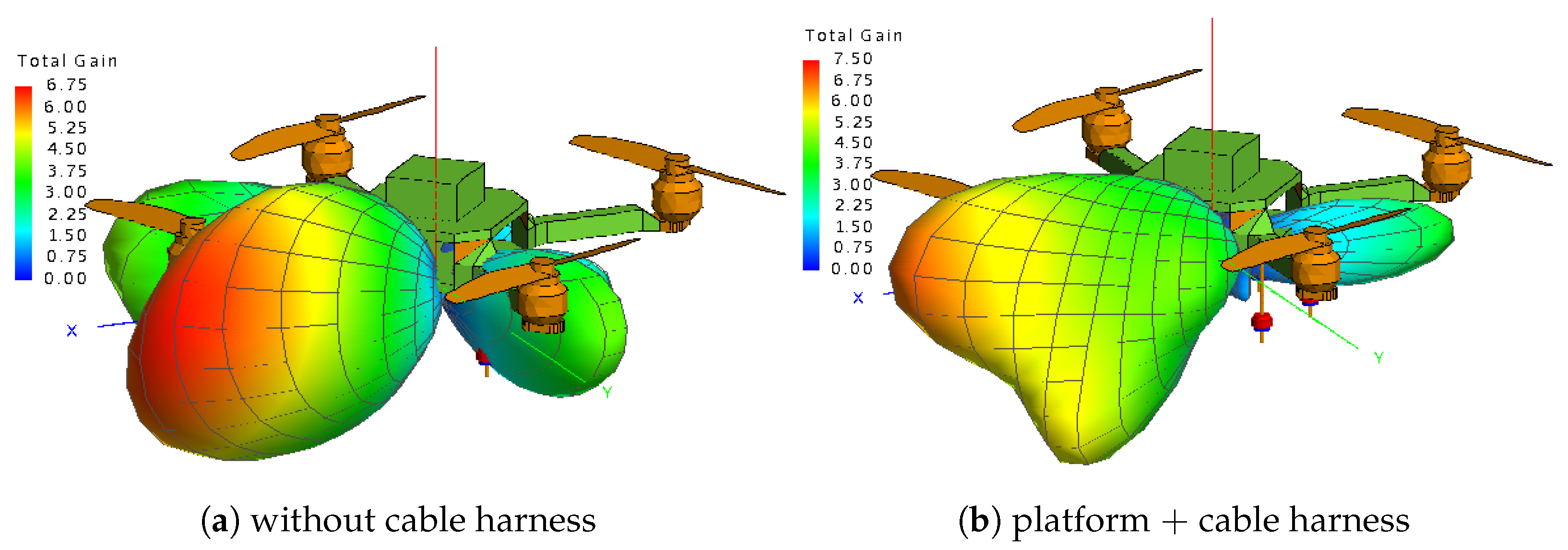
The realized gain ranges from 6–7.5 dB in the main lobe direction, providing adequate directivity for DoA estimation. The 3D visualization also illustrates the tradeoff between beamwidth and sidelobe control at different steering angles.

3. Integration with UAV

3.1. UAV Platform Model and Material Assignment

A UAV CAD model was imported into CADFEKO and healed to remove sub-$\lambda /20$ details at 2.4 GHz ($\lambda \approx 125$ mm). The quadcopter and UCA are defined in a common body–frame coordinate system. The six-element UCA is placed such that the inter-element spacing and azimuth angles match the UCA design in the previous section. To obtain a realistic mounting surface, the imported quadcopter CAD model was uniformly scaled such that the central plate accommodates the chosen UCA radius. The UCA is then rigidly attached to this plate, and the element coordinates and inter-element distances are checked within CADFEKO.

Platform components were assigned materials as summarized in

Table 5. Material assignment for the UAV platform at 2.4 GHz.

Component	FEKO Model	${\mathit{\epsilon }}_{\mathit{r}}$	$tan\mathit{\delta }$	$\mathit{\sigma }$ [S/m]	${\mathit{\mu }}_{\mathit{r}}$
Body/centre plates	ABS (dielectric)	2.7	0.01	-	1.0
Arms	ABS (dielectric)	2.7	0.01	-	1.0
Motors & mounts	PEC	-	-	∞	1.0
Propellers	Free space (omitted)	-	-	-	1.0

. The body and arms are modeled as ABS to reflect the library geometry’s molded-plastic construction; using a homogeneous dielectric (${\epsilon }_r=2.7$, $tan\delta =0.01$) captures platform loading while keeping the mesh lightweight. These are standard properties listed in the FEKO database. Motors and mounts are set to PEC to represent metallic cans whose wall thickness is many skin depths at 2.4 GHz, so finite-$\sigma$ losses are negligible for DoA behavior; this also captures realistic shadowing. Propellers are omitted (treated as free space) because their rotating, thin plastic blades add little to steady-state beam shapes but greatly increase meshing complexity. This assignment captures the dominant effects, dielectric loading from the body/arms and metallic shadowing from the motors, at minimal solver cost.

The UAV with the UCA is shown in Figure 7. The different colors show different material assignments as summarised in Table 5.

3.2. Cable Harness Modeling

To capture reradiation and common-mode effects, a coaxial harness was modeled using CADFEKO’s cable engine. An RG316-like cross-section was defined with copper conductors ($\sigma =5.8\times {10}^7$ S/m), PTFE dielectric (${\epsilon }_r\approx 2.1$), core radius 0.25 mm, dielectric outer radius 0.76 mm (OD ≈ 1.52 mm), and shield outer radius 1.25 mm (OD ≈ 2.5 mm). The electrical harness is modeled as four PEC cable runs representing the DC power/signal wiring from the central battery/ESC bay to each motor. For every arm, a straight line cable path is defined in CADFEKO, starting at the vehicle center and following the underside of the arm out to the motor mount. For embedded-element pattern (EEP) calculations, the excited element was driven with a 1 V source (50 $\Omega$), while all non-excited elements were terminated in 50 $\Omega$ at the cable ends. This configuration preserves realistic feed/return currents and their interaction with the platform.

3.3. Simulation Matrix and Solver Settings

Three configurations were solved to isolate platform contributions:

• (A) Isolated UCA (baseline);
• (B) Platform with metals/CFRP (no cables);
• (C) B + cables.

3.4. Platform Effects on Embedded-Element Patterns (EEPs)

Figure 8 shows the 3D total-gain lobe of a UCA in two cases. One case considers the effect of the UAV (platform only), and the other case adds the cables/harness. The platform introduces two dominant mechanisms: (i) dielectric loading from the ABS body/arms that broadens the pattern and reduces peak gain and (ii) metallic shadowing by the motors/mounts that creates azimuthal sectors with suppressed radiation. The principal lobe remains roughly horizontal, but its shape becomes clearly non-circular with shadowed “valleys” co-located with motor azimuths.

A quantitative comparison is given by the $\varphi =0^{°}$ cuts in Figure 9, plotted in linear gain. For the platform-only case the main lobe is centred near $\theta \approx {85}^{°}$ with an HPBW of ≈${73}^{°}$.

Adding the cable harness routed along the UAV arms produces three clear changes that are consistent across frequency points around 2.4 GHz:

• The main-lobe peak shifts slightly in $\theta$ and its relative level changes with respect to neighboring lobes, reflecting additional reradiation from the cables.
• The broad null region around $\theta \approx {145}^{°}$ deepens and additional shallow minima appear, consistent with stronger induced currents on the motor cans, brackets, and harness.
• There are additional ripples in the gain plot which can be attributed to currents on the cables.

The horizontal coverage of the element remains largely intact and the UCA retains a usable gain. For DoA operation, this implies that platform-aware embedded-element patterns must be used to construct the array manifold. Otherwise, the observed distortions will translate into bias and increased error.

Using EEPs from configuration (C) in the steering-vector construction preserves the correct amplitude/phase weighting per element, which is critical for subspace methods. In this case, the cable-induced asymmetry primarily alters amplitude tapering (raising effective SLL by ≈1–2 dB) rather than the main-beam pointing, so MUSIC/PA_MUSIC resolution is largely maintained while detection probability dips in the shadow sectors. This matches the measured cuts (refer to the main beam (HPBW $\approx {73}^{°}$) being preserved, while deep minima become deeper and slightly wider with cables. The quantified changes in EEPs across the three configurations (A–C) are summarized in

Table 6. Quantified platform effects on EEPs.

Metric (at $\mathit{f}=2.4$ GHz, $\mathit{\varphi }=0^{°}$)	A: Isolated	B: Platform Only	C: Platform + Cables	Change (C vs. B)
Peak elevation angle ${\theta }_{\mathrm{pk}}$	–	≈${85}^{°}$	≈${85}^{°}$	slight tilt (few °)
HPBW (elevation)	–	≈73°	≈${73}^{°}$	≈$0^{°}$ (no material change)
First sidelobe level (SLL)	–	≈$-14$ dB	higher sidelobe floor	increased by ∼1–2 dB
Main-lobe peak gain	–	reference	reference $-0.5$ to $-1.0$ dB	decreased by 0.5–1.0 dB
Notable nulls/shadowing	–	broad null near $\theta \approx {145}^{°}$	deeper nulls in motor sectors	deeper by a few dB
Ripple near broadside	–	mild	visible common-mode ripple	increased ripple

.

4. Pose and Doppler-Aware MUSIC with WAA for a Moving UAV-Mounted UCA

4.1. Classical MUSIC with a UCA

In the classical MUSIC algorithm for UCA, we consider a narrowband, far-field source at carrier $f_0$ and wavelength $\lambda$, impinging on an M-element Uniform Circular Array (UCA) of radius R. The m-th element lies at an angle ${\gamma }_m=2\pi m/M$ with position $p_m={[R\cos {\gamma }_m,R\sin {\gamma }_m,0]}^T$. For a direction of arrival (DoA) $(\theta ,\varphi )$ with unit vector $r={[-\sin \theta \cos \varphi ,-\sin \theta \sin \varphi ,\cos \theta ]}^T$, the relative delay and phase are

$${\tau }_m=-{\displaystyle \frac{R}{c}}\sin \theta \cos (\varphi -{\gamma }_m),{\phi }_m(\theta ,\varphi )=-\beta R\sin \theta \cos (\varphi -{\gamma }_m),\beta =\frac{2\pi }{\lambda },$$

and the UCA steering vector is

$$a(\theta ,\varphi )={\left[e^{-j{\phi }_0(\theta ,\varphi )},\dots ,e^{-j{\phi }_{M-1}(\theta ,\varphi )}\right]}^T.$$

(5)

For K uncorrelated sources with the response matrix $A={\left[a({\theta }_k,{\varphi }_k)\right]}_{k=1}^K$, the array model is $x\left[n\right]=As\left[n\right]+v\left[n\right]$. From N snapshots, the sample covariance matrix $\widehat{R}$ is estimated as

$$\widehat{R}={\displaystyle \frac{1}{N}}\sum _{n=1}^{N}x\left[n\right]x{\left[n\right]}^H$$

(6)

The sample covariance admits the eigen-decomposition.

$$\widehat{R}=U_S{\Lambda }_S{U}_S^H+U_N{\Lambda }_N{U}_N^H,$$

(7)

where $U_S$ and $U_N$ span the signal and noise subspaces, respectively. The MUSIC pseudospectrum is

$$P_{\mathrm{MUSIC}}(\theta ,\varphi )={\displaystyle \frac{1}{a^H(\theta ,\varphi )U_N{U}_N^{H}a(\theta ,\varphi )}},$$

(8)

whose peaks estimate the DoAs. (Equations (5)–(8) in this form are laid out for a UCA in our reference.)

UCAs provide 360° azimuth coverage but exhibit elevation-angle sensitivity and azimuthal ambiguities near the array plane. Practical systems, therefore, need careful calibration and robust processing. In related UCA-based 2D-DoA work, Mei et al. [16] study a switching UCA (SUCA) architecture with fewer RF chains and use a deep feedforward network to complete the covariance matrix of a fully sampled UCA (FUCA) before applying classical MUSIC, demonstrating that FUCA-level performance can be approached with reduced hardware complexity. Zhu et al. [1] build a real-time UAV RF direction-finding system using a six-element UCA and a hybrid MUSIC-WAA search, showing that a weighted-average refinement can reduce the number of spectral evaluations by orders of magnitude while maintaining good 2D accuracy. Our PA–MUSIC and Hybrid CTF+WAA formulation follows the same broad paradigm of UCA-based 2D–DoA estimation, but focuses on pose-aware manifolds and drone platform loading, with WAA used as a principled continuous refinement step within a platform-calibrated simulation framework.

4.2. Pose- and Doppler-Aware MUSIC for a Moving UCA

4.2.1. Pose-Aware Steering and Stacking

Let $R_{b\to i}\left(t\right)$ be the rotation from the UAV body frame to an inertial/world frame at time t. Let $u_i(\theta ,\varphi )$ denote the unit vector expressed in the inertial coordinates. The corresponding body–frame direction at time t is then

$$u_b\left(t\right)=R_{b\to i}{\left(t\right)}^T{u}_i(\theta ,\varphi )$$

(9)

We evaluate the UCA manifold at $u_b\left(t\right)$, i.e., $a({\theta }_b\left(t\right),{\varphi }_b\left(t\right))$, and stack several short, pose-bounded time slices into an augmented vector:

$$a_{\mathrm{aug}}(\theta ,\varphi )=\left[\begin{array}{c}a({\theta }_b\left(t_1\right),{\varphi }_b\left(t_1\right))\\ ⋮\\ a({\theta }_b\left(t_K\right),{\varphi }_b\left(t_K\right))\end{array}\right],x_{\mathrm{aug}}\left[n\right]=\left[\begin{array}{c}x\left(t_1\right)\left[n\right]\\ ⋮\\ x\left(t_K\right)\left[n\right]\end{array}\right]$$

(10)

We then form an augmented covariance ${\widehat{R}}_{\mathrm{aug}}={\displaystyle \frac{1}{N}}{\sum }_n{x}_{\mathrm{aug}}\left[n\right]x_{\mathrm{aug}}{\left[n\right]}^H$ (optionally with exponential forgetting and forward-backward averaging) and compute the MUSIC cost with the pose-aware steering:

$$P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )={\displaystyle \frac{1}{a_{\mathrm{aug}}^H(\theta ,\varphi )U_N{U}_N^H{a}_{\mathrm{aug}}(\theta ,\varphi )}}$$

(11)

Here $U_N$ collects the noise-subspace eigenvectors of ${\widehat{R}}_{\mathrm{aug}}$, and the denominator $a_{\mathrm{aug}}^{\mathrm{H}}(\theta ,\varphi )U_N{U}_N^{\mathrm{H}}{a}_{\mathrm{aug}}(\theta ,\varphi )$ measures how much of the pose-aware steering vector lies in the noise subspace. True DoA directions lie almost entirely in the signal subspace, so this projection becomes small and $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$ forms sharp peaks at the correct angles.

The changing attitude creates a synthetic angular aperture, stacking pose-bounded slices “virtually stabilises” the array in the world frame while preserving MUSIC’s subspace property.

4.2.2. Doppler De-Rotation from Platform Motion

For a static emitter and moving receiver, the Doppler is (approximately) common across channels:

$$f_D\left(t\right)={\displaystyle \frac{v_{\mathrm{rx}}\left(t\right)·u_i(\theta ,\varphi )}{\lambda }}$$

(12)

Before stacking, we de-rotate the baseband data with a kinematic carrier frequency offset (CFO) estimate:

$$\tilde{x}\left(t_k\right)\left[n\right]=e^{-j2\pi {\widehat{f}}_D(\theta ,\varphi )t_k}x\left(t_k\right)\left[n\right]$$

(13)

then use $\tilde{x}$ to form ${\widehat{R}}_{\mathrm{aug}}$ and evaluate (11). (Equivalently, a light 1-D co-search in $f_D$ can be added around the kinematic prior).

In the current study, the rotation matrices $R_{b\to i}\left(t\right)$ are driven by synthetic roll–pitch–yaw trajectories generated in MATLAB 2025a to emulate small quadcopter maneuvers. No real IMU data are used at this stage, and the pose is assumed to be known exactly by the estimator. A full experimental validation with measured IMU logs and explicit attitude-error modeling is left to future work.

In a practical UAV implementation, the quantities used in (9)–(13) would be obtained directly from the onboard sensors. The rotation $R_{b\to i}\left(t\right)$ is constructed from the attitude and velocity estimate (yaw-pitch-roll) provided by the flight controller (or IMU onboard). In the case of GNSS-denied environments, the velocity can be obtained from alternative estimators such as visual odometry or radar/optical flow sensors. These sensor streams are fed into the PA-MUSIC processing chain in real time, so that pose rotation and Doppler de-rotation are driven by the same navigation data already used for vehicle control.

4.3. Search Methods for PA-MUSIC: CTF, WAA, and Hybrid

4.3.1. Coarse-to-Fine (CTF) Grid Refinement

Given $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$, a two-stage coarse-to-fine scan evaluates on a coarse grid ${\mathcal{G}}_c={\mathrm{\Theta }}_c\times {\mathrm{\Phi }}_c$,

$$({\widehat{\theta }}_c,{\widehat{\varphi }}_c)=arg\underset{(\theta ,\varphi )\in {\mathcal{G}}_c}{max}{P}_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi ),$$

(14)

then refines within a local fine grid ${\mathcal{G}}_f={\mathrm{\Theta }}_f\times {\mathrm{\Phi }}_f$ centered at $({\widehat{\theta }}_c,{\widehat{\varphi }}_c)$,

$$({\widehat{\theta }}_{\mathrm{CTF}},{\widehat{\varphi }}_{\mathrm{CTF}})=arg\underset{(\theta ,\varphi )\in {\mathcal{G}}_f}{max}{P}_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi ).$$

(15)

The cost scales with grid sizes,

$$N_{\mathrm{eval}}^{\mathrm{CTF}}=|{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+|{\mathrm{\Theta }}_f\left|\right|{\mathrm{\Phi }}_f|,$$

(16)

and discretization induces a gridding floor,

$$\left|{\widehat{\theta }}_{\mathrm{CTF}}-{\theta }^{𓇼}\right|\lesssim \frac{1}{2}{\delta }_{\theta },\left|{\widehat{\varphi }}_{\mathrm{CTF}}-{\varphi }^{𓇼}\right|\lesssim \frac{1}{2}{\delta }_{\varphi }.$$

(17)

4.3.2. WAA–MUSIC (Continuous, Seedless)

WAA–MUSIC replaces dense gridding with a population-based continuous maximization of (11),

$$(\widehat{\theta },\widehat{\varphi })=arg\underset{\theta ,\varphi }{max}{P}_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi ),\mathcal{J}(\theta ,\varphi )=-log{P}_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi ).$$

(18)

Here, $J(\theta ,\varphi )$ is the cost function to be minimized by the WAA optimizer.

Conceptually, the WAA–MUSIC scheme adaptively concentrates its search density near high-likelihood DoA regions, functioning analogously to simulated annealing but without relying on a discrete angular grid. A scout pass proposes multiple seeds, at each iteration t, a population around the current mean ${\mu }^{\left(t\right)}$ is reweighted with temperatured soft weights

$$w_i^{\left(t\right)}\propto exp\left(\frac{1}{{\tau }^{\left(t\right)}}log{P}_{\mathrm{PA}-\mathrm{MUSIC}}({\theta }_i,{\varphi }_i)\right),\sum _i{w}_i^{\left(t\right)}=1,$$

(19)

and the mean/spread are updated with circular averaging in azimuth and annealed variances:

$${\mu }_{\theta }^{(t+1)}=\sum _i{w}_i^{\left(t\right)}{\theta }_i,{\mu }_{\varphi }^{(t+1)}=atan2\left(\sum _i{w}_i^{\left(t\right)}\sin {\varphi }_i,\sum _i{w}_i^{\left(t\right)}\cos {\varphi }_i\right),{\sigma }^{(t+1)}=\alpha {\sigma }^{\left(t\right)}.$$

(20)

This removes gridding bias and caps evaluations by population × iterations × restarts.

Equation (19) assigns a probability-like weight to each candidate angle in the current population, with higher $P_{\mathrm{PA}-\mathrm{MUSIC}}({\theta }_i,{\varphi }_i)$ values receiving larger weights. The temperature parameter $\tau \left(t\right)$ plays the same role as in Boltzmann or softmax models: it controls how selective this reweighting is. At high temperatures, the weights are relatively flat, so even weaker candidates retain non-negligible weight and the population explores a broader region. As $\tau \left(t\right)$ decreases, the distribution becomes sharply peaked around the strongest pseudospectrum values, guiding the population from broad exploration toward exploitation of the dominant DoA modes.

4.3.3. Hybrid CTF+WAA (Discrete Seeds, Continuous Refinement)

The Hybrid scheme first evaluates the coarse map and selects the top K peaks after non-maximum suppression,

$${\mathcal{S}}_K={\left\{({\tilde{\theta }}_k,{\tilde{\varphi }}_k)\right\}}_{k=1}^K\subset {\mathcal{G}}_c,$$

(21)

then runs local WAA around each seed to obtain $({\widehat{\theta }}_k,{\widehat{\varphi }}_k)$ and score $P_k$, with the final estimate

$$({\widehat{\theta }}_{\mathrm{HYB}},{\widehat{\varphi }}_{\mathrm{HYB}})=arg\underset{k\in \{1,\dots ,K\}}{max}{P}_{\mathrm{PA}-\mathrm{MUSIC}}({\widehat{\theta }}_k,{\widehat{\varphi }}_k),$$

(22)

at a cost

$$N_{\mathrm{eval}}^{\mathrm{HYB}}\approx |{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+KST,$$

(23)

which is typically far smaller than a dense fine grid while mitigating the gridding floor in Equation (17). Equation (23) follows by counting calls to the PA-MUSIC cost function. The coarse stage evaluates $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$ once at each point on the grid ${\mathrm{\Theta }}_c\times {\mathrm{\Phi }}_c$, giving $|{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|$ evaluations. The WAA stage then refines K seeds, each with a population of S candidates over T iterations, adding approximately $KST$ further evaluations and yielding $N_{\mathrm{eval}}^{\mathrm{HYB}}\approx |{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+KST$.

Relative to the coarse-to-fine grid in Equation (16), whose cost is $N_{\mathrm{eval},\mathrm{CTF}}= |{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+|{\mathrm{\Theta }}_f\left|\right|{\mathrm{\Phi }}_f|$, the hybrid scheme replaces the dense fine grid by $KST$ local evaluations around a few coarse peaks. For the parameter choices used in Section 5, this leads to a lower median number of pseudospectrum evaluations for the Hybrid method than for CTF at comparable display resolution, as reported in Section 5.6 later (in Table 9), where the median evaluation count decreases from 7452 (CTF) to 5400 (Hybrid).

5. Concept Validation

Before integrating full electromagnetic models from FEKO, the proposed Pose-Aware MUSIC (PA-MUSIC) algorithm was first validated in MATLAB to ensure the correctness of the signal processing chain. The rationale for this staged validation is that MUSIC relies fundamentally on the array manifold, covariance formation, and subspace decomposition. Therefore, the algorithmic behavior can be verified using an analytically defined dipole-based UCA before introducing platform-specific distortions. The validation process followed the flow illustrated in Figure 10.

This section validates the proposed pose and Doppler-aware MUSIC processing on UAV-mounted UCAs and compares three practical solvers for the 2D DoA search: (i) pose-aware Coarse-to-Fine (CTF) MUSIC, (ii) robust global WAA–MUSIC (seedless), and (iii) a hybrid method that seeds WAA from the top K coarse peaks. All three methods optimize the same pose-aware pseudospectrum $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$ in (11).

5.1. Pose-Aware CTF–MUSIC

CTF–MUSIC evaluates the pose-aware pseudospectrum $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$ on a coarse grid ${\mathcal{G}}_c$ and refines the maximum within a small neighborhood using a finer local grid. This approach inherits the robustness of grid search while remaining simple to implement. Its principal limitations are (i) computational cost that scales with the product of azimuth and elevation grid sizes (still significant if a very fine display resolution is desired) and (ii) a gridding floor, i.e., a residual bias on the order of half the grid step, even at high SNR. In practice, the method provides a strong baseline and reliable seeds for continuous optimizers. The implementation follows the steps in Algorithm A1 (Appendix A), which outlines pose-aware data generation, covariance formation, subspace decomposition, and a two-stage coarse-to-fine grid refinement of $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$.

5.2. Pose Aware WAA–MUSIC

WAA–MUSIC replaces exhaustive gridding with a population-based, continuous maximization of $P_{\mathrm{PA}-\mathrm{MUSIC}}(\theta ,\varphi )$. The implementation uses a scout pass to propose multiple starting means, followed by weighted–annealed updates (temperatured soft weights and decaying spreads) with retention and stagnation bursts. This eliminates gridding bias and caps the number of pseudospectrum evaluations roughly by population × iterations × restarts, independent of display resolution. The trade-offs are a higher sensitivity to low-SNR sidelobes without good seeding and a need to tune annealing/restart settings for stability. Under moderate–high SNR, the method converges competitively to CTF-quality solutions with fewer evaluations. The detailed WAA–MUSIC procedure is given in Algorithm A2 (Appendix A), including the scout phase, population updates, annealing schedule, and restart logic.

5.3. Hybrid CTF+WAA

The Hybrid CTF+WAA implementation is summarized in Algorithm A3 (Appendix A), where a coarse map is first computed and the top K peaks are then refined by local WAA searches. By restricting WAA to small neighborhoods, it preserves the robustness of CTF while removing grid bias and substantially reducing incremental computing relative to a dense fine grid. The single tunable lever, K, trades resilience to coarse-map anomalies against cost; small K (e.g., 2–5) typically suffices. In short, the hybrid system achieves near-CTF accuracy at a fraction of the additional evaluations and shows the most consistent behavior across SNRs and poses.

5.4. Findings

The three solvers-CTF–MUSIC, WAA–MUSIC, and Hybrid CTF+WAA MUSIC were evaluated on the ten DoA+pose cases in

Table 7. True DoA and UAV pose for the 10 cases.

Case	$\mathbf{az}{(}^{°})$	$\mathbf{el}{(}^{°})$	$\mathit{y}{(}^{°})$	$\mathit{p}{(}^{°})$	$\mathit{r}{(}^{°})$
01	−25.0	35.0	30.0	−6.0	4.0
02	−123.9	63.3	21.6	−1.1	−2.2
03	−82.4	49.4	−0.4	9.3	6.0
04	−15.2	58.1	−22.9	5.4	−9.9
05	−70.4	46.7	20.7	−4.0	−5.0
06	56.6	69.3	−1.6	−7.5	8.3
07	151.7	26.7	1.0	−6.9	−9.7
08	−59.8	69.5	0.7	7.5	−8.7
09	−73.4	38.1	13.1	8.5	−2.1
10	145.9	40.0	15.1	7.9	−0.4

. The processing pipeline was pose- and Doppler-aware (Section 5), using (9), (12), and (13) with $N=256$ snapshots per run.

Table 8. Summary of the 10 cases at $\parallel v_{\mathrm{rx}}\parallel =15$ m/s (along $+x$). MAE = mean absolute error.

Method	MAE$\left|\mathbf{\Delta }\mathbf{az}\right|$	MAE$\left|\mathbf{\Delta }\mathbf{el}\right|$	RMSEaz	RMSEel	Median Time (s)	Median Evals
CTF–MUSIC	0.35009	0.26283	0.47758	0.39805	0.053198	7452
WAA–MUSIC	0.33869	0.27923	0.45802	0.39612	0.045290	5700
Hybrid	0.34203	0.27184	0.44899	0.38395	0.039474	5400

summarizes performance aggregated over the ten cases. All methods attain sub-degree RMSE in both elevation and azimuth. WAA and Hybrid achieve comparable accuracy to CTF while requiring fewer pseudospectrum evaluations, with the hybrid system yielding the lowest median runtime and the smallest evaluation count owing to local continuous refinement seeded from the coarse map.

The median search times of order ${10}^{-2}$ s in Table 8 correspond to a single DoA estimation on one augmented data window. Hence, processing a longer mission (with more points) would repeat this operation for each window.

Figure 11 plots mean absolute elevation and azimuth errors versus SNR (0:5:25 dB). The curves for the three solvers nearly overlap at each SNR: elevation MAE decreases from $\approx 1.{78}^{°}$ at 0 dB to $\approx 0.{07}^{°}$ at 25 dB, azimuth MAE decreases from $\approx 2.{26}^{°}$ to $\approx 0.{09}^{°}$ over the same range. The reduction with SNR is expected: higher SNR yields a lower-variance sample covariance, a larger eigengap between the signal and noise subspaces, and a sharper MUSIC pseudospectrum. Consequently, peak localization improves, gridding/optimizer ambiguities are reduced, and both CTF (discrete) and WAA/Hybrid (continuous) converge to the true DoA with smaller bias and variance (consistent with CRLB scaling $\propto 1/\mathrm{SNR}$).

Figure 12 reports mean absolute errors alongside median compute and evaluation counts across the ten cases. While accuracy is within $0.2^{°}$ across all cases, the hybrid method achieves the best compute profile due to restricting the continuous search to a few coarse seeds. Seedless WAA reduces evaluations relative to CTF without relying on a dense fine grid, at the cost of restarts and annealing.

Finally, it is important to note that classical subspace estimators such as Root-MUSIC and ESPRIT are usually derived for static, pose-invariant arrays (typically ULAs) and do not directly handle a 3-D UCA mounted on a maneuvering UAV. Implementing root-MUSIC/ESPRIT for such a platform would result in high errors due to the dynamic nature of the UAV. Nevertheless, for completeness,

Table A1. Summary of DoA estimation performance over 10 DoA+pose cases (SNR = 12 dB).

Method	$\mathbf{Mean}\left|\mathbf{\Delta }\mathit{\varphi }\right|$	$\mathbf{Mean}\left|\mathbf{\Delta }\mathit{\theta }\right|$	RMSEϕ	RMSEθ	Median t [s]	Median Evals
CTF–MUSIC	0.3501	0.2628	0.4776	0.3981	0.051861	7452
WAA–MUSIC	0.3387	0.2792	0.4580	0.3961	0.044713	5700
Hybrid	0.3420	0.2718	0.4490	0.3840	0.036498	5400
Root–MUSIC	75.737	12.877	108.03	16.645	0.000831	0
ESPRIT	77.610	17.774	94.455	21.560	0.000587	0

in Appendix B provides a comparison with pose-unaware root-MUSIC and ESPRIT (no pose or Doppler compensation) on the same UAV array data. As shown there, these baselines incur mean azimuth errors in excess of ${70}^{°}$, confirming that pose-unaware formulations are not meaningful comparators for the proposed Pose-Aware MUSIC estimators.

5.5. Takeaways

• Accuracy: CTF and the hybrid system deliver comparable localization accuracy; the hybrid system marginally improves peak placement by continuous refinement near the coarse maximum. Seedless WAA attains similar accuracy at moderate–high SNR but can deviate at very low SNR unless restarts and annealing are sufficiently aggressive.
• Computation: CTF cost scales with grid density; WAA and the hybrid system scale with population, iterations, and restarts. For matched quality, the hybrid system requires markedly fewer incremental evaluations than a dense fine grid, while WAA avoids gridding entirely.
• Robustness: The hybrid system is the most forgiving to hyperparameters due to CTF seeding. WAA benefits strongly from a scout phase and multiple restarts. Coarse grid design (step sizes and NMS radii) matters for good hybrid seeds.
• Kinematics: With a single short block, the Doppler induced by UAV translation is common across channels and cancels out spatial covariance; when stacking multiple pose slices, Doppler de-rotation (using a kinematic prior or a light 1-D co-search) preserves inter-block coherence and improves stability.
• Practical guidance: For real-time UAV DoA with a UCA, Hybrid CTF+WAA is recommended as the default: use a moderate coarse grid, pick $K\in [2,5]$, and run a short local WAA. Reserve global WAA for scenarios demanding gridding-free operation or when display resolution is decoupled from compute.

These findings motivate the system-level analysis in Section 6, where we quantify how coupling with the drone airframe, and current-carrying cables, modify the array manifold, and impact PA-MUSIC performance.

5.6. Computational Complexity and Runtime

Let $L=M{K}_{\mathrm{blk}}$ be the augmented array size (where M is the number of antenna elements and $K_{blk}$ is the number of poses, i.e., time/attitude slices stacked in the augmented covariance). Each run using the three methods discussed before has two parts:

(1) Setup (one-off per run). The algorithm forms the augmented covariance ${\widehat{R}}_{\mathrm{aug}}\in {\mathbb{C}}^{L\times L}$ and computes its eigendecomposition to obtain the noise subspace used in Equation (16)/(23). For dense matrices, this step grows roughly with the cube of L, written as $O\left(L^3\right)$. For example, doubling L makes this setup step about $2^3=8$ times slower.

Why $O\left(L^3\right)$? Standard dense eigensolvers first reduce ${\widehat{R}}_{\mathrm{aug}}\in {\mathbb{C}}^{L\times L}$ to tridiagonal (Hermitian) or Hessenberg (general) form using Householder transforms in $\mathrm{\Theta }\left(L^3\right)$ flops, then apply QR or divide-and-conquer iterations whose total cost is also $\mathrm{\Theta }\left(L^3\right)$. This is the basis for the widely cited cubic scaling of dense EVD/SVD [27].

(2) Search (many small, repeated steps). The solver then probes the PA–MUSIC pseudospectrum $P(\theta ,\varphi )=1/\left(a^{\mathrm{H}}{U}_N{U}_N^{\mathrm{H}}a\right)$ (Equation (16)) at many angle pairs. Because the projector $P_N=U_N{U}_N^{\mathrm{H}}$ is already precomputed in the setup, each probe reduces to one quadratic form on an L-length vector and costs $O\left(L^2\right)$. If the solver makes $N_{\mathrm{eval}}$ such probes, the total time becomes

$$T(L,N_{\mathrm{eval}})=O\left(L^3\right)+O\left(N_{\mathrm{eval}}{L}^2\right).$$

What is the difference between “evaluations” and “time”? Evaluations counts how many $(\theta ,\varphi )$ points are tested (this depends on the method and its settings). Time adds the one-off $O\left(L^3\right)$ setup plus $N_{\mathrm{eval}}$ probes at $O\left(L^2\right)$ each. Put simply, setup is “pay once, cubic”; probing is “pay many times, quadratic”. The computational complexity and run time evaluated for the discussed methods are summarised in

Table 9. Complexity and measured-runtime comparison. $\left|\mathrm{\Theta }\right|,\left|\mathrm{\Phi }\right|$ are grid sizes; S population, T iterations, $R_s$ restarts, K coarse seeds. Evaluations counts PA-MUSIC probes of $P(\theta ,\varphi )$ (Equation (16)). Search times are medians over repeated runs on fixed hardware (in this case, MATLAB run on PC).

Method	Asymptotic Time $\mathit{T}(\mathit{L},{\mathit{N}}_{\mathbf{eval}})$	${\mathit{N}}_{\mathbf{eval}}$ (Median)	Search Time (s) (Median)	$\mathbf{\Delta }{\mathit{N}}_{\mathbf{eval}}$ vs. CTF	$\mathbf{\Delta }$ Time vs. CTF
CTF-MUSIC	$O\left(L^3\right)+O\left(\left(\right|{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+|{\mathrm{\Theta }}_f\left|\right|{\mathrm{\Phi }}_f\left|\right)L^2\right)$	7452	0.053198	—	—
WAA–MUSIC	$O\left(L^3\right)+O\left(ST{R}_s{L}^2\right)$	5700	0.045290	$-23.5\%$	$-14.9\%$
Hybrid (CTF+WAA)	$O\left(L^3\right)+O\left(\left(\right|{\mathrm{\Theta }}_c\left|\right|{\mathrm{\Phi }}_c|+KST)L^2\right)$	5400	0.039474	$-27.5\%$	$-25.8\%$

below.

All methods use the same augmented dimension $L=M{K}_{\mathrm{blk}}$ and identical angle bounds; only the evaluation policy differs, which explains the observed search-time reductions consistent with the $O\left(N_{\mathrm{eval}}{L}^2\right)$ term.

6. Effect of Drone on DoA Estimation

Drone-mounted arrays do not behave like ideal free-space arrays. The airframe, wiring, and payload introduce mutual coupling between elements, small per-element gain/phase imbalances, and  position jitter (mm-level placement errors). Flight adds multipath (modeled well by a Rician K-factor) [28], pose changes (yaw–pitch–roll), and  Doppler from motion. Together, these effects distort the array’s steering vector, so the received data follow an effective manifold

$$a_{\mathrm{eff}}(\theta ,\varphi \mid R)=CG{a}_0(\theta ,\varphi \mid R,\Delta r),$$

rather than the ideal $a_0$. Here, C models coupling (with magnitude/phase summarized by $\kappa$), G captures per-element complex gains, and $\Delta r$ represents the placement errors. If the estimator still uses $a_0$, MUSIC peaks shift and broaden, producing bias floors and loss of resolution. This is visible in our results: mismatch heatmaps highlight angles where ${\parallel a_{\mathrm{eff}}-a_0\parallel }_2$ is largest, and sweeps versus K, $\kappa$, and jitter quantify how bias grows as the platform departs from ideal conditions.

A practical remedy is to build and use a platform-aware manifold [29,30]. The existing Lua beam-steering script can automate this by sweeping programmed beams (TX reciprocity) or sequentially exciting elements under a probe/beacon to tabulate ${\widehat{a}}_{\mathrm{eff}}(\theta ,\varphi )$ for a few representative poses. At run time, IMU pose rotates candidate directions into the body frame; the estimator interpolates the measured manifold and then runs the Hybrid CTF→WAA search (coarse grid seeds followed by local refinement) on the MUSIC pseudospectrum. Using ${\widehat{a}}_{\mathrm{eff}}$ suppresses platform-induced bias and recovers resolution in realistic flight, while the same heatmaps and effect sweeps guide calibration priorities (reduce $\kappa$, tighten mechanics, or operate at higher K) and provide concrete system requirements for the airframe and RF chain.

The platform impact is evaluated by generating a platform–aware array manifold on the full airframe model. For each look direction $(\theta ,\varphi )$ and pose R (yaw–pitch–roll), embedded-element responses are obtained and converted into steering vectors $a_{\mathrm{FEKO}}(\theta ,\varphi \mid R)$ (phase/gain referenced and unit–norm). Using the same data window and noise conditions as in the ideal study, two MUSIC pseudospectra are then formed for comparison with the previous section: (i) an ideal case, where both the covariance and the search manifold use the free-space model $a_0$, and (ii) a drone-loaded case, where the covariance reflects the FEKO-derived manifold (i.e., coupling, gain/phase imbalance, position jitter, and scattering), while the search still uses the ideal manifold $a_0$ to expose mismatch. The resulting normalized pseudospectra are shown in Figure 13.

Figure 13 visualizes the Hybrid PA-MUSIC pseudospectrum for case 01. The left panel (‘Ideal manifold’) forms the covariance with uncoupled, perfectly calibrated dipoles and free-space propagation, and searches with the corresponding ideal dictionary. The right panel (‘With drone effects’) forms the covariance with mutual coupling, per-element gain/phase imbalance, Doppler and pose effects, while the search manifold is still ideal. In both panels, the pseudospectrum is normalized by its global maximum and plotted in dB so that 0 dB corresponds to the strongest peak and the color bar indicates relative levels. The main lobe is therefore simply the global maximum, and the ground-truth DoA is marked by ‘×’. In the ideal case, the peak is sharp and centered on the truth, with a narrow mainlobe and a sidelobe floor roughly 20–25 dB below the maximum. On the heatmap, these sidelobes appear as the fainter vertical streaks next to the main bright ridge. When drone effects are included, the mainlobe broadens and its peak shifts by about 5–$6^{°}$ in azimuth/elevation on average (and up to ≈13° in the worst of the ten cases in

Table 10. Hybrid (CTF→WAA) estimation errors for 10 DoA+pose cases under platform-loading.

Case	$\widehat{\mathbf{Az}}$	$\widehat{\mathbf{El}}$	$\mathit{d}\mathbf{Az}$	$\mathit{d}\mathbf{El}$	Time (s)
case_01	$-25.288$	$44.495$	$-0.288$	$9.495$	$0.06636$
case_02	$-118.190$	$67.320$	$5.744$	$4.048$	$0.04305$
case_03	$-76.745$	$53.879$	$5.672$	$4.437$	$0.04168$
case_04	$-9.969$	$64.206$	$5.261$	$6.143$	$0.04013$
case_05	$-73.745$	$51.997$	$-3.300$	$5.343$	$0.03773$
case_06	$50.440$	$77.170$	$-6.133$	$7.918$	$0.03566$
case_07	$147.110$	$30.965$	$-4.575$	$4.303$	$0.03862$
case_08	$-46.969$	$71.677$	$12.788$	$2.223$	$0.03616$
case_09	$-68.001$	$44.563$	$5.387$	$6.429$	$0.04036$
case_10	$149.000$	$46.272$	$3.106$	$6.295$	$0.05187$

). At the same time, the sidelobe floor rises to only about 10–12 dB below the peak, yielding a visibly flatter and less symmetric pseudospectrum. These changes illustrate how manifold mismatch from coupling, RF imbalance, jitter, and multipath introduces systematic bias and reduces sidelobe contrast when an ideal manifold is used in the search.

The changes arise because the received data follow an hleffective manifold $a_{\mathrm{eff}}(\theta ,\varphi \mid R)$ rather than the ideal $a_0$. Mutual coupling (C) and RF imbalances (G) reshape the array response; mm-level position jitter ($\Delta r$) adds direction-dependent phase errors; and low-K multipath injects coherent components that reduce signal/noise-subspace orthogonality, all of which flatten the pseudospectrum and displace the maximum. For DoA estimation, this means that, if the search uses an ideal manifold, one should expect systematic bias(peak shift), reduced resolution (broader mainlobe, higher sidelobes), and lower robustness to close sources. Using a platform-aware (measured or calibrated) manifold in the Hybrid CTF→WAA estimator restores peak sharpness and contrast, thereby suppressing bias floors and preserving resolution under realistic flight conditions.

The electromagnetic degradations in Table 6 translate into DoA accuracy penalties when the search manifold ignores platform loading;

Table 11. Effect of platform loading on DoA accuracy (Hybrid PA-MUSIC).

Statistic (10 Cases)	Ideal Manifold (Hybrid)	Platform-Loaded Data (Hybrid)
MAEaz	≈$0.{34}^{°}$	≈$5.{23}^{°}$
MAEel	≈$0.{27}^{°}$	≈$5.{66}^{°}$
RMSEaz	≈$0.{45}^{°}$	∼$6^{°}$
RMSEel	≈$0.{38}^{°}$	∼$6^{°}$

summarizes this effect over ten cases. Compared with the ideal free-space case, the errors are larger (mean absolute $\approx 5–6^{°}$, RMSE $\approx 6^{°}$) because the received data are generated by a platform-loaded manifold (coupling, gain/phase imbalance, element jitter, multipath, and motion), whereas the MUSIC search continues to assume an ideal textbook manifold. This deliberate mismatch, used to isolate the penalty of ignoring platform effects and to represent a no-calibration baseline, shifts and broadens the pseudospectrum peak, yielding the observed $5–6^{°}$ average error. In the experiments, the covariance is formed from drone-loaded data while the steering vectors remain ideal. Substituting a platform-aware (FEKO/OTA-measured) manifold, pose-rotated at run time, is expected to suppress bias and recover resolution.

Analysis of Platform Effects on Hybrid PA-MUSIC Using FEKO Manifolds

Platform effects were obtained from full-wave FEKO simulations of the complete airframe and antenna installation. For each look direction and representative pose (yaw–pitch–roll), FEKO provided embedded-element patterns and port-to-port S-parameters, from which a platform-aware steering dictionary $a_{\mathrm{FEKO}}(\theta ,\varphi \mid R)$ and coupling matrix C were derived in MATLAB. The Rician K-factor was swept by adjusting the relative weighting of the FEKO direct (LOS) and scattered fields, while mechanical tolerances were emulated by re-solving the FEKO model with element coordinates. The Hybrid PA-MUSIC estimator (coarse CTF seeds followed by WAA refinement) was then evaluated by forming covariances consistent with the FEKO manifold and, for isolation of platform penalties, comparing against a search that still assumes an ideal free-space manifold. This setup exposes the mismatch that would arise if platform-aware calibration were omitted.

Mutual coupling is incorporated at the manifold level by premultiplying the ideal steering vector $a_0(\theta ,\varphi \mid R,\Delta r)$ with the coupling matrix C, so that the effective manifold is consistent with

$$a_{\mathrm{eff}}(\theta ,\varphi \mid R)=CG{a}_0(\theta ,\varphi \mid R,\Delta r).$$

If we stack the effective steering vectors into $A_{\mathrm{eff}}$ and denote the source covariance by $R_s$, then the array covariance takes the form

$$R_{xx}=A_{\mathrm{eff}}{R}_s{A}_{\mathrm{eff}}^{\mathrm{H}}+{\sigma }^{2}I.$$

Thus, the impact of coupling, per-element gain/phase imbalance and position jitter is fully embedded in the signal and noise subspaces used by PA–MUSIC.

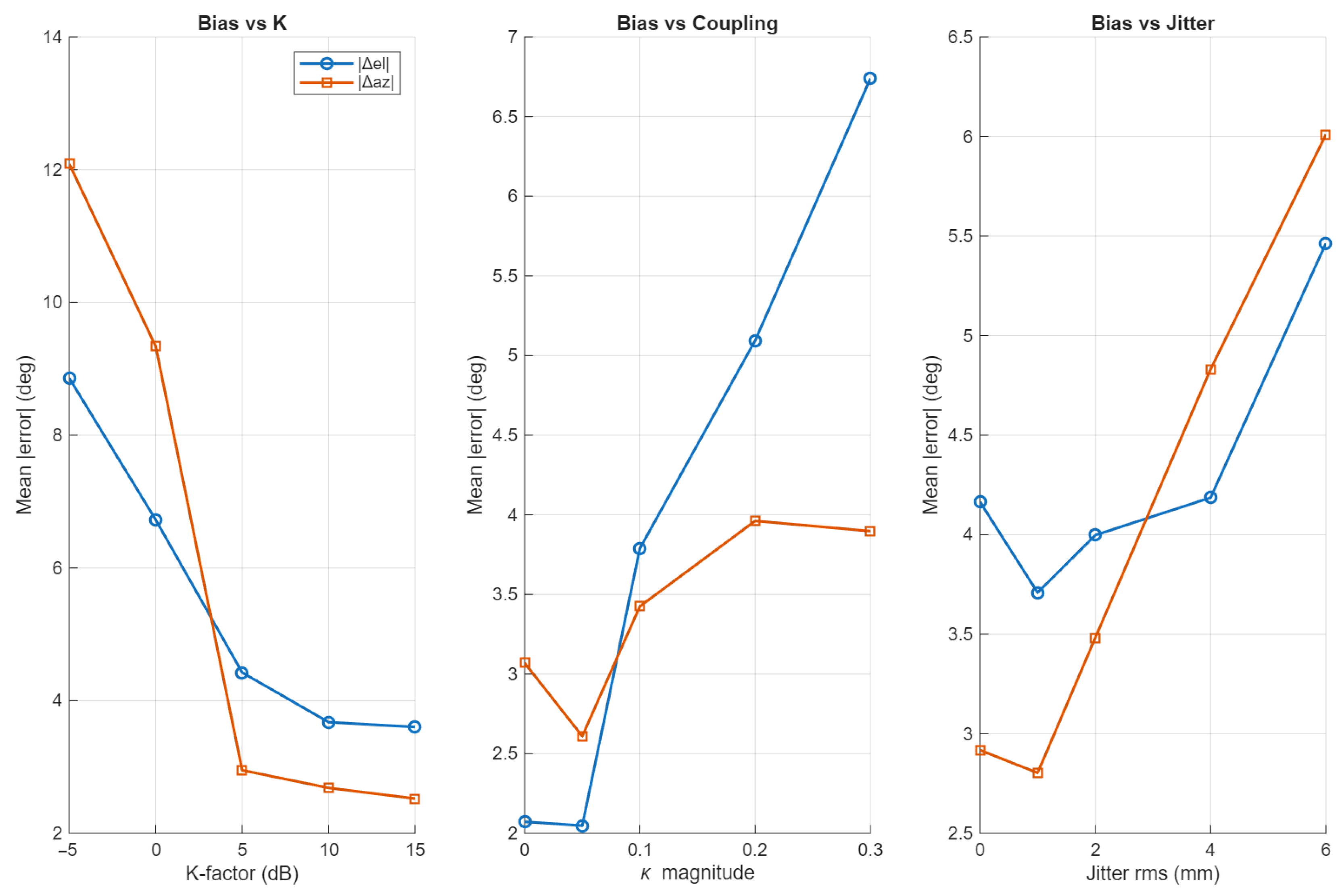
Figure 14 shows that mean absolute errors decrease strongly with K: when scattered energy dominates (low K), coherent multipath distorts the effective manifold and enlarges bias. As K increases (clearer LOS), the MUSIC peak recenters and errors fall to ≈3–$4^{°}$. Qualitatively, lower K values are representative of more cluttered/urban-like conditions, whereas higher K values correspond to more open, LOS-favorable links (e.g., suburban or rural), consistent with typical Rician K-factor ranges reported in measurement studies. Bias grows with coupling magnitude $\kappa$ extracted from FEKO S-parameters: elevation error rises from ≈$2^{°}$ to ≈5–$7^{°}$ as $\kappa$ moves into the 0.2–0.3 range, reflecting manifold reshaping by mutual coupling. Subspace robustness under increasing coupling was assessed by sweeping the coupling magnitude $\kappa \in \{0,0.05,0.10,0.20,0.30\}$, recomputing $R_{xx}$ and the noise subspace for each value, and plotting the resulting DoA bias and two-source resolution probability (Figure 14). Within this range, the PA-MUSIC subspace remains usable, with a gradual increase in bias and loss of resolution rather than a catastrophic breakdown. Jitter studies show a monotonic increase in azimuth bias (from ≈$3^{°}$ toward ≈$6^{°}$ over 0–6 mm), consistent with direction-dependent phase errors from placement tolerances. These trends quantify how far a free-space dictionary deviates from the FEKO-informed manifold under realistic platform conditions.

Figure 15 reports the probability of resolving two equal-power sources separated by $8^{°}$ in azimuth. Resolution remains low across the sweeps (highest at modest K and small $\kappa$/jitter), and degrades to near-zero as coupling and jitter increase. With the present aperture and element count, platform-induced mismatch remains at $8^{°}$ near the practical separation limit unless a platform-aware dictionary is used.

The study demonstrates that ignoring platform effects leads to systematic bias and loss of resolution even at moderate SNR. Before field deployment, a platform-aware manifold should be assembled directly from FEKO (or OTA measurements), incorporating embedded patterns and pose dependence. This dictionary should be pose-rotated at run time and used within the Hybrid PA-MUSIC search. In the present work, the platform-aware manifold is obtained from FEKO simulations of the UAV-mounted array. The curves provide actionable targets: operate in higher-K conditions when possible and design and calibrate to keep $\kappa$ small, and control mechanical tolerances (jitter) to a few millimeters. If close-source resolution is critical, increase aperture/element count and/or apply coherent-multipath mitigation (e.g., forward-backward averaging or spatial smoothing) together with the platform-aware manifold.

7. Discussion

This work examined Direction-of-Arrival (DoA) estimation on a small UAV for ISAC using a compact six-element UCA and a Pose-Aware MUSIC (PA–MUSIC) algorithm. Embedded-element patterns of the installed array provided a realistic basis for received fields, while channel and hardware effects (Rician LOS/NLOS mixing, mutual coupling, per-element gain/phase imbalance, and element–position jitter) were added in post-processing to emulate flight. The proposed estimator rotates candidate look vectors by the instantaneous yaw–pitch–roll and compensates platform-induced Doppler across the snapshot window, then employs a hybrid coarse-to-fine search with local refinement to locate pseudospectrum maxima efficiently.

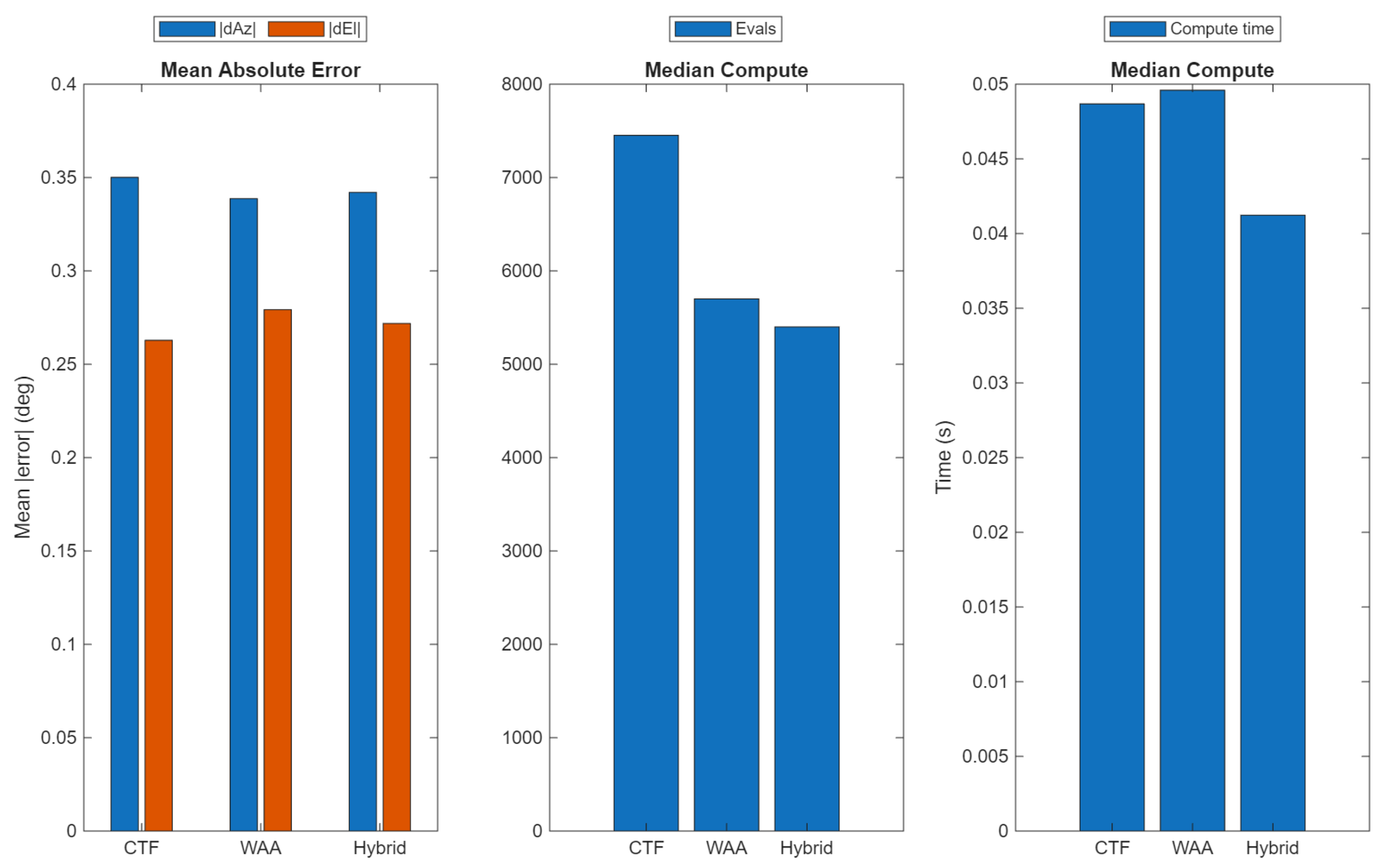
The results show three salient points. First, pose and Doppler compensation materially stabilize the pseudospectrum in motion, preserving narrow peaks and preventing drift that would otherwise inflate errors. Second, the dominant residual errors arise from manifold mismatch, primarily coupling and mechanical jitter, because the search still uses an ideal steering model. This appears as several-degree bias floors and lowered separability for closely spaced sources, consistent with the manifold–mismatch heatmaps and the bias/resolution trends versus K, $\kappa$, and jitter. Third, the hybrid solver meets real-time constraints on modest hardware (fixed evaluation budget and short runtimes), making the method practical for onboard use in GNSS-denied conditions where only inertial pose and platform velocity are available.

8. Conclusions

This work presented a pose- and Doppler-aware formulation of MUSIC for UAV-mounted arrays that explicitly incorporates instantaneous attitude and velocity into the steering vector used in the pseudospectrum. The study integrated antenna design, platform modeling, and signal processing into a single evaluation framework: a six-element UCA at 2.4 GHz with radius $R=0.3\lambda$ was designed for compact multirotor platforms and analyzed using full-wave simulations to quantify platform loading. A two-stage search policy was proposed, combining a coarse grid pass (CTF) with local weighted-annealed refinement (Hybrid), thereby removing gridding bias while retaining efficiency. Across 0–25 dB SNR, the proposed estimator achieved sub-degree RMSE (<$0.5^{°}$ in both azimuth and elevation) with ideal manifolds (Section 5), and when platform loading was introduced but the search manifold was kept ideal to expose mismatch, the mean absolute errors were approximately 5–$6^{°}$ (Table 11), consistent with the platform-induced gain and sidelobe changes summarized in Table 6.

8.1. Limitations

This study evaluates a pose- and Doppler-aware MUSIC framework together with a compact UCA design using full-wave electromagnetic simulation in Altair FEKO and algorithmic validation in MATLAB. The results therefore reflect high-fidelity simulations rather than field measurements. This choice isolates platform-coupling mechanisms and search-policy behaviour without confounding factors such as regulatory constraints, safety restrictions, or uncontrolled interference. The analysis focuses on a six-element UCA optimized for small multirotors and uses an ideal search manifold to intentionally expose the effect of platform loading. Larger or sparse arrays, alternative element types, embedded real-time execution, and long-term drift effects are outside the current scope. These boundaries are consistent with the objective of establishing a controlled baseline before undertaking hardware integration and flight testing.

8.2. Future Work

Future efforts will extend the present baseline to practical testing in a dedicated follow-on study. The next step is hardware-in-the-loop evaluation and flight trials that combine the proposed estimator with live IMU and GNSS data while characterizing interference, cable effects, and temperature drift in representative missions. Further work will also explore platform-calibrated or learned manifolds to close the mismatch observed with ideal search, scale to larger or sparse arrays, and investigate MIMO ISAC configurations that enable finer angular resolution and waveform or resource co-design for ISAC link optimization under power, spectral, and latency constraints. Additional directions include lightweight online calibration for gain and phase imbalance and adaptive pose stacking for real-time operation on edge computing. These activities are planned as a separate paper that focuses on experimental methods and results, building directly on the simulation-backed foundations reported here.