Active and Passive Control Strategies for Ride Stability and Handling Enhancement in Three-Wheelers
Abstract
1. Introduction
2. Motivation
3. Scope of the Work
4. Fundamental Vehicle Dynamics Model for Three-Wheelers
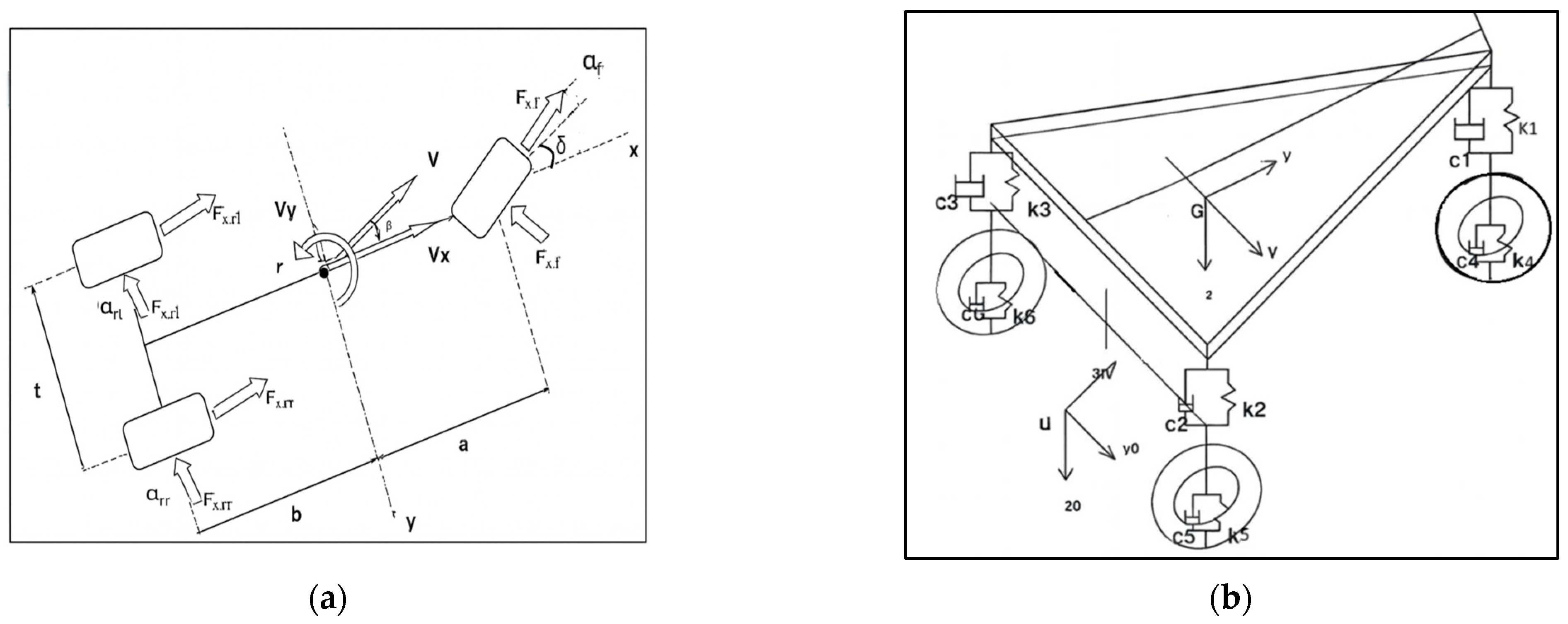
4.1. Model Overview
Equations of Motion
- a = Length between the CG and front tire patch;
- V = Vehicle velocity vector;
- b = Length between the CG and rear tire patch;
- Vf = Front tire velocity vector;
- δ = Steer angle;
- Vr = Rear tire velocity vector;
- FY = Tire lateral forces;
- Vx = Vehicle velocity in the x-axis;
- Vy = Vehicle velocity in the y-axis;
- Izz Vertical axis moment inertia;
- ax, ay = Longitudinal and Lateral acceleration.
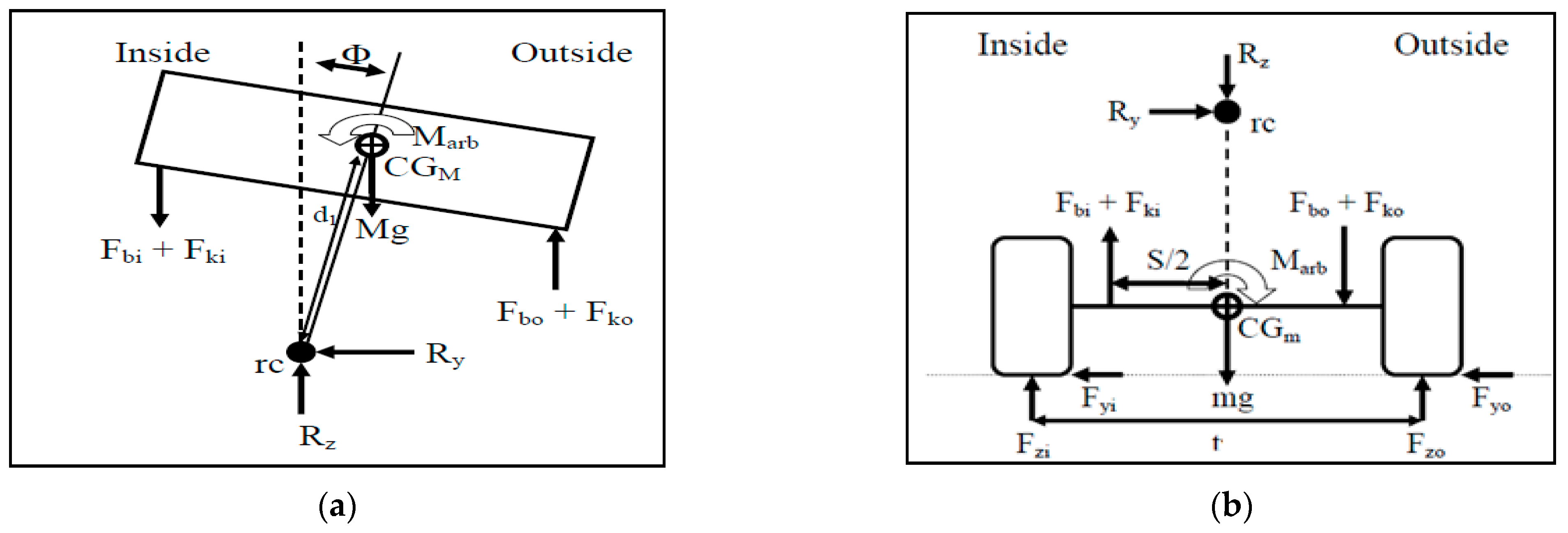
4.2. Vehicle Roll Model of Three Wheeled Vehicle
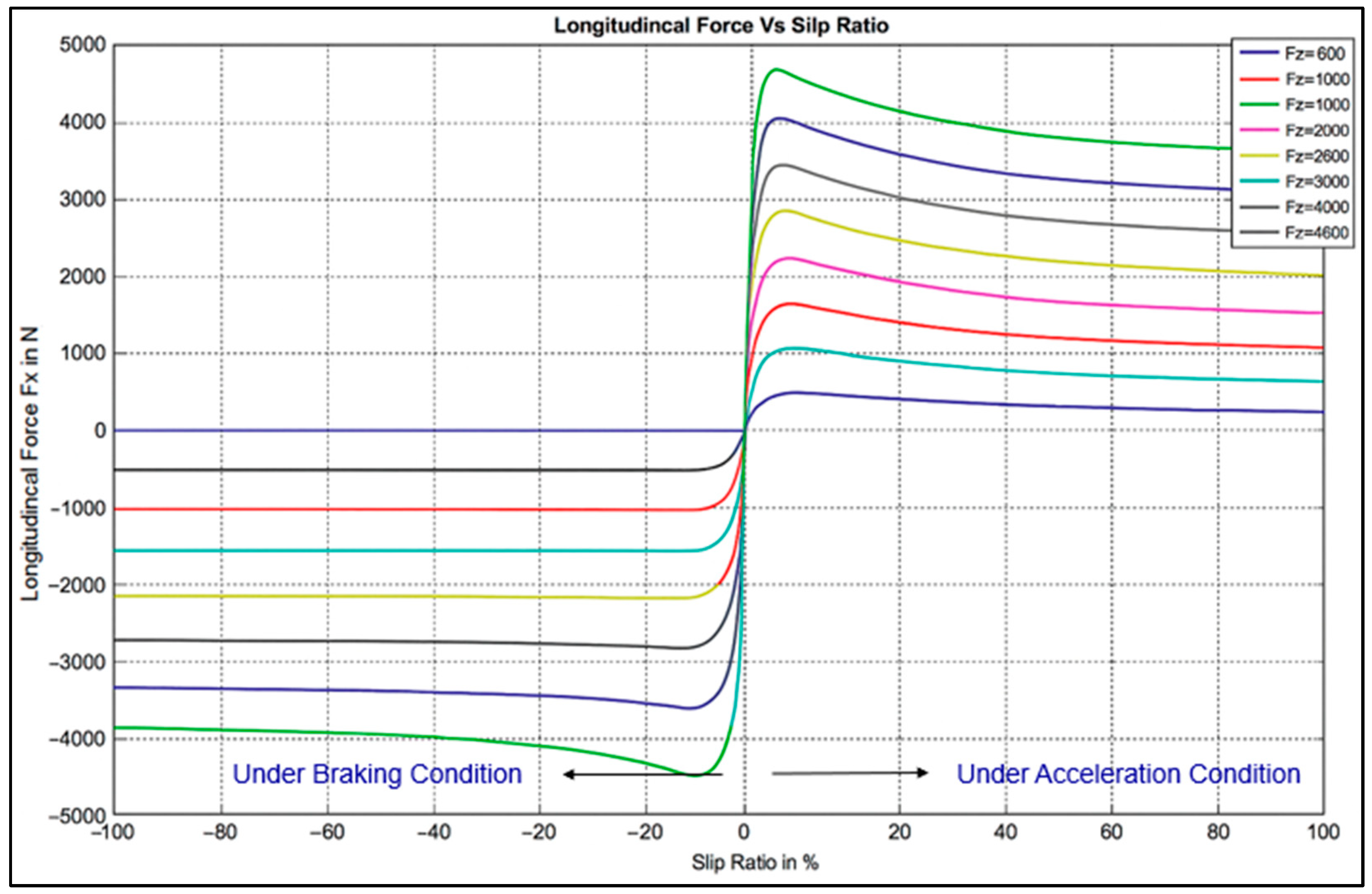
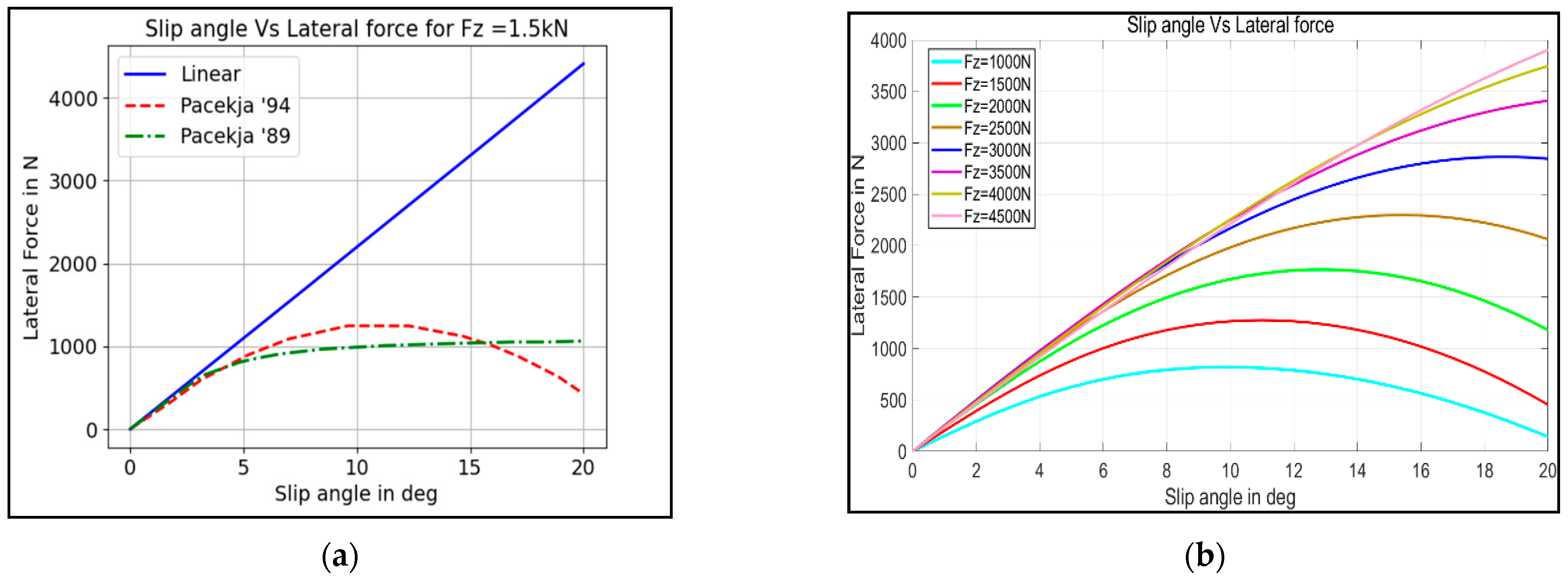
4.3. Tire Modelling
5. Virtual Model Development
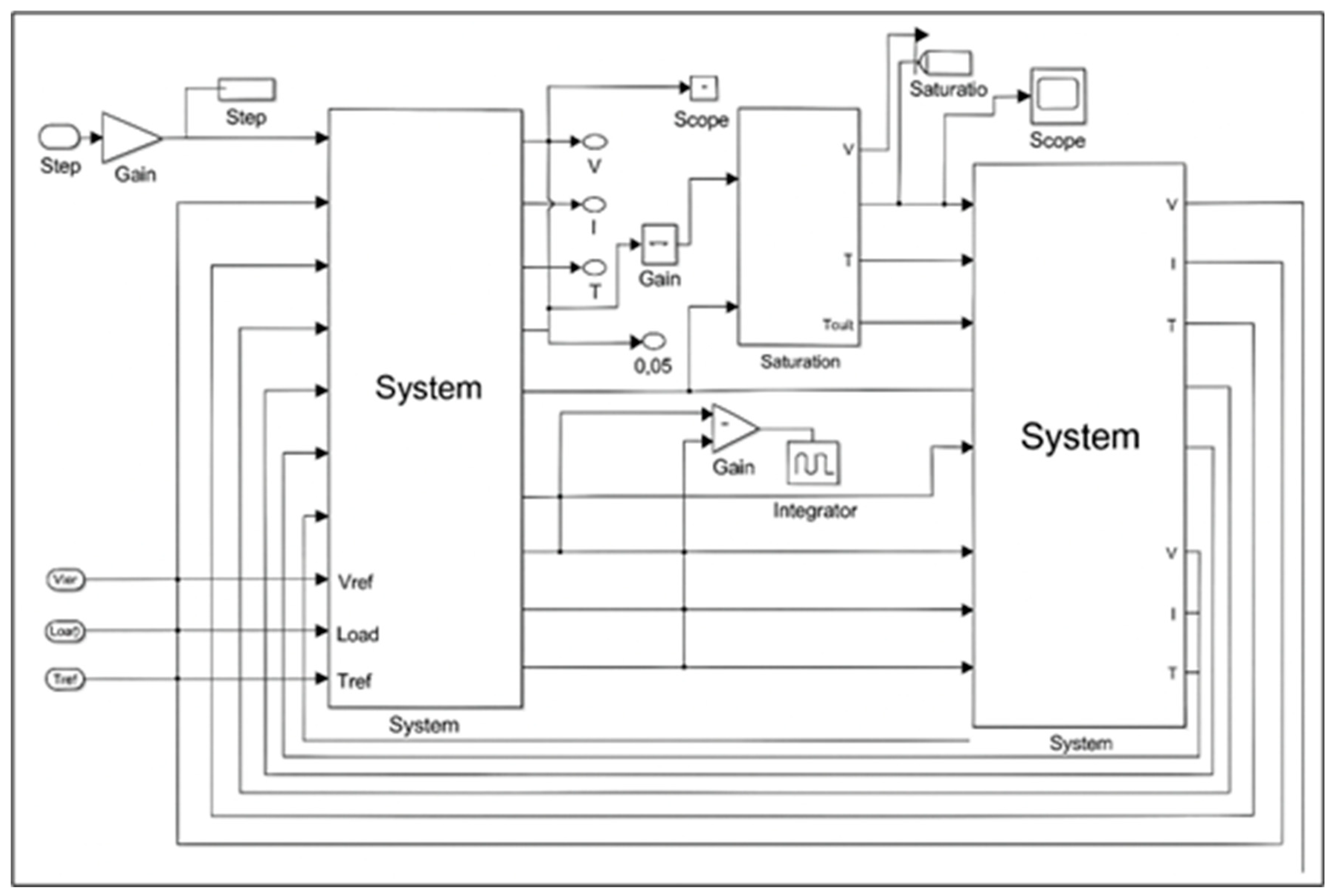
5.1. MATLAB Simulink Model
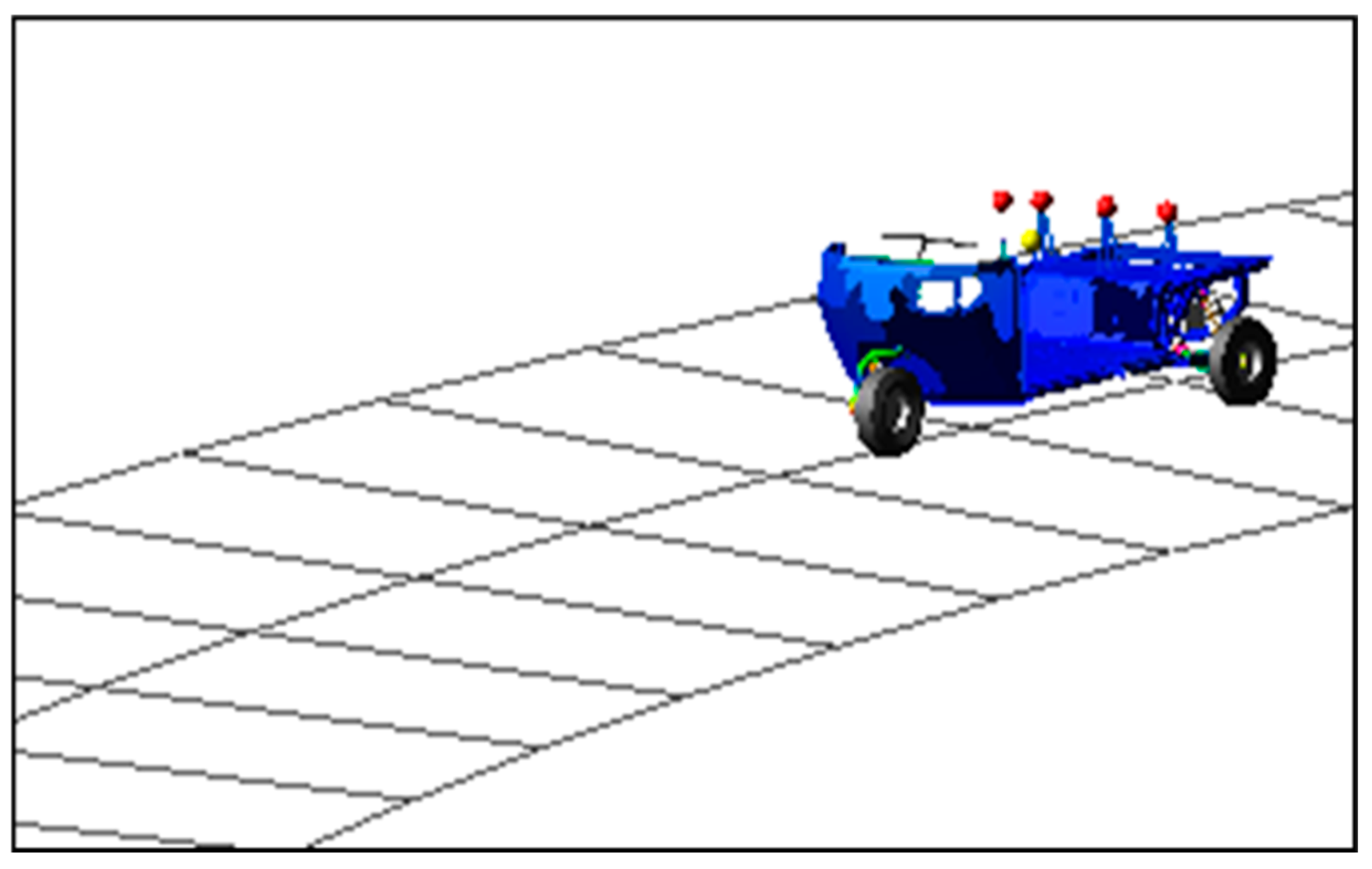
5.2. Multi-Body Dynamics Model
5.3. Powertrain Integration
6. Handling Dynamics Analysis of a Three-Wheeled Vehicle Using MBD and MATLAB/Simulink Simulation
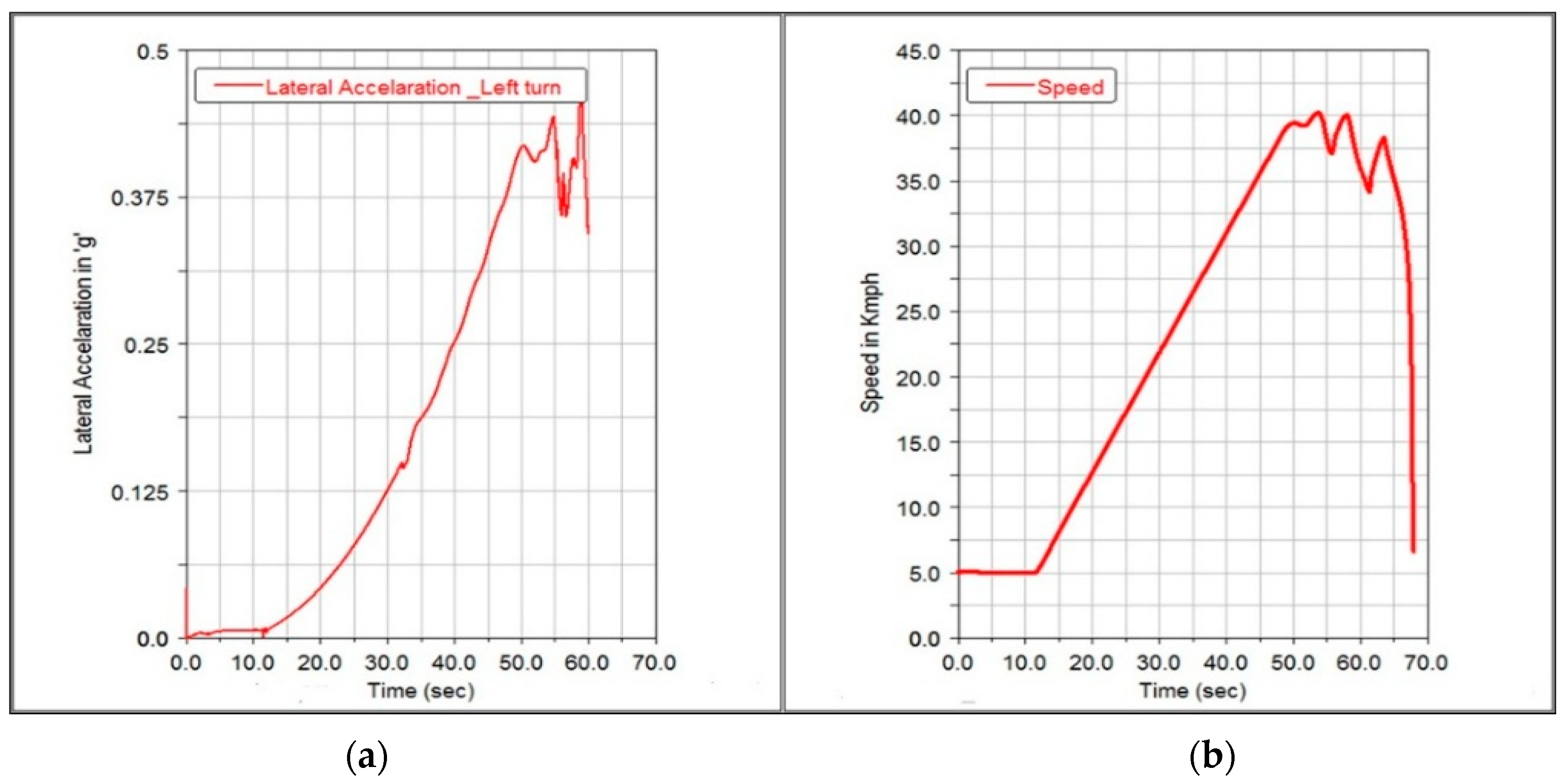
6.1. Open-Loop Handling Simulations
6.1.1. Step Steer Manoeuvre
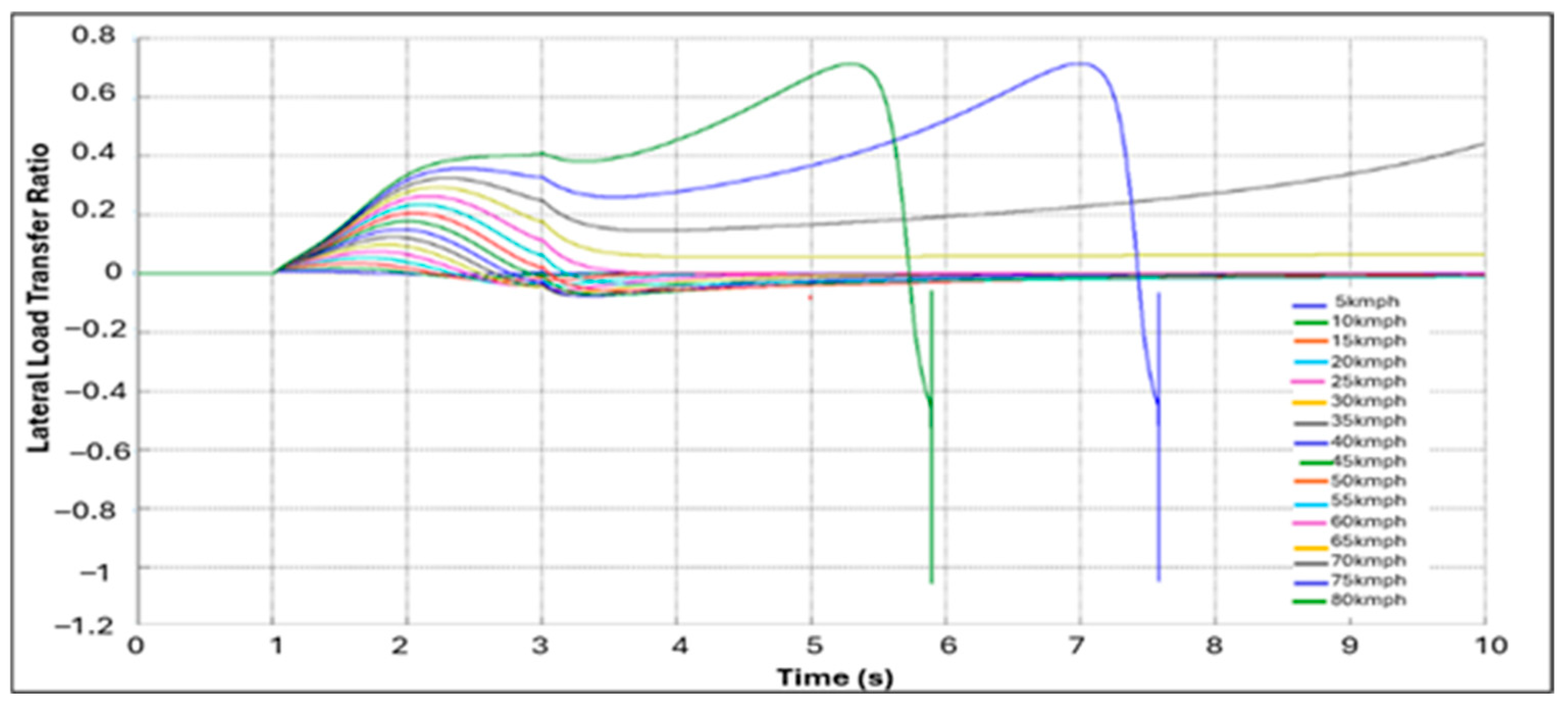
6.1.2. Constant Radius Cornering (CRC)
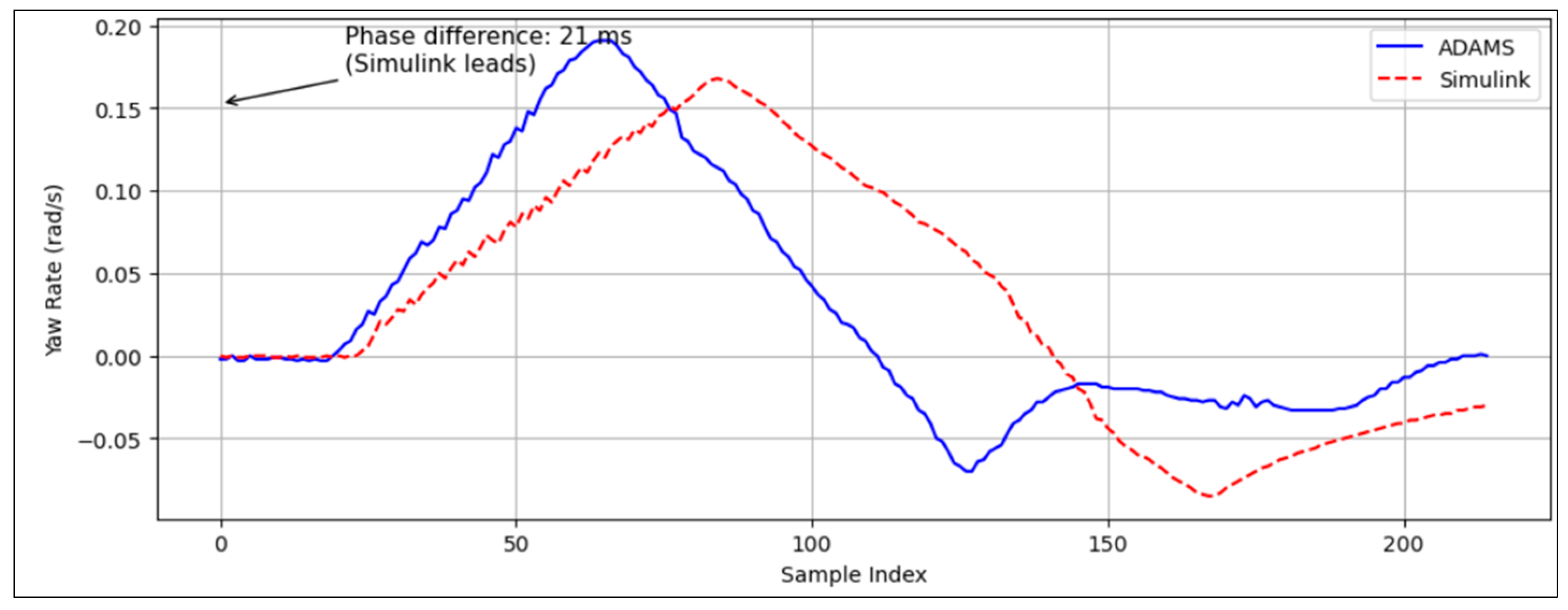
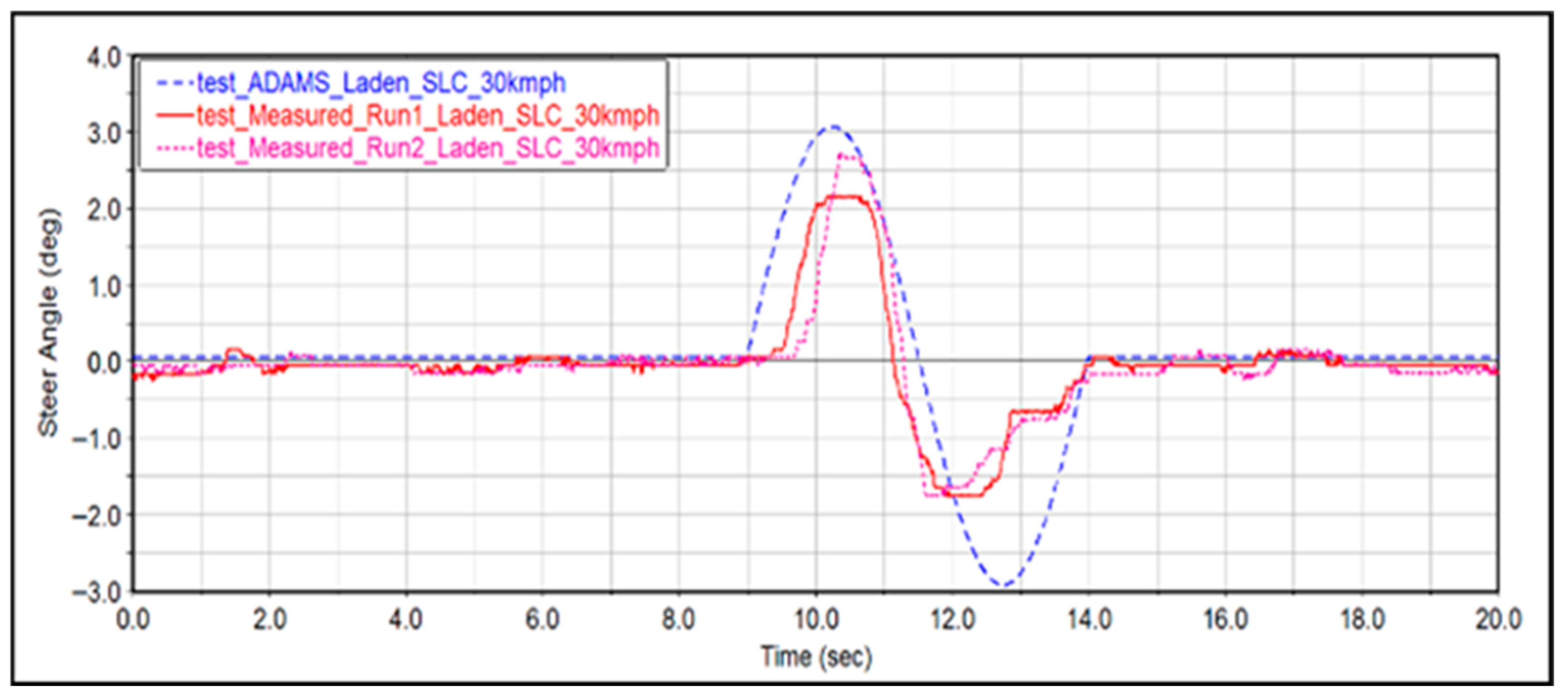
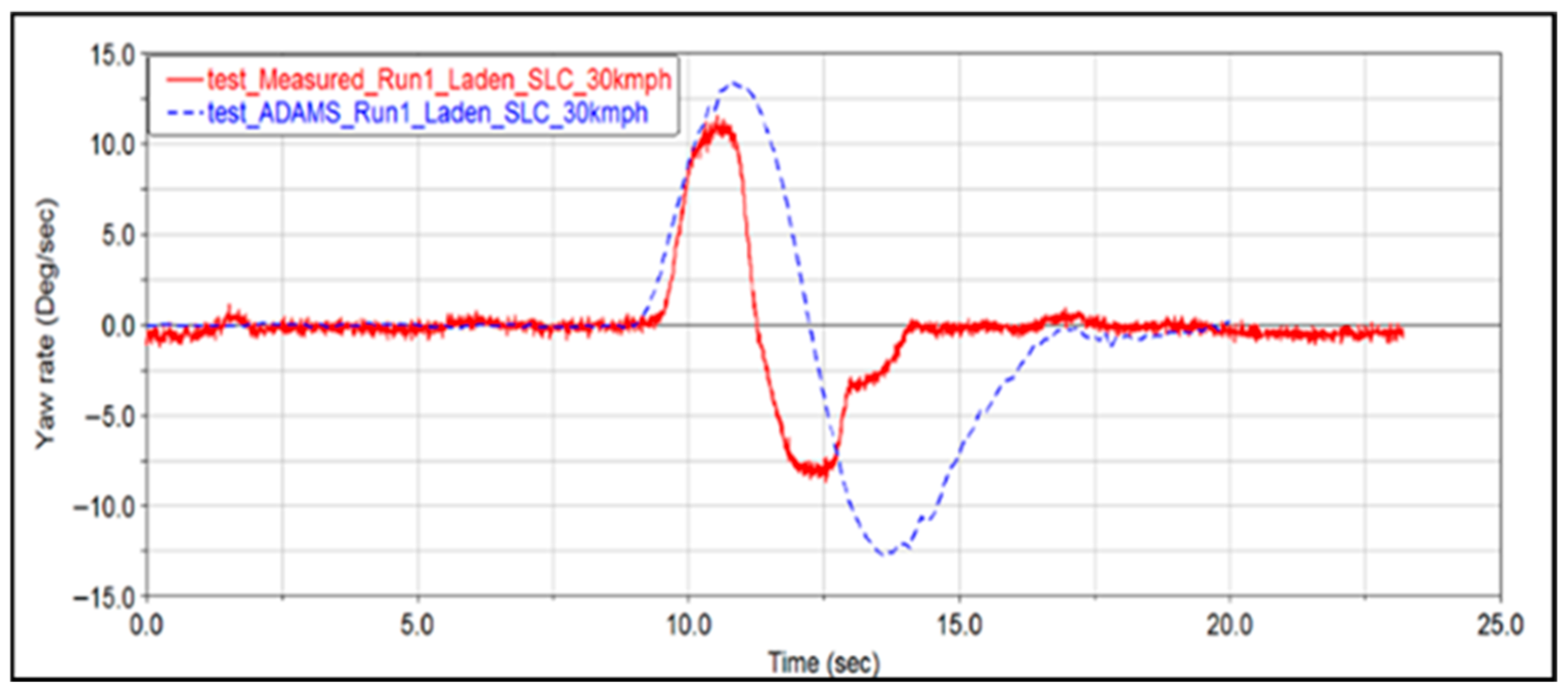
6.2. Comparative Validation with MATLAB/Simulink
7. Experimental Validation of Vehicle Dynamics Simulation
7.1. Instrumentation
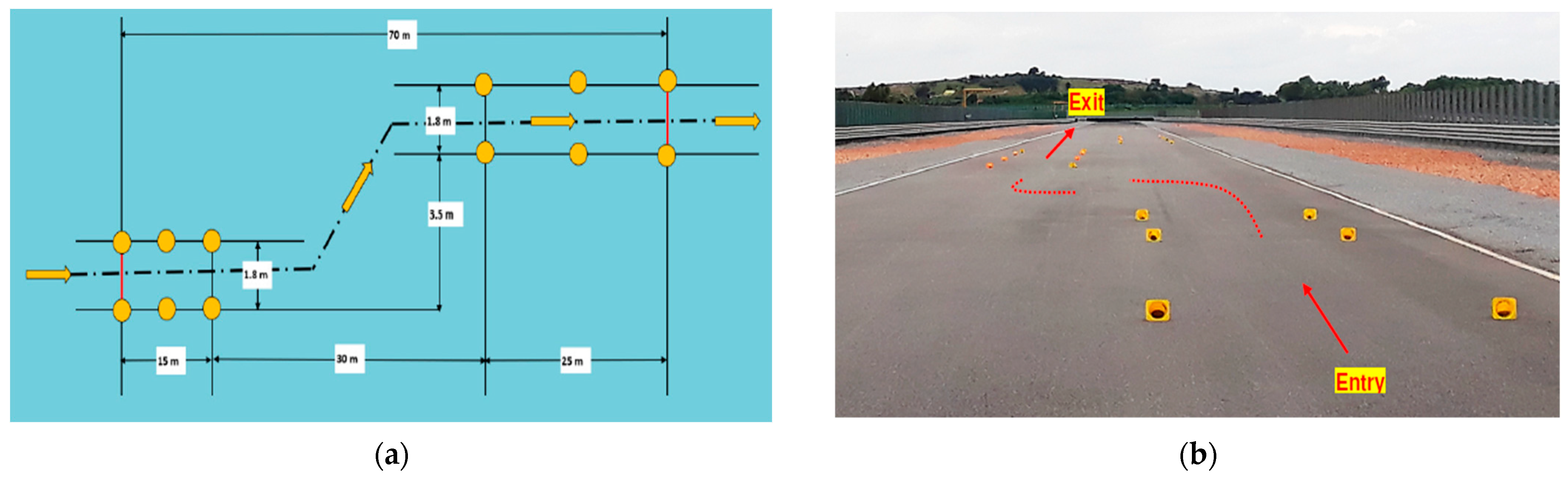
7.2. Road Data and Lane Change Manoeuvres
7.3. Steady-State Circular Test
7.4. Testing Methodology
- Phase I (≤28 km/h): Small speed increments to capture linear behaviour.
- Phase II (>28 km/h): Higher speeds to assess roll saturation and stability.
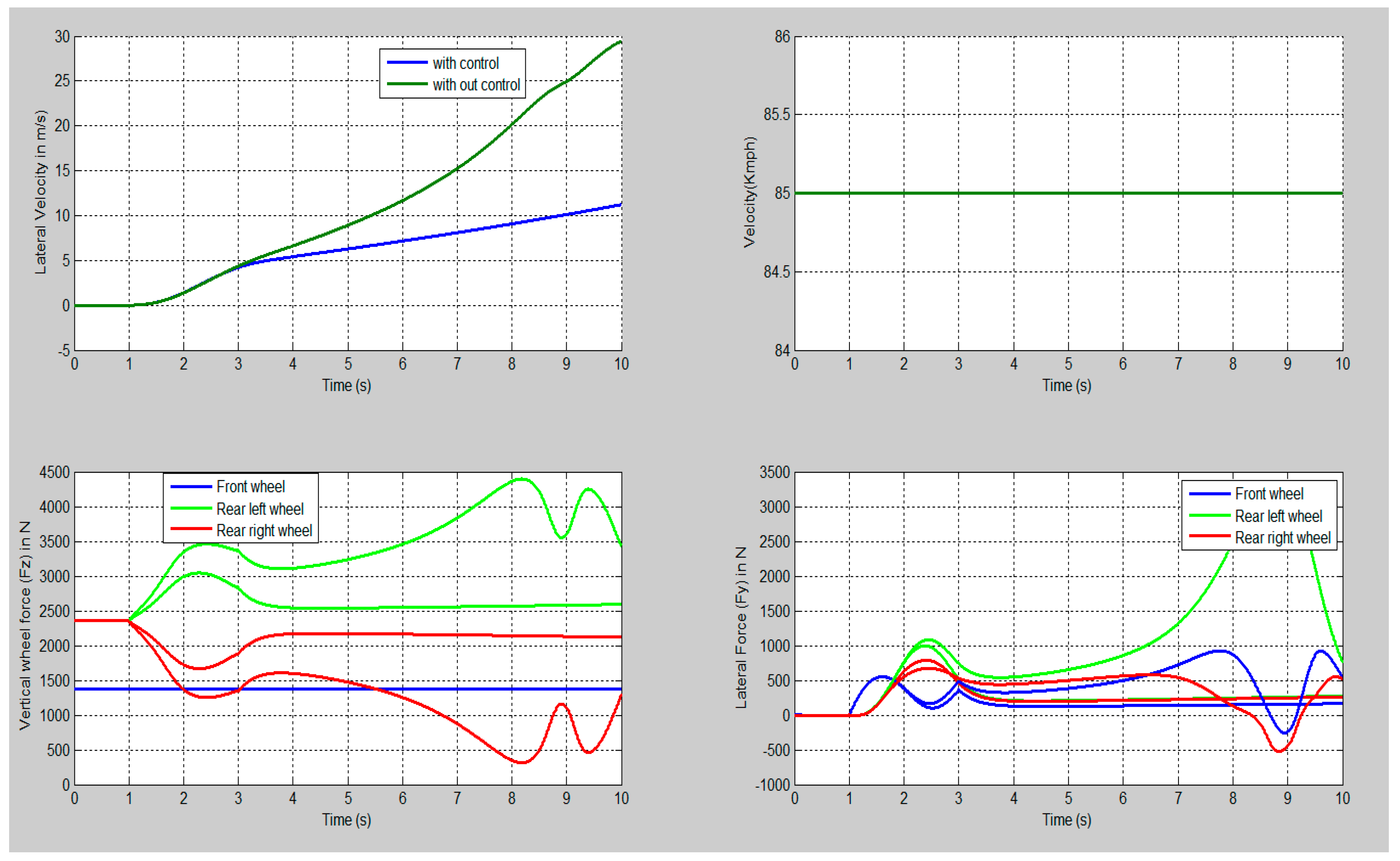
8. Observations and Data Analysis
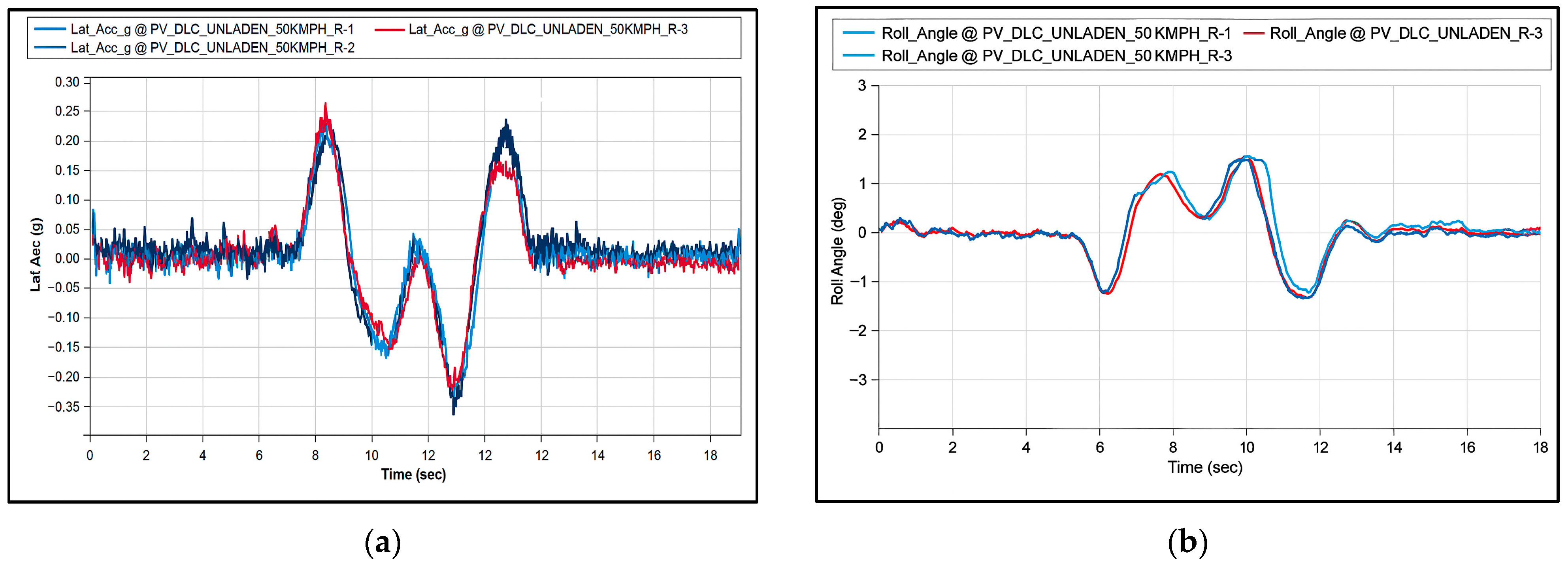
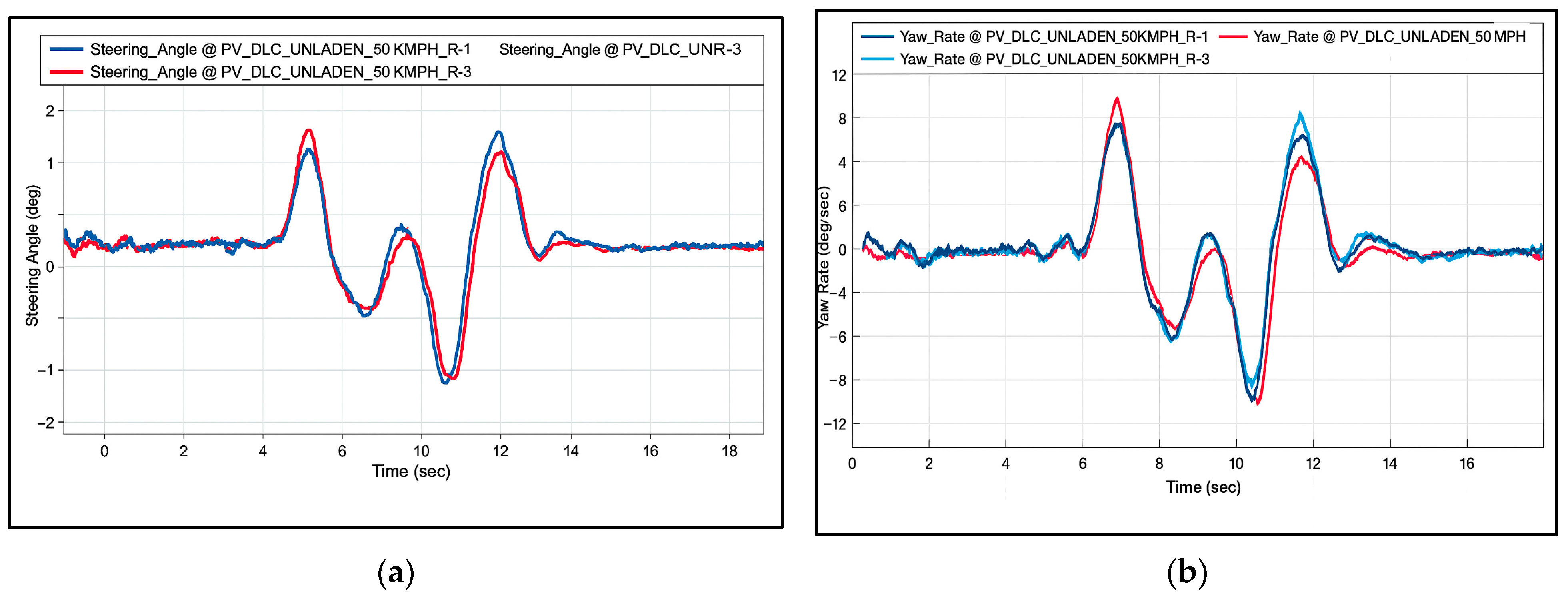
Transient Handling (Lane Change Manoeuvres)
9. MATLAB-Simulink Model with PID Control and Algorithmic Framework for Vehicle Dynamics
Vehicle Dynamics Control Framework
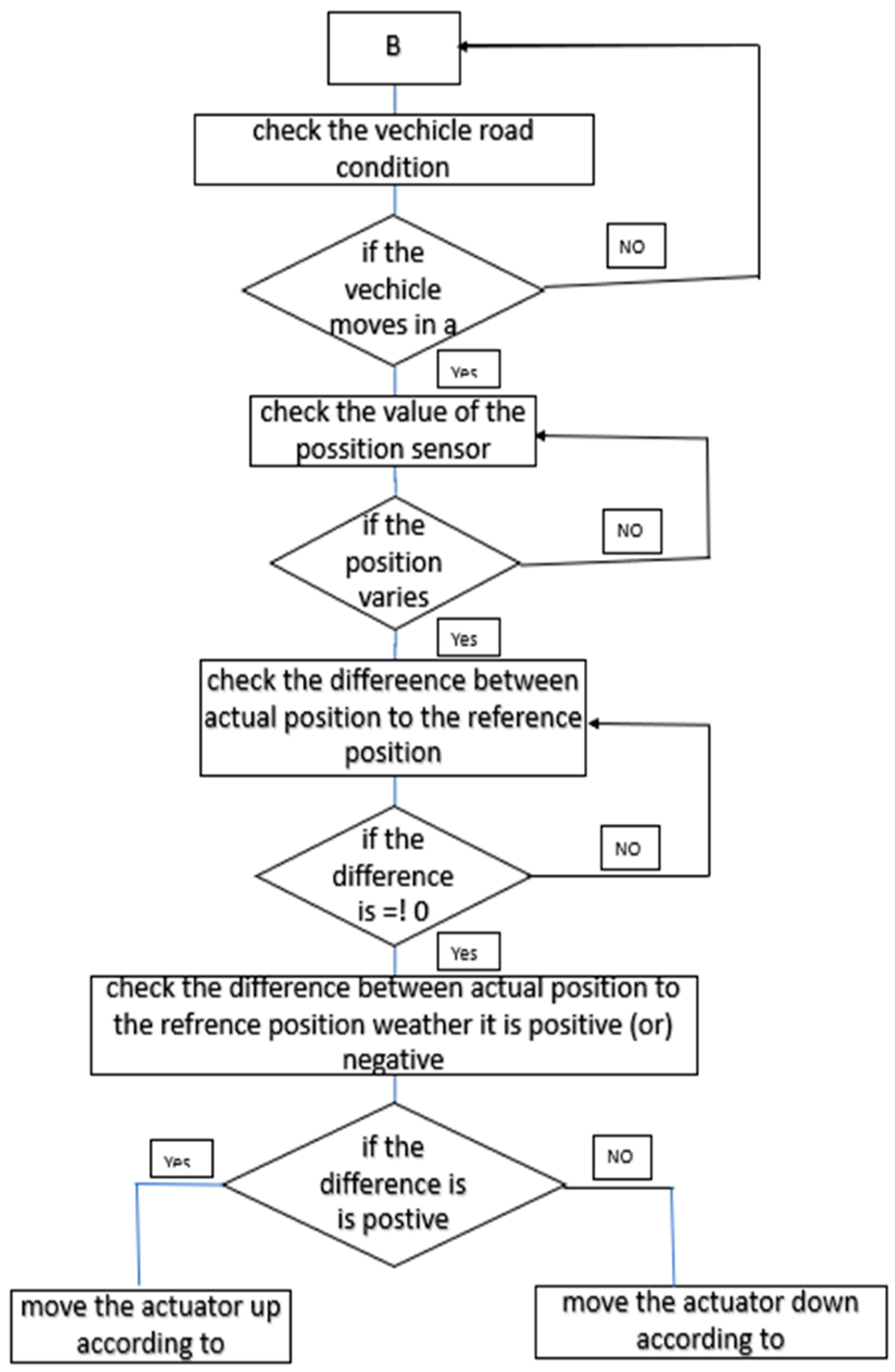
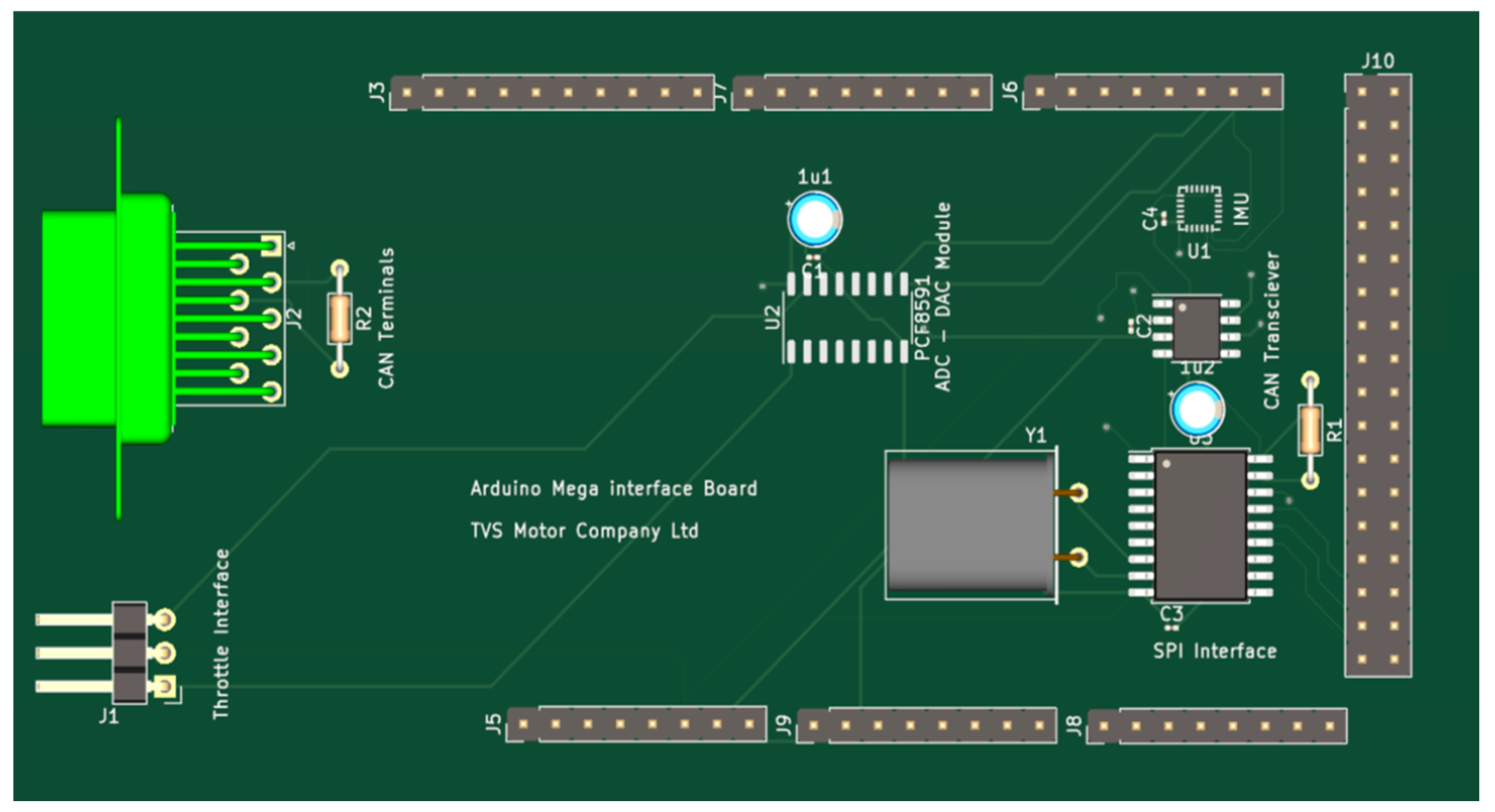
10. Active Control Strategy
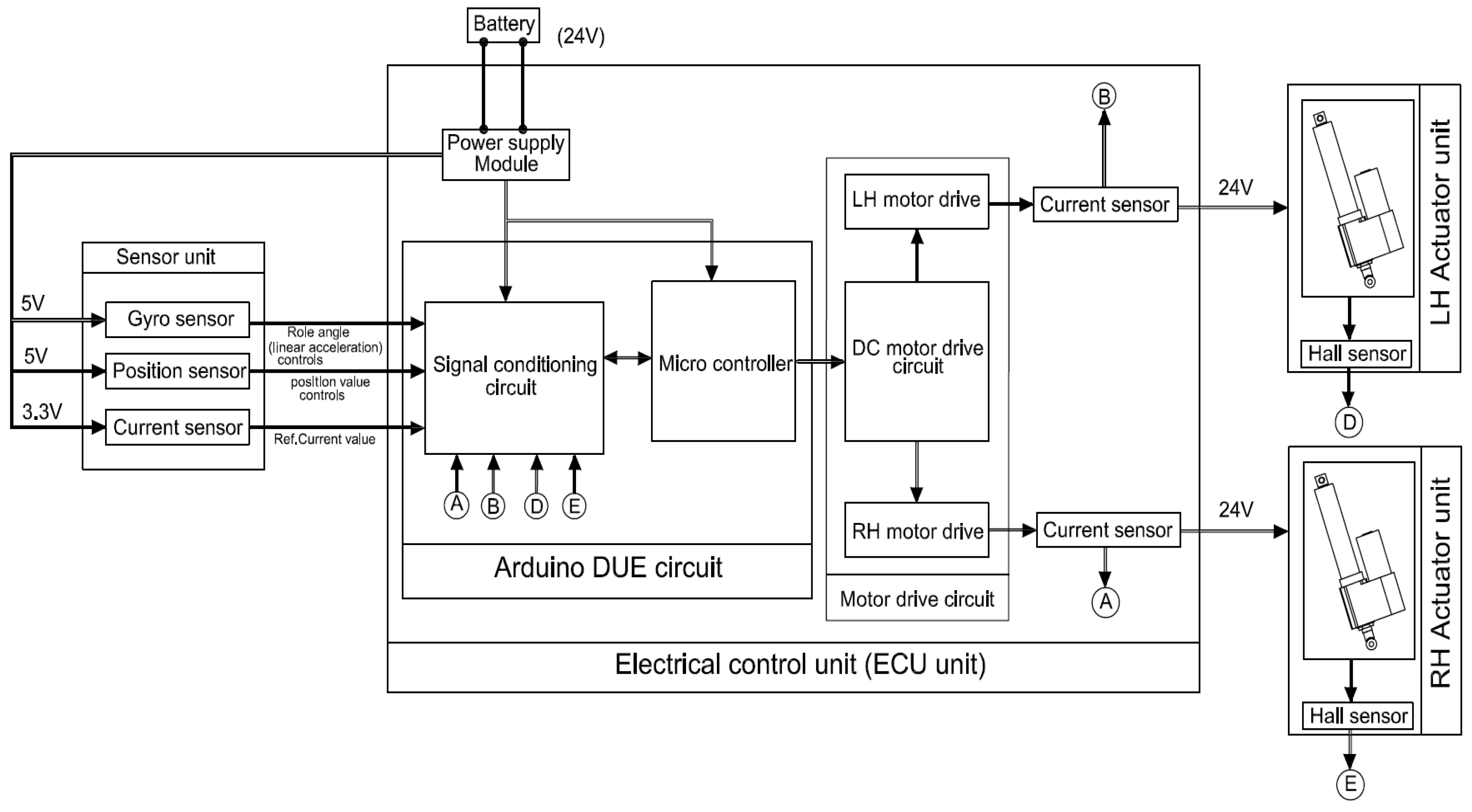
Arduino DUE-Based Experimental Vehicle Control System
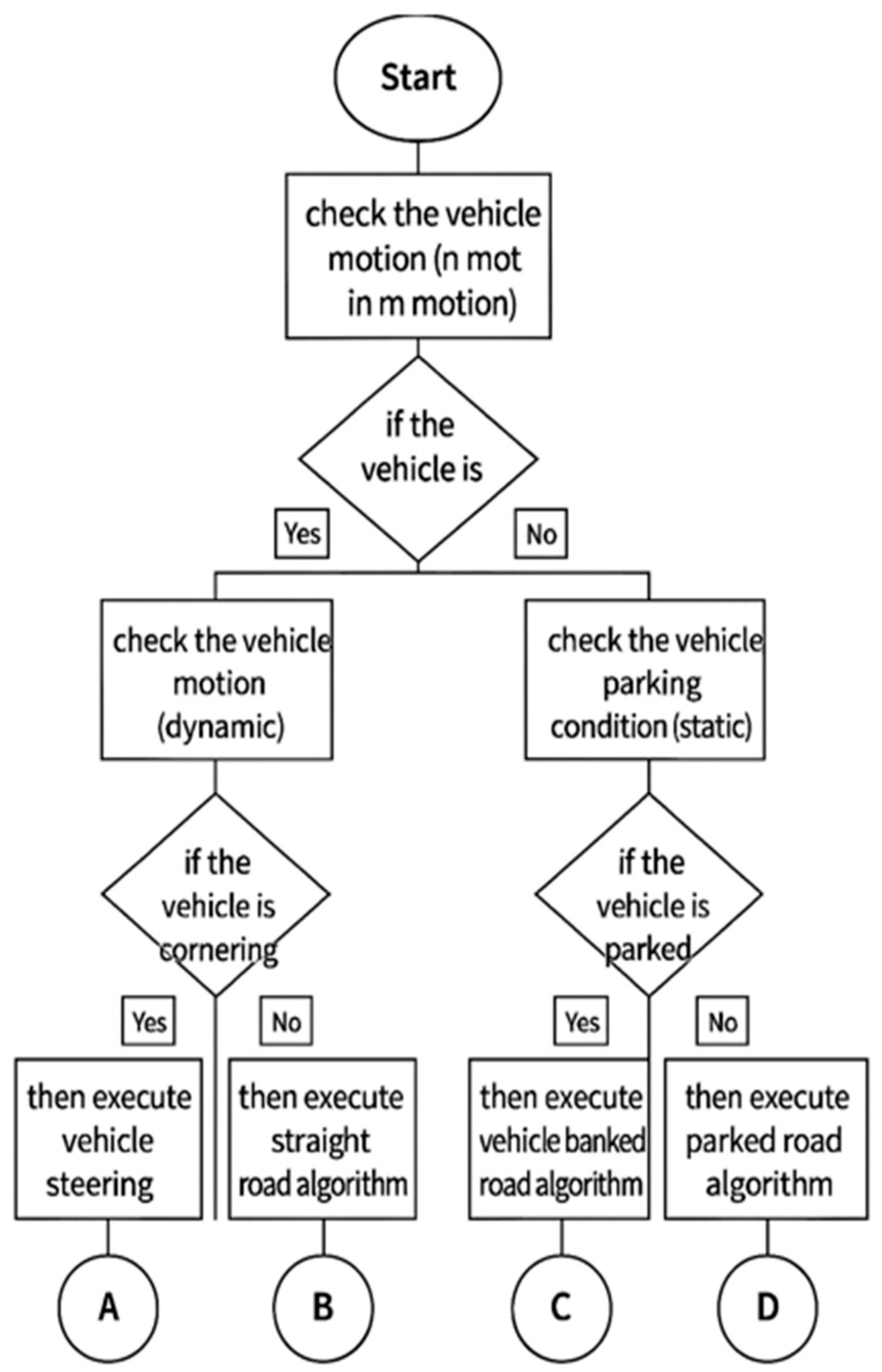
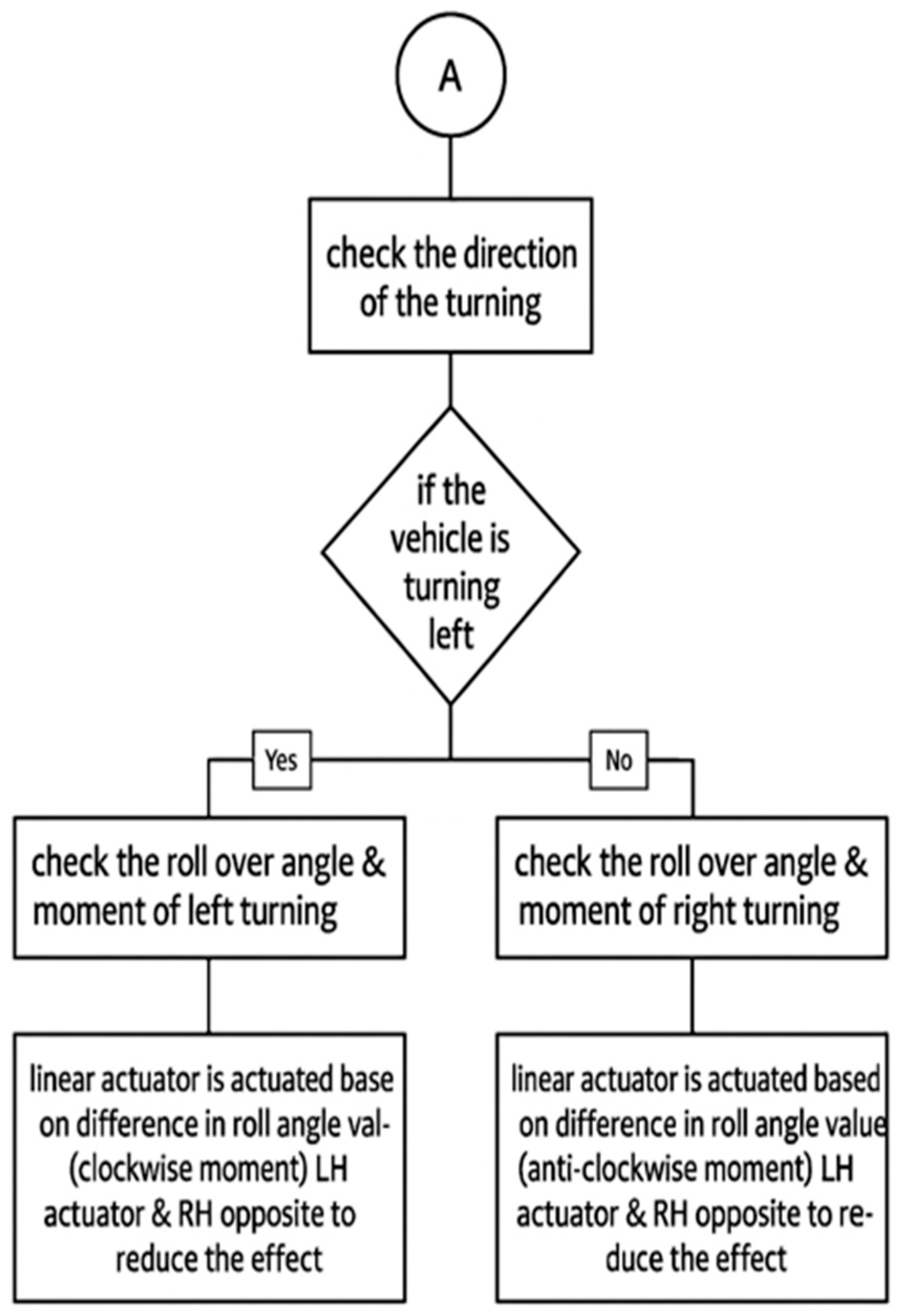
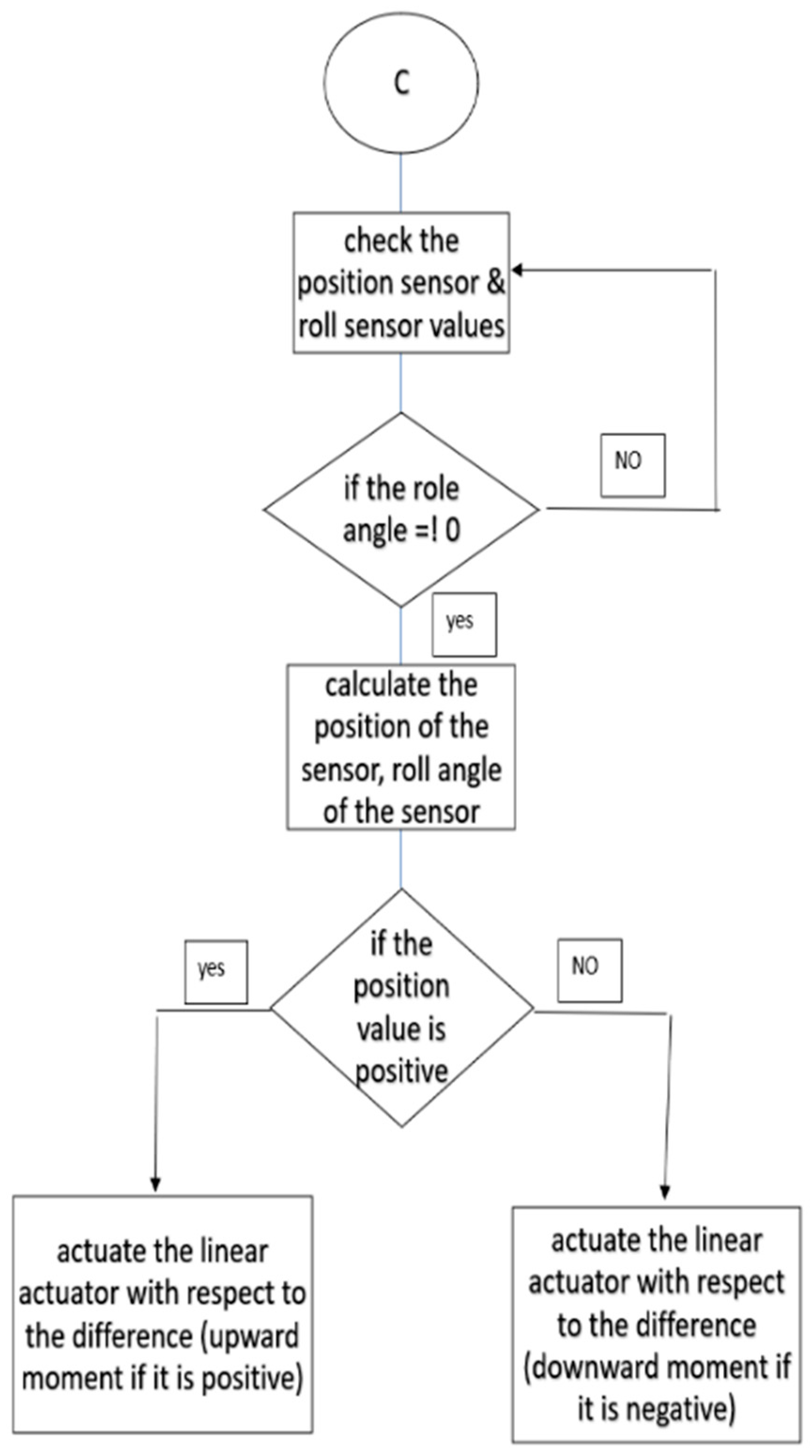
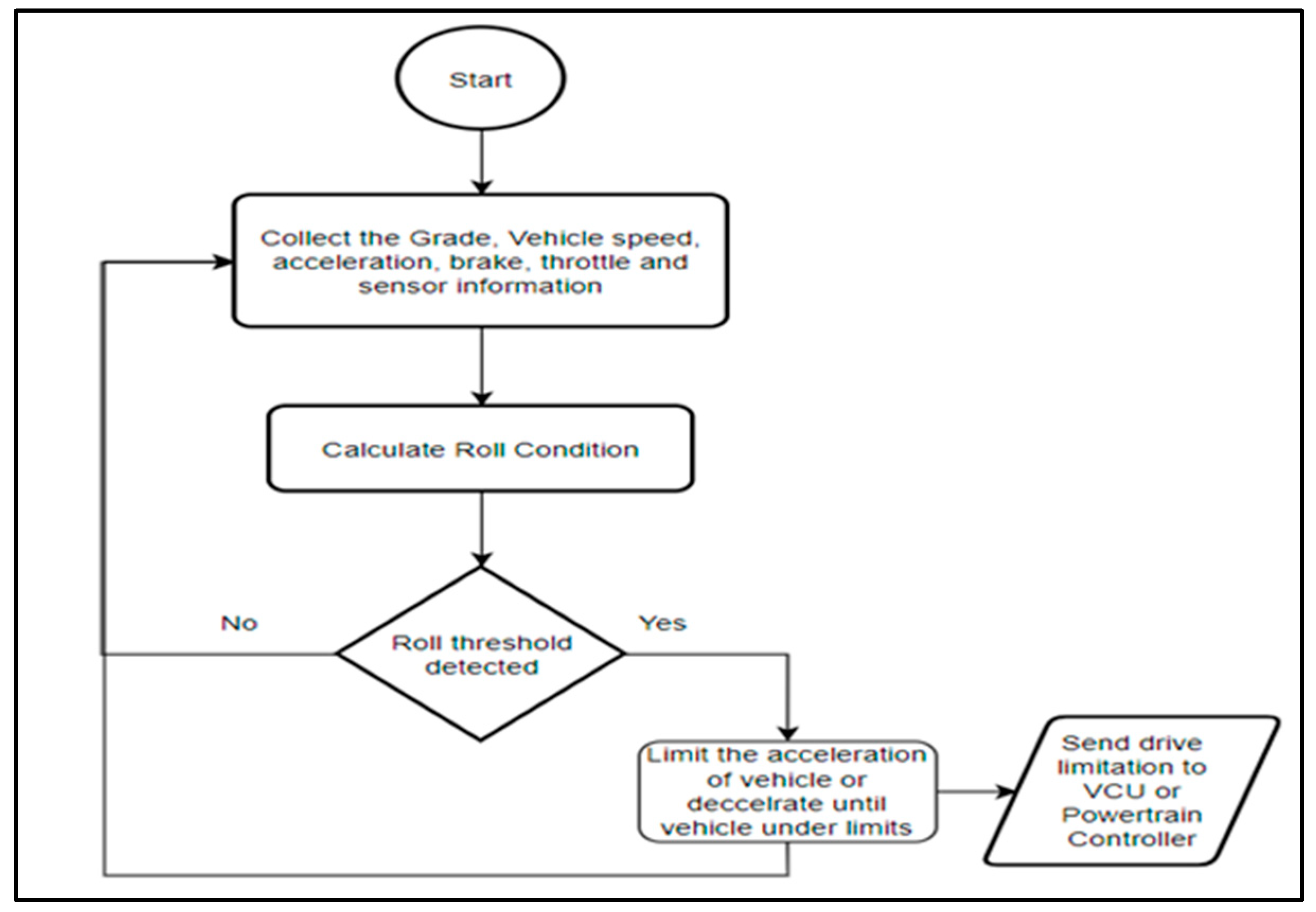
11. Passive Control Strategy
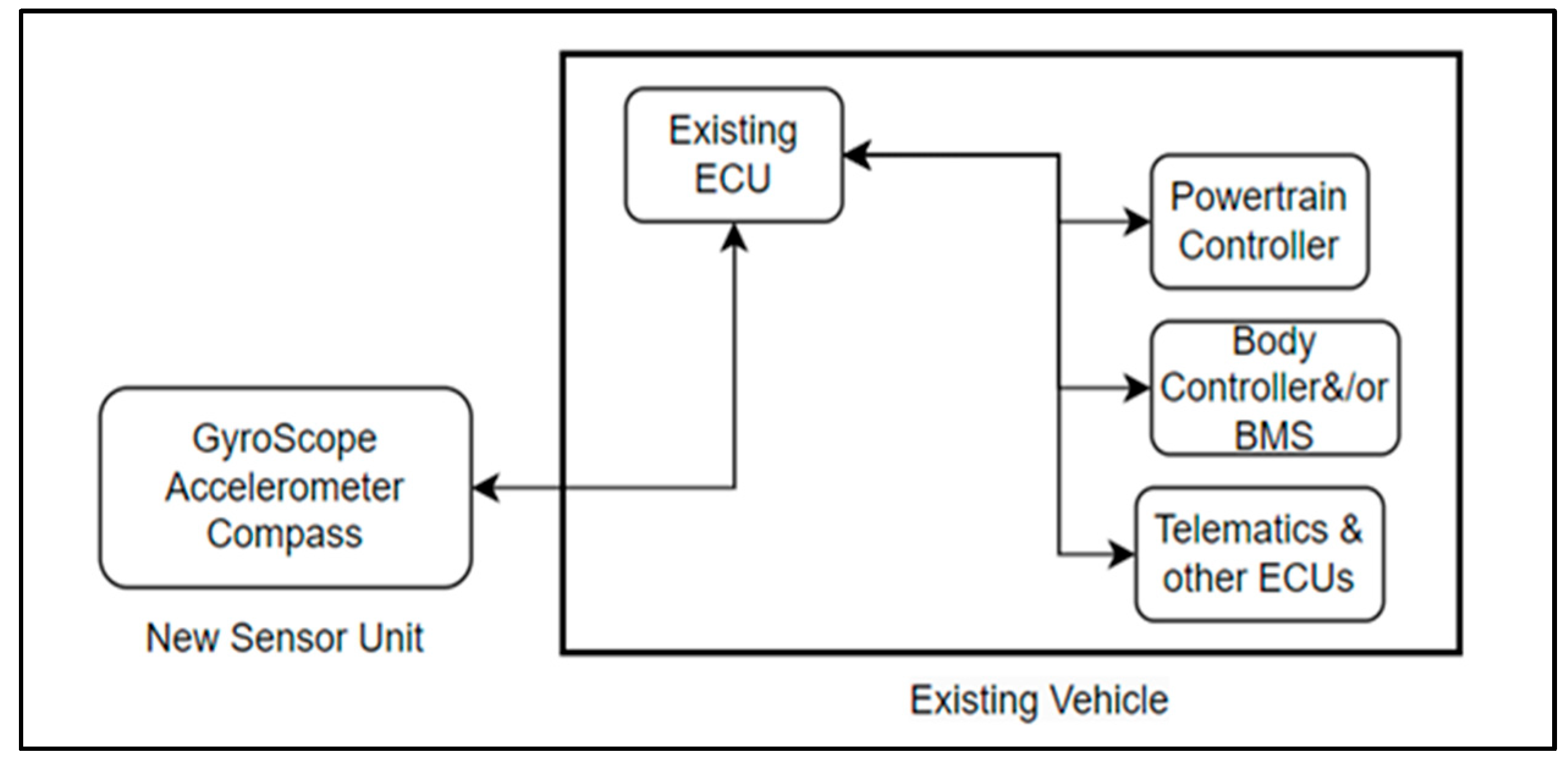
11.1. Communication Between Sensor Unit and ECU
11.2. ECU Functional Architecture
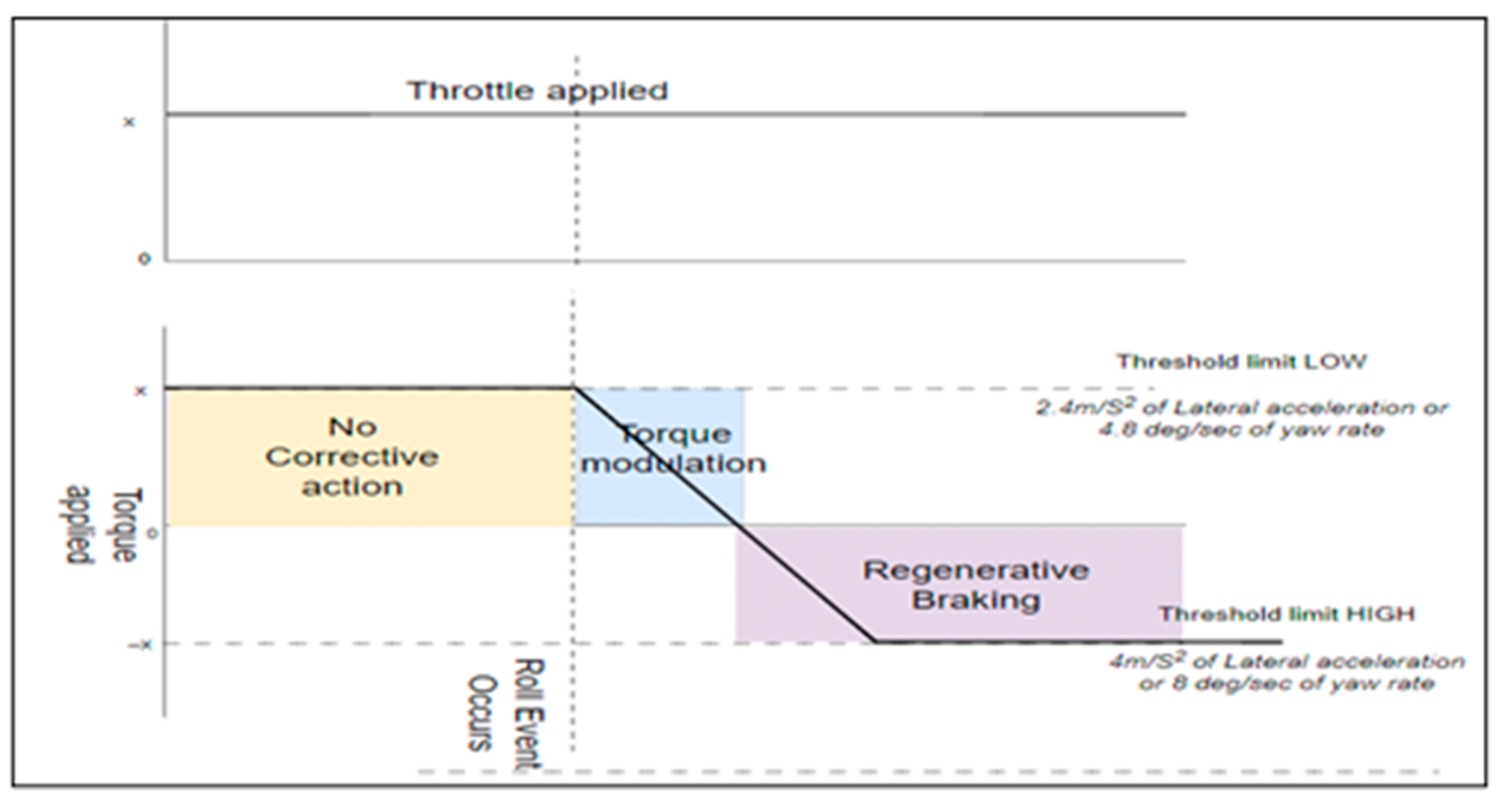
11.3. Threshold Management
11.4. Roll Mitigation
12. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leng, B.; Han, W.; Solmaz, S.; John, R.; Xiong, L. Modeling, Analysis, and Control on Vehicle Lateral Dynamics of Three-Wheeled Vehicles. Chin. J. Mech. Eng. 2025, 38, 187. [Google Scholar] [CrossRef]
- Saxena, S.N. Two- and Three-Wheeler Electric Vehicles in India—Outlook 2019. Int. J. Electr. Eng. Technol. 2019, 9, 1–13. [Google Scholar]
- How Delhi’s Unsafe E-Rickshaws Turn Daily Commute into Gamble; 3 Lives Lost Monthly. Times of India, 8 March 2025.
- Magar, B.; Gangele, A.; Mahajan, G. Electric Three-Wheeler: A Next-Gen Transport System for Developing Countries. Int. J. Recent Technol. Eng. (IJRTE) 2020, 8, 966–970. [Google Scholar] [CrossRef]
- Ministry of Road Transport and Highways (MoRTH). Road Accidents in India—2023; Government of India: New Delhi, India, 2024.
- Moneycontrol. Overspeeding Caused Maximum Road Accidents, Deaths in India in 2023: MoRTH Report. 29 August 2025. Available online: https://www.moneycontrol.com/automobile/overspeeding-caused-maximum-road-accidents-deaths-in-india-in-2023-morth-report-article-13502483.html (accessed on 29 August 2025).
- Drexler, D.; Hou, Z.-C. Simulation Analysis on Vertical Vehicle Dynamics of Three-Wheeled Vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 1041–1052. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. Active wheel steering and yaw moment control combination to maximize stability and vehicle responsiveness during quick lane change for active vehicle handling safety. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2002, 216, 115–124. [Google Scholar] [CrossRef]
- Naidu, M.K.; Srinivasa Rao, S.; Tejesh, T. Ride analysis of three wheeled vehicle using MATLAB/Simulink. Proc. Int. Conf. Adv. Mech. Eng. 2012, 93, 22–26. [Google Scholar]
- Nguyen, X.N.; Tran, T.T. Rollover Stability Dynamic Analysis of Passenger Vehicle in Moving Conditions. Math. Model. Eng. Probl. 2023, 10, 16–21. [Google Scholar] [CrossRef]
- Dumpala, G.R.; Ramarathnam, K.K. Development and validation of a 12-DOF vehicle model for ride and handling analysis for 3-wheeled vehicle. In Proceedings of the VEHICULAR 2025: The Fourteenth International Conference on Advances in Vehicular Systems, Technologies and Applications, Lisbon, Portugal, 9–13 March 2025; IARIA. pp. 11–17, ISBN 978-1-68558-233. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1992. [Google Scholar]
- Gawade, T.; Mukherjee, S.; Mohan, D. Six degrees-of-freedom three-wheeled vehicle model validation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 487–498. [Google Scholar] [CrossRef]
- Esmaeilzadeh, E.; Goodarzi, A.; Vossoughi, G.R. Optimal Yaw Moment Control Law for Improved Vehicle Handling; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Pacejka, H.B. Tire and Vehicle Dynamics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Pacejka, H.B.; Bakker, E. The combined slip Magic Formula tire model. In Vehicle System Dynamics, Supplement 21, Proceedings of 1st Colloquium on Tire Models for Vehicle Analysis, Delft, The Netherlands, 21–22 October 1991; TRID: Washington, DC, USA, 1993. [Google Scholar]
- Blundell, M.; Harty, D. The Multibody Systems Approach to Vehicle Dynamics, 1st ed.; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Furukawa, Y.; Abe, M. Advanced chassis control systems for vehicle handling and active safety. Veh. Syst. Dyn. 1997, 28, 59–86. [Google Scholar] [CrossRef]
- ISO 3888-2:2011; Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre—Part 2: Obstacle Avoidance. ISO: Geneva, Switzerland, 2011.
- ISO 4138:2021; Passenger Cars—Steady-state circular driving behaviour—Open-Loop Test Methods. ISO: Geneva, Switzerland, 2021.
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2005. [Google Scholar]
- Saeddi, M.A.; Kazemi, R. Stability of three-wheeled vehicles with and without control systems. Int. J. Automot. Eng. 2013, 3, 343–355. [Google Scholar]












| Component | DOF | Description |
|---|---|---|
| Vehicle Body | 6 | Translational: X (longitudinal), Y (lateral), Z (vertical) Rotational: Roll (rotation about X-axis), Pitch (rotation about Y-axis), Yaw (rotation about Z-axis) |
| Front Left Wheel | 2 | Vertical translation (Z-axis), Spin about wheel axis (Y-axis) |
| Front Right Wheel | 2 | Vertical translation (Z-axis), Spin about wheel axis (Y-axis) |
| Rear Wheel | 2 | Vertical translation (Z-axis), Spin about wheel axis (Y-axis) |
| Front Wheel Steering | 1 | Rotation about Z-axis (steering) |
| Tire Slip Angle, α, [deg] | 2.5º | 5 º | 7 º |
|---|---|---|---|
| Lateral force difference between linear and non-linear tire Pacejka ‘89’ model | 4% | 33% | 65% |
| Lateral force difference between linear and non-linear tire Pacejka ‘94’ model | 14% | 25% | 40% |
| a0 = 0.5; | a9 = 0.0; |
| a1 = −1300; | a10 = 0.0; |
| a2 = 2400; | a11 = 0.0; |
| a3 = −250; | a12 = 0.0; |
| a4 = −3; | a13 = 0.0; |
| a5 = −0.0024; | a14 = 0.0; |
| a6 = −1.6; | a15 = −0.1; |
| a7 = 1.6; | a16 = 0.0; |
| a8 = 0.0; | a17 = 0.2 |
| Model | TVS King | ||||||
|---|---|---|---|---|---|---|---|
| Engine | Petrol 200cc-1-cyl | ||||||
| Transmission | Manual | ||||||
| Drive | RWD | ||||||
| Tyre type | TVS Tyres Auto 150 | ||||||
| Tyre size | 4.00-8-76F-8PR | ||||||
| Wheelbase (mm) | 2018 | ||||||
| Track(mm) | Front | n/a | |||||
| Rear | 1150 | ||||||
| Tyre pressure (psi) Front/Rear | Driver only | 30/30 | |||||
| GVW | 30/34 | ||||||
| Test Mass—Kerb (kg) | Left | Right | Total | ||||
| Front | 120.0 | 358.5 | |||||
| Rear | 118.5 | 120.0 | |||||
| Test Mass—Driver Only (kg) | Left | Right | Total | ||||
| Front | 162.5 | 437.5 | |||||
| Rear | 134.0 | 141.0 | |||||
| Test Mass—GVW (kg) | Left | Right | Total | ||||
| Front | 197.5 | 658.5 | |||||
| Rear | 224.0 | 237.0 | |||||
| Wheel Alignment (measured at test mass) | Kerb | Driver only | GVW | ||||
| Front toe | n/a | ||||||
| Front Camber | 0.1° top to right | 0.2° top to right | 0.6 ° top to right | ||||
| Rear toe | 0.5° total toe in | 0° | 0.1 ° total toe-out | ||||
| Rear Camber | −0.75° | 0.1.25° | 0.75° | 1.50° | 0.75° | 1.50° | |
| SLC | Steering Angle | Steering Torque | Lateral Acceleration | |||||
|---|---|---|---|---|---|---|---|---|
| PEAK | PEAK | PEAK | PEAK | PEAK | PEAK | |||
| 1 | 2 | 1 | 2 | 1 | 2 | |||
| 30 Kmph | Laden | R-1 | 2.36 | 1.35 | 18.44 | 11.32 | 0.16 | 0.15 |
| R-2 | 2.83 | 1.65 | 19.18 | 7.74 | 0.2 | 0.13 | ||
| R-3 | 2.57 | 1.54 | 17.7 | 12.35 | 0.19 | 0.13 | ||
| Unladen | R-1 | 2.2 | 1.7 | 13.2 | 8.45 | 0.14 | 0.12 | |
| R-2 | 2.19 | 2.02 | 11.15 | 12.19 | 0.14 | 0.14 | ||
| R-3 | 2.24 | 1.5 | 11.5 | 8.94 | 0.15 | 0.1 | ||
| 40 Kmph | Laden | R-1 | 2.17 | 1.54 | 19.81 | 13.52 | 0.27 | 0.16 |
| R-2 | 1.68 | 1.13 | 20.25 | 11.52 | 0.26 | 0.15 | ||
| R-3 | 2.49 | 1.41 | 18.74 | 13.26 | 0.22 | 0.15 | ||
| Unladen | R-1 | 2.49 | 1.41 | 17.18 | 10.12 | 0.25 | 0.14 | |
| R-2 | 1.9 | 1.81 | 15.13 | 11.79 | 0.23 | 0.18 | ||
| R-3 | 2.5 | 1.4 | 17.88 | 13.32 | 0.27 | 0.16 | ||
| 45 Kmph | Laden | R-1 | 1.83 | 1.64 | 20.68 | 15.12 | 0.26 | 0.17 |
| R-2 | 1.77 | 1.73 | 20.91 | 12.09 | 0.28 | 0.21 | ||
| 50 Kmph | Unladen | R-1 | 1.9 | 1.1 | 18.4 | 12.11 | 0.03 | 0.2 |
| R-2 | 1.6 | 1.41 | 16.89 | 13.45 | 0.29 | 0.21 | ||
| R-3 | 2.18 | 1.11 | 18.81 | 11.27 | 0.35 | 0.17 | ||
| SLC | Slip Angle | Roll Angle | Yaw Rate | |||||
|---|---|---|---|---|---|---|---|---|
| PEAK | PEAK | PEAK | PEAK | PEAK | PEAK | |||
| 1 | 2 | 1 | 2 | 1 | 2 | |||
| 30 Kmph | Laden | R-1 | 1.53 | 0.91 | 2.1 | 1.49 | 11.17 | 8.36 |
| R-2 | 1.97 | 0.91 | 2.52 | 1.4 | 13.42 | 8.21 | ||
| R-3 | 1.52 | 1.1 | 2.29 | 1.35 | 12.19 | 7.94 | ||
| Unladen | R-1 | 1.13 | 0.28 | 1.25 | 0.95 | 9.21 | 7.34 | |
| R-2 | 1.34 | 0.33 | 1.34 | 1109 | 9117 | 8.96 | ||
| R-3 | 1.43 | 0.57 | 1.42 | 0.8 | 9.68 | 6.35 | ||
| 40 Kmph | Laden | R-1 | 2.63 | 2.06 | 2.57 | 2.2 | 15 | 9.93 |
| R-2 | 2.31 | 1.95 | 2.81 | 1.67 | 14.43 | 7.11 | ||
| R-3 | 2.27 | 1.54 | 2.56 | 1.69 | 11.88 | 7.78 | ||
| Unladen | R-1 | 1.77 | 0.54 | 2.09 | 0.99 | 13.4 | 7.27 | |
| R-2 | 1.33 | 0.83 | 1.7 | 1.46 | 11.61 | 9.07 | ||
| R-3 | 1.89 | 0.72 | 2.03 | 1.26 | 14.97 | 8.52 | ||
| 45 Kmph | Laden | R-1 | 2.99 | 1.84 | 2.63 | 1.94 | 14.83 | 9.49 |
| R-2 | 2.9 | 2.05 | 2.74 | 2.05 | 13.46 | 10.53 | ||
| 50 Kmph | Unladen | R-1 | 2.15 | 1.24 | 2.2 | 1.33 | 13.92 | 6.96 |
| R-2 | 2.15 | 1.3 | 2.09 | 1.53 | 12.84 | 8.66 | ||
| R-3 | 2.53 | 0.96 | 2.19 | 1.47 | 14.77 | 6.52 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reddy, D.G.; Kumar, R.K. Active and Passive Control Strategies for Ride Stability and Handling Enhancement in Three-Wheelers. Vehicles 2025, 7, 126. https://doi.org/10.3390/vehicles7040126
Reddy DG, Kumar RK. Active and Passive Control Strategies for Ride Stability and Handling Enhancement in Three-Wheelers. Vehicles. 2025; 7(4):126. https://doi.org/10.3390/vehicles7040126
Chicago/Turabian StyleReddy, Dumpala Gangi, and Ramarathnam Krishna Kumar. 2025. "Active and Passive Control Strategies for Ride Stability and Handling Enhancement in Three-Wheelers" Vehicles 7, no. 4: 126. https://doi.org/10.3390/vehicles7040126
APA StyleReddy, D. G., & Kumar, R. K. (2025). Active and Passive Control Strategies for Ride Stability and Handling Enhancement in Three-Wheelers. Vehicles, 7(4), 126. https://doi.org/10.3390/vehicles7040126








