A Systematic Review of Sustainable Ground-Based Last-Mile Delivery of Parcels: Insights from Operations Research

Abstract

The importance of Last-Mile Delivery (LMD) in the current economy cannot be overstated, as it is the final and most crucial step in the supply chain between retailers and consumers. In major cities, absent intervention, urban LMD emissions are projected to rise by >30% by 2030 as e-commerce grows (top-100-city “do-nothing” baseline). Sustainable, innovative ground-based solutions for LMD, such as Electric Vehicles, autonomous delivery robots, parcel lockers, pick-up points, crowdsourcing, and freight-on-transit, can revolutionize urban logistics by reducing congestion and pollution while improving efficiency. However, developing these solutions presents challenges in Operations Research (OR), including problem modeling, optimization, and computations. This systematic review aims to provide an OR-centric synthesis of sustainable, ground-based LMD by (i) classifying these innovative solutions across problem types and methods, (ii) linking technique classes to sustainability goals (cost, emissions/energy, service, resilience, and equity), and (iii) identifying research gaps and promising hybrid designs. We support this synthesis by systematically screening 283 records (2010–2025) and analyzing 265 eligible studies. After the gap analysis, the researchers and practitioners are recommended to explore new combinations of innovative solutions for ground-based LMD. While they offer benefits, their complexity requires advanced solution algorithms and decision-making frameworks.

1. Introduction

Last-Mile Delivery (LMD) has become increasingly central to modern supply chains as e-commerce expands and service expectations tighten. LMD involves delivering products from a warehouse to the end consumer, and its impact has grown significantly due to the rise of e-commerce and the demand for quick deliveries [1]. LMD costs contribute considerably to shipping expenses, accounting for 53% of the total [2]. The global autonomous LMD market is expected to reach around USD 84.72 billion by 2030 [3]. Additionally, according to a 2023 survey, over half (53%) of consumers chose not to complete their purchases due to excessively protracted shipping times [4]. Efficient LMD not only influences purchasing decisions but also shapes urban planning, sustainability efforts, and transportation logistics [5,6,7].

Beyond the economic benefits, LMD has both environmental and societal significance. While delivery vehicles constitute a small share of total urban vehicles, their activity is concentrated in dense cores with frequent stop-and-go operations. Consistent scenario studies indicate that, in the top 100 cities and under a no-intervention baseline, urban LMD emissions could increase by >30% by 2030 alongside higher congestion [8]. At the same time, cities and operators are accelerating the adoption of zero-emission vehicles; however, uptake remains uneven across regions and vehicle classes (e.g., electric vans constitute a single-digit share of new registrations in many markets) [9,10]. Environmentally, its carbon footprint necessitates sustainable approaches, such as the use of Electric Vehicles (EVs) and optimized routes, to reduce emissions and air pollution. Utilizing local fulfillment centers to establish the last-mile supply chain can mitigate last-mile emissions by $17\%$ to $26\%$ by 2025 [11]. In addition, on a societal level, LMD improves accessibility for people with mobility limitations, supports local employment, and plays a crucial role during emergencies.

Innovative solutions for sustainable LMD can revolutionize urban logistics, minimizing congestion and pollution while enhancing efficiency and customer satisfaction in the evolving landscape of e-commerce and urban mobility [12]. Innovative ground-based solutions include EV delivery, Autonomous Delivery Robots (ADRs), Parcel Lockers (PLs), Pick-up Points (PPs), Crowdsourcing (CS), and Freight-on-Transit (FOT). In recent times, due to the efficacy and sustainability of EVs, Walmart intends to acquire 4500 all-electric delivery vehicles. Domino’s purchases 800 Chevy Bolt EVs to facilitate deliveries across its U.S. outlets, and Amazon deploys numerous customized EVs across over 100 cities [13]. ABI Research predicts an impressive $850\%$ growth in ADR technology advancements over the next ten years, benefiting warehouse usage and the delivery market [14]. Moreover, PLs and PPs have gained significant attention and popularity in recent years as practical solutions for the LMD [15].

Developing sustainable innovative solutions such as EVs, ADRs, PLs, PPs, CS, and FOT for LMD presents a multifaceted set of challenges from an Operations Research (OR) perspective. These challenges encompass modeling (problem definition), intricate optimization problems, uncertainty, and computations involving route planning, vehicle (e.g., EV and ADR) scheduling, resource allocation, and infrastructure planning, necessitating advanced algorithms to achieve efficient and cost-effective LMD networks. Furthermore, integrating diverse technologies requires novel modeling techniques to address uncertainties arising from traffic congestion, adverse weather conditions, and complex urban environments. Balancing environmental considerations with economic viability and adapting to evolving consumer preferences adds another layer of complexity to OR-driven decision-making processes in the pursuit of establishing sustainable and resilient LMD systems.

Conducting a systematic review to identify the challenges of innovative sustainable solutions for LMD from the OR perspective is of paramount significance in the LMD literature. Such a survey serves as a comprehensive synthesis of existing research, offering a consolidated understanding of the multifaceted challenges inherent in deploying technologies like EVs, ADRs, PLs, CS, and FOT for LMD optimization. This review paper examines the intricate challenges posed by optimization problems (models) and environmental factors (sustainability), identifies gaps in existing knowledge, and proposes directions for future research. It serves as a crucial reference point for researchers and practitioners, fostering a deeper appreciation of the interdisciplinary nature of sustainable LMD innovations and encouraging the development of novel methodologies that effectively address the intricate OR-related challenges, ultimately advancing both the academic and practical realms of LMD.

According to the literature, Last-Mile Logistics (LMLs) encompasses last-mile distribution, last-mile fulfillment, last-mile transport, and LMD. Several review papers have focused on LML, such as [16,17,18,19,20]. Moreover, LMD has been reviewed by researchers based on three classes of approaches: (i) traditional approaches (e.g., using trucks), such as, Vehicle Routing Problem (VRP) [21,22,23], and Traveling Salesman Problem (TSP) [24]; (ii) combination of traditional and innovative solutions [1,6,12,25,26]; and (iii) sustainable innovative solutions [27,28,29,30,31], which designed to minimize life-cycle environmental and social impacts (energy use, emissions, noise, congestion) while maintaining or improving service levels and economic viability through optimization, modeling, and solution algorithms. The last category of approaches can be studied from both OR and non-OR (e.g., stakeholder) perspectives.

In this systematic review, we focus on sustainable, innovative ground-based solutions in LMD from an OR perspective, which, to the best of our knowledge, has not been studied in the literature. Additionally, to the best of the authors’ knowledge, this literature review is a first attempt to investigate combined (hybrid) innovative solutions. Conducting a review from an OR perspective not only highlights existing shortcomings but also provides a structured framework for identifying, analyzing, and recommending strategies that bridge gaps in the literature. Previous reviews of ground-based LMDs exist in the literature, but our work differs from them in both focus and approach. For example, the works of [27,28,32,33,34] reviewed innovative solutions in LMD, but their perspectives were not from an OR perspective. In addition, ref. [35] reviewed the LMD and transportation logistics from a non-OR (i.e., stakeholder) perspective, which differs from our focus in the present work. Moreover, ref. [1] studied innovative solutions in LMD, but they investigated LMD in terms of efficiency, rather than sustainability. Two review works of [12,17] are the most similar works to this present paper in terms of studying the innovative solution in ground-based LMD from an OR perspective; however, the former work has not focused on sustainability, and also our work is more complete and detailed than the later work by investigating more problems and sub-problems in terms of OR. Additionally, the work of [12] did not review the CS, unlike our current review. To organize the review conceptually rather than descriptively, we introduce a conceptual framework that maps OR technique classes to sustainability goals and metrics; this framework precedes the per-innovation sections and anchors the comparative analysis presented later.

Moreover, the recent literature offers complementary perspectives: Shuaibu et al. [36] review optimization with Artificial Intelligence (AI), the Internet of Things (IoT), and drone integration. Bonilla et al. [37] provide a management-oriented taxonomy of sustainable e-retail practices. Alverhed et al. [38] focus specifically on autonomous delivery robots. In contrast, our review is intentionally ground-based and OR-centric approaches, linking problem structures to method classes and to people-planet-profit objectives, and synthesizing combined EV/ADR/PL/PP/CS/FOT designs. We complement recent reviews by providing a goal-technique framework, comparative OR studies, and insights into the deployment of hybrid systems. Additionally, as a broad baseline, Liu and Hassini [39] provide a unified terminology and bibliometric map of freight LMD across commercial and humanitarian settings (2010–2021). Additionally, a comprehensive synthesis of environmental sustainability approaches in B2C LMD by [40] provides valuable background on logistics- and consumer-side levers, along with reported trade-offs. Our review, in contrast, focuses on ground-based innovations and OR methods, with an update on technical advances from 2022 to 2025.

Throughout this review, sustainability follows a triple-bottom-line lens, planet (environmental impact), people (social impact), and profit (economic viability) [41,42], with resilience as a cross-cutting property. Planet covers life-cycle-aware use-phase indicators such as CO₂ emission per parcel, energy use, local pollutants (NO_x, PM), noise, and congestion externalities. People cover access to equity (e.g., the share of the population within a walking radius of PL/PP), customer service reliability (including failed deliveries and lateness), and safety/curb-conflict proxies. Profit covers total generalized cost, unit delivery cost, asset utilization, and on-time service as a viability criterion. We use this lens to motivate the goal-technique mapping and comparative guidance.

Contributions to theory and practice. Theoretically, we synthesize sustainable, ground-based LMD from an OR perspective by (i) unifying prior models under decision layers (strategic, tactical, and operational) and sustainability goals (cost, emissions/energy, service, resilience, and equity), (ii) formalizing a goal-technique mapping that links problem structure to appropriate OR method classes, and (iii) distilling cross-cutting insights and method selection guidance. In practice, we translate these insights into deployable guidance, including a comparative study of technique choice under real constraints, a reporting checklist for reproducible evaluation, and consolidated practice snapshots that summarize outcomes from real deployments and pilots. Together, these elements position the review as a reference for both academics and practitioners.

Methodological approach. We conduct a protocolled systematic review adapted from established guidance for operations and supply chain research. Searches covered Scopus, Google Scholar, IEEE Xplore, EBSCO, and Web of Science with pre-specified keywords (2010–2025; English; ground-based LMD; OR methods). We identified 283 records, screened titles/abstracts, assessed full texts against inclusion/exclusion criteria, and analyzed 265 eligible studies. A PRISMA-style flow diagram summarizes the identification, screening, eligibility, and inclusion processes. We then classify each study by innovation (EV, ADR, PL, PP, CS, FOT, hybrid), problem/sub-problem, and methodology, overlay the conceptual framework, and synthesize cross-cutting insights with comparative studies.

In Section 2, the methodology of this systematic review is explained in more detail. Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8 describe the sustainable innovative solutions and introduce the challenges of using EV, ADR, PL, PP, CS, and FOT, respectively, in ground-based LMD from the OR perspective. Section 9 explains the combined innovative solutions in the literature from an OR perspective. Section 10 presents the comparative study, practical insights, and critical synthesis. In Section 11, the study gaps and future research directions are given. Finally, the concluding remarks are presented in Section 12.

2. Review Methodology

To conduct the systematic literature review, a methodology described in [43] was adapted to the research area. The systematic literature review consists of the following steps: (1) stating the research questions (Section 2.1), (2) identifying the scope of the work (Section 2.2), (3) identifying the database and search keywords (Section 2.3), (4) identifying the inclusions and exclusion criteria (Section 2.4), (5) reviewing and choosing the most relevant papers (Section 2.5), (6) defining a classification scheme to organize the literature (Section 2.6) and introducing a conceptual framework that maps OR technique classes to sustainability goals and metrics (Section 2.7), and (7) gap analysis and suggesting the future research directions (Section 11). These steps, along with their descriptions, are illustrated in Figure 1 for ease of understanding.

2.1. Research Questions

It is crucial to formulate research questions with precision and provide explanations for their formulation at the beginning of a review study. The research question determines the research design and sets expectations for the results. The research questions of the present review work are presented as follows:

• RQ1: What are the challenges of employing sustainable innovative ground-based solutions in LMD from an OR perspective?
• RQ2: Which OR methods are deemed most efficient for optimizing ground-based LMD with innovative technologies in terms of sustainability, and what are their essential characteristics?
• RQ3: What are the research directions and study gaps in the sustainable employment of innovative ground-based solutions in LMD in terms of OR challenges?

2.2. Scope of the Work

By exploring the complexities of optimization challenges and considering environmental factors related to sustainable, innovative ground-based solutions in LMD from an OR perspective, this review helps pinpoint deficiencies in the existing understanding and proposes potential directions for future research.

2.3. Database and Keywords Selection

Identifying related work was based on the title, further refinement on the abstract, and reading the crucial parts of the papers when the abstract was insufficient for assessing alignment with the analysis’s scope. The first author collected and screened the papers. A total of 283 English papers published since 2010 were chosen for initial examination. A search was conducted using keywords across search engines and library databases, including Scopus, Google Scholar, IEEE, EBSCO, and ISI Web of Knowledge. The chosen keywords were a combination of terms related to LMD, such as, “last mile,” “parcel delivery,” “e-commerce,” “freight,” “sustainability,” “operations research,” “innovative solutions,” “EV,” “ADR,” “autonomous vehicles,” “ground-based,” “crowdsourcing,” “crowdshipping,” “parcel lockers,” and “pick-up points.” The search was limited to business and management, engineering, decision sciences, and social sciences journals. The individual scientific papers were chosen from published literature (journals) and conference proceedings.

2.4. Inclusion and Exclusion Criteria

The papers were also filtered based on specific criteria. For example, delivery of products not ordered online and delivery of services were excluded, as they fell outside the scope of the study. Only the ground-based last-mile forward flow was considered, excluding work on reverse and aerial-based logistics. Additionally, only papers that used OR as the methodology were selected, so papers that employed empirical, policy, or conceptual methods were excluded. Therefore, according to these inclusion and exclusion criteria, the collected articles resulted in 265 eligible papers for in-depth examination (including 23 review papers).

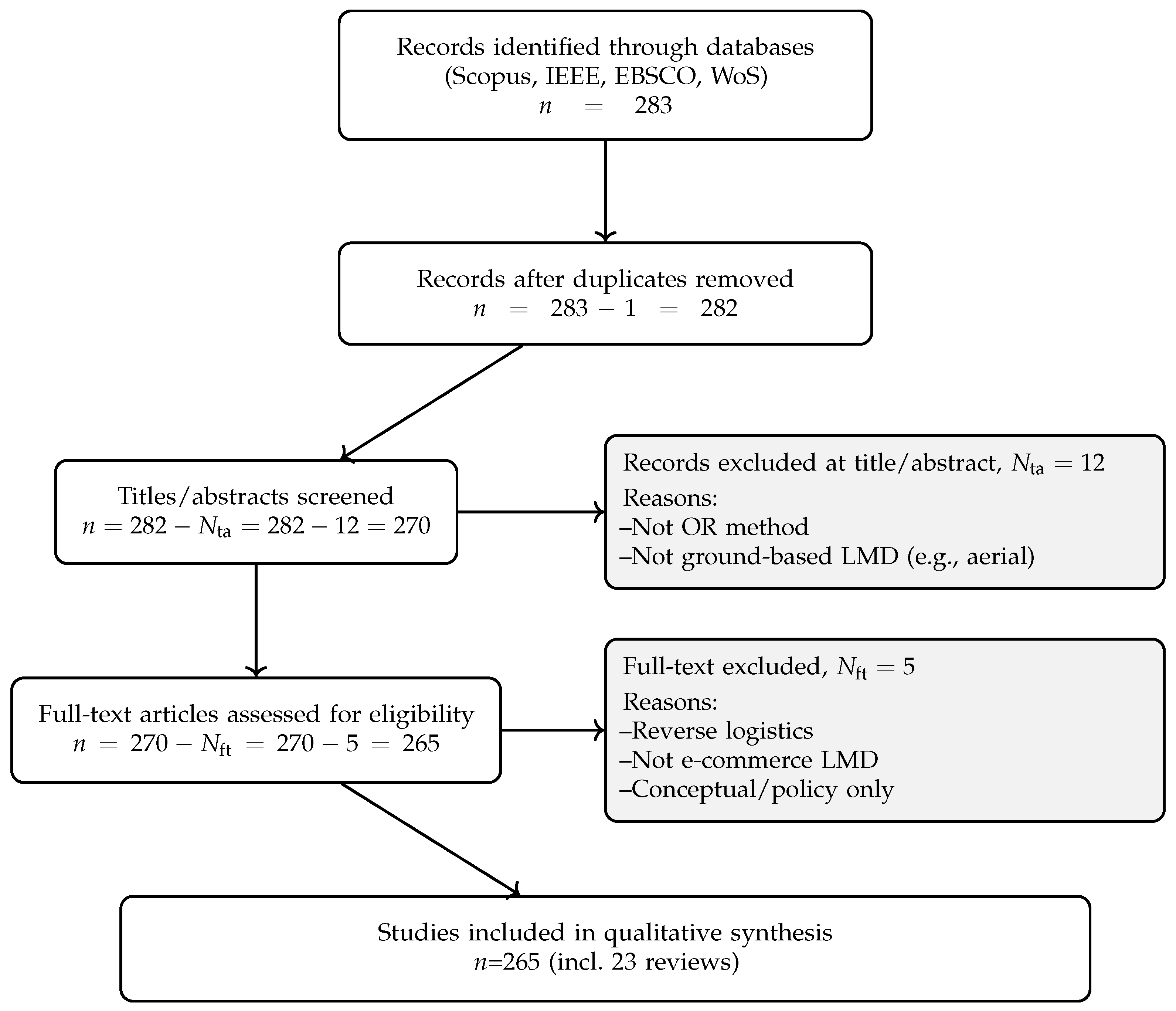
2.5. Screening and Inclusion Flow (PRISMA-Style)

Figure 2 summarizes the screening pipeline based on Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA)-style [44]. We identified 283 English records (2010–present) from Scopus, Google Scholar, IEEE Xplore, EBSCO, and Web of Science. After deduplication, we screened titles/abstracts, excluded out-of-scope items (e.g., non-OR methods, aerial/reverse logistics, service deliveries not tied to e-commerce), and assessed the remainder at full text. We included 265 articles for in-depth analysis (including 23 review papers). Counts in the diagram are aligned with our scope and are reproducible from the query strings and criteria reported in Section 2.3 and Section 2.4. This systematic review was prospectively registered on the Open Science Framework (OSF) under the title “A Systematic Review of Sustainable Ground-Based Last-Mile Delivery of Parcels: Insights from Operations Research.” The registration type is Generalized Systematic Review Registration, and it is available under a CC-BY 4.0 International License. The registration DOI is https://doi.org/10.17605/OSF.IO/STXZQ.

2.6. Classification Scheme

The selected contributions were reviewed and categorized based on various criteria, including their characteristics, research methods, and the problems addressed, as shown in Figure 3. The classification scheme of the present review work is based on three categories: (I) type of innovative solution, (II) type of problems and sub-problems, and (III) type of solution methodology. The first criteria, type of innovative ground-based solutions, include EV, ADR, PL, PP, CS, FOT, and combined solutions. The second criterion classifies papers by the problems and sub-problems within each innovative solution. Finally, the third criterion indicates the OR-oriented research method for each paper. Using these three criteria, the articles on sustainable and innovative solutions in ground-based LMD are classified and distinguished. In Section 3, Section 4, Section 5, Section 6, Section 7, Section 8 and Section 9, the papers related to each innovative solution with their type of problems and solution methodologies—starting from EVs to combined solutions—are reviewed to see the similarities and differences between them and find the research gaps.

2.7. Conceptual Framework: OR Techniques to Sustainability Goals

This study structures sustainable LMD as a multi-objective decision problem spanning three layers: strategic (siting/infrastructure), tactical (routing/scheduling), and operational (real-time dispatch). The sustainability goals considered are as follows: environmental impact (energy use, noise, and emissions), service quality (on-time performance, walking distance, and access equity), cost-effectiveness (total generalized cost), and resilience (robustness and recovery under perturbations). Let x collect first-stage decisions (e.g., siting and fleet mix) and $y\left(\xi \right)$ recourse decisions (e.g., dispatch and recharging) under uncertainty $\xi$. A canonical formulation is

$$\underset{x}{min}\left(C\left(x\right),E\left(x\right),S\left(x\right)\right)\mathrm{s}.\mathrm{t}.x\in \mathcal{X},y\left(\xi \right)\in \mathcal{Y}(x,\xi ),$$

with robust or stochastic variants such as ${min}_x{max}_{\xi \in \mathcal{U}}C(x,\xi )$ or two-stage ${min}_x{\mathbb{E}}_{\xi }\left[C(x,\xi )\right]$; trade-offs can be explored via $ϵ$-constraint (e.g., $minC$ s.t. $E\le {ϵ}_E$, $1-S\le {ϵ}_S$). Metrics include: cost (in currency), energy (in kWh), and emissions (in CO₂), as well as service (late deliveries, mean/percentile lateness), resilience (worst-case regret, expected shortfall of lateness, recovery time), and equity (population within walking distance). As presented in

Table 1. Goal–technique–metric map for sustainable LMD.

Decision Layer	Technique Class	Primary Goals	Modeling Feature	Typical Metrics
Strategic (siting, sizing)	Exact MILP/Benders	Cost, equity	Network design with capacity/access; policy transparency	Total cost; coverage share; average walking distance
Strategic-tactical (EV infrastructure + routing)	Decomposition (CG, Lagrange)	Cost, emissions	Location-routing split; resource-constrained paths	Cost; kWh; CO2; solver bounds/gaps
Tactical (routing/scheduling)	Matheuristics and metaheuristics	Cost, emissions, service	Energy/battery, time windows, synchronization neighborhoods	Cost; on-time rate; energy; runtime vs. instance size
Operational (real-time dispatch)	Rolling-horizon + learning	Service, resilience	Prediction (arrival times, acceptance), receding horizon control	On-time %; average delay; recovery time; re-optimization count
Cross-cutting (uncertainty)	Stochastic/robust optimization	Resilience, service	Scenario recourse; uncertainty sets; risk measures	Lateness; worst-case regret; service reliability
Evaluation (trade-offs)	Multi-objective (e.g., Non-dominated Sorting Genetic Algorithm (NSGA-II), $ϵ$-constraint)	Cost, emissions, service balance	Pareto set construction; decision support	Pareto spread; dominance counts; knee points

, different technique classes naturally emphasize certain goals and constraints. Exact Mixed-Integer Linear Programming (MILP) models and decomposition methods offer transparency and policy sensitivity at strategic/tactical levels. Matheuristics and metaheuristics scale effectively on rich tactical models involving energy/synchronization. Robust and stochastic programs enhance resilience, while learning-assisted heuristics support operational responsiveness. Practitioners identify their dominant goals and constraints, select the decision layer, and then choose technique classes that best realize the mechanisms for those goals. For example, if resilience and service under timetable drift are critical (e.g., FOT), a Time-Expanded Network (TEN) with stochastic recourse and Column Generation (CG) is preferable; if city-scale EV routing with nonlinear charging is central, matheuristics with energy-aware neighborhoods dominate. This framework anchors the per-innovation reviews (Section 3, Section 4, Section 5, Section 6, Section 7, Section 8 and Section 9) and complements the comparative analysis in Section 10. Note that the existing classification (shown in Figure 3) organizes prior work by innovation type, problem/sub-problem, and solution methodology. However, the conceptual framework overlays two additional dimensions: (i) decision layer (strategic/tactical/operational) and (ii) sustainability goals/metrics (cost, emissions/energy, service/equity, resilience), providing a mapping from each classified item to goals and suitable technique classes.

Table 2. Sustainability dimensions: example metrics and OR modeling levers.

Dimension	Example Metrics (Units)	Typical OR Levers (Objective/Constraints)	Data/Proxies
Planet	CO2e per parcel; energy (kWh/parcel); NOx, PM (g/km); noise (dB); congestion proxy (empty vehicle kilometers traveled, curb dwell minutes)	Minimize emissions/energy; cap local pollutants/noise; penalize curb dwell; $ϵ$-constraint on CO2e	Telematics traces; emission factors; noise maps; traffic data
People	Access equity (population within 400–800 m of PL/PP); average walking distance; service reliability (failed deliveries, on-time %); safety proxies (conflicts per 100k stops)	Maximize coverage/equity; bound walking distance; penalize failures/lateness; soft/hard time windows	Census/land-use; locker/PP usage; carrier KPIs; curb/incident logs
Profit	Total generalized cost; unit cost (USD/parcel); asset utilization (%); on-time service (as viability)	Minimize cost; capacity/crew constraints; service-level constraints; fleet sizing	Cost ledgers; depot/crew schedules; demand forecasts
Resilience (cross-cutting)	Lateness; worst-case regret; recovery time; feasibility under perturbations	Two-stage stochastic or robust optimization; rolling-horizon recourse; buffer/slack constraints	Delay distributions; demand uncertainty; scenario sets

links sustainability dimensions to measurable metrics and typical OR levers. This mapping enables multi-objective or $ϵ$-constraint formulations that balance environmental, social, and economic goals, with resilience captured via risk-sensitive objectives and feasibility under perturbations. In practice, we recommend either (i) a multi-objective formulation that constructs Pareto sets over {cost, emissions/energy, service, equity} with resilience captured via risk measures, or (ii) an $ϵ$-constraint approach (e.g., minimize cost subject to CO₂e $\le {ϵ}_E$, on-time $\ge {ϵ}_S$, coverage $\ge {ϵ}_Q$). This makes people, planet, and profit goals explicit and traceable in solution design.

3. Electric Vehicles

The EVs, including e-bikes, e-vans, e-tricycles, e-trucks, and e-Tuk-tuks, have emerged as a transformative solution for urban LMD, offering significant environmental benefits by reducing emissions and fossil fuel dependence. However, integrating EVs also introduces operational challenges, such as range limitations, charging logistics, and fleet heterogeneity. The OR methods provide a systematic framework for tackling these complexities through optimization models, heuristic techniques, and simulation-based approaches.

3.1. Routing and Scheduling Models

Due to their limited battery range and longer charging times, EVs pose unique routing and scheduling challenges. EVs generally support 160–500 km on a full charge, depending on vehicle type and technological advancements [45,46]. OR models for routing with EVs, such as the Green Vehicle Routing Problem (G-VRP) and the Electric Vehicle Routing Problem (E-VRP), extend classical VRPs by including battery constraints and charging requirements. G-VRP focuses on alternative-fuel vehicles with limited range and sparse refueling stations [47]. E-VRP integrates battery consumption and charging dynamics, often under time-window constraints [48], which are solved using hybrid heuristics such as Variable Neighborhood Search (VNS) and Tabu Search (TS). For a detailed review, see [49,50,51].

3.1.1. Charging Strategies and Dynamics

Charging behavior is another layer of complexity; early models assumed full recharging, while later models introduced partial charging [52,53,54] and battery swapping [55,56,57,58]. Heuristics such as Adaptive Large Neighborhood Search (ALNS) [52,59,60,61,62], VNS [54], Simulated Annealing (SA) [63], Iterated Local Search (ILS) [64], matheuristics [53], and exact branch-price-and-cut [65] methods have been employed. For more details, please see [66].

3.1.2. Variable Vehicle Speed

Moreover, the assumption of a constant speed for EVs is unrealistic in many applications. Liu et al. [67] studied the E-VRP with variable vehicle speed and soft time windows for perishable products. They proposed a Mixed-Integer Programming (MIP) model and an Adaptive Hybrid Ant Colony Optimization (AHACO) with a two-stage speed optimization strategy for the problem. Including more decision variables related to EV features could better reflect real-world situations. For example, Xiao et al. [68] proposed a comprehensive model that includes energy-loss functions, piecewise linear charging, and continuous decision variables. They developed a mathematical model for this problem.

3.1.3. Charging/Consumption Rate Pattern

Moreover, the State of Charge (SoC) at each charging station may be modeled as a nonlinear function of charging time, typically a piecewise-linear function. The nonlinear charging function was first introduced by Montoya et al. [69]. They proposed a metaheuristic, ILS, to solve the large-scale E-VRP with a nonlinear charging function. Next, Froger et al. [70] developed more effective MIP models for the same problem. Initially, they created a method to track time and charge levels using arcs. This approach proved to be more effective than the traditional node-based method [69] for tracking these variables. In addition to the nonlinear charging function, [71] studied load-dependent discharging with capacitated charging stations, extending the classic E-VRP in which the discharging rate was constant and independent of the EV’s load, and the capacity of each station was unlimited. They proposed a MIP model and an ALNS metaheuristic algorithm to solve the problem. A recent work by [72] studied the E-VRP with SoC-dependent charging and discharging rates. They developed a new MIP model and an ILS-based heuristic for the addressed problem.

3.2. Charging Infrastructure Planning

OR models aid in infrastructure planning by determining the optimal locations and capacities of charging stations. Approaches include Genetic Algorithm (GA)-based heuristics [73,74,75], Particle Swarm Optimization (PSO) [76], hybrid PSO-GA [77], MIP [78], exact methods [79,80,81,82], simulation–optimization model [83], and multi-criteria decision making [84]. Realistic constraints, such as grid interaction, renewable energy sources, and traffic data, are integrated [85,86]. Review papers include [87,88,89,90].

3.3. Simultaneous Routing and Infrastructure Optimization

The Electric Location Routing Problem (EV-LRP) and Battery Swap Station Location-Routing Problem (BSS-EV-LRP) integrate routing and infrastructure decisions. BSS-EV-LRP was first introduced by [91] and further advanced by [84,92]. Recent approaches use skewed general VNS [93] and branch-and-price [94]. For EV-LRP, Schiffer and Walther [95] proposed a robust approach under demand uncertainty using a parallelized ALNS. Wang et al. [96] introduced a two-phase evolutionary algorithm leveraging historical learning. Other works address stochastic demands [97], ambient temperature [98], and motion dynamics [99].

3.4. Fleet Management and Optimization

Efficient fleet management involves decisions on fleet size, allocation, and vehicle heterogeneity. Models either minimize the number of EVs used [100,101] or assume a fixed-size fleet [102]. Heterogeneous EV fleets are addressed in [103,104], with optimization via Benders decomposition and hybrid methods.

3.5. Balancing Efficiency and Sustainability

The integration of EVs into LMD offers environmental benefits such as reduced greenhouse gas emissions and improved air quality. However, achieving a balance between environmental sustainability and operational efficiency presents challenges. The OR methods play a crucial role in addressing these trade-offs by incorporating environmental metrics and emissions models into multi-objective optimization frameworks. These models typically aim to minimize both environmental impact (e.g., emissions and energy consumption) and operational costs (e.g., transportation, charging, and penalties). Numerous studies have applied OR techniques to various multi-objective EV routing and scheduling problems. Cai et al. [105] addressed the EVRPSPDTW using NSGA-II, focusing on cost and power consumption under time windows and congestion. Gholami et al. [106] optimized the allocation of EV charging stations and PV inverters using fuzzy Pareto dominance and differential evolution. Kapoor et al. [107] developed a framework that minimizes charging costs and power losses using PSO for stakeholder-aligned scheduling. Zakariazadeh et al. [108] employed the $ϵ$-constraint method and Benders decomposition for V2G scheduling under economic and environmental constraints. Sarker et al. [109] proposed MORP for wireless in-motion charging, balancing energy use, travel time, and driver anxiety using adaptive constraint techniques. Zhou and Zhao [110] developed a whale-optimization algorithm for the EVRP with battery swaps and mixed time windows, optimizing cost and battery utilization.

Overall, EVs in LMD present new challenges and opportunities that OR can address across routing, charging, infrastructure, and sustainability dimensions. By leveraging optimization and data analytics, OR enables informed decisions that enhance the feasibility and impact of EV adoption in urban logistics. Exact MILPs are suitable for calibration on small-to-medium EVRP instances or for simplified charging. For city-scale routing with time windows and energy, ALNS/VNS/ILS provide near-optimal solutions within practical time budgets, while decomposition helps when charging or location decisions are coupled. Nonlinear charging or SoC-dependent rates favor matheuristics with tailored neighborhoods over monolithic exact solves.

4. Autonomous Delivery Robots

The ADRs are ground-based EVs that can deliver packages independently. According to SAE’s classification of automation (ranging from Level 0 to Level 5), ADRs can operate up to full autonomy (Level 5) [111]. Despite their growing potential, the application of ADRs in urban LMD still faces various operational and strategic challenges. Unlike autonomous vehicles, which are primarily studied for passenger transport [112], ADRs remain underexplored in freight applications [113]. Two major categories of ADRs include Sidewalk ADRs (SADRs), which operate on pedestrian pathways, and Road-based ADRs (RADRs), which operate in mixed traffic environments [113].

4.1. Pure ADR-Based Routing and Scheduling

ADR-exclusive delivery systems aim to optimize routes without involving conventional vehicles. This is known as the Robot-Only Routing Problem (RRP), focusing solely on ADRs for parcel transport [114]. Sonneberg et al. [115] proposed strategic positioning and routing models for urban autonomous ground vehicles (AUGVs). Kronmueller et al. [116] examined dynamic on-demand grocery delivery using a decentralized network of local depots and ADRs. More recently, Wang et al. [117] developed a space-time route-planning and task-assignment model with enhanced TS to minimize fleet travel distance. Moradi et al. [101] formulates a routing model for multi-stop Autonomous Delivery Vehicles (ADVs) in urban last-mile logistics, aiming to minimize route and vehicle usage costs while respecting constraints on ADV load and battery capacity, maximum route duration, and customers’ walking distance. For robot-only operations with soft time windows, Gnegel et al. [118] formulate a Mixed-Integer Quadratic Programming (MIQP) that minimizes squared delays under battery/partial-charging constraints and solve it via a layered time-SoC graph with Iterative Refinement and Branch-and-Refine, which outperform direct MIQP solves on Solomon-style instances. In dynamic settings, Jeong and Moon [119] formulate a DPDP-AR for an airport terminal with online order arrivals, hard deadlines, and battery charging; a reassignment policy and peak-time battery management improve service robustness during surges. For the strategic, city-scale design of sidewalk ADR systems, a continuous approximation model by [120] with bounded makespans yields closed-form guidance on fleet size, station density, and service regioning. A New York City case study demonstrates how policy/operational constraints influence optimal designs.

4.2. Truck-and-Robot Collaborative Delivery

4.2.1. Single-Vehicle Systems

Truck-assisted ADR delivery has gained attention in hybrid models. Boysen et al. [121] introduced the CSVSP-TBAR model, in which a truck deploys robots from city depots. Simoni et al. [122] investigated a “mothership” system using SADRs and proposed heuristics for coordinated routing. Jennings and Figliozzi [123] assessed regulatory constraints, robot performance, and time–cost tradeoffs in the U.S. The CAVADP, proposed by Reed et al. [124], combines ADRs with delivery personnel, reducing parking time and increasing delivery speed. Their results showed up to $77\%$ time savings under specific scenarios. Later, the authors adapted the model to more realistic urban-rural configurations. Additionally, Reed et al. [125] developed an integer programming model (CAVADP) to evaluate the benefits of ADR-assisted LMD across urban and rural settings, finding that ADRs reduce delivery time and costs, particularly in urban areas. Ostermeier et al. [126] optimized cost-based routing in truck-and-ADR systems, accounting for time windows and limited robot availability. Alfandari et al. [127] presented the URSP, where trucks launch robots from facilities to reduce tardiness, which is solved using a branch-and-Benders-cut scheme. Heimfarth et al. [128] extended these ideas by formulating the MTR-RP, where both trucks and robots serve customers. Their VNS-based algorithm significantly outperformed previous methods, reducing delivery costs by up to $43\%$.

4.2.2. Multi-Vehicle Systems

Chen et al. [129] introduced the VRPTWDR problem, in which trucks and ADRs jointly handle deliveries under synchronization constraints and time windows. Their matheuristic [129] and ALNS-based [130] approaches proved effective in reducing delivery times and operational costs. Unlike CSVSP-TBAR and URSP, this model does not rely on dedicated robot facilities. To address scale, Ostermeier et al. [131] proposed MVTR-RP-D, a multi-vehicle variant with robot depots. Their SINS heuristic achieved up to $62\%$ cost savings compared to truck-only systems. Meanwhile, Scherr et al. [132] studied tactical-level service network design with a mixed ADR fleet. The model integrates platooning with manual vehicles for areas outside autonomous zones, aiming to optimize fleet mix and routing. For hybrid ADR-van designs, Klar et al. [133] developed an integer program that, given zonal demand estimates, allocates parcels to robots or vans to jointly minimize cost and energy, clarifying when dense, short-haul zones favor robots and when dispersed zones favor vans. Accounting for congestion explicitly, Wei et al. [134] modeled a two-echelon truck and Unmanned Ground Vehicle (UGV) routing problem with time-dependent travel times and solved it via ALNS; a Dalian case and sensitivity analysis (congestion, UGV capacity) indicate notable efficiency gains and clarify deployment conditions. Two-echelon designs with ADVs have been formalized in a study by [135] via a MILP model (2E-VRP-ADV), showing conditions under which robot-assisted second-level distribution outperforms truck-only tours.

4.3. Safety and Security Considerations

Safety is a critical concern for ADRs. They must navigate complex environments without disrupting traffic or causing accidents. Li et al. [136] detailed the system architecture and safety strategies of an autonomous delivery platform. Bentley et al. [137] addressed coordination challenges, using Constrained Optimization in Learned Latent Space (COIL) to schedule ADRs under supervision constraints. Their results demonstrated improved safety and throughput compared to standard GAs. Beyond technical safety, user acceptance matters: a hospitality study finds that framing ADRs as a lower-carbon option increases consumers’ choice of robot delivery, yet the effect collapses when perceived service risk (e.g., cold/late food) is high [138]. User acceptance shapes feasible deployment: survey evidence shows that motivated consumer innovativeness (functional, hedonic, social, and cognitive) significantly increases intention to choose ADR delivery, partly via perceived usefulness/enjoyment [139]. Beyond routing and control, the feasibility of ADR deployment depends on urban planning and governance choices (e.g., sidewalk/curb design, conflict management, and accessibility). A recent planning chapter synthesizes design principles for integrating autonomous robots into people-oriented streets and public spaces [140]. Public attitudes toward delivery robots are mixed. A study by [141], which combines text mining and user studies, highlights the usefulness versus intrusiveness, safety/privacy concerns, and etiquette concerns, and derives design implications for ADR behavior in public spaces.

Real-world HRI evidence from 117 user-generated videos shows recurring interaction breakdowns and communication needs (multi-party path negotiation, transparency for unexpected behavior, and help-seeking cues), informing eHMI and etiquette for ADRs in public space [142]. A deployment-oriented account of the Ona ADR details street-sidewalk navigation, safety/teleop, and early city pilots, offering practical integration lessons that complement optimization models [143]. At the local control layer, a campus study [144] contrasts A*, RRT, and RRT* with pure-pursuit tracking on an outdoor delivery robot: A* is more consistent but slower, whereas RRT/RRT* are faster yet variable; in minimum-cost cases, RRT* yields smoother steering and slightly shorter runs, underscoring a consistency-speed trade-off in motion planning. Survey evidence by [145] suggests that trust, transparency, and user-centered design significantly influence public willingness to adopt ADR delivery. Human factors evidence by [146] shows that robot lighting can shape public comfort: a nighttime study finds SADR light colors significantly affect pedestrians’ perceived safety during approach interactions.

A German consumer study [147] finds that acceptance of delivery robots varies by meal/parcel scenarios and is shaped by TAM constructs (usefulness, ease, etc.), supported by SEM and qualitative interviews. At the sidewalk navigation layer, Zhou et al. [148] developed a multi-modal socially aware stack (sidewalk segmentation; RGB-D 3D pedestrian detection + social force-based trajectory selection; state lattice planning with etiquette costs) and validated it in simulation and on a Husky platform, improving ADE/FDE and yielding behaviors like “keep left/overtake right”. A recent work by [149] enumerates the principal ADR challenges (energy/charging, navigation and public safety/HRI, reliability, regulation, and infrastructure readiness). It links them to managerial levers, providing a deployment-oriented complement to optimization models. Consumer acceptance of ADRs depends less on raw features per se and more on how they shape perceived value and perceived risk: a 500-respondent study by [150] shows compatibility, convenience, privacy/security, and reliability act via full mediation, yielding concrete levers for deployment and communication. Practice evidence from a European pilot [151] highlights governance, regulatory coordination, and infrastructure readiness as decisive factors for ADR deployment, offering concrete managerial recommendations on scoping, stakeholder alignment, and tech adaptation.

4.4. Trade-Off Between Efficiency and Sustainability in Autonomous Delivery Robots

The environmental performance of ADR-based delivery is under active investigation. Li et al. [152] assessed life-cycle greenhouse gas emissions for various levels of automation and vehicle types. Their findings show that small electric vans remain more eco-efficient than ADR-based systems in specific contexts, while the environmental benefits of full automation are moderate. Figliozzi [113] compared ADRs, including drones, SADRs, and RADRs, to traditional vans and customer pickups using a continuous approximation model. The study quantified vehicle miles, energy use, and emissions, highlighting efficiency trade-offs that depend on delivery density, vehicle choice, and travel distance. Complementing micro-level routing studies, a 14-city comparative analysis finds that ADRs are most effective in pedestrian-focused, traffic-restricted areas. In contrast, cargo bicycles dominate in dense cores, and light commercial vehicles retain advantages as dispersion grows [153]. Using continuous approximation with Monte Carlo uncertainty analysis, Lemardelé et al. [154] showed that a two-echelon van-and-ADR scheme via urban micro-hubs can cut operating costs by over $10\%$ in small/medium European cities under appropriate conditions, while quantifying input-driven cost variability.

In summary, integrating ADRs into LMD systems offers significant benefits in terms of cost efficiency, delivery speed, and environmental sustainability. However, these benefits come with challenges in routing complexity, fleet coordination, infrastructure planning, and safety. OR models, through MIP formulations, metaheuristics, and hybrid algorithms, are essential in developing efficient ADR-based solutions. Also, synchronization and launch/retrieval constraints limit exact scalability. Matheuristics and Benders-aided formulations handle medium- to large-scale instances, and policy learning supports real-time dispatch. Reliable handling times and curb operations data are pivotal; sensitivity to these inputs should be reported. For further reading, several review works offer detailed overviews of ADRs in LMD [38,114,155,156,157,158,159].

5. Parcel Lockers

The continued rise of e-commerce has intensified the need for efficient LMD. The PLs have emerged as an innovative solution that supports unattended delivery, offering benefits such as reduced failed deliveries, lower courier costs, and increased customer convenience [1,160,161]. PLs, typically located in public or commercial spaces, enable flexible, secure access via digital authentication. However, their integration poses operational challenges that require optimization via OR methods.

5.1. Parcel Locker Location Optimization

The optimal placement of PLs is essential for balancing accessibility, logistics efficiency, and investment cost. Deutsch and Golany [162] formulated the Parcel Locker Facility Location Problem (PL-FLP) to maximize profit, accounting for setup and delivery costs. Simulation optimization frameworks have also been utilized to guide deployment strategies, as demonstrated in the Automated Parcel Locker (APL)-focused work by Rabe et al. [163] and Sawik et al. [164], which employed real data and multi-period models. Multi-objective models, such as MOPLNDP by Luo et al. [165], strike a balance between cost and accessibility by utilizing active-learning evolutionary algorithms. In China, Yang et al. [166] introduced a bilevel programming model to align user satisfaction and provider profitability. Kahr [167] studied integrated locker location and compartment design under uncertainty as the SMCLLP. Schwerdfeger and Boysen [168] explored Mobile PLs (MPLs), who found that locker fleets dynamically reposition during the day, thereby reducing the overall fleet size. Stochastic approaches, such as those by Mancini et al. [169], address demand and capacity uncertainties in locker box location planning using scenarios and matheuristics. These models highlight how OR can enhance planning under both deterministic and uncertain environments. PL siting can be coupled with volume design: a study by [170] models profit-maximizing locations where each PL selects from discrete volume options to serve heterogeneous parcel sizes, improving performance over fixed-size deployments.

5.2. Integration of Parcel Lockers with Vehicle Routing Optimization

Several models have integrated PLs into vehicle routing to enhance delivery efficiency. Orenstein et al. [171] proposed the Flexible Parcel Delivery (FPD) problem, incorporating customer preferences for delivery locations. Sitek and Wikarek [172] developed the CVRPPAD model, integrating pick-up, delivery, and locker points using hybrid CLP/MP techniques. Time window-based extensions were later explored [172,173]. Other formulations include the TSP-L-TW [174], which minimizes delivery and customer travel costs, and the VRP-L-TW [175], which is solved using branch-and-cut algorithms. Two echelon variants, such as the 2E-VRP-CO [176] and 2EVRP-LF [177], incorporate both satellite facilities and lockers for final deliveries. More complex hybrid models, such as 2E-VRPTW-IF-OD [178], incorporate delivery flexibility and customer preferences. Other innovations include the VRPPL [179], VRPDO [180], and VRP-HL [181], which incorporate shared locations, multiple parcel sizes, and heterogeneous lockers. Several solution approaches have been proposed for VRPDO in the literature, including the branch-price-and-cut algorithm [182] and data-driven ALNS [183]. Recent studies have also explored simultaneous locker location and routing [184,185,186], mixed delivery systems [187], and VRPSPDPL models that combine pickup and delivery [188]. Novel systems involving Autonomous Mobile Lockers (AMLs) have been modeled in the AML-C2-E-LRP and its multi-depot extension [136,189], showing significant operational savings. Finally, Liu et al. [190] proposed the MPLP and solved it using a hybrid reinforcement learning technique, thereby further improving the efficiency of mobile locker deployment.

5.3. Locker Assignment and Scheduling

Wang et al. [191] considered mixed fixed-mobile locker deployments and solved a location-routing-scheduling model using a GA-based algorithm. These studies show how OR can guide both strategic location design and operational scheduling. A stated-choice study by [192] comparing stationary versus MPLs reports that access distance dominates choice, with a general preference for stationary lockers; short MPL dwell times reduce attractiveness; younger users are more open to MPLs; and stationary PLs are preferred on rainy weekdays and for time-sensitive parcels.

5.4. Trade-Offs Between Efficiency and Sustainability in Parcel Lockers

Studies suggest PL-based delivery systems can outperform home delivery in terms of cost, emissions, and reliability. Zurel et al. [193] reviewed international PL deployments and outlined regulatory challenges. Dong et al. [194] analyzed PL network expansion in Norway and found reduced environmental impact and improved service efficiency. Klein and Popp [195] examined customer preferences and perceptions of sustainability across various delivery types, highlighting the importance of convenience and perceived value. White-label PLs were explored by Hohenecker et al. [196] as part of the alBOX project. The pilot in urban and rural areas revealed insights into user behavior and social acceptance. Finally, Bonomi et al. [197] introduced a multi-objective optimization model for PL-based LMD that minimizes both environmental impact and travel distance. A simulation study by [198] for Dortmund shows that when customer trips to lockers are explicitly included, the CO₂ advantage of APLs can diminish or reverse in outer districts, making locker density and user behavior key parameters in sustainability comparisons. MPLs can outperform both stationary lockers and home delivery under suitable dwell-time and coverage policies. An operational design study by [199] quantifies the cost and CO₂ trade-offs and identifies key levers in mobility patterns and siting density.

PLs offer a compelling alternative to conventional delivery, enhancing efficiency and sustainability in LMD. However, their optimal deployment, integration, and scheduling require advanced OR techniques that handle both logistical and behavioral uncertainties. When siting and routing are tightly coupled, decomposition or matheuristics dominate; if siting is strategic and slow-moving, an exact siting phase followed by heuristic routing is effective. Under uncertain compartment usage and time windows, scenario-based matheuristics are more stable than single-scenario exact solves. For a broader understanding, readers may consult review works by [200,201,202].

6. Pick-Up Points

The PPs are increasingly popular alternatives in LMD, offering customers a centralized location to pick up parcels. Unlike the PLs, PPs are typically manned kiosks or stores and operate only during specific hours [1,160]. Their integration into LMD networks introduces various challenges related to location planning, vehicle routing, and sustainability that can be effectively addressed using OR tools.

6.1. Pick-Up Point Location Optimization

The location of PPs plays a crucial role in optimizing accessibility and delivery consolidation. Morganti et al. [203] compared PPs and locker-based alternatives in France and Germany, examining their operational models, consumer behavior, and service providers’ strategies. These alternatives were found to consolidate deliveries and reduce fragmentation. From a spatial planning perspective, Russo et al. [204] evaluated the accessibility of PPs in an urban center in Sicily. Using spatial syntax and walkable isochrones, they proposed a methodology that integrates pedestrian infrastructure into location analysis. Their findings emphasized the importance of walkability and proximity in sustainable urban logistics. A consumer study by [205] highlights which PP attributes most influence choice, accessibility (walking distance), opening hours, safety/security, queueing/parking convenience, and information/fees, suggesting these factors be encoded as equity and service constraints in PP siting and routing. On the strategic side, siting is naturally modeled via p-median, covering, or maximal accessibility formulations with time-dependent capacities; exact MILPs are tractable at city block granularity. Multi-objective formulations balance delivery cost, access equity (the share of the population within a target walking radius), and robustness to no-show/late pick-up rates. For uncertain demand and operating hours, two-stage stochastic programs with recourse or robust counterparts can stabilize performance. Scenario-based matheuristics (e.g., ALNS with site-opening neighborhoods) scale well and preserve solution interpretability. PPs are most effective where retail density provides coverage within a short walking distance and where opening hours align with customer availability.

6.2. Integration of Pickup Points with Vehicle Routing Optimization

PPs can be integrated into vehicle routing models to improve sustainability, especially in the food supply chain. Saad and Bahadori [206] compared home delivery and PP systems using a VRPTW formulation, focusing on CO₂ emissions. Their implementation found that PP models offer substantial environmental advantages, reducing vehicle kilometers and emissions in urban food delivery systems. Demand steering to PPs can be co-optimized with routing: a two-stage stochastic model with decision-dependent uncertainty and a branch-and-bound algorithm achieves 4-8% lower costs than common baselines, with optimal incentives often targeting customers near PPs rather than the farthest ones [207]. A realistic OR model for PPs accounts for: (i) opening/closing schedules and lunch breaks that restrict feasible customer pick-ups; (ii) clerk capacity and service times that induce queuing or time window effects; (iii) maximum customer walking distance to a selected PP; and (iv) inventory/holding constraints for parcels awaiting pick-up. A time-windowed facility location with capacity can represent these elements, and by a VRPTW with delivery to PP nodes, often with a penalty or soft time window for customer retrieval. When siting and tours are coupled (joint location-routing to PPs), decomposition is effective: a master problem selects PP sites and capacities, and a subproblem plans VRPTW tours given those sites. Empirically, PP deployments consolidate stops and reduce failed deliveries, with case studies reporting substantial reductions in fleet size and vehicle kilometers when home deliveries are redirected to staffed PPs in densely populated areas. Notably, including clerk capacity helps avoid over-optimistic service assumptions and explains the observed evening peaks; coupling PP siting with VRPTW yields better network-wide performance than sequential decisions in high-demand districts.

6.3. Trade-Offs Between Efficiency and Sustainability in Pickup Points

The adoption of PPs can significantly reduce LMD’s carbon footprint. Brown and Guiffrida [208] compared traditional in-store pickup with e-commerce home delivery. By modeling break-even points in emissions based on distance and delivery volume, they provided insights into the environmental impact of each method and helped guide sustainable logistics decisions. Beckers and Verhetsel [209] studied the spatial distribution of Collection and Delivery Points (CDPs) in Belgium. They found that only one courier provided walking distance access to more than half of the population, advocating for multi-carrier CDPs and urban planning support to enhance sustainability and reduce reliance on cars for last-mile trips. Masteguim and Cunha [210] assessed the operational and environmental viability of redirecting home deliveries to PPs in São Paulo, Brazil. Using an optimization-based model, they demonstrated that routing parcels to PPs could reduce fleet size and total mileage by over $50\%$. Their results supported PPs as an effective alternative for dense urban regions aiming to reduce externalities associated with traditional LMD.

The PPs offer a viable alternative to home delivery in urban logistics, helping reduce congestion, emissions, and delivery failure rates. The successful implementation depends on optimal location planning, customer accessibility, and integration with routing models, areas where OR techniques play a vital role. PP networks favor simple siting with routing heuristics at scale, given their low capital expenditure and retail coverage. However, limited opening hours and human handling constrain reliability, making exact time window models practical only for small instances. For comprehensive insights, conceptual frameworks, and reviews, the works of [211,212] offer valuable contributions.

7. Crowdsourcing

The CS (Crowdsourcing), also known as crowdshipping, refers to the delegation of LMD tasks to a network of ordinary individuals, commonly referred to as the “crowd” who utilize their routes and vehicles to deliver parcels [213]. This model enhances delivery responsiveness and efficiency, often enabling same-hour services, while posing novel OR challenges due to its dynamic, decentralized nature.

7.1. Scheduling, Assignment, and Operational Models

Efficiently assigning delivery tasks to a dynamic, heterogeneous pool of drivers, each with unique availability, routes, and preferences, constitutes a core optimization problem. The Vehicle Routing Problem with Occasional Drivers (VRP-OD) was first introduced by Archetti et al. [214], considering in-store customers as potential Occasional Drivers (ODs). This model was enhanced by Macrina et al. [215] through the use of VRP-OD with Time Windows (VRP-ODTW), which enabled drivers to serve multiple deliveries under temporal constraints. Subsequent studies advanced solution techniques using VNS, GRASP-VNS hybrids, and Machine Learning (ML)-assisted heuristics [216]. Soto Setzke et al. [217] developed route matching algorithms evaluated on real mobility data. Mancini and Gansterer [218] proposed VRP-OD with Order Bundles (VRP-OD-OB), using bidding mechanisms to assign bundles. A chance-constrained stochastic version of VRP-ODTW was later proposed to handle uncertainty in travel times [219]. Reinforcement learning also emerged in this domain. Ahamed et al. [220] used Deep Q-Networks (DQN) to assign courier tasks under capacity and availability constraints. Behrendt et al. [221] applied neural networks for real-time scheduling, achieving near-optimal results. To address uncertainty in driver capacity, Ulmer and Savelsbergh [222] proposed continuous approximation models for staff scheduling.

Kafle et al. [223] modeled the integration of pedestrian- and cyclist-based CS with truck carriers for urban delivery; the MIP model determined relay points, truck routes, and crowdsourced assignments. TS-based heuristics achieved high-quality solutions efficiently. Tao et al. [224] proposed a multi-depot delivery system using both regular and ODs. The model employed an event-based, rolling-horizon approach, dynamically updating assignments in real time based on driver availability. Wu et al. [225] introduced the 2EOVRP-CS, which involves transferring trucks to crowdsourced shippers at relay points. A Nested Genetic Algorithm (NGA) optimized crowdshipper selection, relay location, and route planning. Empirical evidence from Xi’an showed $14\%$ cost and $26\%$ VMT reductions compared to truck-only models. Arslan et al. [226] proposed a service platform that coordinates ad hoc and dedicated drivers in dynamic settings. A rolling-horizon optimization approach yielded up to a $37\%$ reduction in VMT. Dayarian and Savelsbergh [227] designed myopic and predictive strategies within rolling horizon frameworks to leverage in-store customer deliveries for same-day services, demonstrating the value of probabilistic modeling in planning. Sampaio et al. [228] introduced transfer points to reduce distance and driver needs. Voigt and Kuhn [229] proposed an MIP model for mixed fleets that improves service flexibility.

7.2. Stochastic and Uncertainty-Based Models

Gdowska et al. [230] introduced a bi-level matching and routing framework, recognizing ODs as autonomous agents who may reject deliveries. Optimization accounted for the probabilistic nature of driver acceptance. Mousavi et al. [231] proposed a two-stage stochastic program for mobile depot placement under crowdshipper uncertainty. CS systems must respond to real-time fluctuations in delivery demand and driver supply. Chen et al. [232] formulated a multi-driver, multi-parcel matching problem and proposed ILP and heuristics that account for parcel transfers and detour constraints. Yıldız [233] employed dynamic programming without making assumptions about arrival distributions, while Tapia et al. [234] showed that CS could increase CO₂ emissions if not optimized carefully.

7.3. Crowdshipping Infrastructure and Transshipment

Macrina et al. [235] incorporated intermediate depots into crowdshipping to reduce traditional vehicle costs. Using VNS heuristics, they optimized delivery assignments to central and intermediate depots. Vincent et al. [236] extended this model by using ALNS to handle multiple delivery modes. Wang et al. [237] formulated crowd-tasking as a network min-cost flow problem, utilizing citizen workers to deliver parcels during their regular commutes. Real-world datasets from Singapore and Beijing demonstrated the method’s scalability and efficiency.

7.4. Parcel Allocation and Network Optimization

Wang et al. [238] addressed joint optimization of parcel allocation to stations and crowd-courier routing. A CG-based set-partitioning model and a rolling-horizon strategy were used to solve large-scale problems. Stokkink and Geroliminis [239] employed a continuum approximation to select depots efficiently.

7.5. Pricing, Incentives, and Compensation

Crowdshipping reliability challenges prompted platforms to offer employees incentives. Behrend and Meisel [240] combined item sharing with CS to enable collaborative consumption. Fadda et al. [241] minimized connectivity costs using mobile device hotspots via a stochastic model. Boysen et al. [242] employed Benders’ decomposition to optimize matching and wages under time constraints. Fatehi and Wagner [243] presented a robust CS model integrating labor planning, routing, and queueing. Chen et al. [232] used a reverse-auction framework to price Occasional Couriers (OCs). He et al. [244] examined insurance schemes for pricing and wage-setting in CS, identifying revenue-sharing as optimal under certain conditions. Additional works further explore pricing mechanisms and incentive structures [245,246,247,248,249]. Le et al. [250] introduced an integrated CS framework that balances matching, routing, and compensation across varying supply-demand scenarios. It presented four pricing models to help platforms maximize profits and user satisfaction.

7.6. Capacity, Quality, and Reliability

Dai et al. [251] addressed workforce planning in O2O logistics with in-house, part-time, and full-time CS drivers. Yildiz and Savelsbergh [252] assessed delivery dynamics on on-demand platforms, such as Uber Eats, providing insights into coverage, profitability, and service design. A key concern in CS is reliability. Buldeo Rai et al. [253] identified trust issues as a significant barrier to adoption. Devari et al. [254] proposed leveraging social networks to enable trusted deliveries, reduce emissions, and lower costs.

7.7. Efficiency vs Sustainability Trade-Off in Crowdshipping Logistics

CS flexibility can compromise sustainability. Gatta et al. [255] evaluated Rome’s crowdshipping via mass transit integration, projecting significant reductions in emissions and accidents. Qi et al. [256] assessed shared mobility for home delivery, highlighting cost savings but limited scalability. Ghaderi et al. [257] proposed a framework combining trajectory analytics with profit-optimized routing, achieving strong results across key metrics.

The OR techniques play a crucial role in resolving the challenges posed by integrating CS into sustainable LMD. From routing and pricing to capacity planning and real-time decision-making, OR-driven models can support reliable, cost-effective, and environmentally responsible crowdshipping systems [258]. Rolling horizon assignment with prediction (acceptance, detours) is practical and scales. Exact stochastic programs remain small. Reported performance depends on incentive design; pricing and matching should be evaluated jointly with routing. Other review works on CS concept in the literature are presented in [259,260,261,262,263,264,265,266].

8. Freight-on-Transit

The FOT is a novel logistics paradigm that integrates freight delivery with Public Transportation (PT) systems to transport passengers and goods simultaneously. This model leverages underutilized capacity in urban transit networks, such as buses, trams, and subways, to support LMD operations. By leveraging existing infrastructure, FOT seeks to reduce delivery costs, traffic congestion, and carbon emissions, contributing to more sustainable and efficient urban logistics.

8.1. Transit-Assisted Two-Tier Urban Delivery

One of the foundational investigations into FOT was conducted by Azcuy et al. [267], who proposed a two-tier system wherein PT routes serve as the primary freight corridors. Parcels are first delivered to strategically selected transfer points, also known as transit stops, after which secondary deliveries are made using smaller, potentially greener vehicles. The study focused on identifying optimal transfer locations using an MIP formulation and heuristic methods. The results demonstrated potential distance savings of up to $7.1\%$, especially for deliveries over longer distances, with stringent deadlines, and customer clusters along the transit line. At the operational level, a recent EvoCOP study by [268] introduces a GA for the three-tier FOT problem (depot → PT stops → green last leg) and shows it attains near-optimal solutions on large instances where a compact MILP becomes intractable. City-level evidence from Zrenjanin (Serbia) [269] shows that integrating parcels on fixed-route buses can improve energy and environmental performance under realistic policy and energy-mix scenarios, providing impact validation for FOT concepts.

8.2. Integrated Public Transit with Emerging Technologies

Expanding on the FOT framework, Kızıl and Yıldız [270] introduced a comprehensive LMD model that integrates PT with several innovative delivery enablers: automated service points, CS, and zero-emission vehicles. This multifaceted system is designed for express urban deliveries. The authors employed a two-stage stochastic program to model uncertainties in delivery operations. They used a branch-and-price algorithm with a novel decomposition branching strategy, thereby improving computational tractability. Their solution reflects real-world delivery dynamics and underscores the feasibility of scalable, eco-friendly urban logistics via FOT. The FOT planning benefits from a TEN that encodes station nodes across discrete time layers. Arc sets represent in-vehicle travel, waiting, transfers, handling, and last-leg dispatch. Capacity on in-vehicle arcs enforces limited freight space on buses/trams; station buffers cap simultaneous parcel handling. Coupling with last-leg modes (e-bikes and foot couriers) is captured via synchronization arcs that respect departure times and service windows. Objective terms typically minimize total generalized cost (line usage, transfers, handling) and last-leg distance or energy, with optional penalties for missed delivery targets. Path-based CG outperforms monolithic flows on the TEN, especially when last-leg coupling is present; pricing subproblems yield feasible transit-plus-last-leg paths that satisfy resource constraints. Benders or logic-based Benders decompose siting or line-activation from operational assignments. Lagrangian relaxations of capacity or synchronization constraints yield tight bounds and good heuristics. In practice, these decompositions solve city-scale instances with minute-level time discretization, whereas exact single-block MILPs remain suitable for pilot corridors and scenario calibration.

8.3. Strategic Design of FOT Networks

Further developing the FOT concept, Delle Donne et al. [271] explored a strategic model that employs mass PT to move freight within cities through a sequence of nodes: parcels travel from central depots to “drop-in” stations on public lines, continue aboard PT to “drop-out” stations, and are finally delivered by green vehicles such as cargo bikes or foot couriers. The core research question was to determine which PT lines and stations should be included in the FOT system. Multiple mathematical formulations were proposed to capture the network design problem. To address them, the authors applied CG heuristics and conducted extensive computational experiments. Their results provided actionable insights into trade-offs between network configuration, operational efficiency, and environmental impact. Cheng et al. [272] presented a comprehensive review of integrated transportation systems that combine passenger and freight movement. Their study categorized practical integration models and mapped out the associated decision-making challenges across tactical, operational, and strategic levels. Topics such as vehicle routing, schedule synchronization, infrastructure requirements, and pricing policies were reviewed. The authors also discussed solution methodologies, highlighting the complexities and trade-offs inherent in implementing such systems. Their review positions FOT within a broader class of people-and-goods integration approaches and serves as a valuable reference for future research.

At the timetable/rolling-stock level, a recent study by [273] shows that integrating freight into an urban rail line via joint optimization of train schedules, rolling-stock rotations, and freight allocation can profitably add trips in off-peak periods, thereby reducing passenger travel times while carrying freight. PT co-modality can be planned on the timetable: a schedule-based parcel assignment model synchronizes deliveries with fixed-route, multi-line bus services and shows cost/emissions benefits from sharing spare capacity [274]. Modular co-modality can share vehicle capacity between passengers and freight: a study by [275] models a two-way corridor with time-dependent demand, using a MIP formulation and a two-stage algorithm to allocate modular units, thereby improving utilization while respecting timetables.

The FOT presents a compelling vision for sustainable LMD by optimizing the dual use of urban PT systems. The OR plays a central role in making this concept viable, offering methods to address key decisions such as transfer point selection, transit network design, resource allocation, and uncertainty modeling. As the body of work grows, from two-tier system optimizations to fully integrated, crowdshipping-supported frameworks, the feasibility and potential of FOT in modern urban logistics become increasingly tangible. Also, TENs are expressive but large. The CG and Benders-type decompositions scale better than monolithic MILPs. Operational viability hinges on station handling times; robustness to timetable perturbations should be shown. Review works on FOT include [272,276,277].

9. Combined Innovative Solutions

This section explores hybrid and integrative strategies that combine EVs, PLs, PPs, ADRs, CS, and FOT within sustainable LMD systems. These integrated models offer potential improvements in operational efficiency, environmental performance, and service quality.

9.1. Electric Vehicles and Autonomous Delivery Robots

Yu et al. [278] introduced a two-echelon LMD system in which each EV is equipped with a delivery robot, facilitating parcel distribution in restricted zones such as pedestrian areas and campuses. A key feature of the model was en-route charging, which enabled the van to recharge during robot deployment, optimizing downtime and enhancing delivery efficiency. The system was modeled as an MIP, incorporating a time-distance-energy trade-off due to battery constraints and energy transfer durations. To improve scalability, an ALNS algorithm and a linear-programming-based route evaluation were proposed. Sensitivity analysis revealed that optimizing charging strategies can significantly reduce total operational cost and travel time. Moradi et al. [279] proposed a new variant (REVRP-LPCP) that integrates EVs, SADRs, and PLs, assigning higher service priority (“prizes”) to Prime members and jointly optimizing EV routes, robot dispatch, and locker assignments to minimize total cost while ensuring Prime customers are served quickly. This model formulated delivery as an MILP complemented by a tailored metaheuristic, achieving up to $53\%$ lower EV route and utilization costs compared to EV-only systems. By prioritizing Prime customers and integrating robots, EVs, and lockers within a unified planning framework, it significantly enhances efficiency and service responsiveness while outperforming commercial solvers in large-scale benchmarks.

9.2. Parcel Lockers with Electric Vehicles

Pan et al. [280] developed a two-level hybrid model that integrates EVs and PLs. At the upper level, a minimum-cost Parcel Network Flow Problem (PNFP) determines the optimal positions for lockers and parcel flows. At the lower level, a Multi-Depot Capacitated VRP (MDCVRP) manages routing between depots, lockers, and customers. A hybrid GA combined with the Lin-Kernighan Heuristic (LKH) was used to optimize delivery flows and vehicle routes. Vukićević et al. [281] tackled the “covering delivery problem,” optimizing routes where an EV either directly delivers to customers or drops parcels at lockers. Charging stations could also serve as lockers. A MIP formulation and a VNS-based heuristic using a sequential-mixed Variable Neighborhood Descent (VND) approach were proposed to solve this problem efficiently. The results confirmed significant improvements in delivery time and energy consumption. Yu V.F. et al. [62] introduced an extension of the EVRP-TW and Partial Recharges (EVRPTW-PR), known as the EVRP-TW, Partial Recharges, and PL (EVRPTW-PR-PL). The focus was on minimizing delivery costs by using a fleet of EVs and offering two customer service options: home delivery and self-pickup via PLs. The paper presented a mathematical formulation for this problem and proposed an ALNS algorithm. Song et al. [282] assessed the environmental impact of delivery failures. They proposed two solutions: using smart lockers as collection points and replacing fuel vans with battery vans. VRP models were used to compare emissions, and results from a Beijing-based case study with 500 customers showed that CO₂ emissions per parcel decreased significantly as the ratio of failed home deliveries increased, underscoring the environmental benefits of lockers. Boroujeni et al. [283] combined EV home deliveries with optional PL self-pickup while prioritizing high-value “Prime” customers to balance fast service and cost efficiency. The study proposes a MILP model and a tailored Large Neighborhood search (LNS) heuristic (with SA), achieving an average $24\%$ lower EV routing cost and a $22.5\%$ reduction in EV utilization cost compared to EV-only strategies, while ensuring prioritized delivery for Prime users. Recently, Yu and Anh [284] extended EVRPTW-PR by integrating covering locations-facilities that combine PLs (for optional customer self-pickup), and charging stations. The goal is to minimize total cost, including travel, fixed operational costs for EVs and active lockers, and customer compensation for self-pickup. To address this issue, the authors develop a MIP formulation and an effective VNS algorithm, enhanced with dynamic programming and set partitioning, that yield new best-known solutions and provide valuable managerial insights on balancing delivery options and cost trade-offs.

9.3. Parcel Lockers with Autonomous Delivery Robots

Schnieder et al. [285] proposed a decision-support model that integrates autonomous vehicles and lockers. The study analyzed real parcel delivery data from London and examined scenarios involving modular and fixed lockers, Road-based Autonomous Lockers (RALs), and different depot locations and fleet compositions. A routing and scheduling algorithm was employed, and findings revealed that modular lockers adjusted weekly offered the best results under moderate to high demand, while RALs were more efficient under low demand. Additionally, Moradi et al. [286] modeled an LMD system in which electric-powered delivery robots (i.e., SADRs) are deployed from trucks acting as mobile satellite depots, and customers can optionally be served via strategically placed PLs. The MILP model jointly optimizes truck routes, locker locations, and robot routes to minimize total cost, while a greedy heuristic effectively tackles larger instances. Sensitivity analysis provides managerial insights into when locker deployment and robot use drive cost-efficient, sustainable delivery operations.

9.4. Pick-Up Points with Autonomous Delivery Robots

Ulmer and Streng [287] developed a same-day delivery model combining PPs and ADRs. Their goal was to optimize real-time vehicle dispatch and goods loading. A Policy Function Approximation (PFA) method was proposed to balance the benefits of speed and consolidation. The study provided managerial insights into dispatch timing and resource allocation, offering a promising alternative to conventional delivery systems for e-commerce applications.

9.5. Crowdsourcing with Electric Vehicles

He and Csiszár [288] investigated integrating crowdsourced delivery into Mobility-as-a-Service (MaaS) using EVs to reduce emissions and energy consumption. The paper proposed a system-oriented approach, detailing functional models and information system architectures. Using numerical simulations and matching theory, the authors quantified the emission and energy savings per parcel. They highlighted potential scenarios where this embedded delivery system could replace traditional courier networks, particularly in densely populated urban environments.

9.6. Crowdsourcing with Parcel Lockers

Dos Santos et al. [289] introduced a novel two-echelon delivery model that combines PLs and OCs. In this model, lockers serve as both PPs and transshipment hubs. Couriers picking up their parcels can volunteer to deliver others’ parcels along their routes for compensation. The system includes fallback strategies to ensure service continuity in the event of OC no-shows. An MIP model encapsulated three delivery options: depot-to-locker, locker-to-home via professional fleet, and locker-to-home via OC. Computational results showed cost savings and reduced travel distance when OCs were used effectively. Similarly, Ghaderi et al. [290] proposed a crowdshipping framework in which strategically located PLs served as exchange points for both single and joint deliveries. A two-phase algorithm first identified task sets (single vs. joint) and then allocated deliveries among crowdshippers. Experiments with real-world data demonstrated strong performance, and large-scale simulations indicated that the joint delivery model could enhance success rates by up to $5\%$, provided PLs were optimally positioned. A multi-criteria framework by [291] integrates automated smart lockers with capillary distribution and CS, articulating objectives for cost, distance/time, utilization, resilience, and sustainability, and embedding VRP-style delivery constraints. The PT-based CS, in which commuters move small parcels between APLs at metro stations, can save vehicle-km and emissions when spare PT capacity is utilized; a Rome case study by [255] quantifies the environmental and economic impacts and outlines the coordination needs. A study by [292] estimates the system effects of PT-based CS, showing that diverting a share of small parcels to commuters’ PT trips can reduce carrier CO₂ and operating effort, with participation and station capacity emerging as key constraints.

9.7. Autonomous Delivery Robots and Freight-on-Transit

De Maio et al. [293] modeled the LMD where ADRs can ride scheduled PT to extend range and save battery, then continue on sidewalks/roads to serve multiple customers. Technically, the city’s PT network is time-expanded, so robot routes must synchronize with bus/metro departure and arrival times; ADRs board/exit using dedicated compartments (so passenger capacity is not the bottleneck), and the optimization minimizes total delivery cost under battery, capacity, and timing constraints. The authors design a destroy-and-repair LNS tailored to the PT timetable structure. On realistic Rome-style instances (up to 500 customers), the approach yields ≈ 7.5% lower cost than a traditional road-only benchmark, and the experiments indicate meaningful emissions reductions relative to both diesel and electric vans, thanks to shifting distance onto PT lines. A recent LRPVR study bases ADRs at selected public transport stations and co-optimizes van and robot routes via a two-step matheuristic (hybrid set-partitioning + location, then routing), showing notable cost and emission reductions versus van-only delivery on Rome-style instances [294].

9.8. Crowdsourcing with Freight-on-Transit

A recent report by [295] proposes a conceptual framework for integrating urban freight with PT and CS, highlighting capacity sharing, timetable coordination, station handling, and regulatory/liability considerations as key design issues before detailed OR modeling. Also, co-modality concepts explicitly integrate small freight with PT by leveraging passengers as ad hoc carriers. A recent work by [296] formalizes a crowd-sourced co-modality transportation system and outlines operational building blocks and expected cost/emissions benefits. A recent work by [297] defines the PT-based CS Problem (PTCP), combining a compact MILP (tightened by valid inequalities) with an ALNS; parcels are staged at PT stations, assigned to commuters along their regular trips, and undelivered items are covered by backup service. Experiments show that the heuristic scales well and that CS vs. backup cost parameters dominate system cost. The PT-based CS feasibility depends on commuters’ willingness to accept parcel tasks. A Latent Class (LC)-based study by [298] on Sydney PT passengers quantifies acceptance as a function of incentive, parcel weight, and detour, yielding segment-specific elasticities that can inform OR assignment and backup policies.

9.9. Crowdsourcing with Parcel Lockers and Freight-on-Transit

Early feasibility evidence for PT-based CS in Rome [299] shows promising willingness to participate and operational viability when parcels are exchanged at/near transit stations via PLs. The PT-based CS can exploit spare metro capacity by exchanging parcels via APLs at/near stations; Rome Stated Preference (SP) surveys in [300] quantified willingness to act as crowdshippers and to buy the service, and identified feasible design/compensation conditions. The PT-based CS can be operationalized by prioritizing spatially outlying parcels, matching them to PT passengers, and co-deciding the number/placement of PLs; a Singapore study by [301] reports up to $11\%$ of parcels diverted, with CO₂, fleet-size, and nearly $20\%$ carrier cost reductions versus truck-only delivery. User acceptance of PT-based CS has been quantified through a stated-choice mixed-logit analysis of 524 passengers in Copenhagen [302], revealing who is likely to participate and the compensation/extra time trade-offs that should guide service and locker design. Passenger acceptance is pivotal for PT-based CS. A study by [303] shows that time availability/flexibility and physical condition are the primary factors driving participation decisions, with youth and riders familiar with PLs more inclined to participate.

In addition, the PL located on PT nodes can be optimized under a capital budget to enable PT-based CS. The study by [304] formalizes this problem and provides a facility-location baseline for PT-locker designs. A Copenhagen case study by [305] combines budgeted PL siting with a downstream carrier VRP to evaluate PT-based CS. Its results show reductions in vans and driver hours, with crowdshipper availability as the key bottleneck. PT-based CS can relay parcels among PLs at PT stations, with multi-hop handoffs via commuting crowdshippers. The study by [306] shows that allowing handovers outperforms single-carrier paths and offers better robustness to delays while balancing stakeholder objectives. Mixed-methods evidence on PT-based PL-CS studied by [307] highlights demographic drivers of participation and operational bottlenecks (e.g., station crowding, liability), providing levers that complement OR models for locker siting and task matching. City-scale microsimulation for a Greek mid-sized city by [308] indicates that PT-based CS with lockers can mitigate last-mile impacts, with outcomes sensitive to participation rates and locker siting. Operationalizing PT-based CS with lockers at stations can be modeled via a probabilistic optimization that embeds passenger task-acceptance behavior, enabling realistic parcel-to-commuter allocation on transit networks [309].

Integrating EVs, ADRs, PLs, and CS provides a multifaceted approach to sustainable ground-based LMD. These hybrid systems address urban delivery challenges by combining flexibility, scalability, and environmental responsibility. The OR models—ranging from MIP to ALNS, GA, and PFA—enable optimized decisions for routing, energy use, facility location, and task assignment. The synergy between these technologies reveals promising paths for designing future-ready, green delivery ecosystems.

10. Comparative Analysis and Practice Insights

At first, this section synthesizes method-level insights across innovations. We compare dominant OR techniques in terms of benefits, drawbacks, scalability, and performance under practical limitations, including time windows, energy and charging dynamics, synchronization between assets (e.g., EVs and robots), stochastic travel times, and data availability. The goal is to guide method selection for a given problem structure and deployment constraints. As presented in

Table 3. Comparative view of OR techniques across ground-based LMD innovations.

Setting	Typical Model Structure	Benefits in Practice	Drawbacks/Limits	Scalability/Runtime
EVs	MILP with energy and charging; time windows	Explicit feasibility respecting the SoC, time; interpretable costs and constraints; suitable for sensitivity and policy testing	Exact methods degrade with tight time windows and nonlinear charging; parameter uncertainty increases solve times	Exact: small/medium; metaheuristics: large (hundreds-thousands stops) with near-optimal solutions in minutes/hours
ADRs	MILP with synchronization, launch/retrieval, coupled capacity	Captures timing and resource coupling; supports what-if on robot counts and speeds	Synchronization explodes state space; exact methods scale poorly; requires reliable travel/handling times	Matheuristics/decomposition: medium instances; hybrid heuristics: larger with good gaps
PLs	Bi-level or joint location-routing MILP	Fewer failed deliveries; consolidates stops; amenable to strategic-operational splits	Coupling of siting and tours is hard; stochastic demand and compartment sizes complicate feasibility	Decomposition or matheuristics handle city-scale; exact is moderate scale if decoupled
PPs	Facility location + routing MILP	Leverages existing retail; simple policies possible	Limited hours; human factors; less secure than lockers	Similarly to PL; heuristics scale well; exact limited by time windows
CS	Stochastic/rolling-horizon assignment + routing	Fast surge capacity; good in peak and sparse areas; platform data enables learning	Acceptance uncertainty; reliability; pricing incentives couple to routing	Myopic + learning or CG with heuristics scale; full stochastic exact is small
FOT	Network design + time-expanded MILP; two-stage modeling	Uses existing capacity; emissions savings; robust for dense corridors	Timetable synchronization; station handling; passenger interference	Decomposition + CG scale; exact monoliths limited
Combined solutions	Multi-layer MILP with synchronization, location-routing, assignment; two-stage modeling; set-partitioning/CG; rolling-horizon control	Synergies from pooling and flexible hand-offs; shifts curb time to lockers; robust under demand spikes; supports multi-objective trade-offs (cost-energy-service)	Strongly coupled decisions (siting-routing-synchronization) inflate state space; more data/parameters to calibrate; higher orchestration complexity	City-scale via matheuristics + decomposition (ALNS/VNS + Benders/CG) heuristics; exact feasible only for small pilot networks

, the decomposition and matheuristics are consistently effective when models include energy or synchronization constraints, offering near-optimality with practical runtimes. (Meta-)Heuristics improve initialization and acceptance prediction in CS and dynamic tours, but they require careful validation under distribution shifts. Also, exact methods remain valuable for calibration, benchmarking, and small-to-medium strategic instances (e.g., siting and limited charging layouts). Finally, realistic evaluation benefits from reporting seeds, time budgets, and convergence diagnostics to contextualize performance claims. Also, according to this table, method choice is driven less by the “innovation” itself than by the constraint structure. When synchronization and multi-resource coupling (e.g., truck-robot timing and locker capacities) are present, decomposition and matheuristics consistently outperform monolithic exact solves at scale. Nonlinear charging and SoC-dependent energy models favor tailored neighborhoods and set-partitioning over single-shot MILPs; exact methods remain valuable for calibration and policy sensitivity on reduced instances. Dynamic and stochastic regimes (crowd acceptance and transit perturbations) benefit from rolling-horizon optimization with prediction, where data are scarce, robust, or two-stage formulations prevent overfitting. In hybrid systems, combining ALNS/VNS with Benders’ decomposition or CG yields city-scale solutions within practical time budgets, while retaining clear levers for managerial trade-offs.

Moreover, this section consolidates real-world implementations and data-driven case studies referenced throughout the review. Each snapshot lists the setting, geography/scale, salient design elements, reported outcomes, and sources.

Table 4. Representative practice cases and implementation evidence across ground-based LMD. Tags: [obs.] observed/operational, [pilot] pilot-scale, [proj.] model-projected.

Setting	Geography/Scale	Design/Constraints	Reported Outcomes (tag)	Source(s)
EV fleet adoption (retail delivery)	U.S., multi-city	Retail EV deployment; depot-charger alignment; partial charging in operations	Emissions reduction potential; curb/charging constraints binding in practice [obs.]/[proj.]	[13]
ADR + modular lockers (routing/siting)	London, U.K.	Road-based autonomous lockers vs. fixed lockers; weekly modular adjustment	Modular lockers outperform fixed under moderate-high demand; fewer failed deliveries [proj.]; limited trials [pilot]	[285]
PL network expansion	Norway, national rollout	Multi-period siting with real demand; environmental accounting	Lower delivery externalities; improved access and service reliability [obs.]/[proj.]	[194]
Collection/Delivery Points (PP/CDP)	Belgium, nationwide	Accessibility/coverage analysis; walking-distance equity	Large coverage gaps without multi-carrier CDPs; policy guidance [obs.]	[209]
Crowd-tasking using commuter flows	Singapore/Beijing, city-scale datasets	Network min-cost flow; citizens deliver along commutes	High scalability/coverage using existing mobility; strong matching rates [obs.]/[proj.]	[237]
CS with relay points	Xi’an, China	2-echelon truck→relay→crowd; nested GA selection/routing	∼14% total cost and ∼26% VMT reductions vs. truck-only [proj.]	[225]
FOT (people+goods)	Rome, Italy	Integration with mass transit; safety/emissions accounting	Substantial projected drops in emissions and accidents [proj.]	[255]
White-label lockers (alBOX pilot)	Austria, urban + rural pilots	Multi-carrier lockers; user acceptance and behavior	Operational feasibility; usage patterns; social acceptance insights [pilot]/[obs.]	[196]
ADR (street+sidewalk)	Barcelona, ES (dense urban core; mixed sidewalk/road)	Prototype build + city pilots; perception/navigation for street-sidewalk operation; safety + teleop fallback; operational envelope definition; curb/sidewalk integration with municipal infra	Reported lessons on infrastructure interfaces, HRI/etiquette, and regulatory coordination; demonstrates practical feasibility and integration considerations for ADR deployments [pilot]	[143]
ADR (sidewalk navigation)	Singapore (NTU campus sidewalks)	Husky platform + RGB-D; Nanyang Sidewalk dataset; social-force-guided intent prediction; state-lattice planner with etiquette cost	Shows how human-space etiquette can be encoded in local planning for ADRs, informing micro-level constraints for OR models [obs.]	[148]
ADR (city pilot)	European city (pilot)	Pilot design; stakeholder alignment; regulatory coordination; infra readiness; change management	Actionable recommendations for scoping use cases and city coordination; complements optimization with deployment guidance [pilot]	[151]
PT-based CS + PL	Rome (city)	Feasibility and willingness analyses; APLs near PT stations; leverages spare capacity	Viable under PL siting and participation assumptions [proj.]	[299]
PT-based CS + PL	Rome (city)	Stated-preference demand/supply; compensation and detour constraints	Participation conditions and policy levers identified [proj.]	[300]
PT-based CS	Singapore (city)	System-level scenario analysis; participation and station-capacity constraints	Lower carrier CO2 and operating effort; capacity/uptake are bottlenecks [proj.]	[292]
PT-based CS + PL (outlier parcels)	Singapore (city)	LOF-based parcel prioritization; locker siting; carrier CVRP evaluation	Up to 11% parcels diverted with 31 lockers; ∼20% cost cut; CO2 down [proj.]	[301]
PT-based CS	Copenhagen (city)	Stated-choice ($n=524$); mixed-logit acceptance model; extra-time/compensation constraints	Acceptance elasticities and target segments for design [proj.]	[302]
PT-based CS + PL + carrier VRP	Copenhagen (district)	Budgeted PL siting at PT; downstream carrier VRP; availability constraints	Fewer vans, reduced VKT and driver hours; crowdshipper availability is binding [proj.]	[305]
PT-based CS	Sydney (metro)	Latent-class acceptance model ($n=2208$); incentive/weight/detour constraints	Segment-specific participation propensities to embed in OR models [proj.]	[298]
PT-based CS + PL	Volos, Greece (city)	City-scale microsimulation; locker siting near PT; participation-rate scenarios	Impact reductions feasible; strong sensitivity to participation and siting [proj.]	[308]
Parcels on fixed-route buses (FOT)	Zrenjanin, Serbia (city)	Stakeholder-informed energy/environmental simulation; policy/energy-mix scenarios	Improved energy and environmental performance vs. truck-only [proj.]	[269]
Mobile vs. stationary PLs vs. home	EU/General (synthetic)	Operational design; dwell-time/coverage policies; emissions-cost trade-offs	MPLs outperform stationary/home under suitable policies; CO2/cost-benefits [proj.]	[199]
PT-CS via locker-to-locker handovers	Subway network (synthetic)	Multi-hop parcel relays at PT lockers; decomposition heuristic; delay robustness	Handover-enabled plans beat single-carrier paths; higher robustness [proj.]	[306]

consolidates real deployments and data-driven case studies cited throughout the review. To clarify evidence types, we tag each snapshot as [obs.] (observed/operational data), [pilot] (pilot trials or limited rollouts), or [proj.] (model-based projections from empirical inputs). “Design/constraints” surface the key operational levers (e.g., charging policy, station handling, clerk capacity), while “Reported outcomes” summarize the measured or projected effects consistent with the sources. According to this table, we observed that (i) PL and PP deployments deliver consistent consolidation benefits when siting considers walking accessibility and operating hours; (ii) ADR + locker hybrids benefit from modular capacity and conservative handling times; (iii) crowdshipping performance hinges on incentive design and acceptance prediction, with relay points amplifying gains; (iv) FOT is most promising on high-frequency corridors with realistic station handling and small freight quotas; (v) EV operations are improved by partial charging policies and charger-route co-design.

Critical Synthesis and Recommendations

Across innovations, the dominant driver of method choice is the underlying constraint structure rather than the innovation’s label. Problems that combine synchronization between resources (e.g., truck-robot launch and retrieval, or transit-last-leg handoffs) with energy and charging dynamics consistently favor decomposition and matheuristics over monolithic exact solutions at scale. Exact MILPs remain valuable for calibration and policy sensitivity on smaller or simplified instances. Still, city-scale planning with rich constraints is more reliably handled by ALNS/VNS/ILS and path-based or Benders-type decompositions (see Table 3). Ensuring resilience requires modeling uncertainty explicitly. At the operational layer, rolling-horizon control supported by prediction (e.g., expected arrival times, acceptance probabilities) improves robustness to day-to-day variability. At both tactical and strategic levels, two-stage stochastic and robust formulations mitigate tail risk in lateness and missed deliveries, particularly when timetables, handling times, or acceptance behavior are volatile (see Table 1). Also, evaluation practices significantly influence conclusions. Reporting random seeds, time budgets, convergence diagnostics, and percentile-based service metrics prevents over-optimistic claims and facilitates replication across datasets.

Furthermore, hybrid systems provide meaningful synergy but introduce orchestration complexity. Designs that combine EVs, ADRs, lockers or PPs, CS, and FOT benefit from flexible hand-offs and the ability to shift curb time to unattended facilities. However, these gains are coupled with siting, routing, and synchronization decisions, and increase data and parameter requirements. In practice, decomposition combined with learning-assisted heuristics scales well while retaining clear managerial levers. Finally, equity and access should be treated as first-class objectives. Locker and PP siting with walking-distance coverage constraints measurably affect emissions, failure rates, and user experience, and sequential “site-then-route” planning can underperform joint formulations in dense districts.

For city-scale EV routing with non-linear or SoC-dependent charging, energy-aware ALNS/VNS/ILS are generally preferable, with exact MILPs used for calibration on reduced instances. For truck-ADR or ADR-locker synchronization, logic-based or Benders-style decomposition, paired with heuristic routing, is effective at the tactical level. In contrast, rolling-horizon dispatch supports real-time operations. For locker/PP systems that jointly choose sites and routes, especially when equity constraints are present, two-phase approaches (exact siting followed by heuristic tours) or CG path models deliver good performance, and robust variants are advisable when opening hours or compartment availability are uncertain. For CS under acceptance uncertainty, rolling-horizon assignment augmented with prediction of acceptance or expected arrival times is practical and should be evaluated jointly with pricing and routing policies. For FOT with timetable drift, TEN models solved by CG work well in combination with explicit station-handling constraints and passenger-first quotas. To facilitate comparability across studies, we recommend publishing instance specifications (including size and spatial density), solver time limits, random seeds, and hardware details; reporting means and percentiles for service quality (on-time rate, lateness) and for energy/emissions (kWh, CO₂); and, when learning components are used, documenting the training-data horizon and monitoring distribution shift between training and evaluation periods. These synthesized insights complement the practice snapshots in Table 4 and the goal-technique mapping in Table 1, positioning the review as a reference for method selection and deployment.

11. Discussion and Future Directions

In the previous sections, the collected papers were reviewed and analyzed with respect to innovative solutions, problems, sub-problems, and OR-based solution techniques. After reviewing and analyzing the relevant papers and contributions, the research gaps and suggestions for future studies are presented below. The suggestions for future studies can be divided into three directions: (I) novel, combined, innovative solutions; (II) new sub-problems and variants; (III) state-of-the-art solution methodologies.

11.1. Introducing Novel Combined Innovative Solutions

The existing literature reveals a notable gap in research focused on integrated innovative solutions for LMD. For instance, a research direction in this field involves integrating EVs with ADRs, a transformative approach that can significantly impact the sustainability of LMD operations. However, it also raises essential safety and privacy considerations that must be carefully addressed. In this innovative concept, EVs, including e-vans, e-trucks, and e-cars, serve as a “mothership van." These EVs are tasked with transporting goods and releasing SADRs (sidewalk-based robots) for the LMD process, serving customers who may be difficult for larger EVs to reach. This symbiotic relationship between EVs and ADRs holds immense promise, particularly in densely populated urban areas where maneuvering e-trucks or e-vans can be challenging. However, successful implementation requires meticulous infrastructure planning, particularly for establishing CSs to recharge EVs. Ensuring a reliable network of CSs is critical to maintaining the efficiency and effectiveness of the EV-ADR delivery system. Another crucial aspect is the synchronization and scheduling of operations within this combined EV-ADR system. Coordinating the movements and tasks of EVs and ADRs to optimize delivery efficiency while minimizing delays is a complex, multifaceted challenge. Advanced OR algorithms and decision-making techniques are essential to achieving this synchronization, ensuring that products reach their intended recipients on time.

Furthermore, an emerging and promising avenue for future research is the integration of RADRs and SADRs in urban LMD systems. These ground-based innovations offer high flexibility and can help reduce environmental footprints by operating on electricity and navigating through urban roadways and sidewalks. However, from an OR standpoint, their joint deployment introduces complex optimization challenges. A key issue is the strategic placement and selection of charging stations tailored to the heterogeneous mobility patterns and energy requirements of RADRs and SADRs, especially in dense urban environments with limited infrastructure. Moreover, ensuring the safety and compliance of these robots with traffic regulations, pedestrian flows, and dynamic road conditions remains a critical concern. Routing problems become significantly more complicated due to the need to coordinate two robot types with different speed profiles, operational zones, and interaction constraints. Future research on OR should develop integrated mathematical models and algorithms that address these challenges under realistic urban conditions, considering stochastic travel times, battery constraints, collision avoidance, and service time windows. Simulation optimization frameworks and multi-agent systems can play a vital role in analyzing such hybrid deployments, providing insights into their feasibility, efficiency, and robustness in real-world city logistics.

Moreover, another promising research direction involves integrating SADRs with the emerging FOT paradigm. FOT leverages the unused capacity of PT systems, such as buses, subways, and trams, to carry freight alongside passengers, offering a cost-effective and environmentally friendly approach to urban logistics. Pairing SADRs with FOT can enable a two-tier LMD system, in which goods are transported via transit networks to intermediate drop-off points (e.g., transit hubs or stations), from which SADRs deliver to doorsteps. However, this hybrid model introduces a range of optimization challenges from an OR perspective. Key concerns include synchronizing SADR dispatch schedules with transit vehicle arrivals, selecting optimal transfer hubs, and coordinating robot routing under spatial and temporal constraints. Also, real-time variability in transit schedules, passenger flows, and sidewalk accessibility can introduce stochastic elements into the problem. Developing robust mathematical models and solution methods, such as TEN formulations, stochastic programming, and agent-based simulations, will be essential for assessing the feasibility and efficiency of SADR-FOT systems. This integration has the potential to reduce urban delivery costs and emissions significantly, but it demands innovative OR tools to address operational complexities and ensure service reliability.

In addition, an innovative approach to modernizing parcel delivery is the hybrid PL-FOT system, which increases the speed and efficiency of product delivery to end customers. This pioneering concept envisions using buses or trams to transport parcels from depots to strategically designated PLs, where customers can conveniently pick up their orders. Since PLs operate as 24/7 access points, there are no restrictions on when orders can be placed inside them. This convenience ensures that customers can collect their parcels at their preferred time, accommodating their busy schedules. However, for same-day delivery services, a more intricate level of planning and coordination is essential. This includes synchronizing the arrival times of buses or trams at the PLs with customers’ expected arrival times. Achieving this synchronization ensures that parcels are ready for pickup when customers arrive, optimizing the overall process and meeting the demands of time-sensitive deliveries. Another complex aspect of this hybrid solution is routing public vehicles to PLs near customers. This entails dynamic routing algorithms that consider real-time traffic conditions, the location of PLs, and the destinations of individual customers. Effective routing ensures that deliveries are both timely and efficient, reducing unnecessary travel and optimizing resource allocation.

Another novel concept is the hybrid EV-ADR-PL system, which combines EVs, ADRs, and PLs. This approach is particularly beneficial in densely populated urban areas, where customers prefer the convenience of picking up their orders from a parcel point, such as a PL. In such urban environments, the EVs serve as the backbone of the delivery fleet, transporting parcels to strategically located PLs. Meanwhile, ADRs complement this system by handling the final mile, autonomously navigating sidewalks and public spaces to reach customers or PLs efficiently. The synergy among EVs, ADRs, and PLs ensures prompt, accessible deliveries that cater to the specific demands of urban customers.

Finally, integrating CS concepts into any hybrid delivery system, such as EV-SADR, PL-FOT, or EV-PL, holds immense potential to deliver an efficient, highly effective solution for LMD. This collaboration streamlines logistics, optimizing parcel flow and enhancing delivery efficiency. Moreover, when sustainable solutions such as EVs and ADRs are incorporated into PL or CS systems, they improve air and environmental quality, aligning with eco-friendly initiatives. However, a pivotal challenge is pricing and incentive strategies to encourage customer participation in CS-aided EV-PL or EV-ADR-PL systems. Convincing customers to adopt these innovative approaches may require carefully designed incentives and pricing models, posing a complex decision problem. As a result, researchers and practitioners are encouraged to explore various combinations of innovative solutions, such as EV-PL-CS, EV-ADR-PL-CS, EV-ADR-PL-CS-FOT, or other integrated LMD systems. These proposals offer versatility in addressing diverse delivery needs and urban environments. However, striking the right balance between operational costs and environmental considerations remains a critical aspect of these decisions. Despite the undeniable benefits of these efficient and sustainable hybrid solutions, it is essential to acknowledge that their complexity escalates as more innovative components are integrated. This complexity challenges researchers in OR to develop sophisticated algorithms and decision-making frameworks that can accommodate the intricacies of these integrated systems. Nevertheless, pursuing these solutions represents a promising path forward for LMD’s evolution, offering both operational efficiency and environmental responsibility.

11.2. Extending New Sub-Problems and Variants

Another future research direction could be to build models that incorporate scenarios and parameters closely resembling the actual conditions encountered by EVs, ADRs, PLs, and FOT. The problems addressed should focus on practical setups and limitations, particularly concerning factors such as expenses, battery longevity (for EVs and SADR), and operational distances. This encompasses considerations such as permitted and off-limits driving areas, diverse safety considerations, and pedestrian pathways designated in the case of SADR applications. To develop more practical routing models that integrate innovative LMD approaches, it is essential to account for uncertainties in dynamic customer demand, order handling, and vehicle travel. These models should mirror real-world scenarios in which the number and type of customer orders remain uncertain over a given timeframe. Addressing strategies for managing such orders, such as day-to-day ordering or aggregating orders over a rolling timetable, presents an intriguing challenge for future research.

Furthermore, other uncertainties in this context include demand patterns, crowd availability in CS, and parcel loading and unloading. These operations must be factored into models of parcel delivery challenges for emerging delivery methods. This is especially crucial as parcel unloading is not always straightforward, and there may be unsuitable locations for EV or ADRs to complete their deliveries. Confronting these variables and assessing their impacts on the overall delivery process represents another engaging research challenge. Furthermore, researchers should consider how various weather conditions, such as rain, dust, and stormy weather, can significantly disrupt the routing and performance of robots.

In summary, future research in the field of LMD should adopt a holistic approach that considers the unique challenges and uncertainties associated with various delivery modes, real-world operational constraints, and environmental factors, ultimately leading to more effective and resilient delivery systems.

11.3. Developing State-of-the-Art Methodologies

A key future research direction in sustainable LMD is advancing data-driven OR models that integrate real-world information into decision-making processes. The increasing availability of granular data—such as GPS trajectories, delivery timestamps, customer preferences, and urban traffic flows—enables researchers to build more accurate and responsive optimization models. These models can capture dynamic urban conditions and customer behavior, enabling logistics systems to adapt in real time. For instance, delivery route optimization for EVs or SADRs can be enhanced by incorporating real-time energy consumption data, weather conditions, and congestion patterns. Data-driven approaches also support demand forecasting, time-window estimation, and customer clustering, all of which are vital inputs to OR models for vehicle routing, fleet composition, and delivery scheduling.

Another promising methodology is stochastic programming, which is well-suited for handling the uncertainty and variability inherent in LMD operations. Unlike deterministic models, stochastic OR models can incorporate uncertain travel times, variable customer demand, unpredictable traffic conditions, and energy consumption variability, especially critical for EVs and autonomous robots with limited range. Two-stage or multi-stage stochastic programs can be used to develop robust delivery schedules and charging strategies, in which first-stage decisions (e.g., vehicle routing) are made before uncertainty is realized. Second-stage choices (e.g., rerouting or charging adjustments) are made afterward. This approach ensures more reliable and cost-effective operations in complex urban environments.

Simulation-based optimization also holds strong potential for evaluating and improving LMD systems that involve multiple interacting components such as lockers, transit networks, and autonomous delivery agents. When analytical models become intractable due to the scale or heterogeneity of the system, discrete-event or agent-based simulation can help capture the temporal evolution of delivery processes and urban dynamics. These simulations can be coupled with metaheuristics, reinforcement learning, or scenario-based analysis to test routing strategies, charging policies, and infrastructure placement across various urban layouts and customer behavior patterns. Simulation-based methods are beneficial for evaluating the performance of hybrid systems, such as SADR + FOT or EV + robot-assisted delivery, under stochastic and dynamic conditions.

In recent years, ML tools have become increasingly valuable in complementing OR methods for LMD. ML can be employed to predict delivery demand, estimate travel time under uncertain traffic conditions, detect delivery failures, or recommend locker locations based on historical usage patterns. Supervised learning models, such as gradient boosting or neural networks, can forecast customer time windows or charging demand, which is then fed into optimization models. Reinforcement learning can be applied to learn dynamic delivery and routing policies in evolving urban networks. Furthermore, ML-based surrogates can replace time-consuming simulations or solve large-scale optimization problems faster, facilitating real-time decision-making. Integration of ML with OR—often referred to as “predict-then-optimize” frameworks—can enhance the responsiveness and intelligence of sustainable urban logistics systems.

Lastly, hybrid approaches combining mathematical programming, heuristics, simulation, and learning-based techniques offer a comprehensive direction for future research. Realistic LMD problems often involve a blend of discrete decisions (e.g., routing and vehicle assignment), continuous decisions (e.g., energy consumption), and dynamic events (e.g., unexpected road closures or customer unavailability). Hybrid models can exploit the strengths of each methodology; for example, using MILP for core routing structures, simulation for evaluating dynamic responses, and ML to predict uncertain inputs. Such integrated frameworks will be key to designing, optimizing, and operating sustainable, ground-based last-mile systems that are not only efficient and robust but also adaptable to the complexities of real-world urban environments.

Practical implications. For implementation, we recommend a constraint-first pathway: (i) diagnose the dominant constraint structure (energy/charging, synchronization, timetable drift, equity) for the target city or corridor; (ii) select technique classes accordingly using the goal-technique framework (Section 2.7, Table 1) and the comparative summary (Table 3); (iii) adopt the reporting checklist to ensure comparable evaluation across pilots (Section 10); and (iv) prototype on a limited district or line before scaling. Typical “quick wins” include partial-charging policies for EV fleets, modular capacity adjustments for lockers, and rolling-horizon dispatch for ADR/crowd systems. This path translates the review’s synthesis into deployable steps for both municipal planners and parcel operators.

12. Conclusions

This systematic review synthesizes sustainable, ground-based Last-Mile Delivery (LMD) from an Operations Research (OR) perspective, linking problem structures to technique classes and to sustainability goals (people-planet-profit) with resilience as a cross-cutting property. It integrates evidence across EVs, ADRs, PLs, PPs, CS, and FOT, and it analyzes hybrid designs that couple these innovations. Our answer to RQ1 (challenges of employing sustainable innovations in LMD from an OR perspective) is that across modes, the dominant challenges are: (i) synchronization of multi-resource operations (e.g., truck-robot launch/retrieval, transit timetables and last legs); (ii) energy/charging dynamics (state of charge, partial/nonlinear charging, charger capacity/queues); (iii) joint siting-routing couplings (e.g., PLs/PPs with equity and walking bounds); (iv) uncertainty in demand, travel/handling times, and crowd acceptance; (v) scalability of rich formulations; and (vi) measurement of sustainability beyond GHGs (equity, noise, curb dwell, reliability). These cut across innovations and motivate decomposition, stochastic/robust modeling, and learning-assisted control (explained previously in Section 3, Section 4, Section 5, Section 6, Section 7, Section 8 and Section 10).

Moreover, our answer to RQ2 (effective OR methods for sustainable ground-based LMD and their characteristics) is that method choice is driven by constraint structure. Energy-aware ALNS/VNS/ILS and path/decomposition schemes are effective for EV routing with charging; logic-/Benders-based decomposition with heuristic routing and rolling-horizon dispatch works for truck-ADR and ADR-locker synchronization; two-phase or CG models handle PL/PP siting–routing with equity constraints; rolling-horizon and prediction addresses crowd acceptance uncertainty; and time-expanded networks with CG fit FOT under timetable drift (previously shown in Table 3 and Section 2.7 and Section 10). Key characteristics include scalability (minutes to hours on city-scale instances), interpretability of levers, and compatibility with multi-objective or $ϵ$-constraint formulations to balance cost, emissions/energy, service, and equity. Also, we answered RQ3 (research directions and gaps) by showing the priorities, which include (i) hybrid/combined designs (e.g., EV+ADR+PL/PP/CS/FOT) with explicit orchestration of hand-offs; (ii) uncertainty-aware models (stochastic/robust) for lateness, charger queues, and acceptance; (iii) data-driven demand/acceptance prediction embedded in optimization; (iv) equity and access as first-class constraints in siting and routing; and (v) transparent evaluation via shared benchmarks, percentile service metrics, and reproducible reporting (described previously in Section 11).

Contributions and beneficiaries. For academics, we provide a goal-technique conceptual framework (Section 2.7), comparative algorithmic guidance (Table 3), and a PRISMA-style synthesis (Figure 2) to structure future research. For parcel carriers and platform providers, we offer guidance on method selection, tied to operational levers (partial charging, curb-time shifting to lockers, rolling-horizon dispatch) and risk-aware objectives. For municipalities and transit agencies, the review clarifies when FOT and ADR hybrids are feasible and how equity constraints (such as coverage/walking bounds) affect siting and routing. For locker/charging planners and software vendors, it identifies joint siting-routing patterns and decomposition schemes that scale across city instances. The practice snapshots (Table 4) and the reporting checklist (Section 10) translate findings into deployable steps and comparable evaluation.

We focus on ground-based LMD (2010–2025) articles; aerial systems and reverse logistics are out of scope. We conclude that by aligning OR technique classes with people–planet-profit objectives and synthesizing cross-cutting constraints common to EVs, ADRs, lockers/PPs, CS, and FOT, this review provides both a conceptual and practical reference for designing scalable, resilient, and sustainable last-mile systems. Future research in the field of LMD should take a comprehensive approach that considers the unique challenges and uncertainties associated with different delivery modes, real-world operational constraints, and environmental factors. This will contribute to the development of more effective and resilient delivery systems. Additionally, the integration of matheuristic and ML-based methodologies has transformed LMD optimization. Data-driven models and ML tools can enhance adaptability and responsiveness, while stochastic programming and simulation-based methods provide robust solutions in the face of real-world variability. The synergy of these techniques, particularly in hybrid frameworks, holds great promise for optimizing innovative ground-based delivery systems. Future research should focus on leveraging these methodologies to develop scalable, intelligent, and resilient logistics solutions that align with urban sustainability goals. To advance LMD operations, it is crucial to continue exploring integrated, innovative solutions (such as EV, ADR, PL, CS, and FOT) and to adopt a holistic perspective.