Flight Routing Optimization with Maintenance Constraints
Abstract
1. Introduction
| Reference | Optimizer | Objective | Constraints |
|---|---|---|---|
| [2] | Branch and price | Min total cost | – |
| [27] | Polynomial-time algorithm | Find feasible routes | – |
| [3] | Deep first and random search | Min maintenance and reassignment cost | M1, M4 |
| [4] | Branch and price | Min number of unused legal flying hours | M2, M4 |
| [5] | CPLEX 10.0 | Min connection and maintenance costs | – |
| [6] | CPLEX 12.1 | Find feasible routes | M1, M2, M3 |
| [7] | Branch and bound, compressed annealing | Max utilization of remaining flying time | – |
| [8] | Large-scale neighborhood search algorithm | Min the sum of remaining flying time | M1, M2, M3 |
| [9] | ACO, GA, SA | Max the through value | M1, M4 |
| [10] | Branch and bound | Min the number of maintenance misalignments | M1, M2, M4 |
| [11] | CPLEX 12.1 | Max total profit | M1, M2, M3, M4, M5 |
| [12] | Heuristic | Min maintenance violations and not airworthy aircraft | M2, M3, M4 |
| [13] | Reinforcement learning vs CPLEX | Max through value of the route | M2, M3, M4 |
| [14] | Hybrid Gasimov’s and ACO | Max the total profit through value of the route | M6 |
| [16] | CPLEX-Heuristic | Max the number of cyclic routes | M1, M6 |
| [15] | Hybrid IACO-CPLEX | Min the sum of aircraft usage, idle time, and fuel-burn related costs | M1, M2, M3, M4 |
| Reference | Mtto. Type | Planning | Network | Model | Data |
|---|---|---|---|---|---|
| [2] | – | Weekly | Connection network | FSM RTNOM | G |
| [27] | A | 3–4 days | Network flow problem | Euler Tour | – |
| [3] | A, B | Weekly | Connection network | MCNF | – |
| [4] | A, B | Daily | Set partitioning | – | – |
| [5] | Night-Transit | Daily | Time–space network | MIP RTNOM | RL US Carrier |
| [6] | A | Daily | Connection network | NAFF | RL (United airlines) |
| [7] | – | Weekly | Connection network | MCNF | RL |
| [8] | A | Weekly | Connection network | MCFP | – |
| [9] | – | 4 days | Connection network | MIP | – |
| [10] | MWD | Weekly | Connection network | – | RL Canadian |
| [11] | A | 4 days | Modified connection network | – | EgyptAir |
| [12] | C | 30 days | – | MMILP | Flightradar24 |
| [13] | A | 4 days | Network flow based/Markov decision process | NAFF | – |
| [14] | A | Daily | Connection network | ATSP | – |
| [16] | A | 3 days | Connection network | ATSP | RL (Florida Express) |
| [15] | A | 4 days | Connection network | – | BTS |
2. Methodology
2.1. Solution Representation
2.2. Parameters to Define a Rotation (Input Data)
- A matrix R, as seen in Equation (9), is a matrix with rows (number of flights), such that the first column, with elements , represents the airports of origin, the first index , indicates a row in the connection matrix E, while the second, 1, indicates that this entry comes from the first column of the matrix E. The second, with elements , is the destination airport; this entry comes from the second column of the matrix E to ensure a real flight connection. For the third column with elements , the first index is the same as the previous elements; that is, refers to the same row index in the E, H, and T matrices. The second index, j, is a column in H that indicates a selected departure time for the corresponding flight. In addition, the flight duration is found in matrix T at position . This representation is suitable for direct human interpretation, but it does not facilitate compact storage and the application of perturbation operators, which are commonly used in most direct search algorithms.
- Matrix X in Equation (10) is a second representation of a rotation. This representation facilitates compact storage and the application of perturbation operators. It has a number of lines ; therefore, the number of rows is the same as that of R. Nevertheless, this representation assumes that the entry is the origin airport while is the destination, and so on. In general, is the origin airport for , and is the destination for . Finally, the last origin airport is , and the last destination airport is . This representation assumes the fulfillment of two constraints: firstly, a destination airport becomes the next origin airport; this is the path constraint, which ensures that connecting flights are possible. Secondly, the last destination airport is the first origin airport; this is the closed path constraint, which ensures that the rotation is repeated cyclically. Nevertheless, these constraints seem obvious; a method for generating and perturbing candidate solutions must ensure that both are fulfilled.
2.3. Objective Functions
- Maximization of flight duration: It assumes that increasing the flight time increases the profit, measures the sum of flight durations of the rotation, using the data from matrix T in Equation (4) and the indexes of rotation in Equation (9), as shown in Equation (11).If available, profit data can be incorporated by substituting the time variable with the profit variable in Equation (11). This substitution does not require substantial alteration to the underlying method.
- Maximization of the number of flights: It assumes that maximizing the number of flights in the rotation increases the profit. This number of flights is the number of rows of rotation, as shown in Equation (12).
2.4. Constraints
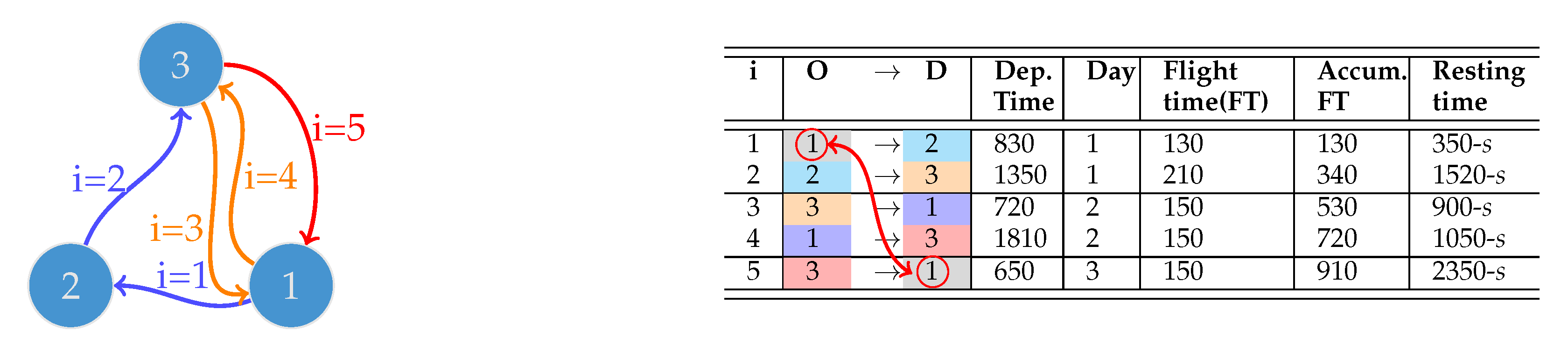
- Path constraint: In rotation R, the flight from for always departs from the previous airport so that . In a mathematical sense, it means that the sequence of visited vertices forms a walk or path. For example, Figure 1 shows that the sequence of visiting nodes is . All connections must exist in the matrix E. For example, the table in Figure 1 illustrates the rotation in the figure; the second and third columns denote the departure and arrival airports, respectively. The right airport is the left airport of the row below. The departure time is in the third column; if the departure time of a flight is earlier than the previous, the departure day in the fourth column is computed to fulfill this constraint.
- Duration constraint: A rotation R is a sequence of flights that repeat every certain number of days. Therefore, the total rotation time must not exceed the period . Note that the rotation duration time is not only the flight time and turnarounds, but also the downtime due to schedule limitations. For example, if a flight arrives at 12:00 p.m. and departs at 11:00 a.m., a full day must pass before departs. In Figure 1, assuming a of 3 days, the relative day of each flight is shown in the Day column, which is assigned automatically by an algorithm to ensure that they do not overlap. Assuming a turnaround time of min, the total rotation time is calculated using the departure time of the first flight (8:30, recorded as 830 in the Dep. time column) on the first day and the arrival time plus turnaround of the last flight. The last flight departs at 6:50 on the third day (row 5, columns 3 and 4), flies for 1 h and 50 min, arrives at 8:40, and undergoes a 40-min turnaround. Thus, the operation ends at 9:20 on the third day. Then, the aircraft rests by 23:50 h minus 40 min, as shown in the Resting time column—that is, 23 h and 10 min—to restart the rotation for the next day (first day again) at 8:30.
- Closed-path constraint: A closed path is one that ends at the vertex at which it started. In our case, it means that the sequence of flights ended at the airport where it started, which is necessary for rotation R to repeat exactly the same flights every time interval . In Figure 1, it is shown with a red arrow from the last destination airport to the first origin airport.
- Constraint of turnaround: The turnaround time s is a minimal gap between landing and taking off. In Figure 1, the last column subtracts the turnaround time from the difference between arrival and the next departure; this value must always be positive to ensure that flights do not overlap.
- Number of maintenance services constraint: The number of maintenance opportunities that are possible within a rotation R is computed by counting the gaps between arrivals and next lading minus the turnaround time that are greater than or equal to the maintenance time. For example, assuming h (800 in our notation) and a turnaround time of min, in Figure 1, the number of maintenance opportunities is the number of resting times that are lesser or equal to 800; in this case there are 4, and only the first flight has a resting time of 3:10 h. Hence, if the number of maintenance opportunities is equal to or lower than the number of maintenance services, the rotation is feasible.
2.5. Candidate Solution Evaluation and Constraint Management
- The path constraint presents two cases: The first case involves proposing the initial random rotation. The first flight is selected from the total possible flights in matrix E. Then, the next flight is randomly selected from the subset of flights that fulfill the constraint (i.e., flights connected to the previous one). The second case is a perturbation, where a block of connecting flights is replaced by another. The algorithm ensures that the block of flights inserted fulfills the path constraint. If no feasible solution is found after several trials (specifically, 30 trials in our implementation), the solution is not perturbed and is returned in its current form.
- For managing the duration constraint, the algorithm computes the total rotation time; if it is greater than the rotation period, then the candidate solution is penalized. The penalization method guarantees that a feasible solution has a better objective function value than an unfeasible one. Let be the total rotation time, be the rotation period, and be the flight time; hence, the penalization for this objective is shown in Equation (13). Notice that for a feasible solution, is always greater than because , and an unfeasible solution is always less than .In the same regard, assuming that a rotation X has at least 2 rows (1 flight), Equation (14) is greater than for a feasible solution and less than for an unfeasible one.
- The closed-path constraint is managed by removing flights from the rotation until the last flight is connected to the first.
- The turnaround constraint is managed by verifying that there is a lapse time s between a flight and the next, or assigning the flight to the next day.
- The number of maintenance services constraint is managed by inserting a maintenance service each time a maintenance airport is visited until the number of desired services is fulfilled. Inserting the maintenance services very possibly increases the duration time; hence, the penalization is applied to the duration time.
2.6. Simulated Annealing
- An initial candidate solution: , which is generated randomly.
- A perturbation, , functions to generate candidate solutions in the neighborhood of another.
- A test solution from the perturbation of the initial solution in a neighborhood: .
- The objective function: .
- Number of steps before recalculating the neighborhood: .
- Number of steps before updating the temperatures: .
- The annealing parameter: to reduce the temperature.
- Maximum number of (while) loops without improving the best solution as a stopping criterion.
| Algorithm 1 Simulated Annealing |
Require: ▷ Initial temperature (high initially). ▷ Annealing factor. ▷ Perturbation function. ▷ Objective function. ▷ Converts the problem to minimization. ▷ Iteration counter. ▷ Initial rotation ▷ Initialize best solution ▷ Evaluation ▷ Best OF initialization; while Until the stop criterion is met do for do for do if then end if if ( then else if then end if end for if then end if end for ; Update and end while |
2.7. Perturbation Operators
- Perturbation 1 (PERT-1): Airport substitutionA randomly chosen index denoted by , corresponding to an airport, is selected and replaced by a random airport from those with a connection with the previous airport at position . Then, it is verified that a connection to the subsequent airport, , exists. Finally, a random schedule is selected for the flights, which is straightforward by selecting a non-empty position in the H matrix, corresponding to the rows for the flights. If the new airport, chosen at random, is the same as the existing one or has no additional flights compared to the current, we repeat the random selection process. Table 3 presents an example of this flight perturbation. The selected airport is that in row 3 (); hence, airport 4 is randomly replaced by airport 3. Then, it is verified that such connection flights exist, specifically 2-3 and 3-1, and new schedules are selected for these flights. The changes are in red.
- Perturbation 2 (PERT-2): Schedule substitutionIn this perturbation, a random airport position is selected, and a new random departure time for the flight from the airport at position to the airport in position is selected. In this case, the first and last airports can be selected.In Table 4, two flights are observed where airport 4 is selected randomly and is connected to airport 5; thus, a new schedule of 1535 (15:35) is assigned, and the two resting times are recomputed.
- Perturbation 3 (PERT-3): Multiple flight deletion and one flight additionIn this perturbation, two positions of the airport column are selected at random, with the beginning and end . The airports between and are removed. Then, we search for new airport connections between and and select one of them at random. If it is not possible to find a connection flight, the process is repeated a maximum of 15 times; otherwise, the rotation is returned as is.Table 5 shows an example of the perturbation. The gray positions from 1 to 4 are selected, both positions have airport 1 in the airport column, then airports 2 and 4 are removed, and airport 2 is inserted, generating the connection flights from 1 to 2 and 2 to 1, marked in red in the second table.
- Perturbation 4 (PERT-4): Combination of PERT-3 and PERT-1Perturbations 3 and 1 are combined by applying them sequentially.
- Perturbation PERT-5: Schedule shiftingThis perturbation operates similarly to the schedule substitution method (PERT-2), with the difference that the departure schedule of a randomly selected flight is changed with a probability of 0.2 to the next available schedule and with a probability of 0.8 to the previous one. The schedules are considered cyclic, meaning that the next schedule after the last one is the first in the sequence.Recall that flights are scheduled sequentially within the same day if the departure time allows; otherwise, the flight is assigned to the next day. The main purpose of this perturbation is to increase the number of flights accommodated within the rotation period. Since departure times are sorted in increasing order, shifting a flight to an earlier or later schedule can improve the overall fit within the rotation period. An example of this perturbation is shown in Table 6, where the affected schedule is highlighted in red. The selected flight in row 4 is moved forward from 1200 to 1915. As a result, the rest time between flights is adjusted, as indicated in the last column.
- Perturbation 6 (PERT-6): Random perturbation or addition of two connection airportsThis perturbation consists of a random selection of the previous perturbations and a new drastic perturbation for adding flights. Considering that adding flights leads to large unfeasible rotations, the previous perturbations alleviate these problems selected at random: PERT-3 is applied with a probability of 0.09, PERT-1 with a probability of 0.18, and PERT-2 with a probability of 0.18, PERT-4 with a probability of 0.45, and finally, with probability of 0.1, the addition of two connection airports is applied as follows: a random index, , is randomly selected from the rotation X (i.e., the index of an airport in the sequence representation X). The previous index is denoted as . Then, we search for the set of airports, denoted by , that has a flight originating from . For each airport in , we look for flights from to such that is the origin of a flight that arrives at . Then, the pair of airports (,) is added to an array of possible flight additions. A pair of airports (,) is randomly selected from the array and added to the rotation X after . Hence, this perturbation adds two airports to the rotation in the X representation and 3 flights in the R representation: from to , from to , and from to . The corresponding flight schedules are assigned randomly. This process is repeated until a successful perturbation is achieved or a maximum of 15 attempts is reached.An example of this perturbation is shown in Table 7, where the search path for the two new flights that are added to the rotation R is observed; as can be seen in the final rotation of Table 7, there is an increase from six to eight flights in the new rotation R.This perturbation consists of a random selection from the previously defined perturbations, along with a new, more drastic perturbation aimed at adding flights. Since adding flights can result in large, infeasible rotations, the previous perturbations are used to help mitigate these issues. The selection is made randomly as follows: PERT-3 is applied with a probability of 0.09, PERT-1 with 0.18, PERT-2 with 0.18, PERT-4 with 0.45, and with a probability of 0.10, the new flight-addition perturbation is applied.In this new perturbation, a random index is selected from the rotation X (i.e., the index of an airport in the sequence representation X). The preceding index is denoted as . We then identify the set of airports that have outgoing flights from . For each airport , we look for flights from to another airport such that is the origin of a flight arriving at . Each valid pair of airports is added to an array of possible flight additions.A pair is then randomly selected from this array and inserted into rotation X immediately after . As a result, this perturbation adds two airports to the rotation in the X representation, and three flights replace one in the R representation: from to , from to , and from to . The corresponding flight schedules are assigned randomly. This process is repeated until a successful perturbation is achieved or a maximum of 15 attempts is reached.
2.8. Rotation Repairing
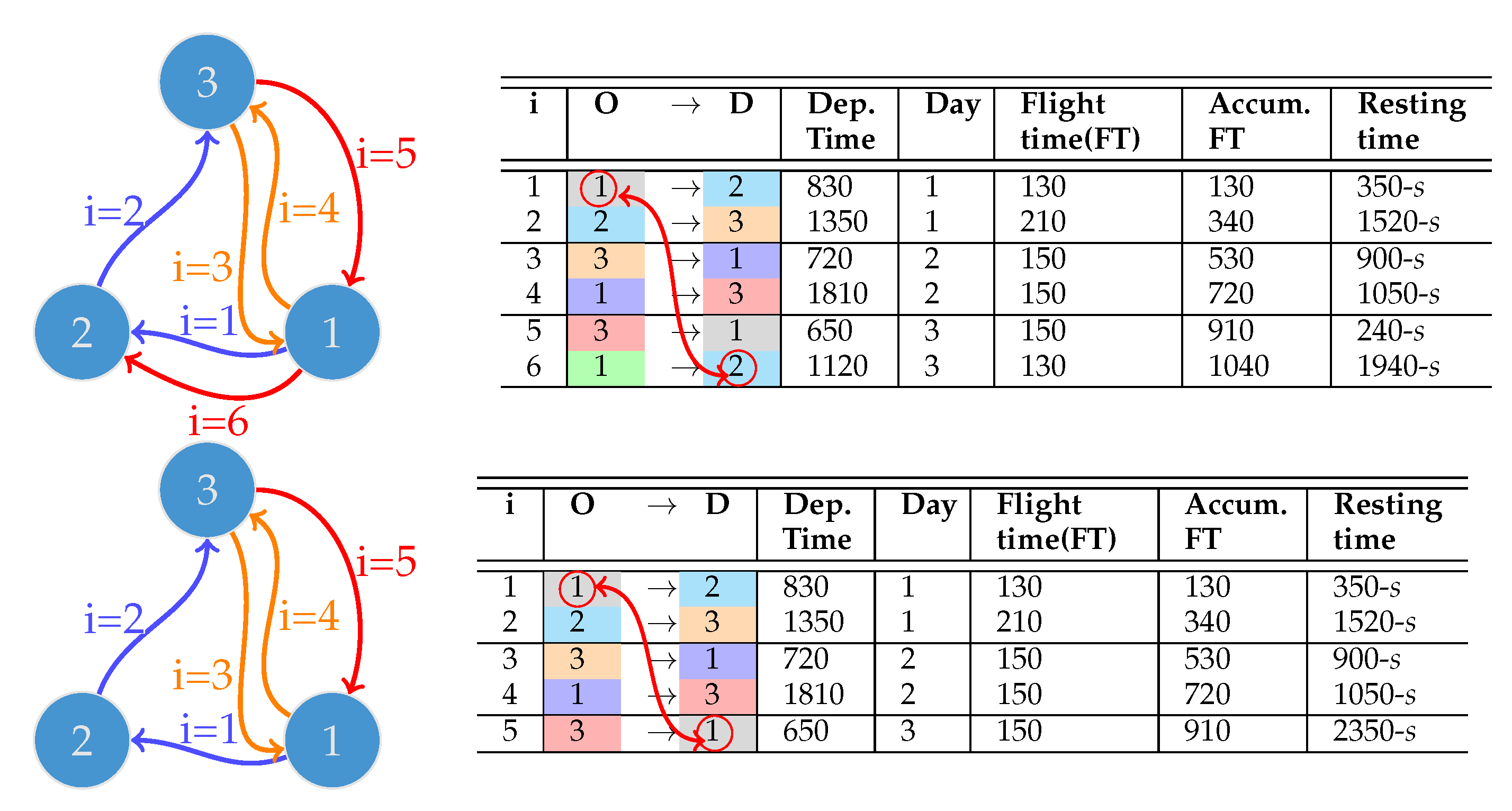
- Remove the last flight. For example, Figure 2 shows a rotation with airport 2 as the last destination and airport 1 as the first origin; hence, there is no closed path. Removing the last flight, in row 6 of the first table, going from airport 1 to 2 alleviates the problem, as noted in row 5 of the second table and in the market with in the graph; the first origin and last destination of the repaired rotation are airport 1.
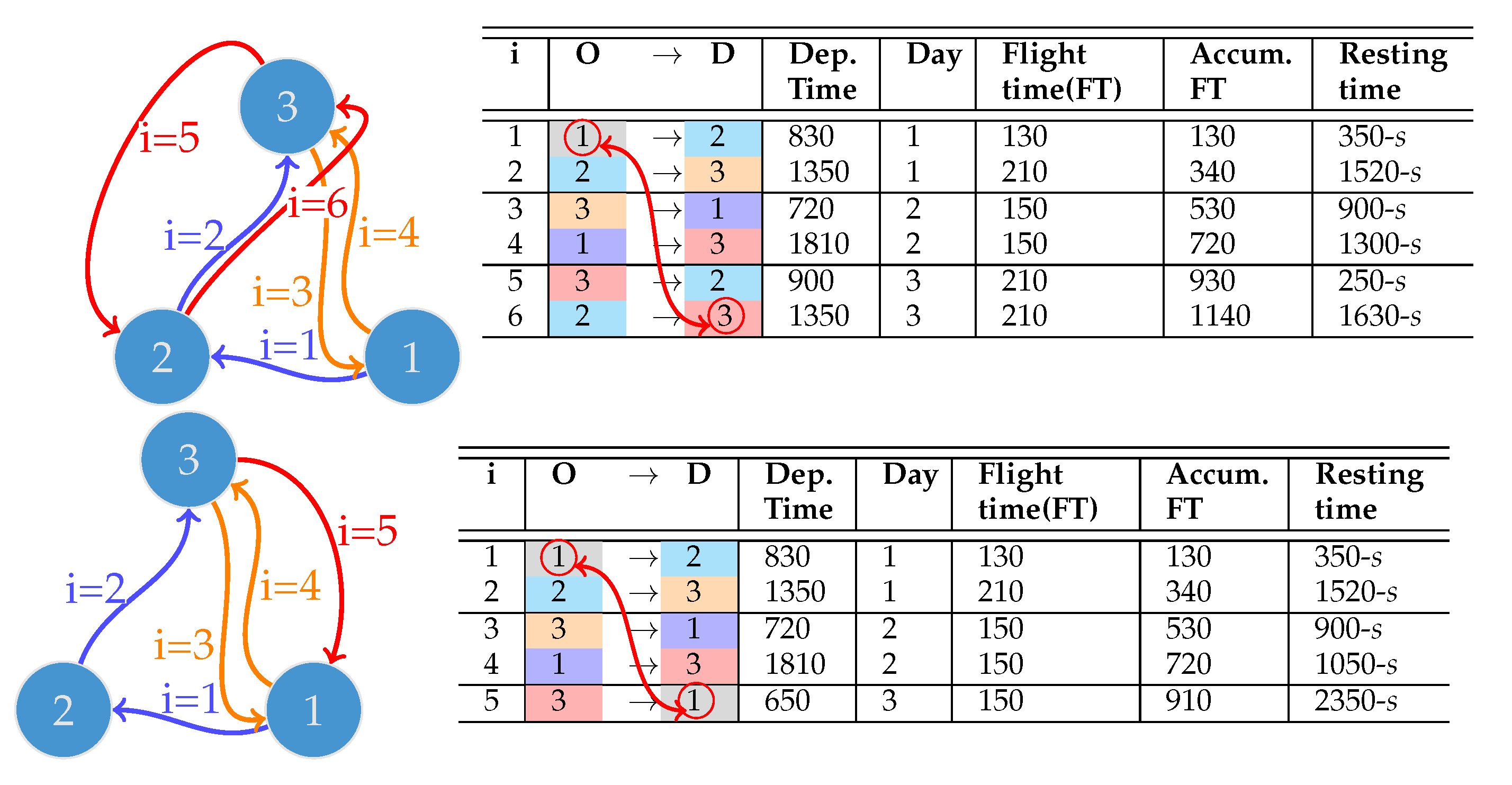
- There are cases that are not repaired by the previous strategy. For example, in Figure 3, in the first table, the flight in row 6 from airport 2 to 3 is removed; nevertheless, the last airport in the modified rotation is 2, so the closed path constraint is not fulfilled. Hence, a second repair step is to look for a flight from the current last origin, that is, airport 3 (since a row has been removed), to the first origin, that is, airport 1. This results in the rotation in the second table and graph, which fulfills the closed path constraint.
- Finally, if neither removing a flight nor looking for connecting flights makes the rotation feasible, the process is repeated.
3. Results
3.1. Study Case 1: Data from Bazargan Book
- Ns: 5
- Nt: 5
- MaxfCount: 5
- rT: 0.95
Results for Study Case 1
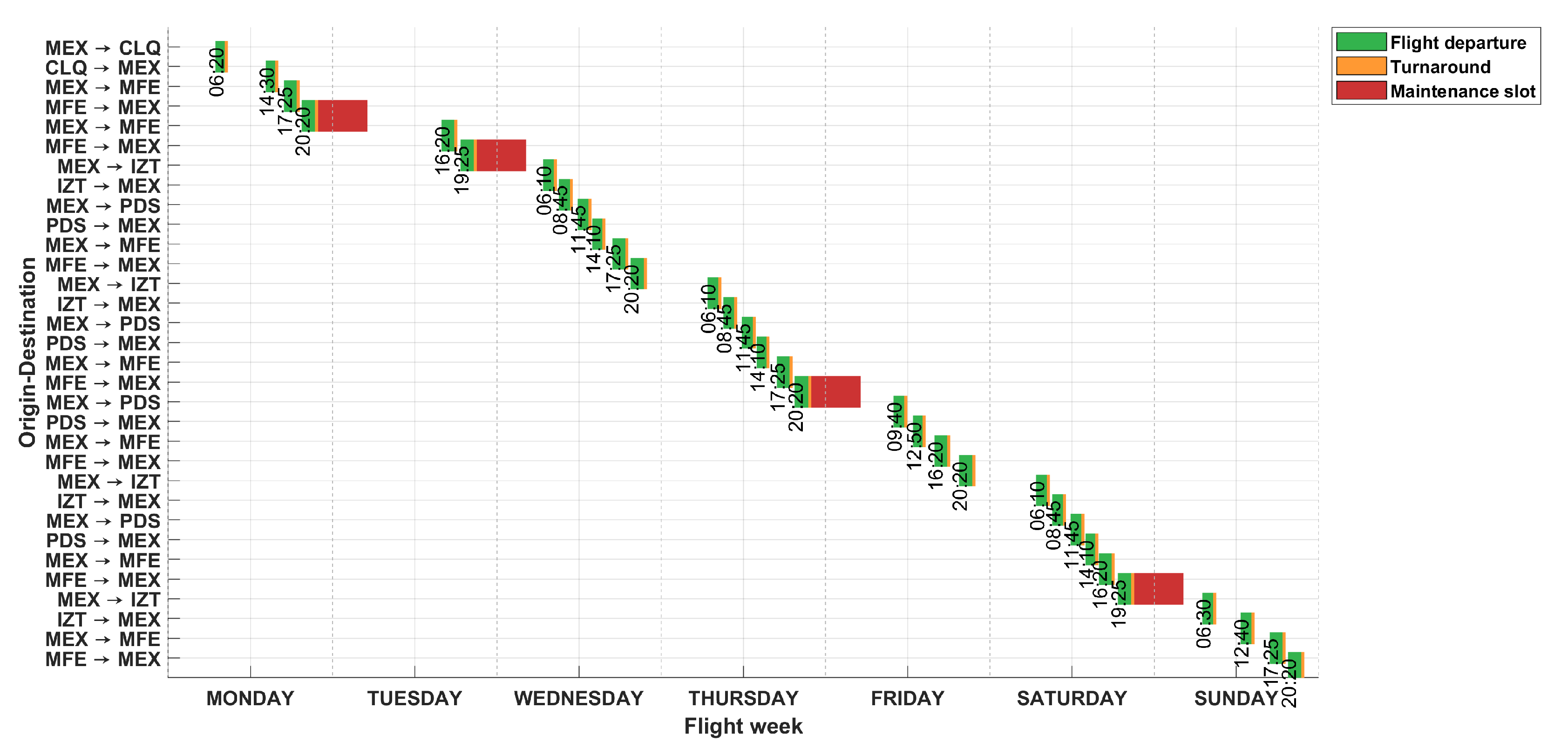
3.2. Study Case 2: Data from a Mexican Airline
- MaxOMin: −1
- Ns: 10
- Nt: 20
- MaxfCount: 50
- rT: 0.95
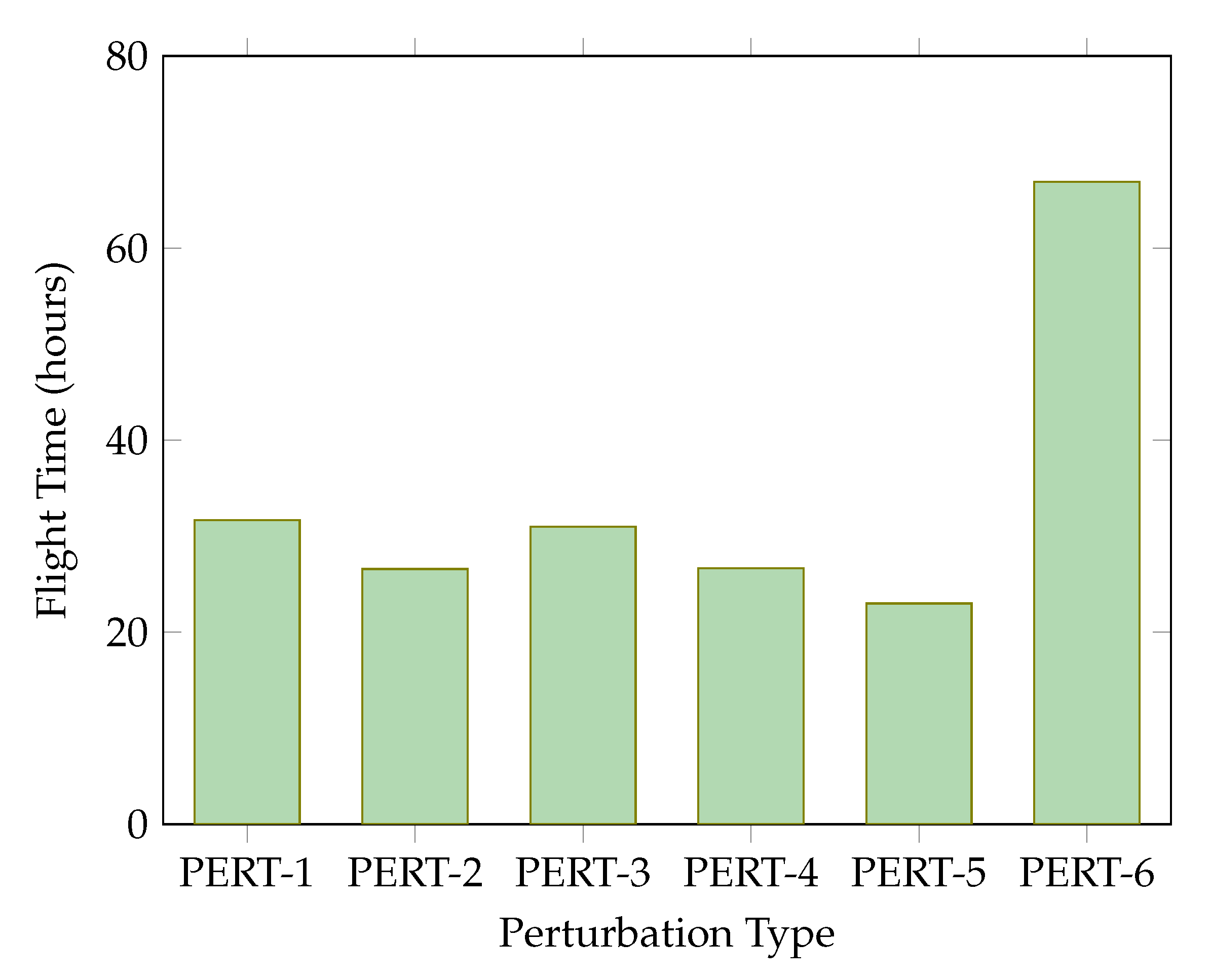
3.2.1. Flight Time Maximization for Study Case 2
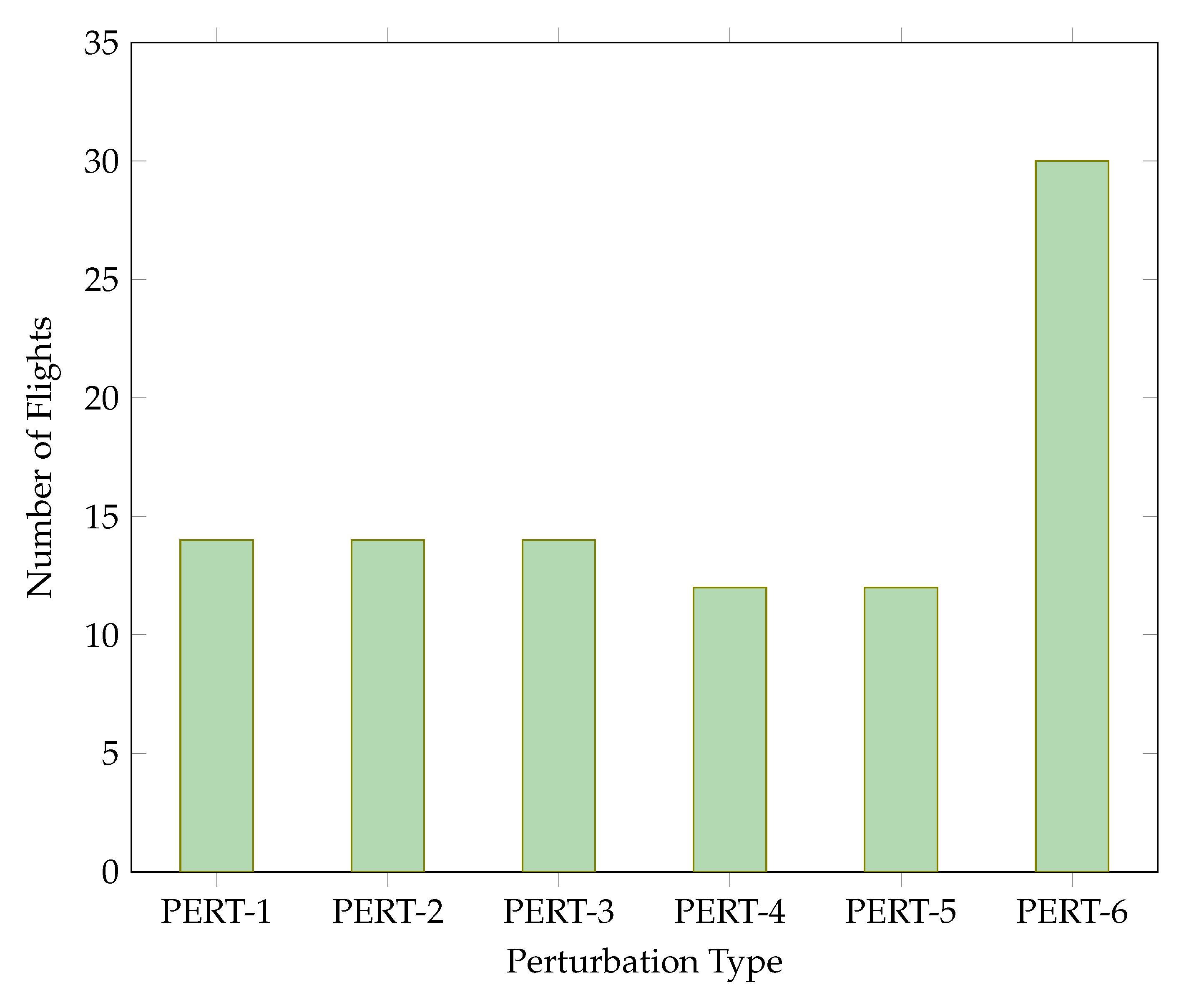
3.2.2. Maximization of the Number of Flights for Study Case 2
3.3. Study Case 3: Maintenance Requirement with Mexican Airline Data
3.3.1. Flight Time Maximization with Two Maintenance Events for Study Case 3
3.3.2. Maximization of the Number of Flights with Two Maintenance Events for Study Case 3
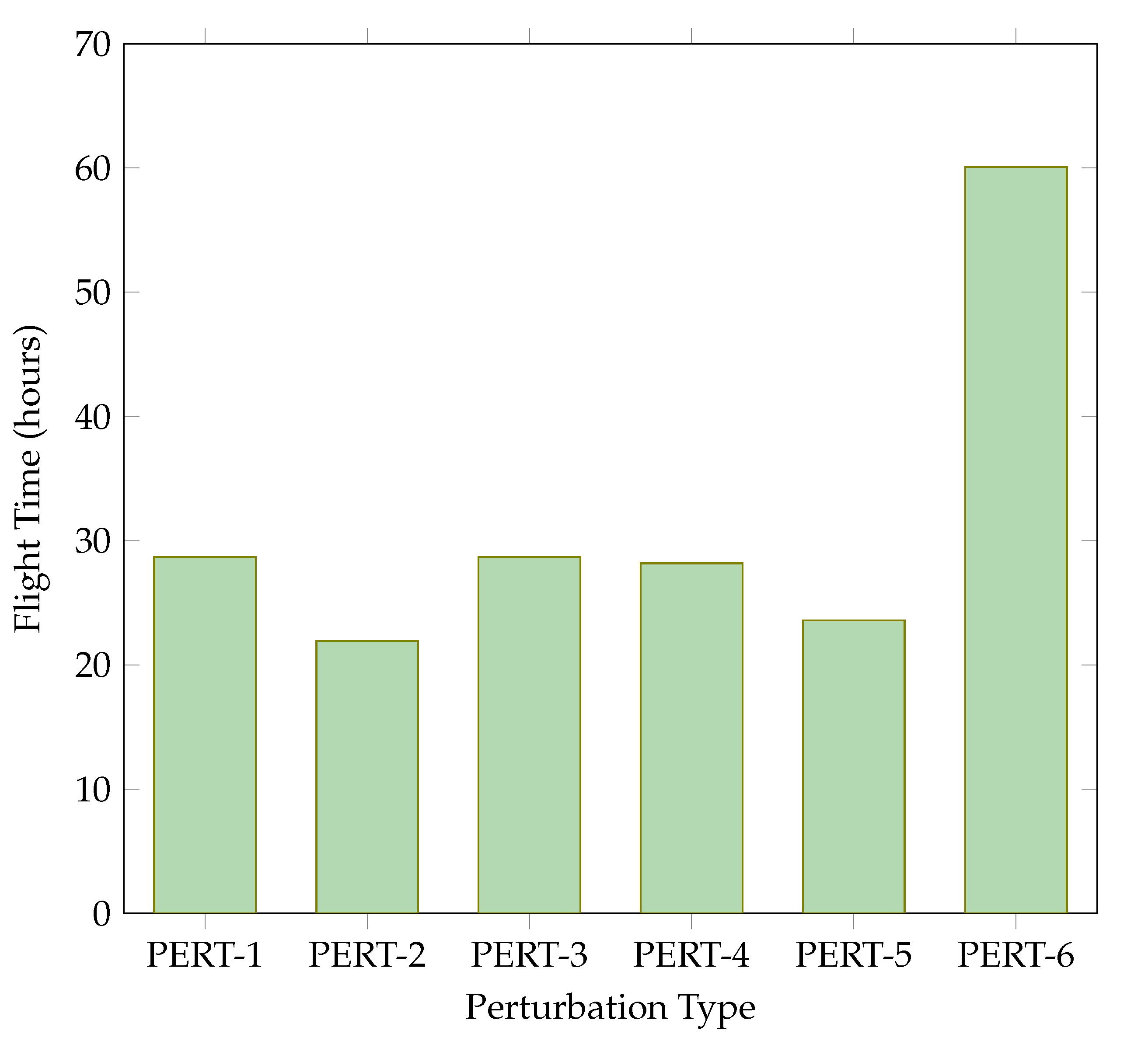
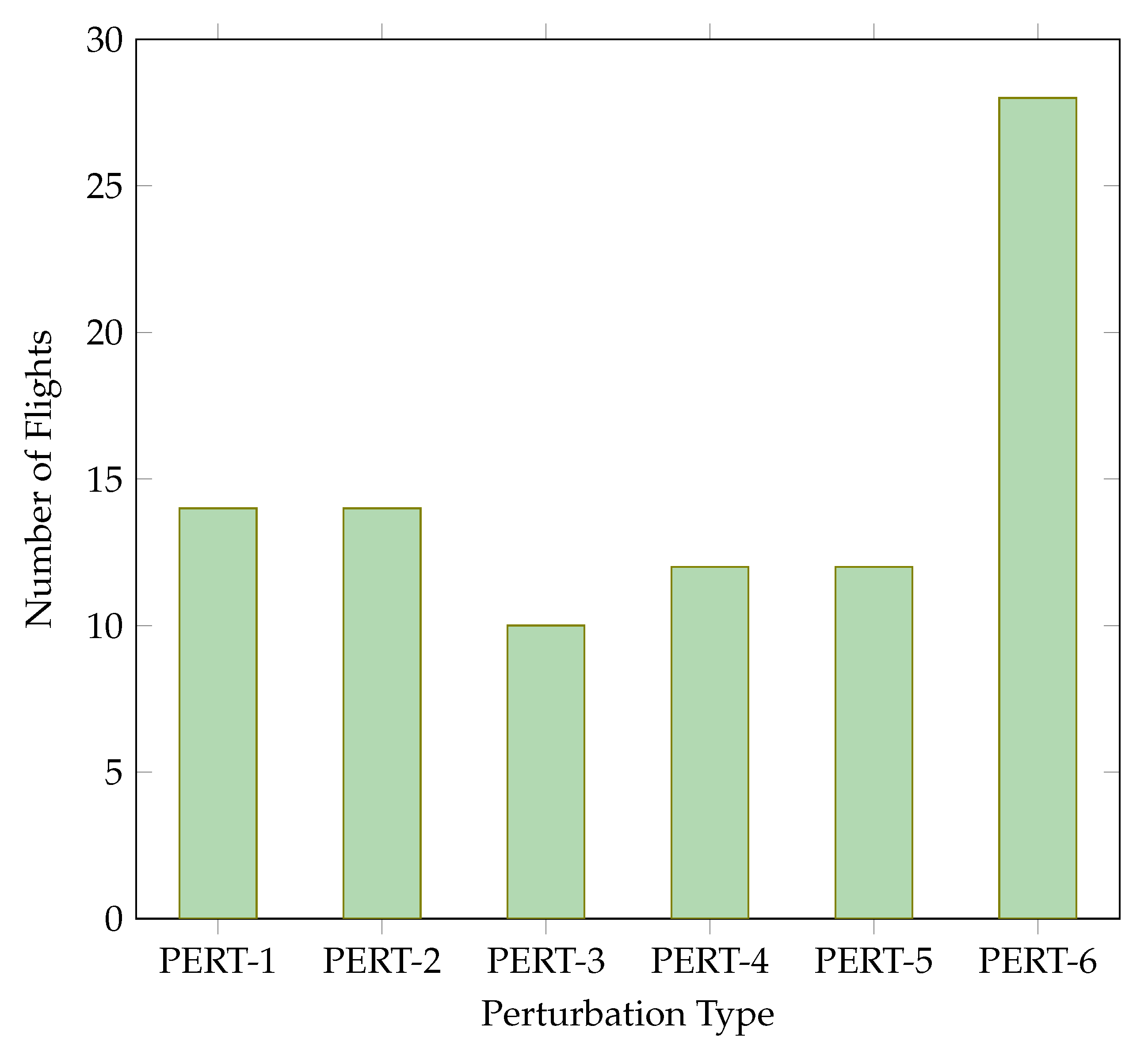
3.4. Summary of Perturbation Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kinnison, H.A.; Siddiqui, T. Aviation Maintenance Management; McGraw-Hill Education: Columbus, OH, USA, 2013. [Google Scholar]
- Barnhart, C.; Boland, N.L.; Clarke, L.W.; Johnson, E.L.; Nemhauser, G.L.; Shenoi, R.G. Flight string models for aircraft fleeting and routing. Transp. Sci. 1998, 32, 208–220. [Google Scholar] [CrossRef]
- Sriram, C.; Haghani, A. An optimization model for aircraft maintenance scheduling and re-assignment. Transp. Res. Part A Policy Pract. 2003, 37, 29–48. [Google Scholar] [CrossRef]
- Sarac, A.; Batta, R.; Rump, C.M. A branch-and-price approach for operational aircraft maintenance routing. Eur. J. Oper. Res. 2006, 175, 1850–1869. [Google Scholar] [CrossRef]
- Liang, Z.; Chaovalitwongse, W.; Huang, H.; Johnson, E. On a New Rotation Tour Network Model for Aircraft Maintenance Routing Problem. Transp. Sci. 2011, 45, 109–120. [Google Scholar] [CrossRef]
- Haouari, M.; Shao, S.; Sherali, H.D. A Lifted Compact Formulation for the Daily Aircraft Maintenance Routing Problem. Transp. Sci. 2013, 47, 508–525. [Google Scholar] [CrossRef]
- Başdere, M.; Bilge, Ü. Operational aircraft maintenance routing problem with remaining time consideration. Eur. J. Oper. Res. 2014, 235, 315–328. [Google Scholar] [CrossRef]
- Al-Thani, N.A.; Ahmed, M.B.; Haouari, M. A model and optimization-based heuristic for the operational aircraft maintenance routing problem. Transp. Res. Part C—Emerg. Technol. 2016, 72, 29–44. [Google Scholar] [CrossRef]
- Eltoukhy, A.; Chan, F.; Chung, S.H.; Niu, B.; Wang, X. Heuristic approaches for operational aircraft maintenance routing problem with maximum flying hours and man-power availability considerations. Ind. Manag. Data Syst. 2017, 117, 2142–2170. [Google Scholar] [CrossRef]
- Safaei, N.; Jardine, A.K. Aircraft routing with generalized maintenance constraints. Omega 2018, 80, 111–122. [Google Scholar] [CrossRef]
- Eltoukhy, A.E.; Chan, F.T.; Chung, S.; Niu, B. A model with a solution algorithm for the operational aircraft maintenance routing problem. Comput. Ind. Eng. 2018, 120, 346–359. [Google Scholar] [CrossRef]
- Sanchez, D.T.; Boyacı, B.; Zografos, K.G. An optimisation framework for airline fleet maintenance scheduling with tail assignment considerations. Transp. Res. Part B Methodol. 2020, 133, 142–164. [Google Scholar] [CrossRef]
- Ruan, J.; Wang, Z.; Chan, F.T.; Patnaik, S.; Tiwari, M. A reinforcement learning-based algorithm for the aircraft maintenance routing problem. Expert Syst. Appl. 2021, 169, 114399. [Google Scholar] [CrossRef]
- Bulbul, K.G.; Kasimbeyli, R. Augmented Lagrangian based hybrid subgradient method for solving aircraft maintenance routing problem. Comput. Oper. Res. 2021, 132, 105294. [Google Scholar] [CrossRef]
- Zhang, Q.; Chan, F.T.; Chung, S.H.; Fu, X. A matheuristic for aircraft maintenance routing problem incorporating cruise speed control. Expert Syst. Appl. 2024, 242, 122711. [Google Scholar] [CrossRef]
- Saltzman, R.M.; Stern, H.I. The multi-day aircraft maintenance routing problem. J. Air Transp. Manag. 2022, 102, 102224. [Google Scholar] [CrossRef]
- Alpos, T.; Iliopoulou, C.; Kepaptsoglou, K. Nature-Inspired Optimal Route Network Design for Shared Autonomous Vehicles. Vehicles 2023, 5, 24–40. [Google Scholar] [CrossRef]
- Zacharia, P.; Stavrinidis, S. The Vehicle Routing Problem with Simultaneous Pick-Up and Delivery under Fuzziness Considering Fuel Consumption. Vehicles 2024, 6, 231–241. [Google Scholar] [CrossRef]
- Kouretas, K.; Kepaptsoglou, K. Planning Integrated Unmanned Aerial Vehicle and Conventional Vehicle Delivery Operations under Restricted Airspace: A Mixed Nested Genetic Algorithm and Geographic Information System-Assisted Optimization Approach. Vehicles 2023, 5, 1060–1086. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, W.; Yu, D.Z.; Liu, S.; Zhang, Y. Multi-Depot Electric Vehicle–Drone Collaborative-Delivery Routing Optimization with Time-Varying Vehicle Travel Time. Vehicles 2024, 6, 1812–1842. [Google Scholar] [CrossRef]
- Moradi, N.; Wang, C.; Mafakheri, F. Urban Air Mobility for Last-Mile Transportation: A Review. Vehicles 2024, 6, 1383–1414. [Google Scholar] [CrossRef]
- Voigt, S. A review and ranking of operators in adaptive large neighborhood search for vehicle routing problems. Eur. J. Oper. Res. 2025, 322, 357–375. [Google Scholar] [CrossRef]
- Benjelloun, R.; Tarik, M.; Jebari, K. Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem. Information 2025, 16, 675. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, Y.; Gajpal, Y.; Chen, X. A Memetic Algorithm for the Green Vehicle Routing Problem. Sustainability 2019, 11, 6055. [Google Scholar] [CrossRef]
- Rezvanian, S.; Husseinzadeh Kashan, A.; Rezvanian, A.; Sabzevari, A. Intelligent vehicle routing for stochastic service times: A grouping evolution strategy approach. Int. J. Transp. Sci. Technol. 2025. in press. [CrossRef]
- Liu, X.; Chen, Y.L.; Por, L.Y.; Ku, C.S. A Systematic Literature Review of Vehicle Routing Problems with Time Windows. Sustainability 2023, 15, 12004. [Google Scholar] [CrossRef]
- Gopalan, R.; Talluri, K.T. The aircraft maintenance routing problem. Oper. Res. 1998, 46, 260–271. [Google Scholar] [CrossRef]
- Peres, F.; Castelli, M. Combinatorial optimization problems and metaheuristics: Review, challenges, design, and development. Appl. Sci. 2021, 11, 6449. [Google Scholar] [CrossRef]
- Sánchez, M.; Cruz-Duarte, J.M.; carlos Ortíz-Bayliss, J.; Ceballos, H.; Terashima-Marin, H.; Amaya, I. A systematic review of hyper-heuristics on combinatorial optimization problems. IEEE Access 2020, 8, 128068–128095. [Google Scholar] [CrossRef]
- Cruz-Rosales, M.H.; Cruz-Chávez, M.A.; Alonso-Pecina, F.; Peralta-Abarca, J.d.C.; Ávila-Melgar, E.Y.; Martínez-Bahena, B.; Enríquez-Urbano, J. Metaheuristic with cooperative processes for the university course timetabling problem. Appl. Sci. 2022, 12, 542. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Díaz-Molina, A.I.; Valdez, S.I.; Hernández, E.E. Code for the Article: Flight Routing Optimization with Maintenance Constraints. 2025. Available online: https://github.com/EEHMatNMSU/Flight-Routing-Optimization-with-Maintenance-Constraints.git (accessed on 10 August 2025).
- Bazargan, M. Airline Operations and Scheduling, 2nd ed.; Ashgate Publishing Company: London, UK, 2010. [Google Scholar]
- Airportinfo.live. Aeromar Estado de Vuelos, n.d. Available online: https://airportinfo.live/es/estado-de-vuelos-aeromar (accessed on 10 January 2023).

| Before PERT-1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | O | → | D | Dep. Time | Day | Flight Time (FT) | Accum. FT | Resting Time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 100-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 640 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| After PERT-1 | ||||||||
| i | O | → | D | Dep. Time | Day | Flight time (FT) | Accum. FT | Resting time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 3 | 1405 | 1 | 150 | 320 | 1605-s |
| 3 | 3 | → | 1 | 800 | 2 | 130 | 450 | 230-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 620 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 810 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 940 | 1700-s |
| Before PERT-2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | O | → | D | Dep. Time | Day | Flight Time (FT) | Accum. FT | Resting Time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 100-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 640 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| After PERT-2 | ||||||||
| i | O | → | D | Dep. Time | Day | Flight time (FT) | Accum. FT | Resting time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 435-s |
| 4 | 1 | → | 3 | 1535 | 2 | 130 | 640 | 1355-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 43-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| Before PERT-3 | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | O | → | D | Dep. Time | Day | Flight Time (FT) | Accum. FT | Resting Time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 100-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 640 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| After PERT-3 | ||||||||
| i | O | → | D | Dep. Time | Day | Flight time (FT) | Accum. FT | Resting time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 1 | 1320 | 1 | 130 | 300 | 2355-s |
| 3 | 1 | → | 3 | 1445 | 2 | 130 | 430 | 1635-s |
| 4 | 3 | → | 2 | 850 | 3 | 150 | 620 | 240-s |
| 5 | 2 | → | 1 | 1320 | 3 | 130 | 750 | 1700-s |
| Before PERT-5 | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | O | → | D | Dep. Time | Day | Flight Time (FT) | Accum. FT | Resting Time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 100-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 640 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| After PERT-5 | ||||||||
| i | O | → | D | Dep. Time | Day | Flight time (FT) | Accum. FT | Resting time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 815-s |
| 4 | 1 | → | 3 | 1915 | 2 | 130 | 640 | 1015-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| Before PERT-6 | ||||||||
|---|---|---|---|---|---|---|---|---|
| i | O | → | D | Dep. Time | Day | Flight Time (FT) | Accum. FT | Resting Time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 800-s |
| 2 | 2 | → | 4 | 1720 | 1 | 210 | 340 | 1400-s |
| 3 | 4 | → | 1 | 930 | 2 | 130 | 510 | 100-s |
| 4 | 1 | → | 3 | 1200 | 2 | 130 | 640 | 1730-s |
| 5 | 3 | → | 2 | 700 | 3 | 150 | 830 | 430-s |
| 6 | 2 | → | 1 | 1320 | 3 | 130 | 1000 | 1700-s |
| After PERT-6 | ||||||||
| i | O | → | D | Dep. Time | Day | Flight time (FT) | Accum. FT | Resting time |
| 1 | 1 | → | 2 | 750 | 1 | 130 | 130 | 100-s |
| 2 | 2 | → | 4 | 1020 | 1 | 210 | 340 | 620-s |
| 3 | 4 | → | 3 | 1850 | 1 | 150 | 530 | 910-s |
| 4 | 3 | → | 4 | 550 | 2 | 150 | 720 | 150-s |
| 5 | 4 | → | 1 | 930 | 2 | 130 | 850 | 100-s |
| 6 | 1 | → | 3 | 1200 | 2 | 130 | 1020 | 1730-s |
| 7 | 3 | → | 2 | 700 | 3 | 150 | 1210 | 430-s |
| 8 | 2 | → | 1 | 1320 | 3 | 130 | 1340 | 1700-s |
| Origin | Destination | Dep. Time 1 | Dep. Time 2 | Dep. Time 3 | Dep. Time 4 | Flight Time (FT) |
|---|---|---|---|---|---|---|
| LAX | JFK | 05:00 | 09:45 | 14:20 | 21:10 | 5 h 30 min |
| SFO | JFK | 05:05 | 15:25 | 21:50 | NA | 3 h 30 min |
| BOS | JFK | 06:15 | 10:00 | NA | NA | 1 h 30 min |
| JFK | IAD | 06:20 | 12:00 | 16:15 | 18:40 | 1 h 00 min |
| ORD | JFK | 07:30 | 12:20 | 17:10 | 19:00 | 2 h 00 min |
| JFK | LAX | 07:35 | 13:00 | 15:30 | 18:25 | 5 h 30 min |
| JFK | BOS | 07:40 | 21:30 | NA | NA | 1 h 30 min |
| IAD | JFK | 08:15 | 14:25 | 18:30 | 20:30 | 1 h 00 min |
| JFK | ORD | 10:05 | 13:25 | 16:00 | 21:00 | 2 h 00 min |
| JFK | SFO | 15:30 | 22:00 | NA | NA | 3 h 30 min |
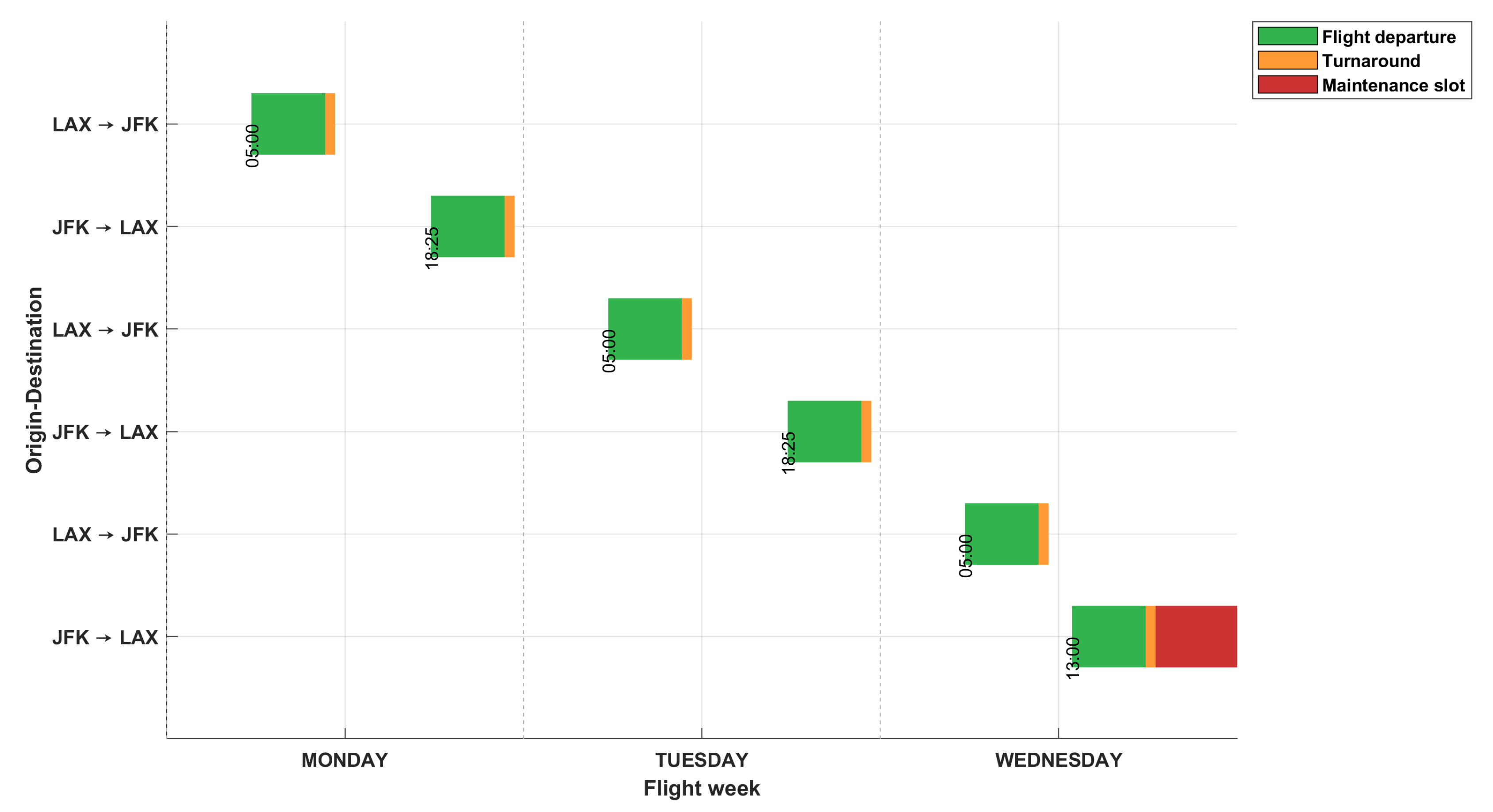
| Flight | Origin | Destination | Dep. Time | Day |
|---|---|---|---|---|
| 1 | LAX | JFK | 05:00 | 1 |
| 2 | JFK | LAX | 18:25 | 1 |
| 3 | LAX | JFK | 05:00 | 2 |
| 4 | JFK | LAX | 18:25 | 2 |
| 5 | LAX | JFK | 05:00 | 3 |
| 6 | JFK | LAX | 13:00 | 3 |
| City | IATA Code | |
|---|---|---|
| 1 | Ciudad de México | MEX |
| 2 | Ciudad Victoria | CVM |
| 3 | Colima | CLQ |
| 4 | Tepic | TPQ |
| 5 | Piedras Negras | PDS |
| 6 | Guadalajara | GDL |
| 7 | Puerto Vallarta | PVR |
| 8 | Aguascalientes | AGU |
| 9 | Ixtepec | IZT |
| 10 | McAllen-Miller | MFE |
| 11 | Villahermosa | VSA |
| 12 | Cancún | CUN |
| 13 | Habana | HAV |
| 14 | Zihuatanejo | ZIH |
| 15 | Managua | MGA |
| 16 | Acapulco | ACA |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Mean | 20:05:20 | 18:02:00 | 16:27:40 | 18:11:00 | 14:28:20 | 58:41:20 |
| Median | 17:10:00 | 17:55:00 | 19:30:00 | 20:00:00 | 15:25:00 | 58:35:00 |
| Max. | 31:40:00 | 26:35:00 | 31:00:00 | 26:40:00 | 23:00:00 | 66:55:00 |
| Min. | 2:30:00 | 9:50:00 | 4:00:00 | 2:40:00 | 3:00:00 | 51:10:00 |
| Std dev | 7:36:52 | 5:15:15 | 8:20:01 | 7:06:59 | 6:06:01 | 4:21:22 |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Media | 9.2 | 9.8 | 9.0 | 8.4 | 9.0 | 24.0 |
| Mean | 10 | 10 | 10 | 8 | 10 | 26 |
| Max. | 14 | 14 | 14 | 12 | 12 | 30 |
| Min. | 4 | 2 | 4 | 2 | 2 | 2 |
| Std dev | 2.8 | 3.1 | 3.1 | 2.9 | 2.8 | 9.1 |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Mean | 23:05:00 | 16:13:30 | 18:06:32 | 18:57:40 | 17:51:55 | 54:30:00 |
| Median | 23:25:00 | 16:50:00 | 17:40:00 | 19:45:00 | 17:00:00 | 54:35:00 |
| Max. | 28:40:00 | 21:55:00 | 28:40:00 | 28:10:00 | 23:35:00 | 60:05:00 |
| Min. | 15:50:00 | 6:40:00 | 6:55:00 | 6:55:00 | 11:40:00 | 48:30:00 |
| Std dev | 4:05:00 | 4:10:38 | 6:05:18 | 6:01:14 | 4:25:11 | 3:58:08 |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Mean | 11.0 | 9.6 | 8.4 | 8.2 | 10.5 | 22.8 |
| Median | 10.0 | 10.0 | 9.0 | 8.0 | 10.0 | 23.0 |
| Max. | 14.0 | 14.0 | 10.0 | 12.0 | 12.0 | 28.0 |
| Min. | 6.0 | 4.0 | 6.0 | 4.0 | 8.0 | 20.0 |
| Std dev | 2.1 | 2.6 | 1.8 | 2.6 | 1.2 | 2.4 |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Mean | 2.6 | 3.5 | 2.7 | 2.9 | 4.3 | 4.6 |
| Median | 2.0 | 3.5 | 2.0 | 2.0 | 4.0 | 4.0 |
| Max. | 6.0 | 5.0 | 5.0 | 7.0 | 6.0 | 7.0 |
| Min. | 1.0 | 2.0 | 2.0 | 2.0 | 2.0 | 3.0 |
| Std dev | 1.5 | 1.0 | 1.0 | 1.4 | 1.1 | 1.4 |
| PERT-1 | PERT-2 | PERT-3 | PERT-4 | PERT-5 | PERT-6 | |
|---|---|---|---|---|---|---|
| Media | 3.5 | 3.6 | 2.8 | 2.9 | 4.8 | 3.7 |
| Mean | 4.0 | 4.0 | 2.0 | 3.0 | 5.0 | 4.0 |
| Max. | 5.0 | 5.0 | 5.0 | 6.0 | 7.0 | 5.0 |
| Min. | 2.0 | 2.0 | 0.0 | 2.0 | 2.0 | 2.0 |
| Std dev | 0.9 | 1.1 | 1.6 | 1.0 | 1.3 | 1.1 |
| Flight Time Obj. Function | Number of Flights Obj. Function | |
|---|---|---|
| Study case 2 | 5:45 | 4:22 |
| Study case 3 | 4:18 | 4:29 |
| Obj | PERT6 > PERT1 | PERT6 > PERT2 | PERT6 > PERT3 | PERT6 > PERT4 | PERT6 > PERT5 |
|---|---|---|---|---|---|
| t no-mtto | 3.885484 × 10−6 | 3.059264 × 10−7 | 3.930226 × 10−6 | 1.678999 × 10−6 | 1.687437 × 10−6 |
| t mtto | 1.674793 × 10−6 | 6.446725 × 10−9 | 6.446725 × 10−9 | 1.687437 × 10−6 | 6.446725 × 10−9 |
| nf no-mtto | 3.066352 × 10−4 | 2.517797 × 10−4 | 3.005682 × 10−4 | 2.128853 × 10−4 | 2.484540 × 10−4 |
| nf mtto | 2.796612 × 10−6 | 4.674529 × 10−6 | 1.872081 × 10−5 | 2.026176 × 10−6 | 6.208650 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Molina, A.I.; Valdez, S.I.; Hernández, E.E. Flight Routing Optimization with Maintenance Constraints. Vehicles 2025, 7, 120. https://doi.org/10.3390/vehicles7040120
Díaz-Molina AI, Valdez SI, Hernández EE. Flight Routing Optimization with Maintenance Constraints. Vehicles. 2025; 7(4):120. https://doi.org/10.3390/vehicles7040120
Chicago/Turabian StyleDíaz-Molina, Anny Isabella, Sergio Ivvan Valdez, and Eusebio E. Hernández. 2025. "Flight Routing Optimization with Maintenance Constraints" Vehicles 7, no. 4: 120. https://doi.org/10.3390/vehicles7040120
APA StyleDíaz-Molina, A. I., Valdez, S. I., & Hernández, E. E. (2025). Flight Routing Optimization with Maintenance Constraints. Vehicles, 7(4), 120. https://doi.org/10.3390/vehicles7040120







