Optimized GOMP-Based OTFS Channel Estimation Algorithm for V2X Communications

Abstract

Vehicle-to-everything (V2X) communication, a current key area of research, has a large impact on traffic safety, traffic efficiency, autonomous driving technology development, and intelligent transport. In order to achieve the low-latency performance and high transmission efficiency required for V2X communication, channel estimation for transmission channels is particularly important. In this regard, this paper proposes an improved general orthogonal match pursuit (GOMP) channel estimation algorithm based on the base extension model for an orthogonal time frequency space (OTFS) system. Firstly, the channel matrix is decomposed using the basis expansion model. Then, the strong sparsity of the basis function is exploited for channel estimation using the GOMP algorithm, while the ordinal difference restriction method and the weak selectivity principle are introduced to improve the system. The obtained improved GOMP algorithm not only shows a greater improvement in terms of normalized mean square error (NMSE) and bit error rate (BER) performance but also greatly reduces computational complexity, enabling it to better satisfy the needs of V2X communication.

1. Introduction

With the development of information and communication technology (ICT), the enhancement of people’s judgment of the environment around a vehicle through vehicle-to-vehicle and vehicle-to-infrastructure communication—as well as the provision of drivers with timely warnings when road hazards are detected, enabling them to avoid traffic collisions, which is referred to as vehicle-to-everything (V2X) telematics [1]—has become a hot research topic for domestic and foreign research institutes and enterprises. The core objective is to achieve a seamless connection between vehicles and the environment through multi-modal communication so as to improve traffic safety, optimize traffic flow, and provide basic support for autonomous driving and intelligent transportation systems [2]. Therefore, low latency and high transmission reliability are particularly critical in V2X networking [3].

In recent years, with the proposal of orthogonal time–frequency space (OTFS) technology, the transmission stability problem and the high-delay problem of Orthogonal Frequency-Division Multiplexing (OFDM) technology under high-speed movement have been satisfactorily solved, meeting the demands of V2X telematics [4,5,6,7,8,9,10]. However, in OTFS systems, in order to know the channel-state information in advance under a double-selective channel with high-speed movement, it is necessary to introduce channel estimation by means of pilots so as to select the appropriate parameters and modulation methods that make it possible to maximize transmission performance. For early OTFS channel estimation algorithms, the authors of [11] proposed an OTFS-embedded pilot channel estimation method based on the threshold method, and the authors of [12] proposed a data-assisted OTFS-superimposed guided-frequency channel estimation method. Later on, researchers started applying compressed sensing algorithms to OTFS channel estimation to further improve its performance. For example, a generalized orthogonal matching tracking method, based on sense-assisted and atomic selection thresholds, was proposed in [13]. This approach optimizes the generalized, compressed orthogonal matching tracking perception algorithm by introducing sense-assisted and atomic selection thresholds. Additionally, a Sparse Bayesian Learning (SBL) turbo compressed perception channel estimation algorithm for joint wireless channels with sparse characteristics in the delay-Doppler (DD) domain was proposed in [14]. This was based on the structure of a turbo compressed sensing algorithm combined with a sparse Bayesian channel estimation algorithm for optimization, which improves the channel estimation performance. The authors of [15] propose a compressed sample-matched, tracking-based OTFS superposition guide channel estimation algorithm, which combines the advantages of superposition guide frequency and optimizes the compressed sample-matched tracking channel estimation algorithm to further improve the performance. The authors of [16] proposed an orthogonal matching pursuit algorithm based on phase rotation optimization, which improves the performance of the orthogonal matching pursuit channel estimation algorithm by performing phase rotation processing on the input signal.

However, the above-mentioned algorithms retain certain deficiencies and are not fully applicable in the field of V2X communications. For example, most of these algorithms demand considerable computational complexity, require long computation times, and thus generate greater latency, which cannot meet the low-latency requirements of V2X communications. At the same time, most of the algorithms fail to maintain high channel estimation accuracy in double-selective high-speed movement, which affects any subsequent channel equalization and link adaptation.

Therefore, based on the above algorithms, this paper combines a base extension model with the GOMP algorithm and introduces a method to limit serial number differences and the principle of weak selectivity in order to further optimize the GOMP algorithm and improve its ability to perform channel estimation. Our experimental results show that the BEM-iGOMP algorithm proposed in this paper, compared with other commonly used compressed sensing algorithms, exhibits considerable improvements in the normalized mean square error (NMSE) and the bit error rate (BER) obtained using the MMSE signal detection algorithm. Also, the computational complexity is lower than that of the BEM-iGOMP algorithm, indicating that it can suitably satisfy the needs of V2X communication.

This paper is organized as follows: Section 2 introduces the system model, including the OTFS system, the pilot insertion, the signal detector, etc. Section 3 introduces the structure and basic principles of the BEM-iGOMP algorithm proposed in this paper. Section 4 introduces the performance results for the algorithm proposed in this paper as obtained by simulation. Section 5 concludes this paper and provides an outlook on future research.

2. System Model

2.1. V2X OTFS System Model

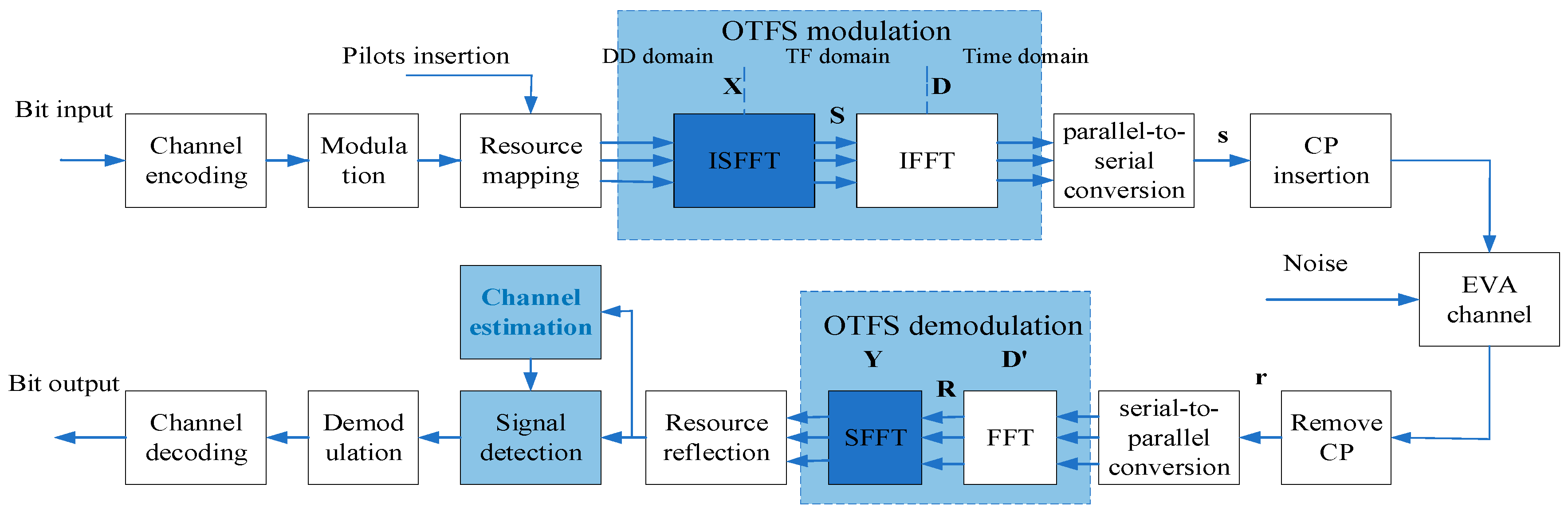
The block diagram of the transmission principle for the V2X-oriented OTFS communication system is shown in Figure 1.

It should be assumed that the total duration of a packet, with the number of symbols $N$ and the number of subcarriers $M$, is $NT$, and the total bandwidth is $M\mathsf{\Delta }f$, where $T$ is the symbol of the time interval, and $\mathsf{\Delta }f$ is the subcarrier frequency interval. The signal is sampled on the DD domain in steps of ${\displaystyle \frac{1}{NT }}$ on the Doppler axis and in steps of ${\displaystyle \frac{1}{M∆f }}$ on the time delay axis, and the resulting discrete sampled grid $L_D$ on the DD domain is

$$L_{\mathrm{D}}=\left\{\left({\displaystyle \frac{k}{NT}},{\displaystyle \frac{l}{M\Delta f}}\right) ,k=0,1,\dots ,N-1,l=0,1,\dots ,M-1\right\}$$

(1)

Therefore, the magnitudes of ${\displaystyle \frac{1}{M∆f}}$ and ${\displaystyle \frac{1}{NT}}$ also determine the resolution of the OTFS, with larger $M$ and $N$ resulting in a more accurate characterization of the channel in the delay-Doppler domain. The signal on the DD domain is then transformed to the TF domain by Inverse Symplectic Finite Fourier Transform (ISFFT) to obtain $X[n,m]$, which can be roughly expressed as

$$X[n,m]={\displaystyle \frac{1}{MN}}{\displaystyle \sum _{k=0}^{N-1}{\displaystyle \sum _{l=0}^{M-1}x}}[k,l]e^{j2\pi \left({\displaystyle \frac{nk}{N}}-{\displaystyle \frac{ml}{M}}\right)}$$

(2)

The signal in the TF domain is then mapped onto the entire time axis by the Heisenberg transform to obtain the signal $s\left(t\right)$ in the time domain, which is emitted and can be roughly represented as

$$s(t)={\displaystyle \sum _{n=0}^{N-1}{\displaystyle \sum _{m=0}^{M-1}X}}[n,m]g_t\left(t-n{T}_{\mathrm{d}}\right)e^{j2\pi m\Delta f_{\mathrm{d}}\left(t-n{T}_{\mathrm{d}}\right)}$$

(3)

where $g_t\left(t\right)$ is the shaped filter function. When $g_t\left(\mathrm{t}\right)$ is an ideal rectangular window function, the Heisenberg transform can then be viewed as a traditional Inverse Discrete Fourier Transform (IDFT). After passing through the EVA channel, it is received by the receiver, and, assuming that the received signal is $r\left(t\right)$, it can be roughly expressed as

$$r(t)={\displaystyle \iint h}(\tau ,v)s(t-\tau )e^{j2\pi v(t-\tau )}d\tau dv+w(t)$$

(4)

The received signal samples in the time domain are then split into the time–frequency domain by the Wegener transform, which can be roughly expressed as

$$Y[n,m]={\displaystyle \int r}(t)g_r^{*}\left(t-n{T}_d\right)e^{-j2\pi m\Delta f_d\left(t-n{T}_d\right)}dt$$

(5)

where $g_r^{*}\left(t\right)$ denotes the matched filter function at the receiver.$g_r^{*}\left(t\right)$ is the ideal moment window function when the Wigner transform degenerates to the conventional discrete Fourier transform. It is then transformed to the DD domain by the Symplectic Finite Fourier Transform (SFFT) to obtain the final signal $y[k,l]$, which can roughly be expressed as

$$y[k,l]={\displaystyle \frac{1}{MN}}{\displaystyle \sum _{k=0}^{N-1}{\displaystyle \sum _{l=0}^{M-1}Y}}[n,m]e^{j2\pi \left({\displaystyle \frac{nk}{N}}+{\displaystyle \frac{ml}{M}}\right)}$$

(6)

Finally, the obtained $y[k,l]$ is subjected to channel estimation and signal detection to restore the initial signal and to complete the evaluation and analysis of the system’s performance. Meanwhile, it is assumed that the OTFS system passes through the channel as a linear time-varying channel, and its input–output relationship can be roughly viewed in the DD domain as

$$\begin{array}{cc}y[k,l]\hfill & ={\displaystyle \sum _{i=1}^p{h}_i}x\left[{\left[k-k_{vi}\right]}_{\mathrm{N}},{\left[l-l_{vi}\right]}_{\mathrm{M}}\right]\hfill \\ & =h[k,l]\ast x[k,l]\hfill \end{array}$$

(7)

Also, taking into account the effect of fractional Doppler, the input–output relationship in the modified DD domain can be expressed as follows:

$$y[k,l]\approx {\displaystyle \sum _{i=1}^p{\displaystyle \sum _{q=-Q}^Q{h}_{i}x\left[{\left[k-k_{vi}+q\right]}_{\mathrm{N}},{\left[l-l_{vi}\right]}_{\mathrm{M}}\right]}}{\alpha }_i\left(k,l,q\right){\xi }_i(q)$$

(8)

where Q is a parameter that approximates the Doppler effect. When Q = 5, the effect of fractional Doppler can be taken into account [9]. This can then be expressed by

$${\alpha }_i\left(k,l,q\right)=\left\{\begin{array}{l}{e}^{j2\pi {\displaystyle \frac{(l-l_i)(k_i-{\kappa }_i)}{MN}}}\hfill \\ {\displaystyle \frac{N-1}{N}}{e}^{j2\pi {\displaystyle \frac{(l-l_i)(k_i-{\kappa }_i)}{MN}}}{e}^{-j2\pi {\displaystyle \frac{{[k_i-{\kappa }_i+q]}_N}{N}}}\hfill \end{array}\right.$$

(9)

$${\xi }_i(q)={\displaystyle \frac{e^{-j2\pi (-q-{\kappa }_i)}-1}{N{e}^{-j\frac{2\pi }{N}(-q-{\kappa }_i)}-N}}$$

(10)

where $l_i,k_i, {\kappa }_i$ denote the magnitude of the delay, the integer Doppler, and the fractional Doppler in the $i$th path of the channel, respectively.

2.2. Pilot Design and Channel Estimation Model

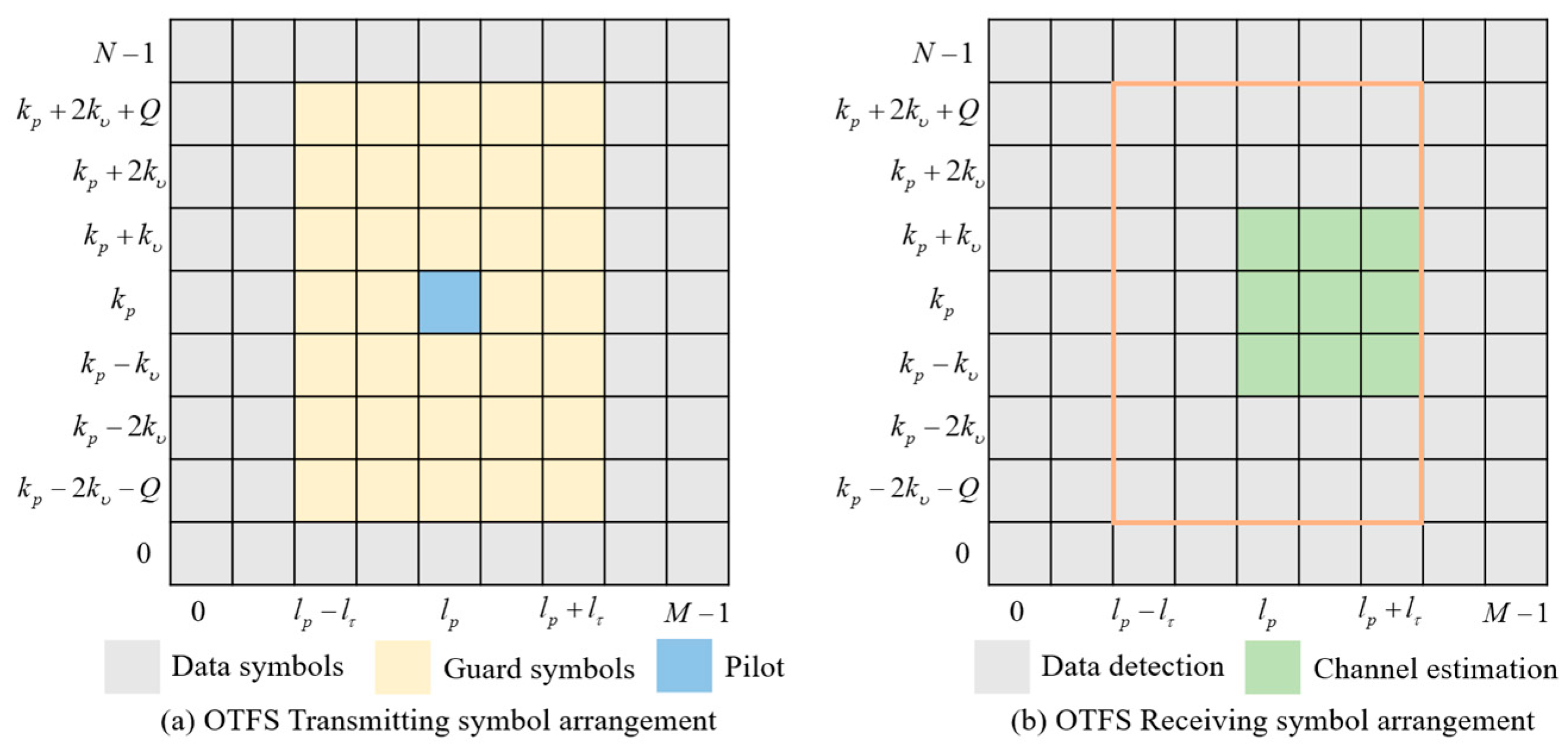
The embedded conduction structure of the channel estimation algorithm designed in this paper is shown in Figure 2. In this structure, no protection interval is set between the conduction symbols and the data symbols, and the conduction power is set to be approximately the same as the data symbol power with the aim of reducing the conduction overhead while reducing the conduction’s signal-to-noise ratio [17].

The signal at the transmitter end of the delay-Doppler domain, as shown in Figure 2, can be expressed as

$$x[k,l]=\left\{\begin{array}{c}{x}_{\mathrm{p}}[k,l],k_{\mathrm{p}}-2k_v-Q⩽k⩽k_{\mathrm{p}}+2k_v+Q,l_{\mathrm{p}}-l_{\tau }⩽l⩽l_{\mathrm{p}}+l_{\tau }\hfill \\ x_{\mathrm{d}}[k,l], \mathrm{else} \hfill \end{array}\right.$$

(11)

where $x_p[k,l]$ denotes the derivative symbol, $x_d[k,l]$ denotes the data symbol, $k_p={\displaystyle \frac{N}{2}}, l_P={\displaystyle \frac{M}{2}}$, $k_{\upsilon }$ denotes the Doppler tap corresponding to the maximum Doppler, and $l_{\tau }$ denotes the delay tap corresponding to the maximum delay.

At the receiver side, the signal received from the delay-Doppler domain, $\mathit{y}[\mathit{k},\mathit{l}]$, $\mathit{k}\in [{\mathit{k}}_{\mathit{p}}-{\mathit{k}}_{\mathit{\upsilon }},{\mathit{k}}_{\mathit{p}}+{\mathit{k}}_{\mathit{\upsilon }}],\mathit{l}\in [{\mathit{l}}_{\mathit{p}},{\mathit{l}}_{\mathit{p}}+{\mathit{l}}_{\mathit{\tau }}]$, is used to perform channel estimation (the detailed process of the channel estimation method devised in this paper is described in Section 3), and the estimated channel information will be used by the Minimal Mean Square Error (MMSE) algorithm for data detection. The number of guides used for channel estimation at the receiver is written as $\mathit{L}=(2{\mathit{k}}_{\mathit{\upsilon }}+1)\times ({\mathit{l}}_{\mathit{\tau }}+1)$, and these $\mathit{L}$ guides cause Doppler shift effects on the $\mathit{P}=(2{\mathit{k}}_{\mathit{\upsilon }}+2\mathit{Q}+1)\times ({\mathit{l}}_{\mathit{\tau }}+1)$ guides around them. Then, the matrix form of the signal received at the guide frequency can be expressed as

$$Y_{\mathrm{p}}=\left(X_{\mathrm{p}}\odot D\right)h+w=Ah+w$$

(12)

where ${\mathbf{X}}_{\mathrm{p}}\in {\mathit{C}}^{L\times P}$ is the guided frequency signal transmission matrix, ${\mathbf{Y}}_{\mathrm{P}}\in {\mathit{C}}^{L\times 1}$ is the pilot signal receipt matrix, $\mathbf{h}\in {\mathit{C}}^{P\times 1}$ is the delay-Doppler domain channel matrix, and $\mathbf{w}\in {\mathit{C}}^{L\times 1}$ is the Gaussian noise matrix. From the above analysis, it can be seen that the effects of time delay and Doppler manifest as a phase shift, so that the corresponding phase compensation is performed at the receiver side, according to the time delay and Doppler shift values, so that $\mathrm{D}$ denotes the phase compensation matrix, and $\mathrm{D}= {\left[conj\left({\alpha }_1\right),...,conj\left({\alpha }_L\right)\right]}^T$, where ${\mathit{\alpha }}_{\mathit{i}}\in {\mathit{C}}^{1\times P}$ is the $\mathsf{\alpha }[k,l,q]$ vector. ⊙ denotes the Hadamard product. From the above analysis, it can be seen that the dimensional high-dimensional channel h (with the dimensions $P\times 1$) will be recovered from the low-dimensional received signal ${\mathbf{Y}}_{\mathrm{P}}$ (with the dimensions $L$ × 1), thus transforming the OTFS system channel estimation problem into a sparse signal recovery problem.

2.3. Signal Detector

At the signal receiving end, the received signal y can be viewed as

$$\mathit{y}=\mathbf{H}\mathit{x}+z$$

(13)

where $\mathbf{H}$ is the channel matrix, $\mathit{x}$ is the transmitted signal, and $\mathit{z}$ is the noise. Therefore, the main task for the signal detector is to use channel estimation in order to obtain the transmitted signal $\mathit{x}$ from the received signal $\mathit{y}$ and the channel matrix $\mathbf{H}$.

Additionally, for the MMSE signal detector, the corresponding MMSE weighting matrix can be expressed as

$${\mathbf{W}}_{\mathrm{mmse}}={\left(H^{\mathrm{H}}H+{\sigma }_z^{2}I\right)}^{-1}{H}^{\mathrm{H}}$$

(14)

where $\mathbf{H}$ is the channel matrix, ${\sigma }_z$ is the variance of the noise, and $\mathbf{I}$ is the identity matrix. Thus, the transmitted signal ${\mathit{x}}_{\mathbf{m}\mathbf{m}\mathbf{s}\mathbf{e}}$, educed by the MMSE signal detector, can be expressed as

$$\begin{array}{cc}{\mathit{x}}_{\mathrm{mmse}}\hfill & ={\mathbf{W}}_{\mathrm{mmse}}\mathit{y}\hfill \\ & ={\left(H^{\mathrm{H}}H+{\sigma }_z^{2}I\right)}^{-1}{H}^{\mathrm{H}}\mathit{y}\hfill \end{array}$$

(15)

Therefore, in practical signal detection, the use of MMSE signal detectors can be suitably implemented for the detection and recovery of the transmitted signal. Consequently, the MMSE signal detector was used for signal detection in the experimental section of this paper.

3. Proposed Algorithm

3.1. GOMP Channel Estimation Algorithm

In the OTFS channel estimation model, since the dimensions of the channel matrix are much larger than those of the received signal, trying to estimate the channel matrix directly using OTFS channel estimation results in underdetermined equations that cannot be computed and solved. As for the GOMP algorithm, it is mainly based on the traditional OMP algorithm, which constructs a support set by fixedly selecting the serial numbers of the column vectors corresponding to the few atoms that are most relevant to the residuals in each iteration [18]. The core objective is to recover the original signal via sparse representation theory in a system of underdetermined linear equations. In the OTFS system, by assuming that the signal is sparse in a certain transform domain, the atoms most correlated with the residuals can be chosen iteratively to approximate the original signal. Therefore, the GOMP algorithm is well suited to OTFS channel estimation. The specific flow and pseudo-code of the GOMP-based channel estimation method are shown in Algorithm 1.

Algorithm 1 Pseudo-code for the GOMP channel estimation algorithm.

Input: Perception matrix $\mathsf{\Psi }$, received signal $\mathbf{Y}$, sparsity $K$, number of atoms selected per iteration $S (S\le K)$, threshold value $\epsilon$

Output: The recovered channel vector $\widehat{\mathbf{H}}$.

(1) Initialize ${\mathbf{R}}_0=\mathbf{Y}$, ${\mathsf{\Omega }}_0=\mathrm{\varnothing }$, ${\mathsf{\Psi }}_0=\mathrm{\varnothing }$ (2) $\mathit{U}=\mathrm{a}\mathrm{b}\mathrm{s}\left[{\mathsf{\Psi }}_{\mathrm{t}}^{\mathrm{T}}{\mathbf{R}}_{\mathrm{t}-1}\right]$ (3) ${\mathit{I}}_0=\left[{\mathit{I}}_1,{\mathit{I}}_2,\dots ,{\mathit{I}}_S\right]$//${\mathit{I}}_S$ denotes the Column number of ${\mathit{U}}_S$ in $\mathit{U}$ (4) ${\mathit{\Omega }}_t={\mathit{\Omega }}_{t-1}\cup {\mathit{I}}_0$ (5) ${\mathsf{\Psi }}_t={\mathsf{\Psi }}_{t-1}\cup {\mathbf{A}}_i$//${\mathbf{A}}_i$ denotes the $i$ th column of $\mathsf{\Psi }$, $i\in I_0$ (6) ${\widehat{\mathbf{H}}}_t = argmin \Vert \mathbf{Y}-{\mathsf{\Psi }}_t{\mathbf{H}}_t\Vert ={\left({\mathsf{\Psi }}_t^T {\mathsf{\Psi }}_t\right)}^{-1}{\mathsf{\Psi }}_t^T\mathbf{Y}$ (7) ${\mathbf{R}}_t=\mathbf{Y}-{\mathsf{\Psi }}_t{\widehat{\mathbf{H}}}_t$ (8) $t=t+1$, if $t>K$ or ${‖{\mathbf{R}}_t‖}_2<\mathsf{\epsilon }$, go to (9), Otherwise return (2) (9) $\widehat{\mathbf{H}}={\widehat{\mathbf{H}}}_t$

3.2. BEM Channel Estimation Model

The basis expansion model (BEM) is a mathematical tool that is used to parameterize complex time-varying channels by linear combinations of basis functions, the core idea being to simplify the complexity of channel estimation and signal processing by representing the channel impulse response as the weighted sum of a set of known basis functions. At the same time, the BEM can capture the time-varying characteristics of the channel more accurately through the time–frequency localization of basis functions, and can also reduce the computational complexity and frequency-conducting overhead.

In the OTFS system, the BEM decomposes the channel matrix in the time domain into the product of the basis function and the coefficients of the basis function, which are expressed as follows:

$${\mathrm{g}}_l={\displaystyle \sum _{q=1}^{Q}diag(b_q)C_q^T}$$

(16)

where $C_q$ is the basis function coefficient, and $b_q$ is the $q$th known basis function of the OGCE-BEM, with a length of MN. The known basis functions are different for different BEMs. The most basic BEM is the polynomial basis expansion model (P-BEM), which is obtained by approximation through Taylor series expansion, and its basis coefficients can be expressed as

$$b_q\left(n\right)={\left(n-{\displaystyle \frac{N}{2}}\right)}^q$$

(17)

The Complex Exponential Base Expansion Model (Complex-Exponential BEM or CE-BEM) was invented on the basis of the P-BEM, a base expansion model based on complex exponential expansion [19]. In the CE-BEM, the main principle is to compress the time-domain channel’s impact response from the perspective of the frequency domain, and its basis coefficients can be expressed as

$$b_q\left(n\right)=e^{j{w}_{q}n}=e^{j{\displaystyle \frac{2\pi \left(q-Q/2\right)}{N}}n}$$

(18)

Later, on the basis of the CE-BEM, the Optimized Generalized Complex Exponential BEM (OGCE-BEM) was proposed; it effectively reduces spectral leakage through more intensive sampling and, at the same time, reduces the modeling error caused by high-frequency basis functions through correction coefficients. Its basis coefficients can be expressed as [20]

$$b_q\left(n\right)=e^{j{w}_{q}n}=e^{j{\displaystyle \frac{2\pi nz\left(q-Q/2\right)}{ZN}}}$$

(19)

where $z=2{\overline{f}}_{max} ZN/M$ is the correction factor, and $Z$ is the intensive sampling factor; $q=1,\dots ,Q, Q\ge 2{\overline{f}}_{max}$, $N$ is the number of OGCE-BEM basis functions, ${\overline{f}}_{max} =f_{max}/\mathsf{\Delta }f$ is the normalized maximal Doppler frequency, $\mathsf{\Delta }f$ is the sub-carrier spacing, $f_{max}= f_{c}v/\mathrm{c}$ is the maximal Doppler frequency, $f_c$ is the carrier frequency, $v$ is the relative velocity between the transmitter and receiver, and c is the speed of light. According to the relationship between the channel matrix in the DD domain and that in the time domain, the obtained channel matrix in the DD domain can be expressed as

$$\begin{array}{cc}{h}_l\hfill & ={\displaystyle \frac{1}{\sqrt{N}}}\left(F_N\otimes I_M\right)g_l\hfill \\ & ={\displaystyle \frac{1}{\sqrt{N}}}\left(F_N\otimes I_M\right)B{c}_l\hfill \\ & =A{c}_l\hfill \end{array}$$

(20)

where $\mathbf{A}={\displaystyle \frac{1}{\sqrt{N}}}\left(F_N\otimes I_M\right)B$, and $\mathbf{B}$ is the basis function matrix. According to the input–output relationship of the OTFS system in the DD domain, it can be obtained from

$$\begin{array}{cc}y\hfill & =\mathit{x}(I_L\otimes A)c_q+z\hfill \\ & =\mathsf{\psi }{\mathit{C}}_q+z\hfill \end{array}$$

(21)

where the observation vector $\mathsf{\psi }=(I_L\otimes A)c_q$ represents the matrix of basis coefficients. Meanwhile, there are many other BEMs—including the Discrete Prolate Spheroidal Sequences BEM (DPSS-BEM) [21], the Discrete Karhunen–Loeve BEM (DKL-BEM) [22], etc.—which will be analyzed individually in the section containing the experimental results.

3.3. BEM-iGOMP Channel Estimation Algorithm

When using the GOMP algorithm for channel estimation, it is necessary to ensure the sparsity of the channel and the uncorrelation of each channel. Meanwhile, since its base coefficients are diagonal matrices, the OGCE-BEM has a very strong sparsity, which can suitably satisfy the requirements of the GOMP algorithm. Therefore, the OGCE-BEM can be combined with the GOMP algorithm to improve its performance, and we call this the BEM-GOMP algorithm. To account for the uncorrelation requirement, we introduced an ordinal difference restriction method that requires that the atoms selected each time satisfy the ordinal difference restriction principle in order to reduce the correlation between the atoms. Meanwhile, the GOMP algorithm requires the sparsity of the channel matrix to be known in advance. However, in practice, the sparsity of the channel usually cannot be predicted in advance. Therefore, we rely on the weak selectivity principle in the Stagewise Weak Orthogonal Match Pursuit (SWOMP) algorithm and adaptively select appropriate atoms by setting a threshold with a coefficient, thereby selecting atoms with a correlation greater than the threshold into the support set, and discarding atoms with a correlation less than or equal to the threshold. This results in the selection of the appropriate atoms without determining the sparsity of the system in advance [23]. We call this optimized BEM-GOMP algorithm, which uses the ordinal difference restriction method and the weak selectivity principle, the BEM-iGOMP algorithm. The specific flow of channel estimation by the BEM-iGOMP algorithm is shown in Algorithm 2. Compared to the OMP and GOMP algorithms, the computational complexity of BEM-iGOMP is $O\left(K\right),$ and the computational complexities of BEM-OMP and BEM-GOMP are $O\left(K^2\right)$ and $O\left(K\right(K-1\left)\right)$, respectively, where $K$ is the channel sparsity. Therefore, the computational complexity of BEM-iGOMP is much lower than those of the BEM-OMP and BEM-GOMP algorithms.

Algorithm 2 Pseudo-code for the BEM-iGOMP channel estimation algorithm.

Input: Perception matrix after BEM decomposition $\mathsf{\Psi }$, received signal $\mathbf{Y}$, sparsity $K$, threshold coefficient $\gamma$, Minimum serial number difference $\rho$, error threshold value $\epsilon$

Output: The recovered Base coefficient matrix ${\widehat{\mathbf{C}}}_q$.

(1) Initialize ${\mathbf{R}}_0=\mathbf{Y}$, ${\mathit{\Omega }}_0=\varnothing$, ${\mathsf{\Psi }}_0=\varnothing$, $\mathit{U}=abs\left[{\mathsf{\Psi }}_t^T{\mathbf{R}}_{t-1} \right]$ (2) for ($S=1; S\le L;S++$) do //L is the number of columns for $\mathit{U}$ (3) if (${\mathit{U}}_S\ge \gamma {\mathit{U}}_{max}$) then (4) ${\mathit{I}}_0=\left[{\mathit{I}}_0\bigcup {\mathit{I}}_S\right]$ (5) end if (6) end for (7) for ($i=1;i\le S;i++$) do (8) $d_i=I_{i+1}-I_i$ (9) if ${(d}_i<\rho )$ then (10) ${\mathit{I}}_i=\left[\right]$ (11) end if (12) end for (13) ${\mathit{\Omega }}_t={\mathit{\Omega }}_{t-1}\cup {\mathit{I}}_0$ (14) ${\mathsf{\Psi }}_t={\mathsf{\Psi }}_{t-1}\cup {\mathbf{A}}_i$ (15) ${\widehat{\mathbf{C}}}_{q_t } = argmin ‖ \mathbf{Y}-{\mathsf{\Psi }}_t{\mathbf{C}}_{q_t}‖={\left({\mathsf{\Psi }}_t^T {\mathsf{\Psi }}_t\right)}^{-1}{\mathsf{\Psi }}_t^T\mathbf{Y}$ (16) ${\mathbf{R}}_t=\mathbf{Y}-{\mathsf{\Psi }}_t{\widehat{\mathbf{C}}}_{q_t }$ (17) $t=t+1$, if $t>K$ or ${‖{\mathbf{R}}_t‖}_2<\epsilon$, go to (18); Otherwise return (2) (18) ${\widehat{\mathbf{C}}}_q={\widehat{\mathbf{C}}}_{q_t}$

4. Results and Discussion

In this paper, the OTFS system is simulated based on the MATLAB (version 2024a) platform as per the 3GPP protocol, and the parameters used are shown in

Table 1. OTFS system simulation parameter design.

Parameters	Value
Symbols	16
Subcarriers	32
Frames	1000
Modulation mode	64 QAM
Carrier frequency	4 GHz
Subcarrier interval	15 kHz
Relative speed of receiver and transmitter Channel model	500 km/h
	EVA channel [24]
Paths of channel	9
Pilot to data ratio	12.5%

.

To evaluate the model’s performance after signal detection using the MMSE signal detector, we selected two major performance metrics, Normalized Mean Square Error (NMSE) and Bit Error Rate (BER). Their respective formulas are as follows:

$$\mathrm{NMSE}=10{\log }_{10}\left({\displaystyle \frac{E\left({‖h-\stackrel{⌢}{h}‖}_2^2\right)}{E\left({‖h‖}_2^2\right)}}\right)$$

(22)

$$\mathrm{BER}={\displaystyle \frac{B_{\mathrm{error}}}{B_{\mathrm{sum}}}}$$

(23)

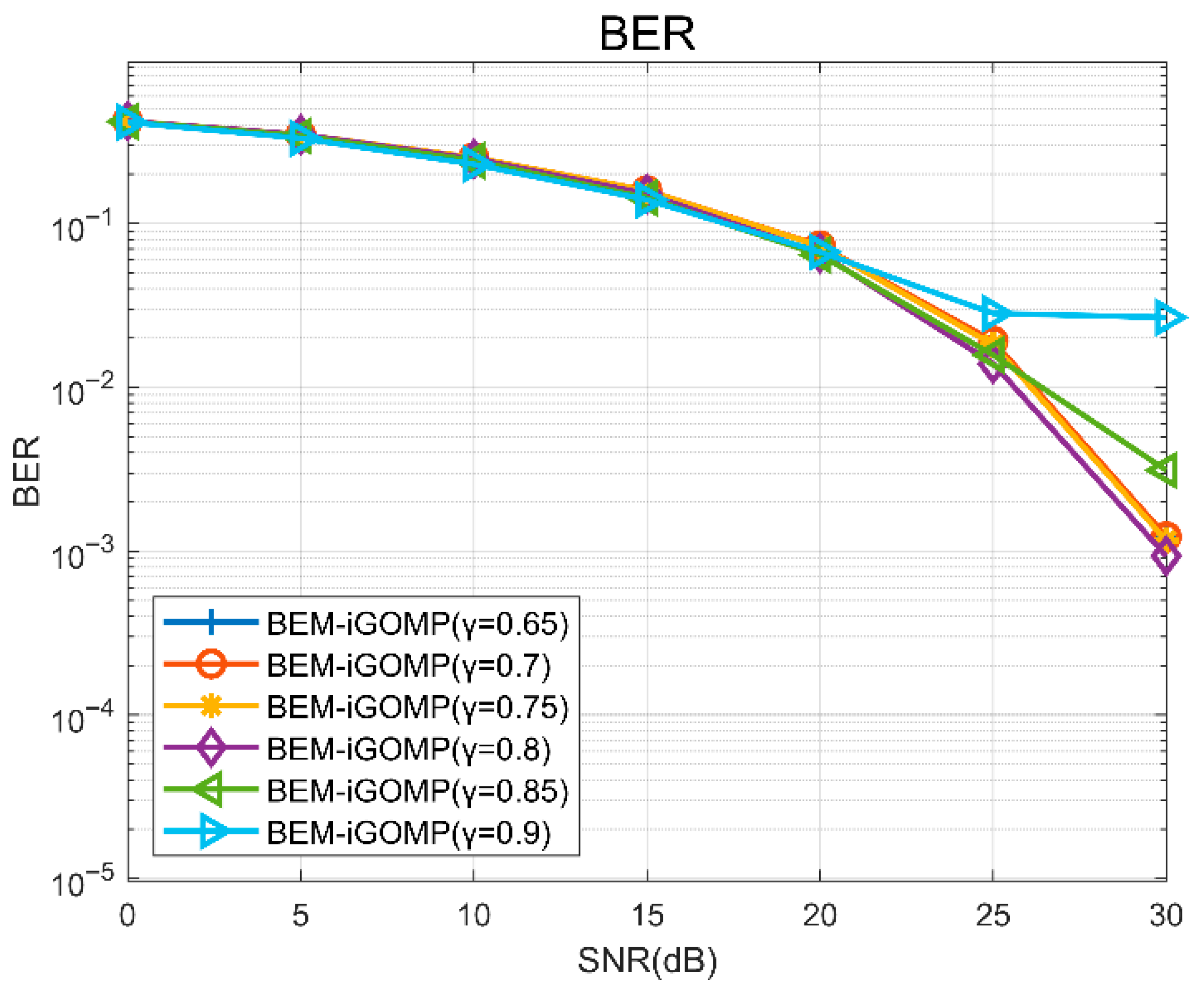
where $h$ denotes the true value of the channel, $\widehat{h}$ denotes the estimated value of the channel, $B_{error}$ denotes the number of bits in the error, and $B_{sum}$ denotes the total number of bits transmitted. In the BEM-iGOMP channel estimation algorithm we designed, we first compared the selection of its threshold. The NMSE and BER results obtained for different SNR environments by selecting different thresholds γ and comparing the obtained model performance results are shown in Figure 3 and Figure 4, respectively.

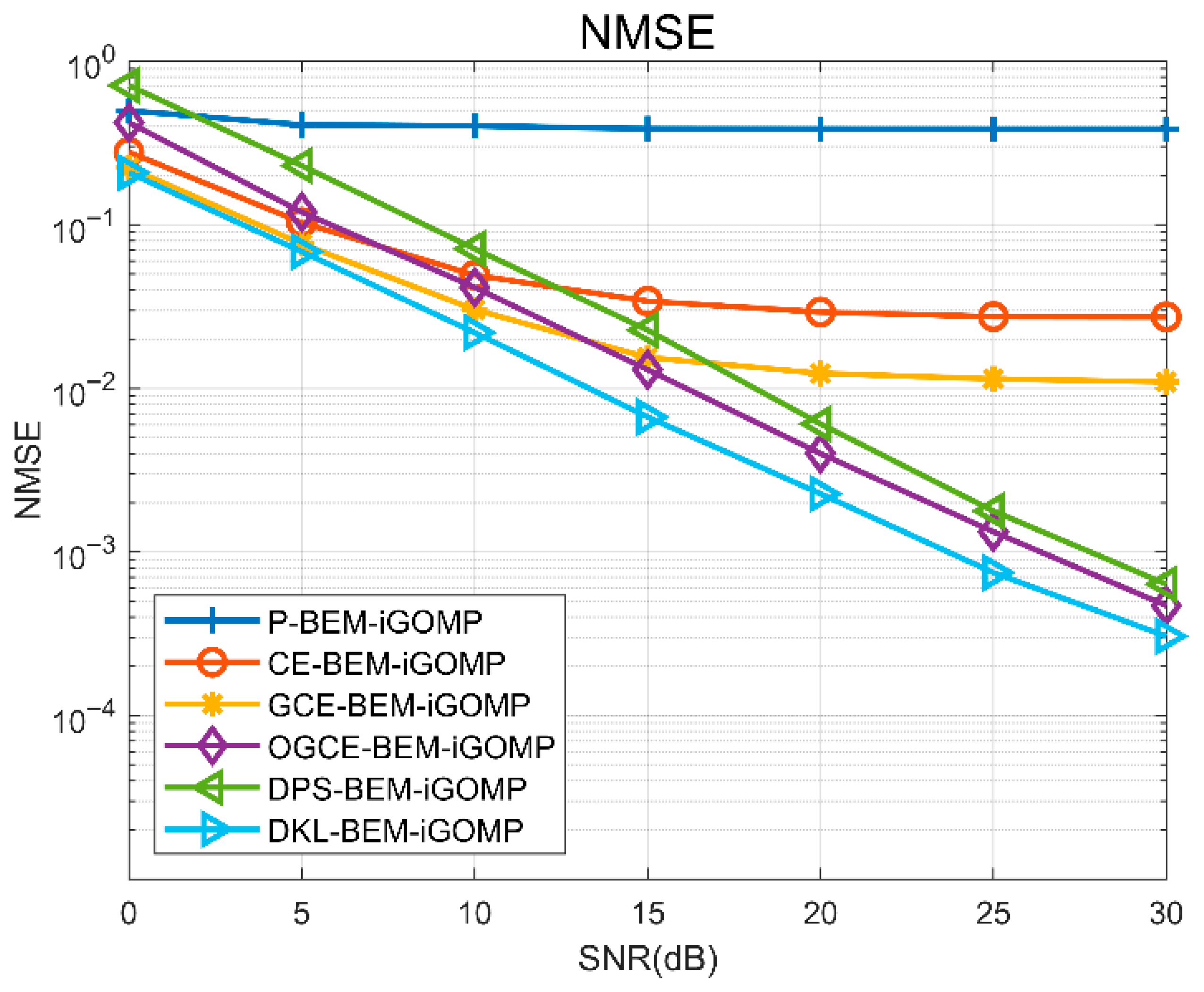
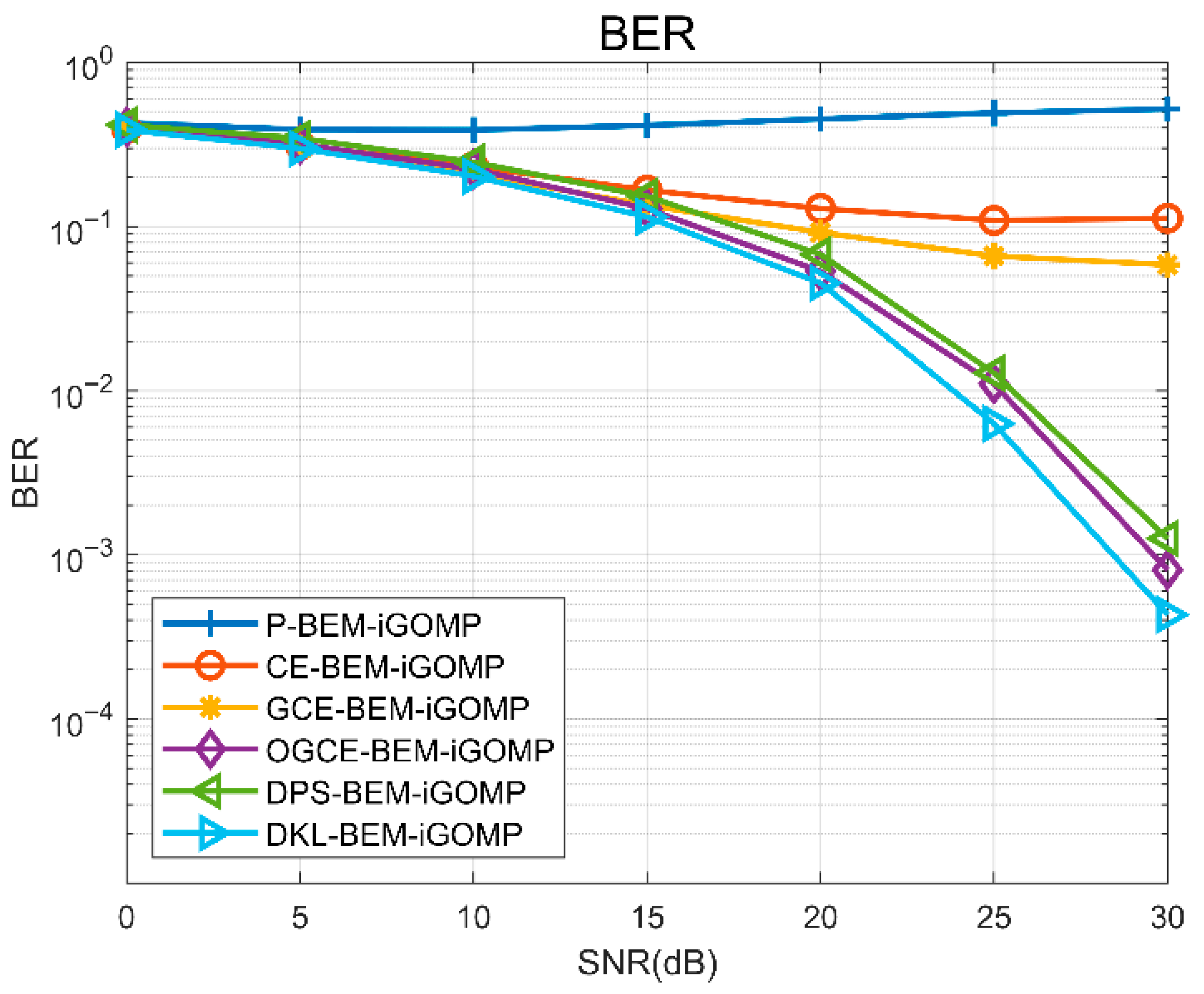
Based on the results, it can be seen that, under high-SNR conditions, the model’s performance is best for a threshold of $\gamma = 0.8$, and therefore this threshold was in the subsequent analysis. Secondly, to select the BEM’s base coefficient model, we compared the models’ performance under different base coefficient conditions in the same way as above, and the obtained NMSE and BER results in different signal-to-noise ratio environments are shown in Figure 5 and Figure 6, respectively.

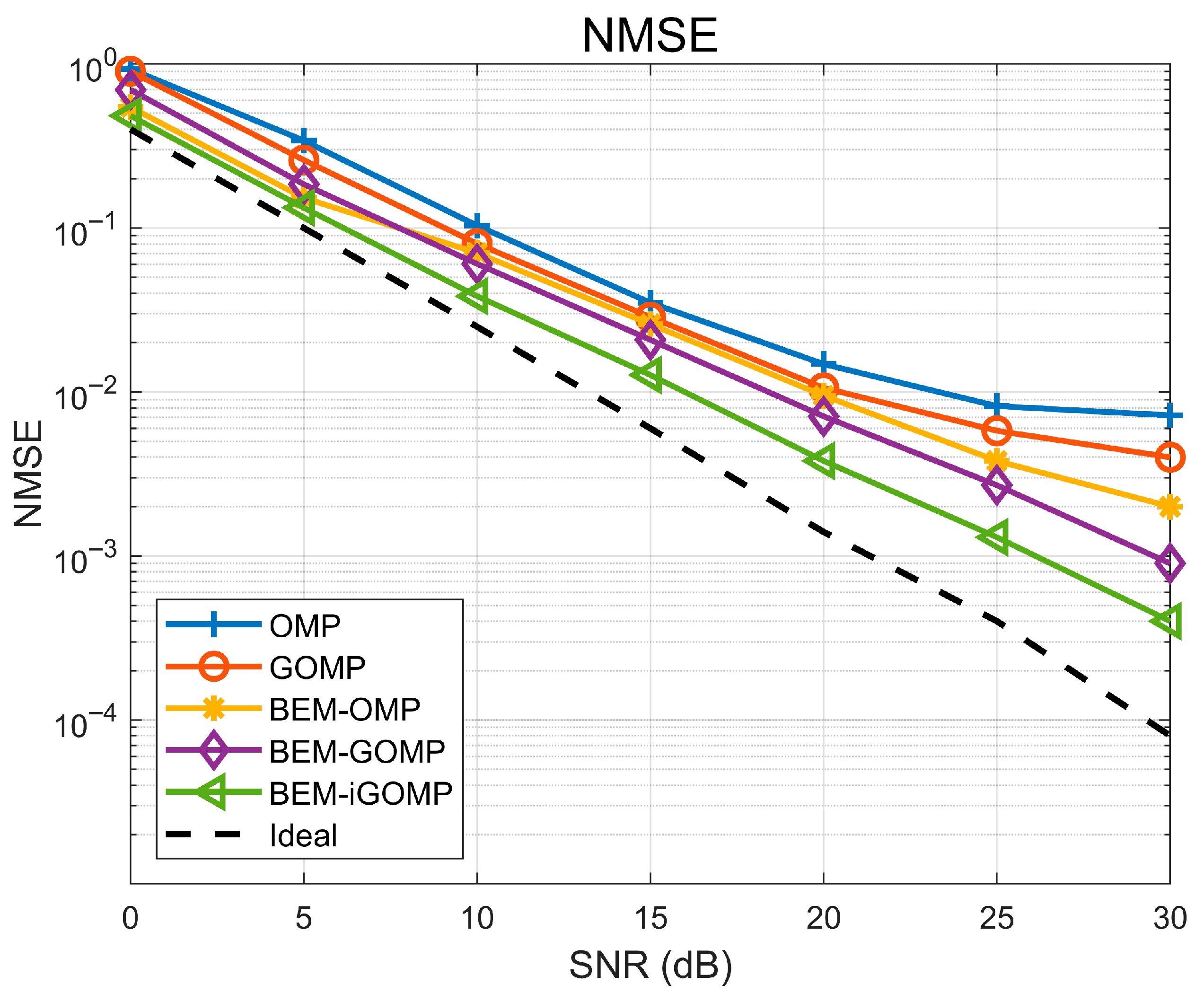
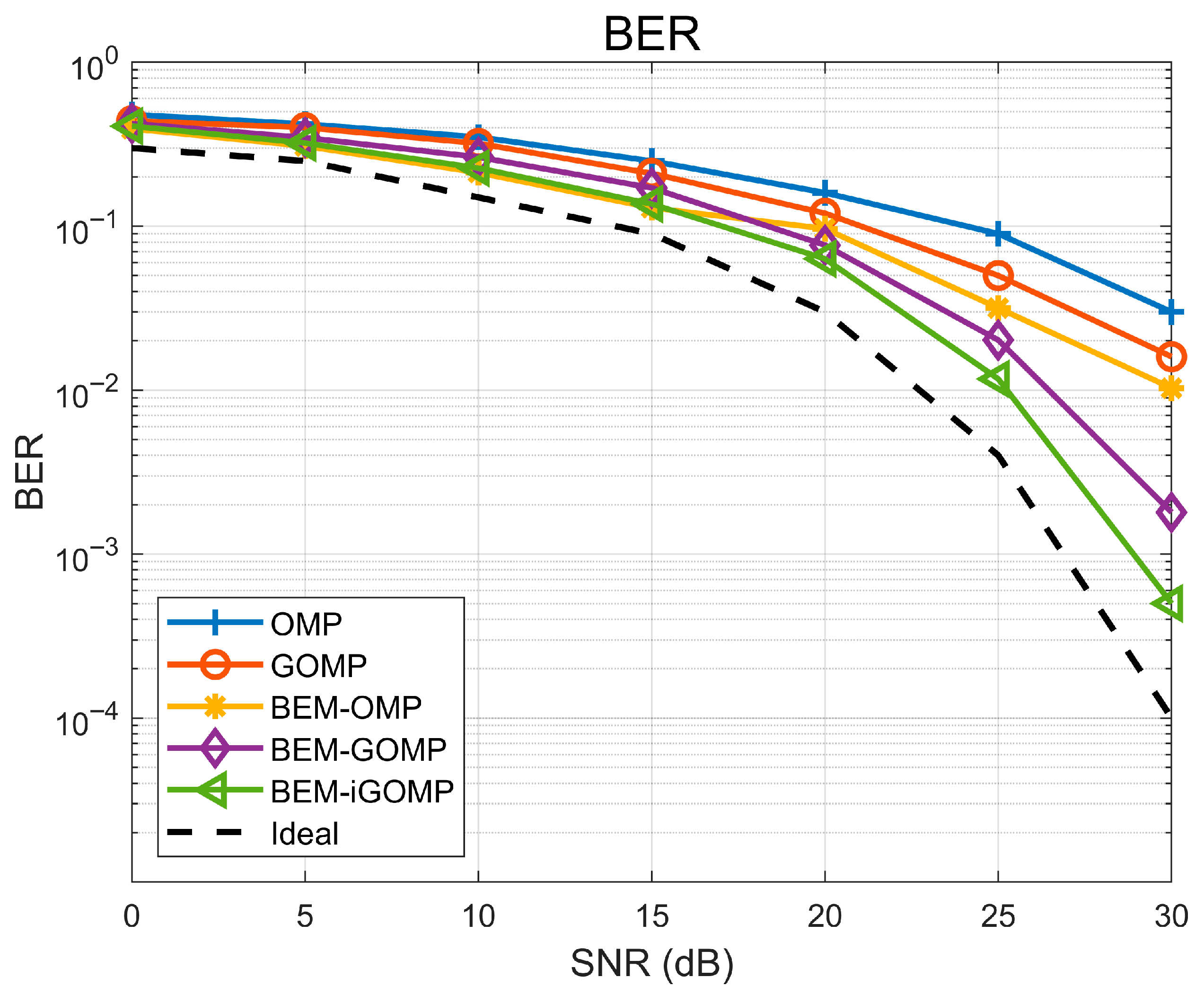
Based on the results, it can be seen that the DKL-BEM is the best-performing model in high-SNR environments, and that this is followed by the OGCE-BEM. However, due to the extremely high computational complexity of the DKL-BEM, we finally chose to optimize the GOMP algorithm using the OGCE-BEM. We also compared the original GOMP algorithm and the BEM-GOMP algorithm, as well as the basic OMP algorithm and the OMP algorithm optimized with the BEM; the NMSE and BER results obtained for different SNR environments are shown in Figure 7 and Figure 8, respectively.

Based on the above results, it can be seen that the BEM-iGOMP channel estimation algorithm proposed in this paper improves on the NMSE and BER performance of the OMP algorithm, the original GOMP algorithm, the BEM-optimized OMP algorithm, and the BEM-GOMP algorithm. In a high-SNR environment (SNR = 30 dB), the algorithm proposed in this paper achieves NMSE performance improvements of about 12–15 dB compared to the OMP algorithm, about 10–13 dB compared to the original GOMP algorithm, about 8–10 dB compared to the BEM-optimized OMP algorithm, and about 5–6 dB compared to the BEM-GOMP algorithm. Meanwhile, the BER performance of the BEM-iGOMP channel estimation algorithm proposed in this paper is about 5 × 10⁻⁴ at SNR = 30 dB, after signal detection by the MMSE signal detector, which is much smaller than the BER results obtained by other channel estimation algorithms. Therefore, it is clear that the NMSE and BER performance of the system are greatly improved when using the channel estimation algorithm proposed in this paper.

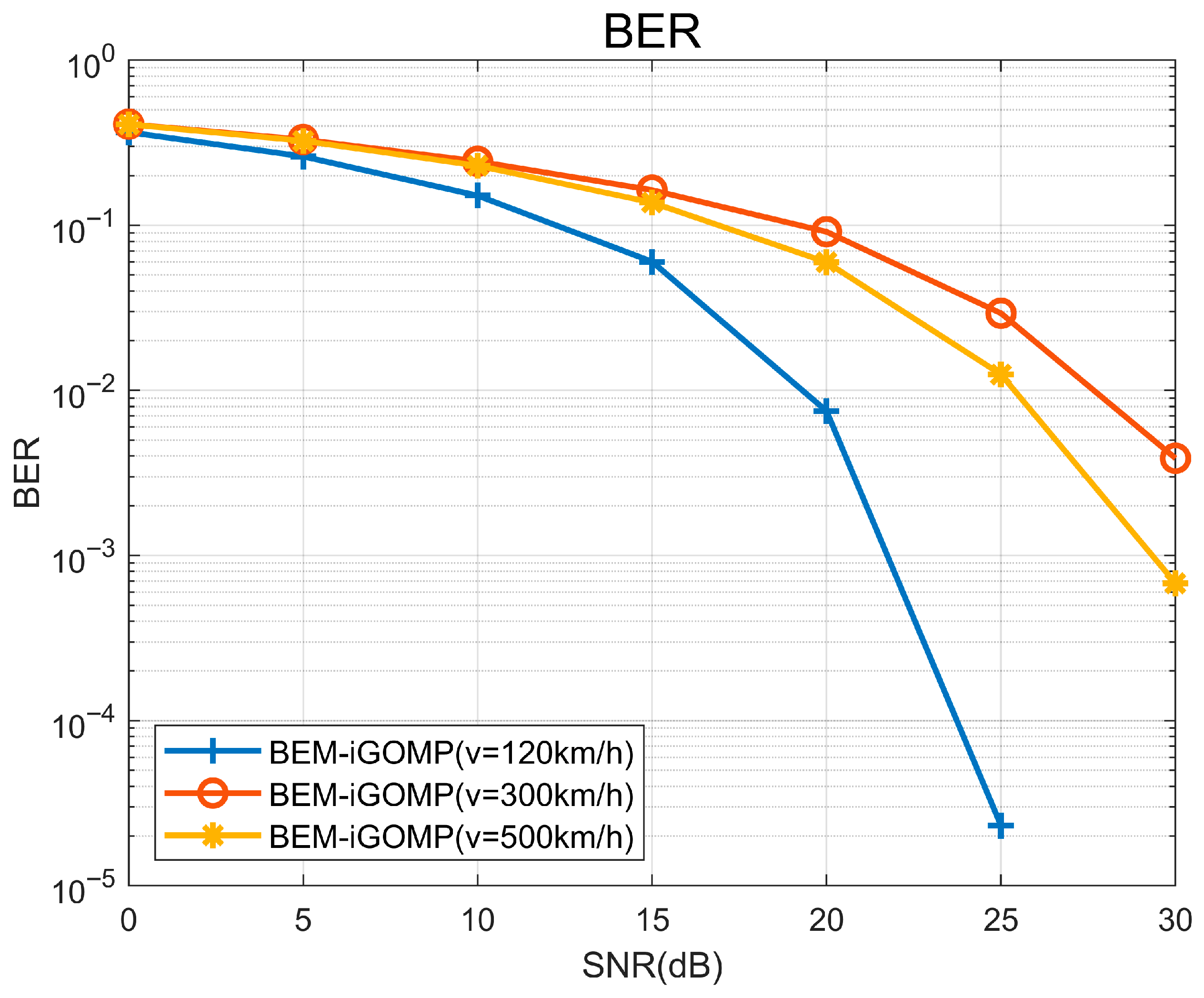
We also compared the performance of this algorithm at different relative speeds, and the obtained NMSE and BER results for different SNR environments are shown in Figure 9 and Figure 10, respectively.

Based on the above results, it can be seen that the best channel estimation performance is obtained when the relative speed between the receiver and the transmitter is 120 km/h, when using the algorithm proposed in this paper for channel estimation. The NMSE performance is similar when the relative speed is 300 km/h and 500 km/h, but in terms of BER performance, the performance is better when the relative speed between the receiver and the transmitter is 500 km/h.

This shows that the NMSE and BER performance obtained at 300 km/h and 500 km/h using the same algorithm are opposed. Therefore, in channel estimation, higher speeds produce stronger inter-carrier interference and faster channel time variation, which destroys the channel estimation performance, and this is why the NMSE performance is better for a relative speed of 300 km/h. However, when performing signal detection in the very high-speed channel environment, since the BEM-iGOMP algorithm proposed in this paper is mainly based on channel sparsity, the system’s BER performance is better at a relative speed of 500 km/h. This is because, at higher speeds, the absolute value of the Doppler shifts produced by the individual paths increases, and, simultaneously, the relative difference between them also increases. This causes channel taps, which are close together on the Doppler axis at slower speeds, to be “pulled apart” and distributed more sparsely, resulting in a higher degree of separation. This compensates, to a certain extent, for the negative impact of the degradation of channel estimation accuracy under high-speed movement but is also the reason why the system’s BER performance is better at a relative speed of 500 km/h.

5. Conclusions and Outlook

In this paper, an optimized GOMP channel estimation method, the BEM-iGOMP algorithm, is proposed. It firstly combines the base extension model for assistance, decomposes the channel matrix, and then introduces the ordinal difference restriction method as well as the weak selectivity principle to optimize the GOMP algorithm. Based on the results, it can be seen that, compared to the OMP algorithm, the original GOMP algorithm, the BEM-optimized OMP algorithm, and the BEM-GOMP algorithm, our algorithm achieves various degrees of improvement in terms of NMSE performance. At the same time, after the use of the MMSE signal detector, the BER performance obtained by our algorithm is also improved to a large extent, which can be very good for channel estimation in a V2X telematics communication environment. In short, the BEM-iGOMP algorithm improves NMSE performance by about 12–15 dB compared to the OMP algorithm, about 10–13 dB compared to the original GOMP algorithm, about 8–10 dB compared to the BEM-optimized OMP algorithm, and about 5–6 dB compared to the BEM-GOMP algorithm. In future work, the optimization of the GOMP and OMP algorithms for OTFS channel estimation will be further investigated in order to continue to explore whether there exists a better-performing BEM to adapt the GOMP algorithm and whether the algorithm can be further optimized by combining it with an AI model. We will also try to implement our proposed algorithm for other channels, not only the EVA channel, to ascertain the universality of our proposed algorithm.