Dynamic Obstacle Avoidance Approach Based on Integration of A-Star and APF Algorithms for Vehicles in Complex Mountainous Environments

Abstract

Complex mountainous environments pose significant challenges for dynamic path planning and obstacle avoidance of transport vehicles. In response, this paper presents an innovative path planning approach that combines an enhanced A* algorithm with the artificial potential field (APF) method. Firstly, the heuristic function of the A* algorithm was improved, and path inflection points were optimized to enhance global path-planning efficiency and smoothness. Secondly, a target distance factor was introduced to modify the APF algorithm’s repulsive field function, solving the traditional APF’s target-unreachable problem. The integrated algorithm uses the A*-optimized inflection points as sub-target points for the APF, meeting real-time obstacle avoidance requirements in dynamic environments and conducting secondary path planning to avoid local minima. Impressively, static environment simulations demonstrated the integrated algorithm’s outstanding path-planning capabilities in complex terrains. Moreover, dynamic obstacle avoidance experiments revealed its remarkable ability to not only detect and evade dynamic obstacles but also maintain a safe distance from static ones. The findings highlight that this method significantly boosts path-planning efficiency while ensuring safety and global optimality in dynamic settings. This breakthrough offers crucial theoretical support for enhancing the navigation of mountain transport vehicles in complex, real-world scenarios, potentially improving their operation.

1. Introduction

Dynamic path planning is a core aspect of mountain transport vehicle research, in-volving the planning of a driving route from a starting point to a destination in complex terrains with dynamic obstacles. It ensures that the vehicle can safely avoid obstacles and maintain stable passage during movement. Depending on the degree of environmental information available during path planning, path planning algorithms can be categorized into global and local path planning. Currently, common global path planning algorithms include the A* algorithm [1], particle swarm optimization [2], and the ant colony algorithm [3], which primarily optimize the global path based on pre-acquired terrain data. Local path planning typically employs methods such as the artificial potential field (APF) [4] and fuzzy logic algorithms [5], which focus on real-time processing of sudden dynamic obstacles encountered during travel, adjusting the path dynamically using sensor data. In obstacle avoidance, geometric and reinforcement learning (RL) approaches address dynamic navigation challenges differently. The VFH+T algorithm [6] enhances traditional VFH+ with memory-based trap recognition. Meanwhile, an optimized TD3 [7] allows the robot to take its own actions based on the observations it makes, without defining any trajectory beforehand.

The A* algorithm is a heuristic search algorithm characterized by its concise implementation and higher operational efficiency compared to algorithms such as particle swarm and ant colony algorithms. However, the traditional A* algorithm has notable drawbacks, including an excessive number of inflection points and non-smooth paths in the generated trajectories. Early researchers aimed to reduce pathfinding time by adjusting the weight ratios within the cost function [8]. Nevertheless, this approach exhibited poor environmental adaptability, particularly in complex mountainous terrains. Subsequent scholars focused on modifying the cost function to enhance the heuristics of the heuristic function. For example, Yu Xiang et al. [9] improved the A* heuristic function using Euclidean distance and projection distance, a modification that significantly reduced the number of iterations. Bao Jiusheng et al. [10] proposed incorporating an exponential function as a weighting coefficient for the heuristic function, a strategy that yielded a moderate improvement in the algorithm’s search efficiency.

The APF algorithm determines the next movement direction based solely on the surrounding environment and the robot’s current state, offering advantages such as high computational efficiency and smooth path generation. However, this method is prone to stagnation at local minima, and traditional APF struggles to meet optimal path criteria when facing dynamic obstacles. To address these limitations, Min Gyu Park et al. [11] addressed the problem that the APF algorithm is prone to getting trapped in local minima during path planning. They proposed a technique that combines the APF algorithm with the simulated annealing algorithm to effectively avoid local minima and achieve path planning. Additionally, Jinseok Lee et al. [12] proposes a random unit total force (RUTF) algorithm and its repulsion-removed variant (RUTF-RR), which dynamically select force strategies based on the positional and directional conditions of the robot, obstacles, and target. This approach is designed to systematically identify and resolve the local minimum trapping issue inherent in potential field methods, particularly under symmetric robot–obstacle–goal configurations.

In complex mountainous environments, unstructured terrains—such as steep slopes, gullies, and irregular obstacles—and dynamic factors including moving obstacles and real-time environmental perception noise pose significant challenges to vehicle path planning. While single global planning algorithms (e.g., the traditional A* algorithm) can generate globally optimal paths based on prior maps, they struggle to respond in real-time to dynamic obstacles and local terrain mutations. Conversely, local obstacle avoidance algorithms (e.g., the artificial potential field (APF) method) can achieve immediate obstacle avoidance but suffer from local minimum traps and lack global path guidance, leading to deviations from optimal paths and even target unreachability. The inherent limitations of these two algorithms are significantly amplified by the complexity of mountainous environments. Therefore, the organic integration of the systematic global planning with the real-time adaptability of local obstacle avoidance to construct a dynamic obstacle avoidance approach that balances global optimality and dynamic adaptability has become a critical breakthrough for solving navigation problems of mountain vehicles in complex environments.

In the fields of autonomous driving and unmanned aerial vehicles (UAVs), improvements to the A* and APF algorithms primarily focus on path smoothing, dynamic obstacle avoidance, search efficiency, and constraint integration. In autonomous driving, cubic B-spline/Bezier curve fitting is introduced to optimize the curvature continuity of A*-generated paths, addressing issues of redundant inflection points [13,14]. Weighted heuristic functions and bidirectional search strategies are employed to enhance search efficiency in complex environments and reduce redundant nodes [15,16]. To tackle the local minimum traps of the APF algorithm, repulsive field functions are improved to be distance-sensitive—for example, by incorporating target distance factors or dynamically adjusting repulsive force intensity—and combined with safety distance models or road boundary constraints (e.g., virtual lane line gravitational forces) to enhance global guidance [17,18]. In the UAV domain, repulsive-force optimized heuristic functions enable safe path planning and load stabilization, while lightweight search strategies drastically reduce search time [19].

To address the above challenges, this paper proposes an algorithm that integrates the A* algorithm and the APF algorithm. The algorithm optimizes the set of inflection points in the global path generated by the improved A* algorithm and uses these optimized inflection points as sub-target points for obstacle avoidance in the improved APF algorithm. This approach not only reduces the iteration time but also shortens the path length.

2. Traditional Path Planning Algorithm

2.1. Traditional A* Algorithm

The core idea of the A* algorithm in path planning is to integrate a heuristic search strategy. It calculates two components: the actual cost function g(n) from the start node to the current node, and the heuristic function h(n) estimating the cost from the current node to the target node. The combined evaluation criterion is the total cost f(n) = g(n) + h(n). A priority queue is used to store nodes to be expanded, sorted by f(n). During the search, the algorithm dynamically updates path information and performs effective pruning. Under the condition that h(n) is an admissible heuristic function, A* guarantees finding the optimal path. Typically, the heuristic function h(n) is represented by the Euclidean distance between the current node and the target node:

$$\mathrm{h}(n)=\sqrt{{(x_n-x_g)}^2+{(y_n-y_g)}^2}$$

(1)

where x_n and y_n represent the X-axis and Y-axis coordinates of the current node, respectively, while x_g and y_g denote the X-axis and Y-axis coordinates of the target node.

The flowchart of the traditional A* algorithm is shown in Figure 1. However, the traditional A* algorithm has notable drawbacks in its computational results. First, it involves an excessive number of search nodes and long computation time: in complex environments, the search space grows exponentially, and the heuristic function struggles to adapt to most environments. Second, issues such as non-smooth explored paths and suboptimal routes arise: the paths are jagged with frequent turns, and the algorithm cannot adjust the path in a timely manner in dynamic environments.

2.2. Traditional APF Algorithm

The traditional APF algorithm is based on the principle of gradient potential fields. The attractive potential field U_att experienced by an object is given by

$${\mathrm{U}}_{att}={\displaystyle \frac{1}{2}}{k}_{att}|\rho {|}^2$$

(2)

where k_att denotes the attractive gain coefficient, and ρ represents the spatial vector from the current position of the vehicle to the target. This vector is directed from the current position to the target, with its magnitude equal to the distance between the two points.

The magnitude of the attractive force acting on the vehicle is given by the negative gradient of the attractive potential field function:

$${\mathrm{F}}_{att}=-\nabla U_{att}=k_{att}\rho$$

(3)

The repulsive potential field U_obs experienced by the vehicle around an obstacle is given by

$$U_{obs}=\left\{\begin{array}{l}{k}_{obs}{\left({\displaystyle \frac{1}{q}}-{\displaystyle \frac{1}{\lambda }}\right)}^2 q\le \lambda \\ 0 q>\lambda \end{array}\right.$$

(4)

where k_obs represents the repulsive gain coefficient, q denotes the shortest distance from the vehicle to the obstacle, and λ is the radius of the obstacle’s repulsive field range.

This means that the obstacle exerts a repulsive force on the vehicle when it enters the repulsive field range, while it has no effect outside this range. Specifically, the repulsive force exerted by the obstacle on the vehicle is given by

$$F_{obs}=-\nabla U_{obs}=\left\{\begin{array}{l}{k}_{obs}\left({\displaystyle \frac{1}{q}}-{\displaystyle \frac{1}{\lambda }}\right){\displaystyle \frac{1}{q^2}} q\le \lambda \\ 0 q>\lambda \end{array}\right.$$

(5)

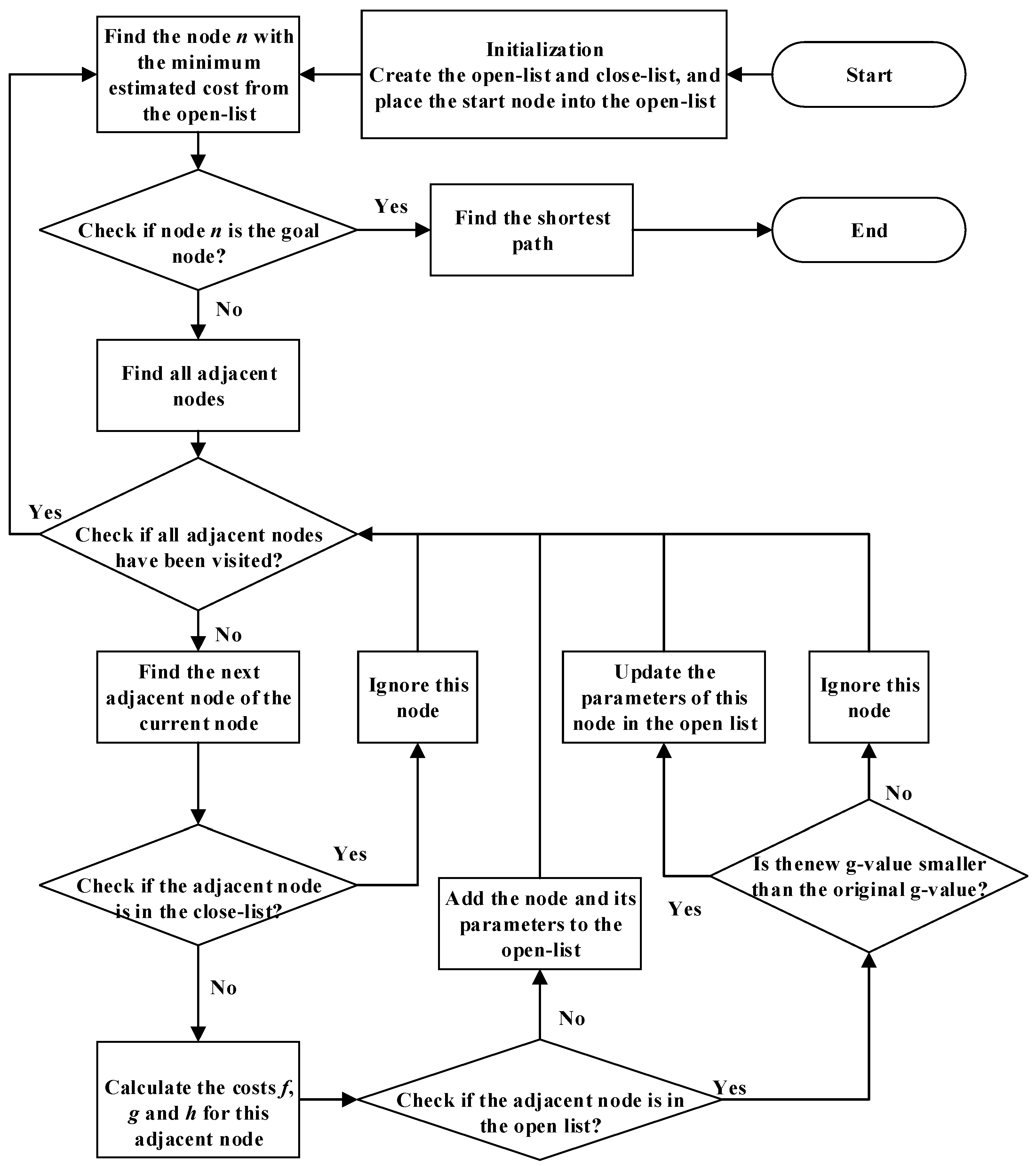
3. Improvement of Path Planning Algorithm

In the operation process of a vehicle, the working environment is a critical factor influencing its path planning. Common methods for constructing environmental maps include the grid method, vector method, and free space method. Among these, the grid method is widely used for its intuitive, simple, and easy-to-establish nature, as well as its good compatibility with the A* algorithm. It works by finely dividing the area where the vehicle operates into numerous grids, thereby constructing an intuitive and easy-to-manipulate representation model.

3.1. Improvement of A* Algorithm

(1)

Improvement of Heuristic Function

The A* algorithm uses the cost function f(n) to calculate each reachable node, selecting the node with the lowest cost to determine the next step. By reasonably modifying the combined cost function f(n) of the traditional A* algorithm and increasing the weight of the heuristic function h(n), search efficiency can be improved. Specifically, when h(n) is always smaller than the actual cost g(n) from the current node to the target, the search space expands, leading to a larger number of explored nodes. Adjusting the weight of h(n) to give it a larger proportion in the calculation can more accurately direct the search direction, reducing unnecessary node exploration and enhancing the algorithm’s search efficiency. However, an excessive weight on the heuristic function can cause the algorithm to over-explore a single direction during pathfinding, ignoring other possible routes. In this case, the resulting path will no longer be optimal. The improvement method is to modify the heuristic function to not only consider the distance from the current node to the target, but also the distance from the current node to the starting point and the line connecting the target.

Reference [7] introduces an additional component to the heuristic function, which considers not only the distance from the current node to the target but also the distance from the current node to the line connecting the start and target points. This approach can narrow the search area and enable the algorithm to approach the target more quickly. Specifically, it modifies the heuristic function h(n) to

$$h(n)={\displaystyle \frac{|a{x}_n+b{y}_n+c|}{\sqrt{a^2+b^2}}}+\sqrt{{(x_n-x_g)}^2+{(y_n-y_g)}^2}$$

(6)

where a, b, and c are the three parameters of the linear equation representing the line connecting the start and target points.

Reference [8] does not modify the heuristic function but instead adopts an exponential function as the weighting coefficient for the heuristic function. The optimized cost function f(n) is given by

$$\begin{array}{cc}\hfill f(n)& =g(n)+{\exp }^{h(\mathrm{n})}\times h(n)\hfill \\ & =g(n)+{\exp }^{h(\mathrm{n})}\times \left({\displaystyle \frac{|a{x}_n+b{y}_n+c|}{\sqrt{a^2+b^2}}}+\sqrt{{(x_n-x_g)}^2+{(y_n-y_g)}^2}\right)\hfill \end{array}$$

(7)

Both of the above methods aim to enhance the heuristics of the cost function by increasing the proportion of the heuristic function. Thus, this paper integrates these two approaches to form a new cost estimation function. Taking an L-shaped obstacle as an example, Figure 2 compares the specific path results of four methods. In Figure 2, white grids represent unexplored nodes; blue grids denote examined nodes; black grids indicate obstacles; the red and blue grids mark the start and target nodes, respectively; and the red solid line shows the final path found by the algorithm.

As shown in Figure 2, the search area of the traditional A* algorithm is significantly larger than that of the other three methods. Modifying the heuristic function clearly restricts the search scope: the inclusion of the distance from the current node to the line connecting the start and target points increases the heuristic value for nodes deviating from this line, thereby reducing their likelihood of being selected. Additionally, a comparison between Figure 2c,d reveals that the improved heuristic function exhibits a pronounced convergent effect, narrowing the search focus effectively. Comparing Figure 2a,c shows that while the exponential weighting method enhances heuristic guidance, it struggles to navigate across rectangular obstacles. In mountainous environments with gullies and fallen trees, relying solely on exponential function improvements is clearly insufficient to adapt to the complex terrain.

The specific data for each algorithm in Figure 2 are shown in

Table 1. Statistical results of path planning under different algorithms.

Algorithm	Number of Searched Nodes	Path Length	Running Time
Traditional A* algorithm	267	39 m	5.994 s	--
Improved heuristic function	99	40.314 m	2.536 s	↓ 57.7%
Exponential weighted A* algorithm	105	46.21 m	2.626 s	↓ 56.2%
Improved exponential weighted A* algorithm	90	40.314 m	2.491 s	↓ 58.4%

. In the “Running Time” column, the first column is the time the algorithm is running, and the second column is the percentage of time saved compared to traditional algorithms In terms of search efficiency, whether by modifying heuristic functions or applying exponential weighting, it has excellent optimization effects compared to traditional algorithms, reducing search time by 57.7% and 56.2%, respectively. However, due to the limitations of exponential weighting, the path generated by this method is significantly longer than those of the other three approaches. Combining the heuristic function modification with exponential weighting overcomes this shortcoming. The results also indicate that the number of nodes has a greater impact on runtime than algorithm complexity to some extent. Since the traditional A* algorithm has weak heuristics and conducts more thorough exploration of surrounding nodes, it is reasonable that it achieves the shortest path among the methods compared.

(2)

Path optimization

In the scenario depicted in Figure 2, even after completing path planning, the resulting path still suffers from issues such as an excessive number of inflection points and a relatively long total length. Therefore, it is necessary to optimize this path. First, all inflection points in the path are extracted in sequence. The inflection point is the path inflection points in the global path generated by the improved A* algorithm, which can serve as sub objectives of the APF algorithm to facilitate dynamic obstacle avoidance. Notably, both the start node and the target node are treated as special inflection points and included in the extraction process. After extracting these points, the algorithm traverses each inflection point starting from the start node. If there are no obstacles between the start node and the current inflection point, the algorithm skips this point. If obstacles exist, it retains the previous inflection point and resumes traversal from that point to the subsequent ones, continuing until reaching the target node. Through this series of operations, the final generated path becomes the theoretically shortest path.

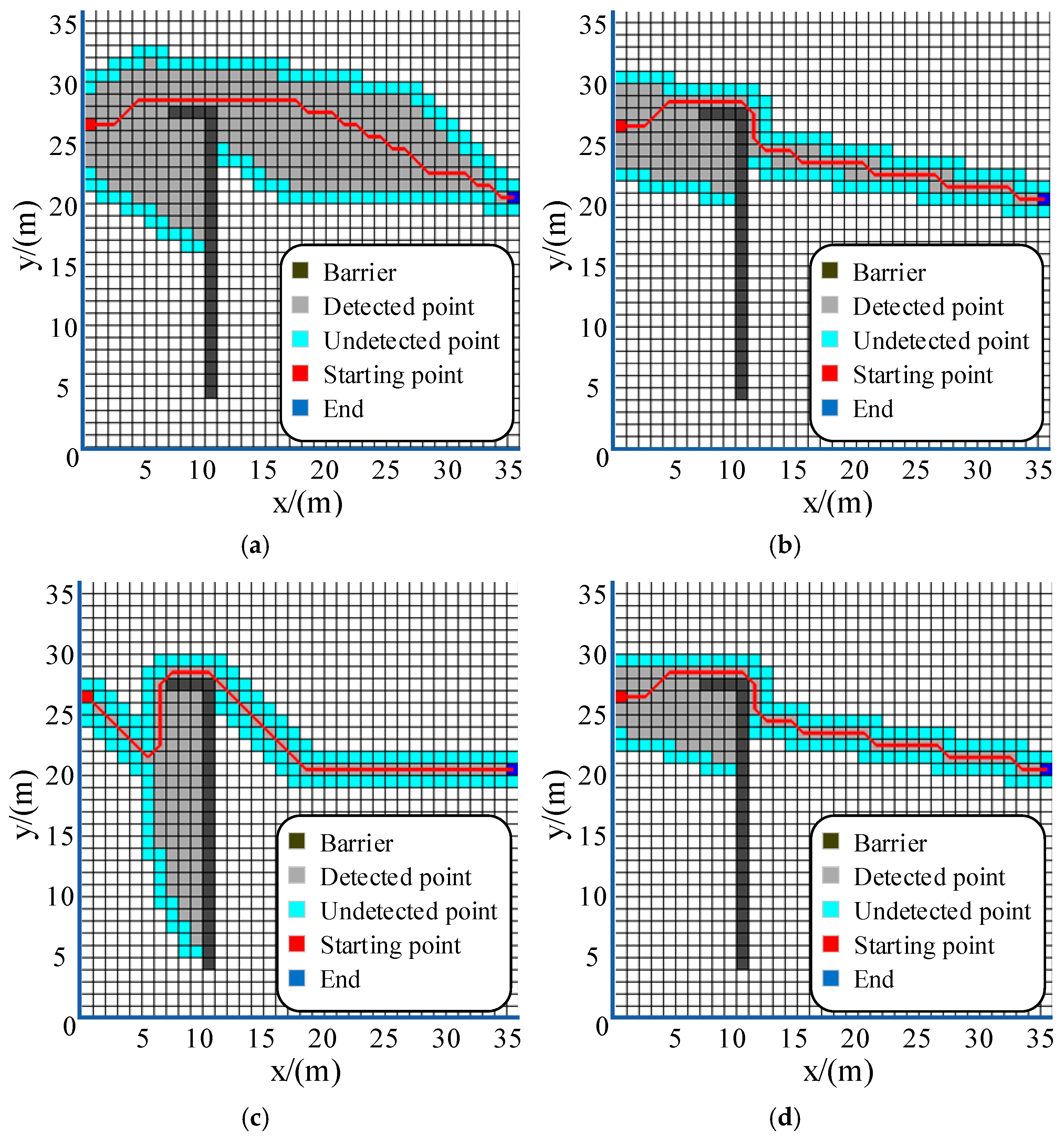
To generate random obstacles more consistent with mountainous environments, as shown in Figure 3, four algorithms were used for path planning in this environment, where the yellow solid line represents the optimized path. As indicated by Figure 3, after path optimization, the number of inflection points in the path is significantly reduced. Through statistical analysis of various data before and after algorithm optimization,

Table 2. Data before and after path optimization.

Algorithm	Number of Searched Nodes	Number of Inflection Points		Path Length
		Before	After	Before	After
Traditional A* algorithm	184	16	5	38.31 m	36.19 m
Improved heuristic function	66	13	5	38.31 m	36.21 m
Exponential weighted A* algorithm	40	19	6	44.46 m	40.07 m
Improved exponential Weighted A* algorithm	41	13	5	38.31 m	36.21 m

is obtained. The results show that this path optimization can substantially reduce the number of inflection points and effectively shorten the path length.

3.2. Improvement of APF Algorithm

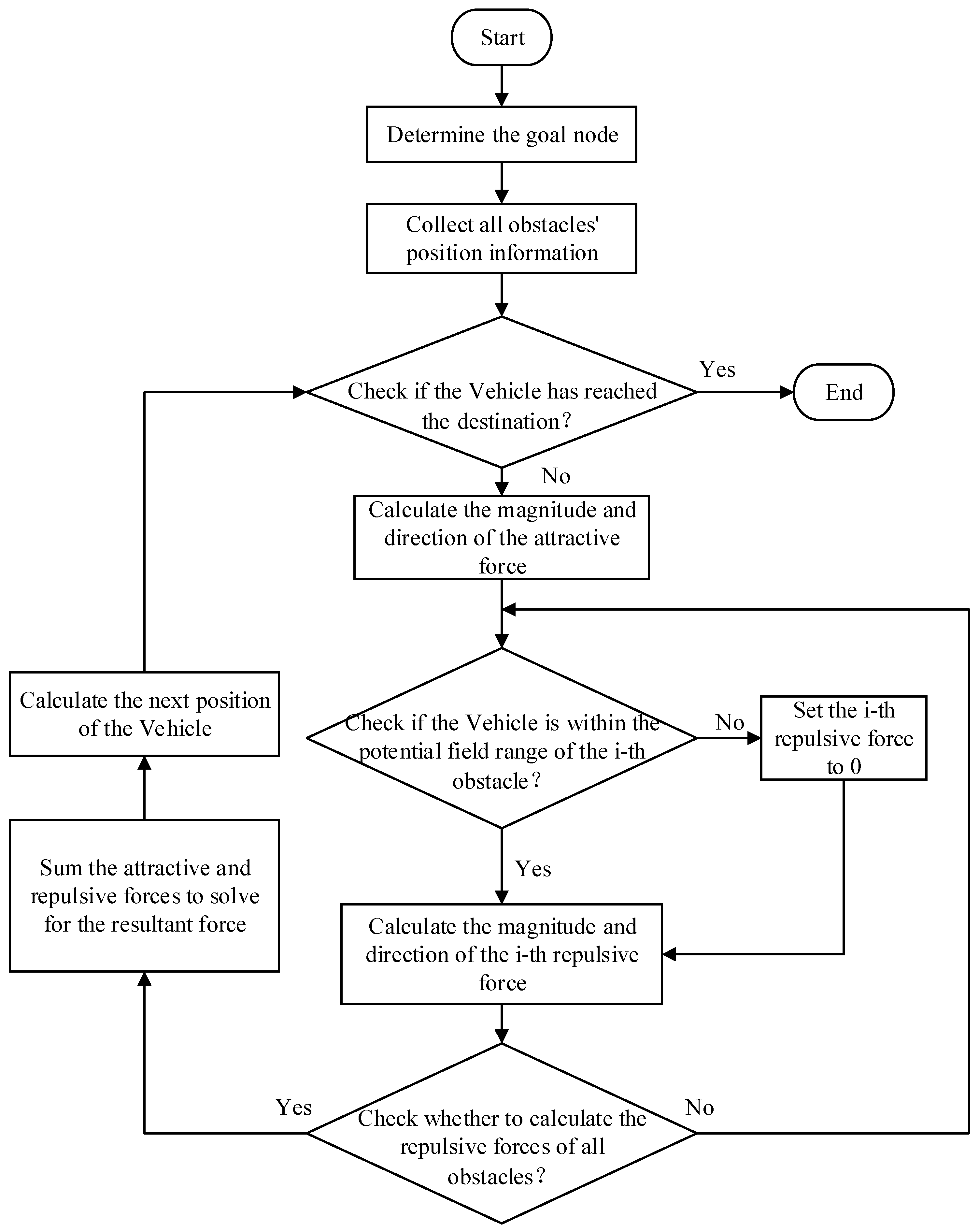
In the process of numerous practical applications, the traditional APF algorithm has two pressing issues to be resolved. The first is the local minimum problem, and the second is the target unreachable problem. Figure 4 shows the basic flowchart of the APF algorithm. The main idea of this paper is to divide the path into multiple sub-target points under the guidance of the A* algorithm, and when a local optimum point is encountered, the path is replanned. Since these are the two major problems of the APF algorithm, the improvement of the APF in this paper mainly focuses on the target unreachable problem.

In certain special environments, such as when obstacles are close to the target point, the traditional APF algorithm may prevent the robot from reaching the target. This is primarily because when the robot approaches the target, the repulsive force remains unchanged while the attractive force decreases significantly, leading to the attractive force being smaller than the repulsive force from obstacles, thus making it impossible for the robot to reach the target. To address this issue, the repulsive field function is modified by incorporating the distance between the robot and the target point. The improved repulsive field function, i.e., the repulsive force function, is given by

$${U^{\prime }}_{obs}=\left\{\begin{array}{l}{\displaystyle \frac{1}{2}}{k}_{obs}\left({\displaystyle \frac{1}{q}}-{\displaystyle \frac{1}{\lambda }}\right){\rho }^n q\le \lambda \\ 0 q>\lambda \end{array}\right.$$

(8)

$${\overrightarrow{F}}_{obs}=-\nabla {U^{\prime }}_{obs}=\left\{\begin{array}{l}{\overrightarrow{F}}_{obs1}+{\overrightarrow{F}}_{obs2} q\le \lambda \\ 0 q>\lambda \end{array}\right.$$

(9)

$$\left\{\begin{array}{c}|F_{obs1}|=k_{obs}\left({\displaystyle \frac{1}{q}}-{\displaystyle \frac{1}{\lambda }}\right){\displaystyle \frac{1}{q^2}}{\rho }^n\\ |F_{obs2}|={\displaystyle \frac{1}{2}}{k}_{obs}\left({\displaystyle \frac{1}{q}}-{\displaystyle \frac{1}{\lambda }}\right){\rho }^{n-1}\end{array}\right.$$

(10)

where n is a real number greater than 0, and F_obs1 and F_obs2 represent the repulsive force components. Specifically, F_obs1 is directed from the obstacle to the vehicle, while F_obs2 is directed from the vehicle to the target. This separation mirrors the potential field’s dual functional form, enabling independent tuning of distance-based repulsion and goal-oriented navigation behaviors.

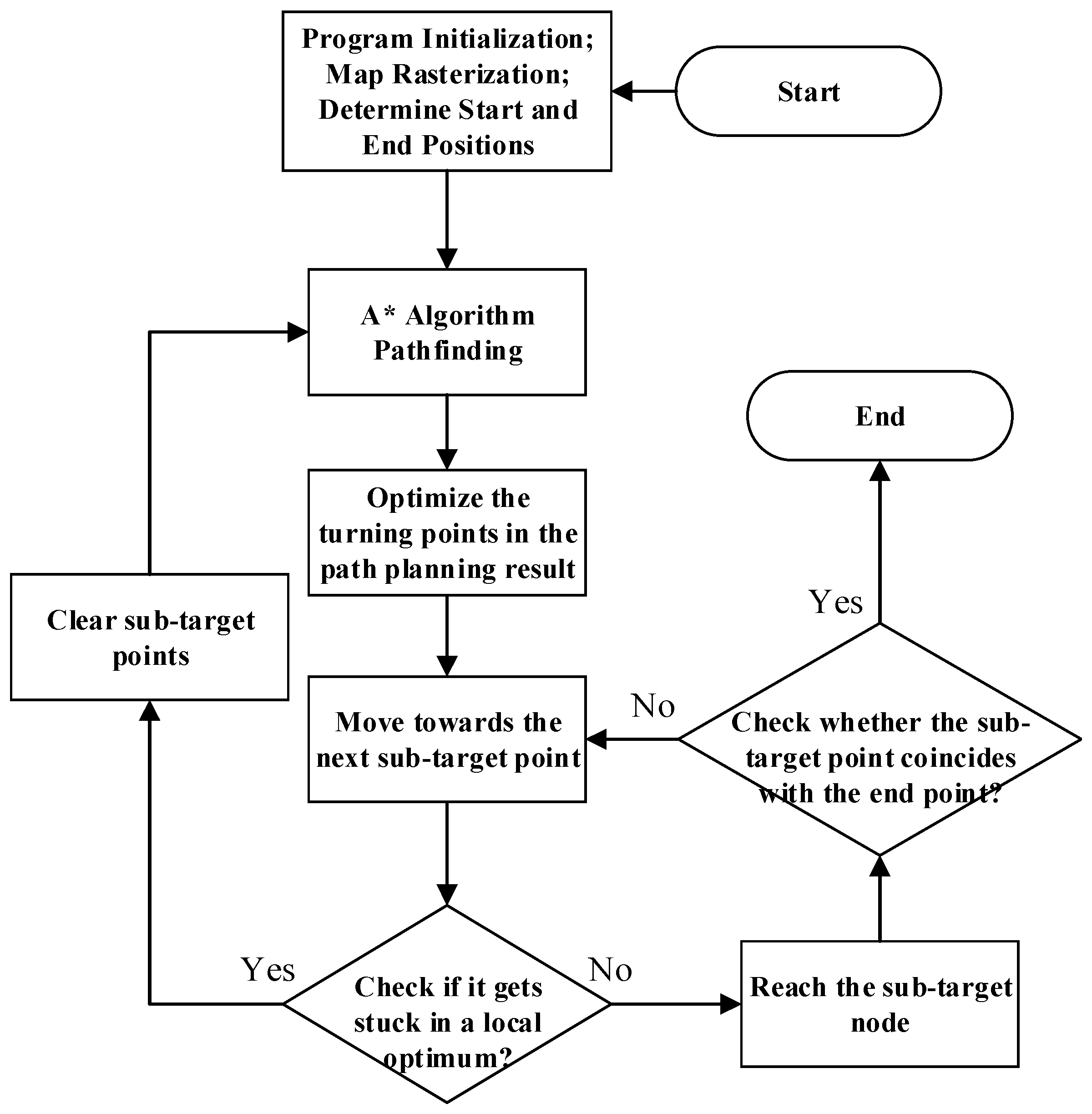
3.3. Improved A* Algorithm Combined with APF Algorithm

Through improvements, the A* algorithm effectively addresses the issue of low search efficiency. After path optimization, it can plan an optimal path. The APF algorithm, built upon the paths generated by the improved A* algorithm, is used to solve obstacle avoidance problems in dynamic environments. Meanwhile, when the APF algorithm encounters a local optimum, it replans the path to avoid this limitation. This paper integrates the two algorithms, enabling the combined approach to exhibit strong path-planning capabilities in both static environments and dynamic scenarios, as shown in Figure 5.

4. Simulation Verification of Fusion Algorithm

4.1. Static Planning

In mountainous environments, the distribution of obstacles is often complex, with narrow areas where planned paths may appear passable but are actually unnavigable in reality. Random obstacles were created on a 36 × 36 grid map, with the vehicle starting at coordinates (1, 27) and ending at (36, 21). Figure 6 shows the pathfinding results of the traditional APF algorithm and the APF algorithm guided by the improved A* algorithm, where blue dashed lines represent the vehicle’s movement trajectory.

As shown, the traditional APF algorithm failed to bypass large obstacles in complex setups (Figure 6a), struggling to navigate long strip-shaped barriers due to its lack of global path prediction. In contrast, the A*-guided APF algorithm generated a more reasonable and shorter path (Figure 6b), leveraging optimized inflection points from the improved A* as sub-targets for dynamic obstacle avoidance. However, single-pass planning may still trap the vehicle in local minima. To address this, the algorithm marked the current position as an obstacle and initiated secondary path planning upon detecting stagnation, ensuring successful destination reachability (Figure 6c). This validation highlights that integrating A*’s global optimization (via heuristic function modification and path pruning) with APF’s local adaptability (via target-distance factor adjustment) effectively balances real-time obstacle avoidance and global path optimality in complex terrains.

4.2. Dynamic Obstacle Avoidance

In mountainous environments, there are not only numerous static obstacles but also a small number of dynamic obstacles. To simplify calculations, this section adds dynamic obstacles to the static environment. Dynamic obstacles were modeled using a constant velocity framework with linear trajectories, spanning velocities of 0.5–1.0 m/s to simulate slow-moving debris or wildlife. Reciprocal linear motion served as the primary dynamic model, while sinusoidal trajectories were included in supplementary simulations to emulate erratic movements. Safety margins were ≥0.5 m for static obstacles and ≥1.0 m for dynamic ones, enforced via adaptive modifications to the APF repulsive field. Among them, three dynamic obstacles that were colored dark green moved reciprocally along diagonal, longitudinal, and lateral directions, respectively. The red line represents the path planned by the global algorithm, while the blue line denotes the real-time route adjusted for dynamic obstacles.

As shown in Figure 7, when the vehicle was approaching dynamic obstacles, the APF algorithm detected whether these obstacles affect its movement. When dynamic obstacles posed a threat, the bike initiated obstacle avoidance in advance. Meanwhile, while evading dynamic obstacles, it maintained a safe distance from static obstacles. After completing the avoidance maneuver, the vehicle returned to the route planned by the global path planning algorithm and eventually reached the target safely, verifying the effectiveness and safety of the local path planning. From the above simulation tests, it can be seen that during several instances of evading dynamic obstacles, the vehicle made significant deviations but successfully returned to the original route and reached the destination smoothly.

5. Conclusions and Discussion

This study focused on developing an efficient path planning solution for mountain transport vehicles in intricate environments. By integrating an improved A* algorithm with the APF algorithm, significant progress was achieved in both static and dynamic path planning scenarios.

In the improvement of the A* algorithm, the newly designed heuristic function, which combines the distance-based and line-distance-based factors, and the exponential weighting strategy effectively reduced the number of searched nodes and running time. The subsequent path optimization step further streamlined the path by minimizing inflection points and shortening its length. These enhancements contribute to a more efficient global path-planning process.

For the APF algorithm, the modification of the repulsive field function by incorporating the target distance factor successfully overcame the target-unreachable issue. When integrated with the improved A* algorithm, the combined approach used the optimized inflection points from the A* algorithm as sub-target points for the APF, enabling real-time obstacle avoidance in dynamic environments.

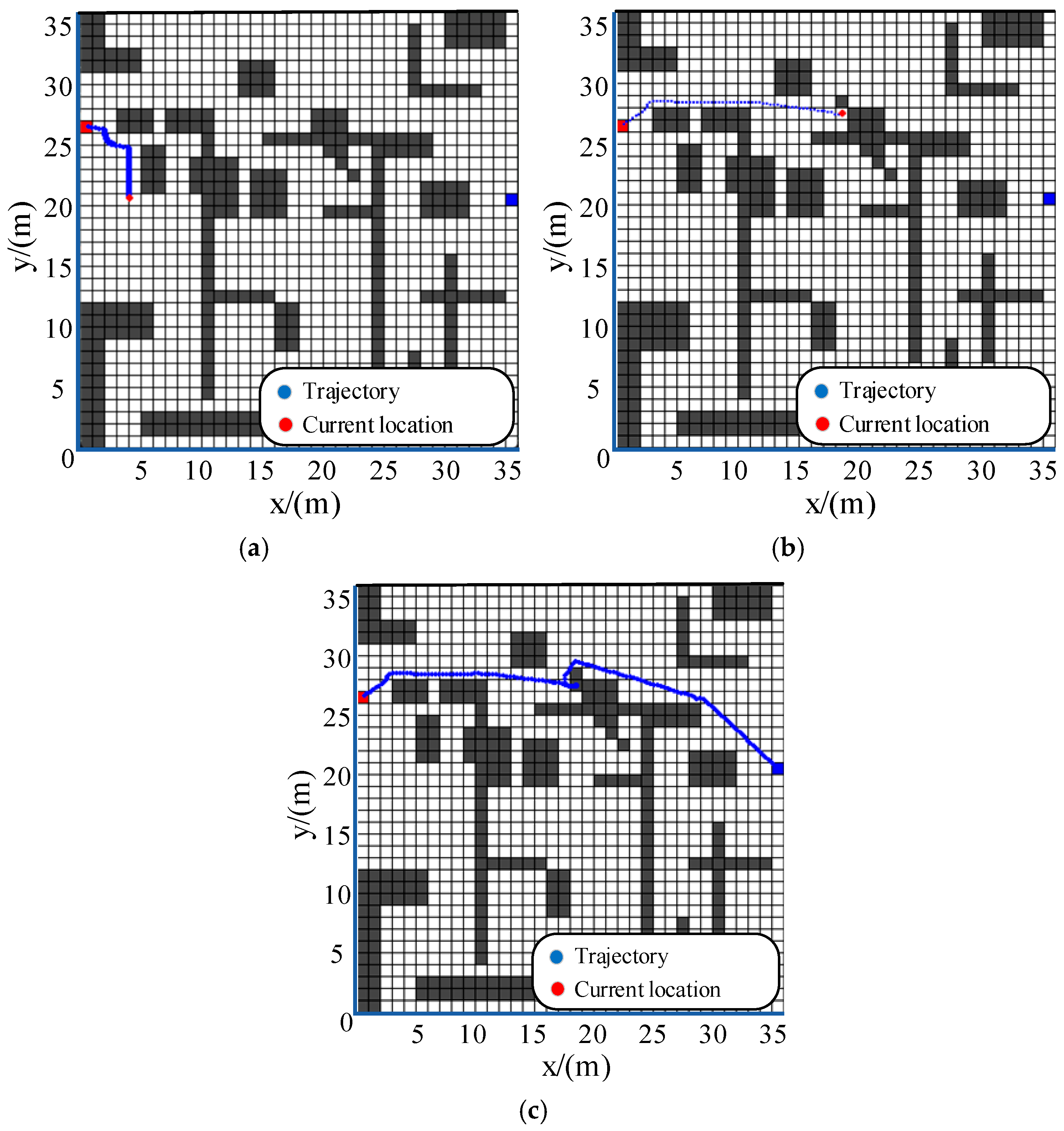
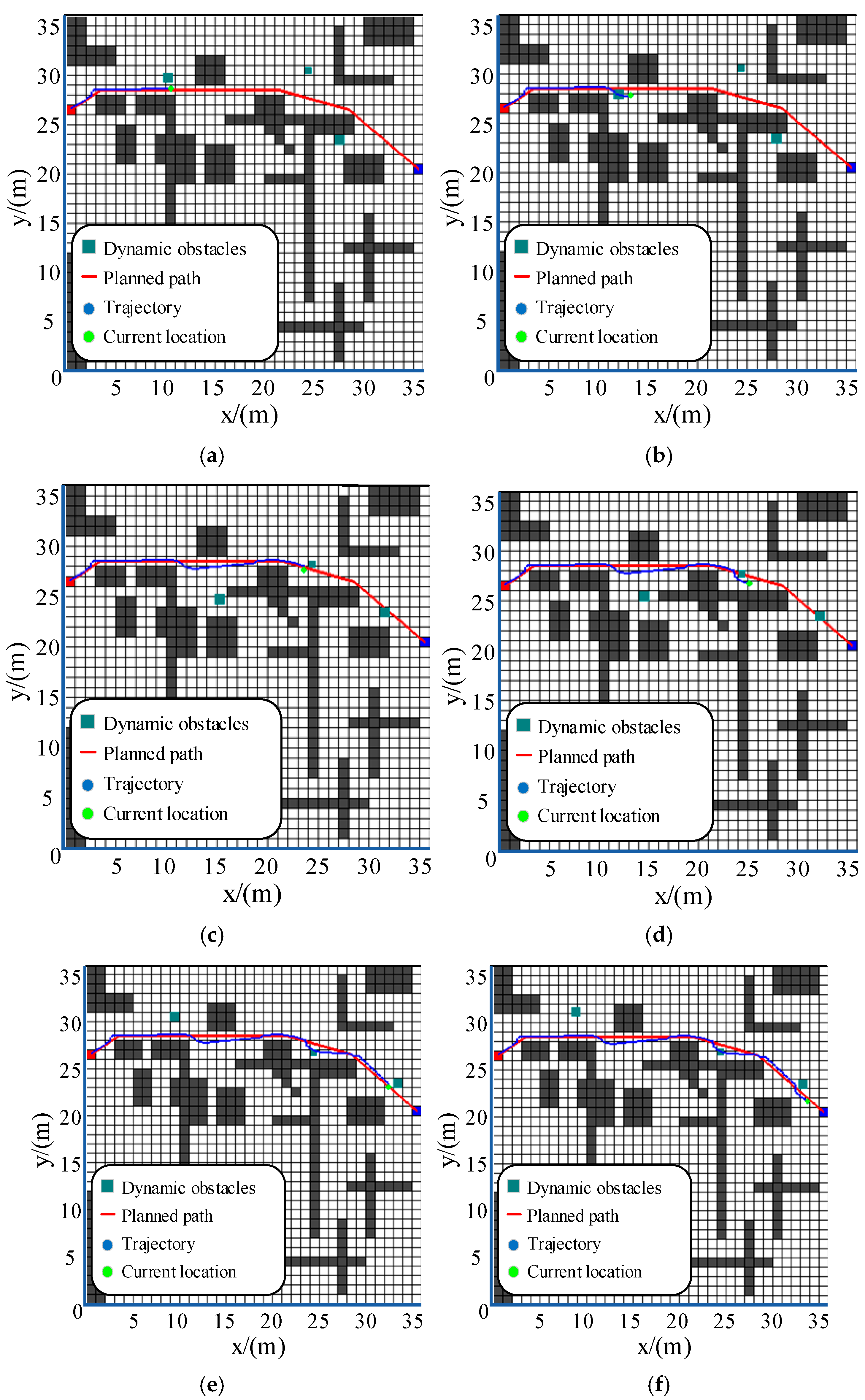
In the simulation verification, in static environments, the integrated algorithm outperformed the traditional APF algorithm. It can plan paths around complex obstacles in mountainous terrains, and the secondary path-planning mechanism effectively resolves local-minimum problems. In dynamic obstacle-avoidance scenarios, the algorithm can accurately detect approaching dynamic obstacles and initiate timely avoidance maneuvers while maintaining a safe distance from static obstacles. This indicates its high adaptability and reliability in dynamic environments.

However, there are still areas for improvement. For example, the computational complexity of the integrated algorithm may increase in extremely large-scale and highly complex environments. Future research could explore ways to further optimize the algorithm’s computational efficiency without sacrificing path-planning quality. Additionally, more real-world experimental data is needed to fully validate the algorithm’s performance in diverse mountainous terrains, and we plan to conduct prototype tests in future work.