Motor Vehicle Brake Pad Wear—A Review
Abstract
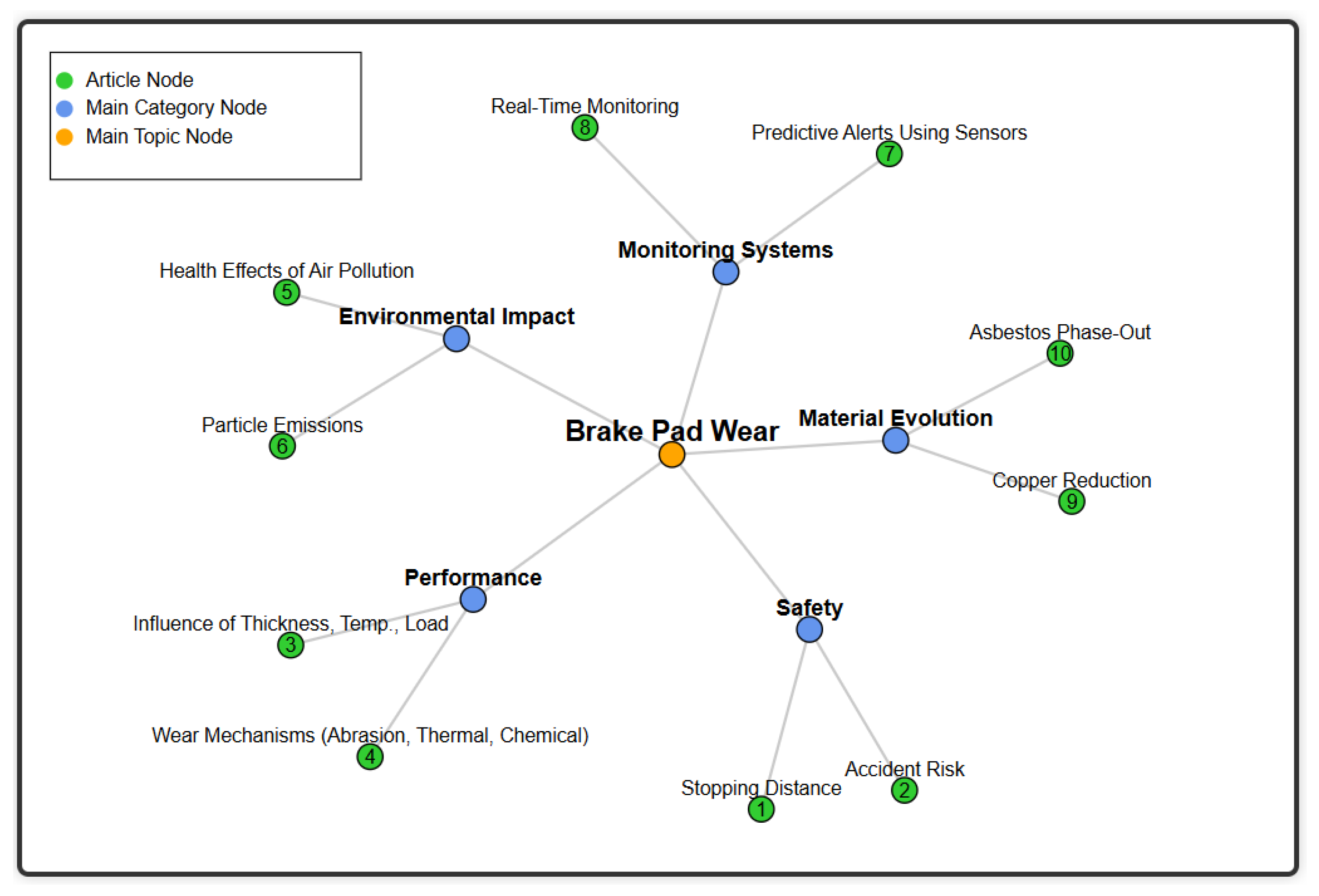
1. Introduction
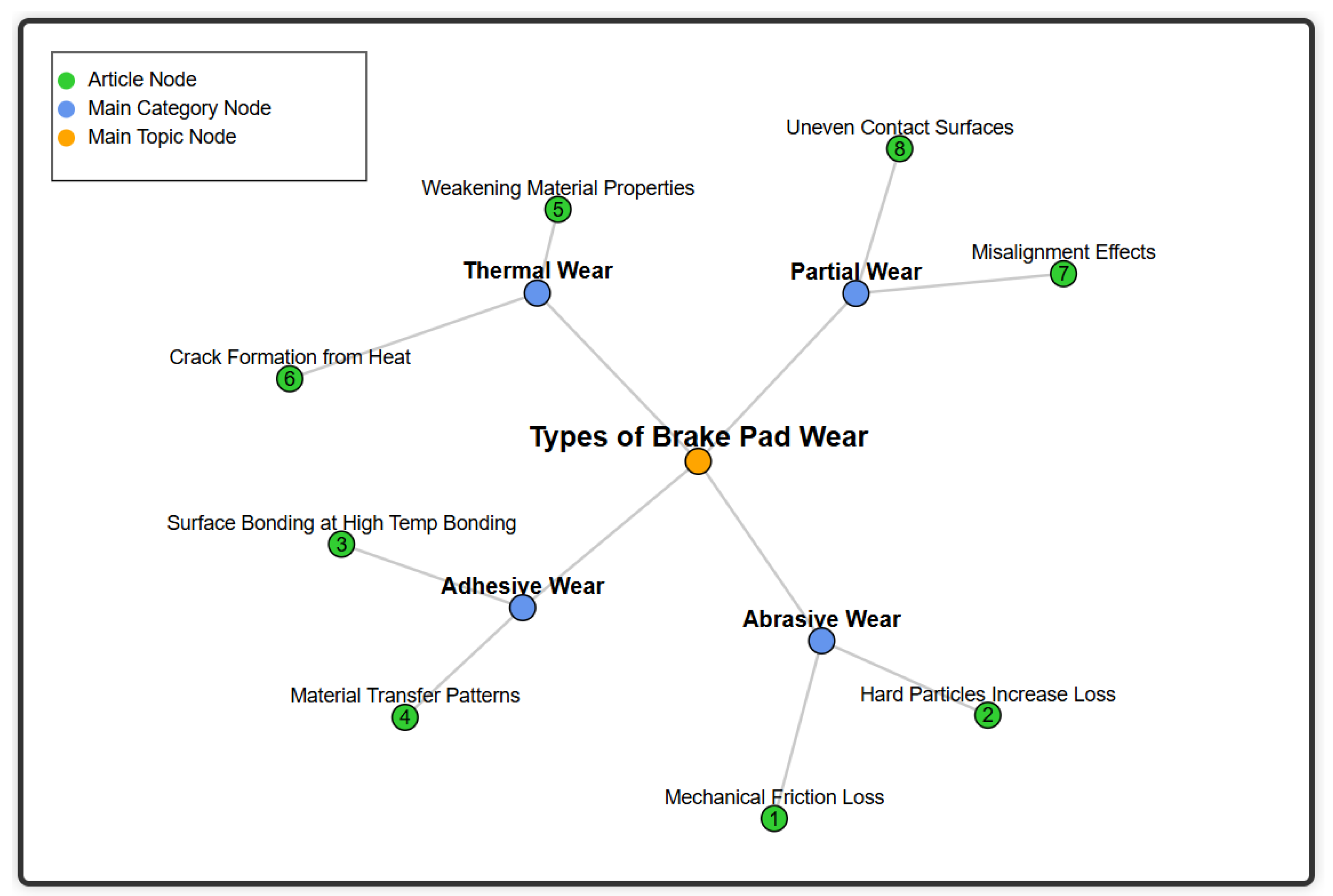
2. Types of Wear on Brake Pads
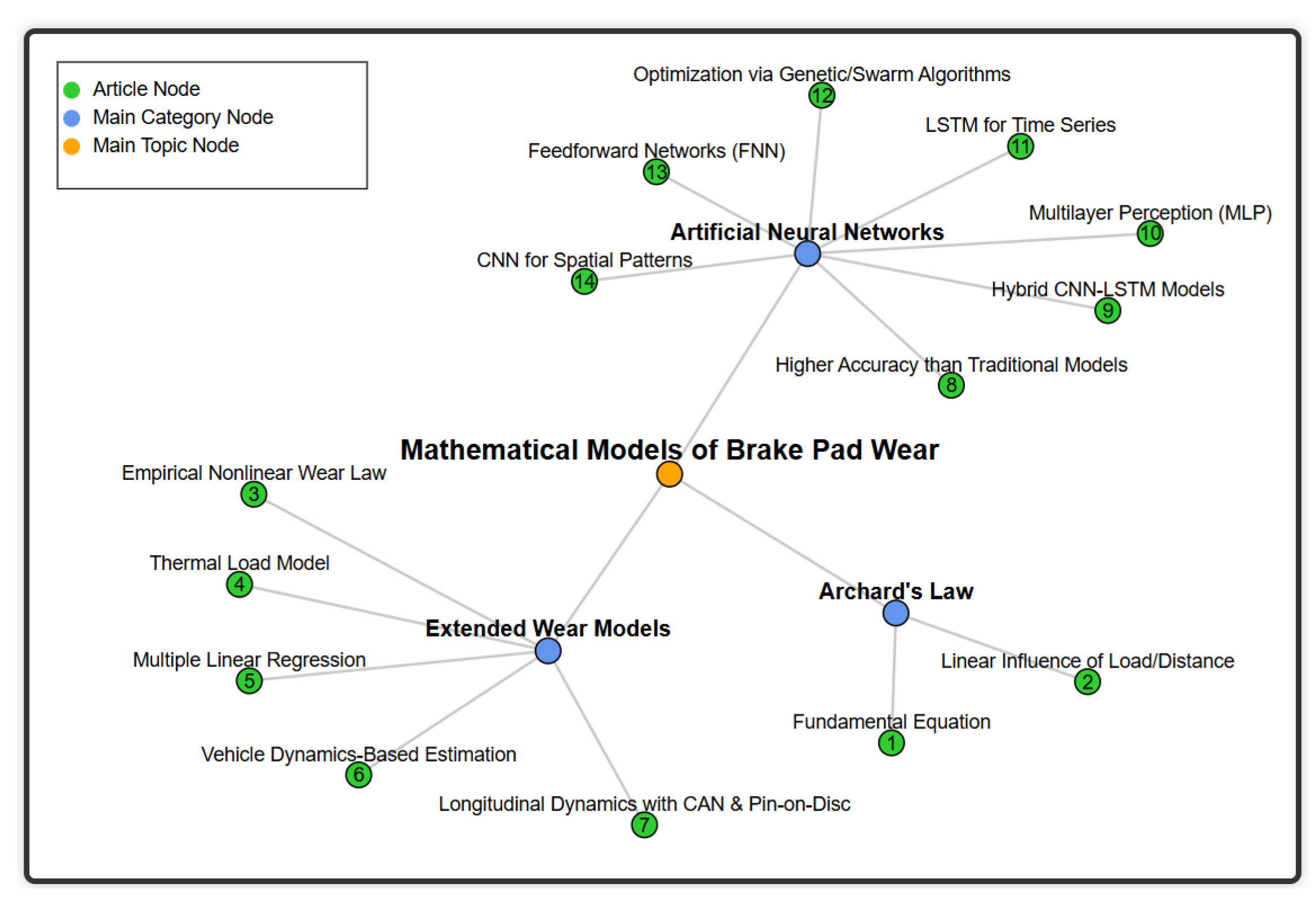
3. Mathematical Analysis of Brake Pad Wear
3.1. Archard’s Law
3.2. Wear Calculation Models
3.3. Artificial Neural Networks (ANNs)
4. Influence Factors of the Wear Coefficient
4.1. The Thermo-Elastic Instability (TEI) Phenomenon
4.2. Surface Quality
4.3. Chemical Affinity Between Disc and Pad Surfaces
5. Wear Detection and Prediction Systems
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.; Yu, Z.; Wang, J.; Chen, S. Research on CNN-LSTM Brake Pad Wear Condition Monitoring Based on GTO Multi-Objective Optimization. Actuators 2023, 12, 301. [Google Scholar] [CrossRef]
- Cao, J.; Bao, J.; Yin, Y.; Wang, Y.; Liu, T.; Cao, T. Intelligent Prediction of Wear Life of Automobile Brake Pad Based on Braking Conditions. Ind. Lubr. Tribol. 2022, 75, 157–165. [Google Scholar] [CrossRef]
- Hao, J.; Yin, X.; Zhu, S.; Ren, J.; Liu, X. Analysis of the Tribological Behavior of the High-Speed and Heavy-Load Braking Interface With Dynamic Wear of Brake Pads. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2023, 237, 1930–1942. [Google Scholar] [CrossRef]
- Li, W.; Zheng, H.; Zong, C. A Brake Pad Wear Control Algorithm for Electronic Brake System. Adv. Mater. Res. 2013, 694, 2099–2105. [Google Scholar] [CrossRef]
- Laguna-Camacho, J.; Juárez-Morales, G.; Calderón-Ramón, C.; Velázquez-Martínez, V.; Hernández-Romero, I.; Méndez-Méndez, J.V.; Vite-Torres, M. A Study of the Wear Mechanisms of Disk and Shoe Brake Pads. Eng. Fail. Anal. 2015, 56, 348–359. [Google Scholar] [CrossRef]
- Yavuz, H.; Bayrakçeken, H. Investigation of Friction and Wear Behavior of Composite Brake Pads Produced with Huntite Mineral. Int. J. Automot. Sci. Technol. 2022, 6, 9–16. [Google Scholar] [CrossRef]
- Rahimi, M.; Bortoluzzi, D.; Wahlström, J. Input Parameters for Airborne Brake Wear Emission Simulations: A Comprehensive Review. Atmosphere 2021, 12, 871. [Google Scholar] [CrossRef]
- Hendre, K.; Bachchhav, B. Friction and Wear Characteristics of Rubber Resin-Bonded Metallic Brake Pad Materials. Int. J. Eng. Adv. Technol. 2019, 8, 1312–1316. [Google Scholar] [CrossRef]
- Ismailov, K.; Shermukhamedov, A.; Alimova, Z.; Rakhmatov, U. Determination of the Quantity of Particles Emitted to the Environment as a Result of Wearing Car Brake Pads. Preprint on ResearchGate, February 2024. Available online: https://www.researchgate.net/publication/231277179_Brake_Wear_Particulate_Matter_Emissions (accessed on 26 May 2025).
- Kalhapure, V.A.; Khairnar, H.P. Taguchi Method Optimization of Operating Parameters for Automotive Disc Brake Pad Wear. Appl. Eng. Lett. J. Eng. Appl. Sci. 2021, 6, 47–53. [Google Scholar] [CrossRef]
- Zhang, S.; Hao, Q.; Liu, Y.; Li, J.; Ma, F.; Sha, Z.; Yang, D. Simulation Study on Friction and Wear Law of Brake Pad in High-Power Disc Brake. Math. Probl. Eng. 2019, 2019, 6250694. [Google Scholar] [CrossRef]
- Han, X.; Zhao, C.; Yang, J.; Su, L.; Fu, R.; Gao, F. Influence of Contacting Shape of Partial Wear on Friction Properties of Copper-Based Materials for Trains. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2023, 237, 1098–1106. [Google Scholar] [CrossRef]
- Kalidas, P.; Vignesh, R.V.; Govindaraju, M.; Kasi, R.K.; Baghad, A. Numerical and Experimental Validation of Tribological Phenomenon in Wind Turbine Brake Pads Using Novel Archard’s Wear Coefficient. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2024, 238, 1103–1120. [Google Scholar] [CrossRef]
- Rhee, S. Wear equation for polymers sliding against metal surfaces. Wear 1970, 16, 431–445. [Google Scholar] [CrossRef]
- Bakar, A.R.A.; Li, L.; James, S.; Ouyang, H.; Siegel, J.E. Wear simulation and its effect on contact pressure distribution and squeal of a disc brake. In Proceedings of the International Conference on Vehicle Braking Technology, York, UK, 7–9 May 2006; pp. 233–242. [Google Scholar]
- AbuBakar, A.R.; Ouyang, H. Wear prediction of friction material and brake squeal using the finite element method. Wear 2008, 264, 1069–1076. [Google Scholar] [CrossRef]
- Patil, S.P.; Chilakamarri, S.H.; Markert, B. A novel nonlinear nano-scale wear law for metallic brake pads. Phys. Chem. Chem. Phys. 2018, 20, 12027–12036. [Google Scholar] [CrossRef]
- Hohmann, C.; Schiffner, K.; Brecht, J. Pad Wear Simulation Model. SAE Trans. 1999, 108, 3389–3397. [Google Scholar]
- Bakar, A.A.A.; Ouyang, H.; James, S.; Li, L. Finite element analysis of wear and its effect on squeal generation. Sage J. 2008, 222, 1153–1165. [Google Scholar] [CrossRef]
- Basista, G.; Hajos, M.; Francik, S.; Pedryc, N. Prediction of Brake Pad Wear of Trucks Transporting Oversize Loads Based on the Number of Drivers’ Braking and the Load Level of the Trucks—Multiple Regression Models. Appl. Sci. 2024, 14, 5408. [Google Scholar] [CrossRef]
- Ikpambese, K.K.; Lawrence, E. Comparative Analysis of Multiple Linear Regression and Artificial Neural Network for Predicting Friction and Wear of Automotive Brake Pads Produced from Palm Kernel Shell. Tribol. Ind. 2018, 40, 565. [Google Scholar] [CrossRef]
- Sawczuk, W.; Merkisz-Guranowska, A.; Cañás, A.M.R.; Kołodziejski, S. New approach to brake pad wear modelling based on test stand friction-mechanical investigations. Eksploat. Niezawodn. Maint. Reliab. 2022, 24, 419–426. [Google Scholar] [CrossRef]
- Hwang, J.Y. Method of Estimating Brake Pad Wear and Vehicle Having a Controller that Implements the Method. US9416835B2, 16 August 2011. [Google Scholar]
- Jensen, K.M.; Santos, I.F.; Corstens, H.J. Estimation of brake pad wear and remaining useful life from fused sensor system, statistical data processing, and passenger car longitudinal dynamics. Wear 2024, 538–539, 205220. [Google Scholar] [CrossRef]
- Jensen, K.M.; Santos, I.F.; Corstens, H.J. Prediction of brake pad wear and remaining useful life considering varying vehicle mass and an experimental holistic approach. Wear 2024, 552–553, 205433. [Google Scholar] [CrossRef]
- Ricciardi, V.; Augsburg, K.; Gramstat, S.; Schreiber, V.; Ivanov, V. Survey on Modelling and Techniques for Friction Estimation in Automotive Brakes. Appl. Sci. 2017, 7, 873. [Google Scholar] [CrossRef]
- Saša, V.; Glisovic, J.; Stojanovic, N.; Grujic, I. Application of neural networks in predictions of brake wear particulate matter emission. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 095440702110363. [Google Scholar] [CrossRef]
- Wang, S.; YU, Z.; XU, G.; CHEN, S. CNN-LSTM Based on Attention Mechanism for Brake Pad Remaining Life Prediction. Mech. Eng. Sci. 2022, 4, 30–38. [Google Scholar] [CrossRef]
- Aleksendrić, D.; Duboka, v.; Mariotti, G.V. Neural Modelling of Friction Material Cold Performance. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2008, 222, 1201–1209. [Google Scholar] [CrossRef]
- Hassan, A.K.F.; Mohammed, S. Artificial Neural Network Model for Estimation of Wear and Temperature in Pin-Disc Contact. Univers. J. Mech. Eng. 2016, 4, 39–49. [Google Scholar] [CrossRef]
- Kato, H.; Todaka, Y. Microstructure and Wear Properties of High-Pressure Torsion Processed Iron. In Materials Science Forum; Trans Tech Publications Ltd.: Baech, Switzerland, 2017. [Google Scholar] [CrossRef]
- Ipate, G.; Ilie, F.; Cristescu, A.C. Finite Element 3D Numerical Simulation Study of Car Braking Systems and Brake Disc/Drum—Pad/Shoe Friction Couple Materials. In E3s Web of Conferences; EDP Sciences: Les Ulis, France, 2020. [Google Scholar] [CrossRef]
- Dani Nandiyanto, A.B.; Al Husaeni, D.N.; Ragadhita, R.; Fiandini, M.; Al Husaeni, D.F.; Aziz, M. Resin Matrix Composition on the Performance of Brake Pads Made From Durian Seeds: From Computational Bibliometric Literature Analysis to Experiment. Automot. Exp. 2022, 5, 328–342. [Google Scholar] [CrossRef]
- Krishnan, G.S.; Jayakumari, L.S.; Vijay, R. Effect of Graphitization Percentage on Fade and Recovery Performance of Copper-Free Non-Asbestos Organic Brake Pads. Ind. Lubr. Tribol. 2022, 74, 901–909. [Google Scholar] [CrossRef]
- Yavuz, H. An Experimental Case Study on the Comparison of the Use of Micronized Quartz and Alumina in Brake Pads. Türk Doğa Ve Fen Dergisi 2023, 12, 9–14. [Google Scholar] [CrossRef]
- Majeed, B.; Baştürk, S. Analysis of Polymeric Composite Materials for Frictional Wear Resistance Purposes. Polym. Polym. Compos. 2020, 29, 127–137. [Google Scholar] [CrossRef]
- Mahale, V.; Bijwe, J. Role of Thermal Conductivity in Controlling the Tribo-Performance of Non-Asbestos Organic Brake-Pads. J. Compos. Mater. 2020, 54, 4145–4155. [Google Scholar] [CrossRef]
- Öktem, H.; Akıncıoğlu, S.; Uygur, İ.; Akıncıoğlu, G. A novel study of hybrid brake pad composites: New formulation, tribological behaviour and characterisation of microstructure. Plast. Rubber Compos. 2021, 50, 249–261. [Google Scholar] [CrossRef]
- Öztürk, B.; Arslan, F.; Öztürk, S. Effects of Different Kinds of Fibers on Mechanical and Tribological Properties of Brake Friction Materials. Tribol. Trans. 2013, 56, 536–545. [Google Scholar] [CrossRef]
- Xiao, X.; Bao, J.; Lu, L.; Feng, X. Review on the friction and wear of brake materials. Adv. Mech. Eng. 2016, 8, 1687814016647300. [Google Scholar] [CrossRef]
- Majuma, R.; Bin Peeie, M.H.; Ondong, K.; Hassan, O.A. Investigation of Brake Pad Wear Effect Due to Temperature Generation Influenced by Brake Stepping Count on Different Road Terrains. Automot. Exp. 2023, 6, 234–244. [Google Scholar] [CrossRef]
- Abu Bakar, A.R.; Ouyang, H.; Khai, L.C.; Abdullah, M.S. Thermal Analysis of a Disc Brake Model Considering a Real Brake Pad Surface and Wear. Int. J. Veh. Struct. Syst. 2010, 2, 20. [Google Scholar] [CrossRef][Green Version]
- Ramkumar, E.; Mayuram, M. Coupled Temperature-Displacement Modeling to Study the Thermo-Elastic Instability in Disc Brakes. Coupled Syst. Mech. Int. J. 2012, 1, 165–182. [Google Scholar] [CrossRef]
- Voloaca, S.; Fratila, G. Concerns Regarding Temperature Distribution Obtained By Experiments Furthermore, Finite Element Analyses For Two Types Of Brake Discs. UPB Sci. Bull. Ser. D Mech. Eng. 2012, 74, 33–42. [Google Scholar]
- Hwang, J.H.; Kim, H.S.; Choi, Y.; Kim, B.S.; Kang, K.W. The Thermal Analysis of Brake Disc With 3-D Coupled Analysis. Key Eng. Mater. 2005, 297, 305–310. [Google Scholar] [CrossRef]
- Cho, C.; Ahn, S. Thermo-Elastic Analysis for Chattering Phenomenon of Automotive Disk Brake. Ksme Int. J. 2001, 15, 569–579. [Google Scholar] [CrossRef]
- Qiao, Y.; Yi, Y.; Wang, T.; Cui, H.; Lian, Z. Effect of Wear on Thermoelastic Instability Involving Friction Pair Thickness in Automotive Clutches. J. Tribol. 2021, 144, 041202. [Google Scholar] [CrossRef]
- Sandip, S.S.; Purohit, P. Digital investigation of friction composites for automotive brake pads. UPB Sci. Bull. Ser. D Mech. Eng. 2024, 86, 119–132. [Google Scholar]
- Vdovin, A.; Gigan, G.L. Aerodynamic and Thermal Modelling of Disc Brakes—Challenges and Limitations. Energies 2020, 13, 203. [Google Scholar] [CrossRef]
- Karabay, S.; Baynal, K.; İğdeli, C. Detecting Groan Sources in Drum Brakes of Commercial Vehicles by TVA-FMEA: A Case Study. Stroj. Vestn. J. Mech. Eng. 2013, 59, 375–386. [Google Scholar] [CrossRef]
- Shinde, D.; Bulsara, M.; Mistry, K.N. Tribological Performance of Non-Asbestos Brake Friction Material in Contact With Brake Disc of Varying Topography. Ind. Lubr. Tribol. 2020, 72, 1277–1283. [Google Scholar] [CrossRef]
- Bucur, F.; Pascu, L.; Birtok Baneasa, C.; Budiul Berghian, A.; Socalici, A. Research on the Production Of Composite Materials for Brake Shoes. UPB Sci. Bull. Ser. B Chem. Mater. Sci. 2022, 84, 227–236. [Google Scholar]
- Fadzli Mokti, M.F.; Abdul Hamid, M.K.; Abu Bakar, A.R. Humidity and Water Effect on Wear Characteristics of Disc Braking System. Appl. Mech. Mater. 2016, 819, 612–617. [Google Scholar] [CrossRef]
- Yavuz, H.; Bayrakçeken, H. Friction and Wear Characteristics of Brake Friction Materials Obtained from Fiber and Huntite Blends. Ind. Lubr. Tribol. 2022, 74, 844–852. [Google Scholar] [CrossRef]
- Stoica, N.A.; Tudor, A. Experimental Results About The Stick-Slip Phenomenon With Application To The Disc-Brake Friction Materials Couple Used In The Automotive Domain. UPB Sci. Bull. Ser. D Mech. Eng. 2018, 80, 155–170. [Google Scholar]
- Sethupathi, P.B.; Chandradass, J. Comparative Study of Different Solid Lubricants Towards Friction Stability in a Non-Asbestos Disc Brake Pad. Ind. Lubr. Tribol. 2021, 73, 897–903. [Google Scholar] [CrossRef]
- Josan, A.; Pinca-Bretotean, C. Effect of the Alloying Elements on the Properties of Gray Cast Iron Used For Automotive Brake Discs. UPB Sci. Bull. Ser. B Chem. Mater. Sci. 2022, 84, 247–258. [Google Scholar]
- Roman, A.; Braga Lemos, G.V.; Gasparin, A.L. Friction Material Wear: Effects and Interactions Between Service Brake Temperature, Lining Contact Pressure, and Vehicle Speed. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2022, 236, 2468–2476. [Google Scholar] [CrossRef]
- Woo, S.H.; Lee, G.; Han, B.; Lee, S. Development of Dust Collectors to Reduce Brake Wear PM Emissions. Atmosphere 2022, 13, 1121. [Google Scholar] [CrossRef]
- Świderski, A.; Borucka, A.; Jacyna-Gołda, I.; Szczepański, E. Wear of Brake System Components in Various Operating Conditions of Vehicle in the Transport Company. Eksploat. I Niezawodn. Maint. Reliab. 2019, 21, 1–9. [Google Scholar] [CrossRef]
- Federici, M.; Alemani, M.; Menapace, C.; Gialanella, S.; Perricone, G.; Straffelini, G. A critical comparison of dynamometer data with pin-on-disc data for the same two friction material pairs—A case study. Wear 2019, 424–425, 40–47. [Google Scholar] [CrossRef]
- Akincioglu, G.; Akincioglu, S.; Oktem, H.; Uygur, I. Brake Pad Performance Characteristic Assessment Methods. Int. J. Automot. Sci. Technol. 2021, 5, 67–78. [Google Scholar] [CrossRef]
- Fahruzi, A.; Wardaya, A.Y.; Suryowinoto, A. Estimation of Brake Pad Wear Using Fuzzy Logic in Real Time. Inf. J. Ilm. Bid. Teknol. Inf. Dan Komun. 2023, 8, 78–83. [Google Scholar] [CrossRef]
- Lamjahdy, A.; Ali, J.K.; Markert, B. Simulation of the Temperature and Wear Behaviour of a Disc Brake. Pamm 2016, 16, 217–218. [Google Scholar] [CrossRef][Green Version]
- Yin, Y.G.; Bao, J.; Yang, L. Wear Performance and Its Online Monitoring of the Semimetal Brake Lining for Automobiles. Ind. Lubr. Tribol. 2014, 66, 100–105. [Google Scholar] [CrossRef]
- Prajapati, D.K.; Tiwari, M. Use of artificial neural network (ANN) to determining surface parameters, friction and wear during pin-on-disc tribotesting. Key Eng. Mater. 2017, 739, 87–95. [Google Scholar] [CrossRef]
- Aleksendrić, D. Neural network prediction of brake friction materials wear. Wear 2010, 268, 117–125. [Google Scholar] [CrossRef]
- Kuncy, I.K.; Abugh, A.; Tyovenda, T.L. Prediction of Wear and Friction Coefficient of Brake Pads Developed from Palm Kernel Fibres Using Artificial Neural Network. J. Eng. Stud. Res. 2017, 20, 45. [Google Scholar] [CrossRef]
- Han, J.H.; Wu, Q.S. Artificial neural network for predicting wear properties of brake lining materials. Adv. Mater. Res. 2011, 328, 237–240. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voloacă, Ş.; Badea-Romero, A.; Badea-Romero, F.; Toma, M.F. Motor Vehicle Brake Pad Wear—A Review. Vehicles 2025, 7, 52. https://doi.org/10.3390/vehicles7020052
Voloacă Ş, Badea-Romero A, Badea-Romero F, Toma MF. Motor Vehicle Brake Pad Wear—A Review. Vehicles. 2025; 7(2):52. https://doi.org/10.3390/vehicles7020052
Chicago/Turabian StyleVoloacă, Ştefan, Alexandro Badea-Romero, Francisco Badea-Romero, and Marius Florin Toma. 2025. "Motor Vehicle Brake Pad Wear—A Review" Vehicles 7, no. 2: 52. https://doi.org/10.3390/vehicles7020052
APA StyleVoloacă, Ş., Badea-Romero, A., Badea-Romero, F., & Toma, M. F. (2025). Motor Vehicle Brake Pad Wear—A Review. Vehicles, 7(2), 52. https://doi.org/10.3390/vehicles7020052






