Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM)
Abstract
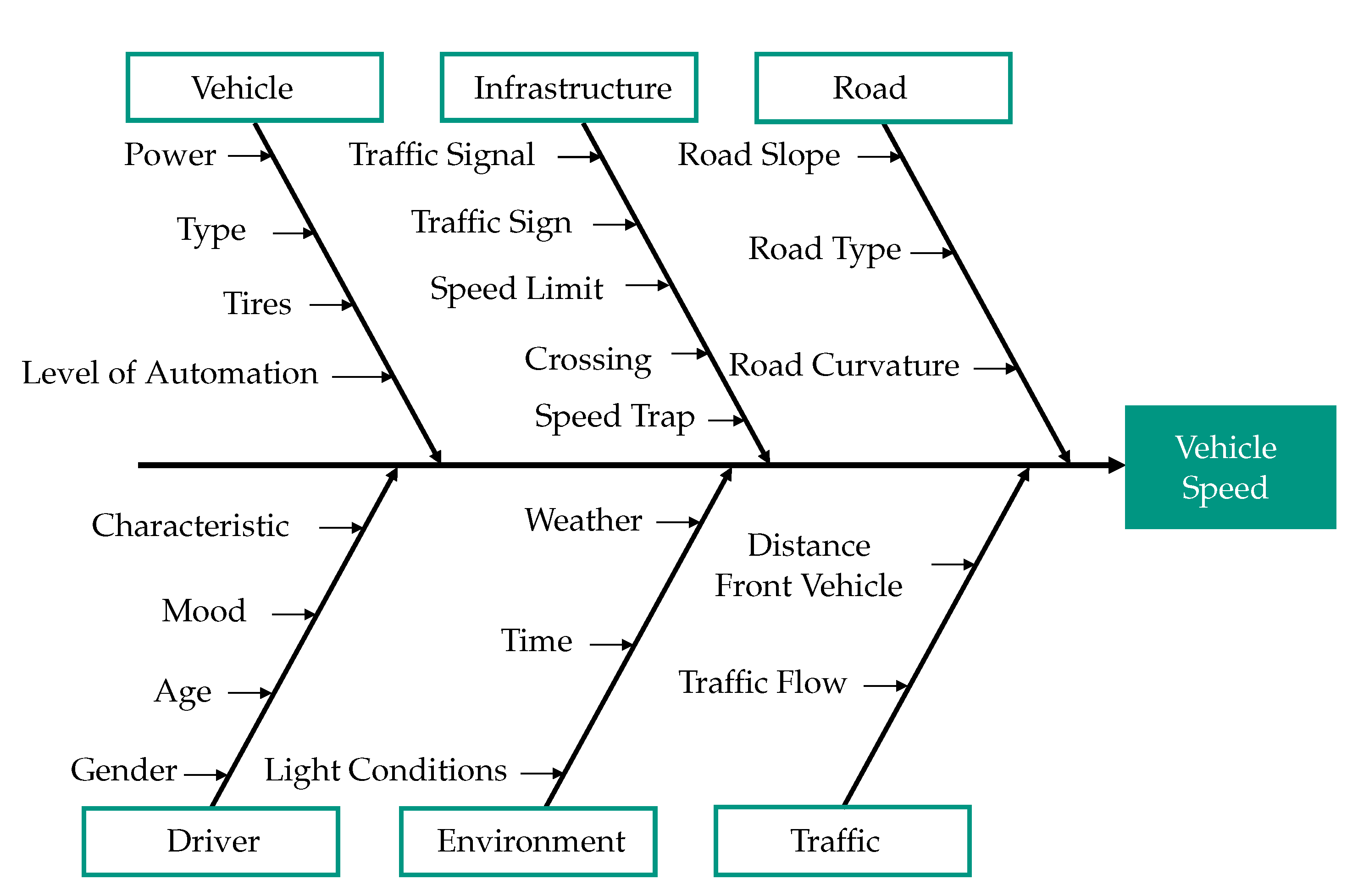
:1. Introduction
2. Related Work
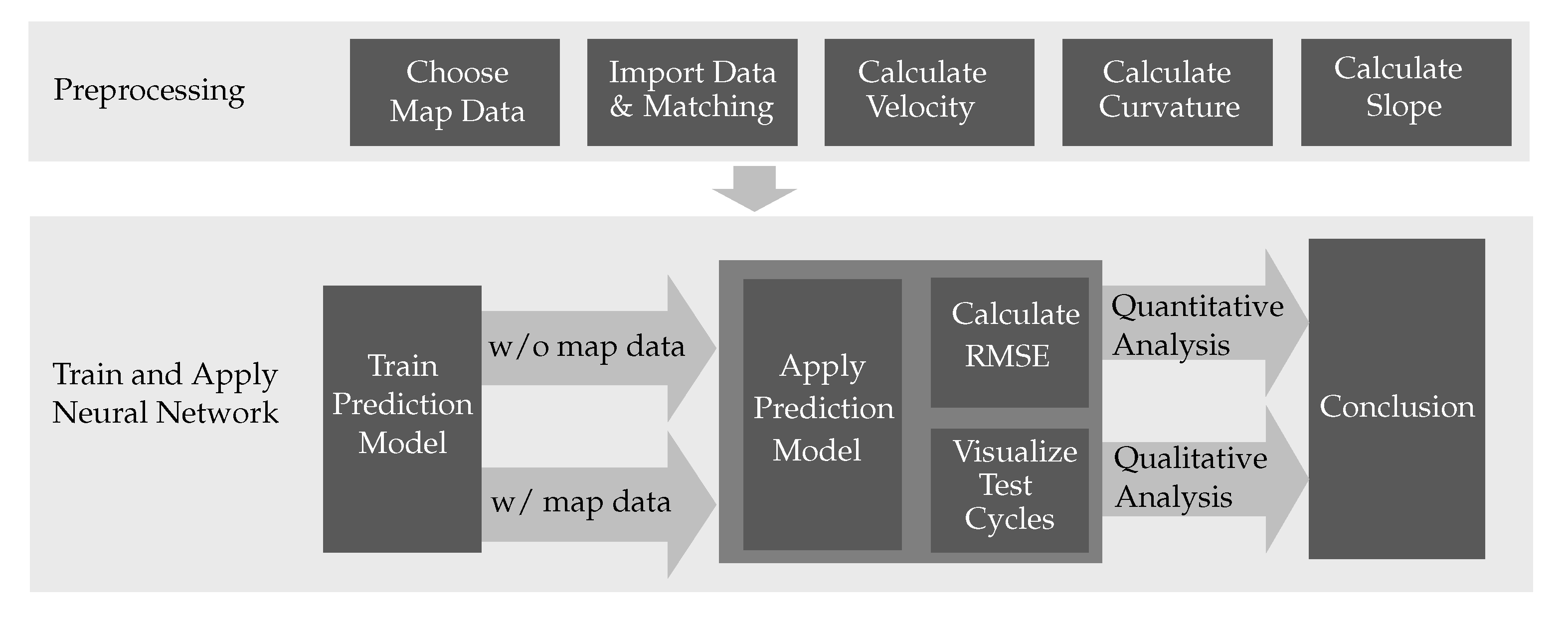
3. Method
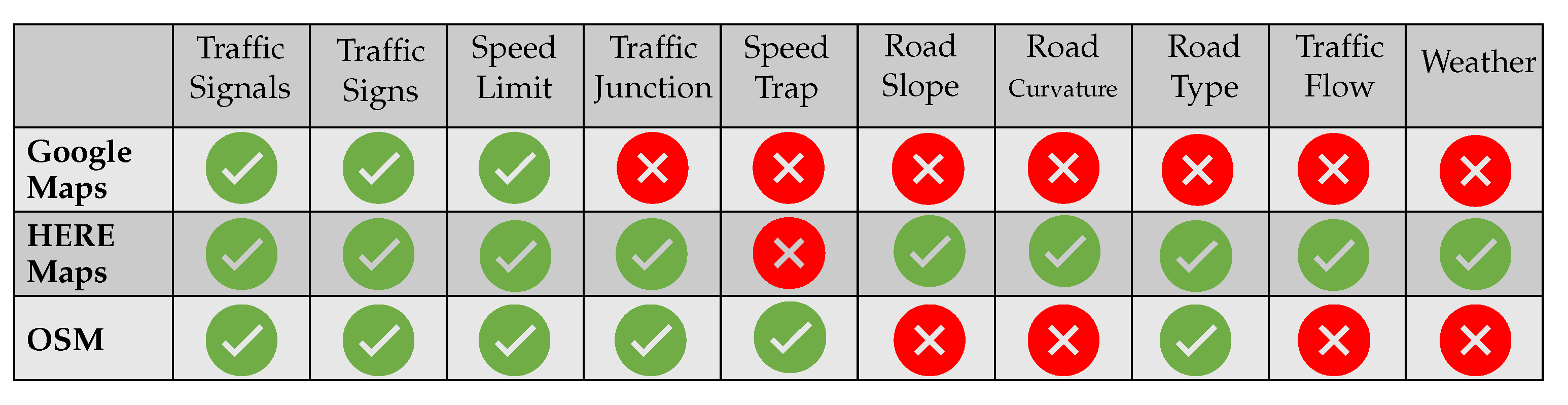
- Choosing a map data source
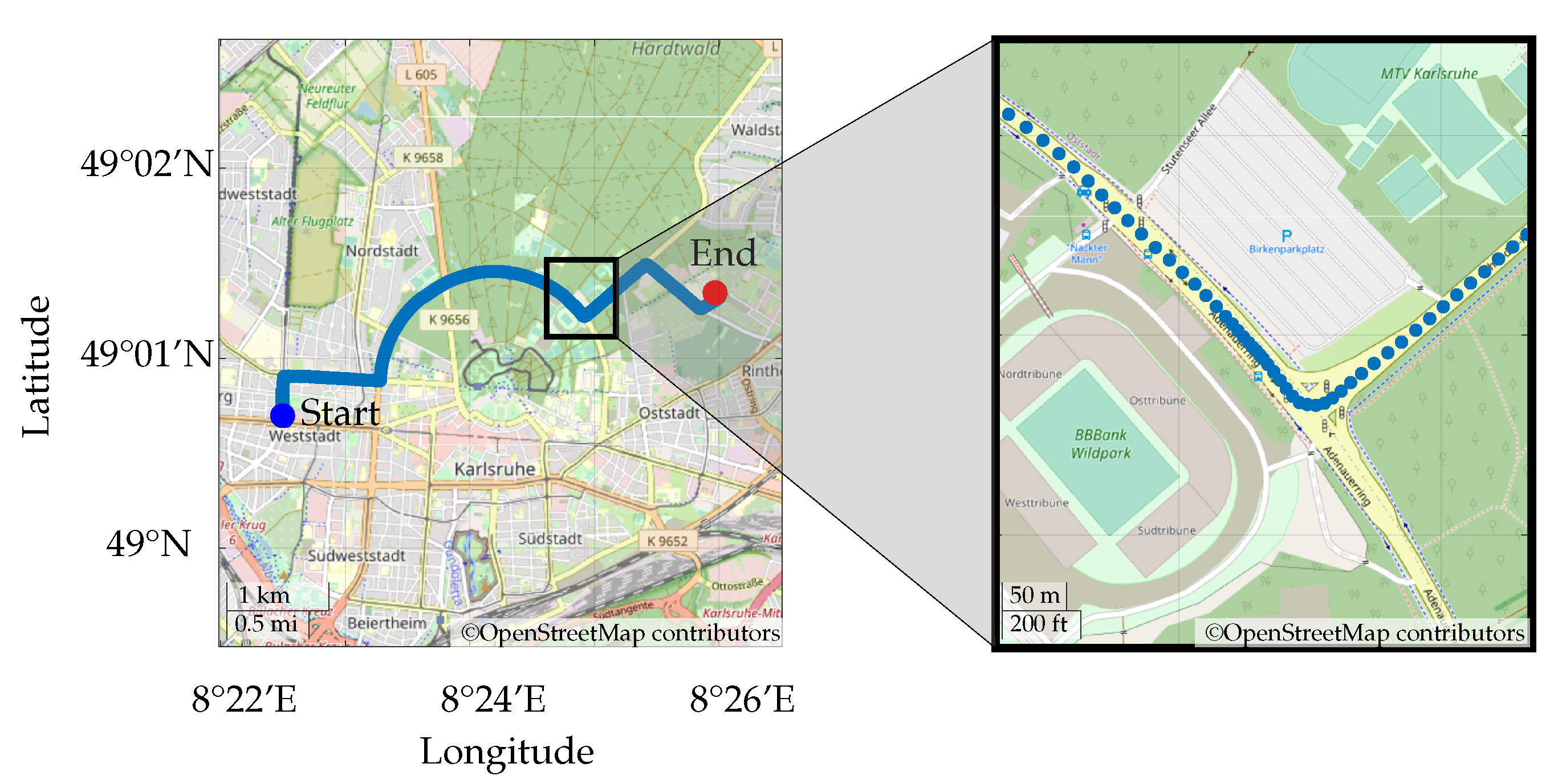
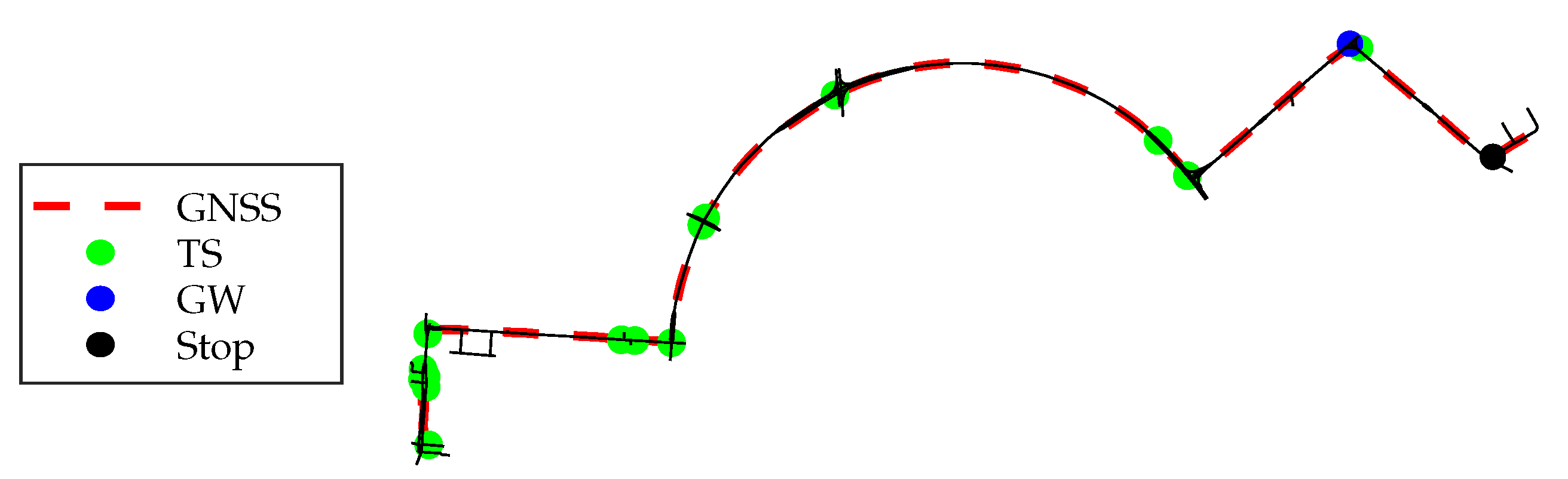
- Importing data from GNSS tracking and matching with map data
- Calculating velocity
- Calculating road curvature
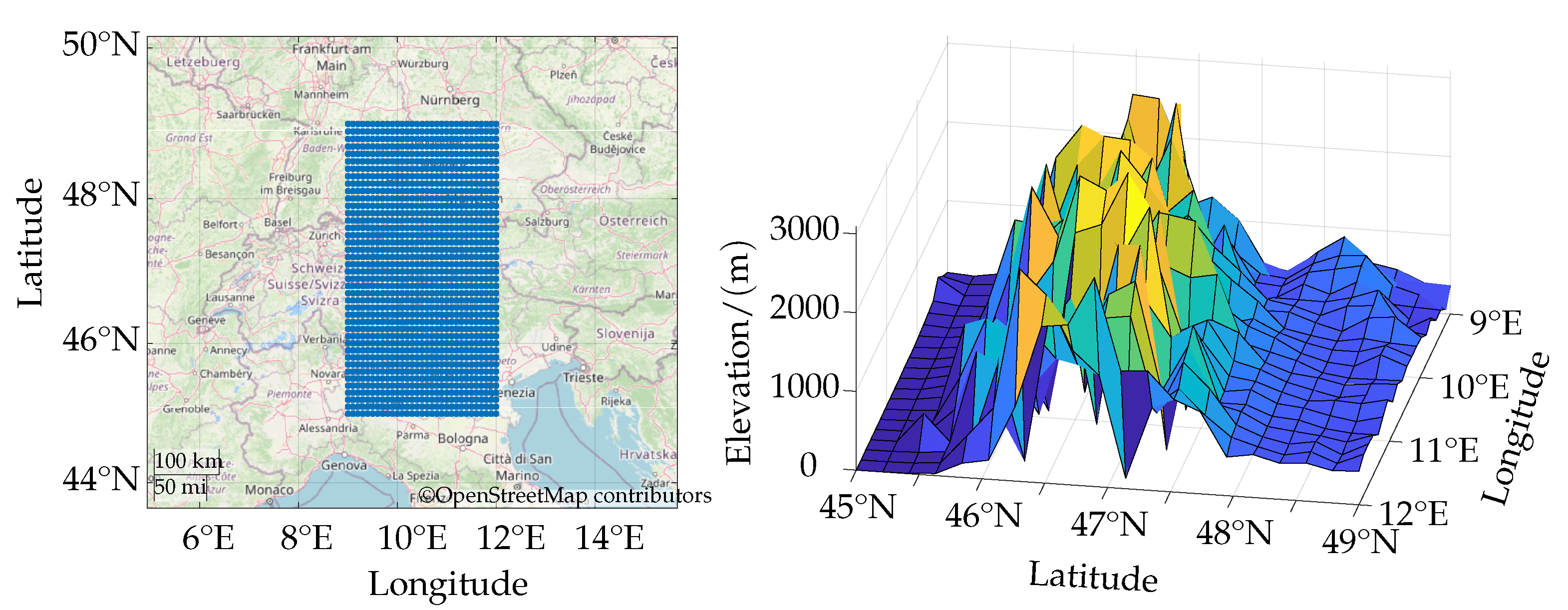
- Calculating road slope
4. Implementation
4.1. Choosing Data Sources
- Available map data and road attributes
- Cost of use of the provider (free availability is to be aimed at)
- Quality of the data (accuracy, completeness, up-to-dateness)
- Effort of data processing
4.2. Importing Data Including Matching
4.3. Calculating Velocity
4.4. Calculating Road Curvature
4.5. Calculating Road Slope
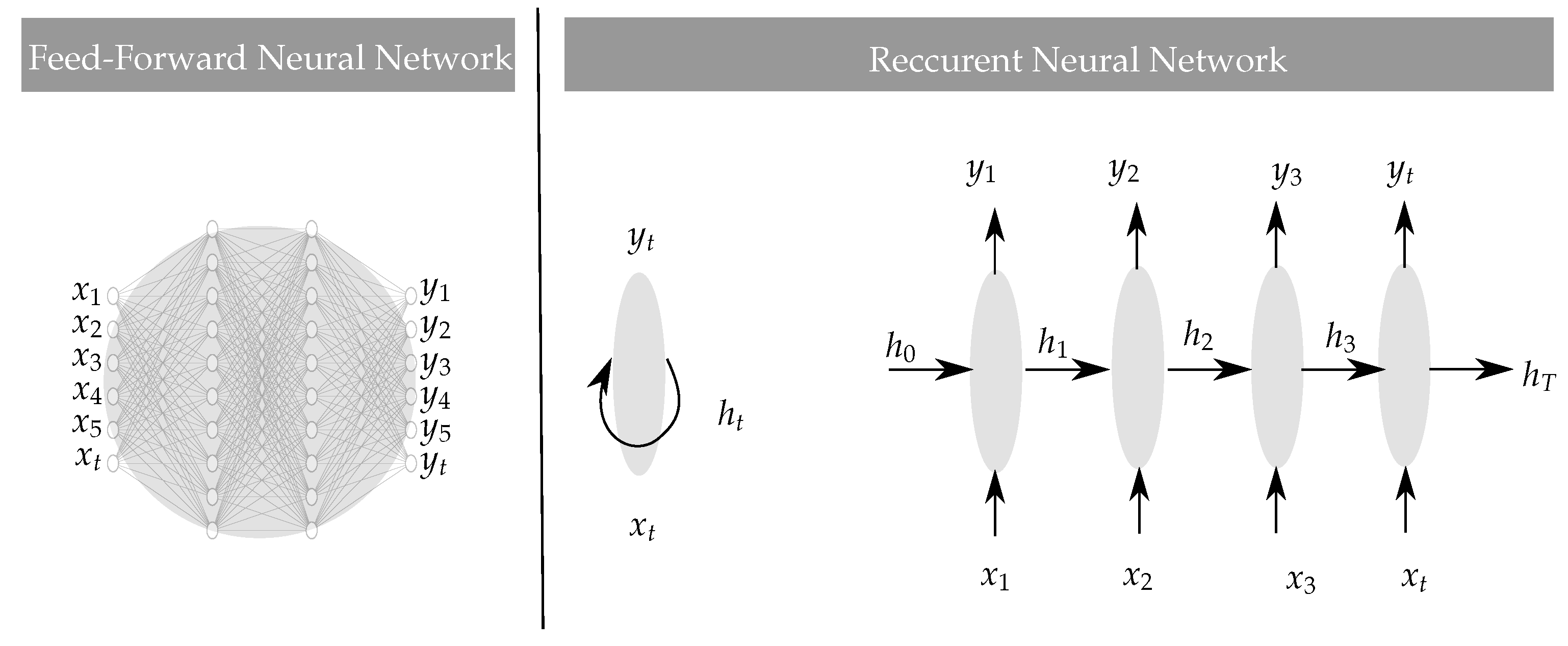
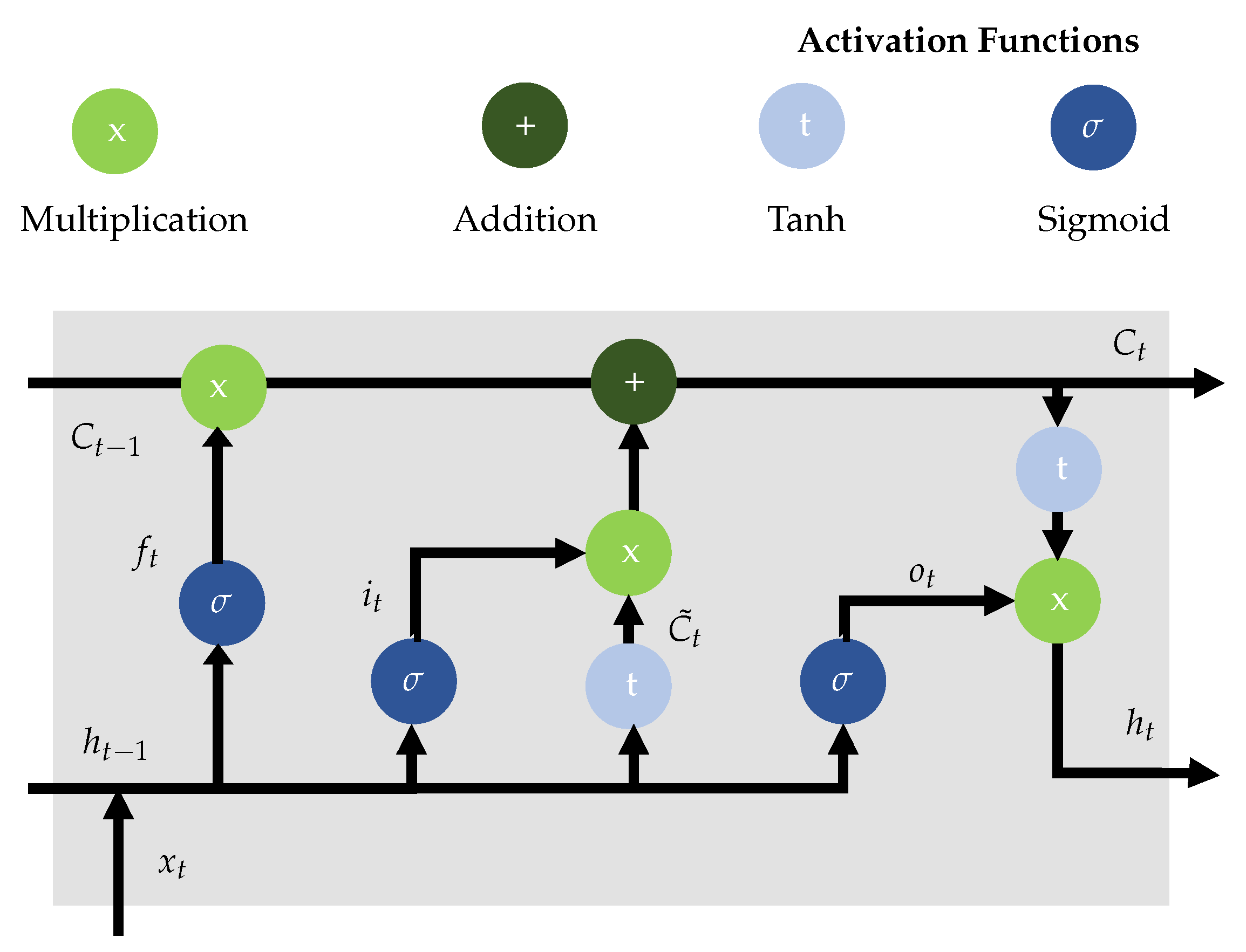
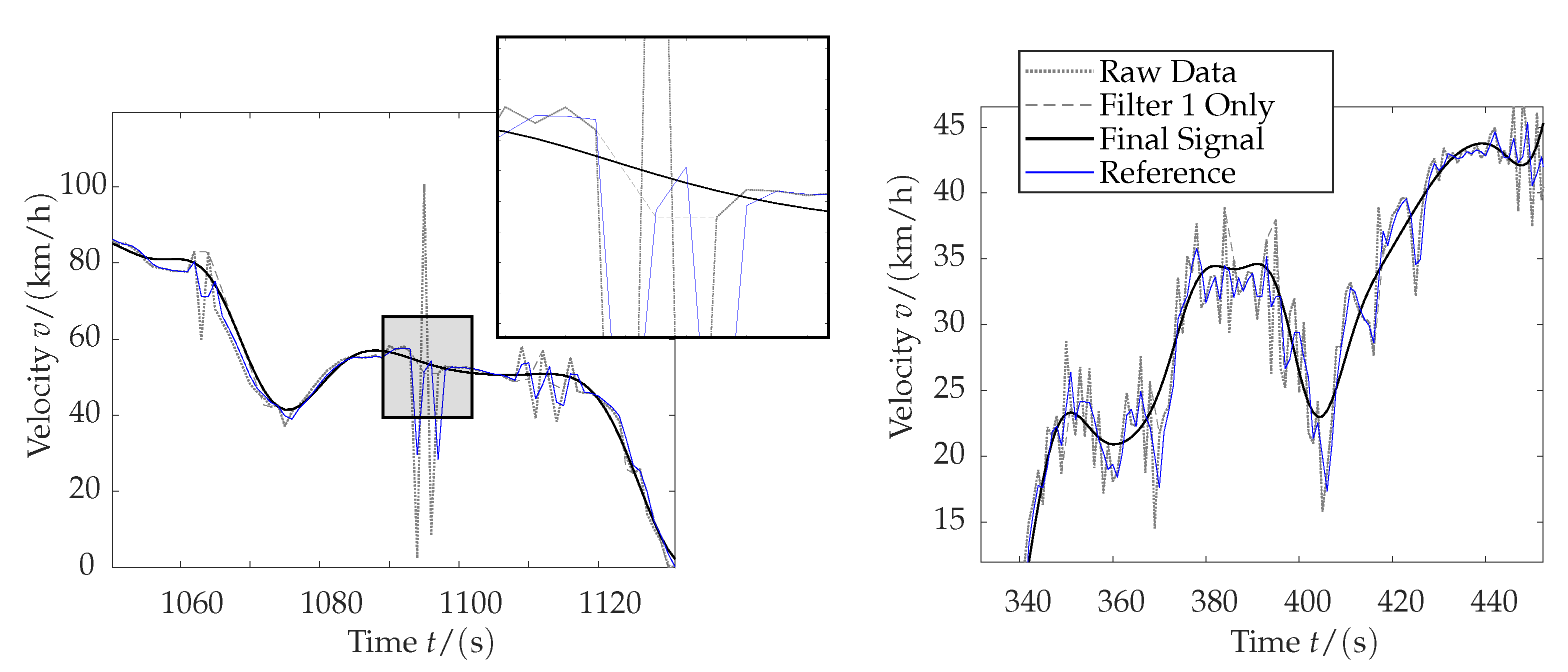
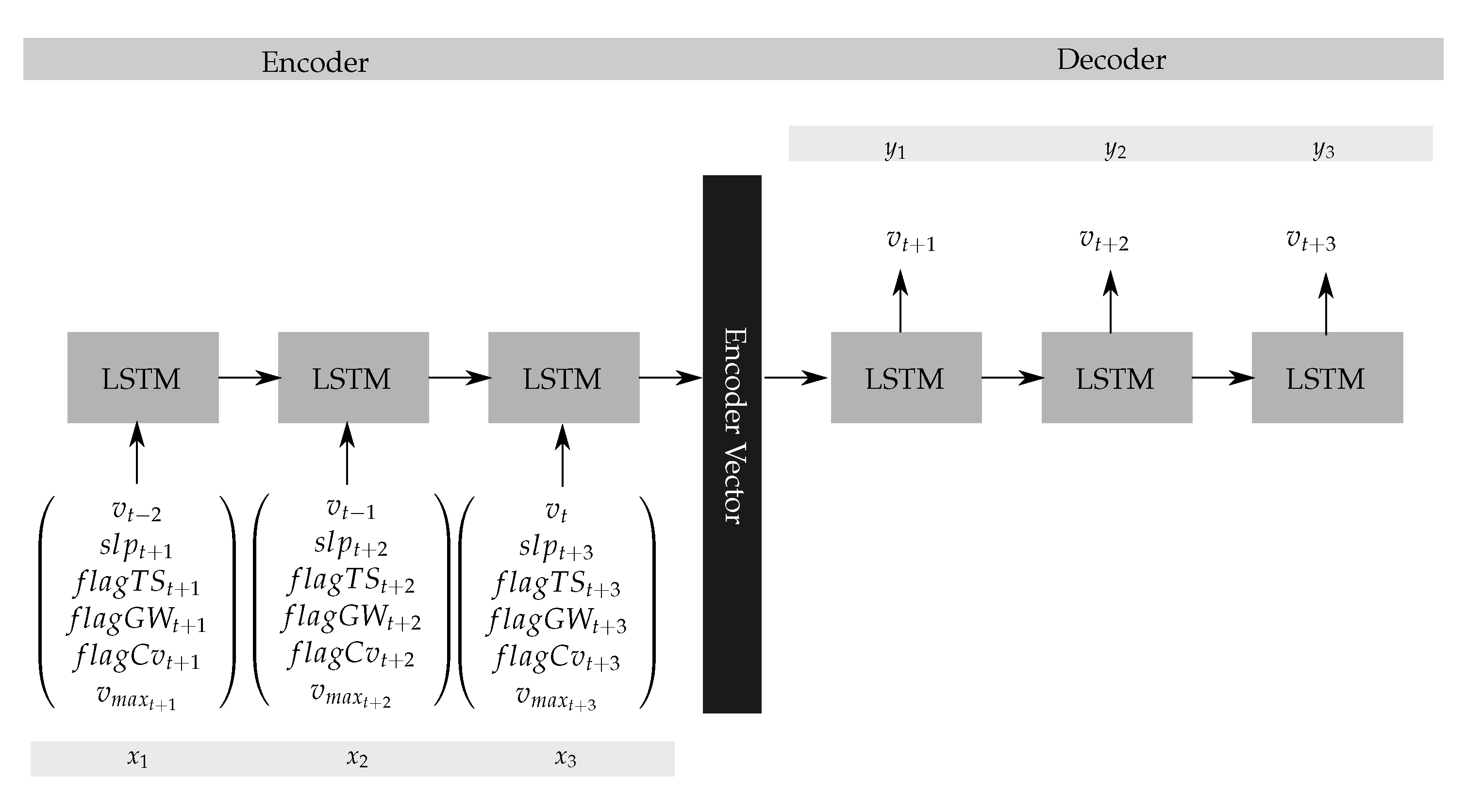
4.6. Short Range Predictions
5. Results
5.1. Analysis of RMSE Values (Quantitative Analysis)
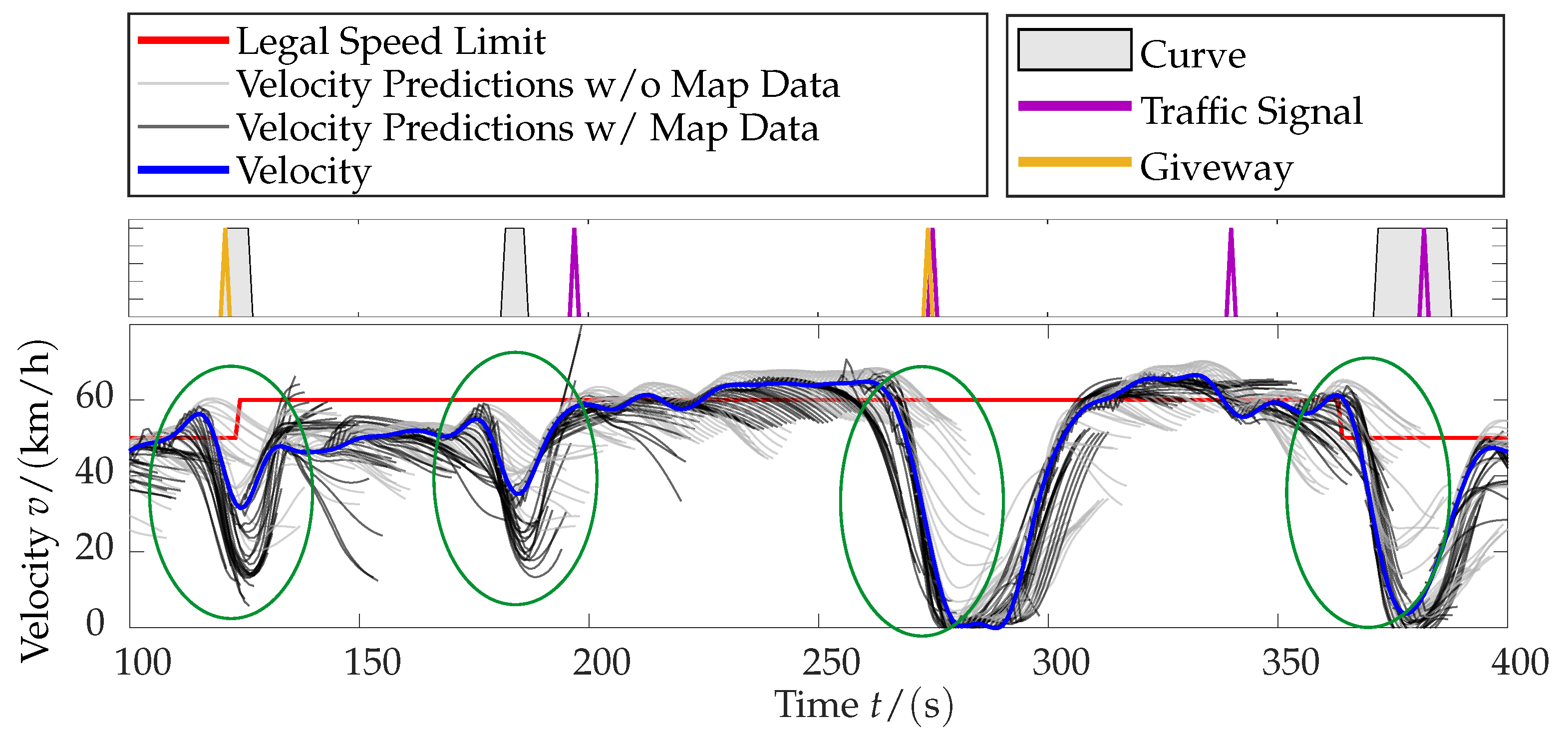
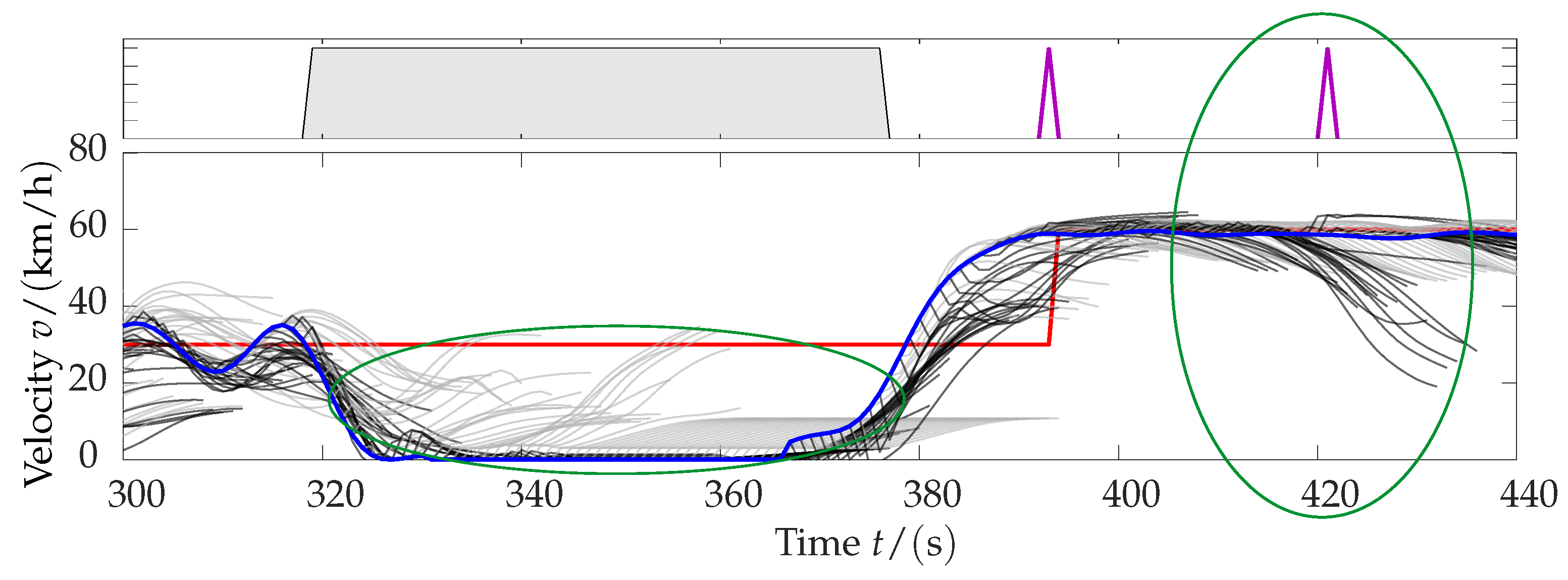
5.2. Analysis in Time Domain (Qualitative Analysis)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, P.; Steinbuch, M. Review of Optimization Strategies for System-Level Design in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef]
- Tran, D.D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Serrao, L. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Rizzoni, G.; Onori, S. Energy Management of Hybrid Electric Vehicles: 15 years of development at the Ohio State University. Oil Gas Sci. Technol. Rev. D’IFP Energies Nouv. 2015, 70, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Xu, N.; Kong, Y.; Chu, L.; Ju, H.; Yang, Z.; Xu, Z.; Xu, Z. Towards a Smarter Energy Management System for Hybrid Vehicles: A Comprehensive Review of Control Strategies. Appl. Sci. 2019, 9, 2026. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Ossart, F.; Marchand, C. Comparative Study of Real-Time HEV Energy Management Strategies. IEEE Trans. Veh. Technol. 2017, 66, 10875–10888. [Google Scholar] [CrossRef] [Green Version]
- Markschlaeger, P.; Wahl, H.G.; Weberbauer, F.; Lederer, M. Assistenzsystem für mehr Kraftstoffeffizienz. In Vernetztes Automobil; Siebenpfeiffer, W., Ed.; Springer: Wiesbaden, Germany, 2014; pp. 146–153. [Google Scholar] [CrossRef]
- Deufel, F.; Gießler, M.; Gauterin, F. A Generic Prediction Approach for Optimal Control of Electrified Vehicles Using Artificial Intelligence. Vehicles 2022, 4, 182–198. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Xi, J. Leveraging Drivers’ Driving Preferences into Vehicle Speed Prediction Using Oriented Hidden Semi-Markov model. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 650–655. [Google Scholar] [CrossRef]
- Lefevre, S.; Sun, C.; Bajcsy, R.; Laugier, C. Comparison of parametric and non-parametric approaches for vehicle speed prediction. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3494–3499. [Google Scholar] [CrossRef]
- Omari, B.H.A.; Jafari, A.A. Roles of driver and vehicle characteristics in speed choice along rural highways. Int. J. Eng. Manag. Econ. 2015, 5, 181. [Google Scholar] [CrossRef]
- Yufang, L.; Mingnuo, C.; Wanzhong, Z. Investigating long–term vehicle speed prediction based on BP–LSTM algorithms. IET Intell. Transp. Syst. 2019, 13, 1281–1290. [Google Scholar] [CrossRef]
- Quimby, A.; Maycock, G.; Palmer, C.; Buttress, S. The Factors That Influence a Driver’s Choice of Speed—A Questionnaire Study; Transport Research Laboratory: Crowthorne, UK, 1999. [Google Scholar]
- Sagberg, F. Factors Infuencing Driving Speed; TOI Report 765/2005; Institute of Transport Economics: Oslo, Norway, 2005. [Google Scholar]
- Laraki, M.; de Nunzio, G.; Thibault, L. Vehicle speed trajectory estimation using road traffic and infrastructure information. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Hellwig, M.; Ritschel, W. The Predictability of Driving in Typical Traffic Conditions. In Proceedings of the 2020 21st International Conference on Research and Education in Mechatronics (REM), Cracow, Poland, 9–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Rezaei, A.; Burl, J.B. Effects of Time Horizon on Model Predictive Control for Hybrid Electric Vehicles. IFAC-PapersOnLine 2015, 48, 252–256. [Google Scholar] [CrossRef]
- Back, M. Prädiktive Antriebsregelung zum Energieoptimalen Betrieb von Hybridfahrzeugen. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2005. [Google Scholar]
- Liu, L.; Zhu, L.; Yang, D. Modeling and simulation of the car-truck heterogeneous traffic flow based on a nonlinear car-following model. Appl. Math. Comput. 2016, 273, 706–717. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 1805–1824. [Google Scholar] [CrossRef] [Green Version]
- Chandra, R.; Goyal, S.; Gupta, R. Evaluation of Deep Learning Models for Multi-Step Ahead Time Series Prediction. IEEE Access 2021, 9, 83105–83123. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Li, F.F.; Johnson, J.; Yeung, S. Lecture 10: Recurrent Neural Networks; Stanford University: Stanford, CA, USA, 2017; Available online: http://cs231n.stanford.edu/slides/2017/cs231n{_}2017{_}lecture10.pdf (accessed on 25 March 2022).
- Werbos, P.J. Generalization of Backpropagation with Application to a Recurrent Gas Market Model. Neural Netw. 1988, 1, 339–356. [Google Scholar]
- Elman, J. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Afshine Amidi and Shervine Amidi. CS 230—Deep Learning; Stanford University: Stanford, CA, USA, 2022; Available online: https://stanford.edu/{~{}}shervine/teaching/cs-230/ (accessed on 10 May 2022).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Phi, M. Illustrated Guide to LSTMs and GRUs: A Step by Step Explanation; Towards Data Science: Toronto, ON, Canada, 2022; Available online: https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21 (accessed on 25 March 2022).
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech Recognition with Deep Recurrent Neural Networks. 2013. Available online: http://arxiv.org/pdf/1303.5778v1 (accessed on 25 March 2022).
- Graves, A. Generating Sequences with Recurrent Neural Networks. 2014. Available online: https://arxiv.org/pdf/1308.0850 (accessed on 25 March 2022).
- Jiang, L.; Hu, G. Day-Ahead Price Forecasting for Electricity Market using Long-Short Term Memory Recurrent Neural Network. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Gers, F.; Schmidhuber, J. Recurrent Nets that Time and Count. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000. [Google Scholar]
- Nowak, J.; Taspinar, A.; Scherer, R. LSTM Recurrent Neural Networks for Short Text and Sentiment Classiication. In International Conference on Artificial Intelligence and Soft Computing; Springer: Cham, Switzerland, 2017; pp. 553–562. [Google Scholar]
- Ciepłuch, B.; Jacob, R.; Mooney, P.; Winstanley, A.C. Comparison of the accuracy of OpenStreetMap for Ireland with Google Maps and Bing Maps. In Proceedings of the Ninth International Symposium on Spatial Accuracy Assessment in Natural Resuorces and Enviromental Sciences, Leicester, UK, 20–23 July 2010; University of Leicester: Leicester, UK, 2010; p. 337. [Google Scholar]
- Cahyono, A.; Angogoro, H. Comparison Study of Crowdsource Geographic Comparison Study of Crowdsource Geographic Information Services for Rural Mapping and Toponym Inventory. In Proceedings of the 1st International Conference on Geography and Education (ICGE 2016), Malang, Indonesia, 29 October 2016; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 275–282. [Google Scholar]
- Ruchti, P.; Steder, B.; Ruhnke, M.; Burgard, W. Localization on OpenStreetMap data using a 3D laser scanner. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5260–5265. [Google Scholar] [CrossRef]
- Basiri, A.; Jackson, M.; Amirian, P.; Pourabdollah, A.; Sester, M.; Winstanley, A.; Moore, T.; Zhang, L. Quality assessment of OpenStreetMap data using trajectory mining. Geo Spat. Inf. Sci. 2016, 19, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Silvas, E.; Hereijgers, K.; Peng, H.; Hofman, T.; Steinbuch, M. Synthesis of Realistic Driving Cycles With High Accuracy and Computational Speed, Including Slope Information. IEEE Trans. Veh. Technol. 2016, 65, 4118–4128. [Google Scholar] [CrossRef]
- Geofabrik. OpenStreetMap Data Extracts; Geofabrik GmbH: Karlsruhe Germany, 2022; Available online: https://download.geofabrik.de/ (accessed on 25 March 2022).
- Migurski, M. Osmosis; Github: San Francisco, CA, USA, 2022; Available online: https://github.com/openstreetmap/osmosis/releases/tag/0.48.3 (accessed on 25 March 2022).
- Falkena, W. xml2struct; MATLAB Central File Exchange: Natick, MA, USA, 2022; Available online: https://www.mathworks.com/matlabcentral/fileexchange/28518-xml2struct (accessed on 25 March 2022).
- Filippidis, I. OpenStreetMap Functions; Github: San Francisco, CA, USA, 2022; Available online: https://github.com/johnyf/openstreetmap (accessed on 25 March 2022).
- USGS. EarthExplorer; U.S. Geological Survey: Reston, VA, USA, 2022. Available online: https://earthexplorer.usgs.gov (accessed on 25 March 2022).
- Burg, H. (Ed.) Handbuch Verkehrsunfallrekonstruktion: Unfallaufnahme, Fahrdynamik, Simulation; mit 152 Tabellen, 2., aktualisierte aufl; Praxis; ATZ-MTZ-Fachbuch; Vieweg + Teubner: Wiesbaden, Germany, 2009. [Google Scholar]
- Forster, D.; Inderka, R.B.; Gauterin, F. Data-Driven Identification of Characteristic Real-Driving Cycles Based on k-Means Clustering and Mixed-Integer Optimization. IEEE Trans. Veh. Technol. 2020, 69, 2398–2410. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. 2014. Available online: https://arxiv.org/pdf/1409.3215 (accessed on 25 March 2022).
- Gangopadhyay, T.; Yong Tan, S.; Huang, G.; Sarkar, S. Temporal Attention and Stacked LSTMs for Multivariate Time Series Prediction. In Proceedings of the Workshop on Modeling and Decision-Making in the Spatiotemporal Domain, 32nd Conference on Neural Information Processing Systems (NIPS 2018), Montréal, Canada, 3–8 December 2018. [Google Scholar]


| LSTM Units | |
| Optimizer | Adam |
| Loss Function | Mean Squared Error (MSE) |
| Activation Function | Rectified Linear Unit (ReLU) |
| Learning Rate | 0.01 |
| Batch Size | 1400 |
| Epochs | 1000 |
| Horizon 10 s | Horizon 20 s | Horizon 30 s | |||||
|---|---|---|---|---|---|---|---|
| ED-LSTM | FNN | ED-LSTM | FNN | ED-LSTM | FNN | ||
| 6.43 | 7.74 | 12.23 | 14.10 | 16.44 | 17.84 | ||
| 0.52 | 0.57 | 0.59 | 0.62 | 0.65 | 0.66 | ||
| Horizon 10 s | Horizon 20 s | Horizon 30 s | |||||
|---|---|---|---|---|---|---|---|
| ED-LSTM | FNN | ED-LSTM | FNN | ED-LSTM | FNN | ||
| 5.33 | 6.46 | 5.77 | 9.29 | 10.31 | 11.82 | ||
| 0.48 | 0.52 | 0.49 | 0.56 | 0.58 | 0.60 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deufel, F.; Jhaveri, P.; Harter, M.; Gießler, M.; Gauterin, F. Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM). Vehicles 2022, 4, 808-824. https://doi.org/10.3390/vehicles4030045
Deufel F, Jhaveri P, Harter M, Gießler M, Gauterin F. Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM). Vehicles. 2022; 4(3):808-824. https://doi.org/10.3390/vehicles4030045
Chicago/Turabian StyleDeufel, Felix, Purav Jhaveri, Marius Harter, Martin Gießler, and Frank Gauterin. 2022. "Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM)" Vehicles 4, no. 3: 808-824. https://doi.org/10.3390/vehicles4030045
APA StyleDeufel, F., Jhaveri, P., Harter, M., Gießler, M., & Gauterin, F. (2022). Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM). Vehicles, 4(3), 808-824. https://doi.org/10.3390/vehicles4030045







